Non-affine Fiber Reorientation in Finite Inelasticity

Abstract

This paper introduces a model for the mechanical response of anisotropic soft materials undergoing large inelastic deformations. The material is considered made by a isotropic matrix with embedded fibers, each component having its own relaxation dynamics. The constitutive equations are provided in terms of the free energy density and the dissipation density, which are both required to be thermodynamically consistent and structural frame-indifferent, i.e., independent of a rotation overimposed on the intermediate natural state of both matrix and fibers. This is in contrast to many of the currently used anisotropic inelastic models, which do not deal with the lack of uniqueness of the intermediate state. This issue is thoroughly discussed and in terms of two possible choices satisfying structural-frame indifference and leading to different flow rules of the inelastic processes. It is shown that different models from the literature can be incorporated in the proposed formulation including anisotropic viscoelasticity and growth.

1 Introduction

Anisotropic soft solids are materials found either in Nature and in artificial structures characterized by a soft matrix with an internal structure usually constituted by stiff fibers. Both the fibers and the matrix contribute to the mechanical response of the solid to actions such as forces or external stimuli like temperature, electrical, magnetic and chemical fields [1, 6, 29]. Modeling the inelastic behaviour of anisotropic soft solids requires the formulation of evolution laws for the dissipative processes. These latter are associated to the inelasticity of the matrix as well as to the reorientation of the internal structure, if this can evolve independently of the matrix. Interesting examples come from biology and material science [11, 17, 19, 25, 30].

Within this field, elastic and inelastic deformations are frequently described by assuming that the overall deformation $\mathbf{F}$ can be (multiplicatively) decomposed into an elastic $\mathbf{F}_{e}$ and an inelastic $\mathbf{F}_{g}$ part [18], which introduce in the modelling two layers of description. One attains to the natural state of the material, where inelastic processes take place; the other to its current state, where stresses and deformations are measured. Usually, the elastic energy and dissipation functions are used to introduce suitable constitutive prescriptions compatible with thermodynamics [13].

One of the issue of the multiplicative decomposition is the lack of uniqueness of the natural state since both $\mathbf{F}_{e}\mathbf{F}_{g}$ and $\mathbf{F}_{e}\mathbf{Q}^{T}\mathbf{Q}\mathbf{F}_{g}$ produces the same macroscopic deformation. This raises several points that have been differently dealt with in the literature [5, 13, 21], in particular in the field of large strain plasticity [13, 14]. Moreover, when anisotropic finite inelasticity is considered, several questions remain open including the proper description of the material anisotropy in the natural state as well as the relationship between the natural state of the matrix and the one of the fibers [20, 28].

In the framework outlined above, this paper aims at addressing some of the open questions. Specifically, we propose a thermodynamically consistent model of inelastic processes, which takes into account different natural states of matrix and fibers and holds under the constitutive hypothesis that elastic energy and dissipation function are structural frame-indifferent, i.e., independent of a rotation overimposed on the natural state.

We start by presenting a short review of the different approaches proposed over the years; then, we describe our contribution and the plan of the paper.

1.1 A Short Review

The lack of uniqueness of the natural state, originating from the multiplicative decomposition, has arisen several questions starting from [12], where the notion of structural frame-indifference was first introduced as an indifference requirement under a change of frame in the natural state, in addition to the conventional frame-indifference, i.e., a change of frame in the current configuration [13]. The issue is particularly significant within the framework of finite inelasticity, where the multiplicative decomposition of the deformation gradient is used to describe a wide variety of inelastic processes.

In [13], the Authors required that the constitutive functions were structural frame-indifferent. This in turn is satisfied by requiring that the energy density is an isotropic function of the deformation tensor, yet the dissipation function must be independent of the inelastic spin. As a consequence, the theory misses three flow rules to fully determine the time evolution of the six inelastic components of the deformation gradient. However, for isotropic materials, the so-called irrotationality theorem was introduced [13] to show that one can set the inelastic spin to zero. For anisotropic materials, different flow rules in terms of the inelastic strain have been formulated in the literature, yet they do not give the full evolution of the natural state [20, 21]. Actually, it was shown in [5] that the evolution of the natural state can be fully determined by viewing the irrotational condition as an internal constraint on the elastic spin, even in the anisotropic case. With this additional equation, the theory has the right number of flow rules governing the time evolution of the inelastic deformation, and the dissipation function is structural frame-indifferent.

In [5], the problem was discussed for anisotropic solids in which the reinforcing fibers were dragged by the inelastic deformation of the matrix. However, there are situations in which the deformation of the fiber is non-affine. In [26], for instance, it was assumed that the internal structure evolved indipendently of the matrix through a rotation field. This approach is indeed similar to the one proposed in this paper, but in [26], despite introducing the kinematical framework of the theory, the evolution equations of the inelastic processes were not provided. A different point of view was presented in [20, 21, 28]. The authors of [28] assumed that the evolution of the internal fiber structure is driven by the inelastic part of the deformation gradient, which is recognized as a further variable of the problem whose evolution is driven by additional equations. Differently, in [21] and [20], it was assumed that the fibers and the matrix can exhibit a distinct time-dependent behaviour and so two different multiplicative decompositions of the deformation gradient for matrix and fiber phases were introduced. As such, the internal structure in the natural state is described by the inelastic deformation tensor of the fiber phase. Coherently, the constitutive prescriptions involve different inelastic stretch measures and free energy densities for matrix and fiber phases, thus separate flow rules were specified.

1.2 Our Contribution

Recently, we have studied fiber reorientation in elastic materials and considered both passive reorientation [2, 4], driven by mechanical loads, and active reorientation [3], driven by magnetic fields. We have also presented and discussed a structurally frame-indifferent model for anisotropic visco-hyperelastic materials [5], based on the evolution laws of the dissipative processes, which are completely determined by the elastic strain energy density and the dissipation density. Therein, fiber reorientation was affine, i.e., completely driven by the visible gradient.

Herein, we extend that approach by allowing fiber structure to reorient independently of the matrix. Our approach falls within the unifying theory of material remodelling [9, 24]. Within the class of constitutive equations which are indifferent to change of observer, we select those which also satisfy the dissipation imbalance and are structurally frame indifferent [7, 12, 13]. The constitutive hypothesis of structural frame-indifference strongly affects the dissipation function, making it dependent on the relative inelastic spin rate defined as the difference between the fiber reorientation spin and the inelastic spin rate induced by the matrix. As a consequence, the flow rules consistent with the dissipation imbalance are not enough to solve the problem and uniquely determine the natural state. The issue is discussed and two different approaches are suggested to solve the problem.

The main focus of the paper is on transversely isotropic materials, yet the theory may be straightforwardly generalized to more complex anisotropy classes. Within this class of materials, it is shown that the proposed theory can describe some relevant examples from the literature, although the requirement of structural frame-indifference and the internal constraint on the spin rate limit the number of scenarios that can be encompassed.

Section 2 describes the two-layers kinematics of the model driven by the balance equations derived in Sect. 3. The constitutive prescriptions, both thermodynamically consistent and structurally frame-indifferent are presented and discussed in Sects. 4 and 5. The evolution equations driving the state variables are introduced in Sect. 6, whereas Sect. 7 present two approximations of those equations in the limit of fast or slow applied deformations.

Throughout the paper we use small bold letters to indicate vectors and capital bold letters for tensors. The inner product is indicated with a dot ⋅ either for vectors and tensors, i.e., $\mathbf{a}\cdot \mathbf{b}=\sum _{i}a_{i}b_{i}$ and $\mathbf{A}\cdot \mathbf{B}=\sum _{i,j}A_{ij}B_{ij}$, where $a_{i}$, $b_{i}$ and $A_{ij}$, $B_{ij}$ are the components. The tensor product between vectors is indicated by $\mathbf{a}\otimes \mathbf{b}$ and represent a tensor with components $(\mathbf{a}\otimes \mathbf{b})_{ij}=a_{i}b_{j}$.

2 Kinematics

We identify the body with the region $\mathcal{B}_{r}$ of the Euclidean three-dimensional space ℰ occupied at the instant $t=t_{0}$, and denote it as reference configuration. We introduce the vector field $\mathbf{a}_{0}:\mathcal{B}_{r} \to \mathcal{V}$, with $\mathcal{V}$ the translation space of ℰ, such that $\mathbf{a}_{0}\cdot \mathbf{a}_{0}=1$, that represents the reference orientation of the fiber at position $X\in\mathcal{B}_{r}$. The corresponding orientation tensor, also called structural (or Finger) tensor, is given by $\mathbf{A}_{0}= \mathbf{a}_{0}\otimes \mathbf{a}_{0}$.

The deformation of the body is the time-dependent map $p :\mathcal{B}_{r}\times \mathcal{T}\to \mathcal{E}$ that assigns at each point $X\in \mathcal{B}_{r}$ a point $x=p(X,t)$ at any instant $t$ of the time interval $\mathcal{T}$. Accordingly, the set $\mathcal{B}_{t}=p(\mathcal{B}_{r},t)$ is the configuration of the body at time $t$ and $\mathcal{B}_{r}=p(\mathcal{B}_{r},t_{0})$. We call $\mathbf{u}(X,t)$ the displacement field such that $\mathbf{u}(X,t)=p(X,t)-p(X,t_{0})$ and we assume it to be twice continuously differentiable, such that

$$ \mathbf{F}(X,t)=\nabla \,p(X,t)\qquad \text{and} \qquad \dot{p}(X,t)= \dfrac{\partial p}{\partial t}(X,t)\,, $$

(2.1)

for the deformation gradient and the referential velocity field, respectively.

According to the Bibly-Kröner-Lee decomposition [18, 27], the deformation gradient (2.1) is decomposed into inelastic $\mathbf{F}_{g}$ and elastic $\mathbf{F}_{e}$ tensors such that at each material point one has

$$ \mathbf{F}(X,t)=\mathbf{F}_{e}(X,t)\,\mathbf{F}_{g}(X,t)\,. $$

(2.2)

The inelastic deformation $\mathbf{F}_{g}$ is a smooth tensor-valued field with positive Jacobian determinant $J_{g}:=\det \mathbf{F}_{g}>0$, that may be the manifestation of inelastic phenomena such as growth, viscous relaxation or plasticity, and, in general, do not affect the orientation of the fibers. We remark that the relaxed (or natural) state of the matrix may not be described by a placement, meaning that $\mathbf{F}_{g}$ may not be the gradient of any map, or in other terms, there is no way to let each body element relaxing to its natural zero-stress state without removing the surrounding elements [9, 24]. Indeed, it is the elastic reversible deformation $\mathbf{F}_{e}$ that makes the tensor field $\mathbf{F}=\mathbf{F}_{e}\mathbf{F}_{g}$ integrable. In the following, we will call $J=\det \mathbf{F}$ and so we write $J=J_{e}\,J_{g}$ with $J_{e}=\det \mathbf{F}_{e}$.

We further admit the existence of a remodelling process defined by a time-dependent rotation, here identified with an orthogonal tensor ${\mathbf{R}:\mathcal{B}\times \mathcal{T}\to \mathbb{O}\mathtt{rth}^{+}}$, that identifies the orientation that the fiber would assume if it were free from any surroundings, i.e., the relaxed state of the fiber. As such, we use the notation

$$ \mathbf{A}(X,t)=\mathbf{R}(X,t)\,\mathbf{A}_{0}(X)\mathbf{R}(X,t)^{T} \,, $$

(2.3)

to indicate the remodeled orientation tensor, with $\mathbf{A}=\mathbf{a}\otimes \mathbf{a}$, and $\mathbf{a}=\mathbf{R}\,\mathbf{a}_{0}$ the remodelled fiber orientation. Here and henceforth, the dependence on the position $X$ and time $t$ will made explicit only when needed.

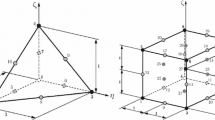
The placement $p$, the inelastic tensor $\mathbf{F}_{g}$ and the reorientation tensor $\mathbf{R}$ represent the state variables of our model and pertain to different layers of description. Placement $p$ belongs to the current state, where strains and stresses are measured, whereas $\mathbf{F}_{g}$ and $\mathbf{R}$ belong to the relaxed state, where the inelastic processes take place, yet they may deliver constitutive information to the current state. It is worth remarking that we have assumed a different relaxed state for the matrix and the fiber, as schematically depicted in Fig. 1. Indeed, $\mathbf{F}_{g}$ acts on a material line element $(X,\mathbf{e}_{0})$ by mapping it into the relaxed state as $(X,\mathbf{F}_{g}\mathbf{e}_{0})$, whereas $\mathbf{R}$ acts on a reference fiber $(X,\mathbf{a}_{0})$, producing the relaxed fiber state $(X,\mathbf{R}\mathbf{a}_{0})$.

Fig. 1

Schematic representation of the different configurations of the matrix and the fiber in our modelling framework. The natural state is represented by a dashed line to indicate that it may not be realizable. Matrix and fiber are represented in different dashed boxes to highlight the fact that no kinematic compatibility between the corresponding relaxed states is required.

As already pointed out in the introductory section, the multiplicative decomposition (2.2) causes the relaxed state to be non-unique. For any $\mathbf{Q}\in \mathbb{O}\mathtt{rth}^{+}$, both $\mathbf{F}_{g}$ and $\mathbf{Q}\mathbf{F}_{g}$ indeed measure the same relaxed state; likewise, $\mathbf{R}$ and $\mathbf{Q}\mathbf{R}$. In fact, the transformations

$$ \mathbf{F}_{e}^{+} = \mathbf{F}_{e}\mathbf{Q}^{T},\qquad \mathbf{F}_{g}^{+} = \mathbf{Q}\mathbf{F}_{g},\qquad \mathbf{R}^{+}=\mathbf{Q}\mathbf{R} $$

(2.4)

keep the visible state unaltered, i.e.,

$$ \mathbf{F}^{+}=\mathbf{F}_{e}^{+}\mathbf{F}_{g}^{+}=\mathbf{F}_{e} \mathbf{Q}^{T}\mathbf{Q}\mathbf{F}_{g}= \mathbf{F}_{e}\mathbf{F}_{g}= \mathbf{F}$$

(2.5)

and

$$ \mathbf{a}_{t}^{+}=\mathbf{F}_{e}^{+}\mathbf{R}^{+}\mathbf{a}_{0}= \mathbf{F}_{e}\mathbf{Q}^{T}\mathbf{Q}\mathbf{R}\mathbf{a}_{0}= \mathbf{a}_{t}\,. $$

(2.6)

Several strategies have been proposed in the literature to deal with this non uniqueness including the assumption that either $\mathbf{F}_{g}$ or $\mathbf{F}_{e}$ were symmetric [20, 21]. A thorough discussion on this matter is presented in Sect. 4.

If the triplet $(p,\mathbf{F}_{g},\mathbf{R})$ represents the local configuration space, the associated velocity triplet is $(\dot{p},\mathbf{L}_{g},\boldsymbol{\varOmega })\in \mathcal{V}\times \mathbb{L}\mathtt{in}\times {\mathbb{S}\textrm{kw}}$ with $\mathbf{L}_{g}=\dot{\mathbf{F}}_{g}\mathbf{F}_{g}^{-1}$ and $\boldsymbol{\varOmega }=\dot{\mathbf{R}}\mathbf{R}^{T}$.

3 Balance Equations

The principle of virtual working defines the weak balance equations of the model and, through the proper localization, allows us to introduce the standard local balance of forces and the new local balance equations of the torques working-conjugate of the fiber reorientation and of the couples working-conjugate of the matrix remodeling actions.

In doing so, we call $\mathbf{z}$ and $\mathbf {s}$ the forces per unit of (reference) volume and area, $\mathbf{Y}$ and $\mathbf{Z}$ the external couple and torque per unit of (reference) volume, that may be interpreted as the mechanical manifestation of processes affecting the hidden layer (growth, magnetic fields, etc...). On the other hand, we assume that internal working is defined in terms of the (first) Piola–Kirchhoff stress tensor $\mathbf{S}$, the stress-couple $\mathbf{G}$ and the stress-torque $\boldsymbol{\varSigma }$. Both the external and internal workings are continuous, linear, real-valued functional on the space of virtual rates $(\tilde{\mathbf{w}},\widetilde{\mathbf{L}}_{g}, \widetilde{\boldsymbol{\varOmega }})$, given by

$$ \mathcal{W}_{e}(\tilde{\mathbf{w}},\tilde{\mathbf{L}}_{g}, \tilde{\boldsymbol{\varOmega }})=\int _{\mathcal{B}_{r}}(\mathbf{z} \cdot \tilde{\mathbf{w}}+ \mathbf{Y}\cdot \tilde{\mathbf{L}}_{g}+ \mathbf{Z}\cdot \tilde{\boldsymbol{\varOmega }}) + \int _{\partial \mathcal{B}_{r}}\mathbf {s}\cdot \tilde{\mathbf{w}}\,, $$

(3.7)

for the external working, and

$$ \mathcal{W}_{i}(\tilde{\mathbf{w}},\tilde{\mathbf{L}}_{g}, \tilde{\boldsymbol{\varOmega }})=\int _{\mathcal{B}_{r}}(\mathbf{S} \cdot \nabla \tilde{\mathbf{w}}+ \mathbf{G}\cdot \tilde{\mathbf{L}}_{g} +\boldsymbol{\varSigma }\cdot \tilde{\boldsymbol{\varOmega }})\,, $$

(3.8)

for the internal one.¹

The principle of virtual working states that for any given subregion $\mathcal{P}\subset \mathcal{B}_{r}$ of the reference configuration, the external and internal workings must be equal for all virtual velocities $(\tilde{\mathbf{w}},\tilde{\mathbf{L}}_{g}, \tilde{\boldsymbol{\varOmega }})\in \mathcal{V}\times \mathbb{L} \mathtt{in}\times {\mathbb{S}\textrm{kw}}$. Therefore, through a standard localization argument, the following strong form of the balance equations can be derived together with the corresponding boundary conditions:²

$$ \begin{aligned} &\mathrm{Div}\,\mathbf{S}+ \mathbf{z}=\textbf{0}\qquad \textrm{in}\, \,\mathcal{B}_{r}\,, \\ &\mathbf{u}=\hat{\mathbf{u}}\qquad \qquad \quad \,\,\;\textrm{in}\, \,\partial _{u}\mathcal{B}_{r}\,, \\ &\mathbf{S}\,\mathbf{m}=\mathbf{s}\qquad \qquad \,\textrm{on}\,\, \partial _{t}\mathcal{B}_{r}\,, \end{aligned} $$

(3.9)

and

$$ \mathbf{G}=\mathbf{Y}\qquad \textrm{and}\qquad \boldsymbol{\varSigma }= \mathbf{Z}\qquad \textrm{in}\, \,\mathcal{B}_{r}\,, $$

(3.10)

with $\partial _{u}\mathcal{B}_{r}$ and $\partial _{t}\mathcal{B}_{r}$ the parts of the boundary $\partial \mathcal{B}_{r}$ where displacements and tractions are prescribed and $\mathbf{m}$ the unit normal to $\partial _{t}\mathcal{B}_{r}$. The former equation (3.9) is the standard balance equation of forces expressed in terms of the first Piola–Kirchhoff stress tensor, whereas the latter (3.10) are the balance equations of the stress-couples and stress-torques.

4 Constitutive Prescriptions Based on Structural Frame-Indifference

The multiplicative decomposition of the deformation gradient (2.2) causes the relaxed state to not be unique since both $(\mathbf{F}_{g},\mathbf{R})$ and $(\mathbf{Q}\mathbf{F}_{g},\mathbf{Q}\mathbf{R})$ gives the same macroscopic deformation as Eqs. (2.5)-(2.6) have evidenced. To this respect, the Authors of [9] wrote: ...there is no reason why the stress response from $\mathbf{Q}\mathbf{F}_{g}$ should be $\mathbf{Q}$-related to the one from $\mathbf{F}_{g}$. This does happen, however, if the body element is isotropic and its relaxed state undistorted [9] (see also [8]).

The $\mathbf{Q}-$ relation cited in [9] is the main idea behind the so called principle of structural frame-indifference (SFI), first formulated in [12]. Accordingly, the non-uniqueness of the relaxed state must not influence the constitutive response of the continuum whether or not the material is isotropic. An immediate consequence is that all constitutive functions must be insensitive to the transformation laws (2.4).

In our model, constitutive prescriptions are given in terms of the strain energy density $\varphi$ and the dissipation density $\delta$ per unit of mass; the two functions completely characterize the material response of the body. Since the material is transversely isotropic and the orientation tensor in the relaxed state is described by $\mathbf{A}=\mathbf{R}\mathbf{A}_{0}\mathbf{R}^{T}$, we assume $\varphi$ to depend on the right Cauchy-Green strain tensor $\mathbf{C}_{e}=\mathbf{F}_{e}^{T}\mathbf{F}_{e}$ and on $\mathbf{A}$, i.e., $\varphi =\varphi (\mathbf{C}_{e},\mathbf{A})$. Then, we require the dissipation function $\delta$ to depend on the inelastic rates $\mathbf{L}_{g}$ and $\boldsymbol{\varOmega }$, such that $\delta =\delta (\mathbf{L}_{g},\boldsymbol{\varOmega })$.³ With these assumptions both $\delta$ and $\varphi$ are frame indifferent, i.e, the theory is objective.

In addition, under the transformation laws (2.4), the arguments of $\varphi (\mathbf{C}_{e},\mathbf{A})$ change as

$$ \mathbf{C}_{e}\mapsto \mathbf{Q}\mathbf{C}_{e}\mathbf{Q}^{T},\qquad \mathbf{A}\mapsto \mathbf{Q}\mathbf{A}\mathbf{Q}^{T}\,. $$

Thus, to satisfy the constitutive hypothesis of structural frame-indifference of the strain energy density, we require that

$$ \varphi (\mathbf{C}_{e},\mathbf{A})=\varphi (\mathbf{Q}\mathbf{C}_{e} \mathbf{Q}^{T},\mathbf{Q}\mathbf{A}\mathbf{Q}^{T})\,, $$

(4.11)

for any $\mathbf{Q}\in \mathbb{O}\mathtt{rth}^{+}$. Equation (4.11) is indeed satisfied for every rotation $\mathbf{Q}$ if and only if $\varphi$ is a isotropic function of the $\mathbf{C}_{e}$ and $\mathbf{A}$, which is equivalent to say that the material is transversely isotropic in the relaxed state. In this sense, the SFI requirement extends what already written in [13] for isotropic materials: a condition both necessary and sufficient that the elastic relation be SFI is that the function (4.11) governing the elastic response be isotropic in its arguments. This allows the energy density to be expressed in terms of the invariants of the two tensors [16].

For what concerns the dissipation function $\delta (\mathbf{L}_{g},\boldsymbol{\varOmega })$, its arguments change as

$$ \mathbf{D}_{g}\mapsto \mathbf{Q}\mathbf{D}\mathbf{Q}^{T}\,,\quad \mathbf{W}_{g}\mapsto \dot{\mathbf{Q}}\mathbf{Q}^{T}+\mathbf{Q} \mathbf{W}_{g}\mathbf{Q}^{T}\,,\quad \boldsymbol{\varOmega }\mapsto \dot{\mathbf{Q}}\mathbf{Q}^{T}+\mathbf{Q}\boldsymbol{\varOmega } \mathbf{Q}^{T}\,, $$

(4.12)

where $\mathbf{D}_{g}=\mathrm{sym}\,\mathbf{L}_{g}$ and $\mathbf{W}_{g}=\mathrm{skw}\,\mathbf{L}_{g}$. Thus, to satisfy the constitutive hypothesis of structural frame-indifference of the dissipation density, we require that, for any $\mathbf{Q}\in \mathbb{O}\mathtt{rth}^{+}$ and for any $\dot{\mathbf{Q}}\mathbf{Q}^{T}\in {\mathbb{S}\textrm{kw}}$, it holds

$$ \delta (\mathbf{D}_{g},\mathbf{W}_{g},\boldsymbol{\varOmega })=\delta ( \mathbf{Q}\mathbf{D}_{g}\mathbf{Q}^{T},\dot{\mathbf{Q}}\mathbf{Q}^{T} + \mathbf{Q}\mathbf{W}_{g}\mathbf{Q}^{T},\dot{\mathbf{Q}}\mathbf{Q}^{T}+ \mathbf{Q}\boldsymbol{\varOmega }\mathbf{Q}^{T})\,. $$

(4.13)

Due to the arbitrariness of $\mathbf{Q}$ and $\dot{\mathbf{Q}}\mathbf{Q}^{T}$, one can choose $\mathbf{Q}=\mathbf{I}$ and $\dot{\mathbf{Q}}\mathbf{Q}^{T}=-\mathbf{W}_{g}$ and write

$$ \delta (\mathbf{D}_{g},\mathbf{W}_{g},\boldsymbol{\varOmega })= \hat{\delta}(\mathbf{D}_{g},-\mathbf{W}_{g} + \mathbf{W}_{g},- \mathbf{W}_{g}+\boldsymbol{\varOmega })=\delta (\mathbf{D}_{g}, \textbf{0},\boldsymbol{\varOmega }-\mathbf{W}_{g})\,, $$

(4.14)

meaning that the dissipation function can only depend on the inelastic stretch rate $\mathbf{D}_{g}$ and on the difference $(\boldsymbol{\varOmega }-\mathbf{W}_{g})$ between the reorientation spin rate and the inelastic spin rate. Therefore, we drop the dependence on $\boldsymbol{\varOmega }+\mathbf{W}_{g}$ from $\delta$ to write, with a slight abuse of notation, the following structurally frame-indifferent form of the dissipation function

$$ \delta =\delta (\mathbf{D}_{g},\boldsymbol{\varOmega }-\mathbf{W}_{g})\,. $$

(4.15)

Let us note that if dependence of $\delta$ on the evolving material structure $\mathbf{A}$ is incorporated in the function, previous results still hold true.

5 Thermodynamic Consistency of the Constitutive Equations

Under isothermal conditions, the second principle of thermodynamics reduces to the local form of the dissipation inequality, which prescribes the time rate of elastic energy be less than or equal to the external actual working, or in other terms that the dissipation function is positive, i.e.,

$$\varrho_{r}\delta dV =(\mathbf{z} \cdot \tilde{\mathbf{w}}+ \mathbf{Y}\cdot \tilde{\mathbf{L}}_{g}+ \mathbf{Z}\cdot \tilde{\boldsymbol{\varOmega }})dV + \mathbf {s}\cdot \tilde{\mathbf{w}}dA -\frac{d}{dt}\varrho_{r}\varphi dV\geq 0\,, $$

with $\varrho _{r}$ the reference mass density. Due to the principle of virtual working, the dissipation inequality can be equivalently written in terms of the internal working and this form used to identify the class of admissible constitutive equations for stresses, stress-couples and stress-torques. It is worth noting that dissipation inequality must hold for any admissible velocity fields; hence, the reactive components of the internal actions do not enter the inequality as they must expend null working on those velocity fields. Hence, the local form of the dissipation inequality is:

$$\begin{aligned} \varrho_{r}\delta = &\hat{\mathbf{S}}\cdot \dot{\mathbf{F}}+ \mathrm{sym}\, \hat{\mathbf{G}}\cdot \mathbf{D}_{g} + \frac{\hat{\boldsymbol{\varSigma }}-\mathrm{skw}\,\hat{\mathbf{G}}}{2} \cdot (\boldsymbol{\varOmega }-\mathbf{W}_{g}) \\ +& \frac{\hat{\boldsymbol{\varSigma }}+\mathrm{skw}\,\hat{\mathbf{G}}}{2} \cdot (\boldsymbol{\varOmega }+\mathbf{W}_{g})-\varrho _{r}\, \dot{\varphi}\geq 0\,, \end{aligned}$$

(5.16)

where we have indicated with a superimposed hat $\hat{\,}$ the constitutively prescribable parts of the Piola-Kirchhoff stress $\hat{\mathbf{S}}$, of the stress-couple $\hat{\mathbf{G}}$ and of the stress-torque $\hat{\boldsymbol{\varSigma }}$, and we have rewritten the internal working (3.8) in terms of sum and difference of the spins $\boldsymbol{\varOmega }$ and $\mathbf{W}_{g}$.

The time derivative of the strain energy density can be written as $\dot{\varphi}={\partial \varphi}/{\partial \mathbf{C}_{e}}\cdot \dot{\mathbf{C}_{e}} +{\partial \varphi}/{\partial \mathbf{A}}\cdot \dot{\mathbf{A}}$ and by making use of the strain rate relationships derived in the Appendix, we obtain

$$ \dot{\varphi}=2\,\mathbf{F}_{e} \frac{\partial \varphi}{\partial \mathbf{C}_{e}}\mathbf{F}_{e}^{T} \cdot \mathbf{D}- 2\,\mathrm{sym}\,\!\big(\mathbf{C}_{e} \frac{\partial \varphi}{\partial \mathbf{C}_{e}}\big)\cdot \mathbf{D}_{g} + [\mathbf{C}_{e}, \frac{\partial \varphi}{\partial \mathbf{C}_{e}}] \cdot (\boldsymbol{\varOmega }-\mathbf{W}_{g})\,, $$

(5.17)

which uses the identity $[\partial \varphi /\partial \mathbf{A},\mathbf{A}]=[\mathbf{C}_{e},{ \partial \varphi}/{\partial \mathbf{C}_{e}}]$, proved true for a transversely isotropic material in [4]. The symbol $[\cdot ,\cdot ]$ is used to indicate the commutator operator (see the Appendix). The quantity $2\varrho _{g}\partial \varphi /\partial \mathbf{C}_{e}$ is the symmetric relaxed (second) Piola-Kirchhoff stress $\hat{\mathbf{S}}$, with $\varrho _{g}=\varrho _{r} J_{g}^{-1}$ being the mass density in the relaxed state, and $\mathbf{M}=\mathbf{C}_{e}\hat{\mathbf{S}}$ is the so-called Mandel stress, for which $\mathrm{skw}\,\hat{\mathbf{M}}= \frac {1}{2} [\mathbf{C}_{e}, \hat{\mathbf{S}}]$ and $\mathrm{sym}\,\hat{\mathbf{M}}= \mathrm{sym}\,(\mathbf{C}_{e} \hat{\mathbf{S}})$. With (5.17) in hand, we rewrite the dissipation inequality (5.16) as

$$\begin{aligned} \varrho_{r}\delta = & \big(\hat{\mathbf{S}}\mathbf{F}^{T}-2\varrho _{r}\, \mathbf{F}_{e}\frac{\partial \varphi}{\partial \mathbf{C}_{e}} \mathbf{F}_{e}^{T}\big)\cdot \mathbf{D}+\big(\mathrm{sym}\, \hat{\mathbf{G}}+2\varrho _{r}\,\mathrm{sym}\,\!(\mathbf{C}_{e} \frac{\partial \varphi}{\partial \mathbf{C}_{e}})\big)\cdot \mathbf{D}_{g} \\ &+\big( \frac{\hat{\boldsymbol{\varSigma }}-\mathrm{skw}\,\hat{\mathbf{G}}}{2} - \varrho _{r}\,[\mathbf{C}_{e}, \frac{\partial \varphi}{\partial \mathbf{C}_{e}}] \big)\cdot ( \boldsymbol{\varOmega }-\mathbf{W}_{g})+ \frac{\hat{\boldsymbol{\varSigma }}+\mathrm{skw}\,\hat{\mathbf{G}}}{2} \cdot (\boldsymbol{\varOmega }+\mathbf{W}_{g})\geq 0 \,, \end{aligned}$$

(5.18)

that must hold true for any admissible $(\mathbf{D},\mathbf{D}_{g},\mathbf{W}_{g},\boldsymbol{\varOmega })\in { \mathbb{S}\textrm{ym}}\times {\mathbb{S}\textrm{ym}}\times {\mathbb{S} \textrm{kw}}\times {\mathbb{S}\textrm{kw}}$. Accordingly, suitable constitutive choices are

$$ \hat{\mathbf{S}}\mathbf{F}^{T}=2\varrho _{r}\,\mathbf{F}_{e} \frac{\partial \varphi}{\partial \mathbf{C}_{e}}\mathbf{F}_{e}^{T}\,, $$

(5.19)

for the first Piola-Kirchhoff stress $\hat{\mathbf{S}}$, and

$$ \begin{aligned} &\mathrm{sym}\,\hat{\mathbf{G}}=-2\varrho _{r}\,\mathrm{sym}\,( \mathbf{C}_{e}\frac{\partial \varphi}{\partial \mathbf{C}_{e}})+ \mathbb{D}\mathbf{D}_{g}\,, \\ &\hat{\boldsymbol{\varSigma }}-\mathrm{skw}\,\hat{\mathbf{G}}=2\varrho _{r} \,[\mathbf{C}_{e}, \frac{\partial \varphi}{\partial \mathbf{C}_{e}}]+2 \,\mathbb{K}(\boldsymbol{\varOmega }-\mathbf{W}_{g})\,, \end{aligned} $$

(5.20)

for the symmetric part of the stress couple $\hat{\mathbf{G}}$ and for the difference between the stress torque $\hat{\boldsymbol{\varSigma }}$ and the skew part of $\hat{\mathbf{G}}$. Therein, $\mathbb{D}$ and $\mathbb{K}$ are fourth-order positive definite tensors, which guarantee $\delta$ be a positive definite quadratic form of the strain rates.⁴

In addition, SFI requires the dissipation inequality (5.18) to be independent of $\boldsymbol{\varOmega }+\mathbf{W}_{g}$ (see Eq. (4.15)), that leads to the two following possible conditions:

$$ \text{(I)}\quad \boldsymbol{\varOmega }+\mathbf{W}_{g}=\textbf{0}\,\qquad \text{or}\qquad \text{(II)}\quad \hat{\boldsymbol{\varSigma }}+ \mathrm{skw}\,\hat{\mathbf{G}}=\textbf{0}\,. $$

(5.21)

Equation (5.21)_I restricts the range of admissible velocity fields by introducing a kinematical constraint, that in turns make reactive components of $\boldsymbol{\varSigma }+\mathrm{skw}\,\mathbf{G}$ appear in the balance equations, yet makes the natural state of the body known at each instant.

On the other hand, equation (5.21)_II restricts the class of external allowable actions, since in this case the balance equations (3.10) yield $\mathbf{Z}+\mathrm{skw}\,\mathbf{Y}=\hat{\boldsymbol{\varSigma }}+ \mathrm{skw}\,\hat{\mathbf{G}}=\textbf{0}$, meaning that the skew part of the external couple must be balanced by the external torque. Indeed, this condition is commonly enforced in the literature where it is customary to assume that the external actions, working-conjugate of the inner inelastic strains, are zero (see for instance [23], [14], [21]). In such a case, the intermediate configuration remains indeterminate, unless further assumptions are made.

The consequences that one or the other choice have on the evolution of the inelastic strains are discussed in the following section.

6 Evolution Equations of the Inelastic Processes

We rewrite the balance equations (3.10) in the equivalent form

$$ \mathrm{sym}\,\mathbf{G}=\mathrm{sym}\,\mathbf{Y}\,,\,\, \boldsymbol{\varSigma }-\mathrm{skw}\,\mathbf{G}=\mathbf{Z}-\mathrm{skw} \,\mathbf{Y}\,,\,\,\boldsymbol{\varSigma }+\mathrm{skw}\,\mathbf{G}= \mathbf{Z}+\mathrm{skw}\,\mathbf{Y}\,, $$

(6.22)

to highlight the working conjugates of $\boldsymbol{\varOmega }-\mathbf{W}_{g}$ and $\boldsymbol{\varOmega }+\mathbf{W}_{g}$, respectively.

The balance equations (6.22)_1,2 and the rate-dependent constitutive equations (5.20) yield

$$ \begin{aligned} &\mathbb{D}\mathbf{D}_{g}=\mathrm{sym}\,\mathbf{Y}+2\varrho _{r}\, \mathrm{sym}\,(\mathbf{C}_{e} \frac{\partial \varphi}{\partial \mathbf{C}_{e}})\,, \\ &2\,\mathbb{K}(\boldsymbol{\varOmega }-\mathbf{W}_{g})=\mathbf{Z}- \mathrm{skw}\,\mathbf{Y}- 2\varrho _{r}\,[\mathbf{C}_{e}, \frac{\partial \varphi}{\partial \mathbf{C}_{e}}]\,. \end{aligned} $$

(6.23)

It is noted that no reactive components appear in previous equations since they are orthogonal to the constraint (5.21)_I, if applied. Equations (6.23) are indeed the evolution equations of the inelastic strains and represent a system of 9 equations (6 symmetric equations and 1 skew-symmetric equation) in the 12 unknowns of the problem $\mathbf{F}_{g}$ and $\mathbf{R}$.

The consideration of the kinematical constraint (5.21)_I brings in the further 3 equations necessary to solve the problem and determine the natural state of the system, that is,

$$ \begin{aligned} &\mathbb{D}\,\mathbf{D}_{g}=\mathrm{sym}\,\mathbf{Y}+2\varrho _{r}\, \mathrm{sym}\,(\mathbf{C}_{e} \frac{\partial \varphi}{\partial \mathbf{C}_{e}})\,, \\ &\mathbb{K}\,\mathbf{W}_{g}=-\frac {1}{4}(\mathbf{Z}+\mathrm{skw}\, \mathbf{Y})+\frac {1}{2} \varrho _{r}\,[\mathbf{C}_{e}, \frac{\partial \varphi}{\partial \mathbf{C}_{e}}]\,, \\ &\boldsymbol{\varOmega }=-\mathbf{W}_{g}\,, \end{aligned} $$

(6.24)

to be solved once the proper initial conditions are specified.

On the other hand, if the range of admissible rates is not restricted and internal actions satisfy (5.21)_II, thus $\mathbf{Z}+\mathrm{skw}\,\mathbf{Y}=\textbf{0}$, the evolution equations (6.23) become

$$ \begin{aligned} &\mathbb{D}\mathbf{D}_{g}=\mathrm{sym}\,\mathbf{Y}+2\varrho _{r}\, \mathrm{sym}\,(\mathbf{C}_{e} \frac{\partial \varphi}{\partial \mathbf{C}_{e}})\,, \\ &\mathbb{K}(\boldsymbol{\varOmega }-\mathbf{W}_{g})=\mathbf{Z}- \varrho _{r} \,[\mathbf{C}_{e}, \frac{\partial \varphi}{\partial \mathbf{C}_{e}}] \,, \end{aligned} $$

(6.25)

which does not allow to determine the solution of the problem unless a particular form of $\mathbf{F}_{g}$ is assumed. If for instance, one restricts the evolution to symmetric inelastic strains, i.e., $\mathbf{F}_{g}=\mathbf{U}_{g}\in {\mathbb{S}\textrm{ym}}$, then $\mathbf{W}_{g}=\textbf{0}$, the previous equations lead to

$$ \begin{aligned} &\mathbb{D}\,\dot{\mathbf{F}}_{g}\mathbf{F}_{g}^{-1}=\mathrm{sym}\, \mathbf{Y}+2\varrho _{r}\,\mathrm{sym}\,(\mathbf{C}_{e} \frac{\partial \varphi}{\partial \mathbf{C}_{e}})\,, \\ &\mathbb{K}\,\dot{\mathbf{R}}\mathbf{R}^{T}=\mathbf{Z}- \varrho _{r} \,[\mathbf{C}_{e}, \frac{\partial \varphi}{\partial \mathbf{C}_{e}}] \,, \end{aligned} \qquad \mathbf{F}_{g}\in {\mathbb{S}\textrm{ym}}\,, $$

(6.26)

that is a system of 9 equations in 9 unknowns. When $\mathrm{sym}\,\mathbf{Y}=\textbf{0}$, Eq. (6.26)₁ is indeed the evolution equation of the viscoplastic model presented in [23] for isotropic materials (with $\varphi$ independent of $\mathbf{A}$ in that case). On the other hand, the equation (6.26)₂ is the remodelling equation introduced in [4] and used in [3] to study the reorientation of fibers under the action of an external magnetic field.⁵ The combination of the two models indeed allows a much richer dynamics to be studied with the relaxation of the matrix uncoupled from the reorientation of the fibers, as shown in the following section.

6.1 Reduced Problems

We discuss both the system of equations (6.24), which hold under the condition I defined by the equation (5.21)_I, and the system of equations (6.26), which hold under the condition II defined by the equation (5.21)_II.

Case I. Let us start by considering an anisotropic material constituted by a viscous matrix reinforced with stiff fibers and by looking for possible solutions of the equations (6.24). As is customary in the literature, the external actions acting on the matrix are considered to be null, that is $\mathrm{sym}\,\mathbf{Y}=\mathrm{skw}\,\mathbf{Y}=\textbf{0}$ (see [5, 23]). On the other hand, fiber reorientation may be driven by external sources, thus we assume $\mathbf{Z}\neq\textbf{0}$ (see for instance [3] for fiber reorientation driven by the magnetic field); we also assume null bulk forces $\mathbf{z}$. In this circumstance, Eqs. (6.24) give

$$ \begin{aligned} &\eta _{d}\mathbf{D}_{g}=2\varrho _{r}\,\mathrm{sym}\,(\mathbf{C}_{e} \frac{\partial \varphi}{\partial \mathbf{C}_{e}})\,, \\ &\eta _{r}\boldsymbol{\varOmega }=\mathbf{Z}+2 \varrho _{r}\,[\mathbf{C}_{e}, \frac{\partial \varphi}{\partial \mathbf{C}_{e}}]\,, \\ &\mathbf{W}_{g}=-\boldsymbol{\varOmega }\,, \end{aligned} $$

(6.27)

to be solved with the initial conditions $\mathbf{F}_{g}(X,0)=\mathbf{I}$ and $\mathbf{R}(X,0)=\mathbf{I}$. In writing Eqs. (6.27), we have assumed that the remodelling tensors are isotropic, that is $\mathbb{D}=\eta _{d}\mathbb{I}$ and $\mathbb{K}=1/4\eta _{r}\mathbb{I}$, with $\eta _{d}$ and $\eta _{r}$ the matrix and fiber viscosity, respectively.

The twelve equations in (6.27) are coupled but can be numerically solved together with the macroscopic balance of forces to get the twelve unknown fields in $\mathbf{F}_{g}$, $\mathbf{R}$ and $p$. It is worth noting that the system does not admit an equilibrium solution, in fact the application of the external field $\mathbf{Z}$ steers the direction of the fibers within the viscous matrix which passively grows and influences fiber reorientation. In such a case, an external source $\mathrm{sym}\,\mathbf{Y}$ would be needed to maintain the equilibrium solution determined by the equations

$$ \mathrm{sym}\,(\mathbf{C}_{e}\hat{\mathbf{S}})=\mathrm{sym}\, \mathbf{Y}\quad \textrm{and}\quad [\mathbf{C}_{e},\hat{\mathbf{S}}]= \mathbf{Z}\,. $$

(6.28)

When no external actions are imposed, i.e., $\mathrm{sym}\,\mathbf{Y}=\textbf{0}$ and $\mathbf{Z}=\textbf{0}$, the only equilibrium solution of (6.27) corresponds to the natural state at which $\mathbf{C}_{e}=\mathbf{I}$ and both $\mathrm{sym}\,\lbrace \mathbf{C}_{e}\hat{\mathbf{S}}\rbrace$ and $[\mathbf{C}_{e},\hat{\mathbf{S}}]$ vanish. However, in this situation $\mathbf{R}$ is indeterminate, since the Mandel stress is zero in the natural state whether rotation $\mathbf{R}$ is considered. This apparent limit of the theory can be overcome by suitably prescribing a different dependence of the elastic energy on the rotation $\mathbf{R}$.

Equations (6.24) also describe the growth problem of a continuum in which the fiber can not reorient independently of the matrix, when the following additional constraint on the rotation matrix is enforced

$$ \mathbf{R}=\mathbf{I}\quad \textrm{or equivalently}\quad \boldsymbol{\varOmega }=\textbf{0}\,, $$

(6.29)

that implies $\mathbf{A}\equiv \mathbf{A}_{0}$, i.e., fibers do not rotate from the reference configuration to the natural state. Equation (6.29) is indeed a constraint acting on the field $\mathbf{R}$, thus limiting the evolution of the state variables of the problem; therefore the proper reactive actions appear. Under the constraint (6.29), the evolution equations reduce to

$$ \eta _{d}\mathbf{D}_{g}=\mathrm{sym}\,\mathbf{Y}+\mathrm{sym}\,( \mathbf{C}_{e}\hat{\mathbf{S}})\quad \textrm{and}\quad \mathbf{W}_{g}= \textbf{0}\,. $$

(6.30)

The remaining balance equation allows the reactive stresses to be determined from the external actions

$$ \tilde{\boldsymbol{\varSigma }}+\mathrm{skw}\,\tilde{\mathbf{G}}= \mathbf{Z}+\mathrm{skw}\,\mathbf{Y}\quad \textrm{and}\quad \tilde{\boldsymbol{\varSigma }}-\mathrm{skw}\,\tilde{\mathbf{G}}= \mathbf{Z}-\mathrm{skw}\,\mathbf{Y}\,. $$

(6.31)

A typical application of Eq. (6.30) is the growth of anisotropic tissues where the reinforcing fiber structure does not evolve from the reference configuration to the natural state, and the external field $\mathrm{sym}\,\mathbf{Y}$ is used to bring into the modelling the effects of external stimuli [11].

Case II. To illustrate the predicting capabilities of the theory when (5.21)_II is enforced, we consider the particular form of the elastic energy

$$ \begin{aligned} \varrho _{g}\,\varphi (I_{1},I_{3},I_{4}) = \frac {\mu }{2} \big(I_{3}^{- \frac {1}{3}}I_{1}-3\big)+\frac {\mu }{2} \frac{\beta _{1}}{\beta _{2}}\big(\exp{(\beta _{2}(I_{4}-1)^{2})}-1 \big) + \frac {\kappa }{2} (I_{3}^{1/2}-1)^{2}\,, \end{aligned} $$

(6.32)

defined in terms of the elastic strain invariants

$$ I_{1} = \mathbf{C}_{e}\cdot \mathbf{I},\qquad I_{4}=\mathbf{C}_{e} \cdot \mathbf{A},\qquad I_{3}=\det \mathbf{C}_{e}\,. $$

Such an energy was introduced in [22] and modifies the model proposed in [10] to correctly account for anisotropic volumetric behaviour; $\mu$ and $\kappa$ are the shear and bulk moduli of the isotropic matrix, and $\beta _{1}$ and $\beta _{2}$ two positive coefficients weighting the reinforcement contribution of the fibers. With (6.32) on hand, the Mandel stress $\mathbf{M}_{e}=2\varrho _{g}\,\mathbf{C}_{e} \frac{\partial \varphi}{\partial \mathbf{C}_{e}}$ becomes

$$ \mathbf{M}_{e}=\mu \,I_{3}^{-1/3}\mathbf{C}_{e}+\mu \beta _{1}(I_{4}-1) \,\exp (\beta _{2}(I_{4}-1)^{2})\,\mathbf{C}_{e}\mathbf{A}+\big( \kappa \,I_{3}^{1/2}(I_{3}^{1/2}-1)-\frac{\mu }{3} \,I_{3}^{-1/3}I_{1} \big)\,\mathbf{I}\,, $$

(6.33)

that upon substitution into (6.26) yields

$$ \begin{aligned} {\tau _{d}}\mathbf{D}_{g} =& I_{3}^{-1/3}\mathbf{C}_{e}+ \frac{\beta _{1}}{2}(I_{4}-1)\exp{(\beta _{2}(I_{4}-1)^{2})}\big( \mathbf{C}_{e}\mathbf{A}+\mathbf{A}\mathbf{C}_{e}\big)+ \\ &\big(\frac{\kappa}{\mu }\,I_{3}^{1/2}(I_{3}^{1/2}-1)-\frac {1}{3} \,I_{3}^{-1/3}I_{1}\big)\,\mathbf{I}\,, \\ {\tau _{r}}\,\dot{\mathbf{R}}\mathbf{R}^{T}=& -\frac{\beta _{1}}{2}(I_{4}-1) \exp{(\beta _{2}(I_{4}-1)^{2})}\big(\mathbf{C}_{e}\mathbf{A}- \mathbf{A}\mathbf{C}_{e}\big)\,, \end{aligned} $$

(6.34)

with $\mathbf{F}_{g}\in {\mathbb{S}\textrm{ym}}$, $\tau _{d}=\mu /\eta _{d}$ and $\tau _{r}=\mu /\eta _{r}$. Equations (6.34) allow the main features of the model to be highlighted. First of all, we note that the reorientation equation (6.34)₂ has two stationary solutions. One of them corresponds to $\mathbf{C}_{e}\mathbf{R}\mathbf{A}_{0}\mathbf{R}^{T}=\mathbf{R} \mathbf{A}_{0}\mathbf{R}^{T}\mathbf{C}_{e}$, meaning that the fibers align themselves to be coaxial with $\mathbf{C}_{e}$, i.e., in the principal directions of $\mathbf{C}_{e}$. The other stationary solution correspond to $I_{4}=\mathbf{C}_{e}\cdot \mathbf{R}\mathbf{A}_{0}\mathbf{R}^{T}=1$, when the fibers re-align to not experiencing any elastic stretches. To further stress this point, we consider an isochoric extension in the direction $\mathbf{e}_{1}$ when the fibers lie in the 1-2 plane. The corresponding macroscopic deformation is

$$ \mathbf{F}=\lambda \,\mathbf{e}_{1}\otimes \mathbf{e}_{1}+ \frac{1}{\sqrt{\lambda}}(\mathbf{e}_{2}\otimes \mathbf{e}_{2}+ \mathbf{e}_{3}\otimes \mathbf{e}_{3})\,, $$

(6.35)

whereas the symmetric inelastic deformation is assumed of the same form,

$$ \mathbf{F}_{g}=\lambda _{g}\,\mathbf{e}_{1}\otimes \mathbf{e}_{1}+ \frac{1}{\sqrt{\lambda _{g}}}(\mathbf{e}_{2}\otimes \mathbf{e}_{2}+ \mathbf{e}_{3}\otimes \mathbf{e}_{3})\,, $$

(6.36)

with both $\lambda$ and $\lambda _{g}$ dependent on time. Accordingly, it holds

$$ \mathbf{D}_{g}=\frac{\dot{\lambda}_{g}}{\lambda _{g}}\big(\mathbf{e}_{1} \otimes \mathbf{e}_{1}-\frac {1}{2}(\mathbf{e}_{2}\otimes \mathbf{e}_{2}+ \mathbf{e}_{3}\otimes \mathbf{e}_{3})\big)\quad \textrm{and}\quad \mathbf{W}_{g}=\textbf{0}\,. $$

(6.37)

In order to maintain the isochoric motion prescribed by (6.37)₁, reactive stresses must appear in (6.34); in particular, since $\mathbf{I}\cdot \mathbf{D}_{g}=0$, only the deviatoric part of the rhs of (6.34)₁ determines the evolution, that is

$$ \tau _{d}\mathbf{D}_{g}=I_{3}^{-1/3}\operatorname{dev}\lbrace \mathbf{C}_{e}\rbrace +\frac{\beta _{1}}{2}(I_{4}-1)\exp{(\beta _{2}(I_{4}-1)^{2})} \operatorname{dev}\lbrace \mathbf{C}_{e}\mathbf{A}+\mathbf{A} \mathbf{C}_{e}\rbrace \,. $$

(6.38)

The reoriented fiber direction $\mathbf{a}=\mathbf{R}\mathbf{a}_{0}$ is expressed in terms of the angle $\theta$ with the $\mathbf{e}_{1}$-axis

$$ \mathbf{a}=\cos (\theta )\,\mathbf{e}_{1}+\sin (\theta )\,\mathbf{e}_{2} \,, $$

(6.39)

such that

$$ \dot{\mathbf{R}}\mathbf{R}^{T}\mathbf{a}=-\dot{\theta}(\sin (\theta ) \mathbf{e}_{1}-\cos (\theta )\mathbf{e}_{2})\,. $$

The evolution equations (6.34) are hence recast in terms of the inelastic stretch $\lambda _{g}$ and of the angle $\theta$ as

$$ \begin{aligned} &3 \tau _{g}\lambda ^{2}\, \lambda _{g}^{4}\,\dot{\lambda}_{g}= && 2 \lambda ^{4} \lambda _{g}^{2}-2 \lambda \lambda _{g}^{5}+\beta _{1} \exp \Big({\beta _{2}\left ( \frac{\lambda ^{2} \cos (\theta )^{2}}{\lambda _{g}^{2}}+ \frac{\lambda _{g} \sin (\theta )^{2}}{\lambda}-1\right )^{2}}\Big)\,, \\ & && \left (2 \lambda ^{3} \operatorname{cos}(\theta )^{2}-\lambda _{g}^{3} \sin (\theta )^{2}\right )\left (\lambda ^{3} \operatorname{cos}( \theta )^{2}+\lambda _{g}^{2}\left (-\lambda +\lambda _{g} \sin (\theta )^{2} \right )\right ) \\ &2\tau _{r} \lambda ^{2} \lambda _{g}^{4}\dot{\theta}=&&\beta _{1} \sin (\theta ) \cos (\theta ) \left (\lambda ^{3}-\lambda _{g}^{3} \right ) \left (\lambda ^{3} \cos ^{2}(\theta )+\lambda _{g}^{2} \left (\lambda _{g} \sin ^{2}(\theta )-\lambda \right )\right ) \\ & &&\exp{\left (\beta _{2}\left ( \frac{\lambda ^{2} \cos ^{2}(\theta )}{\lambda _{g}^{2}}+ \frac{\lambda _{g} \sin ^{2}(\theta )}{\lambda }-1\right )^{2}\right )} \,, \end{aligned} $$

(6.40)

with the following initial conditions: $\lambda _{g}(0)=1$ and $\theta (0)=\theta _{0}$.

The evolution of the inelastic processes under a macroscopic deformation $\lambda$ with a constant stretch rate, i.e., $\lambda (t)=\exp (\varepsilon _{0}\,t)$ is followed through numerical integration of the equations (6.40). The results are shown in Fig. 2. The simulations were carried out with $\varepsilon _{0}=1\text{ s}^{-1}$, $\tau _{d}=0.5$ s, $\tau _{r}=0.05$ s, $\beta _{1}=1$, $\beta _{2}=0.5$ and different values of the initial fiber angle $\theta _{0}=\lbrace 0^{\circ},30^{\circ},60^{\circ},80^{\circ},90^{ \circ}\rbrace$.

Fig. 2

Different characteristics of the isochoric extension under constant stretch rate for different values of $\theta_{0}$. The gray curves in panel (c) represent the fiber orientation in the current configuration.

Figure 2a shows that the elastic stretch $\lambda _{e}=\lambda /\lambda _{g}$ reaches a steady state values for $\lambda$ larger than 2.5 for all the fiber angles. This in turn causes the stress component $S=\mathbf{S}\cdot \mathbf{e}_{1}\otimes \mathbf{e}_{1}$ in Fig. 2b to achieve a stationary value with a horizontal asymptote. In this situation, the macroscopic deformation keeps increasing, yet the flow is totally viscous and does not produce any stress increase.

The evolution of the fiber orientation angle $\theta$ is plotted against the stretch $\lambda$ in Fig. 2c for different values of $\theta (0)=\theta _{0}$. For $\theta _{0}=0^{\circ}$ and $\theta _{0}=90^{\circ}$, the fibers are aligned with the principal direction of the strain tensor $\mathbf{C}_{e}$, in this case $\mathbf{e}_{1}$ and $\mathbf{e}_{2}$, and the rhs of (6.40)₂ is zero, meaning that no evolution occurs. On the other hand for $0^{\circ}<\theta _{0}<90^{\circ}$, $\theta$ evolves towards an angle slightly lower than $60^{\circ}$ at which $I_{4}=1$ and the fiber are unstretched as shown by the plots in Fig. 2d. The grey curves in Fig. 2c represent the fiber orientation in the current configuration, defined as the angle between the vector $\mathbf{F}_{e}\mathbf{a}/\vert \mathbf{F}_{e}\mathbf{a}\vert$ and $\mathbf{e}_{1}$: for the considered constant stretch rate case, the current orientation reaches a stationary value, lower than the relaxed orientation $\theta$, due to the fact that either $\lambda _{e}$ and $\theta$ have reached an asymptotic value.

7 Asymptotic Approximations

In order to further exploit the peculiarities of the proposed theory, we investigate the solutions of the evolution equations (6.24) in the limit of slow and fast applied deformations, when no external actions are present. We rewrite the equations (6.24) in the following form

$$ \mu \,\tau _{d}\mathbf{D}_{g}=\mathrm{sym}\,(\mathbf{C}_{e} \hat{\mathbf{S}})\quad \textrm{and}\quad \mu \,\tau _{r}\mathbf{W}_{g}= \big[\mathbf{C}_{e},\hat{\mathbf{S}}\big]\quad \textrm{and}\qquad \mathbf{W}_{g}+\boldsymbol{\varOmega }=\textbf{0}\,, $$

(7.41)

to make explicit the dependence of the evolution on the characteristic times $\tau _{d}$ and $\tau _{r}$ defined from $\eta _{d}$ and $\eta _{r}$ as $\tau _{d}=\eta _{d}/\mu$, $\tau _{r}=\eta _{r}/\mu$, where $\mu$ is the shear modulus of the matrix. In addition, we define the characteristic deformation time as

$$ \tau _{c}^{-1} = \vert \mathbf{D}\vert ,\qquad \text{such that}\quad \overline{\mathbf{D}}=\tau _{c}\,\mathbf{D},\quad \text{and}\quad \overline{\mathbf{D}}_{g} = \tau _{c} \,\mathbf{D}_{g}\,, $$

to obtain the following dimensionless evolution equations

$$ \mu \,\frac{\tau _{d}}{\tau _{c}}\,\overline{\mathbf{D}}_{g}= \mathrm{sym}\,(\mathbf{C}_{e}\hat{\mathbf{S}})\quad \textrm{and}\quad \mu \,\frac{\tau _{r}}{\tau _{c}}\,\overline{\mathbf{W}}_{g}= \big[ \mathbf{C}_{e},\hat{\mathbf{S}}\big]\quad \textrm{and}\quad \overline{\mathbf{W}}_{g}+\overline{\boldsymbol{\varOmega }}=\textbf{0}\,. $$

(7.42)

We consider two evolution regimes: the first one, that we call slow deformation regime, in which the characteristic deformation time is much longer that the characteristic times of the inelastic processes; the second one, that we call fast deformation regime, in which the characteristic times of the deformation are much shorter than those driving the evolution.

Slow deformation. We first examine the case in which the applied deformation is slow by formally writing that ${\text{max}\lbrace \tau _{d},\tau _{r}\rbrace}/{\tau _{c}}\ll 1$, meaning that the matrix has had time to relax around the natural configuration. We introduce the smallness parameter $\varepsilon ={\tau _{d}}/{\tau _{c}}\ll 1$; it holds: ${\tau _{r}}/{\tau _{c}} = \varepsilon \, {\tau _{r}}/{\tau _{d}}$. Hence, all the variables can be expanded around the natural configuration in terms of the smallness parameter $\varepsilon$:

$$\begin{aligned} &\mathbf{F}_{e} = \mathbf{I}+ \varepsilon \;\mathbf{F}_{1}\,, \end{aligned}$$

(7.43)

$$\begin{aligned} &\mathbf{F}_{g} = \big(\mathbf{I}-\varepsilon \mathbf{F}_{1}\big) \mathbf{F}+ \text{o}(\varepsilon )\,. \end{aligned}$$

(7.44)

Accordingly, it holds

$$\begin{aligned} &\mathbf{C}_{e} = \mathbf{I}+ \varepsilon \big(\mathbf{F}_{1}+ \mathbf{F}_{1}^{T}\big)+\text{o}(\varepsilon )\simeq \mathbf{I}+2\, \varepsilon \,\mathbf{E}_{e}\,, \end{aligned}$$

(7.45)

$$\begin{aligned} &\overline{\mathbf{L}}_{g} = \overline{\mathbf{L}} - \varepsilon \big(\dot{\overline{\mathbf{F}}}_{1}+\big[\mathbf{F}_{1}, \overline{\mathbf{L}}\big]\big) + \text{o}(\varepsilon )\,, \end{aligned}$$

(7.46)

where the symbol ≃ stands for first order approximation in $\varepsilon$ and the strain tensor $\mathbf{E}_{e}$ in (7.45) is defined by $\mathbf{E}_{e}= \frac {1}{2} \big(\mathbf{F}_{1}+\mathbf{F}_{1}^{T} \big)$. The constraint (7.42)₃ gives

$$ \overline{\boldsymbol{\varOmega }} = -\overline{\mathbf{W}}_{g} \simeq - \overline{\mathbf{W}}\,. $$

In addition the Mandel stress tensor takes the form

$$ \mathbf{C}_{e} \hat{\mathbf{S}}_{e} = \big(\mathbf{I}+2\varepsilon \mathbf{E}_{e} \big)\big(\hat{\mathbf{S}}_{e}(\mathbf{I},\mathbf{R})+ \varepsilon \mathbb{C}[\mathbf{E}_{e}] \big) + \text{o}(\varepsilon ) \simeq \varepsilon \,\mathbb{C}[\mathbf{E}_{e}]\,, $$

(7.47)

where it was used the fact that the symmetric Piola stress tensor vanishes in the natural state, i.e., $\hat{\mathbf{S}}_{e}(\mathbf{I},\mathbf{R})=\textbf{0}$. The fourth order tensor $\mathbb{C}:=4\varrho _{r}{\partial ^{2} \varphi}/{\partial \mathbf{C}_{e}\partial \mathbf{C}_{e}}$ is the elasticity tensor evaluated around the natural state with symmetries dictated by $\mathbf{R}\mathbf{A}_{0}\mathbf{R}^{T}$. In this sense, Eq. (7.47) shows that, at the first order, the approximation of the Mandel stress coincides with the Cauchy stress of a transversely isotropic material. It is further noted that at the zero-th order the model predicts zero stress, which is a plausible result since the expansion has been carried out around the natural state.

Fast deformation. When the characteristic deformation time $\tau _{c}$ is much smaller than the relaxation times governing he evolution problem, the deformation is considered fast. Formally, we assume that $\text{min}\lbrace \tau _{d},\tau _{r}\rbrace \gg 1$ and introduce the smallness parameter $\epsilon = \tau _{c}/\tau _{d} \ll 1$. Accordingly, $\tau _{c}/\tau _{r} = \epsilon \tau _{d}/\tau _{r}$ and the following formal expansions can be considered

$$\begin{aligned} &\mathbf{F}_{g} = \mathbf{I}+ \epsilon \, \mathbf{F}_{1}\,, \end{aligned}$$

(7.48)

$$\begin{aligned} &\mathbf{F}_{e} = \mathbf{F}\big(\mathbf{I}-\epsilon \,\mathbf{F}_{1} \big)+\text{o}(\epsilon )\,, \end{aligned}$$

(7.49)

$$\begin{aligned} &\mathbf{C}_{e} = \mathbf{C}-2 \epsilon \,\mathrm{sym}\,\lbrace \mathbf{C}\mathbf{F}_{1} \rbrace +\text{o}(\epsilon )\,, \end{aligned}$$

(7.50)

corresponding to an inelastic deformation rate given by

$$ \overline{\mathbf{L}}_{g} = \epsilon \,\dot{\overline{\mathbf{F}}}_{1}+ \text{o}(\epsilon )\,. $$

(7.51)

In such a regime, the Mandel stress tensor is evaluated as follows

$$\begin{aligned} \mathbf{C}_{e}\hat{\mathbf{S}}&= \big( \mathbf{C}-2\,\epsilon \, \mathrm{sym}\,(\mathbf{C}\mathbf{F}_{1})\big)\big(\hat{\mathbf{S}}( \mathbf{C},\mathbf{R})-\epsilon \,\hat{\mathbb{C}}[\mathrm{sym}\,( \mathbf{C}\mathbf{F}_{1})]\big)+\text{o}(\epsilon ) \end{aligned}$$

(7.52)

$$\begin{aligned} &\simeq \mathbf{C}\,\hat{\mathbf{S}}(\mathbf{C},\mathbf{R})-\epsilon \big(2\,\mathrm{sym}\,( \mathbf{C}\mathbf{F}_{1})\hat{\mathbf{S}}( \mathbf{C},\mathbf{R})+\mathbf{C}\,\hat{\mathbb{C}}[\mathrm{sym}\,( \mathbf{C}\mathbf{F}_{1})]\big)\,, \end{aligned}$$

(7.53)

where the elasticity tensor $\hat{\mathbb{C}}$ is evaluated around the current configuration at $\mathbf{C}_{e}=\mathbf{C}$ and $\mathbf{R}$. Therefore, the model predicts at zero-th order a stress tensor $\mathbf{C}\,\hat{\mathbf{S}}(\mathbf{C},\mathbf{R})$ coincident with the one of a purely elastic anisotropic material with symmetries dictated by $\mathbf{R}\mathbf{A}_{0}\mathbf{R}^{T}$. On the other hand, the evolution problem at the first order becomes

$$ \epsilon \, \mathrm{sym}\,\dot{\overline{\mathbf{F}}}_{1} = {\epsilon} \,\mathrm{sym}\,(\mathbf{C}\,\hat{\mathbf{S}}_{e}(\mathbf{C}, \mathbf{R})),\quad \text{and}\quad \epsilon \, \mathrm{skw}\, \dot{\overline{\mathbf{F}}}_{1} = \epsilon \frac{\tau _{d}}{\tau _{r}}\,\big[\mathbf{C},\hat{\mathbf{S}}_{e}( \mathbf{C},\mathbf{R})\big]\,, $$

(7.54)

together with the constraint equation $\overline{\boldsymbol{\varOmega }}+\mathrm{skw}\, \dot{\overline{\mathbf{F}}}_{1}$ that completely determine the evolution of the system.

8 Conclusions and Perspectives

We have introduced a modelling framework capable of describing the mechanical response of anisotropic soft materials undergoing large inelastic deformations, which act differently on the matrix and the fibers, such that the matrix and the internal fiber structure have two different relaxed states. This assumption has allowed us to partially decouple the evolution of the fiber structure from the one imposed by the matrix, making the interaction between the fiber and the matrix non–affine.

Within this framework, the consistency of the model with thermodynamics was carefully analysed. It was further required that the state functions, i.e., strain energy density and dissipation density, are independent of a rotation overimposed on the natural state or, in other terms, are structurally frame–indifferent. Such a requirement is a constitutive prescription of the theory, which strongly affects the form of the dissipation density whereas is easily satisfied by the anisotropic strain energy density. In particular, it was shown that the elastic energy must be a isotropic function of the strain tensor and of the orientation tensor that conveys information on the fiber direction, whereas the dissipation function must be independent of the difference between the fiber reorientation spin and the matrix spin. Two possible modelling assumptions that satisfy this constitutive restriction were discussed. One of them allowed us to fully determine the relaxed state, and corresponded to the introduction of a kinematical constraint linking the inelastic spin rate, governing the evolution of the matrix, to the reorientation spin rate of the fibers. From one hand, the constraint equation, together with the flow rules, naturally arising from the dissipation inequality, make the evolution problem of the 12 unknowns of the problem, the placement $p$, the inelastic deformation $\mathbf{F}_{g}$ and the rotation tensor $\mathbf{R}$, fully determined. On the other hand, the constraint limits the scenarios attainable by the model, granted the considered constitutive assumptions, which are indeed shared by other Authors in the literature [15, 26]. The second road restricts the class of external allowable actions and allows the complete determination of the relaxed state only if further hypotheses on the form of $\mathbf{F}_{g}$ hold, as it is usually assumed in the Literature.

The theory can be extended by assuming different constitutive prescriptions for $\varphi$ and $\delta$ with a stronger interactions between fibers and matrix, as is the case in which the reoriented fibers are dragged by the inelastic processes that remodel the matrix. Interestingly, another possibility would be to make weaker the kinematical constraint by an elastic-type interaction such that $\boldsymbol{\varOmega }+\mathbf{W}_{g} = \mathbb{M}(\mathbf{Z}+ \mathrm{skw}\,\mathbf{Y})$.

Appendix: Deformation Rates

It is worth deriving and listing the relationships between the rates of the different kinematical quantities defined above.

We call $\mathbf{L}=\dot{\mathbf{F}}\mathbf{F}^{-1}$ the gradient of the velocity field and $\mathbf{L}_{e}=\dot{\mathbf{F}}_{e}\mathbf{F}_{e}^{-1}$ and $\mathbf{L}_{g}=\dot{\mathbf{F}}_{g}\mathbf{F}_{g}^{-1}$ the elastic and inelastic deformation rate tensors. The relationship between these quantities follows as

$$ \mathbf{L}= \mathbf{L}_{e} + \mathbf{F}_{e}\,\mathbf{L}_{g}\, \mathbf{F}_{e}^{-1}\,. $$

The rate of the right-Cauchy Green strain tensor $\mathbf{C}_{e}= \mathbf{F}_{e}^{T}\mathbf{F}_{e}$ is

$$ \dot{\mathbf{C}}_{e} = 2\,\mathbf{F}_{e}^{T}\mathbf{D}\mathbf{F}_{e} - 2\,\mathrm{sym}\,(\mathbf{C}_{e}\mathbf{L}_{v})\,, $$

(9.55)

where $\mathbf{D}=\mathrm{sym}\,\mathbf{L}$ is the symmetric part of the velocity gradient, i.e., the stretch-rate. Throughout the paper $\mathrm{sym}$ and $\mathrm{skw}$ will be used to indicate the symmetric and skew-symmetric part of tensors, i.e., $\mathrm{sym}\,\mathbf{A}= \frac {1}{2} (\mathbf{A}+\mathbf{A}^{T})$ and $\mathrm{skw}\,\mathbf{A}= \frac {1}{2} (\mathbf{A}-\mathbf{A}^{T})$.

To highlight the effects of the interaction between the matrix and the fiber, it is worth computing the rate of evolution of the remodelled fiber $\mathbf{a}=\mathbf{R}\mathbf{a}_{0}$ and compare it to the rate of the remodelled line element $\mathbf{e}=\mathbf{F}_{g}\mathbf{e}_{0}$. These are

$$\begin{aligned} \dot{\mathbf{a}} = \boldsymbol{\varOmega }\,\mathbf{a}\qquad \text{and} \qquad \dot{\mathbf{e}} = \mathbf{L}_{g}\,\mathbf{e}\,. \end{aligned}$$

(9.56)

Figure 3 shows this difference for a fiber and a line element, that coincide at time $t=\overline{t}$. We remark that since $\mathbf{R}$ is an orthogonal tensor the length of $\mathbf{a}_{0}$ is unchanged whereas $\mathbf{e}$ can be stretched (with a stretching rate $\mathbf{D}_{g}\mathbf{e}$).

Fig. 3

Illustration of the deformation rates for a remodelled fiber $\mathbf{a}=\mathbf{R}\mathbf{a}_{0}$ and a remodelled line element $\mathbf{e}=\mathbf{F}_{g}\mathbf{e}_{0}$, which coincide at time $t=\bar{t}$. The difference between the two rates is given by the $\mathbf{L}_{g}-\boldsymbol{\varOmega }$

Finally, since $\mathbf{a}=\mathbf{R}\mathbf{a}_{0}$ and $\dot{\mathbf{a}}=\boldsymbol{\varOmega }\mathbf{a}$, the time rate of the remodeled orientation tensor $\mathbf{A}$ is

$$ \dot{\mathbf{A}}=\dot{\mathbf{a}}\otimes \mathbf{a}+ \mathbf{a} \otimes \dot{\mathbf{a}}=[\boldsymbol{\varOmega },\mathbf{A}]\,, $$

(9.57)

where we have made use of the commutator operator $[\cdot ,\cdot ]:\mathbb{L}\mathtt{in}\times \mathbb{L}\mathtt{in} \to {\mathbb{S}\textrm{kw}}$ such that $[\mathbf{A},\mathbf{B}]=\mathbf{A}\mathbf{B}-\mathbf{B}\mathbf{A}\,, \ \forall \mathbf{A}$, $\mathbf{B}\in \mathbb{L}\mathtt{in}$.