1 Introduction

The classic deformation known as simple shear has long been investigated within the framework of nonlinear elasticity for isotropic incompressible hyperelastic materials in a large variety of contexts. This deformation has been widely used in recent years in the analysis of the mechanical behavior of various types of soft matter. One of the major difficulties in providing a realistic physical interpretation of this idealized homogeneous deformation is the fact that the conventional mathematical model of simple shear using a plane stress assumption to determine the hydrostatic pressure implies that a normal traction must be applied to the slanted faces of the deformed specimen. However, such a traction is not applied in practice. Thus, it has long been recognized that the classic model of simple shear is at best an approximation to the actual deformation that occurs when two rigid platens enclosing a soft material are transversely displaced relative to one another. One approach to resolving this dilemma has been to abandon the plane stress assumption and instead assume at the outset that the normal traction on the slanted faces is identically zero. This approach was first suggested by Rivlin [1] but not subsequently used by him. It was advocated more emphatically as a physically realistic assumption by Gent et al. [2] and further examined in detail by Horgan and Murphy [3, 4].

Here we consider yet another possibility. We retain the classic plane stress assumption to determine the hydrostatic pressure but modify the basic kinematics to consider a simple shear deformation superposed on a uniform lateral extension or compression of the specimen. The amount of lateral stretch is considered as a stabilising factor determined in such a way that the predicted normal traction that needs to be applied to the slanting faces of the deformed specimen is minimised. This optimal choice of the lateral stretch should therefore enhance the fidelity of the mathematical modelling with experimental data. The analysis is simplified by noting that typical simple shear protocols for soft matter prescribe only moderate amounts of shear (see, for example, Sugerman et al. [5]) and the normal traction is an even function of the amount of shear. This enables the normal traction on the slanted faces to be accurately approximated using only the second term in a Maclaurin series in the amount of shear. The coefficient of this term is a function only of the material constants of the model used and the lateral stretch and it is this term that is optimised here.

The focus on minimising the normal traction on the slanted faces within this non-linear context is motivated primarily by its absence in typical experimental protocols and also by its absence in the linear theory. This is the so-called normal stress effect of the non-linear theory. This distinguishes it from the shear traction on the slanted faces that is predicted by both the linear and non-linear theories to be necessary to effect simple shear. Other measures of the fidelity of the model with experiments such as the magnitude of the traction vector might be alternatively considered but the analysis might not be as accessible as that considered here.

The outline for the paper is as follows. In Sect. 2, we present the basic kinematics for simple shear superimposed on a state of uniform lateral compression or extension of the specimen. The constitutive law for the incompressible isotropic nonlinearly elastic materials considered here is first formulated in terms of principal stretches in Sect. 3. This general approach that is independent of the choice of strain invariant means that simple shear superposed on a lateral stretch can be considered for all strain-energy functions that have been used to model the mechanical behaviour of soft matter. In Sect. 4, we discuss the normal traction on the inclined faces. In a recent paper [6], the present authors have described the role played by a particular strain-energy density, namely the one-term Ogden model [7] in recent theoretical and experimental modelling of the mechanical response of a wide variety of soft matter specimens. A non-exhaustive list of some of these applications can be found in [6]. We will consider this model also here in Sect. 5 and show that the minimisation of the normal traction depends crucially on the exponent of the Ogden model.

The general approach of Sect. 3 can, of course, can be adopted to consider the soft tissue models based on the classical Rivlin invariants based on the Cauchy-Green deformation tensors. It is shown in Sect. 6 that the classical formulation of the constitutive law in terms of these invariants considerably reduces the complexity of the analysis. The minimisation of the normal traction for the Mooney-Rivlin, Gent and exponential models that have been widely used in the modelling of soft matter is then considered.

These sample materials show that it is sometimes possible to choose the lateral stretch so that the normal traction is essentially zero. Typically there is a finite lateral stretch for which the normal traction on the slanted faces is minimised but for some materials the minimisation of the normal traction is only possible in the limit of an infinite lateral stretch. It is anticipated that these results could optimise the fidelity of hyperelastic models of simple shear with experiments, especially for soft biological tissue for which only moderate amounts of shear are possible.

2 Kinematics

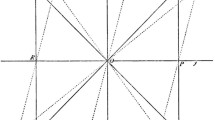
Protocols to determine the mechanical response of soft matter in simple shear experiments are considered here. We are only concerned with soft matter that can be considered to be incompressible, which is typically soft matter with a high water content such as hydrogels and biological soft tissue such as brain tissue. Motivated by the observed configurations of deformed specimens of soft matter (see, for example, Fig. 4 of Rashid et al. [8]), it seems reasonable to assume a deformation of the form

$$ x_{1}=\lambda ^{-\frac{1}{2}}X_{1}+\kappa \lambda X_{2}, \quad x_{2}= \lambda X_{2}, \quad x_{3}=\lambda ^{-\frac{1}{2}}X_{3}, $$
(2.1)

which preserves volume and where \((X_{1},X_{2},X_{3})\) and \((x_{1},x_{2},x_{3})\) denote the Cartesian coordinates of a typical particle before and after deformation respectively. Here \(\kappa >0\) is an arbitrary dimensionless constant called the amount of shear. The parameter \(\lambda \) describes the amount of lateral compression \((\lambda <1)\) or extension \((\lambda >1)\) imposed on the specimen before shear and it is the effect of \(\lambda \) as a stabilising factor in simple shear experiments that is of primary interest here. Because of incompressibility, there will also be an axial and out-of-plane extension or compression of amount \(\lambda ^{-\frac{1}{2}}\). The type of experiment envisaged is depicted in Fig. 1 for the case of lateral compression. Setting \(\lambda \equiv 1\) recovers the classical model of these experiments proposed by Rivlin [1].

Fig. 1
figure 1

A schematic of simple shear superimposed on a compressed specimen with lateral stretch \(\lambda <1\) and axial extension \(\lambda ^{-\frac{1}{2}}\)

Full size image

The corresponding deformation gradient tensor \(\boldsymbol{F}\) is given by

$$\begin{aligned} (\textbf{F})_{ij}= \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \lambda ^{-\frac{1}{2}} & \kappa \lambda & 0 \\ 0 & \lambda & 0 \\ 0 & 0 & \lambda ^{-\frac{1}{2}} \\ \end{array}\displaystyle \right ]. \end{aligned}$$
(2.2)

The corresponding Cauchy-Green deformation tensors \(\boldsymbol{B} = \boldsymbol{F F}^{T}\) and \(\boldsymbol{B}^{-1}\) have the form

$$\begin{aligned} (\textbf{B})_{ij}= \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \lambda ^{-1}+\kappa ^{2}\lambda ^{2} & \kappa \lambda ^{2} & 0 \\ \kappa \lambda ^{2} & \lambda ^{2} & 0 \\ 0 & 0 & \lambda ^{-1} \\ \end{array}\displaystyle \right ], \quad (\textbf{B}^{-1})_{ij}= \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \lambda & -\kappa \lambda & 0 \\ -\kappa \lambda & \lambda ^{-2}+\kappa ^{2}\lambda & 0 \\ 0 & 0 & \lambda \\ \end{array}\displaystyle \right ] \end{aligned}$$
(2.3)

and therefore the principal invariants are

$$ I_{1}\equiv \text{tr}\boldsymbol{B}= \lambda ^{2}+\frac{2}{\lambda}+ \kappa ^{2}\lambda ^{2},\quad I_{2}\equiv \text{tr}\boldsymbol{B}^{-1}= \lambda (2+\kappa ^{2})+\frac{1}{\lambda ^{2}}, \quad I_{3}=1. $$
(2.4)

The in-plane stretches \(\Lambda _{1},\,\Lambda _{2}\) are therefore determined from the quartic

$$ \Lambda ^{4}-\Lambda ^{2}\left (\frac{1}{\lambda}+\lambda ^{2}+ \lambda ^{2}\kappa ^{2}\right )+\lambda =0, $$
(2.5)

while the out-of-plane stretch is \(\Lambda _{3}=\lambda ^{-\frac{1}{2}}\). This quartic can be rewritten as

$$ \frac{\Lambda ^{2}}{\lambda ^{\frac{1}{2}}}+ \frac{\lambda ^{\frac{1}{2}}}{\Lambda ^{2}}- \frac{1+\lambda ^{3}+\lambda ^{3}\kappa ^{2}}{\lambda ^{\frac{3}{2}}}= \left (\frac{\Lambda}{\lambda ^{\frac{1}{4}}}- \frac{\lambda ^{\frac{1}{4}}}{\Lambda}\right )^{2}- \frac{(1-\lambda ^{\frac{3}{2}})^{2}+\lambda ^{3}\kappa ^{2}}{\lambda ^{\frac{3}{2}}}=0, $$
(2.6)

which yields the following quadratic for \(\Omega \equiv \frac{\Lambda}{\lambda ^{\frac{1}{4}}}\):

$$ \Omega -\frac{1}{\Omega}=\pm \alpha , \quad \alpha ^{2}\equiv \frac{(1-\lambda ^{\frac{3}{2}})^{2}+\lambda ^{3}\kappa ^{2}}{\lambda ^{\frac{3}{2}}}. $$
(2.7)

Solving yields

$$ \Omega _{1}=\frac{\alpha +\sqrt{4+\alpha ^{2}}}{2}, \quad \Omega _{2}= \frac{1}{\Omega _{1}}=\frac{-\alpha +\sqrt{4+\alpha ^{2}}}{2}. $$
(2.8)

Therefore

$$\begin{aligned} \Lambda _{1}=\lambda ^{\frac{1}{4}} \Omega _{1}= \frac{\lambda ^{\frac{1}{4}}}{2}(\alpha +\sqrt{4+\alpha ^{2}}), \quad \Lambda _{2}=\lambda ^{\frac{1}{4}} \Omega _{2}= \frac{\lambda ^{\frac{1}{4}}}{2}(-\alpha +\sqrt{4+\alpha ^{2}}), \end{aligned}$$
(2.9)

with

$$ \Lambda _{1}^{2}\Lambda _{2}^{2}=\lambda , \quad \Lambda _{1}^{2}+ \Lambda _{2}^{2}=\frac{1}{\lambda}+\lambda ^{2}(1+\kappa ^{2}). $$
(2.10)

There are two special cases of interest: that of pure extension/contraction with \(\kappa =0\) and that of pure simple shear with \(\lambda =1\). If \(\kappa =0\), then

$$ \Lambda _{1}(=\Lambda _{3})=\lambda ^{-\frac{1}{2}}, \quad \Lambda _{2}= \lambda , $$

while if \(\lambda =1\),

$$ \Lambda _{1}=\frac{\kappa +\sqrt{4+\kappa ^{2}}}{2}, \quad \Lambda _{2}= \frac{1}{\Lambda _{1}}=\frac{-\kappa +\sqrt{4+\kappa ^{2}}}{2}. $$
(2.11)

3 A General Constitutive Law

The principal Cauchy stresses \(t_{i} , i = 1, 2, 3\), for homogeneous isotropic incompressible hyperelastic materials are given by

$$ t_{i}=-p+\Lambda _{i}\frac{\partial W}{\partial \Lambda _{i}}, \quad \text{(no sum)} $$
(3.1)

where \(p\) is an arbitrary scalar field. Here \(W = W(\Lambda _{1}, \Lambda _{2},\Lambda _{3})\) is the strain-energy density per unit undeformed volume and is a symmetric function of the principal stretches. Since the Cauchy stress \(\boldsymbol{T}\) is coaxial with \(\boldsymbol{B}\) it has the spectral decomposition

$$\begin{aligned} \boldsymbol{T} =&\sum _{i=1}^{3}t_{i}\boldsymbol{v}^{(i)}\otimes \boldsymbol{v}^{(i)} \\ =&-p\boldsymbol{I}+\Lambda _{1} \frac{\partial W}{\partial \Lambda _{1}}\boldsymbol{v}^{(1)}\otimes \boldsymbol{v}^{(1)}+\Lambda _{2} \frac{\partial W}{\partial \Lambda _{2}}\boldsymbol{v}^{(2)}\otimes \boldsymbol{v}^{(2)}+\Lambda _{3} \frac{\partial W}{\partial \Lambda _{3}}\boldsymbol{v}^{(3)}\otimes \boldsymbol{v}^{(3)}, \end{aligned}$$
(3.2)

using an obvious notation for the eigenvectors of \(\boldsymbol{T},\,\boldsymbol{B}\).

For simple shear superimposed on a triaxial stretch described by (2.1) and with \(\Omega _{1},\,\Omega _{2}\) defined in (2.8), the two in-plane perpendicular eigenvectors of \(\boldsymbol{B}\) are easily found to be

$$\begin{aligned} \boldsymbol{v}^{(1)}=\left ( \frac{\Omega _{1}^{2}-\lambda ^{\frac{3}{2}}}{\sqrt{(\Omega _{1}^{2}-\lambda ^{\frac{3}{2}})^{2}+\kappa ^{2}\lambda ^{3}}}, \frac{\kappa \lambda ^{\frac{3}{2}}}{\sqrt{(\Omega _{1}^{2}-\lambda ^{\frac{3}{2}})^{2}+\kappa ^{2}\lambda ^{3}}},0 \right ), \\ \boldsymbol{v}^{(2)}=\left ( \frac{\Omega _{2}^{2}-\lambda ^{\frac{3}{2}}}{\sqrt{(\Omega _{2}^{2}-\lambda ^{\frac{3}{2}})^{2}+\kappa ^{2}\lambda ^{3}}}, \frac{\kappa \lambda ^{\frac{3}{2}}}{\sqrt{(\Omega _{2}^{2}-\lambda ^{\frac{3}{2}})^{2}+\kappa ^{2}\lambda ^{3}}}, 0\right ), \end{aligned}$$
(3.3)

and \(\boldsymbol{v}^{(3)}=\boldsymbol{e}_{3}\), using an obvious notation for the unit vectors in the directions of the Cartesian axes.

Noting that (see the Appendix)

$$ (\Omega _{1}^{2}-\lambda ^{\frac{3}{2}})^{2}+\kappa ^{2}\lambda ^{3}= \frac{(\Lambda _{1}^{4}-\lambda )(\Lambda _{1}^{2}-\lambda ^{2})}{\lambda \Lambda _{1}^{2}} , $$
(3.4)

the Cartesian components of the normal stresses are therefore

$$\begin{aligned} T_{11} =&-p+ \frac{\Lambda _{1}^{3}(\Lambda _{1}^{2}-\lambda ^{2})}{\Lambda _{1}^{4}-\lambda} \frac{\partial W}{\partial \Lambda _{1}}+ \frac{\Lambda _{2}^{3}(\Lambda _{2}^{2}-\lambda ^{2})}{\Lambda _{2}^{4}-\lambda} \frac{\partial W}{\partial \Lambda _{2}}, \\ T_{22} =& -p+ \frac{\lambda \Lambda _{1}(\lambda \Lambda _{1}^{2}-1)}{\Lambda _{1}^{4}-\lambda} \frac{\partial W}{\partial \Lambda _{1}}+ \frac{\lambda \Lambda _{2}(\lambda \Lambda _{2}^{2}-1)}{\Lambda _{2}^{4}-\lambda} \frac{\partial W}{\partial \Lambda _{2}}, \\ T_{33} =&-p+\Lambda _{3}\frac{\partial W}{\partial \Lambda _{3}}, \end{aligned}$$
(3.5)

with the in-plane Cauchy shear stress for the deformation (2.1) given by

$$\begin{aligned} T_{12} =&\kappa \lambda ^{\frac{3}{2}} \frac{\Omega _{1}^{2}-\lambda ^{\frac{3}{2}}}{(\Omega _{1}^{2}-\lambda ^{\frac{3}{2}})^{2}+\kappa ^{2}\lambda ^{3}} \left (\Lambda _{1}\frac{\partial W}{\partial \Lambda _{1}}-\Lambda _{2} \frac{\partial W}{\partial \Lambda _{2}}\right ) \\ =&\kappa \lambda ^{2} \frac{\Lambda _{1}^{2}}{\Lambda _{1}^{4}-\lambda}\left (\Lambda _{1} \frac{\partial W}{\partial \Lambda _{1}}-\Lambda _{2} \frac{\partial W}{\partial \Lambda _{2}}\right ) \\ =&\frac{\kappa \lambda ^{2}}{\Lambda _{1}^{2}-\Lambda _{2}^{2}} \left (\Lambda _{1}\frac{\partial W}{\partial \Lambda _{1}}-\Lambda _{2} \frac{\partial W}{\partial \Lambda _{2}}\right ), \end{aligned}$$
(3.6)

where (2.10) has been used in the last step. Trivially, it is predicted that

$$ T_{13}=T_{23}=0. $$

There is no consensus on the best approach to determining the arbitrary pressure term \(p\) in the normal stresses (see, for example, Horgan and Murphy [3] for a discussion) but a common assumption proposed originally by Rivlin [1] is that plane stress conditions hold so that \(T_{33}=0\). Adopting this here yields

$$\begin{aligned} T_{11} =& \frac{\Lambda _{1}^{3}(\Lambda _{1}^{2}-\lambda ^{2})}{\Lambda _{1}^{4}-\lambda} \frac{\partial W}{\partial \Lambda _{1}}+ \frac{\Lambda _{2}^{3}(\Lambda _{2}^{2}-\lambda ^{2})}{\Lambda _{2}^{4}-\lambda} \frac{\partial W}{\partial \Lambda _{2}}-\lambda ^{-\frac{1}{2}} \frac{\partial W}{\partial \Lambda _{3}} \\ =& \frac{\Lambda _{1}^{2}-\lambda ^{2}}{\Lambda _{1}^{2}-\Lambda _{2}^{2}} \Lambda _{1}\frac{\partial W}{\partial \Lambda _{1}}+ \frac{\Lambda _{2}^{2}-\lambda ^{2}}{\Lambda _{2}^{2}-\Lambda _{1}^{2}} \Lambda _{2}\frac{\partial W}{\partial \Lambda _{2}}-\lambda ^{- \frac{1}{2}}\frac{\partial W}{\partial \Lambda _{3}}, \\ T_{22} =& \frac{\lambda \Lambda _{1}(\lambda \Lambda _{1}^{2}-1)}{\Lambda _{1}^{4}-\lambda} \frac{\partial W}{\partial \Lambda _{1}}+ \frac{\lambda \Lambda _{2}(\lambda \Lambda _{2}^{2}-1)}{\Lambda _{2}^{4}-\lambda} \frac{\partial W}{\partial \Lambda _{2}}-\lambda ^{-\frac{1}{2}} \frac{\partial W}{\partial \Lambda _{3}} \\ =& \frac{\lambda (\lambda \Lambda _{1}^{2}-1)}{\Lambda _{1}(\Lambda _{1}^{2}-\Lambda _{2}^{2})} \frac{\partial W}{\partial \Lambda _{1}}+ \frac{\lambda (\lambda \Lambda _{2}^{2}-1)}{\Lambda _{2}(\Lambda _{2}^{2}-\Lambda _{1}^{2})} \frac{\partial W}{\partial \Lambda _{2}}-\lambda ^{-\frac{1}{2}} \frac{\partial W}{\partial \Lambda _{3}}. \end{aligned}$$
(3.7)

4 Normal Traction on the Slanted Faces

The unit normal to the slanted faces of the specimen in the final deformed configuration is given by

$$ \boldsymbol{n}=\frac{1}{\sqrt{1+\kappa ^{2}}}(1,-\kappa ,0), $$
(4.1)

and the normal traction \(N\) on these faces therefore has the form

$$\begin{aligned} N^{SF} =& \frac{T_{11}-2\kappa T_{12}+\kappa ^{2}T_{22}}{1+\kappa ^{2}}. \end{aligned}$$
(4.2)

It follows from (3.6), (3.7) that for simple shear superposed on a lateral stretch \(\lambda \) that

$$\begin{aligned} N^{SF} =&-\lambda ^{-\frac{1}{2}} \frac{\partial W}{\partial \Lambda _{3}}+ \frac{\lambda \Lambda _{1}(\Lambda _{1}^{2}-\lambda ^{2})}{(\lambda \Lambda _{1}^{4}-\Lambda _{1}^{2}+\lambda ^{2})(\Lambda _{1}^{4}-\lambda )} \frac{\partial W}{\partial \Lambda _{1}} \\ &{}+ \frac{\lambda \Lambda _{2}(\Lambda _{2}^{2}-\lambda ^{2})}{(\lambda \Lambda _{2}^{4}-\Lambda _{2}^{2}+\lambda ^{2})(\Lambda _{2}^{4}-\lambda )} \frac{\partial W}{\partial \Lambda _{2}}. \end{aligned}$$
(4.3)

The focus here is on the judicious choice of the lateral stretch/compression \(\lambda \) so that the normal traction on the slanted faces is minimised in some sense, which is assumed here to enhance the fidelity of the mathematical model (2.1) with typical experimental protocols for simple shear which do not require such normal tractions. The general analysis is obviously unwieldy even for the simplest models. However, noting that the amount of shear in experiments rarely exceeds \(50\%\), and is much lower when shearing soft materials, and that the normal stresses are even functions of the amount of shear, a Maclaurin series expansion of \(N^{SF}\) in the amount of shear \(\kappa \) truncated at the quadratic term, denoted here by \(N\kappa ^{2}\), should be an excellent approximation of the general response. Given that

$$ \frac{d\Lambda _{1}^{2}}{d\kappa}|_{\kappa =0}= \frac{d\Lambda _{2}^{2}}{d\kappa}|_{\kappa =0}=0, $$

it follows from (4.2) that to \(\mathcal{O}(\kappa ^{4})\)

$$\begin{aligned} N^{SF} \approx &N\kappa ^{2} \\ =&\left [ \left (\frac{\partial T_{11}}{\partial \Lambda _{1}^{2}} \right )^{(0)}\frac{\lambda ^{2}}{1-\lambda ^{3}}- \left ( \frac{\partial T_{11}}{\partial \Lambda _{2}^{2}} \right )^{(0)} \frac{\lambda ^{5}}{1-\lambda ^{3}}-2\frac{dT_{12}}{d\kappa}^{(0)} +T_{22}^{(0)} \right ]\kappa ^{2}, \\ =&\frac{1}{1-\lambda ^{3}}\left [\lambda ^{2}\left ( \frac{\partial T_{11}}{\partial \Lambda _{1}^{2}} \right )^{(0)}- \lambda ^{5}\left (\frac{\partial T_{11}}{\partial \Lambda _{2}^{2}} \right )^{(0)}+\lambda (1+\lambda ^{3})\left ( \frac{\partial W}{\partial \Lambda _{2}}\right )^{(0)}\right. \\ &{}-\left. \lambda ^{- \frac{1}{2}}(1+\lambda ^{3})\left ( \frac{\partial W}{\partial \Lambda _{1}}\right )^{(0)} \right ] \kappa ^{2}, \end{aligned}$$
(4.4)

where the \((0)\) superscript denotes evaluation of the principal stretches at \(\kappa = 0\). The goal therefore is to choose \(\lambda \) so that the magnitude of the coefficient \(N\) of \(\kappa ^{2}\) in the Maclaurin series is minimised, with the hypothesis advanced here that the fidelity of model with experiment is therefore enhanced.

5 One Term Ogden Model

The one term incompressible Ogden model [7]

$$ W=\frac{2\mu}{n^{2}}\left (\Lambda _{1}^{n}+\Lambda _{2}^{n}+\Lambda _{3}^{n}-3 \right ), \quad n\ne 0, $$
(5.1)

where \(\mu \) is the infinitesimal shear modulus, has been widely used to model the mechanical response of soft matter (see, for example, Horgan and Murphy [6]). For the special case when \(n=2\), the strain energy (5.1) reduces to the neo-Hookean model. The normal stress on the slanted faces follows from (4.3) and has the form

$$ N^{SF}=\frac{2\mu}{n}\left (-\lambda ^{-\frac{n}{2}}+ \frac{\lambda \Lambda _{1}^{n}(\Lambda _{1}^{2}-\lambda ^{2})}{(\lambda \Lambda _{1}^{4}-\Lambda _{1}^{2}+\lambda ^{2})(\Lambda _{1}^{4}-\lambda )}+ \frac{\lambda \Lambda _{2}^{n}(\Lambda _{2}^{2}-\lambda ^{2})}{(\lambda \Lambda _{2}^{4}-\Lambda _{2}^{2}+\lambda ^{2})(\Lambda _{2}^{4}-\lambda )} \right ). $$
(5.2)

Thus even for the simplest implementations of this simple form of strain energy, it is difficult to see how progress can be made with choosing the lateral stretch \(\lambda \) so that \(N^{SF}\) is minimised in some sense. However, there is an exception: Horgan and Murphy [6] observed that \(N^{SF}\equiv 0\) for \(\lambda =1\) and \(n=6\), i.e., there is no normal traction on the slanted faces predicted in plane strain simple shear for the Ogden material with exponent \(n=6\).

However, progress can be made using the quadratic approximation to \(N^{SF}\) given in (4.4). It follows that for this model

$$ \left (\frac{\partial W}{\partial \Lambda _{1}}\right )^{(0)}= \frac{2\mu}{n}\lambda ^{\frac{1-n}{2}} , \quad \left ( \frac{\partial W}{\partial \Lambda _{2}}\right )^{(0)}=\frac{2\mu}{n} \lambda ^{n-1} , $$

and from (3.7)1 that

$$ T_{11}=\frac{2\mu}{n}\left ( \frac{(\Lambda _{1}^{2})^{1+\frac{n}{2}}(\Lambda _{1}^{2}-\lambda ^{2})}{\Lambda _{1}^{4}-\lambda} + \frac{(\Lambda _{2}^{2})^{1+\frac{n}{2}}(\Lambda _{2}^{2}-\lambda ^{2})}{\Lambda _{2}^{4}-\lambda} -\lambda ^{-\frac{n}{2}} \right ). $$

Therefore

$$ \frac{\partial T_{11}}{\partial \Lambda _{1}^{2}}= \frac{\mu \Lambda _{1}^{n}}{n} \frac{n\Lambda _{1}^{6} +\lambda ^{2}(2-n)\Lambda _{1}^{4} -\lambda (4+n)\Lambda _{1}^{2}+\lambda ^{3}(2+n)}{(\Lambda _{1}^{4}-\lambda )^{2}}, $$

and consequently

$$\begin{aligned} \left ( \frac{\partial T_{11}}{\partial \Lambda _{1}^{2}}\right )^{(0)} =& \frac{\mu}{n} \frac{\lambda ^{1-\frac{n}{2}}((2+n)\lambda ^{3}-n)}{\lambda ^{3}-1}, \\ \left ( \frac{\partial T_{11}}{\partial \Lambda _{2}^{2}}\right )^{(0)} =& \frac{2\mu}{n} \frac{\lambda ^{n+1}}{\lambda ^{3}-1}. \end{aligned}$$
(5.3)

Therefore for the one term Ogden model we find from (4.4) that

$$ N^{SF}\approx N\kappa ^{2}=\frac{\mu}{n(\lambda ^{3}-1)^{2}}\left ( 2 \lambda ^{n}-2\lambda ^{-\frac{n}{2}}+n\lambda ^{3-\frac{n}{2}}(1- \lambda ^{3}) \right )\kappa ^{2}. $$
(5.4)

The Hencky model (5.5)

$$ W=\mu \left [\left (\ln (\Lambda _{1})\right )^{2}+\left (\ln ( \Lambda _{2})\right )^{2}+\left (\ln (\Lambda _{3})\right )^{2} \right ], $$
(5.5)

can be obtained from the Ogden model (5.1) on setting \(n\rightarrow 0\). Hencky [9] proposed that finite deformations of elastic solids could be modelled through the simple expedient of replacing the infinitesimal strain measure in the strain energy by a logarithmic measure of finite strain in terms of the principal stretches. In the limit \(n\rightarrow 0\), (5.4) becomes

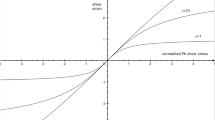
$$ N^{SF}\approx N\kappa ^{2}=\mu \frac{3\ln \lambda +\lambda ^{3}(1-\lambda ^{3})}{(\lambda ^{3}-1)^{2}} \kappa ^{2}. $$
(5.6)

The dimensionless coefficient \(N^{*}\equiv N/\mu \) of \(\kappa ^{2}\) in (5.4) depends only on the pre-stretch \(\lambda \) and the exponent \(n\). In Fig. 2 we plot \(N^{*}\) versus \(\lambda \) for various values of \(n\). It can be seen that there is a wide variety of response depending on the value of the exponent \(n\). When \(n\) is negative, a compressive normal traction needs to be applied on the slanted faces and there is an optimal lateral stretch for which this traction is minimized. As the exponent becomes more negative, the magnitude of this optimal compressive normal traction increases. When \(n=0\), corresponding to the response for the Hencky strain energy (5.5), \(N^{*}\rightarrow -1\) as \(\lambda \rightarrow \infty \). When \(0< n\le 4\), a compressive normal traction again needs to be applied and the larger the lateral stretch, the smaller the traction required. For \(4< n<6\), there is a lateral stretch for which \(N^{*}=0\) and for \(n>6\) there is a lateral compression for which \(N^{*}=0\). As previously remarked, the value \(n=6\) is exceptional with \(N^{SF}\), and not just its second order approximation \(N^{*}\), identically zero for \(\lambda =1\).

Fig. 2
figure 2

Plot of the non-dimensional normal traction \(N^{*}\equiv N/\mu \) versus \(\lambda \) for various values of \(n\). There is a wide variety of response depending on the value of the exponent \(n\)

Full size image

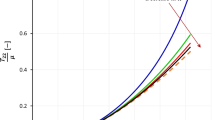
To illustrate the effectiveness of our approximate approach in using a second-order theory to minimise the normal traction of the slanted faces of sheared specimens, a sample value of the Ogden exponent is chosen. For \(n=10\), the optimal lateral stretch predicted by the determining equation (5.4) is \(\lambda =0.651\). The results of substituting this optimal value of the lateral stretch into the expression for the full normal traction (5.2) on the slanted faces are plotted to three decimal places in Fig. 3. There it is seen that the normalised normal traction \(\frac{N^{SF}}{\mu}\) is infinitesimal for the moderate amounts of shear that are typical of simple shear protocols, strongly supporting the hypothesis that our second order approach is likely to be highly effective in promoting the fidelity of model and data in simple shear.

Fig. 3
figure 3

Plot of \(\frac{N^{SF}}{\mu}\) versus \(\kappa \) for \(n=10\) using the optimal lateral stretch \(\lambda =0.651\). The predicted normalised normal traction on the slanted faces is infinitesimal even for the moderate amounts of shear considered here

Full size image

6 The Classical Hyperelastic Model

The classical approach of Rivlin [1] assumed that the strain energy is an arbitrary function of the invariants of the Cauchy-Green deformation tensors (2.4). The leading order term of the normal traction on the slanted faces \(N^{SF}\) could be obtained from (4.4) as was done previously for the Ogden invariants, but the general form can be found much more easily from consideration of the constitutive law in terms of these invariants

$$ \boldsymbol{T}=-p\boldsymbol{I}+2W_{1}\boldsymbol{B}-2W_{2} \boldsymbol{B}^{-1}, $$
(6.1)

where \(W(I_{1},I_{2})\) is the strain energy per unit undeformed volume and the subscripts attached to \(W\) denote partial differentiation with respect to the appropriate invariant. The so-called Empirical Inequalities

$$ W_{1}>0, \quad W_{2}\ge 0, $$
(6.2)

will be assumed to hold.

It therefore follows from (6.1) that the shear stress for materials being deformed as in (2.1) has the form

$$ T_{12}=2\kappa \lambda ^{2}( W_{1}+\frac{1}{\lambda}W_{2}). $$
(6.3)

The corresponding normal stresses are given by

$$\begin{aligned} T_{11} =&-p+2W_{1}(\lambda ^{-1}+\kappa ^{2}\lambda ^{2})-2W_{2} \lambda , \\ T_{22} =&-p+2W_{1}\lambda ^{2}-2W_{2}(\lambda ^{-2}+\kappa ^{2} \lambda ), \\ T_{33} =&-p+2W_{1}\lambda ^{-1}-2W_{2}\lambda . \end{aligned}$$
(6.4)

In (6.3), (6.4) the derivatives are evaluated at the values of the invariants given in (2.4). As before, it will be assumed that

$$ T_{33}=0, $$

and therefore the in-plane normal stresses take the form

$$ T_{11}=2W_{1}\kappa ^{2}\lambda ^{2}, \quad T_{22}=2W_{1} \frac{\lambda ^{3}-1}{\lambda}+2W_{2} \frac{\lambda ^{2}(1-\kappa ^{2})-1}{\lambda}, $$
(6.5)

and the normal traction \(N^{SF}\) on the slanted faces therefore has the form

$$\begin{aligned} N^{SF} =& \frac{T_{11}-2\kappa T_{12}+\kappa ^{2}T_{22}}{1+\kappa ^{2}} \\ =&-\frac{2\kappa ^{2}}{\lambda (1+\kappa ^{2})}\left (W_{1}+W_{2}(1+ \lambda ^{2}+\kappa ^{2})\right ). \end{aligned}$$
(6.6)

By virtue of (6.2), this quantity is always compressive.

Trivially then

$$ N^{SF}\approx N\kappa ^{2}=-\frac{2}{\lambda}\left (W_{1}^{(0)}+W_{2}^{(0)}(1+ \lambda ^{2})\right )\kappa ^{2}, $$
(6.7)

where the 0 superscript denotes evaluation of the strain energy at

$$ I_{1}= \lambda ^{2}+\frac{2}{\lambda},\quad I_{2}=2\lambda + \frac{1}{\lambda ^{2}}. $$

Some of the more common models for soft matter based on this classical approach will now be considered in turn.

6.1 Mooney-Rivlin Material

Although proposed initially as a model for the mechanical response of rubbers, the Mooney-Rivlin material with a strain energy of the form

$$ W=c_{1}(I_{1}-3)+c_{2}(I_{2}-3), \quad c_{1}>0,\, c_{2}\ge 0, $$
(6.8)

where \(2(c_{1}+c_{2})=\mu \), has been widely used as a model of soft matter, as can be seen from Table 1.

Table 1 Applications of the Mooney-Rivlin model
Full size table

It follows immediately from (6.7), (6.8) that

$$ N=-\frac{2}{\lambda}\left (c_{1}+c_{2}(1+\lambda ^{2})\right )=- \frac{\mu}{\lambda}-2c_{2}\lambda . $$
(6.9)

The compressive traction therefore has a maximum, and therefore a minimum absolute value, when

$$ \lambda =\sqrt{\frac{\mu}{2c_{2}}}=\sqrt{1+\frac{c_{1}}{c_{2}}}, \quad c_{2}>0. $$
(6.10)

Thus a lateral extension is required to minimise the compressive normal traction since \(2c_{2}<\mu \). Some values for the optimal lateral stretch \(\lambda \) for some applications of the Mooney-Rivlin material to the modelling of biological soft tissue are given in Table 1. The minimum compressive value of \(N\) is given by \(N_{min}=2\sqrt{2c_{2}\mu}\). For the special case of a neo-Hookean material where \(c_{2}=0\), it follows from (6.9) that \(N=-\frac{2}{\lambda}c_{1}\) so that \(N\) tends to zero for large \(\lambda \). This is also reflected in Fig. 2 for the case \(n=2\) in the Ogden model.

6.2 The Gent Material

We now consider the celebrated Gent phenomenological model [14] which we recall has the form

$$ W=-\frac{\mu J_{m}}{2}\log \left (1-\frac{I_{1}-3}{J_{m}}\right ), \quad I_{1}< J_{m}+3, $$
(6.11)

where \(\mu \) is the infinitesimal shear modulus and \(J_{m}\) is a dimensionless parameter. The constraint in (6.11), imposed so that the log function is well defined, implies a maximum allowable strain. This model reflects the severe strain-stiffening at large strains observed experimentally for non-crystallizing rubber and a variety of biological soft tissues and involves just two material parameters namely the shear modulus for infinitesimal deformations and a parameter that measures a maximum allowable value of strain. See, e.g., Horgan [15] and Puglisi and Saccomandi [16] for background and applications of the Gent model (6.11) and its generalizations. It is well known that in the limit as \(J_{m}\rightarrow \infty \), the Gent model reduces to the neo-Hookean strain-energy. For rubber, typical values for the dimensionless parameter for simple extension range from 30 to 100 whereas for biological tissue, much smaller values are appropriate. For example, for human arterial wall tissue, values on the order of \(0.4-2.3\) have been suggested (see, e.g., Horgan and Saccomandi [17] based on experimental work of Lawton and King [18]).

It follows from (6.7), (6.11) that

$$ N=\frac{\mu J_{m}}{\lambda ^{3}-\lambda (J_{m}+3)+2}. $$
(6.12)

The compressive normal traction has a minimum absolute value at

$$ \lambda =\sqrt{1+\frac{J_{m}}{3}}. $$
(6.13)

This equation for the optimising lateral extension was previously obtained by Horgan and Saccomandi [17] as the critical stretch for the inversion point for models of pressurised arteries (see [17] for a full discussion).

6.3 An Arterial Model

A commonly used model for soft biological tissues is the exponential model due to Demiray [19] who proposed a strain energy of the form

$$ W=\frac{\mu}{2b}\left (e^{b(I_{1}-3)}-1\right ), \quad b>0. $$
(6.14)

As \(b \rightarrow 0\) in (6.14) one recovers the neo-Hookean model. A variety of soft tissues have been modelled by (6.14) with various values of the positive dimensionless parameter \(b\). See, for example, Horgan [15], Horgan and Saccomandi [17] and Horgan and Smayda [20] and references cited therein for discussions. Substitution into (6.7) yields

$$ N=-\frac{\mu}{\lambda}e^{b( \lambda ^{2}+\frac{2}{\lambda}-3)}. $$
(6.15)

The compressive normal traction thus has a minimum absolute value for positive \(\lambda ,\,b\) when

$$ 2b=\frac{\lambda}{\lambda ^{3}-1}. $$
(6.16)

Since \(b>0\), the relation (6.16) can hold only for \(\lambda >1\), i.e., lateral extension. It also follows that for moderate and large values of the parameter \(b\) the critical stretch is approximately \(\lambda =1\), the classical assumption of Rivlin [1] for pure simple shear.

Delfino et al. [21] proposed that \(b=8.35\), a value obtained from pressure-radius measurements of human carotid arteries. From Fig. 4 it is seen that the normalised compressive traction \(N^{*}\equiv N/\mu \) is minimized at a value of lateral stretch close to one (i.e., close to pure simple shear) and that any departure from this deformation leads to large compressive tractions on the slanted faces.

Fig. 4
figure 4

A plot of \(N^{*}\equiv N/\mu \) versus \(\lambda \) for the Demiray model (6.14) for \(b=8.35\), the value obtained from pressure-radius measurements of human carotid arteries by Delfino et al. [21]

Full size image

7 Concluding Remarks

One of the major difficulties in a physical interpretation of the classical simple shear deformation for isotropic incompressible hyperelastic materials is the fact that the conventional mathematical model of simple shear using a plane stress assumption to determine the hydrostatic pressure implies that a normal traction must be applied to the slanted faces of the deformed specimen. However, such a traction is not applied in practice. To resolve this dilemma, the basic kinematics here have been modified to consider a simple shear deformation superposed on a uniform lateral extension or compression of the specimen. Recognising that the normal traction on the slanted faces is an even function of the amount of shear, a Maclaurin series in the amount of shear truncated after the quadratic term should be an excellent approximation to this predicted normal traction for soft materials for which only moderate amounts of shear are possible. The coefficient of the quadratic term is then treated as a stabilising factor that can be used to minimise the normal traction on the slanted faces of the specimen being sheared. It is shown that a judicious choice of the lateral stretch can minimise the predicted normal traction on the slanted faces for a variety of classical strain-energy densities for isotropic hyperelastic materials that have been proposed to model the mechanical response of a variety of soft matter. It is hypothesised that such an optimal choice will improve the fidelity of the model with experimental data. The proposed approach yields important insights into how to design and interpret experiments for determining the mechanical properties of very soft materials.