Sensitivity of the Second Order Homogenized Elasticity Tensor to Topological Microstructural Changes

Abstract

The multiscale elasticity model of solids with singular geometrical perturbations of microstructure is considered for the purposes, e.g., of optimum design. The homogenized linear elasticity tensors of first and second orders are considered in the framework of periodic Sobolev spaces. In particular, the sensitivity analysis of second order homogenized elasticity tensor to topological microstructural changes is performed. The derivation of the proposed sensitivities relies on the concept of topological derivative applied within a multiscale constitutive model. The microstructure is topologically perturbed by the nucleation of a small circular inclusion that allows for deriving the sensitivity in its closed form with the help of appropriate adjoint states. The resulting topological derivative is given by a sixth order tensor field over the microstructural domain, which measures how the second order homogenized elasticity tensor changes when a small circular inclusion is introduced at the microscopic level. As a result, the topological derivatives of functionals for multiscale models can be obtained and used in numerical methods of shape and topology optimization of microstructures, including synthesis and optimal design of metamaterials by taking into account the second order mechanical effects. The analysis is performed in two spatial dimensions however the results are valid in three spatial dimensions as well.

1 Introduction

The study of synthesis and design of materials involving multiscale effects gave rise to a wide interest in Engineering, Mechanics, and Mathematics during the two past decades, and it broadened the application scope, among others structural mechanics, biomechanics, aerospace engineering, wave propagation in solids, and acoustics. The research works on this subject have increased with the emergence of recent experimental and manufacturing techniques, computational methods and tools, and theoretical developments. The various length scales of this type of materials allow the elaboration of multiscale constitutive theories, the so-called theory of homogenization, in order to explain, more accurately than standard phenomenological approaches, their macroscopic response under loading for example. The first developments has been made for periodic structures [18, 30, 34, 36, 45, 46, 54, 61], and since then the framework has not stopped expanding to fit more general and complex models. An introduction to homogenization and related mathematical framework can be found in [23, 62].

In this context, the design of the microstructure is a major issue, as well for a mixture of different materials, as for the arrangement of a single one. For example, in [6] and [42] microstructural topologies that produce negative macroscopic Poisson’s ratio are obtained with a relaxation-based technique. To find out new microstructures producing exotic behaviours at the macroscopic scale, we can cite the use of classical shape optimization method (see, e.g., [35, 60]), based on shape gradient of the desired criterion, with respect to a smooth variation of the boundary. More recently, the combination of shape gradient concept and level-set method (investigated in [53]), has produced several results in structural optimization, the reader can see for instance [2, 5, 20, 52, 55, 63]. This approach depends deeply on the initial guess for the microstructure, because it does not allow for topology changes. Relaxed formulation based on homogenization theory has been developed in [1, 3, 4, 17], and provide topology variations in certain cases.

Another strategy is based on the concept of topological derivative, which was rigorously introduced in [57]. The idea is to compute a topological asymptotic expansion of the investigated criterion with respect to an infinitesimal topological perturbation of the domain. The reader may find the use of this concept in topology optimization in [5, 9, 21]. In the framework of homogenized model of elastic materials, the topological derivative of the first order homogenized elasticity tensor has been calculated in [31, 32] in the case of void and soft inclusion, respectively, and in [12] in the case of a soft material inclusion, completed with a numerical investigation. More recently the topological derivative of the second-order macroscopic model associated with scalar waves in periodic media has been evaluated in [19], making use of integral equations together with the periodic Green’s function.

In the present paper, the elasticity system in periodic media is considered. The microstructure of the underlying material is topologically perturbed by the nucleation of a small circular inclusion endowed with different material properties from the background. In this case, the asymptotic behaviour of the perturbed displacement solutions is computed, allowing the evaluation of the sensitivity of the second-order homogenized elasticity tensor with respect to topological microstructural changes. The resulting topological derivative is given by a symmetric sixth-order tensor field over the RVE (Representative Volume Element) domain that measures how the second-order homogenized elasticity tensor changes when a small circular inclusion is introduced at the microscale level. This information is crucial for the synthesis and optimal design of microsctructures having a macroscopic behaviour depending on the second order derivative of the average displacement. We start by describing in Sect. 2 a homogenization scheme (see [56]), which leads to the formal definition of higher-order homogenized tensors. For this we need the solutions of auxiliary problems posed on the RVE, in the framework of periodic homogenization by asymptotic expansions. Then we undertake in Sect. 3 a perturbation of the RVE by including a new material characterised by a finite contrast, and contained in a small ball. After a substantial introduction to the topological derivative concept through Sect. 3.1, we recall in Sect. 3.2 the formula of the topological asymptotic of the classical first-order homogenized tensor derived in [12, 31, 32]. We also calculate the topological derivative associated with a simple higher-order homogenized tensor for introducing the method. In Sect. 3.3 we finally derive in details the topological derivative of the second-order homogenized tensor. The paper ends with some concluding remarks in Sect. 4. The proofs of certain lemmas are send back to Appendix B.

2 Homogenization

This section describes the multi-scale method to calculate the homogenized coefficients of an elasticity problem written for a periodic media, in order to calculate their topological sensitivities with respect to a configurational perturbation in the periodic cell. Let be two domains. We denote by $\mathbf{D}^{\tau }$ the periodic medium consisting of the domain $T\mathbf{D}$, for $T>0$, paved with the periodic cell $t\Omega$, for $t > 0$, where we have set $\tau = t/T$. We define $y=x/t$ and $Y=x/T$ for all $x\in \mathbf{D}^{\tau }$ (see Fig. 1). Let the vector field be the displacement, solution of the elasticity system in $\mathbf{D}^{\tau }$. We assume that $u$ can be expanded as

$$ u^{\tau }(x) = T( u^{0}(Y,y) + \tau u^{1}(Y,y) + \cdots + \tau ^{n}u^{n}(Y,y) + \cdots ) , $$

(2.1)

where the functions $u^{i}(Y, \cdot )$ are $\Omega$-periodic for $i\geq 0$. Using this expansion in the equilibrium and constitutive equations, we obtain a family of auxiliary problems, and we can write $u^{\tau }$ thanks to a sequence of tensor fields $(H^{\nabla i}(y))_{i\geqslant 0}$ called corrector fields, each one of order $i+2$, and thanks to a sequence of macroscopic vector fields $(U^{i}(Y))_{i\geqslant 0}$ assumed to be constant on a cell. This gives

$$\begin{aligned} T^{-1} u^{\tau }(x) &= U^{0}(Y) \\ &+ \tau \big( U^{1}(Y) + H^{\nabla 1}(y)\nabla ^{s}_{Y}U^{0}(Y) \big) \\ &+ \tau ^{2} \big( U^{2}(Y) + H^{\nabla 1}(y)\nabla ^{s}_{Y}U^{1}(Y) + H^{\nabla 2}(y)\nabla _{Y}\nabla ^{s}_{Y}U^{0}(Y) \big) \\ &+ \tau ^{3} \big( U^{3}(Y) + H^{\nabla 1}(y)\nabla ^{s}_{Y}U^{2}(Y) + H^{\nabla 2}(y)\nabla _{Y}\nabla ^{s}_{Y}U^{1}(Y) + H^{\nabla 3}(y) \nabla _{Y}^{2}\nabla ^{s}_{Y}U^{0}(Y) \big) \\ &+ \cdots , \end{aligned}$$

(2.2)

where the $(i+2)$-order tensor $H^{\nabla i}$ operates for all $j\geq 0$ on the $(i+1)$-order tensor $\nabla _{Y}^{i-1}\nabla ^{s}_{Y}U^{j}$, denoting the resulting vector by $H^{\nabla i}\nabla _{Y}^{i-1}\nabla ^{s}_{Y}U^{j}$. Writing formally $U(Y) = \sum _{i=0}^{\infty }\tau ^{i} U^{i}(Y)$, the above expansion suggests to seek approximations of $u^{\tau }$ in the form of truncations with respect to different order of $\tau$ of the following form

$$ T^{-1}u^{\tau }(x) = U(Y) + \tau H^{\nabla 1}(y)\nabla ^{s}_{Y}U(Y) + \cdots + \tau ^{k} H^{\nabla k}(y)\nabla ^{k-1}\nabla ^{s}_{Y}U(Y) \quad \hbox{for } k\geq 0. $$

(2.3)

Therefore, we seek the total field $u^{\tau }$ as the sum of a macroscopic displacement field $U$ and its $i$-th derivative weighted by $\tau ^{i}$ and a corrector field, for $1\leq i \leq k$. Calculating the homogenized elastic energy induced by this truncations, we can identify the homogenized tensors. We recall how to obtain formally the auxiliary equations and the corrector fields in the framework of the multi-scale method (see, e.g., [23, 28]).

Fig. 1

The domain $\mathbf{D}$ is paved with the unit cell domain $\Omega$, weighted by the parameter $\tau$

2.1 Auxiliary Equations

Let us write the auxiliary problems in their strong formulations. For a load $f\in L^{2}(\mathbf{D}^{\tau })$, and a Dirichlet data $u_{D}\in H^{1/2}(\partial \mathbf{D}^{\tau })$, the displacement vector field $u^{\tau }$ from (2.1) is given by the solution of the following boundary value problem:

$$ \left \{ \textstyle\begin{array}{l} \textstyle\begin{array}{rll@{\quad}c@{\quad}l} -\hbox{div}_{x} ( \sigma _{x}(u^{\tau }) ) & = & f & \text{in} & \mathbf{D}^{\tau } , \\ u^{\tau } & = & u^{D} & \text{on} &\partial \mathbf{D}^{\tau } , \end{array}\displaystyle \end{array}\displaystyle \right . $$

(2.4)

where the second order tensor field $\sigma _{x}(u^{\tau })$, called the total stress tensor, is specified throughout the constitutive law (2.5), and it depends linearly on the total strain tensor $\varepsilon _{x}(u^{\tau })$. The right lower index of a differential operator denotes the differentiation variable. We first determine the convention used for classical tensor calculus. Let $u$ and $v$ be two vectors, $A$ and $B$ be two second order tensors, and $\mathbb{T}$ be a fourth order tensor, we write $\mathbb{T}A = \mathbb{T}_{ijkl}A_{kl} \, \mathrm{e}_{i} \otimes \mathrm{e}_{j}$, $AB=A_{ik}B_{kj} \, \mathrm{e}_{i} \otimes \mathrm{e}_{j}$, $A\cdot B = A_{ij}B_{ij}$, $Au = A_{ij}u_{j} \, \mathrm{e}_{i}$, and $u\cdot v = u_{i}v_{i}$, where $(\mathrm{e}_{1} , \mathrm{e}_{2})$ is an orthonormal basis of , using the Einstein summation convention. Then we define

$$\begin{aligned} \sigma _{x}(u^{\tau }) &:= \mathbb{C}^{t} \varepsilon _{x}(u^{\tau }), \end{aligned}$$

(2.5)

$$\begin{aligned} \varepsilon _{x}(u^{\tau }) &:=\nabla _{x}^{s}u^{\tau } :=\frac{1}{2} \left (\nabla _{x}(u^{\tau }) + \nabla _{x}(u^{\tau })^{\top } \right ), \end{aligned}$$

(2.6)

$$\begin{aligned} \mathbb{C}^{t}(x) &:= \mathbb{C}(x/t), \end{aligned}$$

(2.7)

where the elasticity tensor $\mathbb{C}=(\mathbb{C}_{ijkl})_{1\leq i,j,k,l \leq 2}$ is a fourth order tensor such that for all indices $i,j,k,l=1,2$ we have: $\mathbb{C}_{ijkl}\in L^{\infty }(\Omega )$, is $\Omega$-periodic, $\mathbb{C}_{ijkl}=\mathbb{C}_{jikl}=\mathbb{C}_{klij}$, and there exists two real numbers $0< a< b$ such that $\lvert \mathbb{C}A \rvert \leq b\lvert A \rvert$ for any second order tensor $A$, and $\mathbb{C}A\cdot A \geq a \lvert A \rvert ^{2}$ when $A$ is symmetric. Assuming that $\partial _{x}=T^{-1}(\partial _{Y} + \tau ^{-1}\partial _{y})$, and in view of ansatz (2.1), we can formally write $\varepsilon _{x}(u^{\tau }) = \tau ^{-1}\nabla ^{s}_{y}u^{0} + \sum _{i=0}^{ \infty }\tau ^{i} \varepsilon ^{i}$ where $\varepsilon ^{i} := \nabla ^{s}_{Y} u^{i} + \nabla ^{s}_{y}u^{i+1}$. Let us define in the same way $\sigma ^{i}:=\mathbb{C} \varepsilon ^{i}$. Introducing expansion (2.1) of $u^{\tau }$ in the equilibrium equation (2.4), we obtain a sequence of equations relating to the order of $\tau$:

$$ \left \{ \textstyle\begin{array}{l} \textstyle\begin{array}{rll@{\quad}c@{\quad}r} \nabla ^{s}_{y}u^{0} & = & 0, & & \text{(a)} \\ \hbox{div}_{y} (\sigma ^{0}) & = & 0, & & \text{(b)} \\ \hbox{div}_{y} (\sigma ^{1}) + \hbox{div}_{Y} (\sigma ^{0})+ Tf & = &0, & & \text{(c)} \\ \hbox{div}_{y} (\sigma ^{i+1}) + \hbox{div}_{Y} (\sigma ^{i}) & = & 0 & \hbox{for }i\geq 1 . & \text{(d)} \end{array}\displaystyle \end{array}\displaystyle \right . $$

(2.8)

Each of these equations is written on a unit cell $\Omega$, with the $\Omega$-periodicity of $u^{i}$ as boundary condition. The corresponding boundary value problems, also named auxiliary problems, can be solved by induction. The first equation (2.8a) determines $u^{0}(Y,y) = U^{0}(Y)$.

Let us rewrite the second equation (2.8b) setting $E^{0}:=\nabla ^{s}_{Y}U^{0}$:

$$\begin{aligned} \hbox{div}_{y} \left (\mathbb{C}\nabla ^{s}_{y}u^{1} + \mathbb{C}( \mathrm{e}_{i}\otimes _{s}\mathrm{e}_{j})E^{0}_{ij}\right ) = 0 , \end{aligned}$$

(2.9)

with

$$ a \otimes _{s} b := \frac{a \otimes b + b \otimes a}{2}, $$

(2.10)

for all vectors . By linearity we can write

$$ u^{1}(Y,y) = U^{1}(Y) + \tilde{u}_{ij}(y)E^{0}_{ij}(Y) , $$

(2.11)

where the vector field $\tilde{u}_{ij}$ is the solution of the $\Omega$-periodic boundary value problem on the unit cell $\Omega$ for the first auxiliary equation:

$$ \hbox{div}_{y} \left (\mathbb{C}\nabla ^{s}_{y}\tilde{u}_{ij} + \mathbb{C}(\mathrm{e}_{i}\otimes _{s}\mathrm{e}_{j}) \right ) = 0 . $$

(2.12)

Before solving the third auxiliary problem, let us evaluate the average on the unit cell of equation (2.8c). We assume that $f=T^{-1}F(Y)$. This gives us that:

$$ \hbox{div}_{Y} ( \langle \sigma ^{0} \rangle ) + F = 0 , $$

(2.13)

where for all tensor fields $A$

$$ \langle A \rangle := \frac{1}{V}\int _{\Omega }A(y) dy , $$

(2.14)

and where $V=\lvert \Omega \rvert$ denotes the scaled area of the RVE, $\lvert \Omega \rvert$ being the Lebesgue measure of $\Omega$. We can show that $\langle \sigma ^{0} \rangle = \mathbb{C}^{h}E^{0}$, where the homogenized tensor $\mathbb{C}^{h}$ is constant. Now let us rewrite the equation (2.8c) setting $E^{1}:=\nabla ^{s}_{Y}U^{1}$ and $K^{0}:=\nabla _{Y} E^{0}$, taking into account (2.13), and defining the vector field $u_{ij}(y) := (\mathrm{e}_{i}\otimes _{s} \mathrm{e}_{j})y + \tilde{u}_{ij} (y)$. We find

$$ \hbox{div}_{y} \left (\mathbb{C}\nabla ^{s}_{y}u^{2}\right ) + \hbox{div}_{y} (\mathbb{C}E^{1}) + [ \hbox{div}_{y} (\mathbb{C}(\tilde{u}_{ij} \otimes _{s}\mathrm{e}_{k} ) ) + ( \mathbb{C}\nabla ^{s}_{y}u_{ij} - \mathbb{C}^{h}(\mathrm{e}_{i}\otimes _{s} \mathrm{e}_{j}) )\mathrm{e}_{k} ] K^{0}_{ijk} = 0 . $$

(2.15)

Once again by linearity we can write the solution $u^{2}$ in the following way

$$ u^{2}(Y,y) = U^{2}(Y) + \tilde{u}_{ij}(y)E^{1}_{ij}(Y) + \tilde{\tilde{u}}_{ijk}(y)K^{0}_{ijk}(Y) , $$

(2.16)

where the vector field $\tilde{\tilde{u}}_{ijk}$ is the solution of the $\Omega$-periodic boundary value problem on the unit cell $\Omega$ for the second auxiliary equation:

$$ \hbox{div}_{y} \left (\mathbb{C}\nabla ^{s}_{y}\tilde{\tilde{u}}_{ijk} \right ) +\hbox{div}_{y} \left (\mathbb{C}(\tilde{u}_{ij}\otimes _{s} \mathrm{e}_{k} )\right ) + ( \mathbb{C}\nabla ^{s}_{y}u_{ij} - \mathbb{C}^{h}(\mathrm{e}_{i}\otimes _{s} \mathrm{e}_{j}) ) \mathrm{e}_{k} = 0 . $$

(2.17)

2.2 First-Order Truncation

We recall that $Y = x/T$, $y = x/t$ and $\tau = t/T$, with . Motivated by expansion (2.3), we introduce the macroscopic displacement field , and the macroscopic deformation is defined as $E(Y) = \nabla ^{s} U(Y)$. We write $\tilde{u}(Y,y) = \tilde{u}_{ij}(y) E_{ij}(Y)$, where $E_{ij}(Y) = E(Y)\cdot ( \mathrm{e}_{i} \otimes _{s} \mathrm{e}_{j})$. We also introduce the expansion

$$ u^{\tau }(Y,y) = U(Y) + \tau \, \tilde{u}(Y,y). $$

(2.18)

The displacement fields $\tilde{u}_{ij}$ are solutions of the following canonical set of variational problems

$$ \tilde{u}_{ij} \in \mathcal{V}\; : \; \int _{\Omega } \sigma _{y}( \tilde{u}_{ij}) \cdot \varepsilon _{y}(\eta ) + \int _{\Omega } \mathbb{C}(\mathrm{e}_{i} \otimes _{s} \mathrm{e}_{j}) \cdot \varepsilon _{y}(\eta ) = 0 , \quad \forall \eta \in \mathcal{W}, $$

(2.19)

where $\sigma _{y}(\tilde{u}_{ij}) = \mathbb{C} \varepsilon _{y} (\tilde{u}_{ij})$ and the spaces $\mathcal{W}$ and $\mathcal{V}$ are defined as follows

(2.20)

(2.21)

where is the completion of the space of functions in which are $\Omega$-periodic, in the norm of . From these elements we have

$$ \varepsilon _{x} (u^{\tau }) = \frac{1}{T}\left [ \varepsilon _{Y} (u^{\tau }) + \frac{1}{\tau } \varepsilon _{y} (u^{\tau }) \right ] = \frac{1}{T}\left ( \varepsilon _{y} (u_{ij}) E_{ij} + \tau (\tilde{u}_{ij} \otimes _{s} \nabla _{Y} E_{ij}) \right ), $$

(2.22)

where

$$ u_{ij} := (\mathrm{e}_{i} \otimes _{s} \mathrm{e}_{j})y + \tilde{u}_{ij} , $$

(2.23)

with $\tilde{u}_{ij}$ solutions to the set of canonical variational problems (2.19). Then we calculate the average of the elastic energy $\frac{1}{2}\sigma _{x}(u^{\tau })\cdot \varepsilon _{x}(u^{\tau })$ on the RVE domain $\Omega$, denoted by $W^{h}$, in order to identify the homogenized elasticity tensors. From now on we set $T=1$ for convenience. We find

$$\begin{aligned} \frac{1}{2V} \int _{\Omega } \sigma _{x}(u^{\tau })\cdot \varepsilon _{x} (u^{\tau }) = \frac{1}{2V} \int _{\Omega } & \Big\lbrace E_{kl}\sigma _{y}(u_{kl}) \cdot \varepsilon _{y} (u_{ij})E_{ij} \\ &+ \tau \left ( E_{kl}\sigma _{y}(u_{kl})\cdot (\tilde{u}_{ij} \otimes _{s}\nabla _{Y} E_{ij})\right. \\ & + \left. E_{ij}\sigma _{y}(u_{ij})\cdot ( \tilde{u}_{kl}\otimes _{s}\nabla _{Y} E_{kl}) \right ) \\ &+ \tau ^{2} (\tilde{u}_{ij}\otimes _{s}\nabla _{Y} E_{ij}) \cdot \mathbb{C} (\tilde{u}_{kl}\otimes _{s}\nabla _{Y} E_{kl}) \Big\rbrace . \end{aligned}$$

(2.24)

We assume that terms of odd order $\tau$ in the expression of the homogenized elastic energy are equal to zero. This property may be proved thanks to the parity of the fields in the case of a centrosymmetric cell (see [56]). Thus, from now on we consider that the unit cell $\Omega$ is centrosymmetric. Denoting $K_{ijk}(Y) = K(Y) \cdot (\mathrm{e}_{i} \otimes \mathrm{e}_{j} \otimes \mathrm{e}_{k})$, with $K(Y) = \nabla E(Y)$, we obtain

$$ W^{h} = W^{h}(E,K) = \frac{1}{2} E_{ij}\mathbb{C}_{ijkl}^{h}E_{kl} + \tau ^{2}\frac{1}{2} K_{ijk}\mathbb{D}^{\sharp }_{ijkpqr}K_{pqr} + o( \tau ^{2}), $$

(2.25)

which defines the two following homogenized elasticity tensors: the fourth order tensor $\mathbb{C}^{h}=(\mathbb{C}_{ijkl}^{h})_{1\leq i,j,k,l \leq 2}$, and the sixth-order tensor $\mathbb{D}^{\sharp }=(\mathbb{D}^{\sharp }_{ijkpqr})_{1\leq i,j,k,p,q,r \leq 2}$ given by

$$ \mathbb{C}^{h}_{ijkl} := \frac{1}{V}\int _{\Omega } \sigma _{y}(u_{ij}) \cdot \varepsilon _{y} (u_{kl}) , $$

(2.26)

and

$$ \mathbb{D}_{ijkpqr}^{\sharp } := \frac{1}{V} \int _{\Omega } \mathbb{C}( \tilde{u}_{ij}\otimes _{s} \mathrm{e}_{k}) \cdot (\tilde{u}_{pq} \otimes _{s} \mathrm{e}_{r}) . $$

(2.27)

2.3 Second-Order Truncation

We introduce the expansion

$$ u^{\tau }(Y,y) = U(Y) + \tau \, \tilde{u}(Y,y) + \tau ^{2} \, \tilde{\tilde{u}}(Y,y), $$

(2.28)

where $\tilde{\tilde{u}}(Y,y) = \tilde{\tilde{u}}_{ijk}(y) K_{ijk}(Y)$, with $K_{ijk}(Y) = K(Y) \cdot (\mathrm{e}_{i} \otimes \mathrm{e}_{j} \otimes \mathrm{e}_{k})$ and $K(Y) = \nabla E(Y)$. The displacement fields $\tilde{\tilde{u}}_{ijk}$ are solutions of the following canonical set of variational problems

$$\begin{array}{c}{\tilde{\tilde{u}}}_{ijk}\in \mathcal{V}:{\int }_{\mathrm{\Omega }}{\sigma }_y({\tilde{\tilde{u}}}_{ijk})\cdot {\epsilon }_y(\eta )+{\int }_{\mathrm{\Omega }}\mathbb{C}({\tilde{u}}_{ij}{\otimes }_s{\mathrm{e}}_k)\cdot {\epsilon }_y(\eta )=\hfill \\ \hfill {\int }_{\mathrm{\Omega }}({\sigma }_y(u_{ij})-{\mathbb{C}}^h({\mathrm{e}}_i{\otimes }_s{\mathrm{e}}_j)){\mathrm{e}}_k\cdot \eta ,\mathrm{\forall }\eta \in \mathcal{W}.\end{array}$$

(2.29)

Let us calculate the strain tensor of $u^{\tau }$:

$$ \varepsilon _{x}(u^{\tau }) = \varepsilon _{y}(u_{ij})E_{ij} + \tau ( \tilde{u}_{ij}\otimes _{s}\mathrm{e}_{k} + \varepsilon _{y}( \tilde{\tilde{u}}_{ijk}) )K_{ijk} + \tau ^{2}(\tilde{\tilde{u}}_{ijk} \otimes _{s}\mathrm{e}_{l})\partial _{y_{l}}K_{ijk} . $$

(2.30)

Same as before, we need to calculate $\frac{1}{2}\sigma _{x}(u^{\tau })\cdot \varepsilon _{x}(u^{\tau })$ in order to evaluate the average of the elastic energy on the cell and then identify the macroscopic energy law. Since the unit cell is assumed to be centrosymmetric, it turns out that the odd order terms in $\tau$ are null, and performing a formal macroscopic integration by parts in order to turn the coupled terms $E_{ij}\partial _{y_{k}}K_{pqr}$ into $K_{ijk}K_{pqr}$ (see [56]), we calculate

$$ W^{h} = \frac{1}{2} E_{ij}\mathbb{C}_{ijkl}^{h}E_{kl} + \tau ^{2} \frac{1}{2} K_{ijk}\mathbb{D}_{ijkpqr}K_{pqr} + o(\tau ^{2}) , $$

(2.31)

where $\mathbb{D}=(\mathbb{D}_{ijkpqr})_{1\leq i,j,k,p,q,r \leq 2}$ is the homogenized sixth-order tensor given by

$$\begin{array}{c}{\mathbb{D}}_{ijkpqr}:=\frac{1}{V}{\int }_{\mathrm{\Omega }}\mathbb{C}({\tilde{u}}_{ij}{\otimes }_s{\mathrm{e}}_k+{\epsilon }_y({\tilde{\tilde{u}}}_{ijk}))\cdot ({\tilde{u}}_{pq}{\otimes }_s{\mathrm{e}}_r+{\epsilon }_y({\tilde{\tilde{u}}}_{pqr}))\hfill \\ \hfill -\frac{1}{V}{\int }_{\mathrm{\Omega }}({\sigma }_y(u_{ij})\cdot ({\tilde{\tilde{u}}}_{pqr}{\otimes }_s{\mathrm{e}}_k)+{\sigma }_y(u_{pq})\cdot ({\tilde{\tilde{u}}}_{ijk}{\otimes }_s{\mathrm{e}}_r)).\end{array}$$

(2.32)

By setting $\eta = \tilde{\tilde{u}}_{pqr}$ as test function in (2.29), we obtain the following equality

$$ \int _{\Omega } \sigma _{y}(\tilde{\tilde{u}}_{ijk}) \cdot \varepsilon _{y} (\tilde{\tilde{u}}_{pqr}) + \int _{\Omega } \mathbb{C}(\tilde{u}_{ij} \otimes _{s} \mathrm{e}_{k}) \cdot \varepsilon _{y} (\tilde{\tilde{u}}_{pqr}) = \int _{\Omega } (\sigma _{y}(u_{ij}) - \mathbb{C}^{h}(\mathrm{e}_{i} \otimes _{s} \mathrm{e}_{j})) \mathrm{e}_{k} \cdot \tilde{\tilde{u}}_{pqr}, $$

(2.33)

which allows to write (2.32) as

$$\begin{array}{c}{\mathbb{D}}_{ijkpqr}=\frac{1}{V}{\int }_{\mathrm{\Omega }}\mathbb{C}({\tilde{u}}_{ij}{\otimes }_s{\mathrm{e}}_k+{\epsilon }_y({\tilde{\tilde{u}}}_{ijk}))\cdot ({\tilde{u}}_{pq}{\otimes }_s{\mathrm{e}}_r)\hfill \\ \hfill -\frac{1}{V}{\int }_{\mathrm{\Omega }}({\mathbb{C}}^h({\mathrm{e}}_i{\otimes }_s{\mathrm{e}}_j)\cdot ({\tilde{\tilde{u}}}_{pqr}{\otimes }_s{\mathrm{e}}_k)+{\sigma }_y(u_{pq})\cdot ({\tilde{\tilde{u}}}_{ijk}{\otimes }_s{\mathrm{e}}_r)),\end{array}$$

(2.34)

since $\sigma _{y}(u_{ij}) \mathrm{e}_{k} \cdot \tilde{\tilde{u}}_{pqr} = \sigma _{y}(u_{ij}) \cdot (\tilde{\tilde{u}}_{pqr} \otimes _{s} \mathrm{e}_{k})$. So far, we have defined the homogenized tensors $\mathbb{C}^{h}$, $\mathbb{D}^{\sharp }$ and $\mathbb{D}$. In the following section, we slightly change the RVE, write the new tensors deriving from the perturbed RVE, and explore their behaviour regarding the size of such a perturbation.

3 Topological Sensitivity

The topological optimization framework is as follows. The original domain $\Omega$ is composed of two phases of isotropic materials, the first one represented by the domain $\Omega _{1}$, and the second represented by $\Omega _{\gamma }$, such that $\Omega = \Omega _{1}\cup \Omega _{\gamma }\cup \Gamma _{\gamma }$, where $\Gamma _{\gamma }= \partial \Omega _{\gamma }\cap \Omega$ with $\partial \Omega$ and $\partial \Omega _{\gamma }$ being Lipschitz continuous. These two phases result in a piecewise constant elasticity tensor denoted by ℂ, which is defined as follows. Let $\mathbb{C}_{0} = 2\mu \mathbb{I} + \lambda \mathrm{I}\otimes \mathrm{I}$, where the so-called Lamé coefficients are chosen such that $\mathbb{C}_{0}$ satisfies the conditions from Sect. 2.1, and with $\mathrm{I}$ and $\mathbb{I}$ used to denote the second and the fourth order identity tensors, respectively. Thus $\mathbb{C} (y) = \mathbb{C}_{0}$ if $y\in \Omega _{1}$, and $\mathbb{C} (y) = \gamma _{0}\mathbb{C}_{0}$ if $y\in \Omega _{\gamma }$, with $0 < \gamma _{0} < \infty$.

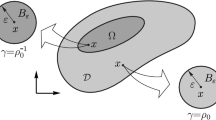
We consider the nucleation of a finite number of small disjoint circular inclusions within the unit cell $\Omega$. The inclusions are spatially distributed far from each other and in such a way that the centrosymmetry of the RVE is preserved, which allows for focusing the attention over a single inclusion. From there, $\Omega$ is subjected to a perturbation confined in a small circular open set $B_{\rho }(\hat{y})$ of radius $\rho$ and center at an arbitrary point $\hat{y}$ of $\Omega$, such that $\overline{B_{\rho }(\hat{y})} \subset \Omega$, and which does not touch the interface $\Gamma _{\gamma }$ (see Fig. 2). Then, the region occupied by $B_{\rho }(\hat{y})$ is filled by an inclusion with different material property from the background. The material properties of the perturbed domain are characterized by the piecewise constant function $\gamma _{\rho }$ of the form

$$ \gamma _{\rho }(x):= \left \{ \textstyle\begin{array}{c@{\quad }l} 1 & \text{if} \, x \in \Omega \setminus \overline{B_{\rho }} \;, \\ \gamma (x) & \text{if} \, x \in B_{\rho }\;, \end{array}\displaystyle \right . \qquad \text{where} \qquad \gamma (x):= \left \{ \textstyle\begin{array}{l@{\quad }l} \gamma _{0} & \text{if} \, x \in \Omega _{1} \;, \\ \gamma _{0}^{-1} & \text{if} \, x \in \Omega _{\gamma }\;. \end{array}\displaystyle \right . $$

(3.1)

Namely the elasticity tensor is given by $\gamma _{\rho }\mathbb{C}$ in the perturbed domain. Henceforth we leave the lower indices of differential operators behind, because we only deal with $y$-variable depending fields. Therefore, the topologically perturbed counterparts of problems (2.19) and (2.29) are respectively given by

$$ \tilde{u}^{\rho }_{ij} \in \mathcal{V}\; : \; \int _{\Omega } \gamma _{ \rho } \sigma (\tilde{u}^{\rho }_{ij}) \cdot \varepsilon (\eta ) + \int _{\Omega } \gamma _{\rho } \mathbb{C}(\mathrm{e}_{i} \otimes _{s} \mathrm{e}_{j}) \cdot \varepsilon (\eta ) = 0 , \quad \forall \eta \in \mathcal{W}, $$

(3.2)

and

$$\begin{array}{c}{\tilde{\tilde{u}}}_{ijk}^{\rho }\in \mathcal{V}:{\int }_{\mathrm{\Omega }}{\gamma }_{\rho }\sigma ({\tilde{\tilde{u}}}_{ijk}^{\rho })\cdot \epsilon (\eta )+{\int }_{\mathrm{\Omega }}{\gamma }_{\rho }\mathbb{C}({\tilde{u}}_{ij}^{\rho }{\otimes }_s{\mathrm{e}}_k)\cdot \epsilon (\eta )=\hfill \\ \hfill {\int }_{\mathrm{\Omega }}({\gamma }_{\rho }\sigma (u_{ij}^{\rho })-{\mathbb{C}}_{\rho }^h({\mathrm{e}}_i{\otimes }_s{\mathrm{e}}_j)){\mathrm{e}}_k\cdot \eta \mathrm{\forall }\eta \in \mathcal{W}.\end{array}$$

(3.3)

Due to Korn’s inequality, the existence and uniqueness of solutions of problems (2.19), (2.29), (3.2) and (3.3) are ensured on $\mathcal{W}$ endowed with the norm $\Vert \cdot \Vert _{\mathcal{W}}$, which is defined as follows

$$ \Vert \eta \Vert _{\mathcal{W}} := \left ( \int _{\Omega } \sigma ( \eta )\cdot \varepsilon (\eta ) \right )^{\frac{1}{2}}, \quad \forall \eta \in \mathcal{W}. $$

(3.4)

Actually, in view of the properties introduced in Sect. 2.1 and satisfied by the elasticity tensor ℂ, the bilinear form of these problems is symmetric, continuous and coercive. We finally fix for each problem a solution belonging to by choosing the representative which satisfies $\langle \cdot \rangle =0$ for problems (2.19), (2.29) and (3.2), (3.3), so that $\tilde{u}_{ij}$ and $\tilde{\tilde{u}}_{ijk}$, as well as $\tilde{u}^{\rho }_{ij}$ and $\tilde{\tilde{u}}^{\rho }_{ijk}$ belong to $\mathcal{V}$.

Fig. 2

Introduction of an inclusion centered at $\hat{y}$ into the domain $\Omega$. The resulting domain is denoted by $\Omega _{\rho , \hat{y} }$

Remark 1

According to Lax-Milgram theorem, the existence and uniqueness of solutions of variational problems on $(\mathcal{W}, \lVert \cdot \rVert _{\mathcal{W}})$ with a symmetric, continuous and coercive bilinear form, are ensured as long as the continuous linear form belongs to the dual space of $\mathcal{W}$, which can be identified with the subspace of the dual space whose the elements are such that $F(c) = 0$ for all . All these conditions are satisfied for the problems (2.19), (2.29), (3.2), and (3.3).

As we did in Sect. 2, we can consequently define the topologically perturbed counterparts of the homogenized tensors, denoted as $\mathbb{C}_{\rho }$, $\mathbb{D}^{\sharp }_{\rho }$ and $\mathbb{D}_{\rho }$. By setting $u_{ij}^{\rho } := (\mathrm{e}_{i} \otimes _{s} \mathrm{e}_{j})y + \tilde{u}_{ij}^{\rho }$, this gives

$$\begin{aligned} (\mathbb{C}_{\rho }^{h})_{ijkl} = &\ \frac{1}{V}\int _{\Omega } \gamma _{\rho }\sigma (u_{ij}^{\rho })\cdot \varepsilon (u_{kl}^{ \rho }), \end{aligned}$$

(3.5)

$$\begin{aligned} (\mathbb{D}_{\rho }^{\sharp })_{ijkpqr} = &\ \frac{1}{V} \int _{\Omega } \gamma _{\rho }\mathbb{C}(\tilde{u}_{ij}^{ \rho }\otimes _{s} \mathrm{e}_{k}) \cdot (\tilde{u}_{pq}^{\rho } \otimes _{s} \mathrm{e}_{r}) , \end{aligned}$$

(3.6)

$$\begin{aligned} (\mathbb{D}_{\rho })_{ijkpqr} = &\ \frac{1}{V} \int _{\Omega } \gamma _{\rho }\mathbb{C}(\tilde{u}_{ij}^{ \rho } \otimes _{s} \mathrm{e}_{k} + \varepsilon (\tilde{\tilde{u}}_{ijk}^{ \rho })) \cdot (\tilde{u}_{pq}^{\rho } \otimes _{s} \mathrm{e}_{r}) \\ -&\ \frac{1}{V} \int _{\Omega } ( \mathbb{C}_{\rho }^{h}(\mathrm{e}_{i} \otimes _{s} \mathrm{e}_{j}) \cdot (\tilde{\tilde{u}}_{pqr}^{\rho } \otimes _{s} \mathrm{e}_{k}) + \gamma _{\rho }\sigma (u_{pq}^{\rho }) \cdot (\tilde{\tilde{u}}_{ijk}^{\rho } \otimes _{s} \mathrm{e}_{r}) ). \end{aligned}$$

(3.7)

3.1 The Topological Derivative Method

We are interested in the behaviour of the homogenized tensors with respect to the size of the topological perturbation. For this purpose, we will use the concept of topological derivative. It has been rigorously introduced in [57] in the context of heat conduction and elasticity problems. Developments of the theory have been led the past two decades in among others [8, 11, 13, 27, 29, 40, 43, 47, 49, 50, 58, 59]. Furthermore, the topological derivative was applied in many fields, such as topology optimization [9, 10, 51], inverse problems [22, 33, 38, 39, 44], and image processing [14, 16, 37].

Let $\Omega _{\rho ,\hat{y}}$ be used to represent the topologically perturbed counterpart of $\Omega$. In the particular case of a perforation, for instance, $\Omega _{\rho ,\hat{y}} = \Omega \setminus \overline{B_{\rho }(\hat{y})}$. For a given shape functional $\Omega _{\rho ,\hat{y}}\mapsto \psi (\Omega _{\rho ,\hat{y}})$ we are looking for the topological asymptotic expansion

$$ \psi (\Omega _{\rho ,\hat{y}}) = \psi (\Omega ) + f(\rho ) D_{T} \psi (\hat{y}) + o(f(\rho )) , $$

(3.8)

where $f(\rho )\rightarrow 0$ and $o(f(\rho ))/f(\rho )\rightarrow 0$ with $\rho \rightarrow 0$. The function $\hat{y}\mapsto D_{T}\psi (\hat{y})$ is called the topological derivative of $\psi$. The sign of the topological derivative indicates whether it is interesting or not regarding the considered criterion $\psi$ to add a small inclusion of material at the point $\hat{y}$. To this end, we will calculate the topological derivative of the homogenized tensors in the next section. Before proceeding, let us introduce a truncated domain of the form

$$ \Omega _{R} := \Omega \setminus B_{R}(\hat{y}). $$

(3.9)

We fix $R$ and consider small positive parameter $\rho \to 0$ with $R>\rho >0$, and such that $\overline{B_{R}(\hat{y})}$ is included in $\Omega$. Note that $B_{R}(\hat{y})$ contains the inclusion $B_{\rho }(\hat{y})$. The existence of the topological derivatives for the components of homogenized tensors is ensured by the following two lemmas. The proofs of these results are relegated to Appendix B.

Lemma 2

Let $\tilde{u}_{ij}$ and $\tilde{u}^{\rho }_{ij}$ be the solutions of original (2.19) and perturbed (3.2) problems, respectively. Then, the following estimates hold true

(3.10)

(3.11)

(3.12)

Lemma 3

Let $\tilde{\tilde{u}}_{ijk}$ and $\tilde{\tilde{u}}^{\rho }_{ijk}$ be the solutions of the original (2.29) and perturbed (3.3) problems respectively. Then the following estimates hold true

(3.13)

(3.14)

(3.15)

3.2 First-Order Truncation

First, let us consider the expansion of the homogenized tensors $\mathbb{C}^{h}$ and $\mathbb{D}^{\sharp }$. To this end, we exclusively need the estimates from Lemma 2. The calculations of the topological derivative of $\mathbb{C}^{h}$ is well-known, and from [12, 31] we have the following result.

Theorem 4

The topological asymptotic expansion of the homogenized elasticity tensor $\mathbb{C}^{h}$ is given by

$$ (\mathbb{C}^{h}_{\rho } - \mathbb{C}^{h})_{ijkl} = \frac{\pi \rho ^{2}}{V} \mathbb{P} \sigma (u_{ij})(\hat{y}) \cdot \varepsilon (u_{kl})(\hat{y}) + o(\rho ^{2}), $$

(3.16)

which, setting $f(\rho ) = \pi \rho ^{2}/V$, allows for identifying the topological derivative of any component of $\mathbb{C}^{h}$, namely

$$ (D_{T} \mathbb{C}^{h})_{ijkl} = \mathbb{P} \sigma (u_{ij}) \cdot \varepsilon (u_{kl}), $$

(3.17)

where $u_{ij}$ is given by (2.23) and the polarization tensor is defined as

$$ \mathbb{P} = -\frac{1-\gamma }{1+\gamma \beta }\left ((1+\beta ) \mathbb{I} + \frac{1}{2}(\alpha -\beta ) \frac{1-\gamma }{1+\gamma \alpha }\mathrm{I} \otimes \mathrm{I}\right ), $$

(3.18)

with the parameters $\alpha$ and $\beta$ given by

$$ \alpha =\frac{\lambda + \mu }{\mu } \quad \textit{and} \quad \beta = \frac{\lambda + 3\mu }{\lambda + \mu }. $$

(3.19)

We are more interested in the topological derivative of $\mathbb{D}$, but the computations performed for $\mathbb{D}^{\sharp }$ are helpful to understand the method applied afterwards. Because the original and perturbed fields $\tilde{u}_{ij}$ and $\tilde{u}_{ij}^{\rho }$ are living in the same functional space $\mathcal{V}$, we can perform a direct calculation. Thus the topological asymptotic expansion of the tensor $\mathbb{D}^{\sharp }$ given by (2.27) is obtained from its definition as follows

$$\begin{aligned} (\mathbb{D}^{\sharp } _{\rho } - \mathbb{D}^{\sharp } )_{ijkpqr} &= \frac{1}{V} \int _{\Omega } \gamma _{\rho }\mathbb{C}(\tilde{u}^{\rho }_{ij} \otimes _{s} \mathrm{e}_{k}) \cdot (\tilde{u}^{\rho }_{pq}\otimes _{s} \mathrm{e}_{r}) - \frac{1}{V} \int _{\Omega } \mathbb{C}(\tilde{u}_{ij} \otimes _{s} \mathrm{e}_{k}) \cdot (\tilde{u}_{pq}\otimes _{s} \mathrm{e}_{r}) \\ &= \frac{1}{V} \int _{\Omega } \mathbb{C}((\tilde{u}^{\rho }_{ij}- \tilde{u}_{ij})\otimes _{s} \mathrm{e}_{k}) \cdot (\tilde{u}_{pq} \otimes _{s} \mathrm{e}_{r}) \\ & + \mathbb{C}(\tilde{u}_{ij}\otimes _{s} \mathrm{e}_{k}) \cdot ((\tilde{u}^{\rho }_{pq}-\tilde{u}_{pq}) \otimes _{s} \mathrm{e}_{r}) \\ &- \frac{1-\gamma }{V} \int _{B_{\rho }}\mathbb{C}(\tilde{u}^{\rho }_{ij} \otimes _{s} \mathrm{e}_{k}) \cdot (\tilde{u}^{\rho }_{pq}\otimes _{s} \mathrm{e}_{r}) + \mathcal{E}_{1}(\rho ), \end{aligned}$$

(3.20)

where the remainder $\mathcal{E}_{1}(\rho )$ is given by

$$\begin{aligned} \mathcal{E}_{1}(\rho ) = \frac{1}{V} \int _{\Omega } \mathbb{C}(( \tilde{u}^{\rho }_{ij}-\tilde{u}_{ij})\otimes _{s} \mathrm{e}_{k}) \cdot ((\tilde{u}^{\rho }_{pq}-\tilde{u}_{pq})\otimes _{s} \mathrm{e}_{r}), \end{aligned}$$

(3.21)

and can be bounded as follows

(3.22)

where we have used Lemma 2. Still evoking Lemma 2, we notice that the last integral on the right-hand side of expression (3.20) gives rise to a $\rho ^{2}$ order term in the asymptotic expansion of $\mathbb{D}^{\sharp }_{\rho }$. But we can not use the same arguments to analyse the first integral (second line) on the right-hand side of (3.20). To overcome this difficult, we make use of the classical adjoint method by introducing suitable adjoint sates $v^{kr}_{ij}\in \mathcal{V}$ for $i,j,k,r \in \lbrace 1,2 \rbrace$, solution of the following set of variational problems:

$$\begin{array}{c}{v}_{ij}^{kr}\in \mathcal{V}:{\int }_{\mathrm{\Omega }}\sigma (v_{ij}^{kr})\cdot \epsilon (\eta )={\int }_{\mathrm{\Omega }}\mathbb{C}({\tilde{u}}_{ij}{\otimes }_s{\mathrm{e}}_k)\cdot (\eta {\otimes }_s{\mathrm{e}}_r)\hfill \\ \hfill -{\int }_{\mathrm{\Omega }}〈\mathbb{C}({\tilde{u}}_{ij}{\otimes }_s{\mathrm{e}}_k)〉\cdot (\eta {\otimes }_s{\mathrm{e}}_r),\mathrm{\forall }\eta \in \mathcal{W}.\end{array}$$

(3.23)

From these elements, we can state the main result of this section, where the details of the calculations can be found in the Appendix A.1.

Theorem 5

The topological asymptotic expansion of tensor $\mathbb{D}^{\sharp }$ is given by

$$\begin{aligned} (\mathbb{D}^{\sharp } _{\rho } - \mathbb{D}^{\sharp } )_{ijkpqr} = &- \frac{\pi \rho ^{2}}{V} \mathbb{P} \sigma (u_{ij})(\hat{y}) \cdot \varepsilon (v^{rk}_{pq})(\hat{y}) -\frac{\pi \rho ^{2}}{V} \mathbb{P} \sigma (u_{pq})(\hat{y}) \cdot \varepsilon (v^{kr}_{ij})( \hat{y}) \\ &-\frac{\pi \rho ^{2}}{V}(1-\gamma ) \mathbb{C}(\hat{y})(\tilde{u}_{ij}( \hat{y})\otimes _{s} \mathrm{e}_{k}) \cdot (\tilde{u}_{pq}(\hat{y}) \otimes _{s} \mathrm{e}_{r}) + o(\rho ^{2}), \end{aligned}$$

(3.24)

where ℙ is the polarization tensor defined in (3.18). By setting $f(\rho ) = \pi \rho ^{2}/V$, the topological derivative of any component of tensor $\mathbb{D}^{\sharp }$ can be identified, namely

$$ (D_{T} \mathbb{D}^{\sharp })_{ijkpqr} = - \mathbb{P} \sigma (u_{ij}) \cdot \varepsilon (v^{rk}_{pq}) - \mathbb{P} \sigma (u_{pq}) \cdot \varepsilon (v^{kr}_{ij}) - (1-\gamma ) \mathbb{C} (\tilde{u}_{ij} \otimes _{s} \mathrm{e}_{k}) \cdot (\tilde{u}_{pq} \otimes _{s} \mathrm{e}_{r}) . $$

(3.25)

Finally, $u_{ij}$ is given by (2.23), $\tilde{u}_{ij}$ are solutions to the set of canonical variational problems (2.19) and the adjoint states $v^{kr}_{ij}$ are solutions to (3.23).

3.3 Second-Order Truncation

Now we want to investigate the topological sensitivity of the tensor $\mathbb{D}$ involved in the macroscopic elastic energy calculated for the second order truncation (2.31). As we did for $\mathbb{D}^{\sharp }$, we perform a direct calculation described in Appendix A.2. By taking into account that $\langle \tilde{\tilde{u}}_{pqr}\rangle =0$ and $\langle \tilde{\tilde{u}}^{\rho }_{pqr}\rangle =0$, we have

$$\begin{aligned} (\mathbb{D}_{\rho } - \mathbb{D})_{ijkpqr} &= \frac{1}{V} \int _{ \Omega } \left (\mathbb{C}(\delta \tilde{u}_{ij}^{\rho } \otimes _{s} \mathrm{e}_{k} ) + \sigma (\delta \tilde{\tilde{u}}_{ijk}^{\rho }) \right ) \cdot (\tilde{u}_{pq} \otimes _{s} \mathrm{e}_{r}) - \!\int _{ \Omega } \!\sigma (\delta u_{pq}^{\rho })\cdot (\tilde{\tilde{u}}_{ijk} \otimes _{s} \mathrm{e}_{r}) \\ &+ \frac{1}{V}\int _{\Omega } \left (\mathbb{C}(\tilde{u}_{ij} \otimes _{s} \mathrm{e}_{k} ) + \sigma (\tilde{\tilde{u}}_{ijk}) \right ) \cdot (\delta \tilde{u}_{pq}^{\rho } \otimes _{s} \mathrm{e}_{r}) -\int _{\Omega } \sigma (u_{pq})\cdot (\delta \tilde{\tilde{u}}_{ijk}^{\rho } \otimes _{s} \mathrm{e}_{r}) \\ &-\frac{1-\gamma }{V}\int _{B_{\rho }} \left (\mathbb{C}(\tilde{u}_{ij}^{ \rho } \otimes _{s} \mathrm{e}_{k} ) + \sigma (\tilde{\tilde{u}}_{ijk}^{ \rho })\right ) \cdot (\tilde{u}_{pq}^{\rho } \otimes _{s} \mathrm{e}_{r}) \\ &+\frac{1-\gamma }{V}\int _{B_{\rho }} \sigma (u_{pq}^{\rho })\cdot ( \tilde{\tilde{u}}_{ijk}^{\rho } \otimes _{s} \mathrm{e}_{r}) + \mathcal{E}_{1} (\rho ) , \end{aligned}$$

(3.26)

where the notation $\delta (\cdot )^{\rho } = (\cdot )^{\rho } - (\cdot )$ has been introduced. The remainder $\mathcal{E}_{1}(\rho )$ is defined as

$$\begin{aligned} \mathcal{E}_{1}(\rho ) &= \frac{1}{V} \int _{\Omega } (\sigma ( \delta \tilde{\tilde{u}}^{\rho }_{ijk}) + \mathbb{C} (\delta \tilde{u}^{\rho }_{ij} \otimes _{s} \mathrm{e}_{k})) \cdot (\delta \tilde{u}^{\rho }_{pq} \otimes _{s} \mathrm{e}_{r}) - \frac{1}{V} \int _{\Omega } \sigma (\delta \tilde{u}^{\rho }_{pq})\cdot (\delta \tilde{\tilde{u}}^{\rho }_{ijk} \otimes _{s} \mathrm{e}_{r}) , \end{aligned}$$

(3.27)

since $u^{\rho }_{ij} := (\mathrm{e}_{i} \otimes _{s} \mathrm{e}_{j})y + \tilde{u}^{\rho }_{ij}$, so that $\delta u^{\rho }_{ij} = \delta \tilde{u}^{\rho }_{ij}$. From Lemmas 2 and 3, the following estimate for the remainder $\mathcal{E}_{1}(\rho )$ given by (3.27) holds true

$$\begin{aligned} |\mathcal{E}_{1}(\rho )| = o(\rho ^{2}). \end{aligned}$$

(3.28)

By taking into account once again Lemmas 2 and 3, we note that the last two integrals in the expansion (3.26) are of order $\rho ^{2}$. However, in order to analyse the first fourth integrals in (3.26), the introduction of convenient adjoint states $p_{ijk}^{r}\in \mathcal{V}$ for $i,j,k,r \in \lbrace 1,2 \rbrace$ are required, which are solutions of the following set of variational problems:

$$\begin{aligned} p_{pqr}^{k} \in \mathcal{V}\; : \; \int _{\Omega } \sigma (p_{pqr}^{k}) \cdot \varepsilon (\eta ) =& \int _{\Omega } \left ( \sigma ( \tilde{\tilde{u}}_{pqr}) + \mathbb{C}(\tilde{u}_{pq}\otimes _{s} \mathrm{e}_{r} ) \right )\cdot (\eta \otimes _{s} \mathrm{e}_{k}) \\ & - \int _{\Omega }\mathbb{C} (\tilde{\tilde{u}}_{pqr}\otimes _{s} \mathrm{e}_{k}) \cdot \varepsilon (\eta ) \\ &-\int _{\Omega } \left \langle \sigma (\tilde{\tilde{u}}_{pqr}) + \mathbb{C}(\tilde{u}_{pq}\otimes _{s} \mathrm{e}_{r} ) \right \rangle \cdot (\eta \otimes _{s} \mathrm{e}_{k}) , \quad \forall \eta \in \mathcal{W}. \end{aligned}$$

(3.29)

Finally, from these elements we can state the main result of the article, where the details of the calculations can be found in the Appendix A.2.

Theorem 6

The topological asymptotic expansion of the tensor $\mathbb{D}$ is given by

$$\begin{aligned} (\mathbb{D}_{\rho } - \mathbb{D})_{ijkpqr} &= - \frac{\pi \rho ^{2}}{V} \mathbb{P} \sigma (u_{ij})(\hat{y}) \cdot ( \varepsilon (p_{pqr}^{k})(\hat{y}) + (\tilde{\tilde{u}}_{pqr}(\hat{y}) \otimes _{s} \mathrm{e}_{k}) ) \\ & - \frac{\pi \rho ^{2}}{V} \mathbb{P} \sigma (u_{pq})(\hat{y}) \cdot ( \varepsilon (p_{ijk}^{r})(\hat{y}) + (\tilde{\tilde{u}}_{ijk}( \hat{y}) \otimes _{s} \mathrm{e}_{r})) \\ & + \frac{\pi \rho ^{2}}{V} \mathbb{P} \left (\sigma ( \tilde{\tilde{u}}_{ijk})(\hat{y}) + \mathbb{C} (\tilde{u}_{ij}( \hat{y}) \otimes _{s} \mathrm{e}_{k})\right ) \cdot \left ( \varepsilon (\tilde{\tilde{u}}_{pqr})(\hat{y})+(\tilde{u}_{pq}( \hat{y}) \otimes _{s} \mathrm{e}_{r}) \right ) \\ & + o(\rho ^{2}), \end{aligned}$$

(3.30)

where ℙ is the polarization tensor defined in (3.18). By setting $f(\rho ) = \pi \rho ^{2}/V$, we can identify the topological derivative of any component of tensor $\mathbb{D}$, namely

$$\begin{aligned} (D_{T} \mathbb{D})_{ijkpqr} &= - \mathbb{P} \sigma (u_{ij}) \cdot ( \varepsilon (p_{pqr}^{k}) + (\tilde{\tilde{u}}_{pqr}\otimes _{s} \mathrm{e}_{k}) ) - \mathbb{P} \sigma (u_{pq}) \cdot ( \varepsilon (p_{ijk}^{r}) + (\tilde{\tilde{u}}_{ijk} \otimes _{s} \mathrm{e}_{r})) \\ & + \mathbb{P} \left (\sigma (\tilde{\tilde{u}}_{ijk}) + \mathbb{C} ( \tilde{u}_{ij} \otimes _{s} \mathrm{e}_{k})\right ) \cdot \left ( \varepsilon (\tilde{\tilde{u}}_{pqr})+(\tilde{u}_{pq} \otimes _{s} \mathrm{e}_{r}) \right ), \end{aligned}$$

(3.31)

where $u_{ij}$ is given by (2.23), $\tilde{u}_{ij}$ are solutions to the set of canonical variational problems (2.19), $\tilde{\tilde{u}}_{ijk}$ are solutions to the set of canonical coupled variational problems (2.29) and the adjoint states $p^{r}_{ijk}$ are solutions to (3.29).

Remark 7

In the particular case of the weak phase material which simulates a void contained in a ball $B_{\rho }$ of radius $\rho$ centered at $\hat{y}$, with the infinitely small contrast $0 < \gamma _{0} \ll 1$, the definitions of the macroscopic and cell boundary value problems should be changed. In such a case the loads are applied on the stiff phase only. For this purpose the characteristic function $\chi$ of the solid domain is introduced. The topologically perturbed counterpart of this characteristic function is written $\chi ^{\rho }= \chi - \chi _{B_{\rho }}$, $\chi _{B_{\rho }}$ being the characteristic function of the ball $B_{\rho }$. Let $\rho _{0} >0$, we define for $0 \leq \rho \leq \rho _{0}$

$$ \boldsymbol{\varphi }^{\rho }(y) := \frac{V}{\int _{\Omega } \chi ^{\rho }}\chi ^{\rho } (y) \quad \text{and} \quad \langle \eta \rangle _{\boldsymbol{\varphi }^{\rho }}:= \frac{1}{V}\int _{\Omega }\boldsymbol{\varphi }^{\rho }\eta . $$

(3.32)

For the macroscopic problem, we assume that $f=T^{-1}\boldsymbol{\varphi }^{\rho _{0}}(y)F(Y)$. We select the periodic solutions of cell problems with null averages on the solid phase. Therefore, the first auxiliary problem remains unchanged, and the second auxiliary problem becomes

$$\begin{array}{c}{\tilde{\tilde{u}}}_{ijk}^{\rho }\in {\mathcal{V}}^{{\gamma }_{\rho }}:{\int }_{\mathrm{\Omega }}{\gamma }_{\rho }\sigma ({\tilde{\tilde{u}}}_{ijk}^{\rho })\cdot \epsilon (\eta )+{\int }_{\mathrm{\Omega }}{\gamma }_{\rho }\mathbb{C}({\tilde{u}}_{ij}^{\rho }{\otimes }_s{\mathrm{e}}_k)\cdot \epsilon (\eta )=\hfill \\ \hfill {\int }_{\mathrm{\Omega }}({\gamma }_{\rho }\sigma (u_{ij}^{\rho })-{\mathit{\phi }}^{\rho }{\mathbb{C}}_{\rho }^h({\mathrm{e}}_i{\otimes }_s{\mathrm{e}}_j)){\mathrm{e}}_k\cdot \eta ,\mathrm{\forall }\eta \in \mathcal{W},\end{array}$$

(3.33)

where

(3.34)

We can calculate the topological derivative of $\mathbb{D}$ in the same way as before, using Lemmas 2 and 3 which are still valid. The normalized characteristic function is introduced into the adjoint boundary value problem. The expression of topological derivative of $\mathbb{D}$ contains some new terms,

$$\begin{aligned} (D_{T} \mathbb{D})_{ijkpqr} &= - \mathbb{P} \sigma (u_{ij}) \cdot ( \varepsilon (p_{pqr}^{k}) + (\tilde{\tilde{u}}_{pqr}\otimes _{s} \mathrm{e}_{k}) ) - \mathbb{P} \sigma (u_{pq}) \cdot ( \varepsilon (p_{ijk}^{r}) + (\tilde{\tilde{u}}_{ijk} \otimes _{s} \mathrm{e}_{r})) \\ & + \mathbb{P} \left (\sigma (\tilde{\tilde{u}}_{ijk}) + \mathbb{C} ( \tilde{u}_{ij} \otimes _{s} \mathrm{e}_{k})\right ) \cdot \left ( \varepsilon (\tilde{\tilde{u}}_{pqr})+(\tilde{u}_{pq} \otimes _{s} \mathrm{e}_{r}) \right ) \\ & + \frac{V}{\int _{\Omega } \chi } \left [( \tilde{u}_{ij}\otimes _{s} \mathrm{e}_{k})\cdot \langle \sigma ( \tilde{\tilde{u}}_{pqr}) + \mathbb{C}(\tilde{u}_{pq}\otimes _{s} \mathrm{e}_{r} ) \rangle - (\tilde{\tilde{u}}_{ijk} \otimes _{s} \mathrm{e}_{r} )\cdot \mathbb{C}^{h}(\mathrm{e}_{p} \otimes _{s} \mathrm{e}_{q}) \right ] \\ & + \frac{V}{\int _{\Omega } \chi } \left [( \tilde{u}_{pq}\otimes _{s} \mathrm{e}_{r})\cdot \langle \sigma ( \tilde{\tilde{u}}_{ijk}) + \mathbb{C}(\tilde{u}_{ij}\otimes _{s} \mathrm{e}_{k} ) \rangle - (\tilde{\tilde{u}}_{pqr} \otimes _{s} \mathrm{e}_{k} ) \cdot \mathbb{C}^{h}(\mathrm{e}_{i} \otimes _{s} \mathrm{e}_{j}) \right ]. \end{aligned}$$

(3.35)

Note that the non-uniform contribution of $\mathbb{C}^{h}$ in equation (3.33) results in corrections to the topological derivative.

Remark 8

We cover as well the case of three spatial dimensions which is important for applications. In particular, the method of asymptotic analysis performed in can be extended to . In three spatial dimensions, the topological expansion of homogenized tensors is obtained by setting $f(\rho ) = (4/3)\pi \rho ^{3}/V$ and replacing the polarization tensor by [7]

$$\begin{aligned} \mathbb{P} = -3 \beta \mathbb{I} - (\alpha - \beta ) \mathrm{I} \otimes \mathrm{I}, \end{aligned}$$

(3.36)

with the coefficients $\alpha$ and $\beta$ redefined as follows

$$\begin{aligned} \alpha = \frac{(1-\nu )(1-\gamma )}{3(1-\nu )-(1+\nu )(1-\gamma )} \quad \hbox{and} \quad \beta = \frac{5(1-\nu )(1-\gamma )}{15(1-\nu )-2(4-5\nu )(1-\gamma )}, \end{aligned}$$

(3.37)

where $E$ is the Young modulus and $\nu$ the Poisson ratio.

Finally, it is important to note that formula (3.31) can be used to evaluate the topological derivative of any differentiable function of $\mathbb{D}$ through the direct application of the conventional calculus rules for composed functions. That is, any such function $\mathbb{D}\mapsto \Psi (\mathbb{D})$ admits the topological derivative of the form

$$ D_{T} \Psi (\mathbb{D}) = \left \langle D \Psi (\mathbb{D}), D_{T} \mathbb{D} \right \rangle , $$

(3.38)

with the brackets $\left \langle \cdot ,\cdot \right \rangle$ denoting the appropriate product between the derivative of $\Psi$ with respect to $\mathbb{D}$ and the topological derivative $D_{T} \mathbb{D}$ of $\mathbb{D}$. In order to fix these ideas, let us consider a pair of third order tensors. Then we obtain the following results, which can be used in numerical methods of synthesis and/or topology design of microstructures analogously to [12]:

Example 9

We consider a function $\Psi (\mathbb{D})$ of the form

$$ \Psi (\mathbb{D}) := \mathbb{D} \Phi _{1} \cdot \Phi _{2}\;. $$

(3.39)

Therefore, according to (3.38), its topological derivative is given by

$$ D_{T} \Psi (\mathbb{D}) = (D_{T} \mathbb{D}) \Phi _{1} \cdot \Phi _{2} \;. $$

(3.40)

If we set $\Phi _{1} = \mathrm{e}_{i} \otimes \mathrm{e}_{j} \otimes \mathrm{e}_{k}$ and $\Phi _{2} = \mathrm{e}_{l} \otimes \mathrm{e}_{m} \otimes \mathrm{e}_{n}$, for instance, we get $\Psi (\mathbb{D}) = (\mathbb{D})_{ijklmn}$ and its topological derivative is given by $D_{T} \Psi (\mathbb{D}) = (D_{T} \mathbb{D})_{ijklmn}$. It means that $D_{T} \Psi (\mathbb{D})$ actually represents the topological derivative of the components $(\mathbb{D})_{ijklmn}$ of the tensor $\mathbb{D}$.

Remark 10

In [24] a pantographic material is investigated, leading to the first order homogenized tensor $\mathbb{C}^{h}$ which is not invertible. In such a case, the addition of the strain-gradient terms $K=\nabla E$ in the macroscopic model is needed to predict more accurately the behaviour of the material. It turns out that an useful information arises from the projection of $\mathbb{D}$ onto the kernel of $\mathbb{C}^{h}$. This fact points strongly to the suitability of the use of (3.31) in a topology design algorithm for the synthesis and optimization of elastic microstructures based on minimization/maximization of cost functions defined in terms of homogenized properties.

4 Conclusion

In this paper, the topological derivative of the second order homogenized elasticity tensor with respect to the nucleation of circular inclusions at the microscopic level has been presented in the framework of periodic Sobolev spaces. The sensitivity has been derived in its closed form with the help of appropriate adjoint states. The limiting case associated with the nucleation of a very weak inclusion has also been considered. As expected, the associated topological derivative leads to a sixth order tensor field over the microstructural domain, measuring the sensitivity of the second order homogenized elasticity tensor to topological microstructural changes. Therefore, this information can be used in the context of synthesis and optimal design of metamaterials, for instance, accounting for second order mechanical effects.

Appendices

Appendix A: Calculation of the Topological Derivatives

1.1 A.1 Proof of Theorem 5

First we rewrite below the topological asymptotic expansion (3.20)

$$\begin{aligned} (\mathbb{D}^{\sharp } _{\rho } - \mathbb{D}^{\sharp } )_{ijkpqr} &= \frac{1}{V} \int _{\Omega } \mathbb{C}((\tilde{u}^{\rho }_{ij}- \tilde{u}_{ij})\otimes _{s} \mathrm{e}_{k}) \cdot (\tilde{u}_{pq} \otimes _{s} \mathrm{e}_{r}) \\ & + \mathbb{C}(\tilde{u}_{ij}\otimes _{s} \mathrm{e}_{k}) \cdot ((\tilde{u}^{\rho }_{pq}-\tilde{u}_{pq}) \otimes _{s} \mathrm{e}_{r}) \\ &- \frac{1-\gamma }{V} \int _{B_{\rho }}\mathbb{C}(\tilde{u}^{\rho }_{ij} \otimes _{s} \mathrm{e}_{k}) \cdot (\tilde{u}^{\rho }_{pq}\otimes _{s} \mathrm{e}_{r}) + o(\rho ^{2}). \end{aligned}$$

(A.1)

In order to simplify the second term on the right-hand side of (A.1), we evoke the adjoint method. We start by subtracting (2.19) from (3.2), to obtain

$$ \int _{\Omega } \sigma (\tilde{u}^{\rho }_{pq}- \tilde{u}_{pq}) \cdot \varepsilon (\eta ) = (1-\gamma )\int _{B_{\rho }} \sigma (u^{\rho }_{pq}) \cdot \varepsilon (\eta ), $$

(A.2)

where $u^{\rho }_{pq} := (\mathrm{e}_{p} \otimes _{s} \mathrm{e}_{q})y + \tilde{u}^{\rho }_{pq}$. By setting $\eta = \tilde{u}^{\rho }_{pq} - \tilde{u}_{pq}$ as test function in the adjoint problem (3.23) for $v_{ij}^{kr}$, and noting that $\langle \tilde{u}^{\rho }_{pq} - \tilde{u}_{pq} \rangle = 0$, we obtain

$$ \int _{\Omega } \sigma (v^{kr}_{ij}) \cdot \varepsilon (\tilde{u}^{ \rho }_{pq} - \tilde{u}_{pq}) = \int _{\Omega } \mathbb{C}(\tilde{u}_{ij} \otimes _{s} \mathrm{e}_{k})\cdot ((\tilde{u}^{\rho }_{pq} - \tilde{u}_{pq})\otimes _{s} \mathrm{e}_{r}). $$

(A.3)

After taking $\eta = v^{kr}_{ij}$ as test function in (A.2), we have

$$ \int _{\Omega } \sigma (\tilde{u}^{\rho }_{pq}- \tilde{u}_{pq}) \cdot \varepsilon (v^{kr}_{ij}) = (1-\gamma )\int _{B_{\rho }} \sigma (u^{ \rho }_{pq}) \cdot \varepsilon (v^{kr}_{ij}). $$

(A.4)

From the symmetry of the bilinear forms we conclude that

$$ \int _{\Omega } \mathbb{C}(\tilde{u}_{ij}\otimes _{s} \mathrm{e}_{k}) \cdot ((\tilde{u}^{\rho }_{pq} - \tilde{u}_{pq})\otimes _{s} \mathrm{e}_{r}) = (1-\gamma )\int _{B_{\rho }} \sigma (u^{\rho }_{pq}) \cdot \varepsilon (v^{kr}_{ij}). $$

(A.5)

Similarly we have, after replacing the indexes ${pq}$ by ${ij}$ in (A.2) and (3.23), that

$$\begin{aligned} \int _{\Omega }\mathbb{C} ((\tilde{u}^{\rho }_{ij} - \tilde{u}_{ij}) \otimes _{s} \mathrm{e}_{k}) \cdot (\tilde{u}_{pq}\otimes _{s} \mathrm{e}_{r}) = (1-\gamma )\int _{B_{\rho }} \sigma (u^{\rho }_{ij}) \cdot \varepsilon (v^{rk}_{pq}). \end{aligned}$$

(A.6)

These results lead to

$$\begin{aligned} (\mathbb{D}^{\sharp } _{\rho } - \mathbb{D}^{\sharp } )_{ijkpqr} &= \frac{1-\gamma }{V} \int _{B_{\rho }} \sigma (u^{\rho }_{ij}) \cdot \varepsilon (v^{rk}_{pq}) +\frac{1-\gamma }{V} \int _{B_{\rho }} \sigma (u^{\rho }_{pq}) \cdot \varepsilon (v^{kr}_{ij}) \\ &-\frac{1-\gamma }{V} \int _{B_{\rho }}\mathbb{C}(\tilde{u}^{\rho }_{ij} \otimes _{s} \mathrm{e}_{k}) \cdot (\tilde{u}^{\rho }_{pq}\otimes _{s} \mathrm{e}_{r}) + \mathcal{E}_{1}(\rho ). \end{aligned}$$

(A.7)

Since we assume that the inclusion $B_{\rho }$ is located neither on the interface nor on the boundary, the solutions of elliptic boundary value problems are smooth in $B_{\rho }$ by the elliptic regularity. Finally, from Lemma 2, and by taking into account the Lebesgue differentiation theorem combined with the Eshelby theorem [25, 26], we can write the topological derivative with the use of the polarization tensor ℙ (see, e.g., [12, 31]), and we deduce Theorem 5.

1.2 A.2 Proof of Theorem 6

The topological asymptotic expansion of the tensor $\mathbb{D}$ given by (2.32) or alternatively by (2.34) is obtained as follows. We start by rewriting expansion (3.26), namely

$$\begin{aligned} (\mathbb{D}_{\rho } - \mathbb{D})_{ijkpqr} &= \frac{1}{V} \int _{ \Omega } \left (\mathbb{C}(\delta \tilde{u}_{ij}^{\rho } \otimes _{s} \mathrm{e}_{k} ) + \sigma (\delta \tilde{\tilde{u}}_{ijk}^{\rho }) \right ) \cdot (\tilde{u}_{pq} \otimes _{s} \mathrm{e}_{r}) - \!\int _{ \Omega } \!\sigma (\delta u_{pq}^{\rho })\cdot (\tilde{\tilde{u}}_{ijk} \otimes _{s} \mathrm{e}_{r}) \\ &+ \frac{1}{V}\int _{\Omega } \left (\mathbb{C}(\tilde{u}_{ij} \otimes _{s} \mathrm{e}_{k} ) + \sigma (\tilde{\tilde{u}}_{ijk}) \right ) \cdot (\delta \tilde{u}_{pq}^{\rho } \otimes _{s} \mathrm{e}_{r}) -\int _{\Omega } \sigma (u_{pq})\cdot (\delta \tilde{\tilde{u}}_{ijk}^{ \rho } \otimes _{s} \mathrm{e}_{r}) \\ &-\frac{1-\gamma }{V}\int _{B_{\rho }} \left (\mathbb{C}(\tilde{u}_{ij}^{ \rho } \otimes _{s} \mathrm{e}_{k} ) + \sigma (\tilde{\tilde{u}}_{ijk}^{ \rho })\right ) \cdot (\tilde{u}_{pq}^{\rho } \otimes _{s} \mathrm{e}_{r}) \\ &+\frac{1-\gamma }{V}\int _{B_{\rho }} \sigma (u_{pq}^{\rho })\cdot ( \tilde{\tilde{u}}_{ijk}^{\rho } \otimes _{s} \mathrm{e}_{r}) + o( \rho ^{2}), \end{aligned}$$

(A.8)

where the notation $\delta (\cdot )^{\rho } = (\cdot )^{\rho } - (\cdot )$ has been introduced. After subtracting (2.29) from (3.3), we obtain $\forall \eta \in \mathcal{W}$

$$\begin{aligned} \int _{\Omega } \sigma (\delta \tilde{\tilde{u}}^{\rho }_{ijk}) \cdot \varepsilon (\eta ) &=\int _{\Omega } (\sigma (\delta \tilde{u}^{\rho }_{ij}) - ( \mathbb{C}^{h}_{\rho } - \mathbb{C}^{h}) (\mathrm{e}_{i} \otimes _{s} \mathrm{e}_{j})) \mathrm{e}_{k} \cdot \eta - \int _{\Omega } \mathbb{C} (\delta \tilde{u}^{\rho }_{ij} \otimes _{s} \mathrm{e}_{k}) \cdot \varepsilon (\eta ) \\ &+(1-\gamma )\int _{B_{\rho }} (\sigma (\tilde{\tilde{u}}^{\rho }_{ijk}) + \mathbb{C} (\tilde{u}^{\rho }_{ij} \otimes _{s} \mathrm{e}_{k})) \cdot \varepsilon (\eta ) - (1-\gamma )\int _{B_{\rho }} \sigma (u^{ \rho }_{ij}) \mathrm{e}_{k} \cdot \eta . \end{aligned}$$

(A.9)

We set $\eta = \tilde{\tilde{u}}_{pqr}$ in (A.9) and $\eta = \delta \tilde{\tilde{u}}^{\rho }_{ijk}$ in (2.29), the equation for $\tilde{\tilde{u}}_{pqr}$, leading to simplification of the terms depending on $\delta \tilde{\tilde{u}}_{ijk}^{\rho }$ in (A.8). Reordering the members of the equation in order to gather the terms of the type $\delta \tilde{u}_{ij}^{\rho }$ and $\delta \tilde{u}_{pq}^{\rho }$, we find

$$\begin{aligned} V(\mathbb{D}_{\rho } - \mathbb{D})_{ijkpqr} &=\; \!\int _{\Omega } \! \big( \mathbb{C}(\delta \tilde{u}_{ij}^{\rho } \otimes _{s} \mathrm{e}_{k} ) \big) \cdot \left ( (\tilde{u}_{pq} \otimes _{s} \mathrm{e}_{r}) + \varepsilon (\tilde{\tilde{u}}_{pqr}) \right ) - \!\int _{\Omega }\! \sigma (\delta \tilde{u}^{\rho }_{ij}) \cdot (\tilde{\tilde{u}}_{pqr} \otimes _{s} \mathrm{e}_{k}) \\ &+\int _{\Omega } \left (\mathbb{C}(\tilde{u}_{ij} \otimes _{s} \mathrm{e}_{k} ) + \sigma (\tilde{\tilde{u}}_{ijk})\right ) \cdot ( \delta \tilde{u}_{pq}^{\rho } \otimes _{s} \mathrm{e}_{r}) -\int _{ \Omega } \sigma (\delta u_{pq}^{\rho })\cdot (\tilde{\tilde{u}}_{ijk} \otimes _{s} \mathrm{e}_{r}) \\ & + (1-\gamma )\int _{B_{\rho }} \sigma (u^{\rho }_{ij})\cdot ( \tilde{\tilde{u}}_{pqr}\otimes _{s} \mathrm{e}_{k}) +(1-\gamma )\int _{B_{ \rho }} \sigma (u_{pq}^{\rho })\cdot (\tilde{\tilde{u}}_{ijk}^{\rho } \otimes _{s} \mathrm{e}_{r}) \\ & - (1-\gamma )\int _{B_{\rho }} \big( \sigma (\tilde{\tilde{u}}^{ \rho }_{ijk}) + \mathbb{C} (\tilde{u}^{\rho }_{ij} \otimes _{s} \mathrm{e}_{k}) \big) \cdot \left ( \varepsilon (\tilde{\tilde{u}}_{pqr})+( \tilde{u}_{pq}^{\rho } \otimes _{s} \mathrm{e}_{r}) \right ) + \mathcal{E}_{1}(\rho ) . \end{aligned}$$

(A.10)

Let us set $\eta = \delta \tilde{u}^{\rho }_{ij}$ and $\eta = \delta \tilde{u}^{\rho }_{pq}$ in the adjoint equation (3.29) for $p_{pqr}^{k}$ and $p_{ijk}^{r}$, respectively. Now, we set in (A.2) $\eta = p^{r}_{ijk}$, and $\eta = p^{k}_{pqr}$ after replacing the indexes ${ij}$ by ${pq}$. After comparing the obtained results, we can conclude that

$$\begin{aligned} (\mathbb{D}_{\rho } - \mathbb{D})_{ijkpqr} &= \frac{1-\gamma }{V}\int _{B_{ \rho }} \sigma (u^{\rho }_{ij}) \cdot ( \varepsilon (p_{pqr}^{k}) + ( \tilde{\tilde{u}}_{pqr}\otimes _{s} \mathrm{e}_{k}) ) \\ &+ \frac{1-\gamma }{V}\int _{B_{\rho }} \sigma (u^{\rho }_{pq}) \cdot ( \varepsilon (p_{ijk}^{r}) + (\tilde{\tilde{u}}_{ijk} \otimes _{s} \mathrm{e}_{r})) \\ &- \frac{1-\gamma }{V}\int _{B_{\rho }} \left (\sigma ( \tilde{\tilde{u}}^{\rho }_{ijk}) + \mathbb{C} (\tilde{u}_{ij} \otimes _{s} \mathrm{e}_{k})\right ) \cdot \left ( \varepsilon ( \tilde{\tilde{u}}_{pqr})+(\tilde{u}_{pq} \otimes _{s} \mathrm{e}_{r}) \right ) + o(\rho ^{2}). \end{aligned}$$

(A.11)

We recall that the inclusion $B_{\rho }$ is located neither on the interface nor on the boundary, so that the solutions of elliptic boundary value problems are smooth in $B_{\rho }$ by the elliptic regularity. Finally, from Lemmas 2 and 3, and by taking into account the Lebesgue differentiation theorem combined with the Eshelby theorem [25, 26], we can write the topological derivative with the use of the polarization tensor ℙ (see, e.g., [12, 31]), and we deduce Theorem 6.

Appendix B: Proofs of Lemmas 2 and 3

For the convenience of the reader we provide the proofs of auxiliary Lemmas which are used to evaluate of the topological derivatives of homogenized tensors.

2.1 B.3 Preliminary Lemmas

We write in this subsection two useful statements for the proof of Lemmas 2 and 3. We consider $\Omega$ an open subset of , and $\hat{y}$ a fixed arbitrary point of $\Omega$. We denote by $B_{\rho }$ be the small disk of radius $\rho$, centered at $\hat{y}$, and take $\rho _{0} > 0$, such that $\overline{B_{\rho }} \subset \Omega$ for all $0 < \rho \leqslant \rho _{0}$. We have the following results.

Lemma 11

Let $\eta \in H^{1}(\Omega )$, $\hat{y}\in \Omega$. Then for all $0 < \delta \leq 1$ there exists a constant $c_{(\delta )}>0$ depending on $\delta$ and $\Omega$, such that for all $0 < \rho \leq \rho _{0}$

$$ \left | \int _{B_{\rho }} \eta (x) dx \right | \leqslant c_{(\delta )} \rho ^{2-\delta } \Vert \eta \Vert _{H^{1}(\Omega )}. $$

(B.1)

Proof

This result derives directly from the Sobolev Embedding Theorem, giving that $H^{1}(\Omega )$ embeds continuously into $L^{p}(\Omega )$ for all $2 \leq p <+\infty$, and with the use of Hölder inequality for $\eta \in L^{p}(B_{\rho })$, $1\in L^{q}(B_{\rho })$, with $q^{-1} = 1 - p^{-1} \in [1/2,1)$, setting $\delta := 2(q-1)/q$. □

Lemma 12

Let . Then we have for all $\delta >0$ a constant $c_{(\delta )}>0$ depending on $\delta$ and $\Omega$ such that for all $0 < \rho \leq \rho _{0}$

(B.2)

Proof

For simplicity we set $\rho _{0}=1$. Let $0 < \rho \leq 1$ and . We introduce $\phi _{\rho } : B_{1} \rightarrow B_{\rho }$ the diffeomorphism defined by $\phi _{\rho } (x)=\rho x$ for all $x\in B_{1}$. The restriction $\phi _{\rho } : \partial B_{1} \rightarrow \partial B_{\rho }$ is also a diffeomorphism, allowing us the following change of variable

(B.3)

where $c_{(1)}>0$ is the fixed constant given by the Trace theorem applied on . Once again, a change of variable yields

(B.4)

and

Then we have

(B.5)

The Sobolev Embedding Theorem gives continuously, for all $2 \leq p < +\infty$. Then from Hölder inequality with $q^{-1} = 1 - (p/2)^{-1}$, $q\in (1, +\infty ]$ we have

(B.6)

where $c_{(p)}$ is the constant depending on $p$ and $\Omega$ given by the Sobolev Embedding Theorem. Thus we can carry on the derivation of inequality (B.5)

(B.7)

for $\delta >0$ as small as we want when $q$ goes to 1. We finally conclude taking the square root of the last inequality. □

We end this preliminary section presenting convenient notation used to name the norms and seminorms of the needed functional spaces. For an open set , bounded, connected and with Lipschitz continuous boundary, is endowed with a norm equivalent to the usual one, due to Korn’s inequality [48], defined by

$$ \left \lVert \eta \right \rVert _{1,\Omega }^{2} := \int _{\Omega }( \sigma (u)\cdot \varepsilon (u) + u\cdot u ) , $$

(B.8)

and we also define in the seminorm

$$ \left \lvert \eta \right \rvert _{1,\Omega }^{2} := \int _{\Omega }\sigma (u)\cdot \varepsilon (u) . $$

(B.9)

We finally denote the usual norms of , and , respectively by $\left \lVert \eta \right \rVert _{0,\Omega }$, $\left \lVert \eta \right \rVert _{1/2,\partial \Omega }$, and $\left \lVert \eta \right \rVert _{-1/2,\partial \Omega }$.

2.2 B.4 Lemma 2

Proof of Lemma 2

Let us introduce an ansatz of the form [41]

$$ \tilde{u}^{\rho }_{ij}(y) = \tilde{u}_{ij}(y) + w^{\rho }_{ij}(y) + z^{ \rho }_{ij}(y), $$

(B.10)

where $w^{\rho }_{ij}$ is solution to the following exterior problem:

$$\{\begin{array}{l}\begin{array}{rllcl}\mathrm{div}({\gamma }_{\rho }\sigma (w_{ij}^{\rho }))& =& 0& \text{in}& {\mathbb{R}}^2,\\ w_{ij}^{\rho }& \to & 0& \text{at}& \mathrm{\infty },\\ 〚w_{ij}^{\rho }〛& =& 0& \text{on}& \partial B_{\rho },\\ 〚{\gamma }_{\rho }\sigma (w_{ij}^{\rho })〛n& =& h& \text{on}& \partial B_{\rho },\end{array}\end{array}$$

(B.11)

where $h = -(1-\gamma )\sigma (u_{ij})(\hat{y})n$, $n$ being the inward normal vector on $\partial B_{\rho }$, and $[\!\![\cdot ]\!\!]$ denotes the jump across the interface of the inclusion:

$$ [\!\![\cdot ]\!\!]= (\cdot )_{\Omega \setminus \overline{B_{\rho }}} - (\cdot )_{B_{\rho }} \quad \text{on} \quad \partial B_{\rho }. $$

(B.12)

The solution $w^{\rho }_{ij}$ of this classical problem is explicitly known [15], and gives rise to these estimates

$$ \Vert w^{\rho }_{ij} \Vert _{ 0,\Omega } = o(\rho ) , \quad \Vert w^{ \rho }_{ij} \Vert _{ 1,\Omega } = O(\rho ), \quad \text{and} \quad \Vert w^{\rho }_{ij} \Vert _{1,\Omega _{R}} = O(\rho ^{2}), $$

(B.13)

with $\Omega _{R}$ defined by (3.9). We want to estimate $z^{\rho }_{ij}$ which compensates the discrepancies introduced by $w^{\rho }_{ij}$. But defined as in (B.10), we don’t have . For having that, let us modify slightly $w^{\rho }_{ij}$ near the boundary $\partial \Omega$. We define the ring

$$ C := \left \{ y\in \Omega \mid \text{dist}(y,\partial \Omega ) < \epsilon \right \} , $$

(B.14)

with $\partial C = \partial \Omega \cup \partial C^{\text{int}}$, $\partial C^{\text{int}} = \left \{ y\in \Omega \mid \text{dist}(y, \partial \Omega ) = \epsilon \right \}$, for a fixed $\epsilon >0$ small enough to have $\overline{B_{R}(\hat{y})}\subset \Omega \setminus \overline{C}$. Then we set

$$ w^{\rho , \epsilon }_{ij}(y):= \textstyle\begin{cases} \ w^{\rho }_{ij}(y) \quad & \hbox{if }y\in \Omega \setminus \overline{C}, \\ \ w^{\rho }_{C, ij}(y) \quad & \hbox{if }y\in C, \end{cases} $$

(B.15)

where $w^{\rho }_{C, ij}$ is solution to the following boundary value problem

$$ \left \{ \textstyle\begin{array}{l} \textstyle\begin{array}{rll@{\quad}c@{\quad}l} \mathrm{div} (\sigma (w^{\rho }_{C, ij})) & = & 0 & \text{in} & C, \\ w^{\rho }_{C, ij} & = & 0 & \text{on} & \partial \Omega , \\ w^{\rho }_{C, ij} & = & w^{\rho }_{ij} & \text{on} & \partial C^{ \text{int}}. \end{array}\displaystyle \end{array}\displaystyle \right . $$

(B.16)

Let us introduce the new ansatz

$$ \tilde{u}^{\rho }_{ij}(y) = \tilde{u}_{ij}(y) + \tilde{w}^{\rho }_{ij}(y) + \tilde{z}^{\rho }_{ij}(y), $$

(B.17)

where $\tilde{w}^{\rho }_{ij} := w^{\rho , \epsilon }_{ij} - \langle w^{ \rho , \epsilon }_{ij} \rangle$, with $\langle \cdot \rangle$ defined as in (2.14), so that $\tilde{w}^{\rho }_{ij}\in \mathcal{V}$, and therefore with $\langle \tilde{z}^{\rho }_{ij} \rangle = 0$. Thus we can calculate the variational problem satisfied by $\tilde{z}^{\rho }_{ij}$. Let us apply the operator $\gamma _{\rho }\sigma$ to (B.17), multiply the obtained expression by $\varepsilon (\eta )$ where $\eta$ is a test function in , and integrate over $\Omega$. Applying the Green formula over $C\cap \Omega$, $(\Omega \setminus \overline{C\cup B_{\rho }})$, and $B_{\rho }$ to the integral term depending on $\tilde{w}^{\rho }_{ij}$, and in view of (2.19), (3.2), (B.11) and (B.16), we find

$$\begin{array}{c}{\tilde{z}}_{ij}^{\rho }\in \mathcal{W}:{\int }_{\mathrm{\Omega }}{\gamma }_{\rho }\sigma ({\tilde{z}}_{ij}^{\rho })\cdot \epsilon (\eta )=(1-\gamma ){\int }_{B_{\rho }}(\sigma (u_{ij})-\sigma (u_{ij})(\hat{y}))\cdot \epsilon (\eta )\hfill \\ \hfill -{\int }_{\partial \mathrm{\Omega }}\sigma (w_{C,ij}^{\rho })n\cdot \eta -{\int }_{\partial C^{\text{int}}}(\sigma (w_{C,ij}^{\rho })-\sigma (w_{ij}^{\rho }))n\cdot \eta ,\mathrm{\forall }\eta \in \mathcal{W}.\end{array}$$

(B.18)

Because of the regularity of $u_{ij}$, we have the following estimate

$$\begin{aligned} \left | \int _{B_{\rho }} ( \sigma (u_{ij}) - \sigma (u_{ij})(\hat{y}) ) \cdot e (\eta ) \right | & \leq c\,\rho ^{2} \Vert \eta \Vert _{1, \Omega } . \end{aligned}$$

(B.19)

In view of the elliptic regularity of the problem (B.16), the continuity of the trace operator, the estimate (B.13), and because we can show that there exists a constant $c>0$ such that for all $\eta \in H^{1}(C,\mathbb{R}^{2})$ satisfying $\mathrm{div}\, \sigma (\eta ) = 0$, we have

$$ \Vert \sigma ( \eta )n \Vert _{-1/2,\partial \Omega } \leq c \left | \eta \right |_{1,C} , $$

(B.20)

then we have the following estimate

$$\begin{aligned} \left | \int _{\partial \Omega }\sigma (w^{\rho }_{C, ij})n\cdot \eta \right | &\leq \Vert \sigma (w^{\rho }_{C, ij})n \Vert _{-1/2, \partial \Omega } \Vert \eta \Vert _{1/2,\partial \Omega } \\ & \leq c \lvert w^{\rho }_{C, ij} \rvert _{1,C} \Vert \eta \Vert _{1, \Omega } \\ & \leq c \Vert w^{\rho }_{ij} \Vert _{1/2,\partial C^{\text{int}}} \Vert \eta \Vert _{1,\Omega } \\ & \leq c \Vert w^{\rho }_{ij} \Vert _{1,\Omega _{R} \setminus \overline{C}} \Vert \eta \Vert _{1,\Omega } \\ & \leq c \rho ^{2} \Vert \eta \Vert _{1,\Omega } . \end{aligned}$$

(B.21)

In the same way we obtain the estimate $O(\rho ^{2})\Vert \eta \Vert _{1,\Omega }$ for the integrals over $\partial C^{\text{int}}$. Noting that the bilinear form of the problem (B.18) is uniformly coercive on $\mathcal{W}$, and because $\tilde{z}^{\rho }_{ij} \in \mathcal{V}$, we can conclude, making use of Poincaré-Wirtinger inequality, that

$$ \Vert \tilde{z}^{\rho }_{ij} \Vert _{\mathcal{W}} = O(\rho ^{2}), \quad \text{and} \quad \Vert \tilde{z}^{\rho }_{ij} \Vert _{ 0,\Omega } = O(\rho ^{2}). $$

(B.22)

We can finally write the following expansion

$$ \tilde{u}^{\rho }_{ij} = \tilde{u}_{ij} + w^{\rho }_{ij} + \big( \tilde{z}^{\rho }_{ij} + \tilde{w}^{\rho }_{ij} - w^{\rho }_{ij} \big), $$

(B.23)

and noting after few calculations that

$${\parallel {\tilde{w}}_{ij}^{\rho }-w_{ij}^{\rho }\parallel }_{\mathcal{W}}=O({\rho }^2),$$

(B.24)

$${\parallel {\tilde{w}}_{ij}^{\rho }-w_{ij}^{\rho }\parallel }_{0,\mathrm{\Omega }}=o(\rho ),$$

(B.25)

we finally find the estimates (3.10), (3.11) and (3.12). □

2.3 B.5 Lemma 3

Before proving Lemma 3, let us make some preliminary calculations, for which the results directly ensue from Lemma 2. We denote by $a_{\rho }$ the bilinear form on $\mathcal{W}$ of problem (3.3), that is to say

$$\begin{aligned} a_{\rho } (u,v) &:= \int _{\Omega } \gamma _{\rho } \sigma (u) \cdot \varepsilon (v) , \quad \forall u,v \in \mathcal{W}. \end{aligned}$$

(B.26)

We want to estimate, for all $\eta \in \mathcal{W}$, the expression $a_{\rho }(\tilde{\tilde{u}}^{\rho }_{ijk},\eta ) - a_{\rho }( \tilde{\tilde{u}}_{ijk},\eta )$. According to expressions (3.3) and (2.29), we find

$$\begin{aligned} a_{\rho }(\tilde{\tilde{u}}^{\rho }_{ijk},\eta ) - a_{\rho }( \tilde{\tilde{u}}_{ijk},\eta ) &= - \int _{\Omega } ( \gamma _{\rho } \mathbb{C}(\tilde{u}^{\rho }_{ij} \otimes _{s} \mathrm{e}_{k}) - \mathbb{C}(\tilde{u}_{ij} \otimes _{s} \mathrm{e}_{k})) \cdot \varepsilon (\eta ) \\ &\quad + \int _{\Omega } (\gamma _{\rho }\sigma (u^{\rho }_{ij})- \sigma (u_{ij}) - \int _{\Omega } ( \mathbb{C}_{ \rho }^{h}- \mathbb{C}^{h})(\mathrm{e}_{i} \otimes _{s} \mathrm{e}_{j})) \mathrm{e}_{k} \cdot \eta \\ &\quad +(1-\gamma )\int _{B_{\rho }}\sigma (\tilde{\tilde{u}}_{ijk}) \cdot \varepsilon (\eta ) . \end{aligned}$$

(B.27)

Recalling the notation $\delta (\cdot )^{\rho } = (\cdot )^{\rho } - (\cdot )$, we start developing the first two terms of the right hand side of this expression.

$$\begin{array}{c}-{\int }_{\mathrm{\Omega }}({\gamma }_{\rho }\mathbb{C}({\tilde{u}}_{ij}^{\rho }{\otimes }_s{\mathrm{e}}_k)-\mathbb{C}({\tilde{u}}_{ij}{\otimes }_s{\mathrm{e}}_k))\cdot \epsilon (\eta )=-{\int }_{\mathrm{\Omega }}{\gamma }_{\rho }\mathbb{C}(\delta {\tilde{u}}_{ij}^{\rho }{\otimes }_s{\mathrm{e}}_k)\cdot \epsilon (\eta )\hfill \\ \hfill +(1-\gamma )\mathbb{C}({\tilde{u}}_{ij}(\hat{y}){\otimes }_s{\mathrm{e}}_k)\cdot {\int }_{B_{\rho }}\epsilon (\eta )+(1-\gamma ){\int }_{B_{\rho }}\mathbb{C}(({\tilde{u}}_{ij}-{\tilde{u}}_{ij}(\hat{y})){\otimes }_s{\mathrm{e}}_k)\cdot \epsilon (\eta ),\end{array}$$

(B.28)

and

$$\begin{array}{c}{\int }_{\mathrm{\Omega }}({\gamma }_{\rho }\sigma (u_{ij}^{\rho })-\sigma (u_{ij})){\mathrm{e}}_k\cdot \eta ={\int }_{\mathrm{\Omega }}{\gamma }_{\rho }\sigma (\delta {\tilde{u}}_{ij}^{\rho }){\mathrm{e}}_k\cdot \eta -(1-\gamma )\sigma (u_{ij})(\hat{y}){\mathrm{e}}_k\cdot {\int }_{B_{\rho }}\eta \hfill \\ \hfill -(1-\gamma ){\int }_{B_{\rho }}(\sigma (u_{ij})-\sigma (u_{ij})(\hat{y})){\mathrm{e}}_k\cdot \eta .\end{array}$$

(B.29)

In view of estimates calculated in Lemma 2, the regularity of $u_{ij}$, and the behaviour of $(\mathbb{C}^{\rho } - \mathbb{C})$ given by (3.16), we have for all $\eta \in \mathcal{W}$

$$ - \int _{\Omega } ( \gamma _{\rho }\mathbb{C}(\tilde{u}^{\rho }_{ij} \otimes _{s} \mathrm{e}_{k}) - \mathbb{C}(\tilde{u}_{ij} \otimes _{s} \mathrm{e}_{k})) \cdot \varepsilon (\eta ) = (1-\gamma ) \mathbb{C}( \tilde{u}_{ij}(\hat{y})\otimes _{s}\mathrm{e}_{k})\cdot \int _{B_{ \rho }} \varepsilon (\eta ) + o(\rho )\lVert \eta \rVert _{1,\Omega } , $$

(B.30)

and

$$\begin{array}{c}{\int }_{\mathrm{\Omega }}({\gamma }_{\rho }\sigma (u_{ij}^{\rho })-\sigma (u_{ij})-({\mathbb{C}}_{\rho }^h-{\mathbb{C}}^h)({\mathrm{e}}_i{\otimes }_s{\mathrm{e}}_j)){\mathrm{e}}_k\cdot \eta ={\int }_{\mathrm{\Omega }}{\gamma }_{\rho }\sigma (\delta {\tilde{u}}_{ij}^{\rho }){\mathrm{e}}_k\cdot \eta \hfill \\ \hfill -(1-\gamma )\sigma (u_{ij})(\hat{y}){\mathrm{e}}_k\cdot {\int }_{B_{\rho }}\eta +o(\rho ){\parallel \eta \parallel }_{1,\mathrm{\Omega }}.\end{array}$$

(B.31)

Let us show that the second term of the right hand side of equation (B.27) is actually $o(\rho )\Vert \eta \Vert _{1,\Omega }$. The estimate from Lemma 11 gives, for $\delta >0$ small enough, a constant $c_{(\delta )}$ such that for all $\eta \in H^{1}(\Omega )$

$$\begin{aligned} \left \rvert \int _{B_{\rho }} \eta (x) dx \right \rvert \leq c_{( \delta )} \rho ^{2-\delta } \Vert \eta \Vert _{1,\Omega } . \end{aligned}$$

(B.32)

In this manner, the first term on the right-hand side of equation (B.31) behaves as follows

$$ -(1-\gamma )\sigma (u_{ij})(\hat{y})\mathrm{e}_{k} \cdot \int _{B_{ \rho }} \eta = o(\rho )\Vert \eta \Vert _{1,\Omega } . $$

(B.33)

Let us develop the second term on the right-hand side of (B.31), $\int _{\Omega }\gamma _{\rho }\sigma (\delta \tilde{u}_{ij}^{\rho }) \mathrm{e}_{k}\cdot \eta$. We apply Green formula to this integral separated over $\Omega \setminus \overline{B_{\rho }}$ and over $B_{\rho }$. Denoting by $n$ the inward normal to the boundary $\partial B_{\rho }$, we obtain

$$\begin{array}{c}{\int }_{\mathrm{\Omega }}{\gamma }_{\rho }\sigma (\delta {\tilde{u}}_{ij}^{\rho }){\mathrm{e}}_k\cdot \eta =-{\int }_{\mathrm{\Omega }}{\gamma }_{\rho }\mathrm{div}(\mathbb{C}(\eta {\otimes }_s{\mathrm{e}}_k))\cdot \delta {\tilde{u}}_{ij}^{\rho }+{\int }_{\partial \mathrm{\Omega }}{\gamma }_{\rho }\mathbb{C}(\eta {\otimes }_s{\mathrm{e}}_k)n\cdot \delta {\tilde{u}}_{ij}^{\rho }\hfill \\ \hfill +(1-\gamma ){\int }_{{\mathrm{\Gamma }}_{\gamma }}\mathbb{C}(\eta {\otimes }_s{\mathrm{e}}_k)n\cdot \delta {\tilde{u}}_{ij}^{\rho }+(1-\gamma ){\int }_{\partial B_{\rho }}\mathbb{C}(\eta \otimes {\mathrm{e}}_k)n\cdot \delta {\tilde{u}}_{ij}^{\rho }.\end{array}$$

(B.34)

The first term of the right hand side of equation (B.34) is $o(\rho )\Vert \eta \Vert _{1,\Omega }$ according to Lemma 2 estimate (3.11). The second one is null because ℂ, $\eta$ and $\delta \tilde{u}_{ij}^{\rho }$ are $\Omega$-periodic. The third term is controlled by $\lVert \mathbb{C}(\eta \otimes _{s} \mathrm{e}_{k} )n \rVert _{-1/2, \Gamma _{\gamma }}\lVert \delta \tilde{u}_{ij}^{\rho }\rVert _{1/2,\Gamma _{\gamma }}$. On one hand we have $\lVert \mathbb{C}(\eta \otimes _{s} \mathrm{e}_{k} )n \rVert _{-1/2, \Gamma _{\gamma }} \leq c \lVert \eta \rVert _{1,\Omega }$, on the other $\lVert \delta \tilde{u}_{ij}^{\rho }\rVert _{1/2,\Gamma _{\gamma }} \leq c \lVert \delta \tilde{u}_{ij}^{\rho }\rVert _{1,\Omega _{R}}$, so that the third term is $O(\rho ^{2})\lVert \eta \rVert _{1,\Omega }$. The fourth term of the right hand side of equation (B.34) is controlled by . And we know from Lemma 12 that for all $\delta >0$ there exists a constant $c_{(\delta )}>0$ such that

(B.35)

The fourth term of the right hand side of equation (B.34) is $O(\rho ^{1-2\delta })\Vert \delta \tilde{u}_{ij}^{\rho } \Vert _{1, \Omega }\Vert \eta \Vert _{1,\Omega }$, which is, regarding the estimate from Lemma 2, $O(\rho ^{2-2\delta }) \Vert \eta \Vert _{1,\Omega }$. Thus

$$ \int _{\Omega }\gamma _{\rho }\sigma (\delta \tilde{u}_{ij}^{\rho }) \mathrm{e}_{k}\cdot \eta = o(\rho ) \Vert \eta \Vert _{1,\Omega } . $$

(B.36)

Finally, we end the preliminary calculations by rewriting the third term of equation (B.27) in view of the regularity of solutions. We find for all $\eta \in \mathcal{V}$

$$\begin{aligned} (1-\gamma )\int _{B_{\rho }}\sigma (\tilde{\tilde{u}}_{ijk}) \cdot \varepsilon (\eta ) &= (1-\gamma )\sigma (\tilde{\tilde{u}}_{ijk})( \hat{y})\cdot \int _{B_{\rho }} \varepsilon (\eta ) \\ &+ (1-\gamma )\int _{B_{\rho }}( \sigma (\tilde{\tilde{u}}_{ijk}) - \sigma (\tilde{\tilde{u}}_{ijk})(\hat{y}) )\cdot \varepsilon (\eta ) , \\ &= (1-\gamma )\sigma (\tilde{\tilde{u}}_{ijk})(\hat{y})\cdot \int _{B_{ \rho }} \varepsilon (\eta ) + o(\rho )\Vert \eta \Vert _{1,\Omega } . \end{aligned}$$

(B.37)

Proof of Lemma 3

We want to introduce the same kind of ansatz for the expansion of $\tilde{\tilde{u}}^{\rho }_{ijk}$ as in Lemma 2. For this purpose, let us set the field $w^{\rho }_{ijk}$ meant to cancel the first terms of the right hand sides of equations (B.30) and (B.37). So $w^{\rho }_{ijk}$ is defined as the solution to the following exterior problem:

(B.38)

where $h = -(1-\gamma )(\sigma (\tilde{\tilde{u}}_{ijk})(\hat{y}) + \mathbb{C} (\tilde{u}_{ij}(\hat{y}) \otimes _{s} \mathrm{e}_{k}))n$. The above boundary value problem admits an explicit solution with the same estimates as in Lemma 2 (see, e.g., [15]). Once again let us introduce

$$ w^{\rho , \epsilon }_{ijk}(y):= \textstyle\begin{cases} \ w^{\rho }_{ijk}(y) \quad & \hbox{if }y\in \Omega \setminus \overline{C}, \\ \ w^{\rho }_{C, ijk}(y) \quad & \hbox{if }y\in C, \end{cases} $$

(B.39)

where $C$ is the ring defined in (B.14), and $w^{\rho }_{C, ij}$ is solution to the following problem:

$$ \left \{ \textstyle\begin{array}{l} \textstyle\begin{array}{rll@{\quad }c@{\quad }l} \mathrm{div} (\sigma (w^{\rho }_{C, ijk})) & = & 0 & \text{in} & C, \\ w^{\rho }_{C, ijk} & = & 0 & \text{on} & \partial \Omega , \\ w^{\rho }_{C, ijk} & = & w^{\rho }_{ijk} & \text{on} & \partial C^{ \text{int}}. \end{array}\displaystyle \end{array}\displaystyle \right . $$

(B.40)

Now we can introduce the new ansatz:

$$ \tilde{\tilde{u}}^{\rho }_{ijk} = \tilde{\tilde{u}}_{ijk} + w^{\rho }_{ijk} + \big( \tilde{z}^{\rho }_{ijk} + \tilde{w}^{\rho }_{ijk} - w^{\rho }_{ijk} \big), $$

(B.41)

where $\tilde{w}^{\rho }_{ijk} = w^{\rho , \epsilon }_{ijk} - \langle w^{ \rho , \epsilon }_{ijk} \rangle$, so that $\tilde{w}^{\rho }_{ijk}\in \mathcal{V}$. In this way, we effectively have , with $\langle \tilde{z}^{\rho }_{ijk} \rangle = 0$. As in the proof of Lemma 2, we write the variational problem satisfied by $\tilde{z}^{\rho }_{ijk}$, applying the bilinear form $a_{\rho }$ to $\tilde{z}^{\rho }_{ijk}$ and a test function $\eta$. In view of (B.41) and the notations introduced before, the problem is expressed by

$$ \tilde{z}^{\rho }_{ijk}\in \mathcal{W}\; : \; a_{\rho }(\tilde{z}^{ \rho }_{ijk},\eta ) = a_{\rho }(\tilde{\tilde{u}}^{\rho }_{ijk},\eta ) - a_{\rho }(\tilde{\tilde{u}}_{ijk},\eta ) - a_{\rho }(\tilde{w}^{ \rho }_{ijk},\eta ) , \quad \forall \eta \in \mathcal{W}. $$

(B.42)

Let us develop this expression thanks to preliminary calculations (B.27), (B.30), (B.31) (B.33), (B.36), and (B.37). We obtain the variational problem

$$\begin{array}{c}{\tilde{z}}_{ijk}^{\rho }\in \mathcal{W}:{\int }_{\mathrm{\Omega }}{\gamma }_{\rho }\sigma ({\tilde{z}}_{ijk}^{\rho })\cdot \epsilon (\eta )=(1-\gamma )\mathbb{C}({\tilde{u}}_{ij}(\hat{y}){\otimes }_s{\mathrm{e}}_k)\cdot {\int }_{B_{\rho }}\epsilon (\eta )\hfill \\ \hfill +(1-\gamma )\sigma ({\tilde{\tilde{u}}}_{ijk})(\hat{y})\cdot {\int }_{B_{\rho }}\epsilon (\eta )-{\int }_{\mathrm{\Omega }}{\gamma }_{\rho }\sigma ({\tilde{w}}_{ijk}^{\rho })\cdot \epsilon (\eta )+o(\rho ){\parallel \eta \parallel }_{1,\mathrm{\Omega }},\mathrm{\forall }\eta \in \mathcal{W}.\end{array}$$

(B.43)

Let us apply the Green formula to $- \int _{\Omega } \gamma _{\rho }\sigma (\tilde{w}^{\rho }_{ijk}) \cdot \varepsilon (\eta )$ on domains $C\cap \Omega$, $(\Omega \setminus \overline{C\cup B_{\rho }})$, and $B_{\rho }$. In view of the definition of $\tilde{w}^{\rho }_{ijk}$ (B.38), and denoting by $n$ the inward normal to the boundary $\partial B_{\rho }$, we finally obtain that $\tilde{z}^{\rho }_{ijk}$ follows the variational problem:

$$\begin{array}{c}{\tilde{z}}_{ijk}^{\rho }\in \mathcal{W}:{\int }_{\mathrm{\Omega }}{\gamma }_{\rho }\sigma ({\tilde{z}}_{ijk}^{\rho })\cdot \epsilon (\eta )=-{\int }_{\partial \mathrm{\Omega }}\sigma (w_{C,ijk}^{\rho })n\cdot \eta \hfill \\ \hfill -{\int }_{\partial C^{\text{int}}}(\sigma (w_{C,ijk}^{\rho })-\sigma (w_{ijk}^{\rho }))n\cdot \eta +o(\rho ){\parallel \eta \parallel }_{1,\mathrm{\Omega }},\mathrm{\forall }\eta \in \mathcal{W}.\end{array}$$

(B.44)

In the same way as in Lemma 2, we find that the two first terms on the right-hand side of equation (B.44) are $o(\rho )\Vert \eta \Vert _{1,\Omega }$, and the bilinear form of the problem (B.18) being uniformly coercive on $\mathcal{W}$, and $\tilde{z}^{\rho }_{ij} \in \mathcal{V}$, we obtain

$$ \Vert \tilde{z}^{\rho }_{ijk} \Vert _{1,\Omega } = o(\rho ) . $$

(B.45)

Furthermore the solution $w^{\rho }_{ijk}$ of the classical problem (B.38) is explicitly known (see, e.g., [15]), gives rise to the same estimates as those written equations (B.13), and few developments lead as well to

$${\parallel {\tilde{w}}_{ijk}^{\rho }-w_{ijk}^{\rho }\parallel }_{1,\mathrm{\Omega }}=O({\rho }^2),$$

(B.46)

$${\parallel {\tilde{w}}_{ijk}^{\rho }-w_{ijk}^{\rho }\parallel }_{0,\mathrm{\Omega }}=o(\rho ).$$

(B.47)

Finally, the expansion (B.41) gives rise to the intended estimates (3.13), (3.14) and (3.15). □