1 Introduction

In recent years, composite materials have been used in many applications in civil and mechanical engineering. In the design of these materials, control and optimization of stress and displacement fields are serious goals. A special class of composite materials, known as Functionally Graded Materials (FGMs), has been gaining considerable attention by researchers and engineers. In these materials, both the composition and the structure change (usually continuously) along specific directions, resulting in corresponding changes in the properties of the material. In the simplest FGMs, two different material constituents change gradually from one to the other. The most common material of this kind compositionally grades from a ceramic material to a metal one.

The general idea of structural gradients was first advanced for composites in the Seventies [1]. However, there was no genuine investigation about how to design, fabricate and evaluate graded structures until the Eighties [2]. More recently, FGMs are present in many engineering applications such as space shuttles, nuclear fusion reactors and energy conversion systems [3]. Since FGMs are not homogeneous materials, it is clear that in order to create them, comprehensive studies need to be performed in design methodology and theoretical modeling as well as in processing and properties evaluation. On the other hand, unlike conventional homogeneous materials, the spatial variation of mechanical and physical properties in FGMs can be exploited to obtain better performances by micro-structural control.

Generally, the variation in material properties of FGMs is exclusively examined within two categories of analyses. While in the first one the mechanical and physical properties are assumed to vary according to specific functions with respect to spatial coordinates by means of the so called heterogeneity factors, the second category is based on the description of the material heterogeneity by means of volume fractions of the constituents. Volume fractions are in turn linked to the material properties through the so called micromechanical models, which may range from explicit traditional rule of mixtures, such as Voigt, Reuss, Mori-Tanaka and Wakashima-Tsukamoto models, to implicit ones (such as Hill-Budianski model) to variational ones (e.g., Hashin-Shtrikman model) [2].

Works pertaining to both categories can be found in the literature concerning, for instance, the torsion in bars [4], the stress concentration factors and the static, buckling, and free- and forced-vibration in plates [5, 6] as well as the out of plane displacement field in inclined cracks [7]. Besides, as far as axisymmetric bodies are concerned, several papers are devoted to the stress analysis in hollow cylinders subject to internal pressure [8], thermal [9] and axial [10] loads, pressure vessels [11] and rotating disks [12].

The optimum response of the material to an actual environment is one of the most important aspects in the design of FGMs [13], leading to interesting results for several different functionally graded structures. However, to the extent of our knowledge, the overwhelming majority of works belongs to the first category, namely dealing with optimization problems in FGMs which consist in finding the values of some tuning parameters of the heterogeneity factors for prefixed types of property variations (e.g., power-law, exponential, trigonometric models, etc.) such that an objective function is minimized or maximized. Gradient-based methods as well as meta-heuristic algorithms led researchers towards these objectives. For instance, a finite element based optimization of a pressure vessel consisting in a finite length hollow cylinder and two spherical closed ends has been performed in [14]. In [15], a combination of a co-evolutionary particle swarm optimization approach coupled with a differential quadrature method is applied to obtain minimized stress and displacement fields through the geometry of a disk under thermo-elastic loads. The thermo-mechanical analysis and optimization of functionally graded rotating hollow disks is dealt with in [16] using the sequential quadratic programming method. Not by chance, all the aforementioned works consider power-law property distributions, as they are simple and allow closed-form solutions amenable for numerical optimization, yet imposing considerable limitations to the generalization of the optimization procedures. In our opinion, another strong limitation not mentioned in the works cited above is that once fixed the class of property variation and once the optimized heterogeneity factors have been found, optimal solutions for material properties do not necessarily give rise to realistic structures, i.e., with unfeasible associated metallic and ceramic volume fractions, being considered a micromechanical model.

1.1 Motivation of the Work

The above mentioned facts entail that a more intrinsic optimization procedure should a priori consist in the search for the best volume fractions and not merely in the tuning of the parameters of prefixed property behaviors. In this case, the formulation of the resulting problem is also useful from the technological viewpoint. In fact, although it must be based on a micromechanical model to relate elastic properties to volume fractions, it does not hinder one to deal with a specified class of functions describing property variations.

To the extent of our knowledge, only a few studies concerning with a material tailoring approach have been addressed. For instance, in [17, 18] the inverse problem of finding the variation with the radius of the shear modulus is considered, yet it is desired that the difference between the radial and the hoop stress satisfies a particular relation along the radius. Moreover, in [19], the shear modulus such that stresses radially evolve in rubber-like cylinders and spheres within a more general functional constraint is sought. These latter works provide interesting solutions, however they have been written in a context different from that of optimal design, which is the framework of the present paper.

1.2 Objectives and Results

The present paper addresses the problem of finding the optimal composition profile of the constituents for axisymmetric bodies subject to mechanical loadings and for which plane elasticity holds. The material is assumed to be functionally graded in the radial direction. In light of these considerations, equilibrium, compatibility and constitutive relations are firstly recalled and a general background on the most used micromechanical models is then presented. The problem of minimizing the maximum equivalent stress is subsequently formulated and analytically solved in the context of dynamic optimization theory by means of Pontryagin’s Principle. Optimal solutions have been found to perform better than classic variations distributions, commonly employed in the literature, leading to promising results in terms of stress reduction. Finally, the effect of technological constraint on optimal solutions is discussed.

A first attempt to deal with the aforementioned optimization problem has been done for the first time in [20] for a functionally graded pressurized thick-walled cylinder within the plane stress condition. Nevertheless, the present paper remarkably presents three novelties that can be summarized as follows.

  • Firstly, different from [20] where only plane stress condition is considered, a unified mathematical approach for both plane stress and plane strain hypotheses is presented.

  • Secondly, goal functions are expressed in terms of constituents volume fractions and not merely in the property variations, making therefore the present framework suitable for technological aspects associated with the manufacture process.

  • Finally, it is shown that the proposed optimization framework can be applicable regardless of the involved micromechanical model, resulting novel from the theoretical viewpoint.

2 Governing Equations

Consider a radially graded axisymmetric hollow body and let \(R_{i}\) and \(R_{o}\) denote the inner and outer radii, respectively (see Fig. 1). Define a cylindrical coordinate system and let the radial, circumferential and axial coordinates be denoted by \(r\), \(\theta \) and \(z\), respectively.

Fig. 1
figure 1

Schematic representation of the axisymmetric hollow body considered in the analysis

Full size image

If the body is subject to an axially-uniform and axisymmetric loading, then deformations are also axisymmetric, i.e., they vary only in the radial direction. In particular, the strains and the internal stresses, denoted by \(\varepsilon _{i}\) and \(\sigma _{i}\) (with \(i=r,\theta ,z\)), respectively, are supposed to be continuous functions of \(r\) only.

According to the theory of elasticity, a problem may be simplified if either one of the stresses or the strains is zero along a particular direction. Such behaviors are referred to as plane stress (in which a generic infinitesimal element is subject to a biaxial stress condition accompanied by a triaxial strain state) and plane strain (in which a generic infinitesimal element is subject to a triaxial stress condition accompanied by a biaxial strain state), respectively. The resulting elastic problem may be formulated following either Beltrami-Michell or Navier approaches, so far as boundary conditions are expressed in terms of radial stresses or displacements, respectively [21]. With reference to the former approach, herein used for convenience, the equilibrium equation written for the infinitesimal element in the radial direction and the consideration of Hooke’s constitutive laws for linear, elastic, isotropic and non-homogeneous materials entail that both the hoop \(\sigma _{\theta }\) and axial \(\sigma _{z}\) stresses may be written in terms of the radial stress \(\sigma _{r}\). Consequently, the stress analysis may be described in terms of \(\sigma _{r}\) only.

In the following, the governing equations are written within the plane stress state assumption, while several remarks are given when the plane strain condition applies.

2.1 Equilibrium, Kinematic and Constitutive Laws

According to the infinitesimal linear elasticity theory (in absence of body forces), the stress equilibrium equation in the radial direction may be written in the form [22]

$$ (r\sigma _{r}(r))'-\sigma _{\theta }(r)=0, $$
(1)

where the prime symbol denotes a first derivative with respect to \(r\). The strain-displacement (or kinematic) equations for an axisymmetric body loaded by axisymmetric forces are

$$ \varepsilon _{r}(r)=u'(r),\ \ \varepsilon _{\theta }(r)=u(r)/r, $$
(2)

where \(u\) is the radial displacement, while the plane stress state Hookean constitutive relations in terms of Young’s modulus \(E(r)\) and Poisson’s coefficient \(\nu \) (assumed constant along the radius due to its marginal variation among a wide range of materials), are

$$ \varepsilon _{r}=\frac{\sigma _{r}-\nu \sigma _{\theta }}{E},\ \ \varepsilon _{\theta }=\frac{\sigma _{\theta }-\nu \sigma _{r}}{E},\ \ \varepsilon _{z}=-\frac{\nu (\sigma _{r}+\sigma _{\theta })}{E}. $$
(3)

In the last equations and hereafter, the dependence on \(r\) is omitted for the sake of a simple notation.

Remark 1

For the plane strain condition, Hookean constitutive relations are obtained substituting \(E\) with \(\frac{E}{1-\nu ^{2}}\) and \(\nu \) with \(\frac{\nu }{1-\nu }\) and imposing \(\varepsilon _{z}=0\).

The radial strain in (2) can be written as

$$ \varepsilon _{r}=(\varepsilon _{\theta }r)'=\left ( \frac{\sigma _{\theta }}{E}r-\nu \frac{\sigma _{r}}{E}r\right )', $$
(4)

which, together with (3), yields

$$ (\sigma _{\theta }-\sigma _{r})(E+\nu E)-(\sigma _{\theta }-\nu \sigma _{r})E'r+Er \sigma _{\theta }'-\nu E r \sigma _{r}'=0. $$
(5)

From (1) the hoop stress \(\sigma _{\theta }\) and its first derivative with respect to \(r\) are

$$ \sigma _{\theta }=\sigma _{r}+r\sigma _{r}' $$
(6)

and

$$ \sigma _{\theta }'=2\sigma _{r}'+r\sigma _{r}'', $$
(7)

respectively. Substituting (6) and (7) in (5) and rearranging the terms one obtains

$$ \mathcal{O}{\sigma }_{r}=0 $$
(8)

where \(\mathcal{O}\) is a differential operator given by

$$ \mathcal{O}(.)={r}^{2}(.)''+{r}(3-{r}{\mathcal{E}}')(.)'-\tilde{\nu }{r}{ \mathcal{E}}'(.) $$
(9)

with \({\mathcal{E}}=\ln (E)\) and \(\tilde{\nu }=1-\nu \).

Remark 2

If the plane strain condition holds, the differential operator reads

$$ \mathcal{O}(.)={r}^{2}(.)''+{r}(3-{r}{\mathcal{E}}')(.)'-\breve{\nu }{r}{ \mathcal{E}}'(.), $$
(10)

where \(\breve{\nu }=1-\frac{\nu }{1-\nu }\).

2.2 Micromechanical Models

Realistic predictions of the stress and strain behavior of FGMs require appropriate constitutive relations. This aspect represents the most significant difficulty in FGM modeling when subjected to thermal or mechanical loading conditions. Efforts to analytically determine the effective properties of heterogeneous structures were initiated more than a century ago by such famous scientists as Maxwell, Lord Rayleigh, and Einstein [2] (see also the work by O.F. Mossotti [23]). Recently, due to the increased interest in composite structures for industrial applications, the subject of composite materials properties has been thoroughly developed, and a large literature nowadays exists. In several extensive review articles and textbooks, both good overviews of the subject and insight into the significant involved complexities are provided (see, e.g., [24, 25, 33]). For simple geometries and reasonably simple material properties (e.g., elastic behavior) analytical solutions are often available in terms of volume fractions. It is worthwhile to note that most of the micromechanical models are expressed in terms of effective bulk \(K\) and shear \(G\) moduli. Because of the isotropic assumption, these latter are linked to the Young’s modulus by the relation

$$ E=\frac{9KG}{3K+G}. $$
(11)

2.2.1 Voigt (V) and Reuss (R) Models

The simplest micromechanical model to achieve the equivalent macroscopic material properties is the rule of mixture which was first formulated by Voigt. Voigt’s idea is to determine material properties by averaging stresses over all phases with the strain uniformity assumption within the material [2]. The resulting model, that is frequently used in most FGM analyses, estimates Young’s modulus of FGMs as a volume based arithmetic average, i.e., [26]

$$ E=E_{m}V_{m}+E_{c}V_{c}, $$
(12)

where \(E_{m}\) and \(E_{c}\) are Young’s moduli of the metal and ceramic constituents and \(V_{m}\) and \(V_{c}\) are their volume fractions, respectively, both functions of \(r\) and related to each other by the relation

$$ V_{c}+V_{m}=1. $$
(13)

It is convenient to rewrite (12) in terms of one volume fraction function only (usually \(V_{c}\)) exploiting (13), namely

$$ E=E_{m}(1-V_{c})+E_{c}V_{c}=E_{m}+(E_{c}-E_{m})V_{c}. $$
(14)

Another well-known mixture rule is that based on the harmonic mean estimate (Reuss model), namely [2]

$$ E=\frac{E_{c}E_{m}}{E_{m}V_{c}+(1-V_{c})E_{c}}. $$
(15)

In their most basic form, the above rules of mixtures are employed using bulk constituent properties, assuming no interactions between phases. They are often used for FGMs, since a single relationship can be used for all volume fractions and micro-structures. However, due to their simplicity, their validity is limited.

2.2.2 Mori-Tanaka (MT) Model

The Mori-Tanaka model provides effective mechanical properties estimation of a graded micro-structure with ceramic and metal phases. The steps for obtaining the overall material properties depend on the bulk and shear moduli of the metal and the ceramic. More precisely, if \(K_{m}\) and \(K_{c}\), \(G_{m}\) and \(G_{c}\) denote bulk and shear moduli of the metal and ceramic, respectively, the effective bulk \(K\) and shear \(G\) moduli are given by [27]

$$ K=\frac{(K_{c}-K_{m})V_{c}}{1+\frac{3(K_{c}-K_{m})}{3K_{m}+4G_{m}}(1-V_{c})}+K_{m} $$
(16)

and

$$ G= \frac{(G_{c}-G_{m})V_{c}}{1+\frac{(G_{c}-G_{m})}{G_{m}+\frac{G_{m}(9K_{m}+8G_{m})}{6(K_{m}+2G_{m})}}(1-V_{c})}+G_{m}. $$
(17)

2.2.3 Other Models

It is worth to note that several other models are covered in the literature, such as the models proposed by Wakashima and Tsukamoto [28], Tamura [29], by Hashin and Shtrikman [30], by Kerner [31] or by Ravichandran [32]. Recently [33], a comparison of various analytical methods with experimental data is graphically made to find out the best suitable micromechanical model.

Notwithstanding the above mentioned models generally yield dissimilar estimates (discrepancies of more than \(50\%\) may be observed in the case of some volume fractions [6]), they are explicit in terms of phases’ volume fractions, offering a possibility to estimate the FGM properties for the whole composition range with a single model.

3 Formulation of the Optimization Problem

In order to formulate the optimization problem in the context of dynamic optimization theory, a state-space representation, boundary conditions and a goal functional are needed.

3.1 State-Space Representation and Boundary States

Firstly, since the Young’s modulus is a function of the ceramic volume fraction, namely \(E=E(V_{c})\), the term \(\mathcal{E}'\) can be written as

$$ \mathcal{E}'=(\ln (E(V_{c})))'=g(V_{c})v_{c}, $$
(18)

where \(v_{c}=\frac{dV_{c}}{dr}\) (the rate of change of the ceramic volume fraction through the domain) is chosen to be the control function and

$$ g(V_{c})=\frac{1}{E(V_{c})}\frac{dE(V_{c})}{dV_{c}}, $$

whose explicit expression is derived from the involved micromechanical model.

Introducing the state variables \(x_{1}={\sigma }_{r}\), \(x_{2}=d{\sigma }_{r}/d{r}\) and \(x_{3}=V_{c}\), the differential equation (8) may be written as the first-order non-linear system

$$ \textstyle\begin{cases} x_{1}^{\prime }=x_{2}\,,\\ x_{2}'=\displaystyle g(x_{3})v_{c}\left (x_{2}+\tilde{\nu }\frac{x_{1}}{{r}} \right )-\frac{3x_{2}}{{r}},\\ x_{3}'=v_{c}, \end{cases} $$
(19)

or, defining \({\mathbf{x}}=(x_{1}\,\,x_{2}\,\,x_{3})\), in more compact form as

$$ \textbf{x}'=\textbf{f}(r,\textbf{x}(r),v_{c}(r)). $$
(20)

Note that not all the boundary states are specified. In particular, \(x_{1}(R_{i})\) and \(x_{1}(R_{o})\) can be deduced from the mechanical loads, yielding

$$ x_{1}(R_{i})=-p_{i}, \ x_{1}(R_{o})=0, $$
(21)

while \(x_{2}(R_{i})\) and \(x_{2}(R_{o})\) are unknown. As far as concerns \(x_{3}\), if the cylinder is compositionally graded from ceramic to metal, then

$$ x_{3}(R_{i})=1, \ x_{3}(R_{o})=0. $$
(22)

3.2 Goal Functional

In this paper, goal functionals of the Mayer form are considered, consisting in a function \(\mathcal{K}\) depending on the initial and final state conditions, namelyFootnote 1

$$ J(v_{c})=\mathcal{K}(\textbf{x} (R_{i}),R_{i},\textbf{x} (R_{o}),R_{o}). $$
(23)

Taking into account the plane-stress condition and using the above introduced state variables and Eq. (6), the equivalent Tresca stress may be written as

$$ {\sigma }_{eq}^{T}=|{\sigma }_{\theta }-{\sigma }_{r}|=|x_{1}+{r}x_{2}-x_{1}|=|{r}x_{2}|. $$

Now if the body is pressurized only internally, \(x_{1}\) strictly increases along the radius (\(x_{2}>0\)) and \(\sigma _{eq}^{T}\) achieves its maximum value at the inner radius. Therefore, taking

$$ \mathcal{K}=x_{2}(R_{i}) $$

leads to the minimization of the maximum Tresca stress, being fixed \(R_{i}\).

Remark 3

The same problem can be stated within the plane-strain condition, taking into account that \(\sigma _{z}=\nu (\sigma _{r}+\sigma _{\theta })=\nu (2x_{1}+rx_{2})\).

3.3 Constraints

According to [13], there are a few optimization studies in which the manufacturability cost is taken into consideration. Adding technological constraints to the optimization studies is highly recommended since it leads to more practical designs with prospects of being produced in large scales. To this purpose, one may model the cost in such a way that steep variations of the volume fractions along the radius are, reasonably, more costly and more difficult to obtain than moderate variations. As a consequence, in the present optimization framework, it is reasonable to assume that \(v_{c}\) be constrained in an admissible range of values. More precisely, we assume, for all values of \(r\), \(v_{c}\in [v_{-},v_{+}]\). Note that the following analysis remains unchanged if, instead of \([v_{-},v_{+}]\), one considers the union of a set of disjoint closed and bounded intervals \([v_{-},v_{1}]\cup [v_{2},v_{3}]\cup \cdots \cup [v_{n},v_{+}]\), with \(v_{-}< v_{1}<\cdots <v_{n}<v_{+}\), thus including in the model also situations for which, for some technological reasons, some values of \(v_{c}\) between \(v_{-}\) and \(v_{+}\) are not admissible. Suitable values for \(v_{-}\) and \(v_{+}\) can be deduced from fixed radial property variations or from technological process data.

3.4 Statement

The optimization problems can now be stated formally. In the formulation of the problem, as well as in the computation of the solution, reference is made to the goal functional (23) in its general form. Hence, solutions to the maximum Tresca stress minimization problem within the plane stress and plane strain conditions can be found in a common fashion.

Problem 1

Given the dynamical system (20) and the boundary conditions (21) and (22), find the control function \(v_{c}:[R_{i},R_{o}]\to [v_{-},v_{+}]\) such that the functional (23) is minimized.

To solve Problem 1 analytically, the dynamic optimization theory is considered [34]. In particular, Pontryagin’s Minimum Principle is applied in order to find the optimal solution. Many engineering problems have been considered using this method, ranging from strongest columns against buckling [35], to cylinders and spheres of minimum strain energy [36], to minimum weight rod hanging under gravitational load from a fixed support [37] and to minimum weight straight pin fins [38] (see also the introductory book [39] where several engineering applications are described).

4 Solution to the Optimization Problem

Pontryagin’s principle applied to Problem 1 states that the optimal control function \(v_{c}\), i.e., the one which minimizes the cost functional \(J(v_{c})\) is, among all admissible functions, the one which, at any value of \({r}\), minimizes the Hamiltonian function \(\mathcal{H}({r},{\mathbf{x}},{\mathbf{p}},v_{c})\) defined by [34]

$$ \mathcal{H}=\textbf{p}^{\top }\textbf{f} $$
(24)

where \({\mathbf{p}}=(p_{1}\,\,p_{2}\,\,p_{3})\) is the vector of the so called co-state variables, all functions of \(r\). Recalling (19), the Hamiltonian function ℋ exhibits a linear dependence on the control function \(v_{c}\), i.e., Eq. (24) can be written as

$$ \mathcal{H}=s+qv_{c}\,, $$
(25)

where \(s\) and \(q\) are functions of the states and co-states, whose explicit expressions for the plane-stress condition are given by

$$ s=p_{1}x_{2}-\frac{3p_{2}x_{2}}{r},\ \ q=g(x_{3})p_{2}\left (x_{2}+\tilde{\nu } \frac{x_{1}}{r}\right )+p_{3}. $$
(26)

Since the problem is characterized by a Hamiltonian function linear with respect to \(v_{c}\) and since the set of admissible values for \(v_{c}\) is compact, Pontryagin’s Principle yields extremal solution for the minimization of (25). More precisely, the optimal control function \(v_{c}^{*}\) is defined by

$$ v_{c}^{*}(r)=\arg {\min _{v_{c}}{\mathcal{H}({r},{\mathbf{x}},{\mathbf{p}},v_{c})}}= \left \{ \textstyle\begin{array}{l@{\quad }l} v_{-}\,, & \text{ if }q(r)>0\,, \\ v_{+}\,, & \text{ if }q(r)< 0\,, \end{array}\displaystyle \right . $$
(27)

that is, the optimal control function only may assume its minimum or maximum value, possibly switching among them when \(q=0\). In the parlance of the control theory, the design admits a “bang-bang” control scenario, jumping in value at certain points \({r}_{j}\) (with \(j=1,2,3,\ldots\)). The roots of \(q\) are called switching points since the control function switches from a bound to the other. Recalling the definition of \(v_{c}\), optimal ceramic volume fraction \(V_{c}^{*}\) turns out to be piece-wise linear with respect to \({r}\). This conclusion is particularly interesting since the piece-wise linearity is supposed to be the simplest volume fraction profile among all possible forms of variation.

4.1 Computational Aspects

Equation (27) does not yet provide the explicit expression of the optimal solution; in fact, it is clear that in order to know the explicit value of \(v_{c}\) for any value of \({r}\) one should know the value of \(q\). In turn, the computation of \(q\) requires the knowledge of the solution of the dynamical system (19) and of the differential equations [34]

$$ p_{k}'=-\frac{\partial \mathcal{H}}{\partial x_{k}} $$
(28)

for the co-states, which for the plane-stress condition are given by

$$ \textstyle\begin{cases} \displaystyle p_{1}'=-\frac{\tilde{\nu }p_{2}g(x_{3})v_{c}}{r}, \\ \displaystyle p_{2}'=-p_{1}-p_{2}g(x_{3})v_{c}+\frac{3p_{2}}{r}, \\ \displaystyle p_{3}'=-p_{2}\frac{dg(x_{3})}{dx_{3}}v_{c}\left (x_{2}+\tilde{\nu } \frac{x_{1}}{r}\right ). \end{cases} $$
(29)

Boundary conditions for co-states are determined by the transversality conditions [34]

$$ p_{2}(R_{i})=-\frac{\partial \mathcal{K}}{\partial x_{2}(R_{i})}, \ p_{2}(R_{o})= \frac{\partial \mathcal{K}}{\partial x_{2}(R_{o})}, $$
(30)

which, once again, for the plane-stress condition, yield

$$ p_{2}(R_{i})=-1,\ p_{2}(R_{o})=0. $$
(31)

Remark 4

The state-space representation, boundary states, co-state equations and boundary co-states for the plane-strain condition are the same as (19)–(22), (28) and (31), provided that \(\tilde{\nu }\) is replaced by \(\breve{\nu }\).

The application of Pontryagin’s Principle, therefore, leads to a system of six first-order and coupled non-linear differential equations described by (19) and (28), that has to be solved taking into account the six boundary conditions (21), (22) and (30).

Remark 5

Usually, to solve a non-linear dynamical systems like (19)–(28), numerical tools (such as the shooting methods or the pseudospectral methods) are needed. The implementation of these algorithms may give raise to convergence and computational issues, due to the non-linear nature of the involved equations, which are beyond the scopes of this article and could be addressed in future investigations.

Remark 6

The optimization problem above could be solved also by searching for the solution to the Hamilton-Jacobi-Bellman (HJB) equation, as in classic dynamic programming [40]. However, Pontryagin’s principle allows one to understand some characteristics of the optimal control function without knowing the explicit solution to the HJB equation which, in the non-linear case under investigation, would not be easy to find. Analogously, the validity of a candidate optimal control function could be analysed according to the verification principle, yet the application of this principle would require the integration of (19) which is beyond the scope of the article.

4.2 Single Switching Point Case

To overcome the computational burden of the numerical approach, special attention is drawn to the case in which \(q\) has only one root, i.e., when the optimal solution admits a single switching point. Beside its simplicity, this choice is justified since the resulting volume fraction profile is amenable for physical realization from the technological viewpoint. Denoting by \(\bar{v}\) the rate of the linear variation between \(x_{3}(R_{i})=1\) and \(x_{3}(R_{o})=0\), namely

$$ \bar{v}=-\frac{1}{R_{o}-R_{i}}\,, $$

two situations may occur. Firstly, if \(\bar{v}\notin [v_{-},v_{+}]\), there is no feasible solution, since no variation \(v_{c}:[R_{i},R_{o}]\to [v_{-},v_{+}]\) is consistent with the boundary conditions (see Fig. 2, left). As a consequence, no optimal solution exists either.

Fig. 2
figure 2

Optimal control function \(V_{c}^{*}\) and definition of \(\bar{v}\), \(v_{-}\), \(v_{+}\), \(r_{1}\) and \(r_{2}\). Case \(\bar{v}\notin [v_{-},v_{+}]\) (left) where no solutions are feasible and \(\bar{v}\in [v_{-},v_{+}]\) (right) where two solutions may exist (black and grey solid lines)

Full size image

On the other hand, if \(\bar{v}\in [v_{-},v_{+}]\), two optimal solutions are possible. More precisely, one characterized by a subinterval in which \(v_{c}=v_{+}\) followed by a subinterval in which \(v_{c}=v_{-}\) (black bold line in Fig. 2, right) and the other one with the opposite situation (first \(v_{c}=v_{-}\) and then \(v_{c}=v_{+}\), as in the grey bold line in Fig. 2, right). With reference to Fig. 2, right, the switching points \(r_{1}\) and \(r_{2}\) can be geometrically determined as

$$ r_{1}=\frac{-1-v_{-}R_{o}-v_{+}R_{i}}{v_{+}-v_{-}},\ \ r_{2}= \frac{1-v_{-}R_{i}+v_{+}R_{o}}{v_{+}-v_{-}}. $$
(32)

Remark 7

It is worth to point out that, in general, not all the dynamic optimization problems admit a formulation or a closed-form solution as in the case considered above. In some cases, one must resort to numerical approximation techniques, including neural networks or genetic algorithms, to which several works available in the literature are dedicated (see, among the others, [41–44]).

5 Numerical Example

We now show a numerical example concerning the design of a family of internally pressurized thick-walled FG cylinders where the material variation has to be chosen to minimize the maximum equivalent Tresca stress. We first show the results obtained with three “classic” material variations widely used in the literature. These results are then compared with the ones associated with the optimal solution described in the previous section where, for simplicity, a single switching point is supposed to exist. The inner radius is selected to be \(20\text{ mm}\), while the outer radius is chosen to vary from \(R_{o,min}=30\text{ mm}\) to \(R_{o,max}=50\text{ mm}\). The hollow cylinder is subject to an internal pressure \(p_{i}=10\text{ MPa}\). Alumina and steel are taken as the ceramic and metallic constituents at the inner and outer radii, respectively. Young’s modulus, as well as bulk and shear moduli of both materials are summarized in Table 1, while Poisson’s ratio is chosen to be \(\nu =0.3\).

Table 1 Mechanical properties of alumina and steel
Full size table

5.1 Results of Classic Variations

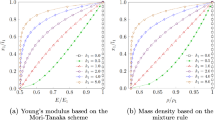
In a first analysis, linear, sinusoidal and sigmoidal volume fraction profiles have been taken into account. They are widely used in the literature and exhibit different stress behaviors throughout the thickness. Employing the micromechanical models introduced in Sect. 2, effective bulk and shear moduli are obtained while the effective Young’s modulus is derived using (11). Figure 3 shows the above mentioned volume fractions and the associated Young’s moduli for a fixed \(R_{o}/R_{i}\) ratio.

Fig. 3
figure 3

Linear, sinusoidal and sigmoidal volume fractions (left) and the associated Young’s moduli (right) by Voigt (solid line), Reuss (dotted line) and Mori-Tanaka (dashed line) micromechanical models

Full size image

A finite element model (whose details are omitted for brevity) has been developed to numerically forecast the stress behavior within the plane-stress and plane-strain conditions. Numerical values for the maximum Tresca stress have been computed for selected \(R_{o}/R_{i}\) ratios. The effect of micromechanical models on the stress responses can be readily seen in Table 2, where the values of the ratio \(\sigma _{max}^{T}/p_{i}\) are reported. Voigt and Reuss estimates yield the lowest and highest normalized maximum equivalent stress values, respectively, for all the aforementioned volume fraction profiles, while results for Mori-Tanaka model present an intermediate stress behavior. Moreover, the employment of a sigmoidal volume fraction leads to lower \(\sigma _{max}^{T}/p_{i}\) values with respect to the linear and sinusoidal ones, regardless of the involved micromechanical model.

Table 2 Numerical values of \(\sigma _{max}^{T}/p_{i}\) for linear, sinusoidal and sigmoidal volume fraction profiles and for Voigt (V), Reuss (R) and Mori-Tanaka (MT) micromechanical models
Full size table

5.2 Results of the Pontryagin Solution

Solutions associated with the Pontryagin’s Principle have been, then, investigated and compared to the three above-mentioned volume fractions. In light of the single switching point assumption, two possible extremal solutions may occur (see Eq. (32)). One of the two solutions corresponds to the minimum value of \(\sigma _{max}^{T}/p_{i}\), while the other one can be discarded.

Upper and lower limits for \(v_{-}\) and \(v_{+}\), respectively, are firstly determined. In particular, from simple geometric considerations, an optimal solution exists for all \(R_{o}/R_{i}\) ratios when

$$ v_{-}< \frac{1}{R_{i}-R_{o,min}}=-1/10,\ \ v_{+}>\frac{1}{R_{i}-R_{o,max}}=-1/30. $$
(33)

Two suitable values for \(v_{-}\) and \(v_{+}\) are therefore preliminary chosen to be −0.2 and −0.02, respectively (\({v_{-}}/{v_{+}}=10\)). The associated extremal solutions for ceramic volume fractions and the effective Young’s moduli obtained by Voigt, Reuss and Mori-Tanaka models are represented in Fig. 4 as \(R_{o}/R_{i}\) increases. The equations for the locus of switching points can be derived easily from (32), showing a linear dependence with respect to \(R_{o}/R_{i}\), being fixed \(v_{-}/v_{+}\). In particular, the switching points \(r_{1}\) and \(r_{2}\) get close to the inner and outer radii, respectively, as \(R_{o}/R_{i}\) increases.

Fig. 4
figure 4

Extremal solutions for ceramic volume fractions and the locus of switching points as \(R_{o}/R_{i}\) increases (left) and the associated effective Young’s moduli (right) by Voigt (solid lines), Reuss (dotted lines) and Mori-Tanaka (dashed lines) micromechanical models with \(v_{-}/v_{+}=10\)

Full size image

Numerical values of \(\sigma _{max}^{T}/p_{i}\) for both extremal solutions are reported in Table 3, showing worse and best stress scenarios when the switching point occurs at \(r_{1}\) and \(r_{2}\), respectively. These considerations allow one to conclude that the optimal solution is the one associated with \(r_{2}\) (grey bold line in Fig. 2, right) while the one associated with \(r_{1}\) (black bold line in Fig. 2, right) has to be discarded.

Table 3 Numerical values of \(\sigma _{max}^{T}/p_{i}\) for both extremal scenarios with \(v_{-}/v_{+}=10\) and for Voigt (V), Reuss (R) and Mori-Tanaka (MT) micromechanical models
Full size table

5.3 Comparison

From the results described above, it is clear that the optimal solution, despite its simplicity, outperform the classical linear, sinusoidal and sigmoidal variations. Taking for instance \(R_{o}/R_{i}=1.50\) and considering Voigt and Mori-Tanaka models, optimal volume fraction profile shows, for the Pontryagin’s solution, a significant normalized maximum equivalent stress reduction of about 10%, 15% and 9% with respect to the linear, sinusoidal and sigmoidal ones, respectively, for both plane-stress and plane-strain conditions. The reduction percentages read slightly higher considering Reuss model for the same \(R_{o}/R_{i}\) ratio. The normalized maximum equivalent stress reduction percentage decreases as \(R_{o}/R_{i}\) increases, reaching averagely 3% for \(R_{o}/R_{i}=2.50\).

To further analyse the performance of the Pontryagin’s solution the effect of the \(v_{-}/v_{+}\) has also been investigated. We have pointed out above that volume fraction profiles switching at \(r_{1}\) can be discarded. As a consequence, numerical analyses have been performed considering only the switching in \(r_{2}\) (grey bold line in Fig. 2, right). In particular, results have been obtained by keeping \(v_{+}\) constant and acting on \(v_{-}\) only. The resulting volume fraction profile is characterized by a switching point \(r_{2}\) getting linearly closer to \(R_{o}\) as \(v_{-}/v_{+}\) increases. Figure 5 shows the optimal volume fraction profiles and the corresponding switching points for \(v_{-}/v_{+}=10, 20, 30\) and for \(R_{o}/R_{i}=1.5, 2\). The corresponding numerical values of \(\sigma _{max}^{T}/p_{i}\) are listed in Table 4 considering only Voigt and Reuss models for the assessment of lower and higher stress behaviors, respectively, showing further maximum stress reduction as \(v_{-}/v_{+}\) increases (see Table 3, where results are reported for \(v_{-}/v_{+}=10\)).Footnote 2

Fig. 5
figure 5

The effect of the variation of \(v_{-}/v_{+}\) on the optimal volume fraction profile for two instances of \(R_{o}/R_{i}\)

Full size image
Table 4 The effect of variation of \(v_{-}/v_{+}\) on the normalized maximum Tresca stress \(\sigma _{max}^{T}/p_{i}\) for two instances of \(R_{o}/R_{i}\)
Full size table

6 Conclusions

Material property variation in functionally graded materials has been reported in the context of dynamic optimization theory. In particular, optimal volume fractions for maximum equivalent stress minimization problem in axisymmetric bodies within the theory of plane elasticity is analytically derived by means of Pontryagin’s Principle. The optimization framework is independent of the involved micromechanical model. Optimal volume fraction profiles turn out to be piece-wise linear along the radius, consequence of a bang-bang control scenario and amenable for physical realization. Comments on a special class of optimal solutions are addressed and a numerical example considering a pressurized functionally graded cylinder is performed. Maximum equivalent stresses are numerically assessed and compared to those obtained by other gradations found in literature. The achieved results are encouraging and future works may be extended to deal with other axisymmetric components with loads of different kinds, e.g., thermal, electric and magnetic.