Abstract
The purpose of this work is the formulation of energetic constitutive relations for thermoelasticity of non-simple materials based on atomistic considerations and equilibrium statistical thermodynamics (EST). In particular, both (unrestricted) canonical, and (restricted) quasi-harmonic, formulations are considered. In the canonical case, (spatial) non-locality results from relaxation of the assumption that atoms subject to continuum deformation change position uniformly and affinely. In the quasi-harmonic case, the analogous assumption on mean atomic position (i.e., Cauchy-Born) is relaxed. Two types of spatial non-locality, i.e., strong and weak, are considered. In the former case, atomic position (or mean position) is a functional of the deformation gradient \(\boldsymbol{F}\), while in the latter, this functional is approximated by a function of \(\boldsymbol{F}\) and its higher-order gradients \(\nabla^{1}\!\boldsymbol{F},\ldots ,\nabla^{n}\!\boldsymbol{F}\). On this basis, canonical and quasi-harmonic non-local model relations are obtained for the thermoelastic free energy, entropy, internal energy, and stress. In addition, such relations are formulated for thermoelastic material properties (e.g., stiffness).
In the second part of the work, basic relations from the continuum thermodynamics of (non-polar) simple materials are generalized to higher-order deformation gradient (i.e., weakly non-local) continua and applied to energetic thermoelasticity. The corresponding formulation is based in particular on (i) Euclidean frame-indifference of the energy balance and (ii) the dissipation principle. As in the standard case, necessary for (i) is linear momentum balance and the symmetry of the (generalized) Kirchhoff stress (i.e., angular momentum balance). In the context of (ii), the free energy density determines in particular the first Piola-Kirchhoff stress \(\boldsymbol{P}\), the higher-order stress measures  conjugate to \(\nabla^{1}\!\boldsymbol{F},\ldots ,\nabla^{n}\!\boldsymbol{F}\), as well as the generalized Kirchhoff stress. Modeling the phenomenological free energy on the corresponding (weakly non-local) canonical free energy yields EST-based constitutive forms for the entropy, all stress measures, and thermoelastic material properties. Alternatively, one can model the former energy as an approximation to the latter. An example of this for the second-order (\(n=2\)) case is discussed both theoretically and computationally in the last part of the work.
conjugate to \(\nabla^{1}\!\boldsymbol{F},\ldots ,\nabla^{n}\!\boldsymbol{F}\), as well as the generalized Kirchhoff stress. Modeling the phenomenological free energy on the corresponding (weakly non-local) canonical free energy yields EST-based constitutive forms for the entropy, all stress measures, and thermoelastic material properties. Alternatively, one can model the former energy as an approximation to the latter. An example of this for the second-order (\(n=2\)) case is discussed both theoretically and computationally in the last part of the work.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
The formulation of continuum constitutive relations based on discrete ab initio and/or atomistic considerations and methods rather than on continuum phenomenology alone has been pursued for many classes of materials in the literature. In the case of solids crystals, for example, Wallace [30, Chaps. 2–3] formulated zero-temperature hyperelasticity for simple materials based on an interatomic potential (see also, e.g., [23, §8.1.2]). This treatment was extended to finite temperature and energetic thermoelasticity (i.e., without heat conduction and viscosity) for simple materials by Wallace [30, Chaps. 4–5] and more recently [31] in the context of (quantum) phonon thermodynamics (see also, e.g., [23, §8.1.3]). Among other things, the establishment of (quantum) density functional theory for the quantitative determination of material properties (for a detailed review, see, e.g., [23, Chaps. 4–5]), as well as continuum modeling of nanoscopic systems and processes, has maintained interest in the formulation of continuum constitutive models based on ab initio and/or atomistic considerations. For example, a quantitative elastic stored energy model for simple materials was recently formulated in [24] based on atomistic considerations and quantum density functional theory (DFT) in terms of material-symmetry-adapted strain tensor components and determined the corresponding elastic stiffnesses.
One purpose of the current work is the generalization of such formulations for energetic thermoelasticity to non-simple materials in the context of equilibrium statistical thermodynamics (EST). As detailed in what follows, this results in general in strongly non-local (SNL) constitutive relations, i.e., relations which are functionals of the deformation gradient \(\boldsymbol{F}\). Also treated in this work is the weakly non-local (WNL) approximation of these, i.e., functions of the deformation gradient \(\boldsymbol{F}\) and its higher-order gradients \(\nabla ^{1}\boldsymbol{F},\ldots ,\nabla ^{n}\boldsymbol{F}\). Both non-local formulations represent broad non-local generalizations of existing treatments (e.g., [23, §§8.1.2–8.1.3]).
To employ such constitutive relations in the continuum modeling of non-simple materials, a formulation of corresponding basic field and balance relations is required. To this end, a second purpose of the current work is the phenomenological formulation of such relations for higher-order deformation gradient (i.e., WNL) continua in the context of continuum thermodynamics (e.g., [29]). Since the pioneering works of Mindlin (e.g., [14, 15]) or Toupin (e.g., [26]), a number of extensions and generalizations have been pursued. For example, direct generalization of the formulation of [14] to geometrically non-linear isothermal gradient hyperelasticity has been carried out in [10]. In contrast to the variational formulation common in these works, a direct formulation is pursued in the current work in the context of the Euclidean frame-indifference of the energy balance (e.g., [9]). As such, the current work represents a generalization of the second-order case in [20] to arbitrary order. Since the focus in this work is on energetic thermoelasticity and EST, additional kinetic / dissipative constitutive relations (e.g., in the second-order case: [20]) are not considered here.
The current work begins in Sect. 2 with the constitutive formulation of energetic thermoelasticity in SNL form based on the (unrestricted) canonical ensemble and corresponding ensemble averaging. The corresponding WNL canonical formulation is given in Sect. 3. SNL and WNL constitutive formulation based on the quasi-harmonic (QH) approximation to the canonical ensemble is carried out in Sect. 4. This is followed in Sect. 5 by the phenomenological formulation of balance and field relations for higher-order deformation gradient continua based on continuum thermodynamics. This is then applied to the case of energetic thermoelasticity in the context of the dissipation principle, resulting i corresponding energetic thermoelastic constitutive relations, e.g., for stress. More detailed relations for these and related material properties (e.g., elastic stiffness) are obtained in Sect. 6 with the help of the free energy models from EST. Lastly, as a computational example, the EST-based WNL free energy is compared in Sect. 7 to second-order (i.e., \(n=2\)) with its approximation via higher-order deformation gradient thermoelasticity in strain-gradient form. The work ends with a summary and discussion in Sect. 8. For completeness, reduced forms of the interatomic potential in the EST-based formulations are summarized in Appendix A in the context of material frame-indifference (e.g., [27, 29]). Corresponding material frame-indifference, reduced forms for the free energy density in higher-order deformation gradient thermoelasticity are discussed in Appendix B. Finally, the boundary-value problem for higher-order deformation gradient thermoelasticity is briefly summarized in Appendix C in variational form.
In this work, Euclidean vectors are represented by lower-case bold italic characters \(\boldsymbol{a},\ldots ,\boldsymbol{z}\), second-order Euclidean tensors by upper-case bold italic characters \(\boldsymbol{A},\ldots ,\boldsymbol{Z}\), and calligraphic characters \(\mathcal{A},\ldots ,\mathcal{Z}\) for Euclidean tensors of arbitrary order. The notation \(\mathcal{A}\cdot \mathcal{B}\) is used for the scalar product of arbitrary tensors. Given this product on vectors, \((\boldsymbol{a}\otimes \boldsymbol{b})\boldsymbol{c}:=(\boldsymbol{b} \cdot \boldsymbol{c})\boldsymbol{a} \) defines the tensor product \(\boldsymbol{a}\otimes \boldsymbol{b}\) of \(\boldsymbol{a}\) and \(\boldsymbol{b}\), and \(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{a} \cdot \boldsymbol{b} :=\boldsymbol{a}\cdot \boldsymbol{A}\boldsymbol{b} \) the transpose \(\boldsymbol{A} ^{\mathrm{T}}\) of \(\boldsymbol{A}\). Let \(\mathop{\mathrm{sym}}\boldsymbol{A} := \frac{1}{2}(\boldsymbol{A}+\boldsymbol{A}^{\mathrm{T}}) \) represent the symmetric part, and \(\mathop{\mathrm{skw}}\boldsymbol{A} :=\frac{1}{2}(\boldsymbol{A}-\boldsymbol{A} ^{\mathrm{T}}) \) the skew-symmetric part, of \(\boldsymbol{A}\) in what follows. Unless otherwise stated, upper-case subscripted slanted sans-serif characters  represent tensorial and non-tensorial quantities of order \(i+2\) for \(i\geqslant 0\) in this work. In particular,
represent tensorial and non-tensorial quantities of order \(i+2\) for \(i\geqslant 0\) in this work. In particular,  is then second-order. For \(i\geqslant 1\), any
is then second-order. For \(i\geqslant 1\), any  satisfying
satisfying  is referred to as symmetric in what follows. Further concepts and notation will be introduced as needed along the way.
is referred to as symmetric in what follows. Further concepts and notation will be introduced as needed along the way.
2 Strongly Non-local Canonical Formulation
As stated above, the current formulation is restricted to the simplest case of unary solids, primitive unit cells, and purely bulk relations (i.e., periodic system). In the corresponding canonical ensemble for a system of \(N\) of mass points at temperature \(\theta \), let \(\boldsymbol{r} _{a}\) represent the position of mass point \(a\) (\(a=1,\ldots ,N\)) and \(\boldsymbol{p}_{a}=m_{a}\dot{\boldsymbol{r}}_{a}\) its momentum. As usual, the system Hamiltonian  consists of kinetic \(K\) and potential \(U\) parts, with
consists of kinetic \(K\) and potential \(U\) parts, with  and
and  . Given these, the partition function and free energy
. Given these, the partition function and free energy

respectively, are determined, as well as ensemble averaging

with respect to the canonical distribution function \(w\). The short-hand notation  and
and  is employed here and in what follows, with \(dv(\boldsymbol{x}) \) the volume element induced by \(d\boldsymbol{x}\).
is employed here and in what follows, with \(dv(\boldsymbol{x}) \) the volume element induced by \(d\boldsymbol{x}\).
Central to the current canonical formulation is the finite, non-affine generalizationFootnote 1
of the "standard" infinitesimal, affine transformation \(\boldsymbol{r}_{ \mathrm{r}a} :=\boldsymbol{F}^{-1} \,\boldsymbol{r}_{a} \) (in the current notation) of phase-space position "coordinates" (e.g., [30, §7], or [23, Eq. (8.45)]). Here, \(\boldsymbol{\chi }\) is the continuum deformation field, \(\boldsymbol{F}=\nabla \boldsymbol{\chi }\) the deformation gradient, and \(\boldsymbol{x}_{\mathrm{r}}\) the reference location of an arbitrary continuum material element with current location \(\boldsymbol{x}_{\mathrm{c}}=\boldsymbol{\chi }(\boldsymbol{x}_{ \mathrm{r}}) \) (Fig. 1). In the context of (3) and Fig. 1, the formulation to follow is with respect to a fixed, but otherwise arbitrary, continuum material element located at \(\boldsymbol{x}_{\mathrm{r}} \) in the reference, and at \(\boldsymbol{x}_{\mathrm{c}}\) in the current, configuration of the material in question. Analogous to its infinitesimal, affine counterpart (e.g., [23, §8.1.3]), (3) couples atomic and continuum kinematics. In particular, (3) induces the transformation \(\dot{\boldsymbol{r}} _{a} =\boldsymbol{F}(\boldsymbol{r}_{\mathrm{r}a}) \,\dot{\boldsymbol{r}}_{ \mathrm{r}a} \) of velocities, and so the "canonical" transformation
of \(K\), with \(\sum_{a}:=\sum_{a=1}^{N}\). This results in the "discrete" functional

of \(\boldsymbol{F}\). In addition, integration of
of (3) yields the functional
of \(\boldsymbol{F}\), and so the corresponding one

for the potential energy. Further, (6)1 and \(d\boldsymbol{p}_{a} =\boldsymbol{F}^{-\mathrm{T}}(\boldsymbol{r}_{\mathrm{r}a}) \,d\boldsymbol{p}_{\mathrm{r}a} \) (at constant \(\boldsymbol{r}_{\mathrm{r}a}\)) from (4)2 imply
for the corresponding volume elements. Then \(dv(\boldsymbol{r}_{a}) \,dv( \boldsymbol{p}_{a}) =dv(\boldsymbol{r}_{\mathrm{r}a}) \,dv(\boldsymbol{p}_{\mathrm{r}a} ) \) is invariant, \(Z\) from (1)1 is equal toFootnote 2

and
holds for the system free energy (1)2.
\(\boldsymbol{\chi }\) maps the position \(\boldsymbol{x}_{\mathrm{r}}+\boldsymbol{s}_{\mathrm{r}}\) of any point in a neighborhood of the reference position \(\boldsymbol{x}_{\mathrm{r}}\) of a material element to \(\boldsymbol{x}_{\mathrm{c}}+\boldsymbol{s}_{\mathrm{c}} =\boldsymbol{\chi }(\boldsymbol{x}_{\mathrm{r}}+\boldsymbol{s}_{\mathrm{r}}) \) in a neighborhood of its current position \(\boldsymbol{x}_{\mathrm{c}}=\boldsymbol{\chi }(\boldsymbol{x}_{\mathrm{r}})\). In the context of (3), this is the case in particular for \(\boldsymbol{r}_{\mathrm{r}a} =\boldsymbol{x}_{\mathrm{r}}+\boldsymbol{s}_{\mathrm{r}a} \) and \(\boldsymbol{r}_{a} =\boldsymbol{x}_{\mathrm{c}}+\boldsymbol{s}_{a} =\boldsymbol{\chi }(\boldsymbol{x}_{\mathrm{r}}+\boldsymbol{s}_{\mathrm{r}a}) \)
System properties derived from (11) include as usual the entropy and internal energy
respectively. In addition, the (functional) derivatives
via ensemble averaging. Note that \((\mathcal{D}_{\smash{\boldsymbol{F}}} \boldsymbol{r}_{a})^{\mathrm{T}} \boldsymbol{a} \cdot \boldsymbol{Z} :=\boldsymbol{a} \cdot (\mathcal{D}_{\smash{\boldsymbol{F}}}\boldsymbol{r}_{a}) \,\boldsymbol{Z} \). In addition, \((\mathcal{D}_{\smash{\boldsymbol{F}}}\boldsymbol{r}_{a}) \, \boldsymbol{Z} =\int _{\boldsymbol{0}}^{\,\boldsymbol{s}_{\mathrm{r}a}} \boldsymbol{Z}(\boldsymbol{x}_{ \mathrm{r}}+\boldsymbol{s}_{\mathrm{r}}) \ d\boldsymbol{s}_{\mathrm{r}} \) from (7) for any \(\boldsymbol{Z}(\boldsymbol{r}_{\mathrm{r}})\). In particular, the choice \(\boldsymbol{Z}(\boldsymbol{r}_{\mathrm{r}}) =\boldsymbol{A} \boldsymbol{F}(\boldsymbol{r}_{\mathrm{r}}) \) yields \((\mathcal{D}_{ \smash{\boldsymbol{F}}}\boldsymbol{r}_{a}) \,\boldsymbol{A}\boldsymbol{F} =\boldsymbol{A}\boldsymbol{r}_{a} \), and so
via "push-forward" of \(\mathcal{D}_{\smash{\boldsymbol{F}}}K_{\mathrm{r}} \) and \(\mathcal{D}_{\smash{\boldsymbol{F}}}U_{\mathrm{r}}\), respectively, from (13). In turn,
then holds from (14).
In the context of material frame-indifference, the reduced form

of (8) follows from (A.3), with \(\boldsymbol{r}_{ab} :=\boldsymbol{r}_{a} -\boldsymbol{r}_{b} \) and
from (7). In particular, (17) results in the reduction
of (13)1 in terms of the bond force \(U_{ab} :=\partial _{\smash{r_{ab}}}\!U_{\mathrm{d}} \) and bond direction \(\boldsymbol{d}_{ab}:=\boldsymbol{r}_{ab}/r_{ab} \), with \(\sum_{a< b}:=\sum_{a=1}^{N}\sum_{b=a+1}^{N}\). Likewise, (15)1 reduces to
and so (16) to the symmetric form
Clearly, the symmetry of \((\mathcal{D}_{\smash{\boldsymbol{F}}}U_{ \mathrm{r}}) \boldsymbol{F}^{\mathrm{T}} \), and so that of \(( \mathcal{D}_{\smash{\boldsymbol{F}}}\varPsi _{\mathrm{r}}) \boldsymbol{F}^{ \mathrm{T}} \), here is a direct consequence of the material frame-indifference of  in (17). This is also true in the WNL formulation of energetic thermoelasticity, to which we now turn.
in (17). This is also true in the WNL formulation of energetic thermoelasticity, to which we now turn.
3 Weakly Non-local Canonical Formulation
This is based on the Taylor series expansionsFootnote 3
where \((\varPi _{i}\boldsymbol{a})\mathcal{A} :=\frac{1}{i!} \,(\cdots ( \mathcal{A}\boldsymbol{a})\boldsymbol{a}\cdots )\boldsymbol{a} \) (\(i\) times) is a projection. From (22) follow

analogous to \(\boldsymbol{r}_{a} {}[ \boldsymbol{F}; \boldsymbol{x}_{\mathrm{r}} , \boldsymbol{s}_{\mathrm{r}a} ] \) and \(\boldsymbol{F}(\boldsymbol{r}_{ \mathrm{r}a})\), respectively, with

In turn, (23) result in

analogous to (5) and (8), respectively, as well as

analogous to (10), and (11), respectively.
As for the SNL case (12),
determine the entropy and internal energy, respectively, now with respect to (25) and (26). On the other hand, in the context of these,

"replace" \(\mathcal{D}_{\boldsymbol{F}}\varPsi _{\mathrm{r}}\) in the WNL case. Here,

from (25) with

via (23). The "push-forward" forms

of (29) determine that

of (28) with

via (30). Whereas \(\boldsymbol{g}_{\mathrm{r}a}^{i}\) has units of length, note that \(\boldsymbol{G}_{\mathrm{r}a}^{i}\) is dimensionless (e.g., like \(\boldsymbol{F}\) and \(\boldsymbol{F}_{\mathrm{r}a}\) in (23)). In contrast to  , which is of order \((2+i)\), note that
, which is of order \((2+i)\), note that  is of order 2 for all \(i\). Related to this is the fact that the former has (SI) units of Jmi, while those J of the latter are independent \(i\).
is of order 2 for all \(i\). Related to this is the fact that the former has (SI) units of Jmi, while those J of the latter are independent \(i\).
Like in the SNL case above, we have the reduced form

of (25)2 in the context of the MFI of \(U\) and (A.3), with

from (23)1 and \((\varPi _{i}\boldsymbol{s}_{ \mathrm{r}})_{ab} :=(\varPi _{i}\boldsymbol{s}_{\mathrm{r}a}) -(\varPi _{i}\boldsymbol{s}_{\mathrm{r}b}) \). In turn, (34) results in the reductions

of (29)1 and (31)1, respectively, with \(\boldsymbol{g}_{\mathrm{r}ab}^{i} :=\boldsymbol{g}_{\mathrm{r}a}^{i} -\boldsymbol{g}_{ \mathrm{r}b}^{i} \). Likewise,

holds for the reduced form of (32). As shown in the continuum thermodynamic formulation of WNL energetic thermoelasticity in Sect. 5 below,  determine for example the WNL form of the Kirchhoff stress. More on this later.
determine for example the WNL form of the Kirchhoff stress. More on this later.
4 Quasi-harmonic Formulation
The quasi-harmonic (QH) approximation (e.g., [23, §11.4]) to the canonical formulation employed in the last two sections is based on the assumption that each mass point remains "close" to its mean position \(\bar{\boldsymbol{r}}_{a}\) on the timescale of interest, i.e.,
In addition, mean atomic positions are assumed to "deform" with the continuum (Cauchy-Born). Consequently, the current QH formulation is based on the (finite, non-affine) generalization
of the (infinitesimal, affine) Cauchy-Born relation \(\bar{\boldsymbol{r}} _{\mathrm{r}a} :=\boldsymbol{F}^{-1}(\boldsymbol{x}_{\mathrm{r}}) \,\bar{ \boldsymbol{r}}_{a} \) (i.e., for primitive lattices; for the case of multilattices, see, e.g., [23, §11.2.2]). Analogous to the formulation of (7) and (23)1 based on (3), then, we have

in the SNL QH, and WNL QH, cases, respectively.
In the context of restricted ensemble averaging (e.g., [23, §11.1]), the assumption (38) facilitates analytic evaluation of the system partition function (1)1, resulting in the corresponding analytic form

(e.g., [23, §11.4]) of the QH approximation to \(\varPsi \) in (1)2. Here, \(\varPsi _{\mathrm{K}} ^{\mathrm{qh}}\) represents the kinetic part of \(\varPsi ^{\mathrm{qh}}\), and
is the spectral form of the symmetric "force-constant" matrix

(summation convention over \(k,l=1,2,3\)) relative to the 3-dimensional \((\boldsymbol{i}_{1},\boldsymbol{i}_{2},\boldsymbol{i}_{3}) \) and \(3N\)-dimensional \((\mathbf{i}_{1}^{1},\mathbf{i}_{2}^{1},\mathbf{i}_{3}^{1}, \ldots , \mathbf{i}_{1}^{N},\mathbf{i}_{2}^{N},\mathbf{i}_{3}^{N}) \) Cartesian bases. In the current bulk (periodic) case, \(m=3N-3\) non-zero eigenvalues \(\lambda _{1},\ldots ,\lambda _{m}\) and corresponding eigenvectors \(\mathbf{e}_{1},\ldots ,\mathbf{e}_{m}\) determine \(\mathbf{\varPhi }_{\ast }\) in (42). With \(U\) given by (A.3), note that

holds, with \(U_{\mathit{abcd}} :=\partial _{\smash{r_{cd}}} \partial _{\smash{r_{ab}}} \!U_{\mathrm{d}} \) the bond stiffness, and \(\delta _{\mathit{abc}}:=\delta _{ab}-\delta _{ac}\). In what follows, the derivatives
of (41) via (42) will be useful. Note that (45)2 is based on the assumption that \(\lambda _{r}\) depends on \(\bar{\boldsymbol{r}}_{ab}\) only through its magnitude \(\bar{r}_{ab}\) (e.g., [23, Eqs. (11.110) and (11.111)]), such that \(\partial _{\smash{\bar{\boldsymbol{r}}_{ab}}}\!\ln \lambda _{r} =( \partial _{\smash{\bar{r}_{ab}}}\!\ln \lambda _{r}) \,\bar{ \boldsymbol{r}}_{ab}/\bar{r}_{ab} \) holds.
Combination of (40) and (41) then results in the QH approximations

to  from (11), and to
from (11), and to  from (26)2, respectively. From (45)2 and the first of these, we have
from (26)2, respectively. From (45)2 and the first of these, we have
as the QH approximation to the SNL relation \((\mathcal{D}_{ \smash{\boldsymbol{F}}}\varPsi _{\mathrm{r}}) \boldsymbol{F}^{\mathrm{T}} \) from (21). Similarly, (45)2 and (46)2 result in the QH approximation

to the WNL relation  from (37). Analogous to the WNL canonical case discussed above,
from (37). Analogous to the WNL canonical case discussed above,  determine in particular the WNL QH form of the Kirchhoff stress in the continuum thermodynamic formulation of WNL energetic thermoelasticity.
determine in particular the WNL QH form of the Kirchhoff stress in the continuum thermodynamic formulation of WNL energetic thermoelasticity.
5 Continuum Thermodynamic Formulation
Since the current treatment neglects heat conduction, the following is restricted to spatially uniform temperature \(\theta \). In this context, a direct generalization of the (referential or "Lagrangian") formulation of the first-order case in [20] to the current \(n{\mathrm{th}}\)-order one is pursued here. For further simplicity, quasi-static conditions are assumed, and supplies are neglecting.
Given these conditions and assumptions, the total energy balance reduces to
in terms of the internal energy density \(\varepsilon _{\mathrm{r}}\) and the (mechanical) referential energy flux density \(\boldsymbol{h}_{ \mathrm{r}}\). In the zeroth-order case of simple materials (e.g., [29, §3.6]), \(\boldsymbol{h}_{\mathrm{r}} =\boldsymbol{P} ^{\mathrm{T}}\dot{\boldsymbol{\chi }} \) is determined by the material velocityFootnote 4\(\dot{\boldsymbol{\chi }}\) and the first Piola-Kirchhoff stress \(\boldsymbol{P}\). Direct generalization of this to the current case yieldsFootnote 5

in terms of the higher-order hyperstresses  . As done here, we work with the notation
. As done here, we work with the notation  analogous to
analogous to  in what follows for simplicity. By analogy with the zeroth- and first-order cases (e.g., [20]), the form of the energy balance resulting from (49) and (50) is Euclidean frame-indifferent (e.g., [29, Chap. 6]) iff linear and angular momentum balance
in what follows for simplicity. By analogy with the zeroth- and first-order cases (e.g., [20]), the form of the energy balance resulting from (49) and (50) is Euclidean frame-indifferent (e.g., [29, Chap. 6]) iff linear and angular momentum balance
respectively, hold, whereFootnote 6

is the (generalized) Kirchhoff stress. As in the first-order case (e.g., [20]), the standard (i.e., zeroth-order) forms (51) of momentum balance apply in the \(n{\mathrm{th}}\)-order case as well. Note that \(\boldsymbol{K}\) from (52) reduces to its standard form  for \(n=0\). Together with energy balance (49) and linear momentum balance (51)1, the entropy balance \(\dot{\eta }_{\mathrm{r}}=\pi _{\mathrm{r}} \) for the current case of uniform temperature implies
for \(n=0\). Together with energy balance (49) and linear momentum balance (51)1, the entropy balance \(\dot{\eta }_{\mathrm{r}}=\pi _{\mathrm{r}} \) for the current case of uniform temperature implies

for the dissipation rate density in terms of the free energy density \(\psi _{\mathrm{r}} :=\varepsilon _{\mathrm{r}}-\theta \eta _{\mathrm{r}} \).
Except perhaps for the energy flux form (50) relevant to higher-order deformation gradient continua without heat conduction, the above formulation is independent of any (further) constitutive assumptions. Restricting attention now to energetic thermoelasticity in this context, we have

Substituting these into (53), we have

In the current energetic thermoelastic context, exploitation of the dissipation principle (e.g., [29, §9.5 for supply-free case]) then yields the thermoelastic relations

and so \(\pi _{\mathrm{r}}=0\). Here,
represents the \(i{\mathrm{th}}\)-order variational derivative operator. On the basis of (54) and (56), we also have the reduced form

for the Kirchhoff stress from (52).
6 Results Based on Free Energy Models from EST
Specific forms of (54) are determined by either the WNL canonical relations (26)2 and (27)1, or by the corresponding WNL QH relations (46)2 and (45)1, respectively. In the WNL canonical formulation based on the reduced MFI form (34) of \(U\),  is determined by (37). Substituting this into (58), we obtain
is determined by (37). Substituting this into (58), we obtain
relative to the reference volume \(V_{\mathrm{r}}\). Since \(\sum_{i=0}^{n}\boldsymbol{g}_{\mathrm{r}ab}^{i} =\boldsymbol{r}_{ab} \) and \(\sum_{i=0}^{n}\boldsymbol{G}_{\mathrm{r}a}^{i} =\boldsymbol{F}_{\mathrm{r}a} \) in the context of (23), the right-hand side of (59) simplifies to
Substituting this back into (58) yields the WNL canonical form
of the Kirchhoff stress. This is the same form as that of \(( \mathcal{D}_{\smash{\boldsymbol{F}}}\psi _{\mathrm{r}}) \boldsymbol{F}^{ \mathrm{T}} \) resulting from (16) in SNL canonical case. Both of these can be compared with the WNL QH relation
for \(\boldsymbol{K}\) resulting from (48), and with the SNL-QH relation for \((\mathcal{D}_{\smash{\boldsymbol{F}}} \psi _{\mathrm{r}}^{\mathrm{qh}}) \boldsymbol{F}^{\mathrm{T}} \) resulting from (47). Since all of these relations are constitutively symmetric via material frame-indifference and (A.3), they satisfy angular momentum balance (51)2 identically.
Finally, consider the second derivatives of \(\psi _{\mathrm{r}}\) based on the WNL canonical formulation, (26)2 and (54), which determine equilibrium thermoelastic material properties (e.g., [29, Chap. 10]). These include the referential heat capacity
the higher-order referential thermal expansion

as well as higher-order referential elastic stiffness

with \(\mathop{\mathrm{cov}}(a,b) :=\langle (a-\langle a\rangle ) \otimes (b-\langle b\rangle )\rangle =\langle a\otimes b\rangle - \langle a\rangle \otimes \langle b\rangle \) the covariance. In particular, note that

is obtained from (29)1 and (36)1. The relations (64) and (65) represent direct generalizations of standard (i.e., \(n=0\)) referential thermoelastic properties (e.g., [29, §§10.5–10.6]) to the current context. As done in the standard case, referential material properties such as  and
and  can also be expressed in spatial form. For example, the latter is transformed into the spatial form
can also be expressed in spatial form. For example, the latter is transformed into the spatial form  via the definition
via the definition

We then have

with \(V_{\mathrm{c}} =(\det \boldsymbol{F}) V_{\mathrm{r}} \),  from (36), and
from (36), and  defined by
defined by

analogous to  . On this basis, one obtains
. On this basis, one obtains

via (30) and (66) in terms of \((\boldsymbol{A}\,\square \,\boldsymbol{B})\boldsymbol{C} :=\boldsymbol{A}\boldsymbol{C}\boldsymbol{B} \) and \((\boldsymbol{A}\,\triangle \, \boldsymbol{B})\boldsymbol{C} :=\boldsymbol{A}\boldsymbol{C}^{\mathrm{T}}\!\boldsymbol{B} \). In contrast to that \((4+i+j)\) of  , note that the order of
, note that the order of  is 4, independent of \(i\) and \(j\). Analogously, the (SI) units J/m\({}^{3-i-j}\) of
is 4, independent of \(i\) and \(j\). Analogously, the (SI) units J/m\({}^{3-i-j}\) of  depend on \(i\) and \(j\), while those J/m3 of
depend on \(i\) and \(j\), while those J/m3 of  do not. Consequently,
do not. Consequently,  has the same units as the fourth-order elastic stiffness tensor in standard equilibrium thermoelasticity for all \(i\) and \(j\).
has the same units as the fourth-order elastic stiffness tensor in standard equilibrium thermoelasticity for all \(i\) and \(j\).
7 Example: Second-Order Gradient Elasticity
As an illustration and example of selected theoretical results in this work, consider lastly approximation of the EST-based WNL free energy (26)2 by specific forms of the phenomenological free energy density (54). For simplicity, attention is restricted to zero temperature and \(n\leqslant 2\) in this section.
7.1 Free Energy
In the context of material frame-indifference (see Appendix B), the phenomenological free energy density (54) takes the reduced formFootnote 7

via (B.2) for \(n=2\) at zero temperature with respect to the right Cauchy-Green deformation  as well as the first-order
as well as the first-order  and second-order
and second-order  strain-gradient-like deformation measures from (B.3). Likewise, the EST-based WNL free energy (26)2 simplifies to
strain-gradient-like deformation measures from (B.3). Likewise, the EST-based WNL free energy (26)2 simplifies to

at zero-temperature for \(n=2\). Here,

is determined by the interatomic potential (A.3), and

follows from (35) with

Assuming centrosymmetry (e.g., [1]), let (71) be given by the specific form

based on second-order Taylor-series expansion of (73) about  with respect to a reference volume \(V_{\mathrm{r}}\). Here,
with respect to a reference volume \(V_{\mathrm{r}}\). Here,  and so on. In the standard \(n=0\) case, this is formally analogous for example to the approach of [24] based on material-symmetry-adapted strain tensor components. In particular, note that
and so on. In the standard \(n=0\) case, this is formally analogous for example to the approach of [24] based on material-symmetry-adapted strain tensor components. In particular, note that  for zero stress (e.g., Kirchhoff stress (85) below), while
for zero stress (e.g., Kirchhoff stress (85) below), while  and
and  vanish identically via centrosymmetry since
vanish identically via centrosymmetry since  is determined by an odd gradient of \(\boldsymbol{F}\). On the other hand, since
is determined by an odd gradient of \(\boldsymbol{F}\). On the other hand, since  is even in this sense,
is even in this sense,

is generally non-zero. Besides this last relation, (73) also yields

with \(U_{ab} :=\partial _{\smash{r_{ab}}}\!U_{\mathrm{d}} \) the atomic bond force, and \(U_{\mathit{abcd}} := \partial _{\smash{r_{ab}}}\partial _{\smash{r_{cd}}} \!U _{\mathrm{d}} \) the atomic bond stiffness. Here,

from (74) with
In particular, then, the isothermal elastic stiffness  as well as the corresponding first-order
as well as the corresponding first-order  and second-order
and second-order  "gradient" stiffnesses, are determined by (78).
"gradient" stiffnesses, are determined by (78).
7.2 Computational Comparisons
The following comparisons are based on the "plane-wave" deformation
of a fcc primitive unit cell with volume \(V_{\mathrm{r}}=a^{3}/4\) and central atom located at \(\boldsymbol{x}_{\mathrm{r}}\). Here, \(a\) is the lattice parameter, \(\boldsymbol{a}\) is the displacement amplitude, \(\boldsymbol{\kappa }\equiv 2\pi {}[ 001] /a\) is a wave vector in the first Brillouin zone, and \(k\in {}[ 0,1] \). In turn, (81) implies

As \(k\) increases, then, gradients of higher-order become increasingly important.
In the undeformed reference configuration (lattice),  are known and prescribed. In this case, (82) determine
are known and prescribed. In this case, (82) determine  from (74). Given in addition \(U_{\mathrm{d}}\),
from (74). Given in addition \(U_{\mathrm{d}}\),  ,
,  ,
,  ,
,  , and
, and  , are then all determined, and so
, are then all determined, and so  from (76).
from (76).
As an example comparison of  from (72) and
from (72) and  from (76), consider the results in Fig. 2 based on the EAM potential for Al of [32, 33] for \(U_{\mathrm{d}}\). The displacement amplitude \(\boldsymbol{a}\) is assumed parallel to \(\boldsymbol{\kappa }\) with magnitude \(\|\boldsymbol{a}\|=0.05\,V_{\mathrm{r}}^{1/3}\) (much smaller than the cutoff radius of the potential). As evident, the zero- and first-order strain-gradient energies (brown and green curves) begin to deviate both qualitatively and quantitatively from the second-order strain-gradient and EST-based cases (blue and red curves) for \(k\) above about 0.09. For \(k\) above about 0.34, even
from (76), consider the results in Fig. 2 based on the EAM potential for Al of [32, 33] for \(U_{\mathrm{d}}\). The displacement amplitude \(\boldsymbol{a}\) is assumed parallel to \(\boldsymbol{\kappa }\) with magnitude \(\|\boldsymbol{a}\|=0.05\,V_{\mathrm{r}}^{1/3}\) (much smaller than the cutoff radius of the potential). As evident, the zero- and first-order strain-gradient energies (brown and green curves) begin to deviate both qualitatively and quantitatively from the second-order strain-gradient and EST-based cases (blue and red curves) for \(k\) above about 0.09. For \(k\) above about 0.34, even  begins to deviate quantitatively from
begins to deviate quantitatively from  .
.
Comparison of  from (72) (red curve) and
from (72) (red curve) and  from (76) as a function of \(k\) for \(\boldsymbol{a}\) parallel to \(\boldsymbol{\kappa }\) (i.e., \([ 001] \)). Brown curve (classical):
from (76) as a function of \(k\) for \(\boldsymbol{a}\) parallel to \(\boldsymbol{\kappa }\) (i.e., \([ 001] \)). Brown curve (classical):  . Green curve (first strain gradient):
. Green curve (first strain gradient):  . Blue curve (second strain gradient):
. Blue curve (second strain gradient):  . See text for discussion (Color figure online)
. See text for discussion (Color figure online)
8 Summary and Discussion
In this work, model relations for the energetic thermoelasticity of non-simple materials have been obtained with the help of equilibrium statistical thermodynamics (EST) as well as phenomenologically via continuum thermodynamics.
In the EST context, both the (unrestricted) canonical formulation, as well as the (restricted) quasi-harmonic (QH) approximation, have been considered. With respect to these, both strongly non-local (SNL) and weakly non-local (WNL) formulations of energetic thermoelasticity have been pursued. Principle results of the formulation include the SNL continuum form (11) for the EST canonical free energy \(\varPsi _{\mathrm{r}}\) and its WNL approximation (26). In addition, the approximations (46) to these have been formulated in the context of the QH approximation to the unrestricted canonical formulation. As discussed in the text, the WNL form of either of these can be used to determine the phenomenological free energy density (54) for higher-order deformation gradient thermoelasticity.
A basic aspect of the continuum thermodynamic formulation of higher-order deformation gradient thermoelasticity in Sect. 5 is the generalization (50) of the (mechanical) energy flux \(\boldsymbol{h}_{\mathrm{r}}\) in terms of the higher-order (hyper)stress measures  conjugate to
conjugate to  . Exploiting the Euclidean frame-indifference of the energy balance (e.g., [29, Chap. 6]), a direct consequence of (50) is the generalized Kirchhoff stress (52). In the context of the dissipation principle, (50) and (54) result in the generalized hyperelastic relations (56) for
. Exploiting the Euclidean frame-indifference of the energy balance (e.g., [29, Chap. 6]), a direct consequence of (50) is the generalized Kirchhoff stress (52). In the context of the dissipation principle, (50) and (54) result in the generalized hyperelastic relations (56) for  and so the corresponding form (58) for the Kirchoff stress. As shown by the variational formulation of the corresponding boundary-value problem in Appendix C, the direct formulation of Sect. 5 is completely consistent with a variational one in the spirit of [14, 15].
and so the corresponding form (58) for the Kirchoff stress. As shown by the variational formulation of the corresponding boundary-value problem in Appendix C, the direct formulation of Sect. 5 is completely consistent with a variational one in the spirit of [14, 15].
Central to the current treatment of atomistic-continuum coupling is the finite, non-affine relation \(\boldsymbol{r}_{a} =\boldsymbol{\chi }(\boldsymbol{r}_{ \mathrm{r}a}) \) from (3) for the effect of continuum deformation on atomic position. For uniform (affine) local deformation \(\boldsymbol{\chi }(\boldsymbol{x}_{\mathrm{r}}) =\boldsymbol{F}\,\boldsymbol{x}_{ \mathrm{r}} \), note that (3) reduces to the "standard" infinitesimal, affine relation \(\boldsymbol{r}_{a} = \boldsymbol{\chi }(\boldsymbol{x}_{\mathrm{r}}) +\boldsymbol{F}(\boldsymbol{x}_{\mathrm{r}}) \, \boldsymbol{s}_{\mathrm{r}a} =\boldsymbol{F}\,\boldsymbol{r}_{\mathrm{r}a} \) (e.g., [23, §8.1.3]). From the point of view of Hamilton’s equations, (3) represents a so-called "canonical" transformation of \(\boldsymbol{r}_{1},\ldots ,\boldsymbol{r}_{N}\) (e.g., [8, 11, 18, 23, §8.1]). Indeed, the corresponding generator takes the form  [cf. 23, Eq. (8.46)]. Then \(\boldsymbol{r}_{a} =-\partial _{\smash{\boldsymbol{p}_{a}}}\!G = \boldsymbol{\chi }(\boldsymbol{r}_{\mathrm{r}a}) \) corresponds to (3), and \(\boldsymbol{p}_{\mathrm{r}a} =- \partial _{\smash{\boldsymbol{r}_{\mathrm{r}a}}}\!G =\boldsymbol{F}^{ \mathrm{T}}(\boldsymbol{r}_{\mathrm{r}a}) \,\boldsymbol{p}_{a} \) to (4)2. This is in contrast to the quasi-harmonic (QH) case, in which the mean atomic positions are assumed to deform with the continuum according to the generalized Cauchy-Born relation (39). As from (3) via in particular (7) and (23) in the canonical case, both SNL- and WNL-based QH formulations of energetic thermoelasticity ensue from (39) via (40).
[cf. 23, Eq. (8.46)]. Then \(\boldsymbol{r}_{a} =-\partial _{\smash{\boldsymbol{p}_{a}}}\!G = \boldsymbol{\chi }(\boldsymbol{r}_{\mathrm{r}a}) \) corresponds to (3), and \(\boldsymbol{p}_{\mathrm{r}a} =- \partial _{\smash{\boldsymbol{r}_{\mathrm{r}a}}}\!G =\boldsymbol{F}^{ \mathrm{T}}(\boldsymbol{r}_{\mathrm{r}a}) \,\boldsymbol{p}_{a} \) to (4)2. This is in contrast to the quasi-harmonic (QH) case, in which the mean atomic positions are assumed to deform with the continuum according to the generalized Cauchy-Born relation (39). As from (3) via in particular (7) and (23) in the canonical case, both SNL- and WNL-based QH formulations of energetic thermoelasticity ensue from (39) via (40).
The WNL formulation of atomistic-continuum kinematics in Sect. 3 and in particular (22)1 can be compared for example with the recent treatment of [1]. They work with the polynomial-map-based approximation

to \(\boldsymbol{\chi }(\boldsymbol{x}_{\mathrm{r}})\). Here, \(\boldsymbol{\chi }_{0}\) is a constant vector, \(\boldsymbol{F}_{0}\) a constant second-order tensor, and  (\(i=1,\ldots ,m\)) constant symmetric tensors of order \(i+2\). The distance \(\tilde{r}^{\alpha \beta } :=| \tilde{\boldsymbol{r}}^{\alpha \beta }| \) between atoms (or primitive unit cells) \(\alpha \) and \(\beta \) with \(\tilde{\boldsymbol{r}}^{\alpha \beta } :=\tilde{\boldsymbol{x}}^{\alpha }-\tilde{\boldsymbol{x}}^{\beta } \) is then determined by \(\tilde{r}^{\alpha \beta } (\boldsymbol{x}_{\mathrm{r}}^{ \alpha },\boldsymbol{x}_{\mathrm{r}}^{\beta }; \boldsymbol{C}_{0},\boldsymbol{C}_{0}^{(1)}, \ldots ,\boldsymbol{C}_{0}^{(m)}) \) in terms of the higher-order continuum deformation measures \(\boldsymbol{C}_{0}^{(i)}:=\boldsymbol{F}_{0}^{\mathrm{T}}\! \boldsymbol{F}_{0}^{(i)} \) formally analogous to
(\(i=1,\ldots ,m\)) constant symmetric tensors of order \(i+2\). The distance \(\tilde{r}^{\alpha \beta } :=| \tilde{\boldsymbol{r}}^{\alpha \beta }| \) between atoms (or primitive unit cells) \(\alpha \) and \(\beta \) with \(\tilde{\boldsymbol{r}}^{\alpha \beta } :=\tilde{\boldsymbol{x}}^{\alpha }-\tilde{\boldsymbol{x}}^{\beta } \) is then determined by \(\tilde{r}^{\alpha \beta } (\boldsymbol{x}_{\mathrm{r}}^{ \alpha },\boldsymbol{x}_{\mathrm{r}}^{\beta }; \boldsymbol{C}_{0},\boldsymbol{C}_{0}^{(1)}, \ldots ,\boldsymbol{C}_{0}^{(m)}) \) in terms of the higher-order continuum deformation measures \(\boldsymbol{C}_{0}^{(i)}:=\boldsymbol{F}_{0}^{\mathrm{T}}\! \boldsymbol{F}_{0}^{(i)} \) formally analogous to  in (B.3). As discussed in [1], this can also be expressed with respect to \(\boldsymbol{E}_{0}\) and \(\boldsymbol{E}_{0}^{(1)}\), with \(\boldsymbol{C}_{0} =\boldsymbol{I}+2\boldsymbol{E}_{0} \), and \(\boldsymbol{C}_{0}^{(1)} =\mathop{\mathrm{cyc}}\boldsymbol{E}_{0}^{(1)} \) analogous to (B.9).
in (B.3). As discussed in [1], this can also be expressed with respect to \(\boldsymbol{E}_{0}\) and \(\boldsymbol{E}_{0}^{(1)}\), with \(\boldsymbol{C}_{0} =\boldsymbol{I}+2\boldsymbol{E}_{0} \), and \(\boldsymbol{C}_{0}^{(1)} =\mathop{\mathrm{cyc}}\boldsymbol{E}_{0}^{(1)} \) analogous to (B.9).
Although not treated explicitly in the text, the energetic constitutive relations formulated in the context of EST satisfy material frame-indifference (MFI). For example, in the (unrestricted) SNL case, \(K_{\mathrm{r}} {}[ \boldsymbol{F} ] =K_{\mathrm{r}} {}[ \boldsymbol{Q}\boldsymbol{F} ] \) holds for (5), \(U_{ \mathrm{r}} {}[ \boldsymbol{F} ] =U_{\mathrm{r}} {}[ \boldsymbol{Q}\boldsymbol{F} ] \) for (17), and so \(\varPsi _{\mathrm{r}} {}[ \theta , \boldsymbol{F} ] =\varPsi _{ \mathrm{r}} {}[ \theta , \boldsymbol{Q}\boldsymbol{F} ] \) for (11), for all orthogonal \(\boldsymbol{Q}\). Likewise,  for (26)2 holds in the (unrestricted) WNL case when
for (26)2 holds in the (unrestricted) WNL case when  is given by (34). On the other hand, neither (11) nor (26)2 are in MFI-based reduced form (e.g., [5, 21]). As discussed in detail in Appendix B,
is given by (34). On the other hand, neither (11) nor (26)2 are in MFI-based reduced form (e.g., [5, 21]). As discussed in detail in Appendix B,  from (B.2), and \(\psi _{\mathrm{s}} (\theta , \boldsymbol{E}, \nabla ^{1}\!\boldsymbol{E}, \ldots , \nabla ^{n}\! \boldsymbol{E}) \) from (B.10), are but two among many possible such reduced forms for \(\psi _{\mathrm{r}} (\theta , \boldsymbol{F}, \nabla ^{1}\!\boldsymbol{F}, \ldots , \nabla ^{n}\!\boldsymbol{F}) \) from (54). Indeed, for example, \(\psi _{\mathrm{i}} \) itself determines a third reduced form
from (B.2), and \(\psi _{\mathrm{s}} (\theta , \boldsymbol{E}, \nabla ^{1}\!\boldsymbol{E}, \ldots , \nabla ^{n}\! \boldsymbol{E}) \) from (B.10), are but two among many possible such reduced forms for \(\psi _{\mathrm{r}} (\theta , \boldsymbol{F}, \nabla ^{1}\!\boldsymbol{F}, \ldots , \nabla ^{n}\!\boldsymbol{F}) \) from (54). Indeed, for example, \(\psi _{\mathrm{i}} \) itself determines a third reduced form

of the free energy density in terms of the Eringen measures  with
with  . Any of these reduced forms, and in particular (B.2), result in turn in corresponding reduced forms of energetic constitutive quantities. For example, the continuum thermodynamic relation (58) for the Kirchhoff stress reduces to
. Any of these reduced forms, and in particular (B.2), result in turn in corresponding reduced forms of energetic constitutive quantities. For example, the continuum thermodynamic relation (58) for the Kirchhoff stress reduces to

in the context of (B.2). Since \(\boldsymbol{K}\) as given by (85) is symmetric, it satisfies angular momentum balance (51)2 identically. Long ago, Noll (see, e.g., [17] or [27, §84]) established the fact that the MFI of \(\psi _{\mathrm{r}}\) implies the symmetry of the Cauchy, and so Kirchhoff, stress for simple materials. As shown by (85), this holds in the more general WNL case as well.
As investigated in previous work (e.g., [6, 7, 16, 19, 22]), other issues from material theory for gradient continua besides MFI include higher-order material symmetry restrictions. As discussed in detail for example in [22], since \(\nabla ^{1}\!\boldsymbol{F},\ldots ,\nabla ^{n}\! \boldsymbol{F}\) do not transform tensorially under change of compatible reference configuration, such material symmetry restrictions invariably involve the consideration of higher-order jets. On the atomistic side, the material symmetry of \(U_{\mathrm{d}}\) from (A.3) is inherited by  . Yet another issue concerns a dependence of free energy on higher-order (e.g., anharmonic) strain terms such as
. Yet another issue concerns a dependence of free energy on higher-order (e.g., anharmonic) strain terms such as  in comparison to strain gradient terms like
in comparison to strain gradient terms like  . Although the corresponding moduli
. Although the corresponding moduli  and
and  are of the same order, they are different in character. Indeed, in contrast to
are of the same order, they are different in character. Indeed, in contrast to  ,
,  is lengthscale-independent. In any case, these and other issues represent work in progress to be reported on in the future.
is lengthscale-independent. In any case, these and other issues represent work in progress to be reported on in the future.
Notes
In this work, the subscript r stands for reference, and c for current.
Since \(\boldsymbol{x}_{\mathrm{r}}\) and so \(\boldsymbol{x}_{ \mathrm{c}}=\boldsymbol{\chi }(\boldsymbol{x}_{\mathrm{r}})\) are fixed, note that \(d\boldsymbol{r}_{a}=d\boldsymbol{s}_{a}\) and \(d\boldsymbol{r}_{\mathrm{r}a}=d \boldsymbol{s}_{\mathrm{r}a}\).
More formally, (22)1 for example defines the \((n+1)\)-jet \((J_{\smash{\boldsymbol{x}_{\mathrm{r}}}}^{n+1}\boldsymbol{\chi }) (\boldsymbol{s}_{\mathrm{r}}) \) of \(\boldsymbol{\chi }\) with "base point" \(\boldsymbol{x}_{\mathrm{r}}\). By varying this point, one obtains a vector-valued polynomial of at most order \(n+1\) at every point of the base manifold.
For simplicity, the notation \(\boldsymbol{\chi }\) is used for both the deformation and motion fields in this work.
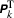 in (50) is defined by
in (50) is defined by 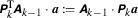 for \(k\geqslant 1\).
for \(k\geqslant 1\).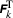 in (52) is defined by
in (52) is defined by 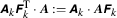 for \(k\geqslant 0\).
for \(k\geqslant 0\).Except where needed, \(\boldsymbol{x}_{\mathrm{r}}\) and
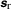 are suppressed in the notation from now on for brevity.
are suppressed in the notation from now on for brevity.
References
Admal, N.C., Marian, J., Po, G.: The atomistic representation of first strain-gradient elastic tensors. J. Mech. Phys. Solids 99, 93–115 (2017)
Admal, N.C., Tadmor, E.B.: A unified interpretation of stress in molecular systems. J. Elast. 100, 63–143 (2010)
Admal, N.C., Tadmor, E.B.: Stress and heat flux for arbitrary multibody potentials: a unified framework. J. Chem. Phys. 134, 184,106 (2011)
Admal, N.C., Tadmor, E.B.: The non-uniqueness of the atomistic stress tensor and its relationship to the generalized Beltrami representation. J. Mech. Phys. Solids 93, 72–92 (2015)
Bertram, A., Svendsen, B.: On material objectivity and reduced constitutive relations. Arch. Mech. 53, 653–675 (2001)
Cross, J.J.: Mixtures of fluids and isotropic solids. Arch. Mech. 25, 1025–1039 (1973)
Epstein, M., Elzanowski, M.: Material Inhomogeneities and Their Evolution. Springer Series on the Interaction of Mathematics and Mechanics. Springer, Berlin (2007)
Goldstein, H.: Classical Mechanics, 2nd edn. Addison-Wesley, Reading (1980)
Green, A.M., Rivlin, R.S.: Simple force and stress multipoles. Arch. Ration. Mech. Anal. 16, 325–353 (1964)
Javili, A., Dell’Isola, F., Steinmann, P.: Geometrically nonlinear higher-gradient elasticity with energetic boundaries. J. Mech. Phys. Solids 61, 2381–2401 (2013)
Lutsko, J.L.: Generalized expressions for the calculation of elastic constants by computer simulation. J. Appl. Phys. 65, 2991–2997 (1989)
Marsden, J., Hughes, T.J.R.: Mathematical Theory of Elasticity. Dover, New York (1984)
Marsden, J.E., Ratiu, T.S.: Introduction to Mechanics and Symmetry. Texts in Applied Mathematics, vol. 17. Springer, New York (1994)
Mindlin, R.D.: Micro-structure in linear elasticity. Arch. Ration. Mech. Anal. 16(1), 51–78 (1964)
Mindlin, R.D.: Second gradient of strain and surface-tension in linear elasticity. Int. J. Solids Struct. 1, 417–438 (1965)
Morgan, A.J.A.: Inhomogeneous materially uniform higher order gross bodies. Arch. Ration. Mech. Anal. 57, 189–253 (1975)
Noll, W.: On the continuity of the solid and fluid states. J. Ration. Mech. Anal. 4, 3–81 (1955)
Ray, J.R., Rahman, A.: Statistical ensembles and molecular-dynamics studies of anisotropic solids. J. Chem. Phys. 80(9), 4423–4428 (1984)
Samohýl, I.: Symmetry groups in the mass conserving, second-grade materials. Arch. Mech. 33, 983–987 (1981)
Svendsen, B.: Continuum thermodynamic and rate variational formulation of models for extended continua. In: Markert, B. (ed.) Advances in Extended and Multifield Theories for Continua. Lecture Notes in Applied and Computational Mechanics, vol. 59, pp. 1–18. Springer, Berlin (2011), Chap. 1
Svendsen, B., Bertram, A.: On frame-indifference and form-invariance in constitutive theory. Acta Mech. 132, 195–207 (1999)
Svendsen, B., Neff, P., Menzel, A.: On constitutive and configurational aspects of models for gradient continua with microstructure. Z. Angew. Math. Mech. 89, 687–697 (2009)
Tadmor, E., Miller, R.: Modeling Materials. Cambridge University Press, Cambridge (2011)
Thomas, J.C., van der Ven, A.: The exploration of nonlinear elasticity and its efficient parameterization for crystalline materials. J. Mech. Phys. Solids 107, 76–95 (2017)
Torres-Sánchez, A., Vargas, J.M., Arroyo, M.: Geometric derivation of the microscopic stress: a covariant central force decomposition. J. Mech. Phys. Solids 93, 224–239 (2016)
Toupin, R.A.: Theories of elasticity with couple-stress. Arch. Ration. Mech. Anal. 17(2), 85–112 (1964)
Truesdell, C., Noll, W.: The Non-Linear Field Theories of Mechanics. Handbuch der Physik, vol. III/3. Springer, Berlin (1965)
Truesdell, C., Toupin, R.: The Classic Field Theories. Handbuch der Physik, vol. III/1. Springer, Berlin (1960)
Šilhavý, M.: The Mechanics and Thermodynamics of Continuous Media. Springer, Berlin (1997)
Wallace, D.C.: Thermodynamics of Crystals. Wiley, New York (1972)
Wallace, D.C.: Statistical Physics of Crystals and Liquids. World Scientific, Singapore (2002)
Zhou, X.W., Johnson, R.A., Wadley, H.N.G.: Misfit-energy-increasing dislocations in vapor-deposited CoFe/NiFe multilayers. Phys. Rev. B 69(14), 144113 (2004)
Zhou, X.W.: EAM alloy potential set table for element Al. compatible with LAMMPS (2018). OpenKIM. https://doi.org/10.25950/276be3c4
Acknowledgements
Open access funding provided by Max Planck Society. We thank the reviewers of the first version of this work for helpful comments which have lead to its improvement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Reduced Forms of the Interatomic Potential
Consider the action
of the Euclidean group on \(U\), including in particular pure translation (\(\boldsymbol{Q}=\boldsymbol{I}\)) and pure orthogonal transformation (\(\boldsymbol{t}=\boldsymbol{0}\)). As usual, the material frame-indifference (MFI) of \(U\) takes the form
For example, \(U (\boldsymbol{r}_{1}, \ldots , \boldsymbol{r}_{N}) =U_{ \mathrm{t}} (\boldsymbol{r}_{12}, \ldots , \boldsymbol{r}_{N-1 N}) \) satisfies translational MFI (recall \(\boldsymbol{r}_{ab}:=\boldsymbol{r}_{a}-\boldsymbol{r} _{b}\)). Using the Cauchy’s representation theorem for simultaneous vector invariants (e.g., [27]), \(U_{\mathrm{t}}\) can be shown (e.g., [2, 3]) to satisfy orthogonal MFI iff it can be expressed as a function of \(\boldsymbol{d}_{12}\cdot \boldsymbol{d}_{23}, \ldots , \boldsymbol{d}_{N-2\,N-1}\cdot \boldsymbol{d}_{N-1\,N} \) (recall \(\boldsymbol{d}_{ab}:=\boldsymbol{r}_{ab}/r_{ab}\)). As usual, the simpler distance-based form
is (at least) sufficient to satisfy orthogonal MFI, and satisfies differential orthogonal MFI \(\sum _{a} \boldsymbol{r}_{a} \times \partial _{\smash{\boldsymbol{r}_{a}}}\!U =\sum _{a< b} r_{ab}^{-1} (\partial _{\smash{r_{ab}}}\!U_{\mathrm{d}} ) \,\boldsymbol{r}_{ab} \times \boldsymbol{r}_{ab} =\boldsymbol{0} \) identically. On the other hand, as discussed by [2, 4, 25], \(U_{\mathrm{d}}\) is not unique for potentials beyond 4-body interactions. For such cases, the "cluster" form
of \(U_{\mathrm{d}}\) is appropriate. In this form, each \(U_{ \smash{l^{n}}}\) is a \(n\)-body potential, and \(M_{n}\leqslant (N/n)\) is the number of \(n\)-body interactions among \(N\) mass points. By requiring that each \(U_{\smash{l^{n}}}\) vanish in the limit as the distance of any one of the interacting mass points to the others approaches infinity, this expansion can be formulated in a unique fashion.
Appendix B: Reduced Forms for the Continuum Free Energy Density
In the context of the continuum thermodynamic formulation from Sect. 5, the requirement of material frame-indifference
on (54)1 and the choice \(\boldsymbol{Q} \equiv \boldsymbol{R}^{\mathrm{T}} =\boldsymbol{U}^{-1}\!\boldsymbol{F}^{\mathrm{T}} \) result for example in the reduced form

of \(\psi _{\mathrm{r}}\), with  (subscript i stands for indifferent), \(\boldsymbol{U}=\boldsymbol{C}^{ \frac{1}{2}}\), \(\boldsymbol{C}=\boldsymbol{F}^{\mathrm{T}}\!\boldsymbol{F}\), and
(subscript i stands for indifferent), \(\boldsymbol{U}=\boldsymbol{C}^{ \frac{1}{2}}\), \(\boldsymbol{C}=\boldsymbol{F}^{\mathrm{T}}\!\boldsymbol{F}\), and

Clearly, (B.2) is a direct generalization of the zeroth-order reduction \(\psi _{\mathrm{r}}(\theta ,\boldsymbol{F}) = \psi _{\mathrm{i}}(\theta ,\boldsymbol{C}) \) to the current \(n \mathrm{th}\)-order case. Since  from (35) reduces to
from (35) reduces to  directly, the reduced form \(\psi _{\mathrm{i}}\) of \(\psi _{\mathrm{r}}\) in (B.2) also follows directly from the statistical thermodynamic treatment in the text.
directly, the reduced form \(\psi _{\mathrm{i}}\) of \(\psi _{\mathrm{r}}\) in (B.2) also follows directly from the statistical thermodynamic treatment in the text.
Note that the deformation measures  defined in (B.3) are strain-gradient-like. This can be seen by considering the change in squared relative distance
defined in (B.3) are strain-gradient-like. This can be seen by considering the change in squared relative distance

via (22)1 in a neighborhood of \(\boldsymbol{x}_{\mathrm{c}} =\boldsymbol{\chi }(\boldsymbol{x}_{\mathrm{r}}) \) (see Fig. 1). Here, \(\boldsymbol{s}_{\mathrm{c}} :=\boldsymbol{\chi }(\boldsymbol{x} _{\mathrm{r}}+\boldsymbol{s}_{\mathrm{r}}) -\boldsymbol{\chi }(\boldsymbol{x}_{ \mathrm{r}}) \), and \(\boldsymbol{E}:=\frac{1}{2}(\boldsymbol{C}-\boldsymbol{I}) \) is the Green strain. Note that the zeroth-order special case \(|\boldsymbol{s}_{ \mathrm{c}}|^{2}-|\boldsymbol{s}_{\mathrm{r}}|^{2} =\boldsymbol{s}_{ \mathrm{r}}\cdot 2\boldsymbol{E}\boldsymbol{s}_{\mathrm{r}} \) of (B.4) is consistent with \(|d\boldsymbol{x}_{\mathrm{c}} |^{2}-|d\boldsymbol{x}_{\mathrm{r}}|^{2} =d\boldsymbol{x}_{\mathrm{r}} \cdot 2\boldsymbol{E} \,d\boldsymbol{x}_{\mathrm{r}} \). Since \(\boldsymbol{C}^{-1}\) and \(\boldsymbol{s}_{\mathrm{r}}\) are non-zero, (B.4) implies that \(|\boldsymbol{s}_{\mathrm{c}}|=| \boldsymbol{s}_{\mathrm{r}}| \) iff  vanish; hence,
vanish; hence,  are strain-gradient-like. Moreover,
are strain-gradient-like. Moreover,  can be expressed as functions of \(\nabla ^{1}\!\boldsymbol{E}\), …, \(\nabla ^{n}\!\boldsymbol{E}\). To show this, consider the identities
can be expressed as functions of \(\nabla ^{1}\!\boldsymbol{E}\), …, \(\nabla ^{n}\!\boldsymbol{E}\). To show this, consider the identities

and

for constant \(\boldsymbol{a}_{1},\ldots ,\boldsymbol{a}_{n}\) with

In particular, note that \(\boldsymbol{\varGamma}_{\!1}\) represents the affine (linear, Kozsul) connection "symbols" induced by \(\boldsymbol{F}\). Analogously, in the context of the interpretation of \(\boldsymbol{C}\) as a Riemann metric (e.g., [12, 13, 28]),  for example represents the corresponding metric connection symbols. Note that the results (B.5)–(B.7) determine
for example represents the corresponding metric connection symbols. Note that the results (B.5)–(B.7) determine  as functions of \(\boldsymbol{C}\),
as functions of \(\boldsymbol{C}\),  ,
,  , …,
, …,  . To proceed further, consider next the identity
. To proceed further, consider next the identity

between \(\nabla \boldsymbol{E}\) and  . Exploiting the symmetry
. Exploiting the symmetry  of
of  induced by that \((\nabla \boldsymbol{F})^{\mathrm{S}} =\nabla \boldsymbol{F} \) of \(\nabla \boldsymbol{F}=\nabla \nabla \boldsymbol{\chi }\), (B.8) can be inverted via cyclic permutation of \(\boldsymbol{a}\), \(\boldsymbol{b}\), \(\boldsymbol{c}\) to yield
induced by that \((\nabla \boldsymbol{F})^{\mathrm{S}} =\nabla \boldsymbol{F} \) of \(\nabla \boldsymbol{F}=\nabla \nabla \boldsymbol{\chi }\), (B.8) can be inverted via cyclic permutation of \(\boldsymbol{a}\), \(\boldsymbol{b}\), \(\boldsymbol{c}\) to yield

with  . Note that (B.9) implies that
. Note that (B.9) implies that  is a linear function of \(\nabla \boldsymbol{E} \). Consequently, (B.9) also implies that
is a linear function of \(\nabla \boldsymbol{E} \). Consequently, (B.9) also implies that  is a linear function of \(\nabla ^{i}\!\boldsymbol{E}\) for \(i=2,\ldots ,n\). In summary, then,
is a linear function of \(\nabla ^{i}\!\boldsymbol{E}\) for \(i=2,\ldots ,n\). In summary, then,  , …,
, …,  are determined by \(\boldsymbol{C}(\boldsymbol{E})\), \(\nabla ^{1} \!\boldsymbol{E}\), …, \(\nabla ^{n}\!\boldsymbol{E}\). Consequently,
are determined by \(\boldsymbol{C}(\boldsymbol{E})\), \(\nabla ^{1} \!\boldsymbol{E}\), …, \(\nabla ^{n}\!\boldsymbol{E}\). Consequently,  always induces
always induces

in the context of higher-order strain-gradient thermoelasticity.
Appendix C: Variational Formulation of the Boundary-Value Problem
In order to connect with previous work for non-simple materials based on variational methods, and for completeness, the boundary-value problem implied by the direct formulation of higher-order deformation gradient energetic thermoelasticity in Sect. 5 is formulated here in variational form. Since the formulation is purely referential, we dispense with the subscript r on referential quantities in the rest of this section.
To this end, note that (51)1 and the result for  from (56) together imply the variational form
from (56) together imply the variational form
for linear momentum balance in the current context. For boundary conditions, attention is restricted to generalized displacement-traction-type (conservative) loading (e.g., [29, §13.3]) here. Let \(B\) represent a reference configuration, and \(\partial B\) its (smooth) boundary with (outward) unit normal \(\boldsymbol{n}\). Generalizing the considerations of [15] to the current \(n{\mathrm{th}}\)-order case, only the "normal" part \(\nabla _{\boldsymbol{n}}^{i}\boldsymbol{\chi }\) of \(\nabla ^{i}\boldsymbol{\chi }\) is kinematically independent on \(\partial B\). In this case,
represents the potential energy of loading in terms of the corresponding tractions \(\boldsymbol{t}_{0},\boldsymbol{t}_{1},\ldots ,\boldsymbol{t}_{n}\) on the flux part \(\partial _{\mathrm{f}}B\) of \(\partial B\). Then
represents the total (canonical) free energy (e.g., [29, §13.4]). Given (C.3), one obtains in turn
for the first variation \(\delta P\) of \(P\). Repeated integration by parts and application of the divergence theorem then yields
for \(\delta P\) with

via (56). Here, \(\boldsymbol{p}_{ij}\) represents the sum of all terms depending on  which contribute to the \(i{\mathrm{th}}\)-order boundary condition. As usual, \(\delta \boldsymbol{\chi }, \nabla _{\boldsymbol{n}}^{1}\delta \boldsymbol{\chi }, \ldots , \nabla _{\boldsymbol{n}}^{n}\delta \boldsymbol{\chi } \) vanish on the kinematic part \(\partial B\setminus \partial _{\mathrm{f}}B\) of \(\partial B\) by definition. Given (C.5), then,
which contribute to the \(i{\mathrm{th}}\)-order boundary condition. As usual, \(\delta \boldsymbol{\chi }, \nabla _{\boldsymbol{n}}^{1}\delta \boldsymbol{\chi }, \ldots , \nabla _{\boldsymbol{n}}^{n}\delta \boldsymbol{\chi } \) vanish on the kinematic part \(\partial B\setminus \partial _{\mathrm{f}}B\) of \(\partial B\) by definition. Given (C.5), then,
in \(B\), and
on \(\partial _{\mathrm{f}}B\), are necessary for \(\delta P=0\). In particular, (C.7) is clearly consistent with (51)1 in the form (C.1).
Determination of \(\boldsymbol{p}_{01},\ldots ,\boldsymbol{p}_{n-1\ n}\) in (C.6) follows via direct generalization of the approach of [15] to the current context. In particular, this is based on the split
of the gradient operator into normal and tangential parts. In addition, the operator identity

induced by the (smooth) surface divergence theorem, and the constraint
are employed in what follows. On this basis, consider the hierarchical system

of relations via (C.9) and (C.10). In particular, \(\boldsymbol{w}=\delta \boldsymbol{\chi }\),  ,
,  , …,
, …,  . As it turns out, this hierarchy is partially recursive with respect to dependence on \(\boldsymbol{w}\), \(\nabla _{\boldsymbol{n}}^{1}\boldsymbol{w}\), …, \(\nabla _{\boldsymbol{n}}^{n} \boldsymbol{w}\), in the following sense. Given (C.12)1, one obtains for example
. As it turns out, this hierarchy is partially recursive with respect to dependence on \(\boldsymbol{w}\), \(\nabla _{\boldsymbol{n}}^{1}\boldsymbol{w}\), …, \(\nabla _{\boldsymbol{n}}^{n} \boldsymbol{w}\), in the following sense. Given (C.12)1, one obtains for example

for the second term in (C.12)2. Together with

via (C.9)–(C.11), (C.13) determines (C.12)2 in terms of \(\boldsymbol{w}\), \(\nabla _{\boldsymbol{n}}^{1}\boldsymbol{w}\), and \(\nabla _{ \boldsymbol{n}}^{2}\boldsymbol{w}\), i.e.,

In recursive fashion, (C.15) also determines the second term on the right-hand side of (C.12)3 in terms of \(\boldsymbol{w}\), \(\nabla _{\boldsymbol{n}}^{1}\boldsymbol{w}\), and \(\nabla _{ \boldsymbol{n}}^{2}\boldsymbol{w}\). Likewise, (C.12)1 and (C.15) determine the last two terms on the right-hand side of

in terms of these. Together with

these determine (C.12)3 in terms of \(\boldsymbol{w}\), \(\nabla _{\boldsymbol{n}}^{1}\boldsymbol{w}\), \(\nabla _{\boldsymbol{n}}^{2}\boldsymbol{w}\), and \(\nabla _{\boldsymbol{n}}^{3}\boldsymbol{w}\). In this fashion, one can successively determine all identities in (C.12) in terms of \(\boldsymbol{w}\), \(\nabla _{\boldsymbol{n}}^{1}\boldsymbol{w}\), …, \(\nabla _{\boldsymbol{n}} ^{n}\boldsymbol{w}\). In turn, these can be used to determine \(\boldsymbol{p}_{ij}\) in (C.6).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Po, G., Admal, N.C. & Svendsen, B. Non-local Thermoelasticity Based on Equilibrium Statistical Thermodynamics. J Elast 139, 37–59 (2020). https://doi.org/10.1007/s10659-019-09745-9
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10659-019-09745-9





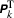 in (
in (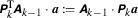 for
for 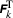 in (
in (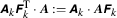 for
for 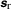 are suppressed in the notation from now on for brevity.
are suppressed in the notation from now on for brevity.