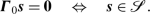Abstract
The homogenization of periodic elastic composites is addressed through the reformulation of the local equations of the mechanical problem in a geometric functional setting. This relies on the definition of Hilbert spaces of kinematically and statically admissible tensor fields, whose orthogonality and duality properties are recalled. These are endowed with specific energetic scalar products that make use of a reference and uniform elasticity tensor. The corresponding strain and stress Green’s operators are introduced and interpreted as orthogonal projection operators in the admissibility spaces. In this context and as an alternative to classical minimum energy principles, two geometric variational principles are investigated with the introduction of functionals that aim at measuring the discrepancy of arbitrary test fields to the kinematic, static or material admissibility conditions of the problem. By relaxing the corresponding local equations, this study aims in particular at laying the groundwork for the homogenization of composites whose constitutive properties are only partially known or uncertain. The local fields in the composite and their macroscopic responses are computed through the minimization of the proposed geometric functionals. To do so, their gradients are computed using the Green’s operators and gradient-based optimization schemes are discussed. A FFT-based implementation of these schemes is proposed and they are assessed numerically on a canonical example for which analytical solutions are available.






Similar content being viewed by others
References
Boffi, D., Brezzi, F., Fortin, M.: Mixed Finite Element Methods and Applications. Springer, Berlin (2013)
Bonnet, M., Constantinescu, A.: Inverse problems in elasticity. Inverse Probl. 21(2), R1 (2005)
Brézis, H.: Functional Analysis, Sobolev Spaces and Partial Differential Equations. Springer, New York (2011)
Brisard, S., Dormieux, L.: FFT-based methods for the mechanics of composites: a general variational framework. Comput. Mater. Sci. 49(3), 663–671 (2010)
Eyre, D.J., Milton, G.W.: A fast numerical scheme for computing the response of composites using grid refinement. Eur. Phys. J. Appl. Phys. 6, 41–47 (1999)
Gélébart, L., Mondon-Cancel, R.: Non linear extension of FFT-based methods accelerated by conjugate gradients to evaluate the mechanical behavior of composite materials. Comput. Mater. Sci. 77, 430–439 (2013)
Kabel, M., Böhlke, T., Schneider, M.: Efficient fixed point and Newton-Krylov solvers for FFT-based homogenization of elasticity at large deformations. Comput. Mech. 54, 1497–1514 (2014)
Khatchaturyan, A.G.: Theory of Structural Transformations in Solids. Wiley, New York (1983)
Kirchdoerfer, T., Ortiz, M.: Data-driven computational mechanics. Comput. Methods Appl. Mech. Eng. 304, 81–101 (2016)
Kröner, E.: Statistical Continuum Mechanics. Springer, Berlin (1971)
Ladeveze, P., Leguillon, D.: Error estimate procedure in the finite element method and applications. SIAM J. Numer. Anal. 20(3), 485–509 (1983)
Ladevèze, P., Pelle, J.P.: Mastering Calculations in Linear and Nonlinear Mechanics. Springer, New York (2005)
Michel, J., Moulinec, H., Suquet, P.: A computational method for linear and nonlinear composites with arbitrary phase contrast. Int. J. Numer. Methods Eng. 52, 139–160 (2001)
Milton, G.W.: The Theory of Composites. Cambridge University Press, Cambridge (2002)
Monchiet, V., Bonnet, G.: A polarization-based FFT iterative scheme for computing the effective properties of elastic composites with arbitrary contrast. Int. J. Numer. Methods Eng. 89(11), 1419–1436 (2012)
Moreau, J.J.: Duality characterization of strain tensor distributions in an arbitrary open set. J. Math. Anal. Appl. 72(2), 760–770 (1979)
Moulinec, H., Silva, F.: Comparison of three accelerated FFT-based schemes for computing the mechanical response of composite materials. Int. J. Numer. Methods Eng. 97(13), 960–985 (2014)
Moulinec, H., Suquet, P.: A fast numerical method for computing the linear and nonlinear properties of composites. C. R. Acad. Sci. Paris II 318, 1417–1423 (1994)
Moulinec, H., Suquet, P.: A numerical method for computing the overall response of nonlinear composites with complex microstructure. Comput. Methods Appl. Mech. Eng. 157, 69–94 (1998)
Moulinec, H., Suquet, P., Milton, G.W.: Convergence of iterative methods based on Neumann series for composite materials: theory and practice. Int. J. Numer. Methods Eng. 114, 1103–1130 (2018). https://doi.org/10.1002/nme.5777
Müller, W.: Mathematical versus experimental stress analysis of inhomogeneities in solids. J. Phys. IV 6(C1), C1-139–C1-148 (1996)
Mura, T.: Micromechanics of Defects in Solids. Springer, Berlin (1987)
Nouy, A., Soize, C.: Random field representations for stochastic elliptic boundary value problems and statistical inverse problems. Eur. J. Appl. Math. 25(3), 339–373 (2014)
Obnosov, Y.V.: Periodic heterogeneous structures: new explicit solutions and effective characteristics of refraction of an imposed field. SIAM J. Appl. Math. 59(4), 1267–1287 (1999)
Paris, L.: Etude de la régularité d’un champ de vitesses à partir de son tenseur deformation. In: Séminaire d’Analyse Convexe, Montpellier, 6(12) (1976)
Schneider, M.: An FFT-based fast gradient method for elastic and inelastic unit cell homogenization problems. Comput. Methods Appl. Mech. Eng. 315, 846–866 (2017)
Staber, B., Guilleminot, J.: Stochastic modeling and generation of random fields of elasticity tensors: a unified information-theoretic approach. C. R., Méc. 345(6), 399–416 (2017)
Suquet, P.: Plasticité et Homogénéisation. Thèse d’État, Université Pierre et Marie Curie, Paris 6 (1982)
Suquet, P.: Elements of homogenization for inelastic solid mechanics. In: Sanchez-Palencia, E., Zaoui, A. (eds.) Homogenization Techniques for Composite Media, vol. 272, pp. 193–278. Springer, Berlin (1987)
Willis, J.: Bounds and self-consistent estimates for the overall properties of anisotropic composites. J. Mech. Phys. Solids 25(3), 185–202 (1977)
Willis, J.: Variational and related methods for the overall properties of composites. Adv. Appl. Mech. 21, 1–78 (1981)
Zeman, J., Vondr̆ejc, J., Novák, J., Marek, I.: Accelerating a FFT-based solver for numerical homogenization of periodic media by conjugate gradients. J. Comput. Phys. 229, 8065–8071 (2010)
Acknowledgements
Fruitful discussions with H. Moulinec and J.-C. Michel are gratefully acknowledged. The Authors have received funding from Excellence Initiative of Aix-Marseille University - A*MIDEX, a French “Investissements d’Avenir” program in the framework of the Labex MEC.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Mathematical Definitions
1.1 A.1 Periodic Fields
Consider a unit-cell \(\mathcal{V}\) allowing to fill the space \(\mathbb{R}^{d}\) by translation along \(d\) vectors \({\boldsymbol{Y}}_{1}, \dots, {\boldsymbol{Y}}_{d}\). The lattice ℛ generated by these vectors is defined as
Define spaces of periodic scalar functions, vector fields and tensor fields as:

1.2 A.2 Fourier Transforms
The Fourier transform \(\hat{f}\) of \(f\) is defined as:
Let \(\mathcal{R}^{*}\) denote the reciprocal lattice of ℛ generated by the vectors
where \((i,j,k)\) is a direct circular permutation. Then, according to Plancherel’s theorem:
and therefore
The original periodic function \(f \) in \(L^{2}_{\text{per}}\! (\mathcal{V} )\) can be reconstructed from its Fourier transform by
Appendix B: Properties of the Green’s Operators
Lemma 3
The strain Green’s operator\({\boldsymbol{\varGamma}}_{0}\)satisfies the following properties:
- 1.
\({\boldsymbol{\varGamma}}_{0}\)satisfies the reciprocity identity:
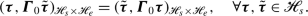 (65)
(65) - 2.
The kernel of\({\boldsymbol{\varGamma}}_{0}\)coincides with the subspace
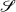 :
:
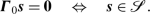 (66)
(66) - 3.
\({\boldsymbol{\varGamma}}_{0}\)is such that:
$$ {\boldsymbol{\varGamma}}_{0} {\boldsymbol{L}}_{0} { \boldsymbol{\varGamma}}_{0} = {\boldsymbol{\varGamma}} _{0}. $$(67)
Properties (66) and (67) were proved in [13]. The additional property (65) derives from the identity

To prove (68), note that, by definition of \({\boldsymbol{\varGamma}} _{0}\), a stress field \({\boldsymbol{s}}={\boldsymbol{L}}_{0} {\boldsymbol{\varGamma}}_{0}{\boldsymbol {\tau}}- {\boldsymbol{\tau}}\) in  can be associated with \({\boldsymbol{\tau}}\) through (17). By Lemma 1:
can be associated with \({\boldsymbol{\tau}}\) through (17). By Lemma 1:

which, according to the definition (9) of the Riesz mapping, proves (68). Note that similar properties can be proved for the stress Green’s operator \({\boldsymbol{\Delta}}_{0}\) owing to the duality principle, see [14].
Remark 6
If one defines the Green’s operator from  , endowed with the standard \(L^{2}\)-scalar product, into itself then the reciprocity identity (65) amounts in the self-adjointness of \({\boldsymbol{\varGamma}}_{0}\), a property which is known since [10].
, endowed with the standard \(L^{2}\)-scalar product, into itself then the reciprocity identity (65) amounts in the self-adjointness of \({\boldsymbol{\varGamma}}_{0}\), a property which is known since [10].
Rights and permissions
About this article
Cite this article
Bellis, C., Suquet, P. Geometric Variational Principles for Computational Homogenization. J Elast 137, 119–149 (2019). https://doi.org/10.1007/s10659-018-09713-9
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10659-018-09713-9
Keywords
- Composite materials
- Helmholtz decomposition
- Green’s operators
- Lippmann-Schwinger equation
- Gradient-based algorithms




 :
: