The Biaxial Moduli of Cubic Materials Subjected to an Equi-biaxial Elastic Strain

Abstract

Formulae for the biaxial moduli along the directions of principal stress for $(\mathit{hkl})$ interfaces of cubic materials are given for situations in which there is equi-biaxial strain within the plane. These formulae are relevant in the consideration of the deposition of thin films on single crystal substrates such as silicon. Within a particular $(\mathit{hkl})$, the directions defining these principal biaxial moduli are shown to be those along which there are the extreme values of the shear modulus and Poisson’s ratio. Conditions for stationary values of the biaxial moduli are also derived, from which the conditions for the global extrema of the biaxial moduli are established.

1 Introduction

In contrast to mathematical expressions and their graphical representations for Young’s modulus, Poisson’s ratio and the shear modulus, as a function of crystal orientation for cubic crystals [1–16], expressions in the literature for the orientation dependence of the biaxial modulus of cubic materials subjected to an equi-biaxial elastic strain are limited to circumstances where this strain is in a {001}, {111} or {011} plane [17–23]. In almost all studies in which biaxial moduli are of interest, the material can reasonably be assumed to be isotropic, e.g., if the material is a glass or a fully annealed polycrystalline metal or ceramic. In such circumstances, it is straightforward to show that if there is zero stress perpendicular to the plane on which there is equi-biaxial strain (the Kirchhoff hypothesis of thin plate theory [20]), the single-valued biaxial modulus is $E/(1- \nu)$, where $E$ is Young’s modulus and $\nu$ is Poisson’s ratio [19, 20, 22].

However, as Janssen et al. note [22], biaxial moduli are important in the deposition of thin films on single crystal substrates, such as in the semiconductor industry where single crystal silicon is a common substrate, and where a state of equi-biaxial strain in the film and substrate has been introduced during deposition and/or by a change in temperature. For example, a polycrystalline metal film might be deposited on the silicon substrate at a high temperature, after which the thin film/substrate assembly is cooled to room temperature. This equi-biaxial strain introduces a state of biaxial stress in the thin film and curvature in the thin film/substrate assembly [19, 20, 22] which can be measured experimentally. This physical situation of an equi-biaxial strain in the material of interest and a zero normal stress also applies to the situation where a single crystal thin film with a $(\mathit{hkl})$ orientation parallel to the substrate and with a cubic crystal structure is deposited onto an isotropic substrate. Janssen et al. comment on the need to use correct mathematical expressions when deducing film stress from wafer curvature measurements and show how biaxial moduli of (001) and (111) silicon substrates can be derived [22].

The purpose of the work reported here is the generation of analytical expressions and their graphical representations for the biaxial moduli of cubic materials relevant for thin film/substrate assemblies in which there is an equi-biaxial elastic strain, and where the substrate is a single crystal, cut so that the interface between the thin film and the substrate is a general $(\mathit{hkl})$ plane, rather than a plane of high symmetry such as (001) or (111). For such a situation, in which the film could be a polycrystalline film isotropic in the plane of the film, the substrate will have induced in it curvature associated with two principal radii of curvature orthogonal to one another. These principal radii of curvature are directly related to the two orthogonal principal biaxial moduli in the $(\mathit{hkl})$ plane. For the high symmetry situations of (001) and (111) cubic substrates, the two principal biaxial moduli are identical and the substrate appears to be transversely isotropic, so that the curvature induced by an equi-biaxial strain is radially symmetric [22].

The paper is organised as follows. A statement of the problem of determining principal biaxial moduli for a plane of a general anisotropic material of undeclared symmetry subjected to in-plane biaxial strain is given in Sect. 2. The process of how the equations generated for a general anisotropic material of undeclared symmetry reduce for equi-biaxial strain when the material is cubic is then presented in Sect. 3. Computations of the principal biaxial moduli for various $(\mathit{hkl})$ for cubic materials and their extrema as a function of $(\mathit{hkl})$ are presented in Sect. 4. Finally, in Sects. 5 and 6, remarks are made on the magnitude of shear stresses out of the plane on which there is an equi-biaxial strain and conclusions drawn on the practical consequences for cubic materials of the results established in Sect. 4.

2 General Tensor Transformation Relations for Biaxial Strains in Thin Plates

Under the assumption that elastic conditions pertain, the symmetric stress and strain tensors, $\sigma_{ij}$ and $\varepsilon_{kl}$ respectively, are related to one another through the equations

$$ \sigma_{ij} = C_{ijkl}\varepsilon_{kl}\quad \mbox{and}\quad \varepsilon_{ij} = S_{ijkl}\sigma_{kl}, $$

(1)

in which $C_{ijkl}$ is the stiffness tensor and $S_{ijkl}$ the compliance tensor, both tensors of the fourth rank, and where $i$, $j$, $k$ and $l$ take all values between 1 and 3 [7, 24, 25]. For an arbitrary rotation of axes from one axis system to another, fourth rank tensors, $T_{ijkl}$, transform as

$$ T'_{ ijkl} = a_{im}a_{jn}a_{kp}a_{lq}T_{mnpq}, $$

(2)

for $i$, $j$, $k$, $l$, $m$, $n$, $p$ and $q$ all taking values from 1 to 3 [7, 24, 25], where the $a_{im}$ are direction cosines specifying the angle between the $i$th axis of the ‘new’ axis system and the $m$th axis of the ‘old’ axis system. Both the ‘old’ axis system and the ‘new’ axis system in this formalism are defined by orthonormal axis systems [7, 24, 25]. For materials with relatively high symmetry, ‘old’ axis systems are straightforward to define with respect to the crystal axis, whereas this is not the case with monoclinic or triclinic symmetry.

Defining axes $1'$, $2'$ and $3'$ in the ‘new’ axis system, it is convenient to choose axis $3'$ to be parallel to the normal to the plane $(\mathit{hkl})$ of interest within the crystal and $1'$ and $2'$ to be parallel to principal strains within the plane of the film. The Kirchhoff hypothesis of thin plate theory requires that $\sigma '_{33} = 0$. Hence, within the plane, we have the three equations

$$\begin{aligned} \sigma '_{11} =& C'_{1111} \varepsilon '_{11} + C'_{1122} \varepsilon '_{22} + C'_{1133} \varepsilon '_{33}, \\ \sigma '_{22} =& C'_{2211} \varepsilon '_{11} + C'_{2222} \varepsilon '_{22} + C'_{2233} \varepsilon '_{33}, \\ \sigma '_{12} =& C'_{1211} \varepsilon '_{11} + C'_{1222} \varepsilon '_{22} + C'_{1233} \varepsilon '_{33}. \end{aligned}$$

(3)

These equations together with the condition

$$ \sigma '_{33} = C'_{3311}\varepsilon '_{11} + C'_{3322}\varepsilon '_{22} + C'_{3333}\varepsilon '_{33} = 0 $$

(4)

determine the problem of an unequal biaxial strain within a thin plate or film. However, for many practical situations, such as those described in Sect. 1, there is good reason to expect the strain to be equi-biaxial, so that $\varepsilon '_{11} = \varepsilon '_{22} = \varepsilon$. Under these circumstances, using the contracted two suffix Voigt notation [7], the biaxial modulus $M$ along $1'$ for a general anisotropic material of undeclared symmetry is defined by the expression

$$ M = \frac{\sigma '_{1}}{\varepsilon} = c'_{11} + c'_{12} - \frac{1}{c'_{33}}\bigl({c'_{13}}^{2} + c'_{13}c'_{23}\bigr). $$

(5)

in which the stiffness components in contracted Voigt notation have been denoted by $c$. A similar result pertains for the biaxial modulus along the direction $2'$ perpendicular to $1'$ within the plane. To ensure that the biaxial moduli along $1'$ and $2'$ are principal biaxial moduli, a further constraint is that $\sigma '_{12}$ in Eq. (3) is zero.

For a general anisotropic material, and for a general $(\mathit{hkl})$, the number of independent components of the stiffness tensor makes evaluation of the principal biaxial moduli computationally challenging, even for this special case of equi-biaxial strain. However, for cubic materials, the effect of crystal symmetry simplifies the problem considerably, as is shown in the next section.

3 Equations Defining the Biaxial Moduli for Cubic Materials when There Is an Equi-biaxial Strain

When a cubic single crystal substrate has a $(\mathit{hkl})$ orientation, it is convenient to define the ‘old’ axis system to be the orthonormal axis system aligned with respect to the $\langle 100\rangle$ directions of the cubic crystal. Sixty coefficients of tensors of the fourth rank for cubic materials are zero in this axis system. The twenty one non-zero $C_{ijkl}$ and $S_{ijkl}$ for cubic crystals are

$$ c_{11} = C_{iiii},\quad c_{12} = C_{iijj}, \quad c_{44} = C_{ijij},\quad s_{11} = S_{iiii},\quad s_{12} = S_{iijj},\quad s_{44} = 4S_{ijij} $$

(6)

[7, 24, 25], in which the contracted two suffix Voigt notation [7] is denoted by $c$ and $s$ for stiffness and compliance to distinguish these from the full tensor $C$ and $S$ components. Hence, there are only three independent elements of $c_{ij}$ and $s_{ij}$. These non-zero $c_{ij}$ and $s_{ij}$ are related to one another through the equations

$$ \begin{aligned}[c] s_{11} &= \frac{c_{11} + c_{12}}{(c_{11} - c_{12}) (c_{11} + 2c_{12})},\qquad s_{12} = \frac{ - c_{12}}{(c_{11} - c_{12}) (c_{11} + 2c_{12})},\qquad s_{44} = \frac{1}{c_{44}}, \\ c_{11} &= \frac{s_{11} + s_{12}}{ (s_{11} - s_{12}) (s_{11} + 2s_{12})},\qquad c_{12} = \frac{ - s_{12}}{(s_{11} - s_{12}) (s_{11} + 2s_{12})},\qquad c_{44} = \frac{1}{s_{44}}. \end{aligned} $$

(7)

The $C_{ijkl}$ and $S_{ijkl}$ transform from axes 1, 2 and 3 to the axes $1'$, $2'$ and $3'$ in such a way that the $C'_{ijkl}$ and $S'_{ijkl}$ can be written in the succinct forms

$$ \begin{aligned}[c] C'_{ijkl} &= c_{12}\delta_{ij}\delta_{kl} + c_{44}( \delta_{ik}\delta_{jl} + \delta_{il} \delta_{jk}) + (c_{11} - c_{12} - 2c_{44}) a_{iu}a_{ju}a_{ku}a_{lu}, \\ 4S'_{ijkl} &= 4s_{12}\delta_{ij} \delta_{kl} + s_{44}(\delta_{ik} \delta_{jl} + \delta_{il}\delta_{jk}) + (4s_{11} - 4s_{12} - 2s_{44}) a_{iu}a_{ju}a_{ku}a_{lu}, \end{aligned} $$

(8)

in which $\delta$ is the Kronecker delta and the dummy suffix $u$ takes the values 1, 2 and 3 [26].

The direction cosines for $3'$, the direction parallel to the normal to $(\mathit{hkl})$, are [$a_{31},a_{32},a_{33}$], where

$$ a_{31} = h/\sqrt{h^{2} + k^{2} + l^{2}}, \qquad a_{32} = k/\sqrt{h^{2} + k^{2} + l^{2}}\quad \mbox{and}\quad a_{33} = l/\sqrt{h^{2} + k^{2} + l^{2}}. $$

(9)

Using Eqs. (8) and (9), it then follows from Eq. (5) and some straightforward mathematical manipulation that the biaxial modulus $M [a_{11},a_{12},a_{13}]$ along the direction $1'$, i.e., along the unit direction [$a_{11},a_{12},a_{13}$] within $(\mathit{hkl})$, is specified by the equation

$$ M [a_{11},a_{12},a_{13}] = \frac{(c_{11} + 2c_{12}) (2c_{44} + (P - Q)H)}{c_{12} + 2c_{44} - QH}, $$

(10)

in which

$$ P = a_{11}^{2}a_{31}^{2} + a_{12}^{2}a_{32}^{2} + a_{13}^{2}a_{33}^{2}\quad \mbox{and}\quad Q = a_{31}^{4} + a_{32}^{4} + a_{33}^{4} $$

(11)

and where

$$ H = 2c_{44} + c_{12} - c_{11} $$

(12)

is the anisotropy factor defined by Hirth and Lothe [27]. For cubic materials, where the anisotropy ratio

$$ A = \frac{2c_{44}}{c_{11} - c_{12}} = \frac{2 (s_{11} - s_{12})}{s_{44}} $$

(13)

[7, 25, 27, 28] is >1, $H > 0$. If $A = 1$, $H = 0$ and if $A < 1$, $H < 0$. Likewise, along the orthogonal unit direction [$a_{21},a_{22},a_{23}$], we have the result

$$ M [a_{21},a_{22},a_{23}] = \frac{(c_{11} + 2c_{12}) (2c_{44} + (R - Q)H)}{c_{12} + 2c_{44} - QH}, $$

(14)

where

$$ R = a_{21}^{2}a_{31}^{2} + a_{22}^{2}a_{32}^{2} + a_{23}^{2}a_{33}^{2}. $$

(15)

Inspection of Eqs. (10) and (14) shows that, for a given plane $(\mathit{hkl})$, the arithmetic mean of two biaxial moduli defined along two orthogonal directions in $(\mathit{hkl})$ is independent of the orientation of these two orthogonal directions with respect to the directions of principal stress within $(\mathit{hkl})$, since we have the identity

$$ P + Q + R = 1. $$

(16)

Hence, the mean value of the biaxial modulus for a plane $(\mathit{hkl})$ of a cubic material subjected to an equi-biaxial strain, $\bar{M} (\mathit{hkl})$, is

$$ \bar{M} (\mathit{hkl}) = \frac{(c_{11} + 2c_{12}) (4c_{44} + (1 - 3Q)H)}{2 (c_{12} + 2c_{44} - QH)}. $$

(17)

The condition specified in Sect. 2 for the biaxial moduli along these two orthogonal directions to be along directions of principal stress within $(\mathit{hkl})$ is that $\sigma '_{12} = 0$, i.e.,

$$ C'_{1211}\varepsilon '_{11} + C'_{1222}\varepsilon '_{22} + C'_{1233}\varepsilon '_{33} = 0. $$

(18)

Using Eqs. (8) and (12) and making the substitution $\varepsilon '_{11} = \varepsilon '_{22} = \varepsilon$, this condition can first be rewritten in the form

$$\begin{aligned} &H \bigl(a_{11}a_{21}\bigl(a_{11}^{2} + a_{21}^{2}\bigr) + a_{12}a_{22} \bigl(a_{12}^{2} + a_{22}^{2}\bigr) + a_{13}a_{23}\bigl(a_{13}^{2} + a_{23}^{2}\bigr)\bigr) \varepsilon \\ &\quad {}+H \bigl(a_{11}a_{21}a_{31}^{2} + a_{12}a_{22}a_{32}^{2} + a_{13}a_{23}a_{33}^{2}\bigr) \varepsilon '_{33} = 0. \end{aligned}$$

(19)

Making use of the orthonormality properties of direction cosines and the orthogonality of [$a_{11},a_{12},a_{13}$] and [$a_{21},a_{22},a_{23}$], so that $a_{11}a_{21} + a_{12}a_{22} + a_{13}a_{23} = 0$, this simplifies to the condition that

$$ H\bigl(\varepsilon - \varepsilon '_{33}\bigr) \bigl(a_{11}a_{21}a_{31}^{2} + a_{12}a_{22}a_{32}^{2} + a_{13}a_{23}a_{33}^{2}\bigr) = 0. $$

(20)

Since $(\varepsilon - \varepsilon '_{33}) \neq$ 0 and in general $H \neq$ 0, this reduces to the condition on [$a_{11},a_{12},a_{13}$] and [$a_{21},a_{22},a_{23}$] that

$$ a_{11}a_{21}a_{31}^{2} + a_{12}a_{22}a_{32}^{2} + a_{13}a_{23}a_{33}^{2} = 0. $$

(21)

This is the same condition as Eq. (19) of Knowles and Howie [16] defining the axes of the sextic equation describing the variation of the shear modulus as a function of shear direction of a particular plane of shear $(\mathit{hkl})$; Knowles and Howie show how this equation can be solved to determine these axes for a general $(\mathit{hkl})$. It is evident from Eqs. (8) and (21) that the condition expressed by Eq. (21) is equivalent to the statement that $C'_{1233} = C'_{3312} = 0$. It is also evident that equivalent descriptions of this condition can be derived by permuting 1, 2, 3 and 3 in Eq. (8), so that, for example, the condition $C'_{1332} = 0$ is also defined by Eq. (21).

It is further shown in Appendix A that the condition described by Eq. (21) is also equivalent to the condition for the extreme values of shear modulus and Poisson’s ratio for a particular $(\mathit{hkl})$ in a cubic material specified by Norris [12]. Hence, we have the interesting result that, on a particular $(\mathit{hkl})$ for a cubic material used as a substrate, the biaxial moduli defining the principal radii of curvature in an isotropic thin film/substrate assembly in which a state of equi-biaxial strain has been induced in both the thin film and the substrate are parallel to extrema in both the shear modulus and Poisson’s ratio on that plane.

4 Computation of Principal Biaxial Moduli for Various $(\mathit{hkl})$

We are now in a position to consider both special and general results from this analysis.

4.1 (001) Interface Orientation

For this interface, $a_{31}= 0$, $a_{32} = 0$ and $a_{33} = 1$. Hence, in Eq. (11), $P = 0$ and $Q = 1$ since $a_{13} = 0$ because [$a_{11},a_{12},a_{13}$] has to be orthogonal to [$a_{31},a_{32},a_{33}$]. It follows from Eq. (10) that

$$ M [a_{11},a_{12},0] = \frac{(c_{11} + 2c_{12}) (2c_{44} - H)}{c_{12} + 2c_{44} - H}, $$

(22)

i.e., using Eq. (12),

$$ M [a_{11},a_{12},0] = \frac{(c_{11} + 2c_{12}) (c_{11} - c_{12})}{c_{11}} \equiv c_{11} + c_{12} - \frac{2c_{12}^{2}}{c_{11}}, $$

(23)

as stated in [18–20, 22, 23]. It is evident that this expression for $M$ is independent of $a_{11}$ and $a_{12}$, confirming the transverse isotropy of $M$ in the (001) plane, so that this $M$ can be designated $M$ (001). Using the equations in (7), an alternative expression for $M$ (001) is

$$ M (001) = \frac{1}{s_{11} + s_{12}} $$

(24)

[17, 21, 22].

4.2 (111) Interface Orientation

Here, $a_{31} = a_{32} = a_{33} = 1/\sqrt{3}$, and since $a_{11}^{2} + a_{12}^{2} + a_{13}^{2} = 1$, $P = Q = 1/3$ in Eq. (11). Hence, $M$ on this plane is also transversely isotropic and can be designated $M$ (111). Using Eqs. (7) and (10),

$$ M (111) = \frac{6c_{44}(c_{11} + 2c_{12})}{c_{11} + 2c_{12} + 4c_{44}} \equiv \frac{6}{4s_{11} + 8s_{12} + s_{44}} $$

(25)

[17–23].

4.3 (011) Interface Orientation

Here, $a_{31}= 0$ and $a_{32} = a_{33} = 1/\sqrt{2}$. Using Eq. (21), it is evident by inspection that direction cosines defining the directions of principal stresses within (011) are $[a_{11},a_{12},a_{13}] = [1, 0, 0]$ and $[a_{21},a_{22},a_{23}] = [0, 1/\sqrt{2}, - 1/\sqrt{2} ]$. Hence, $P = 0$ and $Q = R = 1/2$, and so using conventional crystallographic nomenclature,

$$ M [100] = \frac{(c_{11} + 2c_{12}) (c_{11} - c_{12} + 2c_{44})}{c_{11} + c_{12} + 2c_{44}} = \frac{2s_{11} - 2s_{12} + s_{44}}{s_{11}s_{44} + 2 (s_{11} - s_{12})(s_{11} + 2s_{12})} $$

(26)

and

$$ M [01\bar{1}] = \frac{4c_{44}(c_{11} + 2c_{12})}{c_{11} + c_{12} + 2c_{44}} = \frac{4 (s_{11} - s_{12})}{s_{11}s_{44} + 2 (s_{11} - s_{12})(s_{11} + 2s_{12})}. $$

(27)

Straightforward algebraic manipulation of the more complicated equations quoted by Nix [19] for $M [100]$ and $M [01\bar{1}]$ in Section IV.B of his paper confirms that Eqs. (26) and (27) expressed in terms of $c_{11}$, $c_{12}$ and $c_{44}$ are equivalent to the equations he has quoted. It is also evident from these two equations that

$$ \frac{M [01\bar{1}]}{M [100]} = \frac{2A}{1 + A}, $$

(28)

so that for $A > 1$, $M [01\bar{1}] > M [100]$ on (011), and for $A < 1$, $M [01\bar{1}] < M [100]$ on (011).

Expressed in terms of $s_{11}$, $s_{12}$ and $s_{44}$, the arithmetic mean of these two biaxial moduli on (011), $\bar{M} (011)$, is

$$ \bar{M} (011) = \frac{6 (s_{11} - s_{12}) + s_{44}}{2s_{11}s_{44} + 4 (s_{11} - s_{12})(s_{11} + 2s_{12})}, $$

(29)

which is Eq. (42) quoted by Lee [21].

4.4 $(0\mathit{kl})$ Interface Orientation

For ($0\mathit{kl}$), i.e., a general plane on the great circle on which (001), (011) and (010) lie on a stereographic representation of a cubic crystal [25], the table of direction cosines between the axis set 1, 2 and 3 and the axis set $1'$, $2'$ and $3'$ defining the directions of principal stress within ($0\mathit{kl}$) can be chosen to be of the form

(30)

with $a_{32}^{2} + a_{33}^{2} = 1$. Hence, for the direction [100], $P = 0$ and $Q = a_{32}^{4} + a_{33}^{4}$, and so from Eq. (10),

$$ M [100] = \frac{(c_{11} + 2c_{12}) (2c_{44} - (a_{32}^{4} + a_{33}^{4})H)}{c_{12} + 2c_{44} - (a_{32}^{4} + a_{33}^{4})H}, $$

(31)

or, equivalently,

$$ M [100] = \frac{(c_{11} + 2c_{12}) (c_{11} - c_{12} + 2a_{32}^{2}a_{33}^{2}H)}{c_{11} + 2a_{32}^{2}a_{33}^{2}H}. $$

(32)

Likewise, $M [0l\bar{k}]$ along the direction perpendicular to [100] within ($0\mathit{kl}$) is

$$ M [0l\bar{k}] = \frac{(c_{11} + 2c_{12}) (2c_{44} + (2a_{32}^{2}a_{33}^{4} - a_{32}^{4} - a_{33}^{4})H)}{c_{12} + 2c_{44} - (a_{32}^{4} + a_{33}^{4})H}, $$

(33)

or, equivalently,

$$ M [0l\bar{k}] = \frac{(c_{11} + 2c_{12}) (c_{11} - c_{12} + 4a_{32}^{2}a_{33}^{2}H)}{c_{11} + 2a_{32}^{2}a_{33}^{2}H}. $$

(34)

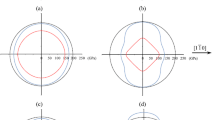
To show how $M [100]$ and $M [0l\bar{k}]$ vary as a function of ($0\mathit{kl}$), it is convenient to examine the portion of the great circle between (001) and (010), setting $a_{32} = \sin \theta$ and $a_{33} = \cos \theta$ for $0 \leq \theta \leq 90^{\circ}$. Graphs of how these vary as a function of angle from (001) towards (010) for Si (for which $A = 1.56$), Cu ($A = 3.21$), Nb ($A = 0.55$) and $\beta$-brass ($A = 8.49$) are shown in Fig. 1. For these graphs, data for $c_{11}$, $c_{12}$ and $c_{44}$ for Si, Cu and Nb were those quoted in Table 6.1 of [25], i.e., 165.7, 63.9 and 79.6 GPa respectively for Si, 168.4, 121.4 and 75.4 GPa respectively for Cu, and 245.6, 138.7 and 29.3 GPa respectively for Nb. The corresponding data for $\beta$-brass were those quoted in Table III of [29], i.e., 129.1, 109.7 and 82.4 GPa respectively. The positions of a number of low index planes between (001) and (010) are also indicated.

Fig. 1

Principal biaxial moduli for ($0\mathit{kl}$) interfaces as a function of angle away from (001) towards (010): (a) Si, (b) Cu, (c) $\beta$-brass and (d) Nb. Both $M [100]$ and $M [0l\bar{k}]$ are symmetric about 0°, 45° and 90°, i.e., the (001), (011) and (010) planes. Other low index planes are (013) at 18.43°, (012) at 26.57°, (021) at 63.43° and (031) at 71.57°

It is evident that the disparity between the values of $M [100]$ and $M [0l\bar{k}]$ is greatest when ($0\mathit{kl}$) is (011). Also noteworthy is the fact that for $A > 1$, both $M [100]$ and $M [0l\bar{k}]$ increase from minima at (001) and (010) to a maximum at (011). For $A < 1$, these trends in $M [100]$ and $M [0l\bar{k}]$ are reversed.

4.5 $(\mathit{hhl})$ Interface Orientation

For $(\mathit{hhl})$, i.e., a general plane on the great circle on which (001), (111) and (110) lie on a stereographic representation of a cubic crystal [25], the table of direction cosines between the axis set 1, 2 and 3 and the axis set $1'$, $2'$ and $3'$ defining the directions of principal stress within $(\mathit{hhl})$ can be chosen to be of the form

(35)

with $2a_{31}^{2} + a_{33}^{2} = 1$. Hence, for the direction [$1\bar{1}0$] defining one of the principal directions, $P = a_{31}^{2}$ and $Q = 2a_{31}^{4} + a_{33}^{4}$, and so from Eq. (10),

$$ M[1\bar{1}0] = \frac{(c_{11} + 2c_{12}) (2c_{44} + (a_{31}^{2} - 2a_{31}^{4} - a_{33}^{4})H)}{c_{12} + 2c_{44} - (2a_{31}^{4} + a_{33}^{4})H}, $$

(36)

or, after some elementary mathematical manipulation to eliminate $a_{31}$ from this expression,

$$ M[1\bar{1}0] = \frac{(c_{11} + 2c_{12}) (4c_{44} - a_{33}^{2}(3a_{33}^{2} - 1)H)}{c_{11} + c_{12} + 2c_{44} - a_{33}^{2}(3a_{33}^{2} - 2)H}. $$

(37)

Similarly, $M [\mathit{ll}\overline{2h}]$ along the direction perpendicular to [$1\bar{1}0$] within $(\mathit{hhl})$ is

$$ M[\mathit{ll}\overline{2h}] = \frac{(c_{11} + 2c_{12}) (c_{11} - c_{12} + 2c_{44} - a_{33}^{2}(6a_{33}^{2} - 5)H)}{c_{11} + c_{12} + 2c_{44} - a_{33}^{2}(3a_{33}^{2} - 2)H}. $$

(38)

It is then straightforward to examine the portion of the great circle between (001) and (110) for $a_{33} = \cos \theta$ for $0 \leq \theta \leq 90^{\circ}$ to show how $M[1\bar{1}0]$ and $M [\mathit{ll}\overline{2h}]$ vary as a function of $\theta$. Graphs of how these quantities vary for Si, Cu, Nb and $\beta$-brass as a function of $\theta$ are shown in Fig. 2. The positions of a number of low index planes between (001) and (110) are also indicated.

Fig. 2

Principal biaxial moduli for $(\mathit{hhl})$ interfaces as a function of angle away from (001) towards (110): (a) Si, (b) Cu, (c) $\beta$-brass and (d) Nb. $M [1\bar{1}0]$ and $M [\mathit{ll}\overline{2h}]$ are identical at 0° (i.e., for a (001) interface) and at 54.74° (for a (111) interface). Other relatively low index planes are (114) at 19.47°, (113) at 25.24°, (112) at 35.26°, (221) at 70.53°, (331) at 76.74° and (441) at 79.98°

For the three materials for which $A > 1$, the maximum in $M [\mathit{ll}\overline{2h}]$ occurs around a value of $\theta$ of 46–47°, while $M [1\bar{1}0]$ increases monotonically from its value at (001) to its value at (110). For Nb, for which $A < 1$, there is a minimum in $M [\mathit{ll}\overline{2h}]$ at a slightly higher value of $\theta$ of ≈ 49°, while for $M [1\bar{1}0]$, its value appears to plateau above $\theta \approx 63^{\circ}$.

Inspection of the mathematics shows that stationary values occur for $M [\mathit{ll} \overline{2h}]$ at values of $\theta$ of 0° and 90°, and where $\cos \theta$ satisfies the equation

$$ a\cos^{4}\theta + b\cos^{2}\theta + c = 0, $$

(39)

where

$$\begin{aligned} a =& 3 ( - c_{11} + c_{12} + 2c_{44}), \\ b =& - 6 (c_{11} + 3c_{12} + 2c_{44}), \\ c =& 3c_{11} + 7c_{12} + 6c_{44}. \end{aligned}$$

(40)

Numerical computation shows that this quadratic for $\cos^{2}\theta$ is satisfied for Si when $\theta = 46.66^{\circ}$, for Cu when $\theta = 47.49^{\circ}$, for $\beta$-brass when $\theta = 46.91^{\circ}$, and for Nb when $\theta = 49.05^{\circ}$.

For $M[1\bar{1}0]$, stationary values occur at values of $\theta$ of 0° and 90° and where cos $\theta$ satisfies Eq. (39) with

$$\begin{aligned} a =& 3 ( - c_{11} + c_{12} + 2c_{44}), \\ b =& 6 (c_{11} + c_{12} - 2c_{44}), \\ c =& - c_{11} - c_{12} + 6c_{44}. \end{aligned}$$

(41)

Restrictions on $c_{11}$, $c_{12}$ and $c_{44}$ from consideration of the strain energy per unit volume require $c_{11} + 2c_{12} > 0$, $c_{11} > \vert c_{12} \vert$ and $c_{44} > 0$ [7]. For $A > 1$, $a > 0$, and for $A < 1$, $a < 0$. For Si, Cu and $\beta$-brass, all of which have $A > 1$, $b$ and $c$ are both >0. Therefore, solutions of Eq. (39) for $\cos^{2}\theta$ are either imaginary, because $b^{2} < 4ac$, as in the case of $\beta$-brass with its high value of anisotropy ratio $A$, or negative, as is the case for Si and Cu.

However, for Nb where $A < 1$, $b > 0$ and $c < 0$, one of the roots of Eq. (39) lies within the range $0 \leq \cos^{2}\theta \leq$ 1, giving a minimum of 136.9 GPa at a value of $\theta = 70.86^{\circ}$, very close to (221) at $\theta = 70.54^{\circ}$. By comparison, the value of $M [1\bar{1}0]$ at $\theta = 63^{\circ}$ is 138.2 GPa and that at $\theta = 90^{\circ}$, when the interface plane is (110), is 138.4 GPa.

Further consideration of Eq. (39) shows that for $b > 0$, a condition which applies to every cubic crystal tabulated in Table 6.1 of [25] and Appendix 1 of [27], the additional constraint that one of the real roots of Eq. (39) lies within the range $0 \leq \cos^{2}\theta \leq 1$ is satisfied only when $a < 0$ and $c < 0$. The condition that $a < 0$ requires $A < 1$; the condition that $c < 0$ requires

$$ \frac{6c_{44}}{(c_{11} + c_{12})} < 1. $$

(42)

This is a significantly more restrictive condition than $A < 1$. Plots of $M [1\bar{1}0]$ on $(\mathit{hhl})$ as a function of $\theta$ are shown in Fig. 3 for six cubic materials for which $A < 1$. Each material has a value of $M [1\bar{1}0]$ at $\theta = 0^{\circ}$ higher than that at $\theta = 90^{\circ}$, with a general levelling off of the curves after $\theta \approx 60^{\circ}$. However, for Nb, KCl ($A = 0.372$) and PbS ($A = 0.510$), for which Eq. (42) is satisfied, there are formal minima at angles less than $\theta = 90^{\circ}$, whereas for NaCl ($A = 0.694$), Mo ($A = 0.775$) and TiC ($A = 0.904$), for which Eq. (42) is not satisfied, the formal minima are all at $\theta = 90^{\circ}$. These trends are emphasised most easily by normalising the plots of $M [1\bar{1}0]$ on $(\mathit{hhl})$ to the value at $\theta = 90^{\circ}$ and examining $\theta$ in the range 60–90°, as shown in Figs. 4 and 5. The minima for Nb and KCl at $\theta = 70.86^{\circ}\mbox{ and }77.25^{\circ}$ respectively are readily apparent in Fig. 4, whereas the minimum for PbS at $\theta = 83.59^{\circ}$ is not; this is because it is only 0.01 % less than $M [1\bar{1}0]$ at $\theta = 90^{\circ}$.

Fig. 3

$M [1\bar{1}0]$ principal biaxial moduli for $(\mathit{hhl})$ interfaces as a function of angle away from (001) towards (110) for six cubic materials with $A < 1$. Data for $c_{11}$, $c_{12}$ and $c_{44}$ are from Table 6.1 of [25] for TiC, NaCl and Nb, from Appendix 1 of [27] for Mo and PbS, and from [29] for KCl

Fig. 4

Detail of the normalised $M [1\bar{1}0]$ principal biaxial moduli for $(\mathit{hhl})$ interfaces of KCl, PbS and Nb as a function of angle away from (001) relative to the magnitude of $M [1\bar{1}0]$ at $\theta = 90^{\circ}$

Fig. 5

Detail of the normalised $M [1\bar{1}0]$ principal biaxial moduli for $(\mathit{hhl})$ interfaces of NaCl, Mo and TiC as a function of angle away from (001) relative to the magnitude of $M [1\bar{1}0]$ at $\theta = 90^{\circ}$

It is evident that the results for the principal values of $M$ for (hll) planes on the boundary of the standard 001–011–111 stereographic triangle are equivalent by symmetry to those principal values for $(\mathit{hhl})$ for $54.74^{\circ} \leq \theta \leq 90^{\circ}$: the relevant values of the biaxial moduli along the directions of principal stress are then $M[01\bar{1}]$ and $M [\overline{2l}\mathit{hh}]$. Thus, for example, for (122), these values can be obtained from Fig. 2 for Si, Cu, $\beta$-brass and Nb by reading the results for $M [1\bar{1}0]$ and $M [\mathit{ll}\overline{2h}]$ for $(\mathit{hhl})$ at 70.53°.

4.6 $(\mathit{hkl})$ Interface Orientation

For a general $(\mathit{hkl})$, the orthonormal directions defining the directions of principal stress within $(\mathit{hkl})$ to an equi-biaxial strain in this plane can be determined either by solving Eq. (21) or by using the method of Norris [12], as discussed in Sect. 3. Equation (10) can then be used to determine the corresponding values of $M$ for these two orthogonal directions. Orthonormal directions for $M$ for selected $(\mathit{hkl})$ within the standard 001–011–111 stereographic triangle are shown in Table 1. Calculated principal values for $M$ for these $(\mathit{hkl})$ are shown in Table 2 for Si, Cu, $\beta$-brass and Nb. Additional $(\mathit{hkl})$ on the edges and at the corners of the standard 001–011–111 stereographic triangle are also included in Table 2 for comparison purposes.

Table 1 Direction cosines defining the directions of principal stress $\eta_{1}$ and $\eta_{2}$ for various $(\mathit{hkl})$ within the standard 001–011–111 stereographic triangle subjected to an equi-biaxial strain. The planes (011), (156), (134), (123), (235) and (112) all lie on the same great circle whose pole is [$1 1\bar{1}$] and share the same value of $Q$ defined in Eq. (11) of 0.5

Table 2 Principal values of $M$ in GPa for various $(\mathit{hkl})$ within the standard 001–011–111 stereographic triangle and at its corners and on its edges for planes parallel to $(\mathit{hkl})$ subjected to an equi-biaxial strain. Directions $\eta_{1}$ and $\eta_{2}$ are specified in Table 1 for $(\mathit{hkl})$ within this stereographic triangle. For $(\mathit{hkl})$ at the corners and on the edge of this stereographic triangle, $\eta_{1}$ and $\eta_{2}$ and the values of $M$ are those determined by the relevant equations in Sects. 4.1–4.5. (001) and (111) are isotropic in their biaxial modulus and so for these planes a single value of $M$ is given

The data in Table 2 confirm that the differences between the principal values of $M$ for a particular $(\mathit{hkl})$ are greatest when $(\mathit{hkl}) = \{011\}$. In this context, the data for the planes (011), (156), (134), (123), (235) and (112) are relevant, because for these planes $Q = a_{31}^{4} + a_{32}^{4} + a_{33}^{4}$ is constant, and so the denominators of Eqs. (10) and (14) are fixed while their numerators vary.

4.7 Global Extrema of $M$ and $\bar{M}$

For the three materials discussed in Sects. 4.4–4.6 for which $A > 1$, the global maxima in $M$ occur for {011} planes in $\langle 01\bar{1}\rangle$ directions, and the global minima occur for {001} planes. For $A < 1$, the global maxima in $M$ occur for {001} planes, whereas the global minima occur for $\{\mathit{hhl}\}$ planes in $\langle 1\bar{1}0\rangle$ directions. If Eq. (42) is not satisfied, these $\{\mathit{hhl}\}$ will be {110}. If Eq. (42) is satisfied, as for Nb, these planes are very close to being {122}. Moving away from (122) towards (125) on the great circle whose pole is $2\bar{1}0$, i.e., through (367), (245) and (123), is consistent with the statement that the global minima in $M$ occur for $\{\mathit{hhl} \} \approx \{122\}$ for Nb (Table 2). For KCl, for which Eq. (42) is also satisfied, the $\{\mathit{hhl}\}$ planes with the global minima for $M$ are close to being {133}.

These results can be confirmed using the formalism established by Norris [11] when determining the conditions for the global extrema of Poisson’s ratio for cubic materials, suitably adapted for biaxial moduli. The formalism, which makes use of expressions for stationary values of engineering moduli in general in anisotropic materials, is used in Appendix B to validate the results quoted in this Section for stationary conditions and global extrema.

It is also useful to describe these results for the magnitudes of the biaxial moduli in the ($X, Y$) space defined by Brańka et al. [15] in which at zero hydrostatic pressure, $X$ and $Y$ are ratios of elastic moduli defined as

$$ X = \frac{3 (c_{11} - c_{12})}{2 (c_{11} + 2c_{12})},\qquad Y = \frac{(c_{11} - c_{12})}{8c_{44}}. $$

(43)

In this parameter space, $X$ and $Y$ must both be positive because of the stability conditions noted in Sect. 4.5. Brańka et al. then used this parameter space for the description of global maximum and global minimum surfaces for Poisson’s ratio in cubic materials. In their nomenclature, the directional dependence of Poisson’s ratio in unit direction $\boldsymbol{m}$ for uniaxial loading along a unit direction $\boldsymbol{n}$ is described by two functions $D(\boldsymbol{n},\boldsymbol{m}) = n_{1}^{2}m_{1}^{2} + n_{2}^{2}m_{2}^{2} + n_{3}^{2}m_{3}^{2}$ and $p(\boldsymbol{n}) = n_{1}^{4} + n_{2}^{4} + n_{3}^{4}$.

In the nomenclature of Brańka et al., Eq. (10) becomes

$$ M(\boldsymbol{n},\boldsymbol{m};X,Y) = 9G\frac{1 + (D(\boldsymbol{n},\boldsymbol{m}) - p(\boldsymbol{n}) (1 - 4Y))}{6Y - 4XY + 3X - 3X p(\boldsymbol{n}) (1 - 4Y)}, $$

(44)

for the biaxial modulus in the unit direction $\boldsymbol{m}$ within the plane whose normal is the unit vector $\boldsymbol{n}$, where $G = (c_{11} - c_{12})/2$. Thus, for example,

$$ M\bigl((110),[1\bar{1}0];X,Y\bigr) = 9G\frac{2}{12Y + 4XY + 3X}, $$

(45)

since, for the biaxial modulus on (110) along $[1\bar{1}0]$, $D(\boldsymbol{n},\boldsymbol{m}) = p(\boldsymbol{n}) = 0.5$.

It is apparent that in the formalism of Brańka et al., the three materials with $A < 1$ for which there is a global minimum in $M$ along [$1\bar{1}0$] on $(\mathit{hhl})$ interfaces away from (110) are at the positions of (0.924, 0.673), (0.781, 0.490) and (0.307, 0.456) within ($X,Y$) space for KCl, PbS and Nb respectively. These regions in ($X,Y$) space are some way from the very limited domain in ($X,Y$) space near $X = 0$ and $Y = 0$, i.e., for materials for which $A \gg 1$, where there are the most extreme maxima and minima in Poisson’s ratio, as documented by Brańka et al.

More interestingly, ($X,Y$) space can be used to explore the possibility for $A > 1$, or equivalently, $Y < 0.25$, that the local maxima in $M$ along [$\mathit{ll}\overline{2h}$] on $(\mathit{hhl})$ interfaces away from (110) can be greater than the value of $M$ along [$1\bar{1}0$] on (110). It is evident from Fig. 2 that, for Si, Cu and $\beta$-brass these local maxima have values which are a significant fraction of $M [1\bar{1}0]$ on (110): 0.965, 0.947 and 0.919 for Si, Cu and $\beta$-brass respectively, the ($X,Y$) values of which are (0.520, 0.160), (0.171, 0.078) and (0.084, 0.029) respectively.

Returning to Eqs. (39) and (40), it is apparent that the value of cos $\theta$ at which there is maximum value of $M [\mathit{ll}\overline{2h}]$ on $(\mathit{hhl})$ for materials with $A > 1$ satisfies the equation

$$a\cos^{4}\theta + b\cos^{2}\theta + c = 0, $$

where, in ($X,Y$) space,

$$\begin{aligned} a =& 9X (1 - 4Y), \\ b =& - 6 (24Y + 3X - 4XY), \\ c =& 60Y + 9X - 4XY. \end{aligned}$$

(46)

As $X \rightarrow 0$, it is evident that $\cos^{2}\theta \rightarrow 5/12$, so that $\theta \rightarrow 49.80^{\circ}$. At this limiting value of $\theta$, $D(\boldsymbol{n},\boldsymbol{m}) = 105/288$ and $p(\boldsymbol{n}) = 99/288$, so that the ratio of $M((\mathit{hhl}),\ [\mathit{ll}\overline{2h}];X,Y)$ to $M((110),\ [1\bar{1}0];\ X,Y)$ as $X \rightarrow 0$ is simply

$$ \frac{M((hhl),[\mathit{ll}\overline{2h}];X,Y)}{M((110),[1\bar{1}0];X,Y)} = 1 + \frac{1}{48} ( 1 - 4Y ), $$

(47)

Hence, as both $X$ and $Y \rightarrow 0$, it is evident that this ratio takes a limiting value of $49/48$, confirming that for $A > 1$ there can be values of $M$ along [$\mathit{ll}\overline{2h}$] on $(\mathit{hhl})$ interfaces away from (110) which can be slightly greater than the value of $M$ along [$1\bar{1}0$] on (110).

Numerical calculations show that for materials with $Y < 0.25$, there will be a restricted range of orientations within limits of $\theta = 45^{\circ}$ and $\theta = 54.74^{\circ}$ for which

$$ \frac{M((\mathit{hhl}),[\mathit{ll}\overline{2h}];X,Y)}{M((110),[1\bar{1}0];X,Y)} > 1 $$

(48)

if, to a good approximation, $X < 0.29 Y$. To satisfy both $Y < 0.25$ and $X < 0.29 Y$, we therefore need to satisfy the inequality

$$ 6c_{11} - 6c_{12} < 12c_{44} < 0.29 (c_{11} + 2c_{12}). $$

(49)

This inequality produces a very restrictive set of conditions to be satisfied in real anisotropic cubic materials: $c_{12}/c_{11} > 0.868$ with $12c_{44} < 0.29 (c_{11} + 2c_{12})$. A search of the Landolt-Börnstein compendium of elastic constants of cubic materials [30] and other information sources shows that there are materials for which $c_{12}/c_{11} > 0.868$ is satisfied, such as certain In−Tl alloys [31], certain compositions of $\beta$-brass [32] and nickel hexamine nitrate, Ni(NH₃)₆(NO₃)₂ [33]. However, the criterion $12c_{44} < 0.29 (c_{11} + 2c_{12})$ is not met in any of these materials. It is most close to being met in nickel hexamine nitrate at −34°C, for which $c_{11} = 9.275~\mbox{GPa}$, $c_{12} = 8.77~\mbox{GPa}$ and $c_{44} = 0.699~\mbox{GPa}$ [33]; were $0.253~\mbox{GPa} < c_{44} < 0.648~\mbox{GPa}$ in this $Fm\bar{3}m$ material, Eq. (48) would be satisfied.

By comparison with the global extrema for $M$, global extrema for $\bar{M}$ are easier to specify. $Q$ has limiting values of 1 at {001} orientations and $1/3$ at {111} orientations. An examination of Eq. (17) shows that for $A > 1$, $\bar{M}$ has maxima at {111} orientations and minima at {001} orientations; for $A < 1$, $\bar{M}$ has maxima at {001} orientations and minima at {111} orientations.

5 Stresses $\sigma '_{13}$ and $\sigma '_{23}$

So far in this analysis we have only considered the stresses $\sigma '_{11}$, $\sigma '_{22}$ and $\sigma '_{12}$ within $(\mathit{hkl})$ and the stress $\sigma '_{33}$ normal to $(\mathit{hkl})$ arising from an equi-biaxial strain within $(\mathit{hkl})$. The constraint that $\sigma '_{33} = 0$ enables a relationship between the principal strains $\varepsilon '_{11} = \varepsilon '_{22} = \varepsilon$ and $\varepsilon '_{33}$ to be established. We have yet to examine the stresses $\sigma '_{13}$ and $\sigma '_{23}$.

Using Eq. (1) it is evident that

$$ \sigma '_{13} = C'_{1311}\varepsilon '_{11} + C'_{1322}\varepsilon '_{22} + C'_{1333}\varepsilon '_{33}. $$

(50)

Using Eq. (8) and making use of the orthogonality relationships of direction cosines,

$$ \sigma '_{13} = H\bigl(a_{11}a_{31}^{3} + a_{12}a_{32}^{3} + a_{13}a_{33}^{3} \bigr) \bigl(\varepsilon - \varepsilon '_{33}\bigr). $$

(51)

Similarly,

$$ \sigma '_{23} = H\bigl(a_{21}a_{31}^{3} + a_{22}a_{32}^{3} + a_{23}a_{33}^{3} \bigr) \bigl(\varepsilon - \varepsilon '_{33}\bigr). $$

(52)

For a plane such as (001), it follows that the terms involving directions cosines in Eqs. (51) and (52) are zero, and so $\sigma '_{13} = \sigma '_{23} = 0$. Likewise, for (111), we require $a_{11} + a_{12} + a_{13} = 0$ and since for (111) $a_{31} = a_{32} = a_{33}$, $\sigma '_{13} = \sigma '_{23} = 0$ when $(\mathit{hkl})$ is (111).

For ($0\mathit{kl}$) planes, with $k$, $l$ both ≠ 0, using Eq. (30) we can choose $1'$ to be [100] and $2'$ to be [$0\ a_{33}\ \overline{a_{32}}$]. While $\sigma '_{13} = 0$, $\sigma '_{23} = 0$ only when $a_{32} = a_{33}$, i.e., only for (011). For all other ($0\mathit{kl}$) planes apart from the special cases of (010) and (001), $\sigma '_{23} \ne 0$. For $(\mathit{hhl})$ planes $\sigma '_{13} = 0$ for $1'$ parallel to [$1 \bar{1} 0$], but $\sigma '_{23} = 0$ along [$\mathit{ll}\overline{2h}$] only if $l = 0$, $h = 0$ or $h^{2} = l^{2}$, e.g., for (001), (111) and (110).

Hence, for a general $(\mathit{hkl})$, both $\sigma '_{13} \ne 0$ and $\sigma '_{23} \ne 0$. These stresses can be argued to be small relative to $\sigma '_{11}$ and $\sigma '_{22}$, even for highly anisotropic cubic materials, since they both depend on $H$ modulated by a direction cosine expression which, from the form of this expression, is small. Even so, it is important to recognise that, for interface planes other than {001}, {111} and {011}, shear stresses out of the plane will arise naturally in cubic materials as a consequence of a state of equi-biaxial strain within the plane and a zero normal stress to the plane. It also follows that any calculation of elastic strain energy per unit volume for a $(\mathit{hkl})$ oriented cubic single crystal subjected to an equi-biaxial strain must include these terms.

6 Discussion and Conclusions

The main results of this paper are Eqs. (10) and (21). Equation (10) specifies the biaxial modulus along a particular direction of choice in a $(\mathit{hkl})$ plane of a cubic crystal subjected to an equi-biaxial strain in the plane, with the additional constraint that the stress normal to $(\mathit{hkl})$ is zero. In this context, $(\mathit{hkl})$ could either be a plane of a cubic crystal substrate or the orientation of planes parallel to the substrate of a single cubic crystal deposited on a suitable substrate, such as a glass slide which would be isotropic, or another cubic crystal with which it has a cube-cube orientation relationship. For two orthogonal directions within a general $(\mathit{hkl})$ plane, the biaxial moduli will be parallel to the directions of principal stress within the $(\mathit{hkl})$ plane. These directions of principal stress are specified by Eq. (21) and are parallel to extrema in both the shear modulus and Poisson’s ratio on that plane. They are necessarily extrema of the biaxial moduli on that plane simply because they are principal stresses.

Examination of the biaxial moduli as a function of $(\mathit{hkl})$ shows that for cubic crystals for which the anisotropy ratio $A > 1$, the minimum value of the biaxial modulus occurs when $(\mathit{hkl})$ is {001}, in which case the biaxial modulus is isotropic in the plane. Apart from specific unusual sets of circumstances discussed in Sect. 4.7, the maximum value of the biaxial modulus occurs on {011} along $\langle 01\bar{1}\rangle$. The maximum difference between the principal biaxial moduli on $(\mathit{hkl})$ occurs on {011} for all cubic crystals for which $A > 1$.

For $A < 1$, the formal minimum value of the biaxial modulus occurs when $(\mathit{hkl})$ is a plane of the form $\{\mathit{hhl}\}$ where $h$ and $l$ are determined by Eqs. (39), (41) and (42) and the direction is $\langle 1\bar{1}0\rangle$. However, in practice, the value of the $\langle 1\bar{1}0\rangle$ biaxial modulus on the (110) plane for a material with $A < 1$ will have a value sufficiently close to any formal minimum away from (110) that it can be regarded from an engineering point of view as being a plane with the minimum value of the biaxial modulus, as the calculations for Nb, KCl and PbS have shown. The maximum value of the biaxial modulus occurs on {001}, in which case the biaxial modulus is isotropic in the plane. As for materials with $A > 1$, the maximum difference between the principal biaxial moduli on $(\mathit{hkl})$ occurs on {011}.

The most obvious context in which to use equations for biaxial moduli is in the deposition of thin films on substrates [19, 20, 22]. While most single crystal silicon substrates used for thin film deposition are (001) and (111), a number of other possible substrate orientations are now offered by manufacturers such as (011), (112) and even (531) (e.g., [34, 35]). For (011) silicon substrates, the elastic biaxial moduli differ by 22 % along [$01 \bar{1}$] and [100], and so any computations of elastic responses of microelectromechanical systems must take this into account, as Hopcroft et al. have recently discussed [23].

A second practical application is in the evaluation of residual stress levels in relatively thick coatings deposited on substrates, where the thickness of the coating is not necessarily small in comparison with the thickness of the substrate [20, 36]. Thus, for example, in the deposition of plasma electrolytic oxidation coatings on metallic substrates, the coatings can be ∼100 μm thick and the substrates 300–500 μm thick [36]. In such a situation, the misfit strains generate significant levels of stress in both the coating and the substrate. Although it is usual for such substrates to be polycrystalline, and therefore isotropic in their elastic response, such substrates could in principle be $(\mathit{hkl})$ planes of cubic single crystals.

Appendices

Appendix A: Directions of Principal Stress Within a Plane $(\mathit{hkl})$ Subjected to Equi-biaxial Strain

From Sect. 3, the condition on the unit vectors with direction cosines [$a_{11},a_{12},a_{13}$] and [$a_{21},a_{22},a_{23}$] lying in the plane $(\mathit{hkl})$ of the cubic single crystal defining the principal stresses when the plane is subjected to an equi-biaxial strain is

$$a_{11}a_{21}a_{31}^{2} + a_{12}a_{22}a_{32}^{2} + a_{13}a_{23}a_{33}^{2} = 0, $$

Eq. (21), where [$a_{31},a_{32},a_{33}$] is the unit vector normal to $(\mathit{hkl})$. From Norris [12], the extreme values of the shear modulus and Poisson’s ratio for a fixed plane $\boldsymbol{n}$ defined by the unit vector [$n_{1},n_{2},n_{3}$] are defined by unit vectors $\boldsymbol{m}_{-}$ and $\boldsymbol{m}_{+}$ lying in $\boldsymbol{n}$, where

$$\begin{aligned} \boldsymbol{m}_{ \pm} =& \rho_{ \pm} \biggl[ \frac{n_{1}}{n_{1}^{2} - \lambda_{ \pm}},\frac{n_{2}}{n_{2}^{2} - \lambda_{ \pm}},\frac{n_{3}}{n_{3}^{2} - \lambda_{ \pm}} \biggr], \end{aligned}$$

(53)

$$\begin{aligned} \rho_{ \pm} =& \biggl[ \frac{n_{1}^{2}}{(n_{1}^{2} - \lambda_{ \pm})^{2}} + \frac{n_{2}^{2}}{(n_{2}^{2} - \lambda_{ \pm})^{2}} + \frac{n_{3}^{2}}{(n_{3}^{2} - \lambda_{ \pm})^{2}} \biggr]^{ - 1/2}, \end{aligned}$$

(54)

$$\begin{aligned} \lambda_{ \pm} =& \bigl(n_{1}^{2}n_{2}^{2} + n_{2}^{2}n_{3}^{2} + n_{3}^{2}n_{1}^{2}\bigr) \pm \sqrt {\bigl(n_{1}^{2}n_{2}^{2} + n_{2}^{2}n_{3}^{2} + n_{3}^{2}n_{1}^{2} \bigr)^{2} - 3n_{1}^{2}n_{2}^{2}n_{3}^{2}}, \end{aligned}$$

(55)

and where the $\lambda_{ \pm}$ are the roots of the quadratic equation

$$ \lambda^{2} - 2\lambda \bigl(n_{1}^{2}n_{2}^{2} + n_{2}^{2}n_{3}^{2} + n_{3}^{2}n_{1}^{2}\bigr) + 3n_{1}^{2}n_{2}^{2}n_{3}^{2} = 0. $$

(56)

Expressed in terms of the nomenclature used by Norris, Eq. (21) becomes the condition

$$ \frac{n_{1}^{4}}{(n_{1}^{2} - \lambda_{ +} ) (n_{1}^{2} - \lambda_{ -} )} + \frac{n_{2}^{4}}{(n_{2}^{2} - \lambda_{ +} ) (n_{2}^{2} - \lambda_{ -} )} + \frac{n_{3}^{4}}{(n_{3}^{2} - \lambda_{ +} ) (n_{3}^{2} - \lambda_{ -} )} = 0. $$

(57)

Noting the identities

$$\begin{aligned} \bigl(n_{1}^{2} - \lambda_{ +} \bigr) \bigl(n_{1}^{2} - \lambda_{ -} \bigr) =& n_{1}^{2}\bigl(n_{1}^{2} - n_{2}^{2}\bigr) \bigl(n_{1}^{2} - n_{3}^{2}\bigr), \\ \bigl(n_{2}^{2} - \lambda_{ +} \bigr) \bigl(n_{2}^{2} - \lambda_{ -} \bigr) =& n_{2}^{2}\bigl(n_{2}^{2} - n_{3}^{2}\bigr) \bigl(n_{2}^{2} - n_{1}^{2}\bigr), \\ \bigl(n_{3}^{2} - \lambda_{ +} \bigr) \bigl(n_{3}^{2} - \lambda_{ -} \bigr) =& n_{3}^{2}\bigl(n_{3}^{2} - n_{1}^{2}\bigr) \bigl(n_{3}^{2} - n_{2}^{2}\bigr), \end{aligned}$$

(58)

Eq. (57) becomes the condition

$$ \frac{n_{1}^{2}}{(n_{1}^{2} - n_{2}^{2}) (n_{1}^{2} - n_{3}^{2})} + \frac{n_{2}^{2}}{(n_{2}^{2} - n_{3}^{2}) (n_{2}^{2} - n_{1}^{2})} + \frac{n_{3}^{2}}{(n_{3}^{2} - n_{1}^{2}) (n_{3}^{2} - n_{2}^{2})} = 0. $$

(59)

Since the first two terms sum to the negative of the third term, the result is shown, as long as $(n_{1}^{2} - n_{2}^{2}) (n_{2}^{2} - n_{3}^{2}) (n_{3}^{2} - n_{1}^{2}) \ne 0$. However, as Norris explains, suitable values of $\boldsymbol{m}$ can be identified where $(\mathit{hkl})$ is of the form ($1p0$) and $(11p); (11p)$ is directly equivalent to $(\mathit{hhl})$ considered here in Sect. 4.5, while ($1p0$) is equivalent by symmetry to ($0\mathit{kl}$) considered here in Sect. 4.4. It is straightforward to verify that these suitable forms of $\boldsymbol{m}$ satisfy Eq. (21) when expressed as unit vectors with direction cosines [$a_{11},a_{12},a_{13}$] and [$a_{21},a_{22},a_{23}$].

Appendix B: Stationary Values and Global Extrema for Biaxial Moduli

Norris [11] derives conditions for stationary values of engineering moduli in anisotropic triclinic materials, applying these conditions to the consideration of Poisson’s ratio, Young’s modulus and the shear modulus. His approach provides a general framework for finding stationary values of any engineering modulus, $f$. The analysis in [11] uses the connection between the fourth order elasticity tensors in 3 dimensions and their corresponding second order symmetric tensors in 6 dimensional space derived by Mehrabadi and Cowin [37] and also expressions derived by Mehrabadi et al. [38] for the representation in a space of six dimensions of a three-dimensional rotation by an angle $\theta$ about a specific axis.

Consideration of the formalism of the fourth order compliance and stiffness tensors shows that the conditions for the rotational derivatives for the elements of the compliance tensor $s_{ij}$ in Voigt notation derived by Norris and presented on page 798 of [11] are also valid for the stiffness tensor $c_{ij}$ by the simple substitution of $c$ for $s$. Hence, the approach in Sect. 3 of Norris can be readily adapted for the biaxial modulus, $M$, of cubic materials.

From Sect. 2, the equation for $M$ to use for determining the extremal conditions for $M$ for cubic materials is

$$M = \frac{\sigma '_{1}}{\varepsilon} = c'_{11} + c'_{12} - \frac{1}{c'_{33}}\bigl({c'_{13}}^{2} + c'_{13}c'_{23}\bigr), $$

(Eq. (5)), noting that in his analysis, Norris dropped the primes when defining a set of orthonormal directions relative to the crystal axes. Norris reserved the use of primes to denote rotational derivatives with respect to an angle of rotation, $\theta$ about a unit vector $\mathbf{q} = q_{1}\mathbf{e}_{1'} + q_{2}\mathbf{e}_{2'} + q_{3}\mathbf{e}_{3'}$, defined in the formalism here relative to the orthonormal set of axes $1'$, $2'$ and $3'$, in which the unit vectors along these three axes are $\mathbf{e}_{1'}$, $\mathbf{e}_{2'}$, and $\mathbf{e}_{3'}$, respectively.

The condition derived by Norris for a stationary value to be obtained of an engineering modulus $f$ for a triclinic material is that a vector $\mathbf{d}^{(f)} = 0$ at a stationary point of $f$ for a suitable vector $\mathbf{d}^{(f)}$ independent of the three-dimensional vector $\mathbf{q}$ about which the rotation takes place. This then leads to three conditions for stationary values of $f$, one from each component of $\mathbf{d}^{(f)}$ along the axes $1'$, $2'$ and $3'$ respectively. The analysis requires differentiation of $f$ with respect to $\theta$ for a general $\mathbf{q}$, evaluated at $\theta = 0$; this in turn requires differentiation of the $c'_{ij}$ in Eq. (5) with respect to $\theta$ for a general $\mathbf{q}$, also evaluated at $\theta = 0$. The vector $\mathbf{d}^{(f)}$ is defined by the condition

$$ \frac{\partial f ( \mathbf{q} )}{\partial \theta} = \mathbf{d}^{(f)} \cdot \mathbf{q}. $$

(60)

It follows from the equivalence of the conditions for the rotational derivatives for the elements of the compliance tensor $s_{ij}$ and $c_{ij}$ that

$$\begin{aligned} \frac{\partial c'_{11} ( \mathbf{q} )}{\partial \theta} =& 4c'_{15}q_{2} - 4c'_{16}q_{3}, \\ \frac{\partial c'_{33} ( \mathbf{q} )}{\partial \theta} =& 4c'_{34}q_{1} - 4c'_{35}q_{2}, \\ \frac{\partial c'_{12} ( \mathbf{q} )}{\partial \theta} =& - 2c'_{14}q_{1} + 2c'_{25}q_{2} + \bigl(2c'_{16} - 2c'_{26}\bigr)q_{3}, \\ \frac{\partial c'_{23} ( \mathbf{q} )}{\partial \theta} =& \bigl(2c'_{24} - 2c'_{34}\bigr)q_{1} - 2c'_{25}q_{2} + 2c'_{36}q_{3}, \\ \frac{\partial c'_{13} ( \mathbf{q} )}{\partial \theta} =& 2c'_{14}q_{1} + \bigl(2c'_{35} - 2c'_{15} \bigr)q_{2} - 2c'_{36}q_{3}, \end{aligned}$$

(61)

where the $c'_{ij}$ are the values at $\theta = 0$, i.e., the values with respect to the $1'$, $2'$ and $3'$ orthonormal set of axes.

Differentiating $M$ with respect to respect to $\theta$ for a general $\mathbf{q}$, we have

$$\begin{aligned} \frac{\partial M ( \mathbf{q} )}{\partial \theta} =& \frac{\partial c'_{11} ( \mathbf{q} )}{\partial \theta} + \frac{\partial c'_{12} ( \mathbf{q} )}{\partial \theta} - \frac{1}{c'_{33}} \biggl( \bigl(2c'_{13} + c'_{23}\bigr)\frac{\partial c'_{13} ( \mathbf{q} )}{\partial \theta} + c'_{13} \frac{\partial c'_{23} ( \mathbf{q} )}{\partial \theta} \biggr) \\ &{}+ \frac{({c'_{13}}^{2} + c'_{13}c'_{23})}{{c'_{33}}^{2}}\frac{\partial c'_{33} ( \mathbf{q} )}{\partial \theta}. \end{aligned}$$

(62)

Hence, from Eqs. (60) and (61),

$$\begin{aligned} \mathbf{d}^{(M)} =& \biggl( - \frac{2 (2c'_{13} + c'_{23} + c'_{33})}{c'_{33}}c'_{14} - \frac{2c'_{13}}{c'_{33}}c'_{24} + \biggl( \frac{2c'_{13}}{c'_{33}} + \frac{4c'_{13}(c'_{13} + c'_{23})}{{c'_{33}}^{2}} \biggr) c'_{34} \biggr) \mathbf{e}_{1'} \\ &{}+ \biggl( \frac{2 (2c'_{13} + c'_{23} + 2c'_{33})}{c'_{33}}c'_{15} + \frac{2 (c'_{13} + c'_{33})}{c'_{33}}c'_{25} \\ &{}- \biggl( \frac{2 (2c'_{13} + c'_{23})}{c'_{33}} + \frac{4c'_{13}(c'_{13} + c'_{23})}{{c'_{33}}^{2}} \biggr) c'_{35} \biggr) \mathbf{e}_{2'} \\ &{}+ \biggl( - 2c'_{16} - 2c'_{26} + \frac{2 (c'_{13} + c'_{23})}{c'_{33}}c'_{36} \biggr)\mathbf{e}_{3'}. \end{aligned}$$

(63)

The three conditions for the stationary values of $M$ are that each of the coefficients of $\mathbf{e}_{1'}$, $\mathbf{e}_{2'}$, and $\mathbf{e}_{3'}$ is zero.

These three conditions valid for triclinic materials can be simplified considerably for cubic materials, making use of the three identities

$$\begin{aligned} &c'_{14} + c'_{24} + c'_{34} = 0, \\ &c'_{15} + c'_{25} + c'_{35} = 0, \\ &c'_{16} + c'_{26} + c'_{36} = 0. \end{aligned}$$

(64)

which follow from a consideration of Eq. (8), and the identity

$$ c'_{13} + c'_{23} + c'_{33} = c_{11} + 2c_{12} > 0, $$

(65)

which also follows from Eq. (8), together with recognition that the bulk modulus of a cubic material is independent of the choice of axes [7]. Hence, we find for a cubic material that the conditions that the coefficient the coefficients of $\mathbf{e}_{1'}$, $\mathbf{e}_{2'}$, and $\mathbf{e}_{3'}$ are zero become

$$\begin{aligned} 2c'_{34}c'_{13} - c'_{14}c'_{33} =& 0, \end{aligned}$$

(66)

$$\begin{aligned} 2c'_{35}c'_{13} + \bigl(c'_{35} - c'_{15}\bigr) c'_{33} =& 0, \end{aligned}$$

(67)

$$\begin{aligned} c'_{36} =& 0. \end{aligned}$$

(68)

It is immediately apparent that these conditions for the stationary values of $M$ are satisfied for isotropic materials because each of the individual terms in the three identities in Eq. (64) is zero.

Since $c'_{36} \equiv C'_{3312}$ in full tensor notation, Eq. (68) is equivalent to Eq. (21), i.e., Eq. (68) is satisfied when $1'$ and $2'$ are along directions of principal stress within the plane whose normal is parallel to $3'$. Without loss of generality we can examine Eqs. (66) and (67) for a general $(\mathit{hkl})$ within the standard 001–011–111 stereographic triangle for a cubic material by choosing axis $1'$ to be parallel to $\boldsymbol{m}_{-}$ and axis $2'$ to be parallel to $\boldsymbol{m}_{+}$. Under these circumstances, using the nomenclature in Appendix A and other results in Eqs. (3.4) and (3.5) of [12],

$$ \begin{aligned}[c] &c'_{34} = -H\rho_{ +},\qquad c'_{35} = -H\rho_{ -},\\ &c'_{14} = -H\frac{\rho_{ +} \lambda_{ -}}{\lambda_{ -} - \lambda_{ +}}, \qquad c'_{15} = -H\rho_{ -} \biggl( \frac{\lambda_{ -}}{\lambda_{ -} - \lambda_{ +}} - 2 \biggr). \end{aligned} $$

(69)

Rewriting Eqs. (66) and (67) in the form

$$ \left ( \textstyle\begin{array}{cc} 2c'_{34} & - c'_{14} \\ 2c'_{35} & c'_{35} - c'_{15} \end{array}\displaystyle \right ) \left ( \textstyle\begin{array}{c} c'_{13} \\ c'_{33} \end{array}\displaystyle \right ) = \left ( \textstyle\begin{array}{c} 0 \\ 0 \end{array}\displaystyle \right ), $$

(70)

it is evident that the determinant of the $2 \times$ 2 matrix in Eq. (70) is

$$ 2c'_{34} \bigl( c'_{35} - c'_{15} \bigr) + 2c'_{35}c'_{14} = 6H^{2}\rho_{ +} \rho_{ -}, $$

(71)

which is non-zero for a general $(\mathit{hkl})$ within the standard 001–011–111 stereographic triangle. Hence, as for Poisson’s ratio for cubic materials [12], the important result is obtained that there are no stationary values of $M$ inside the standard stereographic triangle. The only possible stationary values are on the edges of this stereographic triangle. By symmetry, we need only examine planes of the form ($0\mathit{kl}$) and $(\mathit{hhl})$, as in Sects. 4.4 and 4.5.

2.1 B.1 $(0\mathit{kl})$ Interface Orientation

If, as in Sect. 4.4, we choose the table of direction cosines between the axis set 1, 2 and 3 and the axis set $1'$, $2'$ and $3'$ defining the directions of principal stress within ($0\mathit{kl}$) to be

(72)

with $a_{32}^{2} + a_{33}^{2} = 1$, Eq. (68) is automatically satisfied. Using Eq. (8),

$$ \begin{aligned}[c] &c'_{34} \equiv C'_{3323} = - Ha_{32}a_{33}\bigl(a_{32}^{2} - a_{33}^{2}\bigr),\qquad c'_{14} \equiv C'_{1123} = 0, \\ &c'_{15} \equiv C'_{1131} = 0,\qquad c'_{35} \equiv C'_{3331} = 0, \end{aligned} $$

(73)

and so Eq. (67) is also automatically satisfied. Equation (66) is satisfied if $a_{32}a_{33}(a_{32}^{2} - a_{33}^{2}) = 0$. Hence, stationary values of $M$ occur at (001), (011) and (010), and orientations related by symmetry to these three planes, and so these are candidates for global extrema for $M$. This conclusion is unchanged if we interchange axes $1'$ and $2'$, so that, for a right-handed axis set, we were to have chosen the table of direction cosines to be

(74)

instead.

2.2 B.2 $(\mathit{hhl})$ Interface Orientation

If, as in Sect. 4.5, we choose the table of direction cosines between the axis set 1, 2 and 3 and the axis set $1'$, $2'$ and $3'$ defining the directions of principal stress within ($0\mathit{kl}$) to be

(75)

with $2a_{31}^{2} + a_{33}^{2} = 1$, Eq. (68) is automatically satisfied. Using Eq. (8),

$$\begin{aligned} &c'_{34} \equiv C'_{3323} = - \sqrt{2} Ha_{31}a_{33}\bigl(a_{31}^{2} - a_{33}^{2}\bigr),\qquad c'_{14} \equiv C'_{1123} = - \frac{H}{\sqrt{2}} a_{31}a_{33}, \\ &c'_{15} \equiv C'_{1131} = 0, \qquad c'_{35} \equiv C'_{3331} = 0, \\ &c'_{13} \equiv C'_{1133} = c_{12} - Ha_{31}^{2};\qquad c'_{33} \equiv C'_{3333} = c_{12} + 2c_{44} - H \bigl(2a_{31}^{4} + a_{33}^{4}\bigr). \end{aligned}$$

(76)

Since $c'_{15} \equiv c'_{35} = 0$, Eq. (67) is also automatically satisfied. Equation (66) is satisfied if

$$ \frac{Ha_{31}a_{33}}{\sqrt{2}} \bigl\{ c_{12} + 2c_{44} - H \bigl(2a_{31}^{4} + a_{33}^{4}\bigr) - 4 \bigl(a_{31}^{2} - a_{33}^{2}\bigr) \bigl(c_{12} - a_{31}^{2}H\bigr) \bigr\} = 0. $$

(77)

Hence stationary values of $M$ occur when $a_{31} = 0$, i.e., for (001), when $a_{33} = 0$, i.e., for (110), and when the term inside the curly bracket is set to zero. If we let $a_{33} = \cos \theta$, and substitute for $H$ using Eq. (10), this term becomes the condition

$$ a\cos^{4}\theta + b\cos^{2}\theta + c = 0, $$

(78)

where

$$\begin{aligned} a =& 3 ( - c_{11} + c_{12} + 2c_{44}), \\ b =& 6 (c_{11} + c_{12} - 2c_{44}), \\ c =& - c_{11} - c_{12} + 6c_{44}, \end{aligned}$$

(79)

i.e., Eq. (39) with the coefficients $a$, $b$ and $c$ defined by Eq. (41). This analysis therefore confirms the conditions for stationary values for $M[1\bar{1}0]$ in Sect. 4.5.

If we interchange axes $1'$ and $2'$, we can choose the table of direction cosines to be

(80)

for a right-handed set of axes, with $2a_{31}^{2} + a_{33}^{2} = 1$. Equation (68) is still automatically satisfied. Using Eq. (8),

$$\begin{aligned} &c'_{34} \equiv C'_{3323} = 0, \qquad c'_{14} \equiv C'_{1123} = 0, \\ &c'_{15} \equiv C'_{1131} = - \frac{Ha_{31}a_{33}}{\sqrt{2}} \bigl(a_{33}^{2} - 4a_{31}^{2} \bigr),\qquad c'_{35} \equiv C'_{3331} = - \frac{Ha_{31}a_{33}}{\sqrt{2}} \bigl(2a_{31}^{2} - 2a_{33}^{2}\bigr), \\ &c'_{13} \equiv C'_{1133} = c_{12} - 3Ha_{31}^{2}a_{33}^{2}, \qquad c'_{33} \equiv C'_{3333} = c_{12} + 2c_{44} - H\bigl(2a_{31}^{4} + a_{33}^{4}\bigr). \end{aligned}$$

(81)

Since $c'_{34} \equiv c'_{14} = 0$, Eq. (66) is also automatically satisfied. Equation (67) is satisfied if

$$ \frac{Ha_{31}a_{33}}{\sqrt{2}} \bigl\{ 4\bigl(a_{31}^{2} - a_{33}^{2}\bigr) \bigl(c_{12} - 3Ha_{31}^{2}a_{33}^{2}\bigr) - 3 \bigl(2a_{31}^{2} - a_{33}^{2}\bigr) \bigl(c_{12} + 2c_{44} - H\bigl(2a_{31}^{4} + a_{33}^{4}\bigr)\bigr) \bigr\} = 0. $$

(82)

Hence, stationary values of this $M$ occur for (001), (011) and (010), and orientations related by symmetry to these three planes, and also when the term inside the curly bracket is set to zero. If we let $a_{33} = \cos \theta$, and substitute for $H$ using Eq. (12), this term can be rearranged into the condition

$$ a\cos^{4}\theta + b\cos^{2}\theta + c = 0, $$

(83)

where the coefficients $a$, $b$ and $c$ are now defined by Eq. (40). This therefore confirms the conditions for stationary values for $M [\mathit{ll}\overline{2h}]$ in Sect. 4.5.

Overall, therefore, this analysis gives a total of four candidates for global extrema for $M$ on the edges of the 001–011–111 standard stereographic triangle for cubic materials: (001), (011), and the two (lhh) orientations related by symmetry to the $(\mathit{hhl})$ orientations defined by Eq. (39), with $a$, $b$ and $c$ given either by Eq. (40) or Eq. (41). As discussed in Sects. 4.4–4.6, examination of each of these stationary conditions shows that for the overwhelming majority of cubic materials with anisotropy ratios $A > 1$, the minimum value of $M$ occurs for {001} and the maximum value of $M$ occurs on {011} along $\langle 01\bar{1}\rangle$. For $A < 1$, the maximum value of $M$ occurs on {001} and the formal minimum value of $M$ occurs when $(\mathit{hkl})$ is a plane of the form $\{\mathit{hhl}\}$ where $h$ and $l$ are determined by Eqs. (39), (41) and (42) and the direction is $\langle 1\bar{1}0\rangle$. For a significant number of cubic materials with $A < 1$, this formal minimum will actually be at {110}, because Eq. (42) is not satisfied. Even if Eq. (42) is satisfied, this formal minimum is likely to have a value sufficiently close to the value of $M \langle 1\bar{1}0\rangle$ at {110} that for all practical purposes, {110} can be regarded as being planes with the minimum values of $M$ along their $\langle 1\bar{1}0\rangle$ directions.