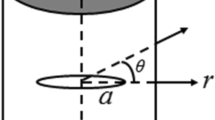
Appendix
1. Expressions of the known functions \(\varLambda_{mj}^{(S)}(\omega,z)\) (m=0,…,3,j=1,…,5), \(\varLambda_{nj}^{(E)}(\omega,z)\) (n=0,1,j=1,…,5) and \(\varLambda_{nj}^{(M)}(\omega,z)\) (n=0,1,j=1,…,5) appearing in Eqs. (66)–(68)
For Case (i)
$$ \begin{aligned} \varLambda_{m1}^{(S)}(\omega,z) &= \bigl[ \varGamma_{m}^{(S)} ( \eta_{1} )\cos (\omega \sigma_{1}z) - \Delta_{m}^{(S)} ( \eta_{1} )\sin (\omega \sigma_{1}z) \bigr]e^{\omega o_{1}z}, \\ \varLambda_{m2}^{(S)}(\omega,z) &= \bigl[ \Delta_{m}^{(S)} ( \eta_{1} )\cos (\omega \sigma_{1}z) + \varGamma_{m}^{(S)} ( \eta_{1} )\sin (\omega \sigma_{1}z) \bigr]e^{\omega o_{1}z}, \\ \varLambda_{m3}^{(S)}( \omega,z) &= \bigl[ \varGamma_{m}^{(S)} ( \eta_{3} )\cos (\omega \sigma_{3}z) - \Delta_{m}^{(S)} ( \eta_{3} )\sin (\omega \sigma_{3}z) \bigr]e^{\omega o_{3}z}, \\ \varLambda_{m4}^{(S)}(\omega,z) &= \bigl[ \Delta_{m}^{(S)} ( \eta_{3} )\cos (\omega \sigma_{3}z) + \varGamma_{m}^{(S)} ( \eta_{3} )\sin (\omega \sigma_{3}z) \bigr]e^{\omega o_{3}z}, \\ \varLambda_{m5}^{(S)}( \omega,z) &= \varPi_{m}^{(S)} ( o_{5} )e^{\omega o_{5}z},\quad m = 0, \ldots,3, \end{aligned} $$
(102)
$$\begin{aligned} & \begin{aligned} \varLambda_{n1}^{(E)}( \omega,z) &= \bigl[ \varGamma_{n}^{(E)} ( \eta_{1} ) \cos (\omega \sigma_{1}z) - \Delta_{n}^{(E)} ( \eta_{1} )\sin (\omega \sigma_{1}z) \bigr]e^{\omega o_{1}z}, \\ \varLambda_{n2}^{(E)}(\omega,z) &= \bigl[ \Delta_{n}^{(E)} ( \eta_{1} )\cos (\omega \sigma_{1}z) + \varGamma_{n}^{(E)} ( \eta_{1} )\sin (\omega \sigma_{1}z) \bigr]e^{\omega o_{1}z}, \\ \varLambda_{n3}^{(E)}( \omega,z) &= \bigl[ \varGamma_{n}^{(E)} ( \eta_{3} ) \cos (\omega \sigma_{3}z) - \Delta_{n}^{(E)} ( \eta_{3} )\sin (\omega \sigma_{3}z) \bigr]e^{\omega o_{3}z}, \\ \varLambda_{n}^{(E)}(\omega,z) &= \bigl[ \Delta_{n}^{(E)} ( \eta_{3} )\cos (\omega \sigma_{3}z) + \varGamma_{n}^{(E)} ( \eta_{3} )\sin (\omega \sigma_{3}z) \bigr]e^{\omega o_{3}z}, \\ \varLambda_{n5}^{(E)}( \omega,z) &= \varPi_{n}^{(E)} ( o_{5} )e^{\omega o_{5}z},\quad n = 0,1, \end{aligned} \end{aligned}$$
(103)
$$\begin{aligned} & \begin{aligned} \varLambda_{n1}^{(M)}(\omega,z) &= \bigl[ \varGamma_{n}^{(M)} ( \eta_{1} )\cos (\omega \sigma_{1}z) - \Delta_{n}^{(M)} ( \eta_{1} )\sin (\omega \sigma_{1}z) \bigr]e^{\omega o_{1}z}, \\ \varLambda_{n2}^{(M)}(\omega,z) &= \bigl[ \Delta_{n}^{(M)} ( \eta_{1} )\cos (\omega \sigma_{1}z) + \varGamma_{n}^{(M)} ( \eta_{1} )\sin (\omega \sigma_{1}z) \bigr]e^{\omega o_{1}z}, \\ \varLambda_{n3}^{(M)}( \omega,z) &= \bigl[ \varGamma_{n}^{(M)} ( \eta_{3} ) \cos (\omega \sigma_{3}z) - \Delta_{n}^{(M)} ( \eta_{3} )\sin (\omega \sigma_{3}z) \bigr]e^{\omega o_{3}z}, \\ \varLambda_{n}^{(M)}(\omega,z) &= \bigl[ \Delta_{n}^{(M)} ( \eta_{3} )\cos (\omega \sigma_{3}z) + \varGamma_{n}^{(M)} ( \eta_{3} )\sin (\omega \sigma_{3}z) \bigr]e^{\omega o_{3}z}, \\ \varLambda_{n5}^{(M)}( \omega,z) &= \varPi_{n}^{(M)} ( o_{5} )e^{\omega o_{5}z},\quad n = 0,1, \end{aligned} \end{aligned}$$
(104)
where known functions \(\varGamma_{m}^{(S)} ( \cdot )\), \(\Delta_{m}^{(S)} ( \cdot )\), \(\varPi_{m}^{(S)}\), \(\varGamma_{n}^{(E)} ( \cdot )\), \(\Delta_{n}^{(E)} ( \cdot )\), \(\varPi_{n}^{(E)}\), \(\varGamma_{n}^{(M)} ( \cdot )\), \(\Delta_{n}^{(M)} ( \cdot )\) and \(\varPi_{n}^{(M)}\) are given as
$$\begin{aligned} &\begin{aligned} \varGamma_{0}^{(S)} ( \eta ) &= c_{11} + c_{16}g_{1}(\eta ) + c_{13} \bigl[ \operatorname{Re} ( \eta )g_{2} ( \eta ) - \operatorname{Im} ( \eta )h_{2} ( \eta ) \bigr] \\ &\quad {} + e_{31} \bigl[ \operatorname{Re} ( \eta )g_{3} ( \eta ) - \operatorname{Im} ( \eta )h_{3} ( \eta ) \bigr] + h_{31} \bigl[ \operatorname{Re} ( \eta )g_{4} ( \eta ) - \operatorname{Im} ( \eta )h_{4} ( \eta ) \bigr], \\ \Delta_{0}^{(S)} ( \eta )&= c_{16}h_{1} ( \eta ) + c_{13} \bigl[ \operatorname{Re} ( \eta )h_{2} ( \eta ) + \operatorname{Im} ( \eta )g_{2} ( \eta ) \bigr] \\ &\quad {} + e_{31} \bigl[ \operatorname{Re} ( \eta )h_{3} ( \eta ) + \operatorname{Im} ( \eta )g_{3} ( \eta ) \bigr] + h_{31} \bigl[ \operatorname{Re} ( \eta )h_{4} ( \eta ) + \operatorname{Im} ( \eta )g_{4} ( \eta ) \bigr], \\ \varPi_{0}^{(S)} ( \eta )&= c_{11} + c_{16}f_{1}(\eta ) + c_{13}\eta f_{2}( \eta ) + e_{31}\eta f_{3}(\eta ) + h_{31}\eta f_{4}(\eta ), \end{aligned} \end{aligned}$$
(105)
$$\begin{aligned} &\begin{aligned} \varGamma_{1}^{(S)} ( \eta ) &= c_{13} + c_{36}g_{1}(\eta ) + c_{33} \bigl[ \operatorname{Re} ( \eta )g_{2} ( \eta ) - \operatorname{Im} ( \eta )h_{2} ( \eta ) \bigr] \\ &\quad {} + e_{33} \bigl[ \operatorname{Re} ( \eta )g_{3} ( \eta ) - \operatorname{Im} ( \eta )h_{3} ( \eta ) \bigr] \\ &\quad {} + h_{33} \bigl[ \operatorname{Re} ( \eta )g_{4} ( \eta ) - \operatorname{Im} ( \eta )h_{4} ( \eta ) \bigr], \\ \Delta_{1}^{(S)} ( \eta ) &= c_{36}h_{1} ( \eta ) + c_{33} \bigl[ \operatorname{Re} ( \eta )h_{2} ( \eta ) + \operatorname{Im} ( \eta )g_{2} ( \eta ) \bigr] + e_{33} \bigl[ \operatorname{Re} ( \eta )h_{3} ( \eta ) + \operatorname{Im} ( \eta )g_{3} ( \eta ) \bigr] \\ &\quad {} + h_{33} \bigl[ \operatorname{Re} ( \eta )h_{4} ( \eta ) + \operatorname{Im} ( \eta )g_{4} ( \eta ) \bigr], \\ \varPi_{1}^{(S)} ( \eta ) &= c_{13} + c_{36}f_{1}(\eta ) + c_{33}\eta f_{2}( \eta ) + e_{33}\eta f_{3}(\eta ) + h_{33}\eta f_{4}(\eta ), \end{aligned} \end{aligned}$$
(106)
$$\begin{aligned} &\begin{aligned} \varGamma_{2}^{(S)} ( \eta ) &= c_{45} \bigl[ \operatorname{Re} ( \eta )g_{1} ( \eta ) - \operatorname{Im} ( \eta )h_{1} ( \eta ) \bigr] + c_{55} \bigl[ \operatorname{Re} ( \eta ) - g_{2} ( \eta ) \bigr] - e_{15}g_{3} ( \eta ) \\ &\quad {} - h_{15}g_{4} ( \eta ), \\ \Delta_{2}^{(S)} ( \eta ) &= c_{45} \bigl[ \operatorname{Im} ( \eta )g_{1} ( \eta ) + \operatorname{Re} ( \eta )h_{1} ( \eta ) \bigr] + c_{55} \bigl[ \operatorname{Im} ( \eta ) - h_{2} ( \eta ) \bigr] - e_{15}h_{3} ( \eta ) \\ &\quad {} - h_{15}h_{4} ( \eta ), \\ \varPi_{2}^{(S)} ( \eta ) &= c_{45}\eta f_{1} ( \eta ) + c_{55} \bigl[ \eta - f_{2} ( \eta ) \bigr] - e_{15}f_{3} ( \eta ) - h_{15}f_{4} ( \eta ), \end{aligned} \end{aligned}$$
(107)
$$\begin{aligned} &\begin{aligned} \varGamma_{3}^{(S)} ( \eta ) &= c_{44} \bigl[ \operatorname{Re} ( \eta )g_{1} ( \eta ) - \operatorname{Im} ( \eta )h_{1} ( \eta ) \bigr] + c_{45} \bigl[ \operatorname{Re} ( \eta ) - g_{2} ( \eta ) \bigr] - e_{14}g_{3} ( \eta ) \\ &\quad {} - h_{14}g_{4} ( \eta ), \\ \Delta_{3}^{(S)} ( \eta ) &= c_{44} \bigl[ \operatorname{Im} ( \eta )g_{1} ( \eta ) + \operatorname{Re} ( \eta )h_{1} ( \eta ) \bigr] + c_{45} \bigl[ \operatorname{Im} ( \eta ) - h_{2} ( \eta ) \bigr] - e_{14}h_{3} ( \eta ) \\ &\quad {} - h_{14}h_{4} ( \eta ), \\ \varPi_{3}^{(S)} ( \eta ) &= c_{44}\eta f_{1} ( \eta ) + c_{45} \bigl[ \eta - f_{2} ( \eta ) \bigr] - e_{14}f_{3} ( \eta ) - h_{14}f_{4} ( \eta ), \end{aligned} \end{aligned}$$
(108)
$$\begin{aligned} &\begin{aligned} \varGamma_{0}^{(E)} ( \eta ) &= e_{14} \bigl[ \operatorname{Re} ( \eta )g_{1} ( \eta ) - \operatorname{Im} ( \eta )h_{1} ( \eta ) \bigr] + e_{15} \bigl[ \operatorname{Re} ( \eta ) - g_{2} ( \eta ) \bigr] + \epsilon _{11}g_{3} ( \eta ) \\ &\quad {} + d_{11}g_{4} ( \eta ), \\ \Delta_{0}^{(E)} ( \eta ) &= e_{14} \bigl[ \operatorname{Im} ( \eta )g_{1} ( \eta ) + \operatorname{Re} ( \eta )h_{1} ( \eta ) \bigr] + e_{15} \bigl[ \operatorname{Im} ( \eta ) - h_{2} ( \eta ) \bigr] + \epsilon _{11}h_{3} ( \eta ) \\ &\quad {} + d_{11}h_{4} ( \eta ), \\ \varPi_{0}^{(E)} ( \eta ) &= e_{14}\eta f_{1} ( \eta ) + e_{15} \bigl[ \eta - f_{2} ( \eta ) \bigr] + \epsilon _{11}f_{3} ( \eta ) + d_{11}f_{4} ( \eta ), \end{aligned} \end{aligned}$$
(109)
$$\begin{aligned} &\begin{aligned} \varGamma_{1}^{(E)} ( \eta ) &= e_{31} + e_{36}g_{1}(\eta ) + e_{33} \bigl[ \operatorname{Re} ( \eta )g_{2} ( \eta ) - \operatorname{Im} ( \eta )h_{2} ( \eta ) \bigr] \\ &\quad {} - \epsilon _{33} \bigl[ \operatorname{Re} ( \eta )g_{3} ( \eta ) - \operatorname{Im} ( \eta )h_{3} ( \eta ) \bigr] - d_{33} \bigl[ \operatorname{Re} ( \eta )g_{4} ( \eta ) - \operatorname{Im} ( \eta )h_{4} ( \eta ) \bigr], \\ \Delta_{1}^{(E)} ( \eta ) &=e_{36}h_{1} ( \eta ) + e_{33} \bigl[ \operatorname{Re} ( \eta )h_{2} ( \eta ) + \operatorname{Im} ( \eta )g_{2} ( \eta ) \bigr] \\ &\quad {} - \epsilon _{33} \bigl[ \operatorname{Re} ( \eta )h_{3} ( \eta ) + \operatorname{Im} ( \eta )g_{3} ( \eta ) \bigr] - d_{33} \bigl[ \operatorname{Re} ( \eta )h_{4} ( \eta ) + \operatorname{Im} ( \eta )g_{4} ( \eta ) \bigr], \\ \varPi_{1}^{(E)} ( \eta ) &= e_{31} + e_{36}f_{1}(\eta ) + e_{33}\eta f_{2}( \eta ) - \epsilon _{33}\eta f_{3}(\eta ) - d_{33}\eta f_{4}(\eta ), \end{aligned} \end{aligned}$$
(110)
$$\begin{aligned} &\begin{aligned} \varGamma_{0}^{(M)} ( \eta ) &= h_{14} \bigl[ \operatorname{Re} ( \eta )g_{1} ( \eta ) - \operatorname{Im} ( \eta )h_{1} ( \eta ) \bigr] + h_{15} \bigl[ \operatorname{Re} ( \eta ) - g_{2} ( \eta ) \bigr] + d_{11}g_{3} ( \eta ) \\ &\quad {} + \mu_{11}g_{4} ( \eta ), \\ \Delta_{0}^{(M)} ( \eta ) &= h_{14} \bigl[ \operatorname{Im} ( \eta )g_{1} ( \eta ) + \operatorname{Re} ( \eta )h_{1} ( \eta ) \bigr] + h_{15} \bigl[ \operatorname{Im} ( \eta ) - h_{2} ( \eta ) \bigr] + d_{11}h_{3} ( \eta ) \\ &\quad {} + \mu_{11}h_{4} ( \eta ), \\ \varPi_{0}^{(M)} ( \eta ) &= h_{14}\eta f_{1} ( \eta ) + h_{15} \bigl[ \eta - f_{2} ( \eta ) \bigr] + d_{11}f_{3} ( \eta ) + \mu_{11}f_{4} ( \eta ), \end{aligned} \end{aligned}$$
(111)
$$\begin{aligned} &\begin{aligned} \varGamma_{1}^{(M)} ( \eta ) &= h_{31} + h_{36}g_{1}(\eta ) + h_{33} \bigl[ \operatorname{Re} ( \eta )g_{2} ( \eta ) - \operatorname{Im} ( \eta )h_{2} ( \eta ) \bigr] \\ &\quad {} - d_{33} \bigl[ \operatorname{Re} ( \eta )g_{3} ( \eta ) - \operatorname{Im} ( \eta )h_{3} ( \eta ) \bigr] - \mu_{33} \bigl[ \operatorname{Re} ( \eta )g_{4} ( \eta ) - \operatorname{Im} ( \eta )h_{4} ( \eta ) \bigr], \\ \Delta_{1}^{(M)} ( \eta ) &= h_{36}h_{1} ( \eta ) + h_{33} \bigl[ \operatorname{Re} ( \eta )h_{2} ( \eta ) + \operatorname{Im} ( \eta )g_{2} ( \eta ) \bigr] \\ &\quad {} - d_{33} \bigl[ \operatorname{Re} ( \eta )h_{3} ( \eta ) + \operatorname{Im} ( \eta )g_{3} ( \eta ) \bigr] - \mu_{33} \bigl[ \operatorname{Re} ( \eta )h_{4} ( \eta ) + \operatorname{Im} ( \eta )g_{4} ( \eta ) \bigr], \\ \varPi_{1}^{(M)} ( \eta ) &= h_{31} + h_{36}f_{1}(\eta ) + h_{33}\eta f_{2}( \eta ) - d_{33}\eta f_{3}(\eta ) - \mu_{33}\eta f_{4}(\eta ). \end{aligned} \end{aligned}$$
(112)
For Case (ii)
$$\begin{aligned} & \begin{aligned} \varLambda_{m1}^{(S)}(\omega,z) &= \bigl[ \varGamma_{m}^{(S)} ( \eta_{1} )\cos (\omega \sigma_{1}z) - \Delta_{m}^{(S)} ( \eta_{1} )\sin (\omega \sigma_{1}z) \bigr]e^{\omega o_{1}z}, \\ \varLambda_{m2}^{(S)}(\omega,z) &= \bigl[ \Delta_{m}^{(S)} ( \eta_{1} )\cos (\omega \sigma_{1}z) + \varGamma_{m}^{(S)} ( \eta_{1} )\sin (\omega \sigma_{1}z) \bigr]e^{\omega o_{1}z}, \\ \varLambda_{mj}^{(S)}(\omega,z) &= \varPi_{m}^{(S)} ( o_{j} )e^{\omega o_{j}z},\quad m = 0, \ldots,3, j = 3,4,5, \end{aligned} \end{aligned}$$
(113)
$$\begin{aligned} & \begin{aligned} \varLambda_{n1}^{(E)}(\omega,z) &= \bigl[ \varGamma_{n}^{(E)} ( \eta_{1} ) \cos (\omega \sigma_{1}z) - \Delta_{n}^{(E)} ( \eta_{1} )\sin (\omega \sigma_{1}z) \bigr]e^{\omega o_{1}z}, \\ \varLambda_{n2}^{(E)}(\omega,z) &= \bigl[ \Delta_{n}^{(E)} ( \eta_{1} )\cos (\omega \sigma_{1}z) + \varGamma_{n}^{(E)} ( \eta_{1} )\sin (\omega \sigma_{1}z) \bigr]e^{\omega o_{1}z}, \\ \varLambda_{nj}^{(E)}(\omega,z) &= \varPi_{n}^{(E)} ( o_{j} )e^{\omega o_{j}z},\quad n = 0,1,\ j = 3,4,5, \end{aligned} \end{aligned}$$
(114)
$$\begin{aligned} & \begin{aligned} \varLambda_{n1}^{(M)}(\omega,z) &= \bigl[ \varGamma_{n}^{(M)} ( \eta_{1} ) \cos (\omega \sigma_{1}z) - \Delta_{n}^{(M)} ( \eta_{1} )\sin (\omega \sigma_{1}z) \bigr]e^{\omega o_{1}z}, \\ \varLambda_{n2}^{(M)}(\omega,z) &= \bigl[ \Delta_{n}^{(M)} ( \eta_{1} )\cos (\omega \sigma_{1}z) + \varGamma_{n}^{(M)} ( \eta_{1} )\sin (\omega \sigma_{1}z) \bigr]e^{\omega o_{1}z}, \\ \varLambda_{nj}^{(M)}(\omega,z) &= \varPi_{n}^{(M)} ( o_{j} )e^{\omega o_{j}z},\quad n = 0,1,\ j = 3,4,5. \end{aligned} \end{aligned}$$
(115)
For Case (iii)
$$\begin{aligned} &\varLambda_{mj}^{(S)}(\omega,z) = \varPi_{m}^{(S)} ( o_{j} )e^{\omega o_{j}z},\quad m = 0, \ldots,3,\ j = 1, \ldots,5, \end{aligned}$$
(116)
$$\begin{aligned} &\varLambda_{nj}^{(E)}(\omega,z) = \varPi_{n}^{(E)} ( o_{j} )e^{\omega o_{j}z},\quad n = 0,1,\ j = 1, \ldots,5, \end{aligned}$$
(117)
$$\begin{aligned} & \varLambda_{nj}^{(M)}(\omega,z) = \varPi_{n}^{(M)} ( o_{j} )e^{\omega o_{j}z},\quad n = 0,1,\ j = 1, \ldots,5. \end{aligned}$$
(118)
In Case (ii) and Case (iii), known functions \(\varGamma_{m}^{(S)} ( \cdot )\), \(\Delta_{m}^{(S)} ( \cdot )\), \(\varPi_{m}^{(S)}\), \(\varGamma_{n}^{(E)} ( \cdot )\), \(\Delta_{n}^{(E)} ( \cdot )\), \(\varPi_{n}^{(E)}\), \(\varGamma_{n}^{(M)} ( \cdot )\), \(\Delta_{n}^{(M)} ( \cdot )\) and \(\varPi_{n}^{(M)}\) are the same forms as those given in Eqs. (105)–(112).
2. Expressions of the known functions T
mj
(ω,0) (m=1,2,3,j=0,…,5) appearing in Eqs. (75)–(77)
For Case (i)
$$\begin{aligned} \begin{aligned} &\mathrm{T}_{m1}(\omega,z) = \bigl[ g_{m + 1}( \eta_{1})\cos (\omega \sigma_{1}z) - h_{m + 1}( \eta_{1})\sin (\omega \sigma_{1}z) \bigr]e^{\omega o_{1}z}, \\ &\mathrm{T}_{m2}(\omega,z) = \bigl[ h_{m + 1}( \eta_{1})\cos (\omega \sigma_{1}z) + g_{m + 1}( \eta_{1})\sin (\omega \sigma_{1}z) \bigr]e^{\omega o_{1}z}, \\ &\mathrm{T}_{m3}(\omega,z) = \bigl[ g_{m + 1}( \eta_{3})\cos (\omega \sigma_{3}z) - h_{m + 1}( \eta_{3})\sin (\omega \sigma_{3}z) \bigr]e^{\omega o_{3}z}, \\ &\mathrm{T}_{m4}(\omega,z) = \bigl[ g_{m + 1}( \eta_{3})\cos (\omega \sigma_{3}z) - h_{m + 1}( \eta_{3})\sin (\omega \sigma_{3}z) \bigr]e^{\omega o_{3}z}, \\ &\mathrm{T}_{m5}(\omega,z) = f_{m + 1}(o_{5})e^{\omega o_{5}z}, \quad m = 1,2,3. \end{aligned} \end{aligned}$$
(119)
For Case (ii)
$$\begin{aligned} \begin{aligned} & \mathrm{T}_{m1}(\omega,z) = \bigl[ g_{m + 1}( \eta_{1})\cos (\omega \sigma_{1}z) - h_{m + 1}( \eta_{1})\sin (\omega \sigma_{1}z) \bigr]e^{\omega o_{1}z}, \\ &\mathrm{T}_{m2}(\omega,z) = \bigl[ h_{m + 1}( \eta_{1})\cos (\omega \sigma_{1}z) + g_{m + 1}( \eta_{1})\sin (\omega \sigma_{1}z) \bigr]e^{\omega o_{1}z}, \\ &\mathrm{T}_{mj}(\omega,z) = f_{m + 1}(o_{j})e^{\omega o_{j}z}, \quad m = 1,2,3, j = 3,4,5. \end{aligned} \end{aligned}$$
(120)
For Case (iii)
$$\begin{aligned} \mathrm{T}_{mj}(\omega,z) = f_{m + 1}(o_{j})e^{\omega o_{j}z}, \quad m = 1,2,3,\ j = 1, \ldots,5. \end{aligned}$$
(121)
3. Expressions of 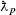 ,
, 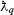 and
and 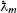 appearing in Eq. (93)
appearing in Eq. (93)
where
4. Expressions of \(\varOmega_{mj}^{(S)}\) and \(\varUpsilon_{mj}^{(S)}\) (m=0,…,3,j=1,…,5), \(\varOmega_{nj}^{(E)}\) and \(\varUpsilon_{nj}^{(E)}\) (n=0,1, j=1,…,5) and \(\varOmega_{nj}^{(M)}\) and \(\varUpsilon_{nj}^{(M)}\) (n=0,1,j=1,…,5) appearing in Eqs. (95)–(97)
$$\begin{aligned} \begin{aligned} &\mathrm{K}_{mj}^{(S)}(x,z) = \left\{ \begin{array}{l@{\quad }l} \varTheta_{mj}^{(S)}(x,z), & \mathrm{Case\ I} \\ \varUpsilon_{mj}^{(S)}(x,z), & \mathrm{Case\ II} \end{array} \right .,\quad (m = 0, \ldots,3,\ j = 1, \ldots,5), \\ & \mathrm{K}_{nj}^{(E)}(x,z) = \left\{ \begin{array}{l@{\quad }l} \varTheta_{nj}^{(E)}(x,z), & \mathrm{Case\ I} \\ \varUpsilon_{nj}^{(E)}(x,z), & \mathrm{Case\ II} \end{array} \right .,\quad (n = 0,1,\ j = 1, \ldots,5), \\ & \mathrm{K}_{nj}^{(M)}(x,z) = \left\{ \begin{array}{l@{\quad }l} \varTheta_{nj}^{(M)}(x,z), & \mathrm{Case\ I} \\ \varUpsilon_{nj}^{(M)}(x,z), & \mathrm{Case\ II} \end{array} \right .,\quad (n = 0,1,\ j = 1, \ldots,5), \end{aligned} \end{aligned}$$
(124)
where Case I denotes the expressions for \(\varOmega_{mj}^{(S)}\), \(\varOmega_{nj}^{(E)}\) and \(\varOmega_{nj}^{(M)}\) and Case II denotes the expressions for \(\varUpsilon_{mj}^{(S)}\), \(\varUpsilon_{nj}^{(E)}\) and \(\varUpsilon_{nj}^{(M)}\).
For Case (i)
$$\begin{aligned} &\begin{aligned} K_{m1}^{(S)}(x,z) &= \frac{1}{2} \bigl[ \varGamma_{m}^{(S)} ( \eta_{1} ) \chi_{11}(x,z) - \Delta_{m}^{(S)} ( \eta_{1} )\chi_{12}(x,z) \bigr],\quad m = 0,1, \\ K_{m2}^{(S)}(x,z) &= \frac{1}{2} \bigl[ \Delta_{m}^{(S)} ( \eta_{1} )\chi_{11}(x,z) + \varGamma_{m}^{(S)} ( \eta_{1} ) \chi_{12}(x,z) \bigr],\quad m = 0,1, \\ K_{m3}^{(S)}(x,z) &= \frac{1}{2} \bigl[ \varGamma_{m}^{(S)} ( \eta_{3} )\delta_{11}(x,z) - \Delta_{m}^{(S)} ( \eta_{3} )\delta_{12}(x,z) \bigr],\quad m = 0,1, \\ K_{m4}^{(S)}(x,z) &= \frac{1}{2} \bigl[ \Delta_{m}^{(S)} ( \eta_{3} )\delta_{11}(x,z) + \varGamma_{m}^{(S)} ( \eta_{3} ) \delta_{12}(x,z) \bigr],\quad m = 0,1, \\ K_{m5}^{(S)}(x,z) &= \varPi_{m}^{(S)} ( o_{5} )\tau_{15}(x,z),\quad m = 0,1, \\ K_{m1}^{(S)}(x,z) &= \frac{1}{2} \bigl[ \varGamma_{m}^{(S)} ( \eta_{1} ) \chi_{21}(x,z) - \Delta_{m}^{(S)} ( \eta_{1} )\chi_{22}(x,z) \bigr],\quad m = 2,3, \\ K_{m2}^{(S)}(x,z) &= \frac{1}{2} \bigl[ \Delta_{m}^{(S)} ( \eta_{1} )\chi_{21}(x,z) + \varGamma_{m}^{(S)} ( \eta_{1} ) \chi_{22}(x,z) \bigr],\quad m = 2,3, \\ K_{m3}^{(S)}(x,z) &= \frac{1}{2} \bigl[ \varGamma_{m}^{(S)} ( \eta_{3} )\delta_{21}(x,z) - \Delta_{m}^{(S)} ( \eta_{3} )\delta_{22}(x,z) \bigr],\quad m = 2,3, \\ K_{m4}^{(S)}(x,z) &= \frac{1}{2} \bigl[ \Delta_{m}^{(S)} ( \eta_{3} )\delta_{21}(x,z) + \varGamma_{m}^{(S)} ( \eta_{3} ) \delta_{22}(x,z) \bigr],\quad m = 2,3, \\ K_{m5}^{(S)}(x,z) &= \varPi_{m}^{(S)} ( o_{5} )\tau_{25}(x,z),\quad m = 2,3, \end{aligned} \end{aligned}$$
(125)
$$\begin{aligned} & \begin{aligned} K_{01}^{(E)}(x,z) &= \frac{1}{2} \bigl[ \varGamma_{0}^{(E)} ( \eta_{1} ) \chi_{21}(x,z) - \Delta_{0}^{(E)} ( \eta_{1} )\chi_{22}(x,z) \bigr], \\ K_{02}^{(E)}(x,z) &= \frac{1}{2} \bigl[ \Delta_{0}^{(E)} ( \eta_{1} )\chi_{21}(x,z) + \varGamma_{0}^{(E)} ( \eta_{1} )\chi_{22}(x,z) \bigr], \\ K_{03}^{(E)}(x,z) &= \frac{1}{2} \bigl[ \varGamma_{0}^{(E)} ( \eta_{3} )\delta_{21}(x,z) - \Delta_{0}^{(E)} ( \eta_{3} )\delta_{22}(x,z) \bigr], \\ K_{04}^{(E)}(x,z) &= \frac{1}{2} \bigl[ \Delta_{0}^{(E)} ( \eta_{3} )\delta_{21}(x,z) + \varGamma_{0}^{(E)} ( \eta_{3} )\delta_{22}(x,z) \bigr], \\ K_{05}^{(E)}(x,z) &= \varPi_{0}^{(E)} ( o_{5} )\tau_{25}(x,z), \\ K_{11}^{(E)}(x,z) &= \frac{1}{2} \bigl[ \varGamma_{1}^{(E)} ( \eta_{1} ) \chi_{11}(x,z) - \Delta_{1}^{(E)} ( \eta_{1} )\chi_{12}(x,z) \bigr], \\ K_{12}^{(E)}(x,z) &= \frac{1}{2} \bigl[ \Delta_{1}^{(E)} ( \eta_{1} )\chi_{11}(x,z) + \varGamma_{1}^{(E)} ( \eta_{1} )\chi_{12}(x,z) \bigr], \\ K_{13}^{(E)}(x,z) &= \frac{1}{2} \bigl[ \varGamma_{1}^{(E)} ( \eta_{3} )\delta_{11}(x,z) - \Delta_{1}^{(E)} ( \eta_{3} )\delta_{12}(x,z) \bigr], \\ K_{14}^{(E)}(x,z) &= \frac{1}{2} \bigl[ \Delta_{1}^{(E)} ( \eta_{3} )\delta_{11}(x,z) + \varGamma_{1}^{(E)} ( \eta_{3} )\delta_{12}(x,z) \bigr], \\ K_{15}^{(E)}(x,z) &= \varPi_{1}^{(E)} ( o_{5} )\tau_{15}(x,z), \end{aligned} \end{aligned}$$
(126)
$$\begin{aligned} &\begin{aligned} K_{01}^{(M)}(x,z) &= \frac{1}{2} \bigl[ \varGamma_{0}^{(M)} ( \eta_{1} ) \chi_{21}(x,z) - \Delta_{0}^{(M)} ( \eta_{1} )\chi_{22}(x,z) \bigr], \\ K_{02}^{(M)}(x,z) &= \frac{1}{2} \bigl[ \Delta_{0}^{(M)} ( \eta_{1} )\chi_{21}(x,z) + \varGamma_{0}^{(M)} ( \eta_{1} )\chi_{22}(x,z) \bigr], \\ K_{03}^{(M)}(x,z) &= \frac{1}{2} \bigl[ \varGamma_{0}^{(M)} ( \eta_{3} )\delta_{21}(x,z) - \Delta_{0}^{(M)} ( \eta_{3} )\delta_{22}(x,z) \bigr], \\ K_{04}^{(M)}(x,z) &= \frac{1}{2} \bigl[ \Delta_{0}^{(M)} ( \eta_{3} )\delta_{21}(x,z) + \varGamma_{0}^{(M)} ( \eta_{3} )\delta_{22}(x,z) \bigr], \\ K_{05}^{(M)}(x,z) &= \varPi_{0}^{(M)} ( o_{5} )\tau_{25}(x,z), \\ K_{11}^{(M)}(x,z) &= \frac{1}{2} \bigl[ \varGamma_{1}^{(M)} ( \eta_{1} ) \chi_{11}(x,z) - \Delta_{1}^{(M)} ( \eta_{1} )\chi_{12}(x,z) \bigr], \\ K_{12}^{(M)}(x,z) &= \frac{1}{2} \bigl[ \Delta_{1}^{(M)} ( \eta_{1} )\chi_{11}(x,z) + \varGamma_{1}^{(M)} ( \eta_{1} )\chi_{12}(x,z) \bigr], \\ K_{13}^{(M)}(x,z) &= \frac{1}{2} \bigl[ \varGamma_{1}^{(M)} ( \eta_{3} )\delta_{11}(x,z) - \Delta_{1}^{(M)} ( \eta_{3} )\delta_{12}(x,z) \bigr], \\ K_{14}^{(M)}(x,z) &= \frac{1}{2} \bigl[ \Delta_{1}^{(M)} ( \eta_{3} )\delta_{11}(x,z) + \varGamma_{1}^{(M)} ( \eta_{3} )\delta_{12}(x,z) \bigr], \\ K_{15}^{(M)}(x,z) &= \varPi_{1}^{(M)} ( o_{5} )\tau_{15}(x,z), \end{aligned} \end{aligned}$$
(127)
where χ
nj
(x,z) (n,j=1,2) are given as
$$\begin{aligned} \begin{aligned} &\chi_{1j}(x,z) = T_{j1}(x,z) + T_{j2}(x,z),\quad j = 1,2,\\ &\chi_{21}(x,z) = T_{21}(x,z) - T_{22}(x,z), \qquad \chi_{22}(x,z) = - T_{11}(x,z) + T_{12}(x,z), \end{aligned} \end{aligned}$$
(128)
$$\begin{aligned} &T_{1j}(x,z) = \left\{ \begin{array}{l@{\quad }l} \dfrac{\sqrt{\rho_{j2}^{2} - x_{Aj}^{2}}}{\rho_{j2}^{2} - \rho_{j1}^{2}}, & \mathrm{Case\ I} \\ \dfrac{\sqrt{\rho_{j2}^{2} - x_{Aj}^{2}} + o_{1}z}{a}, & \mathrm{Case\ II} \end{array} \right.,\quad j = 1,2, \\ & T_{2j}(x,z) = \left\{ \begin{array}{l@{\quad }l} \operatorname{sgn}(x_{Aj})\dfrac{\sqrt{x_{Aj}^{2} - \rho_{j1}^{2}}}{\rho_{j2}^{2} - \rho_{j1}^{2}}, & \mathrm{Case\ I} \\ \dfrac{x_{Aj} - \operatorname{sgn}(x_{Aj})\sqrt{x_{Aj}^{2} - \rho_{j1}^{2}}}{a}, & \mathrm{Case\ II} \end{array} \right .,\quad j = 1,2, \end{aligned}$$
(129)
where sgn(⋅) is the sign function and
$$\begin{aligned} &\rho_{11} = \frac{1}{2} \bigl( \sqrt{(x_{A1} + a)^{2} + (o_{1}z)^{2}} - \sqrt{(x_{A1} - a)^{2} + (o_{1}z)^{2}} \bigr), \end{aligned}$$
(130)
$$\begin{aligned} &\rho_{12} = \frac{1}{2} \bigl( \sqrt{(x_{A1} + a)^{2} + (o_{1}z)^{2}} + \sqrt{(x_{A1} - a)^{2} + (o_{1}z)^{2}} \bigr), \end{aligned}$$
(131)
$$\begin{aligned} &\rho_{21} = \frac{1}{2} \bigl( \sqrt{(x_{A2} + a)^{2} + (o_{1}z)^{2}} - \sqrt{(x_{A2} - a)^{2} + (o_{1}z)^{2}} \bigr), \end{aligned}$$
(132)
$$\begin{aligned} &\rho_{22} = \frac{1}{2} \bigl( \sqrt{(x_{A2} + a)^{2} + (o_{1}z)^{2}} + \sqrt{(x_{A2} - a)^{2} + (o_{1}z)^{2}} \bigr), \end{aligned}$$
(133)
$$\begin{aligned} &x_{A1} = \sigma_{1}z + x,\quad x_{A2} = \sigma_{1}z - x, \end{aligned}$$
(134)
and δ
nj
(x,z) (n,j=1,2) are given as
$$\begin{aligned} \begin{aligned} &\delta_{1j}(x,z) = \mathrm{H}_{j1}(x,z) + \mathrm{H}_{j2}(x,z),\quad j = 1,2, \\ &\delta_{21}(x,z) = \mathrm{H}_{21}(x,z) - \mathrm{H}_{22}(x,z), \qquad \delta_{22}(x,z) = - \mathrm{H}_{11}(x,z) + \mathrm{H}_{12}(x,z), \end{aligned} \end{aligned}$$
(135)
$$\begin{aligned} \begin{aligned} & H_{1j}(x,z) = \left \{ \begin{array}{l@{\quad }l} \dfrac{\sqrt{\gamma_{j2}^{2} - x_{Bj}^{2}}}{\gamma_{j2}^{2} - \gamma_{j1}^{2}}, & \mathrm{Case\ I} \\ \dfrac{\sqrt{\gamma_{j2}^{2} - x_{Bj}^{2}} + o_{3}z}{a}, & \mathrm{Case\ II} \end{array} \right.,\quad j = 1,2, \\ & H_{2j}(X,Z) = \left \{ \begin{array}{l@{\quad }l} {\mathop{\mathrm{sgn}}} (x_{Bj})\dfrac{\sqrt{x_{Bj}^{2} - \gamma_{j1}^{2}}}{\gamma_{j2}^{2} - \gamma_{j1}^{2}}, & \mathrm{Case\ I} \\ \dfrac{x_{Bj} - {\mathop{\mathrm{sgn}}} (x_{Bj})\sqrt{x_{Bj}^{2} - \gamma_{j1}^{2}}}{a}, & \mathrm{Case\ II} \end{array} \right .,\quad j = 1,2, \end{aligned} \end{aligned}$$
(136)
where
$$\begin{aligned} & \gamma_{11} = \frac{1}{2} \bigl( \sqrt{(x_{B1} + a)^{2} + (o_{3}z)^{2}} - \sqrt{(x_{B1} - a)^{2} + (o_{3}z)^{2}} \bigr), \end{aligned}$$
(137)
$$\begin{aligned} & \gamma_{12} = \frac{1}{2} \bigl( \sqrt{(x_{B1} + a)^{2} + (o_{3}z)^{2}} + \sqrt{(x_{B1} - a)^{2} + (o_{3}z)^{2}} \bigr), \end{aligned}$$
(138)
$$\begin{aligned} & \gamma_{21} = \frac{1}{2} \bigl( \sqrt{(x_{B2} + a)^{2} + (o_{3}z)^{2}} - \sqrt{(x_{B2} - a)^{2} + (o_{3}z)^{2}} \bigr), \end{aligned}$$
(139)
$$\begin{aligned} & \gamma_{22} = \frac{1}{2} \bigl( \sqrt{(x_{B2} + a)^{2} + (o_{3}Z)^{2}} + \sqrt{(x_{B2} - a)^{2} + (o_{3}Z)^{2}} \bigr), \end{aligned}$$
(140)
$$\begin{aligned} & x_{B1} = \sigma_{3}z + x, \quad x_{B2} = \sigma_{3}z - x. \end{aligned}$$
(141)
The functions τ
nj
(x,z) are
$$\begin{aligned} \begin{aligned} &\tau_{1j}(x,z) = \left \{ \begin{array}{l@{\quad }l} \dfrac{\sqrt{\lambda_{2j}^{2} - x^{2}}}{\lambda_{2j}^{2} - \lambda_{1j}^{2}}, & \mathrm{Case\ I} \\ \dfrac{\sqrt{\lambda_{2j}^{2} - x^{2}} + o_{j}z}{a}, & \mathrm{Case\ II} \end{array} \right., \\ & C_{2j}(X,Z) = \left\{ \begin{array}{l@{\quad }l} {\mathop{\mathrm{sgn}}} (X)\dfrac{\sqrt{X^{2} - \lambda_{1j}^{2}}}{\lambda_{2j}^{2} - \lambda_{1j}^{2}}, & \mathrm{Case\ I} \\ \dfrac{X - {\mathop{\mathrm{sgn}}} (X)\sqrt{X^{2} - \lambda_{1j}^{2}}}{a}, & \mathrm{Case\ II} \end{array} \right., \end{aligned} \end{aligned}$$
(142)
$$\begin{aligned} \begin{aligned} & \lambda_{1j} = \frac{1}{2} \bigl( \sqrt{(x + a)^{2} + (o_{j}z)^{2}} - \sqrt{(x - a)^{2} + (o_{j}z)^{2}} \bigr), \\ &\lambda_{2j} = \frac{1}{2} \bigl( \sqrt{(x + a)^{2} + (o_{j}z)^{2}} + \sqrt{(x - a)^{2} + (o_{j}z)^{2}} \bigr). \end{aligned} \end{aligned}$$
(143)
For Case (ii)
$$\begin{aligned} & \begin{aligned} K_{m1}^{(S)}(x,z) &= \frac{1}{2} \bigl[ \varGamma_{m}^{(S)} ( \eta_{1} ) \chi_{11}(x,z) - \Delta_{m}^{(S)} ( \eta_{1} )\chi_{12}(x,z) \bigr],\quad m = 0,1, \\ K_{m2}^{(S)}(x,z) &= \frac{1}{2} \bigl[ \Delta_{m}^{(S)} ( \eta_{1} )\chi_{11}(x,z) + \varGamma_{m}^{(S)} ( \eta_{1} ) \chi_{12}(x,z) \bigr],\quad m = 0,1, \\ K_{mj}^{(S)}(x,z) &= \varPi_{m}^{(S)} ( o_{j} )\tau_{1j}(x,z),\quad m = 0,1,\ j = 3,4,5, \\ K_{m1}^{(S)}(x,z) &= \frac{1}{2} \bigl[ \varGamma_{m}^{(S)} ( \eta_{1} ) \chi_{21}(x,z) - \Delta_{m}^{(S)} ( \eta_{1} )\chi_{22}(x,z) \bigr],\quad m = 2,3, \\ K_{m2}^{(S)}(x,z) &= \frac{1}{2} \bigl[ \Delta_{m}^{(S)} ( \eta_{1} )\chi_{21}(x,z) + \varGamma_{m}^{(S)} ( \eta_{1} ) \chi_{22}(x,z) \bigr],\quad m = 2,3, \\ K_{mj}^{(S)}(x,z) &= \varPi_{m}^{(S)} ( o_{j} )\tau_{2j}(x,z),\quad m = 2,3,\ j = 3,4,5, \end{aligned} \end{aligned}$$
(144)
$$\begin{aligned} &\begin{aligned} K_{01}^{(E)}(x,z) &= \frac{1}{2} \bigl[ \varGamma_{0}^{(E)} ( \eta_{1} ) \chi_{21}(x,z) - \Delta_{0}^{(E)} ( \eta_{1} )\chi_{22}(x,z) \bigr],\\ K_{02}^{(E)}(x,z) &= \frac{1}{2} \bigl[ \Delta_{0}^{(E)} ( \eta_{1} )\chi_{21}(x,z) + \varGamma_{0}^{(E)} ( \eta_{1} )\chi_{22}(x,z) \bigr],\\ K_{0j}^{(E)}(x,z) &= \varPi_{0}^{(E)} ( o_{j} )\tau_{2j}(x,z),\quad j = 3,4,5, \\ K_{11}^{(E)}(x,z) &= \frac{1}{2} \bigl[ \varGamma_{1}^{(E)} ( \eta_{1} ) \chi_{11}(x,z) - \Delta_{1}^{(E)} ( \eta_{1} )\chi_{12}(x,z) \bigr], \\ K_{12}^{(E)}(x,z) &= \frac{1}{2} \bigl[ \Delta_{1}^{(E)} ( \eta_{1} )\chi_{11}(x,z) + \varGamma_{1}^{(E)} ( \eta_{1} )\chi_{12}(x,z) \bigr], \\ K_{1j}^{(E)}(x,z) &= \varPi_{1}^{(E)} ( o_{j} )\tau_{1j}(x,z), \quad j = 3,4,5, \end{aligned} \end{aligned}$$
(145)
$$\begin{aligned} &\begin{aligned} K_{01}^{(M)}(x,z) &= \frac{1}{2} \bigl[ \varGamma_{0}^{(M)} ( \eta_{1} ) \chi_{21}(x,z) - \Delta_{0}^{(M)} ( \eta_{1} )\chi_{22}(x,z) \bigr], \\ K_{02}^{(M)}(x,z) &= \frac{1}{2} \bigl[ \Delta_{0}^{(M)} ( \eta_{1} )\chi_{21}(x,z) + \varGamma_{0}^{(M)} ( \eta_{1} )\chi_{22}(x,z) \bigr], \\ K_{0j}^{(M)}(x,z) &= \varPi_{0}^{(M)} ( o_{j} )\tau_{2j}(x,z),\quad j = 3,4,5,\\ K_{11}^{(M)}(x,z) &= \frac{1}{2} \bigl[ \varGamma_{1}^{(M)} ( \eta_{1} ) \chi_{11}(x,z) - \Delta_{1}^{(M)} ( \eta_{1} )\chi_{12}(x,z) \bigr], \\ K_{12}^{(M)}(x,z) &= \frac{1}{2} \bigl[ \Delta_{1}^{(M)} ( \eta_{1} )\chi_{11}(x,z) + \varGamma_{1}^{(M)} ( \eta_{1} )\chi_{12}(x,z) \bigr], \\ K_{1j}^{(M)}(x,z) &= \varPi_{1}^{(M)} ( o_{j} )\tau_{1j}(x,z),\quad j = 3,4,5. \end{aligned} \end{aligned}$$
(146)
For Case (iii)
$$\begin{aligned} &\begin{aligned} K_{mj}^{(S)}(x,z) = \varPi_{m}^{(S)} ( o_{j} )\tau_{1j}(x,z),\quad m = 0,1,\ j = 1, \ldots,5, \\ K_{mj}^{(S)}(x,z) = \varPi_{m}^{(S)} ( o_{j} )\tau_{2j}(x,z),\quad m = 2,3,\ j = 1, \ldots,5, \end{aligned} \end{aligned}$$
(147)
$$\begin{aligned} &\begin{aligned} K_{0j}^{(E)}(x,z) = \varPi_{0}^{(E)} ( o_{j} )\tau_{2j}(x,z),\quad j = 1, \ldots,5, \\ K_{1j}^{(E)}(x,z) = \varPi_{1}^{(E)} ( o_{j} )\tau_{1j}(x,z),\quad j = 1, \ldots,5, \end{aligned} \end{aligned}$$
(148)
$$\begin{aligned} &\begin{aligned} K_{0j}^{(M)}(x,z) = \varPi_{0}^{(M)} ( o_{j} )\tau_{2j}(x,z),\quad j = 1, \ldots,5, \\ K_{1j}^{(M)}(x,z) = \varPi_{1}^{(M)} ( o_{j} )\tau_{1j}(x,z),\quad j = 1, \ldots,5. \end{aligned} \end{aligned}$$
(149)
In Case (ii) and Case (iii), known functions χ
nj
(x,z), δ
nj
(x,z) and τ
nj
(x,z) are the same forms as those given in Case (i) with eigenvalues changed to the related ones.








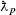 ,
, 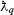 and
and 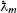 appearing in Eq. (93)
appearing in Eq. (93)