Abstract
We consider the nonlocal formulation of continuum mechanics described by peridynamics. We provide a link between peridynamic evolution and brittle fracture evolution for a broad class of peridynamic potentials associated with unstable peridynamic constitutive laws. Distinguished limits of peridynamic evolutions are identified that correspond to vanishing peridynamic horizon. The limit evolution has both bounded linear elastic energy and Griffith surface energy. The limit evolution corresponds to the simultaneous evolution of elastic displacement and fracture. For points in spacetime not on the crack set the displacement field evolves according to the linear elastic wave equation. The wave equation provides the dynamic coupling between elastic waves and the evolving fracture path inside the media. The elastic moduli, wave speed and energy release rate for the evolution are explicitly determined by moments of the peridynamic influence function and the peridynamic potential energy.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Peridynamics, introduced by Silling in 2000, [30] is a nonlocal formulation of continuum mechanics expressed in terms of regular elastic potentials. The theory is formulated in terms of displacement differences as opposed to spatial derivatives of the displacement field. These features provide the flexibility to simultaneously simulate kinematics involving both smooth deformations and defect evolution. Numerical simulations based on peridynamic modeling exhibit the formation and evolution of sharp interfaces associated with defects and fracture [6, 31, 32, 35], and [15]. These aspects are exploited in the peridynamic scheme for dynamic fracture simulation where the crack path is determined as part of the solution [20, 24]. This type of solution is distinct from the classical setting where the crack path is specified a priori see, [19].
We consider peridynamic formulations with constitutive laws that soften beyond a critical shear strain. Here we discover new quantitative and qualitative information that is extracted from the peridynamic formulation using scaling arguments and by passing to a distinguished small horizon limit. In this limit the dynamics correspond to the simultaneous evolution of elastic displacement and fracture. For points in spacetime not on the crack set the displacement field evolves according to the linear elastic wave equation. The wave equation provides the dynamic coupling between elastic waves and the evolving fracture path inside the media. The limit evolutions have bounded energy expressed in terms of the bulk and surface energies of linear elastic fracture mechanics. They also satisfy an energy inequality expressed in terms of the kinetic energy of the motion together with the bulk elastic energy and a Griffith surface energy. These energies are described by the density ρ, elastic shear modulus μ and energy release rate \(\mathcal{G}_{c}\). The parameters μ and \(\mathcal{G}_{c}\) have explicit formulas given in terms of the moments of the peridynamic influence function and the peridynamic potential energy see, (2.8). These formulas provide a rigorous means to calibrate peridynamic potentials with experimentally measured values of elastic shear modulus and critical energy release rate.
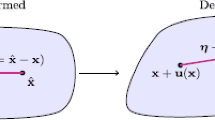
To present the ideas we focus on antiplane shear problems posed over a bounded convex domain \(D\subset\mathbb{R}^{2}\). The antiplane displacement transverse to D is written u(t,x). In the peridynamic formulation one considers pairs of points x, x′ in \(\mathbb{R}^{2}\) and the relative displacement η(t,x)=u(t,x′)−u(t,x). The antiplane shear strain is given by \(\mathcal{S}=\eta/|x'-x|\). The family of points x′ that interact with x is confined to a neighborhood \(\mathcal{H}_{\epsilon}(x)\) of x of diameter 2ϵ. Here ϵ is the horizon for the peridynamic interaction and \(\mathcal{H}_{\epsilon}(x)\) is a disk of radius ϵ centered at x. The peridynamic influence function is defined inside \(\mathcal{H}_{\epsilon}(x)\) and is written \(J(\frac{|x'-x|}{\epsilon})\), with M>J(r)≥0 for 0≤r≤1 and zero outside. Next we will introduce the nonlocal analogue of boundary conditions for the problem. We define the set D α , with D⊂D α defined as the set of points x for which \(\operatorname{dist}(x,D)<\alpha\), see Fig. 1. For points x residing in D α ∼D we set the displacement u(t,x)=0 for all 0≤t≤T; this gives the nonlocal analogue of “Dirichlet” boundary conditions for peridynamic problems introduced in [13].
In this paper we are interested in the small horizon limit ϵ→0 and we make the change of variable x′=x+ϵξ, where ξ belongs to the unit disk \(\mathcal{H}_{1}(0)\) centered at the origin. The peridynamic potential energy density is a function of x′−x=ϵξ and η(x) and we consider the family of regular peridynamic potentials parameterized by ϵ given by
see Fig. 2. The potential functions \(f:[0,\infty)\rightarrow\mathbb{R}\) considered here are positive, smooth and concave with the properties
The limiting values of f′ near zero and f near infinity determine the linear elastic properties and critical energy release rate seen in the limiting dynamics. The precise relationship between f′(0) and f ∞ and the linear elastic shear modulus μ and critical energy release rate \(\mathcal{G}_{c}\) are given by formulas (2.8) of Sect. 2.1. The potentials W ϵ can be thought of as the smooth analogues of potentials used to describe the peridynamic bond stretch models introduced in [30, 31]. This class of potential energies is convex-concave with respect to the magnitude of the shear strain \(\mathcal{S}\) with infection point \(\overline{\eta}/(\epsilon|\xi|)\) see, Fig. 2. This delivers the constitutive relation
Here the softening behavior occurs when the antiplane shear strain \(\mathcal{S}\) exceeds the critical value \(\overline{\eta}/(\epsilon|\xi|)\) see, Fig. 3.
The peridynamic potential energy is obtained by integrating the energy density over the neighborhood \(\mathcal{H}_{\epsilon}(x)\) and is given in terms of the rescaled coordinates by
The total strain energy of the displacement is given by
The peridynamic evolution is described by the Lagrangian
with
where ρ is the mass density of the material and b(t,x) is the body force density. The initial conditions u ϵ(0,x)=u 0(x) and \(u^{\epsilon}_{t}(0,x)=v_{0}(x)\) are prescribed and the action integral for the peridynamic evolution is
For a given unit vector n and h in \(\mathbb{R}\) we define the difference quotient of ψ(x) by
Writing \(e=\frac{\xi}{|\xi|}\) and ξ=e|ξ|, we set
The Euler Lagrange Equation for this system delivers the peridynamic equation of motion given by
where
In what follows we examine the family of peridynamic deformations {u ϵ(t,x)} ϵ>0 defined for suitable initial data u 0,v 0 and investigate the dynamics of the limit u 0(t,x)=lim ϵ→0 u ϵ(t,x). To do this we describe peridynamic deformations as trajectories in function space. The nonlocal Dirichlet boundary conditions are incorporated into the function space by defining the class of functions \(L^{2}_{0}(D)\) that are square integrable over D and zero on D α ∖D.Footnote 1 In this context we view peridynamic evolutions as functions of time taking values in the space \(L^{2}_{0}(D)\). It follows from the evolution equation (1.12) that u ϵ(t,x) is twice differentiable in time taking values in \(L^{2}_{0}(D)\). This space of functions is denoted by \(C^{2}([0,T];L^{2}_{0}(D))\) see, e.g., [17]. The initial value problem for the peridynamic evolution (1.12) is shown to be well posed on \(C^{2}([0,T];L^{2}_{0}(D))\) see, Sect. 2.2. We apply a scaling analysis to show that the peridynamic evolutions u ϵ(t,x) approach a limit evolution u 0 in the ϵ→ limit. The limit evolution u 0(t,x) is shown to have bounded linear elastic energy and bounded Griffith surface energy for a wide class of initial conditions. The limit evolution satisfies an energy inequality expressed in terms of the kinetic energy of the motion together with a linear elastic energy in terms of the antiplane shear strain ∇u 0 and a Griffith surface energy associated with the evolving jump set \(S_{u^{0}(t)}\) of u 0(t,x) see, Sect. 3.1. The jump set \(S_{u^{0}(t)}\) is the crack set and distinguished limit of the peridynamic model is given by the displacement—crack set pair u 0(t,x), \(S_{u^{0}(t)}\). The wave equation provides the dynamic coupling between elastic waves and the evolving fracture path inside the media.
Motivated by the approach given in [34] we investigate the effect of the softening constitutive law (1.3) on the nucleation of fracture inside a peridynamic body. We consider a generic peridynamic neighborhood \(\mathcal{H}_{\epsilon}(x)\) of radius ϵ about the point x. For points x′ inside \(\mathcal{H}_{\epsilon}(x)\) we say that the material between x and x′ (the bond) is critically strained if the magnitude of the shear strain \(|\mathcal{S}^{\epsilon}|=|\eta^{\epsilon}(x)|/(\epsilon|\xi|)>\overline {\eta}/(\epsilon|\xi|)\), otherwise the shear strain is called subcritical. A linear stability analysis is given that identifies necessary conditions for fracture nucleation inside \(\mathcal{H}_{\epsilon}(x)\). These conditions are directly linked to the appearance of subsets of critically strained bonds inside \(\mathcal{H}_{\epsilon}(x)\) with nonzero area fraction. The fracture nucleation condition given by Proposition 2.1 implies that if the neighborhood contains a nonzero area fraction of critically strained bonds then the neighborhood can be linearly unstable and a displacement jump can be nucleated. These results are presented in Sect. 2.3.
We focus on the peridynamic neighborhoods \(\mathcal{H}_{\epsilon}(x)\) that contain critically strained bonds over an area fraction larger than ϵ α with exponent 0<α<1 and 0<ϵ α<1. These neighborhoods are referred to as unstable neighborhoods. Under this definition unstable neighborhoods have the potential to nucleate jump discontinuities. We apply this definition to identify a set where unstable neighborhoods for the flows u ϵ(t,x) concentrate as the peridynamic horizon approaches zero. To present the idea we fix α and consider the collection of centroids x of all the unstable neighborhoods \(\mathcal{H}_{\epsilon}(x)\) with critically strained bonds over an area fraction greater than ϵ α for a family of flows with δ>ϵ>0. This collection is denoted by the set \(C^{\alpha}_{\delta}\). It is shown that the area of \(C^{\alpha}_{\delta}\) vanishes as δ→0 and that the collection of centroids for unstable neighborhoods concentrate onto a set \(C^{\alpha}_{0}\) of zero area as δ→0. This is shown to be true for every choice of 0<α<1 and we take the intersections of these sets denoted here by \(C^{0}_{0}\). The set \(C^{0}_{0}\) is associated with centroids of neighborhoods for which all bonds have become soft. The dynamics associated with each point in the reference configuration belonging to the set \(C_{0}^{0}\) is not affected by the motion of its surroundings. With these ideas in mind the set \(C^{0}_{0}\) presents itself as an alternate description of the crack set in the small horizon limit.
It is shown that the concentration of instability is inevitable for convex-concave peridynamic potentials and is directly linked to the energy budget associated with the peridynamic motion. The analysis shows that for a family of peridynamic flows {u ϵ(t,x)} ϵ>0 all driven by the same initial conditions and body forces that the peridydnamic potential energy of each flow is bounded uniformly in time 0≤t≤T independently of the radius of the horizon, see Sect. 4.2. This bound is shown to force the localization see Theorem 2.3. These observations are presented in Sect. 2.4 and established in Sect. 4.5.4.
Within the context of Sect. 3.2 we will apply these observations and adopt the hypothesis that the crack set \(S_{u^{0}}\) for the limit evolution and \(C^{0}_{0}\) are one and the same, see Hypotheses 3.3. We employ a scaling analysis to the peridynamic equation of motion to discover that the limit evolution u 0(t,x) satisfies the wave equation at every point in spacetime where ∇u 0 is defined see Theorem 3.4. The wave equation provides the dynamic coupling between elastic waves u 0(t,x) and the evolving fracture path \(S_{u^{0}(t)}\) inside the media. It is important to point out that the limiting dynamic fracture evolution described here follows from scaling arguments and on passing to a distinguished limit in the peridynamic formulation. These results are presented in Sects. 3.1 and 3.2. The mathematical tool set appropriate for extracting the limit behavior from this class of peridynamic models is based on Γ-convergence and comes from the literature associated with the analysis of the Mumford Shah functional and free discontinuity problems see, [21, 22], and [23].
We point out here that other related recent work focuses on passing to the small horizon limit for linear peridynamic formulations; establishing a link between linear elasticity and peridynamics see [14, 16, 27, 33].
In closing we note that there is a vast literature on fracture modeling and a complete survey is beyond the scope of this paper. Instead we point out recent proposals for computing crack propagation in dynamic and quasi static settings. Approaches using a phase field for the damage set and a linear elastic field, to represent crack propagation have been proposed and developed in [9, 26], and [7]. Wave equations for fields inside domains with evolving cracks are posed in [11] and variational aspects of sharp interface models are discussed in [25]. For quasi static problems variational phase field methods are developed in the pioneering work of [8, 18]. More recently a two field method using eigen-deformations for the fracture field is developed for quasi static problems in [29]. Alternative nonlocal formulations have been developed for quasi static crack propagation in [5, 10].
2 Peridynamic Evolution
We begin this section by introducing a suitable class of initial conditions appropriate for describing the evolution of deformations that can have smooth variation as well as jumps. Here we will choose initial conditions with bounded elastic energy in the sense of fracture mechanics. We show that well posed peridynamic evolutions exist for this class of initial data. These peridynamic evolutions satisfy an energy balance between potential and kinetic energy at each time during the deformation. Next we develop a necessary criterion for fracture initiation inside a peridynamic neighborhood. Here fracture initiation is defined to be the nucleation of a jump in the displacement inside a peridynamic neighborhood. We develop a criterion for the orientation of the nucleated crack based upon the notion of the most unstable direction. The approach taken here is consistent with the analysis of crack nucleation developed in [34]. We conclude with a discussion of the localization of instability in the limit of vanishing peridynamic horizon.
2.1 Initial Conditions and Motivation
Our choice of initial conditions is motivated by Linear Elastic Fracture Mechanics (LEFM). Here we investigate Mode III fracture in the context of antiplane shear. The initial condition is specified by a crack set K and displacement u 0. The gradient ∇u 0 is defined off the crack set and the displacement u 0 can suffer jumps across K. Griffith’s theory of brittle fracture asserts that the energy necessary to produce a crack K is proportional to the crack length ℓ. For LEFM the total energy associated with bulk elastic and surface energy is given by
where μ is the shear modulus and \(\mathcal{G}_{c}\) is the critical energy release rate for the material. In what follows we chose initial conditions associated with bounded LEFM elastic energy.
In order to pass to the small horizon limit of peridynamics and to understand the elastic energy associated with this limit we cast the problem in a functional analytic context. The function space used in the mathematical formulation of free discontinuity problems including fracture is the space SBV developed in [3] see also, [1, 2]. Functions in this space belong to L 1(D) and are approximately continuous almost everywhere. Here we recall that points x of approximate continuity for the function u 0 satisfy
where B(x,r) is the ball of radius r centered at x. The discontinuity set \(S_{u_{0}}\) for elements of SBV are characterized by at most a countable number of smooth rectifiable curves across which u 0 has a jump discontinuity. Here the notion of arc length corresponds to the one dimensional Hausdorff measure of \(S_{u_{0}}\) and is denoted by \(\mathcal{H}^{1}(S_{u_{0}})\). We choose an orientation and define the unit normal ν to the jump set \(S_{u_{0}}\). For points x belonging to the jump set we denote the intersection of B(x,r) with the half spaces (y−x)⋅ν<0 and (y−x)⋅ν>0 by B −(x,r) and B +(x,r) respectively. The left and right limits of the function u 0 for a point on the jump set are denoted by \(u^{-}_{0}\), \(u^{+}_{0}\) and satisfy the identities
The approximate gradient denoted by ∇u 0 of an SBV function is defined almost everywhere on \(D\setminus S_{u_{0}}\) and satisfies
Distributional derivatives Du 0 of SBV functions are constructed from the approximate gradient and jump sets and satisfy
for every continuous test function \(\varPhi:D \rightarrow\mathbb{R}^{2}\) with support on D. Here \(d\mathcal{H}^{1}\) corresponds to an element of arc length for sufficiently regular curves. Functions in SBV have distributional derivatives with bounded total variation. Detailed descriptions of the properties of SBV functions are provided in [4] and [5].
Deformations of class SBV(D) are easily interpreted as deformations with cracks in D: the crack set K is identified with the jump set \(S_{u_{0}}\) and ∇u 0 represents the usual shear strain in the elastic part of the body outside the crack see, [1, 2]. With this in mind we take the initial displacement \(u_{0}\in L^{2}_{0}(D)\) and require that it belong to the space SBV(D). For this choice of initial data the bulk and surface energy of LEFM is given by
Definition 2.1
We refer to initial data \(u_{0}\in L^{2}_{0}(D)\), \(v_{0}\in L^{2}_{0}(D)\) with the restriction of u 0 on D belonging to SBV(D) that satisfy
as LEFM initial data.
We coordinate our choice of shear modulus μ and critical energy release rate \(\mathcal{G}_{c}\) with the peridynamic potential f and influence function J through the relations:
where f ∞ is defined by (1.2). The correspondence between the shear modulus and critical energy release rate and the peridynamic quantities f and J follows directly from the limit analysis, see Theorem 3.1, Sect. 4.3, and equation (4.49).
2.2 Peridynamic Evolutions and Energy Balance
We choose the initial data (u 0,v 0) to be LEFM initial data and the initial crack set at t=0 is prescribed by \(K=S_{u_{0}}\). There is a unique peridynamic evolution for this choice of initial data. This is stated in the following theorem.
Theorem 2.1
(Existence of unique solution for nonlinear peridynamics)
For LEFM initial data (u 0,v 0) and body force b(t,x) in C 1([0,T];L 2(D)) there exists a unique peridynamic evolution u ϵ(t,x) in \(C^{2}([0,T];L^{2}_{0} (D))\) taking the initial values u ϵ(0,x)=u 0(x), \(u_{t}^{\epsilon}(0,x)=v_{0}(x)\), and satisfying
This theorem follows from the Lipschitz continuity of ∇PD ϵ and is established in Sect. 4.1.
Multiplying both sides of (2.9) by \(u^{\epsilon}_{t}\) delivers the identity
and integration over time from 0 to t delivers the energy balance associated with the peridynamic evolution given by
Theorem 2.2
(Energy balance)
where
and
2.3 Instability and Fracture Initiation
In this section we present a fracture initiation condition that arises from the unstable peridynamic constitutive law relating antiplane shear strain to force. Fracture nucleation conditions have been identified for peridynamic evolutions in [34]. Here we investigate the nucleation criteria for the case at hand and provide an additional condition for the most unstable direction along which the crack can nucleate. We introduce a jump perturbation at x associated with a direction ν on the unit circle. Set \(E_{\nu}^{+}(x)=\{y:(y-x)\cdot\nu^{\perp}>0\}\) and \(E_{\nu}^{-}(x)=\{y:(y-x)\cdot\nu^{\perp}\leq0\}\) and introduce the local coordinate basis at x given by ν and ν ⊥. Consider a time independent body force density b and a smooth equilibrium solution u of (1.12). We now perturb u by adding a function δ ν with a jump discontinuity of height δ across the line \(\{y\in\mathcal{H}_{\epsilon}(x);(y-x)\cdot\nu^{\perp}=0\}\) that is piecewise constant in \(\mathcal{H}_{\epsilon}(x)\) and δ ν =δ for points in \(E_{\nu}^{+}\cap\mathcal{H}_{1}(0)\) and δ ν =0 for points in \(E_{\nu}^{-}\cap\mathcal{H}_{1}(0)\). Here the direction ν points along the direction of the discontinuity and ν ⊥ is the normal to the line of discontinuity. We write u p=u+δ ν and apply the ansatz
We regard δ as a small perturbation and expand the integrand of ∇PD ϵ(u p) in a Taylor series to recover the linearized evolution equation for the jump δ at x across the line with normal ν ⊥. The evolution equation is given by
where
here \(E_{\nu}^{+}(0)=\{\xi:\xi\cdot\nu^{\perp}>0\}\) and \(E_{\nu}^{-}(0)=\{\xi :\xi\cdot\nu^{\perp}\leq0\}\). Recalling that \(\eta=\mathcal{S}\epsilon|\xi|\) and calculation shows that
where \(f'(\epsilon|\xi|\mathcal{S}^{2})>0\), \(f''(\epsilon|\xi|\mathcal{S}^{2})<0\) and the critical value \(\overline{\eta}\) is the root of \(\partial_{\eta}^{2}W^{\epsilon}(\eta,\epsilon\xi)=0\) with
and
Here \(\overline{\eta}=\sqrt{\epsilon|\xi|}\overline{r}\) where \(\overline{r}\) is the inflection point for the function r:→f(r 2). For \(\mathcal{A}_{\nu}>0\) the jump can grow exponentially. It is evident that this can occur if there are critically strained bonds, \(|\mathcal{S}|>\overline{\eta}/(\epsilon|\xi|)\) or equivalently \(|\eta|>\overline{\eta}\), inside the neighborhood. We summarize these results in the following.
Proposition 2.1
(Facture nucleation condition)
Given a point x and a direction ν, a condition for crack nucleation at x along direction ν is \(\mathcal{A}_{\nu}>0\). The directions ν ∗ along which cracks grow are the most unstable ones which satisfy the condition
Proposition 2.1 together with (2.19) provides the explicit link between dynamic instability and the critical shear strain where the constitutive law begins to soften.
2.4 Concentration of Fracture Nucleation Sites in the Small Horizon Limit
Here we present results that show that peridynamic neighborhoods likley to nucleate jump sets become concentrated in the small horizon limit. The discussion focuses on the basic unit of peridynamic interaction: the peridynamic neighborhoods \(\mathcal{H}_{\epsilon}(x)\) of diameter ϵ>0 with centroids x∈D. Here we investigate the family of peridynamic evolutions u ϵ(t,x) at a fixed time t.
Consider a prototypical neighborhood \(\mathcal{H}_{\epsilon}(x)\). The collection of points y inside \(\mathcal{H}_{\epsilon}(x)\) for which the relative shear strain \(\mathcal{S}^{\epsilon}\) beyond critical, i.e., \(|\mathcal{S}^{\epsilon}|=|u^{\epsilon}(t,y)-u^{\epsilon}(t,x)|/(\epsilon|\xi |)>\overline{\eta}/(\epsilon|\xi|)\) is called the unstable subset of \(\mathcal{H}_{\epsilon}(x)\) and is written in terms of the relative displacement as
where \(\overline{\eta}=\sqrt{|y-x|}\overline{r}\), and \(\overline{r}\) is the inflection point for the map r:→f(r 2). The weighted area fraction of the neighborhood \(\mathcal{H}_{\epsilon}(x)\) occupied by the unstable subset is denoted by
Here P is defined in terms of the indicator function χ +,ϵ(x,y) for the unstable subset with, χ +,ϵ(x,y)=1 for y in the unstable subset and 0 otherwise, and
where the normalization constant \(m=\int_{\mathcal{H}_{1}(0)}|\xi|J(|\xi |)\,d\xi\) is chosen so that \(P(\mathcal{H}_{\epsilon}(x))=1\).
Definition 2.2
The neighborhood \(\mathcal{H}_{\epsilon}(x)\) is said to be unstable at time t if there is an exponent 0<α<1 for which
To proceed choose δ>0, 1>α>0, and consider a family of radii \(\epsilon_{j}=\frac{1}{2^{j}}\), j=1,… and the collection of neighborhoods \(\mathcal{H}_{\epsilon_{j}}(x)\) with centroids x in the reference domain D. The set of centroids associated with unstable neighborhoods for ϵ j <δ at time t is denoted by \(C^{\alpha}_{\delta,t}\). This set is expressed as
Here \(C^{\alpha}_{\delta,t}\subset C^{\alpha}_{\delta',t}\) for δ<δ′ and \(C^{0}_{\delta,t}\subset C^{\alpha}_{\delta,t}\subset C^{\alpha'}_{\delta,t}\) for 0<α<α′ where the set \(C^{0}_{\delta,t}\) is the collection of centroids for failed neighborhoods \(C^{0}_{\delta,t}=\cap_{{0<\alpha <1}}C^{\alpha}_{\delta,t}\) given by
Let \(C^{0}_{0,t}={\cap}_{{0<\delta}} C^{0}_{\delta,t}\) denote the concentration set for the set of centroids associated with unstable neighborhoods. In what follows the Lebesgue measure (area) of a set \(\varOmega\subset \mathbb{R}^{2}\) is denoted by \(\mathcal{L}^{2}(\varOmega)\) and we state a theorem on the localization of bond instability as the peridynamic horizon shrinks to zero.
Theorem 2.3
(Localization of bond instability in the small horizon limit)
The collection of centroids for unstable neighborhoods concentrate onto \(C^{0}_{0,t}\). The set of centroids \(C^{0}_{\delta,t}\) is decreasing with δ→0 and there is a positive constant C independent of t and δ for which
Moreover \(C^{\alpha}_{\delta,t}\) concentrate on the set \(C^{\alpha}_{0,t}\), where \(C^{\alpha}_{0,t}\) is a set of Lebesgue measure zero and
Theorem 2.3 is established in Sect. 4.5.4. This theorem shows that the nucleation sites concentrate on the centroids associated with the collection of failed neighborhoods \(C^{0}_{0,t}\) for which all bonds have become soft. For points x belonging to \(C^{0}_{0,t}\) the dynamics of the surrounding motion no longer influences the dynamics at x. Intuitively this set of points provides an alternative description of the crack set in the reference configuration as seen in the small horizon limit. The concentration of instability is inevitable for this model and is directly linked to the energy budget associated with the peridynamic motion. It is shown that for a family of peridynamic flows {u ϵ(t,x)} ϵ>0 all driven by the same initial conditions and body forces that the peridydnamic potential energy of each flow is bounded uniformly in time 0≤t≤T independently of the radius of the horizon, see Sect. 4.2. This bound forces the localization as shown in Sect. 4.5.4.
3 The Small Horizon, Sharp Interface Limit
In this section we identify the ϵ↘0 limit of the solutions u ϵ to the peridynamic initial value problem with LEFM initial data. A limit evolution u 0(t,x) is identified that:
-
Has uniformly bounded linear elastic bulk energy and Griffith surface energy for 0≤t≤T.
-
Satisfies an energy inequality involving the kinetic energy of the motion together with the bulk elastic and surface energy associated with linear elastic fracture mechanics for 0≤t≤T.
-
Satisfies the wave equation for points in spacetime not on the crack set.
3.1 Convergence of Peridynamics to Sharp Interface Dynamics Associated with Brittle Fracture
We consider the family of solutions \(u^{\epsilon_{k}}\) to the peridynamic initial value problem with LEFM initial data for a sequence ϵ k , k=1,2,… . We shall see that we can pass to the limit ϵ k ↘0 to identify a limit evolution u 0(t,x) for 0≤t≤T. The limit flow is found to have an approximate gradient ∇u 0(t,x) almost everywhere in D and the jump set \(S_{u^{0}(t)}\) is the countable union of rectifiable arcs. Moreover the limit evolutions u 0(t,x) have uniformly bounded energy in the sense of linear elastic fracture mechanics over 0≤t≤T. We begin by making the following hypothesis.
Hypothesis 3.1
We suppose that the magnitude of the deformations do not become infinite for 0≤t≤T, i.e.,
for 0≤t≤T. This hypothesis is consistent with the bounds on the kinetic energy for peridynamic evolution given in Theorem 4.1 of Sect. 4.2 and is also motivated by simulations carried out in the peridynamic literature see, for example [24, 31].
Theorem 3.1
(Limit evolution with bounded LEFM energy)
Suppose Hypothesis 3.1 holds true then there exists a subsequence of peridynamic evolutions \(u^{\epsilon_{k}}\) with LEFM initial data that converge as trajectories in \(C([0,T];L^{2}_{0}(D))\) to u 0(t,x) in \(C([0,T];L_{0}^{2}(D))\). The limit flow has an approximate gradient ∇u 0(t,x) almost everywhere in D and the jump set \(S_{u^{0}(t)}\) is the countable union of rectifiable arcs. Furthermore there exists a constant C depending only on T bounding the LEFM energy of the limit flow, i.e.,
for 0≤t≤T. The relations between the peridynamic potential f, influence function J, shear modulus μ, and critical energy release rate \(\mathcal {G}_{c}\) are given by (2.8).
Theorem 3.1 is established using Gronwall’s inequality see, Sect. 4.2 and the Γ-convergence associated with peridynamic energies see, Sect. 4.3. The proof of Theorem 3.1 is given in Sect. 4.3.
We now present an energy inequality for the limit evolution. We denote the LEFM energy for the limit evolution u 0(t) at time t as
and the LEFM energy for the initial data is written
The sum of energy and work for the deformation u 0 at time t is written
The sum of energy and work for the initial data u 0,v 0 is written
The energy inequality for the limit evolution u 0 is given in the following theorem.
Theorem 3.2
(Energy Inequality)
For 0≤t≤T,
The proof of Theorem 3.2 given in Sect. 4.4.
Motivated by the energy inequality Theorem 3.2 we conclude this section by showing that the length of the set cracked the by the limiting evolution over the time interval 0≤τ≤t is bounded. Recall the jump set for the deformation u 0 at time τ is \(S_{u^{0}(\tau)}\) and its length is given by its one dimensional Hausdorff measure \(\mathcal{H}^{1}(S_{{u^{0}(\tau)}})\). The bound follows from the following theorem.
Theorem 3.3
Hence
This shows that the total length of the set cracked by the evolution from t=0 to t=T is bounded. Theorem 3.3 is established in Sect. 4.5.
3.2 Wave Equation for the Displacement
It is shown that the limit evolution u 0 solves the wave equation. The following hypothesis on the regularity of the crack set is made.
Hypothesis 3.2
We suppose that the crack set given by \(S_{u^{0}(t)}\) is a closed set for 0≤t≤T.
The next hypotheses applies to the concentration set associated with unstable neighborhoods and its relation to the crack set for the limit flow.
Hypothesis 3.3
Theorem 2.3 shows that the centroids of failed neighborhoods for which all bonds have become soft, see (2.26), concentrate on the lower dimensional set \(C^{0}_{0,t}\). Recall that the dynamics associated with every point in the reference configuration belonging to the set \(C^{0}_{0,t}\) is not affected by the motion of its surroundings. Motivated by this observation we assume \(S_{u^{0}(t)}=C^{0}_{0,t}\) for 0≤t≤T.
The next hypotheses applies to neighborhoods \(\mathcal{H}_{\epsilon_{k}}(x)\) for which the shear strain is subcritical, i.e., \(|u^{\epsilon_{k}}(t,y)-u^{\epsilon_{k}}(t,x)|/|y-x|<\overline{\eta}/|y-x|\), for y in \(\mathcal{H}_{\epsilon_{k}}(x)\). These neighborhoods will be referred to as neutrally stable.
Hypothesis 3.4
We suppose that \(\epsilon_{k}=\frac{1}{2^{k}}<\delta\) and 0≤t≤T. Consider the collection of centroids \(C^{0}_{\delta,t}\). We fatten out \(C^{0}_{\delta,t}\) and consider \(\tilde{C}^{0}_{\delta,t}=\{x\in D: \operatorname{dist}(x,C^{0}_{\delta ,t})<\delta\}\). We suppose that all neighborhoods \(H_{\epsilon_{k}}(x)\) that do not intersect the set \(\tilde{C}^{0}_{\delta,t}\) are neutrally stable.
Passing to subsequences if necessary we apply Theorem 3.1 and take u 0 to be the limit evolution of the family of peridynamic evolutions \(\{u^{\epsilon_{k}}\}_{k=1}^{\infty}\) characterized by horizons of radii \(\epsilon_{k}=\frac{1}{2^{k}}\).
Theorem 3.4
(Wave equation)
Suppose Hypotheses 3.2, 3.3 and 3.4 hold true then the limit evolution u 0(t,x) is a solution of the wave equation
Here the second derivative \(u_{tt}^{0}\) is the time derivative in the sense of distributions of \(u^{0}_{t}\) and \(\operatorname{div}(\nabla u^{0})\) is the divergence of the approximate gradient ∇u 0 in the distributional sense.
The proof of Theorem 3.4 is given in Sect. 4.5.
Remark 3.1
The sharp interface limit of the peridynamic model is given by the displacement—crack set pair u 0(t,x), \(S_{u^{0}(t)}\). The wave equation provides the dynamic coupling between elastic waves and the evolving fracture path inside the media.
Remark 3.2
We point out that the peridynamic constitutive model addressed in this work does not have an irreversibility constraint and the constitutive law (1.3) applies at all times in the peridynamic evolution. Because of this the crack set at each time is given by \(S_{u^{0}(t)}\). Future work will investigate the effects of irreversibility (damage) in the peridynamic model.
Remark 3.3
We conjecture that Hypotheses 3.2, 3.3 and 3.4 hold true. It is also pointed out that these hypotheses are only used to establish Lemma 4.3 which identifies the directional derivative of u 0 at x along the direction e=ξ/|ξ| with the weak \(L^{2}(D\times\mathcal{H}_{1}(0))\) limit of the shear strain \(\mathcal{S}^{\epsilon_{k}}=\frac{\eta^{\epsilon_{k}}}{\epsilon_{k}|\xi |}\) restricted to pairs (x,ξ) for which the shear strain is subcritical, i.e., \(|\mathcal{S}^{\epsilon_{k}}|<\overline{\eta}/(\epsilon _{k}|\xi|)\).
4 Mathematical Underpinnings and Analysis
From the physical perspective the convex-concave nonlinearity of the peridynamic potential delivers the unstable constitutive law relating force to shear strain. On the other hand from the mathematical viewpoint this class of peridynamic potentials share the same convex-concave structure as the function r:→arctan(r 2) proposed by De Giorgi [21] and analyzed and generalized in the work of Gobbino [21, 22], and Gobbino and Mora [23] for the analysis of the Mumford Shah functional used in image processing [28]. Here we apply the methods developed in these investigations and use them as tools for extracting the limit behavior from the peridynamic model.
In this section we provide the proofs of the theorems stated in sections two and three. The first subsection asserts the Lipschitz continuity of \(\nabla\mathit{PD}^{\epsilon_{k}}(u)\) for u in \(L^{2}_{0}(D)\) and applies the standard theory of ODE to deduce existence of the peridynamic flow see, Sect. 4.1. A Gronwall inequality is used to bound the peridynamic elastic energy and kinetic energy uniformly in time see, Sect. 4.2. We introduce Γ-convergence for peridynamic functions in Sect. 4.3 and identify compactness conditions necessary to generate a sequence of peridynamic flows converging to a limit flow. We take limits and apply Γ-convergence theory to see that the limit flows have bounded elastic energy in the sense of fracture mechanics. In Sect. 4.4 we pass to the limit in the energy balance equation for peridynamic flows (2.11) to recover an energy inequality for the limit flow. The wave equation satisfied by the limit flow is obtained on identifying the weak L 2 limit of the sequence \(\{\nabla \mathit{PD}^{\epsilon_{k}}(u^{\epsilon_{k}})\}_{k=1}^{\infty}\) and passing to the limit in the weak formulation of (1.12) see, Sect. 4.5. We conclude with the proof of Theorem 2.3.
4.1 Existence of Peridynamic Evolution
The peridynamic equation (2.9) is written as an equivalent first order system. We set \(y^{\epsilon_{k}}=(y^{\epsilon _{k}}_{1},y^{\epsilon_{k}}_{2})^{T}\) where \(y^{\epsilon_{k}}_{1}=u^{\epsilon_{k}}\) and \(y_{2}^{\epsilon_{k}}=u_{t}^{\epsilon_{k}}\). Set \(F^{\epsilon_{k}}(y^{\epsilon _{k}},t)=(F^{\epsilon_{k}}_{1}(y^{\epsilon_{k}},t),F^{\epsilon_{k}}_{2}(y^{\epsilon _{k}},t))^{T}\) where
The initial value problem for \(y^{\epsilon_{k}}\) given by the first order system is
with initial conditions \(y^{\epsilon_{k}}(0)=(u_{0},v_{0})^{T}\) satisfying LEFM initial conditions. In what follows we consider the more general class of initial data (u 0,v 0) belonging to \(L^{2}_{0}(D)\times L^{2}_{0}(D)\). A straight forward calculation shows that for a generic positive constant C independent of η, ξ, and ϵ k , that
From this it easily follows from Hölder and Minkowski inequalities that \(\nabla\mathit{PD}^{\epsilon_{k}}\) is a Lipschitz continuous map from \(L^{2}_{0}(D)\) into \(L^{2}_{0}(D)\) and there is a positive constant C independent of 0≤t≤T, such that for any pair of vectors y=(y 1,y 2)T, z=(z 1,z 2)T in \(L^{2}_{0}(D)\times L^{2}_{0}(D)\)
Here for any element w=(w 1,w 2) of \(L^{2}_{0}(D)\times L^{2}_{0}(D)\) we have \(\Vert w \Vert_{L^{2}(D)^{2}}=\Vert w_{1}\Vert_{L^{2}(D)}+\Vert w_{2}\Vert_{L^{2}(D)}\). Since (4.3) holds the standard theory of ODE in Banach space [12] shows that there exists a unique solution to the initial value problem (4.1) with \(y^{\epsilon_{k}}\) and \(\partial_{t} y^{\epsilon_{k}}\) belonging to \(C([0,T]; L^{2}_{0}(D))\) and Theorem 2.1 is proved.
4.2 Bounds on Kinetic and Potential Energy for Solutions of PD
In this section we apply Gronwall’s inequality to obtain bounds on the kinetic and elastic energy for peridynamic flows. The bounds are used to show that the solutions of the PD initial value problem are Lipschitz continuous in time. The bounds are described in the following theorem.
Theorem 4.1
(Bounds on kinetic and potential energy for peridynamic evolution)
There exists a positive constant C depending only on T and independent of the index ϵ k for which
Proof
We apply (2.9) and write
Adding \(\mathit{PD}^{\epsilon_{k}}(u^{\epsilon_{k}})\) to the right hand side of (4.5) and applying Gronwall’s inequality gives
From (4.10) of Sect. 4.3 we have the upper bound
where LEFM(u 0,D) is the elastic potential energy for linear elastic fracture mechanics given by (3.4). Theorem 4.4 now follows from (4.6) and (4.7). □
Theorem 4.1 implies that PD solutions are Lipschitz continuous in time; this is stated explicitly in the following theorem.
Theorem 4.2
(Lipschitz continuity)
There exists a positive constant K independent of t 2<t 1 in [0,T] and index ϵ k such that
Proof
We write
where the last inequality follows from the upper bound for \(\Vert u_{t}^{\epsilon_{k}}(t)\Vert_{L^{2}(D)}\) given by Theorem 4.1. □
4.3 Compactness and Convergence
In this section we prove Theorem 3.1. We start by introducing the relationship between the elastic energies \(\mathit {PD}^{\epsilon_{k}}(u)\) and LEFM(u,D) given by (1.5) and (3.3) respectively. An application of Theorem 4.3 of [23] together with a straight forward computation using the formula for the peridynamic strain energy delivers the following inequality
We now recall the properties of Γ-convergence in order to apply them to the problem considered here. Consider a sequence of functions {F j } defined on a metric space \(\mathbb{M}\) with values in \(\overline{\mathbb{R}}\) together with a function F also defined on \(\mathbb{M}\) with values in \(\overline {\mathbb{R}}\).
Definition 4.1
We say that F is the Γ-limit of the sequence {F j } in \(\mathbb{M}\) if the following two properties hold:
-
1.
for every x in \(\mathbb{M}\) and every sequence {x j } converging to x, we have that
$$\begin{aligned} F(x)\leq\liminf_{j\rightarrow\infty} F_j(x_j), \end{aligned}$$(4.11) -
2.
for every x in \(\mathbb{M}\) there exists a recovery sequence {x j } converging to x, for which
$$\begin{aligned} F(x)=\lim_{j\rightarrow\infty} F_j(x_j). \end{aligned}$$(4.12)
We shall see that we can pass to the limit ϵ k ↘0 to find that the limit evolution u 0(t,x) belongs to the class of Generalized SBV functions denoted by GSBV(D). This class of functions has been introduced for the study of free discontinuity problems in [3] and are seen here to naturally arise in the small horizon limit of peridynamics. The space GSBV(D) is composed of all measurable functions u defined on D whose truncations u k =(u∧k)∨(−k) belong to SBV(B) for every compact subset B of D, see [4, 5]. Every u belonging to GSBV(D) has an approximate gradient ∇u(x) for almost every x in D and the jump set S u is the countable union of rectifiable arcs up to a set of Hausdorff \(\mathcal{H}^{1}\) measure zero.
For u in \(L^{2}_{0}(D)\) define \(\mathit{PD}^{0}:L^{2}_{0}(D)\rightarrow [0,+\infty]\) by
A straight forward application of Theorem 4.3(iii) of [23] to the sequence of peridynamic energies \(\{\mathit{PD}^{\epsilon_{k}}\}\) shows that
Now it is shown that the family of peridynamic flows \(\{u^{\epsilon_{k}}\} _{k=1}^{\infty}\) is relatively compact in C([0,T];L 2(D)) and that the limit flows have bounded elastic energy in the sense of fracture mechanics. For each t in [0,T] we apply Theorem 4.1 and Hypothesis 3.1 to obtain the bound
where C<∞ and is independent of ϵ k , k=1,2,… , and 0≤t≤T. With this bound we can apply Theorem 5.1 and Remark 5.2 of [23] to assert that for each t the sequence \(\{u^{\epsilon_{k}}(t)\}_{k=1}^{\infty}\) is relatively compact in L 2(D). From Theorem 4.2 the sequence \(\{u^{\epsilon_{k}}\}_{k=1}^{\infty}\), is seen to be uniformly equa-continuous in t with respect to the L 2(D) norm and we immediately conclude from the Ascoli theorem that \(\{u^{\epsilon_{k}}\}_{k=1}^{\infty}\) is relatively compact in C([0,T];L 2(D)). Therefore we can pass to a subsequence also denoted by \(\{u^{\epsilon_{k}}(t)\}_{k=1}^{\infty}\) to assert the existence of a limit evolution u 0(t) in C([0,T];L 2(D)) for which
Observe that since the sequence of peridynamic energies \(\{\mathit {PD}^{\epsilon_{k}}\}\) Γ-converge to PD 0 in L 2(D) we can apply the lower bound property (4.11) of Γ-convergence to conclude that the limit has bounded elastic energy in the sense of fracture mechanics, i.e.,
This concludes the proof of Theorem 3.1.
4.4 Energy Inequality for the Limit Flow
In this section we prove Theorem 3.2. We begin by showing that the limit evolution u 0(t,x) has a weak derivative \(u_{t}^{0}(t,x)\) belonging to L 2([0,T]×D). This is summarized in the following theorem.
Theorem 4.3
On passage to subsequences as necessary the sequence \(u_{t}^{\epsilon_{k}}\) weakly converges in L 2([0,T]×D) to \(u^{0}_{t}\) where
for all compactly supported smooth test functions ψ on [0,T]×D.
Proof
The bound on the kinetic energy given in Theorem 4.1 implies
Therefore the sequence \(u^{\epsilon_{k}}_{t}\) is bounded in L 2([0,T]×D) and passing to a subsequence if necessary we conclude that there is a limit function \(\tilde{u}^{0}\) for which \(u_{t}^{\epsilon_{k}}\rightharpoonup\tilde{u}^{0}\) weakly in L 2([0,T]×D). Observe also that the uniform convergence (4.17) implies that \(u^{\epsilon _{k}}\rightarrow u^{0}\) in L 2([0,T]×D). On writing the identity
applying our observations and passing to the limit it is seen that \(\tilde{u}^{0}=u_{t}^{0}\) and the theorem follows.
To establish Theorem 3.2 we require the following inequality.
Lemma 4.1
For every t in [0,T] we have
Proof
For every non-negative bounded measurable function of time ψ(t) defined on [0,T] we have the inequality
and together with the weak convergence given in Theorem 4.3 one easily sees that
Applying (4.20) and invoking the Lebesgue dominated convergence theorem we conclude
to recover the inequality given by
The lemma follows noting that (4.26) holds for every non-negative test function ψ. □
Theorem 3.2 now follows immediately on taking the ϵ k →0 limit in the peridynamic energy balance equation (2.11) of Theorem 2.2 and applying (4.15), (4.17), (4.18), and (4.22) of Lemma 4.1. □
4.5 Stationarity Conditions for the Limit Flow
In this section we prove Theorems 3.3 and 3.4. In the first subsection we give the proof of Theorem 3.3. In the second subsection we provide the proof of Theorem 3.4 using Theorem 4.4. In the last subsection we prove Theorem 4.4.
4.5.1 Proof of Theorem 3.3
We consider the integral
and apply the energy bound (4.4) to obtain the inequality
Since \(\mathit{PD}^{\epsilon_{k}}(u^{\epsilon_{k}}(t))\) and \(\Vert u_{t}^{\epsilon_{k}}(t)\Vert_{L^{2}(D)}^{2}\) are non-negative we apply Fatou’s Lemma to see that
Applying (4.18) and (4.22) delivers the upper bound
Here we have used the fact that \(\mathit{PD}^{\epsilon_{k}}(u^{0}(t))\) is continuous in t and the pointwise convergence \(\mathit{PD}^{\epsilon_{k}}(u^{0}(t))\rightarrow\mathit{LEFM}(u^{0}(t),D)\) to assert the integrability of LEFM(u 0(t),D) with respect to t. Theorem 3.3 now follows from (4.30).
4.5.2 Proof of Theorem 3.4
We introduce the following integration by parts identity that holds for any pair of functions u, v belonging to \(L_{0}^{2}(D)\) with either u or v having compact support inside D given by
Note further if v is infinitely differentiable and has compact support in D then
where the convergence is uniform in D. Here e is the unit vector e=ξ/|ξ|.
Taking the first variation of the action integral (1.8) gives the Euler equation in weak form
where the test function δ=δ(x,t)=ψ(t)ϕ(x) is smooth and has compact support in [0,T]×D. Integrating by parts in the second term of (4.33) using (4.31) gives
Where \(\eta^{\epsilon_{k}}=u^{\epsilon_{k}}(x+\xi)-u^{\epsilon_{k}}(x)\) and observe that \(\eta^{\epsilon_{k}}/(\epsilon_{k} |\xi|)=D_{e}^{{\epsilon_{k}}|\xi |} u^{\epsilon_{k}}\). Next we make the change of function and write \(F_{s} (r)=\frac{1}{s}f(sr^{2})\) and on setting s=ϵ k |ξ| and \(r=D_{e}^{{\epsilon_{k}}|\xi|} u^{\epsilon_{k}}\) we transform (4.34) into
where
For future reference observe that F s (r) is convex-concave in r with inflection point \(\overline{r}_{s}=\overline{r}/\sqrt{s}\) where \(\overline{r}\) is the inflection point of f(r 2)=F 1(r). One also has the estimates
We send ϵ k →0 in (4.35) applying the weak convergence Theorem 4.3 to the first term to obtain
Theorem 3.4 follows once we identify the limit of the second term in (4.39) for smooth test functions ϕ(x) with support contained in D. We state the following convergence theorem.
Theorem 4.4
Given any infinitely differentiable test function ϕ with compact support in D then
where \(\mu=\pi f'(0)\int_{0}^{1} r^{2}J(r)\,dr\).
Theorem 4.4 is proved in Sect. 4.5.3. The sequence of integrals on the left hand side of (4.40) are uniformly bounded in time, i.e.,
this is demonstrated in (4.55) of Lemma 4.4 in Sect. 4.5.3. Applying the Lebesgue bounded convergence theorem together with Theorem 4.4 with δ(t,x)=ψ(t)ϕ(x) delivers the desired result
and we recover the identity
from which Theorem 3.4 follows.
4.5.3 Proof of Theorem 4.4
We decompose the difference \(D_{e}^{\epsilon_{k} |\xi|}u^{\epsilon_{k}}\) as
where
where \(\overline{r}\) is the inflection point for the function F 1(r)=f(r 2). Here \(D_{e}^{\epsilon_{k} |\xi|,+}u^{\epsilon_{k}}\) is defined so that (4.44) holds. We prove Theorem 4.4 by using the following two identities described in the Lemmas below.
Lemma 4.2
For any ψ in \(C^{\infty}_{0}(D)\)
Lemma 4.3
Assume that Hypotheses 3.2, 3.3 and 3.4 hold true and define the weighted Lebesgue measure ν by ν(S)=∫ S |ξ|J(|ξ|) dξ dx for any Lebesgue measurable set \(S\subset D\times\mathcal {H}_{1}(0)\). Passing to subsequences as necessary \(\{D_{e}^{\epsilon_{k} |\xi |,-}u^{\epsilon_{k}}\}_{k=1}^{\infty}\) converges weakly in \(L^{2}(D\times \mathcal{H}_{1}(0);\nu)\) to e⋅∇u 0 where e=ξ/|ξ|, i.e.,
for any test function ϕ(x,ξ) in \(L^{2}(D\times\mathcal{H}_{1}(0);\nu)\).
We now apply the Lemmas. Observing that \(D_{e}^{\epsilon_{k} |\xi|}\psi\) converges strongly in \(L^{2}(D\times\mathcal{H}_{1}(0):\nu)\) to e⋅∇ψ for test functions ψ in \(C^{\infty}_{0}(D)\) and from the weak \(L^{2}(D\times\mathcal{H}_{1}(0):\nu)\) convergence of \(D_{e}^{\epsilon_{k} |\xi|,-}u^{\epsilon_{k}}\) we deduce that
A calculation shows that
where μ is given by (2.8). Theorem 4.4 now follows immediately from (4.48) and (4.46).
To establish Lemmas 4.2 and 4.3 we develop the following estimates for the sequences \(D_{e}^{\epsilon_{k} |\xi |,-}u^{\epsilon_{k}}\) and \(D_{e}^{\epsilon_{k} |\xi|,+}u^{\epsilon_{k}}\). We define the set \(K^{+,\epsilon_{k}}\) by
We have the following string of estimates.
Lemma 4.4
We introduce the generic positive constant 0<C<∞ independent of 0<ϵ k <1 and 0≤t≤T and state the following inequalities that hold for all 0<ϵ k <1 and 0≤t≤T and for C ∞(D) test functions ϕ with compact support on D.
Proof
For \((x,\xi)\in K^{+,\epsilon_{k}}\) we apply (4.37) to get
and in addition since |ξ|≤1 we have
where Theorem 4.1 implies that the right most element of the sequence of inequalities is bounded and (4.51) follows noting that the inequality (4.57) is equivalent to (4.51). More generally since |ξ|≤1 we may argue as above to conclude that
for 0≤p. We apply (4.38) and (4.58) to find
and (4.52) follows.
A basic calculation shows there exists a positive constant independent of r and s for which
so
and
where Theorem 4.1 implies that the right most element of the sequence of inequalities is bounded and (4.53) follows.
To establish (4.54) we apply Hölders inequality to find that
and (4.54) follows from (4.58) and (4.53), and (3.1).
We establish (4.55). This bound follows from the basic features of the potential function f. We will recall for subsequent use that f is smooth positive, concave and f′ is a decreasing function with respect to its argument. So for A fixed and \(0\leq h\leq A^{2}\overline{r}^{2}\) we have
The bound (4.55) is now shown to be a consequence of the following upper bound valid for the parameter 0<A<1 given by
We postpone the proof of (4.65) until after it is used to establish (4.55). Set \(h_{\epsilon_{k}}=D_{e}^{\epsilon_{k} |\xi|,-}u^{\epsilon_{k}}\) to note
Applying Hölders inequality, (4.52), (4.53), (4.66), and (4.65) gives
and (4.55) follows.
We establish the inequality (4.65). Set \(h_{\epsilon _{k}}=D_{e}^{\epsilon_{k} |\xi|,-}u^{\epsilon_{k}}\) and for 0<A<1 introduce the set
To summarize \((x,\xi)\in K^{+,\epsilon_{k}}_{A}\) implies \(A^{2}\overline {r}^{2}\leq\epsilon_{k}|\xi||h_{\epsilon_{k}}|^{2}\leq\overline{r}^{2}\) and \((x,\xi)\not\in K^{+,\epsilon_{k}}_{A}\) implies \(\epsilon_{k}|\xi||h_{\epsilon _{k}}|^{2}<A^{2}\overline{r}^{2}\) and \(|f'(\epsilon_{k}|\xi||h_{\epsilon _{k}}|^{2})-f'(0)|\leq|f'(A^{2}\overline{r}^{2})-f'(0)|\). Inequality (4.53) implies
the last inequality follows since 1≥|ξ|>0. Hence
and it follows that
Collecting observations gives
and (4.65) follows.
We now prove Lemma 4.2. Write
and from (4.52) it follows that
To finish the proof we identify the limit of the right hand side of (4.74). Set \(h_{\epsilon_{k}}=D_{e}^{\epsilon_{k} |\xi|,-}u^{\epsilon_{k}}\) and apply Hólder’s inequality to find
We estimate the first factor in (4.75) and apply (4.66), Hölder’s inequality, (4.53), and (4.65) to obtain
Lemma 4.2 follows on passing to the ϵ k zero limit in (4.76) and noting that the choice of 0<A<1 is arbitrary.
We now prove Lemma 4.3. For τ>0 sufficiently small define K τ⊂D by \(K^{\tau}=\{x\in D:\operatorname{dist}(x,S_{u^{0}(t)})<\tau\}\). From Hypothesis 3.3 the collection of centroids associated with unstable neighborhoods \(C^{0}_{\delta,t}\) lie inside K τ for δ sufficiently small. (Otherwise the collection \(C^{0}_{\delta,t}\) would concentrate about a component of \(C^{0}_{0,t}\) outside K τ; contradicting the hypothesis that \(S_{u^{0}(t)}=C^{0}_{0,t}\)). The collection of all points belonging to unstable neighborhoods associated with centroids in \(C^{0}_{\delta,t}\) is easily seen to be contained in the slightly larger set \(K^{\tau,\delta}=\{x\in D; \operatorname{dist}(x,K^{\tau})<\delta\}\). From Hypothesis 3.4 we may choose test functions \(\varphi\in C_{0}^{1}(D\setminus K^{\tau,2\delta})\) such that for ϵ k sufficiently small
We form the test functions ϕ(x,ξ)=φ(x)ψ(ξ), with \(\varphi\in C_{0}^{1}(D\setminus K^{\tau,2\delta})\) and \(\psi\in C(\mathcal{H}_{1}(0))\). From (4.53) we may pass to a subsequence to find that \(D_{e}^{\epsilon_{k} |\xi|,-}u^{\epsilon_{k}}\) weakly converges to the limit g(x,ξ) in \(L^{2}(D\times\mathcal{H}_{1}(0);\nu)\). With this in mind we write
Noting that \(D_{-e}^{\epsilon_{k} |\xi|}\varphi(x)\) converges uniformly to −e⋅∇φ(x) and from the strong convergence of \(u^{\epsilon_{k}}\) to u 0 in L 2 we obtain
where we have made use of Du 0⌊D∖K τ,2δ=∇u 0 dx on the third line of (4.79). From the density of the span of the test functions we conclude that g(x,ξ)=∇u 0⋅e almost everywhere on \(D\setminus K^{\tau,2\delta}\times\mathcal{H}_{1}(0)\). Since K τ,2δ can be chosen to have arbitrarily small measure with vanishing τ and δ we conclude that g(x,ξ)=∇u 0⋅e on \(D\times\mathcal{H}_{1}(0)\) a.e. and Lemma 4.3 is proved. □
4.5.4 Proof of Theorem 2.3
The set \(K^{+,\epsilon_{k}}\) defined by (4.50) has the equivalent description given by
where \(\overline{\eta}\) is the critical relative displacement given by \(\overline{\eta}=\sqrt{\epsilon_{k}|\xi|}\overline{r}\). We rewrite the lefthand side of the inequality (4.51) as
where for each x∈D, \(\chi^{+,\epsilon_{k}}(x,\xi)\) is defined to be the indicator function given by
Making the change of variable y=ϵ k ξ+x the inner integral on the right hand side of (4.81) is given by
Recall that (4.57) shows that the inequality (4.51) is uniform both in time and in the length scale of the horizon ϵ k . This follows from the uniform bound on the peridynamic potential given by Theorem 4.1. Application of (4.51) gives
For A>0, Tchebyshev’s inequality gives
Choosing \(A=\epsilon_{k}^{\alpha}\), and applying (4.84) delivers
Here C is a constant independent of t and ϵ k . The collection of centroids x for neighborhoods \(\mathcal{H}_{\epsilon _{k}}(x)\) associated with the instability condition given by
is denoted by \(U^{\alpha}_{\epsilon_{k},t}\). Choose \(\epsilon_{k}=\frac {1}{2^{k}}\) and (4.86) implies \(\mathcal{L}^{2}(U^{\alpha}_{\epsilon _{k},t})<C(\frac{1}{{2}^{k}})^{1-\alpha}\). The unstable set defined by (2.25) is written as
and from the geometric series we find
Theorem 2.3 follows noting further that \(C^{0}_{0,t}\subset C^{0}_{\delta,t}\subset C^{\alpha}_{\delta,t}\).
5 Summary
The nonlocal continuum model of peridynamic type presented here does not require extra constitutive laws such as a kinetic relation between crack driving force and crack velocity or a crack nucleation condition. Instead this information is intrinsic to the formulation and encoded into the nonlocal constitutive law. Crack nucleation criteria are recovered here by viewing nucleation as a dynamic instability, this is similar in spirit to [34] and the work of [15] for phase transions. The scaling analysis shows that the limit evolution has bounded linear elastic energy and bounded Griffith surface energy and that these are expressed in terms of shear moduli μ and energy release rate \(\mathcal{G}_{c}\). These parameters are determined explicitly by the peridynamic potential f and influence function J. The formulas for μ and \(\mathcal{G}_{c}\) follow directly from the scaling limit without extra hypotheses. With these observations in hand we can turn this correspondence around and use measured values of μ and \(\mathcal{G}_{c}\) to choose peridynamic potentials and influence functions appropriate for a particular material of interest. It is pointed out that the constitutive model (1.3) does not include the effects of damage and bonds strained beyond critical can return to their subcritical constitutive behavior. However with this caveat in mind the theoretical results presented here strongly support the notion that the peridynamic model can be used as a numerical tool for analyzing crack paths associated with brittle fracture by choosing the scaling parameter ϵ sufficiently small in (1.12) and running numerical simulations. In closing we note that future work will attempt to uncover kinetic relations relating crack driving force and velocity for the dynamics in the small horizon limit.
Notes
We denote A∖B=A∼B=A∩B c, where B c is the complement of B in A.
References
Ambrosio, L.: A compactness theorem for a special class of functions of bounded variation. Boll. Unione Mat. Ital. 3-B, 857–881 (1989)
Ambrosio, L., Brades, A.: Energies in SBV and variational models in fracture mechanics. In: Cioranescu, D., Damlamian, A., Donnato, P. (eds.) Homogenization and Applications to Materials Science 9, pp. 1–22. Gakuto/Gakkotosho, Tokyo (1997)
Ambrosio, L., De Giorgi, E.: Un nuovo tipo di funzionale del calcolo delle variazioni. Atti Accad. Naz. Lincei, Rend. Cl. Sci. Fis. Mat. Nat. 82, 199–210 (1989)
Ambrosio, L., Fusco, N., Pallara, D.: Functions of Bounded Variation and Free Discontinuity Problems. Oxford Mathematical Monographs. Clarendon, Oxford (2000)
Attouch, H., Buttazzo, G., Michaille, G.: Variational Analysis in Sobolev and BV Spaces: Applications to PDEs and Optimization. MPS-SIAM Series on Optimization. SIAM, Philadelphia (2006)
Bobaru, F., Hu, W.: The meaning, selection, and use of the peridynamic horizon and its relation to crack branching in brittle materials. Int. J. Fract. 176, 215–222 (2012)
Borden, M., Verhoosel, C., Scott, M., Hughes, T., Landis, C.: A phase-field description of dynamic brittle fracture. Comput. Methods Appl. Mech. Eng. 217–220, 77–95 (2012)
Bourdin, B., Francfort, G., Marigo, J.-J.: The variational approach to fracture. J. Elast. 91, 5–148 (2008)
Bourdin, B., Larsen, C., Richardson, C.: A time-discrete model for dynamic fracture based on crack regularization. Int. J. Fract. 168, 133–143 (2011)
Braides, A.: Discrete approximation of functionals with jumps and creases. In: Homogenization, Naples, 2001. Gakuto Internat. Ser. Math. Sci. Appl., vol. 18, pp. 147–153. Gakkotosho, Tokyo (2003)
Dal Maso, G., Larsen, C.J.: Existence for wave equations on domains with arbitrary growing cracks. Atti Accad. Naz. Lincei, Rend. Lincei, Mat. Appl. 22, 387–408 (2011)
Driver, B.: Analysis Tools with Applications E-Book. Springer, Berlin (2003)
Du, Q., Gunzburger, M., Lehoucq, R., Zhou, K.: A nonlocal vector calculus, nonlocal volume-constrained problems, and nonlocal balance laws. Math. Models Methods Appl. Sci. 23, 493–540 (2013)
Du, Q., Gunzburger, M., Lehoucq, R., Zhou, K.: J. Elast. 113(2), 193–217 (2013)
Dyal, K., Bhattacharya, K.: Kinetics of phase transformations in the peridynamic formulation of continuum mechanics. J. Mech. Phys. Solids 54, 1811–1842 (2006)
Emmrich, E., Weckner, O.: On the well-posedness of the linear peridynamic model and its convergence towards the Navier equation of linear elasticity. Commun. Math. Sci. 5, 851–864 (2007)
Evans, L.C.: Partial Differential Equations. Graduate Studies in Mathematics, vol. 19. Am. Math. Soc., Providence (2010)
Francfort, G., Marigo, J.-J.: Revisiting brittle fracture as an energy minimization problem. J. Mech. Phys. Solids 46, 1319–1342 (1998)
Freund, L.B.: Dynamic Fracture Mechanics. Cambridge Monographs on Mechanics and Applied Mathematics. Cambridge University Press, Cambridge (1998)
Gerstle, W., Sau, N., Silling, S.: Peridynamic modeling of concrete structures. Nucl. Eng. Des. 237, 1250–1258 (2007)
Gobbino, M.: Finite difference approximation of the Mumford–Shah functional. Commun. Pure Appl. Math. 51, 197–228 (1998)
Gobbino, M.: Gradient flow for the one-dimensional Mumford–Shah functional. Ann. Sc. Norm. Super. Pisa, Cl. Sci. XXVII(4), 145–193 (1998)
Gobbino, M., Mora, M.G.: Finite difference approximation of free discontinuity problems. Proc. R. Soc. Edinb. A 131, 567–595 (2001)
Hu, W., Ha, Y.D., Bobaru, F.: Modeling dynamic fracture and damage in a fiber-reinforced composite lamina with peridynamics. Int. J. Multiscale Comput. Eng. 9, 707–726 (2011)
Larsen, C.J.: Models for dynamic fracture based on Griffith’s criterion. In: Hackl, K. (ed.) IUTAM Sympo-sium on Variational Concepts with Applications to the Mechanics of Materials, pp. 131–140. Springer, Berlin (2010)
Larsen, C., Ortner, C., Suli, E.: Existence of solutions to a regularized model of dynamic fracture. Math. Models Methods Appl. Sci. 20, 1021–1048 (2010)
Mengesha, T., Du, Q.: Nonlocal constrained value problems for a linear peridynamic Navier equation. J. Elast. (2013). doi:10.1007/s10659-013-9456-z
Mumford, D., Shah, J.: Optimal approximation by piecewise smooth functions and associated variational problems. Commun. Pure Appl. Math. 17, 577–685 (1989)
Schmidt, B., Fraternali, F., Ortiz, M.: Eigenfracture: an eigendeformation approach to variational fracture. Multiscale Model. Simul. 7, 1237–1266 (2009)
Silling, S.A.: Reformulation of elasticity theory for discontinuities and long-range forces. J. Mech. Phys. Solids 48, 175–209 (2000)
Silling, S.A., Askari, E.: A meshfree method based on the peridynamic model of solid mechanics. Comput. Struct. 83, 1526–1535 (2005)
Silling, S.A., Bobaru, F.: Peridynamic modeling of membranes and fibers. Int. J. Non-Linear Mech. 40, 395–409 (2005)
Silling, S., Lehoucq, R.: Convergence of peridynamics to classical elasticity theory. J. Elast. 93, 13–37 (2008)
Silling, S., Weckner, O., Askari, E., Bobaru, F.: Crack nucleation in a peridynamic solid. Int. J. Fract. 162, 219–227 (2010)
Weckner, O., Abeyaratne, R.: The effect of long-range forces on the dynamics of a bar. J. Mech. Phys. Solids 53, 705–728 (2005)
Acknowledgements
The author would like to thank Stewart Silling, Richard Lehoucq and Florin Bobaru for stimulating and fruitful discussions. This research is supported by NSF grant DMS-1211066, AFOSR grant FA9550-05-0008, and NSF EPSCOR Cooperative Agreement No. EPS-1003897 with additional support from the Louisiana Board of Regents.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Lipton, R. Dynamic Brittle Fracture as a Small Horizon Limit of Peridynamics. J Elast 117, 21–50 (2014). https://doi.org/10.1007/s10659-013-9463-0
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10659-013-9463-0