From Gradient Damage Laws to Griffith’s Theory of Crack Propagation

Abstract

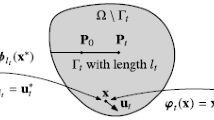
This paper is devoted to the comparison of the evolution of damage governed by a gradient damage model with the evolution of a crack predicted by Griffith’s law. The analysis is made in a two-dimensional setting, assuming that damage is concentrated inside thin bands whose width is proportional to the internal length of the material. Taking advantage of the variational formulation based on the three principles of irreversibility, stability and energy balance, one introduces a generalized Rice path integral which contains terms involving the gradient of damage. Assuming that the internal length of the material is small by comparison with the dimension of the body, a separation of scales is achieved. Owing to the energy balance and the stability condition, one first proves some properties of this path integral with respect to the path. Then, one shows that the evolution of the damage zone is governed by Griffith’s law, the dissipated surface energy being given by the energy dissipated in the damage process zone.

Appendix: Sketch of the Proof of Property (24)

The proof of property (24) for the general class of strongly brittle materials is not available at the present time. Indeed it needs a complete analysis of the singularities at the tip of the crack. Such an analysis requires additional hypotheses on the state function W. Consequently, we merely give the proof in the particular case of the damage model (14) given in Example 1. The analysis of the singularities is made near the tip of the crack and hence we use a polar system of coordinates (r,θ) with pole the tip of the crack, θ=0 corresponding to the axis tangent to the crack. Accordingly the lips of the crack correspond to θ=±π. Since the time is fixed, the index t is removed from all fields.

Let us denote v=1−α, we only consider singular parts of the displacement and damage fields of the following form:

$$v(r, \theta)=r^{p}V(\theta)+\cdots,\qquad\mathbf{u}(r, \theta )=r^{q} \bigl( U_r(\theta)e_{r}+U_{\theta}( \theta)e_{\theta} \bigr)+\cdots, $$

where p and q will be called the order of the singularity. In order that the total energy be finite the orders p and q must be such that p>0 and p+q>0. The damage criterion (17)₁ reads

$$ v^{-3}\mathsf {S}_0\boldsymbol{\sigma}\cdot\boldsymbol{\sigma}-\mathsf {w}_1-\mathsf {w}_1\eta^2\Delta v\le0. $$

(45)

Since the first term of (45), v ⁻³ S ₀ σ⋅σ, is non negative, it cannot be more singular than the two other terms of (45) whose orders are respectively 0 and at least p−2. We can merely consider the case p≤2 because otherwise the proof is trivial. Therefore, the order of v ⁻³ S ₀ σ⋅σ must be greater or equal to p−2. This condition is automatically satisfied when the singular displacement field corresponds to a rigid displacement and in such a case q∈{0,1}. Otherwise v ⁻³ S ₀ σ⋅σ is of order p+2q−2. Hence, in any case q must be non negative.

From the two inequalities p>0 and q≥0, it is easy to check that lim _r→0 I _r =0. Moreover the only terms in J _r which can give a non null contribution are the gradient damage terms. Since ∇α⋅∇α and q _r α _,1 are both of order 2p−2, J ₀=0 if p>1/2. Therefore, it remains to consider the cases when p≤1/2.

Let us prove that even if q=0, the order of ${\frac {1}{2}}v^{-3}\mathsf {S}_{0}\boldsymbol{\sigma}\cdot\boldsymbol{\sigma}$ is greater than p−2. It is true when q>0. If q=0, then the order of the strains is at least −1, the order of ε _rr is greater than −1 and the order of the stresses is at least 2p−1. Since the stress field σ must satisfy the equilibrium equations, assuming that the body forces are not singular, the singular part of $\operatorname{div}\boldsymbol{\sigma}$ must vanish. This is equivalent to introduce an Airy function of order 2p+1, say ϕ(r,θ)=r ^2p+1 F(θ), and to set

$$ \sigma_{rr}=\frac{1}{r^2}\frac {\partial^2\phi}{\partial\theta^2}+ \frac {1}{r}\frac{\partial\phi}{\partial r}+\cdots,\qquad\sigma_{r\theta }=- \frac{\partial}{\partial r} \biggl(\frac {1}{r}\frac{\partial\phi}{\partial\theta} \biggr)+\cdots,\qquad \sigma_{\theta\theta}=\frac{\partial^2\phi}{\partial r^2}+\cdots. $$

(46)

From the stress-strain relation v ² E ₀ ε _rr =(1−ν ²)σ _rr −ν(1+ν)σ _θθ , where E ₀ is the Young modulus of the sound material and ν the (invariable) Poisson ratio, one deduces that F(θ) must satisfy

$$0=(1-\nu)F''(\theta) +(1-\nu(2p+1))(2p+1)F(\theta). $$

Since the lips of the crack are stress free, F must satisfy the boundary conditions F(±π)=F′(±π)=0. Therefore, the unique solution is F=0, the order of the stresses is greater than 2p−1 and hence the order of ${\frac{1}{2}}v^{-3}\mathsf{S}_{0}\boldsymbol {\sigma}\cdot\boldsymbol{\sigma}$ is greater than p−2.

Writing (45) at the order p−2, one deduces that V must be a non null function which satisfies

$$V''+p^2V\ge0\quad\mbox{and}\quad V\ge0\quad\mbox{in}\ (-\pi,\pi ),\qquad V(\pm\pi)=0. $$

Let us prove that p≥1/2. Multiplying the inequality V″+p ² V≥0 by V, integrating over (−π,π), integrating by parts the first term and taking into account the boundary conditions lead to

$$ p^2\ge\frac{\int_{-\pi}^\pi V'(\theta)^2\mathrm{d}\theta}{\int_{-\pi }^\pi V(\theta)^2\mathrm{d}\theta}\ge\min_{{\varphi\ge0\atop\varphi (\pm\pi)=0}}\frac{\int_{-\pi}^\pi\varphi'(\theta)^2\mathrm{d}\theta}{\int _{-\pi}^\pi \varphi(\theta)^2\mathrm{d}\theta}=\frac{1}{4}, $$

(47)

where the last equality is a classical result the proof of which is left to the reader. Moreover, all inequalities become equalities in (47) if and only if p=1/2 and V(θ)=Kcos(θ/2) with K>0. This matches the classical singularity of the laplacian with Dirichlet boundary conditions on the lips of the crack. In such a case, a straightforward calculation gives

$$\mathsf{J}_0=-\frac{\pi}{4} \mathsf{w}_1\eta^2K^2<0, $$

which completes the proof.

Remark 3

Note that the stresses remain bounded since p≥1/2. Moreover, by virtue of Proposition 2, $\mathsf{J}_{0}\dot{\ell}=0$. That means that the gradient of damage can be singular only when the crack does not propagate. Its singular part is then given by

$$\nabla\alpha= \frac{K}{2\sqrt{r}} \biggl(-\cos\frac{\theta }{2} \mathbf{e}_r+\sin \frac{\theta}{2}\mathbf{e}_\theta \biggr)+ \mbox{regular terms},\quad K\ge0. $$

But K must vanish and hence the singularity disappears when the crack propagates.