Abstract
A mathematical framework for the fundamental objects of continuum mechanics is presented. In the geometric setting of general differentiable manifolds, velocity fields over bodies, modeled as sections of a vector bundle W, are generalized using notions of homological integration theory such as flat chains and cochains. The class of bodies includes fractal sets whose irregular boundaries may have infinite measures. Stresses, initially modeled as smooth differential forms valued in the dual of the jet bundle of W, are generalized to cochains represented by L ∞-sections whose weak divergences are also L ∞. The divergence of a stress field, defined in an earlier work, is generalized to apply to stress cochains. The co-divergence of a velocity field is a weak form of the jet extension mapping and it is the counterpart of the boundary operator for real valued flat chains.
Similar content being viewed by others
References
Barnsley, M.: Fractals Everywhere. Academic Press, New York (1988)
Capriz, G.: Continua with Microstructure. Springer, Berlin (1989)
Capriz, G., Mariano, P.: Symmetries and Hamiltonian formalism for complex materials. J. Elast. 72, 57–70 (2003)
de Rham, G.: Differentiable Manifolds. Springer, Berlin (1984)
Degiovanni, M., Marzocchi, A., Musesti, A.: Cauchy fluxes associated with tensor fields having divergence measure. Arch. Ration. Mech. Anal. 147, 197–223 (1999)
Federer, H.: Geometric Measure Theory. Springer, Berlin (1969)
Federer, H., Fleming, W.: Normal and integral currents. Ann. Math. 72(3), 458–520 (1960)
Giaquinta, M., Modica, G., Soucek, J.: Cartesian Currents in the Calculus of Variations I. Springer, Berlin (1998)
Gol’dshtein, V., Kuz’minow, V., Shvedov, I.: Integration of differential forms of the classes
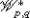 . Sib. Mat. Zh. 23, 63–79 (1982). English translation published by Plenum
. Sib. Mat. Zh. 23, 63–79 (1982). English translation published by Plenum
Gol’dshtein, V., Kuz’minow, V., Shvedov, I.: Differential forms on Lipschitz manifolds. Sib. Mat. Zh. 23, 16–30 (1982). English translation published by Plenum
Gol’dshtein, V., Kuz’minow, V., Shvedov, I.: Wolfe’s theorem for differential forms of classes
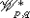 . Sib. Mat. Zh. 24, 31–42 (1983). English translation published by Plenum
. Sib. Mat. Zh. 24, 31–42 (1983). English translation published by Plenum
Mariano, P.: Multifield theories in mechanics of solids. Adv. Appl. Mech. 38, 1–93 (2002)
Mariano, P.: Cracks in complex bodies: covariance of tip balances. J. Nonlinear Sci. 18, 99–141 (2008)
Mariano, P., Modica, G.: Ground states in complex bodies. ESAIM Control Optim. Calc. Var. 15, 377–402 (2009)
Mermin, N.: The topological theory of defects in ordered media. Rev. Mod. Phys. 51, 591–646 (1979)
Noll, W.: The foundation of classical mechanics in light of recent advances in continuum mechanics. In: The Axiomatic Method, with Special Reference to Geometry and Physics. North-Holland, Amsterdam (1959)
Palais, R.S.: Foundations of Global Non-Linear Analysis. Benjamin, Elmsford (1968)
Rodnay, G.: Cauchy’s flux theorem in light of Whitney’s geometric integration theory. Ph.D. thesis, Ben-Gurion University of the Negev (2002)
Rodnay, G., Segev, R.: Cauchy’s flux theorem in light of geometric integration theory. J. Elast. 71, 183–203 (2003)
Segev, R.: Forces and the existence of stresses in invariant continuum mechanics. J. Math. Phys. 27, 163–170 (1986)
Segev, R.: The geometry of Cauchy’s fluxes. Arch. Ration. Mech. Anal. 154, 183–198 (2000)
Segev, R.: Metric-independent analysis of the stress-energy tensor. J. Math. Phys. 43, 3220–3231 (2002)
Segev, R., Rodnay, G.: Cauchy’s theorem on manifolds. J. Elast. 56(2), 129–144 (1999)
Silhavy, M.: Cauchy’s stress theorem for stresses represented by measures. Contin. Mech. Thermodyn. 20, 75–96 (2008)
Silhavy, M.: The divergence theorem for divergence measure vectorfields on sets with fractal boundaries. Math. Mech. Solids 14, 445–455 (2009)
Whitney, H.: Geometric Integration Theory. Princeton University Press, Princeton (1957)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Segev, R., Falach, L. Velocities, Stresses and Vector Bundle Valued Chains. J Elast 105, 187–206 (2011). https://doi.org/10.1007/s10659-011-9316-7
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10659-011-9316-7
Keywords
- Continuum mechanics
- Velocity
- Stress
- Vector valued
- Vector bundle
- Flat chains
- Geometric integration theory
- Geometric measure theory
- de Rham currents
- Divergence
- Boundary operator


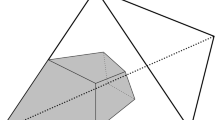

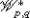 . Sib. Mat. Zh. 23, 63–79 (1982). English translation published by Plenum
. Sib. Mat. Zh. 23, 63–79 (1982). English translation published by Plenum
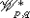 . Sib. Mat. Zh. 24, 31–42 (1983). English translation published by Plenum
. Sib. Mat. Zh. 24, 31–42 (1983). English translation published by Plenum