Summary of relationships between exchangeability, biasing paths and bias

Abstract

Definitions and conceptualizations of confounding and selection bias have evolved over the past several decades. An important advance occurred with development of the concept of exchangeability. For example, if exchangeability holds, risks of disease in an unexposed group can be compared with risks in an exposed group to estimate causal effects. Another advance occurred with the use of causal graphs to summarize causal relationships and facilitate identification of causal patterns that likely indicate bias, including confounding and selection bias. While closely related, exchangeability is defined in the counterfactual-model framework and confounding paths in the causal-graph framework. Moreover, the precise relationships between these concepts have not been fully described. Here, we summarize definitions and current views of these concepts. We show how bias, exchangeability and biasing paths interrelate and provide justification for key results. For example, we show that absence of a biasing path implies exchangeability but that the reverse implication need not hold without an additional assumption, such as faithfulness. The close links shown are expected. However confounding, selection bias and exchangeability are basic concepts, so comprehensive summarization and definitive demonstration of links between them is important. Thus, this work facilitates and adds to our understanding of these important biases.

Appendix 1

In the Appendix 1, we define additional terms, state assumptions and provide proofs of Claims 1B, 2A, 3, and 4. Throughout, we assume that the causal model is Markovian [13], defined below.

Causal models

Following Pearl [13, p. 27], a functional causal model, or just causal model, is a set of structural equations that determines the potential outcome x _i of X _i for each dependent variable by:

$${\text{X}}_{i} (pa_{i} ,u) = \, f_{i} (pa_{i} ,u),\quad {\text{ for}}\,i = 1, \ldots ,{\text{n}},$$

(4)

where: i indicates the variable, f _i (.) is a function; pa _i is a value of the variables PA _i which are the parents of X _i (i.e., the immediate causes of X _i ); and, u is a value of the error term U_i and n is the number of variables. The errors, sometimes called disturbances, are often unobserved and could be viewed as representing omitted factors. In Eq. (3) of the main text, X_i could represent D, and then PA_D consists of E and C, and U_i is U₁.

The Eq. (4) give the effect on each X _i that would result from changing PA _i or U _i from one value to another. They are assumed to represent autonomous, causal mechanisms or effects. When the form of the f _i (.) is unspecified they define a non-parametric structural-equations model (NPSEM), which generalizes the linear structural-equations models with Gaussian errors often found in the econometric and social literature [13]. The set of structural equations provide formulas for determining potential outcomes that would occur for actions of setting specific combinations of the relevant parents [13].

Without some restriction, D _i (e) could depend on the exposure of other individuals as might, for example, be true of communicable diseases. Rubin describes independence (no interference), wherein exposure of one individual doesn’t affect outcomes of others. Here, to avoid this interference, we make a “stable unit treatment value assumption”: D _i (e) $\mathop \coprod \nolimits$ E _i* for i and i* ≠ i.

Markovian causal model

If we draw an arrow from the direct causes of each variable X _i (from each member of PA _i ) to X _i in a causal model, we obtain a causal diagram for the model. Here, each node or letter in a DAG represents a variable (X_i) and each arrow represents a causal effect with the arrowhead pointing to the effect. We call each variable (X _i ) a node and each arrow an effect. If the causal diagram contains no cycles and the errors of each variable are jointly independent, we call the causal model Markovian [13, p. 30]. Each Markovian causal model induces a compatible probability distribution [13] which we use here. With the appropriate distribution for U_i, we could write P(X _i  = x _i |PA _i  = pa _i ) = P(U _i  = u, u $\in$ {u: f _i (pa _i , u) = x _i }). This model is a nonparametric structural model with independent errors (NPSEM-IE). It differs from the “finest fully randomized causally interpretable tree graph” (FFRCITG) of Richardson and Robins [24] because the errors are assumed independent. The NPSEM-IE is a special case of the FFRCTIG.

Further note on DAGs

Other models, both causal and non-causal, can be represented by DAGs. Here, we use only the causal interpretation and independent errors (represent by a U) for DAGs so that they represent Markovian causal models. With this link and restrictions, we can use either the non-parametric structural equations (Appendix Eq. 4) or the graphical representation of a Markovian causal model. In a Markovian causal model, a compatible induced probability distribution always exists and can be factored as: P(X₁ = x ₁,…, X _n  = x _n ) = $\prod\nolimits_{i} {{\text{P}}({\text{X}}_{i} = x_{i} |PA_{i} = pa_{i} )}$ [13, p. 30].

Confounding

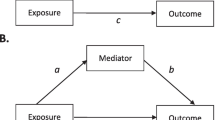
As noted in the main text, many definitions of confounding (and other concepts) are available. Our main focus concerns the relationships between exchangeability, bias and biasing paths but for completeness, we provided one precise definition of confounding [11]. Although highly overlapping, the presence of confounding under this definition does not always coincide with presence of a confounded exposure-disease association. For example, suppose that E precedes D and consider the three DAGs in Fig. 4. The upper DAG shows no confounding (under our definition [11] )—since E and D would be unassociated if all effects of E were removed, but the association is confounded since there is a confounding path (conditioning on the collider C₁, indicated by the box, opens the path). The middle DAG shows confounding—since E and D would be associated if all effects of E were removed, but the association is not confounded since there is no confounding path (the biasing path does not end with an arrow into D). This middle DAG nevertheless illustrates a biasing path [1]; since it involves conditioning on a common effect of exposure and disease, referred to as structural selection bias.

Other definitions of confounding and of other biases, while similar to those used here, are available and can differ. We adopted one set of definitions from the literature so we could illustrate and summarize the inter-relationships between some of the different conceptualizations. Use of a single set of definitions allowed us to focus on the inter-relationships between conceptualizations in different frameworks; we avoid some of discussion about strengths, weakness and preferability of one option over another. Nevertheless, it might be useful for the wider epidemiologic community to move towards adoption of a single set of definitions.

Structural selection bias is defined as bias that results from conditioning on a variable caused by two other variables; one is exposure or a cause thereof, and the other is disease or a cause thereof [17]. As such it’s a type of collider bias. In the DAG framework, this situation would be represented by a biasing path. However, the definition of confounding path used here [1] includes some situations that represent both a confounding path and structural selection bias (e.g., the uppermost DAG of Fig. 4). Hence, here we primarily refer to “biasing paths.” There are a few biasing paths, perhaps unusual, that do not meet this definition of structural selection bias (but more inclusive definitions are available, see Appendix of Ref. [17] ) or a confounding path (lowest DAG of Fig. 4).

We now sketch proofs of Claims 1B, 2B, 3, 4A and 4B.

Proof of Claim 1B

(Exchangeability and faithfulness imply absence of a biasing path). We prove a contrapositive: a biasing path and faithfulness imply non-exchangeability. Presence of a biasing path implies the DAG includes an open, undirected path. An example is illustrated in Fig. 5, where n and m are the number of additional variables intermediate between E and C, and between C and D, respectively, along the path. Additional variables not on the path can also be present. Each factor in the path is determined by its parents along the path plus other parents not in the path, according to the structural equations:

Fig. 5

Causal graph, illustrating a biasing path with m descendants of C that are ancestors of exposure E, and n descendants of C that are ancestors of outcome D (see Appendix 1)

$$\begin{aligned} {\text{E}}\left( {{\text{y}}_m ,{\text{pa}}_{\text{E}} ,{\text{u}}_{\text{E}} } \right) & = {\text{f}}_{\text{E}} \left( {{\text{y}}_m ,{\text{pa}}_{\text{E}} ,{\text{u}}_{\text{E}} } \right); \\ {\text{Y}}_{i} \left( {{\text{y}}_{i - 1} ,{\text{pa}}_{\text{Yi}} ,{\text{u}}_{\text{Yi}} } \right) & = {\text{f}}_{\text{Yi}} \left( {{\text{y}}_{i - 1} ,{\text{pa}}_{\text{Yi}} ,{\text{u}}_{\text{Yi}} } \right)\quad {\text{for}}\,i = 2, \ldots ,m;\quad {\text{Y}}_{1} \left( {{\text{c}},{\text{pa}}_{{{\text{Y}}1}} ,{\text {u}}_{\text {Y1}} } \right) = {\text{f}}_{\text{Y1}} \left( {{\text{c}},{\text{pa}}_{\text{Y1}} ,{\text{u}}_{\text{Y1}} } \right) \\ {\text{C}}\left( {{\text{pa}}_{\text{C}} ,{\text{u}}_{\text{C}} } \right) & = {\text{f}}_{\text{C}} \left( {{\text{pa}}_{\text{C}} ,{\text{u}}_{\text{C}} } \right) \\ {\text{Z}}_{1} \left( {{\text{c}},{\text{pa}}_{\text{Z1}} ,{\text{u}}_{\text{Z1}} } \right) & = {\text{f}}_{\text{Z1}} \left( {{\text{c}},{\text{pa}}_{\text{Z1}} ,{\text{u}}_{\text{Z1}} } \right);\quad {\text{Z}}_{i} \left( {{\text{z}}_{i - 1} ,{\text{pa}}_{\text{Zi}} ,{\text{u}}_{\text{Zi}} } \right) = {\text{f}}_{\text{Zi}} \left( {{\text{z}}_{i - 1} ,{\text{pa}}_{\text{Zi}} ,{\text{u}}_{\text{Zi}} } \right)\quad {\text{for}}\,i = 2, \ldots ,n \\ {\text{D}}\left( {{\text{z}}_{n} ,{\text{ pa}}_{\text{D}} ,{\text{u}}_{\text{D}} } \right) & = {\text{f}}_{\text{D}} \left( {{\text{z}}_{n} ,{\text{pa}}_{\text{D}} ,{\text{u}}_{\text{D}} } \right), \\ \end{aligned}$$

In the expression E(y _m , pa_E, u_E) = f_E(y _m , pa_E, u_E) is the potential value of E if Y _m , were set to y _m , PA_E, to pa_E and the independent, random error term U_E to u _E, with analogous statements for the other expressions; where PA_X are the parents of X excluding U_X and the factors explicitly included on the path shown. The path depicted is a special type of biasing path—a backdoor path, without any conditioning on colliders in the path and with an arrow into E; However, the n + m + 3 equations above can be modified to reflect other biasing paths; for each type we still have n + m + 3 equations for variables on the paths. [For example, the path in Fig. 6, is a biasing path with one, controlled collider (Y₁). We would need to modify 2 equations, setting E(pa_E, u_E) = f_E(pa_E, u_E) and Y _m (e, pa_Yi, u_Yi) = f_Yi(e, pa_Yi, u_Yi) to reflect this modification.]

Fig. 6

Causal graph, illustrating a biasing path with m − 1 descendants of C that are parents of a descendant (Y _m ) of exposure E, conditioning on collider (Y _m ) which opens the path between C and E, and n descendants of C that are ancestors of outcome D (see Appendix 1). A box indicates control for the variable

We show that one can always choose parameters so that P(D(e)|E = 1) ≠ P(D(e)|E = 0), for e = 0, 1. The functions are unspecified, so we can define and parameterize each function (e.g., f_D) so that it depends on the unmeasured terms (e.g., U_D) and on the immediate parent on the path (e.g., Z_n), but negligibly on other variables (e.g., PA_D). We first consider the simplest case (Fig. 1a), where C affects both E and D directly, and Y_i and Z_i aren’t present. We can define:

$$\begin{array}{*{20}l} {{\text{f}}_{\text{E}}({\text{c}},{\text{u}}_{\text{E}} )} \hfill & { = 1\quad{\text{if}}\,{\text{expit}}\left( {\upalpha_{1} c + \upalpha_{2} {\text{u}}_{\text{E}} } \right) > 0.5,} \hfill \\{} \hfill & { = 0\quad {\text{if}}\,{\text{expit}}(\upalpha_{1} c + \, \upalpha_{2} {\text{u}}_{\text{E}} ) \le 0.5} \hfill \\{{\text{f}}_{\text{C}} ({\text{u}}_{\text{c}} )} \hfill & { =1\quad {\text{if}}\,{\text{expit(}}\upgamma {\text{u}}_{\text{c}} )> 0.5} \hfill \\ {} \hfill & { = 0\quad{\text{if}}\,{\text{expit(}}\upgamma {\text{u}}_{\text{c}} )\le 0.5} \hfill \\ {{\text{f}}_{\text{D}}(e,c,{\text{u}}_{\text{D}} )} \hfill & { = 1\quad{\text{if}}\,{\text{expit(}}\upbeta_{0} e + \upbeta_{1} c +\upbeta_{2} {\text{u}}_{\text{D}} )> 0.5,} \hfill \\{} \hfill & { = 0\quad {\text{if}}\,{\text{expit(}}\upbeta_{0} e +\upbeta_{1} c + \, \upbeta_{2} {\text{u}}_{\text{D}} )\le 0.5,\,{\text{and}}} \hfill \\{{\text{u}}_{\text{E}} ,{\text{u}}_{\text{c}}\,{\text{and}}\,{\text{u}}_{\text{D}}\,{\text{have}}\,{\text{independent}},{\text{standard}}\,{\text{normal}}\,{\text{distributions}}}\hfill & {} \hfill \\ \end{array}$$

Then with α₁ = β₁ = 1,000, α₂ = β₂ = γ = 1, and β₀ = 0, E has no effect: D(1) = D(0). Also D(e) will be 1, to a close approximation, if and only if C = 1, so: P(D(e) = 1|E = 1) ≈ P(C = 1|E = 1) ≈ 1 and P(D(e) = 1|E = 0) ≈ P(C = 1|E = 0) ≈ 0 implying P(D(e)|E = 1) ≠ P(D(e)|E = 0) for e = 0, 1 and by consistency P(D|E = 1) ≠ P(D|E = 0).

For more complicated situations (e.g., Fig. 5), one can show by induction on the number of equations that it is always possible to choose functions (f_E f_Ym , …, f_Y1, f_C, f_Z1,…, f_Zn f_D) and parameterizations for those functions such that P(D(e)|E = 1) ≠ P(D(e)|E = 0) for e = 0, 1.

Faithfulness now implies that exchangeability cannot hold: the induction argument implies that parameters can be chosen that would “destroy” the independence P(D(1)|E = 1) = P(D(1)|E = 0) required by exchangeability (see Note 2) and destroy P(D|E = 1) = P(D|E = 0)—which is not consistent with faithfulness. (In other words, a probability distribution which implies P(D(e)|E = 1) = P(D(e)|E = 0) for e = 0, 1 under the structure implied by a biasing-path-containing graph could not be faithful). Thus, if a biasing path is present and the distribution is faithful in this way, then exchangeability cannot hold, establishing Claim 1B.

Proof of Claim 2A

(Absence of a biasing path implies exchangeability.) Absence of a biasing path implies that E $\mathop \coprod \nolimits$ A_D, where A_D is the set of D’s parents including the U’s that are implicit in the DAG for each node. If E $\mathop \coprod \nolimits$ A_D did not hold, the DAG would need to include an open path from E to some X $\in$ A_D, which would then be part of a biasing path from E to X and then to D, conditionally on controlled factors (if any). But, by G-computation or the do-calculus, the parents of D determine the counterfactual distribution of D, under interventions setting e to 0 or 1. Since the distribution of D’s -parents is the same among the exposed and the unexposed by independence, the distribution of counterfactuals for D must be the same in the exposed and unexposed. In particular, D(e) $\mathop \coprod \nolimits$ E. (A possible subtlety is that absence of an open path from E to X $\in$ A_D immediately implies E and each X $\in$ A_D are pairwise independent, whereas the argument assumed that E is independent of A_D. However, this last independence is implied, for example, by Theorem 1.2.5 of Pearl, since E and A_D are d-separated [13], conditionally on controlled factors, if any).

Proof of Claim 3

(In a Markovian causal model, exchangeability need not imply absence of a biasing path). We start with the DAG in Fig. 2 which has a confounding path and the corresponding structural equations (Example 1) and show that exchangeability can hold for some parameterization. We consider the following parameterization:

$$\begin{array}{*{20}l} {{\text{U}}_{\text{D}} \,{\text{has}}\, 6\,{\text{categories: P}}\left( {{\text{U}}_{\text{D}} = {\text{u}}} \right) > 0\quad {\text{ for}}\,\,u = 1, \ldots ,6;} \hfill & {{\text{P}}\left( {{\text{U}}_{\text{D}} = 5} \right) = {\text{P(U}}_{\text{D}} = 6 );} \hfill \\ {{\text{f}}_{\text{D}} (e,c,1) = 0\quad {\text{for}}\,\,{\text{all}}\,\,e,c;} \hfill & {{\text{f}}_{\text{D}} (e,c,2) = 1\quad {\text{if}}\,\,e = 0,\,{\text{and}}\,\,0\,\,{\text{otherwise}};} \hfill \\ {{\text{f}}_{\text{D}} (e,c,3) = 1\quad {\text{for}}\,\,e = 1\,\,{\text{and}}\,\,0\,\,{\text{otherwise}}} \hfill & {{\text{f}}_{\text{D}} (e,c,4) = 1\quad {\text{for}}\,\,{\text{all}}\,\,e,c;} \hfill \\ {{\text{f}}_{\text{D}} (e,c,5) = 1\quad {\text{if}}\,\,c = 0\,{\text{and}}\,\,0\,\,{\text{otherwise;}}} \hfill & {{\text{f}}_{\text{D}} (e,c,6) = 1\quad {\text{for}}\,\,c = 1\,{\text{and}}\,\,0\,\,{\text{otherwise}} .} \hfill \\ \end{array}$$

With this parameterization, D(1) = 1 if and only if: U_D = 3; U_D = 4; U_D = 5 and C = 0; or, U_D = 6 and C = 1. These events are mutually exclusive so:

$$\begin{aligned} {\text{P}}\left( {{\text{D}}\left( 1 \right) = 1|{\text{E}} = 1} \right) & = {\text{P}}\left( {{\text{U}}_{\text{D}} = 3} \right) + {\text{P}}\left( {{\text{U}}_{\text{D}} = 4} \right) + {\text{P}}\left( {{\text{C}} = 1|{\text{E}} = 1} \right) \times {\text{P}}\left( {{\text{U}}_{\text{D}} = 6} \right) \\ & \quad + {\text{P}}\left( {{\text{C}} = 0|{\text{E}} = 1} \right) \times {\text{P}}\left( {{\text{U}}_{\text{D}} = 5} \right) \\ & = {\text{P}}\left( {{\text{U}}_{\text{D}} = 3} \right) + {\text{P}}\left( {{\text{U}}_{\text{D}} = 4} \right) + {\text{P}}\left( {{\text{U}}_{\text{D}} = 6} \right) \\ \end{aligned}$$

Similarly, P(D(1) = 1|E = 0) = P(U_D = 3) + P(U_D = 4) + P(U_D = 6) so D(1) $\mathop \coprod \nolimits$ E; similar results show D(0) $\mathop \coprod \nolimits$ E, proving exchangeability. With the same parameterization, a stronger form of exchangeability $\vec{p} = \vec{q}$ also holds. Thus, exchangeability (not even the stronger form) does not imply absence of a biasing path as Fig. 2 does, in fact, have a biasing (confounding) path.

Proof of Claims 4A and 4B

(Absence of bias does not imply absence of a biasing path, and a biasing path does not imply bias.). We prove this claim through an Example that has a Biasing path but no bias (and exchangeability). We again use the causal relationships in Fig. 2, where there is a biasing path. Appendix Table 4 parameterizes the causal relationships, in terms of the structural equations. We also assume that C has 3 categories with P(C = 1) = 0.4, P(C = 2) = 0.3, P(E = 1|C = 1) = 0.4, P(E = 1|C = 2) = 0.5 and P(E = 1|C = 3) = 0.1. The latter three equations represent causal effects of C on E.

Table 4 Structural equations for example used in proof (Appendix 1) of claim 4

With this parameterization, E[D(1)] = P(D = 1|E = 1) = 0.1375 and E[D(0)] = P(D = 1|E = 0) = 0.1225 and so there is no bias. Similarly, exchangeability holds. In this example, we have “fine-tuned” the parameters, so bias would be absent even though C affects both E and D, a common situation for confounding. Bias would be present for most minor changes in the parameters and so the absence of bias is unstable in some sense. The distribution would be technically be unfaithful, since for example with most parameter changes D(e) would no longer be independent of E.