Abstract
In observational studies, selection of confounding variables for adjustment is often based on observed baseline incomparability. The aim of this study was to evaluate this selection strategy. We used clinical data on the effects of inhaled long-acting beta-agonist (LABA) use on the risk of mortality among patients with obstructive pulmonary disease to illustrate the impact of selection of confounding variables for adjustment based on baseline comparisons. Among 2,394 asthma and COPD patients included in the analyses, the LABA ever-users were considerably older than never-users, but cardiovascular co-morbidity was equally prevalent (19.9% vs. 19.9%). Adjustment for cardiovascular co-morbidity status did not affect the crude risk ratio (RR) for mortality: crude RR 1.19 (95% CI 0.93–1.51) versus RR 1.19 (95% CI 0.94–1.50) after adjustment for cardiovascular co-morbidity. However, after adjustment for age (RR 0.95, 95% CI 0.76–1.19), additional adjustment for cardiovascular co-morbidity status did affect the association between LABA use and mortality (RR 1.01, 95% CI 0.80–1.26). Confounding variables should not be discarded based on balanced distributions among exposure groups, because residual confounding due to the omission of confounding variables from the adjustment model can be relevant.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Selection of covariates for adjustment in randomized trials is still frequently based on observed baseline imbalances between the study groups [1], even though this strategy is flawed and hence not recommended [2–4]. For example, relatively small imbalances (indicated by large P values) of strong prognostic factors may still result in bias, when omitting such variables from an adjustment model [3].
In observational studies, the selection of covariates for adjustment should not be based on baseline imbalances either [5, 6]. Nevertheless, it is likely that this practice is even more common in observational studies than in trials [7], since adjustment for confounding is known to be an important issue in observational designs. Similar to the situation in trials, a variable that is a strong prognostic risk factor of the outcome, yet weakly associated with exposure may not be selected for adjustment, yet such omission may result in confounding. Also, adjusting for variables that are related to the exposure under study, yet are no true confounding variables, may actually introduce bias, rather than remove it. Examples include so-called M-bias, Z-bias, and adjustment for variables that are intermediates in the causal chain [8, 9]. Hence, baseline imbalances should not guide selection of covariates for adjustment in observational research.
Using observational data on the effects of long-acting beta-agonist use on mortality risk in patients with obstructive pulmonary disease, we here illustrate that even a situation of ‘perfect’ balance of prognostic characteristics between study groups should not result in omitting such variables from being selected for adjustment for confounding. Before turning to this clinical example, we first illustrate the invalidity of this strategy for selecting confounding variables using a numerical example on hypothetical data.
Numerical example
Suppose an observational study was conducted among 20,000 subjects on the effects of a certain exposure. Two variables (e.g., age and gender) were considered potential confounding variables, because both were known risk factors for the outcome of interest. Age (dichotomized at e.g. 50 years), was imbalanced between the exposure groups: of those exposed 75% were of old age, whereas 25% of those unexposed were of old age. Gender, however, was equally distributed among the exposure groups, since both groups included 50% females (Table 1).
The incidence of the outcome (e.g., mortality) among those exposed was 13.5%, and among those unexposed 19.5%, resulting in an estimated risk ratio (RR) of 0.69. Since gender was clearly balanced between the exposure groups, stratification by gender was not expected to result in a difference between the crude (i.e., unadjusted) RR and gender-adjusted RR. Indeed, after adjustment for gender the RR was equal to the crude RR (i.e., RR = 0.69).
Clearly, age was unevenly distributed among the exposure groups. Stratification by age controlled for the confounding by age and resulted in a change in the risk ratio: RR = 0.44. What is more, in these hypothetical data old age and female gender were related, such that women tended to be older (odds ratio = 6). However, by adjusting (stratifying) for age, the gender distribution that was initially balanced between exposure groups changed: the proportion females among exposed and unexposed subjects of young age became 20 and 40%, respectively. Among exposed and unexposed subjects of old age, the proportion females became 60 and 80%, respectively. Hence, due to the relation between age and gender, stratification by age resulted in an uneven distribution of gender among the exposure groups within age strata.
As a result, gender is likely to be considered a confounding variable within strata of young and old subjects. Indeed, stratification by gender after stratification by age resulted in another change in the risk ratio: RR = 0.50 (age- and gender-adjusted) versus RR = 0.44 (age-adjusted RR). In Table 2, the cell counts of the two-by-two tables for the exposure-outcome associations are given for the different age-gender strata. By merging these tables, the steps described above can be replicated in detail.
Clinical example
It has been suggested that inhaled beta-agonist therapy for pulmonary obstructive diseases (i.e., asthma and COPD) increases the risk of major cardiovascular events [10]. To study the effects of ever versus never inhaled long-acting beta agonist (LABA) use on all-cause mortality, we used a sample from the Netherlands University Medical Center Utrecht General Practitioner Research Network on the period 1995–2005. Subjects were included in the cohort when a diagnosis of asthma [ICPC code R96], or COPD [ICPC code R95] was mentioned in the electronic database. Ever versus never exposure to LABA was based on ATC coding [ATC R03AC12, R03AC13, R03AK06, or R03AK07]. The relation between LABA use and mortality was analyzed using a Poisson regression model with robust standard errors to estimate risk ratios [11]. Potential confounding variables were age, gender, and a diagnosis of cardiovascular co-morbidity, because these are known risk factors for myocardial infarction. For this example age was arbitrarily dichotomized at 50 years: those older than 50 years, were considered ‘old’, the others ‘young’. Cardiovascular co-morbidity was considered present when a subject was treated with a cardiovascular drug (antithrombotic drugs [ATC B01], cardiac therapy [ATC C01], diuretics [ATC C03], beta-blockers [ATC C07], or agents acting on the renin-angiotensin system [ATC C09]).
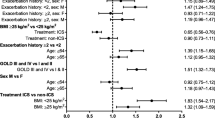
Among 2,394 asthma and COPD patients included in the analyses, the LABA ever-users were considerably older than never-users (Table 3). These groups did not differ, however, with respect to cardiovascular co-morbidity status (P = 0.99), or gender (P = 0.98). Consequently, adjustment for cardiovascular co-morbidity status or gender did not change the observed risk ratio (RR) for mortality: unadjusted RR 1.19 (95% CI 0.93–1.51), RR 1.19 (95% CI 0.94–1.50) after adjustment for cardiovascular co-morbidity status, and RR 1.19 (95% CI 0.94–1.51) after adjustment for gender. However, adjustment for age affected the RR considerably: RR 0.95 (95% CI 0.76–1.19). In this clinical example, old age and presence of cardiovascular co-morbidity were related (odds ratio = 11). As a result, within age strata, cardiovascular co-morbidity was no longer balanced between groups of LABA users. For example, after stratification by age, the proportions of cardiovascular co-morbidity among ever-users and never-users of old age were 33.6 and 42.0%, respectively (P = 0.002). Due to these imbalances, additional adjustment for cardiovascular co-morbidity status indeed changed the risk ratio: RR 1.01 (95% CI 0.80–1.26). The stratum-specific RRs were indeed approximately similar (Table 4).
Since old age was also related to female gender (odds ratio = 1.3), after stratification by age the groups of LABA users were no longer comparable with respect to gender either (e.g., proportions females among users among young ever-users and never-users were 40.5 and 46.5%, respectively (P = 0.04)). Consequently, additional adjustment for gender resulted in another change in the risk ratio: RR 0.98 (95% CI 0.79–1.23).
Discussion
In observational studies, the selection of variables in a model to adjust for confounding is often based on known associations with the outcome under study (i.e., the variables are known risk factors for the outcome), and observed associations with the exposure of interest [7]. Potential confounding variables with an uneven distribution among the exposure groups are then selected for (multivariable) adjustment, whereas evenly distributed ones are omitted from the adjustment model. Both the hypothetical and clinical example show that this approach is incorrect and can result in relevant residual confounding.
The observation that a variable is equally distributed among exposure groups indicates that it is marginally (i.e. unconditional on other variables) independent of the exposure under study. If, however, two variables are marginally independent and both are related to a third variable, they are dependent, conditional on that third variable [12]. This means that although exposure and gender (hypothetical example) or LABA use and cardiovascular co-morbidity status or gender (clinical example) were marginally independent, they were dependent conditional on age, because both were related to age.
The amount of (residual) confounding by the initially balanced confounding variable after adjustment for age alone likely depends on the strength of the association between the two variables as well as the strength of the association between the initially balanced confounding variable and the outcome. In both examples these associations were substantial. Obviously, if age is not related to the initially balanced confounding variable, stratification by age will not result in an uneven distribution of the latter variable within age strata, and hence no residual confounding due to that variable. In the clinical example, two initially balanced confounding variables became imbalanced after stratification by age. In practice, the number of initially balanced confounders could be even larger and residual confounding due to omitting all these variables from the adjustment model may become substantial, especially when these variables are strong risk factors for the outcome. Likewise, adjusting only for imbalanced baseline covariates in a randomized trial may actually induce bias by imbalancing other baseline covariates that are strong risk factors for the outcome.
In textbooks on epidemiology, a confounding variable is defined as a variable that is a risk factor for the outcome under study and also related to the exposure of interest [13, 14]. Furthermore, an intermediate to the causal chain is by definition not a confounding variable. Thus, what is considered a confounding variable depends on the outcome of interest and exposure under study and hence the clinical research question. However, it also depends on the stage of analysis, since in the examples presented here, gender and co-morbidity status did not confound the observed crude association, but they were confounding variables for the age-adjusted association.
Different strategies for selecting confounding variables have been proposed. A frequently applied strategy is based on some change-in-estimate criterion (e.g. 10% change in OR), but variables may then be falsely identified as confounding variables due to non-collapsibility [15]. Statistical tests to assess whether a certain variable is associated with either the exposure, the outcome, or both, are typically insensitive in small datasets, but raising the significance level can reduce this problem [16]. However, even ‘perfect’ balance of prognostic characteristics among exposure groups can result in confounding (as shown in our examples). Based on prior knowledge, common causes of both exposure and outcome (or causes of either exposure or outcome [17]) may be identified. Obviously, this relies on available knowledge, but in any case established risk factors for the outcome will be selected. Even if these variables are not related to exposure, statistical power will likely increase with adjustment for such risk factors [18]. Hence, selection of confounding variable for adjustment starts with identifying risk factors for the outcome.
In conclusion, a risk factor for the outcome under study that is evenly distributed among exposure groups can still be a confounding variable. Hence, observed balance of important prognostic variables among the exposure groups in a baseline table should not result in omitting such variables from the model to adjust for confounding.
References
Austin PC, Manca A, Zwarenstein M, Juurlink DN, Stanbrook MB. A substantial and confusing variation exists in handling of baseline covariates in randomized controlled trials: a review of trials published in leading medical journals. J Clin Epidemiol. 2010;63:142–53.
Senn SJ. Covariate imbalance and random allocation in clinical trials. Stat Med. 1989;8:467–75.
Senn S. Testing for baseline balance in clinical trials. Stat Med. 1994;13:1715–26.
Altman DG, et al. Baseline comparisons in randomized clinical trials. Stat Med. 1991;10:797–802.
Greenland S. Invited commentary: variable selection versus shrinkage in the control of multiple confounders. Am J Epidemiol. 2008;167:523–9.
Brookhart MA, Stürmer T, Glynn RJ, Rassen J, Schneeweiss S. Confounding control in healthcare database research: challenges and potential approaches. Med Care. 2010;48:S114–20.
Groenwold RH, van Deursen AM, Hoes AW, Hak E. Poor quality of reporting confounding bias in observational intervention studies: a systematic review. Ann Epidemiol. 2008;18:746–51.
Greenland S. Quantifying biases in causal models: classical confounding vs. collider-stratification bias. Epidemiology. 2003;14:300–6.
Brookhart MA, Schneeweiss S, Rothman KJ, et al. Variable selection for propensity score models. Am J Epidemiol. 2006;163:1149–56.
Salpeter SR, Ormiston TM, Salpeter EE. Cardiovascular effects of beta-agonists in patients with asthma and COPD: a meta-analysis. Chest. 2004;125:2309–21.
McNutt LA, Wu C, Xue X, Hafner JP. Estimating the relative risk in cohort studies and clinical trials of common outcomes. Am J Epidemiol. 2003;157:940–3.
Hernan MA, Robins JM. Letter to the editor of biometrics. Biometrics. 1999;55:1316–7.
Grobbee DE, Hoes AW. Clinical epidemiology, principles, methods, and applications for clinical research. 1st ed. Sudbury: Jones and Bartlett; 2008.
Rothman KJ. Epidemiology: an introduction. 1st ed. New York: Oxford university Press; 2002.
Groenwold RH, Moons KG, Peelen LM, Knol MJ, Hoes AW. Reporting of treatment effects from randomized trials: a plea for multivariable risk ratios. Contemp Clin Trials. 2011;32:399–402.
Maldonado G, Greenland S. Simulation study of confounder-selection strategies. Am J Epidemiol. 1993;138:923–36.
Vanderweele TJ, Shpitser I. A new criterion for confounder selection. biometrics. 2011 May 31. doi: 10.1111/j.1541-0420.2011.01619.x. [epub ahead of print].
Robinson LD, Jewell NP. Some surprising results about covariate adjustment in logistic regression models. Int Stat Rev. 1991;59:227–40.
Acknowledgment
The research leading to these results was conducted as part of the PROTECT consortium (Pharmacoepidemiological Research on Outcomes of Therapeutics by a European ConsorTium, www.imi-protect.eu) which is a public–private partnership coordinated by the European Medicines Agency. The research leading to these results has received funding from the European Union’s Seventh Framework Programme (FP7/2007–2013) for the Innovative Medicine Initiative (www.imi.europa.eu) under Grant Agreement no 115004. In the context of the IMI Joint Undertaking (IMI JU), the Department of Pharmacoepidemiology, Utrecht University, also received a direct financial contribution from Pfizer. The views expressed are those of the authors only and not of their respective institution or company.
Conflicts of interest
The department of Pharmacoepidemiology and Clinical Pharmacology, Utrecht Institute for Pharmaceutical Sciences, employing the authors RG, and OK, has received unrestricted funding for pharmacoepidemiological research from GlaxoSmithKline, private–public funded Top Institute Pharma (www.tipharma.nl) and includes co-funding from universities, government, and industry, the Dutch Medicines Evaluation Board and the Dutch Ministry of Health. OK has been consultant to Sanofi-Aventis on issues not related to this paper.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Additional information
A. W. Hoes—On behalf of PROTECT WP2 (Framework for pharmacoepidemiology studies, full list of collaborators in Appendix). The PROTECT consortium (Pharmacoepidemiological Research on Outcomes of Therapeutics by a European ConsorTium) is a private–public partnership coordinated by the European Medicines Agency (EMA).
Appendix
Appendix
The research leading to these results was conducted as part of the PROTECT consortium (Pharmacoepidemiological Research on Outcomes of Therapeutics by a European ConsorTium) which is a public–private partnership coordinated by the European Medicines Agency. Members of PROTECT WP2 (Framework for pharmacoepidemiology studies): Y. Alvarez, J. Slattery, X. Kurz (European Medicines Agency), M. Rottenkolber, J. Hasford, A. Sassenfeld (Ludwig-Maximilians-Universität-München), F. J. (de) Abajo Iglesias, M. Gil, C. Huerta, D. Montero (Agencia Espanola de Medicamentos y Productos Sanitarios), L. A. Garcia-Rodriguez, A. Ruigomez (Fundación Centro Español de Investigación Farmacoepidemiológica), P. Souverein, D. de Bakker, A. de Boer, R. Groenwold, S. Belitser, W. Pestman, K. Roes, A. Hoes, V. Abbing-Karahagopian, F. de Vries, T. P. van Staa, A. C. G. Egberts, H. G. M. Leufkens, L. van Dijk, O. H. Klungel (Utrecht University, The Netherlands), A. M. Gallagher, D. Patel (The UK General Practice Research Database), P. Helboe, J. Lyngvig, AM Clemensen, TS Engraff, U. Hesse, J. Poulsen (Lægemiddelstyrelsen, Danish Medicines Agency), J. Weil (GlaxoSmithKline Research and Development LTD), L. Bensouda-Grimaldi, L. Abenhaim (L.A. Sante Epidemiologie Evaluation Recherche), R. F. Reynolds, N. Gatto, A. Bate (Pfizer), G. F. Downey, R. Brauer, S. Yeboa, K. L. Goh, M. F. Tepie, A. Roddam (Amgen NV), E. Velthuis (Genzyme Europe), M. Miret (Merck KgaA), S. Johansson (AstraZeneca AB), P. Primatesta, R. Schlienger, J. Fortuny, E. Rivero (Novartis), G. Quartey, H. Petri, M. Schuerch, J. Robinson (F.Hoffmann-La Roche AG), J. R. Laporte, L. Ibañez, M. Sabaté, E. Ballarin, P. Solari (Fundació Institut Català de Farmacologia).
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Groenwold, R.H.H., Klungel, O.H., Grobbee, D.E. et al. Selection of confounding variables should not be based on observed associations with exposure. Eur J Epidemiol 26, 589–593 (2011). https://doi.org/10.1007/s10654-011-9606-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10654-011-9606-1