Analysis of individual drug use as a time-varying determinant of exposure in prospective population-based cohort studies

Abstract

In pharmaco-epidemiology, the use of drugs is the determinant of interest when studying exposure-outcome associations. The increased availability of computerized information about drug use on an individual basis has greatly facilitated analyses of drug effects on a population-based scale. It seems likely that many negative findings in the early days of pharmaco-epidemiology can be explained by non-differential misclassification because of too simple (yes/no) exposure measures. In this paper, the authors discuss the importance of an adequate definition of drug exposure in pharmaco-epidemiological research and how this time-varying determinant can be analyzed in cohort studies. To reduce the risk of non-differential misclassification, a precise definition of exposure is mandatory and it is important to distinguish the complete follow-up period of a population into mutually exclusive episodes of non-use, past use and current use for each individual. By analyzing exposure to drugs as a time-dependent variable in a Cox regression model, cohort studies with complete coverage of all filled prescriptions can provide us with valid and precise risk estimates of drug-outcome associations. However, such estimates may be biased in the presence of time-dependent confounders which are themselves affected by prior exposure.

Introduction

In pharmaco-epidemiology, the use of drugs is the determinant of interest when studying exposure-outcome associations. The increased availability of computerized information about drug use on an individual basis has greatly facilitated analyses of drug effects on a population-based scale. This stimulated the development of pharmaco-epidemiology as a branch within epidemiology as can be seen on epidemiological congresses [1].

In the last decades of the preceding century, many pharmaco-epidemiologic studies employed a case–control design. Case–control studies of the association between diethylstilboestrol against habitual abortion and vaginal carcinoma in female offspring [2], and of salicylate-attributed Reye syndrome [3] have clearly shown the benefits of this design thanks to their valid and relevant results despite small numbers of cases in both studies. However, in hindsight this design may also have risen spurious associations such as that between use of reserpine and breast cancer [4].

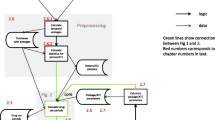
Because information about drug use in these early studies had to be obtained from interview, they suffered from two important potential limitations. First, the suspicion that patients with severe diseases would tend to have a better recall than non-diseased controls. This type of information bias (so-called ‘recall bias’) was suspected to be partly responsible for the association between X-ray exposure during pregnancy, and the subsequent occurrence of congenital malformations in off-spring [5]. In a subsequent similar study with hospital records, the significant risk increase of 90% found earlier was brought back to 40%, albeit still statistically significant [6]. Unfortunately, even hospital records may be incomplete when information of drug use is retrospectively gathered [7]. Second, whereas recall bias leads to differential (i.e., non-random) misclassification of exposure, also non-differential (i.e., random) misclassification may jeopardize the validity of drug-effect estimates as can be seen in Fig. 1. The argument which is often brought forward that such misclassification is less serious because it leads to a more conservative estimate, is questionable as also underestimations are non-valid and therefore unwanted. It seems likely that many negative findings in the early days of pharmaco-epidemiology can be explained by non-differential misclassification because of too simple (yes/no) exposure measures. But even with extensive scrutiny of drug history during interview, long-term exposure such as might be relevant to development of end-stage renal failure [8] will inevitably lead to both differential and non-differential exposure misclassification. It would not be fair to blame researchers for this, as laborious investigation of serious diseases should be praised and because most of them do not ignore the limitations of their data.

Fig. 1

Assume a prospective cohort study with 10% non-differential misclassification of exposure. Without misclassification, the true relative risk would be calculated as [30/100]/[10/100] = 3.0 in those treated with drug A in comparison to those on drug B. However, because in diseased as well as non-diseased 10% of individuals switches from A → B and vice versa, the number of exposed changes for each cell, i.e. cell a (30 − 3+1 = 28); cell b (70 − 7+9 = 72); cell c (10 − 1+3 = 12); cell d (90 − 9+7 = 88). Consequently, we calculate the relative risk as [28/100]/[12/100] = 2.3

In this paper, we discuss the importance of an adequate definition of drug exposure in pharmaco-epidemiological research and how this time-varying determinant can be analyzed in cohort studies.

Drug assessment in populations

The two types of above-mentioned exposure misclassification can be effectively circumvented when drug use in populations is prospectively gathered, i.e., before onset of the event of interest and consequently unbiased. Prospective data collection prevents the occurrence of ‘recall bias’ or other types of differential exposure information bias. Non-differential misclassification, however, can still occur if the exposure definition is imprecise or if drug use falls outside the biologically plausible risk window, as can be seen in Fig. 2. Although we know that prolonged use of high doses of estrogens is a strong risk factor for liver adenoma [9], for instance, it is clear that in a woman who started using the drug 1 month before diagnosis, liver adenoma can not be caused by the estrogen. Apparently, exposure status is not merely a matter of using/non-using a drug before the event occurs but also of timing. In real life situations, the effect of exposure will depend on dose, duration of use, timing in relationship to the event, concurrent medication, and adherence to therapy.

Fig. 2

Assume a prospective cohort study on the risk of cancer induction after long-term exposure to a drug A. To reduce the effect of non-differential misclassification as much as possible, cumulative exposure should only be calculated during the induction period (exposure window 2). If use during the latent period is included (exposure window 1), the measured relative risk (RR) will be diluted from RR = 5 towards RR = 2. This will be brought down even further to a RR = 1 if cumulative exposure is only measured during the latent and disease period (exposure window 3)

Of course, the fundamental question is: “what is exposure ?”. In an ideal situation, it tells us what the drug concentration is at the receptor site which is responsible for the biological effect. Obviously, such a situation can be achieved at best in small groups of diseased or volunteers and even there, it is a rather theoretical option and is approached nearest with the assessment of drugs and their metabolites in blood or plasma. As blood levels tell us little about, for instance, the concentration of psychotropic drugs in brain tissue, the contribution to large-scale population-based pharmaco-epidemiology is modest although it will add to interpreting the study results. Instead, large studies rely on three types of health care data which are currently becoming more and more readily available: drug exposure information from health insurance companies or sick funds [10]; from general practitioners [11], and from pharmacies. Data from general practitioners are of great value because they consist of both drug prescriptions and information on disease, and can not only show changes in prescribing [11] but can also be pooled in large-scale collaborative research [12] to study rare events. However, a limitation is that specialist prescriptions are incompletely registered in general practice databases, and that not all of their own prescriptions are filled at pharmacies. As for health insurance companies, not all of them register the daily dose of the patient. Consequently, drug filling data from pharmacies come closest to true exposure of prescription-only drugs. This holds especially in those who use chronic medication. People who come back at regular intervals for refills of a drug, usually have a high compliance to therapy. Dividing the number of filled tablets or capsules by the daily prescribed number makes it possible to calculate when a patients is expected to come for the next vial of medicines. In this way, adherence to therapy can be assessed reliably. All mentioned data sources, however, miss over-the-counter (OTC) drugs.

Converting filled prescriptions into exposure variables

For the analysis of drug-event associations, the dose, the duration, and timing of use are highly important. Unfortunately, individual medication histories may contain a plethora of different drugs, doses, switching between drugs, and types of administration. Most western countries have some 10,000 different marketed drug products and it is an administrative and pharmacological challenge to convert this information into an analyzable dataset. Suppose, for instance, that one would be interested to study the association between long-term use of anti-inflammatory drugs (NSAIDs) and cancer. Then, use of several different pharmaceutical products over the years by one person has to be brought back to the numbers of days of use of each pharmacological entity, and to a standardized dose to facilitate comparison between products. For instance, the recommended daily dose for treatment of arthritic pain is 100 mg for diclofenac and 500 mg for naproxen. Taking the average dose without standardization would be meaningless. A well-known scheme for dose standardization is the ATC-DDD scheme of the World Health Organisation (http://www.whocc.no).

Drug-event analyses

Epidemiologists usually underline the importance of awareness of potential confounding in study designs to prevent non-validity [13]. For obvious reasons, appropriate epidemiologic methods are a prerequisite for valid study results. This includes the validation of exposure measurement tools [14]. An adequate assessment of the role of drug exposure requires knowledge of the biologically relevant period during which the drug must be used to induce or modify the event of interest, and of the pharmacokinetic and pharmacodynamic properties of the drug. If we are interested in the question whether a drug may cause an event, we should only assess the exposure status during the induction period as any assessment outside this period will introduce non-differential misclassification of exposure (Fig. 2). On the other hand, if we investigate whether a drug is not a cause but modifies the disease process, we will only assess the exposure status during the latent and/or disease period. The pharmacodynamic effects of the drug should be compatible with causation, although this may not always be clear. The pharmacokinetic properties of a drug are very important for assessing the duration of exposure. For instance, a drug against cystitis such as nitrofurantoin is excreted completely within hours while the notorious carcinogenic diagnostic agent thorium dioxide which was used between the 30 and 50 s of the 20th century has a biological half-life of 400 years and a physical half-life of 5,000 years. Drugs such as the antiarrhythmic agent amiodaron and the anxiolytic diazepam have prolonged carry-over effects because of their long half-life. Apparently, the exposure period is not merely the time during which the drug was actually taken but may have to be extended with a carry-over period of 1–2 half-lives.

Analysis of drug exposure as a time-varying determinant in prospective population-based cohort studies

As mentioned above, the prospective gathering of drug use facilitates unbiased risk estimates provided exposure is precisely defined by reference to a well-defined event with a clearly recognizable onset. Thanks to prospectively gathered and complete medication histories, exposure status can be assessed on every day of the follow-up. This is a great advantage over population-based studies where drug use is assessed on the basis of interview during repeated rounds of cross-sectional measuring. Although the analyses in this paper pertain to cohort studies, this includes nested case–control studies where the prospective exposure data come from the cohort but there are efficiency reasons to perform a case–control analysis. This may occur, for instance, when tissue samples have to be taken or when additional data gathering from medical records makes it unfeasible to perform this in the whole study cohort.

Unlike constant features such as sex and certain genetic traits, drug use is essentially a time-varying determinant. In a traditional Cox regression model [15], the hazard function in the total population at time point t is defined as:

$$ \lambda \left( t \right) = \lambda_{0} \left( t \right) * \exp \left( {\beta x} \right) $$

(1)

in which λ(t) represents the event rate at time t conditional on being still event free before time t. In this model the event rate is assumed to be equal to a baseline risk λ₀(t), which is the same for everybody in the population, i.e., independent of the determinants. This baseline risk is multiplied by a term exp(βx), dependent on the determinants x, which are different between individuals. The parameters β quantify the effect of the determinants on the event rate. They have to be estimated from the data, together with the baseline risk λ₀(t). There are different choices possible for the time scale t, for instance, t = age (when age is strongly and exponentially associated with event occurrence), t = time since entry in the cohort, or t = calendar time. In the simplest case, x represents only one determinant x ₁, for instance sex, with x ₁ = 1 (males) and x ₁ = 0 (females). Then λ(t) gives the hazard function for developing the event at time point t in males or females. For females, the hazard is λ₀(t) and for males the hazard is λ₀(t) multiplied by exp(β₁). In this model, the determinants x are not necessarily constant during follow-up, but may vary in time, such as drug use. In a study sample, the unknown hazards are then estimated from the data as:

$$ h\left( t \right) = h_{0} \left( t \right) * \exp \left( {b_{1} x_{1} } \right) $$

(2)

Suppose that we performed a study in which m individuals developed the event of interest during follow-up. The follow-up times at which the events (the “cases”) occurred are denoted with t ₁,…, t _m . (for simplicity, we assume that events do not coincide). In a Cox proportional hazards regression analysis with drug exposure as a time-varying determinant [16], the exposure status x ₁[t _j] on the index day t _j of the case number j, is compared to the exposure status of all other cohort members on the same day of the follow-up. In this way, j = 1,…, m strata are formed of one case each and the other cohort members who were still in the follow-up and event free at time t _j as controls. In an earlier analysis in The Rotterdam Study [17], for instance, it was investigated whether thiazide diuretics protect against hip fracture, thanks to their calcium-retaining effect [18]. An analytical matrix would look like the ones given in Table 1a and b. On the index date t _j , all cohort members have a history of thiazide use up to that time. In its simplest form, we can characterize this history as use on the index date as 1 (‘yes’) or 0 (‘no’) like in Table 1a. If i denotes the number of an arbitrary cohort member that is under follow-up at the index date t _j , the model states for this individual i

$$ h\left( {t_{i} } \right) = h_{0} \left( {t_{j} } \right) * \exp \left( {b_{1} x_{1i} \left[ {t_{j} } \right]} \right) $$

(3)

in which the time-varying determinant x _1i [t _j ] has the numerical value ‘1’ (exposed) or ‘0’ (unexposed) depending on whether cohort member i is exposed or non-exposed at time point t _j . For each event time t _j , there is a set R _j (the “risk set”) containing all individuals who were under observation at t _j . So, R _j contains case number j and its corresponding controls. Given the event at t _j , the conditional probability that out of all cohort members in R _j the cohort member with number j (the one who was observed to develop the event) will develop the event is:

$$ h_{0} \left( {t_{j} } \right) * \exp \left( {b_{1} x_{1j} \left[ {t_{j} } \right]} \right)/\sum\limits_{{i\,{\text{from}}\,R_{j} }} {\left\{ {h_{0} \left( {t_{j} } \right) * \exp \left( {b_{1} x_{1i} \left[ {t_{j} } \right]} \right)} \right\}} \, $$

(4)

Table 1 Apart from unique patient number, sex and age in years, the columns respectively represent: case status (1 = ‘yes’; 0 = ‘no’); stratum; follow-up in days; cumulative number of days of current use; number of days since last intake in past users; defined daily dose (DDD) [for hydrochlorothiazide: 25 mg and for chlorothiazide: 500 mg]; and total numbers of days of use since study entry

Notice that the baseline hazard rate h ₀(t _j ) is present in numerator and denominator and cancels out. Therefore, the conditional likelihood function of all the data, defined as the product of the probabilities as given in (4) over all event times t _j , is equal to:

$$ L\left( \beta \right) = \mathop \Uppi \limits_{j = 1}^{m} \{ \exp \left( {b_{1} x_{1j} \left[ {t_{j} } \right]} \right)/\sum\limits_{{ \, i\,{\text{from}}\,R_{j} }} {\exp \left( {b_{1} x_{1i} \left[ {t_{j} } \right]} \right)} \} $$

However, this straightforward but simple analysis with only the status exposed/unexposed would mean that we use only a very limited part of the information that is contained in the thiazide use history and thereby introduce non-differential misclassification. As can be seen in Table 1a, knowing the numbers of days of continuous use on the index date of each cohort member facilitates calculation of more valid risk estimates as it is unlikely that only 1 day of thiazide use would already be protective while the model would consider even those people as exposed who started thiazides 1 day before the index date. There are pharmacological reasons to assume that a protective effect on hip fracture may become visible only after at least 6 weeks of calcium retention by thiazide treatment and reaches a maximum after ~1 year. Hence, more information, and consequently less non-differential misclassification, is obtained with the introduction of extra determinants x ₂, and x ₃, where the cumulative continuous exposure to thiazides at the index date is categorized as: x ₁ = 1 through 42 days; x ₂ = 42 through 365 days; x ₃ > 365 days.

$$ h\left( t \right) = h_{0} \left( t \right) * \exp \left( {b_{1} x_{1} \left[ t \right] + b_{2} x_{2} \left[ t \right] + b_{3} x_{3} \left[ t \right]} \right) $$

(5)

In this way, the risk for these two exposure categories is expressed in comparison to non-use and yields a more valid representation of the drug-event association than in (3) or when thiazide exposure in days would be introduced as a continuous exposure determinant.

Even more information, and therefore less non-differential misclassification, may follow from the introduction of determinants for ‘past use’ when one expects that a carry-over period should be taken into account. For instance, if thiazide use for more than 1 year results in a higher calcification of the hip, it will take a certain time period before discontinuation of thiazides results in returning to the situation before starting treatment. This can be done by introducing determinants for past exposure, defined as the number of days since last intake of thiazides (Table 1b). In the previously mentioned study, additional categorical determinants were created as extra determinants x ₄, x ₅, and x ₆ where the number of days since last intake of thiazides, counting back from the index date, was categorized as: x ₄ = 1 through 60 days; x ₅ = 61 through 365 days; and x ₆ > 365 days.

For obvious reasons, the determinants x ₁ through x ₆ should be introduced in one model. After all, it is important that the complete follow-up time of each study member is expressed in mutually exclusive episodes of non-use, past use, and current use to decrease the degree of non-differential misclassification as much as possible. Then, the full model is:

$$ h\left( t \right) = h_{0} \left( t \right) * \exp (b_{1} x_{1} \left[ t \right] + b_{2} x_{2} \left[ t \right] + b_{3} x_{3} \left[ t \right] + b_{4} x_{4} \left[ t \right] + b_{5} x_{5} \left[ t \right] + b_{6} x_{6} \left[ t \right]) $$

(6)

This model can be extended with the inclusion of other non-time-varying determinants such as gender and baseline age x _a , x _b , …, x _j , …, x _z , provided usual precautions against overfitting of the model are taken into account. Adjusting for dosage may be performed by including it as a continuous determinant in mg/day or categorized, for instance by splitting current use as: current use with >1 defined daily dose (DDD); current use with ≤1 DDD.

The analytical matrix in Table 1c facilitates different type of analyses. For instance, would we be interested to find out whether cumulative use of nonsteroidal antiinflammatory drugs (NSAID) are associated with an increased risk of cancer, we might prefer to use the determinant ‘total use’. However, if we would be interested in induction, rather than promotion, we might subtract a theoretical episode of 5 years from the index date of cancer diagnosis and calculate total use in days until that date, or in dose as cumulative DDDs. We would do this to avoid non-differential misclassification by restricting ourselves to the induction period. Would we only be interested in promotion, we would treat NSAID as an effect modifier and restrict our analysis to total use in the 5 years before cancer diagnosis because we would expect that malignant cells would already be present during that latent period.

Limitations

The method described above facilitates a clear insight into the data structure but may have some practical limitations. First, in patients who use drugs very irregularly, it may be difficult to calculate the cumulative period of continuous current use at the index date as in such patients these periods will usually be short and irregular. However, this can often be circumvented by combining current and total use. Second, because for every case the remainder of non-censored cohort members serves as a reference, huge strata may lead to substantial computational time to run analyses. For instance, with 1000 cases in a cohort of 50,000 people, each stratum would have slightly less than 50,000 observations at the index date of that stratum, leading to a data file of ~50,000,000 records. As there are techniques to deal with such a problem, however, this may only be relevant to the less well-equipped researcher.

A methodological limitation may arise when the model is adjusted for a time-dependent co-variable which is a risk factor for the event of interest and may be influenced by the drug exposure [19]. Standard methods for estimating the effect of a time-varying exposure on survival may be biased in the presence of time-dependent confounders which are themselves affected by prior exposure. This problem can be overcome by inverse probability weighted estimation of Marginal Structural Cox Models (Cox MSM) or G-estimation of Structural Nested Cumulative Failure Time Models (SNCFTM). For this situation, the reader is referred to recent literature about such a scenario [20].

Conclusion

In pharmaco-epidemiology, the use of drugs is the determinant of interest when studying exposure-effect associations. It seems likely that many negative findings in the early days of pharmaco-epidemiology can be explained by non-differential misclassification because of too simple (yes/no) exposure measures. To reduce the risk of non-differential misclassification, a precise definition of exposure is mandatory and it is important to distinguish the complete follow-up period of a population into mutually exclusive episodes of non-use, past use and current use for each individual. By analyzing exposure to drugs as a time-dependent variable in a Cox regression model, cohort studies with complete coverage of all filled prescriptions can provide us with valid and precise risk estimates of drug-outcome associations. However, such estimates may be biased in the presence of time-dependent confounders which are themselves affected by prior exposure.