Experimental and numerical study of unsteady flows in a compound open channel

Abstract

Unsteady flows are investigated in a compound open-channel flume, consisting of a Main Channel (MC) and an adjacent Flood Plain (FP). Two types of inflow hydrographs are studied, i.e., a discharge hydrograph with, at any time: a slightly unbalanced inflow partition between MC and FP (Case I); and a noticeably unbalanced inflow partition (Case II). Ensemble averages of the time-varying discharges, water depths and velocities are estimated based on 100 successive runs. The main focus of the experimental study is on assessing (i) the time-varying lateral discharge and depth-averaged Reynolds stress at the MC/FP interface, and (ii) the influence of the inflow partition on the downstream flow parameters. The experimental flows are then simulated using a 1D (one-dimensional) code that was adapted to implement the 1D+ Independent Sub-sections Model (ISM) (Proust et al. in Water Resour Res 45:1–16, 2009). The numerical study aims at validating the ISM under unsteady flow conditions, using classical 1D simulations as benchmark. It is experimentally found that 90 successive runs are required to get convergence of the ensemble averages of sub-section discharges and flow depth, while interfacial velocity is not fully converged after 100 runs. The influence of the inflow partition on the downstream parameters is felt along the whole flume. The ISM simulations are closer to the measurements than the classical 1D simulations. The ISM can accurately predict the time-varying flow depths and interfacial lateral discharge, and can approximate the interfacial Reynolds stresses.

1 Introduction

River floods affect hundred of millions of people worldwide and cause numerous casualties and devastating economic damages. For instance, the river floods in Central Europe in July 2021 caused estimated overall losses of US$ 54 billions, the costliest natural catastrophe in modern Europe history [2]. In France, river floods is the most frequent flood type, and also the flood type that affects more people, with 17.1 million people (25$\%$ of the population) exposed to the overflow of rivers [3]. Crucially, the number of people wordlwide exposed to high river flood events is expected to increase with climate change [4], with significant spatial variation [4, 5].

In such a context, as recently recalled by Bates [6], ‘mapping the areas at risk of flooding is critical to reducing casualties and economic losses’. This requires a good knowledge of the hydrodynamics of overflowing rivers, i.e. of the overbank flows or flows in a Compound open Channel (CC), which is composed of the river Main Channel (MC) and one or two adjacent Flood Plains (FPs). In addition, this knowledge should be correctly introduced in numerical models with satisfying prediction capabilities. In this area, although Navier–Stokes equations can be numerically solved in either one, two or three dimensions, within reasonable computational time, either two-dimensional (2D) or three-dimensional (3D) models are still too time-consuming for some specific operational applications such as flood management (requiring real time computing) or optimisations in the design of hydraulic works (requesting hundreds of runs in order to optimize the hydraulic design or to process automatic model calibration). Therefore, there is still a deep interest for improvements in one-dimensional (1D) modelling techniques since 1D models are generally fast enough for those purposes whereas they suffer from a poor modelling of the different terms of head losses − mainly treated as bed-friction head losses as pointed out by Visse et al. [7]. The influence of this poor representation of the physical processes is somehow compensated by some calibration techniques that could benefit from numerous routine data [8]. While such calibration processes have been proven to deliver satisfying results in the range of the available calibration data, the predicting capabilities of such calibrated models are still questionable when they are run in situation of very high flows (e.g., for modelling extreme flood events as required for safety studies or hydraulic works conception).

Fig. 1

High flood events along the Rhône River at: (left) Arles in 2003 (100-year return period flood); and (right) Pont-Saint-Esprit, $\copyright$CNR

Coming back to the physics of overflowing rivers, an overbank flow or CC flow features a complex 3D structure arising from the interplay between: (i) the transverse shear layer developing at the interface between MC and FP; (ii) the vertical boundary layers developing over the MC and FP bottoms; (iii) the lateral boundary layers forming on the sidewalls of MC and FP; and (iv) the helical secondary currents with a longitudinal axis caused by turbulence anisotropy or/and centrifugal effects. This flow structure was thoroughly experimentally investigated for: steady streamwise uniform flows in straight CCs [9,10,11,12,13,14,15,16]; steady non-uniform flows in straight CCs [17,18,19]; and steady non-uniform flows in non-prismatic geometries [14, 20,21,22]. The present laboratory experiment and numerical study focus on CC flows whose structure has been far less explored, namely unsteady flows in CCs.

The structure of unsteady flows in CC was studied in the laboratory by Tominaga et al. [23] and Lai et al. [24]. Tominaga et al. [23] measured the time-dependent velocity field across a CC section using a micro-propeller and repetitive hydrographs (starting with a base inbank flow in the MC). Estimating the sub-section-averaged velocities in MC and FP, $U_m$ and $U_f$, and plotting these velocities as a function of time, they highlighted different loop patterns in the MC and FP. They also found that the peak velocity value appears earlier in the MC than in single rectangular channel. Lai et al. [24] investigated the flood-wave propagation in a CC flume, for long, moderate, and short duration floods. In particular, they analyzed the flood peak attenuation, the wave front speed, and the relationship between water depth and surface velocities (measured by flow visualization).

Unsteady flows in CC were also numerically studied by several authors. By comparing simulations of three different 1D models with observed water levels, Abida and Townsend [25] showed that accounting for the effects of the MC/FP interaction and the meandering of MC [25, Eq. (4)] can improve the prediction of water levels. Rashid and Chaudry [26] showed that, when using a 1D model to simulate unsteady water levels, it is better to consider FPs as storage areas (no contribution of the FP flow to momentum exchange) than using a total-cross-section-averaged velocity combined with a momentum coefficient accounting for non-uniform velocity distribution. However, both approaches overestimate the peak water levels. Bousmar et al. [27] proposed a 1D model that takes into account both the lateral mass exchange and momentum transfer at the MC/FP interface, and simulated the data of Tominaga et al. [23]. They showed that during the rising stage, the momentum transfer increases the FP discharge without interfering with the MC, while during the falling stage, the MC head losses are increased by the momentum exchange, which delays the emptying of FPs. Tang et al. [28] compared two variants of numerical schemes for 1D flood routing, focusing on the relationship between flood wave celerity and discharge. Unfortunately, the numerical results were not validated against laboratory or field data. The relationship between wave celerity and discharge was also analyzed by Fleischmann et al. [29] using the 1D code HEC-RAS along a 175 km river reach. Helmiö [30] used a 1D model to simulate unsteady flows in a CC with vegetated FPs. A specific treatment of the friction caused by vegetation was carried out, while flow non-uniformity across the channel was accounted for by a momentum coefficient. The effect of density vegetation and FP width on the peak flow depths were numerically assessed. Then, Helmiö [31] applied this model to a 28-km reach on the Upper Rhine river for two unsteady flood events. A good agreement was observed between computed discharges and water levels and measured data. Last, we can mention the works of Liu et al. [32], who recently studied the hyporheic exchanges between a CC unsteady flow and the water table using 2D and 3D numerical simulations.

In addition to investigating the flood wave propagation [23,24,25,26,27,28,29,30,31], the present laboratory experiment aims at investigating: (i) the time-varying lateral discharge between MC and FP (called herein sub-sections); (ii) the time-varying depth-averaged Reynolds stress at the MC/FP interface; and (iii) the influence of the upstream flow partition between sub-sections on the downstream transient flow parameters. At this stage, it is important to recall that: (1) the lateral discharge at the MC/FP interface is a key parameter as it is involved in both the connectivity between river and FPs [33] and the transport and deposit of materials between the river MC and FPs or deltas during flood events [34,35,36,37]; (2) to the authors’ knowledge, time-varying mean velocities in CC flows were experimentally studied only by Tominaga et al. [23] and Lai et al. [24]; and (3) the study of time-varying Reynolds stresses in CC flows has never been conducted.

The numerical part of the present study focuses on an improved 1D (denoted as ‘1D+’) approach, termed ‘the Independent Sub-sections Model (ISM)’, which was initially developed for steady non-uniform flows in non-prismatic idealized compound geometries [1], by relying on the works of Yen et al. [38] and Bousmar and Zech [39]. Unlike classical 1D approaches that solve a dynamic equation (energy or momentum conservation equations) on the total compound cross-section, the ISM solves the dynamic equation in each sub-section (MC, left-hand and right-hand FPs). This enables to explicitly model the depth-averaged lateral exchanges of mass and momentum at the MC/FP interface, and to take into account the upstream flow partition between MC and FP. Prior to the present study, the ISM was validated against experimental measurements in various CC flumes for steady flows, either uniform or non-uniform in the streamwise direction [1, 40], but has never been validated for unsteady river flood events that are more realistic hydrological situations for overflowing rivers. As a result, the present numerical study aims at validating the ISM under unsteady flow conditions in (as a first step) an idealized prismatic compound geometry, and using classical 1D simulations as benchmark.

Table 1 Numerical modelling of a high flood event along the Rhône River, France, on 16/11/2002

Note that, the present numerical study just follows a test-simulation with the ISM of real floods along the Rhône River (Fig. 1), which was carried out to perform a feasibility test [41]. Interestingly, by optimizing the turbulent exchange coefficient at the MC/FP interface, the ISM was shown to reproduce the water surface elevations as well as a classical calibrated 1D code as reported in Table 1. In the latter, FudaaCrue [8] is the operational code developed by Compagnie Nationale du Rhône (C.N.R), and based on the Divided Channel Method (DCM) [42] to address overbank flows. MAGE is a research code developed by INRAE that can be coupled either with the DEBORD method [9]—a corrected DCM accounting for the turbulent exchange between MC and FP−, or with the 1D+ISM [1] to model CC flows. The maximum (resp. mean) bias Max $\epsilon (x)$ (resp. Mean $\epsilon (x)$) is the maximum (resp. mean) value of the absolute difference between computed water level and observed water mark along the 3.5-km studied reach (see Fig. 5.12 in Kaddi et al. [41]). The root mean square error (RMSE) is computed from the squared differences in water levels [7]. Since the results of the 1D simulations on the water levels are mostly driven by the total discharge and the bed-friction coefficients (e.g., Strickler or Manning roughness coefficients [43]), these first results suggested that the turbulent exchange coefficient introduced in the ISM played a significant role in the modelling of the global head losses and could efficiently correct the well-known weaknesses of the classical 1D modelling [41].

Section 2 describes the flume used in the experiments, the flow conditions (inflow discharge hydrographs and steady base flow conditions), the repetition of the discharge hydrographs and the ensemble averaging of the flow parameters (discharge, velocity and flow depth), and the measuring techniques. The unsteady flow data processing is developed in Sect. 3. The 1D+ model (ISM) and the 1D approach used as benchmark are presented in Sect. 4, as well as the adaptation of the 1D code MAGE to implement the 1D+ ISM. The experimental and numerical results are presented in Sect. 5 (flood wave propagation) and Sect. 6 (flow parameters at the MC/FP interface). Relying on the ISM results, the three various contributions to the sub-section head losses are estimated in Sect. 7.1, namely: (1) the head losses caused by the shear layer turbulence at the MC/FP interface; (2) the head losses related to the lateral momentum exchange by the mean flow at this interface; and (3) the head losses caused by bed-friction. Section 7.2 is dedicated to the study of the sensitivity of the ISM to its calibrating parameters. Conclusions are eventually drawn in Sect. 8.

2 Experiments

2.1 Experimental facility

The experiments were conducted in an 18 m long and 2 m wide CC flume (Fig. 2a) at INRAE Lyon-Villeurbanne, France. The flume bed slope in the longitudinal direction, $S_o$, is $1.05\times 10^{-3}$. The compound cross-section is asymmetrical (Fig. 2b), consisting of a 1 m wide rectangular MC and a 1 m wide adjacent FP. The bed and sidewalls of the MC are made of glass, and the FP bottom is covered by dense synthetic grass. This grass consists of 1 mm wide and 5 mm high thin rigid blades with a density of 256 blades per square centimeter (8 by 8 bunches of 4 blades). The vertical distance from the MC glass bed to the FP bottom is 0.117 m. The Manning roughness coefficients in the FP, $n_f$ = 0.0114 m$^{-1/3}$s, and in the MC, $n_m$ = 0.0096 m$^{-1/3}$s, were calibrated independently by separating both sub-sections with a wall in a previous study in the same flume [15].

At the flume entrance, the MC and FP are supplied with water by two independent inlet tanks (Fig. 2c). Each inlet tank is filled with water through a tower with a constant water level reservoir. The flow rate in the MC, $Q_m$, and the flow rate in the FP, $Q_f$, can be varied independently using two electromagnetic valves thanks to a PID (Proportional, Integral, Derivative) system that relates the valve opening to the discharge measurement. The minimum variation step of the valve corresponds to 0.1$\%$ of the full opening. Note that the inflow partition between MC and FP is maintained until the trailing edge of a 75 cm long vertical splitter plate (Fig. 2c, $\#$2).

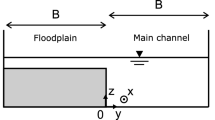
A Cartesian right-handed coordinate system is used in which x-, y-, and z-axes are aligned with the streamwise (parallel to flume bottom), spanwise, and vertical (normal to flume bottom) directions (Fig. 2b and c). The origin is defined as: x = 0 at the trailing edge of the upstream splitter plate; y = 0 at the vertical interface between MC and FP; and z = 0 at the FP bottom. At the downstream end of the flume (x = 17.25 m), two vertical weirs (one per sub-section) enable the water surface to be controlled (Fig. 2c, $\#$4). These weirs are separated by a 50 cm long vertical splitter plate (Fig. 2c, $\#$2). For each total discharge tested ($Q = Q_f+Q_m$), the weirs heights are set to get a water surface parallel to flume bottom under steady base flow conditions. Then, these heights are unchanged for the unsteady flow experiments.

In the following, the streamwise and spanwise distances are normalized by the FP width $B_f$ (Fig. 2b), i.e., $x^*=x/B_f$ and $y^* = y/B_f$. The vertical distance is normalized by the peak flow depth over the FP, denoted as $h^p_f$, i.e., $z^*=z/h^p_f$.

Fig. 2

Compound open-channel flume with a working length = 18 m and a working width = 2 m (left-hand 2/3 of the total flume width): a view downstream; b sketched of a cross-section (view downstream) in which $h_f$ and $h_m$ are the average water depths over the Flood Plain (FP) and in the Main Channel (MC), and $B_f$ and $B_m$ are the widths of FP and MC, respectively; and c sketch of a right-hand side view of the Compound Channel (CC), displaying the sidewall separating the two inlet tanks ($\#1$), the upstream and downstream vertical splitter plates ($\#2$), a honeycomb ($\#3$), and tailgate weirs ($\#4$)

To assess the influence of the flow partition between sub-sections at the flume entrance [17, 19, 44], two types of inflow conditions were studied: (i) a total discharge hydrograph Q(t) (where $Q(t)=Q_m(t)+Q_f(t)$), with at any time t, a slightly unbalanced inflow partition between sub-sections with respect to a uniform flow partition of same Q(t)-value; and (ii) a hydrograph Q(t) with a noticeably unbalanced inflow partition. These two inflow conditions will be identified as ‘Case I’ and ‘Case II’, respectively. The discharge hydrographs associated with Case I and Case II are shown in Fig. 3, and their main features are reported in Table 2, using ensemble averages of the flow parameters (to be detailed in Sect. 3.2.).

In Fig. 3, the measured time-varying discharges $\langle Q\rangle$, $\langle Q_m\rangle$ and $\langle Q_f\rangle$ are normalized by their analogous values under steady Base Flow (BF) conditions, denoted as $\langle Q^b \rangle$, $\langle Q_m^b \rangle$ and $\langle Q_f^b \rangle$. The BF conditions correspond to constant total and sub-section discharges for 300 s and 200 s for Case I and Case II, respectively. In addition, time is scaled by the duration of the rising limb of the total flow rate, $T_Q^r$ (with $t/T^r_Q=0$ when the total discharge Q starts rising and $t/T^r_Q=1$ at Peak Flow (PF)). For Case I and Case II (Table 2), the rising time of the total discharge $T^r_Q$ equals 90 s and 150 s, respectively, while the falling time (to reach for the next BF) $T^f_Q$ equals 170 s and 230 s.

To quantify the disequilibrium in inflow partition at any time t (Fig. 3), the measured discharges in the MC and FP are compared to the theoretical sub-section discharges of a uniform flow of same total flow rate Q. The latter are estimated using the DEBORD formula developed by Nicollet and Uan [9] (to be seen in Sect. 4.3, Eqs. (16) to (19)). Figure 3 shows that the inflow partition between sub-sections is more unbalanced for Case II than for Case I, especially around the peak flow.

Fig. 3

Inflow discharges in the MC and FP, $\langle Q_m \rangle$ and $\langle Q_f \rangle$, and total discharge ${\langle Q \rangle = \langle Q_m \rangle + \langle Q_f\rangle }$, scaled by the base flow values ($\langle Q_m^b \rangle$, $\langle Q_f^b \rangle$, and $\langle Q^b \rangle$) as a function of time t scaled by the rising time to the peak total discharge $T_Q^r$: experimental data (—) vs. theoretical discharges for a uniform flow of same total flow rate Q (- - -) [9]. Operator $\langle \ \rangle$ refers to ensemble averaging

Table 2 Features of the two inflow discharge hydrographs (Case I and Case II) at Base Flow (BF) and Peak Flow (PF)

2.2 Repetition of the discharge hydrographs and unsteadiness levels

For Case I or Case II, 100 consecutive runs were performed to estimate ensemble averages of the time-varying flow parameters, i.e.: (i) the sub-section inflow discharges ($Q_m$ and $Q_f$); (ii) the flow depths in the MC and FP ($h_m$ and $h_f$) at various streamwise position $x^*$; and (iii) the three components of the velocity ($U_x$, $U_y$, and $U_z$ along x-, y-, and z- axes) at one $x^*$-position at the MC/FP interface for each $z^*$-elevation. Note that, two consecutive discharge hydrographs are separated by a steady BF. As shown in Fig. 4 by the time series of the inflow discharge $Q_m(t)$, flow depth $h_m(t)$ at ${x^* = 10}$, and of the interfacial velocities $U_x(t)$ and $U_y(t)$ at ${x^* = 10}$ and ${z^* = 0.18}$, the repeatability of the flow parameters is fairly good at first sight. However, we will see in Sect. 3.2 that a large number of runs are required for the ensemble averages to converge within the measurement uncertainty range.

Fig. 4

Synchronous time series (see Sect. 2.3) of the measured flow parameters for four consecutive runs (Case I): inflow discharge in the MC ($Q_m)$, flow depth in the MC ($h_m$) at ${x^* = 10}$ and ${y^* = -0.5}$, streamwise and spanwise velocities ($U_x$ and $U_y$) at ${x^* =10}$, ${y^* = 0}$ and ${z^*=0.18}$. The windowing used in the segmentation (Sect. 3.2.1) with a duration of 520 s is depicted by a yellow rectangle

Table 3 Features of the stage hydrographs in MC and FP at $x^*$ = 10 for Cases I and II at Base Flow (BF) and Peak Flow (PF)

Regarding the level of unsteadiness of Case I and Case II, they are comparable based on the unsteadiness coefficient defined by Takahashi [45], which reads in each sub-section:

$$\begin{aligned} \lambda _i = \frac{\langle h^p_i\rangle -\langle h^b_i\rangle }{T^r_{h_i}\sqrt{g\langle h^p_i\rangle }S_o} \end{aligned}$$

(1)

where $\langle h^p_i\rangle$ is water depth at PF in sub-section i, $\langle h^b_i\rangle$ is water depth at BF in sub-section i, with $i =m$ for the MC and $i = f$ for the FP.

The values of $\lambda _m$ and $\lambda _f$ (Eq. (1) with $i =m$ and $i = f$, respectively), measured at $x^* = 10$, are reported in Table 3, along with the flow depths $\langle h_m\rangle$ and $\langle h_f\rangle$, the relative flow depth $\langle h_r\rangle = \langle h_f\rangle / \langle h_m\rangle$, the rising time to reach for the peak flow depth in MC $T_{h_m}^r$, and the falling time $T_{h_m}^f$ from the PF to the next BF. The $\lambda _m$- and $\lambda _f$- values are in the lower range of the values found in the literature on unsteady flows in CCs. For instance, the $\lambda _m$-values range from 0.19 to 0.75 in the experiments of Tominaga et al. [23], and from 0.38 to 5.03 in the experiments of Lai et al. [24]. As a result, Cases I and II can be considered as weakly unsteady discharge hydrographs. However, the results will show a posteriori a noticeable hysteresis loop in the time evolution of the flow parameters (as will be seen in Sect. 6.1, Fig. 9).

No noticeable transverse gradient of the water surface was measured. For instance, at PF at $x^* = 10$, the difference $<h_m>-(<h_f>+0.117)$ is approximately 1 mm (see the values in Table 3, with bank full depth in MC = 0.117 m in Fig. 2). Nevertheless, this order of magnitude should be compared with the accuracy of the ultrasonic sensor (± 0.3 mm) and with the standard deviation of the measurements around the ensemble average (from 0.5 to 2 mm for BF and PF, Cases I and II [46, Fig. 3.12, p. 95]).

2.3 Measurement techniques

The inflow discharges in MC and FP, $Q_m$ and $Q_f$, are monitored with two electromagnetic flowmeters (Waterflux) manufactured by Krohne, with an acquisition rate of 50 Hz, and with an accuracy better than 0.3 $\%$ of the measured value. The two flowmeters are placed along the inlet pipes between the tower and the two inlet tanks.

Water surface elevations were measured using six ultrasonic sensors manufactured by Baumer (UNDK 20I6912/S35A). Each sensor has an acquisition rate of 50 Hz, and an accuracy better than 0.3 mm. Measurements were taken at streamwise positions ${x^*=6}$, 7, 10, 13, 14 and 15, both in the MC (at $y^*= -0.5$) and over the FP (at $y^*= 0.5$). First, six sensors were simultaneously measuring at $x^*=6$, 10 and 13, in both sub-sections for 100 runs. Second, four sensors were measuring at $x^*=7$ and 14 for 100 runs. Last, two sensors were measuring at $x^*=15$ for 100 runs.

Velocity was measured using an Acoustic Doppler Velocimeter (ADV) with a side-looking probe (Vectrino+), and with a sampling rate of 100 Hz. The sampling volume is 5 cm away from the probe in the lateral direction, and can be approximated as a 7 mm long cylinder with a 6 mm diameter. The flow was seeded with 40 $\mu$m polyamide particles to increase both the signal-to-noise ratio and the correlation level within the measuring volume. Measurements were essentially taken at the vertical interface between MC and FP (at $y^*= 0$) at $x^*=$ 10 and at various elevations (i.e., 8 to 12 measuring points over the water depth depending on the flow case). Last, according to the manufacturer, the accuracy was $0.5 \%$ of the measured velocity. Note that, based on recent measurements in the same flume for steady flows in a CC [19], the sampling standard errors for time-averaged flow parameters and turbulence statistics were approximately: 1$\%$, 9$\%$, and 16$\%$ for the time-averaged velocities, $\overline{U_x}$, $\overline{U_y}$ and $\overline{U_z}$, respectively; 3$\%$, 2$\%$, and 3$\%$ for the turbulence intensities $\sqrt{\overline{{U_x'}^2}}$, $\sqrt{\overline{{U_y'}^2}}$ and $\sqrt{\overline{{U_z'}^2}}$; and 10$\%$ for the Reynolds shear stress $-\overline{U_x'U_y'}$.

Note that the sub-section inflow discharges $Q_m$ and $Q_f$, the flow depths $h_m$ and $h_f$ at various x-positions, and the interfacial velocities $U_x$, $U_y$ and $U_z$ at ${x^*=10}$, are measured and recorded simultaneously using the program Labview (National Instruments).

3 Experimental data processing

3.1 Initial filtering and angular correction of the velocity data

As the ADV probe is fixed at a given z-elevation during the whole duration of a discharge hydrograph, the measuring volume of the probe can be outside water for high z (higher than the BF surface level), resulting in some erroneous velocity data. The latter have been discarded relying on the values of the Signal-to-Noise Ratio (SNR) for each velocity component and of the percentage of correlation within the measuring volume (COR). Only velocity measurements with SNR $\ge 22$ dB and COR $\ge 85\%$ were considered. Note that no additional despiking filter was used.

In addition, as the spanwise velocity $U_y$ is small compared to the streamwise velocity $U_x$, a potential misalignment of the ADV probe can have a strong impact on the measured values of $U_y$ [47]. The data of $U_y$ were therefore corrected based on steady uniform flow data (BF of Case I). Twenty measurements were carried out over the depth at the centerline of the MC ($y^* = -0.5$) and $x^* = 10$. We then assumed that the depth- and time-averaged spanwise velocity was zero as the flow was uniform. This procedure resulted in a rotation around the vertical axis of a yaw angle $\theta _z=-0.48^\circ.$

3.2 Ensemble averaging of the data

3.2.1 Windowing

To perform ensemble averaging of the hydrographs of discharge, stage, and velocities, times series of the instantaneous data were segmented. The segmentation is based on a windowing centered on the peak total inflow discharge, and the temporal window width was chosen to include the measurements of water depth and velocity of the two BFs from either side of each transient hydrograph. This width equals 520 s and 550 s for Case I and Case II, respectively. As illustrated in Fig. 4, this windowing was then applied to segment the time series of sub-section discharges, $Q_m(t)$ and $Q_f(t)$, sub-section flow depths, $h_m(t)$ and $h_f(t)$, and interfacial streamwise and spanwise velocities, $U_x(t)$ and $U_y(t)$.

Note that, the easiest windowing method would have been to drag a window (with a constant width) along the time series. This could not be done because, notably, the duration of a BF separating two successive transient hydrographs was slightly variable.

3.2.2 Convergence and dispersion of the ensemble averages

As previously mentioned in Sect. 2.2, for each measuring point of flow depth or velocity, each discharge hydrograph (Case I or Case II) was repeated 100 times, two consecutive hydrographs being separated by a steady BF. The objective was to compute ensemble averages over the set of transient data. The number of discharge hydrograph repetitions was set in order to get a satisfying convergence of the ensemble average of the key parameters used to describe the flow: inflow sub-section discharges ($Q_m$ and $Q_f$), flow depths in MC and FP ($h_m$ and $h_f$), and streamwise and spanwise velocity at the MC/FP interface ($U_x$ and $U_y$). For this purpose, the average over the i first runs was compared to the ensemble average over the 100 runs for each of the key parameters by computing the resulting bias. The required number of runs was estimated to be sufficient once the relative bias previously computed has become smaller than the sensor accuracy. The results of these tests are displayed in Fig. 5. Strictly speaking, the previous criterion does not fit the mathematical definition of a convergence test, but it makes possible to check that the ensemble average is contained in a reasonably small interval to assume the pointed variable as converged. Note that, to the authors’ knowledge, this kind of tests were not performed in the previous experimental studies on unsteady flows in CCs [e.g. 23, 24].

In Fig. 5, we present the difference between the ensemble average over the first i runs and the ensemble average over the 100 runs, normalized by the latter for the sub-section inflow discharges $\langle Q_m\rangle$ and $\langle Q_f\rangle$, and interfacial streamwise velocity $\langle U_x\rangle$. This normalization stems from the accuracy given by the manufacturers in percentage of the measured values (see Sect. 2.3), i.e., $\pm 0.3\%$ for the flow meter and $\pm 0.5\%$ for the ADV probe. We also analyze the convergence of the FP flow depth $\langle h_f\rangle$, but using dimensional data as the accuracy of the ultrasonic sensor is of $\pm 0.3$ mm.

Figure 5 shows that approximately 90 runs are required to obtain converged ensemble-averaged sub-section discharges and water depth. In contrast, 100 runs are not sufficient to get convergence of the ensemble average of interfacial velocity $U_x$, when considering the manufacturer accuracy ($\pm 0.5\%$). We then end up with residual fluctuations in the ensemble average that are due to the variability of the initial conditions (see Fig. 4), and to the high level of turbulence at the MC/FP interface, where Kelvin–Helmholtz coherent structures form under uniform flow conditions [15], and where velocity fluctuations are the strongest for steady non-uniform flows in CC [19].

The ensemble averages of the total discharge and sub-section discharges were previously shown in Fig. 3, and ensemble-averaged flow depths in MC and FP will be shown in Fig. 6 and 7. Ensemble-averaged time-varying mean velocity and Reynolds stress will be shown in Fig. 8 and 9. Kaddi [46] has calculated the standard deviation $\sigma$ associated to the ensemble averages of each flow parameter for Case I [46, Figure 3.12]. The maximum values of $\sigma$ for the sub-section discharges and flow depths were approximately $0.04 \langle Q_m\rangle$, $0.08 \langle Q_f\rangle$, $0.03 \langle h_m\rangle$, and $0.08 \langle h_f\rangle$. For the interfacial velocity, the maximum standard deviation is far much higher, i.e. approximately $0.27 \langle U_x\rangle$ and $2 \langle U_y\rangle$.

From a practical point of view, it is interesting to estimate the uncertainty on the key parameters when using less runs, e.g. 20. According to Fig. 5, the uncertainty on $Q_m$ is ±1.5$\%$, on $Q_f$ is ±4$\%$, on $U_x$ is ±25$\%$, and on $h_f$ is $-$0.3 mm to 1 mm. The latter should be compared to the standard deviation of the measurements around the ensemble average of $h_f$ $\approx$ 0.5 mm at x = 6 m at BF and PF [46, Fig. 3.12, p. 95].

Fig. 5

Convergence of the ensemble averages of the sub-section discharges, $\langle Q_m\rangle$ and $\langle Q_f\rangle$, interfacial streamwise velocity $\langle U_x\rangle$ (at ${x^*=10}$, ${y^*=0}$, and ${z^*= 0.18}$), and FP flow depth $\langle h_f\rangle$ (at ${x^*=6}$ and ${y^* = 0.5}$). The area bounded by the two horizontal lines represents the accuracy on the measured parameter: $\pm 0.3 \%$ for the discharges, $\pm 0.5\%$ for the velocity, and $\pm 0.3$ mm for the flow depth

3.2.3 Separating time-varying mean velocity and turbulence statistics

It was already mentioned that the ensemble averages of the instantaneous streamwise and spanwise velocities, $\langle U_x\rangle$ and $\langle U_y\rangle$, were not fully converged after 100 runs, due to both variations in the inflow conditions and high levels of turbulence at the MC/FP interface. In order to eliminate the residual velocity fluctuations caused by the Kelvin–Helmholtz coherent structures, a moving average over 4 s was applied to the unsteady data of $\langle U_x\rangle$ and $\langle U_y\rangle$. This duration of 4 s corresponds to the turbulence integral time-scale at the MC/FP interface, which was estimated based on a time autocorrelation function of the streamwise velocity fluctuations for some samples at PF and during the BF [46, Fig. 3.15]. The resulting smoothed data of time-varying mean velocity are denoted as $U_x(t)$ and $U_y(t)$, the streamwise and transverse turbulent velocity fluctuations being accordingly defined as

$$\begin{aligned} U'_x(t) = \langle U_x \rangle (t) - U_x(t) \end{aligned}$$

(2)

$$\begin{aligned} U'_y(t) = \langle U_y \rangle (t) - U_y(t) \end{aligned}$$

(3)

and the ensemble-averaged Reynold stresses are defined as:

$$\begin{aligned} \langle \tau _{xy}(t) \rangle= & {} -\rho \langle U'_x(t)U'_y(t) \rangle \end{aligned}$$

(4)

$$\begin{aligned} \langle \tau _{xx}(t) \rangle= & {} -\rho \langle U'_x(t)^2 \rangle \end{aligned}$$

(5)

$$\begin{aligned} \langle \tau _{yy}(t) \rangle= & {} -\rho \langle U'_y(t)^2 \rangle \end{aligned}$$

(6)

Importantly, we should keep in mind that fluctuations $U'_x(t)$ and $U'_y(t)$ are actually caused by both turbulence and small variations in the inflow conditions (between runs), resulting in slightly over-estimated values of $U'_x(t)$ and $U'_y(t)$. Note that, separating both influences is complex, since this comes down to distinguishing two different uncertainties within an overall uncertainty, which was not done during the present study.

4 1D+ and 1D numerical models

The 1D+ and 1D models used in the present study were implemented in the code MAGE developed at INRAE. These models are based on a Preissmann semi-implicit numerical scheme.

4.1 The 1D+ independent sub-sections model (ISM)

As previously mentioned in Sect. 1, the 1D+ model termed ‘Independent Sub-sections Model (ISM)’, was initially developed by Proust et al. [1] for modelling steady non-uniform overbank flows in idealized non-prismatic geometries, by relying on the research works of Yen et al. [38] and Bousmar and Zech [39]. The key issue was how to accurately predict both flow depth and mean velocity in the FP. To this end, the ISM solves a momentum conservation equation in each sub-section (left-hand FP, right-hand FP, and MC), instead of solving a momentum (or energy) conservation equation on the total compound cross-section like the classical 1D approaches (e.g., the Divided Channel Method (DCM) of Lotter [42], the DEBORD method of Nicollet  and Uan [9] used herein, or the Exchange Discharge Model (EDM) of Bousmar and Zech [39]). This enables the water level and the sub-section averaged velocities to be simultaneously calculated, without priority to any variable. In addition, as shown in Proust et al. [1, Table 2], it enables to explicitly model the lateral exchange of mass and momentum between sub-sections, and to take into account the actual flow partition between MC and FP at the upstream boundary of a river reach. Last, unlike the DCM, the DEBORD method, and the EDM, the ISM does not assume equal head loss gradients in all sub-sections, which gives a certain degree of freedom in the evolution of each sub-section discharge. For the 46 flow configurations experimentally investigated in various geometries (straight CCs, skewed CCs, CCs with narrowing or enlarging FPs, abrupt FP contraction) by Proust et al. [1], the ISM predicted FP flow depth, $h_f$, and FP mean velocity, $U_f$, with a maximum relative error of 8$\%$ and 19$\%$, respectively.

For a CC with two sub-sections (configuration studied here), the ISM consists in a set of three coupled ordinary differential equations, i.e., one mass conservation equation across the total section (Eq. 7) and two momentum conservation equations (one in each sub-section) (Eqs. 8 and  9):

$$\begin{aligned} \frac{\partial A}{\partial t} + \frac{\partial (Q_m + Q_f)}{\partial x} = 0 \end{aligned}$$

(7)

$$\begin{aligned} \frac{\partial Q_m}{\partial t} + \frac{\partial }{\partial x}\left( \frac{Q_m^2}{A_m}\right) +gA_m\frac{\partial Z}{\partial x} = -gA_mS_m^f - \frac{{\tau _{xy}}_d h_f}{\rho } + U_{{x}_d}q \end{aligned}$$

(8)

$$\begin{aligned} \frac{\partial Q_f}{\partial t} + \frac{\partial }{\partial x}\left( \frac{Q_f^2}{A_f}\right) + gA_f\frac{\partial Z}{\partial x} = -gA_fS_f^f + \frac{{\tau _{xy}}_d h_f}{\rho } - U_{{x}_d}q \end{aligned}$$

(9)

where A is total wet area, Z is water level, g is gravity acceleration, $A_m$ and $A_f$ are the wet areas in MC and FP, $S_m^f$ and $S_f^f$ are the bed-friction slopes in MC and FP, $\rho$ is water density, ${\tau _{xy}}_d$ is the interfacial depth-averaged Reynolds stress, q is the interfacial lateral discharge (q being positive when a net mass transfer occurs from MC to FP), and $U_{{x}_d}$ is the interfacial depth-averaged streamwise velocity.

In addition, the lateral discharge per unit length is defined as:

$$\begin{aligned} q = \frac{\partial A_f}{\partial t} + \frac{\partial Q_f}{\partial x} = -\frac{\partial A_m}{\partial t} - \frac{\partial Q_m}{\partial x} \end{aligned}$$

(10)

and the interfacial depth-averaged Reynolds stress, which is derived from a mixing length model proposed by Bousmar and Zech [39], reads

$$\begin{aligned} {\tau _{xy}}_d = \rho \psi ^t (U_m-U_f)^2 \end{aligned}$$

(11)

In Eq. (11), the streamwise and spanwise velocity fluctuations are both assumed to be proportional to $U_m-U_f$. The interfacial turbulent exchange coefficient $\psi^t$ equals 0.02, the default value proposed by Proust et al. [1] that was estimated from steady uniform flow data in various CC flumes with smooth FPs. The same $\psi^t$-value will be used for modelling the experimental unsteady flows. This value differs from the $\psi^t$-value calibrated along the Rhône river reach on field measurements (Table 1). The latter (0.03$-$0.08) is higher than the former (0.02), as it accounts for all the head losses not related to bed friction.

The interfacial depth-averaged streamwise velocity is defined as

$$\begin{aligned} {U_{x}}_d = \phi U_m + (1-\phi ) U_f \end{aligned}$$

(12)

where $\phi$ is a weighting coefficient. As a first approximation, we can consider than ${\phi \approx 1 }$ when water leaves the MC (i.e., ${q >0}$), or ${\phi \approx 0 }$ when water leaves the FP (i.e., ${q <0}$) [1].

The sub-section bed-friction slope is computed using Manning’s formula (Eq. 13), where $R_i$ is the hydraulic radius of sub-section i and $n_i$ is the Manning roughness in sub-section i.

$$\begin{aligned} S_{i}^f = \frac{Q_i^2 n_i^2}{R_i^{4/3}A_i^2} \end{aligned}$$

(13)

with i = m and f in MC and FP, respectively.

Last, it should be noted that, in the ISM, the lateral momentum exchange by the secondary currents and the associated head losses are considered to be nil at the MC/FP interface, in agreement with the measurements of Dupuis et al. [15, Fig. 11] for steady uniform flows, and of Proust and Nikora [19, Fig. 18] for steady uniform and non-uniform flows.

4.2 Adaptation of the 1D code MAGE to implement the 1D+ ISM

The passage from one momentum conservation equation formulated on the total compound cross-section in the case of the 1D DEBORD method [9] to three momentum conservation equations in the case of the 1D+ ISM, requires building a new modeling of the geometry in order to be able to distinguish the left-hand and right-hand FPs, and requires calculating their geometrical parameters (wetted width, area and perimeter) according to the water level. Note that, the lack of distinction between left and right FPs in the classical 1D approach is specific to the code MAGE, and is not a restriction imposed by the DEBORD method.

In order to ensure the backward compatibility of MAGE and thus to be able to continue to use the DEBORD method, we used an object modeling of the river geometry and its hydraulic data. For example, a ‘discharge’ object was created, which could have one or three components depending on whether the DEBORD method or ISM is used. This allows to manipulate these objects (value assignment, addition, subtraction, multiplication by a scalar, etc.) independently of the underlying DEBORD or ISM modeling.

Of course, all the discretization of the Saint-Venant equations to apply the Preissmann numerical scheme had to be redone for the ISM, managing in particular the couplings between the flows in the three sub-sections.

In MAGE, the solution of the nonlinear discretized system is obtained by an iterative method of Newton–Raphson type. At each iteration a linear system must be solved. With DEBORD method we apply the so-called double-sweep method, which is actually an adaptation of the Gauss method to the particular form of the matrix. In the ISM, the transposition of the double-sweep from two to four equations does not work. We had to implement a direct method to solve the linear system. This is more expensive than the double-sweep would be if it was numerically stable.

The implementation of the boundary conditions also had to be adapted for the ISM. At the downstream boundary condition, the situation is simple as the water level across the channel is always unique when considering either a stage hydrograph or a rating curve. It is only when the downstream flow is taken into account (rating curve) that the choice was made to consider only rating curves based on the total flow rate (sum of the flow rates in the three sub-sections). At the upstream boundary condition, the situation is more complex as it is necessary to inject an inflow hydrograph in each of the sub-sections. In the case of a laboratory experiment such as the present one, these inflow hydrographs were measured, while in the case of a river, the hydrological models give us the total flow rate only. It is thus required to desegregate this total flow rate into three sub-section inflow discharges. It was therefore necessary to adapt the format of the boundary conditions file so that it could contain three flows instead of one (as a function of time) and to implement a method for desegregating the total inflow in the case of overbank flows.

Last, as ISM does not allow to model the local absence of overflow in one of the FPs, it was necessary to implement an automatic switchover mechanism between ISM and DEBORD method for the situations where ISM fails. At each time step, we try to solve with the ISM. If the calculation fails (e.g. in absence of water over one or two FPs), we solve with the DEBORD method. The problem can also occur at the beginning or end of the overflow.

Note that the current implementation of the ISM is not completely isofunctional with DEBORD method. In particular, it still lacks the consideration of meshed networks and a fine management of the mixing of flows at confluences. This last point is important to couple MAGE-ISM with the AdisTS code of pollutant and sediment transport developed at INRAE.

4.3 Benchmark 1D modelling

The 1D+ ISM simulations of the experimental flows (described in Sect. 2) were compared with 1D simulations based on the DEBORD method [9]. In this 1D approach, both mass conservation equation (Eq. 14) and momentum conservation equation (Eq. 15) are solved on the total compound cross-section.

$$\begin{aligned} \frac{\partial A}{\partial t} + \frac{\partial Q}{\partial x} = 0 \end{aligned}$$

(14)

$$\begin{aligned} \frac{\partial Q}{\partial t} + \frac{\partial }{\partial x}\left( \frac{\beta Q^2}{A}\right) + gA\frac{\partial Z}{\partial x} = -gAS^f \end{aligned}$$

(15)

where the bed-friction slope on the total cross-section is defined as:

$$\begin{aligned} S^f = \frac{Q^2}{D^2} \end{aligned}$$

(16)

where D is the total conveyance capacity, with

$$\begin{aligned} D = D_m + D_f = 1/n_mBA_mR_m^{2/3} + 1/n_f\sqrt{A_f^2 + A_mA_f(1-B^2)}R_f^{2/3} \end{aligned}$$

(17)

where $B<1$ is a function of $n_f$, $n_m$, and $R_f/R_m$ [9] accounting for the turbulent momentum exchange at the MC/FP interface, which is responsible for the FP flow acceleration and the MC flow deceleration under steady uniform flow conditions. Note that, in Eq. (17), it is implicitly assumed that $S^f= S_m^f = S_f^f$ like in the DCM of Lotter [42].

In Eq. (15), $\beta$ is the Boussinesq coefficient accounting for the non-uniformity of the velocity across the CC, with

$$\begin{aligned} \beta = \left( \frac{\eta ^2}{A_m} + \frac{1}{A_f}\right) \frac{A}{1+\eta ^2} \end{aligned}$$

(18)

and

$$\begin{aligned} \eta = \frac{Q_m}{Q_f}=\frac{n_f}{n_m}\frac{BA_m}{\sqrt{A_f^2 + A_mA_f(1-B^2)}}\left( \frac{R_m}{R_f}\right) ^{2/3} \end{aligned}$$

(19)

We can also recall that, in the DEBORD method, it is assumed that the flow partition between the MC and FP is the same (i.e. same $\eta$-value) for a uniform flow and a non-uniform flow of same total discharge Q.

5 Flood wave

5.1 Stage hydrographs

Fig. 6

Measured flow depths in the MC and FP, $\langle h_m\rangle$ and $\langle h_f\rangle$, normalized by the local base flow depth values, $\langle h_m^b\rangle$ and $\langle h_f^b\rangle$, as a function of time t, at various downstream x-positions. Operator $<>$ refers to ensemble averaging

Fig. 7

1D and 1D+ (ISM) simulations of the FP flow depth, $h_f$, against experimental data at various x-positions. Operator $<>$ refers to ensemble averaging

The stage hydrographs measured in MC and FP are shown in Fig. 6. The flow depths $\langle h_f\rangle$ and $\langle h_m\rangle$ are scaled by the respective BF depths $\langle h_f^b\rangle$ and $\langle h_m^b\rangle$. Figure 6 shows that, for both Cases I and II, the depth hydrographs feature a rising limb faster than the recession. This results in a positive skewness parameter—as defined by Fleischmann et al. [29] by replacing the derivative of discharge by the derivative of flow depth−, which is commonly observed along real streams.

Figure 7 additionally shows a comparison between simulated (using both 1D and 1D+ models) and measured flow depths in the FP, $\langle h_f\rangle$. Based on the measurements and 1D+ ISM simulations (which are in very good agreement with the measurements, see data at $x = 6$ m, 10 m, and 13 m), the flood wave attenuation along the flume is found to be small. Between x = 1 m and x = 14 m, the ISM calculated a decrease by ${-3 \%}$ of the MC peak flow depth for Case I, and a decrease by $-5.5\%$ for Case II. We compared these attenuation rates with the exponential decay law proposed by Lai et al. [24], which was derived from their experimental data set (composed of 18 test cases):

$$\begin{aligned} h^p / h^{p0} = A \exp (-B x/ (h^b/S_0). \end{aligned}$$

(20)

with $A = 1$ and $B = 0.42$ for long duration floods [24, Fig. 7], the latter being defined based on the unsteady parameter ($\lambda _m$ in Table 3 for the MC). Using Eq. (20) leads to a decrease by $-4 \%$ and $-3.8 \%$ between $x = 1$ m and 14 m for Case I and Case II, respectively. These percentages are of the same order of magnitude as those previously calculated using ISM.

As regards the longitudinal propagation of the PF depth, no noticeable time lag was observed between x = 6 m and 15 m, when considering the total duration of the discharge hydrograph as a reference time-scale. This could be expected since, if we consider $\sqrt{gh_m^p}$ as a first approximation of the flood wave celerity in MC, the time the wave takes to cross the flume is 14 s and 13 s for Case I and Case II, respectively.

5.2 Influence of the upstream flow partition

Figure 7 shows that, for Case I, comparable results are obtained for the 1D+ ISM and the 1D model, both simulations being close to the measured FP flow depth at x = 6 m, 10 m, and 13 m. In contrast, for Case II, the 1D+ simulations are closer to the measurements than the classical 1D simulations during the transient phase at x = 6 m and 10 m. This could be due to the inflow partition between MC and FP that is imposed by the models as upstream boundary condition. For the 1D+ ISM, the measured inflow partition is imposed at x = 0 m, whereas the 1D classical model considers at this position a uniform inflow partition calculated using the DEBORD Method (Fig. 3). We recall that for Case I, measured inflow partition and uniform flow partition are little different, while they significantly differ for Case II. This led the 1D model to underestimate the peak flow depth at x = 6 m and x = 10 m for Case II (Fig. 7). Based on the comparison between 1D+ and 1D simulations, this underestimate of the flow depth for Case II is maximum near the flume entrance (data at $x^*=1$). We will see in the next sections that, if the flow partition between sub-sections differs from the uniform flow partition, it causes a lateral discharge q between sub-sections and associated head losses due to momentum exchange by the mean flow ($S_i^m$).

At this stage, the present results would suggest that (i) accounting for the actual upstream flow partition, and (ii) explicitly modelling the lateral discharge q and associated head losses $S_i^m$ could be of primary importance when predicting the water surface profiles. Note that a large variation in the inflow partition can lead to dramatic changes in the flow depth as experimentally observed for non-uniform flows in a straight CC [18, 19].

6 Time-varying flow parameters at the MC/FP interface

Fig. 8

FP flow depth $h_f$ at ${y^*=0.5}$ and ${x^*=10}$. Interfacial parameters at ${y^*=0}$ and ${x^*=10}$: lateral discharge q, depth-averaged streamwise and transverse mean velocities, ${\langle U_x \rangle }_d$ and ${\langle U_y \rangle }_d$, and depth-averaged Reynolds stresses, ${{\langle \tau _{xy} \rangle }_d = -\rho {\langle U_x'U_y' \rangle }_d}$, and ${\langle \tau _{yy} \rangle }_d = -\rho {\langle U_y'^{2} \rangle }_d$

The measured and simulated flow parameters at the MC/FP interface are shown in Figs. 8, 9, and 10. The experimental measurements are time-varying depth-averaged data for both the mean flow and turbulence statistics. To the authors’ knowledge, this type of velocity data for unsteady overbank flows has been very rarely collected experimentally (with the exception of the propeller data of $U_m$ and $U_f$ measured by Tominaga et al. [23] and simulated by Bousmar et al. [27]).

6.1 Depth-averaged mean spanwise velocity and lateral discharge

The measured depth-averaged mean spanwise velocity ${\langle U_y \rangle }_d = \frac{\langle q \rangle }{\langle h_f \rangle }$ is shown in Fig. 8e and f. For Case I, the lateral flow occurs from MC to FP (${\langle U_y \rangle _d >0}$) at the beginning of the rising limb, then takes the opposite direction from FP to MC (${{\langle U_y \rangle }_d <0}$) during the rest of the hydrograph. For Case II, the lateral flow occurs from FP to MC during all the hydrograph. The ${\langle U_y \rangle }_d$-values simulated by the ISM fairly match the experimental data for both test cases.

Usually, during the rising limb of a discharge hydrograph, the mass exchanges are directed towards the FPs [24], while they are directed towards the MC during the falling limb. The present results would suggest that the mass exchanges between sub-sections are strongly influenced by the inflow partition. Indeed, for Case II (Fig. 3), we imposed an excess in FP discharge (compared with the uniform FP discharge) during the whole hydrograph, which results in a mass transfer towards the MC over the whole duration of the transient phase. This is supported by the stage discharge hydrographs in Fig. 7, which shows that for Case II, at x = 10 m, the 1D+ results are closer to the measurements than the 1D results (highlighting that considering the actual upstream flow partition is required). As regards Case I, the negative ${\langle U_y \rangle }_d$-values observed during the second part of the rising limb would also suggest that imposing a (quasi-)uniform flow partition at the flume entrance is also a forcing of the lateral mass exchange, as the rising limb is usually associated with a deficit in FP flow. This is confirmed by the streamwise evolution of the lateral discharge q for Case I shown in Fig. 10, see the data at x = 1 m and 5 m, for which the simulated discharge q is negative during all the hydrograph duration, while when moving downstream (data at x = 10 m and 13 m) the ‘classical’ mass transfer towards the FP can be observed at the first phase of the rising limb. Figure 10 additionally confirms that for Case II the high forcing in the upstream flow partition is felt along the whole measuring domain.

The results on the lateral discharge q (Fig. 8g and h) are very similar to the results on ${\langle U_y \rangle }_d$. We are therefore in the presence of a river-floodplain connectivity that is influenced by the upstream boundary condition for both cases, especially during the rising stage phase. Figure 9a and b show that the 1D+ ISM fairly well reproduce the dynamic evolution of this river-floodplain connectivity (which cannot be calculated by a classical 1D model), with better results for Case I than for Case II.

6.2 Depth-averaged mean streamwise velocity

The depth-averaged streamwise mean velocity ${\langle U_x \rangle }_d$ measured at $x^*=10$ is shown in Figs. 8 and 9. In Fig. 8c and d, we can notice that the peak value of ${\langle U_x \rangle }_d$ is reached before the peak value of FP flow depth. This result was also observed by Tominaga et al. [23] when considering the sub-section-averaged streamwise velocities $U_m$ and $U_f$. The hysteresis loops displayed in Fig. 9c and d highlight that, for a fixed water depth, the streamwise velocity during the rising limb is higher than that during the falling limb (as previously observed in CC [24] an in rectangular channel [48, 49]), owing to accelerated and decelerated vertical profiles of streamwise mean velocity, respectively.

Surprisingly, it can also be noticed that ${\langle U_x \rangle }_d$ decreases below the BF value immediately after the falling limb (Fig. 8c and d). This result was not observed in the literature on unsteady flows in CC or single channel [23, 24, 48,49,50]. This can actually be explained by the relationship between the interfacial depth-averaged streamwise velocity ${U_x}_d$ and streamwise sub-section velocities, $U_m$ and $U_f$, in the presence of an interfacial lateral mass exchange by the mean flow. According to Proust et al. [1, 40], the ${U_x}_d$-value is partly controlled by the direction of the lateral discharge, i.e. ${U_x}_d \approx U_i$ when mass transfer occurs from sub-section i to j. This hypothesis is based on experimental mean velocity profiles with mass transfers from narrowing FPs to MC [20, 22] or with mass transfers from MC to enlarging FPs [20, 40]. As a result, in the present experiments, as the flow occurs from FP to MC during the falling limb (${\langle U_y \rangle }_d<0$ in Figs. 8e, f and 10), we can assume than ${U_x}_d \approx U_f$. Considering that $U_f \le {U_x}_d \le U_m$ during the BF (e.g., ${U_x}_d = (U_f+U_m)/2$ if $B_f = B_m$ for Yen at al. [38]), just after the falling limb we observe an overshoot in ${U_x}_d$ with ${U_x}_d$ increasing from $U_f$ to approximately $(U_f+U_m)/2$.

In Fig. 9c and d, we can notice that, while both 1D and 1D+ models qualitatively reproduce the shape of the hysteresis loops in the relationship ${\langle U_x \rangle }_d$ vs. $\langle h_f \rangle$, the ISM results are better than those of the 1D model (see also Fig. 8c and d) since the former are relevant approximations of the relationship between either ${\langle U_y\rangle }_d$ or ${\langle U_x\rangle }_d$ and $\langle h_f \rangle$ during the falling limb. Note that ${U_x}_d$ is computed in the ISM using a weighting coefficient of ${\phi = 0.3 }$, i.e. a more important weight is given to the FP velocity $U_f$ than to the MC velocity as the flow is preferentially directed from FP to MC for both cases (Fig. 8e and f). In the 1D model, ${U_x}_d$ is not explicitly calculated, but calculated a posteriori from $U_m$- and $U_f$-values by assuming that ${U_x}_d = (U_m+U_f)/2$ at any time t.

Fig. 9

1D and 1D+ (ISM) simulations vs. experimental data at ${x^* = 10}$: a, b time-varying depth-averaged mean spanwise velocity at the interface ${\langle U_y \rangle }_d$ as a function of time-varying FP flow depth $\langle h_f \rangle$; and c, d time-varying depth-averaged mean streamwise velocity at the interface ${\langle U_x \rangle }_d$ as a function of $\langle h_f \rangle$

Fig. 10

1D+ (ISM) simulation of the lateral discharge $\langle q \rangle$ at the MC/FP interface (${y^*=0}$) and $x^*$ = 1, 5, 10 and 13

6.3 Depth-averaged Reynolds stresses

Measured depth-averaged turbulence statistics are shown in Fig. 8. The transverse Reynolds stress ${{\langle \tau _{xy} \rangle }_d = -\rho {\langle U_x'U_y' \rangle }_d}$ (Fig. 8i and j) experienced a noticeable decrease as the flow depth increases from BF to PF (Fig. 8a and b). This could be expected as, with an increasing flow depth, the velocity difference $U_m-U_f$ decreases, the latter being a driver of the shear layer turbulence and especially of the Kelvin–Helmholtz vortices [19, 51, 52]. Note that a drop in turbulence intensity ${{\langle \tau _{yy} \rangle }_d}$ is also observed from BF to PF.

In the ISM, the transverse Reynolds stress ${{\langle \tau _{xy} \rangle }_d}$ is modelled by Eq. (11). The 1D+ ISM gives a good estimate of the highest values of ${{\langle \tau _{xy} \rangle }_d}$ at BF, while the classical 1D model well predict the lowest values of ${{\langle \tau _{xy} \rangle }_d}$ at PF (Fig. 8i and j). To explain these results, three hypotheses can be put forward.

First, can we assume that Kelvin–Helmholtz vortices develop at the FP/MC interface during the whole hydrograph duration? A necessary condition for the emergence of Kelvin–Helmholtz structures in shallow flows is that ${\lambda =(U_2-U_1)/(U_2+U_1)>0.3}$ [16, 19, 51, 52], where $U_2$ and $U_1$ are characteristic streamwise velocities outside the mixing layer on the high-speed stream side and low-speed stream side, respectively. Kaddi [46] calculated the $\lambda$-values from the ISM results, assuming than $U_2 \approx U_m$ and $U_1 \approx U_f$. For Case I, $\lambda$ ranges from 0.6 (BF) to 0.4 (PF), while for Case II, $\lambda$ ranges from 0.55 (BF) to 0.25 (PF). As a result, Kelvin–Helmholtz structures should be present for Case I during the whole hydrograph, and for Case II during a big part of the hydrograph except around the PF (assuming that there is no time and space inertia to dissipate them, a rough approximation). The noticeable decrease in the measured data of ${{\langle \tau _{xy} \rangle }_d}$ cannot thus be attributed to the absence of Kelvin–Helmholtz structures −which could have explained the overestimate of ${{\langle \tau _{xy} \rangle }_d}$ by the ISM during the transient phase (Fig. 8i and j).

Second, we can wonder if the turbulence measured at x = 10 m is a free-mixing-layer-like turbulence as modelled in the mixing length model (Eq. 11) or a shallow-mixing-layer turbulence hindered by bed-induced turbulence [52, Figure 26]. According to Proust et al. [52], the free-mixing-layer-like turbulence in shallow flows can only be observed not far away from the merging of the two incoming flows, i.e. when the bed friction number, S [53], is lower than 0.01. In this region, the scaled turbulence statistics are constant and equal to that of free-mixing layers. Further downstream, when $0.01 \lessapprox S \lessapprox 0.1$, the Kelvin–Helmholtz structures are longitudinally stretched (altered by bed-induced turbulence that de-correlates the transverse and streamwise velocity fluctuations); and when $S \gtrapprox 0.1$ the Kelvin–Helmholtz structures vanish and turbulence at the interface becomes negligible. Based on these results, it is reasonable to assume that 10 m downstream of the splitter plate, shear layer turbulence can be altered by the bed-induced turbulence. This could explain the overestimate by the mixing length model of the ${{\langle \tau _{xy} \rangle }_d}$-values for both cases (Fig. 8i and j). Note that the S-values could not be evaluated in the present experiment, as it would require the measurements of the shear layer width (i.e. of the transverse profiles of the mean streamwise velocity).

Last, the reduced values of turbulence statistics at the MC/FP interface during the transient phase could be partly due to the lateral shift of the region of high Reynolds stresses in the presence of a significant lateral discharge q, as observed by Proust et al. [17].

We can thus conclude that the overestimate of the transverse Reynolds stress by the ISM could reflect an alteration of shear layer turbulence by bed-induced turbulence or could be due to a transverse displacement of the peak Reynolds stress from either side of the interface.

7 Sub-section head losses and calibrating parameters in the 1D+ ISM

7.1 The three contributions to sub-section head losses

Fig. 11

The three contributions to head losses in MC and FP (see Eqs. 21−22), expressed as the ratio of the head losses by turbulent exchange to the bed-friction slope $S_i^t/S_i^f$ (dashed pink line ‘- - -’), and the ratio of the head losses by depth-averaged lateral mean flow exchange to the bed-friction slope $S_i^m/S_i^f$ (continuous blue line ‘—’), where i = m or f in MC and FP, respectively

One of the advantages of the 1D+ ISM is that the mass and momentum exchanges between sub-sections are explicitly modelled (Sect. 4.1, Eqs. 8−12). These lateral exchanges result in head losses in each sub-section [40]. The head losses caused by the shear layer turbulence reads in sub-section i:

$$\begin{aligned} S^t_{i} = \frac{{\tau _{xy}}_d h_i}{\rho gA_i} \end{aligned}$$

(21)

and the head losses related to the lateral momentum exchange by the mean flow reads

$$\begin{aligned} S^m_{i} = \frac{q({U_{x}}_d-U_i)}{gA_i} \end{aligned}$$

(22)

Based on comparisons between measurements and ISM results in prismatic and non-prismatic CCs, for steady non-uniform flows, Proust et al. [1, 40] showed that: (1) when approaching equilibrium, the head losses due to shear layer turbulence $S^t_{i}$ was predominant with respect to $S^m_{i}$, and of the same order of magnitude than the friction slope ${S^f_{i} = \frac{Q_i^2 n_i^2}{R^{4/3}_iA_i^2}}$; and (2) far from flow uniformity, $S^m_{i}>>S^t_{i}$ in narrowing FPs or in the presence of mass transfers from FPs to MC in straight CCs, and $S^m_{i} \approx S^t_{i}$ in enlarging FPs or in the presence of mass transfers from MC to FPs in straight CCs.

The sub-section head losses $S^m_{i}$ and $S^t_{i}$ are shown in Fig. 11, with a normalization by the bed-friction slope $S^f_{i}$. In the downstream part of the flume, where small lateral discharges are estimated by the ISM (Fig. 10), $S^t_{i}$ and $S^f_{i}$ are the two predominant contributions to head losses in both MC and FP and for both cases. In the upstream part of the flume, the three contributions $S^m_{i}$, $S^t_{i}$, and $S^f_{i}$ can be of the same order of magnitude as both lateral discharge q and velocity difference $U_m-U_f$ (imposed by the inflow partition) are high.

In such a context, the calibrating parameters $\psi^{\text {t}}$ and $\phi$ present in $S^t_{i}$ and $S^m_{i}$ become as important as the manning roughness coefficients $n_i$ in the friction slope $S^f_{i}$.

Fig. 12

Influence of the calibrating parameters in the 1D+ (ISM) modelling on the FP flow depth $\langle h_f \rangle$ and interfacial depth-averaged streamwise velocity ${\langle U_x \rangle }_d$: a, c weighting coefficient $\phi$ in the ${U_x}_d$-formula (Eq. 12); b, d turbulent exchange coefficient $\psi^{\text {t}}$ in the interfacial depth-averaged Reynolds stress formula (Eq. 11)

7.2 Sensitivity of the 1D+ ISM to calibrating parameters $\psi^t$ and $\phi$

In Fig. 12, we present the sensitivity of the FP flow depth $h_f$ and interfacial depth-averaged streamwise velocity ${U_x}_d$ to the interfacial velocity weighting coefficient $\phi$ (panels (a) and (c)) and to the turbulent exchange coefficient $\psi^{\text {t}}$ (panels (b) and (d)). As expected, ${U_x}_d$ significantly varies with $\phi$-coefficient (Eq. 12). Note that the variation range in ${U_x}_d$ is constant when $\phi$-coefficient is changed. In contrast, a change in $\phi$-coefficient has no impact on the flow depth hydrograph. The sensitivity of $h_f$ to $\psi^{\text {t}}$ is slightly higher than to $\phi$, but remains small.

The sensitivity of the interfacial depth-averaged Reynolds stress to $\psi^{\text {t}}$ is highlighted in Fig. 13. Surprisingly, we can observe that the initial value of 0.02 calibrated in various CC flumes of different sizes, with smooth FPs [1], is still relevant (in the present study) with a roughened FP. As a result, we could wonder if the value calibrated along the Rhône river in Sect. 1, i.e., ${\psi^{\text {t}} = 0.08}$ (Table 1), would not artificially include some effects of the flow non-uniformity (head loss caused by lateral discharge q between MC and FP, $S_i^m$). We can also mention a possible effect of the emergent rigid vegetation in the field, which enhances the turbulent exchange between sub-sections [15, 18], resulting in an increase in the $\psi^{\text {t}}$-coefficient ($\psi^{\text {t}} =0.035$ in Dupuis et al. [15]).

Fig. 13

Sensitivity of the interfacial depth-averaged transverse Reynolds stress (Eq. 11) to a variation in the turbulent exchange coefficient $\psi^{\text {t}}$ for Case I

8 Conclusions

Unsteady flows in a CC were investigated by focusing on the transient depth-averaged flow exchanges between MC and FP, and on the effect of the inflow partition on the downstream transient flow parameters. The experimental data were also used for validating the 1D+ Independent Sub-sections Model (ISM) under unsteady flow conditions (using a classical 1D model as benchmark).

The experiments show that 80−90 repetitions of the inflow hydrograph are required so that the dispersion of the ensemble average of the time-varying flow depths and sub-section discharges can be lower than the measurement uncertainty range. Due to high levels of interfacial turbulence, the ensemble average of the interfacial velocity is not fully achieved after 100 runs. For this kind of data processing, the run number should be adjusted for each variable of interest to the required accuracy.

The flood wave attenuation is small (decrease in the FP flow depth $h_f$ by $-3\%$ and $-5\%$ between x = 1 m and x = 14 m for Case I and Case II, respectively). For both cases, the peak interfacial streamwise velocity is reached before the peak of $h_f$. We also observed, just after the falling limb of the hydrograph, an overshoot in the interfacial streamwise velocity $U_{x_d}$, which went down below the BF value. Both cases present noticeable hysteresis loops in the relationship $h_f$ vs. $U_{x_d}$. For a given $h_f$-value, $U_{x_d}$ is higher during the rising limb than during the falling limb. For both cases, the direction of the interfacial lateral discharge q is partly controlled by the inflow partition. The interfacial Reynolds stress values would reveal the presence of horizontal Kelvin–Helmholtz vortices during the BFs and a major part of the transient phases. The comparison between ISM results and measurements would also reveal (i) a possible damping effect of bed-induced turbulence on the shear layer turbulence (at x = 10 m), or/and (ii) a lateral shift of the peak Reynolds stress from the interface to the MC or FP by the lateral discharge q.

The stage hydrographs simulated by the 1D+ ISM are closer to the measurements than the hydrographs computed by the 1D model. This would highlight the advantage of explicitly modelling the interfacial flow exchanges, and of accounting for the inflow partition between MC and FP. The influence of the inflow partition is demonstrated when comparing 1D and 1D+ models, as only the 1D+ ISM accounts for the actual (measured) discharges in MC and FP. Assuming at any time t a flow partition equal to that of a uniform flow of same total flow rate (1D model) results in an underestimate of the PF depths, which rises when moving upstream. The interfacial depth-averaged spanwise velocity ${U_y}_d$ and lateral discharge q are well predicted by the ISM for all the duration of both inflow hydrographs. Note that ${U_y}_d$ and q cannot be calculated by the classical 1D approaches. The hysteresis loops in the relationship ${U_y}_d$ vs. $h_f$ are also fairly well reproduced by the ISM. Last, the ISM can approximate the interfacial Reynolds stress without tuning the turbulent exchange coefficient (the initial value ${\psi^t = 0.02}$ [1] was used). The ISM values of the Reynolds stresses are higher than the measured ones (but of the same order of magnitude). This could be due to (i) the limit of using a free-mixing length model that does not take into account the damping effect of the bed-induced turbulence on the shear layer turbulence, or (ii) the lateral shift of the peak Reynolds stress by the lateral discharge q.

Last, the 1D+ ISM simulations showed that the three contributions to head losses, $S_i^t$ (turbulence), $S_i^m$ (mean flow exchange), $S_i^f$ (bed-friction) can be of the same order of magnitude near the flume entrance, while $S_i^t \approx S_i^f>> S_i^m$ further downstream (during the whole hydrographs). The effect on the stage hydrographs of the turbulent exchange $\psi^t$-coefficient, is small (when multiplied by 3, the change in $h_f$ is less than 5% at PF) while the effect of the interfacial velocity $\phi$-coefficient is negligible.