1 Introduction

The study of three-phase flows of gas–liquid–solid mixtures is an open, emerging and relevant scientific field with a wide number of applications, including in environmental eco-systems, in many processes resulting from the use and human control of natural resources, industrial development and urbanisation. There are many examples that can be mentioned, as for instance: drilling and mining industries (e.g. for hydrocarbons or petroleum extraction), pipelines for oil or gas transport, solids transport and sedimentation in natural water streams or artificial channels, storm water networks, municipal wastewater systems, and wastewater treatment processes.

The transport or deposition of solid particles, and the boundary conditions for which any of the processes can begin to occur, in two-phase flows of mixtures of water-solids, or air-solids, have been intensively investigated since a long time ago. Many research works have predominantly focussed on open-channel flows because of their particular relevance to natural configurations on the earth’s surface at micro and macro-scales [1, 2, 22, 28, 35]. Other studies have been developed around two-phase flows in enclosed pipes, particularly in the petroleum industry, and many other industrial, or engineering applications (e.g. [15, 21, 29]).

Most natural single-phase flows of air or water in the real-world are turbulent, incorporating all inherent complexity of turbulence which has not yet been fully solved, scientifically. The difficulty greatly increases when one or more additional phases flow simultaneously in the same global physical space that is submitted to turbulence, but with characteristics and behaviours very different. Most of the scientific progress in the field of solids transport has been typically achieved by experimental investigation, complemented by the development of numerical models and the use of computational fluid dynamics (CFD) in recent decades. Three-phase flows of mixtures of gas–liquid–solids can occur and be applied in very different areas, but their scientific development seems to be still predominately in an initial exploratory stage. In fact, these flows are currently a fertile field of investigation with multiple research aspects that seem completely open (see, for example, [4, 27], or [17]). Several relatively recent research works have been performed with experimental investigations, including the transport of water or viscous fluids in pipelines horizontal, or close to horizontal (e.g. [8, 18, 19, 34]).

The boundary condition that is required to avoid the deposition and retention of solid particles transported in a main flow, or that is necessary to begin the transport of non-cohesive materials deposited in a bed is frequently called self-cleansing condition, in the first case, or critical condition, in the second. Such processes are often difficult to identify with exactness, but may generally be considered practically reciprocal, in average terms along the time, particularly due to the principle of mass conservation. They are typically described as being mainly related with the average velocity of the main flow, which is normally referred to as the self-cleansing velocity, critical velocity, or (although less commonly) pick-up velocity, and with the average shear stress of the solid boundary, which is frequently called critical average shear stress [21, 31, 33].

In the case of municipal sewerage systems, in general, or separate sanitary sewer networks, more specifically, the guarantee of solid transport (in order to allow a good hydraulic performance and to avoid undesirable obstructions), and the guarantee of natural or artificial airing assume particular relevance, due to the materials and organic pollution which are drained or collected from the community and transported in the wastewaters, before reaching the treatment plants. The systems typically work, predominantly, by gravity, with free surface or as open channel flow in descending lines, in order to avoid sedimentation of the transported materials and to allow the natural ventilation of the wastewater through the upper part of the sewer pipe that is occupied by atmospheric air. Aerobic conditions prevent the generation of sulphide gas (H2S) and the subsequent corrosive acids (e.g. sulfuric acid, H2SO4) that may be troublesome for the integrity of the infrastructures. Acceptable dissolved oxygen concentrations in the wastewater allow the avoidance of unhealthy surrounding environments, given that H2S is a toxic gas that, when present in a confined environment, may be very dangerous, particularly in high ratios or over long periods of contact.

In open channel flow, solids transport is mainly guaranteed in the planning and design phases by imposing suitable slopes for the sewers at predicted flow rates, in order to allow average velocities and average shear stresses above the self-cleansing or critical values that avoid sedimentation [6, 23]. The pipes, frequently of circular shape in the current separate systems, are partially filled with air in the upper part of their cross section to promote the required ventilation [32, 37]. For cold or temperate climates, the imposition of a maximum relative-depth of wastewater that should not be exceeded, guaranteeing the ventilation, and such slopes and average velocities are frequently sufficient to avoid septic conditions in the environment of the sewer networks, under normal circumstances and temperatures not very high. However, for large systems and/or hot climates, additional measures may be required [24].

Additionally, large systems rarely work completely in open channel flow, due to topography and natural or artificial obstacles, which normally have to incorporate or to be crossed. Pumping systems and other complementary installations, like inverted siphons, which operate with conduits at full bore (or pipe flow) without natural ventilation, are frequently required. In such circumstances, air injection in force mains of pumping systems (i.e. in the wastewater pressurized pipes), normally performed immediately after the pumping equipment, is relatively common, and has typically been considered as one of the possible suitable measures for sulphide control since a long time ago (see, for example, [36]).

Inverted siphons are very attractive options for potentially crossing natural or artificial obstacles in storm water or sanitary sewer systems, when no increase of the invert elevation of the sewer pipe is required and the topography allows pipe flow governed by gravity. However, their use has been traditionally considered inadvisable and is frequently avoided in the project practice, due to the enormous difficulties which are normally encountered in their design and operation. In fact, the high total head loss required between the inlet and outlet chamber, the high average flow velocity necessary to avoid sedimentation, the low retention time required to avoid sulphide generation and septic conditions, the frequent deposition of solids and obstructions, and the requirement for regular cleaning operations and maintenance are difficulties which are widely recognised and typically reported. Nevertheless, all these problems may be efficiently solved by air injection in steady flow at the base of the rising leg of the inverted siphons.

The air injection in the base of an inclined rising leg of an inverted siphon operating in steady flow was preliminarily proposed in the planning phase of a large sanitary siphon in a tropical region, included in a large regional wastewater collection, treatment and reuse system from an International project [9]. The main purpose of the air injection was the sulphide control and the hydraulic performance improvement of the siphon, due to the well-known air lift effect which has typically been studied in (vertical) air-lift pumps (see, for example, [38]). A research project was initiated since then in the area of multiphase flows in sewerage systems in the Laboratory of Hydraulics, Water Resources and Environment (LHWRA) of Coimbra University.

The different aspects of the two-phase steady flows of air–water mixtures in the inclined rising leg of inverted siphons were studied in great detail by the first Author and his co-workers in the Laboratory along of about 1 decade, mainly with respect to hydraulic performance, efficiency of the air-lift pumping, and sulphide control. For that purpose, one experimental installation was built, and different experimental conditions were established and measured for steady air–water flows. A numerical hydraulic model and a simplified hydraulic model were developed and compared with the experimental results [3, 10,11,12, 14].

In the sequence and development of the different stages of the mentioned research project initiated in 2008, the previous experimental installation was adapted and upgraded to allow the inclusion and measurement of solids flows. A new experimental campaign regarding the solids transport in two and three-phase steady flows was undertaken in the installation in 2021 by the Authors, with sets of assays performed in a new transparent upward acrylic test pipe of 84 mm internal diameter carrying water-solid flows and three-phase flows of air–water–solid mixtures. The installation can be easily adapted to transport viscous fluids, hydrocarbons, and even eventually sludge, muds or other non-Newtonian fluids in order to investigate multiple relevant issues in the field of multiphase flows, like for example the critical velocity with different liquids, and several physical interactions of different phases in the transportation of granular materials.

Based on the fundamental theorem of dimensional analysis (commonly known as Buckingham π theorem), on the physical analysis of the phenomenon, and on the experimental observations and measurements obtained in the campaign for the new testing capabilities, this work proposes a new model for mathematically describing the critical condition, or self-cleansing velocity, in three-phase flows of an upward pipe, for different angles of inclination. The conditions for the beginning of the solids transport in an upward pipe subject to three-phase steady flows of mixtures of gas–liquid–solids with non-cohesive materials, like any pressurised upward pipe transporting any Newtonian fluid, a force main from a pumping system or a rising leg from an inverted siphon, are conceptually modelled based on dimensional analysis. The improvement that the presence of air is able to promote in steady pipe-flow in the self-cleansing condition is then presented, analysed, and discussed.

Two dimensionless parameters, namely a modified Shields number, Shmixc, and a modified critical Reynolds number, Remixc, both adapted for mixtures of gas–liquid–solids under critical conditions, are proposed, calculated using experimental data, graphically plotted, and related experimentally. By analysing the results of the modelling devised and experiments performed, it is shown in this paper that Shmixc varies with Remixc according to a power law of the type Shmixc = a Remixc−b. The law is valid for both flows of air–water-solids and flows of water-solids (which is a particular case of the former, when the air superficial velocity, Uair, is null), and a and b are positive constants that are encountered with a coefficient of determination R2 clearly above 90%. It is also demonstrated that the general equation obtained can be used for explicitly determining the water self-cleansing velocity in steady flow, when Uair = 0, and for determining Uairc implicitly by an iterative numerical method, when the water flow rate is insufficient to guarantee this critical condition without air.

2 Experimental setup description and experimental procedure

2.1 Experimental setup

The experimental set-up used in the Laboratory of Hydraulics, Water Resources and Environment of Coimbra University is represented schematically in Fig. 1. The installation basically comprises an enclosed hydraulic circuit, impelled by three equal submersible pumps of 1 kW power (each installed in parallel in a main tank with 1 m3 capacity), a compressed air injection system (fed by a 2.25 kW power compressor with a 50 L capacity tank), equipment for solid particles accommodation, and an upward transparent acrylic main test pipe with 84 mm internal diameter, D, and 6.125 m length. The apparatus also includes several measuring and control devices.

Fig. 1
figure 1

Experimental setup. a General schema. b Schematic details of piezometric head measurement, air injection equipment, initial sand/gravel bed, and acrylic pipe exit

Full size image

The pumping equipment pumps the water from the main tank to a secondary tank (with base dimensions of 1.25 m × 0.60 m and 0.475 m total height), installed at a higher level. Three flexible plasticised polyvinyl chloride (PVC) pipes of 35 mm internal diameter are directly connected to the pumps and to a low density polyethylene (LDPE) pipe with 94.5 mm internal diameter (nominal 110 mm), which is connected in series to the 84 mm transparent acrylic main test pipe (with nominal diameter 90 mm). The secondary tank has two compartments in series, separated by a stabiliser plate, and the second compartment discharges the pumped flow freely through a thin crest triangular weir with a 90° opening to the main tank, closing the circuit (see Fig. 1a). The main test pipe can simulate any real-world upward pipeline, and also either the rising force main of a pumping system or the rising leg of an inverted siphon governed by gravity. Two static pressure taps connected to two piezometric tubes are located in the Sects. 1 and 2 represented in Fig. 1. In the case of Sect. 2, the static pressure tap is only used for flow of water-solids (i.e. when the air is not injected in the system). The last part of the 94.5 mm LDPE pipe, between the static pressure taps at Sects. 1 and 2, has a total length of 16.64 m and can indirectly simulate the downing leg of an inverted siphon. The elevation of the free surface in the siphon inlet chamber is then simulated by the piezometric level (piezometric head) that is reached in the piezometric tube connected to the tap located at Sect. 1. For the higher pressures at Sect. 1, the piezometric tube is replaced by a differential air–water manometer with the second branch connected to a chamber whose determined/known water level is kept constant (see detail 1 of Fig. 1b).

The water flow in the circuit is regulated by three valves installed in the 35 mm plasticised PVC pipes and the 1 kW pumps can reach each up to a maximum total head of 9 m (the limit for a null water flow rate) and have maximum individual capacity up to 18 m3/h (limit for null total head). For the establishment of flows of air–water and air–water-solids, the compressed air is injected in the PEBD pipe by a tee accessory (in Sect. 2), about 0.5 m before a PVC U 84 mm reduction accessory linked to a 90 mm flexible plastic joint that assures a suitable connection to the upward main test pipe (which can have different inclination angles). The compressed air coming from the 50 L tank of the compressor crosses a camera, where the establishment of a stagnation point is assumed, and flows through a converging nozzle, producing an imposed steady sonic flow at the throat. The air is then conveyed by a relatively small diameter flexible plasticised PVC pipe to the T enlargement accessory that is connected to the PEBD pipe (see schematic detail 2 in Fig. 1b). The camera is equipped with a thermometer, a manometer and a valve that allows to regulate its internal static pressure. This equipment, in conjunction with the converging nozzle, allows the establishment and the measurement of the intended steady air flow rate to be injected in the system. Four converging nozzles with throat diameters of, respectively, 1.05, 1.50, 2.00 and 2.50 mm are used, according to the characteristics of the compressed air system and the intended steady air flow rates that can be injected. These selected diameters allow to maintain, for the injected air flows, a suitable pressure gradient between the air inside the camera and inside the plasticised PVC pipe, which is required for the sonic flow condition in the throat.

The upward acrylic pipe is laid parallel to a steel support beam (with a constant inclination, and the test pipe over the beam), and the inclination of both can be adjusted as needed. The support beam is articulated in a section close to its upper end, by a mechanism that uses two vertical concentric iron tubes. The external tube is fixed and supports the internal tube, which is movable. The latter is connected to the beam at the articulation point and has a height adjustable above the fixed tube. After the intended elevation had been regulated according to the level required for the upper extremity of the beam (i.e. the intended inclination of the installation main test pipe is obtained), the internal tube is then supported/fixed by a screw.

A T accessory is installed in the upper part of the acrylic main pipe, with the same diameter, and it is equipped with a screw cap that allows the manual introduction of the solid particles in the installation in still water, prior to the execution of the tests. The granulometric curve of sedimentary material containing medium to coarse sand and fine gravel from River Mondego in Tentugal, with a density of about 2650 kg/m3, was previously analysed. Four groups of samples with different grain size diameters between 0.425 and 1.18 mm, 1.18 and 2.36 mm, 2.36 and 4.76 mm, and 4.76 and 7.20 mm, respectively, were separated and selected for the solid transport testing. Before each assay, a given sand/fine gravel sample is manually introduced inside the main test pipe in still water. The grains move by gravity from the T accessory to the lower part of the pipe and region of the flexible joint, and then forms a small sand/fine gravel bed (see detail 3 in Fig. 1b).

The main test acrylic pipe freely discharges the transported mixture at atmospheric pressure (see detail 4 of Fig. 1b) in the first compartment of the secondary tank, which is equipped with a screen/net basket for collecting the transported grains. The second compartment of the secondary tank has two graduated rulers in its lateral walls, in order to allow the reading of the water height above the crest of the downstream weir and the subsequent computation of the water flow rate in steady flow. It is separated from the first compartment by a stabiliser plate with two rectangular openings equipped with a thin steel net, in order to maintain a stable water level in steady flow at the measuring points upstream of the triangular weir and avoid any eventual residual transport of abrasive materials to the pumps.

2.2 Experimental procedure

Two-phase flows of mixtures of water-solids and three-phase flows of mixtures of air–water-solids were tested experimentally in the laboratory installation, in order to evaluate the solids transport obtained, with and without air injection immediately before the lower extremity of the upward testing acrylic pipe. The hydraulic performance of the installation for the three-phase flows observed is presented in Moura [25]. Although the solids transport was measured in the experimental campaign performed for a wide range of operating conditions, at this stage and in the context of the specific research work that is developed and presented in this paper, only the measurements obtained in the region of the beginning of the solids transport, with and without air injection, are considered and treated, and the corresponding results are analysed in detail.

Several volumes of the selected River Mondego granular material were initially tested to form the sand/fine gravel bed in the lower region of the acrylic pipe in the vicinity of the flexible joint. A dry mass of 1618.3 g was measured in a high precision balance, corresponding to a volume of about 1 L of a sample with intermediate particle diameters (ds) between 2.36 and 4.76 mm, and was selected as a constant dry reference mass (mTD) to be inserted/guaranteed in the sand/fine gravel bed for all the grain samples, prior to any testing. Each of the four different samples considered (with the dry reference mass mTD of 1618.3 g, measured in the balance) was wetted with clean water and the wet mass (mTW) was measured in the high precision balance in comparable/similar conditions of compaction and humidity. The wet masses obtained for the dry mass of 1618.3 g were 1860.9, 1778.8, 1676.4, and 1660.3 g for the four samples with grain diameters between 0.425 and 1.18 mm, 1.18 and 2.36 mm, 2.36 and 4.76 mm, and 4.76 and 7.20 mm, respectively.

Three angles of inclination (α) of the upward testing pipe were tested: 30°, 46° and 58°. For each given settled inclination, the selected sand/gravel sample is inserted in still water in the acrylic pipe prior to each test, and the grain bed is then formed in comparable conditions. After completing each test, the mass of wet grain collected in the basket (mw) for a given time interval (Δt) is removed from the basket and from the net and measured in the precision balance under comparable wet conditions to those initially considered for the total wet mass of the sample, mTW. The time interval Δt was measured and/or controlled using a chronometer. The mass solid flow rate Ms in SI units of mass per unit of time, is then approximated by:

$$M_{s} = \frac{{m_{W} }}{{{\Delta t}}} \times \frac{{m_{TD} }}{{m_{TW} }}$$
(1)

In the two-phase flow case, successive tests for successive increments of the water flow rate in steady flow, Qw, were established through the regulation of the water flow valves, beginning with low flows for which no solids transport occurs, up to flows reaching the maximum capacity of the installation (i.e. the three pumps working in parallel and the three valves fully opened). In each test, the variables required for the determination of the water volumetric flow rate, Qw, the solid flow rate (in mass per unit of time), Ms, and the piezometric elevations, (Z + p/γ), are then measured. This experimental procedure was systematically repeated for all subsequent sand and fine gravel samples and for all subsequent inclination angles, α.

In the tests performed with three-phase flows, after the inclination angle α had been set and the grain bed formed, an initial water flow rate Qw0 is then established, corresponding to a predetermined average velocity in the acrylic pipe, Uw0. In such conditions, successive increasing air flow rates, in steady flow, Qair, are injected through the T accessory in the experimental installation, in successive tests, beginning with low air flow rates until reaching the maximum capacity of the compressor under steady flow conditions. Initial average water velocities Uw0 of about 0.30, 0.45 and 0.60 m/s were selected and regulated using the water flow valves installed in the 35 mm PVC pipes. In each test, all of the variables required for the determination of the real water volumetric flow rate, Qw, the volumetric air flow rate, Qair, the solid flow rate (in mass per unit of time), Ms, and the piezometric head at Sect. 1 of the LDPE pipe (Z + p/γ)1 are then measured. Once all tests for a given grain sample, initial average water velocity, or inclination angle had been completed, the subsequent sample, subsequent initial water velocity, or subsequent angle was selected and established. The process was systematically repeated until completing the whole range of possible combinations for all the established values of all the experimental parameters considered.

The thin-crest triangular 90° weir installed in the secondary tank that is used to calculate the volumetric water flow rate, Qw, presents complete contraction. The device was calibrated in previous studies [10, 13] and Qw is determined (in SI units) by:

$$Q_{w} = 1.400 \times h^{{\left( {5/2} \right)}}$$
(2)

where h is the height of the water above the weir crest observed in the graduated rulers installed in the lateral walls of the secondary tank.

The volumetric air flow rate, Qair (Qair = Mair/ρair, where Mair is the air flow rate in mass per unit of time and ρair is a given air density of reference), is calculated for a sonic flow on the throats of the converging nozzles, assuming a frictionless isentropic flow [16]. Qair is then determined by (in SI units):

$$Q_{air} = \frac{{M_{air} }}{{\rho_{air} }} = { }\sqrt {\frac{k}{R} \times \left( {\frac{2}{{\left( {k + 1} \right)}}} \right)^{{\frac{{\left( {k + 1} \right)}}{{\left( {k - 1} \right)}}}} } \times \frac{{p_{0} }}{{\rho_{air \times } \sqrt {T_{0} } }}{ } \times { }\frac{{{\uppi } \times { }D_{T}^{2} }}{4}{ }$$
(3)

where p0 and T0 are, respectively, the absolute pressure and the absolute temperature (in Kelvin degrees, K) in the measuring camera/chamber that is considered to be a stagnation point. k is the adiabatic constant and R is the constant of the ideal gases, being k = 1.4 and R = 287 Nm/kg/K for the air, and DT is the diameter of the throats. The air density considered as reference is ρair = 1.205 kg/m3, for an ambient temperature of 20 °C and the normal atmospheric pressure that is set in 101,234 N/m2. The manometer connected to the chamber measures the relative pressure in the stagnation point. The absolute local atmospheric pressure was assumed (by simplification) to be practically constant during the experiments and approximately equal to 100,700 N/m2.

The piezometric elevation reached at Sect. 1, (Z + p/γ)1, is the elevation given by the level of liquid reached in the piezometric tube, to which the static pressure tap 1 is connected. In the case of the use of the differential air–water manometer, (Z + p/γ)1 is given by:

$$\left( {Z + \frac{p}{\gamma }} \right)_{1} = {\Delta y} + Z_{CT}$$
(4)

where ZCT is the elevation of the water level in the control tank connected to the second manometer branch (ZCT was set at 4.5 m with respect to the reference plane horizontal considered that is at the floor level of the laboratory in the vertical of the upward pipe discharge point), and Δy is the vertical difference between the water levels in the manometer branches, connected, respectively, to Sect. 1 and to the control tank.

When air is injected, the piezometric elevation and the total head in the LDPE pipe upstream from the rising acrylic pipe, particularly in Sect. 1, decrease significantly, due to the well-known air-lift effect. The pumps, under a lower total head, drive a slightly higher water volumetric flow rate in steady flow, and the initial average superficial water velocity, which was fixed for the acrylic pipe, increases, in steady flow. The total head reduction and the subsequent increment of the water flow rate, Qw, as well as the superficial average velocity, increase with the injected air flow rate, Qair. However, in a similar way to the previous observations in air–water flows for an inverted siphon working by gravity for a fixed initial average water velocity [11], the increase in maximum flow rate observed in steady flow for the maximum air flow rate injection is normally residual, given that it does not exceed a corresponding increase of about 3 mm in the graduated ruler that measures the water height, h, above the crest of the triangular weir.

The time interval, Δt, of each test was prolonged for as long as possible, in order to guarantee steady flow conditions with a large margin of safety in the performed experiments, and minimise the eventual relative errors in the averaged values of the measured variables. Δt was established frequently at about 10 min, particularly for three-phase flows. The maximum relative tolerances/errors in the measurement of the variables that are necessary to compute the water and air steady flow rates, according to the used devices, h, DT, p0, and T0, can be estimated in about ± 1.4, ± 2.0, ± 4.0, and ± 0.5%, respectively. This gives a maximum cumulative propagated tolerance/error of about ± 3.5 and ± 8.5%, respectively, for Qw and Qair [10, 12]. However, it is very likely that the real propagated errors in the calculated flows Qw and Qair are frequently significantly inferior.

3 Devised approach

3.1 General formulation and variables of the model

The transport of solids, and particularly the boundary flow conditions for which the transportation of solid particles begins to occur in turbulent gas–liquid-solid flows, is a very complex phenomenon that, as in many other real-world problems of fluid mechanics and hydraulics, has not yet been solved by conventional fundamental research. Alongside the use of currently available computational tools for solving complex theoretical differential equations, normally by numerical models, most of the scientific progress in this research area in recent decades, particularly in turbulent steady water-solids (two-phase) flow in open channels, has occurred due to the results obtained through the experimental investigations which have been developed. See, for example, the well-known and proficient works of Shields [5, 35], Meyer-Peter and Müller [20, 22], or Ackers and White [1, 2, 28].

In order to obtain the mathematical relations that describe diverse complex physical phenomena by experimental means, dimensional analysis and its fundamental theorem (the Buckingham π Theorem or Theorem of Vaschy-Buckingham) are well-known useful tools that have been typically used in hydraulics, with some success. The π Theorem is applied in this work, in order to obtain the algebraic equations that might be able to mathematically describe the experimental results of the three-phase flows that were measured in the laboratorial installation at the region of the commencement of the transportation of solids.

According to the theorem [16, 30], any homogeneous relation/equation of/with N physical variables that are relevant for a given phenomenon (Vi, i = 1, N), (a relation/equation is homogeneous if the two members of the two sides of the equation have the same dimensions in a given system of units, for example an MLT system, in the International System case), can be replaced by a relation/equation of N–Nf dimensionless parameters (πi, i = 1, N–Nf), where Nf is the number of dimensionally independent variables. In fluid mechanics, in general, Nf maximum comprises three variables: a geometric, a kinematic and a dynamic, which are called fundamental, and which should be selected from between all the identified variables, with a total number of N. Each πi parameter may be defined by the quotient between each remaining variable Vi not selected as fundamental (in number N–Nf) and the product of the Nf variables selected as fundamental, with each one elevated to a real exponent determined under the condition that πi is dimensionless. The great advantage of the theorem is that it allows the reduction of the initial number (N) of variables that are required to describe the problem, using a lower number of dimensionless parameters (N–Nf) which are then easier to relate through the experimental measurements that are obtained for all the initial N variables.

The selection of a suitable set of variables that may be able describe the phenomenon is essential for the success of the mathematical modelling. Too many variables could hamper the analysis (high N–Nf), while an insufficient number of variables could produce results which are only valid for particular situations. Given the complexity of the turbulent three-phase flows and the subsequent large number of variables that may be under consideration, the elementary approach that was devised in this research work and is proposed in this paper is based on an analytic effort to incorporate and adapt the variables present in the Shields number and to consider, at least, a total minimum of five variables (N = 5), selected according to their observed relevance for the phenomenon under consideration. Shields parameter was originally developed for open-channel two-phase flows (water-solids), and the adaptation of their variables for three-phase flows in enclosed pipes is non-trivial. The approach proposed in this work is able produce excellent results, as can be observed through the experimental measurements and analytical results obtained.

The first two variables that were selected are: (1) the critical average tangential stress/tension on the solid frontier of the air–water mixture, τmixc (i.e. the minimum average tangential tension on the solid frontier of the air–water mixture for which the solid transport begins), with τmixc =  γmix Jmixc D/4, where γmix represents the weight per unit of volume of the air–water mixture, Jmixc is the head loss per unit of pipe length of the mixture under critical conditions, and D is the internal diameter of the rising pipe; and (2) the submerged specific weight of the solid particles in the air–water mixture, γs′ = γs—γmix, where γs is the weight per unit of volume of the solid particles. The remaining three variables considered are: (3) the diameter of the solid particles, ds; (4) the critical average velocity of the air–water mixture, i.e. the minimum average velocity of the air–water mixture for which the solids transport begins, Umixc; and (5) the kinematic viscosity of the air–water mixture νmix. The initial equation may then be expressed generically by:

$$\phi { }\left( {{\uptau }_{mixc } ,{\upgamma }_{s }^{\prime} ,d_{s } ,{ }U_{mixc} { },{ }\nu_{mix} } \right) = 0$$
(5)

The arguments of the function φ, ds, Umixc, γs′, are variables geometric, kinetic, and dynamic, respectively. They are then dimensionally independent (Nf = 3) and are selected as the set of fundamental variables. The two dimensionless parameters (N–Nf = 2), π1 and π2, obtained by the application of the theorem, are the Shields Number (or Shields parameter) for the steady flow averaged air–water mixture under critical conditions, π1 = Shmixc, when τmixc, is the variable considered,

$${\text{Sh}}_{mixc} = \frac{{{\uptau }_{mixc} }}{{{\upgamma }_{s}^{\prime} { } \times { }d_{s} }}$$
(6)

and the inverse of the Reynolds number, calculated with the critical average velocity in steady flow and the kinematic viscosity of the air–water mixture, π2 = 1/Remixc, when the considered variable is νmixc,

$${\uppi }_{2} = \frac{{{\upnu }_{mix} }}{{{\text{ U}}_{mixc} \times { }d_{s} }} = \frac{1}{{Re_{mixc} }}$$
(7)

The dimensionless parameter Shmixc is proportional to the quotient between the average drag force in the solid frontier per unit of internal wall surface in the three-phase flow commencement and the submerged weight of the solid particles per unit of their projection area over a plane. Shmixc measures the relative importance between the drag force required for the commencement of the particle movements and their submerged weight. The dimensionless parameter Remixc is proportional to the quotient between the inertial forces and the viscosity forces in the three-phase flow commencement, and is a measurement of the relative importance of both for the critical condition. The mathematical equation that describes the critical condition of the solids transport in three-phase flow, according to the considered approximations, may then be expressed generically by:

$${\text{F }}\left( {{\uppi }_{1} , 1/{\uppi }_{2} } \right) = 0$$
(8)

or

$${\text{F }}\left( {{\text{Sh}}_{mixc} , Re_{mixc} } \right) = 0$$
(9)

Replacing the expressions obtained for the dimensionless parameters gives:

$$\frac{{{\uptau }_{mixc} }}{{{\upgamma }_{s}{\prime} { } \times { }d_{s} }} = {\psi }\left( {\frac{{{\text{U}}_{mixc} \times { }d_{s} }}{{{\upnu }_{mix} { }}}} \right)$$
(10)

The specific algebraic form of the equation and their parameters are then selected and adjusted using a suitable adjustment criterion, according to the experimental measurements obtained.

It is worth noting that the experiments were performed for a smooth pipe and, thus, the influence of the pipe equivalent absolute roughness, k, may be neglected, particularly in the presence of a sand/gravel bed with grains of diameter, ds which are much larger than k. The conduit roughness may just be considered in the flow resistance law that is required to compute Jmixc and τmixc (for example if the Colebrook-White equation for a single-phase flow is used). For rough pipes, however, it may eventually be required to include k and the corresponding dimensionless parameter π3 = k/ds in the analysis.

3.2 Model implementation

Several two-phase flow resistance laws can be used to compute Jmixc and τmixc. In this work, the head losses per unit of pipe length of the mixture, Jmix, are determined using the Chisholm and Laird [7] empirical equation:

$$J_{mix} = J_{w} + C_{wair} \times \left( {J_{w} \times J_{air} } \right)^{\frac{1}{2}} + J_{air}$$
(11)

where Jw and Jair are the head losses per unit of pipe length for the superficial average velocity of water, Uw = Qw/A, and for air, Uair = Qair/A, respectively. In these continuity equations, A is the flow cross-sectional area, and in Eq. (11) Jw and Jair are referenced to the same fluid specific weight or to the same fluid density from Jmix. Cwair is an experimentally determined coefficient [26] that varies with the flow regimens of the gas and liquid phases, when separately considered.

Under the analysed conditions in this work, the flow of the liquid phase and of the mixture is always clearly turbulent. However, for the smaller air flow rates separately considered, the gas phase regime can also be theoretically laminar or can be inside the critical zone, with Reynolds numbers, generically defined by Re = U \(\times\) D/ν, of the air phase, Reair, below 3000. In this definition, U is the average velocity in the cross section of the flow and ν is the fluid kinematic viscosity (with U = Uair and ν = νair, in the case of Reair). Several alternatives were considered for computing Jmix and Jair of the isolated air flows, particularly in the critical zone between laminar and turbulent, using laminar and turbulent single-flow resistance laws. The best results were achieved when Cwair is assumed to be always equal to 21 (value close to the originally proposed for turbulent regimes of both phases) regardless of the flow resistance used for the gas phase. This coefficient was considered in Yoshinaga and Sato [38] and proved to produce acceptable results in previous works also, even for low liquid fractions [12, 14]. On the other hand, for very small air flow rates below 0.5 L/s, with Reynolds numbers of the gas phase Reair below about 500 and with the use of the laminar flow resistance law, Cwair was reduced to 12. In all these computations, Qair is referenced to the local atmospheric pressure and water temperature (at the exit discharge section, and with isothermal flow in the upward pipe).

Jw and Jair can be calculated using any suitable existing turbulent single-phase flow resistance law between those frequently used in current practice. In this case (smooth pipe and Reynolds number not too high, i.e. Re between 3000 and 105), the well-known Blasius empirical equation was considered to determine the head loss per unit of pipe length, J, both for water and for air flow,

$${\text{J }} = \frac{{0,3164 \times \left( {{\raise0.7ex\hbox{$4$} \!\mathord{\left/ {\vphantom {4 \pi }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\pi $}}} \right)^{1,75} \times \nu^{0,25} { }}}{2g} \times \frac{{Q^{1,75} }}{{D^{4,75} }}$$
(12)

where g is the gravitational acceleration (in this work, it was assumed that g ≈ 9.8 m/s2), and Q is the volumetric flow rate. For single-phase air flow rates with Reair < 3000, the Hagen–Poiseuille equation was additionally used\(: J_{air} { } = 32{ } \times \frac{{\nu_{air} }}{g} \times \frac{{U_{air} }}{{D^{2} }}\). An approximated averaged value of 15 × 10–6 m2/s is considered for the air kinematic viscosity, νair, in the experiments performed and, by simplification, the influence of air viscosity variation is ignored. The water temperature Tw was measured in the main tank at the beginning of each set of tests, and the water kinematic viscosity, νw, is approximated for the measured Tw (in Celsius degrees) by the following equation [13]:

$$\nu_{w} = \frac{0,00000178}{{1 + 0,0337 \times T_{w} + 0,000221 \times T_{w}^{2} }}$$
(13)

Several alternatives were tested to compute the variables γmix, νmix, and Umixc (and subsequently Jmixc and τmixc) that are present in the dimensionless parameters, including, in particular, several approximations for the well-known slippage that occurs between the phases.

However, good results and the best adjustments were obtained when the variables and parameters are calculated without the slippage consideration. γmix is then calculated by \({\upgamma }_{{{\text{mix}}}} = {\upgamma }_{{\text{w}}} \times {\text{f}}_{{\text{w}}} + {\text{g}} \times {\uprho }_{{{\text{airE}}}} \times \left( {1 - {\text{f}}_{{\text{w}}} } \right)\), with \({\text{f}}_{{\text{w}}} = { }\frac{{{\text{Q}}_{{\text{w}}} }}{{{\text{Q}}_{{\text{w}}} + {\text{Q}}_{{{\text{airE}}}} }}\), where γw is the water specific weight, fw is the water fraction at the pipe exit section as if no slippage occurred, and ρairE and QairE are the air density and the air flow rate at the pipe exit section, respectively. νmix is determined by \({\upnu }_{{{\text{mix}}}} = ({\uprho }_{{\text{w}}} \times {\upnu }_{{\text{w}}} \times {\text{f}}_{{\text{w}}} + {\uprho }_{{{\text{airE}}}} \times {\upnu }_{{{\text{air}}}} \times \left( {1 - {\text{f}}_{{\text{w}}} } \right))/{\uprho }_{{{\text{mix}}}}\), where ρw and ρmix are the water and the mixture density, respectively. Umixc is computed by \({\text{U}}_{{{\text{mixc}}}} { } = { }\frac{{\left( {{\text{Q}}_{{\text{w}}} + {\text{Q}}_{{{\text{airE}}}} } \right)}}{{\text{A}}}\), with Qw and QairE corresponding to the critical condition, i.e. the inferior limit for the beginning of the solids transport, and A is the flow cross-sectional area in the acrylic pipe. The standard average approximated value of 1000 kg/m3 is used in the computations for the water density, ρw, and the variation of ρw in the observed steady flows is ignored.

3.3 Model input critical experimental volumetric flow rates

Even in steady single-phase turbulent flow, it is normally very difficult to determine deterministically with a very high degree of accuracy the exact liquid average velocity for which the solids transport begins to occur in an upward pipe. The difficulty greatly increases for the required superficial average velocities of gas and liquid in steady two-phase turbulent flow of air–water mixtures. In fact, it was observed, experimentally, in the transparent acrylic pipe that for flows of air–water mixtures in the region of the beginning of the solids transport, the hydrodynamic forces acting over the solid particles may be able to temporarily suspend or slightly drag them. This may induce small chaotic advances which are practically instantaneous in the longitudinal direction, but the particles may return swiftly to regions close to their previous positions in the bed, without any real average transportation in time, neither by saltation and suspension nor by rolling and dragging as bed load.

The criterion used to determine the conditions for which the solids transport effectively begins was to plot the experimental observed curves Ms versus Qw for water-solid two phase flows (for each given pipe inclination angle and sand/fine gravel sample) and Ms versus Qair for air–water-solid flows (for each given pipe inclination angle, grain sample, and initial fixed Uw0) and analyse their behaviour, particularly in the region close to the flows for which Ms ≈ 0. It can be observed that the curves in this zone normally show a behaviour close to a power law of the type \(M_{s} = {\upalpha } + {\beta } \times Q_{air}^{\gamma }\) and/or \(M_{s} = {\upalpha } + {\beta } \times Q_{w}^{\gamma }\). The coefficients α, β, and γ are then determined for each curve, adjusting the power equations to the plotted data observed.

A positive residual value for Ms corresponding to a minimum mass of effectively transported sand/fine gravel particles (i.e. deposited in the net/screen basket and measured in the precision balance) is defined as the condition in steady flow for which the solids transport effectively begins. This residual value is then introduced to the obtained equations and Qw and Qair, corresponding to the searched critical condition, can finally be determined. Although any real value can be naturally chosen (including logically Ms0 = 0, as a lower criterion), the mentioned residual value that was selected, for the results presented in this paper, is Ms0 = 0.05 g/s (i.e. 3 g/min), according to the best criterion found (somehow on the balanced side) for the grain samples used and all the remaining laboratorial conditions considered. Table 1 presents the estimated approximations for the critical volumetric flow rates that are obtained for the observed two and three-phase flows, according to the methodology described above.

Table 1 Water and air volumetric flow rates required to start the transport of solids in two and three-phase upward steady pipe flows. (In the case of three-phase flows, with initial water average velocities of 0.30, 0.45 and 0.60 m/s, insufficient for solids transport before the introduction of air)
Full size table

4 Results and discussion

4.1 Experimentally observed average superficial critical velocities of air and water

Figure 2 presents the variation of the average superficial water and air velocities in critical conditions for the solid particle diameters, under the tested conditions for angles of inclination α of the upward acrylic pipe of 30°, 46°, and 58°. The superficial average velocities of air (Uair) and water (Uw) are represented in Fig. 2a, the average velocity of the mixture, Umix = Uair + Uw is represented in Fig. 2b, and the ratio of water and air flow rates, as a percentage of the total flow rate of the mixture, in Fig. 2c. The air–water mixture in steady flow, inside the entire upward acrylic pipe, shows an improvement in the available conditions for the beginning of the solids transport, particularly when compared with the corresponding single-phase water flow. This was observed for all the tests performed, and is due to the air-lift effect and increased average velocity of the mixture, requiring an initial lower water volumetric flow rate and lower water average velocity for the solids transport occurrence when the air is present. The air injection in steady flow at the lower point, or minimum level, before the beginning of a rising leg or an upward pipe shows a positive effect, facilitating the solids transport conditions, which may avoid the deposition of materials and the occurrence of obstructions in the lower points both of the pressurised pipelines, in general, and of the upward pipes of sanitary or stormwater sewer networks, in particular.

Fig. 2
figure 2figure 2figure 2

Average superficial water and air velocities in critical conditions versus solid particle diameters for the tested angles of inclination α of the upward acrylic pipe. a Superficial average velocities of air, Uair, and of water, Uw. b Average velocity of the mixture, Umixc = (Uw + Uair)c. c Ratio (%) between the water and air flow rates (or superficial average velocities), and the total flow rate (or average velocity) of the mixture

Full size image

For all tested angles, the critical average velocity clearly increases with the diameter of the solid particles and the average water velocity seems to be the determining factor that governs the beginning of the solids transport. It should be highlighted that, according to the tested experimental conditions, the air-lift effect was mainly mobilised for the reduction of the upstream total head, with a mere residual increase of the water volumetric flow rate and the average velocity in steady flow. In a real sewer system governed by gravity this would correspond, for example, to a gain of hydraulic head in an inverted siphon between the inlet and the outlet chamber (which would occur in the rising leg), maintaining the influent wastewater flow arriving at the siphon practically invariable. On the other hand, the results obtained show that air injection in the base of a rising force main of a pumping system, which is frequently mentioned as a good measure for sulphide control, is also able to increase the solids transport in the upward pipe.

A laboratory test with air injection in steady flow was performed in the experimental installation maintaining the upstream total head (which can simulate, for example, a constant water level at the inlet chamber of a real-world inverted siphon of a sewer network). The introduced air, due to the occurrence of air-lift, greatly increased the water flow rate and the average velocity of the mixture under steady flow conditions, and the solids transport was strongly mobilised, with a very high flux of mass of solids per unit of time. However, under normal operating conditions in steady flow of an inverted siphon of a sewer network, what really changes, normally, is that the upstream head at the inlet chamber, and/or at the downing leg, decreases, due to the air injection in the base of the rising leg and the corresponding air-lift. The experimental campaign performed and the measurements that led to the results that are presented in this paper are thus suitable to simulate exactly a similar situation to that should be normally considered with an inverted siphon subject to air injection in its base. Nevertheless, a recirculation scheme between the chambers, using the second siphon barrel normally constructed in parallel with the first, as the water recirculation pipe, with the return single-phase flow controlled by adjustable and removable weirs located at the outlet chamber may be able to guarantee the mentioned condition at the siphon inlet.

Additional tests for lower initial average water velocities between 0.0 and 0.3 m/s can be performed in further studies, particularly for particles with the smaller diameters. However, for the larger particle diameters, it is expected that such experiments will require an air compressor with a capacity in steady flow much larger than the actual capacity of the compressor that was used in this experimental study. The performed experiments were limited to a maximum established steady air flow rate of approximately 4.45 L/s, corresponding to a maximum superficial average velocity in the acrylic pipe of about 0.8 m/s.

For water-solid flows, although based on different experimental conditions and diverse definitions, both for the self-cleaning velocity and for the critical velocity, some results of the same order of magnitude, or comparable, can be found in May [21] for fine gravel with concentrations of about 50 ppm in volume in rising pipes and in Leporini et al. [19] for medium sand transport in a horizontal test pipe.

4.2 Results of the performed modelling

Several computations were executed varying Cwair in the Chisholm and Laird formula and the single-phase flow resistance law used for the gas flow, according to the Reair of the air phase reached in the experiments, particularly in the critical zone between laminar and turbulent flows. All the results presented in this subsection (i.e. in Figs. 3 and 4 and in the Tables 2 and 3) were obtained considering Cwair = 21, when Reair > 500, and 12, if Reair ≤ 500, and the application of the Blasius equation, separately for the water superficial velocity and for the air superficial velocity, when Reair > 3000, and the formula of Hagen-Poiseuille for the air phase, when Reair ≤ 3000. Nevertheless, acceptable results were also achieved using always Cwair = 21 and the Blasius equation, regardless Reair that is reached in the air phase.

Table 2 Constants a and b from Eqs. (14) and (17), and coefficient of determination R2 obtained for the power trend lines represented in Fig. 3
Full size table
Table 3 Constants a and b from Eqs. (16) and (18) that use Re*mixc as the second dimensionless parameter, and coefficient of determination R2 obtained experimentally for the power trend lines represented in Fig. 4
Full size table
Fig. 3
figure 3figure 3

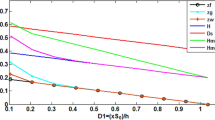
Variation of the modified Shields number for mixtures of air–water-solids, Shmixc, with the critical Reynolds number of the solid particles computed with the critical average velocity of the mixture, Remixc, according to the performed tests and the model proposed. a Results of the three-phase flows (including when Qair = 0) grouped according to the inclination angles α of 30°, 46° and 58° of the upward acrylic pipe. b Results of the three-phase flows (including when Qair = 0) regardless of the inclination angles α for which they were experimentally obtained. c Results of the two-phase flows (Qair = 0) grouped according to the inclination angles α of 30°, 46° and 58° of the upward acrylic pipe. d Results of the two-phase flows (Qair = 0), regardless of the inclination angles α for which they were experimentally obtained

Full size image
Fig. 4
figure 4

Variation of the modified Shields number for mixtures of air–water-solids, Shmixc, with the critical Reynolds number of the solid particles computed with the critical average friction velocity of the mixture, Re*mixc, according to the performed tests for all three-phase flows (including when Qair = 0). (a) Results grouped according to the inclination angles α of 30°, 46° and 58° of the upward acrylic pipe. b Results of all tests, regardless of the inclination angles α for which they were experimentally obtained

Full size image

Figure 3 presents the graphical plotting of Shmixc versus Remixc that was obtained for the tested angles of inclination α of 30°, 46° and 58° of the upward acrylic pipe, according to the considerations, experimental procedure, equations and data presented in Sect. 3. In Fig. 3a and c, all points calculated for the critical average velocities are grouped and plotted in three series according to the inclination angle for which they were experimentally obtained. Figure 3a includes the results obtained for all three-phase flows and all two phase-flows and Fig. 3c includes just the flows of water-solids. In fact, a two-phase flow can be regarded as a particular case of a three-phase flow with a null air flow rate or null superficial average velocity, and should then be included on the corresponding graph. In Fig. 3b and d, all of the plotted points mentioned are presented together in two single sets, a set for all tested flows, and a set just for flows of water-solids, respectively.

It is possible to observe that the plotted points in all of these four graphs seem to follow, more or less regularly, curves that can be approximated by a power law equation of the generic type

$$Sh_{mixc} = a \times \left( {Re_{mixc} } \right)^{ - b}$$
(14)

where a and b are constants that can be determined by a suitable adjustment criterion between this generic mathematical equation and the experimental data observed. Constants a and b and the coefficient of determination R2, for each one of the eight curves represented in the graphs, were computed by the method of least squares for the selected power trend lines and are presented in Table 2.

Regardless if the pairs of values (Shmixc, Remixc) computed for three-phase flows are included, or are not included, in the figures, the influence of the upward pipe inclination on the critical condition for the beginning of the solids transport seems relatively small for all the tested angles, in comparison with the remaining variables. A requirement for a slightly higher Shmixc seems to occur for α = 46° in the three-phase flows and for α = 30° in two-phase flows, with curves being very close for the remaining tested angles in both cases. However, the differences do not seem very significant. The trend lines of all the points that were observed experimentally can, generally, be well represented (i.e. with a good approximation) by single curves, both for all flows (Fig. 3b), and just for two-phase flows (Fig. 3d). According to the results obtained, and when all air flows are considered (including Qair = 0), a varies from 0.24 to 0.29 and b varies from 0.33 to 0.37 (see Table 2A).

All the coefficients of determination R2 for all of the eight plotted curves are clearly above 0.90, which shows an excellent adjustment between the models, the type of equation proposed, and the experimental data measured. For all four curves of the two-phase flows, R2 reaches even values that are always superior than or equal to 0.97, but the number of total points considered to obtain these results in the trend analysis is much smaller than the total number that was used for all the curves of the three-phase flows.

The variation of the Shields parameter for critical conditions of the mixture of air–water-solids, Shmixc, with the critical friction Reynolds number of the mixture, Re*mixc, was also analysed in this work. Re*mixc, is calculated with the critical average friction velocity for the three-phase mixture, U*mixc = √(τmixc/ρmix) = √(g \(\times\) Jmixc \(\times\) D/4), and is then given by:

$$Re_{mixc}^{*} = \frac{{\sqrt {g {\text{J}}_{mixc} \times \frac{D}{4}} \times d_{s} }}{{\upnu _{mix} }}$$
(15)

Analogously to the previous definition considered for the Reynolds number in this study, i.e. defined with Umixc, the different tested inclination angles α of the upward acrylic pipe are taken as parameters. Pairs of values of Shmixc and Re*mixc were computed for the data obtained experimentally, the corresponding points were plotted graphically, and the results are presented in Fig. 4a in three series according to the angle α. In Fig. 4b, the results are presented as a single series for all observed points. The general qualitative layout of the plotted points and their relative position according to the angle α of the upward pipe is very similar to those previously presented in Fig. 3, following curves that can be approximated by a similar generic power law, expressed by:

$$Sh_{mixc} = a \times \left( {Re_{mixc}^{*} } \right)^{ - b}$$
(16)

Power trend lines curves were also added to the graphs and the constants a and b for the equations, obtained for each curve by the least squares method, are presented in Table 3. The constants a and b vary between about 0.09 and 0.10 and between about 0.34 and 0.38, respectively. The coefficients of determination R2 are very close to those obtained when the Reynolds number is calculated with the critical average velocity of the mixture, showing an excellent adjustment between the algebraic equation proposed with Re*mixc and the experimental data observed too.

4.3 Computation of the average superficial water and air velocity required

Replacing the definitions of Shmixc, Remixc and Re*mixc in Eqs. (14) and (16) yields the following two equations that can alternatively be used for computing the average velocities required to guarantee the solids transport in an upward pipe, after the constants a and b have been determined and set:

$$\frac{{{\uptau }_{mixc} }}{{(\gamma_{s} - \gamma_{mix} ){ } \times { }d_{s} }} = a \times \left( {\frac{{{\text{U}}_{mixc} \times { }d_{s} }}{{{\upnu }_{mix} { }}}} \right)^{ - b}$$
(17)

and

$$\frac{{\uptau _{mixc} }}{{(\gamma_{s} - \gamma_{mix} ) \times d_{s} }} = a \times \left( {\frac{{\sqrt {g {\text{J}}_{mixc} \times \frac{D}{4}} \times d_{s} }}{{ \nu_{mix} }}} \right)^{ - b}$$
(18)

These two equations are valid for three-phase flows of air–water-solids and for two-phase flows of water-solids. Two-phase flows can be considered a particular case of the former when Qair = 0, τmixc = τWc, Umixc = UWc, Jmixc = JWc, γmix = γw, and νmix = νw, i.e. when the air–water mixture is replaced by water.

To compute the head loss per unit of pipe length of the liquid phase, Jw, a general approximated empirical flow resistance law for turbulent pipe-flow of the following generic type can be used:

$$U_{w} = K \times {\text{D}}^{\alpha } \times J_{w}^{\beta }$$
(19)

where K, α, and β are constants for a given material of the pipe internal surface. This expression is equivalent to

$$J_{w} = {\text{K}}^{ - 1/\beta } \times {\text{D}}^{ - \alpha /\beta } \times U_{w}^{1/\beta }$$
(20)

Equation (20) yields the Blasius empirical formula that is generally accepted to be a good approximation for turbulent smooth pipe flows up to Rew = 105, when K = (2 × g × νw0.25/ 0.3164) (1/1.75), α = 1.25/1.75, and β = 1/1.75, and the well-known empirical Manning formula that is valid for fully rough turbulent regimes, when K = 1/(n 4(2/3)), α = 2/3, and β = 1/2, where n is the roughness coefficient of the Manning formula. Transitional turbulent flows have typically been approximated by experimentally obtained coefficients, with 1/β varying between 1.75 and 2. For example, the exponents of Scimemi and Hazen-Williams empirical formulas for pipe flow, in current use, can be regarded as particular cases of the generic Eq. (19) for these regimes.

Equation (17) can be used to determine the critical average water velocity and the corresponding water volumetric flow rates that satisfy the solids transport flow condition for two-phase flows of water-solids. Introducing Eq. (20) into Eq. (17), with τmixc = τWc = γw \(\times { }\) JWc \(\times { }\) D/4, and rearranging and solving for UWc, allows to explicitly determine the average minimum water flow that is required to guarantee solids transport in steady flow:

$$U_{Wc} = (4 \times {\text{a}} \times {\text{K}}^{{\frac{1}{\beta }}} \times \nu_{w}^{\beta } \times \left( {{\text{s}} - 1} \right){ } \times {\text{D}}^{{\left( {\frac{\alpha }{\beta } - 1} \right)}} \times d_{s}^{{\left( {1 - b} \right)}} )^{{1/\left( {b + \frac{1}{\beta }} \right)}}$$
(21)

where s is the specific density, or specific weight per unit of volume, of the solid particles (s = γs/γw). If Blasius Equation is used as the water flow resistance law, UWc can be expressed by:

$$U_{Wc} = \left( {\frac{{8 \times {\text{a}} \times {\text{g}}}}{0.3164} \times \nu_{w}^{{\left( {b - 0.25} \right)}} \times \left( {{\text{s}} - 1} \right){ } \times {\text{D}}^{0.25} \times d_{s}^{{\left( {1 - b} \right)}} } \right)^{{1/\left( {b + 1.75} \right)}}$$
(22)

According to Eq. (22), the average critical water velocity, UWc, is proportional to the power (b − 0.25)/(b + 1.75) of the water kinematic viscosity, νw, power 1/(b + 1.75) of the submerged specific weight, (s − 1), power 0.25/(b + 1.75) of the pipe diameter, D, and power (1 − b)/(b + 1.75) of the solid particles diameter, ds. Under the tested conditions for two-phase flows, b varied between 0.341 and 0.408, with a value of 0.374 for all data (see Table 2B). Thus, the exponents of νw, (s − 1), D, and ds are all positive and vary between 0.04 and 0.07, 0.46 and 0.48, 0.116 and 0.12, and 0.27 and 0.32, respectively, with estimated values for all data of 0.06, 0.47, 0.12, and 0.29, respectively. These obtained results show that UWc increases with the four variables of the right-hand side of Eq. (22) and, very significantly, with (s − 1) and ds (higher exponents).

Once UWc has been determined, the critical average shear stress, τWc, can be computed directly from Eq. (17) by:

$${\uptau }_{Wc} = a \times (\gamma_{s} - \gamma_{w} ) \times d_{s}^{{\left( {1 - b} \right)}} \times {\upnu }_{w}^{b} \times U_{Wc}^{ - b} { }$$
(23)

If a given water volumetric flow rate and the corresponding average water velocity is insufficient to guarantee the solids transport, UW < UWc (or τW < τWc), it is then appropriate and may be relevant the determination of the average superficial air velocity and the corresponding air volumetric flow rate necessary be present, or required to be inserted, so that such a condition can be guaranteed in steady flow. However, with the flow resistance law for three-phase flows considered in this work, both Eqs. (17) and (18) cannot be explicitly solved with respect to Umixc, nor τmixc (or τmixc), for a given Uw (or Qw), becoming then necessary the research of a numerical iterative process.

The set of equations that solves the problem needs to be established and prepared to develop an efficient iterative procedure that might allow the computation of the required average superficial air velocity in critical conditions, Uairc. For that purpose, Jw, Jair and Jmix of Eq. (11) from Chisholm and Laird can be referenced to the specific weigh of the mixture (Jw × γw /γmix and Jair × γair/γmix), applied to the critical condition, and the resulting Jmixc can then be introduced into the expression of τmixc, τmixc = γmix Jmixc D/4, yielding,

$$\tau_{mixc} = \left( {J_{w} \times \gamma_{w} + J_{airc} \times \gamma_{air} + C_{wair} \times \sqrt {J_{w} \times \gamma_{w} \times J_{airc} \times \gamma_{air} } } \right) \times {\text{D}}/4$$
(24)

and Eq. (17) can be rearranged and solved with respect to τmixc,

$${\uptau }_{mixc} = \left( {\gamma_{s} - \gamma_{mix} } \right) \times {\text{a}} \times \nu_{mix}^{b} \times d_{s}^{{\left( {1 - b} \right)}} \times (U_{w} + U_{air} ) ^{ - b}$$
(25)

with

$$\gamma_{mix} { } = \frac{{\gamma_{w} \times U_{w} + { }\gamma_{air} \times U_{airc} { }}}{{U_{w} { } + { }U_{airc} { }}}$$
(26)
$$\nu_{mix} { } = \frac{{\nu_{w} \times \gamma_{w} \times U_{w} + { }\nu_{air} \times \gamma_{air} \times U_{airc} { }}}{{\gamma_{mix} \times \left( {U_{w} { } + { }U_{airc} { }} \right)}}$$
(27)

and with (for the current single-phase flow resistance laws used)

$$J_{w} = {\text{K}}^{ - 1/\beta } \times {\text{D}}^{ - \alpha /\beta } \times U_{w}^{1/\beta }$$
(20)
$$J_{airc} = { }C_{air} \times U_{{{\text{airc}}}}^{1,75}$$
(28)

where Cair in Eq. (28) is a constant for a fixed geometry and air kinematic viscosity, which can be expressed by \(C_{air} = \frac{{0,3164 \times \nu_{{{\text{air}}}}^{0,25} { }}}{{2g \times D^{1,25} }}\). A similar expression, with \(J_{w} = { }C_{w} \times U_{{\text{w}}}^{1,75}\) and νW, for replacing Eq. (20), can be also derived when JW is calculated with Blasius. For low air flow rates, including in the critical zone of the gas phase separately considered, with Reynolds numbers Reair up to about 2500 to 3000, Jairc can also be approximated using the Hagen-Poiseuille formula \(J_{airc} = { }C_{air} \times U_{airc}\), with \(C_{air} = \frac{{32 \times \nu_{air} { }}}{{g \times D^{2} }}\), instead of Eq. (28). Cwair can be set always in 21 for Reair > 500, regardless of the flow resistance law used. However, for Reair ≤ 500, and when the Hagen-Poiseuille formula is used, Cwair requires to be reduced to 12, or eventually even a little less for very small Reynolds numbers.

A model using successive approximations was devised to solve iteratively this system of equations. Replacing the value of τmixc calculated by Eq. (25), for a given Uairc obtained in a previous iteration step (i), on the left-hand side of Eq. (24) and solving Eq. (24) with respect to the resulting Uairc inside the radicand, yields Uairc for the next iteration (i + 1):

$${\text{U}}_{airc } = \left( {C_{air} \times \gamma_{air} \times J_{w} \times \gamma_{w} } \right)^{{\left( { - \frac{1}{1,75}} \right)}} \times \left( {\frac{1}{21} \times \left( {\frac{4}{D} \times \tau_{mixc} - J_{airc} \times \gamma_{air} - J_{w} \times \gamma_{w} } \right)} \right)^{{\left( {\frac{2}{1,75}} \right)}}$$
(29)

Therefore, Eqs. (25) and (29) are successively applied for the iteration i + 1, calculating, respectively and successively, τmixc (i+1) (by Eq. (25)) and Uairc (i+1) (by Eq. (29)), using the corresponding values determined in the previous iteration i, Uairc (i) (in Eq. (25)) and τmixc (i) (in Eq. (29)), respectively. All the remaining variables (which are required to solve the Eqs. 25 and 29) are calculated for each iteration applying the Eqs. (20), (26), (27) and (28) for the Uairc (i) considered in the iteration. The process is repeated until a convergence criterion is reached, which is given by an acceptable approximation level for which, practically, no changes occur in the variables between successive iterations.

When Hagen–Poiseuille formula is used, instead of Eq. (28), for computing Jairc, the constant 1.75 presented twice in Eq. (29) is (needs to be) replaced by 1 (Jairc varies linearly with Uairc), with the remaining terms of the equation and the above described process unchanged. The initial value of Uairc, required for the beginning of the iterative process, can generally be any air velocity of the same order of magnitude or even equal to the given average superficial water flow velocity (Uairc = UW), with UW always positive and lower than the two-phase average critical flow velocity (0 < UW < UWc). The described iterative procedure proved to reach a relatively rapid convergence, normally requiring just a small number of iterations, even for very small water flow rates and high air flow rates. The developed model by successive approximations considers that the average superficial water velocity cannot be negative nor null, but this does not seem to be a practical limitation. In fact, if with air flow and in the presence of water, the uplift of the liquid does not occur (due to the slippage between phases, for example) then it is generally unlikely that the transport of solids can occur, particularly for solid particles denser than the liquid.

The procedure described above can be extended or adapted for any other single-phase flow resistance law that might be suitable for the liquid phase. In the case of the Colebrook-White equation use, for example, Jw can be calculated iteratively at once as usually (e.g. by successive approximations) for the given Uw. However, for other single-phase flow resistance law of the air phase (e.g. the Colebrook-White equation) and/or for other non-trivial flow resistance law of three-phase mixtures, which might be able to determine Jmixc and replace subsequently the current Eq. (24), it may be necessary to develop or consider different iterative procedure to solve the new equations in conjunction with Eq. (25). A possible general numerical solution, for example, is to eliminate τmixc in the equations by equalising them and solving the resulting equation, which is exclusively a function of Jairc and Uairc, and, ultimately, of Uairc, by the conventional bisection method.

In the case of the eventual testing/consideration of other Newtonian fluids, like hydrocarbons, for example, in turbulent flow, the liquid single-phase flow resistance law to be used in Chisholm and Laird Equation can be also the Blasius Equation or the Colebrook-White Equation, and for Newtonian viscous liquids, in laminar flow, the Hagen Poiseuille formula. Nevertheless, for hydrocarbons, simplified equations can be always derived or obtained inside fixed intervals of Reynolds Number of a general type similar to the Scimemi Equation, whose existing coefficients were developed for water at ambient temperature. According to the above described, it may be then possible to obtain experimentally the coefficients to be used in the equations proposed in this work and to determine numerically what is the volumetric gas flow rate in steady flow that is required to avoid the deposition of granular non-cohesive material, particularly in the lower parts of any rising conduit for a given flow rate of any given Newtonian liquid.

It should be highlighted that the base data that were used for computing the constants a and b for three-phase flows considered herein were obtained experimentally for a smooth pipe with angles of inclination between 30° and 58°, for water with initial average superficial velocities between 0.30 and 0.60 m/s below the critical condition in single-phase flow for the corresponding grain samples, for solid particles with diameters between 0.425 and 7.20 mm and a specific density of 2.65, for an average superficial air velocity up to 0.8 m/s, and without relevant mobilisation of the air-lift effect in increasing the water flow rate. Previous studies have shown that the purely hydraulic performance, due to the air-lift effect in a two-phase flow of air–water, improves when the vertical column component of the mixture increases and the initial average water flow velocity decreases (see, for example, [14]).

Values of about a ≈ 0.25 and b ≈ 0.35 for three-phase flows and a ≈ 0.30 and b ≈ 0.375 for two-phase flows for the application of Eq. (17) are proposed in this work as a possible approximation that may be acceptable inside the limits of the tested conditions. The relative differences between Shmixc computed with the two resulting equations are less than or equal to 6.5% for values of Remixc up to 18,000 (well above the maximum Remixc observed in the performed experiments). For the different criteria tested when computing Jmixc for air flows with Reair < 3000, the coefficient a varied between about 0.23 and 0.27 and b between about 0.33 and 0.36. The above proposed coefficients represent also intermediate values in these observed intervals.

The model proposed in this paper is general and potentially valid for different experimental conditions, including other tested fluids, with the necessary adaptations. The results obtained experimentally in this research work with air, water, sand and fine gravel seem reliable and robust and are well-described with a very good approximation by the model. However, tests under different experimental conditions, particularly lower initial average water velocities, higher average air flow velocities, other angles of the upward pipes, or even eventually other fluids may be useful, and are strongly encouraged. They may allow to establish, in particular, a larger spectrum of the values for the proposed parameters to be used in the potential practical applications. Additionally, further studies, predominantly based on a systematic bibliometric search particularly related with mining and the petroleum industry, can be eventually performed, in order to provide a more comprehensive understanding of the multidisciplinary relevance of the obtained findings.

5 Conclusions

Experimental observations and measurements have shown that the introduction of air in steady flow at the base of an upward pipe facilitates and increases the transport of solid particles, even without mobilising the water flow rate increase in the upward pipe due to the air-lift effect.

An equation obtained by dimensional analysis, which uses two dimensionless parameters for describing the conditions that are required for the beginning of the solids transport in three-phase steady pipe flows of gas–liquid–solid particles in an upward pipe, is proposed and their coefficients are experimentally determined. Such equation allows the determination of the self-cleansing velocity of the three-phase mixture in steady upward pipe-flow, which guarantees to avoid the sedimentation and obstruction of rising pipes, either governed by gravity or forced, particularly in sanitary or storm water networks. The resulting parameters are a modified Shields number and a modified Reynolds number, which are defined and related experimentally for the critical average velocity of the three-phase mixture, considered as the condition for which no sedimentation occurs or solids transport begins. The equation obtained follows a power law, both for mixtures of air–water solids and for mixtures of water solids, with an excellent agreement between the experimental data obtained and the type of law considered. A two-phase flow may be regarded as a particular case of the three-phase flows when the air flow rate is null.

The superficial average liquid velocity was shown to be one of the most relevant variables in steady flow for the mobilisation of solids transport in three-phase flows of gas–liquid–solids in an upward pipe. In the case of sanitary or storm water sewer systems, with upward pipes working in steady pipe-flow, a large improvement in the solids transport conditions can be achieved with air injection at the lowest point of the pipes, position that maximizes also the period of contact and the oxygen transference to the wastewater, keeping the upstream total head, due to the important increase of the average water velocity. This may be reached when air is injected in the base of the inclined rising leg of an inverted siphon, maintaining the water level at the siphon inlet chamber and with the entire downing leg working in steady single-phase pipe-flow, particularly using a recirculation scheme between the chambers, and also when the air is injected for sulphide control into a sanitary force main, after the pumping equipment in a wastewater pumping station, particularly if the pumping system has relatively low friction losses (system and pump curves intersection).

The mathematical model proposed in this paper allows the explicit computation of the average self-cleansing liquid velocity in the case of two-phase flows (through Eqs. (21) or (22), depending on the flow resistance law considered). For three-phase flows, when the average liquid flow velocity is lower that this critical value, iterative procedures by successive approximations and by the bisection method are proposed to iteratively determine the average superficial gas velocity required in three-phase flow to initiate the solids transport or to avoid sedimentation.

New measurements under different experimental conditions may be required to develop or extend the coefficients obtained for the model to a larger field of application, particularly with lower average superficial water velocities, higher average superficial air velocities, rough and/or large pipes, different angles of inclination of the rising pipes, particularly below 30° or above 60°, and different fluids. Beyond the average conditions, the analysis of instantaneous turbulent velocities and turbulent pressure fluctuations, particularly using measurement equipment and tools such as Acoustic Doppler Velocimetry (ADV) and computational fluid dynamics (CFD), may be useful to complement the study and also eventually extend the obtained results.