On the rotation of melting ice disks

Abstract

This investigation was inspired by the work of Dorbolo et al. (Phys Rev E 93(3):15, 2016), which was the first to study, at a laboratory scale, the phenomenon observed in the natural world of floating disks of ice rotating. They conclude that, in controlled conditions, ice disks are able to induce their own rotation. Whilst their work successfully exposes multiple aspects of the kinematics of such disks, and the buoyancy-driven flow generated beneath them as they melt, the mechanism by which rotation is triggered remains unsubstantiated. We therefore return in this work to the study of floating ice disks, focusing specifically on the importance of experimental technique in obtaining reliable measurements of disk behaviour. Our investigation reveals that the motion of ice disks placed on a nominally quiescent body of fresh water is unpredictable, with some disks remaining motionless, and others rotating clockwise or anticlockwise. For those in motion, the average rate of rotation observed was less than half of that recorded by Dorbolo et al., a discrepancy possibly explained by residual background motions in the nominally quiescent surrounding body of water. However, given our observation that non-melting disks of high-density polyethylene (HDPE) cooled to the same temperature as the ice (comparable HDPE and ice disks differing by only $\sim 4$% in mass) consistently rotated at rates less than those made of ice, it is hypothesised that, within the confines of the freshwater environment, the motion of the turbulent meltwater plume that forms beneath an ice disk amplifies the effect of residual background motions. From our observations, it is concluded that residual motions are an underlying physical trigger for disk rotation.

Article Highlights

• The trigger for the rotation of freely floating ice disks on a nominally quiescent body of freshwater is investigated.

• The requisite ‘settling’ time for residual background motions to decay, such that the initial experimental conditions can be considered as quiescent, is measured.

• No systematic trends in the rate and sense of ice disk rotation with disk radius were observed.

• Our data supports the notion that the negatively buoyant meltwater plume that forms beneath an ice disk may amplify rotation, once this has been triggered by residual background motions.

1 Introduction

On rare occasions, floating disks of ice with diameters as large as 100 m or more have been observed rotating on cold rivers and lakes, typically taking minutes to complete a revolution. Figure 1 is an image taken from what we understand to be the first recorded observation of this phenomenon, over 125 years ago by Bates [1] and reported in a letter to the Editor of Scientific American. Since this initial observation, naturally occurring ice disks have been photographed on numerous occasions throughout the 20th century, for instance by Carstens [2] and A.G.U. [3]. However, few observers recorded in detail the conditions in which the disks were found, or the disk dimensions. There has been some discussion as to how these disks form, in particular by Nordell and Westerstrom [4], but almost no discussion as to why they rotate.

Fig. 1

Drawing taken from Bates [1] of an ice disk “about 25 or 30 feet in diameter”

The work of Dorbolo et al. [5], henceforth referred to as D16, was the first which sought to isolate the physical mechanism underlying rotation, studying the motion of ice disks floating in nominally quiescent surroundings. Based on controlled, laboratory scale experiments, D16 concluded that floating ice disks “self induce” rotation, identifying the following mechanism from particle image velocimetry (PIV) measurements of the negatively buoyant flow beneath an ice disk:

“The ice disk melts and decreases locally the water temperature close to the bottom surface of the disk. Eventually, the water reaches locally the temperature of 4 °C. At this temperature the density of the water is the highest and the fluid sinks towards the bottom of the pool and generates a plume. [...] The plume induces the horizontal rotation of the fluid, i.e., a vertical vortex close to the bottom face of the ice disk. We assess that the vortex puts the ice disk in rotation by a viscous entrainment process.”

Although D16 did not expand on this mechanism, their description provides a first insight into the physical basis for self-induced rotation, identifying the generation of vorticity by the meltwater plume as pivotal. In the new experiments reported herein we investigate what may provide an initial trigger for motion, seeking to corroborate their proposed mechanism, including through attempts to visualise the vertical vortex D16 refer to (Sect. 5.2). In addition to rotating, D16 noted that freely floating disks translated during the course of an experiment (Fig. 2). There would not, however, appear to be a physical basis for the aforementioned vertical vortex to induce translation. This observation therefore potentially indicating the existence, and significance, of residual background motions in the nominally quiescent body of water, prior to the introduction of an ice disk. In the experiments of D16, this translation was ultimately constrained non-intrusively using a magnetic field. Investigating constrained disks, D16 observed that disk rotation rate was not consistent across experiments, with the variation in the reported rate being typically as large as the mean.

These intriguing results beg the question of whether the meltwater plume is entirely responsible for initiating disk rotation or whether, even in carefully controlled experiments, residual background motion within the confines of the surrounding environment may be the trigger for disk rotation. The possibility of residual background motion within the freshwater environment driving rotation has not previously been considered and investigating its effect provides the primary motivation for our current study - our goal being to ascertain whether there is a link between the residual motions established when preparing/initialising an experiment and disk rotation.

Fig. 2

The result of tracking ellipses stained onto disks in D16. Translation was constrained by embedding a ferrous bead into disks and positioning a magnet immediately above the position from which the disk was released. Reproduced with permission from Physical Review E

A similar phenomenon has previously been studied and understood by Kouraev et al. [6]; ice ‘rings’, several kilometres across (Fig. 3), have often been observed on Russia’s Lake Baikal. The rings have not been observed to rotate but the authors reason they form from Coriolis-driven eddies in the body of water in which they reside. The water at the edge of the eddy moves more rapidly than at the centre, resulting in a greater transfer of heat to the ice at the edge. It is thought this melts the ice locally to form the near-circular outline seen in Fig. 3.

Fig. 3

An ice ‘ring’ on Lake Baikal; note the scale. Photo taken by NASA [7]

Ice disks at laboratory scale are both smaller and rotate more rapidly than the eddies observed within Lake Baikal; hence the Earth’s rotation cannot be responsible for inducing their motion. However, the possibility of pre-existing motion(s) within a nominally quiescent body of water driving rotation remains. In a laboratory setting, unless a body of water is left to quiesce for a suitable period of time, the largest background disturbances are typically tank-filling eddies—i.e. those formed as the experiment is being prepared. Personal correspondence with Dorbolo [8] revealed that an assessment of the strength and persistence of residual motions after filling the visualisation tank was not performed as part of the experiments reported in D16.

2 Rationale and scene setting

The work presented herein is essentially devoted to the question of the reliability of experimental data obtained in the study of self-induced rotation of floating ice disks on the surface of a quiescent body of water. Intrigued by the novel experiments of D16, and mindful of the challenges faced by any experimentalist, we questioned if residual background motions in the surrounding body of water, such as those present in even the most careful of experiments, could trigger disk rotation.

If one begins from the premise that the question of whether an ice disk may self induce rotation remains open, where ‘self induced’ refers purely to motion generated by the melting of the disk or the associated negatively buoyant meltwater flow below the disk, then it is useful to proceed by considering the dynamics of a perfectly cylindrical ice disk of uniform density in two idealised situations:

• (i) An ice disk floated in a smooth background flow which is initially homogeneous in the horizontal plane. In this situation, the resulting forces exerted by the flow on the disk, both due to viscous forces at the water-ice boundary and pressure forces, will be symmetrical about the vertical axis through the disk centre. Such forces are unable to generate a net moment on the disk, and therefore in this situation a floating disk would not be expected to rotate (although it would translate across the water surface).

• (ii) An ice disk floated in a background flow composed of small-scale eddying motions which are spatially random, both in velocity magnitude and direction. In this situation the viscous forces exerted on the disk surface will, evidently, be neither uniform, nor symmetrical. This, however, does not imply directly that the disk will be subjected to a net moment. It is possible to conceive of configurations of random motions in which the integral effect on the disk is such that no net moment is generated, and therefore no rotation would be expected.

These idealised situations illustrate how the presence of background motions alone is not sufficient to trigger rotation. Moreover, situation (ii) shows that to ‘measure’, in an absolute sense, a link between background motions and rotation one must determine both the spatial irregularity, and the integral moment contribution of such motions. Making measurements of this kind presents a significant experimental challenge, and fell beyond the scope of the investigations detailed herein.

We reason, however, that where background motions are residual due to the ‘random’ process of tank filling (as they are in our work), a strong correlation should exist between the magnitude of the spatial irregularities of the background motions and the mean magnitude of these motions. The latter of these metrics is something we are able to measure experimentally. Thus, whilst establishing definitively a relation between rotation and residual background motions is beyond the scope of this work, we sought to address some aspects of conducting repeatable and reproducible experiments on floating ice disks.

Following the insight that the novel work of D16 provides, our aim was firstly to corroborate whether freely floating ice disks at laboratory scale are capable of inducing their own rotation, in particular under the same essential conditions as those underpinning the work in D16, and then to investigate whether residual background motion is a trigger for the initiation of rotation. The following objectives were identified to meet this aim:

• 1. Establish the magnitude of residual background motions in a body of water as a consequence of tank filling.

• 2. Conduct a programme of controlled experiments to quantify the rotation rate of floating ice disks.

• 3. Compare the motion of disks of ice to that of a non-melting ‘control’ disk—the underlying premise being to isolate the role of meltwater on rotation.

• 4. Visualise the flow beneath an ice disk to seek independent verification of the vertical vortex reported in D16—the objective being to attempt to throw additional light on the mechanism underpinning rotation.

The remainder of this paper is laid out in the order of these objectives: Sect. 3 quantifying background motion, Sect. 4 reporting on rotation rates and Sect. 5 on the meltwater plume beneath an ice disk.

3 Background motion

An investigation into the magnitude of residual background motion resulting from tank filling served two primary purposes: firstly, to confirm the validity of the method presented in D16 and secondly, to inform the methodology of further experiments, including those we report in Sects. 4 and 5.

A specific goal was to ascertain the duration, post filling, that the water in the visualisation tank should be allowed to quiesce for prior to floating an ice disk on the free surface. Only in the absence of residual background motions would one be in the position to begin to isolate the mechanism that potentially triggers, and initially drives, the rotation of an ice disk. We do not claim to have reached a state of absolutely zero initial background motion in our experiments due, for example, to external influences (see Sect. 3.2). However, by quantifying the strength of residual motions we are better positioned to gain insight into the underlying cause for the onset of ice disk motion.

This type of question is by no means new as, for example, in the early 20th century, Einstein discussed the solution to the Tea Leaf Paradox [9]. Additionally, in rotating fluid dynamics the associated question concerning the transient behaviour of liquids in vessels that spin-down, or are spun-up, has long captured the interest of fluid dynamicists on account of the numerous applications to geophysical, astrophysical and industrial systems (Greenspan and Howard [10], van Heijst et al. [11], Watkins and Hussey [12], Wedemeyer [13], Weidman [14]). Herein, however, we are concerned with the decay rate in the mean velocity of residual background motions and, as is set out in Sect. 2, do not consider the details of the patterns of flow within the visualisation tank as motion dissipates.

3.1 Background motion: method

Figure 4 shows the basic arrangement of the apparatus: a camera was positioned perpendicular to a light sheet (a Metaphase 1.5 million lux collimated line light) which illuminated the central vertical cross-section of the visualisation tank. Particle image velocimetry (PIV) was used to measure how residual background motion varied over time in the body of water contained in the tank. A ‘worst-case’ scenario was examined, whereby the freshwater environment was initially stirred as though filling had induced a single large-scale rotational flow with an initial mean velocity of circa 30mm/s, a value chosen to be significantly larger than the disturbances anticipated on slowly filling the tank in preparation for an ice disk experiment (Sect. 4).

The PIV technique followed that laid out by Ciriello and Hunt [15] for their measurements of saline plumes conducted using the same basic apparatus.

Fig. 4

Illustration of the experimental arrangement used for making PIV measurements of residual background motions. The camera was positioned 2 m (approx.) from the light sheet and was fitted with a 75 mm focal length lens. The region of interest of the camera (not marked) captured essentially the full section illuminated by the light sheet, excluding only 50 mm at the tank base, and 25 mm from each of the left- and right-hand sides

Accordingly, the clear acrylic flow visualisation tank, of dimensions 1000 $\times$ 1000 $\times$ 750 mm (depth), was seeded with 50$\mu$m diameter polyamide particles. Video of the 700 $\times$ 900 mm² PIV window was recorded with a resolution of 5 Megapixels at 12.5 frames per second (fps). This resulted in a minimum (true) resolvable velocity of 4 mm/s, chosen such that velocities reported in the experiments of D16 were resolvable. Based on sub-pixel correlations, however, velocities as low as 0.5 mm/s were identifiable.

Computational limits resulted in non-continuous data; video was captured in four minute bursts, approximately every eight minutes. This cycle ended after 40 min of recording, with a final video taken at 80 min as a reference for possible residual background motion for the subsequent ice disk experiments. Raw footage was processed using the PIVlab MATLAB application developed by Thielicke and Stamhuis [16]: a Wiener denoise filter was applied, and a two-pass 50% overlap interrogation technique was used, with respective areas of 160 $\times$ 160 and 80 $\times$ 80 pixels². The raw data is shown in Fig. 5; by averaging the magnitude of velocity within the window, the typical speed of the freshwater within the tank was quantified.

3.2 Residual background motion: results and discussion

Fig. 5

Magnitude of average velocity in a vertical section of the visualisation tank over a single 88-minute duration experiment following a disturbance. The resulting $1.8\times 10^{4}$ datapoints were regressed to an equation of the form $ae^{bt}$, where t is time in seconds and the constants $a = 18.9$ mm/s and $b = -2.45\times 10^{-3}$/s

Tank-filling eddies dissipate through the effects of viscosity. Thus, deceleration of the residual background motion is proportional to the magnitude of velocity; an exponential decay of velocity magnitude with time was to be expected, viz. the analytical solution for the spin down of liquid in a cylindrical container [17]. Figure 5 plots the magnitude of velocity averaged over the PIV window as a function of time. Regression to an exponential fit was good, with an adjusted correlation coefficient value of $R^2=0.93$. However, the residual errors at velocities below 3 mm/s are significant. This is potentially due to other disturbances, such as those created by air currents over the tank surface or convection currents created as a result of heat transfer from the tank walls.

Any further investigation into the dissipation of tank-filling eddies could improve upon the methodology presented here in several ways. A lower frame rate would allow video recording further into an experiment, i.e. where the magnitude of motions are smaller, as well as longer periods of continuous recording, or a second light sheet could examine motion within a horizontal plane. Measures could also be taken to isolate the apparatus from other disturbances, for example, vibrations through the floor.

However, the results presented here are still valid: leaving the water in the tank to settle for 45 min following a disturbance would ensure the magnitude of residual velocities was less than 0.5 mm/s, small relative to the motions observed in D16. The methodology described in Sect. 4 therefore included leaving the apparatus for at least this duration between tank filling and the start of the first experiment with a disk, and following this between one experiment ending and the next beginning.

Whilst this 45 min ‘settling time’ may have been overly conservative in some cases, given that it was measured based upon a ‘worst-case’ large-scale rotational flow, it was infeasible to determine some reduced settling time corresponding to a more typical tank filling disturbance. Indeed, in preliminary scoping experiments related to quantifying the rotation rate of an ice disk (i.e. in which the tank was not agitated artificially), it was found that the source of the most significant disturbance preceding an experiment would vary between experiments. In some cases it was a consequence of tank filling, whilst in others it was a consequence of removing the remnants of a partially melted disk following the conclusion of a previous experiment. Given the most significant source of disturbance preceding a typical experiment could not be reliably assumed a priori, the conservative approach to allow the full 45 min settling time prior to all experiments was adopted.

4 Quantifying rotation

The following programme of experiments was conducted to answer two questions. Firstly, can the results presented in D16 be replicated after allowing the body of surrounding freshwater to quiesce, and secondly, does the motion of an ice disk differ from that of a non-melting ‘control’ disk?

In contrast to the worst-case-scenario disturbances created during the tests described in Sect. 3, for all experiments concerning ice disk rotation, the tank was filled slowly so as to limit disturbances from the very outset—the water in the tank was then allowed to settle for 45 min prior to lowering a disk onto the free surface. As such, circa 0.5 mm/s (Fig. 5) represents an extreme upper bound for the initial disturbances.

4.1 Quantifying rotation: method

A number of ice disks were prepared. To form an ice disk, a silicone mould was first half-filled with tap water before being cooled to −23 °C. The mould was insulated on all sides but underneath. The ice would then form first at the base of the mould and crystallise upwards, preventing air bubbles from being trapped in the ice. Once this had frozen, three slender nylon lines, each with a diameter of 0.45 mm, were embedded in a second layer of ice atop the first to form a single complete disk, as depicted in Fig. 6a. The lines were used to slowly lower each disk horizontally onto the surface of the water in the visualisation tank, following the procedure described below; freezing the lines in a second layer ensured that, as the disk melted, they would not become exposed to water beneath or become detached within the time frame of an experiment. Finally, two wooden markers were rigidly fixed on the surface of each disk to form a cross.

The procedure adopted to float the ice disks was required to place, and then release, the disks in such a way that neither they, nor the surrounding body of water, were perturbed prior to the start of an experiment. Disks were lowered slowly onto the water surface, using the nylon lines in a pulley arrangement over a stainless steel super-structure above the tank. Throughout the lowering process the horizontal orientation of the disk was confirmed using a spirit level placed on the top surface of the disk, with the three nylon lines allowing for precise adjustments to the disks orientation. When the disk contacted the water surface, the tension in the nylon lines was gently released simultaneously to allow the disk to float freely and, once slack, the lines were cut away from the disk close to the top surface.

This procedure prevented ‘pitching’ of the disk when released, by placing it horizontally. Disks were susceptible to ‘bobbing’ if the tension in the lines was released too quickly, however if any visible bobbing was observed then the experiment was terminated. The only disturbances caused to the body of water were tiny ripples (capillary waves) created as a disk first touched the free surface before settling to its equilibrium position, the latter evidenced by a slackening of the supporting lines. These ripples were perceptible only on account of the changing pattern of light reflecting from the free surface. No bobbing or pitching of the disk due to these capillary waves, or further wave motion, was observed. This method of release was shown to not impart motion onto an ice disk; an HDPE disk at ambient temperature released in the same manner was initially motionless. Once released, the motion of each disk was then observed by tracking the cross.

Fig. 6

Illustration of the experimental arrangement. a The ice disk with embedded nylon lines and reference cross. b The ice disk released centrally on the free surface. The surface forms the $x-y_\phi$ plane, with the $x-$axis perpendicular to the camera. A wide-angle 16 mm lens was used given the angle at which the recording had to take place

A 230 mm diameter and 60 mm thickness ‘control’ disk was fabricated from high density polyethylene (HDPE) sheet material using a waterjet cutter. The cutter resulted in deviations from a perfect circle of approximately 0.5 mm, less than 0.5% of the radius and deemed insignificant. HDPE was selected for this purpose as its density and specific heat capacity are similar to that of ice, see Appendix A for details. The difference in mass between an ice disk and an HDPE disk of equivalent dimensions was approximately $4\%$.

Video recording at 6.25fps resulted in 3750 frames over a ten-minute period for each ice disk. Footage was manually processed; the angle of the markers was re-measured whenever they appeared to have rotated by more than 5 °, typically resulting in eight angle measurements over the course of an experiment.

The procedure used to lower the disks vertically downwards onto the free surface via the nylon lines, and the available vertical space in the laboratory, meant that the camera could not be positioned centrally above (and perpendicular to) the surface. The camera was instead positioned at an angle to the vertical as depicted in Fig. 6b. This introduced two kinds of perspective error, shown in Fig. 7:

• (i) if a marker on a disk rotated, the angle through which this occurred would appear to the camera to be distorted; and

• (ii) if a disk translated towards or away from the camera, the shape of the disk as seen by the camera would change.

Fig. 7

The two types of perspective error. a, b Images of the same cross after being rotated by approximately 45 °. c Three images of the same disk when positioned at the (i) front, (ii) middle, and (iii) back of the tank as seen by the camera

The first error was addressed by developing a function to map between the angle as seen by the camera and the angle through which a disk physically rotated. The second error was addressed by adjusting this mapping according to which of nine sections of a frame the marker was located. The function selected is described by (1):

$$\begin{aligned} \phi = \gamma + {c_1}\text{ sin }(2{\gamma }) \end{aligned}$$

(1)

where $\phi$ and $\gamma$, see Fig. 8, are the angles (in radians) measured from the positive x-axis to a marker as would be seen from directly above and as seen by the camera, respectively. The constant $c_1$ was found from calibration and varied depending on which section of a frame the marker was located. Calibration was performed by floating a protractor in the tank, giving angles in the $x-y_{\phi }$ plane and their corresponding values in the $x-y_{\gamma }$ plane upon which the function could be regressed.

Fig. 8

Angle and coordinate system definitions. The $y_\gamma$ axis is the result of rotating the $y_\phi$ axis through $(\frac{\pi }{2} - \theta )$ radians about the positive x-axis, where $\theta$ is the angle of the cameras line of sight from horizontal (i.e. elevation). Subscripts refer to which of the two markers an angle corresponds

Discussion supporting the choice of function (1) is provided in Appendix B; it should be noted that this function is not the true mapping but an accurate albeit simpler form.

The accuracy of the mapping was assessed in two ways. The correlation coefficient $R^2$ of the calibration data with the function varied based on which section of the frame a marker was in, but was always at least $R^2 = 0.98$. Additionally, the angle between the two markers in each experiment had to be constant. This angle varied in $\gamma$-space due to the perspective error, but once mapped into $\phi$-space it remained constant, a strong indicator that the mapping was accurate.

4.2 Quantifying rotation: results and discussion

Disks of different diameter were used to establish whether there was a systematic variation in rotation rate with disk diameter. The variation in marker angle $\phi$ with time for 11 experiments is presented in Fig. 9; 10 of the disks observed were made of ice, with diameters of 150, 200 or 230 mm, and initial thickness 50 mm. The eleventh (control) disk was made of HDPE and also cooled to −23 °C. Experiments with an HDPE disk at ambient temperature were conducted but the results are not plotted; the disk was completely motionless. The final two datapoints of each experiment were used to calculate the rate of rotation of each disk. This was to establish the ultimate rotation rate of the disk, i.e. at the conclusion of each experiment, and allow the results to be directly compared to those of D16. These results are presented in Table 1, with entries in the fourth column giving the tangential speed at the disk circumference.

Fig. 9

Angle through which disks were observed to rotate over time. Data from D16 includes average rate of rotation and range of their results at the same water temperature. Data could not be obtained prior to t = 80 s (with $t\,=\,$ 0 s being the time at release) as the camera line of sight was obscured during the disk release procedure

Neglecting direction, the average rate of rotation of an ice disk was 0.85 °/s, with a standard deviation of 0.64 °/s. No disk rotated at greater than the average rate reported in D16 for water at the same temperature (1.9 °/s), although six were above the lower bound of their data range (0.9 °/s). The remaining five rotated at less than 0.5 °/s, with two of those effectively motionless. The control disk rotated slowly, with a rate higher than just two of the ice disks.

Table 1 Rates of rotation for disks floating on a $1\times 1\times 0.65$ m³, 12 °C body of water that was allowed to settle for 45 min between any disturbance and the experiment beginning. The average rate observed in D16 at the same temperature was 1.9 °/s

The highest tangential speeds of rotation evidently occurred when the largest diameter disk rotated at its fastest rate (2.5 mm/s, Table 1). Of all the observed tangential speeds, however, the majority were of the same order of magnitude as the residual background motions expected following tank filling and settling ($\sim 0.1-0.5$mm/s as reported in Sect. 3). This suggests that residual background motions are capable of being a driver for the observed disk motion. Furthermore, having conducted similar experiments to those in D16 but with greater emphasis on reducing residual background motion, slower rates of rotation were recorded. Therefore, it is proposed here that residual background motion triggers the rotation of ice disks.

Additional corroboration for this proposal can be obtained by drawing a comparison between the expected magnitude of residual background motions, and the velocities which will be induced in the surroundings by the meltwater plume which forms beneath each ‘cold’ disk. A first-order estimate of these induced velocities is made in Appendix C, which reveals that both the depth-averaged, and peak, values of horizontal velocity (resulting from turbulent entrainment into the plume) are approximately equivalent to the residual motions present after allowing an extreme disturbance to settle. We thus believe these induced velocities will be several times larger than the residual motions which may be present in a carefully initialised experiment. This suggests both that the procedure developed to minimise residual background motions (Sect. 3) is appropriate (and moreover necessary), but also that those motions which may still remain are of sufficient magnitude to play a significant role in driving disk motion. Note that the peak induced vertical velocity, as estimated in Appendix C, is both relatively small and would be observed at a location distant to the floating disk. This velocity is therefore deemed negligible in the context of driving disk motion.

The large variation in observed motion, specifically in the direction of rotation and the mean rotation rate, is indicative of randomness and indeed that there is no single driver of rotation; the results are what one would expect from an unconstrained object with some small and unpredictable shear force applied to it. However, an HDPE disk at ambient temperature was completely motionless. Nine ice disks and a cooled HDPE disk did show motion; perhaps the thermal gradients they induced within the tank amplified any underlying motion.

Despite the relatively limited number of tests, no systematic variation in the rate or sense of rotation was observed with disk diameter—findings that do not clearly point to the need for repeat experiments to investigate this further.

5 Flow visualisation

A cold disk placed on the surface of a body of freshwater (above 4 °C) cools the nearby fluid, increasing its density. Exceeding the density of its surroundings, this fluid is subject to a buoyancy force which drives convection and, consequently, it was expected that a plume-like structure would be observed beneath both a melting ice disk, and the cooled control disk. Perhaps, as proposed by D16, the behaviour of this buoyancy-driven flow could explain the differing behaviours of disks of ice and ambient temperature HDPE.

5.1 Flow visualisation: method

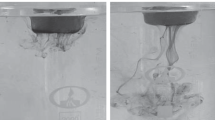
Methylene blue dye was used to stain the water that comprised the ice disks used in the flow visualisation experiments, which upon melting would serve to highlight the path of meltwater on backlighting the setup. This choice of flow visualisation enabled the flow beneath the disk to be clearly visualised and thereby for evidence of the ‘vertical vortex’ reported in D16 to be collected.

This method of flow visualisation does not, however, show the entire plume, as heat transfer forms a thermal plume around the meltwater ‘core’. Attempts were made to visualise the entire plume using a shadowgraph technique: the density differences involved were sufficiently small, however, that the resulting variations in refractive index did not enable the flow to be visualised as clearly with the available apparatus as with the backlighting approach.

Video recording of an initially 230 mm diameter ice disk as it melted was centred approximately 100 mm below the free surface, a depth at which the plume was expected to contract to a ‘neck’. As the ice melts, the negatively buoyant meltwater produced accelerates downward. Conservation of volume acts to reduce the cross-sectional area of the flow. If this dominates the effect of entrainment (which acts to expand the plume), the flow contracts to a neck before the flow subsequently expands downstream.

As in Sect. 3, a 75 mm focal length lens was used. Video was processed using MATLAB: contrast was increased and colours inverted for clarity. Edge detection was performed with the Prewitt operator [18]. Each disk was weighed before and after an experiment, the difference giving the mass of ice $\Delta m$ which had melted.

5.2 Flow visualisation: results and discussion

Our flow visualisation results provide no indication as to the presence of the ‘vertical vortex’ structure described by D16. As a consequence, the description of the mechanism proposed by D16 would appear to require amendment.

Figure 10 shows the path of meltwater from an ice disk. Following the perimeter of the meltwater-freshwater interface, a pronounced contraction of the flow to a minimum width close to one quarter of a disk diameter below the underside of the disk, followed by an expansion in width, is clearly evident. As such, the morphology of the meltwater flow closely resembles the observations of contracting lazy plume flows (e.g. Kaye and Hunt [19]) produced by low-momentum releases of saline solution from large area sources into freshwater environments. Here, ‘lazy’ refers to the classification of the plume source and specifically to the fact that the source momentum flux is less than that which would be required to produce a pure plume at source [20]. Drawing the analogy between the meltwater plume and the previously observed behaviour of highly lazy aqueous-saline plumes, it is evident that whilst turbulent entrainment of the surrounding freshwater into the meltwater plume acts to increase the plume width in the far field, the near-source contraction observed (Fig. 10) indicates that the acceleration of the flow (which in the absence of entrainment would result in a strongly contracting flow) dominates entrainment in the near-source region. Furthermore, in the far field, the rate of expansion of the plume width appears to reduce with distance below the disk, indicating a reduction in the rate of entrainment into the plume. This observation is consistent with there being enhanced entrainment in the near field (following the neck) of lazy plumes, as indicated by Marjanovic et al. [21] and others.

Fig. 10

Colour-inverted image (1/6th second frame) of turbulent plume flow under a melting ice disk

The observed plume was compared to the shape predicted analytically by Ciriello and Hunt [15] for a turbulent plume from a circular source with entrainment varying with local Richardson number: such a theoretical plume model with variable entrainment coefficient was key due to the non-pure plume local conditions in the meltwater plume that forms beneath the ice disk.

The classification of turbulent plumes and the plume source in terms of the Richardson number ${\Gamma }$, as described in Hunt and van den Bremer [20], has a direct bearing on plume morphology. The source Richardson number $\Gamma _0$, where

$$\begin{aligned} {\Gamma _0} = \frac{5}{8\alpha }\frac{{b_0 g_0'}}{w_0^2}= \frac{5}{8\alpha \sqrt{\pi }}\frac{{g_0'}{{A_0}^{\frac{5}{2}}}}{{Q_0}^2}, \end{aligned}$$

(2)

characterises the ratio of the inertial and buoyancy forces at the source of the plume of interest relative to a pure plume, in other words, the ‘laziness’; $\Gamma =1$, $\Gamma <1$ and $\Gamma >1$ correspond to pure, forced and lazy plumes, respectively, and theoretically it is well established that only suitably lazy plumes contract. In (2), $b_0$ is the source radius, $w_0$ a vertical velocity characteristic of plume fluid at the source, $\rho _0$ and $\rho _a$ the density of the plume at source and the surrounding environment, respectively, and $g_0' = g{\frac{{\rho }_a-\rho _0}{{\rho }_a}}$ the reduced gravity of the fluid that emanates from the source,¹ where g is the acceleration due to gravity.

Whilst pure plumes are dynamically invariant and well described by theoretical models based on a constant entrainment formulation where, specifically, the entrainment coefficient $\alpha$ is invariant, the flow within a lazy plume is in a non-equilibrium state and so dynamically varies with distance z from the source ((Ezzamel et al. [24], van Reeuwijk et al. [25]) with behaviour characterised by $\Gamma \rightarrow 1$ as $z \rightarrow \infty$, so that local conditions in the plume, including entrainment, are expected to depend on the local Richardson number. This behaviour has been confirmed by measurements in thermal and aqueous-saline plumes (Papanicolaou and List [26]; Wang and Law [27]; Kaye and Hunt [19]; Ezzamel et al. [24]) with further support from direct numerical simulation and theoretical studies (van Reeuwijk et al. [25], Marjanovic et al. [21]). Ciriello and Hunt [15] provide the first analytical solutions to the plume conservation equations for such non-equilibrium plumes based on the variable entrainment model

$$\begin{aligned} \alpha = {d_1} + {d_2}\Gamma \end{aligned}$$

(3)

where $d_1$ and $d_2$ are coefficients. The historical numerical predictions and experimental measurements of these coefficients may be estimated from the summary table in Ciriello and Hunt [15]. Herein, we adopt the values given by Marjanovic et al. [21].

The time-averaged source volume flux for an ice disk $\overline{Q_0}=\frac{{\Delta }m}{{\rho _i}T}$ was calculated for each experiment, where $\rho _i$ is the density of ice and T the duration of an experiment. We make the assumption that $Q_0\approx \overline{Q_0}$ is reasonable given the duration of an experiment ($T=550$s) is long relative to the time taken for the plume to form ($\approx 20$s).

Three different disk diameters were used over 12 experiments, resulting in three different values of ${\Gamma }_0$ (see table 2). The variable entrainment model was then applied using the lazy plume parameters from Marjanovic et al. [21], i.e. with $d_1=0.085$ and $d_2=0.24$, and the resulting prediction of the plume outline compared to the observed shape in Fig. 11.

Table 2 Scaled source Richardson number $\frac{8\alpha \sqrt{\pi }}{5}\Gamma _0$, cf. (2), and standard deviation $\sigma$ for the three disk sizes, each entry based on an average across four individual experiments. For the purposes of comparison with D16, the characteristic Rayleigh number based on a vertical length scale of $L=D$, $Ra =g_{0}'L^3/(\kappa \nu ) \sim \mathcal {O}(10^{8})-\mathcal {O}(10^{9})$ for all experiments; the physical properties of water were taken to be $\kappa =1.5 \times 10^{-7}\,$m$^2$s$^{-1}$ and $\nu =1.2 \times 10^{-6}\,$ m$^2$s$^{-1}$

Whilst qualitative agreement is good, quantitatively the outline of the meltwater plume differs from the outline predicted. For the 230 mm diameter disk, the plumes narrowest point, or neck, was 50 mm below the source, whereas the model predicted necking considerably closer to the source.

Notably, the plume model we adopt is based on a number of key assumptions, including that the flow is steady, slender and turbulent. Given the disk appeared unchanged during the period the plume was interrogated, in other words the characteristic timescale for disk melting was large relative to the timescale for plume formation, the steady assumption is reasonable. However, in the context of the meltwater plumes under consideration the other key assumptions are less viable. In the context of area source plumes, Hunt and van den Bremer [20] explain the falsity of the slender assumption near the source as follows: “the length scale for the entraining turbulent eddies scales on the vertical distance from the source in this region rather than on the plume width.” This results in classical plume theory underestimating near-field entrainment from highly lazy area source plumes. The variable entrainment model improves on this, but evidently the model overestimates the change in $\Gamma$ with distance from the source, and so entrainment is again underestimated. Additionally, the flow does not appear to be fully turbulent immediately beneath a melting ice disk. Moreover, meltwater from an ice disk is an atypical plume source compared with those more routinely analysed using plume theory as volume flux is driven by a phase change and not a release of fluid with an already established momentum.

Fig. 11

a Prewitt edge detection applied to the single frame in Fig. 10. b Plume shape predicted by the analytical model of Ciriello and Hunt [15] using the lazy plume parameters of Marjanovic et al. [21]

6 Discussion and conclusions

Inspired by the novel experiments of Dorbolo et al. [5] on the self-induced rotation of floating ice disks, we sought to gain further insight into the mechanism(s) potentially responsible for triggering and sustaining disk rotation. Our focus was on disks at laboratory scale that are freely floated on an initially uniform temperature body of nominally quiescent freshwater. Identifying the underlying mechanism(s) via a controlled set of experiments under highly repeatable conditions is fraught with challenges, particularly given the inherent difficulties of releasing an ice disk without imparting a net torque, or creating waves on the free surface of an environment, such that the influence of unwanted background motions can be categorically ruled out. In this laboratory setting, we questioned whether eddies resulting from the process of filling the flow visualisation tank with freshwater or, in other words, residual background motions, may trigger the rotation of a disk in what may otherwise be regarded as a nominally quiescent environment.

Prior to conducting experiments with floating ice disks, particle image velocimetry was used to quantify the dissipation of eddies following an artificial initial disturbance of significantly greater magnitude than that produced by careful tank filling. Taking the average velocity, on a PIV window comparable in area to the full vertical cross section through the visualisation tank, as a measure of the residual motion indicated that a 45 min settling time was necessary to reduce this average to 0.5 mm/s, approximately $2\%$ of the initial value. Water in the tank was therefore left to settle for at least this duration prior to each disk experiment. Before drawing any conclusions, it is informative to first reflect on the main findings of our disk experiments which may be summed up as follows:

• (i) For ice disks:

  • some disks rotated clockwise, some anticlockwise, and some remained effectively motionless;

  • no systematic variation in the rate or sense of rotation was observed with disk diameter (and, given all ice disks had identical initial thickness, in disk mass);

  • the ensemble average rate of rotation was comparable with the standard deviation in these measurements;

  • for disks in motion, the tangential speed at the disk circumference was comparable with a representative measure of the speed of residual motions created on tank filling; and

  • a contracting meltwater plume formed beneath the disk (a ‘vertical vortex’ was not observed).

• (ii) For a (non-melting) control disk of HDPE at the temperature of the water in the visualisation tank:

  • the disk was motionless.

• (iii) For a (non-melting) control disk of HDPE cooled to the same temperature as the ice:

  • the disk rotated at a low rate of rotation, comparable to the lowest observed rates for rotating ice disks.

Based on these findings we may draw some overriding conclusions, although, as the ambient temperature control disk did not rotate, definitively pinning down the triggering mechanism still eludes us - the stalling point from our own observations being that if rotation were triggered exclusively by residual background motion, rather than by plume motion or a combination, then one would have expected the non-melting disk at ambient temperature to have rotated. However, that this disk did not rotate does not rule out the potential triggering role of residual background motions. Our experiments only captured their bulk effect and were not designed to, and could not, produce a complete picture of the individual eddying motions in contact with the disk. Whilst the integral effect of these eddies evidently resulted in zero net torque and thus an absence of rotation, other residual disturbances with an identical average velocity could have resulted in a non-zero net torque and, thus, in rotation. Resolving the role on rotation of individual residual eddying motions local to the disk and their integral effect, whilst tremendously challenging, could prove decisive in identifying the triggering mechanism. That a cooled non-melting control disk rotated (at a slow rate, comparable to some of the ice disks) but remained perfectly still when at ambient temperature points to the convective motions driven by small density differences as magnifying the effect of residual background motions.

Whilst we have made inroads into procedures that improve the reliability of experimental data obtained in ice disk studies, comparing our own measurements with those of D16 raises a number of interesting questions. For example, although our disks were initially thicker and, thereby, of a greater mass, it remains unclear why the nominally steady rotation rates we recorded were so much lower (by $\sim$55%)—the steady rotation rate not having an obvious anticipated dependence on mass, an idea supported by our observations of disks of varying mass.

Owing to the arrangement we designed to release the disks in a disturbance-free fashion, it was not possible to gather footage during a period of time immediately following release. It would be informative to interrogate this initial transient motion, potentially to establish a dependence on disk mass, and simultaneously capture the developing meltwater plume and its induced flow field—for example, to establish whether asymmetries in this entrainment field could be responsible for consistently triggering rotation or whether the motion is established on a shorter timescale.

Finally, the highest speed of rotation recorded was of the same order of magnitude as the residual background motion, while some disks were near motionless. This supports the concept of the rotation we observed as being triggered by random motions such as the residual background motions studied here.

Appendices

Appendix A: Material selection for a control disk

Figures 12 and 13 are taken from the materials selection programme Cambridge Engineering Selector (CES). To have heat transfer properties comparable to ice, the control disk had to have a similar specific heat capacity (2.1kJ/kg K) and density as close as possible to that of ice, but certainly less than that of water (1000 kg/m³). The material also had to be machinable, inexpensive, and impermeable to water: the options meeting these criteria were natural rubber, polyethylene or polypropylene, of which polyethylene was easiest to source.

Fig. 12

Plotting specific heat capacity against density. Note x-axis log scale. Using a material substantially less dense than ice was infeasible as the resulting disk would need to be very large to have the same thermal mass as an ice disk

Fig. 13

Plotting specific heat capacity against material cost per unit mass. Note x-axis log scale

Appendix B: Function to correct perspective error

To calculate an exact mapping from $\gamma$ to $\phi$ would have required considerable effort; the geometry of the lens in use, as well as exact distances and angles in the experiment, would be needed. As such, an approximate mapping was chosen, that required all of the following traits: $\gamma = \phi$ at 0, $\pi /2$, $\pi$ and $3\pi /2$; $d\phi /d\gamma$ is largest when $\gamma =0$; $d\phi /d\gamma = 0$ at $\gamma =\pi /2$; the function must be strictly increasing; and finally, the function must be collapsible to $\phi =\gamma$ (for the case of a camera positioned vertically above the free surface, i.e. $\theta =\pi /2$). The simplest function meeting these requirements, as given in Sect. 4 and expressed in radians, is:

$$\begin{aligned} \phi = \gamma + {c_1}\text {sin}(2{\gamma }) \end{aligned}$$

with the requirement of $0\le c_1 \le 0.5$. This function is plotted in Fig. 14 for several values of $c_1$.

Fig. 14

The chosen mapping function with varying $c_1$

Appendix C: Scalings for plume-induced background motions

On appealing to the established scalings for the time-averaged bulk flow in turbulent plumes [28], first-order estimates for the magnitudes of the principal secondary motions that are induced by the plume descending from a disk can be readily established, as outlined below. These estimates can then be compared with the magnitude of the residual background motions expected following the process of tank filling and settling (cf. Sect. 3).

The secondary plume motions of interest are two-fold: first, the predominantly horizontal secondary flow that occurs as a consequence of plume entrainment (i.e. the classic plume-induced flow) and, second, the predominantly vertical ‘filling-box’ flow (cf. Baines and Turner [29]) that occurs as a consequence of the plume being confined within the boundaries of a visualisation tank - this vertical flow manifesting as a deepening pool of cool meltwater at the base of the tank. For the former, the magnitude of the horizontal entrainment velocity u is of primary interest and for the latter, the vertical velocity $\mathcal {W}$ associated with the rate of deepening of the meltwater pool. Our estimates that follow are based on the asymptotic behaviour of a plume and thus do not account for the contraction observed in the near-source region (Sect. 5.2), or overturning motions within the confines of a filling box, as quantified by Kaye and Hunt [30]. As such, the approach taken below provides a guide and the order of magnitude estimates we sought.

1.1 C.1 Horizontal background velocities

The time-averaged asymptotic vertical velocity in a quasi-steady (as opposed to ‘starting’) plume emanating from an axisymmetric area source in uniform quiescent surroundings may be expressed as

$$\begin{aligned} w(B,z)=cB^{1/3}(z+z_v)^{-1/3}, \end{aligned}$$

(4)

where c is a constant, B the source buoyancy flux, and the virtual origin offset $z_v$ accounts for the non-zero area of the plume source (the disk) at $z=0$—the vertical coordinate z increasing downwards. Thus, a representative average plume fall velocity over the depth H of the tank is

$$\begin{aligned} \bar{w}=cB^{1/3} \frac{1}{H} \int _0^H (z+z_v)^{-1/3} dz=\frac{3cB^{1/3}}{2H} \left( (H+z_v)^{2/3} - z_v^{2/3} \right) . \end{aligned}$$

This compares with the vertical plume velocity at the base of the initially unstratified tank (the peak plume velocity) of

$$\begin{aligned} w(B,z=H)=cB^{1/3}(H+z_v)^{-1/3}. \end{aligned}$$

Whilst, with knowledge of the source fluxes, the virtual origin offset may be predicted from the analytical solution of Hunt and Kaye [31] or Ciriello and Hunt [15] for constant or variable entrainment formulations, respectively, for simplicity we take $z_v=D$, with D the disk diameter. In our notionally ‘deep’ tank, $H \gg z_v$ so that $H \gg D$ and, thus, the depth-averaged and peak vertical plume velocities reduce to

$$\begin{aligned} \bar{w}\approx \frac{3cB^{1/3}}{2H} \left( H^{2/3} - D^{2/3} \right) \quad \text{ and } \quad w(B,z=H)\approx cB^{1/3}H^{-1/3}, \end{aligned}$$

respectively. The horizontal velocity induced in the ambient, u, is related to the vertical velocity of the plume w via the entrainment coefficient $\alpha$, i.e. $u=\alpha w$. For ‘top hat’ cross-stream profiles of velocity and buoyancy, $\alpha \approx 0.13$ [32] and, as such, the horizontal velocity induced in the ambient at the plume perimeter is roughly one-eighth of the local vertical velocity in the plume. Accordingly, the following estimates are obtained:

$$\begin{aligned} u(B,z=H)\approx 0.13 cB^{1/3}H^{-1/3} \quad \text{(peak } \text{ horizontal } \text{ velocity) }, \end{aligned}$$

(5)

and

$$\begin{aligned} \bar{u}\approx 0.13 \times \frac{3cB^{1/3}}{2H} \left( H^{2/3} - D^{2/3} \right) \quad \text{(depth-averaged } \text{ horizontal } \text{ velocity) }. \end{aligned}$$

(6)

1.2 C.2 Vertical background velocities

The volume flux in the plume at the base of the tank may be approximated as

$$\begin{aligned} Q(B,z=H)= CB^{1/3}(z+z_v)^{5/3}|_{z=H}, \end{aligned}$$

with C a constant. If we now make the assumption that the horizontal cross-sectional of the plume is small compared with the cross-sectional area $W \times L$ of the visualisation tank, the peak vertical velocity $\mathcal {W}$ in the ambient associated with the deepening meltwater pool at the tank base may be expressed as

$$\begin{aligned} \mathcal {W}(z=H)\approx -CB^{1/3}\frac{(H+D)^{5/3}}{WL}. \end{aligned}$$

(7)

The minus sign in (7) signifies that this velocity is counter to that in the descending plume.

1.3 C.3 Velocity estimates

Based on the assumption of ‘top hat’ cross-stream profiles, the constants

$$\begin{aligned} c=(5/6\alpha )(9\alpha /10)^{1/3}{\pi }^{2/3} \quad \text{ and } \quad C=(6\alpha /5)(9\alpha /10)^{1/3}{\pi }^{-1/3}, \end{aligned}$$

(8)

see Morton et al. [28], giving $c\approx 7$ and $C\approx 0.05$ for $\alpha \approx 0.13$. Substitution into (5), (6) and (7), respectively, yields the following estimates - peak horizontal velocity $u(B,z=H)\approx 1.0$mm/s, depth-averaged horizontal velocity $\bar{u}\approx 0.84$mm/s and peak vertical velocity $\mathcal {W}(z=H)\approx -0.053$mm/s.