1 Introduction

A vortex formation around bridge piers can be destructive by causing complex flow interactions and scouring at riverbed. There is a huge research interest among literature in the field of hydrodynamics around the flow obstruction [5, 8, 16, 22, 23, 25, 26, 29, 45, 49]. Most researches have been conducted on the turbulent characteristics of flow over smooth and rough boundaries around single pier or obstruction [2, 35, 46, 47], and fewer studies have been conducted on coherent flow structures to study the burst cycle dynamics and to understand the burst cycles correlation to flow [7, 18, 24, 34].

Kline et al. [28] first used the idea of a burst cycles for particle movement between turbulence and laminar zones near wall-boundary. This effort has been followed by Brodkey et al. [6] who re-examined sweep and ejection events that could significantly affect the Reynolds shear stress (RSS). Since then, the study of turbulent coherent structures in a boundary layer has become a prominent research topic. A review study by Adrian and Marusic [1] discussed significant advances made over the past few decades in the fundamental study of wall turbulence over smooth and rough surfaces, focusing on coherent structures and their role at high Reynolds number flows. The purpose of their study is to determine how such analysis can be used to improve hydraulic engineering design.

Experimental studies were conducted by Bauri and Sarkar [4] to investigate the effect of submerged circular and square cylinders on turbulence bursting events and sediment transport to gain a better understanding of wall-wake flow. Their quadrant analysis confirms that in wall-wake flows, sweeps are the governing mechanism. Other studies have found similar results using quadrant analysis around single circular bridge pier [24], around a sphere placed on rough bed [15], and for rough wavy bed [36]. However, according to the study by Motion [32] in an open channel flume with varying bed roughness, the most common event during a burst cycle is multi-ejection, which can push existing settled particles into suspension. Cellino and Lemmin [7] showed in their investigation how the burst cycle influences the suspended sediment transport under clear water condition. They explained the mechanism of erosion, transport and particle deposition, which showed that instantaneous sediment suspension is significantly determined by the near-bed bursting events.

To analyse the flow turbulence and to relate the sediment entrainment and deposition around bridge piers, a quadrant analysis has been conducted by Chavan et al. [9]. It was observed that strong wake occurs between piers (i.e. tested on two different diameters of pier) for non-uniform sand bed. Hamed et al. [17] and Huai et al. [20] have also conducted research on the hydrodynamics of turbulent flow and sediment transport through submerged flexible vegetation using acoustic Doppler velocimeter (ADV), which their results have been conclude in the review study by Huai et al. [19]. According to those studies, sediment transport capacity can be diminished in the vegetated zone, while flow resistance increases.

In present study, a three square-piers group induced turbulence has been experimentally studied. The quadrant analysis has been used to quantify in detail how bursting events contribute to turbulence after each pier. As a result of analysing the flow surrounding piers, vortices formation exhibits a coherent structure. In addition, the probability of each bursting event is assessed. The piers-group presents complex constructive-destructive turbulence coupling. This complex phenomenon is crucial for engineer to design the bridge piers and assess the interaction between flow and pier. In the view of the importance to understand flow behaviour within group of bridge piers, this study will analyse the bespoke phenomenon by the quadrant’s contribution of Reynolds shear stress after each pier. To demonstrate how coherent flow structures affect the flow region, three parallel paths have been measured and discussed from the flume streamline at distances of 0 m (first row), 0.025 m (second row) and 0.05 m (third row) from the centreline of the piers.

2 Experiment and methods

2.1 Experimental setup

Experiments were conducted in a smooth-bed rectangular open channel located at the University of Bradford's Hydraulic Laboratory with a flume length of 12 m, a height of 0.5 m, and a width of 0.45 m. Three long square piers with dimensions of 0.05 × 0.05 m were placed at 0.1 m distance from each other, where the first pier was located at 3 m downstream from the entrance of the flume. Water discharge and bed slope were set at 0.072 m3/s and 0.0033, respectively, with a uniform flow depth of 0.21 m achieved throughout the flume before placing the piers.

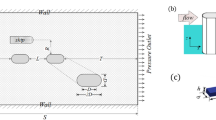
For this study, the ratio of pier to channel width (b/w) was 11%, and the distance between the piers (dp) was twice the pier width. It was also suggested by Chiew and Melville [10] that b/w should be about 10% to avoid sidewall interference to the turbulence zone created by pier. A side-looking Acoustic Doppler Velocimeter (ADV) by Nortek was used to measure velocity profile. The data for each measured point was recorded for 5-min duration at 100 Hz sampling frequency. This allowed the collection of 30,000 samples for each point. The utilised duration and sampling size have been adopted from Khaple et al. [27], as they were suggested to be sufficient to obtain time-averaged turbulence structures and velocity. The ADV profile re-alignment method proposed by Pu et al. [38] and Pu [37] has been used to ensure the profile’s locational precision. A minimum correlation coefficient of 70% and a minimum signal-to-noise (SNR) ratio of 15 dB have been maintained for all measured points. In total, 60 different locations were measured based on Fig. 1’s schematic plan. At each location, at least 15 vertical positions were recorded across the flow depth. The lowest measurement point was 0.005 m from bed.

Fig. 1
figure 1

Schematic Plan of the experiment and measuring point by using ADV on the right side of the piers in three rows

Full size image

2.2 Quadrant analysis

Burst cycles are common phenomena in the turbulence generation layer near bed, in which strong vortices are generated because of ejection and sweep events [44]. Low-speed ejections and high-speed sweeps were suggested to occur irregularly [42], and they are primarily responsible for vortices generation. In natural flow, bed particles are lifted by ejections and moved by sweeps, therefore most of the particles incipient motion boosted during bursting events.

In this study, the analysis of streamwise (\({u}^{^{\prime}}\)) and vertical (\({w}^{^{\prime}}\)) velocity fluctuations were divided into four burst quadrants [30, 47]. There are: (Q1): Outward interaction, reflected high-speed flow by the wall (within limit of \(w^{\prime} > 0\), \(u^{\prime} > 0\)), (Q2): Ejection, away from the boundary by low-speed flow (within limit of \(w^{\prime} > 0\), \(u\prime < 0\)), (Q3): Inward interaction, pushed backward by low-speed flow (within limit of \(w^{\prime} < 0\), \(u^{\prime} < 0\)), and (Q4): Sweep, toward the boundary by high-speed flow (within limit of \(w^{\prime} < 0\), \(u^{\prime} > 0\)) [25, 26, 33]. \({u}^{^{\prime}}\) and \(w^{\prime}\) can be defined as:

$$u_{i}^{\prime } = u_{i} - \overline{u}$$
(1)
$$w_{i}^{\prime } = w_{i} - \overline{w}$$
(2)

where \(u\) and \(w\) are the instantaneous velocity components in the streamwise and vertical directions, respectively, i = 1, 2, 3, …, n is an index in which n is the total number of samples. \(\overline{u}\) and \(\overline{w}\) are time-averaged velocity components in the streamwise and vertical directions, respectively, which can be calculated as follows:

\(\overline{u} = \frac{1}{n}\mathop \sum \limits_{i = 1}^{i} u_{i}\), and,

$$\overline{w} = \frac{1}{n}\mathop \sum \limits_{i = 1}^{i} w_{i}$$

For the convenience of quadrant analysis, concept of Fig. 2 has been adopted. The cross-hatched region bounded by curves is called ‘hole’. The hole is defined by the parameter H in the plane \(u^{\prime } w^{\prime }\) [11, 12, 48].

$$\left| {u^{\prime}w^{\prime}} \right| = H\sqrt {\overline{{u^{^{\prime}2} }} } \sqrt {\overline{{w^{^{\prime}2} }} }$$
(3)
Fig. 2
figure 2

Quadrant interactions in \(u^{\prime } w^{\prime }\) plane

Full size image

As H is the hole size, those events that occur within the hole are excluded from the quadrant analysis. In large values of the hole size, only strong events are considered [7, 9, 31].

Based on a threshold level of the hyperbolic hole region, the contribution of each quadrant to the RSS was determined by Dey et al. [15] and Balachandar and Bhuiyan [3], and the fractional contributions, Si,H, to RSS for each event can be estimated as follows [13, 21, 43]:

$$I_{{i,H}} \left( {z,t} \right) = \left\{ \begin{gathered} 1,~~when~\left| {u^{\prime } w^{\prime } } \right| \ge H\left| {\overline{{u^{\prime } w^{\prime } }} } \right| \hfill \\ 0,~~otherwise \hfill \\ \end{gathered} \right.$$
(4)
$$\left\langle {u^{\prime } w^{\prime } } \right\rangle _{{i,H}} = \mathop {\lim }\limits_{{T \to \infty }} \frac{1}{T}\mathop \int \limits_{0}^{T} u^{\prime } \left( t \right)w^{\prime } \left( t \right)I_{{i,H}} \left( {z,t} \right)dt$$
(5)
$$S_{{i,H}} = \frac{{\left\langle {u^{\prime } w^{\prime } } \right\rangle _{{i,H}} }}{{\left| {\overline{{u^{\prime } w^{\prime } }} } \right|}}$$
(6)

where t is the time, T is the time interval and \({I}_{i,H}\left(z,t\right)\) is a detection function.

3 Results and discussions

3.1 Velocity distribution

Figure 3 shows the time-averaged streamwise velocity, uave, in the inner and outer flow regions (IFR and OFR), which can be defined by z/h ≤ 0.2 and 0.2 < z/h < 1, respectively. These regions have been suggested by Nezu and Rodi [35] to give clear characteristic division of inner and outer flow velocity profiles, hence it has been adopted in this study. Streamwise reversal flow can be observed following each pier in both IFR and OFR. The darker part of the graph represents slower depth-averaged velocity, and the arrow face indicates positive or negative mean velocity after depth-averaging. In Fig. 3b, uave in the OFR are observed with the greatest reversal streamwise velocity value of − 0.197 m/s (at T1 location). This shows the existence of a vortex behind Pier 1 at T1 location. In H1, this value in OFR has been reduced to − 0.145 m/s. Exploring the turbulence mechanism, the reversed averaged value of uave has been caused by circulation at the OFR to surface zone where strong vortex after each pier can be observed (agreed with findings from Dey and Raikar [14].

Fig. 3
figure 3

Depth-averaged of time-averaged streamwise velocity distribution flow in IFR and OFR in three rows

Full size image

Behind Pier 2, a contradicting pair of vectors can be constantly observed throughout IFR and OFR. This observation is resulted from the formed vortex behind that pier, which evolves and expand from IFR to OFR. At IFR, the strong vortex occurs at relatively smaller space (lateral and longitudinal-wise). However, this vortex is evolving to weaker strength but occupying larger flow domain at OFR. When considering the space just in front of Pier 3, due to the space for vector forming is larger, a positive flow field can be detected at IFR; whereas further at OFR, an observed negative vector is caused by the smaller space left by the evolved vortex (i.e. to restrict the vector formation in front of Pier 3). As a result a reversal velocity can be found at point L1 in the OFR layer. In Fig. 3, the red curve-arrows summarises the fundamental flow motion induced by piers and the turbulence resulted from that motion. It is evident from the large negative uave values is associated with between-pier circulation, indicating the formation of eddies.

Studies by Pu et al. [38,39,40] and Vijayasree et al. [47] defined the normalized velocity profiles (\({U}^{+}, {V}^{+}, {W}^{+}\)) for smooth-bed flow. In Fig. 4, the variation of its values for different elevations in the IFR along three measured rows has been used to identify the mechanism of flow turbulence. To better understand the flow behaviour in IFR, three average flow-depths have been considered (z/h = 0.05, 0.13 and 0.2). Due to the flow-mixing process, there is a discrepancy in the near-bed values. It can be observed that a near-wake flow reversal and an afflicted far-wake flow gradually recover to their undisturbed approach velocity at downstream. The reversal velocity is preserved by the near-wake flow, which implies the long-life developed turbulence within flow. Also, the wall-wake flow experiences a spatial acceleration across depth in the recovery, resulted from the flow mixing effect that impact the time-averaged flow momentum balance as well as the spatial structure of turbulence which contribute to the momentum transport.

Fig. 4
figure 4

Normalised velocity profile of average \({\mathrm{U}}^{+}\) in xz plane in IFR; z/h = 0.05, 0.13 and 0.2 in three rows

Full size image

From Fig. 5, each characteristic of W+ profiles remain almost the same in all the three rows. Negative trend after the first pier in the first row indicates its higher magnitude compared to the other locations especially when moving upwards in IFR. W+ in second and third rows also records significant magnitude which is resulted from mixing processes associated with strong vortices.

Fig. 5
figure 5

Normalised velocity profile of average \({\mathrm{W}}^{+}\) in xz plane in IFR; z/h = 0.05, 0.13 and 0.2 in three rows

Full size image

3.2 Reynolds shear stress (RSS)

Figure 6 depicts RSS for \(-\overline{{u }^{^{\prime}}{w}^{^{\prime}}}\) and \(-\overline{{v }^{^{\prime}}{w}^{^{\prime}}}\) profiles. There is a stronger reversed RSS at near-wake flow areas compared to the undisturbed profile, i.e. at D1 location. It is found that the RSS variation through the whole depth is primarily caused by the dispersion and formation of vortices. In the blocked zone, the magnitude of \(-\overline{{u }^{^{\prime}}{v}^{^{\prime}}}\) and \(-\overline{{u }^{^{\prime}}{w}^{^{\prime}}}\) are larger than the undisturbed location. \(-\overline{{u }^{^{\prime}}{v}^{^{\prime}}}\) and \(-\overline{{u }^{^{\prime}}{w}^{^{\prime}}}\) has more obvious variation compared to \(-\overline{{v }^{^{\prime}}{w}^{^{\prime}}}\) due to the dominant u component and its significant slowing down by the pier. As showing by Fig. 6b, there is a significant alteration of positive to negative value of \(-\overline{{u }^{^{\prime}}{w}^{^{\prime}}}\) after each pier indicating a transfer in flow momentum across flow direction resulted by pier hindering effect.

Fig. 6
figure 6

RSS profiles at disturbed and undisturbed zones

Full size image

3.3 Sweep and ejection events

In Fig. 7, the gaps between each and after the third pier (T, N, H, S, M, G, R, L and F lines) have been investigated using two-dimensional quadrant analysis. These measurements were taken through the entire flow depth to evaluate the full fluctuation terms based on Eqs. (1) and (2), where the same bursting analysis has also been used by Cellino and Lemmin [7]. The burst cycle is dominated by sweep at T1. Due to the low-speed dominance at N1, turbulence activity may be enhanced during burst cycles. At H1 location, low-speed flows in the OFR contribute to turbulence energy in a similar manner to high-speed flows in the IFR.

Fig. 7
figure 7

Burst cycle analysis for three locations after each pier and an unaffected location in three rows

Full size image

During the burst cycle, T2 in the second row exhibits a greater sweep than T1. Energy dissipation in a negative depressive wave causes increased turbulence due to inward and outward interactions. The sweep quadrant at N2 has also experienced significant events. As the low-speed flow at H2 moves downward during burst cycles, energy is dissipated through sweeps and inward interactions. Similarly, a significant amount of energy dissipates at the T3 in the sweep and inward interaction quadrants (i.e. at the third row). High-energy sweep events occur at T3 and H3, while low-speed flows at N3 dissipate constructive flow energy.

The ejection event at S1 in the first row represents the flow spreading upwards in low-speed. However, at M1, due to enhanced energy dissipation, burst cycles are induced primarily by high-speed flow. Compared to S1, S2 has a disrupted sweep quadrant, indicating turbulent energy bursts. Outward and inward interactions are evident in M2, and the high-speed downward flow is the most commanding mechanism for turbulence at that location.

Within the near bed layer, G2 exhibits a burst cycle, where upwards moving flow is minimal. This is evident from the lack of outward interactions and ejection events. Inward interactions are reduced as slow-speed flow decreases caused by reduced energy dissipation. S3 displays the reduced outward and inward interactions. Besides, a high-speed flow upwards from the bed dissipates most energy in G3. This leads to insignificant slowing of downward flow, i.e. inward interactions. In addition, ejection and sweep events are observed within the bed layer at location G3 throughout the burst cycle.

Sweep events become more significant as the flow approaches the piers. At L1 and L2, where high-speed flow clearly plays a significant role, the burst cycle shows considerable energy dissipation. Due to the absence of high-speed downward flow in the second row, the burst cycle at R2 differs significantly from that at R1. An ejection event occurs at R3, representing a burst of turbulent incentive. The turbulence energy generated by ejections and sweeps at L3 is dissipated by inward interactions further downstream.

3.4 Quadrant contribution

As shown in Fig. 8, the characteristics of the burst cycle at the unaffected locations has been compared with those at the locations after each pier. In the figure, < u′ > represents streamwise velocity fluctuations in each quadrant contribution, where subscripts 1, 2, 3 and 4 represent the quadrant number. Based on H = 0, a clear distinction is made between strong and weak events. For a wall-wake flow, u′ and w' are important pairs associated with high frequency events. In unaffected locations, it is evident that all turbulent quadrant changes are insignificant.

Fig. 8
figure 8

Quadrant analysis for effected and unaffected locations in three rows

Full size image

Q1 and Q3 quadrants at T1 location are having small change benchmarked by Q2 and Q4 (between − 0.271 and 0.252); while at location T2, the sweep event dominates with a maximum value of 0.367 near the bed. There is an ejection event (− 0.4 ± 0.015) at location T3, which is more dominant than the two previous locations within same the measurement line and has greatly energised the flow. Moreover, Q4 events have been affected in IFR by a magnitude of 0.3 to 0.34. In summary, high Q4 and Q1 interactions happens to gain effective bursting mechanism.

In the location N1, weak quadrants are observed which decrease in strength from the bed to flow surface. Q1 and Q3 are ruling in IFR with 0.21 and − 0.22 respectively; whereas in locations N2 and N3, Q4 and Q2 events for z/h < 0.2 is stronger than OFR burst cycles [0.21 < (Q1 and Q4) < 0.3 and − 0.261 < (Q2 and Q3) < − 0.314]. A strong correlation exists for all four quadrants at H2 before z/h = 0.5, which indicates that burst cycles have become weaker from upstream to downstream. Conclusively, a sequence of high-speed flow rescinds the effect of low-speed flow, creating a dominant faster-moving process i.e. Q1. However, at increase depth position, Q2 events become more imperative mechanism.

3.5 Quadrant distribution

Figure 9 shows the quadrant distribution plot of velocity fluctuation terms. Roughly 30,000 measurement points are considered (across u′ and w′) in the region of IFR, where the measurements using hole size H = 0 has been analysed. Q2 and Q4 are the most important quadrants with sufficient energy contain. Significant events distribution has been shown in the first row, which is dominated by ejections at N1 and H1. However, ejections in T2 and T3 are dominant in the third row. The contributions from Q2 and Q4 after the first pier are more dominant than those behind other piers which is an important factor affecting bursting events in the lateral flow within the channel boundaries. This phenomenon has also been observed by Chavan et al. [9]. As a result, vortices have been observed after first pier due to strong ejection energy transfer to the outer flow region.

Fig. 9
figure 9

Quadrant distribution in three rows in IFR (z/h = 0.05)

Full size image

3.6 Ratio contribution

In the investigation for the ratio of sweep to ejection (STE), the stress friction ratio has been evaluated in relation to shear stress. \({S}_{i,H}\) represents the stress friction for each quadrant as defined by i and H (refer to Eq. 6). When the ratio is close to zero, sweep is more likely to influence the pier induced flow. Figure 10 shows that after the piers, STE has a value between 0.67 and 1.183. Weak events are dominated in IFR. As the depth increases, the STE ratio increases to about 1.3 in value.

Fig. 10
figure 10

Ratio of sweep to ejection (STE) contributions in the first row in three separate locations compare with unaffected flow

Full size image

Away from the centerline, the STE ratio in the second row is lower (ranging from 0.417 to 1.149). The OFR is evidenced to be affected by flow mixing processes. On the other hand, in the second row, ejection contribution is observed along the piers, which is reduced from upstream to downstream because of weakening burst cycles and variation in RSS. However, in the third row, it is observed that the higher ratio of STE (1.14) in OFR is caused by ejection events, resulting in a significant variation in outer flow; and in contrast to IFR that is primarily caused by sweeps due to its low STE ratio (0.4).

There is also evidence that in theoretical development, larger hole sizes may contribute to overprediction of burst turbulence, as demonstrated by Raupach [41] and Balachandar and Bhuiyan [3] who calculated the difference between the contributions of sweeps and ejections. Nevertheless, there is a higher proportion of ejection and inward interaction events in OFR, indicating that outward interaction and sweep events have greater impact to IFR. This is also supported by findings of Hanmaiahgari et al. [18].

4 Conclusion

To better understand the effect of piers-group to flow, an experimental study has been conducted to analyse its burst cycle events and Reynolds shear stress (RSS) distributions. Measurements at multiple rows surrounding the piers and at different depths have been performed by Acoustic Doppler Velocimeter (ADV). Further, different outer and inner flow region (OFR and IFR) data have been used for the analysis. It has been found that different OFR and IFR play a crucial role in the mixing process of flow from upstream to downstream locations. A reversal of flow direction in quadrant analysis after each pier has evidenced that inward and outward interactions were dominant near bed which has a profound impact on turbulence distribution. From the analysis, low-speed flow motion in the IFR near bed between piers has experienced turbulence generated by Q2 and Q4 quadrants to cause vortices to form. From the quadrant analysis, the STE ratio was more dominant by sweep (STE = 0.9) at T1 and T2 locations (i.e. locations directly after the first pier), which indicated a high degree of turbulence interaction. Turbulence fluctuation was greater in T locations due to the higher RSS in the IFR as compared to the other locations. For future research, the measurements can be conducted on a rough or movable bed, in order to investigate piers-group induced flow in closer condition to the natural streams.