1 Introduction

The present publication is written in honour of recently retired Professor Peter Davies. The first author remembers with great joy and gratitude and with high respect, his enthusiasm for the Gerhard Jirka EFM Summer School [22], where the first author had the lucky fortune to be involved (Fig. 1). Peter was fascinated by our contributions on small-scale observations from the natural environment of lakes. For this reason, we decided to focus in this publication on a unique example of lake double diffusion (DD). The specific novelty of this contribution is the documentation of the entire lifespan—from birth to death—of a singular double-diffusive (DD) event. To our knowledge, such an observation has never been reported for a natural water body.

Fig. 1
figure 1

Professor Peter Davies (left) together with Professor Gerhard Jirka (deceased 14 Feb 2010), in Jan 2009 on the occasion of the Environmental Fluid Mechanics Summer School (later called Gerhard Jirka Summer School) in Santiago de Chile. Peter has been a passionate and a constant lecturer in those courses

Full size image

The location of this unique event is Lake Nyos, the well-known 209 m deep Cameroonian crater lake. Lake Nyos gained notoriety for its limnic carbon dioxide (CO2) eruption in 1986, causing a human tragedy [3, 5]. The origin of the high CO2 abundance are deep subaquatic sources, supplying warm, salty and CO2-enriched water into the hypolimnion. At the time of our observations in the early 2000s, the lake was permanently density-stratified below 50 m depth with temperature (T), salinity (S) and CO2 concentrations increasing with depth (Fig. 2). As all these three constituents affect the water density, Lake Nyos featured an exceptional density structure. While the fast-diffusing T destabilised the density profile, the slow-diffusing S and CO2 had a stabilizing effect (Fig. 2). This setting of largely different molecular diffusivities can lead to localised density instabilities known as double diffusion. Therefore, Lake Nyos is a particularly unusual example of the family of DD-type of stratifications.

Fig. 2
figure 2

Embedding of the DD zone (grey, 53 to 95 m depth) within the vertical stratification and to the degassing of Lake Nyos. Left: the contributions of temperature T (red), plus salinity S (blue), plus CO2 (black) to the density profile. The peculiarity of this DD-stratification, besides the compensating effects of temperature and salinity (blue), is the strong contribution by CO2 (black). Right: self-siphoning pipe flow and subsequent subsidence of ~ 0.48 cm day−1

Full size image

Double-diffusive stratification is generally rare in lakes, because usually T decreases and S increases with depth leading to classical diffusively stable water columns. However, prominent exceptions of DD-developing stratification were found above former salt depositions, such as in Lake Vanda [9, 10] and several other lakes in the Antarctic Dry Valley [34, 35], or over volcanic underground, such as in Lake Kivu [18, 33]. Another set of DD-type lakes can be found on the Norwegian and Canadian West Coast, where former estuarine fjords were transformed to lakes after the last ice-age and still hold ancient saltwater in their deepest realms. Powell Lake in British Columbia is the most prominent representative of this category [24, 36]. With three and four density-relevant water constituents, there are examples of lakes showing triple-diffusion [23], such as the present study, and quadruple-diffusion, such as Lake Kivu [33]. More DD-type lake examples are reviewed in Wüest et al. [42]. The second type of DD, the so-called finger regime [28], is even rarer in lakes. The constellation of saltier and warmer water layers residing on top of fresher and cooler layers is not a setting, which is favoured by geochemical and geothermal processes. However, evaporation in salt lakes may cause such vertical profile structures, such as in the Dead Sea, where during summer an especially high saline and warm water surface forms, which triggers DD salt fingering through the pycnocline [1].

DD is a widely researched fluid dynamics phenomenon occurring in oceans and lakes [11, 21]. The most important feature of DD is the enhancement of the vertical transport of water constituents, relative to molecular diffusion, by transforming gradual density gradients into staircases of convectively mixed layers, separated by thin stable interfaces. The mechanical energy for this process stems from extraction of potential energy from the stratification. Such staircases can develop when two agents that diffuse at different molecular rates contribute in opposing ways to the stability of the vertical density profile [14, 33, 38, 39]. Given that temperature was destabilizing, whereas S and CO2 were stabilizing the density profile (Fig. 2), made Lake Nyos a probable candidate for the development of a DD staircase of a triple-diffusive type.

From early laboratory experiments [37], we know that the density ratio Rρ (stabilising density gradients divided by destabilizing density gradients; see definition in Eq. 2 below) and the interface T step are the two dominant parameters for generation and maintenance of staircase structures and the heat fluxes [13], which drive the convective turbulence in the mixed layers. The most detailed analysis, over thousands of layer-interface pairs in Lake Kivu, confirmed the so-called 4/3 flux law for the low range of Rρ but deviated for larger values of Rρ [30]. The close agreement with the Kelley [13] parameterisation was also found in the earlier report from Lake Nyos, where it was possible to quantify the heat fluxes from the DD layering as well as from the heat budget based on measured T profiles [26].

Important for the present study are the observations made on the layer-interface pairs of Lake Kivu, that the most frequently observed Rρ values were at ~ 4, while Rρ > 8 was extremely rare [30]. This finding was confirmed with corresponding Direct Numerical Simulations [32]. In Powell Lake, three DD-active depth sections were found with \({R}_{\rho }\) values ranging from 1.6 to 6 within the layering zones and larger values outside the layers [24]. All these lake observations are consistent with typical ranges of Rρ in natural DD environments [14]. It will be interesting to analyse how Rρ restricted the dynamic development of the DD staircase in Lake Nyos.

Almost all reports on DD staircases in natural waters stem from stratifications that are in a quasi-steady equilibrium. The boundary conditions, such as background stratification and its supporting fluxes in and out of the DD staircase region are usually long-term sustained and subsequently, the driving forces and the stimulated convection are balanced and vary only slowly with time. In this publication, we focus on the limited duration of an unsustained (one-time “run-down”) stratification, where a DD staircase could develop temporarily until the boundary conditions for the zone of the mixed layers had changed to a degree that the staircase pattern could not be maintained. The energy source for forming mixed layers and enhancing the vertical fluxes through the staircase stems from potential energy, which is delivered by the warm subaquatic water inflow. The fact, that the DD event had limited duration, means practically that the extraction of potential energy due to DD was too large in relation to the potential energy supply from the subaquatic sources. We describe the initiation and dynamic development of the staircase and discuss the formation and dissolution of layers. Of special interest for other natural systems are the conditions at the time when the staircase collapsed, raising the question why the DD process did not adjust to a sustainable steady state functioning.

The complete start–to–end observation of this unique DD-event was pure luck. The dates of the fieldwork were originally chosen for the analysis of the degassing project [7, 8] and the coincidence with the entire lifetime of the simultaneous DD-event was discovered as a by-product.

2 Field site and methods

2.1 Lake Nyos

Lake Nyos is world-renowned for its limnic eruption in Aug 1986, when it released a large cloud of carbon dioxide (CO2), asphyxiating ~ 1700 people [5, 15]. Most convincing is the explanation that CO2 of volcanic origin had continuously accumulated to saturation concentrations. It was suddenly released by an unknown trigger (such as baroclinic displacement or rockfall), which led to local supersaturation, from where subsequent bubble formation invaded the entire lake.

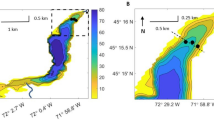
Lake Nyos is a small crater lake situated on 1091 m above sea level in the north-west of Cameroon, with a maximum depth of 209 m, a surface area of 1.58 km2 and a volume of 0.15 km3. At the time of the presented measurements (2002–2005), the water column consisted of three major layers, separated by two chemoclines at ~ 50 and ~ 170 m depth (Fig. 2). The usual seasonal mixing and stratification was restricted to the top 50 m layer (Fig. 2), whereas the hypolimnetic layers below were permanently stratified. In those deep waters, T, S and CO2 increased with depth (Fig. 2), which led to double-diffusively stable density stratification. The DD zone, which is the focus of this publication, evolved in the range between 53 and 95 m depth.

The fact that CO2 already accumulated substantially since the 1986 eruption [16], led to the decision to degas the lake by using self-syphoning over deep vertical pipes (Fig. 2; [7, 8, 27]) to avoid future disasters. As the intake was close to the deepest location and the degassed lake water was sprinkled onto the surface, the profiles of the DD zone were only partly affected by the degassing operation (Fig. 2). Over the 1200 days of data collection, the DD staircase zone was drawn down by ~ 6 m (Fig. SI-1).

2.2 Measurements

The data for this publication stem from a mooring from Nov 2001 to Dec 2002 and 39 CTD profiles, of which some are of high vertical resolution. On the mooring, T was measured every 10 or 15 min at 0, 10, 20, 41, 62, 103, 144, 175, 185, 195 and 200 m depth with VEMCO minilogs, as well as a SeaBird SBE-39 and a RBR TR-1050 for references. The CTD profiles were collected with a Sea-Bird SBE-19 on eight dates (Table 1) over 1200 days between 19 Jul 2002 (first profile, day no. 166) and 27 Oct 2005 (last profile, day no. 1362). The three slowest recorded CTD profiles had a vertical resolution of < 4 cm. Given the short period considered, the CO2 profile from Kusakabe et al. [16] was used for the density calculation. This approximation led to negligible additional errors in the water column stability \({N}^{2}(\mathrm{z})\) and the density ratio Rρ, which are both defined below (Eqs. 4 and 5).

Table 1 Evolution of DD zone characteristics from 3 Feb 2002 to 27 Oct 2005
Full size table

2.3 Data analysis

In Lake Nyos, the density profile depends on T [°C], S [g kg−1], and CO2 [mmol L−1]. As the lake ionic composition is different to oceanic water, the meaning of salinity in this publication is different from the standard oceanic definition. Here, equivalent to ocean water, salinity S [g kg−1] stands for the total concentration of dissolved solids including non-ionic silica. Therefore, the conversion to density, using the haline contraction coefficient, will also be slightly different from ocean water. To determine S, the T-dependent in-situ measured conductivity CT [μS cm−1] was transformed first to the T-independent conductivity C25 [μS cm−1] at T = 25 °C. The CT to C25 conversion depends on the specific ionic composition, taken from Evans et al. [3]. According to the procedure provided in Wüest et al. [40], we can use the following polynomial transformation for the Lake Nyos ionic composition:

$$C_{25} = C_{T} \cdot \left( {1.82163 - 0.047257 \cdot T + 6.87055 \cdot 10^{ - 4} \cdot T^{2} - 4.4567 \cdot 10^{ - 6} \cdot T^{3} } \right) \quad \left[ {\mu{\text{S}}\,{\text{cm}}^{ - 1} } \right]$$
(1)

where T is the in-situ temperature in °C. Again, for this specific ionic composition, the relation between C25 and \(S\) can be approximated by [25]

$$S = 0.0071 + 9.965 \times 10^{ - 4} C_{25} \quad \left[ {{\text{g}}\,{\text{kg}}^{ - 1} } \right]$$
(2)

which includes all major ions, such as the charged HCO3−, and CO3−2, and the non-ionic silica, but not H2CO3, the uncharged dissolved aqueous form of CO2. For one profile (Jul 2003), the conductivity cell was not working properly and therefore the S-gradients have been used from the two neighbouring profiles but the absolute S is not reported.

The concentration of H2CO3 for Dec 2002 was calculated from alkalinity and pH. The dissociation constants K1(T) and K2(T), were calculated conditional for T and the resulting activity of H2CO3 was corrected with the activity coefficient for the ionic strength to result in H2CO3 concentration [26]. The concentrations of H2CO3 in the considered DD zone, from 53 to 95 m depth were approximated, assuming that the relation between dissolved CO2 and conductivity had not changed.

Finally, the water density was calculated as a function of T and the two dissolved substances S and H2CO3 using:

$$\rho = \rho \left( T \right) \cdot \left( {1 + \beta_{S} \cdot S + \beta_{CO2} \cdot \left[ {H_{2} CO_{3} } \right]} \right)\quad \left[ {{\text{kg}}\,{\text{m}}^{ - 3} } \right]$$
(3)

For the T-dependent ρ(T) [kg m−3] we followed Chen and Millero [2]. The haline contraction coefficient \(\beta_{S} { }\) = 0.760·10–3 kg g−1 was calculated according to Wüest et al. [40] and for H2CO3, \(\beta_{CO2}\) = 1.25 10–5 L mmol−1 = 0.284 10–3 L g−1 [19] was used. Although \(\beta_{H2CO3}\) would be the logic symbol for the corresponding density coefficient, we use the established nomenclature \(\beta_{CO2}\) [25, 30]. The water column stability \(N^{2}\) follows the usual definition

$$N^{2} = - \left( {\frac{g}{\rho }} \right)\cdot \partial \rho /\partial z\quad \left[ {{\text{s}}^{ - 2} } \right]$$
(4)

where \(g =\) 9.81 m s−2 and \(z\) is the depth, positive upward. The density ratio Rρ [−], expressing the quotient of the stability of the slow-diffusing water constituents divided by the instability of the fast-diffusing T, we estimated by defining:

$$R_{\rho } = \frac{{\beta_{S} \cdot \partial S/\partial z + \beta_{CO2} \cdot \partial \left[ {H_{2} CO_{3} } \right]/\partial z}}{{\alpha \left( T \right) \cdot \left( {\frac{\partial T}{{\partial z}} - \Gamma } \right)}}\quad \left[ { \, - \, } \right]$$
(5)

where α and Γ are the thermal expansivity and the adiabatic gradient, respectively.

As shown below, the considered CTD profiles developed staircase structures typical for DD stratification. The staircase consists of a series of homogeneously mixed layers separated by stable interfaces. To define the boundaries between layers and interfaces, we plotted the profiles and identified the upper and lower limits by eye. For this manual procedure, the uncertainty of the respective thicknesses is typically one scan of the CTD profile or a few cm in absolute distance.

3 Observations

On eight occasions, from 19 Jul 2002 to 27 Oct 2005, 39 CTD profiles were collected over the full depth range of Lake Nyos. Figure 3 provides an overview of the evolution of T and S over the entire 1200 days of observation (day no 166 to day no 1362; Table 1). The surface layer, which was well-mixed during the dry seasons and never dipped below 55 m depth, is not discussed any further, as our focus is solely on the development of the upper hypolimnetic stratification.

Fig. 3
figure 3

Evolution of T (a) and S (b) over the entire measurement period of 1200 days from 19 Jul 2002 (first profile) to 27 Oct 2005 (last profile). The subsidence of the surface layer due to degassing (Fig. 2) is well visible for S = 0.5 g kg−1 at ~ 60 m depth, as well as in the deepest reaches. Below 65 m depth, S was almost constant due to only weak DD-induced fluxes of S, while T decreased due to subsidence and heat removal by DD. The grey shading indicates the DD zone from 53 to 95 m depth (Fig. 2)

Full size image

Figure 3 reveals that the changes in the hypolimnion were tiny overall. Given the low mechanical energy input to this wind-protected hole-like water body and given the strong permanent density stratification by S and CO2, negligible turbulence could be expected. The main modifications on the profiles took place directly below the base of the surface layer. The profile of 7 Dec 2002, which was collected at an especially low profiling rate, revealed a staircase structure, indicating active double diffusion (Fig. 4). The reanalysis of the previous profiles showed that already in the Jul 2002 profile some vague indications of DD structures were visible (Fig. SI-2).

Fig. 4
figure 4

Two examples of DD-layering profiles shown for S for the dates of 7 Dec 2002 and 17 Mar 2004 within the depth range of the DD zone. For both profiles, 27 layer-interface pairs had been identified (Tables 1, SI-2 and SI-5)

Full size image

Initiation of double diffusion Indeed, the DD event started at the top of the stratified hypolimnion in Feb 2002 due to cooling during the dry season, which increased the T-gradient at the transition from the surface layer to the hypolimnion. We can accurately identify the starting point of the DD process, both in depth and time, by using the T data of the mooring, installed from Nov 2001 to Dec 2002. This T record shows that in 61.6 m depth, the heat flux increased abruptly by orders of magnitude, within hours on 23 Mar 2002 (Fig. 5 in Schmid et al. [26]). This signature indicates the local arrival of the DD front from above. From the Nov 2001 and the Jul 2002 CTD profiles, we can conclude that the depth of the transition from the convectively mixed surface layer to the maximal vertical gradients of T and S was in the range between 52 and 53 m depth at that time ([26]; Fig. 3). Based on the meteorological forcing, we assume that the rate of vertical expansion of the DD zone was similar during the previous few weeks, and conclude that DD layering started on 3 Feb 2002 at ~ 53 m depth. Realistically, these estimates have uncertainties of a few days and up to 1 m in the vertical. We ignore both errors in view of the dimension and duration of the following vertical expansion of the DD zone over almost three years. In the following analysis (Table 1), we define this date as time zero and 53 m depth as the upper bound of the DD zone.

Fig. 5
figure 5

Four examples of highly-resolved T-S profiles over the depth range of the DD zone. While a and d show the beginning (19 Jul 2002) and the disintegration (9 Mar 2005) of the DD-layering, respectively, the profiles b and c are representatives of the quasi-steady phase of expansion with 27 layer-interface pairs each. In those two well-resolved profiles b, c, the layers are better defined (sharper edges) for S than for T. Some layers are numbered to guide the eyes. The profiles of 19 Jul 2002 a are shown at higher resolution in Fig. SI-2

Full size image

Expansion of the DD staircase Following the manual procedure presented in Sect. 2.3, we identified all upper and lower boundaries of the mixed layers from all eight CTD profiles. Because of the 70-times larger molecular diffusivity of T compared to S, we can expect that the mixed layers show edges that are more distinct in the S profile, as shown in detail in Sommer et al. [31]. For some profiles, when the conductivity cell was not working optimally, we used the T profiles to identify layers and interfaces. Figure 5 shows four examples out of the eight profiles with some layers indicated. The complete data sets of the manual analysis are provided in the Supporting Information Tables SI-1 to SI-8, where the characteristics of the individual layers are compiled. Comparing Figs. 3 and 5 reveals that the vertical section of substantial modifications in the T profiles was identical with the DD zone exhibiting staircases.

In the profile of Jul 2002 (day no 166), we find the first four layers ranging over the DD zone of \({H}_{DD}\)= 6.2 m (54.7 to 60.9 m depth; Table 1; Figs. 5a and SI-2). 140 days later, in Dec 2002, the number of layers had rapidly jumped up to 27, with a vertical expansion of \({H}_{DD}\) = 22.3 m (52.9 to 75.2 m depth; Table 1; Fig. 5b). Interestingly, for the following ~ 450 days, the number of layers remained constant at 27, within the uncertainty of about 1 to 2 layers, while the vertical extension of the DD zone expanded to 36.7 m (55.0 to 91.7 m depth) in Mar 2004 (Table 1; Fig. 5c). In the following, we call this period of active expansion of the DD zone the quasi-steady phase. With this term, we express the steady character of this period, consisting of continuous and balanced generation and degeneration of layers, as compared to the unsteady phases of build-up at the beginning and decay at the end of the DD event. After the maximal extension between Mar and Aug 2004, the number of layers decayed, the identifiability of the layers increasingly worsened and the DD zone shrank quickly. In Mar and Oct 2005, only 4 and 2, respectively, poorly-defined layers remained (Table 1; Fig. 5d).

Evolution of the staircase characteristics The characteristic staircase properties evolved over time differently during the three phases of DD layering (Fig. 6). The average layer thickness \({H}_{L}\) increased from ~ 0.5 to ~ 1 m during the active quasi-steady phase and subsequently expanded quickly while the staircase decayed (Table 1; Fig. 6b). Interface thicknesses were only estimable during the quasi-steady phase. No trend could be detected and the average thickness was ~ 25 cm (Table 1). The temperature gradient, which is the key prerequisite for the driving force of DD convection, showed the strongest trend (Fig. 6c). After the initiation of DD (Feb. 2002), \(\partial T/\partial z\) dropped drastically followed by a gradual decline from the first to the last CTD profile, when \(\partial T/\partial z\) decreased continuously by a factor of ~ 4 (Fig. 6c), while the DD zone expanded downwards into deeper regions of lower stratification and lower T-gradients. At the end of the DD event, \(\partial T/\partial z\) taken over the entire DD zone dropped to the level of \(\partial T/\partial z\) at 95 m depth (Fig. 6c), demonstrating the loss of driving force for DD. Similarly, as the stratification decreased towards greater depth, the water column stability \({N}^{2}\) dropped from the uppermost to the deepest layers by an order of magnitude over the DD zone (Tables SI-2 to SI-5; Supporting Information).

Fig. 6
figure 6

Characteristics within the DD zone during the DD event: a Evolution of the cooling of the T profiles; b Thickness of the DD zone (red) and the layers (blue; without interfaces) during expansion and collapse. The left red line in b shows the expansion according to a diffusion coefficient of 1.0 × 10–5 m2 s−1; c Vertical T gradients over the DD zone and at 95 m depth during expansion and collapse; d Histogram of the density ratios \({R}_{\rho }\) during the phase of quasi-steady expansion

Full size image

For the susceptibility of DD layering, the density ratio \(R_{\rho }\) is the most important parameter. The initiation of DD in 53 m depth occurred when \(R_{\rho }\) was in the range of ~ 2 [26, 36]. The accuracy is unknown, as \(R_{\rho }\) was not directly measured at this particular moment. Tables SI-1 to SI-8 show that the variations of \(R_{\rho }\) values between different parts in the staircase did not exhibit strong trends. Although, the values cover a range of up to 7 over the entire DD event, the histogram for the individual layer-interface pairs demonstrates that ~ 50% of the \(R_{\rho }\) values ranged between 2 and 4 (Fig. 6d). The values of \(R_{\rho }\), estimated over the full DD zones, varied only in the quite narrow range of 3 to 4 among the different profiles (Table 1). In addition, there is a consistent vertical structure with larger \(R_{\rho }\) values near the upper bounds and lower \(R_{\rho }\) near the lower bounds of the DD zones (Tables SI-2 to SI-6).

Consistent with the cooling of the DD zones (Figs. 3 and 6a), the upward heat fluxes into the DD zones were typically a factor ~ 5 lower than the fluxes out of the DD zones (Tables SI-2 to SI-6; Fig. SI-3, Supporting Information). The divergence of the heat flux, with ~ 0.1 W m−2 in-flux and ~ 0.5 W m−2 out-flux, was largest at the beginning of the DD layering. As the DD zone moved further down to deeper regions with weaker T-gradients, the divergence decreased, but out-fluxes were always larger than in-fluxes. Therefore, the heat flux was not only driving convective mixing in the staircase layers, it simultaneously cooled the DD zone as well.

4 Discussion

In this section, we discuss the evolution of the staircase characteristics along the three phases of the DD event. We relate the developments to the energetics for layer formation and the boundary conditions during expansion and collapse of the DD zone. Of special interest is the self-destructing character of the unsustained temperature stratification.

Adequacy of the one-dimensional approach The presented CTD profiles were all taken near the deepest location, close to the center of the lake. Although the subaquatic water inflow of ~ 18 L s−1 is not well known [3, 25], the water residence time in the hypolimnion is of the order of hundred years, whereas horizontal spreading in such a small lake takes only days to weeks [6]. On 21 Mar 2004, we collected several profiles in the lake, including some at the vertical sidewall, which confirmed that the DD layering extended nearest to the wall, indicating that boundary mixing had no effect on the layer-interface pairs. For the following discussion, we therefore adhere to only one-dimensional considerations.

DD zone subduction by degassing The T-S profiles changed overall only little during the DD event (Fig. 3). As shown by the T-S diagram in Fig. SI-1 (Supporting Information), the observed modifications were (i) due to downwelling caused by the degassing operation (Fig. 2) and (ii) due to DD-induced vertical fluxes). Whereas the decrease in S were almost entirely due to downwelling, the T changes were due to both downwelling and DD-induced upward heat fluxes (Fig. SI-1). The downwelling at depth z is given by the pipe flow divided by the cross-sectional area at z. Over the entire period of the 1200 days, the chemocline subduction, at the level S = 0.5 g kg−1, was ~ 6 m, corresponding to an average pipe flow of ~ 45 L s−1, which is realistic for the early degassing phase [7, 8, 27]. During the period of the quasi-steady expansion of the DD zone (Dec 2002 to Mar 2004), the subduction was ~ 2.25 m, which fits well to the observation that the uppermost (first) mixed layer migrated downwards from 52.9 to 55.0 m depth (Table 1). We conclude that the T-S profiles in the DD zone have been vertically dislocated by subduction, but the vertical structure within the DD zone was only slightly stretched. As the cross-sectional areas of the lake were 0.81 and 0.64 km2 in 53 and at 95 m depth, respectively, the downdraught were only 20% different. In other words, the DD zone was dislocated, yet with only 1% internal distortion over the 40 m vertical layer.

Divergence of the upward heat fluxes The upward heat flux through the stable stratification is the key driver for staircase formation. While S and CO2 stabilize the water column, only the heat flux could cause local density instabilities and provide the necessary buoyancy flux to mix layers. It is not possible to accurately estimate the upward heat fluxes, as the temperature changes due to the subsidence (cooling) interfere with the changes by DD (cooling first and warming later). As those T changes are of the same magnitudes, the heat balance remains uncertain (Fig. SI-3; Supporting Information). Therefore, we use earlier results to estimate the DD-induced heat fluxes, relaying on empirical relations [13, 17, 37], which have been confirmed by observational data from Lake Nyos [26] and Lake Kivu [30]. Although these estimates cannot be precise because of the continuous transformation of the DD-layering, these empirical heat fluxes agree well with observations for Lake Nyos conditions with \({R}_{\rho }\) from 2 to 7 [30]. We approximate the heat flux \({F}_{h}\) within the DD zone using the formulations by [13]

$$F_{h} = \frac{{(\rho C_{p} ) }}{13} \cdot \left( {\frac{{g\cdot \alpha \cdot \Delta T \cdot H^{3} }}{{D_{T } \cdot \nu }}} \right)^{0.27} \cdot \frac{{\Delta T \cdot D_{T } }}{H}\quad \left[ {{\text{W m}}^{{ - {2}}} } \right]$$
(6)

as well as by Turner [37] and Linden and Shirtcliffe [17]

$$F_{h} = C\left( {R_{\rho } } \right) \cdot \left( {\rho C_{p} } \right) \cdot \left( {\frac{{D_{T}^{2} \cdot g \cdot \alpha }}{\nu }} \right)^{\frac{1}{3}} \cdot \Delta T^{4/3 } \,{\text{with}} \,C\left( {R_{\rho } } \right) = 0.0032 e^{{{{4.8} \mathord{\left/ {\vphantom {{4.8} {R_{\rho }^{0.72} }}} \right. \kern-\nulldelimiterspace} {R_{\rho }^{0.72} }}}} \quad \left[ {{\text{W}}\,{\text{m}}^{ - 2} } \right]$$
(7)

where \(\rho C_{p}\) is the heat capacity of water, \(\Delta T\) is half of the temperature step between neighbouring layers, H is the layer thickness, including half of the interfaces, and \({D}_{T}\) and \(\nu\) are the thermal diffusivity and the kinematic viscosity, respectively. The resulting heat flux values in Tables SI-2 to SI-5 are shown in Fig. SI-3 together with heat budget estimates over the entire quasi-steady period (Dec 2002 to Mar 2004) for the lower region of the DD zone. Although these estimates are not directly comparable, as they mirror different local flux information, the magnitudes and the vertical structure of the upward flux reveal a consistent pattern. From Tables SI-2 to SI-5, and Fig. SI-3 we can conclude that the typical heat flux shows a substantial vertical divergence with ~ 0.5 W m−2 and of ~ 0.1 W m−2 at the upper and lower bounds of the DD zone, respectively. In comparison, for the steepest T-gradient found in Dec 2002, the corresponding molecular flux was only ~ 0.05 W m−2. The same comparison at the lower bound of the DD zone indicates an even larger flux enhancement by DD. We can conclude that DD increased the upward heat flux by approximately one order of magnitude. The difference between the heat flux into the DD zone at the lower bound (~ 0.1 W m−2) and the flux out at the upper end (~ 0.5 W m−2) led to a typical heat divergence of ~ 0.01 W m−3 (average over 53 to 95 m depth). This heat extraction corresponded to a cooling of ~ 0.08 K yr−1, which is orders of magnitudes stronger than the changes below the DD zone. This cooling is well visible in the T-S diagram of Fig. SI-1, where the T decrease during the quasi-steady phase was even slightly larger in the deepest region of the DD zone.

Heat flux induced turbulence A heat flux of ~ 0.5 W m−2 generates a buoyancy flux of ~ 2.7 × 10–10 W kg−1. This value is much higher than typical turbulent dissipation rates in the interior of hypolimnia of even wind-exposed lakes [4, 29, 41]. The comparison with Lake Kivu, the undoubted marvel of lake DD with more than 300 layers in its deep staircase [30, 33], reveals that the buoyancy flux in Lake Nyos is about 5-times stronger, despite the large surface and corresponding long wind fetch of Lake Kivu. Given the topographically well-protected small surface of Lake Nyos and given its deep hole-like structure, the mechanical excitations (currents or baroclinic oscillations) in the hypolimnion were negligible and background turbulence had no effect on the water column. This was confirmed in Mar 2004 by CTD profiles taken directly at the rock wall, which showed identical layering as in the open water and even boundary mixing had obviously no effect on the DD layering.

An alternative indication for the level of turbulence in a water column of stability N2 is offered by quantifying the activity of turbulent mixing. In order to sustain active mixing, the turbulent dissipation has to exceed νN2 by at least an order of magnitude [12]. At the upper bound of the DD zone, with stabilities of N2 ≈ 10–3 s−2 (Tables SI-1 to SI-8), active mixing would therefore require a dissipation of at least 1.5 × 10–8 W kg−1. The above mentioned buoyancy flux of ~ 2.7 × 10–10 W kg−1 is subsequently two orders of magnitude away from active turbulence. However, before DD enhanced the vertical heat fluxes, the energetics in the water column was even lower than during the DD event. Therefore, we can safely assume that before the onset of DD in Feb 2002, the vertical heat flux was on a molecular level only.

Range of density ratios For the establishment of staircase structures, the relative stability of the water column, expressed by the density ratio \({R}_{\rho }\), is the critical parameter. The susceptibility to DD convection rises with decreasing \({R}_{\rho }\). For the smallest value of \({R}_{\rho }=1\), the water column stability would drop by definition to \({N}^{2}=0\). Such a configuration would not be stable and the lowest possible \({R}_{\rho }\) for DD-layering is \({R}_{\rho }\) > 1. When DD was initiated in Feb 2002, \({R}_{\rho }\) was ~ 2, which is realistic, as even smaller values had been observed for natural waters [20]. For large \({R}_{\rho }\), the temperature gradient becomes too small and the heat flux too weak to drive the required convection for mixed layers formation [37]. Interestingly, the distribution of \({R}_{\rho }\) was rather stable during the quasi-steady expansion (Tables 1 and SI-2 to SI-5) and clustered close to \({R}_{\rho }\approx 3\) (Fig. 6d). There was, however, a vertical structure with up to 50% higher values at the upper bound compared to lower values near the lower bound of the DD zone (Tables SI-2 to SI-5). This is consistent with the observation that layers disappeared near the upper end and new layers formed at the lower end, which led to a downward migration of the DD zone. According to Tables SI-2 to SI-5, \({R}_{\rho }\) values varied around 2 to 3 at depth of new layer formation, which agrees with the model by Toffolon et al. [36], where \({R}_{\rho }\) values dropped after new layer formation and oscillated around 2 (Fig. 10c in Toffolon et al. [36]). After the event reached maximal vertical expansion, \({R}_{\rho }\) increased in the lower zone and led the DD-event collapse.

Rates of new layer formation and layer decay During the quasi-steady expansion of the DD zone, the number of observed layers remained constant, within the uncertainty of about 1 to 2, at 27 ± 1. As the layers found in those four profiles did not keep their identity from one profile to the next, the constancy of the number implies that for every newly formed layer at the base of the staircase, a layer must have eroded or two layers must have merged. The new layers formed during the quasi-steady phase at the lower end of the DD zone with average layer and interface thicknesses of ~ 80 and ~ 35 cm, respectively (Table 1; Fig. 6b). Given the vertical expansion of ~ 3.5 cm day−1 during this phase (Table 1), it takes ~ 32 days to form a new layer-interface pair of 1.15 m thickness (80 + 35 cm). We can conclude that during the quasi-steady expansion, the rates of layer generation and layer dissipation were identical at ~ 1 per month.

This observation is consistent with the above presented heat flux divergence \(\partial {F}_{h}/\partial z\) within the T-stratification at the lower bound of the DD zone. To cool a layer of thickness \({H}_{L}\) within a T-gradient \(\partial T/\partial z\) to homogeneous temperature, the heat content of \({\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}\cdot\left( {\rho C_{p} } \right)\cdot{\text{H}}_{L}^{2} \cdot\partial T/\partial z\) needs to be extracted, following purely geometrical arguments. This amount of heat can be set equal to the cooling effect of the flux divergence \(\partial {F}_{h}/\partial z\) acting for duration \({\tau }_{F}\) over the layer\({H}_{L}\). The time scale \({\tau }_{F}\) to generate a new layer of thickness \({\mathrm{H}}_{L}\) is then given by

$$\tau_{F} = \frac{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}} \cdot \left( {\rho C_{p} } \right) \cdot {\text{H}}_{L} \cdot \partial T/\partial z }}{{\partial F_{T} /\partial z}}\quad \left[ {\text{s}} \right]$$
(8)

For typical values at the lower DD zone (Tables SI-2 to SI-5) of \(\frac{\partial T}{{\partial z}} \approx 0.016\, {\text{K }}\,{\text{m}}^{ - 1}\), thickness \({\text{H}}_{L} \approx 0.8 \,{\text{m}}\) and divergence \(\partial F_{h} /\partial z\) \(\approx\) 0.01 W m−3 (0.5 versus 0.1 W m−2 over ~ 42 m DD zone) leads to a time scale of \(\tau \approx\) 31 days. This duration is well consistent with the observed rate of layer generation based on the vertical expansion during the quasi-steady phase (Table 1), when it lasted on average ~ 32 days to form a new layer-interface pair of 1.15 m thickness (see above). Although the numerical agreement is coincidental, it is a logical consequence of the geometrical setting.

The new layer formation is in competition to the layer decay due to diffusive smoothing by \(D_{T }\). The diffusive decay time \(\tau_{D }\) for a layer thickness \({\text{H}}_{L}\) is given by \(H_{L}^{2} = 2 \cdot D_{T } \cdot \tau_{D }\). For an average \(H_{L} \approx 0.8 \,{\text{m}}\), the expected decay time was \(\tau_{D } \approx\) 25 days. This comparison confirms that during quasi-steady expansion, the two time scales (\(\tau_{F} , \tau_{D}\)) almost equalled, and layer merging / decay were in balance with new layer formation. We can expect that layer merging contributed to the observed increase of the average layer thickness (Fig. 6b).

Collapse of the DD layering Interestingly, the vertical widening of the DD zone followed a diffusion-type expansion (Fig. 6b) with an apparent diffusivity of ~ 1.0 × 10–5 m2 s−1. This implies that the expansion was faster at the beginning and slowed down over time. We explain this observation by the fact that the stronger temperature gradients and the higher heat fluxes in the shallower reaches of the DD zone led to larger flux divergences, which caused faster cooling of the DD zone. This stronger heat export led subsequently to faster generation of new layers and a more rapid expansion. As the DD zone expanded deeper towards weaker T-gradients (Table 1; Fig. 6c) and weaker heat fluxes (Tables SI-2 to SI-5), the subsequent flux divergence decreased. In addition, below 95 m depth, the \({R}_{\rho }\) stratification was less favourable for DD staircase formation [26]. In combination, a critical point was reached, when the time scale for new formation (Eq. 8) exceeded the time scale of decay \({\tau }_{D}\). By then, the intensity of DD forcing was weakened, layers eroded faster than new ones were formed and the DD event eventually ended as the layering collapsed after ~ 850 days (Fig. 6b).

A key feature of this type of DD is the efficient upward removal of heat while dissolved substances remain in the deep reaches. This is the consequence of the DD flux laws for heat and for salt, which express that the T-related density flux is larger than the opposing S-related density flux [17, 37]. For typical density ratios \({R}_{\rho }\), as observed in Lake Nyos, the positive heat-driven buoyancy flux is about 7-times stronger as the opposing negative salt-induced buoyancy flux [37]. In effect, this discrepancy of the vertical fluxes of heat and salt intensifies density stratification and increases the water column stability. In Lake Kivu, this phenomenon [33] allows the accumulation of methane and CO2 to extremely high concentrations. The same can be expected for CO2, which was intruding into Lake Nyos until oversaturation was reached in the past. The practical consequence of DD is a “fortunate” conservation of methane energy in Lake Kivu, but it led to a human disaster in Lake Nyos. Considering that after such a DD event ended in the past, heat could had accumulated again in the deep waters, and subsequently another cycle of DD layering could follow. What we have observed may therefore not be a unique phenomenon for Lake Nyos, but it was unique that we had the fortune to observe it by chance.

5 Conclusions

By analysing 39 fine-scale CTD profiles and temperature records from moored thermistors, both collected in Lake Nyos over a period of four years, we have been able to observe a complete lifecycle of a double-diffusive (DD) staircase. To our knowledge, this is the first report of the entire lifetime of a DD event in a natural water body, which lasted ~ 850 ± 50 days. Based on the data analysis we conclude as follows:

  1. (1)

    The DD lifetime consisted of (i) a build-up period of less than 300 days, while up to 27 layers-interfaces pairs were formed, (ii) a quasi-steady period of ~ 450 days of vertical expansion of the DD zone, where the number of pairs remained constant, and finally (iii) a decay phase of a few dozen days when the molecular diffusion of heat eroded the DD layering.

  2. (2)

    The DD zone was initiated in a depth of 53 m in Feb 2002, and expanded to a maximal vertical extension down to ~ 95 m depth after ~ 850 days. The DD zone widened vertically proportional to (time)1/2, indicating a diffusive-type of expansion with an “apparent diffusivity” of 1.0 × 10–5 m2 s−1, orders of magnitude faster than molecular diffusivities. During this expansion, the layers grew up to ~ 1.3 m thick, while the DD zone cooled off.

  3. (3)

    During the build-up phase, the new layer generation rate exceeded the decay rate and the number of layers increased rapidly. During the period of quasi-steady expansion, the number of layers and interfaces remained constant, indicating that the rate of new layer generation was equal to the rate of layer decay. Differences between subsequent CTD profiles indicated that the rates of formation and decay was ~ 1 per month. New layers formed at the lower bound of the DD zone, which continuously expanded downward. Embedded in the vertical profiles of increasing temperature and salinity with depth, the new layers were warmer and saltier.

  4. (4)

    The rates of new layer formation and decay can be explained by the vertical divergence \(\partial {F}_{h}/\partial z\) of the upward heat flux \({F}_{h}\), which was found in good agreement with the DD flux laws of Kelley [13]. The formation time scale was proportional to the temperature gradient \(\partial T/\partial z\) and inversely proportional to the divergence \(\partial {F}_{T}/\partial z\). This relationship is consistent with the observation that during the build-up phase the time scale for generation was shorter than the decay time by diffusion. DD enhanced the vertical heat fluxes and led to strong divergence in the lower DD zone. Subsequently, the generation time scale shortened at the lower bound of the DD zone and the DD-enhanced heat flux sustained the downward expansion.

  5. (5)

    With the expansion of the DD zone, the vertical gradient \(\partial T/\partial z\) decreased and the density ratio \({R}_{\rho }\) increased. The decreasing divergence \(\partial {F}_{h}/\partial z\) reduced the buoyancy flux for convective mixing in the layers. As an effect, the time scale for new layer generation exceeded the decay time scale. In consequence, the staircase structure gradually eroded and within a few weeks, DD layering could not be recognized anymore.

  6. (6)

    Whereas the initiation of the DD event and the subsequent staircase formation could be identified exactly to within less than one week of uncertainty, the end of the lifetime after ~ 850 ± 50 days was not-well defined as the distinct well-mixed homogeneous layers and sharp interfaces faded away over several months.

  7. (7)

    As an overall effect, the DD-enhanced heat fluxes removed heat out of the DD zone into the layer above and thereby weakened the temperature-induced convective instability and killed the DD event itself.