Lock-release gravity currents propagating over roughness elements

Abstract

The influence of bottom roughness on the development of lock-release gravity currents is investigated through laboratory experiments using Particle Image Velocimetry. The bottom roughness is represented by arrays of vertical LEGO bricks with a constant spacing while varying $\lambda$, the relative height of the roughness elements to the gravity current depth. Depending on $\lambda$, the roughness elements may affect the gravity current propagation: for small $\lambda$ the current behaves like moving over a smooth bottom, while for larger $\lambda$ the propagation speed is reduced and the internal structure of the current, including both the head and the tail, is significantly modified. As $\lambda$ increases, stronger recirculation areas between the roughness elements develop interacting with the overlying layer and giving rise to small-scale vortical structures of opposite sign within the whole depth of the current. The additional drag force induced by the bottom roughness adds significant complexity to the flow dynamics and modifies the characteristics of the current.

Article Highlights

• Experimental study on gravity currents flowing over roughness elements.

• The dynamics of the current is deeply affected by the interaction with the bottom roughness.

• The flow pattern and the shape of the current depend on the roughness height.

1 Introduction

Gravity currents are geophysical flows resulting from differences in temperature, salinity, or caused by suspended sediment particles. These flows develop mainly in the horizontal direction and can occur spontaneously in nature or result from anthropic intervention. Oceanic currents, sand storms, the release of pollutants into rivers and desalination plant outflows are examples of gravity currents [1]. In the last decades, gravity currents have been studied extensively by means of theoretical investigations, laboratory experiments, and numerical simulations. Most of these studies focused on gravity currents travelling along a flat, horizontal surface [2,3,4,5,6,7] or flowing over a sloping bottom [8,9,10,11,12,13,14,15].

Recently attention has been paid to topographic features and how they affect the propagation of dense bottom gravity currents. Several studies analyze gravity currents interacting with a single large isolated structure [16,17,18,19,20] showing how a topographic discontinuity, as an obstacle placed on a horizontal bottom, deeply modifies the structure of the gravity current and enhances dilution.

Recent studies focused on the interaction of gravity currents with a rough bottom. The quantification of the roughness effect on gravity currents dynamics is a challenging task, due to the large variability of the roughness dimensions, shape and spatial arrangement [21] which cause a complex flow pattern. [22] investigated the effects of a rough bottom on the interfacial instabilities for a two-layer exchange flow over a sill using sparse and dense roughness elements. They found that bottom roughness can inhibit the formation and growth of shear instabilities at the interface.

Gravity currents flowing over rough beds made by natural sediments were investigated by [23,24,25]. They found that the current velocity decreases for increasing roughness; furthermore they showed how the bed material induces a homogenizing effect throughout the current height, less large-scale billows being observed. [26] investigated gravity currents propagating over a mobile sediment bed. They found that the size of the sediments of the mobile bed influences the hydrodynamics of the current due to the occurrence of feedback mechanisms between the mobile bed and the current itself. Gravity currents interacting with array of obstacles were investigated by [27] by LES. [28] studied gravity currents flowing over roughness elements by LES showing how bottom roughness significantly alters the front characteristics and the mixing within the current. Entrainment in rotating gravity currents flowing down a rough sloping bottom was analyzed by [29].

Moreover, [30] investigated experimentally the dynamics of dense gravity current flowing through an array of vertical rigid cylinders, by varying the spacing between the elements. They observed different flow regimes: for large spacing between the cylinders the currents travel through the cylinder arrays, while for dense arrays the current propagates over the top of the roughness elements. A similar configuration was adopted in the numerical investigation of [31].

In this study we present a novel laboratory investigation on the effects of roughness elements on lock-release gravity currents. In particular, we focus on how the roughness height affects the inner velocity of gravity currents by means of PIV measurements. Three classes of submerged roughness can be defined by the ratio of flow depth, H, to obstacles height, $h_{0x}$: deeply submerged or unconfined ($H/h_{0x} > 10$), shallow submergence ($H/h_{0x} < 5$), and emergent ($H/h_{0x} = 1$) [32]. Following this classification, we explore deeply and shallow submergence cases and for the first time, we analyze a case with random roughness heights.

The paper is organized as follows: details of the experimental apparatus and measurements are given in Sect. 2. Experimental results are discussed in Sect. 3, with a focus on the front propagation and on the front velocity in Sect. 3.1; a description of the inner velocity flow is in Sect. 3.2 and 3.3; the description of the current height profiles is presented in Sect. 3.4. Finally, the conclusions are given in Sect. 4.

2 Experimental details

2.1 Experimental set-up

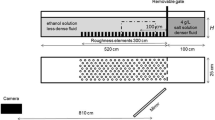
Experiments were conducted in a 6 m long, 0.5 m deep and 0.5 m wide tank, in which an elevated (0.3 m) horizontal channel of a total length of $D=2.30$ m and of reduced width ($s=0.25$ m) was divided into two portions. A sketch of the experimental facility is shown in Fig. 1a.

The tank was first filled with fresh water to a height of $h_0=9.8 \pm 0.2$ cm in the channel. A Plexiglas barrier was then placed at a distance of $x_0=50$ cm from the left end side of the elevated channel to divide it in two portions. A reduced gravity of $g'_0=g \Delta \rho /\rho _a=5 \pm 0.5$ cms$^{-2}$ was produced by adding NaCl to the water in the left portion of the reservoir, which had a total volume of 75 l. Herein, $\Delta \rho =\rho _s-\rho _a$ was the density difference between the saline and the ambient quiescent water. The density of the fresh and of the salty water were determined based on the water temperature ($15\pm 1.5\;^\circ$C measured to $0.1\;^\circ$C) and salt concentration (weighted to 0.1 g) with a high-precision density meter (AntonPaar, DMA5000). Therefore the error in the reduced gravity $g'$ was estimated to be less than $1\%$. The gravity flow was then produced using the lock-release technique by removing the barrier.

Fig. 1

Sketch of the experimental set-up. a Side-view of the tank. b Plan view. c Details of the roughness elements. The PIV acquisition windows FOV1, FOV2 and Zoom, are located respectively at $0.16 \le (x-x_0)/x_0 \le 1.45$, $1.03 \le (x-x_0)/x_0\le 2.32$ and $0.88 \le (x-x_0)/x_0 \le 1.25$

LEGO bricks were used as bottom roughness elements with a constant squared section of 0.78 $\times$ 0.78 cm$^2$. They were placed staggered with a constant spacing of 5.2 cm in both x and y directions fixed on a 0.1 cm thick plate; the latter had a total length of 1.2 m and the same width of the channel, it was positioned on the horizontal bottom of the channel as depicted in Fig. 1b. Five series of experiments were performed by varying the roughness elements height $h_{0x}$. Three series of experiments were performed with a constant height of the roughness elements (R1 with $h_{0x}= 0.64$ cm, R2 with $h_{0x}= 1.6$ cm and R3 with $h_{0x}= 2.56$ cm), series R4 considers a random combination of the previous elements height (R4 with $0.64\le h_{0x}\le 2.56$ cm) and moreover a reference set of experiments under smooth conditions without the use of the roughness plate (R0 with $h_{0x}= 0$ cm) was performed. In the present experiments, the Reynolds number, $Re=(U_fh_0)/\upsilon$, where $U_f$ is the front speed of the current and $\upsilon$ is the kinematic viscosity, varied between $2200 \div 2900$, while the Froude number, $Fr=U_f/\sqrt{g'_0h_0}$, varied between $0.33 \div 0.43$. To characterize the bottom roughness, the relevant non dimensional numbers related to the roughness elements, proposed by [32] and also given in [29] and [30], have been calculated. Due to the fixed position of the roughness adopted in this study some geometric parameters were unchanged in all the tests with roughness; i.e. the area of the field covered by the bricks in elevation as seen by the advancing current, measured from the bottom to the top of the bricks, $A_e$, the total area of the field in elevation measured from the bottom to the top of the bricks, $A_{te}$, the area of the base covered by the bricks in plan, $A_p$, and the total area of the base in plan, $A_{tp}$. Indeed, the elevation density, $\mu =A_e/A_{te}$, and the plan density, $\sigma =A_p/A_{tp}$, assumed a constant value, respectively 0.15 and 0.026. On the other hands, the aspect ratio of the roughness elements, $\alpha =h_{0x}/b$ and the ratio of the bricks height to the water depth, $\lambda =h_{0x}/h_0$, raged between $0.82 \div 3.28$ and $0.07 \div 0.26$, respectively. $h_{0x}$ and b indicate the height and width of the LEGO brick. In run R4 an average of the quantities involved was adopted. All the main experimental parameters are summarized in Table 1.

Table 1 Main parameters of the experimental runs

2.2 Measurement technique

The flow velocities were determined using the optical, non-intrusive experimental technique of Particle Image Velocipedes (PIV). The PIV set-up consisted of a light source, light sheet optics, seeding particles, a camera, and a PC equipped with a frame grabber and image acquisition software. Polyamide particles (Orgasol) with a diameter of $d_p = 50$ $\mu$m with a specific density of $\rho _p = 1.016$ g/cm$^3$ were added in both sides of the channel containing fresh and salt water with a concentration of 0.04 g/l as tracer material for the PIV measurements. A 6 W Argon-Ion laser operating in multimode ($\lambda _b =488$ nm, $\lambda _g=514$ nm) has been used as continuous light source. The beam was transmitted through a fiber optic cable to a line generator with spherical lenses (OZ Optics Ltd., Nepean, Ontario). The generated laser sheet had a length of approximately 1 m and a width of 5 mm and was positioned in the middle of the channel.

Three sets of PIV acquisitions with different image sizes have been performed: in the longitudinal section, two fields of view (FOV1 and FOV2) were captured, with a size of 64.7 $\times$ 11.3 cm, one starting at $x = 8$ cm after the location of the gate removal ($x_0 = 50$ cm) and one starting at $x = 51.3$ cm (Fig. 1). An additional zoomed view of size 18.5 $\times$ 11.3 cm have been captured at $x = 44$ cm. The images were captured with a CCD camera (FlowMaster3, 14bit, 1600 $\times$ 1200 pixels) at a frame rate of 21.5 Hz and an exposure time of 12, 000 $\mu s$. A wide angle lense (SIGMA AF EX 1.8/24 DG Macro AF for Nikon) was used at a distance of 2 m to the field of view for the large size longitudinal acquisitions FOV1 and FOV2, and a smaller angle lens (NIKON AF EX 1.2/49) was used for the zoomed longitudinal view.

Each experiment was repeated between three to five times using the same initial conditions and for each field of view to check the repeatability of the experiment.

Time series of 45 s leading to 1000 raw images for each experiment were stored in real time on a raid system. The raw images were then processed using a PIV algorithm to compute the velocity fields, between two consecutive raw images. With the software package DaVis (LaVision) the velocity fields were computed using a cross-correlation PIV algorithm. For this purpose an adaptive multipass routine was used, starting with an interrogation window of 32 $\times$ 32 pixels and a final window size of $8$ $\times$ 8 pixels for the large size images and 48 $\times$ 48 to 16 $\times$ 16 for the zoomed view, all with $50\%$ overlap. Each vector of the resulting vector field represents an area of roughly 1.6 $\times$ 1.6 cm$^2$ and 0.92 $\times$ 0.92 cm$^2$ for the large size longitudinal view and the zoomed longitudinal view, respectively. The velocity vectors were post-processed using a local median filter and checked by the error that was estimated by $E_n=\overline{\sqrt{u'(t_n)u'(t_{n-1})}}$, where $u'$ represents the velocity fluctuation with respect to the time averaged velocity at the instant $t_n$ and the overline denotes temporal average. Given the velocities encountered in the experiments, the experimental error in the instantaneous velocity is estimated to be $5\%$ maximum. In order to check the results, the velocity fields were also computed using the UVmat software developed at LEGI-Coriolis (Grenoble, France). The comparison showed differences of less than $1\%$ in the instantaneous velocity profiles. The zero time reference was associated to the gate removal.

3 Results and discussion

3.1 Front characteristics

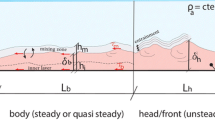
According to the shallow-water theory, gravity currents produced by the lock-exchange technique over a smooth bed present three distinct phases: the slumping phase, the self-similar phase and the viscous phase [33]. After the instantaneous release of the dense flow through a sliding gate at $t_0=0$, an initial slumping phase is observed; in this phase the front position varies linearly with time, i.e. the front advances with a constant velocity. Subsequently, if the flow is confined within a channel of limited length, when a bore generated at the end wall of the channel overtakes the front, the initial constant-velocity phase, merges into a second phase, called the self-similar phase [33]. From this time, the front position advances as $t^{2/3}$, with front speed decreasing as $t^{-1/3}$, where t is the time after the gate removal. In both these phases, the current spread is governed by the balance between buoyancy and inertial forces. When viscous effects overcome inertial effects, a third phase develops and the current front velocity decreases more rapidly following the theoretical power law $t^{-4/5}$, with the front position advancing as $t^{1/5}$. Usually, to define the experimental front position of a 2D dense current, the spanwise-averaged density fields are used, adopting a density threshold value [5, 34,35,36] or identifying the inflection point along the front interface between the current and the ambient fluid through the evaluation of the maximum and the minimum density value [28]. In this work the front position, namely the foremost point of the current along the streamwise direction, $x_f$, is defined as the point where the spatial derivative of the longitudinal velocity u in the streamwise direction $\partial u / \partial {x}$ is maximum. The dimensionless front position $x_{f}^*$, vertical scale $y^*$ and time $t^*$ are defined as:

$$\begin{aligned} x_{f}^*=\frac{x_f-x_0}{x_0}, \quad y^*=\frac{y}{h_0}, \; t^*=\frac{t}{x_0}\sqrt{g'_0h_0} \end{aligned}$$

(1)

Fig. 2

Dimensionless front position ${x_f}^*$ versus dimensionless time $t^*$ for all the experiments performed. Theoretical front position for the slumping and the self-similar phases are indicated by solid and dashed lines, respectively

Fig. 3

a Dimensionless front velocity ${U}^*$ versus dimensionless front position ${x_f}^*$ for all the experiments performed. Theoretical front velocity for the slumping phase is indicated by solid black line. b Non-dimensional front velocity ${U}^*$ dependence on $\lambda$

Figure 2 shows log-log plots of $x_{f}^*$ versus the $t^*$ of the dense currents for all the experiments performed.

The slumping phase is developed in all the cases, and it is represented by the solid line with slope equal to 1 shown in the plot. The R0 and the R1 runs show exactly the same behaviour until the end of the window of analysis, thus highlighting how the current regime for run R1 is not affected by the presence of bottom roughness. By increasing the height of the bottom roughness, R2, R3 and R4 runs show a slight transition from the slumping regime, underlined by the different inclinations of the curves $x_{f}^*$ vs $t^*$. The current does not enter into the inertial regime shown in the graph by a black dotted line with the slope= 2/3.

The time rate of change of $x_f$ represents the front velocity ($U_f=dx_f/dt$). The latter is calculated as the ratio between the distance travelled by the current and the time. Figure 3a shows the dimensionless front velocity $U^{*}=U_f/\sqrt{g'_0h_0}$ versus the dimensionless front position ${x_f}^*$. Previous measurements of $U^{*}$ for full-depth lock exchanges [3, 20, 37] found that during the slumping phase the front velocity is roughly constant ($U^{*}=0.46\pm 0.02$) for sufficiently high Reynolds numbers. The theoretical front velocity for the slumping phase is depicted with a dashed black line in Fig. 3a. As previously discussed, the R0 and the R1 runs do not show noteworthy differences between them; the front velocity is approximately constant in reasonable agreement with the theoretical value for a gravity current propagating over a flat horizontal bottom within the slumping phase. Then small rough elements do not affect the front spread. When increasing the height of the bottom roughness, the velocity $U^{*}$ decreases as the roughness height increases.

Figure 3b shows the effect of $\lambda$ on the non-dimensional front velocity ${U}^*$. An increase in $\lambda$ produces a reduction of ${U}^*$ which can be up to $40\%$ of the velocity for a flat horizontal bottom for runs R3 and R4. Furthermore ${U}^*$ is not only a function of $h_{0x}$, but also of the bricks distribution. Indeed, with almost the same $\lambda$, run R4 shows a lower ${U}^*$ value than run R2, highlighting how a random bricks size distribution produces greater changes in the dynamics of the current than a uniform one.

In the following analyses the results of run R1 are not shown due to the not noteworthy differences with run R0.

3.2 Velocity fields

The leading edge of a gravity current is characterized by a head thicker than the following tail [25, 33, 38]. This zone is distinguished for intense mixing and plays an important role in the dynamics of the current. In a gravity current flowing on a horizontal smooth bottom the head exhibits a quasi-steady behaviour and usually has a ‘nose’, or foremost point, raised at short distance above the ground [33]. In order to investigate how the flow structure is modified by the presence of the bed roughness, the analysis of the velocity fields is here presented for selected runs, but similar characteristics are observed in the remaining runs. The instantaneous dimensionless maps of the streamwise and vertical velocity components, $u^*$ and $v^*$, are shown in Fig. 4 at the time at which the current reaches the end of the measurement field. The grey areas represent the bottom roughness sections present in the PIV measurement plane or areas where PIV data are not available, while the black areas represent the bottom elements that are not really present in the analysis plan considering the staggered arrangement of the elements. The boundary between current and ambient fluid is represented by a black dotted line; the latter is obtained by considering the condition $u\approx 0$ for the upper limit and ${\partial v}/{\partial {x}} \approx 0$ for the frontal limit [39].

In run R0 the typical shape of the current is shown (Fig. 4a). The core of the current is characterized by relatively high $u^*$ values, while at the interface between the ambient fluid and the salty water there are relatively low values of $u^*$. Focusing on the vertical component of the velocity, $v^*$, the high values can be observed in the frontal region of the current (Fig. 4e), while negative values of $v^*$ can be noted at the boundary between the dense current and the ambient fluid, due to the presence of large instabilities at the rear of the head, i.e. Kelvin-Helmoltz billows. A different behavior occurs in case of a rough bottom. The roughness introduces significant complexity in the gravity current flow pattern mainly dependent on geometrical characteristics. Indeed, in run R2 the current flows over the bricks, whereas when the height of the roughness increases, the current moves also around them, developing a three-dimesional flow pattern. As a consequence, the front loses definition as its thickness is comparable with the roughness elements (cf. Fig. 4b-d). The loss of definition of the frontal region is expected to be also dependent on the spatial arrangement of the bricks. Similar results on the 3D nature of the flow were found by [28] who, through 3D LES simulations, show how the current front loses its momentum locally crossing over and surrounding the bottom roughness and how this behavior exhibits strong coupling to the distribution, shape and height of roughness features.

Fig. 4

Dimensionless streamwise velocity field, $u^*$, and dimensionless vertical velocity field, $v^*$, respectively for R0 (a, e), R2 (b, f), and R3 (c, g) and R4 (d, h) after the current has travelled the distance $x^*=2.2$

Figure 4b,c shows that the backflow velocity in the ambient fluid decreases as the intensity of the streamwise velocity $u^*$ decreases. This deceleration is related to the bricks height, the larger is the bricks height the larger is the deceleration. Moreover, the higher velocity regions within the dense flow are mostly positioned above the roughness level, while recirculation patterns are observed between the elements that separate the main current from the bottom area. Run R4 exhibits a general behavior similar to R2 and R3 but even more complex (Fig. 4d). The recirculation patterns are also observed in this case, and their vertical development dependent on the height of the bottom roughness, the greater the height of the roughness, the greater the recirculation patterns.

Also the vertical velocity fields, $v^*$, show a greater complexity due to the rough bottom (Fig. 4f–h). High values as well as negative values of $v^*$ are located between the bricks indicating the formation of turbulent structures.

Fig. 5

Dimensionless streamwise velocity field, $u^*$, and dimensionless vertical velocity field, $v^*$, for R2 are represented in panel (a) and (e) respectively after the current has travelled the distance $x^*\approx 1.2$. The solid white lines represent the vertical sections at $x^*=0.97$, while the dashed white lines represent the vertical sections at $x^*=1.08$. Time series of instantaneous velocity components u and v, black and red lines respectively, for run R2 at $x^*=0.97$ (b, c, d) and $x^*=1.08$ (f, g, h) and different vertical locations $y^*=0.08$ (d, h), $y^*=0.18$ (c, g), $y^*=0.28$ (b, f)

The zoomed views of run R2, shown in Fig. 5, are used to better characterize the flow patterns. Figure 5a, e show instantaneous dimensionless maps of the streamwise and vertical velocity distributions highlighting two vertical sections at $x^*=0.97$ (solid line) and $x^*=1.08$ (dashed line) downstream of a brick, that are reported in Fig. 5b–d and Fig. 5f–h for three different vertical locations $y^*=0.28, y^*=0.18, y^*=0.08$, respectively. In the left panels of Fig. 5 the arrival of the gravity current can be identified for all chosen $y^*$ highlighted by an increase in both the velocity components $(u^*,v^*)$. However, while $u^*$ remains almost constant, after the front of the current has passed, the vertical velocity component, $v^*$, decreases and approaches a zero value (cf. Fig. 5b–d). A different behavior occurs instead at $x^*=1.08$, downstream of a bottom element present in the plane of analysis (right panels of Fig. 5), where a recirculation area is shown (see Fig. 5a). In this case, at $y^*=0.08$ the passage of the front of the current is highlighted by small fluctuations of both velocity components, after which both velocities tend to zero (Fig. 5h). A similar behaviour occurs at $y^*=0.18$ where, after the passage of the current, $u^*$ and $v^*$ are almost zero. At $y^*=0.28$, just above the bricks (Fig. 5f) an increase of both velocity components $u^*$ and $v^*$ appears as the current front passes. Fig. 5 also shows that the recirculation areas between the roughness elements extend above the roughness elements and persist during the whole duration of the experiment.

3.3 Flow structures

In this section we present the vorticity component normal to the plane of measurement, $\zeta =\partial _x v - \partial _y u$, and the Okubo-Weiss parameter OW, defined as:

$$\begin{aligned} OW=S^2- \zeta ^2 \end{aligned}$$

(2)

where $S^2=S^{2}_n+S^{2}_s$ with $S_n= \partial _x u -\partial _y v$ the normal component of strain and $S_s=\partial _x v +\partial _y u$ the shear component.

Regions dominated by vorticity are characterized by high negative values of OW, while high positive values of OW highlight regions dominated by strain. The threshold $OW_0 = 0.2 \sigma _{OW}$, with $\sigma _{OW}$ being the spatial average standard deviation in the whole domain, is usually adopted to isolate the regions dominated by strain ($OW > OW_0$) and the regions dominated by vorticity ($OW<-OW_0$) [40].

Fig. 6

Dimensionless vorticity field, $\zeta ^*$, and dimensionless Okubo-Weiss parameter, $OW^*$, respectively for R0 (a, e), R2 (b, f), R3 (c, g) and R4 (d, h) after the currents have travelled the distance $x^*=2.2$

In Fig. 6 the dimensionless vorticity field $\zeta ^*$ (a–d panels) and the dimensionless Okubo-Weiss parameter $OW^*$ (e–h panels), are plotted for runs R0 (a,e), the R2 (b,f), the R3 (c,g) and the R4 (d,h), after the currents have travelled the distance $x^*=2.2$. In all runs the interface between the dense current and the ambient fluid is characterized by a positive vorticity (cf. Figs. 6a–d), resulting from the shear that causes the development of Kelvin-Helmholtz instabilities. In runs R0 and R2 the highest values of $\zeta ^*$ are located at the interface near the head of the current (Fig. 6a,b). As the height of the bottom roughness increases, the maximum vorticity $\zeta ^*$ decreases. R4 run shows a even more complex behavior compared to R2 and R3. The maximum vorticity $\zeta ^*$ are located at the interface downstream the highest bricks and near the head of the current (Fig. 6d). The region of negative vorticity, resulting from the shear between upper flow and low velocities close to the bottom, is located at the boundary layer for run R0 in Fig. 6a. On the other hands, in runs with roughness elements, the region of negative vorticity increases in intensity and is concentrated at the top of the roughness elements and it may expand down to the bottom in the rough cases. The areas of highest negative vorticity are very close to the region characterized by the vorticity with opposite sign.

This is even more evident in the e-h panels displaying the $OW^*$ parameter: in the R0 case, we see organized structures which mostly alternate high vorticity and high strain regions, concentrated at the interface between the dense flow and ambient water. This regular pattern disappears when employing bottom roughness and the distribution of positive/negative $OW^*$ values becomes more chaotic and is extended to the full depth of the current, including the interstices between the roughness elements. The roughness elements at the bottom, by decreasing the current velocity inhibit the development of the Kelvin-Helmholtz instabilities. The amplification rates of the instabilities are therefore reduced and the roughness elements contribute to their rapid break down. In run R3, the head of the current is no longer characterized by the highest $\zeta ^*$ values, which are distributed along the thin interface just above the roughness elements within the whole measurement window. R4 run shows intermediate characteristics between R2 and R3; the head of the current is still characterized by the highest $\zeta ^*$ values but the the presence of high bricks inhibits the instability structures more than R2.

Fig. 7

Zoom view of vorticity field, $\eta$, and Okubo-Weiss parameter, OW, respectively for R0 (a, e), R2 (b, f), R3 (c, g) and R4 (d, h) after the currents have travelled the distance $x^*=2.3$

Fig. 8

Zoom velocity vectors for the R0 run (a) and R2 run (b). The colour distribution is in accordance with the streamwise velocity field u

Figure 7 is similar to Fig. 6, but showing the zoomed vorticity $\zeta ^*$ and $OW^*$ fields. From the vorticity fields in the left panels, it is seen how the shape of the gravity current is strongly affected by the presence of the bottom roughness elements: while the highest vorticity regions are continuous and uniformly distributed along a line, in the rough cases the shape starts oscillating following the roughness elements and the highest values are concentrated above the roughness. Both positive and negative vorticity structures are present in the interstices. Eddy structures at the current interface are clearly seen in all the runs under analysis by the appearance of areas of high vorticity. Fig. 7b–d shows how the bottom roughness leads to a decrease of vorticity, i.e. a decrease in intensity of the interfacial eddies causing their decay. This phenomenon is shown in Fig. 8b in which a detail of velocity vectors on the experimental streamwise velocity distribution is displayed. As the current passes over the roughness elements, the portion of the current over the roughness peaks slows down and a recirculation zone develops. As expected no recirculation region is present in run R0 (Fig. 8a).

3.4 Current height profiles

To have a global picture of the current profile, the height of the dense flow is evaluated. According to previous studies [3, 41] lock-release gravity currents rapidly develop an elevated head which contains most of the fluid from the lock. Moreover, during the slumping regime, the mean head height of the current over the smooth bed, remains almost constant.

Fig. 9

Dimensionless height profiles of a gravity current for R0 (a), R2 (b), R3 (c) and R4 (d) runs. The profiles depicted by black,dark gray and light gray solid line correspond respectively to a distance traveled by the current equal to $x^*=1.4$, $x^*=1.8$ and $x^*=2.2$

Figure 9 shows three snapshots of the current height profiles for runs R0, R2, R3 and R4, after the current has traveled $x^*=1.4$, $x^*=1.8$ and $x^*=2.2$, indicated by a solid black, dark gray and light gray line respectively. All the bottom elements, present in the whole section of the tank under analysis, are outlined with a thin red line. In run R0 we can observe the typical current profile characterized by a head higher than the current body (Fig. 9a). In runs R2, R3 and R4, on the other hand, there is a totally different behavior. The presence of bottom roughness modifies the behaviour of the current front and as the height of the roughness increases, it becomes more complex to distinguish the head from the body of the current. Indeed, as the front encounters the roughness peak, it deflects upwards, and consequently the depth of the current body increases. The local variation of the current height is much higher for run R3 compared to other cases (Fig. 9c), while in the random run, R4, the height of the current seems to be more uniform between two highest bricks (Fig. 9d).

Fig. 10

Dimensionless height of the current, $h_c/h_0$ for the experiments R0 (a), R2 (b), R3 (c) and R4 (d)

Fig. 11

Mean profiles of the current ${\bar{h}}$, normalized by the water depth $h_0$, after the current front has passed the analysis window, for the experiments R0 (a), R2 (b), R3 (c) and R4 (d). Red areas surrounding the mean profile correspond to the standard deviation

Fig. 12

Evolution of the Froude number Fr considering a the initial height of dense fluid $h_0$, b the maximum equivalent height $h_{max}$ and c the mean height behind the head ${\bar{h}}_m$

To better understand the changes in the flow structure induced by the interaction between the head and the bottom elements, the space-time evolution of the dimensionless gravity current highs $h_c/h_0$ are analysed in Fig. 10. In the latter there are four Hovmöller diagrams, in which the shades of blue represent the different levels of the current height in space-time. The vertical white stripes, which create discontinuity in the height measurements, indicate the presence of the bottom elements in the tank (Fig. 10b–d). In the flat-bed condition, the size of the head region and the interface height do not change significantly as time increases (Fig. 10a), confirming what has already been observed by [34]. In contrast, in the bottom roughness cases, the height does not maintain a regular structure, but distinctive characteristics can be observed. In figure Fig. 10b, at the white stripes, i.e. bottom elements, high current height values are observed. This behavior is due to the dense flow projected upwards as the flow impacts the upstream face of bottom brick, causing a backward-propagating hydraulic jump forms, also observed by [27], which leads to an increase in the height of the current. This local increase in the height of the current is less evident in R3 and R4 due to the reduced longitudinal current velocity which causes a smaller backward hydraulic jump. Moreover, it is interesting to note, how the roughness implies the presence of an extra drag, which results in an increase in the height of the body of the current. This behavior, also observed by [27, 28], is shown in Fig. 10b for $t^*>2.5$ and in Fig. 10c–d for $t^*>4$.

For each run, a time-averaged height ${\bar{h}}(x)$ is evaluated from its instantaneous current profile h(x, t) after the current front has left the analysis window. Fig. 11 show ${\bar{h}}(x)$ normalized by the initial water depth $h_0$. The red regions surrounding the mean profiles represent the standard deviation of the current height $\sigma _h$. In the R0 run the current depth behind the head assumes a constant value for the whole run (Fig. 11a), while in the runs with roughness ${\bar{h}}(x)/h_0$ is no more uniform. As the height of the roughness increases, there is a greater decrease of ${\bar{h}}(x)/h_0$. Runs R3 and R4 show a similar behavior, but the variations of ${\bar{h}}(x)/h_0$ are more marked in R3 characterized by a higher roughness.

During the constant-velocity phase a lock-release gravity current flowing over a flat bed is characterized by a nearly constant depth from the head to the point reached by the reflected disturbance from the lock. This allows to define a current depth ahead of this disturbance which can be used to determine the Froude number of the current [3, 41]. However, when the current flows over a rough bottom, even if the front velocity of the dense current is still constant, there is a difference between the height of the current head and the following current body. As a consequence the definition of a characteristic height of the current for determining the Froude number, Fr, is more complex due to the variation of the current profile exerted by the presence of the roughness elements. Then, we assess Fr by using different characteristic heights. Fig. 12 shows Fr evaluated by using the front velocity $U_f$, and three different heights: the lock height, $h_0$, the maximum height of the current, $h_{max}$, determined by taking the maximum value of current height, and the average height of the current body, ${\bar{h}}_m$. The Froude number $Fr_{h_0}$ based on the initial lock height is approximately constant in all the runs due to the constant front velocity of the current. The value found for the initial phase in run R0 is consistent with previous measurements [3, 24, 41]. In the tests in which the roughness is present, on the other hand, we have a decrease in the front velocity which leads to a decrease of $Fr_{h_0}$ [24]. As already noted in the Sect. 3.1 an increase in the height of the bottom bricks causes a decrease of the front velocity and runs R3 and R4 show a similar behavior. Fig. 12b shows the Froude number based on the maximum height of the current, $Fr_{h_{max}}$. Typically, for the gravity current propagating over a flat surface, $h_{max}$ is located on the head of the current and assumes an almost constant value during the slumping phase. This does not happen in the presence of a bottom elements where the depth of the current body assumes an higher height compared to the current head due to the presence of hydraulic jumps caused by the bottom roughness. R0 and R2 exhibit similar $Fr_{h_{max}}$ as well as R3 and R4. Finally, the Froude number, $Fr_{{\bar{h}}_m}$, based on the mean average height of the current body, is shown in Fig. 12c. $Fr_{{\bar{h}}_m}$ has higher values, but we are always in the case of a subcritical regime. We notice that run R2 exhibits a $Fr_{{\bar{h}}_m}$ slightly higher than R0, despite the roughness slows down the front due to enhanced drag, while runs R3 and R4 still exhibit a similar behaviour.

4 Summary and conclusion

In the present study lock-exchange gravity currents experiments are performed to characterize the influence of bottom roughness elements on the dense flow through Particle Image Velocimetry PIV. LEGO bricks, with a constant quadratic section, are used as bottom roughness elements and the height of the elements is changed. Three different homogeneous roughness configurations (R1, R2, R3) are adopted, additionally a random test (R4) and a smooth test (R0), without bed roughness, are performed. The results obtained show how the bottom roughness adds significant complexity to the flow dynamics. The distribution and the height of roughness elements play a fundamental role in the velocity distribution above and around roughness elements. The analyses carried out highlight how the front velocity and the inner streamwise velocity are reduced as the height of the bottom roughness increases. The highest velocity reduction, about $40\%$, is observed in run R3 which is the experiment characterized by the highest bed roughness. Moreover, the instantaneous maps of the velocity field hint the presence of recirculation areas between the bricks. The recirculation areas developing among the background elements are constant over time with a longitudinal development and height depending on the height of the bricks; the greater the height of the elements and the greater the size of the recirculation areas. The detailed study of the vorticity and OW parameter highlights how these quantities are affected by the increase of the roughness elements; the boundary between the dense current and the ambient fluid is characterized by a greater homogenization of the velocity distribution inside the stream and by a reduction of the maximum velocity gradient, while the bottom dynamics becomes more complex. Furthermore, from the study carried out, it emerged that the gravity current’s dynamics depends not only on the roughness elements height, but also on its distribution. Indeed, a random distribution of the bottom roughness heights adds further complexity in the characterization of the dynamics of the current. The analysis of the current height profiles shows how the shape of the current propagating over a bottom roughness differs from the one propagating over a flat surface. Roughness elements slow down the front due to enhanced drag that involves a decrease of the current head height and an increase of the current tail depth. The greater the height of the roughness, the greater the increase in the height of the current tail. Finally the measurements of the Froude number, considering the variation of the height of the current in space and time and the constant front velocity propagation, suggests how the bottom roughness affects the current dynamics.