A joint velocity-intermittency analysis reveals similarity in the vertical structure of atmospheric and hydrospheric canopy turbulence

Abstract

Turbulent flow through and over vegetation continues to draw significant research attention given its relevance to a plethora of applications in earth and environmental science. Canopy flows are characterized by three-dimensional coherent vortical motions not directly accessible from single-point measurements, which pose a challenge to formalizing links between vegetation structure and turbulent motion. A joint velocity-intermittency technique is applied to velocity data collected within and above aquatic vegetation in a hydraulic flume and above a forested canopy. The approach reveals behavior that provides greater insight into canopy flow dynamics than may be inferred from the vertical profiles of mean velocity, turbulence intensity and Reynolds stresses, which are the quantities usually studied. There is a remarkable similarity in the structure of such flows between the forest canopy and the flume study despite large differences in morphology and stem rigidity. In particular, these results determine an outer flow type arising above 1.5 canopy heights, while turbulent in-rushing events are most significant at the zero-plane displacement. The approach also implies ways in which improved models for canopy turbulence may be developed.

Introduction

The complexity of turbulent flow through vegetation has proven to be a barrier to describing a range of environmental flow phenomena such as carbon dioxide exchange in and over forests [1, 2], seed dispersal by wind [3], as well as carbon retention in rivers and seagrass meadows [4, 5]. As a consequence, it is a topic that has been the focus of much interest in boundary-layer meteorology [6, 7] as well as hydraulic engineering [8,9,10]. The complexity of such flows results from the significant alteration of an already complex boundary-layer physics [11] by the blockage effect of vegetation that at sufficient spatial density, induces strong shear across its upper surface. The aforementioned shear produces coherent flow structures [12] that share striking resemblance to a mixing layer [13, 14]. This, in turn, is complicated by the innate porosity of the canopy. In addition, wake shedding is induced by what is an intrinsically multi-scale, and flexible object (a stand of vegetation). Thus, the length scales involved include the plant stem/trunk diameters, the canopy height and length scales associated with the effective porosity of the array [15], and those associated with plant flexure [16]. In the case of aquatic environments, the limited flow depth imposes an important additional length scale on the flow dynamics [17].

All of these processes induce intermittency to the flow physics, i.e. a spatial and temporal intermittency in the intensity of turbulent fluctuations. This occurs intrinsically in turbulence at small scales because of the action of dissipation on vortical structures [18], and in boundary-layers because of the ejection-sweep cycle [19, 20]. However, it also arises for canopy flows because of the complex nature of the forcing of the flow, which has clear implications for momentum and scalar exchange [21]. Intermittent turbulence excited by multiple scales is also an area of contemporary and fundamental concern [22, 23] and this leads to an absence of equilibrium between turbulence production and dissipation that gives new scaling laws for the cascade dynamics in turbulence [24]. The implications for the role played by vortical structures in these dynamics remains a subject of inquiry (see the recent collection of papers on this theme in Fluid Dynamics Research [25]). The practical consequences of intermittency may be seen in Lagrangian stochastic models in which adding intermittency to the turbulent kinetic energy dissipation rate within canopies creates a semi-heavy tail to the mean concentration far from the scalar source [26].

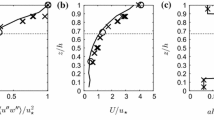
Key features of the vertical structure of depth-limited canopy flows are summarized in Fig. 1 as a function of the vertical coordinate, $x_{3}$, non-dimensionalized by canopy height, h. There is a vertical displacement to the profile for the time mean longitudinal velocity, ${\overline{u}}_{1}$, (the zero-plane displacement), which for the aquatic canopy data used in this study [27] equates to $x_{3} / h \approx 0.7$. A maximum for the longitudinal turbulence intensity for $u_{1}$, where $\sigma (\ldots )$ is a standard deviation, occurs at the top of the canopy. This is also where there is a peak magnitude in the velocity covariance, $\overline{u_{1}^{'}u_{3}^{'}}$, where a Reynolds decomposition of the instantaneous, measured velocity, $u_{i}(t)$, is used

$$\begin{aligned} u_{i}^{'}(t) = u_{i}(t) - {\overline{u}}_{i}. \end{aligned}$$

(1)

Given that the dominant shearing component of the Reynolds stress tensor in a boundary layer is $\tau _{13} = -\rho \overline{u_{1}^{'}u_{3}^{'}}$, where $\rho$ is the fluid density, this peak equates to a maximum for the turbulent stress. These and other features of canopy flow are discussed further in the review paper by Nepf [28].

Fig. 1

Sketch of the flow structure in a canopy flow according to the classification by Ghisalberti and Nepf [27]. The wake, exchange and shear zones are delimited at $x_{3}/h \in \{0.4, 1.0, 2.5\}$ by black dotted lines, where h is the canopy height (137 mm for the hydrodynamic data). The thin, vertical, black lines are origins for the variables shown and $L_{sh}$ denotes the shear layer thickness. From left to right we show typical vertical profiles for the mean longitudinal velocity, ${\overline{u}}_{1}$, velocity covariance, $\overline{u_{1}^{'}u_{3}^{'}}$, and turbulence intensity, $\sigma (u_{1})$

The aim of this study is to highlight new features of the vertical structure of canopy turbulence by using a technique developed to elucidate aspects of the coherent motion and associated intermittency of turbulence from single-point measurements [29]. The passage of coherent structures through the sensing region are thought to be responsible for intermittent behavior at large scales, which may differ from the intermittency associated with fine-scale dissipation in the energy cascade that arises even for locally homogeneous and isotropic turbulence [18]. The dynamics of such large-scale coherent structures are often studied based on the eigenvalues (or the invariants) of the velocity gradient tensor [30,31,32,33]. However, typical field instrumentation used in environmental turbulence research obtains velocity data at a single-point, and (planar) gradients are often surrogated to Taylor’s frozen turbulence hypothesis. This means that the velocity gradient tensor is usually inaccessible, and the variables shown in Fig. 1, or closely related terms, are those typically studied. By studying intermittency in the flow, anchored to single-point statistics, we can obtain information on the dynamics that complements that obtained from conventional analyses.

It was observed in earlier work that the pointwise Hölder regularity of the velocity time series (a measure of the intermittency of the time series signal, defined more formally, below) was highly correlated between velocity components [34], and that the dimensionality of “active periods” within the flow could be determined using this measure [35]. From these observations a velocity-intermittency technique has been developed to illustrate the difference in turbulent structure between jets, wakes, and boundary-layers [29], and to show how the flow over bed-forms and in the wake of wind turbines has a unique structure compared to these canonical flows [36,37,38]. In this study, the technique is further developed and applied to both atmospheric and aquatic vegetation flows to unfold their common characteristics, thereby opening up the possibility to formulate new Lagrangian models for turbulent canopy flows.

Turbulence and intermittency

Fig. 2

Velocity time series realized from two different Hölder functions are shown in a and c. In the upper instance, a fractional Brownian motion (fBm) is generated with a constant Hölder exponent of $\alpha _{1} = 1/3$ where, as described in greater detail in the text, $|u_{1}(t) - u_{1}(t+\delta t)| \sim C|\delta t|^{\alpha _{1}(t)}$. This fBm has the same second moment increment statistics as turbulence. In the lower case the velocity series is a multifractional Brownian motion (mBm) realized from a sinusoidal Hölder function with a mean value of $\alpha _{1} = 1/3$ and an amplitude of 0.1. Regions of relatively smooth and rough behavior correspond to high and low values, respectively. Panel b shows how Hölder exponents are estimated for a fBM with $\alpha _{1} = 1/3$ at $t = 0$. The solid, dot-dashed and dashed curves are for $|t - t_{0}|^{0.15}$, $|t - t_{0}|^{0.33}$, and $|t - t_{0}|^{0.51}$, respectively. It is clear that it is $\alpha _{1} = 1/3$ that bounds the signal. Panel d showns the histograms for the increments of the two $u_{t}$ series for $\delta t = 1.221 \times 10^{-4}$ with a logarithmic ordinate. The fBm results are shown with a solid line and those for the mBm with a dot-dashed line. The respective kurtosis values are 2.99 and 6.22

Describing their experimental study in 1949, Batchelor and Townsend stated

“These space variations in activation can be described as fluctuations in the spectrum at large wave-number...As the wave-number is increased the fluctuations seem to tend to an approximate on-off, or intermittent variation.” [39].

This notion of intermittency in turbulence was implicit in Kolmogorov’s reworking of his 1941 theory to deal with Landau’s objection [40], and Frisch and co-workers provide a useful study of the history of this issue [41]. It was only later that the change from a Gaussian to a log-normal distribution for the dissipation rate was shown explicitly to induce intermittency, and Kolmogorov’s mathematical argument was re-framed as a physical process, whereby the passage of flow structures through the sampling volume would result in longer tails to the increment statistics, as a consequence of large magnitude variations. This may be characterized in terms of the kurtosis (fourth moment) of the velocity increments, $\varDelta u_{1}(\delta t) = u_{t+\delta t}-u_{t}$, at a particular $\delta t$ as shown in Fig. 2d, where the increment kurtosis for the non-intermittent fractional Brownian motion (fBm) shown in Fig. 2a is 2.99 (similar to the value of 3.0 for a Gaussian), while it is 6.22 for the multifractional Brownian motion (mBm) shown in Fig. 2c. This latter signal switches between more ($\alpha _{1} < \frac{1}{3}$) and less ($\alpha _{1} > \frac{1}{3}$) active periods in anti-phase with the generating Hölder function.

A more revealing way to think about intermittency is to consider all $\delta t$ (or strictly, a spatial increment, $\delta r$, rather than temporal increment). This can be achieved using the structure functions for absolute velocity increments [42, 43]. For $n > 1$, the nth order statistical moment for the magnitude of these increments is

$$\begin{aligned} |\varDelta _{n}| = \langle |\varDelta u_{1} |^{n}\rangle , \end{aligned}$$

(2)

where the angled braces are a statistical expectation. For large $\delta r$, the mean-squared velocity fluctuations impact $\varDelta _n$ whereas for very small $\delta r$, velocity gradients dominate $\varDelta _n$. For intermediate $\delta r$, the structure function of order n is given by the power law dependence of $\varDelta _{n}$ on separation $\delta r$,

$$\begin{aligned} \varDelta _{n} \propto \delta r^{\xi _{n}}. \end{aligned}$$

(3)

In Kolmogorov’s original, monofractal formulation, the dependence between $\xi _{n}$ and n is linear according to $\xi _{n} = \frac{1}{3}n$. Thus, the 2/3 law for the scaling exponent of the second moment and the 4/5 law proscribing the coefficient for the third moment, [44], are recovered precisely, where the latter is written as $\langle \varDelta u_{1}^{3}\rangle = - \frac{4}{5} \epsilon r$. Intermittency induces a convexity to this relation and a variety of statistical models have been developed to characterize this curve [18, 45, 46]. We have previously shown how a complex, multi-scale forcing to a flow (as happens in a canopy) induces a departure of this relation from the linear form, indicating the importance of intermittency [47]. This statistical scaling approach is one of the means for providing overall intermittency characteristics for a dataset, but is not able to provide at-a-point results for all $\delta t$. Hence, as outlined below, we utilize a pointwise Hölder exponent to convey this information.

Classical theory for locally homogeneous and isotropic turbulence hypothesizes an independence between the magnitude of turbulent longitudinal velocity in time t, $u_{1}(t)$, and the magnitude of the velocity increments $|\varDelta u_{1}(\delta t)|$ [48]. Note that this result is not between $u_{1}(t)$ and $\varDelta u_{1}(\delta t)$ as these cannot be linearly independent as a consequence of the limiting form for the correlation at large $\delta t$, [49]. This can be shown by writing down the correlation coefficient and then taking the limit that $\langle u_{1}(t)u_{1}(t+\delta t)\rangle = 0$ at large $\delta t$:

$$\begin{aligned} \rho (u_{1},\varDelta u_{1})&= \frac{\langle u_{1}(t)u_{1}(t+\delta t)\rangle - \langle u_{1}(t)^{2}\rangle }{\sqrt{\langle u_{1}(t)^{2}\rangle } \left( \langle u_{1}(t+\delta t)^{2}\rangle + \langle u_{1}(t)^{2}\rangle - 2 \langle u_{1}(t)u_{1}(t+\delta t)\rangle \right) ^{1/2}}, \end{aligned}$$

(4)

$$\begin{aligned}&= \frac{ - \langle u_{1}(t)^{2}\rangle }{\sqrt{\langle u_{1}(t)^{2}\rangle } \left( \langle u_{1}(t+\delta t)^{2}\rangle + \langle u_{1}(t)^{2}\rangle \right) ^{1/2}}\,\,\,\text{ as }\,\, \delta t \rightarrow \infty ,\nonumber \\&= -\sqrt{2} / 2. \end{aligned}$$

(5)

Kolmogorov’s revised theory not only permitted intermittency to emerge in the velocity increment statistics, but also stated that a dependence between the increments and the flow macrostructure was possible [40]. The relation between $|\varDelta u_{1}(\delta t)|$ and $|u_{1}|$ was studied by Praskovsky and co-workers [50], who were concerned with the Tennekes random-sweeping decorrelation hypothesis, which implies an independence between large-scale motions (governed by the velocity, $u_{1}$) and small-scale motions, governed by $\varDelta u_{1}$. Analysis of the correlation between these terms led to the conclusion that such a dependence is significant, and consistency with Kolmogorov’s ideas required an additional dependence such that the small scale excitations were coupled to a large-scale velocity. Taking a different approach, theoretical analysis has shown a dependence between the velocity increments and the local velocity sum [51]. Using a Fokker-Planck equation for the evolution of the probability density function of the conditional velocity increments, it has also been shown that further conditioning on the velocity can improve the convergence of results [52].

This conditional distribution function technique [52] is suited to the analysis of long experimental datasets consisting of millions of samples, but converging the statistics when further conditioning is undertaken on the velocity is difficult. In addition, in environmental fluid mechanics, sampling strategies are typically designed to capture the spatially inhomogeneous nature of the flow, meaning that obtaining samples for millions of integral scales is not feasible. This is even more the case in field studies where stability or flow discharge are unlikely to be stationary for such durations. Hence, a velocity-intermittency analysis framework better suited to the study of shorter duration time series has been proposed for [29] and applied in various experimental and numerical contexts [20, 38, 53].

Pointwise Hölder exponents and their estimation

Instead of the structure functions, an alternative means of characterizing intermittency in turbulence is in terms of the multifractality of the flow field, or equivalently, the sets of pointwise Hölder exponents, $\alpha _{1}(t)$, present in the measured field [54,55,56]. Informally, this can be thought of as saying that the 2/3 exponent in Kolmogorov’s original theory [48] yields a time series with a constant ${\overline{\alpha }}_{1}= 1/3$ (a monofractal, as seen in Fig. 2a). The presence of significant variations in $\alpha _{1}(t)$ introduces intermittency and indicates that the time series may be characterized as a multifractal process as seen in Fig. 2c. These various concepts are unified by the Frisch-Parisi conjecture [42], which states that

$$\begin{aligned} D(\alpha _{1}) = \min _{n} (\alpha _{1} n - \xi _{n} + 1), \end{aligned}$$

(6)

where $D(\alpha _{1})$ is the set of pointwise Hölder exponents, and $\xi _{n}$ is the structure function scaling exponent. When $D(\alpha _{1})$ admits more than one value, there will be periods when the signal contains a high degree of relative variability and $\alpha _{1}(t)$ is relatively small, and periods where the flow field is much smoother ($\alpha _{1}(t)$ is relatively large).

While the terms in (6) provide summary measures of the behaviour of a full dataset, we require the Hölder function, i.e. the pointwise Hölder exponents at each point in time. The definition of $\alpha _{1}(t)$, proceeds from consideration of the differentiability of a function relative to polynomial approximations about a location of interest, $t_{0}$. For turbulence, where we are studying variations in the first derivative then, necessarily, $0< \alpha _{1}(t) < 1$. For the longitudinal velocity component, we have that [57]:

$$\begin{aligned} |u_{1}(t) - u_{1}(t+\delta t)| \sim C|\delta t|^{\alpha _{1}(t)}. \end{aligned}$$

(7)

Figure 2b shows a fBm series with $\alpha _{1} = 0.33$, together with $|\delta t|^{0.15}$, $|\delta t|^{0.33}$, and $|\delta t|^{0.51}$, where it is clear that the appropriate choice of $\alpha _{1} = 0.33$ bounds the increment statistics. There are various ways in which the $\alpha _{1}(t)$ may be estimated, including time- and wavelet-based methods [55, 58]. In a previous study we tested a number of such methods [59], and found that a rapid and precise method is based on a log-log regression of the signal oscillations, $O_{t_{0} \pm \varDelta _{t}}$ against $\varDelta _{t}$ [60]:

$$\begin{aligned} O_{t_{0} \pm \varDelta _{t}} = \text{ max } \, (u_{t \in (t_{0}-\varDelta _{t},\ldots ,t_{0}+\varDelta _{t})}) - \text{ min } \, (u_{t \in (t_{0}-\varDelta _{t},\ldots ,t_{0}+\varDelta _{t})}), \end{aligned}$$

(8)

where $\varDelta _{t}$ is distributed logarithmically. As explained by Peltier and Lévy Véhel [61], this approach can be linked to a windowed variance ($\sigma _{u}^{2}$) operation because

$$\begin{aligned} \frac{u_{t+\varDelta _{t}} - u_{t}}{\varDelta _{t}^{\alpha _{1}}} \underset{\varDelta _{t} \rightarrow 0}{\rightarrow }N(0,\sigma (u_{1})^{2}), \end{aligned}$$

(9)

where $N(\ldots )$ is the normal/Gaussian distribution. The left-hand side of (9) shows why (8) is an appropriate means to estimate the pointwise Hölder exponent: the log-log regression probes the $\varDelta _{t} \rightarrow 0$ limit that gives $\alpha _{1}(t)$. Note that this statement is purely about the efficacy of the fitting method; it does not constrain results to a Gaussian distribution. This finding can be seen in panel (d) of Fig. 2, where the fractional Brownian motion yields Gaussian increment statistics but the intermittent, multifractional Brownian motion generates increments at the same $\delta t$ with a kurtosis of 6.22.

Velocity-intermittency quadrant analysis

With a well-resolved time series for $u_{1}(t)$ and using the oscillation method described above, it is possible to obtain $\alpha _{1}(t)$. The proposed technique for studying the mutual coupling between velocity and intermittency adopts the framework of quadrant analysis commonly used in boundary-layer studies for disaggregating contributions to the Reynolds stress, $\tau _{13}$ [62]. Thus, as is well-known, ejections (quadrant 2: $u_{1}^{'} < 0; u_{3}^{'} > 0$) and sweeps (quadrant 4: $u_{1}^{'} > 0; u_{3}^{'} < 0$) dominate the statistics near the wall in a boundary-layer, resulting in positive Reynolds stresses [63]. The positive Reynolds stresses seen at $x_{3} = h$ in Fig. 1 imply related processes arise at the top of the canopy [27, 64, 65]. Clearly, any relation between conventional quadrants and our formulation depends on the extent to which variations in $\alpha _{1}(t)$ are coupled to $u_{3}^{'}(t)$. Following the argument that the active periods in the flow, defined as when $\alpha _{1}^{'} < 0$ [35], reflect the passage of flow structures through the sampling volume of the probe [18], then near the wall in a boundary-layer one might expect a positive or negative correlation depending on whether or not ejections or sweeps are more strongly associated with strong vortical motions at the height of the probe.

Note that our examination of the correlation between $u_{1}(t)$ and $\alpha _{1}(t)$ has an analogy with the work of Praskovsky and co-workers on the correlation between $u_{1}$ and $\varDelta u_{1}$ discussed in Sect. 2. However, breaking the joint velocity-intermittency distribution into quadrants provides greater information on this behavior and has an analogy with the manner in which conventional quadrants give a greater insight into the processes underpinning the generation of Reynolds stresses.

Fig. 3

A thirty second segment from one of the ninety six time series for $u_{1}^{*}(t)$ from the hydraulic flume experiment (black line in the main panel). Accompanying this time series is that for $\alpha _{1}^{*}(t)$ (red line). The measurement was made on the central location of the three transverse sampling positions at a height of $x_{3} / h = 1.49$. The lower panel gives the time series for the hole size, H(t), with any occurrence of $H \ge 2$ shown. Gray vertical lines of four types then delimit the quadrants defined in this study based on the joint distribution for $u_{1}^{*}(t)$ and $\alpha _{1}^{*}(t)$: dot-dashed = Q1; dashed = Q2; dotted = Q3; solid = Q4

Fig. 4

An illustration of the two basic forms for analysis used in this study. Panel a shows the velocity-intermittency quadrants, with example data plotted in this space as black points and two hole sizes ($H \in \{1,2\}$) shown as gray, solid and dot-dashed lines, respectively. Panel b is a polar histogram (rose diagram) of the results in a at $H = 0$

Table 1 A summary of the properties of the velocity-intermittency quadrants used in this study

The quadrant representation is re-cast in terms of dimensionless, centered and standardized variables, $u_{1}^{*}(t)$ and $\alpha _{1}^{*}(t)$, based on the dimensionless variables

$$\begin{aligned} u_{1}^{*}(t)&= \frac{u_{1}^{'}(t)-{\overline{u}}_{1}}{\sigma (u_{1})}, \nonumber \\ \alpha _{1}^{*}(t)&= \frac{\alpha _{1}^{'}(t)-{\overline{\alpha }}_{1}}{\sigma (\alpha _{1})}, \end{aligned}$$

(10)

as summarized in Table 1. As with standard quadrant analysis, a threshold hole size H is introduced such that an exceedance occurs when $|u_{1}^{*}(t)\alpha _{1}^{*}(t)| \ge H$ (i.e. a hyperbolic hole). The upper panel of Fig. 3 shows a short segment for $u_{1}^{*}(t)$ and $\alpha _{1}^{*}(t)$ at $x_{3} / h = 1.49$, with the lower panel showing the points in time where $H = 2$ is exceeded. The standard deviation of the $\alpha _{1}^{*}(t)$ series for this record is $\sigma (\alpha _{1}) = 0.042$, which was the 12th smallest from the 96 datasets, yet periods with varying intermittency can be observed as described in the next paragraph. We demonstrate the strong degree of statistical significance of these results for even this relatively weak degree of intermittency in the “Appendix”.

The ten vertical lines in Fig. 3 highlight the major exceedances of this threshold, which illustrate all four types of quadrant event. This figure illustrates the difference between smooth and rough behavior as seen, in particular, by comparing the sudden changes in velocity that occur at $t = 205.5$ s which produce the minimal values for $\alpha _{1}^{*}(t)$ seen in this segment, with the more gradual variation seen at $t = 200$ s which results in the maximal values for $\alpha _{1}^{*}(t)$. Because $u_{1}^{*}(t) > 0$ in the latter case a Q1 event occurs (dot-dashed line). The two events highlighted at $t \sim 205.5$ s are both where $u_{1}^{*}(t) < 0$, giving a Q3 response. At $t \sim 183$s, pronounced local variability in the velocity occurs when $u_{1}^{*}(t) > 0$ resulting in a Q4 occurrence (solid gray line), while the extended region of relatively low velocity variability from $187\text{ s } \lesssim t \lesssim 193$ s occurs when $u_{1}^{*}(t) < 0$, showing Q2 behavior (dashed lines).

In addition, an example dataset with choices for the hole size of $H = 1$ and $H=2$ are shown in Fig. 4a. The proportion of time that the flow occupies the ith quadrant, $p_{Qi}(H)$, may then be determined as function of H and normalized at each H such that $\sum _{i = 1}^{4} p_{Qi} | H = 1$. Hence, the importance of four relative flow states at different distances from the center of the joint distribution function for velocity-intermittency is delineated and may be used to elucidate the different nature of turbulence for various flows (Fig. 5). To summarize the $p_{Qi}(H)$ relation with H, we return values for the slope, $dp_{Qi}/dH$ [37]. Thus, a large positive value of $dp_{Q}/dH$ in a particular quadrant implies that in the limit of the high H (i.e. extremum states), this quadrant dominates the velocity-intermittency relation. This approach to analyzing turbulence has also been used to study the amplitude modulation of small scale turbulence by the larger scales in neutral turbulent boundary layers [20].

Fig. 5

An analysis of velocity-intermittency for various experiments. The data for flow over mobile bedforms [36] are shown as a solid black line, while other lines correspond to data from a turbulent jet experiment [66] (red), wake data at 8.5 $\hbox {ms}^{-1}$ (gray dotted) and 24.3 $\hbox {ms}^{-1}$ (gray) [67], and data below 150 wall units (solid lines) and higher into the flow (dotted lines) at 6 $\hbox {ms}^{-1}$ (blue) and 8 $\hbox {ms}^{-1}$ (green) for a neutral boundary layer [47]. This figure is modified from: Keylock, C.J., Singh, A., Foufoula-Georgiou, E. 2013. The influence of bedforms on the velocity-intermittency structure of turbulent flow over a gravel bed, Geophysical Research Letters 40, 1-5, doi:10.1002/grl.50337. (copyright American Geophysical Union) and is reproduced with the permission of the AGU

For a given H, more detail on the distribution of data in a given quadrant can be determined using a polar/angular histogram, or rose diagram. Thus, with each quadrant allocated a range of angles, $\theta$, as stated in Table 1, the angular histogram illustrates if $u_{1}^{*}$ or $\alpha _{1}^{*}$ is driving the behavior in that quadrant. In this study, all rose diagrams include all the data recorded unless otherwise stated. That is, they are defined for $H = 0$. An example of such an analysis is shown in Fig. 4b for the data in Fig. 4a. Thus, the mode for these data ($p = 0.041$) lies in quadrant Q2 (where $\frac{\pi }{2} < \theta \le \pi$) and, because it is at $0.8\pi$, lies nearer the $u_{1}^{*}$ axis than the $\alpha _{1}^{*}$ axis.

Experimental data and analysis

Two published sources (laboratory and field data) are used to compute the velocity-intermittency interactions. The first are based on flume measurements through model vegetation designed to be dynamically similar to eelgrass (Zostera marina), with 15 mm high stems (6.4 mm diameter) and six blades per stem made from polyethylene film, which were 203 mm by 3.8 mm by 0.2 mm [27]. The flume data were obtained with an acoustic Doppler velocimeter, sampling at 25 Hz, at three horizontal positions transverse to the longitudinal direction, $x_{1}$. The flow was fully developed by this point and measurements were made at 32 heights from 3.9 mm to 391 mm (flow depth of 467 mm). The association of each height to a specific flow zone is given in Fig. 1. The field measurements were collected at the Duke forest (near Durham, North Carolina) and obtained at a single point about 3.2 m above a stand of $h = 17$ m tall Loblolly pine [64, 68]. Hence, the forest data were obtained at 1.19h, which is equivalent to 163 mm in the flume study, where the deflected meadow height $h = 137$ mm. The velocities in the field experiment were sampled at 10 Hz using a triaxial sonic anenometer (CSAT3, Campbell Scientific, Logan UT) for unstable conditions (with a negative Obukhov length). For both datasets, three orthogonal velocity components were measured and rotations were undertaken so that ${\overline{u}}_{2} = 0$ and ${\overline{u}}_{3} = 0$) for the forest data and $\langle {\overline{u}}_{2}\rangle = 0$, $\langle {\overline{u}}_{3}\rangle = 0$ for the flume data, where the outer braces indicate an average over all positions. Because the distance from a vegetative stem for the three transverse positions in the hydraulic flume at a given vertical position, $x_{3}$, was not fixed, we focus on results averaged over these three transverse positions.

Results

Fig. 6

Rose diagrams indicating the probability of different velocity-intermittency quadrants and the orientation of data, $\theta$, on the $u_{1}^{*}$ and $\alpha _{1}^{*}$ axes for $H = 1$. Results are amalgamated over the three transects and are shown for six choices of $x_{3}/h$ in the first two columns, with height increasing from bottom to top and then left to right. Results in the last two columns are averages over replicated experiments for five vertical positions in a neutral, turbulent boundary-layer for a momentum thickness Reynolds number of 70,000 [47] and range from 5% of the boundary-layer height, $x_{3}/BL$, to 77%, or if non-dimensionalized by the shear velocity and fluid viscosity, then $50 \le z^{+} \le 750$. The radii are plotted in units of 0.02 probability, and extend to a maximum of $p = 0.012$ for the canopy data and $p = 0.08$ for the boundary-layer data

The vertical profiles for the mean velocity, turbulence intensity, and Reynolds stresses for the hydraulic flume data were published previously [27] and are summarized in Fig. 1. Angular histograms (rose diagrams) are used to summarize the velocity-intermittency results at a hole size of $H = 1$ for the hydraulic flume data at six vertical positions in the first two columns of Fig. 6. These may be compared to boundary-layer turbulence data [47] obtained at six vertical positions in the right-most two columns of Fig. 6, also at $H = 1$, and also based on a use of forty bins for the histogram over the $2\pi$ interval. In both cases, as one moves away from the wall (working through each set of panels from bottom to top and then left to right), there is a transition from the dominance of Q2 or Q4, to dominance by Q1 or Q3. The rose diagram within the wake zone ($x_{3}/h < 0.4$) closely resembles that for the boundary-layer at $x_{3}/BL = 0.051$, or $z^{+} \sim 50$, where BL is the boundary-layer thickness. However, $x_{3}/h = 0.49$ there is an increasing concentration of values in Q2 and Q4 than seen very near the wall. This trend continues with height, reaching a maximum at the top of the exchange zone ($x_{3}/h = 1.00$). A transition in the velocity-intermittency structure is clearly taking place at $x_{3}/h = 1.49$ and by $x_{3}/h = 2.02$ the transition to Q1 and Q3 dominance has occured. As height increases further, there is an increasing emphasis on Q3 dominance. That there is a stronger tendency for the canopy data to occur within a single bin for the histograms is clear from the extent of the radii, which extend to $p = 0.012$ for the canopy data, but only $p = 0.08$ for the boundary-layer.

The changes in velocity-intermittency structure shown in Fig. 6 are not readily discernible from the velocity and Reynolds stress profiles used to derive the classification in Fig. 1. That the velocity-intermittency results highlight different aspects of the flow structure compared to more conventional variables has been shown previously for the case of flow over bed-forms [37].

Fig. 7

Profiles of median values for $dp_{Qi}/dH$ for each velocity-intermittency quadrant are shown in the upper set of panels. The hydraulic flume data are shown by crosses (pluses if the range of values across the three transverse profiles crosses zero) and the Duke Forest data by a large circle. The short, horizontal lines indicate $\pm \,1.96$ residual standard deviations for the fitted data. The vertical dash-dotted line highlights the origin, while the horizontal, dotted lines correspond to the values for $x_{3}/h$ delimited in Fig. 1. The horizontal, dashed line indicates a key transition based on the velocity-intermittency results. The symbols in the region $x_{3}/h < 0$ are the $dp_{Qi}/dH$ results by quadrant for the data shown in Fig. 5 [36]. Data shown are for a turbulent jet (*), the far-wake of a circular cylinder (diamond), boundary-layer with $z^{+}\lesssim 150$ ($\triangledown$), boundary-layer where $z^{+}>700$ ($\vartriangle$), and data for flow over bed-forms ($\square$). The labels (i) and (ii) highlight features discussed in the text

Looking at the results as a function of hole size, profiles of $dp_{Qi}/dH$ for each quadrant, i are shown in Fig. 7. A horizontal, dashed line at $x_{3}/h = 1.5$ delimits the change to Q3 dominance, as measured by large and positive slopes, which may also be discerned in the rose diagram results in Fig. 6. The vertical structure is therefore characterised by Q4 dominance near the wall, which reaches a maximum at $x_{3}/h \sim 0.7$, indicated by (i) in Fig. 7 (i.e. at the mid-height of the exchange zone and similar to the zero-plane displacement). Above this height, the $dp_{Q4}/dH$ slopes decay to attain zero at the canopy height, $x_{3}/h = 1.0$. There is then a region of weaker Q2 dominance for $1< x_{3}/h < 1.5$ shown by label (ii), before the emergence of Q3 dominance in the outer part of the shear zone, which has an approximately constant value for $x_{3}/h > 2.0$. That no particular quadrant is dominant at $x_{3} / h =1.49$ is shown in a qualitative fashion by all four quadrant types exceeding $H = 2$ in Fig. 3 in a short time duration.

It is notable that the $dp_{Qi} / dH$ are large compared to the values for the canonical turbulent flows shown in Fig. 5, with their slopes summarized beneath the origin in each panel of Fig. 7. The maximum median value for $dp_{Q2} / dH$ over the three transects that data were obtained, indicated by the (ii), is $dp_{Q2} / dH > 0.1$ and is near double that for a jet (asterisk), which is the only canonical flow with $dp_{Q2} / dH > 0$. For Q3, the equivalent result of $dp_{Q3} / dH \sim 0.2$ is double that found for flow over bed-forms (square) and for a boundary-layer far from the wall (triangle), while the peak value for $dp_{Q4} / dH$, indicated by the (i), is even more extreme; some three times larger than that for a boundary-layer near the wall (downward triangle).

Fig. 8

Rose diagrams are shown in a for the data from the Duke Forest ($x_{3}/h = 1.19$) in black and the data closest to these from the flume experiment in terms of the root-mean square error (RMSE) between the rose diagrams (which occurred at $x_{3}/h = 1.06$) in gray. The vertical variation in the RMSE between the flume data and the Duke Forest data (expressed in terms of a difference in values for $\text {d}p_{Q}/\text {d}H$ for each quadrant) is shown in panel b

The Duke Forest data are compatible with the hydraulic data at similar dimensionless height for this analysis, exhibiting positive slopes for both Q2 and Q4 as indicated by the circles in Fig. 7. These data are also shown in Fig. 8a in rose diagram form as black lines. The smallest root-mean squared error (RMSE) between the $\text {d}p_{Q}/\text {d}H$ values for the Duke Forest and the hydraulic data in Fig. 7 was for a site at $x_{3}/h = 1.06$ as shown in Fig. 8b. The rose diagram for this location is given by the gray line in Fig. 8a. Given that the height of the canopy for both datasets varies in space and time, it can be seen from Fig. 8b that the rose diagrams for the hydraulic data are a good fit to the forest data for several choices of $x_{3}/h$ close to the canopy height, including the height where the forest measurements were made ($x_{3}/h = 1.19$). These heights are where $dp_{Q2} / dH$ dominates the statistics, i.e. the nature of the joint velocity-intermittency distribution function at high H is dictated by relatively slow moving flow events that have relatively low turbulence intensities compared to the mean characteristics at these heights.

Discussion

A previous study using the hydraulic flume data analyzed in this paper found that the Reynolds stresses and turbulence intensities attain maxima at $x_{3}/h = 1.0$ [27], as shown in Fig. 1, which is a distillation of the results from that paper. The velocity-intermittency relations have the strongest tendency to be dominated by a single quadrant (Q4) at $x_{3}/h \sim 0.7$ (the (i) in Fig. 7). However, the specific height of this peak is likely dependent on canopy density as it appears to correspond to the zero-plane displacement, which typically varies inversely with canopy density (e.g. see Fig. 4 in the study by Luhar et al. [69]). The rose diagrams in Fig. 6 show that these Q4 data reside preferentially between $7\pi /4$ and $2\pi$, i.e. it is $+u_{1}^{*}$ rather than $-\alpha _{1}^{*}$ that contributes more strongly to this relation. Hence, the occasional in-rush of fast flow that has swept up turbulent structures is driving this mechanism. Because $dp_{Q}/dH$ is still strongly positive for Q4 at $x_{3}/h = 0.2$, either these intense events can penetrate this far into the canopy, although at a decreased frequency, or a similar sweeping mechanism is originating within the canopy, with the former explanation more probable [69]. Above $x_{3}/h = 0.7$, larger values for $u_{1}^{'}$ make these Q4 events less extreme relative to the background flow state, causing the strength of $dp_{Q4}/dH$ to decline. The sweeping events detected here are serving a similar function to the “sweep” events that accompany “ejections” near the wall in a boundary-layer [63, 70]. This is why such data (inverted triangle) have the closest signature to the canopy dynamics for Q4 in Fig. 7. Indeed, for $x_{3}/h < 0.2$ we recover a value for $dp_{Q4}/dH$ that is not much greater than this near-wall signature. However, the canopy process is much more intense in its extremes compared to a boundary-layer near the wall, meaning that these sweep events are larger scale phenomena. The implications of this for modeling transport phenomena are that passive scalars and, potentially, inertial particles, are transported greater distances by the turbulence than predicted from a simple representation of turbulence as a random forcing. This is considered in Sect. 6, below.

For $0.9< x_{3}/h < 1.5$ there is a region where Q2 events dominate the statistics, indicated by the (ii) in Fig. 7 and shown in the comparison with the forest data in Fig. 8. The rose diagrams show that these values plot preferentially at $\frac{\pi }{2} < \theta \le \frac{3\pi }{4}$. Hence, in contrast to Q4, it is extreme values for $+\alpha _{1}^{*}$ that drive the extreme states. For the canonical flows, Q2 dominance is a feature of a turbulent jet (asterisk), rather than a wake, for example (diamond), and this is caused by the entrainment of quiescent flow as the jet expands. Given the high turbulence production and increasing velocity for $0.9< x_{3}/h < 1.5$, the origin of these Q2 events is the extrusion of slower moving, relatively quiescent fluid from within the canopy into the outer flow, i.e. the ejection-like events that correspond to the sweep-like events already described. However, there is a major difference in the nature of these events: boundary-layer ejections are slow moving but intensely turbulent leading to a Q3 dominance (the upward triangle in Fig. 7); the ejections in a canopy flow are generated within a region of lower turbulence intensity and move into a region where there is strong shear taking place.

For $x_{3}/h > 1.5$, we are in the outer part of the shear region and the turbulence characteristics have a Q3 dominance, similar to the outer flow over bed-forms (the square in Fig. 7). Hence, shearing at the top of the canopy (or the crest of the dune) generates turbulence that is advected upwards into the flow, into a higher velocity region, resulting in the turbulent events locally having $u_{1}^{*} < 0$. The rose diagrams in Fig. 6c show that it is these negative $u_{1}^{*}$ states that are more important for the sample higher into the flow ($x_{3} / h = 2.58$). However, as the Q3 dominance emerges as $x_{3}$ increases from the highest samples in Fig. 6b to the lowest in Fig. 6c, the $-\alpha _{1}^{*}$ values are just as important. Thus, in this region in particular, it is important to consider how effective a turbulence closure is likely to be that couples dissipative processes to rates of strain independent of sign.

This pattern of Q4 dominance lower in the flow, through Q2 and then into Q3 is similar to that seen for the velocity-intermittency structure of flow over bed-forms [53]. However, the Q2-dominated region was much more vertically extensive in the dune case, at the expense of the Q4 region. This is explained by the extensive recirculation region that exists in the dune case, resulting in flow beneath a separated shear layer that is relatively quiescent. The absence of a large recirculation region for a porous canopy flow restricts the Q2 realm to a small region immediately above the canopy where flow from within the canopy is extruded. On the other hand, the porous nature of the canopy forces the flow at multiple scales, causing high intermittency [47] and a Q4 dominance that is more extreme than seen for other flows.

Potential implications for modeling canopy flows

As well as highlighting important features of the nature of flow through plant canopies, our work also has implications for the modeling of such processes, which is necessary for improving management of pollutant dispersal in rivers, or understanding of carbon dioxide fluxes in forests. The strong velocity-intermittency coupling we have observed relative to canonical flows impacts upon the modeling of large scale flow structures and causes difficulties for modeling dissipation and pressure-strain coupling in conventional model closures. Such concerns can be seen in efforts to develop Reynolds-averaged Navier-Stokes (RANS) turbulence closures for canopy flows [71]. They also relate to fundamental issues regarding the assumption of equilibrium in many turbulence closures, where production and dissipation balance instantaneously and locally. We have recently discussed several aspects of these phenomena, their connections to flow topology, and their implications for the next generation of models in environmental fluid mechanics [22]. Turbulence closures for RANS that relax equilibrium assumptions have now begun to emerge [72]. Among the defining attributes of canopy turbulent flows are non-Gaussian statistics, highly dissipative rate of turbulent kinetic energy, and the lack of a well-defined inertial subrange in the energy cascade. In certain instances, the role of fine-scale wake generation and its destruction lead to an enhanced intermittency to the dissipation rate above and beyond conventional descriptions from locally homogeneous and isotropic turbulence. This enhanced dissipation rate intermittency is partly due to vegetation-flow (or solid-fluid) interactions that imprint itself at multiple scales - large and small and adds distinguishing features to the temporal intermittency in the velocity statistics studied here. The approach proposed here interrogates these features by comparing velocity intermittency in differing canopies (rods, forest) and several canonical turbulent flows where an inertial subrange exist.

Recent progress in understanding dissipation scalings in turbulence is also relevant for developing new RANS or large-eddy simulation (LES) closures [23, 24]. For example, a recent direct numerical simulation of the Navier-Stokes equations by Goto and Vassilicos [73] using a steady state forcing showed that the variation in the integral scale, $\ell (t)$, was significant and $\approx 90^{\circ }$ out of phase with $\sigma (u)$, which in turn was $\approx 90^{\circ }$ out of phase with the dissipation rate $\epsilon (t)$. Because increases in $\ell (t)$ indicate the presence of large structures that dominate changes in $u_{1}$, and an increase in $\sigma (u)$ causes a decrease in $\alpha _{1}(t)$, thereby enhancing subsequent dissipation in the Goto and Vassilicos study, future experimental work on canopy flows should probe the extent to which our clearly discerned velocity-intermittency coupling in quadrant 4 (in the exchange zone) largely reflects integral scale effects, or incorporates the general phasing between higher macroscale velocities and enhanced dissipation. This is important as the high velocities and low values for $\alpha _{1}'$ potentialy imply that local dissipation is higher here than production, a phenomenon that a closure model for a canopy flow should reflect.

A central tenet of how turbulence dissipates in classic closure models is the empirical relation that the dissipation coefficient $C_{\epsilon } \equiv \epsilon {\mathcal {L}} / {\mathcal {U}}^{3} \approx \text {const}$, where ${\mathcal {L}}$ is a suitable length scale (the integral scale) and ${\mathcal {U}}$ a suitable velocity scale (the root-mean-square velocity). However, the situation when production and dissipation cannot reasonably expected to be in equilibrium due to the complexity of wake interaction leads to very different conclusions [24], with a dependence on the ratio of global and local Reynolds numbers, $\text {Re}_{L}$, seen up to $x_{*} \sim 1.5$, where $x_{*}$ is the wake interaction length scale. Work done so far on this indicates that $C_{\epsilon } \propto \text {Re}_{L}^{-1}$ [74], but it is recognized that this could vary for different forcings [23]. Additional research is needed to determine the precise scaling for canopy turbulence in the exchange and wake zones, given the potential for interaction with boundary-layer structures with their own velocity-intermittency signature, shown by the green and blue lines in Fig. 5 and the triangles in Fig. 7. However, such a scaling can then be readily implemented in to RANS closure equations by replacing $C_{\epsilon } = \text {const}$ with $C_{\epsilon } \propto \text {Re}_{L}^{-k}$, where k captures the canopy turbulence behavior and the local Reynolds number, $\text {Re}_{L} = \sigma (u){\mathcal {L}} / \nu$ is a means to incorporate information on the size of the flow structures and the velocity variability that are clearly related to large-scale intermittency in a manner amenable to time-averaged simulations. An experimental program is then needed to determine values for k as function of vegetation stand age, species type and density would then be needed to provide the appropriate information for such a bespoke, canopy closure scheme.

Table 2 A summary of the key results from this study and their implications for flow modeling

Fig. 9

Horizontal distribution functions for experimental results (crosses and circles) and Lagrangian simulations using six different models: “B” indicates the basic model, while “DI” is that with dissipation intermittency; “CT” includes the crossing trajectories effect, while “IP” is the inertial particle model. This figure is modified from [75] and is reprinted by permission from Springer: T. Duman, A. Trakhtenbrot, D. Poggi, M. Cassiani, and G. Katul, Dissipation intermittency increases long-distance dispersal of heavy particles in the canopy sublayer, Boundary-Layer Meteorol.159, 41-68, copyright, 2016

Intermittency and scalar/inertial particle transport

Because our approach highlights the extremal intermittency conditions that result in skewed Lagrangian statistics, it also provides a potential new means to formulate and test relevant transport models. This large-scale intermittency has implications for transport processes such as seed dispersion [75] and pollutant concentrations [17]. However, our observed dependence of intermittency and, thus, dissipation on the larger scale velocity is suggestive of ways to proceed in the modeling of processes associated with canopy flows. For example, when formulating a Lagrangian stochastic trajectory model for seed dispersion, one may write a Langevin stochastic differential equation for the velocities, $u_{i}$, as a function of time, and a zero-mean, Gaussian, increment $\text {d}W_{j}$, with a variance, $\text {d}t$, sampled independently, in each direction, j

$$\begin{aligned} \text {d}u_{i} = a_{i} \text {d}t + b_{ij} \text {d}W_{j}, \end{aligned}$$

(11)

where a and b are chosen to replicate the small-scale statistics of turbulence, with the former typically written in terms of the Eulerian variances and covariances and the latter in terms of the mean turbulence dissipation rate, $\epsilon _{0}$. In terms of large scale intermittency and the advection term, because $a_{u}$ contains (vertical) spatial derivatives of the Reynolds stress [26], which may be equated to the Lamb vector in Navier-Stokes, $\ell = \varvec{\omega }\times {\mathbf {u}}$, it is clear that in principle, large-scale intermittency induced by flow structures with high vorticity will impact on $a_{u}$. However, to make this explicit requires information on the time varying nature of vorticity, or a time history of velocity covariances where the averaging operation is undertaken at time scales corresponding to the vortical advection rather than the full duration of the dataset.

In terms of the diffusion coefficient, $b_{11} = b_{33} = \sqrt{C_{0}\epsilon _{0}}$ is a means to estimate the diffusion using a mean dissipation rate and $C_{0}$, the scaling constant for the Lagrangian structure function. To incorporate small-scale intermittency, the constant dissipation is replaced by an additional transport equation for the instantaneous dissipation along a Lagrangian trajectory, $\chi = \log _{e}[\epsilon (t) / \epsilon _{0}]$ of the form

$$\begin{aligned} \text {d}\chi = -\frac{\chi - \frac{1}{2}\sigma _{\chi }^{2}}{T_{\chi }}\text {d}t + \sqrt{\frac{2\sigma _{\chi }^{2}}{T_{\chi }}}\text {d}W_{\chi }, \end{aligned}$$

(12)

where $T_{\chi }$ is the Lagrangian integral timescale for the quantity, $\chi$, and $\sigma _{\chi }$ is its standard deviation. Because this is the standard deviation of the logarithm of instantaneous dissipation, Kolmogorov-like, log-normal intermittent dissipation statistics may be obtained [40]. Experiments on particle dispersion were previously undertaken in a hydraulic flume with 0.12 m high, 4 mm cross-section steel cylinders used to represent vegetation [76]. Particles with 3 mm diameter, but variable mass were released at the centre of the canopy test section via a tube that replaced one of the rods [75]. The basic model selected to represent the dynamics of the particle dispersion was based on (11) with a constant drift term used to derive particle trajectories from the velocity data. The first modification was to adjust the mean dissipation rate to account for the crossing trajectories effect where inertial particles pass through different fluid elements under the effect of gravity. The further modification was to model the inertial forces explicitly to obtain particle acceleration statistics. Figure 9 shows the results we obtained in a previous study exploring the utility of these differing model formulations, which are denoted by “B”, “CT”, and “IP”, respectively. The final set of three models were based on (12), and are indicated by “DI”, with the addition of crossing trajectory and inertial particle effects. It is clear from these results that both dissipation intermittency and particle inertial terms are needed to capture the long-tail statistics, with the inertial effect needed to move the mode of the distribution to the right, and dissipation intermittency to increase the mass in the right tail, implying that this effect is of greatest importance for long distance modeling [75]. In order to improve the modeling of long distance dispersion further, the results from this study suggest the next generation of such models should construct an explicit dependence between $\chi$ and $u_{i}$. That is, in the terminology of stochastic processes, $\chi$ is considered as a self-regulating process [77, 78]. This is a topic for future research.

More generally, intermittency in transported scalars is typically greater than for the underlying fluid field as can be seen by postulating a Gaussian velocity field and showing that while the odd moments of the velocity distribution vanish, they do not for the transported quantity, which is a nonlinear function of the flow forcing. This results in a skewness to the distribution function and, therefore a greater potential for intermittency than in the underpinning turbulence field [79, 80]. In canopy turbulence, we have previously demonstrated that intermittency for scalars is significantly greater within the canopy than for the velocity field, and that variability in their amplitudes was less important than the on-off aspect of intermittency measured by the density of the zero-crossings [81]. The distribution function for scalar intermittency was found to consist of two components, with smaller scale variation coupled to variability in the scalar source strength and longer scale variation to turbulence convection. Hence, velocity-intermittency studies such as that undertaken here have the potential to improve model parameterization for scalars as well as inertial particles.

Summary and conclusion

Fig. 10

Sketch of the flow structure in a canopy flow incorporating the results from this study. Many of the features here are as described in Fig. 1. The new results are presented on the right-hand side under the “quadrants” heading and are a synthesis of those for three of the velocity-intermittency quadrants, ($Q_{2}$ to $Q_{4}$). They are shown by the gray solid, dot-dashed, and dashed lines, respectively and labelled at the bottom of the plot. The horizontal, gray dashed lines and italicized labels at $x_{3}/h \in \{0.7, 1.5\}$ delimit features of the turbulence structure revealed by our approach

Velocity-intermittency analysis provides a means to obtain information on turbulence structure from single-point measurements that complements traditional measurements of mean velocity, turbulence intensity and Reynolds stress. For the first time we have applied this method to determine the vertical structure of velocity-intermittency for canopy flows. Our results demonstrate that these effects are strong for canopy turbulence relative to canonical flows and flow over bed-forms. They are also consistent for the aquatic vegetation and terrestrial canopy data. The results are shown in detail in Fig. 7, where there is a comparison to the properties of jets, wakes and boundary-layers, as well as schematically for three of the quadrants in Fig. 10. Compared to the classification based on conventional variables shown in Fig. 1 and reproduced in Fig. 10, velocity-intermittency analysis highlights three key features of the profile. The first is a change at $x_{3}/h = 1.5$ where Q3 begins to dominate the statistics and the outer part of the shear region arises. Thus, in the region where mean velocity is high and Reynolds stresses are correspondingly small, the dominant velocity-intermittency relation is one driven by slower moving, relatively turbulent events. The second is the region between the top of the canopy and $x_{3}/h = 1.5$ where the dominant quadrant is Q2, i.e. slower moving, relatively quiescent fluid structures compared to the sheared flow in this mixing layer region. This attains a maximal dominance of the velocity-intermittency statistics approximately halfway into this region where the turbulence intensity is greatest. The origin for these events is the ejection of fluid from within the porous vegetative canopy. The final major feature is the dominance of Q4 beneath the canopy height, which attains a maximum at $x_{3}/h = 0.7$, close to the zero-plane displacement, where there is an inflection in the mean velocity profile. This is where in-rushing events from higher in the canopy are of particular importance to the dynamics (Table 2).

These results not only add to our knowledge of canopy turbulence, and demonstrate the utility of the velocity-intermittency method for studying large-scale flow structures from single-point measurements, but they also suggest means by which the modeling of environmental turbulence may be enhanced. We have discussed briefly some of the more fundamental aspects that such work reveals, which goes to the heart of current work on nonequilibrium turbulence [22, 24]. However, we have also shown how this information may be used in the future for developing enhanced models for practical problems such as seed dispersion by canopy flows [75]. In this study we have focused on the longitudinal velocity component and its intermittency characteristics, which provides a means to compare a range of flows, as seen in Fig. 5, because this is the most commonly measured velocity component. We have also previously shown that the intermittency is highly correlated across velocity components [34]. However, when one is specifically interested in boundary-layers, there may be an advantage to focusing on the vertical velocity component at the expense of the longitudinal or supplementing classical quadrant analysis (that considers both) with an intermittency variable. This is something to be investigated in future work.

Appendix: statistical significance of observed intermittency

In Fig. 3 we showed an excerpt of the time series for $u_{1}^{*}(t)$ and $\alpha _{1}^{*}(t)$ for the dataset with the 12th lowest degree of intermittency (as measured by the standard deviation of $\alpha _{1}^{*}(t)$) from the 96 samples obtained in the hydraulic flume. The simplest means to test for significant intermittency is using a Fourier phase randomization method where we preserve the Fourier amplitude spectrum of the original signal in the linearized surrogates, but destroy, except by chance, the intermittency, which resides in the Fourier phases [82]. That is, with the discrete Fourier transform of an observed, standardized longitudinal velocity component, $u_{1}^{*}(t)$, given by

$$\begin{aligned} {\mathcal {F}}(\omega ) = \sum _{t=0}^{T-1} u_{1}^{*}(t)\,\, \text {exp}\, \frac{i 2 \pi \omega t}{T}, \end{aligned}$$

(13)

for wavenumber, $\omega$, and dataset duration, T, then this may be re-expressed as

$$\begin{aligned} {\mathcal {F}}(\omega ) = |{\mathcal {F}}(\omega )|\,\, \text {exp}\,\, i \theta . \end{aligned}$$

(14)

The amplitudes of the original signal, $|{\mathcal {F}}(\omega )| / N$ are retained, but the phases for the original signal,

$$\begin{aligned} \theta = -i \,\,\text {ln}\left( \frac{{\mathcal {F}}(\omega )}{|{\mathcal {F}}(\omega )|}\right) \end{aligned}$$

(15)

are replaced by random variants, ${\hat{\theta }}$. The easiest way to do this is to undertake a random shuffle of the $u_{1}^{*}(t)$ to give ${\hat{u}}_{1}^{*}(t)$, take its Fourier transform, and store these phases using equations (13–15). Thus, given that $\hat{{\mathcal {F}}}(\omega ) = |{\mathcal {F}}(\omega )|\,\, \text {exp}\,\, i {\hat{\theta }}$, the inverse Fourier transform yields the series ${\hat{u}}^{*}_{1}(t)$, with the surrogate velocity series given by ${\hat{u}}_{1}(t) = {\hat{u}}^{*}_{1}(t)\sigma (u_{1}) + {\overline{u}}_{i}$. Using the Hölder estimation methods described in the main text, the Hölder series, ${\hat{\alpha }}_{1}(t)$, series may then be obtained from the surrogate velocity series and statistical moments extracted. A significant difference is deemed to exist at a significance level, a, if the value for the standard deviation of ${\alpha }_{1}(t)$, $\sigma [{\alpha }_{1}(t)]$ exceeds that for the $(1/a)-1$ surrogate series $\sigma [{\hat{\alpha }}_{1}(t)]$.

Fig. 11

Vertical profiles of values for $\sigma [\alpha _{1}(t)]$ shown as circles together with the IAAFT surrogate values, $\sigma [{\hat{\alpha }}_{1}(t)]$, with their range given by a horizontal line, and the median as an asterisk. Cases where the intermittency is significantly greater than that contained in the IAAFT surrogates are shown as open circles; while insignificant cases are solid black

Fig. 12

Boxplots of the values for 39 IAAFT surrogates of the values for $d p_{Q}/dH$ for the four quadrants for the data at $x_{3}/h = 1.685$ for the central transect. Values for the data are given by triangles, the median for the surrogates is the emboldened line in the center of the box, the box edges are the lower and upper quartiles and the whiskers extend up to 1.5 times the inter-quartile deviation

An alternative is to use the iterated, amplitude adjusted Fourier transform (IAAFT) method to impose both the Fourier amplitudes, and the original time series values, while randomizing the Fourier phases as described above [83, 84]. This approach has been applied in a variety of ways for studying nonlinear time series generated by turbulence [35, 85, 86] although this is not just a test for intermittency; it is a test for intermittency given that the velocities of the synthetic data are sampled from the same distribution as the original data, and Fig. 2d and the associated discussion make this explicit: As the velocity and its derivatives are co-constituted by the flow to some extent [41, 51], imposing the velocity distribution on the synthetic data implies finding a significant difference will be more difficult than a test based on phase-randomized synthetic data alone.

Using this approach, we obtain the results in Fig. 11 where significant differences in the standard deviations are shown by the open circles and insignificant results are given by the solid black circles. Results are shown for all three transects as the variability in the distance between the probe and the stems at a given height induces different degrees of intermittency. At all heights apart from that marked with an arrow ($x_{3}/h = 1.685$) there is at least one transect where a significant difference is found at the 5% level. Expressing the distance between $\sigma [\alpha _{1}(t)]$ and the mean for $\sigma [{\hat{\alpha }}_{1}(t)]$ in multiples of the standard deviation for $\sigma [{\hat{\alpha }}_{1}(t)]$, there were only two $x_{3}/h$ where the average over all transects at a given height was less than 1.96 (critical value for a 5% significance level): $x_{3}/h \in \{1.685,2.299\}$. Overall, the average was 4.54.

Because our method probes more than the second moment of the distribution function of the Hölder exponents, it is still possible to obtain significant results for the velocity-intermittency structure relative to IAAFT surrogate data with no significant difference for $\sigma [\alpha _{1}(t)]$. An example is given in Fig. 12, which shows the velocity intermittency quadrant structure for $x_{3}/h = 1.685$ on the central transect as triangles and that for the IAAFT surrogates of these data as boxplots. In this case it is clear that even though $\sigma [\alpha _{1}(t)]$ may not exhibit a significant difference, the velocity-intermittency structure does so.