1 Introduction

Standing waves within enclosed and semi-enclosed bodies of water are known as seiches and are divided into two categories: shorter period, lower amplitude barotropic (surface) seiches where the free surface of the water oscillates and the restoring force is due to the relative density difference between air and water, and longer period, higher amplitude baroclinic (internal) seiches, where oscillation of the thermocline occurs and the restoring force is due to the relative density difference due to varying water temperature between the hypolimnion and epilimnion [1, 2]. For both types of seiche the restoring force is gravity. The traditional view of surface seiches is that their periods are dependent on the bathymetry of the lake basin and on the effects of gravity and Coriolis forces [3], with the primary damping of seiches being due to frictional effects between the water mass and the lake bed. Cushman-Roisin et al. [4] further shows that the stratification also influences both the period and damping of surface seiches, due to the interference which develops between internal and surface seiches of differing periods.

Surface or barotropic seiches are typically associated with wind stress acting on the surface of a lake, causing upwelling of the water at the leeward end of the water body. The magnitude of this upwelling is influenced by factors including wind direction, lake orientation, depth, bathymetry and shear stress at the air–water and sediment–water interfaces. The effect of this upwelling and the subsequent seiche can be catastrophic under extreme atmospheric conditions and may lead to flooding of locations in both the leeward and windward shores, damage to structures along or within the lake perimeter [5], and damage to boats caused by seiche action within harbors and enclosed coastal bays [6,7,8]. Once the forcing subsides or undergoes a significant change in magnitude or direction, the water oscillates as a standing wave. The oscillation is damped through two primary mechanisms; friction at the boundary layer of the lake (sediment–water and air–water interfaces) and internal friction between water molecules [9]. These frictional forces lead to a steady reduction in the amplitude of the seiche oscillations and, where no other forcing is present, a slight increase in the period of oscillation [3, 4].

The quantification of surface seiche motion and damping is one of the key issues facing any dynamic analysis of lakes, as it is a factor in the understanding of the energy budget within lakes. This field of research is rapidly growing with the development of computational lake simulations for issues as diverse as shoreline erosion, tsunami prediction, water mixing and groundwater seepage [10,11,12]. Wind on the lake surface is a primary mechanism through which energy is transferred to the lake, principally through the induction of surface and internal seiches within the water body, as described previously. These seiches may induce mixing throughout the water column and accurate quantification of the damping of these motions is essential for determining how wind energy is dissipated, thus allowing closure of the lake energy budget.

While numerous observations exist for the periods of surface seiches for a wide variety of lakes, little work has been carried out into obtaining their associated damping ratios. One of the few pieces of work into the subject was published in 1934 by A. Endrös and later reproduced by A. Defant in Physical Oceanography Volume II [3, 13, Table 25, p. 187]. This work was based upon existing water elevation records, collected from published literature for 35 lakes, including a series of records for 147 longitudinal seiches on Lake Geneva collected by Forel [13]. Endrös noted the difficulties of obtaining damping ratios from such records, most notably the small amplitude of the seiche oscillation in shallow lakes, which may be on the order of millimeters, and the effects of further disturbance of the lake surface by further wind forcing or other external influences. For these reasons, there was a high degree of subjectivity within the calculation of the damping ratios. It appears that they were calculated by identifying 5 consecutive waves which appeared to decay in amplitude, with no significant external forcing. The analysis would have been further complicated by the limited accuracy of the instruments used to obtain the water elevation records, which Endrös estimates to be a maximum of 4 mm. While this is largely insignificant in the records for the larger lakes, it accounts for a great deal of the amplitude of the oscillations in smaller and shallower lakes.

The damping ratio of the lakes was expressed by Endrös through the logarithmic decrement, \(\lambda\), and a damping constant or factor of friction, \(\beta\). For the mth and nth peaks in each oscillation the logarithmic decrement is given by:

$$\begin{aligned} \lambda =\frac{\log {(A_{m})}-\log {(A_{n})}}{m-n}=\frac{\beta .T}{2} \end{aligned}$$
(1)

where T is the period of the oscillation in minutes and A is the amplitude of the peak. The amplitude of the nth wave is therefore given by:

$$\begin{aligned} A_n= A_1.e^{-\beta .\frac{n.T}{2}} \end{aligned}$$
(2)

For the sake of clarity, in this paper, all damping is presented as a percentage of energy lost between oscillations, expressed by:

$$\begin{aligned} \text {Energy loss}\,(\%)=100\left[ 1-\frac{1}{e^{2\pi .\delta }}\right] \end{aligned}$$
(3)

where \(\delta\) is the damping ratio given by:

$$\begin{aligned} \delta =\frac{\beta }{2\pi /T} \end{aligned}$$
(4)

Hence

$$\begin{aligned} \text {Energy loss}\,(\%)=100\left[ 1-\frac{1}{e^{\beta /T}}\right] \end{aligned}$$
(5)

The majority of the research on surface seiche damping has been based upon the measurements made by Endrös. Despite numerous reproductions and reference to these measurements [3, 14,15,16,17,18] no verification of the values he obtained, reproduced in “Appendix 1” (Table 4), has ever been carried out. This paper seeks to present a method through which the damping ratios and periods of surface seiches may be extracted using existing data without the need for labor intensive and subjective visual inspection of water elevation records.

At present the damping ratio of seiches is typically extracted manually, with areas of potential seiches first identified visually by the researcher and the damping ratio calculated based upon the reducing magnitude of peaks of the signal. This method has numerous disadvantages. It is both time consuming and subjective, relying on the researcher to trawl through time-series data. It also does not account for additional forcing of the lake by further wind stresses which have occurred since the seiche oscillation was set in motion. This additional forcing can cause the damping ratio of the lake basin to be miscalculated as it may interrupt the decay of the oscillation. The presence of noise within the signal, due to electrical interference in the sensor or localised non-linear fluctuation of the thermocline, may also lead to the presence of further oscillations in the data which are not associated with the seiche motion.

Alternatively, frequency-domain spectral methods may be employed through which the frequency response of the system is visually inspected to identify spectral peaks, and damping ratios extracted through analyses such as the peak-amplitude method (quality factor analysis) [19]. However these techniques are highly dependent on the filtering and windowing of the data during the frequency domain transformation, and may struggle to extract accurate damping estimates for lakes with close-modes. In this paper, we present a novel alternative method for extracting the period and damping ratio of seiches which does not require transformation to the frequency domain, called the random decrement technique (RDT). This method is described in detail below and then applied to datasets from Lake Geneva and Lake Tahoe.

2 Methodology

2.1 The random decrement technique

The random decrement technique [20] was originally designed to provide an on-board warning mechanism of failure and unwanted vibrations in experimental aircraft operated by the National Aeronautics and Space Administration (NASA) [21]. From the original work conducted at NASA, the technique has spread to other fields including the rail industry [22], offshore oil and gas [23], surface geology [24], and high-rise buildings [25,26,27].

The RDT starts by describing the response of a linear dynamic system, such as those shown in Parts 1 and 2 of Fig. 1, as a sum of three components:

  1. 1.

    The response of the system due to the initial displacement.

  2. 2.

    The response of the system due to the initial velocity.

  3. 3.

    The response of the system due to any forcing during the time section being observed.

If either of the first two components can be isolated, they can be used for modal analysis as they represent the free response and impulse response of the dynamic system respectively. Using the RDT, this isolation is achieved by setting a triggering condition relating to either displacement or velocity, and extracting a series of sections from the measured time-history. When the mean of many of those sections is taken, components of the response with a mean of zero tend towards zero. Thus, if the force applied to the system has a mean value of zero, then the contribution of part (3) tends towards zero as consecutive time-samples are averaged. The mean of the sections obtained through the RDT is known as the Random Decrement Signature (RDS).

The triggering condition first used by Cole Jr [21] is now known as the level-crossing trigger. A section is taken to start each time the displacement crosses a set trigger level (a given amplitude of displacement). As the trigger level is defined such that a segment of data is collected on both up and down crossing of the triggering value there are therefore an equal number of trigger points with positive and negative velocity and, with sufficient averages, part (2) tends towards zero, as shown in Stage 3 of Fig. 1. The response of the system due to the initial displacement is not averaged to zero during the RDT analysis due to the nature of the triggering condition. Each time the triggering condition is satisfied, and a new data section is collected, the data section has the same initial displacement value. In a linear system, the component of the waveform due to the initial displacement is consistent across all the sections to be averaged, and so is unchanged by the averaging process, as illustrated in Stages 3 and 4 of Fig. 1.

A more rigorous analysis [28] demonstrates that, if the RDS is to be exactly equal to the transient response to the initial condition, then the applied force must be stationary, Gaussian, with zero mean, and have equal magnitude across the frequency range. That is, it should be white noise. Natural processes such as the action of the wind, however, may have a sufficiently wide bandwidth to give a response similar to that produced by white noise [29, 30]. A full explanation of the RDT can be found in Fu and He [31].

Fig. 1
figure 1

Procedure for the application of the RDT to the analysis of water level data utilizing a level crossing triggering condition

Full size image

The parameters estimated by the RDT can depend on the triggering condition and level chosen. It is therefore important, particularly in applying the technique in a new field, that a sensitivity analysis is carried out to show that the trigger level chosen is low enough to collect sufficient time sections to be averaged, but high enough to exclude noise. These two conditions specify a range within which consistent estimates of modal frequency and damping are obtained. There may still be a systematic variation of modal parameters in that range, and this may reflect important behaviour in the system being measured. In building vibration, the variation of frequency or damping with amplitude of vibration of the building is shown to be reflected in a variation with trigger level when measured by the RDT [25, 27].

2.2 Application of the random decrement technique to seiche analysis

Currently, the modal properties of seiche motion of surface seiches are extracted primarily through power spectral density, coherence and least-squares harmonic analyses [32], analysis of a Fourier transformed surface elevation/pressure data set, as well as visual inspection of water elevation records [9]. Spectral methods struggle to accurately extract the periods of seiches which occur in different directions in lake basins which are of similar bathymetry across both their length and breadth [33], without a priori knowledge of the likely harmonic modes of the lake, such as may be extracted from a spatial model [12]. Frequency domain analyses have further issues with extracting the damping of close modes due to the overlap of the spectral peaks, and the windowing required for transformation into the frequency domain requires careful consideration to avoid affecting the measured modal parameters.

The RDT described above produces an estimate of the autocorrelation function, which is closely related to the free-vibration response of the system (they are equal if the excitation is white noise [28]), and as the RDT relies upon averaging a large number of sections of data it is possible to use data with low sampling rates whilst still extracting the damping ratios and periods of harmonic oscillations with a high degree of accuracy [31]. The resulting RDS can then be analysed by any time-domain modal analysis technique or may be transferred to the frequency domain by Fast Fourier Transform (FFT) for frequency-domain modal analysis. The frequency power spectra of the RDS is notably less noisy than the FFT of the unprocessed time-series data due to the averaging within the RDT, as illustrated in Fig. 6. This allows more accurate estimation of modal parameters extracted using frequency domain techniques, such as the peak-amplitude method, whilst simultaneously avoiding some of the issues with filtering and windowing of the data, and the masking of close-modes which may result from smoothing of the frequency spectral density.

In this study, we use a time-domain curve-fitting technique; the Matrix Pencil Method [34], applied to the RDS, to establish the periods and damping ratios of surface seiches based on RDSs of readily available water level data. The Matrix Pencil Method is utilised to deconstruct the RDS into a series of complex exponentials through the identification of response function poles as the solution of the generalised eigenvalue problem, carried out on the assumption that the signal being deconstructed is comprised entirely of damped sinusoids.

Within this paper the term ‘dominant’ seiche is defined as the lowest frequency seiche which is observable within the data analysed. For both lakes included within the analysis, the dominant seiche observed correlates with the lowest frequency surface seiche oscillation recorded within the literature.

2.3 Formation of the random decrement model

The Random Decrement Model was formed of three sections; filtering of the data, application of the RDT, and RDS signal decomposition using the Matrix Pencil Method. The RDT was applied to the data for both Lake Tahoe and Lake Geneva using MATLAB; pseudo-code for the RDT analysis is provided in “Appendix 2”. The data was first bandpass filtered to remove the low frequency diurnal and long term trends from the data. The RDT was then applied as described earlier in this paper to generate the RDS for a given trigger level. The trigger level was defined as a multiple of the standard deviation of the signal. The RDS could then be used for modal analysis in the time domain to identify the dominant frequencies and their corresponding damping ratios. The signals contained large amplitude non-harmonic components over a range of low frequencies, with a substantial amplitude at frequencies near that of the seiche oscillation. Due to these larger amplitude frequencies, the RDS often showed a frequency component at the lower cut-off of the band pass filter, due to undesirable triggering of the RDT by the lower frequency motions. Three dominant frequencies were extracted from the RDS to ensure that the seiche oscillation was identified, as it was found that the signal induced by the filter cut-off was often the first frequency extracted, as shown by the spectral density plots presented later in this paper.

3 Case studies

3.1 Study site 1: Lake Geneva

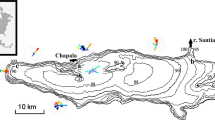
Lake Geneva, located on the border of France and Switzerland, is the largest freshwater lake in Western Europe. It is a perialpine lake with a surface area of \(580\,\hbox {km}^2\), an average depth of 154 m and a maximum depth of 309 m [3]. The lake takes the form of a crescent, with the northern and southern shores of the lake having lengths of 95 km and 72 km respectively, with a maximum width of 14 km (Fig. 2a). It should be noted that the altitude of the water level is artificially controlled, with a fixed minimum of 371.30 m above sea level and an upper limit of 372.30 m above sea level [35]. The lake is stratified for an average of 125 days per year [36].

Fig. 2
figure 2

Clockwise from top left. a Bathymetry of Lake Geneva showing location of sampling sites, b Bathymetry of Lake Tahoe showing location of sampling site, c Filtered 30-day sample of water level data for Lake Geneva and d Filtered 30-day sample of water level data for Lake Tahoe

Full size image

Prevailing winds in the area are north-easterlies and south-westerlies with a small degree of seasonal variation through most years. Two dominant barotropic seiches have been observed in Lake Geneva, each running along the East–West axis of the lake. The first and second mode barotropic seiches have observed periods of 73.5 min and 36.7 min respectively [35]. The amplitudes of the surface seiches varies across the length of the lake, with a mean value of 17.5 cm for the first mode barotropic seiche at the western end of the lake. The amplitude of the seiche at the western end of the lake is significantly larger than that at the eastern end of the basin (mean amplitude of 4 cm), due to the narrowing of the bathymetry at Yvoire combined with shallower waters at the west end of the basin [37].

The time series data used in the RDT analysis of Lake Geneva took the form of water elevation data collected at three locations; location 2026, 2027 and 2028. This data had a sampling rate of 10 min and was continuously collected between 00:00 on 1 January 1974 and 23:50 on 7 January 2013. A sample of the filtered data for location 2028 is presented in Fig. 2c.

3.2 Study site 2: Lake Tahoe

Lake Tahoe is an ultra-oligotrophic lake straddling the border between California and Nevada in the western United States of America. The lake is famed for its exceptional water clarity and is the largest alpine lake in North America with a surface area of \(490\,\hbox {km}^2\), an average depth of 300 m and a maximum depth of 501 m [38]. Due to the steep banks of Lake Tahoe, it is believed to be particularly resonant with low levels of seiche damping [10]. The maximum length of the lake north–south is approximately 35 km with a maximum width of approximately 19 km (Fig. 2b). The lake is strongly stratified for an average of 185 days per year [39] but remains stratified throughout the year, with a weak density stratification persisting throughout the winter months [40]. The prevailing winds in the area are from the south–west, with the first and second modal barotropic seiches being excited along the north–south axis of the water basin and the third and fourth modal barotropic seiches excited about the east–west axis of the lake. The typical barotropic seiche amplitudes is between 2.5 and 5 cm at the north and south ends of the lake for the first dominant seiche mode [41, p. 6.9].

The RDT analysis for Lake Tahoe was carried out using water level data collected at a thermistor chain located at Homewood, highlighted on Fig. 2b. Three time-series data sets were utilized in the analysis; 30 July 2013 00:00:00–6 December 2013 23:59:30, 1 January 2014 00:00:00–10 May 2014 23:59:30, 6 January 2015 00:00:00–15 May 2015 23:59:30. A sample of the filtered data used within this analysis is presented in Fig. 2d. All data sets had a sampling rate of 30 s. A fourth data set was created through combining the three datasets sequentially to allow the three datasets to be compared to a mean value which included all seiche events. This allowed for the comparison of the frequency of the triggering of the RDT between datasets and an analysis of whether the mean period and damping values obtained were dominated by data sections from a single dataset.

3.3 Results of random decrement technique analysis

Where multiple channels measure the response of a system at different points, the RDT is applied using one channel for triggering, and sampling all the other channels at the times defined by that trigger [42]. In order to identify a particular mode of oscillation, the chosen channel should measure that mode with a good signal to noise ratio [43]. The power spectral densities for each of the three channels measured for Lake Geneva are provided in Fig. 3. They show that Location 2028, presented in orange, has a higher signal to noise ratio than either of the other locations. This is shown by the difference between the peak value at the seiche frequency and the level of the surrounding background noise, and is quantified for each of the datasets in Table 1. To quantify the noise present either side of the first dominant seiche frequency, the signal to noise ratio is based on the ratio of the power spectral density of the first dominant seiche period to the mean magnitude at 1.85 cycles per hour and 0.79 cycles per hour. These points were selected based on the visual inspection of the power-spectral densities presented in Fig. 3 and fall outside the spectral peaks associated with the various surface seiche modes. While this additional noise is removed during the averaging process of the RDT, it may affect the final RDS due to the averaging of data sections which do not contain the seiche oscillation.

Fig. 3
figure 3

Power spectral density plot of elevation data for Lake Geneva. Power spectra filtered through band-averaging of the power spectral density with a rectangular window of length 120 samples. Confidence intervals calculated using a Chi-square distribution with 120 degrees of freedom [44]

Full size image
Table 1 Comparison of signal to noise ratios for power spectral densities for Lake Geneva, Locations 2026–2028
Full size table

As the seiche motion is present across the entire lake basin, a seiche detected at one location should also be present at the other two locations and hence present in the data at the same instance. Therefore, once the triggering value is exceeded at Location 2028, data sections are taken at all three locations to create the location-specific RDS. This allows data to be extracted from all locations, despite the high levels of noise present in locations 2026 and 2027. Through this approach, the period of dominant seiche oscillation has been extracted using a triggering value of 4 standard deviations of the filtered mean of the time-series data, and are provided in Table 2 for each of the three data collection locations on Lake Geneva. The results of the associated energy loss for the dominant seiche oscillation was obscured in the resulting RDSs for Location 2026 and Location 2027 due to the greater levels of noise and the lower amplitude of the seiche motion at these locations. Consistent results for the energy loss associated with the dominant seiche were obtained for Location 2028 and are provided in Table 2. These results show strong agreement with the dominant seiche period of 73.5–74.2 min obtained by Graf [35] using spectral methods, and the dominant seiche period of 73.5 min obtained by Endrös [9] through visual inspection of time-series data collected by Forel [13]. The measured energy loss for Lake Geneva is 4.72%. This is higher than the 2.96% reported by Endrös [9], but of a similar magnitude.

Table 2 Dominant seiche period obtained for Locations 2026–2028 on Lake Geneva through use of the linked triggering RDT analysis and energy loss for dominant seiche period for Location 2028
Full size table

Varying the trigger level led to some variation in the measured period and energy loss, as shown in Fig. 4a, b for the dominant seiche period and the energy loss per seiche oscillation respectively. In studies of lateral vibration of buildings, it has been suggested that the variation of measured parameters with trigger level gives an indication of the variation of those parameters with the amplitude of the oscillation [25, 27]. However, it is only possible to obtain an accurate measurement of parameters over a certain range of trigger levels. Trigger levels that are too low are strongly affected by measurement noise, and trigger levels that are too high do not result in sufficient samples for averaging. In this case, a trigger level equal to one standard deviation of the data was found to be a reasonable lower bound, and the upper bound was set where the number of data sections included in the RDS fell below 2000, following guidance by Tamura et al. [45] for building vibration measurements.

These limits were verified as appropriate for the analysis of surface seiches through extensive sensitivity analyses of the RDT, discussed in later sections, and were found to produce consistent results for the seiche period and energy loss between oscillations for both Lake Tahoe and Lake Geneva. Using these limits, the percentage variation from the mean value for the dominant seiche period was found to be between 0.01 and 0.21% across the three locations. The energy loss varied between approximately 4% and 4.9% over this fivefold increase in trigger level. This suggests a trend of increasing energy dissipation with amplitude in this range.

Fig. 4
figure 4

a Variation in dominant seiche period and b Variation in energy loss per seiche oscillation with varying triggering value for Location 2028. The resulting number of data segments averaged to produce the RDS is also plotted

Full size image

The amplitude of the seiche obtained is an order of magnitude larger at Location 2028 than at either of the other two locations, as illustrated in Fig. 10, fitting with the observed increase in seiche amplitude recorded in the shallower western end of the lake basin. The RDS for Location 2028, where Location 2028 is the triggering channel and the triggering value is 4 standard deviations, is presented in Fig. 5 and illustrates sinusoidal oscillations which are clearer than those obtained through visual inspection of the raw water level data. This plot represents all the seiche events for location 2028, identified as when the variation in water depth exceeds 4 standard deviations from the mean variation in water depth, averaged together to form a single RDS. A comparison of the power spectral density obtained through the Fourier analysis of the filtered data and the RDS for Location 2028 is provided in Fig. 6.

Fig. 5
figure 5

RDS for Location 2028, where Location 2028 is utilized as the triggering channel with a triggering value of four standard deviations. Amplitude scaled based on maximum seiche amplitude for Location 2028

Full size image
Fig. 6
figure 6

Comparison of the power spectral density for the filtered data for Location 2028 and the RDS obtained through the RDT analysis of Location 2028 using a triggering value of four standard deviations. Power spectra for Location 2028 filtered through band-averaging of the power spectral density with a rectangular window of length 120 samples. Confidence intervals calculated using a Chi-square distribution with 120 degrees of freedom [44]. No filtering of the power spectral density for the RDS was applied

Full size image

The results for the dominant surface seiche at Lake Tahoe are provided in Table 3 alongside values obtained from the literature. An extensive literature review found no evidence of previous calculation of the damping ratio for surface seiches on Lake Tahoe and as such the energy loss between oscillations obtained through the RDT cannot be compared to prior results. Presented in Fig. 7 is the variation in the results obtained for the dominant seiche period compared to varying trigger values. As with the data for Lake Geneva, presented previously in Fig. 4, consistent results are obtained when a lower bound of one standard deviation for the trigger value is used and an upper bound of when the number of signatures falls below 2000. A similar pattern was observed for the values of energy loss, but with a slightly higher variation in the values obtained depending on the trigger value specified. Based on the limits for the trigger value previously discussed for Lake Geneva, the percentage variation from the mean value for the 2013 to 2015 combined time-series dataset is 3.24% for the dominant seiche period and 14.07% for the energy loss per oscillation.

Table 3 Dominant period and associated energy loss obtained through RDT analysis for Lake Tahoe for individual annual datasets (2013–2015) and for all data combined sequentially into a single dataset
Full size table
Fig. 7
figure 7

Comparison of seiche period (crosses and triangles) extracted for Lake Tahoe, 2013–2015 water level data, using RDT, and number of data sections in the RDT analysis (circles) for varying trigger values. Dashed line corresponds to limit of 2000 data sections proposed by Tamura et al. [45] for the extraction of meaningful results. Once the number of data sections included within the RDS falls below 2000, the obtained damping ratio begins to display random behaviour. Note: the following data points fall outside the plotted data range—2013: 0.25 and 2–4 standard deviations used as trigger. 2014: 4 standard deviations used as trigger. 2015: 0.25, 2.25, 2.5 and 3.25 standard deviations used as trigger

Full size image

4 Discussion

4.1 Seiche period

For Lake Geneva, the seiche period obtained shows excellent agreement with existing literature, with the results for all three locations being within the range previously observed. As the water level in the lake is artificially maintained [46] it would be expected that there would be little variation of these periods across the range of observations made since 1895.

The simplest equation for the theoretical surface seiche period is Merian’s formula [3] and is defined for a rectangular basin as:

$$\begin{aligned} T=\frac{2L}{\sqrt{gh}} \end{aligned}$$
(6)

where T is the period of the surface seiche in seconds, L is the length of the lake in meters, g is the gravitational constant and h is the mean depth of the lake in meters. Lake Geneva, which is far from a rectangular basin, has a mean depth of 154.4 m and an approximate length of 72 km giving a theoretical seiche period of approximately 61.2 min. The true value of the seiche period is approximately 73.5 min [13]. This difference is likely due to the variation in bathymetry along the length of the lake, however it does provide a rough basis for comparison of the surface seiche period obtained.

The seiche periods obtained for Lake Tahoe also show excellent agreement with those obtained from the literature. The values obtained for the separate yearly data sets give a mean period of 11.29 min, with a coefficient of variance of 1.06% across the yearly datasets, compared to values of 11.22 min and 11.7 min recorded by Ichinose et al. [10] and the Tahoe Environmental Research Center [41] respectively. These results are also largely insensitive to the trigger value, with coefficients of variance of 0.13%, 0.01% and 3.19% for the 2013–2015 datasets respectively for triggering conditions between 1 standard deviation and when the number of data sections included within the RDS falls below 2000. The full sensitivity analyses of these results can be found in “Appendix 3”.

Lake Tahoe is closer to the idealized rectangular basin which forms the basis of Merian’s formula with a mean depth of 305 m and a width of 19 km, giving a theoretical seiche period of 11.58 min, close to the observed seiche period of approximately 11.3 min and within the range of historically observed values.

4.2 Damping ratios

The observed energy loss for Lake Tahoe for the years 2013–2015 was 1.09%, 1.95% and 1.79% respectively with a value for the combined datasets of 1.96%, based on a trigger value of 1.5 standard deviations. This appears to be in line with what would be expected for a lake which has both a greater mean depth and less variable bathymetry than Lake Geneva; with less energy lost due to reduced frictional effects and the lack of sills in the lake. However, the values of energy loss obtained for the individual yearly datasets are highly sensitive to the initial triggering condition specified, due in large part to the short length of the datasets. Fewer data sections included within the RDS lead to the amplification of the effects of noise and other signals within the lake not associated with the seiche motion. When all three datasets are combined, the variation in the energy loss based on the initial triggering condition falls significantly. Through access to further data it is expected that this variation would continue to decrease as further data sections are used to generate the RDS.

For comparison, reproduced in full in Table 4, provided in “Appendix 1”, are the damping ratios obtained by Endrös [9] for several lakes. As previously discussed these damping ratios were obtained through visual inspection of water level records and, though widely reproduced, are unverified. The results obtained for both Lake Geneva and Lake Tahoe fit with the general trend of lakes with greater depths having lower energy loss than shallower lakes, as highlighted in Fig. 8a, b for the energy loss per oscillation versus the mean and maximum lake depth respectively. The results obtained through the RDT are presented as red circles for Lake Tahoe and red triangles for Lake Geneva, with all other plotted values based on those presented in Table 4.

Fig. 8
figure 8

a Mean lake depth versus energy lost to damping per oscillation. b Maximum lake depth versus energy lost to damping per oscillation. RDT results for Lake Tahoe (Table 2) and Lake Geneva (Table 3) presented as a red circle and triangle respectively. All other values taken from Table 4, provided in “Appendix 1”. Error bars for Lake Tahoe energy loss show the range of results obtained across the three annual datasets used within the RDT analysis. Error bars for Lake Geneva energy loss show the range of results obtained across the three locations used within the RDT analysis

Full size image

4.3 Sensitivity analyses

To verify the sensitivity of the results obtained using the RDT, extensive sensitivity analyses of the effects of varying inputs upon the RDT model outputs have been undertaken and are documented in full in “Appendix 3”. It was found that the filter cut-off values used for bandpass filtering of the time-series data had little effect of the results obtained provided that the low and high pass filter cut-off values were higher and lower respectively than the seiche period predicted using Merian’s formula. The selection of a length for the RDS signature was found to require an iterative process. If the RDS was too short in length to encompass a sufficient number of oscillations, the damping ratio obtained was more sensitive to the selection of a trigger level. Once the signature became too great in length, the latter part of the RDS is dominated by background noise, and additional RDS length reduced the consistency of the damping ratio and period obtained. The trigger value selected has the greatest impact on the results obtained. It was found for both Lake Tahoe and Lake Geneva that when a trigger value of less than one standard deviation was used many sections of data which were dominated by noise were included in the RDS, reducing its clarity, and that once the number of data sections included within the RDS fell below 2000 the results obtained for both the damping ratio and seiche period varied widely due to insufficient removal through the averaging process of random noise and system forcing not associated with the seiche motion.

4.4 Lake Geneva mode shape

A further benefit of linked triggering RDT for the analysis of the three Lake Geneva datasets is that it allows the mode shape of the lake to be extracted. As samples of data are taken from the 2026 and 2027 datasets at the point where the trigger value is exceeded in the 2028 datasets, the RDSs obtained retain their relative phase and magnitude throughout the analysis, as shown in Fig. 9. This is a further strength of the RDT and allows approximated mode shapes, such as that shown in Fig. 10, to be created. A straight line is drawn between each point at the same time step. This analysis shows the high seiche amplitude at the shallow, narrow western end of the lake, and a node between location 2028 and 2027. Since the variation in amplitude between locations would not be expected to be linear, data from intermediate measurement points would be necessary to more accurately determine the location of this nodal point, but this simple approximation suggests that it would be much closer to location 2027 than 2028. This would be expected for a first dominant seiche motion, with locations 2026 and 2027 being in phase with one another and in perfect anti-phase with location 2028.

Fig. 9
figure 9

Normalised RDSs for the three Lake Geneva datasets (2026, 2027 and 2028) illustrating phase relationship

Full size image
Fig. 10
figure 10

Linear approximation of Lake Geneva mode shape created using one oscillation (80 min) of the RDSs for locations 2026 (71 km), 2027 (49 km) and 2028 (4 km). Locations of data collection marked in red. All distances reported based on centre line of lake

Full size image

5 Challenges and limitations of the random decrement technique

Despite the promise which the RDT holds for seiche analysis it still has several issues which should be noted in its application, alongside those already discussed in the previous section. The first of these is the requirement for a large data set, the size of which is dependent on the frequency which surface seiches are induced within the body of water. There are conflicting reports on how many data sections included within the RDS are required to obtain the true wave form of the oscillation. Yang et al. [47] set a minimum of between 400 and 500, while Tamura et al. [45] set the lower limit as 2000 [26]. The results for both Lake Tahoe and Lake Geneva support a limit of 2000 data sections per RDS for the analysis of surface seiches, as the limit put forward by Yang et al. leads to far higher variation in the obtained damping ratio. However, for the extraction of the seiche periods only, a lower number of data sections included within the RDS is sufficient to obtain consistent results. This is illustrated in Fig. 11, based on data from Location 2028, Lake Geneva. As the number of data sections included within the RDS reduces, the signal visibly deviates from the smooth exponential decay, leading to inconsistent damping ratio extraction and individual data sections dominating the averaged RDS. A full analysis of the effect of the number of data sections included in the RDS can be found in Kareem and Gurley [26].

Fig. 11
figure 11

Comparison of signal clarity of RDS with varying triggering values and associated numbers of data sections included within the RDS extracted for Lake Geneva, Location 2028. Triggering values defined as multiple of standard deviation of filtered elevation data

Full size image

There is also promise for the application of the RDT to the analysis of baroclinic (internal) seiches. At present the work of Shimizu and Imberger [48] is the only technique, other than the visual inspections of the time-series temperature data, for the estimation of damping rates of internal seiches. Their method is based upon the use of fitting coefficients to fit numerically calculated internal waves to recorded isotherm displacements. These fitting coefficients were then taken to be equivalent to the damping ratio. The key disadvantage of such a method is the requirement to first numerically calculate the predicted amplitude of the seiche, to then be matched with the isotherm displacement to identify an internal seiche, and the inability of the method to deal with non-linear effects.

An initial attempt has been made at applying the RDT to the analysis of internal seiches using time-series thermistor chain data, with the variation in temperature recorded at a thermistor close to the thermocline utilized in the same manner as the water level data used in the RDT analysis of surface seiches. While results were obtained, the number of seiche oscillations in the available data was insufficient for consistent period and damping ratios to be extracted.

In the RDT analysis of both Lake Geneva and Lake Tahoe, the periods of other surface seiche modes were extracted. These results were more highly sensitive to the input conditions discussed previously and occurred less frequently within the time-series data than the dominant seiche modes. Initial attempts at extracting the periods and damping ratios of these modes found that the periods could be extracted with little difficulty but extracting their associated damping ratios was more difficult, since the higher-amplitude, lower frequency modes dominate the signal. This difficulty could perhaps be overcome by decomposing the signal into its modal components by using a signal decomposition approach such as that presented by Chen and Wang [49], and excluding all but the mode of interest, before application of the RDT. This same technique could further be applied to larger bodies of water, such as the Great Lakes; and the Adriatic, Baltic and Black Seas; where the frequency of seiche oscillation may be close to the frequencies of diurnal tides. The impact of diurnal tides upon the water surface elevation could be filtered out as it presents a highly consistent and predictable oscillation with low levels of damping. This component could be identified after the application of the RDT using the matrix pencil method, discussed previously, with the RDS reconstructed without the diurnal tide oscillation to allow for further analysis.

The RDT may be applied to semi-enclosed water bodies; such as harbours, Fjords and bays; as previously described for the extraction of seiche periods and damping ratios. Due to the lack of a fixed-boundary for the oscillation, the damping ratio extracted will be the balance of energy added to the system at the open-boundary (seaward boundary), and the energy lost at the open boundary and due to frictional damping of the seiche, averaged over the full dataset being analysed. A further consideration of longer-period seiches is the increased difficulty of obtaining a dataset of sufficient length so as to extract the required number of data segments for the RDS.

6 Conclusion

Experimental measurements of the damping ratio of surface seiches, in particular, are extremely rare, with no new measurements apparent in the literature since the study by Endrös [9], who analysed individual, manually selected instances of seiche oscillation. This would appear to be due, at least in part, to the lack of an efficient method of processing long-term measurements. This study presents a method which makes use of data collected over a period of years, and extracts representative values of seiche period and damping ratio over that time, key parameters in understanding the energy budget within lakes and a crucial step towards the simulation of basin-scale processes such as eutrophication. The results obtained using the RDT on data collected at Lake Tahoe and Lake Geneva have shown excellent agreement with published literature. The damping ratio extracted for Lake Geneva is of a similar magnitude to that observed by Endrös [9] and that obtained for Lake Tahoe represents the first measurement of its kind. Alongside this, the applicability of the RDT to the field of limnology has been demonstrated for the first time. Both sets of results are in line with the general trend of decreasing damping ratios with an increase in lake depth observed by Endrös [9]. This method also shows promise for assessment of secondary surface seiches and internal seiches. The RDT technique provides a robust data-driven approach to determining the pathways of wind energy within a lake, where the wind energy is dissipated, and the resultant impact on mixing and fluxes within a lake system.