1 Introduction

The characterisation and measurement of turbulent stratified mixing remains a central problem for developing models of oceans, lakes and the atmosphere [15]. Mixing in stratified flows can be quantified in a variety of ways. One common means to describe how the density field is modified in a free turbulent flow, such as a plume, jet, or gravity current, is through use of an entrainment coefficient that models the incorporation of ambient fluid into the turbulent region. For a plume, the entrainment coefficient \(\alpha = u_e/U\), where U is a streamwise velocity scale for fluid in the plume and \(u_e\) is a transverse velocity scale for ambient fluid drawn into the plume [16]. This description of the turbulent entrainment is suggested by dimensional analysis and has been used successfully on plumes with a wide range of length scales [12]. The entrainment coefficient for plumes has recently been linked to the production of turbulent kinetic energy [18] and buoyancy variance [4], tying the entrainment coefficient to both viscous dissipation and irreversible mixing.

Another measure of mixing in a stratified flow is based on the fact that mixing of a stratification modifies the gravitational potential energy budget. Increases in potential energy in a stratified flow can be reversible (e.g., in an internal wave) or irreversible (e.g., when two parcels of fluid mix, changing the density of both), but only the irreversible increases correspond to mixing. The most common framework for differentiating between irreversible and reversible changes in potential energy splits the gravitational potential energy into available potential energy and background potential energy, described below [14, 20]. Irreversible mixing increases the background potential energy of the system. Stratified mixing can then be characterised by the mixing efficiency, which compares the energy used in irreversible diabatic mixing to the energy that was available for mixing [17]. In this paper, we use an energetics framework to examine mixing in the filling box and the emptying-filling box.

The background potential energy, \(E_b\), is the gravitational potential energy of the system if every parcel of fluid were allowed to rise or fall without changing its density until the system reaches a state of minimum gravitational potential energy. This minimum potential energy is equivalent to the potential energy of the fluid volume if the rearranged density profile increases monotonically in the direction of the gravitational vector [14]. In a closed system, the gravitational potential energy of this rearranged profile can only increase as a result of mixing, i.e., changing the density of fluid parcels, which raises the centre of mass of this reference state. As mixing is irreversible, for an open system in steady state, net buoyancy fluxes across the boundaries must result in a reduction of the background potential energy at the same rate that mixing increases the background potential energy within the system.

The available potential energy, \(E_a\), of a given state is the energy that would be released by rearranging fluid parcels into a state of gravitational equilibrium and is energy that is available to do work in the system. It is non-zero when the profile is not in a state of gravitational equilibrium, such as if kinetic energy in the flow moves a parcel of fluid away from its height of neutral buoyancy. Available potential energy can also be added directly to the flow by introducing buoyancy forcing or advection of fluid across the boundaries of the system.

The energy consumed by mixing can be measured using the background potential energy, \({E}_b\). The energy available for mixing is the sum of kinetic energy, \({E}_k\), and available potential energy, \({E}_a\), present in the system. As we will consider an unsteady flow in this paper, we make use of the instantaneous mixing efficiency, which can be expressed as

$$\begin{aligned} \eta = \frac{\dot{E}_b}{\left| \dot{E}_a + \dot{E}_k\right| } \end{aligned}$$
(1)

for a closed system, where \(\dot{E}_b\) is the rate of change of background potential energy (positive when irreversible mixing takes place) and \(\dot{E}_a\) + \(\dot{E}_k\) is the rate of change of available energy. For a closed system, \(\dot{E}_b\), \(\dot{E}_a\) and \(\dot{E}_k\) represent rates of conversion within the system. For an open system, where mass or energy transfers across the boundaries are permitted, these represent sources or sinks of energy that must also be taken into account.

In situations where the mixing is buoyancy-driven (i.e., the source of energy in the system is initially entirely \({E}_a\)), high mixing efficiencies have been observed, with values of the cumulative mixing efficiency greater than 75% measured in experiments of Rayleigh–Taylor instability [6], and tending towards 100% in experiments of horizontal convection [9]. In some cases of buoyancy-driven stratified mixing, the mixing efficiency depends on the density profile in regions remote from where the mixing takes place [7]. Nevertheless, the mixing efficiency is often discussed in the literature as if it were a constant value or some property of the turbulence itself, therefore it is useful to examine and understand cases where this is not true, to extend our intuition about such cases. The filling box and the emptying-filling box are both simple, well-defined systems in which the steady-state dynamics are well understood, making them useful test-cases.

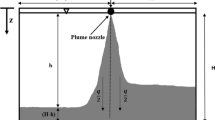
A simplified model of a plume within a closed container is known as a ‘filling box’, sketched in Fig. 1a. Without loss of generality, we will assume that the plume originates from a point source of pure buoyancy and falls through a box that is of height H. As a result of entrainment into the plume, a stable stratification will develop in the box [1]. This stable stratification can be predicted using plume theory, which assumes that entrainment of fluid from the ambient into the plume at some height is proportional to the mean vertical velocity in the plume at that height [16]. Time-dependent density profiles for a plume in a box have also been derived, along with approximate analytic expressions for the density profile [21]. The density profile in a filling box reaches an asymptotic state, at which point the shape of the density profile is no longer changing with time, although the mean density in the box is still increasing [1].

Fig. 1
figure 1

Filling box and emptying-filling box: a a point source of pure buoyancy (whose specific buoyancy flux is \(F_0\)) produces a plume in a closed box of height H. This plume falls to the floor, entraining fluid as it falls, creating a stratified layer that fills the box. This diagram shows the filling box at early times, before the stratified layer has filled the box. At late times an asymptotic steady state is established. b Steady state of an emptying-filling box containing a point source of pure buoyancy. The flow through the upper and lower openings is matched by the flow in the plume as it crosses the interface into the buoyant mixed layer. H is the vertical separation between the openings, h is the distance from the upper opening to the interface. The buoyant mixed layer and ambient densities are labelled \(\rho _m\) and \(\rho _a\) respectively

Full size image

The emptying-filling box (Fig. 1b) is a conceptual extension of the filling box, which introduces openings through the top and bottom [13]. Due to the stratification within the box, there is a resulting pressure difference between the openings that drives a ventilation flow. Ambient fluid enters the box through the opening at the top and mixed fluid exits through the opening at the bottom. The emptying-filling box can reach a steady state when the removal of dense fluid by the ventilation flow is balanced by addition of dense fluid in the plume to a well-mixed layer. For a single source of buoyancy, the steady state consists of a layer of ambient fluid of thickness h and density \(\rho _a\) that sits above a dense mixed layer, which has constant density \(\rho _m > \rho _a\). The depth of the mixed layer within the box is independent of the magnitude of the source buoyancy flux and controlled only by the entrainment coefficient \(\alpha \) of the plume and a ratio of the height of the box to a quantity \(A^*\), which is a function of the areas of the two openings [13].

The emptying-filling box is a common model for buoyancy-driven natural ventilation and has been used to study steady states [13] and transients [3, 11, 19]. Natural ventilation of buildings makes use of wind or temperature differences to drive ventilation flow, rather than mechanical forcing [12]. Displacement ventilation uses existing buoyancy sources to draw cool, fresh air into a building through an opening near the floor, while removing warm air through an opening near the ceiling. Note that in the example shown in Fig. 1, the plume is dense and falls into a less dense ambient, whereas in natural ventilation warm plumes would rise through a cool ambient.

In this paper, we examine how the mixing efficiency and entrainment coefficient associated with a plume in a filling box and an emptying-filling box relate to the turbulent mixing that takes place. In Sect. 2 we examine the filling box, calculating the mixing efficiency for both the asymptotic state (Sect. 2.1) and the transient state (Sect. 2.2). In Sect. 3, we examine the emptying-filling box, again analysing the mixing efficiency of both the steady state (Sect. 3.1) and the transient state (Sect. 3.2). We discuss the difference in mixing efficiencies of open and closed systems in Sect. 4.

2 The filling box

2.1 Mixing efficiency of the asymptotic state

The (closed) filling box reaches an asymptotic state [1], in which the density gradient in the interior is a function of height z only, and the rate of change of density is both spatially uniform and constant, i.e., \(\partial \rho (z,t)/\partial t\) is constant. Thus irreversible mixing in the filling box arranges itself so that the rate of change of density is uniform in space.

If the plume has specific buoyancy flux \(F_0\) (\(\hbox {m}^4\hbox {s}^{-3}\)) and the room has constant cross-sectional area, then the rate of change of density at all heights in the box is

$$\begin{aligned} \frac{\partial \rho }{\partial t} = \frac{\hat{\rho }F_0}{gV} \end{aligned}$$
(2)

where \(\hat{\rho }\) is a reference density, g is gravitational acceleration and V is the volume of the filling box. If we assume the volume of the plume is small compared with V, and that fluid in the filling box is everywhere close to its equilibrium level, then the rate at which the potential energy of fluid in the box (i.e., the background potential energy) increases owing to irreversible mixing is given by

$$\begin{aligned} \dot{E}_b = g\int _{V} \frac{\partial \rho }{\partial t} z \,\mathrm {d}V - \hat{\rho } F_0 z_0 = \frac{\hat{\rho } F_0 H}{2}, \end{aligned}$$
(3)

where the bottom of the box is at \(z_0\). This expression is obtained by comparing the background potential energy in the system with a hypothetical state in which the density anomaly added by the plume falls to the bottom of the box without dilution by mixing. The expression for the rate \(\dot{E}_b\) in (3) may be readily evaluated without loss of generality by defining the origin (\(z_0\)) to be zero at the bottom of the box.

The buoyancy forcing that maintains the plume is the only source of energy for the filling box. The rate of addition of available potential energy by the plume source is equal to the change in potential energy if the buoyancy released by the plume were to traverse the depth of the box without mixing, a process equivalent to sorting the unstable density profile. The rate at which available potential energy is supplied to the system by the buoyancy source is

$$\begin{aligned} \dot{E_a} = \hat{\rho } F_0 H. \end{aligned}$$
(4)

This buoyancy forcing results in parcels of fluid close to the plume source that are buoyant, i.e., they have available potential energy. These parcels of fluid pass through the box depth, converting available potential energy to kinetic energy in the process. Turbulence and density gradients arise on small scales, and energy is consumed by irreversible mixing and viscous dissipation.

The turbulent mixing efficiency \(\eta \) for the asymptotic state of a filling box can thus be estimated as the ratio of the rate of irreversible mixing, \(\dot{E_b}\), and the rate of release of available potential energy,

$$\begin{aligned} \eta = \frac{1}{2}. \end{aligned}$$
(5)

In using this result to characterise turbulent mixing in the filling box, it is assumed that the kinetic energy dissipated from the mean overturning flow is negligible (i.e., \(\dot{E}_k \ll \dot{E}_a\)). The contribution to irreversible mixing associated with molecular diffusion down the mean background gradient through the box depth is also assumed to be unimportant.

Equation 5 is an interesting result in that the mixing efficiency of the asymptotic state is not a function of the entrainment coefficient or any other parameter. It is also independent of the model used to describe the plume and only requires that an asymptotic state is reached, without depending on any of the details of that state. A mixing efficiency of 1/2 has been found in other flows [5] where mixing is driven by available potential energy—the maximum for any 1D monotonic unstable stratification [7, Appendix A].

2.2 Mixing efficiency of the transient state

We can also examine the time dependent evolution of an axisymmetric plume in a box [1]. An axisymmetric plume is maintained below a point source and, at any height z, the vertical velocity and buoyancy are assumed to have mean Gaussian profiles, where w, F and b are the maximum vertical velocity, maximum buoyancy and Gaussian half-width, respectively. As in our last example, we consider a dense plume in a less dense ambient.

The equations that govern the time evolution of the density profile as the box fills are given by Worster and Huppert, who also calculated an approximate analytical solution [21]. We follow their analysis to compute the density profile in the tank as a function of height and time \(\rho (z,t)\). The dimensionless quantities for height, density, time, buoyancy flux, volume flux, and momentum are defined as

$$\begin{aligned} \begin{aligned} \zeta&= z H^{-1}, \quad \delta = 4 \pi ^{\frac{2}{3}} \alpha ^{\frac{4}{3}} H^{\frac{5}{3}} F_0^{-\frac{2}{3}} g \frac{\rho - \hat{\rho }}{\hat{\rho }}, \\ \tau&= 4 \pi ^{\frac{2}{3}} \alpha ^{\frac{4}{3}} H^{\frac{2}{3}} A^{-1} F_0^{\frac{1}{3}} t, \quad f = \frac{1}{2} \pi F_0^{-1} b^2 w F, \\ q&= \frac{1}{4} \pi ^{\frac{1}{3}} \alpha ^{-\frac{4}{3}} H^{-\frac{5}{3}} F_0^{-\frac{1}{3}} b^2 w, \quad m = \frac{1}{2} \pi ^{\frac{1}{3}} \alpha ^{-\frac{1}{3}} H^{-\frac{2}{3}} F_0^{-\frac{1}{3}} b w. \end{aligned} \end{aligned}$$
(6)

The non-dimensionalised governing equations are

$$\begin{aligned} \frac{\,\mathrm {d}q}{\,\mathrm {d}\zeta } = m, \quad \frac{\,\mathrm {d}{m^2}}{\,\mathrm {d}\zeta } = \frac{q f}{m^2}, \quad \frac{\,\mathrm {d}f}{\,\mathrm {d}\zeta } = q \frac{\partial \delta }{\partial \zeta }, \quad \frac{\partial \delta }{\partial \tau } = q \frac{\partial \delta }{\partial \zeta }. \end{aligned}$$
(7)

These are equations for the fluxes of volume, momentum, and buoyancy in the plume, respectively, and describe the evolution of the density profile in the ambient. We solve Eqs. 7 numerically using a layered Germeles model and a second order Runge–Kutta scheme [10]. At each time-step, a new layer is introduced to the bottom of the density profile, with the volume and density in the layer computed from the turbulent plume equations (for more details see [10, 19]). The change in volume of other layers due to exchange with the plume is calculated from mass conservation, with the assumption that the volume taken up by the plume is much smaller than the volume of the box. The evolution of the dimensionless density profile is plotted in Fig. 2a. The position of the upper edge of the mixing region \(\zeta _0\),—also known as the first front—is plotted in Fig. 2b.

Fig. 2
figure 2

Filling box: a dimensionless density profile at \(\tau = 0.25, 1, 2, 4, 12\), b mixing efficiency \(\eta \) (blue, dashed) and the height of the stratified layer \(\zeta _0\) (orange, solid) against time non-dimensionalised by a filling box time scale, as defined in Eq. 6

Full size image

Calculation of the instantaneous mixing efficiency requires the rate of supply of available potential energy in the system and the rate of increase of background potential energy. In the non-dimensionalised problem all rates of energy transfer are in effect normalised by the rate of supply of available potential energy. Therefore the mixing efficiency is equal to the rate of increase of the normalised background potential energy, which is equal to the rate of increase of the normalised potential energy. We will assume the box volume is large compared to the volume taken up by the plume and therefore neglect the contribution of fluid in the plume to the potential energy budget.

The evolution of the mixing efficiency as the box fills is shown in Fig. 2b. At early times the mixing efficiency is low as parcels of fluid that are mixed in the plume are dense and always fall to the stratified layer at the bottom of the box, having transferred all their available potential energy into kinetic energy that is then dissipated viscously. The mixing efficiency increases monotonically with the height of the stratified layer, tending towards a maximum value of 1/2. At late times, the increase in density of the box induced by the presence of the buoyancy source is equally distributed through the full depth.

Another way of thinking about this is that a parcel of dense fluid introduced at the top of the box has an initial centre of mass associated with the anomalous density at \(z = H\). The resulting density change in the box is uniform as the parcel falls through the depth (assuming the fall time scale is much less than the filling time scale). Therefore the final centre of mass associated with the uniformly redistributed density anomaly is \(z = H/2\), or equivalently, half the initially available potential energy has been transformed by mixing into background potential energy.

3 The emptying-filling box

3.1 Mixing efficiency of the steady state

A plume model based on the use of an entrainment constant can be used to model the flow in an emptying-filling box. It has been shown, both theoretically and in laboratory experiments, that the emptying-filling box establishes a steady state [13]. In the steady state, the depth of the upper layer satisfies

$$\begin{aligned} \left( \frac{\xi ^{5}}{1-\xi }\right) ^{1/2} = \frac{A^*}{C^{3/2}H^2}, \end{aligned}$$
(8)

where \(\xi = h/H\) is the dimensionless depth of the ambient layer, \(C = \pi (\frac{5}{2\pi \alpha })^\frac{1}{3} (\frac{6 \alpha }{5})^\frac{5}{3}\) for an axisymmetric plume with Gaussian profiles, \(A^* = a_1a_2/\sqrt{\frac{1}{2}(a_1^2/c + a_2^2)}\), \(a_1\) and \(a_2\) are the areas of the upper and lower openings, and c is an order one constant associated with the loss coefficients of the two openings [11]. As the dimensionless effective opening area \(A^*\) is reduced towards zero, the dimensionless depth of the ambient layer \(\xi \) decreases. When \(A^*\) is increased, the dimensionless depth of the ambient layer increases towards one.

The steady state reached in the emptying-filling box has constant background potential energy, in contrast to the filling box. The rate of removal of background potential energy from the system by the flow through the box is exactly offset by irreversible mixing.

We calculate the rate of removal of potential energy from the system by recognising it must be equal to the instantaneous rate of increase in potential energy if the through flow were momentarily halted (while holding the other parameters constant). In calculating this rate we neglect the volume of gravitationally unstable fluid in the plume and consider only the globally stable two-layer stratification in the box. The potential energy (which is equal to the background potential energy) of the box at time t is

$$\begin{aligned} E_b(t) = \frac{g(\rho _m - \rho _a)(H-h)^2}{2} + \frac{g \rho _a H^2}{2}. \end{aligned}$$
(9)

For convenience, the vertical origin has been taken to be located at the bottom of the box. If the ventilation flow were switched off, but the plume forcing maintained, after a short time \(\varDelta t\) the background potential energy would be

$$\begin{aligned} E_b(t + \varDelta t) = \frac{g(\rho _m - \rho _a)(H-h + \varDelta t \, Q)^2}{2} + \frac{g \rho _a H^2}{2}, \end{aligned}$$
(10)

where Q is the flow rate of fluid across the interface in plume. The rate of removal of background potential energy from the system by the through flow is given by

$$\begin{aligned} E_b(t + \varDelta t) - E_b(t)&= \frac{g \varDelta t \, Q}{2}(\rho _m - \rho _a)(2(H - h) + \varDelta t \, Q). \end{aligned}$$
(11)

Dividing by \(\varDelta t\) and taking the limit \(\varDelta t \rightarrow 0\), gives the instantaneous increase in background potential energy as

$$\begin{aligned} \dot{E_b} = g(\rho _m - \rho _a)(H - h)Q. \end{aligned}$$
(12)

As buoyancy is conserved, \(g (\rho _m - \rho _a) Q = \hat{\rho } F_0\), therefore

$$\begin{aligned} \dot{E_b} = (H - h)\hat{\rho } F_0. \end{aligned}$$
(13)

This is the energy input required to maintain the height of the mixed layer against the action of the through flow. The result in (13) is independent of the choice of vertical origin.

The mixing efficiency is the ratio between the rate of increase in background potential energy and the rate at which available potential energy is supplied to the system (Eq. 1). We assume that any kinetic energy associated with the openings is dissipated without mixing the density profile, therefore the energy available for mixing is the available potential energy. Substituting the values for the background potential energy (Eq. 13) and available potential energy (Eq. 4), we find

$$\begin{aligned} \eta = 1 - \xi , \end{aligned}$$
(14)

where \(\xi = h/H\) is the non-dimensional depth of the ambient layer. If there is a thick mixed layer (i.e., a thin ambient layer, \(\xi = h/H \rightarrow 0\)), the mixing efficiency increases towards 1, while if the mixed layer thickness decreases (i.e., the ambient layer depth increases), the mixing efficiency decreases towards zero.

We can understand this by considering the balance between available potential energy and kinetic energy in the flow. As the plume falls, fluid loses available potential energy to kinetic energy, until the plume reaches the mixed layer. When the plume enters the mixed layer little further mixing can occur as the mean density in the plume is equal to the density of the mixed layer. If the mixed layer is relatively thin the plume falls almost the entire height of the box before being arrested, losing almost all available potential energy to kinetic energy, which is then dissipated, resulting in a low mixing efficiency.

Fig. 3
figure 3

Emptying-filling box in steady state: mixing efficiency \(\eta \), as a function of the opening area \(A^*\), box height H, and entrainment coefficient \(\alpha \)

Full size image

By substituting for the layer depth in Eqs. 14 and 8, the mixing efficiency may be expressed implicitly as a function of the dimensionless effective opening area \(A^*\), box height H and the entrainment coefficient \(\alpha \),

$$\begin{aligned} \frac{\eta }{(1 - \eta )^5} = \frac{1}{3 \pi ^2} \left( \frac{5}{6}\right) ^4 \frac{(H \alpha )^4}{A^{*2}} \end{aligned}$$
(15)

The behaviour of \(\eta \) as a function of \(\frac{H \alpha }{\sqrt{A^*}}\)is plotted in Fig. 3. Dimensional analysis of the problem shows that the mixing efficiency is a function of the non-dimensional groups \(A^*/H^2\) and \(\alpha \). The above analysis has identified the form of this function.

The entrainment coefficient is often considered as a constant for a plume, but in other flows the entrainment coefficient is different from the value measured for plumes [8]. As a thought experiment we can examine the effect on the mixing efficiency of varying the entrainment coefficient while holding \(A^*/H^2\) constant. Decreasing the entrainment coefficient reduces the mixed layer depth and decreases the mixing efficiency. However, the value of the mixing efficiency is not solely determined by the entrainment coefficient, as the full range of values from 0 to 1 is theoretically possible by varying only \(A^*\).

3.2 Mixing efficiency of the transient state

We can create a simple model for the transient density profile in an emptying-filling box by adding an equation for the ventilation rate to our model from Sect. 2.2 [2]. The ventilation rate is driven by the pressure difference between the top and bottom openings, which is determined by the density profile in the tank. In our model, the ventilation rate is given by

$$\begin{aligned} Q_{v} = A^* \left( \int _{0}^{H} g' \,\mathrm {d}z\right) ^{\frac{1}{2}}, \end{aligned}$$
(16)

where \(g'\) is the reduced gravity [19]. When we non-dimensionalise (as in Eq. 6), Eq. 16 becomes

$$\begin{aligned} q_{v}&= \frac{1}{8 \pi }\, \frac{A^*}{\alpha ^2 H^2} \left( \int _{0}^1 \delta \,\mathrm {d}\zeta \right) ^{\frac{1}{2}} \end{aligned}$$
(17)

where \(q_{v}\) is the non-dimensional ventilation rate and \(\delta \) is the density at height \(\zeta \). A similar model for the emptying-filling box was used by Sandbach and Lane-Serff, who used a modified version of the equation that links plume volume flow rate and layer heights in the ambient [19].

In our model, we calculate the effect of the plume on the stratification in the box as before (Sect. 2.2). The ventilation flow is included by shifting the stratification down by \(\zeta _v = q_v \varDelta \tau \) and then removing a layer of dimensionless thickness \(\zeta _v\) from the bottom. The potential energy of the box \(E_{box}\) and the change in potential energy before and after the ventilation occurs are calculated at each time step.

Fig. 4
figure 4

Emptying-filling box for \(A^* C^{-3/2} H^{-2} = 0.02\): a dimensionless density profile in an emptying-filling box at \(\tau = 0.5, 1, 2, 5, 20\), b mixing efficiency of an emptying-filling box \(\eta \) (solid, blue), normalised rate of change of potential energy inside the box \(\dot{E}_{box}\) (dashed, orange), normalised rate of loss of potential energy due to ventilation \(\dot{E}_{vent}\) (dashed, yellow) and the height of the stratified layer \(1 - \xi \) (dotted, green) against non-dimensional time

Full size image

The evolution of the density profile for \(\frac{A^*}{C^{3/2} H^2} = 0.02\) is plotted in Fig. 4a. A stratified layer grows until the stack pressure difference across the box is sufficient to drive a strong enough ventilation flow through the box to match the flow into the mixed layer by the plume. There is some overshoot of the steady state mixed layer height (cf. \(\tau =5\) and \(\tau = 20\)). By \(\tau = 20\) the box has essentially reached a steady state two-layer stratification.

We calculate the potential energy of the evolving stratification in the box, \(E_{box}\). The evolution of the normalised \(\dot{E}_{box}\) is plotted in Fig. 4b (dashed, red). At early times, \(\dot{E}_{box}\) is positive as the potential energy of the box grows with time. At \(\tau \approx 2\) the rate of increase of potential energy reaches a peak. At late times the box is in steady state, therefore the potential energy of fluid in the box does not change with time and \(\dot{E}_{box} = 0\). Our energetics analysis reveals that the rate of change of potential energy of fluid in the box peaks before the height of the mixing region reaches its maximum.

The rate of potential energy loss due to ventilation, \(\dot{E}_{vent}\), is equal to the rate of potential energy increase if the ventilation flow was momentarily switched off in the model (e.g., if the lower vent were closed). The evolution of the normalised \(\dot{E}_{vent}\) is plotted in Fig. 4b (dashed, yellow). There is initially little stratification within the box to drive a ventilation flow, therefore \(\dot{E}_{vent}\) is small. As a stratified layer builds up, a ventilation flow is established and \(\dot{E}_{vent}\) increases.

The total rate of change of background potential energy for the system is \(\dot{E}_b = \dot{E}_{box} + \dot{E}_{vent}\). The instantaneous mixing efficiency of the transient case can be calculated from \(\dot{E}_b\). As we have normalised quantities by the available potential energy input, for our system \(\eta = \dot{E}_b\). The instantaneous mixing efficiency, \(\eta \), is plotted in Fig. 4b (solid, blue). Note that although the stratified layer height in the box overshoots, the mixing efficiency increases monotonically up to a maximum value of \(1 - \xi \). At early times the mixing efficiency is dominated by the growing stratification in the box, with little loss of background potential energy due to the ventilation flow. At \(\tau > 2\) the rate of change of background potential energy, and therefore the value of the mixing efficiency, begins to be dominated by the ventilation flow rate, which increases monotonically. The mixing efficiency approaches \(1 - \xi \) as the box approaches a steady state.

4 Discussion

As our purpose for this paper is to extend understanding of the mixing efficiency, we will discuss various ways to interpret and compare the two examples described above.

The filling box has a maximum mixing efficiency of \(\eta = \frac{1}{2}\) that occurs when the filling box reaches an asymptotic state in which the potential energy of the box is constantly increasing, but the density profile has reached a self-similar shape and the density gradient is no longer a function of time. In this asymptotic state, the rate at which the density changes is independent of height, with the position of the centre of mass remaining unchanged in the box. In other words, buoyancy introduced by the plume source travels through a vertical distance that is on average equal to half the height of the box, resulting in a mixing efficiency of \(\eta = \frac{1}{2}\). Importantly, this is a result of the uniform distribution of the rate of density change and is independent of both the exact shape of the density profile and the value of the entrainment coefficient.

For the emptying-filling box, a true steady state is reached, where both the density profile and background potential energy are constant. The steady state consists of an ambient layer and a mixed layer; the density of the mixed layer is approximately constant and equal to the average density of the plume at the height of the interface with the ambient layer. The ventilation flow removes mixed fluid from the bottom of the box and draws ambient fluid into the top of the box. To keep the box in steady state, buoyancy from the plume mixes with incoming ambient fluid to maintain the mixed layer. The maximum mixing efficiency is attained when the mixed layer fills the box. The buoyancy produced by the plume is then diluted in the vicinity of the source and the mixed fluid effectively remains near the top of the box. This situation results in a maximum mixing efficiency of \(\eta = 1\).

It is instructive to note that reducing the effective opening area \(A^* \rightarrow 0\) for the emptying-filling box does not recover the same mixing efficiency as the filling box. The filling box is a closed system and the mixing efficiency is limited by how much mixing can occur. Assuming an asymptotic state is reached (in which the vertical density gradient remains unchanged at a given height), subsequent changes in density with time must be uniformly distributed through the depth, leading to the result that the mixing efficiency is \(\eta = \frac{1}{2}\). However, the through-flow in the emptying-filling box allows the system to have a mixing efficiency in excess of \(\frac{1}{2}\)—fluid mixed near the plume source enters the well-mixed layer, in which it can reside at any height without energetic cost. Thus, the mixed fluid can be interpreted from an energetics perspective as remaining at the top of the mixed layer, and when the mixed layer nearly fills the box almost all the initial available potential energy is converted to background potential energy.

Another way of understanding this result is by considering the work that the plume does on the flow. For the closed circulation to exist in the filling box, the ambient stratification needs to be continuously displaced in the vertical at all heights in the box. This circulation requires work against buoyancy throughout the box and necessarily accounts for a portion of the available potential energy supplied by the plume source. In contrast, when the emptying-filling box reaches steady state, there is no recirculation that requires a continual input of energy to maintain it. Fluid in the plume is buoyant only as it passes through the ambient layer, and conversion of available potential energy to kinetic energy is therefore limited to this part of the box. Thus, as the ambient layer thickness decreases in the emptying-filling box, the plume transforms less of the available potential energy into kinetic energy, decreasing the proportion of energy that is dissipated viscously and increasing the mixing efficiency.

In this paper, we have quantified stratified turbulent mixing in filling boxes and emptying-filling boxes using the mixing efficiency. The entrainment coefficient also measures mixing in these flows, as it parameterises the approximately self-similar physics that govern entrainment of ambient fluid into a turbulent free-shear flow, a process that occurs throughout the depth for a plume in a filling box. The entrainment process is modified in the emptying filling box; incorporation of buoyancy and momentum (i.e., plume-like behaviour) is confined to the ambient layer, and buoyancy becomes unimportant in the mixed layer (i.e., jet-like behaviour). In reality, there is a variation of density across the plume cross-section and some mixing will occur in the mixed layer. Although this effect is likely to have a minor effect on the overall mixing efficiency, three-dimensional measurements of the buoyancy field from laboratory experiments or direct numerical simulations could be used to confirm the expectation. This would be an interesting area for future research.

To summarise, we have seen that a closed system with continuous net buoyancy forcing can only establish an asymptotic time-evolving density stratification, which has an energetic cost that tends to lower the mixing efficiency. In contrast, a steady density stratification can be established in an open system with continuous net buoyancy forcing. Where that buoyancy forcing produces mixed fluid that is close to its neutral buoyancy level in the background density distribution, the mixing efficiency can approach one.