Experimental investigation of a line plume in a filling box

Abstract

A series of experiments were conducted to quantify the dynamics of a filling box driven by a line plume that spans the full width of the enclosure. Three configurations were tested namely symmetric (centrally located plume), wall-bounded (plume attached to an end wall), and asymmetric. The front movement for the symmetric and wall-bounded configurations was well described by the standard filling box model. The front movement results indicate that the typical value of the entrainment coefficient $\left( \alpha \right)$ for an unconfined plume ($\alpha = 0.16$) could be used to accurately predict the front movement for both the centrally located plume and the wall-attached plume. This is in contrast to other studies that suggest that wall-bounded plumes have a significantly lower entrainment coefficient. The standard filling box model broke down for the asymmetric configuration. As the plume was closer to one wall than the other, the plume outflows that spread out and reflected off the end walls returned to the plume at different times. This created a pressure imbalance across the plume that caused the plume to bend sharply toward the nearest wall. Analysis of the plume outflow as a constant flux gravity current showed that the outflow velocity scaled on the cube root of the plume buoyancy flux per unit width $f$, a result confirmed by further experiments. This result was used to quantify the time at which the plume bends and the standard filling box model breaks down.

1 Introduction

The filling box model, first proposed by Baines and Turner [1], considers a localized source of buoyancy in an enclosure that is initially unstratified. The localized buoyancy source forms a plume that rises to the top of the enclosure and spreads out forming a buoyant upper layer. Over time the buoyant upper layer thickens as more buoyant fluid is added to it from the plume and the interface between the upper buoyant layer and lower ambient layer, the so-called first front, descends toward the buoyancy source. Herein the buoyancy source is taken to be positively buoyant though, for Boussinesq plumes, the flow development is the same regardless of the sign of the buoyancy source.

The initial model was proposed as a conceptual model for the development of a stratification in a lake or sea due to localized convection though it has been extended and applied to many other flows including analyzing liquefied natural gas tanks [2], smoke spread in compartment fires [3], and natural ventilation of buildings [4]. A variety of buoyancy source geometries, other than simple point sources, have also been considered in filling box flows including vertically distributed line sources [5], horizontal lines sources next to a wall [6], and buoyancy sources evenly distributed along a vertical wall [6,7,8]. While the original paper by Baines and Turner [1] covers the theoretical modeling of a filling box model for a line plume, there is a dearth of experimental data on the front movement for a filling box flow driven by a line plume that is not attached to a side wall.

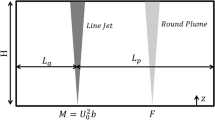
Line plumes from a horizontal line source are ubiquitous in the natural and built environments. For example, line plumes can form below cracks in ice sheets where there is preferential freezing and salt rejection [9]. Line plumes can also be formed at the front of wildfires [10, 11] or above lines of computers in a data center. The entrainment modeling approach, first presented by Morton et al. [12], when applied to horizontal line sources leads to the following equation for the vertical volume flow rate per unit width

$$ q = \left( {\frac{f}{2\alpha }} \right)^{{\frac{1}{3}}} 2\alpha z = Cf^{{\frac{1}{3}}} z $$

(1.1)

Herein $f$ is the source buoyancy flux per unit width, $z$ is the vertical distance from the source to the interface and $\alpha$ is the entrainment coefficient appropriate for a turbulent line plume with an assumed top-hat velocity and buoyancy profile. There are a broad range of values of the entrainment coefficient reported in the literature. A review by Lee and Chu [13] cites the values of $\alpha$ ranging from $\alpha = 0.1$ [14] to $\alpha = 0.22$ [15]. They reported $\alpha = 0.16$ based on measurement of the entrainment flow. A review of the growth rate of the plume width by Chu [16] indicates a value of $\alpha = 0.17$. There is also evidence that the value of the entrainment coefficient decreases when the line plume is attached to a vertical wall [6] though, again, there are a broad range of reported values.

While there is extensive literature on the filling box model and on experimental measurements of line plumes, there is, to the best of the authors’ knowledge, almost no published research on line plumes in a filling box other than the recent paper by George et al. [17] that reports results of a LES simulation of the meandering on a centrally located line plume in a filling box but does not report data on the front movement.

This paper reports results of a series of experiments to examine the flow in a rectangular enclosure induced by a turbulent line plume that spans the full width of the box. Results are presented for experiments in which the plume is centrally located within the enclosure, for when the plume is next to one of the end walls, and for when the plume is located between the enclosure end wall and centerline. When the plume is located off-center but away from the wall the plume is observed to tilt toward the nearest wall part way through the filling process. The time at which the plume tilts is also reported and discussed. The remainder of the paper is structured as follows. The basic filling box model is reviewed in Sect. 2 and extended for the case of an asymmetrically located plume. The experimental methods used in this study are presented in Sect. 3 including a detailed description of the nozzle design used for generating a steady line plume. Qualitative flow descriptions and experimental results for the movement of the first front are described in Sect. 4 and Sect. 5 respectively. Measurements and analysis of the plume outflow and its influence on the bending time for the plume are presented in Sect. 6. Conclusions are drawn in Sect. 7.

2 Model development

This paper considers a line plume in an enclosure of height $H$, length $L$ and width $W$. The plume has a buoyancy flux per unit width $f$, spans the full width $W$ of the enclosure, is normal to the side walls, and is located a distance $\lambda L$ from the right-hand side end of the enclosure. See Fig. 1 for a schematic diagram of this configuration. This can be reduced to a two-dimensional problem with flow parameters expressed per unit width. Without loss of generality, it is assumed that $\lambda \le 0.5$, that is, it is assumed that the right-hand-side has a width that is either equal to or less than that of the left-hand-side.

Fig. 1

Schematic diagram of an asymmetrically located line plume in a filling box showing the buoyant layers on each side of the plume filled by the symmetric outflow from the plume

In the following analysis it is assumed that the plume remains vertical and symmetric and effectively divides the enclosure into distinct left-hand-side (subscript ‘$l$’) and right-hand-side (subscript ‘$r$’) zones. When the plume reaches the base of the enclosure it spreads out away from the plume toward the side walls. As the plume is assumed to be vertical and symmetric the volume entrained into the plume from each side is the same and, therefore, conservation of volume requires that the outflow volume flux is also the same on both sides. However, this is not the case when the plume is attached to the wall ($\lambda = 0$) as fluid is only entrained on one side of the plume and the outflow is unidirectional. Further, as it will be shown in the experimental results section, the symmetry breaks down as soon as the plume outflow on the right-hand side reflects back off the end wall and reaches the plume. At this point the plume bends toward the right-hand wall. The timing and nature of this bending is discussed in detail in Sect. 6.

The outflow creates buoyant lower layers in each side of the plume that thicken over time as more plume outflow fluid is added to them. The vertical distance from the plume source to the top of each layer are denoted by $h_{l}$ and $h_{r}$. Conservation of volume for the buoyant layers on each side results in

$$ \frac{{d\left( {1 - \lambda } \right)L\left( {H - h_{l} } \right)}}{dt} = \frac{1}{2}Cf^{{\frac{1}{3}}} h_{l} \;{\text{and}}\;\frac{{d\lambda L\left( {H - h_{r} } \right)}}{dt} = \frac{1}{2}Cf^{{\frac{1}{3}}} h_{r} $$

(2.1)

for the right-hand-side and left-hand-side respectively. The solutions to (2.1) for the interface height over time are

$$ h_{i} = He^{{ - \frac{t}{{T_{fill.i} }}}} $$

(2.2)

where $T_{fill.i}$ are the filling times for the particular sides $i$ and are given by

$$ T_{fill.l} = \frac{{2\left( {1 - \lambda } \right)L}}{{Cf^{{\frac{1}{3}}} }}\;{\text{and}}\;T_{fill.r} = \frac{2\lambda L}{{Cf^{{\frac{1}{3}}} }} $$

(2.3)

respectively. For the asymmetric case ($0 < \lambda < 0.5$) the filling time for the right-hand-side is less than the filling time for the left-hand-side and will fill up more rapidly. When $\lambda$ = 0.5 the problem is symmetric and both filling times are the same. For the case when the plume is attached to the side wall ($\lambda = 0$) the outflow will be exclusively away from the wall. However, the plume will only be entraining fluid from one side and should be modeled as a plume of buoyancy flux $2f$ for which half the plume volume flux flows out into the enclosure and the other half flows into a mirrored virtual enclosure on the other side of the wall. In this case

$$ T_{fill.l} = \frac{2L}{{C\left( {2f} \right)^{{\frac{1}{3}}} }}. $$

(2.4)

These results are dependent on the underlying assumptions of the original filling box model. In particular, the model assumes that (1) the plume outflow is instantaneous and infinitesimally thin and (2) that there is no mixing of ambient fluid into the buoyant layer and that it is supplied with fluid only by the plume outflow. This is a reasonable approximation for a point source plume in an enclosure that is substantially wider than it is tall as the plume outflow will slow down as it spreads radially (see Kaye and Hunt [18]). However, the outflow from a confined line plume will be a constant flux gravity current [19] with constant velocity as opposed to a radial constant flux gravity current [20] with a velocity that decreases with distance from the plume. Therefore, it is possible that the plume outflow thickness may be significant in the flow development and that there could be overturning at the end walls. The modeling of the outflow is presented in Sect. 5. The goal of the experiments presented below is to evaluate the filling box model presented above and to assess the applicability of the standard filling box model assumptions to the case of a confined line plume.

3 Experimental setup

A series of experiments were conducted to better understand the flow development from a line plume in a filling box. Experiments were run in two visualization tanks one that was 61.0 cm by 31.5 cm and 42.5 cm deep and a larger tank that was 244.5 cm by 30.5 cm and 30.5 cm deep. The line plume was formed by the release of a dense salt solution along a line across the short horizontal dimension at the top of the tank. The tank was filled with freshwater and the saltwater was dyed with red food coloring for flow visualization. While it is possible to measure the concentration of the dye by backlighting the tank and careful calibration (see Algayer and Hunt [21]), the space available for these experiments could not be sufficiently darkened to allow accurate results. As such, the dye was used for visualization and tracking the front movement.

The line source of buoyancy was developed using an innovative nozzle design that was built for this project. The nozzle consisted of two concentric tubes. The inner tube was supplied with fluid from a constant head tank from both ends and had a series of small holes evenly distributed along the length of the tube. The outer tube encased the inner tube and had a narrow slot (3.2 mm wide and 230 mm long for the small tank of width 315 mm, and 210 mm long for the large tank of width 305 mm) cut along the length of the tube pointing downward. Due to the fittings at either end of the tube, the slot did not extend to the full width of the tank. However, the plume that formed rapidly spread out at each end and reached the side walls well above the base of the tank such that, for the vast majority of the plume height, it was spread across the full width of the tank. A schematic diagram of the nozzle showing the two tube configuration is shown in Fig. 2 along with a photograph of one of the nozzles used.

Fig. 2

a Schematic diagram of the nozzle design showing the outer tube with the slot and the concentric perforated inner tube. b Photograph of the nozzle showing the slot and the connectors used to supply salt solution to each end of the inner tube

The combination of feeding the inner tube from both ends and the use of small holes that dominated the head loss in the tube ensured that there was a fairly even distribution of outflow along this tube. The saltwater discharged upward flooding the outer tube and then fell evenly out of the lower slot. Provided flow rate was large enough (at least 250 cubic centimeters per minute) then the outflow was observed to be uniform across the length of the tube. This was checked by observing the front of the fluid that initially fell from the nozzle when the saltwater supply was first turned on.

The nozzle was fed with dyed saltwater that was supplied by a constant head tank that had the supply water surface located 95 cm above the top of the tank. The flow rate into the nozzle was measured using an inline rotameter flow rate meter that had a built-in needle valve to control the flow rate. A quarter turn control valve was located downstream of the flow rate meter to rapidly turn the flow rate on and off. A schematic diagram of the experimental setup is shown in Fig. 3.

Fig. 3

A schematic of the experiment showing a reservoir with constant head of dyed fluid, flowmeter, plume nozzle, ambient fluid in quiescent environment in a rectangular transparent tank, and a buoyant line plume flowing downward

The inline rotameter flow rate meters were calibrated for freshwater and so had to be re-calibrated for various salt solutions. This was done by measuring the time taken for a known volume of fluid to pass through the flow rate meter into a measuring cylinder. The measured flow rate was then plotted against the flow rate reading on the rotameter and a linear calibration curve was fitted. This was done for two different saltwater densities. The linear calibration curves are given by the equations of $Q = 0.923 \times R + 0.524$ and $Q = 0.987 \times R + 8.58$ respectively for the densities of 1.102 gm/cm³ and 1.15 gm/cm³. Both the measured flow rate $Q$ and the rotameter reading $R$ have units of cubic centimeters per minute (CCM).

All experiments were filmed using a Canon JVC AP-V20U digital camera recording color video at 30 frames per second. The camera was mounted to face the long side of the tank such that the plume axis was normal to the plane of view. For the small tank experiments, the tank was backlighted using a square LED photographic soft box. The large tank experiments were conducted with ambient light with the tank located in front of a lightly colored wall.

Each experiment was conducted using the same procedure. First, the salt solution was produced, dye added, and the constant head tank pump turned on to generate the recirculation required to maintain the constant head. The tubing downstream of the control valve was detached and the needle valve turned on so that the tube flooded with saltwater up to the location of the control valve that was then turned off (leaving the needle valve on). The visualization tank was then filled with fresh water and disturbances were allowed to settle out. The density of the freshwater $\rho_{f}$ and saltwater $\rho_{s}$ were then measured using an Anton Paar DMA 35 84138 digital density meter. Finally, the nozzle was immersed into the visualization tank to remove any air bubbles and the nozzle was then connected to the feeder tube downstream of the control value. When any further disturbances in the visualization tank had settled down, the camera started recording, the control valve was turned on and the experiment began. Once the experiment started the rotameter reading was recorded. The needle valve was then adjusted as needed during the experiment to ensure that the reading remained constant. Once the first front reached the nozzle the camera recording was stopped, and the control valve closed.

After each experiment the video was downloaded for post-processing and the experimental settings were recorded (fluid densities and rotameter reading $R$). This data was then used to calculate the plume source reduced gravity

$$ g^{\prime} = g\frac{{\left( {\rho_{s} - \rho_{f} } \right)}}{{\rho_{f} }}, $$

(3.1)

the source flow rate $Q$ based on the reading $R$ and the appropriate calibration curve, and the plume buoyancy flux $F = g'Q$. Experiments were run for values of $\lambda =$ 0, 0.1, 0.2, 0.25, 0.33, 0.4, and 0.5 in the small tank and for $\lambda =$ 0.25 and 0.5 in the large tank.

The video for each experiment was analyzed using a MATLAB script that cropped the image, corrected it for variations in the background light intensity, converted to greyscale, took a horizontal average of each frame, and then concatenated the horizontal averages to give a time series of the horizontal average of vertical light intensity. While the video was recorded at 30 frames per second, only one frame per second was analyzed. The cropped image from each frame did not cover the entire height of the experiment as, at the base of the tank, there was a structural black plastic strip. The top of the image was cropped at the height of the nozzle outlet. However, this is the height of the physical source whereas the filling box model assumes an idealized infinitesimally thin line source. To correct for this a first order virtual origin correction was made that projected back to the virtual origin based on the half width of the plume spreading rate and the half width of the nozzle slot. See Hunt and Kaye [22] for details on this and higher order virtual origin corrections. A sample image of one of the concatenated images re-scaled based on the scaled height and non-dimensional time is shown in Fig. 4.

Fig. 4

False color image of the concatenated light intensity for an experiment with $\lambda = 0$. The arrows indicate the top and bottom of the cropped image with the white space indicating the image loss to the structural strip at the base (red arrow) and the virtual origin correction at the top (green and purple arrows show the locations of original source and virtual source respectively)

4 Flow description

A series of experiments were run to better understand the behavior of a line-plume filling box flow. Experiments were run for seven different values of $\lambda$ and a variety of source buoyancy fluxes (see “Appendix”). The configurations can be broadly broken down into three categories, namely wall-bound ($\lambda = 0$), symmetric ($\lambda = 0.5$) and asymmetric ($0 < \lambda < 0.5$). While the symmetric and wall-bounded flows were somewhat similar the asymmetric configuration was distinctly different.

For the wall-bounded configuration the plume formed at the base of the nozzle and bent toward the end wall attaching to the wall just below the nozzle. The plume then flowed down the wall and spread out. The outflow spread across the base of the tank and then rose most of the way back up the opposite end wall before slumping back down and propagating back toward the plume. Waves propagating along the surface of the fresh-water to salt-water interface persisted for some time after the initial outflow returned to the plume side. A series of images from a sample experiment is shown in Fig. 5. One thing to note is that the plume outflow is quite thick and is a larger fraction of the tank depth than has been observed for round plumes in a filling box [18, 23].

Fig. 5

Images from a sample experiment where λ = 0, taken at a 0 s, b 24 s, c 50 s, and d 186 s

The symmetric case ($\lambda = 0.5$) behaved in a similar manner to the wall-bounded case as can be seen in Fig. 6. However, in this case, there appears to be some degree of overturning by the flow after it rises up the end walls. This will lead to a thickening of the dense layer at a slightly faster rate than predicted by the standard model.

Fig. 6

Images from a sample experiment where λ = 0.5, taken at a 0 s, b 24 s, c 50 s, and d 186 s

The asymmetric case is initially similar, the plume reaches the base of the enclosure, spreads out, reflects off the end wall and propagates back to the plume. See Fig. 7a, b for images from a sample experiment with $\lambda = 0.33$. However, due to the asymmetry, the return flow on the short side (right in this case) returns to the plume before the return flow from the long side. At this time the plume bends sharply toward the short side of the enclosure. See Figs. 7c, d for images of this bending. Later in the experiment, the plume returns to being more vertical (see Fig. 7e, f). A number of things are worth noting about this behavior. First, as the plume deflects to the short side the plume is no longer vertical when it impinges on the base of the tank and the outflow will not be symmetric. However, this does not result in preferential outflow in the direction in which the plume bends. Rather there is a higher hydrostatic pressure force on the short side (the side toward which the plume bends) compared to the long side which drives much of the outflow back toward the long side. This is shown schematically in Fig. 7d.

Fig. 7

Images from a sample experiment where λ = 0.33, taken at a 0 s, b 15 s, c 24 s, d 35 s, e 50 s and f 122 s. Also show in d is a schematic of the plume centerline (dashed line) and the outflow paths on either side of the plume

There are a number of possible explanations as to why the plume bends so dramatically when the short side return flow reaches the plume. One possibility is that the dense layer on the short side is considerably deeper than that on the long side and, as such, there is a hydrostatic pressure imbalance at the base of the plume that drives flow from the short to the long side. This flow must be balanced by a flow in the other direction higher up that pushes the plume over toward the short side. This is analogous to the bending of an air curtain (vertical planar jet) by the temperature difference across the curtain as shown by Hayes and Stoecker [24, 25].

A second explanation is that when the return flow reaches the plume the plume becomes aware, so to speak, of the finite nature of the enclosure on the short side. There is, therefore, a limited volume of fluid from which to entrain and there is an induced low pressure on the short side due to blockage of the entrainment field by the side wall. This would be similar to the mechanism that leads the wall-bounded plume to attach to the end wall despite being released about 1 cm away from the wall and flowing down (see Fig. 5), a mechanism commonly termed as the Coanda effect [26].

5 First front movement

For each experiment, the front movement was tracked using the concatenated horizontal averages of the light intensity for windows cropped from each side of the plume. Though, for $\lambda = 0$ the plume was attached to the wall so there is only one window. The concatenated images are then re-scaled and plotted with the vertical axis representing the non-dimensional height $h_{i} /H$ and the horizontal axis being non-dimensional time $\tau_{i} = t/T_{fill.i}$. This means that the non-dimensional time for each side of the plume is scaled on the filling time for that side of the plume (see 2.3). Overlaid on these images is the theoretical prediction (2.2) using a value of $\alpha = 0.16$ ($C = 0.47$) that is in the middle of the range of values reported in the literature.

Front movement plots for the wall-bounded ($\lambda = 0$) and symmetric ($\lambda = 0.5$) cases in the small tank are shown in Figs. 8 and 9 respectively. In both cases the model does a good job of tracking the front movement over time. There is an initial discrepancy when the layer thickens rapidly due to the plume outflow and reflection from the end walls. However, this process was observed to result in minimal overturning such that the total volume of the dense layer is due almost entirely to fluid from the plume. Therefore, after these initial spikes, the front movement settles down and is well described by the model.

Fig. 8

False color image of the concatenated light intensity for an experiment with $\lambda = 0$ with the model prediction (2.2) overlaid in the thick black line

Fig. 9

False color image of the concatenated light intensity for an experiment with $\lambda = 0.5$ with the model prediction (2.2) overlaid in the thick black line. Results are for the a left hand side and b right hand side

One interesting point to note is that the results presented herein show that the value of $\alpha = 0.16$ that is typical for a free line plume, that is one not attached to a wall, well describes the front position for the filling box with the wall-bounded plume. This is in contrast with some previous studies of wall source plumes that seem to show substantially reduced entrainment. See, for example, Bonnebaigt et al. [6], Kaye and Cooper [7], and Cooper and Hunt [8]. Though this is not a direct comparison as these studies focused on plumes where the buoyancy source was distributed over the wall surface not simply injected next to the wall and then allowed to flow along with it. However, it is clear from Fig. 8 that the results presented herein do not indicate a significant change in entrainment as a result of the line plume attaching to a wall. To emphasize this point the data in Fig. 8 are re-plotted in Fig. 10 with additional model plots for the upper and lower bounds of the entrainment coefficient cited above. It is clear that the experimental front movement is bounded by the model predictions and that it does not support the idea that the entrainment is significantly reduced by the presence of the wall [6, 8]. However, it is important to note that this is a single data point and is therefore not conclusive and that this is not the focus of this study.

Fig. 10

Comparison of front movement predictions for different values of the entrainment coefficient $\alpha$ for wall-bounded plume (λ = 0); red—$\alpha = 0.22$ ($C$ = 0.57), black—$\alpha = 0.16$ ($C$ = 0.47), and white—$\alpha = 0.1$ ($C$ = 0.34)

The results for the asymmetric cases show considerably less agreement with the model of (2.2). This is not particularly surprising as the sharp bending of the plume and the resulting return flow across the plume within the dense layer violates the assumptions of the model, namely that the plume remains vertical and effectively sub-divides the enclosure. See Fig. 11 for experimental front position plots for asymmetrically located line plumes.

Fig. 11

False color image of the concatenated light intensity for the asymmetric experiments with the model prediction (2.2) overlaid in the thick black line. Results on the left and right are for the left hand side and right hand side of the tanks respectively. From top to bottom $\lambda$ increases in the plots which are for $\lambda = 0.1$ (a, b), $\lambda = 0.2$ (c, d), $\lambda = 0.25$ (e, f), $\lambda = 0.33$ (g, h), and $\lambda = 0.4$ (i, j). $\tau$ is the non-dimensional time appropriate for the given side of the tank. As such, the left-hand-side images (a, c, e, g, i) are cropped so that both images for a given $\lambda$ end at the same non-dimensional time

The data in Fig. 12 shows that the front position for the left-hand side (long side) is always under-predicted by the model, though it is the closest to the model for $\lambda = 0.4$ which is the case tested that is the nearest to the symmetric case. The interface height is higher, that is, the dense layer is thicker, because the outflow from the plume flows preferentially to the left after it tilts to the right as described above. The images for the right-hand-side are less clear in part because the cropping window was at times quite small and, after the plume bent over, the plume was often within the image window that was horizontally averaged. This is particularly clear in the plot for the right-hand-side for $\lambda = 0.1$ (Fig. 11b).

Fig. 12

Control volume for the impingement zone showing the inflow and outflow, outflow depth and front velocity. Note that H is measured from the plume virtual origin to the base of the tank

6 Outflow movement and plume bending time

The bending of the plume towards the nearest end wall of the enclosure has a significant influence on the resulting front movement. To better understand the time scale for this process a series of experiments were run to measure the time at which the plume bends. Observations of these experiments showed that the bending occurs when the plume outflow returns back to the plume having reflected off the nearest wall. The process is, therefore, controlled by the velocity of the plume outflow. A separate set of experiments were run in the large enclosure to track the front velocity of the plume outflow for a range of buoyancy fluxes. For each experiment, the position of the front was measured every second until the front reached the end wall. Results showed that the front velocity was constant with time for a given plume buoyancy flux and increased with increasing buoyancy flux. This is consistent with the literature on constant flux gravity currents [19]. We note that a similar problem has been addressed by [27] for the case where there is a mean flow along the channel and the buoyancy source is localized, rather than spanning the entire width of the channel.

It is assumed that, prior to the plume bending, the plume outflow is divided evenly between the two sides. Further, it is assumed that the outflow thickness is approximately constant and is denoted herein by $h'$. Drawing a finite control volume around the impingement zone (see Fig. 12), applying conservation of volume for the steady flow, and assuming that the outflow velocity is uniform both vertically and horizontally leads to

$$ \frac{1}{2}Q_{plume} \left( {z = H - h^{\prime}} \right) = \frac{1}{2}Cf^{{\frac{1}{3}}} \left( {H - h^{\prime}} \right) = h^{\prime}U_{f} $$

(6.1)

here $H$ is the distance from the plume line source (virtual origin) to the base of the tank and $U_{f}$ is the front velocity of the outflow. Solving for $U_{f}$ leads to

$$ U_{f} = \frac{1}{2}Cf^{{\frac{1}{3}}} \left( {\frac{H}{{h^{\prime}}} - 1} \right) = \frac{1}{2}Cf^{{\frac{1}{3}}} \left( {\frac{1}{\phi } - 1} \right) $$

(6.2)

where $\phi = h^{\prime}/H$.

The dynamics of a constant flux gravity current are controlled by a frontal Froude number constraint given by

$$ Fr = \frac{{U_{f} }}{{\sqrt {g^{\prime}h^{\prime}} }} = \left( {\frac{2 - \phi }{{1 - \phi^{2} }}} \right)^{{\frac{1}{2}}} . $$

(6.3)

See Simpson (1982) for more details on constant flux gravity currents. The outflow buoyancy,$g'$ will be the buoyancy of the plume as it enters the control volume and is given by

$$ g^{\prime} = \frac{f}{q} = \frac{{f^{{\frac{2}{3}}} }}{{C\left( {H - h^{\prime}} \right)}}. $$

(6.4)

Solving (6.2)–(6.4) simultaneously leads to

$$ \phi = 0.19,Fr = 1.37\;{\text{and}}\;U_{f} = 1.0f^{{\frac{1}{3}}} $$

(6.5)

for $C = 0.47$ ($\alpha = 0.16$). Figure 13 shows an experimental image of an outflow experiment with the predicted outflow depth overlaid. The image shows good agreement between the experiments and model prediction.

Fig. 13

Image from a plume outflow experiment with the theoretical prediction of the outflow thickness ($h' = 0.19H$) shown as a thick black line

The front position versus time data from each outflow experiment was plotted and a line fitted to establish the front velocity. The fitted velocity data from six experiments performed over a range of source buoyancy fluxes were plotted against the source buoyancy flux raised to the one-third power in Fig. 14. A line of best fit through the data shows that the front velocity can be well approximated by

$$ U_{f} = 0.93f^{{\frac{1}{3}}} $$

(6.6)

which is very close to the model prediction of $U_{f} = 1.0f^{{\frac{1}{3}}}$ in (6.5).

Fig. 14

Plot of the measured front velocity versus the source buoyancy flux raised to the one-third power along with the results of a linear regression forced through the origin

Once the plume outflow reaches the nearest wall it reflects off the wall and, flowing over the plume outflow, travels back toward the plume. When it reaches the plume, the plume bends toward it. The dynamics of counter-flowing overlaid gravity currents flowing beneath a third fluid layer are beyond the scope of this paper. However, it is reasonable to assume that, to first order, the return flow velocity will be linearly related to the outflow velocity. That is, the return velocity is given by $U_{return} = aU_{f}$ where $a$ is an unknown constant. As such, the time is taken for the plume outflow to reach the far wall and then return to the plume will be

$$ T_{bend} \sim \frac{\lambda L}{{U_{f} }} + \frac{\lambda L}{{aU_{f} }} = K\frac{\lambda L}{{f^{{\frac{1}{3}}} }}. $$

(6.7)

where $K$ is to be determined empirically though, given that $a$ is likely equal to or less than 1, one would expect $K \ge 2$. Lane-Serff et al. (1995) [28] examined the velocity of the return flow for a gravity current flowing over a triangular obstruction and showed that, if the obstruction is tall enough that the entire gravity current is reflected back toward its source, then the return flow is slower than the outflow velocity. For an outflow depth of $\phi = 0.19$ their model predicts that the return flow velocity would be about $U_{return} \approx 0.95U_{f}$. However, their experimental velocity measurements were consistently slower than their model (25% slower based on a linear fit through their data). This suggests that the return flow should be even slower, that $a < 1$ and $K > 2$ though a direct comparison between the measurements in [28] and the measurements herein is not possible as their reported data does not distinguish between fully blocked and partially blocked gravity currents. A detailed analysis of the return flow mechanics is beyond the scope of this paper which is focused on the filling box model and the conditions under which it breaks down.

A series of measurements were made to validate this scaling result and to establish the value of $K$. The time taken from the moment the plume initially reached the base of the enclosure to the time that the plume was visually observed to bend, termed as bending time, was recorded for a range of plume buoyancy fluxes and $\lambda$ values. This data is plotted against $\lambda L/f^{{\frac{1}{3}}}$ in Fig. 15. A line was fitted through the data and forced through the origin that resulted in a value of $K = 3.0$ with the fit $R^{2} = 0.82$. This is qualitatively consistent with the model prediction of (6.7).

Fig. 15

Plot of the observed bending time against $\lambda L/f^{{\frac{1}{3}}}$ along with the line of best fit forced through the origin

It is worth noting that the bending time is linearly proportional to the filling time for the short side of the enclosure (2.3). Taking $\alpha = 0.16$ ($C = 0.47$) we can write

$$ T_{bend} = 3\frac{\lambda L}{{f^{{\frac{1}{3}}} }} = 0.705T_{fill} $$

(6.8)

7 Discussion and conclusions

A series of experiments were conducted to better understand the dynamics of a confined line plume. The line plume in a filling box differs from the classic round plume flow as, if the plume spans the full width of the enclosure, it can segment the enclosure creating two distinct regions where the stratification develops. Three different configurations were explored, namely the symmetric (centrally located plume), wall-bounded (plume attached to an end wall), and the asymmetric case (plume located off-center but away from the wall). Experimental results showed that front movement for the symmetric and wall-bounded cases were well predicted by the standard filling box modeling approach. It was also observed that the front movement for the wall-bounded case was well predicted using a typical value of the entrainment coefficient for a line plume that is far from any obstructions. This is in contrast to some studies that have suggested that the presence of a wall on one side of the plume inhibits entrainment and reduces the plume entrainment coefficient.

The asymmetric cases studied showed a dramatic departure from the standard model. Initially, the behavior was similar to that of the symmetric cases. The plume impinged on the base of the tank, spread out along the floor, reflected off the end walls and flowed back toward the plume. However, due to the asymmetry, the outflow on the short side of the plume returned to the plume before the outflow on the long side. At this point, the plume bent dramatically toward the short side of the enclosure producing a counter-flow under the plume toward the long side of the enclosure. As such, the front position over time was not well predicted by the standard modeling approach that requires that the plume remains vertical and acts as a barrier segmenting the enclosure into two distinct and non-interacting regions.

The dynamics of the plume outflow was then investigated to quantify the time at which the plume bends and the filling box model breaks down. The plume outflow was modeled as a constant flux gravity current. Applying the appropriate Froude number condition at the outflow front and using conservation of volume and buoyancy in the plume impingement zone it was established that the outflow front velocity should be $U_{f} = 1.0f^{{\frac{1}{3}}}$. This closely matched the experimentally measured value of $U_{f} = 0.93f^{{\frac{1}{3}}}$. This led to establishing that the time at which the plume will bend will scale on the distance from the plume axis to the near wall divided by the plume buoyancy flux raised to the one-third power. Experimental measurements confirmed this showing that the bending time is given by $T_{bend} = 3.0\lambda L/f^{{\frac{1}{3}}} = 0.705 \times T_{fill}$.

This result indicates that the standard filling box model breaks down quite rapidly for the asymmetric cases. Taking the basic front position result (2.2) one would expect the first front to have reached $h/H = e^{ - 0.705} \approx 0.5$ on the short side at the time when the plume outflow has returned to the plume. However, during that time there is no clear first front on either side of the plume as the layer thickness is controlled by the thickness of the outflow and return flow. Therefore, for the asymmetric case, the model standard is never truly valid as either the buoyant layer thickness is controlled by the outflow thickness ($t < 0.7T_{fill}$) or the plume is no longer vertical ($t > 0.7T_{fill}$). However, the filling box model is still of value to this problem as it clearly provides the appropriate time scale for the stratification development even if it is not appropriate for accurate prediction of the first front position (see Fig. 11). For the symmetric cases ($\lambda = 0.5$ which is symmetric about the box centerline and $\lambda = 0$ which is virtually symmetric about the end wall) the model performs better (see Figs. 9 and 10). There is still the issue of the first front position being controlled by the outflow thickness and overturning at the end walls at early times as indicated by the waves in the front position figures. However, at later times the model is consistent with the measurements. As discussed earlier, one issue with applying the filling box model to a line plume as opposed to a round plume is that the plume outflow is approximately 50% thicker meaning that the initial outflow transient is responsible for filling a greater portion of the box.

Constraints on the available experimental setup prevented detailed measurements of the stratification behind the first front. This would be an obvious next step for future research. It would also be of significant value to measure the velocity field within the enclosure. This would be particularly useful at the time when the plume bends toward the near wall as that is where the standard model breaks down. Quantifying and parameterizing the underflow velocities would enable a more detailed model for the filling box problem to be developed.

Appendix

See Table 1.

Table 1 Details of the experiments