Abstract
Tidal sand ridges are large-scale rhythmic bedforms that are observed on the offshore parts of shelf seas where sand is abundantly available. Spacings between successive ridges are several kilometres, they evolve on centennial time scales, and their crests are cyclonically rotated with respect to the direction of the principal tidal currents. Here, an overview will be presented of the current knowledge about these ridges with respect to their manifestation in different seas, their observed behaviour, the basic mechanisms that explain their initial formation and their evolution towards finite heights and the ability to model them. It will be shown that both tides, waves and changes in mean sea level have a profound impact on the evolution of the ridges.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
This review focuses on linear and nonlinear dynamics of tidal sand ridges in the offshore area of shelf seas. First, in Sect. 1.1 the general geographical and physical aspects of shelf seas are introduced. Next, in Sect. 1.2 different types of bedforms that are observed on the outer continental shelves of these seas are briefly described. From thereon, tidal sand ridges are considered, where in Sect. 1.3 their relevance is discussed and an overview of subsequent sections is given.
1.1 Geographical and physical aspects of shelf seas
A shelf sea is a body of water, with depths of 0–200 m, which extends from the shoreline to the seaward end of the continental shelf, the shelf break. The latter marks the beginning of the continental slope (average slope of order 0.1) that separates the shelf from the deep ocean (depths of several kilometers). Figure 1 shows a sketch of a shelf sea. Examples of shelf seas are the East China Sea, the Celtic Sea off the south coast of Ireland, the Bering Sea between Alaska and Russia and the Argentina shelf sea. Semi-enclosed shelf seas also exist, e.g., the Gulf of Carpentara in northern Australia, and the North Sea that is bordered by Great Britain, Scandinavia, Germany, the Netherlands, Belgium, and France. Although shelf seas take up only approximately 8% of the total surface area of the world oceans [89], they are of great value from both social and economic perspectives, and they play an important role in marine ecosystems and ocean dynamics [64].
Shelf seas are highly dynamic due to the joint presence of tides, waves and bottom changes in these waters. Often, shelf seas are divided into three parts (Fig. 1), i.e., the shore area (between the coastline and the water level of low tide), the shoreface or inshore area (cross-shore slopes of order 0.01 to 0.001), and the offshore area (cross-shore slopes less than 0.001). In the first two areas, typically wind generated surface waves with periods of order 10 seconds dominate the water motion, while tides induce changes in the water level on a time scale of several hours. In the offshore area, tides become more important while waves still play a role.
1.2 Types of bedforms in shelf seas
In shelf seas with a sandy bed, a variety of rhythmic bottom patterns are observed, with spacings \(\lambda\) (mean distance between successive crests) ranging from several decimeters to tens of kilometers. In the shore area, ripples with \(\lambda\) of order 10 cm, megaripples with \(\lambda\) of order 10 m and beach cusps with \(\lambda\) ranging between 1 and 100 m ([26, 49, 79], and references therein) are observed. In the shoreface area, besides ripples and megaripples, sand bars and sand waves with \(\lambda\) of order 100 m, and shoreface-connected sand ridges with \(\lambda\) ranging between 2 and 10 km ([42, 47, 69], and references therein) occur. Furthermore, on inner continental shelves sorted bedforms (also called rippled scour depressions) are observed, with \(\lambda\) of order 100 m, which have a subtle relief and are characterised by abrupt changes in mean grain size [12, 73].
In the offshore area, megaripples and sand waves are still present. In addition, two types of large-scale bedforms occur, viz. long bed waves with \(\lambda\) of 1–3 km [41, 78] and tidal sand ridges with \(\lambda\) between 5 and 20 km ([23, 45, 51, 53], and references therein).
1.3 Focus, relevance and overview
In this review, the dynamics of tidal sand ridges are investigated. There are several reasons why knowledge of these specific bedforms is of interest. First, as stated by Off [51], they are relevant because they may potentially contain oil reservoirs. Second, due to increasing demand of sand in human activities, such as land reclamation, beach nourishment and construction works, offshore large-scale bedforms are considered as potential sand resources for marine sand mining [83]. An example is sand mining from the Kwinte Bank (belonging to the Flemish Banks) on the Belgian Continental Shelf [20].
Third, it should be noted that these bedforms provide habitats for marine organisms [78], while removal of sand will change the local environment and thereby have an impact on those organisms [11, 44, 76]. Moreover, the ridges dissipate wave energy during storms and thereby protect the coast (see e.g. [67]). Last but not least, active bedforms may cause damage to the underwater structures such as pipelines, telecommunication cables and electricity cables from offshore windmill parks [27]. Hence, knowledge of these seabed features and their dynamics is desirable for practical issues, such as strategic planning of marine sand mining [80], maintaining the balance of the marine ecosystem and assessment of the stability of underwater structures.
The contents of the subsequent sections are as follows. In Sect. 2 characteristics of observed tidal sand ridges are presented. This is followed in Sect. 3 by models that explain their initial formation. The main theory that will be discussed is based on morphodynamic self-organisation, which explains the development of free instabilities due to interactions between the hydrodynamics and the sandy seabed. Next, in Sect. 4 models are discussed that describe how the ridges evolve on the long term towards finite heights. Here, the role of tidal currents, wind waves and changes in mean sea level will be discussed. Finally, Sect. 5 contains an outlook for further studies.
2 Characteristics of observed tidal sand ridges
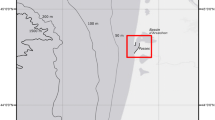
Figure 2 shows where tidal sand ridges occur in the southern North Sea. Generally, tidal sand ridges have crests that are \(5^{\circ }\)–\(30^{\circ }\) cyclonically (clockwise in the Northern Hemisphere) rotated with respect to the direction of the principal tidal current (see Fig. 2), their height is in the order of 10 m, and they evolve on time scales of centuries. Although most of the observed ridges have nearly straight crestlines, ridges with meandering crestlines occur (e.g. in the region of the Norfolk Banks shown in panel c of Fig. 2). Both symmetrical and asymmetrical cross-crest (or cross-sectional) profiles of these ridges are detected. Here, the symmetry refers to the position of the crests. Asymmetrical ridge profiles indicate migration of the ridges in the direction of the crest towards the steepest slope. Figure 3 shows an example of an asymmetrical cross-sectional profile of observed ridges in the region of the Flemish Banks, which suggests that the ridges migrate northwest. Small-scale bedforms with a spacing of order 100 m superimposed on the ridges are also identified. Over tidal sand ridges, variation of the surficial grain size is observed: usually the sediment at the crests (in the case of symmetrical profiles) or at the steeper sides (in the case of asymmetrical profiles) is coarser than that at the other parts of the ridges ([58], and references therein).
a Bathymetry of the southern North Sea. The black circles indicate the areas where tidal sand ridges are located: (1) the Dutch Banks, (2) the Flemish Banks, and (3) the Norfolk Banks. Black lines inside the circles qualitatively indicate the principal direction of the tidal current based on Davies and Furnes [19]. The map is obtained using GeoMapApp [60]. b and c Are zoom-ins of the areas of the Flemish Banks and the Norfolk Banks, respectively
A cross-crest seismic profile (in the southeast direction, SE) of the Middelkerke Bank in the region of the Flemish Banks, after Trentesaux et al. [74]. The gray layer represents (solid) Tertiary (from 66 to 2.6 million years ago) deposits and layers above are the (unconsolidated) Quaternary (from 2.6 million years ago to the present) deposits. The medium bounding surfaces (m.b.s.), which separate layers of material of different sizes and densities, suggest that the ridge migrates to the northwest (NW)
Tidal sand ridges occur in a wide range of water depths, for instance, the southern North Sea (20–40 m), the East China Sea (60–120 m, Fig. 4a) and the Celtic Sea (120–170 m, Fig. 4b). According to their present-day morphodynamic activity, ridges are classified as ‘active’, ‘quasi-active’ and ‘moribund’. Active and moribund mean that sand transport is, respectively, present and absent in the entire area where the ridges occur, and quasi-active means that sand transport occurs in only part of the ridge area. Generally, active ridges are found in relatively shallow waters (10–50 m) where strong tidal currents occur (typically above \(0.5\,{\text {m}}\,{\text{s}}^{-1}\), e.g., in the southern North Sea [39]. In contrast, moribund ridges are observed in relatively deep waters (100–200 m) where tidal currents are weak (maximum velocity is insufficient to move the sand near bed), e.g., in the Celtic Sea [68], or in areas with limited availability of sand (limited thickness of the erodible bed). In shelf seas where the water depth and the current strength are between those for active and moribund ridges, such as the East China Sea [46], quasi-active ridges occur. Usually active/quasi-active ridges have asymmetrical cross-sectional profiles, and smaller-scale bedforms such as sand waves are superimposed on them (see e.g. Fig. 3), while moribund ridges have almost symmetrical cross-sectional profiles and no small-scale bedforms superimposed on them.
3 Initial formation of tidal sand ridges
3.1 The first models
Generally, there are three types of theories for the initial formation of tidal sand ridges ([23, 52], and references therein). The first one is that ridges form directly due to local hydrodynamical conditions. It means that ridges occur as a result of spatial variations in flow conditions, such as spatially varying secondary flow (see e.g. [30, 51]) caused by e.g. gradients in bottom roughness. The second theory explains the ridges as being generated during the post-glacial sea level rise in the presence of a relict core of sediment (see e.g. [3, 4, 70]). The presence of a relict core of sediment in some ridges, e.g. the Middelkerke Bank in the southern North Sea [3] and the Kaiser-I-Hind Ridge in the Celtic Sea [4], supports this theory. The third type of theory is based on the concept that ridges form due to positive feedbacks between water motion and erodible bed (through sand transport), i.e., morphodynamic self-organisation ([6, 16, 22], and references therein). Small-amplitude bedforms can spontaneously grow, because they influence water motion in such a way that net convergence of sand transport takes place in the crest areas. It has been demonstrated in those studies that the latter theory is able to explain the formation of the other bedforms mentioned in Sect. 1.2.
In this review, the focus is on the theory of self-organisation applied to tidal sand ridges. This is done by investigating the stability of a basic state is investigated, characterised by a spatially uniform tidal current (the so-called background tidal current that exists in the absence of bottom undulations) over a flat horizontal bed, subject to bottom perturbations with small amplitudes. The latter consist of bottom modes, which are Fourier modes with arbitrary wavelength and orientation with respect to the direction of the principal tidal current. A linear stability analysis concerns the initial behaviour of the basic state. As initially the amplitude of the perturbation is small, the bottom modes evolve independently of each other, and their amplitudes grow or decay exponentially. Thus, each bottom mode is characterised by a growth rate \(\varGamma\). The mode that grows fastest in the amplitude is called the fastest growing mode or the preferred mode/bedform, which is expected to dominate the bottom pattern after some time. Besides, a linear stability analysis provides information about the migration speeds of the bottom modes. Such migration speeds are to be expected if the background tidal current is skewed, i.e., maximum flood currents differ from maximum ebb currents.
Huthnance [35] was the first to apply the self-organisation theory to the initial formation of tidal sand ridges by using linear stability analysis. He used depth-averaged shallow water equations for the tidal current, a bottom evolution equation that follows from mass conservation of sand, together with a simple sand transport formulation (cubic in velocity, including correction for favoured downslope transport). The explicit expression of the sand transport is given in “Appendix A”. He further assumed the background tidal current to be a symmetrical block flow (constant flood current and constant ebb current, with the same intensity and duration). It turns out that linear stability analysis yields a wavelength \(\lambda _p\) and an orientation \(\vartheta _p\) of the initially preferred bedform that are in fair agreement with those of observed ridges.
Contour plot of the dimensionless growth rate \(\varGamma\) of the bottom modes as a function of the dimensionless topographic wavenumber k and the angle \(\vartheta\) between the principal current direction and the crests, from Huthnance [35]. The growth rate is scaled by a typical morphological time scale of about 150 year, and the wavenumber is scaled by a length scale of about 10 km. The Coriolis force was neglected and the plot is symmetric about \(\vartheta =0\)
Figure 5 shows the contour plot of the dimensionless growth rate \(\varGamma\) of the bottom modes as a function of topographic wavenumber k and the angle \(\vartheta\) between the principal current direction and the crests obtained by Huthnance [35]. In this specific case the Coriolis force was neglected. The reciprocal \(\varGamma ^{-1}\) of the growth rate represents the e-folding growth time of the amplitude of the modes. The mode with the maximum growth rate corresponds to a bedform of which the spacing is 7.5 km (in a water depth of 30 m) and the angle between the crest and the principal current direction is \(28^{\circ }\).
3.2 The mechanism for ridge growth
Huthnance [35] also provides a physical explanation for his results. He argues that bottom frictional forces and Coriolis forces create tidal current asymmetry, such that sand transport is, both during flood and ebb, larger on the upstream side of the ridge than on its downstream side. The details of the current asymmetry were discussed by Huthnance [34] and Zimmerman [94], while Robinson [55] and Zimmerman [95] considered the qualitative aspects. Below, the reasoning of Zimmerman [95] is adopted, which is based on vorticity arguments.
Figure 6a shows, for the Northern Hemisphere and during flood, two water columns (light blue squares) on either side of the crest of a ridge that is cyclonically rotated with respect to the direction of the background tidal current. Both water columns experience Coriolis forces (red arrows, which act to the right when viewing in the direction of the current) and bottom frictional forces (green arrows, which oppose the currents). The magnitudes of both these forces increase with increasing current speed, which occurs when depth becomes smaller because of continuity. Thus, both forces induce torques that create anticyclonic vorticity on the upstream side of the crest, and cyclonic vorticity on the downstream side. Consequently, the tidal current transports anticyclonic vorticity towards the crest and it transports cyclonic vorticity away from the crest. As this happens during both flood and ebb (during ebb the signs of both the current and the torques change, hence the transports of vorticity remain unchanged), anticylonic residual vorticity occurs in the crest area, which results in a residual current.
a Topview, showing the background tidal current (blue arrow), which exists in the absence of bedforms, and two water columns (lightblue squares) on the upstream and downstream side of a cyclonically rotated crest of a tidal sand ridge on the Northern Hemisphere. Here, upstream and downstream are defined with respect to the direction of the background tidal current. Red and green arrows indicate Coriolis forces and bottom frictional forces, respectively, which are both larger in shallower water than in deeper water. These forces exert torques on the water columns. On the upstream side of the ridge, both torques generate anticyclonic (negative) vorticity (indicated by the ‘−’ sign), which is transported by the background tidal current towards the crest. On the downstream side, the Coriolis and frictional torques generate cyclonic vorticity (‘+’ sign) that is transported away from the crest. As a result, anticyclonic vorticity builds up around the crest. b Same view, but showing the background tidal current (blue arrows), residual current (purple arrows) and total current (red arrows). The total current is the vector sum of the background current and the residual current
Figure 6b shows both the background current (blue arrows), the residual current (purple arrows) as well as the total current (red arrows) for the same ridge. The latter is defined as the vector sum of the background tidal current and the residual current. Clearly, the magnitude of the total current is larger on the upstream side, where the residual current acts with the background tidal current, than on the downstream side where the residual current opposes the background flow. Thus, there is current asymmetry. In “Appendix B” a quantitive explanation of the vorticity dynamics of tidal currents over an irregular bottom is given. As was subsequently argued by Huthnance [35], since sand transport is proportional to the magnitude of the total current, sand transport converges above the crest. The same occurs during ebb, as the background tidal current reverses sign, but the residual current remains unchanged. Hence, averaged over a tidal cycle, sand accumulates above the crest and thus the ridge grows. This process is counteracted by divergence of sand transport that is induced by bottom slopes. This suggests that on the long term steady ridges could form, albeit that this can not be investigated with linear stability analysis.
The reason that the mechanism favours crests that are cyclonically rotated with respect to the tidal current is that in that case Coriolis forces and bottom frictional forces create vorticity with the same signs, hence in that case strong residual currents develop. If the crests are rotated in the opposite direction, Coriolis torques and bottom frictional torques have opposite signs and thus a weaker current asymmetry will occur. Furthermore, Huthnance demonstrated that if the tidal current is symmetrical, i.e., the strength of flood and ebb is equal, sand accumulates exactly at the crests of the ridges. In contrast, if the current is asymmetrical, e.g. the maximum flood current is larger than the maximum ebb current, sand accumulates in the area that (with respect to the dominant current direction) is downstream of the crest. This causes the ridges to both grow and migrate. The presence of residual currents around sand ridges and the convergence of sand transport in the ridge areas has indeed been observed in the field [15, 29, 53].
3.3 Further studies on initial ridge formation
After Huthnance [35], several other studies were conducted on the initial formation of tidal sand ridges. Instead of using a block flow, Hulscher et al. [33] employed a background tidal current that is smooth, a semidiurnal lunar \(M_2\) tidal current, which is the dominant tidal constituent in most shelf seas. In the case of a rectilinear tidal current (the end point of the velocity vector moves in a straight line in a tidal cycle), they obtained bedforms with a wavelength and an orientation that agree well with those of tidal sand ridges. Carbajal and Montaño [13] explored the sensitivity of the wavelength \(\lambda _p\) and orientation \(\vartheta _p\) of the initially preferred bedform to the mean water depth H and the velocity amplitude of the tidal current U. By modifying the values of the parameters (H and U) separately, they showed that \(\lambda _p\) increases as H increases, and it also increases as U increases. Roos et al. [56] and Walgreen et al. [84] imposed several rectilinear tidal constituents (residual current \(M_0\), semidiurnal tide \({M_2}\) and quarter-diurnal tide \({M_4}\)) to study the effect of asymmetrical tidal currents on the characteristics (migration rate, growth rate, wavelength and orientation) of tidal sand ridges. They confirmed the finding in Huthnance [35] that the ridges migrate in the presence of asymmetrical tidal currents. Walgreen et al. [85] and Roos et al. [58] took into account the effect of grain sorting (spatial distribution of different grain sizes) over tidal sand ridges during their initial formation. Their results explain most of the observed grain size variation over the ridges, i.e. coarser sediments on the crests and finer sediments in the troughs.
Blondeaux et al. [8] considered elliptical tidal currents (horizontally the end point of the current velocity vector traces out an ellipse in a tidal cycle), a nonlinear bottom stress, a formulation of sand transport that includes the critical shear stress for sand erosion ([66], and references therein) and anisotropic bottom slope-induced sand transport [71]. Their formulation of sand transport is given in “Appendix A”. They demonstrated that, under the conditions that the tidal current is elliptical and the maximum current velocity is just above the threshold for sand erosion, both tidal sand ridges and long bed waves emerge. Yuan et al. [91] further built on the study of Blondeaux et al. [8] by investigating the sensitivity of sand ridge characteristics (i.e., growth time, wavelength and orientation of crests) to the formulations of bottom stress (linear/nonlinear), slope-induced sand transport (isotropic/anisotropic), and to critical velocity for erosion, ellipticity of the tidal current and mixed tidal forcing (variations on the spring-neap cycle and/or at diurnal time scales). It was found that all of these formulations or parameters affected the ridge characteristics, but only in a quantitative manner. Ridge characteristics only marginally depend on the formulation of the bottom stress (linear/nonlinear) and on the slope-induced transport (istropic/nonisotropic). With increasing critical velocity for sand erosion, the ridges grow slower, their preferred wavelength becomes smaller and the angle \(\vartheta\) between crests and the tidal current decreases. The influence of tidal ellipticity on growth time, wavelength and angle \(\vartheta\) of the preferred ridges is shown in Fig. 7. Here, \(\epsilon\) is defined as the ratio between the minor axis and the major axis of the tidal ellipse, and positive (negative) \(\epsilon\) refers to a current vector that in time follows an elliptical path in a counter-clockwise (clockwise) manner.
a The growth time, b wavelength and c orientation angle \(\vartheta\) of the fastest growing mode as a function of tidal ellipticity \(\epsilon\). From Yuan et al. [91]
Clearly, behaviour in \(\epsilon\) is not symmetrical with respect to \(\epsilon =0\), e.g., the fastest growing ridges occur for negative \(\epsilon\) and the shortest ridges for positive \(\epsilon\). This symmetry breaking is caused by the joint action of Coriolis and frictional torques. To understand this, note that any elliptical tide can be decomposed into two circular tides. with current vectors that have different magnitudes and rotate clockwise and counter-clockwise, respectively [54]. Each of these circular tides generates, for any bottom mode, Coriolis torques that are either 90\(^{\circ }\) or -90\(^{\circ }\) out of phase with the frictional torque. Consequently, they result in different tidal vorticity patterns and hence in a different growth of the bottom mode. It turns out that in the cases of negative \(\epsilon\), contour plots of the growth rate as a function of wavenumber k and angle \(\vartheta\) between the crests of the bedforms and the direction of the maximum tidal current have different local maxima. This explains the observed ‘kinks’ in Fig. 7b, c.
In all the works mentioned above, depth-averaged tidal currents were used based on the fact that the water depth is much smaller than the horizontal scale of tidal sand ridges. The vertical flow structure was accounted for in Hulscher [32] and Besio et al. [5]. In these studies, the initial formation of both tidal sand ridges and tidal sand waves was explained, and it was shown that including the vertical flow structure is necessary for the formation of tidal sand waves.
4 Finite-height behaviour of tidal sand ridges
4.1 Early models
To study the characteristics of tidal sand ridges with a finite height, a nonlinear stability analysis is needed. In Huthnance [35], besides the initial formation of tidal sand ridges, finite-height equilibrium ridges were shown to exist, but rather strong simplifications were made. In his model, the topography only varied in one horizontal direction (1D configuration), the tidal current was modelled as a block flow, and the Coriolis force was neglected. Also, it was not shown how the ridges emerge in the course of time. Ridges only remained submerged in the case that either stirring of sand by surface waves, asymmetrical tidal currents or limited availability of sand was considered. It was also shown that asymmetrical tidal currents give rise to asymmetrical equilibrium ridge profiles, and that the ridges migrate in the direction from their gentler side to their steeper side with respect to the crests.
The long-term evolution of topographies that varied in two horizontal dimensions (2DH configuration) was investigated in Huthnance [36] by solving the vorticity equation (to obtain the current velocity) and the equation of bottom evolution numerically. The domain was rectangular and at the boundaries vanishing normal components of the topographically induced flow were imposed. The near-parallel depth contours in the equilibrium state for a single initial bump bottom perturbation suggested that in an open sea, ridges with long straight crests would form under spatially uniform tidal forcing. Note that the same simplifications in the forcing as those in Huthnance [35] were used, and the equilibrium state was only obtained under the condition of limited availability of sand.
Using a two-dimensional vertical model (2DV model) that accounts for currents in the vertical and one horizontal directions, Komarova and Newell [43] investigated the nonlinear interactions between tidal sand waves with crests normal to the principal current direction and different wavelengths. They found that the nonlinear interactions between sand waves could generate bedforms with spacings similar to those of tidal sand ridges. However, the crests of the bedforms generated from the interactions between tidal sand waves were normal to the principal current direction, which are different from those of the observed ridges. Idier and Astruc [37] determined the saturation height of tidal sand ridges by the growth rate of the initially preferred bottom mode with different initial heights subject to a steady flow or a block flow. If the growth rate of the bottom mode with a certain height is zero, the ridge height is said to be saturated. In this way, the nonlinear interactions between bottom modes with different spacings were neglected, and the cross-sectional ridge profiles in time could not be obtained.
In Roos et al. [57], a 1D nonlinear morphodynamic model was presented and used to simulate the time evolution of the cross-sectional profiles of finite-height tidal sand ridges, and stirring of sand by wind waves was parametrically accounted for (for details see “Appendix A”). In that study, unlike Huthnance [35, 36], a rectilinear tidal current rather than a block flow was employed and unlimited availability of sand was assumed. Furthermore, periodic conditions were imposed at the boundaries of the domain. Equilibrium ridges were shown to exist, and they were asymmetrical and migrated in the case of asymmetrical tidal currents (consisting of a semidiurnal tide \(M_2\) together with either a residual current \(M_0\) or an overtide \(M_4\)). In the absence of waves, the crests of the ridges grow until the water surface. With increasing wave stirring intensity, the height of the crests decreases. Figure 8 shows the symmetrical and asymmetrical (flood dominant) tidal currents used by Roos et al. [57] and the modelled cross-sectional ridge profiles in their study. The ridges with asymmetrical profiles migrate in the flood direction (positive x-direction).
a time evolution of velocity u of background symmetrical \(M_2\) (solid line) and asymmetrical \(M_2+M_4\) (dashed and dotted lines, flood dominant) tidal currents in a tidal period T, the sum of the amplitudes of the currents is \(U_{M_2}+U_{M_4} =U=1\,{\hbox {ms}}^{-1}\) and the percentage indicates \(U_{M_4}/U\), and b modelled cross-sectional equilibrium ridge profiles using bed load and the tidal currents in (a). From Roos et al. [57]
Tambroni and Blondeaux [72] carried out a weakly nonlinear stability analysis to investigate the behaviour of finite-height ridges in a 2DH (depth-averaged) model. Their method is fast and yields insight into the mechanism that causes saturation of the height of the ridges, but it is only applicable for tidal currents with large ellipticity \(\epsilon\). Many tidal sand ridges are actually observed at locations where tidal currents are close to rectilinear (\(\epsilon \sim 0\)), for instance, in the southern North Sea [17]. Interestingly, this study is the first study in which the effect of the critical bed shear stress for sand erosion on the evolution of finite-height tidal sand ridges has been considered.
Motivated by all previous results, Yuan et al. [92] studied the evolution of tidal sand ridges towards finite height with a two-dimensional, vertically averaged model. They considered the morphodynamic system in a domain with lengths \(L_x\) and \(L_y\) with periodic boundary conditions. The x-axis and y-axis were chosen such that the crests of the initially preferred mode were along the x-axis. They found two types of end states in their model. In the first state, ridges have straight crests that are aligned in the same direction as those of the initially fastest growing mode. These solutions are similar as those obtained with a 1D model. The other state is characterised by ridges with meandering crests that oscillate in time. As an example, Fig. 9 shows modelled bottom patterns at different times, starting from an almost flat bed with small random perturbations. The parameter values are such that they are representative for typical North Sea conditions (mean depth of 30 m, background tidal current amplitude of \(1\,{\text {ms}}^{-1}\)) and the domain has sizes \(L_x=8\,{\hbox {km}}\) and \(L_y=9\,{\hbox {km}}\). The fastest growing mode has a wavelength of 9 km, so it fits into the domain. For convenience, the bottom patterns are shown in a domain with sizes that are three times larger than those of the computational domain. This is possible because periodic conditions at all horizontal boundaries are used. Results show that the extent of the meanders is 2.4 km and the oscillation period is about 300 years. Yuan et al. [92] also studied the sensitivity of model results to values of parameters such as the critical velocity for erosion, tidal ellipticity, multiple components in the tidal forcing and size of the domain. Overall, quantitative, but no qualitative differences in the results were found, so ridges with meandering crests that oscillate in time are robust phenomena.
a–e Bottom patterns at different times, as calculated by the two-dimensional model of Yuan et al. [92] for typical North Sea conditions. The axes are chosen such that the initially fastest growing mode has crests that are parallel to the x-axis. The computations were done for a domain of \(8\times 9\,{\hbox {km}}\), with periodic boundary conditions. For convenience, results are shown on a domain that is three times larger in both x and y-direction. Panel f: contour plot of bed elevation along a transect \(x=3.2\,{\hbox {km}}\) as a function of coordinate y and time t
It turns out that necessary conditions for meanders occur are that sea waves have a relatively low significant height, such that ridges attain a considerable height, and that the ratio \(L_x/L_y\) is larger than about 0.5. The latter implies the possibility of resonant nonlinear interactions between a bottom mode that is characterised by wavevector (0, \(k_p\)) and two other modes that have wavenumbers \(\pm\,2\pi /L_x\) in the x-direction and wavenumber \(k_p/2\) in the y-direction. As shown by Craik [18] for fluid instabilities, and later also by e.g. Blondeaux and Vittori [7] for tidal sand waves, these interactions result in rich three-dimensional dynamics.
Many observed tidal sand ridges also feature meandering crests, e.g. some of the Norfolk Banks in the North Sea [15] and the Noordhinder Bank on the Belgian shelf [65]. Based on field data, Caston [14] proposed a conceptual model, in which differences in the rates of sand transport on either side of the crests would cause the development of a kink in an initially straight crestline. The kink eventually becomes so large that the ridge would break into three separate ridges. Harris and Jones [29] found evidence for this theory in the case of the sand ridges in Moreton Bay, eastern Australia. In contrast, Smith [65] analysed a kink in the Noordhinder Bank over a period of 135 years and did not find evidence for the mechanism of Caston. Instead, he proposed a different mechanism in which sand waves present at the crest play a key role. In this conceptual model the ridge would eventually break into two ridges. Deleu et al. [21] argued that the latter mechanism explains the behaviour of the kink in the Westhinder Bank on the Belgian shelf.
Crest meandering as well as bank breaking were found in a recent nonlinear model study by van Veelen et al. [82]. They construct solutions of the depth-averaged shallow water equations, supplemented with the sand transport formulation of Roos et al. [57] and a bed evolution equation, on a two-dimensional domain by means of truncated expansions of the state variables in a parameter that is the ratio of the maximum bank elevation and mean water depth. Whether crests of ridges break or evolve into kinks depends on the initial orientation of the ridge with respect to its preferred orientation. If these orientations differ breaking will occur, otherwise kinks develop. Such differences in orientation might in nature result from changing external conditions, such as changes in mean depth due to sea level rise. The latter will be discussed in the next subsection.
It turns out that nonlinear morphodynamic models of sand ridges are able to simulate the gross characteristics (wavelength and height) of observed sand ridges. Regarding the Dutch sand ridges, it was found that modelled saturation heights are larger than the actual height of the ridges. This suggests that these ridges are still in their process of development. There are also certain environmental conditions that could cause limited growth, or even absence of growth of tidal sand ridges. One is the presence of erosion-resistant layers in the subsoil [36]. Others are the presence of river flow from a nearby estuary [40] or that strong wind waves occur so often that the conditions are not favourable for growth. However, none of the three latter conditions apply to the area of the Dutch sand ridges.
4.2 Effect of sea level rise (SLR) on the behaviour of tidal sand ridges
In the studies for the nonlinear evolution of tidal sand ridges mentioned above, the sea level and the characteristics of the background tidal current were kept constant in time. However, these bedforms evolve on a time scale of many hundreds of years, during which both the sea level and the characteristics of the tidal current change. Figure 10 shows the time evolution of local sea level in the southern North Sea [1] and that of the eustatic (opposed to local) sea level [24]. It is seen from Fig. 10a that the sea level for the continental shelves of Belgium and the Netherlands at 8 ka BP (8000 years before present) was about 15 m lower than the present sea level. At the Last Glacial Maximum lowstand, the eustatic sea level was \(125\pm 5\,{\hbox {m}}\) lower than that in the present day (Fig. 10b). As the growth rate of the height of the ridges is in the same order of the rate of SLR, it is to be expected that SLR plays a role in the long-term evolution of these ridges. It seems plausible that present-day quasi-active/moribund ridges were initially formed during a low sea level (e.g., around \(20\,{\hbox {ka}}\) BP for ridges in the Celtic Sea), and subsequently became less active or inactive as the sea level rose [2, 61, 88].
Modelled \(M_2\) current amplitude in the northwest European shelf seas at 16, 12, 10, 8 ka BP (1000 years before present) and the present. Reprinted from Uehara et al. [75]
Regarding the tidal current, van der Molen and de Swart [81] showed that during the Holocene period large variations of tidal conditions occurred in the southern North Sea. Extensions of their work to the full northwest European shelf seas were given by Uehara et al. [75] and Ward et al. [86]. Figure 11 shows modelled \(M_2\) tidal current in the northwest European shelf sea from the Last Glacial Maximum to present [75], in which significant changes in the amplitude of the \(M_2\) current were observed in the Celtic Sea. Since the strength of the tidal current determines the sand transport rate and the principal current direction affects the ridge orientation, variation in the strength and principal direction of the current also affects the evolution of the ridges.
In a model study by Yuan and de Swart [90], the effect of changes in mean sea level and related changes in tidal currents on the evolution of tidal sand ridges was systematically explored. It was found that the dynamics of the ridges strongly depends on the time evolution of mean depth H (due to sea level rise), of the effective velocity \(U_e=(U^2+\frac{1}{2} u_w^2)^{1/2}\) (with U the tidal current amplitude and \(u_w\) the amplitude of near-bed wave orbital motion) and the critical depth-averaged velocity for sand erosion \(U_c\). Clearly, \(U_e\) must be larger than \(U_c\) in order to have erosion and transport of sand. Furthermore, with increasing depth \(u_w\) decreases and \(U_c\) slowly increases.
In Fig. 12 two typical cases are shown. In panel a, \(U_e\), \(u_w\) and \(U_c\) are plotted versus depth for typical North Sea conditions and a fixed \(U=0.5\,{\text {ms}}^{-1}\). This figure reveals that ridges are active as long as the depth is less than 120 m, which is the case in this sea. In panel b the time evolution is shown of mean sea level, crest level and trough level of ridges for a rate of sea level rise \(R=1.875\,{\hbox {mm}}\) per year and an initial mean water depth of 15 m. It shows that the ridges initially grow and after some time keep pace with the rising sea level. With regard to their pattern, meandering ridges that oscillate in time were still obtained for realistic choices of the initial depth at which ridges started to form and the rate R of sea level rise.
a Dependence of effective velocity amplitude \(U_e=(U^2+\frac{1}{2} u_w^2)^{1/2}\), with U the tidal current amplitude, near-bed wave orbital velocity \(u_w\) and critical depth-averaged velocity for sand erosion \(U_c\) versus mean water depth H. Parameter settings representative for North Sea conditions and tidal current amplitude \(U=0.5\,{\text {ms}}^{-1}\). Top-right of this panel shows a zoom-in of the main figure for depths in the range 115–125 m (horizontal axis). b Time evolution of sea level (dashed curve), crest level and trough level of sand ridges for typical North Sea conditions (initial mean depth \(H=H_0=15\,{\hbox {m}}\), sea level rise is 1.875 mm per year). c Time evolution of depth, U, \(u_w\), \(U_e\) and \(U_c\) for a setting that resembles the Celtic Sea. d As panel b, but for Celtic Sea conditions. From Yuan and de Swart [90]
In Fig. 12c,d results are shown for a setting that resembles the situation in the Celtic Sea. In panel c the time evolution of mean depth H, as well as of \(U, U_e, u_w\) and \(U_c\), is plotted. Panel d shows the time evolution of mean sea level, as well as the levels of the crests and troughs. In this case, while mean sea level rose the tidal current amplitude declined. It resulted after some time in the situation that \(U_e\) dropped below the critical velocity for sand erosion, after which the ridges became inactive and drowned.
5 Conclusions and outlook
This contribution has provided an overview of current knowledge about the linear and nonlinear dynamics of tidal sand ridges. The main findings are that tidal sand ridges form due to inherent feedbacks between currents, waves and the sandy bed and that their evolution is strongly affected by changes in mean sea level and related changes in hydrodynamic conditions (both tides and wind waves).
With regard to future research, several extensions are suggested.
- 1.
Most models of tidal sand ridges are based on the depth-averaged shallow water equations, which means that the vertical flow structure (e.g. [63]) is neglected and sand waves do not appear [5, 32]. Sand transport is determined by the near-bed currents, the direction of which may differ from that of depth averaged currents. Thus considering a three-dimensional (3D) flow may bring about a better agreement between modelled and observed orientations of the ridges. Note that it is quite difficult to study tidal sand ridges alone in a 3D flow configuration, as sand waves also form and typically they have a larger growth rate (corresponding growth time scale is several years to decades) than that of sand ridges. At the same time, this seems the way to proceed, as both conceptual models [65] and process-based models [43] suggest that sand ridges and sand waves are nonlinearly coupled.
- 2.
Replacing prescribed background tidal currents, as are used in all studies, by tidal currents from larger scale models in which sea level rise is taken into account, would add more realism. One possibility is to ‘nest’ the model of Yuan and de Swart [90] into models like that of Uehara et al. [75] and Ward et al. [86]. In this way, detailed output of tidal currents from paleotidal simulations serves as input for the present model. Alternatively, including a module of bottom evolution (through sand transport) in large-scale models that simulate paleotides could be considered.
- 3.
Improving the modelling of waves including variation of wave conditions is important. The presently available models use quite simple parameterisations. To gain insight into the effect of wave transformation on the long-term evolution of the ridges, a sophisticated wave model like SWAN [9] is needed. Furthermore, it has been shown that wave conditions change both in the long term and in the short term, and these changes affect the evolution of the ridges, especially the short-term extreme wave conditions [31]. Improvement in modelling the waves can be achieved by using paleo wave models [48], or by prescribing long-term (decades to centuries) and seasonal variations in the wave height and wave period as well as sudden events (storms). The latter can be parameterized as events that are computed from a given probability distribution.
- 4.
In the presently available models several aspects that relate to sand transport could be improved, which are listed below. To explore the effect of both bed load and suspended load on the long-term evolution of sand ridges, a challenge is to account for suspended load based on the characteristics of the flow and the sediment [66]. Roos et al. [57] considered both bed load and suspended load to study the nonlinear dynamics of tidal sand ridges, and they found that using suspended load leads to lower and more rounded crests than those using bed load. Note that in that study bed load and suspended load were included in an isolated way by prescribing coefficients that control the relative importance of bed load and suspended load. Another important generalisation is to take into account a mixture of sand of different sizes, as in Walgreen et al. [85] and Roos et al. [58], such that knowledge of the grain size variation over finite-height ridges (instead of ridges with small heights in previous studies) will be obtained. Besides, considering the availability of sand according to the thickness of local erodible seabed is an interesting topic, which may provide better description of the characteristics of sand ridges. Huthnance [35] showed that the cross-sectional profiles of the ridges are sensitive to the availability of sand. In addition, limited source of sand prevents ridges from keeping pace with SLR, thus accelerates the process that active ridges turn quasi-active/moribund.
- 5.
It is quite a challenge to examine the natural evolution of the wavelength and orientation of tidal sand ridges in the long term. This could be addressed by conducting experiments with the model of Yuan and de Swart [90] on considerably larger 2D domains than those that were used so far. To do such kind of simulations, computational efficiency of the model needs to be improved, possibly by using parallel computation.
- 6.
To gain further insight into transient response of finite-height ridges to human interventions [80, 93], it is important to use a nonlinear 2D model to study the long-term behaviour of finite-height ridges subject to sand extraction, land reclamation, etc. Gaining such knowledge will likely help to understand why e.g. the Kwinte Bank on the Belgian Continental Shelf is closed for sand extraction, because of apparent destabilisation due to past sand extraction ([20], and references therein). Several studies ([38], and references therein) have been conducted to investigate the impact of offshore sand extraction on the local hydrodynamic and morphodynamic conditions. However, those studies either were limited in computation efficiency for simulations longer than a century or they employed simplified topography, i.e., a 1D configuration or a 2D configuration with perturbations of small amplitudes ([59], and references therein). Sand extraction could be applied in the same way as that of Nnafie et al. [50], in which the effect of sand extraction on shoreface-connected sand ridges was investigated.
- 7.
It would be worthwhile to study the interaction between tidal sand ridges and local ecology. A case study by van Dijk et al. [78] clearly showed that benthic habitats wre more dense and more diverse in the muddy, poorly sorted troughs of ridges in the North Sea than on their sandy well sorted crests. Moreover, model studies by Borsje et al. [10] have demonstrated that the presence of biota affect the formation process of bedforms, in their case tidal sand waves. Extensions of such studies are certainly important.
- 8.
There is a large potential to apply the present model to ridges at locations other than the European shelf seas, such as the shelf seas of China [45, 87] and the Australian shelf seas [28]. Attention needs to be paid to suspended load transport of sand, sediment input and outflow from rivers. This holds in particular for areas like the Yellow Sea and the East China Sea on the continental shelf of China, where generally the grain size is less than 0.25 mm, and which receive large amounts of sediment and fresh water from big rivers. Knaapen [40] shows from observation that interaction between the tidal current and outflow of a river affects the formation of sand ridges. It is feasible to account for sediment input and outflow from rivers in the present model by adjustment of its boundary conditions.
- 9.
Besides tidal sand ridges, the present model can also be used to unravel the nonlinear behaviour of long bed waves as observed by Knaapen et al. [41] and van Dijk et al. [77], where their initial formation was studied). This can be achieved by conducting a nonlinear stability analysis for cases that the maximum current velocity is slightly above the critical velocity for sand erosion.
References
Beets DJ, van der Spek AJF (2000) The Holocene evolution of the barrier and the back-barrier basins of Belgium and the Netherlands as a function of late Weichselian morphology, relative sea-level rise and sediment supply. Geol Mijnb/Neth J Geosci 79(1):3–16
Belderson RH, Pingree RD, Griffiths DK (1986) Low sea-level origin of celtic sea sand banks-evidence from numerical modelling of \(M_2\) tidal streams. Mar Geol 73:99–108
Berné S, Trentesaux A, Stolk A, Missiaen T, De Batist M (1994) Architecture and long term evolution of a tidal sandbank: the Middelkerke Bank (southern North Sea). Mar Geol 121(1–2):57–72
Berné S, Lericolais G, Marsset T, Bourillet JF, De Batist M (1998) Erosional offshore sand ridges and lowstand shorefaces: examples from tide-and wave-dominated environments of France. J Sediment Res 68(4):540–555
Besio G, Blondeaux P, Vittori G (2006) On the formation of sand waves and sand banks. J Fluid Mech 557:1–27. https://doi.org/10.1017/S0022112006009256
Blondeaux P (2001) Mechanics of coastal forms. Ann Rev Fluid Mech 33:339–370
Blondeaux P, Vittori G (2009) Three-dimensional tidal sand waves. J Fluid Mech 618:1–11
Blondeaux P, de Swart HE, Vittori G (2009) Long bed waves in tidal seas: an idealized model. J Fluid Mech 636:485–495
Booij N, Ris R, Holthuijsen LH (1999) A third-generation wave model for coastal regions: 1. model description and validation. J Geophys Res 104(C4):7649–7666
Borsje BW, Vries MBd, Bouma TJ, Besio G, Hulscher SJMH (2009) Modeling bio-geomorphological influences for offshore sandwaves. Cont Shelf Res 29:1289–1301. https://doi.org/10.1016/s12665-016-6275-0
Boyd SE, Limpenny DS, Rees HL, Cooper KM (2005) The effects of marine sand and gravel extraction on the macrobenthos at a commercial dredging site (results 6 years post-dredging). ICES J Mar Sci 62:145–162
Cacchione DA, Drake DE, Grant WD, Tate GB (1984) Rippled scour depressions on the inner continental shelf off central California. J Sediment Petrol 54:1280–1291
Carbajal N, Montaño Y (2001) Comparison between predicted and observed physical comparison between predicted and observed physical features of sandbanks. Estuar Coast Shelf Sci 52:425–443
Caston VND (1972) Linear sand banks in the southern North Sea. Sedimentology 18:63–78
Caston VND, Stride AH (1970) Tidal sand movement between some linear sand banks in the North sea off northeast Norfolk. Mar Geol 9:M38–M42
Coco G, Murray AB (2007) Patterns in the sand: from forcing templates to self-organization. Geomorphology 91(3):271–290. https://doi.org/10.1016/j.geomorph.2007.04.023
Collins MB, Shimwell S, Gao S, Powell H, Hewitson C, Taylor JA (1995) Water and sediment movement in the vicinity of linear sandbanks: the Norfolk Banks, southern North Sea. Mar Geol 123:125–142
Craik ADD (1985) Wave interactions and fluid flow. Cambridge University Press, Cambridge
Davies AM, Furnes GK (1980) Observed and computed M 2 tidal currents in the North Sea. J Phys Oceanog 10:237–257
Degrendele K, Roche M, Schotte P, Lancker VV, Bellec V, Bonne W (2010) Morphological evolution of the Kwinte Bank central depression before and after the cessation of aggregate extraction. J Coast Res SI(51):77–86. https://doi.org/10.2112/SI51-007
Deleu S, Lancker VV, den Eynde DV, Moerkerke G (2004) Morphodynamic evolution of the kink of an offshore tidal sandbank: the Westhinder Bank (southern North Sea). Cont Shelf Res 24:1587–1610. https://doi.org/10.1016/j.csr.2004.07.001
Dodd N, Blondeaux P, Calvete D, de Swart HE, Falqués A, Hulscher SJMH, Rozynski G, Vittori G (2003) Understanding coastal morphodynamics using stability methods. J Coast Res 19(4):849–865
Dyer KR, Huntley DA (1999) The origin, classification and modelling of sand banks and ridges. Cont Shelf Res 19:1285–1330
Fleming K, Johnston P, Zwartz D, Yokoyama Y, Lambeck K, Chappell J (1998) Refining the eustatic sea-level curve since the last glacial maximum using far- and intermediate-field sites. Earth Planet Sci Lett 163:327–342
Fredsøe J, Deigaard R (1992) Mechanics of coastal sediment transport. World Scientific, Singapore
Gallagher EL (2011) Computer simulations of self-organized megaripples in the nearshore. J Geophys Res Earth Surf 116:F01004. https://doi.org/10.1029/2009JF001473
Games KP, Gordon DI (2015) Study of sand wave migration over five years as observed in two windfarm development areas, and the implications for building on moving substrates in the North Sea. Earth Environ Sci Trans R Soc Edinb 105(4):241–249. https://doi.org/10.1017/S1755691015000110
Harris PT (1994) Comparison of tropical, carbonate and temperate, siliciclastic tidally dominated sedimentary deposits: examples from the Australian continental shelf. Aust J Earth Sci 41(3):241–254. https://doi.org/10.1080/08120099408728133
Harris PT, Jones MR (1988) Bedform movement in a marine tidal delta; air photo interpretations. Geol Mag 125:31–49
Houbolt J (1968) Recent sediments in the southern bight of the North Sea. Geol Mijnb 47(4):245–273
Houthuys R, Trentesaux A, De Wolf P (1994) Storm influences on a tidal sandbank’s surface (Middelkerke Bank, southern North Sea). Mar Geol 121(1–2):23–41. https://doi.org/10.1016/0025-3227(94)90154-6
Hulscher SJMH (1996) Tidal-induced large-scale regular bed form patterns in a three-dimensional shallow water model. J Geophys Res 101(C9):20727–20744
Hulscher SJMH, de Swart HE, de Vriend HJ (1993) The generation of offshore tidal sand banks and sand waves. Cont Shelf Res 13(11):1183–1204
Huthnance JM (1973) Tidal current asymmetries over the Norfolk Sandbanks. Estuar Coast Mar Sci 1:89–99
Huthnance JM (1982a) On one mechanism forming linear sand banks. Estuar Coast Shelf Sci 14:79–99
Huthnance JM (1982b) On the formation of sand banks of finite extent. Estuar Coast Shelf Sci 15:277–299
Idier D, Astruc D (2003) Analytical and numerical modeling of sandbanks dynamics. J Geophys Res 108(C3):3060. https://doi.org/10.1029/2001JC001205
Idier D, Hommes S, Brière C, Roos PC, Walstra DJR, Knaapen MAF, Hulscher SJMH (2010) Morphodynamic models used to study the impact of offshore aggregate extraction: a review. J Coast Res SI(51):39–52. https://doi.org/10.2112/SI51-004
Kenyon NH, Belderson RH, Stride AH, Johnson MA (1981) Offshore tidal sand-banks as indicators of net sand transport and as potential deposits. Spec Publ Int Assoc Sedimentol 5:257–268
Knaapen MAF (2009) Sandbank occurrence on the Dutch continental shelf in the North Sea. Geo-Mar Lett 29:17–24. https://doi.org/10.1007/s00367-008-0105-7
Knaapen MAF, Hulscher SJMH, de Vriend HJ (2001) A new type of sea bed waves. Geophys Res Lett 28(7):1323–1326
Komar PD (1998) Beach Processes and Sedimentation, 2nd edn. Prentice-Hall, Englewood Cliffs
Komarova NL, Newell AC (2000) Nonlinear dynamics of sand banks and sand waves. J Fluid Mech 415:285–321
Kubicki A, Manso F, Diesing M (2007) Morphological evolution of gravel and sand extraction pits, Tromper Wiek, Baltic Sea. Estuar Coast Shelf Sci 71:647–656. https://doi.org/10.1016/j.ecss.2006.09.011
Liu Z, Xia D, Berné S, Wang K, Marsset T, Tang Y, Bourillet J (1998) Tidal deposition systems of China’s continental shelf, with special reference to the eastern Bohai Sea. Mar Geol 145:225–253
Liu Z, Berné S, Saito Y, Yu H, Trentesaux A, Uehara K, Yin P, Liu JP, Li C, Hu G, Wang X (2007) Internal architecture and mobility of tidal sand ridges in the East China Sea. Cont Shelf Res 27(13):1820–1834. https://doi.org/10.1016/j.csr.2007.03.002
McCave I (1971) Sand waves in the north sea off the coast of holland. Mar Geol 10(3):199–225
Neill SP, Scourse JD, Bigg GR, Uehara K (2009) Changes in wave climate over the northwest European shelf seas during the last 12,000 years. J Geophys Res 114(C06):015. https://doi.org/10.1029/2009JC005288
Nelson TR, Voulgaris G (2015) A spectral model for estimating temporal and spatial evolution of rippled seabeds. Ocean Dyn 65(2):155–171
Nnafie A, de Swart HE, Calvete D, Garnier R (2014) Modeling the response of shoreface-connected sand ridges to sand extraction on an inner shelf. Ocean Dyn 64:723–740. https://doi.org/10.1007/s10236-014-0714-9
Off T (1963) Rhythmic linear sand bodies caused by tidal currents. Bull Am Assoc Pet Geol 47:324–341
Pattiaratchi C, Collins M (1987) Mechanisms for linear sandbank formation and maintenance in relation to dynamical oceanographic observations. Progress Oceanogr 19:117–176
Pattiaratchi CB, Harris PT (2002) Hydrodynamic and sand-transport controls on en echelon sandbank formation: an example from Moreton Bay, eastern Australia. Mar Fresh Water Res 53:1101–1113
Prandle DA (1982) The vertical structure of tidal currents and other oscillatory flows. Cont Shelf Res 1:191–207
Robinson IS (1981) Tidal vorticity and residual circulation. Deep Sea Res 28A(3):195–212
Roos PC, Hulscher SJMH, Peters B, Nemeth A (2001) A simple morphodynamic model for sand banks and large-scale sand pits subject to asymmetrical tides. In: Ikeda S (ed) Proceedings of the 2nd IAHR symposium on river, coastal and estuarine morphodynamics, IAHR, Hokkaido, Japan, pp 91–100
Roos PC, Hulscher SJMH, Knaapen MAF (2004) The cross-sectional shape of tidal sandbanks: modelling and observation. J Geophys Res 109:F02003. https://doi.org/10.1029/2003JF000070
Roos PC, Wemmenhove R, Hulscher SJMH, Hoeijmakers HWM, Kruyt NP (2007) Modeling the effect of nonuniform sediment on the dynamics of offshore tidal sandbanks. J Geophys Res 112(F02):011. https://doi.org/10.1029/2005JF000376
Roos PC, Hulscher SJMH, de Vriend HJ (2008) Modelling the morphodynamic impact of offshore sandpit geometries. Coast Eng 55:704–715. https://doi.org/10.1016/j.coastaleng.2008.02.019
Ryan WBF, Carbotte SM, Coplan JO, O’Hara S, Melkonian A, Arko R, Weissel RA, Ferrini V, Goodwillie A, Nitsche F, Bonczkowski J, Zemsky R (2009) Global multi-resolution topography synthesis. Geochem Geophys Geosyst. https://doi.org/10.1029/2008GC002332
Scourse J, Uehara K, Wainwright A (2009) Celtic Sea linear tidal sand ridges, the Irish Sea Ice Stream and the Fleuve Manche: palaeotidal modelling of a transitional passive margin depositional system. Mar Geol 259(1):102–111. https://doi.org/10.1016/j.margeo.2008.12.010
Seminara G (1998) Stability and morphodynamics. Meccanica 33:59–99
Shapiro GI, van der Molen J, de Swart HE (2004) The effect of velocity veering on sand transport in a shallow sea. Ocean Dyn 54:415–423. https://doi.org/10.1007/s10236-004-0089-4
Simpson JH, Sharples J (2012) Introduction to the physical and biological oceanography of shelf seas. Cambridge University Press, Cambridge
Smith DB (1988) Stability of an offset kink in the North Hinder Bank. In: de Boer PL, van Gelder A, Nio SD (eds) Tide-influenced sedimentary environments and facies, D. Reidel Publishing Company, Dordrecht, pp 65–78
Soulsby RL (1997) Dynamics of marine sands: a manual for practical applications. Thomas Telford, London
Spencer T, Brooks SM, Evans BR, Tempest JA, Möller I (2015) Southern North Sea storm surge event of 5 December 2013: water levels, waves and coastal impacts. Earth-Sci Rev 146:120–145
Stride AH, Belderson RH, Kenyon NH, Johnson MA (1982) Offshore tidal deposits: sand sheet and sand bank facies. In: Stride AH (ed) Offshore tidal sands: processes and deposits. Chapman and Hall, London, pp 95–125
Swift DJ, Parker G, Lanfredi NW, Perillo G, Figge K (1978) Shoreface-connected sand ridges on american and european shelves: a comparison. Estuar Coast Mar Sci 7(3):257–273
Swift DJP (1973) Tidal sand ridges and shoal retreat massifs. Mar Geol 18:105–134
Talmon A, Struiksma N, Mierlo MV (1995) Laboratory measurements of the direction of sediment transport on transverse alluvial-bed slopes. J Hydraul Res 33(4):495–517
Tambroni N, Blondeaux P (2008) Sand banks of finite amplitude. J Geophys Res 113(C10):028. https://doi.org/10.1029/2007JC004658
Thieler ER, Pilkey OH, Cleary WJ, Schwab WC (2001) Modern sedimentation on the shoreface and inner continental shelf at Wrightsville Beach, North Carolina, U.S.A. J Sediment Res 71(6):958–970
Trentesaux A, Stolk A, Berné S (1999) Sedimentology and stratigraphy of a tidal sand bank in the southern North Sea. Mar Geol 159:253–272
Uehara K, Scourse JD, Horsburgh KJ, Lambeck K, Purcell AP (2006) Tidal evolution of the northwest European shelf seas from the last glacial maximum to the present. J Geophys Res 111:C09025. https://doi.org/10.1029/2006JC003531
van Dalfsen JA, Essink K, Madsen HT, Birklund J, Romero J, Manzanera M (2000) Differential response of macrozoobenthos to marine sand extraction in the North Sea and the Western Mediterranean. ICES J Mar Sci 57:1439–1445
van Dijk T, van der Tak C, de Boer W, Kleuskens M, Doornenbal P, Noorlandt R, Marges V (2011) The scientific validation of the hydrographic survey policy of the Netherlands Hydrographic Office, Royal Netherlands Navy. Tech. Rep. 1201907-000-BGS-0008, Deltares
van Dijk TAGP, van Dalfsen JA, Lancker VV, van Overmeeren RA, van Heteren S, Doornenbal PJ (2012) Benthic habitat variations over tidal ridges, North Sea, the Netherlands. In: Harris PT, Baker EK (eds) Seafloor geomorphology as benthic habitat-GeoHAB Atlas of seafloor Ggeomorphic features and benthic, Elsevier Inc, pp 241–249. https://doi.org/10.1016/B978-0-12-385140-6.00013-X
van Gaalen JF, Kruse SE, Coco G, Collins L, Doering T (2011) Observations of beach cusp evolution at Melbourne Beach, Florida, USA. Geomorphology 129(1):131–140. https://doi.org/10.1016/j.geomorph.2011.01.019
van Lancker VR, Bonne W, Garel E, Degrendele K, Roche M, den Eynde DV, Bellec V, Brière C, Collins MB, Velegrakis AF (2010) Recommendations for the sustainable exploitation of tidal sandbanks. J Coast Res 51:151–164. https://doi.org/10.2112/SI51-005.1
van der Molen J, de Swart HE (2001) Holocene tidal conditions and tide-induced sand transport in the southern North Sea. J Geophys Res 106(C5):9339–9362
van Veelen TJ, Roos PC, Hulscher SJMH (2018) Process-based modelling of bank-breaking mechanisms of tidal sandbanks. Cont Shelf Res 167:139–152. https://doi.org/10.1016/j.csr.2018.04.007
Velegrakis AF, Ballay A, Poulos S, Radzevicius R, Bellec V, Manso F (2010) European marine aggregates resources: origins, usage, prospecting and dredging techniques. J Coast Res SI(51):1–14. https://doi.org/10.2112/SI51-002.1
Walgreen M, Calvete D, de Swart HE (2002) Growth of large-scale bed forms due to storm-driven and tidal growth of large-scale bed forms due to storm-driven and tidal currents: a model approach. Cont Shelf Res 22:2777–2793
Walgreen M, de Swart HE, Calvete D (2004) A model for grain-size sorting over tidal sand ridges. Ocean Dyn 54:374–384. https://doi.org/10.1007/s10236-003-0066-3
Ward SL, Neill SP, Scourse JD, Bradley SL, Uehara K (2016) Sensitivity of palaeotidal models of the northwest European shelf seas to glacial isostatic adjustment since the last glacial maximum. Quart Sci Rev 151:198–211. https://doi.org/10.1016/j.quascirev.2016.08.034
Wu Z, Jin X, Cao Z, Li J, Zheng Y, Shang J (2010) Distribution, fomation and evolution of sand ridges on the east china sea shelf. Sci China Earth Sci 53(1):101–112. https://doi.org/10.1007/s11430-009-0190-0
Yang C (1989) Active, moribund and buried tidal sand ridges in the East China Sea and the southern Yellow Sea. Mar Geol 88:97–116
Yool A, Fasham MJ (2001) An examination of the “continental shelf pump” in an open ocean general circulation model. Glob Biogeochem Cycles 15(4):831–844
Yuan B, de Swart HE (2017) Effect of sea level rise and tidal current variation on the long-term evolution of offshore tidal sand ridges. Mar Geol 390:199–213. https://doi.org/10.1016/j.margeo.2017.07.005
Yuan B, de Swart HE, Panadès C (2016) Sensitivity of growth characteristics of tidal sand ridges and long bed waves to formulations of bed shear stress, sand transport and tidal forcing: a numerical model study. Cont Shelf Res 127:28–42. https://doi.org/10.1016/j.csr.2016.08.002
Yuan B, de Swart HE, Panadès C (2017) Modelling the finite-height behavior of offshore tidal sand ridges, a sensitivity study. Cont Shelf Res 137:72–83. https://doi.org/10.1016/j.csr.2017.02.007
Zhu Q, Wang YP, Ni W, Gao J, Li M, Yang L, Gong X, Gao S (2018) Effects of intertidal reclamation on tides and potential environmental risks: a numerical study for the southern Yellow Sea. Environ Earth Sci 75:1472. https://doi.org/10.1007/j.csr.2017.02.007
Zimmerman JTF (1980) Vorticity transfer by tidal currents over an irregular topography. J Mar Res 38(4):601–630
Zimmerman JTF (1981) Dynamics, diffusion and geomorphological significance of tidal residual eddies. Nature 290(5807):549–555
Acknowledgements
The second author was financially supported by the China Scholarship Council (No. 201206250029). We thank the referees for constructive comments that helped to improve the manuscript.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendices
A Formulation of sand transport
In the models for tidal sand ridges different formulations of sand transport are used. In Huthnance [35], Huthnance [36] and Hulscher et al. [33] it is assumed that this transport takes place as bedload, for which they use the parameterisation
Here, \({\mathbf {q}}\) is the volumetric sediment transport vector (units of its components \(q_x\) and \(q_y\) are \({\hbox {m}}^3{\hbox {m}}^{-1}{\hbox {s}}^{-1}\)), \({\mathbf {u}}\) is the depth-averaged velocity vector, h is the elevation of the bed with respect to the reference bottom level, \(\alpha\) a dimensional coefficient, n is an exponent and \(\varLambda\) a bed slope coefficient. Typical values of the parameters are that \(|{\mathbf {q}}|\) is of order \(10^{4}\,{\hbox {m}}^3{\hbox {m}}^{-1}{\hbox {s}}^{-1}\)) in case of a current speed of \(1\,{\text {m}}\,{\text{s}}^{-1}\), \(n=2\) and \(\varLambda =2\). Note that for \(n=2\) the transport is cubic in the velocity.
In Roos et al. [57] and van Veelen et al. [82] the formulation of Eq. (1) is extended with an additional stirring term due to wind waves, by replacing \(|{\mathbf {u}}|^n\) by \(\left( |{\mathbf {u}}|^2+\frac{1}{2}u_w^2\right) ^{n/2}\) and taking \(n=2\). In this expression \(u_w\) is the amplitude of near-bed wave orbital motion, which is computed from a parameterisation that is based on linear wave theory. Moreover, Roos et al. [57] and Besio et al. [5] consider, besides bedload transport, also suspended load transport. The former study shows that the addition of suspended load transport results in finite height ridges with more flattened crests, while the latter study shows that this additional transport component is only important in the case of fine sediment and large tidal currents.
In Besio et al. [5], as well as in later studies by Tambroni and Blondeaux [72], Blondeaux et al. [8] and Yuan et al. [91] , two additional effects are accounted for that are not present in formulation (1). The first is that transport includes a critical velocity for erosion and the second is that transport due to longitudinal and lateral bed slopes differ. Typically, the formulation of Fredsøe and Deigaard [25] is used, which reads
In this expression, \({\hat{q}}\) is a coefficient, \(U_c\) is the critical depth-averaged velocity for erosion and \({\mathbf {G}}\) is a second-rank tensor, represented by a \(2\times 2\) matrix, of which the coefficients are given in Seminara [62], and \({{\mathcal {H}}}\) is the Heaviside function. In the case that \(U_c=0\) and \({\mathbf {G}}=\varLambda {\mathbf {\delta }}\), with \({\mathbf {\delta} }\) the unity tensor, the formulation (2) reduces to that given in Eq. (1). Results of Yuan et al. [91] demonstrated that anistropic slope-induced sand transport has little effect on the model results.
Finally, in Yuan et al. [92] and Yuan and de Swart [90] employed an extended version of formulation (2), in which \(|{\mathbf {u}}|^2\) is replaced by \(u_e^2=|{\mathbf {u}}|^2+\frac{1}{2}u_w^2\). Hence, account is made of additional stirring of sand by wind waves, with \(u_w\) the amplitude of near-bed wave orbital motion.
B Vorticity dynamics of tidal currents over an irregular topography
In this appendix, a quantitative description of generation of vorticity by tide-topgraphy interaction will be given. Starting point are the depth-averaged shallow water equations in Cartesian coordinates x and y, under the rigid lid approximation and with a linearised bottom shear stress:
These are, respectively, the two momentum equations and the continuity equation. Here, u, v are the depth-averaged velocity in the x- and y-direction, \(\zeta\) is the elevation of the free surface with respect to still water level and D is water depth. Furthermore, t is time, f the Coriolis parameter and r a linear friction coefficient.
Taking the x derivative of Eq. (4) and subtracting the y derivative of Eq. (3) results in the vorticity equation
with
the vorticity (twice the angular speed of rotation of water columns around the vertical axis). Here, the continuity equation has been used to rewrite the Coriolis term. The left-hand side of Eq. (6) consists of the local inertial term and the divergence of the vorticity flux, where the latter has the components \(u\omega\) and \(v\omega\) in, respectively, the x- and y-direction. The first two terms on the right-hand side represent the torques due to the Coriolis force and the bottom frictional force. The last term represents the dissipation of vorticity by bottom friction.
In Sect. 3.2 the situation is considered of a spatially uniform tidal flow that, in the absence of bottom undulations, is directed in the y-direction. Its velocity is given by \(v_0=V\cos \sigma t\), with V the velocity amplitude and \(\sigma\) the angular frequency. This so-called background velocity field has no vorticity. Furthermore, by writing \(D=H-h\), with H the constant undisturbed bed and h the elevation of the bed with respect to the mean bottom level, and assuming \(|h|\ll H\), the vorticity equation becomes
The two terms on the right hand side represent the Coriolis and frictional torques that are discussed in Sect. 3.2 and in Fig. 6. Note that they are both negative (on the Northern Hemisphere, where \(f>0\)) if \(\partial h/\partial y\) and \(\partial h/\partial x\) are both positive. Further, note that the tidally averaged vorticity equation reads
Here, the bar denotes an average over the tidal period. So residual vorticity is generated by the divergence of the residual vorticity flux.
Next, the vorticity field is determined for arbitrary bottom undulations on the open shelf. Both can be represented as Fourier integrals:
where k and l are topographic wavenumbers in the x- and y-direction. Upon substitution of these expressions in the vorticity Eq. (8), it follows
This equation has an exact solution (see [94]), but it is more insightful to solve it by expanding the vorticity response \({\hat{\omega }}\) into a truncated Fourier series in time:
Substitution of this expression into the vorticity and collecting the different harmonic terms results in a set of algebraic equations for the harmonic coefficient \(\omega _0, \omega _c, \omega _s\), etc. In particular, truncation of the harmonic series after the first harmonic yields
which has the following solution for the residual vorticity component:
In the term between brackets in the numerator the (Fourier transform of the) Coriolis torque and frictional torque appear. The mechanism is that the torques create tidal vorticity that oscillates with frequency \(\sigma\). This tidal vorticity is transported by the background tidal flow, which leads to a residual vorticity flux. Convergence of that flux yields residual vorticity. Note that if \(f>0, k>0, l>0\) it follows that \(\omega _0\) is negative if \({\hat{h}}\) is positive. Thus, in that case, negative vorticity occurs in the crest areas, and positive vorticity in the trough areas. The condition \(k,l >0\) means that crests are cyclonically rotated with respect to the direction of the background tidal flow \(v_0\).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
de Swart, H.E., Yuan, B. Dynamics of offshore tidal sand ridges, a review. Environ Fluid Mech 19, 1047–1071 (2019). https://doi.org/10.1007/s10652-018-9630-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10652-018-9630-8