Gravity currents with tailwaters in Boussinesq and non-Boussinesq systems: two-layer shallow-water dam-break solutions and Navier–Stokes simulations

Abstract

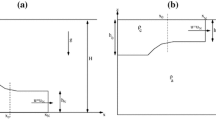
We consider the dam-break initial stage of propagation of a gravity current of density $\rho _{c}$ released from a lock (reservoir) of height $h_0$ in a channel of height $H$. The channel contains two-layer stratified fluid. One layer, called the “tailwater,” is of the same density as the current and is of thickness $h_T (< h_0)$, and the other layer, called the “ambient,” is of different density $\rho _{a}$. Both Boussinesq ($\rho _{c}/\rho _{a}\approx 1$) and non-Boussinesq systems are investigated. By assuming a large Reynolds number, we can model the flow with the two-layer shallow-water approximation. Due to the presence of the tailwater, the “jump conditions” at the front of the current are different from the classical Benjamin formula, and in some circumstances (clarified in the paper) the interface of the current matches smoothly with the horizontal interface of the tailwater. Using the method of characteristics, analytical solutions are derived for various combinations of the governing parameters. To corroborate the results, two-dimensional direct numerical Navier–Stokes simulations are used, and comparisons for about 80 combinations of parameters in the Boussinesq and non-Boussinesq domains are performed. The agreement of speed and height of the current is very close. We conclude that the model yields self-contained and fairly accurate analytical solutions for the dam-break problem under consideration. The results provide reliable insights into the influence of the tailwater on the propagation of the gravity current, for both heavy-into-light and light-into-heavy motions. This is a significant extension of the classical gravity-current theory from the particular $h_T=0$ point to the $h_T > 0$ domain.

Appendices

Appendix 1: The $R \rightarrow 0$ limit

The dam-break of water-in-air is a practical, important problem; see [8, 9]. This case is close to our system in the density limit $\rho _{a}/\rho _{c}= R \rightarrow 0$. However, we considered a gravity current in a channel, not in the open atmosphere. One can argue that the $H \rightarrow \infty$ limit is expected to be a fair approximation.

We therefore compare our solution in this limit with the results of Stansby et al. [8]. We scale height with $h_0$ and speed with $(g h_0)^{1/2}$.

Consider the equation of motion (2.15)–(2.20). In the present limit, $A=0, D=1$, and therefore the equations of the characteristics reduce to the one-layer SW formulation, in particular

$$\begin{aligned} \frac{dh}{du} = \mp \sqrt{h} \quad {\text {on}}\quad \frac{dx}{dt}= c_\pm = u \pm \sqrt{h}. \end{aligned}$$

(6.1)

The contact between the current and the reservoir is a rarefaction wave, therefore the initial conditions on a $c_{+}$ characteristic from the reservoir to the nose are $h=1, u=0$, and integration of $dh/du$ gives

$$\begin{aligned} u = 2( 1 - \sqrt{h}). \end{aligned}$$

(6.2)

When $\rho _{a}/\rho _{c}\rightarrow 0$, at the front a jump is always present, according to (2.7). The kinematic conditions (2.8) is valid, i.e.,

$$\begin{aligned} u_{N} = V_N(1 - b/a). \end{aligned}$$

(6.3)

We use (2.9)–(2.10) with $\rho _{a}/\rho _{c}\rightarrow 0$, and keep $a/b$ finite while $a,b \rightarrow 0$ (because $h_N, h_T$ are finite while the height of the ambient become large), while $\rho _{a}/\rho _{c}\rightarrow 0$. We obtain the dimensionless

$$\begin{aligned} V_N= \left[ \frac{2}{1 + b/a} \right] ^{1/2}h_N^{1/2}. \end{aligned}$$

(6.4)

The height and speed of the front, $h_N, V_N$ are obtained by the intersection of (6.2) and (6.3), subject to (6.4). Substitution of (6.3)–(6.4) into (6.1) shows that $V_{N} < c_{+}$ at the nose, and hence the jump is of Type1; see Fig. 3.

We note that Eqs. (6.1)–(6.3) are in full agreement with the solution of Stansby et al. [8]. However, that paper uses a different nose boundary condition, namely

$$\begin{aligned} V_N= \left[ \frac{1}{2}(1 + a/b) \right] ^ {1/2}h_N^{1/2}. \end{aligned}$$

(6.5)

A closer inspection reveals that the difference is due to the fact that Stansby et al. [8], following Stoker [9], take into account the open-atmosphere pressure condition at the interface before and after the jump. Our channel-flow solution uses the counterpart condition that the bottom is a stagnation-pressure-conserving line, and this assumption can be validated only if a second layer of fluid is present. There is indeed some built-in inconsistency at the front between our model and the water open-to-atmosphere problem. However, as expected, the difference in the results is quite small. In particular, we immediately observe that for $a/b \approx 1$ the difference between (6.4) and (6.5) is insignificant. In this case, both jump-speed formulas reduce to the rarefaction wave result (2.20), which is a unique and non-dissipative limit.

The conclusions are: the present SW solution and that of Stansby et al. [8] are in agreement about the wave into the reservoir and general shape of the current, but differ concerning the value of $h_N$ and $V_N$. The magnitude of the discrepancy is illustrated by the solutions for $b=0.1$ and $b=0.45$, presented and compared with experiments in Stansby et al. [8] (see Fig. 8b,c there). For the first case, the paper shows $h_N = 0.37, V_N= 0.99$, while our values are $0.45, 0.85$. The experimental data is quite ambiguous: the height is in better agreement with the present solution, the speed is closer to the solution of Stansby et al. [8].

For the second case, the paper shows $h_N =0.70, V_N= 0.94$, while our values are $0.70, 0.92$. Here the discrepancy between the theoretical results is rather insignificant, and the agreement with the experiment is fair. The experimental data display some spread of the jump, which prevents a sharp evaluation of $V_N$, and renders the difference between the models in the range of the experimental error.

We reiterate that we do not claim that our theory is accurate for the open-surface gravity current. We just show that, as could be expected, when the density of the ambient is very small, the flow of the gravity current with tailwaters in a channel is close to that in an open-surface system.

Appendix 2: The shape of the current

Our investigation is focused on the formation and propagation of the jumps in lock-released current, using the SW approximation and method of characteristics. However, it is well known that, after the calculation of these jumps (or rarefaction wave) at the front and back of the current, the shape of the interface during the dam-break stage can also be obtained by the same method (see [10, 11]).

Figure 12 illustrates the SW-shape result for a Boussinesq system with $H=3.33, b=0.1$. This is compared with the simulations for $Re=3500, Sc = 1$, free-slip bottom. Here $x_0 = h_0$, speed is scaled with $U = (g' h_0)^{1/2}$, and time with $x_0/U$.

Fig. 12

Height-shape of Boussinesq case with $H=3.33, b= 0.1$, at two times after release. SW (blue line) and NS (black line). The initial shape is shown by the red line

The SW current-shape is, briefly, determined as follows. The layer of fluid above the lock is of thickness $2.33$, and since $2.33/H > 1/2$, the disturbance into the lock is a rarefaction wave (see (2.7) with $\rho _{c}/\rho _{a}= 1$). Using this information, we integrate $du/dh$ (with initial conditions $h=1,u=0$) on a $c_+$ characteristic to obtain $u(h)$. This also provides the values of $c_+, c_-$ and $u/(1-b/a)$ as functions of $h$ (here $a=h/H$). The results are plotted in Fig. 13. Also shown in this figure is the value of front condition $V_N$ calculated from (2.18) for $R=1, b=0.1$ and, again, $a=h/H$. The intersection of this curve with $u/(1-b/a)$, at point $N$, provides the height and speed of the nose, $(h_N, V_N) = (0.635,0.778)$. We see in the diagram that the nose is sub-critical ($V_{N}<c_+$), hence the domain of fluid behind the nose is a rectangle of constant height $h_N$, until it is matched with the expansion domain $LM$. Point $M$ is on a $c_-$ characteristic with $h=h_N, u=u_N$, and the corresponding speed is $-0.408$. Point $L$ moves with the velocity of the rarefaction wave,

$$\begin{aligned} V_L = c_-(h=1, u=0) = -(1 - 1/H)^{1/2}= -0.836. \end{aligned}$$

(6.6)

(We can take additional points on the $LM$ interface. For example, consider a point A at $h_A=0.80$: this $A$ point moves with the corresponding $c_- = - 0.645$.)

Fig. 13

SW solution diagram: $u$ (red), $u/(1-b/a)$ (green), $V_N$ (blue), $c_+, c_-$ (dash-dot lines) as functions of $h$. The vertical dashed-line marks the position $h_N = 0.635$

This construction demonstrates that the main computational effort for the entire SW solution is the integration of $du/dh$ and the calculation of the intersection with the front condition. This is a tremendous simplification as compared to the Navier–Stokes simulation on a two-million-point grid which is used to produce the more accurate flow-field solution.

We see that the Navier–Stokes interface displays oscillations; the matching of the backward-moving rarefaction wave with the reservoir, and the matching of the front with the tailwaters, are not so sharp as the SW profile. These are expected effects, due to the complicated dynamics of the real interface in presence of local vortices, shear, and mixing. However, we observe that, overall, the SW model reproduces fairly well the averaged outline of the current during propagation. We therefore think that this comparison also supports the idea that the present SW approximation is a useful and insightful tool for gaining first estimates on the motion of the gravity current in presence of tailwaters. In spite of its simplicity, the model apparently captures well the dynamic balances that dominate the motion.