Abstract
The eddy covariance (EC) method is a standard micrometeorological technique for monitoring the exchange rate of the main greenhouse gases across the interface between the atmosphere and ecosystems. One of the first EC data processing steps is the temporal alignment of the raw, high frequency measurements collected by the sonic anemometer and gas analyser. While different methods have been proposed and are currently applied, the application of the EC method to trace gases measurements highlighted the difficulty of a correct time lag detection when the fluxes are small in magnitude. Failure to correctly synchronise the time series entails a systematic error on covariance estimates and can introduce large uncertainties and biases in the calculated fluxes. This work aims at overcoming these issues by introducing a new time lag detection procedure based on the assessment of the cross-correlation function (CCF) between variables subject to (i) a pre-whitening based on autoregressive filters and (ii) a resampling technique based on block-bootstrapping. Combining pre-whitening and block-bootstrapping facilitates the assessment of the CCF, enhancing the accuracy of time lag detection between variables with correlation of low order of magnitude (i.e. lower than \(-1\)) and allowing for a proper estimate of the associated uncertainty. We expect the proposed procedure to significantly improve the temporal alignment of the EC time-series measured by two physically separate sensors, and to be particularly beneficial in centralised data processing pipelines of research infrastructures (e.g. the Integrated Carbon Observation System, ICOS-RI) where the use of robust and fully data-driven methods, like the one we propose, constitutes an essential prerequisite.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Combating climate changes requires an accurate quantification of greenhouse gases (GHG) emitted to and removed from the atmosphere by terrestrial ecosystems. To this end, an important research frontier in ecology is directed toward measuring the rates of exchange (or flux densities) of GHGs over natural and anthropogenic ecosystems (Houghton 2005; Bonan 2008; Pan et al. 2011). Surface layer fluxes of energy, water (H2O), carbon dioxide (CO2), methane (CH4) and nitrous oxide (N2O) are currently estimated by the eddy covariance (EC) technique (Foken et al. 2012). The EC technique employs a sonic anemometer (SA) for wind velocity components and a gas analyser (GA) for scalar atmospheric concentrations and requires high-frequency sampling rates (e.g. 10 observations per s). Eddy fluxes are derived from the covariance (normally within an averaging time of 30 min) between instantaneous fluctuations about the mean of the vertical wind speed (W) and the scalar of interest (S), which can be temperature, atmospheric concentrations of water vapour, carbon dioxide or any other trace gas.
The calculation of EC fluxes requires the instantaneous quantities of vertical wind velocity and scalar to be simultaneously measured. Such a condition is seldom fulfilled in field measurements because, in general, there is not a perfect co-location of the SA and the GA sampling points to avoid possible wind flow distortions. This causes the same air parcel to first pass through one sensor and then through the other, creating a delay (time lag) in its wind and concentration measurements. In addition, in closed-path systems (i.e. those GAs with an internal sampling cell and an inlet tube), the sampled air parcel, sucked by a pump, has to travel from the intake to the measurement cell in the analyser (potentially for tens of metres) before being measured and merged with the concurrent wind data. This necessarily causes an additional and undesirable temporal delay with respect to time series sampled by the SA. Physical distance between sensors is not the only source of temporal mis-alignment. Also data flow delays, digital clock drifts, and artefacts in the data acquisition strategy could be responsible for introducing a significant temporal mis-alignment between EC time series measured by different instruments (Fratini et al. 2018).
Correcting such mis-alignments between raw data is a key step in the calculation of fluxes. Failure to correctly synchronise the time series causes a systematic error on covariance estimates (Taipale et al. 2010; Langford et al. 2015). The use of a constant time lag derived from the physical characteristics of the sampling system is often inappropriate since the temporal mis-alignment between time series may vary during the sampling period. For open-path systems (i.e. those GAs without tube inlet), while keeping the physical distance between the sensors fixed, the temporal mis-alignment may vary according to wind speed and wind direction. For closed-path systems instead, while keeping the characteristics of the sampling line geometry (e.g. tube length, tube inner diameter, intake air flow rate, distance between sonic anemometer and tube inlet) unchanged, the temporal mis-alignment may vary with pump ageing, filter contamination, accumulation of dirt in the sampling line, which all impact the stability of the flow rate and therefore the travel time of air parcels through the sampling tube (Massman 2000; Shimizu 2007). Also the way some non-inert gases interact with the tube walls (e.g. adsorption–desorption) is responsible for generating a temporal mis-alignment between time series. For example, the transit time of water vapour along the intake tube of a closed-path system can vary substantially with relative humidity, due to adsorption/desorption processes at the tube walls (Ibrom et al. 2007; Massman and Ibrom 2008; Mammarella et al. 2009; Fratini et al. 2012).
To overcome the limitations of using a constant time lag based procedure, the prevalent solution in EC data processing is to assess the cross-covariance function between W and S. The cross-covariance function provides a measure of the linear dependence between two time series, one of which is delayed with respect to the other. In ideal situations and according to the EC theory, the highest dependence occurs when W and S are perfectly aligned. Therefore, the actual time lag can be detected in correspondence of the step lag that maximises (in absolute terms) the cross-covariance between the two time series (Moncrieff et al. 1997; Rebmann et al. 2012). We refer to such an approach as covariance maximisation (CM hereinafter).
Illustrative examples of cross-covariance function (right panels) between vertical wind velocity component (W, left panels) and nitrous oxide (N2O, middle panels) atmospheric concentrations sampled at 20 Hz scanned frequency (i.e. 20 obs per sec) and collected in 60 min raw data file length. Numbers on the top of the x-axis indicate the time lag detected by the covariance-maximisation (CM) procedure in correspondence with the peak (in absolute terms) of the cross-covariance function
However, the effectiveness of the CM procedure depends on the shape of the cross-covariance function, which in turn depends on the stochastic properties of the variables involved and on the amount of random uncertainty affecting flux estimates (Billesbach 2011; Nemitz et al. 2018; Vitale et al. 2019). Generally, the procedure is effective under second order stationary conditions and when the flux magnitude is moderate/high. In these circumstances, the cross-covariance function exhibits a distinct and pronounced peak (either positive or negative) and the actual time lag can be easily detected (see Fig. 1a). In other circumstances, in particular when fluxes are of small magnitude, the cross-covariance function can be characterised by multiple local extrema of similar magnitude (Fig. 1b–e). In some cases the time lag detection for fluxes of low magnitude can be facilitated by modern GAs capable of simultaneously measuring several GHGs species. For such instruments, and in case of inert gases, the detection of the time lag for low magnitude fluxes can be obtained by dynamically ascribing delays detected from co-measured variables having a stronger signal, generally CO\(_2\) (Nemitz et al. 2018). However, in absence of reference high-magnitude fluxes or when trace gases are measured by different GAs with potential different time lags (e.g. due to their relative position or the use of different data acquisition systems), the detection of the actual time lag becomes challenging, in particular in automated EC data processing pipelines.
A tentative solution to this problem has been described in Taipale et al. (2010) who suggested applying a preliminary smoothing filter on the cross-covariance function before detecting time lag in correspondence of the absolute maximum. While smoothing can help in reducing the influence of sporadic and isolated peaks significantly, the determination of the extremum in the covariance curve often fails for low magnitude fluxes, resulting in unreasonable time lags and, consequently, potentially biased flux estimates (Langford et al. 2015; Nemitz et al. 2018; Schallhart et al. 2018; Kohonen et al. 2020; Striednig et al. 2020).
In addition, a further limitation of the CM-based procedures (with or without smoothing) is that the alignment of time series when the true unknown flux is null or very close to zero can never be achieved. Fluxes are in fact calculated as covariances between W and S and a method which maximises the covariance will always search and select a time lag in correspondence of flux values different from 0 (either positive or negative), a phenomenon known as mirroring effect (Langford et al. 2015; Kohonen et al. 2020). In this regard, it should be noted that flux estimates equal to zero fall within the physical range of possible values and they are not to be understood as a rare event, in particular during periods of low background fluxes. Moreover, from an eco-physiological point of view, zero fluxes could occur not only in the absence of exchange between the atmosphere and the ecosystem, but also when there is a perfect balance between amounts assimilated and released by the ecosystem, for example during the switch between emission and assimilation of CO\(_2\) in the morning and in the evening. Discarding zero fluxes can cause not only a systematic overestimation of the absolute flux, but also affects the density distribution of the observed data for values close to zero.
The aim of this work is to propose a new approach that overcomes the limitations of the CM-based procedures. To this end, we developed a fully data-driven procedure where time lag is detected by assessing the cross-correlation function (CCF) between raw EC data subject to (i) a preliminary filtering procedure based on pre-whitening and (ii) a resampling technique based on block-bootstrapping. As recommended in leading textbooks on time series analysis (see for example Hamilton 1994; Cryer and Chan 2008), a proper assessment of the CCF between time series requires the variables to be stationary and pre-whitened. Stationarity is defined by a constant mean and equal variance at all times and can be achieved by detrending or differencing. Stationary condition is essential when assessing the CCF because dominant long-term trends may hide the correlation between short-term fluctuations. Pre-whitening consists instead of transforming (at least one of) the time series involved in CCF into a white noise (WN) process with the twofold purpose of reducing the influence the serial correlation has on the CCF estimates and making it possible to assess their statistical significance with standard criteria. However, even applying such arrangements, when the peak of the CCF has magnitude similar to those of the conventional confidence intervals the risk of detecting erroneous time lag increases drastically. By combining pre-whitening and bootstrapping, such a risk is avoided and the assessment of the CCF for time lag detection becomes more realistic, informative and suitable for variables having correlation of low order of magnitude, as in the case of low magnitude EC fluxes.
The paper is structured as follows. In the following section a detailed description of the procedure is presented with special emphasis on the decision rules for the choice of the optimal time lag suitable for the alignment of raw EC data. Having described the EC data in Sect. 3, an application of the proposed approach and a comparison with commonly used time lag detection procedures are reported in Sect. 4. Final remarks are provided in Sect. 5.
2 Methods
2.1 Time lag detection via assessment of the cross-correlation function after pre-whitening
In this section we describe the time lag detection procedure based on the assessment of the CCF between pre-whitened variables, focusing on the theoretical aspects motivating such preliminary data filtering. The following definitions are derived from Cryer and Chan (2008).
Let \(Y = {Y_t}\) and \(X = {X_t}\) be two stationary time series of length n indexed by time t, the correlation between X and Y at lag \(k=\pm 1, \pm 2, \ldots , \pm n\) can be estimated by the sample CCF defined by:
where \({\overline{X}}\) and \({\overline{Y}}\) are the sample mean of X and Y, respectively, and the summations are done over all data where the summands are available.
For white noise (WN) processes (i.e. sequences of uncorrelated random variables, each with zero mean and variance \(\sigma\)), \(\rho _k\) is approximately normally distributed with zero mean and variance 1/n, where n is the total number of paired data. This leads to the conventional 5% significance limits of the CCF estimates equal to \(\pm 1.96/\sqrt{n}\). That is, any peak outside the interval \(\pm 1.96/\sqrt{n}\) (or plus/minus two standard errors) is deemed significantly different from zero at 0.05 level. The approximate variance of 1/n applies only when data are independent and identically distributed (iid), a condition that is almost never met for any real, observed time series, because of the presence of autocorrelation (i.e. the current value of the series is dependent on preceding values and can be predicted, at least in part, on the basis of knowledge of those values). Under the assumption that both X and Y are stationary and that they are independent of each other, the sample variance of \(\rho _k\) is approximately:
where \(r_k(X)\) and \(r_k(Y)\) are the autocorrelation estimates at lag k of X and Y, respectively.
Suppose for simplicity that X and Y are both first-order autoregressive processes with coefficients \(\phi _X\) and \(\phi _Y\), respectively, then \(\rho _k\) is approximately normally distributed with zero mean and variance approximately equal to:
From Eq. (3) it can be seen that when \(\phi _X\) and \(\phi _Y\) are close to 1, the ratio of the sampling variance of \(\rho _k\) to the nominal value of 1/n approaches infinity. As a consequence, using the \(\pm 1.96/\sqrt{n}\) rule in deciding the significance of the sample CCF may lead to many more false positives than the nominal 5% error rate, even when time series are independent of each other.
The statistical significance of the CCF estimates is a typical representation of the so-called spurious correlations problem often encountered when analysing the relationship between time series variables (Yule 1926; Hamilton 1994). To avoid the risk of spurious correlations, a viable solution is to disentangle the linear association between X and Y from their autocorrelation. By examining Eq. (2), it can be seen that the approximate variance of \(\rho _k\) is 1/n if at least one of X and Y is an iid sequence. Such a condition can be achieved by transforming one of the variables in a new process that is close to a WN, a procedure known as pre-whitening (Cryer and Chan 2008). Since the purpose of pre-whitening is to filter the serial correlation, and it is not crucial to find the best and most parsimonious model for X exactly, pre-whitening can be achieved by means of autoregressive models of order p, AR(p):
where \({\tilde{X}}_t\) is a WN, \(\pi _i\) are the AR coefficients and B is the backshift operator such that \(B^mX_t=X_{t-m}\). In this work, the choice of p was automatically selected by minimising the Akaike (1998) Information criterion (AIC). Once identified the p order, the AR coefficients were estimated via Yule–Walker method (Lütkepohl 2005).
After transforming the X-variable, the same filter is used to transform the Y-variable in \({\tilde{Y}}_t\), which does not need to be a WN. Since pre-whitening is a linear operation, any linear relationship between the original series will be preserved and can be retrieved by assessing the CCF between transformed \({\tilde{X}}_t\) and \({\tilde{Y}}_t\) variables (Cryer and Chan 2008).
The time lag to be used for temporal alignment of raw EC time series can be retrieved in correspondence of the peak (in absolute terms) of the CCF between pre-whitened variables:
provided it is statistically significant at a pre-specified significance level.
We will refer to such an approach for time lag detection of raw EC data using the name of the procedure, i.e. as pre-whitening (PW hereinafter).
2.2 Time lag detection via assessment of the cross-correlation function after pre-whitening with bootstrap
A time lag detection procedure based solely on the assessment of the CCF between pre-whitened variables (Sect. 2.1) is effective when the order of magnitude of the correlation is equal to \(-1\). This is true for moderate/high magnitude EC fluxes because the signal dominates over the noise and the estimate of the CCF in correspondence of the true time lag will be far greater than the conventional significance limits. When the correlation is low, as is often the case with trace gases, things become more complicated because the peak of the CCF in correspondence of the true (unknown) time lag will not be so pronounced as to dominate over the other estimates of the CCF at different lags. For example, in the case of a sample size of 36000 paired observations and an order of magnitude of the correlation between variables \(<-1\), the peak of CCF is close to the 5% significance limits (\(\pm 1.96/\sqrt{36000}\approx \pm 0.01\)). Therefore, it can often happen that the peak of the CCF is detected in correspondence of an erroneous time lag.
If measurements from repeated sampling under the same conditions were available, it would be easier to distinguish between true and false peaks of the CCF, as the former would remain more stable than the latter, which instead would tend to cancel out after averaging.
With this idea in mind, we mimicked a repeated sampling by means of a block bootstrapping (Härdle et al. 2003) with the twofold aim of (i) increasing the accuracy of time lag detection and (ii) obtaining a quantification of the associated uncertainty. Block bootstrap consists of breaking the series into roughly equal-length blocks of consecutive observations and resampling the block with replacement. Dividing the data into several blocks can preserve the original time series structure within a block. In particular, we built \(N_B=99\) bootstrap samples of paired \({\tilde{X}}_t\) and \({\tilde{Y}}_t\) values of size N equal to the length of time series, and where each sample is formed by randomly choosing N/L blocks (with replacement) with \(L=20\) s, a temporal window large enough to include the true (unknown) time lag and preserve the correlation structure between variables in short time intervals.
The CCF was then estimated for each of the \(N_B\) block bootstrap samples and, to further eliminate the presence of erratic peaks due to noise, a smoothed version (\(\rho _{k,j}^{S}\)) through a centred moving average of width \(hz/2+1\) time steps, where hz is the scanned acquisition frequency of raw data (i.e. 10 or 20 Hz), is computed. For each \(\rho _{k,j}^{S}\), the jth estimated time lag (TL\(_j\)) is then detected in correspondence of the peak (in absolute terms):
By analysing the distribution of the resulting \(N_B\) time lags, regardless of their significance level, the most frequently observed value is selected as the reference time lag:
The 95% highest density interval (HDI), i.e. the shortest interval for which there is a 95% probability that the true (unknown) time lag would lie within the interval, provides a measure of the associated uncertainty.
We will refer to such an approach for time lag detection of raw EC data as pre-whitening with bootstrap (PWB hereinafter).
2.3 Optimal time lag selection for temporal alignment of long-term EC data
Irrespective of the chosen procedure, time lag detection of EC data needs to be performed between the high-frequency (e.g. 10–20 observations per s) time series of 30–60 min (averaging period), usually collected in raw EC data files of the same length. To cope with such large datasets (e.g. 17,520 raw data files per year), the availability of robust and automated procedures is essential for EC data processing pipelines.
In this context, uncertainty estimates are not only important for the accuracy evaluation of individual time lags of each scalar variable/raw data files, but also for defining a fully data-driven strategy for the temporal alignment of long-term EC datasets. While the actual time lag may vary over time for various reasons (see the introductory section for more details), it is expected to be fairly stable during the averaging time intervals.
In this perspective, a low uncertainty indicates a low variability of time lags detected for each of the \(N_B\) bootstrapped samples during the averaging time. Consequently, the reference time lag detected by the PWB procedure is more likely to be the actual one. In contrast, the highest level of uncertainty occurs when the correlation between variables is zero (i.e. for zero fluxes), since the detected time lag will be randomly chosen within the temporal window of lags, in each bootstrapped sample.
With these concepts in mind and with the aim of identifying, for each averaging time, the optimal time lag (PWB\(^\text {OPT}\) hereinafter) to be used for the temporal alignment of long-term EC data, we propose the following strategy articulated in three steps:
-
S1. In the first step, time lags detected by PWB and characterised by a low uncertainty are considered reliable and flagged as optimal. In this work, uncertainty is defined as low when the range of the 95% HDI is less than 0.5 s;
-
S2. In the second step, time lags with larger uncertainty (i.e. range of the 95% HDI > 0.5 s) are also considered reliable and flagged as optimal if they show no significant deviation from the optimal time lag identified in Step 1 in the closest preceding averaging period. In this work, deviation is considered as significant if greater than 0.5 s;
-
S3. Finally, the remaining time lags not satisfying the above criteria are considered unreliable and replaced with the optimal time lag identified in the closest preceding averaging period, according to S1 or S2 criteria.
In the above strategy, the only parameters to be set are the threshold values that define the uncertainty associated with the estimated time lag as low (S1) and the deviation between detected time lags (S2). As reported earlier, we recommend setting them equal to 0.5 s, a conservative threshold value that can be considered as an upper limit of the time lag variability can take over 30–60 min or between consecutive averaging periods.
2.4 Algorithmic details and additional data pre-processing
2.4.1 Variable selection
Time lag detection for EC data is commonly computed by assessing the CCF between S measured by a GA and W measured by a SA. As said in the introductory section, once variables have been aligned, flux exchange rates can be derived from the covariance between S and W.
Sonic anemometers also provide an indirect measure of the air temperature, the so-called sonic temperature (T). Being sampled by the same instrument, W and T are perfectly aligned and sensible heat fluxes can be derived from the covariance between them, without resorting to any temporal alignment procedure. Since air parcels movement is governed by the laws of thermodynamics, any scalar S is correlated with T, and this correlation may be stronger than that existing between S and W. That could facilitate the time lag detection procedure as the CCF between S and T would show a more pronounced peak compared to the CCF between S and W.
For the pre-whitening phase, since the aim is to ensure that at least one of the transformed series is free of autocorrelation, it does not matter which variable is selected as X. For this reason, the PWB procedure considers all (four) possible combinations of S, W and T, for which at least one of X- and Y-variable is the atmospheric scalar concentration. Among the four time lags identified, the one to which a higher correlation (in absolute value) corresponds is chosen as the reference, regardless of its statistical significance.
2.4.2 Despiking and detrending
Time lag detection procedures were performed on despiked and detrended raw data. Wind components were preliminary subject to anemometer tilt correction via double rotation method (Rebmann et al. 2012). For despiking, the procedure described in Vitale (2021) was performed. Different detrending procedures were adopted.
The CM procedure was performed on variables subjected to a linear trend removal, as one of the most used methods in EC data processing (Sabbatini et al. 2018; Nemitz et al. 2018).
For PW and PWB procedures, any trend affecting raw data was removed by differencing, according to the results of the non-parametric variance ratio (VR) test described in Breitung (2002). Differencing is the sequential subtraction of consecutive values of a time-series to obtain sequential changes in time. Besides highlighting other useful properties, differencing a variable eliminates any trends present in it, whether deterministic (e.g. linear) or stochastic (Box et al. 2015). For the purpose of time lag detection, both X- and Y-variables were preliminary differentiated if the VR test provided evidence about the presence of a stochastic trend in one or in both the variables subjected to the pre-whitening procedure.
2.4.3 Software implementation
The PWB procedure is implemented in the RFlux package (downloadable at https://github.com/icos-etc/RFlux) taking advantage of the capabilities of the boot package (Canty and Ripley 2021) that allow to run in parallel mode the processing of the \(N_B\) block-bootstrapped samples.
3 Data, benchmark methods and evaluation criteria
3.1 EC data
In this work, raw data sampled from the following EC sites were used:
-
CH-Cha: Chamau, Switzerland (CH), managed grassland located in a pre-alpine valley (47.2102 N, 8.4104 E, 393 m asl).
-
DE-GsB: Grosses Bruch, Germany (DE), grassland (52.0296 N, 11.1048 E, 81 m asl).
-
FI-Kvr: Kuivajärvi, Finland (FI), small humic lake (2.6 km long, 0.4 km wide, surface area of 0.6 km\(^2\)) surrounded by mixed coniferous forest (61.8466 N, 24.2804 E, 141 m asl).
-
UK-EBu: Easter Bush, Scotland (UK), grazed, managed grassland (55.8655 N, 3.2065 W, 190 m asl).
In addition to the wind components measured by SA, scalar variables of CO\(_2\), CH\(_4\) and N\(_2\)O atmospheric concentrations were sampled, and considered in this work (see Table 1 for a description of the EC flux-station sites setup).
The EC system at UK-EBu was equipped with an inlet overflow system (Nemitz et al. 2018), by which a high concentration of N\(_2\)O was injected at set time intervals to measure the time delay between injection and detection by the closed-path analyser. This time delay, which is a function of the physical properties of the setup (e.g. flow rate through the sampling line and instrument response time), was the largest component of the total time lag and used in the derivation thereof. Time lags estimated by means of such an experimental approach (EXP hereinafter) were used for comparison with our data-driven approach.
3.2 Benchmark methods and evaluation criteria
To aid in comparison and achieve a better interpretation of the results, the following procedures were considered:
-
CM-W: maximisation of the cross-covariance function between S and W;
-
CM-T: maximisation of the cross-covariance function between S and T;
-
CM-W\(^\text {CTR}\): maximisation of the cross-covariance function between S and W constrained within a narrow window of plausible time lags;
-
CM-T\(^\text {CTR}\): maximisation of the cross-covariance function between S and T constrained within a narrow window of plausible time lags;
-
PW-W: assessment of the CCF between S and W after pre-whitening (Sect. 2.1);
-
PW-T: assessment of the CCF between S and T after pre-whitening (Sect. 2.1);
-
PWB: assessment of the CCF after pre-whitening with bootstrap estimated for all (four) possible combinations of S, W and T, for which at least one of X- and Y-variable is the atmospheric scalar concentration (see Sects. 2.2 and 2.4);
-
PWB\(^\text {OPT}\): optimal time lag derived from PWB results according to the strategy described in Sect. 2.3.
Except for CM-W\(^\text {CTR}\) and CM-T\(^\text {CTR}\), each procedure was performed within a broad window of time lags (e.g. ±10 s) with the aim to evaluate their sensitivity in absence of constraints. The definition of the (narrow) window of plausible time lags for the constrained CM approaches was based on a preliminary data analysis to statistically evaluate the most likely time lags and their ranges of variation. Additional constraints based on EC system characteristics were also considered (for example for closed-path GAs a delay of the scalar respect to W greater than zero). For the constrained procedures, time lags detected at the window boundaries were discarded and replaced with a default value. In this work the modal value computed for the entire sampling period was used as the default reference.
The evaluation of each procedure was carried out by looking at the stability of the detected time lags over the sampling periods, separately for each trace gas and for each EC site. To achieve this goal, descriptive statistics (minimum, first and third quartile, maximum, modal value and interquartile range—IQR) of the distribution of time lags detected by each of the above procedures for CO\(_2\), CH\(_4\) and N\(_2\)O trace gases were compared. For N\(_2\)O sampled at the UK-EBu, time lags derived from the EXP approach were additionally used for comparison.
4 Results and discussion
In the following sections, we first report an application of the proposed PWB procedure on a selection of raw EC data files with the aim to highlight its advantages compared to the existing approaches. Then a performance evaluation over long-term periods of the procedures listed in Sect. 3.2 is reported and discussed in Sect. 4.2. An overall evaluation of the impact of different time lag detection procedures on flux covariance data distribution is provided in Sect. 4.3. All statistical analyses were entirely performed in the R programming language (R Core Team 2023, version 4.3.1).
4.1 Application results on a selection of raw EC data files
In this section, we report the advantages of the PWB procedure over the widely used approach in EC data processing pipelines based on the covariance-maximisation using W (CM-W) and the one based on the assessment of the CCF between pre-whitened variables (without bootstrapping) via conventional confidence intervals (for illustrative purposes here we report the results obtained via PW-W specification).
To this end, illustrative examples of time lags detected by each procedure on a selection of raw EC data are shown in Fig. 2. Data refer to W and N\(_2\)O atmospheric concentrations sampled at UK-EBu and depicted in Fig. 1. To better appreciate the pros and cons, the above mentioned procedures were performed without setting a proper temporal window of plausible time lags, i.e. by detecting the time lag over a broad search temporal window of ±10 s.
Illustrative examples of time lag detection via covariance-maximisation using vertical wind speed (CM-W, left panels), cross-correlation function after pre-whitening using vertical wind speed (PW-W, middle panels) and after pre-whitening with bootstrap (PWB, right panels). Raw EC data refer to vertical wind speed (W) and nitrous dioxide (N\(_2\)O) atmospheric concentrations depicted in Fig. 1. Numbers on the top of the x-axis indicate the time lag detected by each procedure. Horizontal dashed lines in the PW-W plots identify the 95% confidence interval. Shadow area in the PWB plots represents the uncertainty (range of the 95% HDI) associated with the detected time lag. Unlike the other methods, the PWB procedure provides consistent results in most examples (panels a–d). For the example in panel e, all methods detect a wrong time lag, but the uncertainty estimate of PWB allows the unreliable result to be identified and discarded
For moderate/high magnitude fluxes, the use of PW-W and PWB procedures in place of the CM-W does not lead to substantially different results. In such cases, the cross-covariance function exhibits a distinct peak and the time lag between variables can be easily derived from it. An example of such a situation is depicted in Fig. 2a. For this data sample, the time lag detected by each procedure resulted in close agreement and equal to 1.6 s, a sensible estimate given the physical properties of this EC system (see Sect. 4.2 for more details). The resulting flux estimate, after temporal alignment, is about \(+\) 2 nmol N\(_2\)O m\(^{-2}\) s\(^{-1}\).
When the cross-covariance function does not exhibit a distinct peak, the detection of the actual time lag becomes more problematic leading to significant biases in flux estimates. For example, by applying the temporal alignment via CM-W procedure, flux estimates for the two examples in Fig. 1b and c would be \(-0.1\) (Fig. 2b) and \(-0.2\) nmol N\(_2\)O m\(^{-2}\) s\(^{-1}\) (Fig. 2c). If, instead, we assume that the actual time lag is around 1.7 s, flux estimates would be of opposite sign. Although such differences are small in magnitude, they have important implications in flux data interpretation. By convention, a positive flux value indicates that the ecosystem is a N\(_2\)O source to the atmosphere, while a negative flux value indicates a sink.
A strategy often advised to prevent bias in flux estimation is to narrow down the temporal window of plausible time lags over which to look for the peak of the cross-covariance function (Rebmann et al. 2012). For this strategy to be effective, however, the peak needs to be well defined. For example, considering the cases shown in Fig. 2, only in the conditions illustrated in panels a–c a narrower temporal window (e.g. 0–5 s) would result in the correct identification of the actual time lag, and thus in an improvement for the two cases shown in panels b and c. In contrast, when the CCF does not exhibit a well-defined peak, as in the cases shown in panels d and e in Fig. 2, detecting the actual time lag remains challenging. Also, constrained CM procedures using a nominal time lag (default), although leading to an improvement in results as shown in the next section, may be ineffective when the shape of the cross-covariance function is such that the absolute maximum does not fall on the temporal window boundaries.
The PW-W approach reduces the risk of spurious correlations through pre-whitening, thus facilitating the time lag detection compared to the CM method. An example is depicted in Fig. 2b, where the actual time lag is detected in correspondence with a statistically significant peak without the need to narrow down the temporal window of plausible time lags. For low magnitude fluxes (Fig. 2c–e), however, the detection of the actual time lag by PW-W remains challenging and the evaluation of peaks by using conventional confidence intervals introduces considerable uncertainty. In fact, for low magnitude fluxes, the peak of the CCF in correspondence with the actual time lag will not be so pronounced as to dominate over the other estimates. In such cases, there is a real risk of detecting erroneous time lags and, consequently, introducing bias into flux estimates.
The advantage that the PWB offers is to better discern well-defined and stable time lags from more uncertain ones. This is done by assessing the uncertainty associated with the detected time lag and quantified, after block-bootstrapping, by means of the 95% HDI. Among these illustrative examples and following the strategy outlined in Sect. 2.3, it turns out that four detected time lags are considered as optimal because the range of 95% HDI is less than 0.5 s (Fig. 2a, b) or because they do not deviate more than 0.5 s from those identified as optimal in preceding averaging periods (Fig. 2c, d), while only one is considered unreliable (Fig. 2e) because too uncertain and anomalous. In cases like this, the closest (in time) PWB optimal time lag detected is recommended.
4.2 Evaluation over long-term periods
In this section, we report a comparison of different time lag detection procedures using the long-term EC data described in Sect. 3.1. Due to space limitations, we report a graphical representation of time lags detected for only three study cases: CO\(_2\) sampled at FI-Kvr (Fig. 3), CH\(_4\) sampled at CH-Cha (Fig. 4) and N\(_2\)O sampled at UK-EBu (Fig. 5). The full set of results is available in the supplementary material (SM). Descriptive statistics (minimum, first and third quartile, maximum, modal value and interquartile range–IQR) of the distribution of time lags detected by different procedures for CO\(_2\), CH\(_4\) and N\(_2\)O trace gases are summarised in Tables 1, 2 and 3 of the SM, respectively.
Comparison of time lags detected by several procedures for carbon dioxide (CO\(_2\)) sampled at FI-Kvr. a–d Covariance maximisation using vertical wind speed (CM-W) and sonic temperature (CM-T) within a broad (± 10 s) and a constrained window (CTR, 0–2 s) of plausible time lags. Red points in c and d indicate time lags detected at the window boundaries. Horizontal red lines in c and d denote the modal value estimated without considering time lags detected at the window boundaries. e- f Assessment of the CCF after pre-whitening using vertical wind speed (PW-W) and sonic temperature (PW-T). Red triangles in PW plots indicate time lags detected in correspondence with a peak statistically non-significant at 0.01 level. g Assessment of the CCF after pre-whitening with bootstrap (PWB). Plus signs in PWB plot indicate time lags with high uncertainty (range of the 95% HDI > 0.5 s). h Optimal time lags (PWB\(^{\text {OPT}}\)) according to the strategy described in Sect. 2.3. i Violin plot with included boxplot of the distribution of detected time lags by each procedure; red lines indicate the modal value, grey areas for CM-W\(^\text {CTR}\) and CM-T\(^\text {CTR}\) indicate the predefined time intervals where plausible time lag must not be searched
Comparison of time lags detected by several procedures for methane (CH\(_4\)) sampled at CH-Cha. a–d Covariance maximisation using vertical wind speed (CM-W) and sonic temperature (CM-T) within a broad (± 10 s) and a constrained window (CTR, 0–2.5 s) of plausible time lags. Red points in c and d indicate time lags detected at the window boundaries. Horizontal red lines in c and d denote the modal value estimated without considering time lags detected at the window boundaries. e-f Assessment of the CCF after pre-whitening using vertical wind speed (PW-W) and sonic temperature (PW-T). Red triangles in PW plots indicate time lags detected in correspondence with a peak statistically non-significant at 0.01 level. g Assessment of the CCF after pre-whitening with bootstrap (PWB). Plus signs in PWB plot indicate time lags with high uncertainty (range of the 95% HDI > 0.5 s). h Optimal time lags (PWB\(^{\text {OPT}}\)) according to the strategy described in Sect. 2.3. i Violin plot with included boxplot of the distribution of detected time lags by each procedure; red lines indicate the modal value, grey areas for CM-W\(^\text {CTR}\) and CM-T\(^\text {CTR}\) indicate the predefined time intervals where plausible time lag must not be searched
Comparison of time lags detected by several procedures for nitrous dioxide (N\(_2\)O) sampled at UK-EBu. a–d Covariance maximisation using vertical wind speed (CM-W) and sonic temperature (CM-T) within a broad (± 10 s) and a constrained window (NW, 0–5 s) of plausible time lags. Red points in c and d indicate time lags detected at the window boundaries. Horizontal red lines in c and d denote the modal value estimated without considering time lags detected at the window boundaries. e-f Assessment of the CCF after pre-whitening using vertical wind speed (PW-W) and sonic temperature (PW-T). Red triangles in PW plots indicate time lags detected in correspondence with a peak statistically non-significant at 0.01 level. gAssessment of the CCF after pre-whitening with bootstrap (PWB). Plus signs in PWB plot indicate time lags with high uncertainty (range of the 95% HDI > 0.5 s). h Optimal time lags (PWB\(^{\text {OPT}}\)) according to the strategy described in Sect. 2.3. i Violin plot with included boxplot of the distribution of detected time lags by each procedure; red lines indicate the modal value, grey areas for CM-W\(^\text {CTR}\) and CM-T\(^\text {CTR}\) indicate the predefined time intervals where plausible time lag must not be searched
Although the actual time lag is not expected to be constant over time for the reasons explained in the introductory section, overall, time lags detected by the proposed PWB\(^\text {OPT}\) approach (see panel i of Figs. 3, 4 and 5) were more stable over time than those identified by CM- and PW-based procedures. Considering the IQR as a measure of the spread of detected time lags distribution, the one estimated for PWB\(^\text {OPT}\) resulted in the lowest IQR for most the cases considered in this work, whereas those estimated for CM-W and PW-W had the largest spread.
Negligible differences in terms of IQR were found for CO\(_2\) at CH-Cha and DE-GsB grassland sites characterised by fluxes of moderate/high magnitude (Table 1 of SM). For CH\(_4\) (Table 2 of SM) and N\(_2\)O (Table 3 of SM), the IQR of PWB\(^\text {OPT}\) was comparable or lower than those estimated for CM-based procedures, even when constrained within a narrow window of plausible time lags. This means that setting a narrower window when performing CM-based procedures, although leading to a marked improvement in results, does not ensure that the detected time lag converges to the actual one. In fact, there is a substantial portion of cases in which most of the time lags detected by CM-based procedures were found to diverge at the boundaries of the pre-fixed search window of plausible time lags, regardless of its width (see panels a-d of Figs. 3, 4 and 5). Such a setting is not strictly required for the proposed PWB strategy, which can instead be performed by setting a wide search temporal window of time lags, without loss in effectiveness.
The assessment of the cross-covariance function using T in place of W facilitates the time lag detection via CM-based procedures, in particular for CH\(_4\) and N\(_2\)O trace gases where a significant reduction in terms of IQR was found. Despite such an improvement, the use of T does not entirely prevent time lags from being identified at the boundaries of the search window (see panel i of Figs. 3, 4 and 5 and Tables 1, 2 and 3 of SM).
Such a risk is drastically reduced when the assessment of the CCF is performed with variables preliminarily subjected to the pre-whitening procedure (see panels e and f of Figs. 3, 4 and 5). For PW-based procedures, in fact, an improvement, in terms of stability of the results, was found when using T in place of W, as confirmed by the reduction of the IQR. However, when variables are characterised by a low order of correlation, as in the case of low magnitude fluxes, the assessment of the statistical significance of the CCF after pre-whitening using conventional confidence intervals was not suitable for detecting reliable time lags. As shown in panels e and f of Figs. 3, 4 and 5 and Figs. 1–5 of the SM, most of the time lags, even those far from the modal value, were detected as statistically significant.
The application of the strategy outlined in Sect. 2.3 to achieve the optimal time lag to be used for temporal alignment, leads to an improvement of the PWB results in terms of stability. In fact, most time lags detected by PWB with large departures from the IQR were characterized by high uncertainty and, then, considered unreliable (panel g of Figs. 3, 4, 5).
The percentage of time lags flagged as optimal during S1 and S2 of the strategy outlined in Sect. 2.3 is reported in Table 2. Among the three gases examined, time lags detected for CO\(_2\) were the least uncertain. In particular, the 89%, 90% and 97% of time lags detected by PWB at FI-Kvr, CH-Cha and DE-GsB, respectively, were considered reliable and flagged as optimal. For most of them (61%, 82% and 92% at FI-Kvr, CH-Cha and DE-GsB, respectively) the 95% HDI range was less than 0.5 s. Referring to CH\(_4\) and N\(_2\)O, characterised by a higher occurrence of low magnitude fluxes, the percentages of reliable time lags detected by PWB were lower than those achieved for CO\(_2\), varying around 70%, except for CH\(_4\) at FI-Kvr (55%).
Focusing on N\(_2\)O sampled at UK-EBu site, 72% of the detected time lags by PWB were flagged as optimal and considered reliable having an associated uncertainty less than 0.5 s (37%) or deviating from time lags detected in preceding averaging periods no more than 0.5 s (35%). The remaining 28% were considered unreliable and occurred in cases of close-to-zero fluxes.
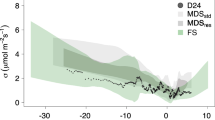
The comparison with the experimental approach by Nemitz et al. (2018) shows that most of time lags achieved by the PWB\(^\text {OPT}\) procedure do not deviate more than ± 0.25 s from direct measurements. Moreover, the actual time lags detected by both approaches seems to follow a common time trend (Fig. 6), the causes of which can have multiple sources not always manageable during field measurements, as said in the introductory section.
Most (80%) of time lags detected by PWB\(^\text {OPT}\) vary between \(+\) 1.45 and \(+\) 2.20 s (1st and 9th deciles, respectively), in strict agreement with the range (from \(+\) 1.50 to \(+\) 2.30 s) of the experimental measurements (see Table 3 of SM).
Such a narrow range of variability was not achieved by any of the others CM- and PW-based procedures.
Comparison of time lags detected by the PWB\(^\text {OPT}\) approach (cyan points) and through the experimental approach (EXP, solid black points) by Nemitz et al. (2018) for nitrous dioxide (N\(_2\)O) sampled at UK-EBu. Panel a shows the temporal dynamics of detected time lags; panel b shows the violin plot with included boxplot of differences between the two approaches based on 283 paired data values
4.3 Impact on flux estimates
The impact on EC fluxes can be appreciated by comparing the flux density distributions computed after temporal alignment of W and the S scalar of interest using different time lag detection procedures.
Figure 7 depicts a graphical representation of the density distributions of flux estimates computed after temporal alignment of time series using time lags detected by CM-W, CM-W\(^\text {CTR}\) approaches and by the proposed PWB\(^\text {OPT}\) procedure.
As shown, the CM-W procedure leads to a significant loss of mass density distribution around zero flux values and is representative of the so-called mirroring effect. There are no eco-physiological reasons that could explain such a behavior, since zero flux values fall within the physical range of possible values and they are not to be understood as a rare event, in particular during the monitoring of greenhouse trace gases having flux exchange rates small in magnitude. Running into this error can have a negative impact on subsequent analyses and should be avoided. For example, errors can propagate during the gap-filling stage and lead to an overestimation of the random uncertainty for procedures based on the use of half-hourly flux data (Richardson et al. 2008; Lasslop et al. 2008; Vitale et al. 2019).
The mirroring effect is only mitigated when the CM is performed with constraints, whereas it completely disappears when fluxes are computed after temporal alignment via the PWB\(^\text {OPT}\) procedure. The limitations of the CM-W\(^\text {CTR}\) in solving the mirroring effect may depend on several interrelated factors such as (i) the number of occurrences of low magnitude fluxes characterising the ecosystem under investigation; (ii) the erratic behaviour of the cross-covariance function even within the prefixed window of plausible time lags which makes the CM ineffective; (iii) the inadequacy of a constant value of the default time lag in presence of drifts during the sampling period, or more in general the selection of a non-representative period for the estimation of the modal value. Such limitations are not of relevance for the PWB procedure, as it is completely data driven and robust to the presence of spurious peaks of the CCF.
5 Conclusions and final remarks
Greenhouse gases monitoring is crucial to combating climate changes. Beyond new instrumentations with increased accuracy and precision, the development and the application of advanced statistical tools in data processing pipelines can facilitate the analysis of such complex phenomena.
In this work, a fully data-driven procedure for the detection of time lag for raw, high-frequency EC data was presented. The proposed PWB approach, based on the assessment of the cross-correlation function after pre-whitening with bootstrap, is designed to overcome the limitations of existing procedures when the correlation between variables is of low order of magnitude (i.e. for low magnitude EC fluxes).
In particular, (i) pre-whitening avoids the risk that time lag is detected in correspondence with spurious peaks of the cross-covariance function as often occurs with the widely used procedure in EC data processing pipelines based on covariance-maximisation, whereas (ii) block-bootstrap allows an estimate of the associated uncertainty useful to reduce the false positives error rate, as occurs with approaches based on the assessment of the CCF after pre-whitening with standard criteria.
The application on real, observed EC data showed that the performance of the proposed PWB method is really promising, in particular for the time lag detection of CH\(_4\) and N\(_2\)O trace gases that are currently under expansion in the global network of eddy covariance stations (see Delwiche et al. 2021), and which are characterised by complex and irregular patterns, like sudden emission peaks alternated to close-to-zero fluxes.
The results achieved by the methods comparison study presented in this work also suggest insights for further improvements of the widely used CM method: (i) we found a better stability in terms of IQR when time lags are detected using T in place of W, in particular for low-magnitude fluxes; (ii) we also found that a default time lag computed as the modal value of the distribution of time lags and based on a preliminary data analysis leads, on average, to results consistent with the PWB method. However, it must be considered that the use of a default value does not ensure to entirely solve the mirroring effect and that the CM method is sensitive to the choice of the predefined search window and to possible drifts of the real time lag during long-period samplings, e.g. due to drifts in the clocks or changes in the tube air flow rate.
Errors in time lag detection could introduce significant biases in flux estimates, with implications on the ecosystem understanding in terms of their full GHGs balance. Similar considerations hold true for all GHGs fluxes measured in ecosystems characterised by low magnitude exchange rates, like in the case of CO\(_2\) measured on water bodies, or during equilibrium phases between photosynthesis and total respiration processes.
We expect that the proposed PWB procedure will become a standard for the centralised data processing pipelines of research infrastructures (e.g. ICOS-RI, Heiskanen et al. 2022) where the use of fully reproducible and objective procedures constitutes an essential prerequisite to move forward in the standardisation and harmonisation efforts ongoing in the context of the global FLUXNET initiatives (Papale 2020). This will be particularly important for non-CO\(_2\) gases, characterised by generally lower magnitude fluxes than CO\(_2\) and by periods with fluxes very close to zero. Although modern multi-species GAs offer the possibility to estimate the time lag by means of CM-based procedures for fluxes with high SNR (i.e. CO\(_2\)) and then use it to temporally align scalars representative of low-magnitude inert gas fluxes (e.g. CH\(_4\) or N\(_2\)O), the proposed PWB constitutes, to the best of our knowledge, the most effective solution currently available.
Code availability
The PWB procedure is implemented in the RFlux R package (R Core Team 2023), downloadable at https://github.com/icos-etc/RFlux.
Change history
22 May 2024
A Correction to this paper has been published: https://doi.org/10.1007/s10651-024-00625-7
References
Akaike H (1998) Information theory and an extension of the maximum likelihood principle. In: Parzen E, Tanabe K, Kitagawa G (eds) Selected papers of Hirotugu Akaike. Springer, New York, pp 199–213. https://doi.org/10.1007/978-1-4612-1694-0_15
Billesbach D (2011) Estimating uncertainties in individual eddy covariance flux measurements: a comparison of methods and a proposed new method. Agric For Meteorol 151(3):394–4. https://doi.org/10.1016/j.agrformet.2010.12.001
Bonan GB (2008) Forests and climate change: forcings, feedbacks, and the climate benefits of forests. Science 320(5882):1444. https://doi.org/10.1126/science.1155121
Box GE, Jenkins GM, Reinsel GC et al (2015) Time series analysis: forecasting and control. Wiley, Hoboken. https://doi.org/10.1002/9781118619193
Breitung J (2002) Nonparametric tests for unit roots and cointegration. J Econ 108(2):343. https://doi.org/10.1016/S0304-4076(01)00139-7
Canty A, Ripley BD (2021) boot: bootstrap R (S-Plus) functions. https://cran.r-project.org/web/packages/boot/index.html, R package version 1.3-30. Accessed 05 March 2024
Cryer JD, Chan KS (2008) Time series analysis with applications in R. Springer, New York. https://doi.org/10.1007/978-0-387-75959-3
Delwiche KB, Knox SH, Malhotra A et al (2021) FLUXNET-CH4: a global, multi-ecosystem dataset and analysis of methane seasonality from freshwater wetlands. Earth Syst Sci Data 13(7):3607. https://doi.org/10.5194/essd-13-3607-2021
Feigenwinter I, Hörtnagl L, Buchmann N (2023) N\(_2\)O and CH\(_4\) fluxes from intensively managed grassland: the importance of biological and environmental drivers vs management. Sci Total Environ 903:16638. https://doi.org/10.1016/j.scitotenv.2023.166389
Foken T, Aubinet M, Leuning R (2012) The eddy covariance method. In: Aubinet M, Vesala T, Papale D (eds) Eddy covariance: a practical guide to measurement and data analysis. Springer, Dordrecht, pp 1–1. https://doi.org/10.1007/978-94-007-2351-1_1
Fratini G, Ibrom A, Arriga N et al (2012) Relative humidity effects on water vapour fluxes measured with closed-path eddy-covariance systems with short sampling lines. Agric For Meteorol 165:53. https://doi.org/10.1016/j.agrformet.2012.05.018
Fratini G, Sabbatini S, Ediger K et al (2018) Eddy covariance flux errors due to random and systematic timing errors during data acquisition. Biogeosciences 15(17):5473–548. https://doi.org/10.5194/bg-15-5473-2018
Hamilton JD (1994) Time series analysis. Princeton University Press, New Jersey. https://doi.org/10.1515/9780691218632
Härdle W, Horowitz J, Kreiss JP (2003) Bootstrap methods for time series. Int Stat Rev 71(2):435–45. https://doi.org/10.1111/j.1751-5823.2003.tb00485.x
Heiskanen J, Brümmer C, Buchmann N et al (2022) The integrated carbon observation system in Europe. Bull Am Meteorol Soc 103(3):E855–E87. https://doi.org/10.1175/BAMS-D-19-0364.1
Houghton R (2005) Aboveground forest biomass and the global carbon balance. Glob Change Biol 11(6):945–95. https://doi.org/10.1111/j.1365-2486.2005.00955.x
Ibrom A, Dellwik E, Flyvbjerg H et al (2007) Strong low-pass filtering effects on water vapour flux measurements with closed-path eddy correlation systems. Agric For Meteorol 147(3–4):140–15. https://doi.org/10.1016/j.agrformet.2007.07.007
Kohonen KM, Kolari P, Kooijmans LM et al (2020) Towards standardized processing of eddy covariance flux measurements of carbonyl sulfide. Atmos Meas Tech 13(7):3957–397. https://doi.org/10.5194/amt-13-3957-2020
Langford B, Acton W, Ammann C et al (2015) Eddy-covariance data with low signal-to-noise ratio: time-lag determination, uncertainties and limit of detection. Atmos Meas Tech 8(10):4197–421. https://doi.org/10.5194/amt-8-4197-2015
Lasslop G, Reichstein M, Kattge J et al (2008) Influences of observation errors in eddy flux data on inverse model parameter estimation. Biogeosciences 5(5):1311–132. https://doi.org/10.5194/bg-5-1311-2008
Lütkepohl H (2005) New introduction to multiple time series analysis. Springer, New York. https://doi.org/10.1007/978-3-540-27752-1
Mammarella I, Launiainen S, Gronholm T et al (2009) Relative humidity effect on the high-frequency attenuation of water vapor flux measured by a closed-path eddy covariance system. J Atmos Ocean Technol 26(9):1856–186. https://doi.org/10.1175/2009JTECHA1179.1
Mammarella I, Nordbo A, Rannik Ü et al (2015) Carbon dioxide and energy fluxes over a small boreal lake in Southern Finland. J Geophys Res Biogeosci 120(7):1296–131. https://doi.org/10.1002/2014JG002873
Massman W (2000) A simple method for estimating frequency response corrections for eddy covariance systems. Agric For Meteorol 104(3):185–19. https://doi.org/10.1016/S0168-1923(00)00164-7
Massman W, Ibrom A (2008) Attenuation of concentration fluctuations of water vapor and other trace gases in turbulent tube flow. Atmos Chem Phys 8(20):6245–625. https://doi.org/10.5194/acp-8-6245-2008
Moncrieff J, Massheder J, De Bruin H et al (1997) A system to measure surface fluxes of momentum, sensible heat, water vapour and carbon dioxide. J Hydrol 188:589. https://doi.org/10.1016/S0022-1694(96)03194-0
Nemitz E, Mammarella I, Ibrom A et al (2018) Standardisation of eddy-covariance flux measurements of methane and nitrous oxide. Int Agrophys 32(4):517–54. https://doi.org/10.1515/intag-2017-0042
Pan Y, Birdsey RA, Fang J et al (2011) A large and persistent carbon sink in the world’s forests. Science 333(6045):988–99. https://doi.org/10.1126/science.1201609
Papale D (2020) Ideas and perspectives: enhancing the impact of the FLUXNET network of eddy covariance sites. Biogeosciences 17(22):5587–559. https://doi.org/10.5194/bg-17-5587-2020
R Core Team (2023) R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria, https://www.R-project.org/, version 4.3-1
Rebmann C, Kolle O, Heinesch B et al (2012) Data acquisition and flux calculations. In: Aubinet M, Vesala T, Papale D (eds) Eddy covariance: a practical guide to measurement and data analysis. Springer, Dordrecht, p 59. https://doi.org/10.1007/978-94-007-2351-1_3
Richardson AD, Mahecha MD, Falge E et al (2008) Statistical properties of random CO\(_2\) flux measurement uncertainty inferred from model residuals. Agric For Meteorol 148(1):38. https://doi.org/10.1016/j.agrformet.2007.09.001
Sabbatini S, Mammarella I, Arriga N et al (2018) Eddy covariance raw data processing for CO\(_2\) and energy fluxes calculation at ICOS ecosystem stations. Int Agroph. https://doi.org/10.1515/intag-2017-0043
Schallhart S, Rantala P, Kajos MK et al (2018) Temporal variation of VOC fluxes measured with PTR-TOF above a boreal forest. Atmos Chem Phys 18(2):815–83. https://doi.org/10.5194/acp-18-815-2018
Shimizu T (2007) Practical applicability of high frequency correction theories to CO\(_2\) flux measured by a closed-path system. Bound-Layer Meteorol 122:417–43. https://doi.org/10.1007/s10546-006-9115-z
Striednig M, Graus M, Märk TD et al (2020) InnFLUX-an open-source code for conventional and disjunct eddy covariance analysis of trace gas measurements: an urban test case. Atmos Meas Tech 13(3):1447–146. https://doi.org/10.5194/amt-13-1447-2020
Taipale R, Ruuskanen TM, Rinne J (2010) Lag time determination in DEC measurements with PTR-MS. Atmos Meas Tech 3(4):853–86. https://doi.org/10.5194/amt-3-853-2010
Vitale D (2021) A performance evaluation of despiking algorithms for eddy covariance data. Sci Rep 11(1):1162. https://doi.org/10.1038/s41598-021-91002-y
Vitale D, Bilancia M, Papale D (2019) Modelling random uncertainty of eddy covariance flux measurements. Stoch Environ Res Risk Assess 33:725–74. https://doi.org/10.1007/s00477-019-01664-4
Wollschläger U, Attinger S, Borchardt D et al (2017) The Bode hydrological observatory: a platform for integrated, interdisciplinary hydro-ecological research within the TERENO Harz/Central German Lowland Observatory. Environ Earth Sci 76:1–2. https://doi.org/10.1007/s12665-016-6327-5
Yule GU (1926) Why do we sometimes get nonsense-correlations between time-series? A study in sampling and the nature of time-series. J R Stat Soc 89(1):1–6. https://doi.org/10.2307/2341482
Acknowledgements
The Integrated Carbon Observation System-Research Infrastructure (ICOS ERIC, https://www.icos-cp.eu/) and the ICOS ETC funding from the Italian Ministry of Research.
Funding
Open access funding provided by Università degli Studi di Roma La Sapienza within the CRUI-CARE Agreement. DP thanks the support of the EU-Next Generation EU Mission 4 “Education and Research”-Component 2: “From research to business”-Investment 3.1: “Fund for the realisation of an integrated system of research and innovation infrastructures”-Project IR0000032-ITINERIS-Italian Integrated Environmental Research Infrastructures System - CUP B53C22002150006. SS thanks the support of the Open-Earth-Monitor Cyberinfrastructure Horizon Europe Project (Grant No. GA101059548). GN thanks the support of the Pilot Application in Urban Landscapes (PAUL) Horizon 2020 Project (Grant No. GA101037319). LH thanks the support of the SNF project M4P (40FA40_154245) and ETH Zurich. IM thanks the support of University of Helsinki via ICOS-HY, the Research Council of Finland project N-PERM (Grant No. 341348) and the EU Horizon Europe-Framework Programme for Research and Innovation (Grant No. 101056921-GreenFeedBack).
Author information
Authors and Affiliations
Contributions
DV and DP conceived the study. DV organised the structure; selected, proposed, implemented the methodologies and performed all the analyses discussing the results with the coauthors. DV wrote all the sections with the supervision of DP and with the contribution of all the coauthors. All authors reviewed the final manuscript, approved it and agreed on the submission.
Corresponding author
Ethics declarations
Conflict of interest
The authors have no conflict of interest to declare.
Additional information
Original Online Version of this article was revised: the given name and surename is swapped for all authors.
Handling Editor: Luiz Duczmal.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Vitale, D., Fratini, G., Helfter, C. et al. A pre-whitening with block-bootstrap cross-correlation procedure for temporal alignment of data sampled by eddy covariance systems. Environ Ecol Stat 31, 219–244 (2024). https://doi.org/10.1007/s10651-024-00615-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10651-024-00615-9