Sequential hypothesis testing for selecting the number of changepoints in segmented regression models

Abstract

Segmented regression is widely used in many disciplines, especially when dealing with environmental data. This paper deals with the problem of selecting the correct number of changepoints in segmented regression models. A review of the usual selection criteria, namely information criteria and hypothesis testing, is provided. We enhance the latter method by proposing a novel sequential hypothesis testing procedure to address this problem. Our sequential procedure’s performance is compared to methods based on information-based criteria through simulation studies. The results show that our proposal performs similarly to its competitors for the Gaussian, Binomial, and Poisson cases. Finally, we present two applications to environmental datasets of crime data in Valencia and global temperature land data.

1 Introduction

Segmented regression is a standard tool in many fields, including epidemiology (Ulm 1991), occupational medicine, toxicology, ecology, biology (Betts et al. 2007), and more recently, higher education (Li et al. 2019; Priulla et al. 2021).

Segmented or broken-line models are regression models where the relationships between the response and one or more explanatory variables are piecewise linear, namely represented by two or more straight lines connected at unknown values. These values are commonly referred to as changepoints or breakpoints. The main advantage of these models lies in the results’ interpretability while also achieving a good trade-off with flexibility, typically achieved by non-parametric approaches.

This paper deals with the task of selecting the number of changepoints in segmented regression models, a topic widely discussed by many authors, as Lerman (1980) and Kim et al. (2000). This is a common problem in segmented regression models. Indeed, if the number of changepoints is too small, the model may not capture all the changes in the relationship between the variables, resulting in bias and reduced model fit. On the other hand, if the number of changepoints is too large, the model may overfit the data and not generalize well to new data.

Other common problems in segmented regression models include the identification of the location of the changepoints in a segmented variable, and the estimation of its effects on the response variable, to cite a few. For instance, Horváth et al. (2004) proposes two classes of monitoring schemes to (sequentially) detect a structural change in a linear model. Aue et al. (2006) develop an asymptotic theory for two monitoring schemes aimed at detecting a change in the regression parameters, showing to have a correct asymptotic size and detecting a change with probability approaching unity. Then, Chen et al. (2011) deal with two problems concerning locating changepoints in a linear regression model, namely, the one involving jump discontinuities (not covered in this paper) in a regression model and the other involving regression lines connected at unknown points. The latter is the main framework covered in our work. Muggeo and Adelfio (2011) present a computationally efficient method to obtain estimates of the number and location of the changepoints in genomic sequences, or, more generally, in mean-shift regression models. Adelfio (2012) introduces a new approach based on the fit of a generalized linear regression model for detecting changepoints in the variance of heteroscedastic Gaussian variables with piecewise constant variance function, and D’Angelo et al. (2022) extend such approach in order to detect changepoints in the variance of multivariate Gaussian variables, allowing to provide simultaneous detection of changepoints in functional time series.

Moving to the main topic of our work, in literature several approaches have been proposed to select the optimal number of changepoints in segmented regression models. One common approach is to use information criteria, such as the Akaike Information Criterion (AIC) (Akaike 1974) or the Bayesian Information Criterion (BIC) (Schwarz 1978), which balance the model’s goodness of fit with the model’s complexity. These criteria penalize models with more parameters, which can prevent overfitting.

Another approach is to use cross-validation (Zou et al. 2020; Pein 2023), which involves splitting the data into training and validation sets, fitting models with different numbers of changepoints to the training set, and then selecting the number of changepoints that minimizes the prediction error on the validation set. The model that performs best on the validation set is selected. Cross-validation can be computationally intensive, but it can also provide a more accurate estimate of model performance than AIC or BIC.

A further approach is hypothesis testing to determine the significance of adding a changepoint to the model. Typically, this consists of performing different hypothesis tests starting from testing ${\mathcal {H}}_0 : K_{0} = 0$ vs ${\mathcal {H}}_1 : K_{0} = K_{max}$ where $K_0$ is the true number of changepoints and $K_{max}$ is the maximum number of potential changepoints fixed a priori, as done by Kim et al. (2000). However, this well-established procedure, which requires sequentially testing for the existence of a changepoint, makes testing for any additional changepoints unfeasible.

In light of this, this paper proposes a novel sequential hypothesis testing procedure that overcomes this problem, having the perk of not being limited to testing for a maximum number of additional changepoints fixed a priori. Starting from the work of Kim et al. (2000), we enhance such a method by proposing a novel sequential hypothesis testing, to identify the correct number of changepoints.

First, we provide an overview of the segmented regression models and a review of the main tools useful for selecting the number of changepoints. Regarding the information-based criteria, we consider the AIC, the BIC and the generalized Bayesian Information Criterion (gBIC). As regards hypothesis testing, we consider Davies’ test (Davies 1977) and the Score test (Muggeo 2016). The performance of the different tools and our proposed procedure is then assessed through simulation studies. Finally, to explore the applicability of the considered framework, two original applications are proposed: the first one deals with the crime events that occurred in Valencia in 2019, available from the stopp package (D’Angelo and Adelfio 2023) of the software R (R Core Team 2023); the second one deals with global temperature anomalies data from the NOAA Merged Land Ocean Global Surface Temperature Analysis Data set (Smith et al. 2008). All the analyses are performed using the segmented package (Muggeo 2008) of the R Core Team (2023) statistical software, and original codes from the authors.

The structure of the paper is as follows. Section 2 introduces the segmented regression model and Section 3 reviews suitable criteria for model selection in this context. Section 4 illustrates our proposal. Section 5 presents simulations to study the performance of the given criteria, and Section 6 proposes two applications dealing with crime events in Valencia and with global anomalies temperature data. The paper ends with conclusions in Section 7. The Appendix contains supplementary material in support of the run experiments.

2 Background on the segmented regression models

The segmented linear regression is expressed as

$$\begin{aligned} g({\mathbb {E}}[Y|x_i,z_i])= \beta _0 +\theta z_i+\beta _1 x_i+\sum _{k=1}^{K_0}\delta _k (x_{i}-\psi _k)_+ \end{aligned}$$

(1)

where g is the link function, x is a broken-line covariate and z is a covariate whose relationship with the response variable is not broken-line. Multiple covariates can be accounted for, but we limit our study to unique covariates. We denote by $K_0$ the true number of changepoints and by $\psi _k$ the $K_0$ locations of the changes in the relationship that we call, from now on, changepoints. These are selected among all the possible values in the range of x. The notation $(x_i-{\psi }_k)_+$ is to be read as $(x_i-{\psi }_k)I(x_i>{\psi }_k)$. The coefficient $\theta$ represents the non-broken-line effect of z, $\beta _1$ represents the effect when $x_i < \psi _1$, while $\varvec{\delta }= \{\delta _k\}_{k=1}^{K_0}$ is the vector of the differences in the effects.

The basic statistical problem dealt in this paper is the identification of the number of changepoints $K_0$. The estimation of their locations, that is the vector of $\psi _k$, and the broken-line effects, represented by $\beta _1$ and the vector $\varvec{\delta }$, may also be of interest.

For estimation purposes, a reparametrization of the segmented model in Equation (1) is considered, dropping the non-segmented covariate z without any loss of generality. This reparametrization has the advantage of an efficient estimating approach via the algorithm discussed in Muggeo (2003, 2008), fitting iteratively the generalized linear model:

$$\begin{aligned} g({\mathbb {E}}[Y|x_i])=\beta _1x_i+\sum _k \delta _k \tilde{U}_{ik}+\sum _k \gamma _k \tilde{V}_{ik}^{-}, \end{aligned}$$

(2)

where $\tilde{U}_{ik}=(x_i-\tilde{\psi }_k)_+$, $\tilde{V}_{ik}^{-}=-I(x_i>\tilde{\psi }_k)$. The parameters $\beta$ and $\delta _k$ are the same as in Equation (1), while the $\gamma$ are the working coefficients useful only for the estimation procedure. At each iteration, the working model in Equation (2) is fitted and new estimates of the changepoints are obtained via: $\hat{\psi }_k=\tilde{\psi }_k+\frac{\hat{\gamma }_k}{\hat{\delta }_k}$ iterating the process up to convergence. Inferences on $\hat{\psi }$ is usually the main interest, and can be drawn by means of bootstrap, likelihood-based or Wald-type methods. In particular, Muggeo (2003) discusses and implements the usage of the Wald statistics. The standard error of $\hat{\psi }$ is obtained through a linear approximation for the ratio of two random variables using the Delta Method: $SE(\hat{\psi })=\{ [\text {var}(\hat{\gamma }) +\text {var}(\hat{\beta })(\hat{\gamma }/\hat{\beta })^2+2(\hat{\gamma }/\hat{\beta })\text {cov}(\hat{\gamma },\hat{\beta })]/\hat{\beta }^2 \}^{\frac{1}{2}},$ with $\text {var}(\cdot )$ and $\text {cov}(\cdot ; \cdot )$ the variance and covariance, respectively.

For further details on the estimation procedure, we refer to Muggeo (2003).

3 Selecting the number of changepoints

In a more general context, with multiple changepoints as in Equation (1), we need to select only the significant changepoints by removing the spurious ones. Indeed, whether the generic $\hat{\psi }_k$ is not significant, the corresponding covariate $V_k$ in Equation (2) should be a noise variable, as it would be $\hat{\delta }_k \approx 0$. Therefore, selecting the number of significant changepoints in model (1) means selecting the significant variables among $V_1, \dots , V_{K^*}$, from model (2), where $K^*$ is the number of estimated changepoints. The fitted optimal model will have $\hat{K} \le K^*$ changepoints selected by any criterion. It is important to notice that these models are not nested, so likelihood ratio tests for model selection cannot be used.

Furthermore, the usual statistics cannot be used to verify the existence of a changepoint, since it is present only under the alternative hypothesis. This leads to a non-linear problem because the regularity conditions of the log-likelihood are not satisfied.

Basically, we need to select the $\hat{\psi }_1,\dots ,\hat{\psi }_{\hat{K}}$ among the $\hat{\psi }_1,\dots ,\hat{\psi }_{K^*}$ via a selection criterion. The changepoints $\hat{\psi }_1,\dots ,\hat{\psi }_{\hat{K}}$ will be a subset of the estimates $\hat{\psi }_1,\dots ,\hat{\psi }_{K^*}$, since one or more changepoints are not included due to the deletion of one or more variables $V_k$ by means of the given selection criterion. Therefore, it should be noticed that, while $\hat{\psi }_1,\dots ,\hat{\psi }_{K^*}$ are the estimates maximising the likelihood with $K^*$ changepoints, there is no guarantee that the subset $\hat{\psi }_1,\dots ,\hat{\psi }_{\hat{K}}$ constitutes also the best estimate for the number of changepoints.

Much of the literature deals with the problem of determining the ‘best’ subset of independent variables: Hocking (1976) summarizes various selection criteria, reviewed below. These can be classified under two major approaches: information criteria and hypothesis testing.

The first information criterion is the well-known Akaike Information Criterion (Akaike 1974), expressed as $AIC=-2\log L + 2 p$, where L represents the likelihood function and p stands for the actual model dimension quantified by the number of estimated parameters, including $\hat{\beta }$, the $\hat{\delta }$ and $\hat{\psi }$ vectors in the segmented regression models, that is $p=1+2\hat{K}$. Given a set of candidate models for the data, the preferred model is the one with the minimum AIC value. Thus, AIC rewards goodness of fit (as assessed by the likelihood function), but also includes a penalty that is an increasing function of the number of estimated parameters. The penalty discourages overfitting, which is desired because increasing the number of parameters in the model almost always improves the goodness of the fit.

The second criterion is the Bayesian Information Criterion (Schwarz 1978) $BIC=-2\log L + p \log (n)$ that includes both a penalty for the number of estimated parameters p and for the logarithm of the number of observations n. In the most common Gaussian case, let’s denote by $y_i$ the response variable and by $\hat{\mu }_i$ the estimated expectation through a generalized linear model. We can therefore express the BIC as $BIC= n\log {\hat{\sigma }^2} + p \log (n),$ where $\hat{\sigma }^2$ is the error variance, defined as $\frac{1}{n-p}\sum _{i=1}^n (y_i-\hat{\mu }_i)^2$, which is an unbiased estimator for the true variance. The one with the lowest BIC is preferred when picking from several models. The BIC is an increasing function of the error variance $\hat{\sigma }^2$ and an increasing function of p. That is, unexplained variation in the dependent variable and the number of explanatory variables increases the value of BIC. Hence, lower BIC implies either fewer explanatory variables, better fit, or both. The BIC generally penalizes parameters more strongly than the AIC, though it depends on n and p. For a typical linear regression model, it is well understood that the traditional best subset selection method with the BIC can identify the true model consistently (Shao 1997; Shi and Tsai 2002). With a fixed predictor dimension, Wang et al. (2009) showed that the tuning parameters for high dimensional model selection procedures selected by a BIC type criterion can identify the true model consistently, and similar results are further extended to the situation with a diverging number of parameters for both unpenalized and penalized estimators. Therefore, the definition of the generalized BIC based on Gaussian distributed iid errors is $gBIC=\log (\hat{\sigma }^2) + p \frac{\log (n)}{n} C_n$, where $C_n$ is a known constant (e.g. 1, $\sqrt{n}$, $\log n$, $\log \log n$). The definition reduces to $gBIC= -2\log L + p \log (n) C_n$ in the case of non-Gaussian errors (which we will also refer to when dealing with Binomial and Poisson responses). In general, the larger $C_n$, the more parsimonious the selected model. Note that the gBIC reduces to the usual BIC when $C_n=1$. The same considerations for the BIC hold, that is, when choosing from several models, the one with the lowest gBIC is the one to be preferred.

An alternative approach to selecting the number of changepoints relies on sequential hypothesis testing. Typically, this consists of performing different hypothesis tests starting from

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathcal {H}}_0 : K_{0} = 0\\ {\mathcal {H}}_1 : K_{0} = K_{max} \end{array}\right. } \end{aligned}$$

where $K_{max}$ is fixed a priori. Depending on the rejection or not of the null hypothesis, the procedure can test for the next hypothesis system by either increasing the number of changepoints specified under ${\mathcal {H}}_0$ or decreasing the one under ${\mathcal {H}}_1$, respectively (Kim et al. 2000).

4 Proposed sequential hypothesis testing

In this paper, we propose a novel sequential procedure to identify the correct number of changepoints resorting to the pseudo-score (Muggeo 2016) or Davies’ test (Davies 1977).

Testing for the existence of a changepoint means that we are dealing with the following system of hypotheses:

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathcal {H}}_{0} : &{} \delta _{k}=0\\ {\mathcal {H}}_{1} : &{} \delta _{k}\ne 0 \end{array}\right. }. \end{aligned}$$

Evaluating the existence of a changepoint is actually a non-regular problem, because $\psi _k$ is present only under the alternative ${\mathcal {H}}_{1}$. This problem makes usual statistical tests, such as the Wald or the likelihood ratio test, useless, because of the lack of a reference null distribution, even asymptotically. Therefore, we review below two tests used to evaluate the presence of a changepoint.

The first test proposed is the Davies’ Test (Davies 1977), an asymptotic test useful for dealing with hypothesis testing with a nuisance parameter present only under the alternative. Assuming fixed and known changepoints, the procedure computes K ‘naive’ test statistics $S(\psi _k)$ for the difference-in-slope $\delta _k$, seeks the lowest value and corresponding naive p-value (according to the alternative hypothesis), and then corrects the selected (minimum) p-value by means of the K values of the test statistic.

Considering the case of multiple changepoints $\psi _{1}$ $<\psi _{2}< \dots <\psi _{k}$ and relevant K test statistics, Davies defined an upper bound for the p-value given by

$$\begin{aligned} \text {p-value} \approx \Phi (-M)+V\exp {(-M^2/2)}(8\pi )^{-1/2} \end{aligned}$$

where $\Phi (\cdot )$ is the cumulative Normal distribution function. M is the supremum of the test statistics $S(\psi )$, that is, $M = \sup \{ S(\psi ) : {\mathcal {L}} \le \psi \le {\mathcal {U}} \}$ where $\{{\mathcal {L}},{\mathcal {U}}\}$ is the range of possible values of $\psi$ (typically, the support of the segmented covariate).

Then, V is the total variation of $S(\psi )$, computed as $V=\int _{{\mathcal {L}}}^{{\mathcal {U}}}\frac{\partial S(\psi )}{\partial \psi } \text {d}\theta =|S(\psi _1)-S({\mathcal {L}})|+|S(\psi _2)-S(\psi _1)|+\ldots +|S({\mathcal {U}})-S(\psi _n)|$, with $\psi _1,\ldots ,\psi _n$ the successive changepoints of $S(\psi )$.

Although Davies’ test is useful to test for the existence of a changepoint, it is not considered ideal to identify the number of changepoints or their location. Indeed, the alternative hypothesis ${\mathcal {H}}_{1}$ actually states the existence of at least one additional changepoint, that is $K_0>k$ when $\delta _k \ne 0$.

The second one is a pseudo-score test proposed by Muggeo (2016), which is based on an adjustment of the score statistic. This approach requires quantities only from the null fit and thus it has the advantage that it is not necessary to estimate the nuisance parameter under the alternative. The proposed statistic has the form:

$$\begin{aligned} s_{0}=\frac{\bar{\varphi }^{T}(I_{n}-A)y}{\sigma \{\bar{\varphi }^{T}(I_{n}-A)y\}^{\frac{1}{2}}} \end{aligned}$$

where $(I_{n}-A)y$ is the residual vector under ${\mathcal {H}}_{0}$, with $I_{n}$ the identity matrix, A the hat matrix, y the observed response vector, and $\bar{\varphi }=\{\bar{\varphi }_{1},\ldots ,\bar{\varphi }_{n}\}^{T}$ the vector of the means of the nuisance parameter $\psi _k$ averaged over the range ${\{{\mathcal L},{\mathcal U}\}}$, i.e. $\bar{\varphi }=K^{-1}\sum _{k=1}^{K}\varphi (x_{i},\psi _{k}), i = 1,\ldots ,n$. This does not depend on $\psi _k$, so the score can be computed even under ${\mathcal {H}}_{0}$ : $\delta _k$ = 0 when $\psi _k$ is not defined. The function $\varphi (x_{i},\psi _{k})$ includes the case of discontinuous changepoint $\varphi (x_{i},\psi _{k}) = I(x_{i} > \psi _{k})$ and the linear segmented $\varphi (x_{i},\psi _{k}) = (x_{i} - \psi _{k})_{+}$, which is the one covered in this paper.

Contrary to the procedure of Kim et al. (2000), our proposal has the advantage of not being limited to testing for a maximum number of additional changepoints fixed a priori. Indeed, the previously explained procedure makes testing for more than two additional changepoints with the pseudo-score unfeasible. Our proposal overcomes this problem by making it possible to test for any number of additional changepoints thanks to the sequential procedure.

Starting from

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathcal {H}}_{0} : K_0=0\\ {\mathcal {H}}_{1} : K_0=1 \end{array}\right. } \end{aligned}$$

and depending on the tests’ results, the procedure ends testing at most

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathcal {H}}_{0} : K_0=K_{max}-1\\ {\mathcal {H}}_{1} : K_0=K_{max} \end{array}\right. } \end{aligned}$$

and selecting up to $K_{max}$ changepoints. The p-value for each hypothesis can be obtained via the Davies’ or the pseudo-score test. Furthermore, we control for over-rejection of the null hypotheses at the overall level $\alpha$ employing the Bonferroni correction, comparing each p-value with $\alpha /K_{max}$. Of course, setting the Bonferroni correction to $\alpha /K_{max}$ means putting ourselves in the most conservative setting.

For simplicity, we outline the algorithm when the maximum number of changepoints is $K_{max}=3$, restricting the analyses to a contained limited number of changepoints.

The procedure works iteratively fitting models following Muggeo (2003), as sketched in Section 2, as follows:

• 1. Fit a segmented model to the data with $K=1$ and test

  $$\begin{aligned} {\left\{ \begin{array}{ll} {\mathcal {H}}_{0} : &{} \delta _{1}=0\quad (K_0=0)\\ {\mathcal {H}}_{1} : &{} \delta _{1}\ne 0\quad (K_0 \ge 1) \end{array}\right. } \end{aligned}$$

  via the Score or Davies’ test. If it is not rejected then $\hat{K}=0$ and the procedure stops at this step. Otherwise, we proceed with the algorithm;

• 2. Fit a segmented model with $K=2$ and test

  $$\begin{aligned} {\left\{ \begin{array}{ll} {\mathcal {H}}_{0} : &{} \delta _{2}=0 \quad (K_0=1)\\ {\mathcal {H}}_{1} : &{} \delta _{2}\ne 0\quad (K_0 \ge 2) \end{array}\right. } \end{aligned}$$

  If ${\mathcal {H}}_{0}$ is not rejected then $\hat{K}=1$ and the procedure stops. Otherwise, we proceed to fit the following model;

• 3. Fit a segmented model with $K=3$ and test

  $$\begin{aligned} {\left\{ \begin{array}{ll} {\mathcal {H}}_{0} : &{} \delta _{3}=0\quad (K_0=2)\\ {\mathcal {H}}_{1} : &{} \delta _{3}\ne 0\quad (K_0 \ge 3) \end{array}\right. } \end{aligned}$$

  If ${\mathcal {H}}_{0}$ is not rejected then $\hat{K}=2$. Otherwise, $\hat{K} \ge 3$.

It is important to remind that when using the Davies’ test, even if, based on the rejection of the last test, the number of changepoints selected is equal to 3 (or in general $K_{max}$), the actual number could be larger, as we are actually testing for (at least) one additional changepoint at each step.

5 Simulation studies

This section is devoted to simulation studies for comparing the performance of our proposed method to the previously introduced criteria for selecting the true number of changepoints, considering Gaussian, Binomial, and Poisson responses.

We simulated from four different scenarios, generating and then fitting models with different true values of the number of changepoints, namely $K_0\in \{0,1,2,3\}$. We consider three different sample sizes $n \in \{100,250,500\}$, including one covariate $x_i$, whose effect on the response is assumed broken-line, taking equispaced values ranging from 0 to 1. An example for each scenario, with $n = 100$, is represented in Figure 3. The segmented models used for the simulations are reported in Table 1, firstly considering iid Gaussian errors with standard deviation equal to $\sigma =0.3$.

Table 1 Linear segmented regression models fitted for the simulations

We set $\alpha =0.05$ for the hypothesis testing, while the penalization of the gBIC is chosen as $C_n=\log \log n$. For each $K_0$, we fit four models with $K\in \{0,1,2,3\}$: the estimated number of changepoints is obtained by fitting segmented models using the segmented library (Muggeo 2003, 2008) over 500 simulations.

Table 2 reports the simulation results in terms of the percentage of the correctly selected number of changepoints for each criterion.

Table 2 Percentages of the correctly selected number of changepoints by each criterion (based on 500 runs and three different sample sizes $n\in \{100,250,500\}$) - Gaussian response variable

With regard to information-based criteria, we select the ‘best’ model by choosing the one with the lowest value of the given information criterion. As for the hypothesis testing, we choose the best model by applying the procedure proposed in Sect. 4. Conditional frequencies are reported in the rows of the Table, and the interpretation of the results is as follows. For instance, simulating a model with $K_0=0$ and $n=100$, the AIC picks the right number of changepoints $60\%$ of the times. Therefore, a criterion that perfectly selects the right number of changepoints should report values equal to 1 in the main diagonal of the table, and zeros in all the other entries.

It appears evident that the AIC overestimates the number of changepoints more frequently than the other considered criteria. This is a reasonable result since it is well known that the AIC tends to overestimate the number of parameters. Also, this is the reason why it might seem to correctly pick the number of changepoints when $K_0=3$, as the percentage of correct identification approaches 1. This is because we have not considered alternative hypotheses with $K_0>3$, that would likely be selected. The BIC and gBIC seem to behave better, as well as the Davies’ and pseudo-score tests. An exception is represented by the case in which $K_0=3$ and $n=100$, since Davies’ test underestimates the number of changepoints on average. Overall, we notice that the gBIC outperforms its competitors in almost all the considered scenarios, especially as n increases. Other simulation studies, omitted for brevity, show that a sample size larger than $n=500$ leads to the same results.

We also explore 5-fold cross-validation (CV). Table 12 of the Appendix contains the percentages of the correctly selected number of changepoints by the CV criterion, based on the same 500 runs and three different sample sizes $n \in \{100, 250, 500\}$ of the Gaussian response variable. We notice that CV leads to similar results if compared to the AIC ones, performing only slightly better as n increases but with the additional disadvantage of requiring much more computational time. Based on these results, we believe the CV criterion is not worth exploring further with other response variables distributions.

Then, we perform other simulations, again considering the same models of Table 1, with an additional non-broken-line variable $z_i$, whose effect is set equal to $\theta =4$. The models considered are reported in Table 13 of the Appendix. We consider both a continuous variable $Z \sim Beta(\alpha _1=1,\alpha _2=2)$ and a dichotomous variable $Z \sim Bernoulli(\pi =0.5)$. These additional results are reported in Tables 14 and 15 of the Appendix, respectively. Overall, we do not identify any relevant differences in the results when a non-broken-line variable is added to the linear predictor, especially as n increases.

In Table 3, we report the results of fitting logit models, whose linear predictors are reported in Table 4. We sum an additional error term to the linear predictors to make data more jittered. This is done to obtain the same degree of variability for the simulations from each considered distribution and to achieve a realistic compromise between simulated and real data.

Table 3 Percentages of correctly selected number of changepoints by each criterion (based on 500 runs and three different sample sizes $n \in \{100, 250, 500\}$) - Binomial response variable

Table 4 Generalized linear segmented regression models fitted for the simulations - Binomial case

Both information criteria and tests struggle to individuate the third changepoint even when n increases. The only exception is the AIC, whose performance is worse for $K_0 \in \{0,1,2\}$, but better with $K_0=3$. As evident from Figure 3, this third changepoint corresponds to a moderate change in the slope of the relationship between the response variable y and the segmented covariate x. The better performance of the AIC in this last scenario could indicate its ability to spot even slight changes in the segmented relation, in the Binomial case.

Finally, we carry out simulations under the Poisson case. Table 5 contains the results of fitting Poisson models, whose linear predictors are reported in Table 6. For ease of comparison, we set the same sample sizes used for the Binomial and Gaussian cases, even though the results show that a larger sample size could be needed to achieve equally good results. In detail, the information criteria, especially the AIC, almost completely fails in selecting the correct number of changepoints. Among the information criteria, the gBIC achieves a good performance when $K_0\ne 0$. The same holds for the Davies' test for all the sample sizes.

Table 5 Percentages of the correctly selected number of changepoints by each criterion (based on 500 runs and three different sample sizes $n \in \{100, 250, 500\}$) - Poisson response variable

Table 6 Generalized linear segmented regression models fitted for the simulations - Poisson case

6 Applications to real data

6.1 Application to crime data

In this subsection, we apply the sequential procedure to select the number of changepoints to the valenciacrimes dataset available in the stopp package in R (D’Angelo and Adelfio 2023). This database includes information about the crime events that occurred in Valencia, Spain, in 2019. Time and space location of the events represent the most important variables of the dataset, but variables based on distances from events to “places of concentration” are also available, including the Euclidean distance from the nearest: atm, bank, bar, cafe, industrial site, marked, nightclub, police, pub, restaurant, or taxi.

In detail, we are interested in exploring the relationship between the number of crimes that occurred and the hour of the event occurrence. To this aim, we compute the hourly number of crimes within a day (number_of_crimes), as the yearly accumulated number of crimes according to the variable week_day. This makes the number of statistical units equal to 168, which is the number of weekdays times the hours within a day. Therefore, we first fit a Poisson regression model

$$\begin{aligned} \log ({\mathbb {E}}[\texttt {number\_of\_crimes}_{i}])=\beta _0+\beta _1 \texttt {crime\_hour}_{i} \end{aligned}$$

(3)

that does not assume any segmented relationship between the covariate crime_hour and the response variable number_of_crimes, i.e. $K=0$.

The summary of the estimated coefficients of model (3) is reported in Table 7.

Table 7 Coefficients of non-segmented model (3)

The second step is to test if this relationship can actually be assumed to be broken-line. This would indicate that the expected number of crimes significantly changes as hours go by. To this aim, we estimate three segmented regression models of the form:

$$\begin{aligned} \log ({\mathbb {E}}[\texttt {number\_of\_crimes}_{i}])=\beta _0 + \beta _1 \texttt {crimes\_hour}_i+\sum _{k=1}^{K}\delta _k (\texttt {crimes\_hour}_{i}-\psi _k)_+ \end{aligned}$$

(4)

with $K=1,2,3$.

In Table 8, we report the information criteria values for each estimated model and the p-values for each step of the sequential hypothesis testing procedure outlined in Section 4.

Table 8 Values of the information-based criteria of the fitted models (4) and p-values of each step of the sequential procedure to be compared to $\alpha / 3 = 0.016$ for the crime data

A segmented relationship is clearly more appropriate compared to a classical linear relationship, given that both the information-based criteria and the sequential procedure never select the model with $K=0$. In detail, all the considered information-based criteria select the model with $K=3$. Differently, the procedure based on sequential hypothesis testing selects the number of changepoints for which the corresponding test is no longer significant, that is unequivocally $K=2$.

Following the results of the simulation studies, which have shown that the proposed sequential procedure outperforms its information-based criteria competitors in Poisson segmented models, we choose the model with $\hat{K}=2$.

The summary of the coefficients of the selected model is reported in Table 9, and the broken-line relationship between the two variables is in Figure 1.

Table 9 Coefficients of the chosen segmented model with $\hat{K}=2$ for the crime data

Fig. 1

Segmented relationship between the number of crimes and the hour of event occurrence for the crime data. The points are located in correspondence with the estimated changepoints

In particular, $\hat{\beta }_1$ is the effect of crime_hour when $x_i<\hat{\psi }_1$, that is, when the crime occurred before 10 am, while $\hat{\delta }_1$ and $\hat{\delta }_2$ are the changes in the slope when $\hat{\psi }_1<x_i<\hat{\psi }_2$ and $x_i>\hat{\psi }_2$, respectively. The positive value of $\hat{\delta }_1$ indicates an increase in the number of crimes after 10 am, while the negative value of $\hat{\delta }_2$ indicates a decrease after 1 pm. Nevertheless, the sum of $\hat{\beta }_1+\hat{\delta }_1+\hat{\delta }_2$ is still positive, indicating a positive relationship.

In summary, the relationship between the number of crimes and the time of crime occurrence is confirmed. Furthermore, we have proven the presence of two changepoints in the hour of crime occurrence, after which the number of crimes changes. In detail, the number of crimes decreases from midnight to 10 am and then increases after 10 am, but more rapidly between 10 am and 1 pm.

This result is achieved thanks to the flexibility of the approach. Note that other non-parametric approaches, such as splines, could well fit the data. Our proposed procedure allows to understand the estimated times of the changing trend, which is potentially crucial to policymakers. In addition, the main advantage of applying segmented models lies in the possibility of estimating and, therefore, interpreting the slopes, that is the risk of observing a crime.

6.2 Application to global land temperature data

In this subsection, we apply the sequential procedure to select the number of changepoints to the global land temperature data available from the https://www.ncei.noaa.gov/access/monitoring/global-temperature-anomalies/anomalies site. This database includes information about the global annual time series on temperature anomalies, with respect to the 20th century average (1901-2000). Monthly and annual global anomalies are available through the most recent complete month and year, respectively.

Here we only analyze land data, excluding ocean temperatures, and we consider all the available years, that is, from 1850 to 2022. As the main interest lies in identifying the years where a shift in the temperature anomalies trend occurred, we fit segmented regression models with Gaussian distribution for the response variable. The only covariate for which a piecewise relationship with the temperature anomalies can be assumed is the year of observation.

Therefore, we fit four models, starting from the one with no changepoints, up to the one with three changepoints.

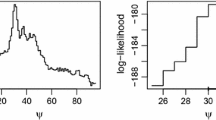
Table 10 reports the information criteria values for each estimated model and the p-values for each step of the sequential hypothesis testing procedure.

Table 10 Values of the information-based criteria of the fitted models (4) and p-values of each step of the sequential procedure to be compared to $\alpha / 3 = 0.016$ for the global land temperature data

Note that the information criteria always select three changepoints, while our proposed procedure always selects one, regardless of using the Davies’ or Score test. This result is in line with the known fact of a uniquely crucial changing trend in recent years (Yu and Ruggieri 2019).

The estimated broken-line relationship is depicted in Figure 2. It is easy to observe the existence of three changepoints, correctly identified by the information criterion methods, while our hypothesis testing method detects the most important unique crucial changing trend.

The coefficients estimated by the selected model are reported in Table 11, indicating 1979 as the changepoint year. Yu and Ruggieri (2019) detected 1963 as the unique changepoint in the temperature anomalies of land-based records. Note, however, that a changepoint for their method could either represent a change in the mean, trend, or variance, while our method is particularly suited for assessing the presence of a change in the effect of the segmented covariate. For this reason, we attribute differences in the location of estimated changepoints to the different nature of the methodologies.

Moving to the estimated effects, we obtain that temperatures were increasing at a rate of 0.05 ${C}^\circ$/decade prior to the changepoint year, while they increased at a rate of 0.28 ${C}^\circ$/decade afterwards. According to Yu and Ruggieri (2019), these temperature increases are 0.06 and 0.27, respectively before and after their estimated changepoint.

Fig. 2

Segmented relationship between the temperature anomalies and the years for the global land temperature data. The red point is located in correspondence with the estimated changepoint

Table 11 Coefficients of chosen segmented model with $\hat{K}=1$ for the global land temperature anomalies data

7 Conclusions

In this paper, we tackle the problem of selecting the optimal number of changepoints in segmented regression models. Firstly, we provide an overview of segmented regression models and a review of various methods used to estimate the number of changepoints. The effectiveness of these methods is assessed through simulation studies.

One well-established procedure, proposed by Kim et al. (2000), uses sequential testing to identify the existence of a single changepoint, but is unable to test for additional changepoints. To address this limitation, we propose a sequential procedure and evaluate its performance through simulations. We also compare the performance of our proposed method with that of information-based criteria in simulated studies. Our results show that the gBIC outperforms the other criteria for Gaussian response variables. Moreover, our sequential procedure performs well in the Gaussian case and is overall superior to information-based criteria for Binomial and Poisson response variables, particularly when multiple changepoints are present. Note, however, that the satisfactory performance of our proposed testing procedure pertains to some specific scenarios, and therefore, one should take this into account when applying the procedure.

These results have some limitations. We run the simulation studies fixing a limited number of changepoints, namely $K_{max}=3$. Of course, our method can be implemented to any fixed $K_{max}$. However, a small $K_{max}$ is often reasonable in real-life applications, as shown in Priulla et al. (2021), which deals with higher education data.

Moreover, a further topic to explore in the future is the quantification of uncertainty of the number of changepoints selected. In addition, a proper criterion to establish a proper Bonferroni correction could be studied, given that the current implementation depends on the a priori chosen $K_{max}$. Note that the applications presented in this paper came out robust to the current choice of the Bonferroni correction.

Furthermore, we have shown the applicability of our methods to the urban context through the analysis of crime data, and to environmental phenomena. In particular, concerning the latter application, our method provides results in line with previous works on temperature anomaly data. In general, segmented regression models are valuable tools for addressing diverse environmental challenges and driving sustainable practices across various fields.

Following such considerations, we believe our automatic procedure for selecting the number of changepoints in regression models will help address many real-life applications in environmental research.

Appendix. Supplementary material

Fig. 3

Simulated data for the Gaussian, Binomial, and Poisson scenarios (by row) and for each of the number of changepoints considered in the experiments (by columns), with $n=100$. On the x-axis, the segmented variables, and on the y-axis, the linear predictors

Table 12 Percentages of the correctly selected number of changepoints by the CV criterion (based on 500 runs and three different sample sizes $n \in \{100, 250, 500\}$) - Gaussian response variable

Table 13 Linear segmented regression models fitted for the simulations, with an additional variable whose effect is non broken-line

Table 14 Percentages of correctly selected number of changepoints by each criterion (based on 500 runs and three different sample sizes $n \in \{100, 250, 500\}$) - Gaussian response variable and covariate $Z \sim Beta(\alpha _1=1, \alpha _2=2)$

Table 15 Percentages of correctly selected number of changepoints by each criterion (based on 500 runs and three different sample sizes $n \in \{100, 250, 500\}$) - Gaussian response variable and covariate $Z \sim Bernoulli(\pi =0.5)$