1 Introduction

The term “circular data,” which is also used to refer to two-dimensional directional data, describes situations in which the observations are expressed in terms of degrees or radians. Since circular data are directions and have no magnitude, they can be easily represented as points on a circle with a unit radius whose center is the origin or as a unit vector in a plane that runs from the origin to the corresponding point.

In numerous scientific fields, measurements involve directions. Cardiology, for example, is a medical specialty where angular differences are common, particularly in the vector heart rate monitor, which is a three-dimensional version of the conventional one-dimensional cardiogram (Downs and Liebman 1969). Physics also uses angular data when describing sound waves or molecular connections, and the distribution of the result of a random sample of unit vectors emerges (Rayleigh 1919). In astronomy, each orbital plane can be thought of as a point on a sphere. Thus, Watson’s hypothesis is identical to the claim that the points are spread evenly on the sphere (Watson 1968). A biologist may be investigate how animals stand or a bird’s flight path (Eckert et al. 2008; Lagona et al. 2015), and with the use of computer image analysis, numerous measurements per sample can be rapidly collected. When dealing with circular data, circular statistical tests that are acceptable for large sample sizes must be used (Capaccioni et al. 1997). In the present time, there are extensive databases of DNA and protein sequences accessible, and structural bioinformatics deals with predicting their associated three-dimensional structure. Mathematically, dihedral angles are often used to describe the structure, assuming ideal bond lengths and angles. Recently, it has been recognized that developing probabilistic models of these angles in proteins can be highly advantageous (Ley and Verdebout 2017). Circular data can be measured not only via a compass, but also through a clock. Whether using a 24-h clock or a 12-month period, it is convenient to represent time data on a circle when the endpoints are naturally linked, such as 0.00 a.m. and 12.00 p.m. or January 1 and December 31. Political scientists (Gill and Hangartner 2010) have recently acknowledged the benefits of this approach in gaining information from circular data.

Circular probability distributions, a particular class of distributions, are frequently used to analyze the behavior of these circumstances. In other words, it is a probability distribution that accepts values that wrap around the circle and is specified in the range \([0,2\pi )\) or \([-\pi ,\pi )\) (Mardia et al. 2000; Jammalamadaka and Sengupta 2001). To broaden the range of possible uses in this situation, many researchers create circular distributions with a variety of properties. Some of these are cardioid, circular normal (Von Mises), wrapped normal, and wrapped Cauchy distributions (Mardia et al. 2000; Jammalamadaka and Sengupta 2001). The first two distributions are continuous probability distributions on a unit circle, while the wrapped normal and wrapped Cauchy distributions were constructed by “wrapping” the corresponding one-dimensional distributions on the real line around the unit circle. The wrapping technique was first articulated by Lévy in his wrapped distributions proposal (Lévy 1939). Wrapped distributions were introduced using Levy’s techniques, and their statistical characteristics and inference strategies have all been investigated in depth by numerous authors, such as the wrapped exponential (Jammalamadaka and Kozubowski 2000), the wrapped Laplace distribution (Jammalamadaka and Kozubowski 2003), the wrapped gamma distribution (Coelho 2007), the wrapped Lindley distribution (Joshi and Jose 2018), the wrapped modified Lindley (Chesneau et al. 2021), the wrapped Akash distribution (Al-khazaleh 2021), and the wrapped two-parameter Lindley distribution (Bhattacharjee et al. 2021).

The XLindley distribution (XLD), a special mixture of the exponential and Lindley distributions, was proposed by Chouia and Zeghdoudi (2021). This distribution was inspired by several factors. Firstly, the XLD is straightforward, and its formulae for the mean, variance, coefficient of variation, skewness, and kurtosis are all simple and can be applied relatively well to analyze many real-life data sets, such as those related to the Ebola, Corona, and Nipah viruses. Additionally, the XLD provides appropriate fits to many data sets. However, in general, it is more relevant to test simpler distributions than more intricate ones. So in this article, we propose a new circular distribution by wrapping the XLD distribution around the unit circle using Lévy’s technique is called the wrapped XLindley distribution (WXL) in Sect. 2. Various characteristic attributes, including the trigonometric moments, means, variance, skewness, and kurtosis coefficients, are covered in Sect. 3 of this article. In Sect. 4, we examine the inserted distribution’s invariance characteristics. The maximum likelihood (ML), least squares (LS), and weighted least squares (WLS) estimates for the unknown parameter are described in Sect. 5, while a simulation study and two lifetime applications are described in Sects. 6 and 7, respectively. Finally, Sect. 8 provide some conclusions

2 A wrapped XLindley distribution

Let a random variable (rv) X have a one-parameter XLD; the probability density function (pdf) of X is

$$\begin{aligned} f(x;\lambda )&= \frac{\lambda ^{2}}{(\lambda +1)^{2}} (2 + x +\lambda ) e^{-\lambda x}\\&= \frac{\lambda ^{2}}{(\lambda +1)^{2}} \left[ (1+\lambda )+(1+x) \right] e^{-\lambda x}\\&= \frac{\lambda ^{2}}{\lambda +1}e^{-\lambda x}+ \frac{\lambda ^{2}}{(\lambda +1)^{2}}(1+x)e^{-\lambda x}\\&=pf_{1}(x;\lambda )+(1-p)f_{2}(x;\lambda ) \quad x,\lambda > 0. \end{aligned}$$

A mixture of two distributions with a mixing proportion p is seen in the XLD pdf, where \(f_{1}(x) = \lambda e^{-\lambda x}\) and \(f_{2}(x) = \frac{\lambda ^{2}}{\lambda +1}(1+x)e^{-\lambda x}\) are, respectively, the probability density functions of the exponential distribution and the Lindley distribution with parameter \(\lambda\), and mixing proportion \(p =\frac{\lambda }{\lambda +1}\).

The wrapped rv produced by XLindley rv X is \(\Theta = X({\text {mod}}\, 2\pi )\) with pdf \(g(\theta ;\lambda )\) stated by

$$\begin{aligned} g(\theta ;\lambda )&= \sum _{k = 0}^{\infty } f(\theta +2k\pi ;\lambda )\\&= p\sum _{k = 0}^{\infty } f_{1}(\theta +2k\pi ;\lambda )+(1-p)\sum _{k = 0}^{\infty } f_{2}(\theta +2k\pi ;\lambda )\\&=p\,g_{1}(\theta ;\lambda )+(1-p)g_{2}(\theta ;\lambda ), \quad \theta \in [0,2\pi ) ,\quad \lambda > 0, \end{aligned}$$
(1)

where \(g_{1}(\theta ;\lambda ) \, \text {and}\, g_{2}(\theta ;\lambda )\) are the pdfs of the wrapped exponential distribution and the wrapped Lindley distribution with parameter \(\lambda\), respectively. Then Eq. (1) can be written as:

$$\begin{aligned} g(\theta ;\lambda )&= p\frac{\lambda e^{-\lambda \theta }}{(1-e^{-2\pi \lambda })}+(1-p)\frac{\lambda ^{2} e^{-\lambda \theta }}{(1+\lambda )(1-e^{-2\pi \lambda })^{2}}\bigg [(1+\theta )(1-e^{-2\pi \lambda })+2\pi e^{-2\pi \lambda }\bigg ] \\&=\frac{\lambda ^{2} e^{-\theta \lambda }}{(\lambda +1)^{2}(1-e^{-2\pi \lambda })^{2}}\bigg [(1-e^{-2\pi \lambda })(\lambda +\theta +2) + 2\pi e^{-2\pi \lambda }\bigg ]. \end{aligned}$$
(2)

Definition

A rv \(\Theta\) on a unit circle follows the WXL distribution with parameter \(\lambda >0\), denoted by \(\Theta \sim WXL(\lambda )\) if the pdf is given by Eq. (2).

Fig. 1
figure 1

Circular and linear representations of the pdf of the WXL distribution at different values of \(\lambda\)

Full size image

The mode of the WXL distribution can be obtained as follows:

$$\frac{\partial g(\theta ;\lambda )}{\partial \theta }=\frac{\lambda ^{2} e^{-\theta \lambda }}{\left( 1-e^{-2 \pi \lambda }\right) (\lambda +1)^{2}}-\frac{\lambda ^{3} e^{-\theta \lambda } \left( \left( 1-e^{-2 \pi \lambda }\right) (\theta +\lambda +2)+2 \pi e^{-2 \pi \lambda }\right) }{\left( 1-e^{-2 \pi \lambda }\right) ^{2} (\lambda +1)^{2}}.$$

Solving \(\frac{\partial g(\theta ;\lambda )}{\partial \theta }=0\), we have

$$\theta = \frac{1-e^{-2 \pi \lambda } (2 \pi \lambda +1)}{\left( 1-e^{-2 \pi \lambda }\right) \lambda }-\lambda -2.$$

\(\hat{\theta } = \frac{1-e^{-2 \pi \lambda } (2 \pi \lambda +1)}{\left( 1-e^{-2 \pi \lambda }\right) \lambda }-\lambda -2\) is a critical point at which \(g(\hat{\theta };\lambda )\) is maximum when \(0<\lambda <0.27602\).

$$Mod(\theta )=\Biggl \{^{\frac{1-e^{-2 \pi \lambda } (2 \pi \lambda +1)}{\left( 1-e^{-2 \pi \lambda }\right) \lambda }-\lambda -2\quad for\, 0<\lambda <0.27602,}_{0\quad \quad \quad \quad \quad \quad \quad \quad otherwise.}$$

The cumulative distribution function (cdf) is easily obtained by integrating Eq. (2) or by \(G(\theta )=\sum _{k=0}^{\infty } \left[ F(\theta +2k\pi )-F(2k\pi )\right]\) to obtain

$$G(\theta ;\lambda ) = \frac{\left( 1-e^{-2 \pi \lambda }\right) (\lambda +1)^{2} \left[ 1-e^{-\theta \lambda } \left( \frac{\lambda \theta }{(\lambda +1)^{2}}+1\right) \right] +2 \pi \lambda e^{-2 \pi \lambda } \left( 1-e^{-\theta \lambda }\right) }{\left( 1-e^{-2 \pi \lambda }\right) ^{2} (\lambda +1)^{2}}.$$
Fig. 2
figure 2

Circular and linear representations of the cdf of the WXL distribution at different values of \(\lambda\)

Full size image

Figures 1 and 2 show the behavior of the pdf and cdf of the new distribution for different values of \(\lambda\).

3 Characteristic properties of the WXL density

3.1 Trigonometric moments and associated parameters

The characteristic function (cf) of a circular distribution can be used to describe it similarly to that over the real line. We begin by discussing a few circular distribution-related concepts (Jammalamadaka and Sengupta 2001).

Due to the periodic nature of the circular rv \(\Theta\), the cf may be determined using

$$\vartheta _{p}(\theta )=\vartheta _{p} = \mathbb {E}(e^{ip\theta })=\mathbb {E}(e^{ip(\theta +2\pi )})=e^{2ip\pi }\mathbb {E}(e^{ip\theta }),$$

where \(i = \sqrt{-1}\), which mean that \(\vartheta _{p} = 0\) or \(e^{2ip\pi }=1\); i.e. p has only integer values.

According to Euler’s equation, the \(p{th}\) trigonometric moment of \(\Theta\) can be determined by

$$\vartheta _{p} = \mathbb {E}(e^{ip\theta })=\mathbb {E}(\cos (p\theta )+i\sin (p\theta ))=\mathbb {E}(\cos (p\theta ))+i\mathbb {E}(\sin (p\theta )) =\alpha _{p}+i\beta _{p},$$
(3)

where \(\alpha _{p}=\mathbb {E}(\cos (p\theta ))\) and \(\beta _{p}=\mathbb {E}(\sin (p\theta ))\).

In the complex plane, \(\vartheta _{p}\) is the mean resultant vector with length \(\rho _{p}=||\vartheta _{p}||=\sqrt{\alpha _{p}^{2}+\beta _{p}^{2}} \in [0,1]\) and direction given by:

$$\mu _{p} = {\left\{ \begin{array}{ll} \tan ^{-1}\left( \frac{\beta _{p}}{\alpha _{p}}\right) ,&{}if\quad \alpha _{p}> 0,\quad \beta _{p}\ge 0,\\ \frac{\pi }{2}, &{}if\quad \alpha _{p}=0,\quad \beta _{p}>0,\\ \tan ^{-1}\left( \frac{\beta _{p}}{\alpha _{p}}\right) +\pi , &{}if\quad \alpha _{p}<0,\\ \tan ^{-1}\left( \frac{\beta _{p}}{\alpha _{p}}\right) +2\pi , &{}if\quad \alpha _{p}\ge 0,\quad \beta _{p}<0,\\ undefined, &{} if\quad \alpha _{p}=0,\quad \beta _{p}=0. \end{array}\right. }$$

The basic measures of concentration and location are, respectively, \(\rho _{1}\) and \(\mu _{1}\). The polar equivalent of \(\vartheta _{p}\) is given by:

$$\vartheta _{p}=\rho _{p} e^{i\mu _{p}}= \rho _{p}\cos (\mu _{p})+i\rho _{p}\sin (\mu _{p})=\alpha _{p}+\beta _{p},$$
(4)

where \(\alpha _{p}=\rho _{p}\cos (\mu _{p})\) and \(\beta _{p}=\rho _{p}\sin (\mu _{p})\).

Furthermore, the p th central trigonometric moment of a circular distribution is given by:

$$\vartheta _{p,\mu _{1}}=\mathbb {E}\left( \cos (p[\theta -\mu _{1}])\right) +i\mathbb {E}\left( \sin (p[\theta -\mu _{1}])\right) =\bar{\alpha }_{p}+i\bar{\beta }_{p},$$

where \(\bar{\alpha }_{p}=\mathbb {E}\left( \cos (p[\theta -\mu _{1}])\right)\) and \(\bar{\beta }_{p}=\mathbb {E}\left( \sin (p[\theta -\mu _{1}])\right)\). The polar representation of \(\vartheta {p,\mu _{1}}\) is given by:

$$\vartheta _{p,\mu _{1}}=\vartheta _{p} e^{-i\mu _{1}}= \rho _{p}\cos (\mu _{p}-p\mu _{1})+i\rho _{p}\sin (\mu _{p}-p\mu _{1}).$$

The trigonometric moment of order p of the WXL distribution is the same as that of the XL distribution, i.e., \(\vartheta (p)=\vartheta _{p} = \vartheta _X(p)\), where

$$\begin{aligned} \vartheta _{p}&= \vartheta _x(p) = \frac{\lambda ^{2}}{(\lambda +1)(\lambda -ip)}+ \frac{\lambda ^{2} (1+\lambda -ip)}{(\lambda +1)^{2}(\lambda -ip)^{2}}, \quad p=0,\pm 1,\pm 2,\ldots \end{aligned}$$
(5)

Using Eq. (5), we can write:

$$\begin{aligned} \vartheta _{p}&=\frac{(\lambda +1)^{2} \lambda ^{4}+(\lambda (\lambda +2)-1) \lambda ^{2} p^{2}}{(\lambda +1)^{2} \left( \lambda ^{2}+p^{2}\right) ^{2}}+i\frac{\lambda ^{2} p \left( 2 \lambda +(\lambda +2) \left( \lambda ^{2}+p^{2}\right) \right) }{(\lambda +1)^{2} \left( \lambda ^{2}+p^{2}\right) ^{2}}. \end{aligned}$$
(6)

Using Eqs. (3) and (6), we can derive the expressions for \(\alpha _{p}\) and \(\beta _{p}\) as:

$$\alpha _{p} =\frac{(\lambda +1)^{2} \lambda ^{4}+(\lambda (\lambda +2)-1) \lambda ^{2} p^{2}}{(\lambda +1)^{2} \left( \lambda ^{2}+p^{2}\right) ^{2}},$$
(7)

and

$$\beta _{p} =\frac{\lambda ^{2} p \left( 2 \lambda +(\lambda +2) \left( \lambda ^{2}+p^{2}\right) \right) }{(\lambda +1)^{2} \left( \lambda ^{2}+p^{2}\right) ^{2}}.$$
(8)

According to Carslaw (1930) the pdf of the WXL distribution can be written as:

$$\begin{aligned} g(\theta ;\lambda )&=\frac{1}{2\pi }\left[ 1+2\sum _{p=1}^{\infty }(\alpha _{p}\cos p\theta + \beta _{p}\sin p\theta )\right] , \quad \theta \in [0,2\pi )\\&=\frac{1}{2\pi }\bigg [1+2\sum _{p=1}^{\infty }\bigg (\frac{(\lambda +1)^{2} \lambda ^{4}+(\lambda (\lambda +2)-1) \lambda ^{2} p^{2}}{(\lambda +1)^{2} \left( \lambda ^{2}+p^{2}\right) ^{2}}\cos p\theta \\&\quad + \frac{\lambda ^{2} p \left( 2 \lambda +(\lambda +2) \left( \lambda ^{2}+p^{2}\right) \right) }{(\lambda +1)^{2} \left( \lambda ^{2}+p^{2}\right) ^{2}}\sin p\theta \bigg )\bigg ]. \end{aligned}$$

To obtain the parameters \(\rho _{p}\) and \(\mu _{p}\) from \(\vartheta _{p}\), we need to determine its polar representation, which can be written as:

$$\vartheta _{p}=\rho _{p}e^{i\mu _{p}}.$$

Starting from Eq. (5), we can express \(\vartheta _{p}\) as:

$$\vartheta _{p} =\frac{\lambda ^{2}}{(\lambda +1)^{2}}((\lambda +1)^{2}-ip(\lambda +2))(\lambda -ip)^{-2}.$$
(9)

Using the identity

$$(a-ib)^{-k} = (a^{2}+b^{2})^{-k/2}e^{i k \,\tan ^{-1}(b/a)}, \quad a,b,k\in \mathbb {R}.$$

Then

$$\left( (\lambda +1)^{2}-ip(\lambda +2)\right) = \left( (\lambda +1)^{4} +p^{2}(\lambda +2)^{2}\right) ^{1/2}e^{-i\,\tan ^{-1}\left( \frac{p(\lambda +2)}{(\lambda +1)^{2}}\right) },$$
(10)

and

$$(\lambda -ip)^{-2} = \left( \lambda ^{2}+p^{2}\right) ^{-1}e^{2i\,\tan ^{-1}(p/\lambda )}.$$
(11)

Substituting Eqs. (10) and (11) into Eq. (9), we obtain the polar representation of \(\vartheta _{p}\) as:

$$\vartheta _{p} = \frac{\lambda ^{2} ((\lambda +1)^{4}+p^{2}(\lambda +2)^{2})^{1/2}}{(\lambda +1)^{2}(\lambda ^{2}+p^{2})}e^{i\left( 2\tan ^{-1}(p/\lambda )-\tan ^{-1}\left( \frac{p(\lambda +2)}{(\lambda +1)^{2}}\right) \right) }.$$
(12)

Now, from Eqs. (4) and (12), we obtain

$$\rho _{p} = \frac{\lambda ^{2} \left( (\lambda +1)^{4}+p^{2}(\lambda +2)^{2}\right) ^{1/2}}{(\lambda +1)^{2}(\lambda ^{2}+p^{2})},$$

and

$$\mu _{p} = 2\tan ^{-1}(p/\lambda )-\tan ^{-1}\left( \frac{p(\lambda +2)}{(\lambda +1)^{2}}\right) .$$

The p th central cosine and sine moments of the WXL distribution are given, respectively, by the following equations:

$$\begin{aligned} \bar{\alpha }_{p}&= \rho _{p} \cos (\mu _{p}-p\mu _{1})\\&= \frac{\lambda ^{2} \left( (\lambda +1)^{4}+p^{2}(\lambda +2)^{2}\right) ^{1/2}}{(\lambda +1)^{2}(\lambda ^{2}+p^{2})}\cos \bigg [2(\tan ^{-1}(p/\lambda )-p\,\tan ^{-1}(1/\lambda ))\\&\quad -\left( \tan ^{-1}\left( \frac{p(\lambda +2)}{(\lambda +1)^{2}}\right) -p\,\tan ^{-1}\left( \frac{\lambda +2}{(\lambda +1)^{2}}\right) \right) \bigg ], \end{aligned}$$

and

$$\begin{aligned} \bar{\beta }_{p}&= \rho _{p} \sin (\mu _{p}-p\mu _{1})\\&= \frac{\lambda ^{2} ((\lambda +1)^{4}+p^{2}(\lambda +2)^{2})^{1/2}}{(\lambda +1)^{2}(\lambda ^{2}+p^{2})}\sin \bigg [2(\tan ^{-1}(p/\lambda )-p\,\tan ^{-1}(1/\lambda ))\\&\quad -\left( \tan ^{-1}\left( \frac{p(\lambda +2)}{(\lambda +1)^{2}}\right) -p\,\tan ^{-1}\left( \frac{\lambda +2}{(\lambda +1)^{2}}\right) \right) \bigg ]. \end{aligned}$$

3.2 Means and related measures

The mean direction and resultant length for the WXL distribution are given, respectively, by

$$\mu = \mu _{1} = 2\tan ^{-1}(1/\lambda )-\tan ^{-1}\left( \frac{\lambda +2}{(\lambda +1)^{2}}\right) ,$$

and

$$\rho = \rho _{1} = \frac{\lambda ^{2} ((\lambda +1)^{4}+(\lambda +2)^{2})^{1/2}}{(\lambda +1)^{2}(\lambda ^{2}+1)},$$

while, the circular variance and standard deviation for the WXL distribution are given, respectively, by

$$\begin{aligned} V&= 1-\rho \\ {}&= 1- \frac{\lambda ^{2} ((\lambda +1)^{4}+(\lambda +2)^{2})^{1/2}}{(\lambda +1)^{2}(\lambda ^{2}+1)}, \end{aligned}$$

and

$$\begin{aligned} \sigma&= \sqrt{-2ln\rho }\\ {}&= \sqrt{\ln \frac{(\lambda +1)^{4}(\lambda ^{2}+1)^{2}}{\lambda ^{4} ((\lambda +1)^{4}+(\lambda +2)^{2})}}.\end{aligned}$$

3.3 Skewness and kurtosis coefficients

The skewness coefficient of the WXL distribution is given by

$$\begin{aligned} \eta _{1}&=\frac{\bar{\beta }_{2}}{V^{3/2}} \\&= \frac{\lambda ^{2} \left( 4 \left( \lambda ^{2}+2\right) ^{2}+(\lambda +1)^{4}\right) ^{1/2} }{(\lambda +1)^{2} \left( \lambda ^{2}+4\right) \left( 1-\frac{\lambda ^{2} \left( \left( \lambda +2\right) ^{2}+(\lambda +1)^{4}\right) ^{1/2}}{(\lambda +1)^{2} \left( \lambda ^{2}+1\right) }\right) ^{3/2}}\sin \left( \mu _{2}-2\mu _{1}\right) . \end{aligned}$$

While the kurtosis coefficient is given by

$$\begin{aligned} \eta _{2}&=\frac{\bar{\alpha }_{2}-\rho ^{4}}{V^{2}} \\&= \left[ \frac{\lambda ^{2} \left( 4 \left( \lambda ^{2}+2\right) ^{2}+(\lambda +1)^{4}\right) ^{1/2} }{(\lambda +1)^{2} \left( \lambda ^{2}+4\right) } \cos \left( \mu _{2}-2\mu _{1}\right) -\frac{\lambda ^{8} \left( \left( \lambda +2\right) ^{2}+(\lambda +1)^{4}\right) ^{2}}{(\lambda +1)^{8} \left( \lambda ^{2}+1\right) ^{4}}\right] \\&\quad \times \left( 1-\frac{\lambda ^{2} \left( \left( \lambda +2\right) ^{2}+(\lambda +1)^{4}\right) ^{1/2}}{(\lambda +1)^{2} \left( \lambda ^{2}+1\right) }\right) ^{-2}. \end{aligned}$$

\(\eta _{1}\) will be almost zero for unimodal symmetric frequency distributions. For unimodal distributions with a normal peak, we would anticipate \(\eta _{2}\) to be almost zero. The distribution is said to be leptokurtic if \(\eta _{2}\) is greater than zero and platykurtic if \(\eta _{2}\) is less than zero.

Table 1 displays some calculated values for several WXL distribution characteristic attributes for varying values of \(\lambda\). We can see that the mean direction, circular variance, standard deviation, and coefficient of skewness decrease when \(\lambda\) increases, contrary to the resultant length and coefficient of kurtosis, which increase when \(\lambda\) increases (i.e., when \(\lambda\) increases, the distribution of data becomes more concentrated in the mean direction and more skewed).

Table 1 Calculated values of various WXL distribution characteristics for different values of \(\lambda\)
Full size table

4 Invariance properties

Circular data probability distributions frequently take on a general structure, with the unit circle acting as support and a closed-form density. However, circular data has several unique characteristics that should be considered in every study. Indeed, circular data have no stated zero (i.e., starting direction) or end, and the assignment of the natural orientation is arbitrary. Despite having tractable forms, the use of well-known circular distributions can lead to incorrect inferences if the difficulties of the initial direction and orientation are disregarded. For example, in some experiments, the scientists take the measurements with the east as the zero direction and anticlockwise as the positive sense of rotation, but in other experiments, the measurements can be taken with the north as the zero direction and clockwise as the positive sense of rotation. To avoid making contradictory or incorrect statistical inferences, the distribution used to analyze circular variables must be invariant concerning changes in starting direction (ICID) and orientation changes (ICO). With \(\mathbb {D}=[a,b)\) where \(b-a=2\pi\) and \(\psi\) is a vector of parameters, circular distributions that have a pdf \(g_{\Theta }(.;\psi )\) of the circular variable \(\Theta \in \mathbb {D}\), with \(\psi \in \Psi\). Let \(\Theta ^{*}=\delta (\Theta +\tau )\), with \(\delta \in \{-1,1\}\) and \(\tau \in \mathbb {D}\), and \(g_{\Theta ^{*}}(.;\psi ^{*})\), \(\psi ^{*}\in \Psi ^{*}\). Then \(g_{\Theta }\) is ICID and ICO iff \(g_{\Theta ^{*}}(\theta ^{*};\psi ^{*})=g_{\Theta }(\theta ^{*};\psi ^{*})\) almost everywhere with \(\Psi ^{*}\equiv \Psi\) (i.e., their characteristic functions must belong to the same functional family) (Mastrantonio et al. 2019).

The characteristic function of \(\theta ^{*}\) for WXL is provided by

$$\begin{aligned} \vartheta _{\theta ^{*}}(p)&=e^{ip\delta \tau }\vartheta _{\theta }(p\delta )\\&=(\cos p\delta \tau )\vartheta _{\theta} (p\delta ) +i(\sin p\delta \tau )\vartheta _{\theta} (p\delta )\\&=\cos (p\delta \tau )\frac{(\lambda +1)^{2} \lambda ^{4}+(\lambda (\lambda +2)-1) \lambda ^{2} p^{2}}{(\lambda +1)^{2} \left( \lambda ^{2}+p^{2}\right) ^{2}}-\sin (p\delta \tau )\frac{\lambda ^{2} p \left( 2 \lambda +(\lambda +2) \left( \lambda ^{2}+p^{2}\right) \right) }{(\lambda +1)^{2} \left( \lambda ^{2}+p^{2}\right) ^{2}} \\&\quad +i\bigg (\cos (p\delta \tau )\frac{\lambda ^{2} p \left( 2 \lambda +(\lambda +2) \left( \lambda ^{2}+p^{2}\right) \right) }{(\lambda +1)^{2} \left( \lambda ^{2}+p^{2}\right) ^{2}}+\sin (p\delta \tau )\frac{(\lambda +1)^{2} \lambda ^{4}+(\lambda (\lambda +2)-1) \lambda ^{2} p^{2}}{(\lambda +1)^{2} \left( \lambda ^{2}+p^{2}\right) ^{2}}\bigg ). \end{aligned}$$
(13)

The WXL is neither ICID nor ICO because the real and imaginary parts of Eqs. (6) and (13) are the same only if \(\delta\) = 1 and \(\tau\) = 0.

If \(g_{\Theta} (.;\psi )\) is not ICO and ICID, the pdf \(g_{\Theta ^{*}}(.;\psi ^{*})\), with \(\Theta ^{*}=\delta (\Theta +\tau )\), \(\delta \in \{-1,1\}\), \(\tau \in \mathbb {D}\),and \(\psi ^{*}=(\psi ,\delta ,\tau )\in \Psi ^{*}\), is ICO and ICID. Then the WXL distribution’s invariant version is provided by

$$g_{\Theta ^{*}}(\theta ^{*};\lambda ,\delta ,\tau )=\left| \frac{\partial \left( \frac{\theta ^{*}}{\delta }-\tau \right) }{\partial \theta ^{*}}\right| g_{\Theta} \left( \frac{\theta ^{*}}{\delta }-\tau ;\lambda \right) .$$
(14)

Since \(\delta \in \{-1,1\}\), then Eq. (14) can be presented by

$$\begin{aligned} g_{\Theta ^{*}}(\theta ^{*};\lambda ,\delta ,\tau )&=\left| \frac{\partial \left( \delta \theta ^{*}-\tau \right) }{\partial \theta ^{*}}\right| g_{\Theta} \left( \delta \theta ^{*}-\tau ;\lambda \right) \\&=\left| \delta \right| g_{\Theta} \left( \delta \theta ^{*}-\tau ;\lambda \right) \\&=\frac{\lambda ^{2} e^{-(\delta \theta ^{*}-\tau )\lambda }}{(\lambda +1)^{2}(1-e^{-2\pi \lambda })^{2}}\bigg [(1-e^{-2\pi \lambda })(\lambda +\delta \theta ^{*}-\tau +2) + 2\pi e^{-2\pi \lambda }\bigg ]. \end{aligned}$$

5 Estimation

In this section, we will study the estimation of the unknown parameter by three different methods: ML, LS, and WLS methods commonly used in the literature.

5.1 Maximum likelihood estimation

Let \(\theta _{1},\theta _{2},\theta _{3},\ldots ,\theta _{n}\) be a random sample from WXL distribution, then the likelihood function is given by

$$\begin{aligned} L(\lambda |\theta _{1},\theta _{2},\ldots ,\theta _{n})&= \prod _{i=1}^{n} g(\theta _{i};\lambda )\\&= \frac{\lambda ^{2n}}{(1+\lambda )^{2n}(1-e^{-2\pi \lambda })^{2n}}\prod _{i=1}^{n}\left[ (1-e^{-2\pi \lambda })(2+\lambda +\theta _{i})+2\pi e^{-2\pi \lambda }\right] e^{-\lambda \theta _{i}}. \end{aligned}$$

The log-likelihood function is therefore given by

$$\begin{aligned} l(\lambda |\theta _{1},\theta _{2},\ldots ,\theta _{n})&= 2n\ln (\lambda )-2n\ln (\lambda +1)-2n\ln (1-e^{-2\pi \lambda })\\&\quad +\sum _{i=1}^{n}\ln \left[ (1-e^{-2\pi \lambda })(2+\lambda +\theta _{i})+2\pi e^{-2\pi \lambda }\right] -\lambda \sum _{i=1}^{n}\theta _{i}. \end{aligned}$$

The log-likelihood function’s derivative with respect to the parameter \(\lambda\) is

$$\begin{aligned} \frac{\partial l(\lambda |\theta _{1},\theta _{2},\ldots ,\theta _{n})}{\partial \lambda }&=\frac{2n}{\lambda }-\frac{2n}{\lambda +1}-\frac{4n\pi e^{-2\pi \lambda }}{1-e^{-2\pi \lambda }}-\sum _{i=1}^{n}\theta _{i} +\sum _{i=1}^{n}\frac{2\pi e^{-2\pi \lambda }(2+\lambda +\theta _{i})+(1-e^{-2\pi \lambda })-4\pi ^{2}e^{-2\pi \lambda }}{(1-e^{-2\pi \lambda })(2+\lambda +\theta _{i})+2\pi e^{-2\pi \lambda }}. \end{aligned}$$
(15)

We may find the ML estimator for the WXL distribution parameter \(\lambda\) by equating the derivative in Eq. (15) to zero and then using numerical methods to solve the resulting equation.

5.2 Least squares estimation

Let’s have a look at the ordered random sample \(\Theta _{(1)}<\Theta _{(2)}<\Theta _{(3)}<\cdots <\Theta _{(n)}\) from the \(WXL(\lambda )\) distribution. Then, we can get the LS estimates of the unknown parameter of the \(WXL(\lambda )\) distribution by minimizing

$$\begin{aligned} \sum _{i=1}^{n}\left( \frac{\left( 1-e^{-2 \pi \lambda }\right) (\lambda +1)^{2} \left[ 1-e^{-\theta _{(i)} \lambda } \left( \frac{\lambda \theta _{(i)}}{(\lambda +1)^{2}}+1\right) \right] +2 \pi \lambda e^{-2 \pi \lambda } \left( 1-e^{-\theta _{(i)} \lambda }\right) }{\left( 1-e^{-2 \pi \lambda }\right) ^{2} (\lambda +1)^{2}}-\frac{i}{n+1}\right) ^{2}, \end{aligned}$$

with respect to \(\lambda\), where \(\frac{i}{n+1}\) is the expected value of the ordered empirical distribution function (Swain et al. 1988). The LS estimations are known to be biased. The WLS is a well-known variant of the LS approach that has less bias than the standard LS. We can calculate the WLS estimates of the unknown parameter of the \(WXL(\lambda )\) distribution by minimizing

$$\sum _{i=1}^{n}\frac{(n+1)^{2}(n+2)}{i(n-i+1)}\left( \frac{\left( 1-e^{-2 \pi \lambda }\right) (\lambda +1)^{2} \left[ 1-e^{-\theta _{(i)} \lambda } \left( \frac{\lambda \theta _{(i)}}{(\lambda +1)^{2}}+1\right) \right] +2 \pi \lambda e^{-2 \pi \lambda } \left( 1-e^{-\theta _{(i)} \lambda }\right) }{\left( 1-e^{-2 \pi \lambda }\right) ^{2} (\lambda +1)^{2}}-\frac{i}{n+1}\right) ^{2},$$

with respect to \(\lambda\).

6 Monte Carlo simulation study

To compare and contrast the estimated performances of the ML, LS, and WLS estimators developed in previous sections, we conduct several Monte Carlo simulation studies in this section. The parameters \(\lambda = 0.1,\, 0.5,\,1,\,\text {and}\, 2\) are used in Monte Carlo simulations. The derived average (\(\hat{\lambda }\)), standard deviation (SD), and mean squared error (MSE) values of estimates based on the 1000 times repeated simulations are shown in Table 2 for the various sample sizes n = 30, 80, 200, and 1000. This section’s computations were all carried out via MATLAB R2019a modules.

Table 2 Monte Carlo simulation results for WXL distribution at different values of \(\lambda\)
Full size table

As is evident from Table 2, the SD and MSE values decrease as the sample size grows for all parameter settings. This demonstrates the estimations’ accuracy and precision, as well as their consistency and unbiasedness. Since the ML estimators are asymptotically unbiased estimators, this is the outcome that may be predicted. Additionally, the outcomes of the simulation demonstrate that LS and WLS estimators have these characteristics as well. It is clear from the simulation results that the ML estimators perform better than the LS and WLS estimators due to their lower MSE values.

7 Applications

In this section, we compare the modeling behavior of the WXL(\(\lambda\)) distribution with five other distributions that have demonstrated good performance in real-life applications: wrapped Lindley (WL(\(\lambda\))) (Joshi and Jose 2018), wrapped modified Lindley (WML(\(\lambda\))) (Chesneau et al. 2021), Von Mises (VM(\(\omega ,\kappa\))) (Mardia et al. 2000), Jones–Pewsey (JP(\(\omega ,\kappa ,\varkappa\))) (Jones and Pewsey 2005), and Kato–Jones (KJ(\(\omega ,\kappa ,\varkappa ,\lambda\))) (Kato and Jones 2015). We evaluate the models’ performance using two real-life applications and show that our proposed WXL model is the best model to fit this data when compared to the WL, WML, VM, JP, and KJ models. We employ the maximum likelihood technique to estimate the models’ unknown parameters. Additionally, we use several statistical measures, including the Akaike information criterion (AIC), Bayesian information criterion (BIC), Watson (W), Kolmogorov–Smirnov (K-Statistic), and corresponding p-values (K P-Value) to compare the models.

7.1 Starhead Topminnows dataset

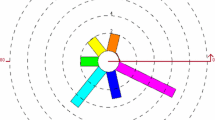
To examine the orientation of Starhead Topminnows in both aquatic and terrestrial environments, they were dispersed to different beaches of a small forest pond. Using a solar compass, these fish were able to move in a direction that would bring them back to the land-water boundary at the place of their capture. By aligning its body for each leap with the position of the sun, the fish was able to move in a certain direction on land. Many fish moved randomly instead of linearly on days with high levels of cloud cover because they were unable to position their bodies in the same way from leap to leap. Individual differences in terrestrial locomotion were significant. The data set includes 50 Starhead Topminnows’ sun compass directions, taken under very gloomy skies (Goodyear 1970; Fisher et al. 1993).

Table 3 The summary of fits for the directional preferences of the Starhead Topminnows dataset
Full size table
Fig. 3
figure 3

Estimated pdfs and cdfs of the considered distributions for the Starhead Topminnows dataset: histogram, rose diagram, and empirical distributions

Full size image

Figure 3 displays several visualizations of the Starhead Topminnows dataset, including a Cartesian histogram, a rose diagram, and empirical. Additionally, we have fitted densities of five different models—WXL, WML, VM, JP, and KJ—to this dataset, as shown in the same figure.

The results for this dataset are presented in Table 3. It is worth noting that the WXL model outperforms all other models in terms of AIC and BIC, indicating a superior fit to the data. However, the VM, JP, and KJ models exhibit better fits than our proposed model in terms of W.

7.2 Bank transaction dataset

Europe suffers annual losses of billions of euros due to credit card fraud. Financial institutions aim to enhance fraud prevention methods, but fraudsters constantly modify their tactics, rendering traditional detection tools, such as expert rules, inadequate (Bahnsen et al. 2014). The pycircular python package provides a genuine dataset of 349 transactions that took place between 1 January and 29 July 2020 (Bahnsen et al. 2023).

Using hour of the day as a scalar variable raises issues due to its cyclic nature, which may result in inaccurate or misleading outcomes. To overcome this, circular statistics techniques, such as circular distribution encoding, can be employed to incorporate the cyclic nature of the data.

Table 4 The summary of fits for the bank transaction dataset
Full size table
Fig. 4
figure 4

Estimated pdfs and cdfs of the considered distributions for the bank transaction dataset: histogram, rose diagram, and empirical distributions

Full size image

In Fig. 4, we present various visual representations of the bank transaction dataset. Specifically, the figure exhibits a Cartesian histogram, a rose diagram, and empirical, alongside the fitted densities of five distinct models—WXL, WML, VM, JP, and KJ—all of which are displayed within the same figure.

Table 4 presents the findings obtained from analyzing the dataset. The results highlight the superior performance of the WXL model compared to WL, WML, and VM in terms of AIC, BIC, and W. This suggests that the WXL model provides a more optimal fit to the data. However, it is worth noting that the JP and KJ models outperform our proposed model solely in terms of AIC and BIC, albeit with a K P-Value approaching zero and a significantly higher W.

8 Conclusion

Using the wrapping strategy, we introduced the wrapped XLindley distribution (WXL), a model circular distribution, in this study. The characteristic function, trigonometric moments, circular variance, circular standard deviation, skewness, and kurtosis are among the essential properties presented in this context. The features of invariance are investigated. The maximum likelihood, least squares, and weighted least squares techniques are used to estimate the model parameter. We find that our distribution is the best model in two-life applications after comparing its results with those of wrapped Lindley, wrapped modified Lindley, Von Mises, Jones–Pewsey, and Kato–Jones distributions. Therefore, it may be said that the suggested distribution adds something valuable to the body of knowledge. The essential calculations and graphics were programmed using MATLAB R2019a modules.