Abstract
Multi-wave-cross-lagged-panel models (CLPMs) of directional ordering are a focus of much controversy in educational psychology and more generally. Extending traditional analyses, methodologists have recently argued for including random intercepts and lag2 effects between non-adjacent waves and giving more attention to controlling covariates. However, the related issues of appropriate time intervals between waves (lag1 intervals across waves) and the possibility of contemporaneous (lag0) effects within each wave are largely unresolved. Although philosophers, theologians, and scientists widely debate sequential (lagged) and simultaneous (lag0) theories of causality, CLPM researchers have mostly ignored contemporaneous effects, arguing causes must precede effects. In a substantive-methodological synergy, we integrated these issues and designed new structural equation models to reanalyze one of the strongest CLPM studies of academic self-concept (ASC) and achievement (five annuals of mathematics data; 3527 secondary school students). A taxonomy of models incorporating various combinations of lag0, lag1, and lag2 effects, random intercepts, and covariates consistently supported a priori reciprocal effect model (REM) predictions—medium or large reciprocal effects of ASC and achievement on each other. Consistent with self-concept theory, effects of ASC on achievement evolved over time (lag1, not lag0 effects), whereas effects of achievement on ASC effects were more contemporaneous (lag0, not lag1 effects). We argue that lag0 effects reflect proximal events occurring subsequent to the previous data wave, suggesting the need for shorter intervals but also leaving open the possibility of contemporaneous effects that are truly instantaneous. We discuss limitations and future directions but also note the broad applicability of our statistical models.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Self-concept is a critical psychological construct that plays a vital role in shaping a person’s perceptions of themselves, impacting how they feel, act, and adjust to a shifting environment. In educational settings, academic self-concept (ASC) is a significant predictor of academic achievement, interest, emotions, school satisfaction, course selection, persistence, and long-term attainment (Guo et al., 2015a, 2015b; Guo et al., 2015a, 2015b; Marsh & Craven, 2006; Marsh & Martin, 2011; Marsh et al., 2005b; Marsh et al., 2018a; Marsh et al., 2022; Pekrun, 2006; Pekrun et al., 2017, 2019; Pekrun et al., 2023; Marsh & O’Mara, 2008). Our study is a substantive-methodological synergy, integrating new and evolving statistical models of the nature of the temporal ordering of ASC and achievement. Extending current structural equation models (SEMs) of panel data, we introduce a new approach incorporating diachronous (lagged) and synchronous (contemporaneous or simultaneous, non-recursive) paths and address the issue of the time intervals in these models.
Much research demonstrates that the positive correlation between ASC and achievement has broad generalizability (e.g., Basarkod et al., 2020; Hansford & Hattie, 1982; Marsh & Hau, 2003; Marsh et al., 2022; Seaton et al., 2009). The interpretation of this correlation has been the focus of much debate and research—whether it reflects a non-causal association, the causal effect of prior ASC on achievement, the causal effect of prior achievement on subsequent ASC, or bidirectional causal effects in both directions (i.e., reciprocal effects). Following Marsh (1990), almost all this research uses traditional cross-lagged panel designs and structural equation models (SEMs) that focus on lagged (lag1) effects linking prior measures of each construct to subsequent measures of the same constructs in immediately adjacent wave (e.g., wave 1→wave 2, wave2→wave 3; see Figs. 1 and 2). The critical concern is the directionality of effects—reciprocal paths leading from prior measures of each construct to subsequent measures of the other construct. Although testing some models with only two waves is possible, more waves are desirable. Thus, when there are more than two waves, it is possible to consider paths between non-adjacent waves (lag2 effects; e.g., wave 1→wave 3, wave 2→wave 4), random intercept models, and the consistency of reciprocal effects over time. Indeed, models without lag2 effects make the critical, typically untested assumption that these lag2 paths are zero, whereas Marsh et al. (2022, 2023; also see Lüdtke & Robitzsch, 2021, 2022) argued that their omission can systematically bias estimates and diminish goodness-of-fit. Marsh et al. (2022, 2023) found consistently significant lag2 stability paths, but reciprocal cross-paths were mostly small and had little effect on substantive interpretations.
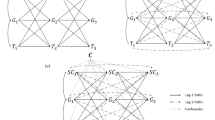
Schematic diagrams illustrating lagged (lag1) and contemporaneous (lag0) reciprocal effects relating academic self-concept (ASC) and achievement (Ach) over three waves of data. Note: Schematic diagram of three basic models positing cross-lagged (lag1; Model A) reciprocal effects, contemporaneous (lag0; Model B) reciprocal effects, and both lag1 and lag0 reciprocal effects (Model C). Model D is a hypothetical model to illustrate the difference between contemporary reciprocal effects that are truly instantaneous and contemporaneous reciprocal effects that may represent proximal (lag1) reciprocal effects associated with shorter time intervals that were not measured
Alternative reciprocal effect models (REMs) positing relations between math self-concept (the X factor) and math achievement (the Y factor) over five annual waves of data. Note. Math self-concept was based on responses to 6 items (the six square boxes); math achievement was based on a single measure (final school grade from school records) for each year. The X and Y variables are measurement factors for math self-concept (X) and achievement (Y). Ax and Ay are autoregressive factors in the structural model representing math self-concept (Ax) and achievement (Ay). The T variables included in RI models are the global trait factors representing the random intercepts for math self-concept (Tx) and achievement (Ty). Ovals represent latent factors, and boxes represent manifest variables. Straight lines with single-headed arrows represent directed paths, and curved lines with double-headed arrows represent covariances (or residual covariances). The dashed lines are lag2 stability paths between non-adjacent waves (lag2 reciprocal paths are not shown but are included in some models; see Table 3). Reciprocal paths from different autoregressive factors (Ax to Ay and Ay to Ax) represent directional ordering. Reciprocal paths can be lagged (from one wave to the next, lag1 paths) or contemporaneous (within the same wave, lag0 paths). Excluded to avoid clutter are correlated uniquenesses relating responses to the same math self-concept item (the set of six boxes) administered in different years
In the present investigation, we extend this research to integrate new statistical models that provide a broader perspective on directional ordering, incorporating a more comprehensive conceptual framework of sequential, simultaneous, and reciprocal theories of directional ordering and the critical role of time intervals. Because time intervals vary as a function of data collection designs (e.g., time lag between measurement waves and temporal focus—current versus past—of measures), and because causal processes themselves might unravel according to different temporalities (e.g., immediate vs. prolonged impact), testing lagged effects of many sorts is necessary to reach a fuller picture of dynamic processes over time. The present research offers a substantive-methodology synergy by articulating new tests of the reciprocal effect model (REM) central to ASC research. More specifically, we posit alternative operationalizations of the time-lapse linking ASC and achievement in CLPMs that have broad implications for other constructs and different disciplines. We begin with brief overviews of the conceptual and theoretical framework underpinning our study, as well as the philosophical, theological, and scientific perspectives of causality and their relation to the chicken-egg conundrum, and then support for the REM in ASC research. We extend this REM research, demonstrating new statistical models to test traditional reciprocal (lag1) effects over sequential waves and contemporaneous (lag0) reciprocal effects of ASC and achievement on each other within the same wave.
Conceptual and Theoretical Framework
Based on self-concept theory, REM hypothesized the directional ordering of causal relations, which becomes empirically testable when both ASC and achievement are measured across at least two, preferably three or more, waves of data. Hence, there is a strong theoretical basis for our a priori hypotheses. More broadly, it is always appropriate to posit a priori hypotheses that the reciprocal directional ordering of self-concept and achievement are “causal” (i.e., the REM hypothesis) and to propose empirical tests to test these hypotheses. However, even when there is support for a priori hypotheses, there typically are alternative interpretations of the results that might qualify this support. Thus, interpretations based on support for the REM hypothesis based on cross-lagged panel data rely on robust assumptions inherent in various statistical models used to test the assumptions.
Our paper, as well as most debates on longitudinal data analysis, adhere to a predictive causality perspective—known as Granger causality—where a cause is equated with the prospective/longitudinal effect of a variable, net of confounding factors of change (Granger, 1969; also see Campbell & Stanley, 1963; Cook & Campbell, 1979; Diener et al., 2022). This framework is explicitly referenced and privileged in SEMs of longitudinal data, due to its inherent temporal focus (Hamaker et al., 2015; Zyphur et al., 2020; Lohmann et al., 2022). Nevertheless, the validity of causal interpretations remains susceptible to threats and might never be fully resolved with statistical models of longitudinal correlational data. Indeed, even random-control and quasi-experimental studies are based on many assumptions that might compromise interpretations of the results (e.g., Campbell & Stanley, 1963; Cook & Campbell, 1979) that are well-known but often disregarded in educational and psychological research (also Diener et al., 2022).
VanderWeele et al. (2020) offered considerable discussion on the issue of causal inference with longitudinal data. Based on their, they proposed a six-level hierarchy of research designs for evidence concerning causality. Our design is level 5 (with a true randomized trial as the only level that is stronger). On this basis, they concluded that “A well-designed longitudinal study with control for prior exposure and outcome, and with robustness to unmeasured confounding assessed through the sensitivity analysis can provide a relatively strong evidence for causality” (p. 1461).
Hübner et al. (2023) made a similar point, emphasizing the strong ignorability/no unobserved confounding assumption requires that all potential confounding variables are measured and adequately considered in the respective model. They suggested that models with neither lag2 nor confounder effects probably make unrealistic assumptions. Whereas lag2 models are more realistic, they argued that such models are still prone to be biased by time-invariant and time-varying confounders that would need to be considered. The RI-CLPM also requires strong ignorability assumptions, but only after controlling for time-invariant differences. However, they also noted Lüdtke & Robitzsch’s (2022) mathematical and simulation research showing that RI-CLPMs led to biased results when the true model had lag2 effects, highlighting the value of CLPM with lag2 effects when cross-lagged effects were of interest. Noting that not many CLPM studies had investigated reasonable approaches for including potentially many covariates, they proposed weighting approaches to this issue rather than traditional multiple regression approaches. Nevertheless, as did Hübner et al., we are concerned about including many covariates without carefully considering their rationale. Indeed, there is the problem of “throwing the baby out with the bath water” by including covariates that are part of the causal process being investigated, particularly for time-varying covariates (see discussion by Marsh et al., 2022; also see VanderWeele et al., 2020).
The Chicken-Egg Conundrum: Simultaneous, Sequential, and Reciprocal Models of Causation
Simultaneous and Sequential Causation
The Chicken-Egg Conundrum is a classic philosophical problem related to causality that asks which came first: the chicken or the egg. This question is at the heart of the interpretation of CLPMs, which is the focus of our study. This conundrum highlights the challenges of determining a clear causal relationship between two mutually dependent events as proposed in sequential, simultaneous, and reciprocal theories of causality. These theories of causality have been a topic of interest among philosophers, religious thinkers, and scientists throughout history. They represent distinct theoretical perspectives on the nature and structure of relations between causes and effects (e.g., Cartwright, 2004; Leuridan & Lodewyckx, 2019; Machamer et al., 2000).
According to literal Biblical representations of creation in the Book of Genesis, God created the universe in 6 days, creating humans on the sixth day. This traditional literal view of creation emphasizes a linear and sequential view of causality, with God being the first cause and all subsequent events occurring in a precise temporal order. However, some religious scholars, such as Saint Augustine, argued for a simultaneous perspective of causation in which God created the universe at once and that God constantly sustains the universe.
Sequential theories of causation posit that causes and effects are temporally distinct, with causes preceding effects. This traditional Western philosophical perspective dates back to ancient Greece when Aristotle argued that the cause must come before the effect and that this ordering of the relation between cause and effect is necessary and invariable. However, it is also fundamental in subsequent work by philosophers David Hume, Bertrand Russell, John Stuart Mill, and George Edward Moore. This perspective emphasizes the importance of necessary connections in causality and rejects the possibility of simultaneous causality. Following these Western philosophical perspectives and subsequent counterfactual theories of causation (e.g., Lewis, 1973; Pearl et al., 2016; Wunsch et al., 2021), this is a traditional theory of causation in psychological research and experimental interventions. However, Cartwright (2004) argues that this notion of causality is too simplistic “because causation is not a single, monolithic concept” (p. 805).
Simultaneous theories of causation challenge the traditional Western emphasis on causality as a linear relationship between cause and effect (e.g., Leuridan & Lodewyckx, 2019). In the second century CE, the Buddhist philosopher Nagarjuna emphasized the interconnectedness of all things and that everything arises in dependence upon multiple causes and conditions (Garfield, 1995). The Japanese Zen master Dogen in the thirteenth century emphasized the concept of non-duality, suggesting that all things are interconnected (Heine, 1994). Descartes (seventeenth century) and Immanuel Kant (eighteenth century) also discussed instantaneous causation. The twentieth-century Japanese philosopher Nishida Kitaro proposed the idea of “absolute nothingness,” which suggests that all things arise in dependence upon a fundamental emptiness or nothingness. Twentieth-century British philosopher Alan Watts (1951) similarly emphasized that everything is interconnected and interdependent, highlighting the importance of multiple perspectives. Huemer & Kovitz (2003) (also see Brand, 1984; Simon, 1977) note numerous examples proposed by eminent philosophers exemplifying this position (e.g., moving one end of the pencil causes the other end to move; a lead ball on a cushion causes an indentation in the cushion; lowering one end of a seesaw causes the other to go up). Theoretical physicist John Cramer (1986) developed the Transactional Interpretation of quantum mechanics, suggesting that causality in the quantum world is simultaneous, bidirectional, and might even transcend time. These perspectives on simultaneous causation challenge traditional Western views and highlight the importance of understanding the interconnectedness of all things. Leuridan & Lodewyckx (2019) also discuss the philosophical and scientific basis for instantaneous causation and real-world examples of simultaneous causation.
Psychologists were introduced to simultaneous effect models from the econometric literature (Klein & Goldberger, 1955) as an example in the highly influential LISREL statistical package developed by Joreskog & Sorbom (1984). Nevertheless, psychological research rarely considers contemporaneous effects, and psychological researchers typically embrace sequential theories. Thus, Gollob & Reichardt (1987, p. 81) contend that the first principle of causal modeling is that “causes take time to exert their effects, and therefore values of a variable can be caused only by values of prior variables” (e.g., Heise, 1975; James et al., 1983; Strotz & Wold, 1960). Gollob & Reichardt (1987) argue that the apparent examples of simultaneous cause-and-effect actually reflect effects that occur in very short intervals (e.g., the speed of light) and that “In all the examples we have come across in the social sciences, it is clear that a time lag exists between cause and effect” (p. 82).
Gollob & Reichardt (1987) also highlighted complications in models of causality associated with time intervals, noting that effect sizes can vary substantially depending on the time interval between waves. Illustrating this issue, they noted that taking an aspirin for a headache is unlikely to have an effect in 2 min, will have its maximum effect after several hours, and is unlikely to have much effect after 24 hours. They further argue that there is no optimal time interval; researchers must consider alternative intervals to fully understand a variable’s causal effects. Dorman & Griffin (2015) similarly noted that overly long time lags could attenuate true relations. Like other methodologists (e.g., Wunsch et al., 2021), they suggest that the choice of time interval should be based on a clear theoretical understanding of the causal processes, considering the research question and the population being studied, conducting sensitivity analyses, and an empirical approach in which different time intervals are considered. Although laudable, this strategy is often impractical, challenging to implement, and rarely pursued. More broadly, the failure to find lagged effects for a given time interval does not mean that lagged effects would not be evident with different time intervals—either longer or shorter (see Singh et al., 2023). To address this issue, we present contemporaneous causation models for cross-lagged panel data to test directional-ordering with each wave (i.e., lag0 paths) as well as between waves (i.e., lag1 and lag2 paths). We also provide a more practical sensitivity analysis concerning time intervals, consistent with recommendations by Dorman and Griffin, Wunsch, and others. By developing a framework for integrating the effects corresponding to multiple time intervals, the current methodological-substantive synergy offers the flexibility needed to implement such a strategy (see “The Present Investigation” section).
Reciprocal Effects Models
Reciprocal causation occurs when two or more variables mutually influence each other, forming a causal loop. Reciprocal causation differs from traditional sequential and simultaneous forms of causation in directionality and temporality. A key difference is that sequential theories of causation posit a unidirectional causal ordering, whereas reciprocal causation posits bidirectional causation. Reciprocal causation is like simultaneous causation in that both variables are a cause and an effect of the other. However, in reciprocal effect models, this represents reciprocal effects over time rather than simultaneous reciprocal effects at the same time. Unlike sequential and simultaneous unidirectional causation, both variables mutually influence each other over time for reciprocal causation. Bandura (1986) and Marsh (1990, 2006) are widely known examples of reciprocal effects models in psychology whereby self-beliefs and outcomes are reciprocally related. However, reciprocal effect models are also influential in biology (e.g., relations between genes and environment; Laland et al., 1999), sociology (relations between social structures and individual actions; Giddens, 1984); economics (relations between supply and demand; Samuelson & Nordhaus, 2010), climate change (relations between human activity and the Earth’s climate system), and ecology (e.g., relations between species and their environment; Ulanowicz, 1997). Thus, reciprocal causation provides a framework for understanding complex, dynamic relationships between variables that mutually influence one another.
In summary, these theories offer different perspectives on causality but have overlapping features. Thus, reciprocal and simultaneous models of causality overlap, as both theories emphasize causality’s complex and interdependent nature. Similarly, the sequential theory of causality might be consistent with reciprocal theories with a feedback loop between cause and effect over time. Moreover, the different theories of causality offer complementary perspectives, which can enrich understanding. For example, sequential theories of causality emphasize the importance of a clear temporal order between cause and effect. On the other hand, simultaneous causality theories highlight causality’s complexity and the importance of understanding the interconnectedness of all things. Finally, reciprocal theories of causality emphasize the temporal pattern of relations between cause and effect over time.
Reciprocal Effects Model (REM) of Academic Self-Concept and Achievement
Historically, self-concept researchers (e.g., Calsyn & Kenny, 1977) took an “either-or” approach—either a skill development model (prior achievement leads to subsequent ASC) or a self-enhancement model (prior ASC leads to subsequent achievement). However, Marsh (1990; also see Pekrun, 1990) integrated theoretical and statistical perspectives, positing a dynamic reciprocal effects model (REM) that incorporated both self-enhancement and skill development models. In contrast to these unidirectional (skill development or self-enhancement) models, Marsh argued for a reciprocal model of effects whereby better ASCs lead to better achievement, and better achievement leads to better ASCs. Marsh (also see Wu et al., 2021) further noted that support for the skill-development model is well-established; a student’s ASC is based at least partly on their prior achievement. Thus, the critical issue is support for the self-enhancement model, irrespective of whether this self-enhancement path is larger or smaller than the skill-development path.
Support for the REM
Based on self-concept theory, we hypothesized the bidirectional ordering of relations (the REM hypothesis). Following Marsh (1990), extensive research supports REM predictions, as evidenced by comprehensive systematic reviews and meta-analyses (e.g., Huang, 2011; Valentine et al., 2004; Wu et al., 2021). Additionally, Marsh and colleagues (Marsh & Craven, 2006; Marsh & Martin, 2011; also see Huang, 2011) perceived support for the REM hypothesis as indicative of causal effects, underscoring the implications for interventions aimed at concurrently enhancing ASC and achievement. Marsh & Craven (2006; also see Huang, 2011) emphasized this point, stating: “If practitioners enhance self-concepts without improving performance, then the gains in self-concept are likely to be short-lived…. If practitioners improve performance without also fostering participants’ self-beliefs in their capabilities, then the performance gains are also unlikely to be long-lasting” (p. 159). Wu et al. (2012) also interpreted the result as supporting an REM hypothesis, particularly for secondary-school students, but cautioned that causal interpretations based on longitudinal correlational models might not be warranted “because the included studies all adopted a correlational design. Therefore, we cannot rule out a third variable that affects both constructs” (p. 1771). Despite advances in statistical methodology used in cross-lag-panel studies that address this “third variable” problem, the issue remains.
Critically, nearly all research supporting these REM predictions in the widely cited systematic reviews and meta-analyses (Huang, 2011; Marsh & Craven, 2006; Valentine et al., 2004; Wu et al., 2021) is based on traditional cross-lagged panel models (CLPM) of longitudinal data with only lag1 effects. Recent research has challenged the appropriateness of CLPMs, arguing that they fail to uncover the within-person effects linking ASC and achievement (Marsh et al., 2022; Núñez-Regueiro et al., 2022; also see Hamaker, 2023; Murayama et al., 2017; Orth et al., 2021). CLPMs with random intercepts (RI-CLPMs) have been proposed as a more robust within-person perspective that better controls for unmeasured covariates (Hamaker et al., 2015). Noting a dearth of research juxtaposing these models, Marsh et al. (2022, 2023; also see Lüdtke & Robitzsch, 2021, 2022; Pekrun et al., 2023) reviewed appropriate research questions and interpretations of RI-CLPMs and CLPMs. They argued that RI-CLPMs and CLPMs with lag2 paths (e.g., additional paths from the first to third waves, from the second to the fourth waves, etc.) were complementary models rather than antagonistic.
New Statistical Models Contrasting Lagged (Lag1) and Contemporaneous (Lag0) Effects
In a review of different approaches to REMs, Muthén & Asparouhov (2022; also see Asparouhov & Muthén, 2022; Muthén & Asparouhov, 2023) extended typical SEMs of REM data by addressing what they referred to as contemporaneous (lag0) effects that might challenge the conclusions based on CLPMs and RI-CLPMs. Although we retain Muthén and Asparouhov’s terminology of contemporaneous effects, we also note that contemporaneous effects are variously referred to as instantaneous, simultaneous, or non-recursive effects and are distinguished from recursive models with no feedback loops between variables (see Paxton et al., 2011). Muthén and Asparouhov noted that their contemporaneous approach had rarely been used (e.g., Greenberg & Kessler, 1982; Ormel et al., 2002), and contrasted CLPMs based on traditional (lag1) cross-lagged with their models with contemporaneous (lag0) effects. They explored these models with simulated and real data, using new options incorporated into the Mplus statistical package. In their discussion of CLPM designs, they noted that the time interval between waves is a critical unresolved issue (see Dorman & Griffin, 2015). Thus, concerning longitudinal panel models, Muthén & Asparouhov (2022; also see Muthén & Asparouhov, 2023) argued that “Cross-lagged effects may be less realistic with long time intervals and may call for allowing contemporaneous (lag0) effects” (p. 6). In this sense, contemporaneous effects might represent the effects of unobserved events between the previous and current waves rather than truly instantaneous effects occurring in the same instance. Although models with both lag1 reciprocal paths and lag0 contemporaneous paths are not identified with only two waves of data, they proposed these models can be identified with three (and preferably more) waves.
Muthén and Asparouhov (Slide 12, 2022; also see Muthén & Asparouhov, 2023) focused on three models (see Fig. 1). Here, we refer to these as the traditional crossed-lagged panel model (CLPM with lag1 reciprocal paths but no lag0 contemporaneous paths), pure contemporaneous panel model (PCPMs) with lag0 contemporaneous reciprocal effects but no lag1 reciprocal paths, and “contemporaneous and cross-lagged panel model” (CCLPM); the CLPM extended to include both contemporaneous and cross-lagged reciprocal effects (with lag1 reciprocal paths and lag0 contemporaneous paths). However, their focus was mainly statistical and heuristic, introducing SEM approaches to test contemporaneous reciprocal effects. Thus, their models were fully manifest (with no multiple indicators to control measurement error), and all included random intercepts (global trait factors, e.g., RI-CLPMs but no CLPMs without RIs). Furthermore, none of their models included lag2 effects or incorporated covariates. In our substantive-methodological synergy, we extend their framework to incorporate these features. Importantly, we highlight substantive issues based on self-concept theory (e.g., Marsh, 2006), integrating them into developing research hypotheses, advancing statistical models, and interpreting results—a substantive-methodological synergy.
Muthén & Asparouhov’s (2022; also see Muthén & Asparouhov, 2023) conclusions about the usefulness of contemporaneous effect models were rather pessimistic. Across diverse applications, they found that their critical models (Fig. 1) could not be readily differentiated in terms of the number of variables and, particularly, goodness-of-fit and argued that some models were formally equivalent. Furthermore, it was difficult to distinguish between models positing lag1 reciprocal effects or lag0 contemporaneous effects, even for the many models that were not formally equivalent. Therefore, they recommended researchers report the results from competing models and focus on the juxtapositions of results from the different models. Furthermore, because convergence problems were common, they also noted the need to consider alternative and more parsimonious versions of these models (e.g., constraining non-significant parameters to be zero and invariant over time). Here, we extend their study methodologically and substantively.
Methodologically, we fit different CLPMs with latent variables (with multiple indicators) and measurement factors (i.e., the X and Y factors in Figs. 2 and 3), incorporating lag2 (as well as lag0 and lag1 effects), and evaluate different approaches to controlling covariates. Substantively, we draw on established ASC theory (e.g., Marsh, 2006) to derive research hypotheses and questions and interpret the results. Model evaluation and interpretation should be based on more than simply goodness-of-fit. Hence, we differentiate alternative models based on substantive interpretations as well as goodness-of-fit. Thus, if interpretations of alternative models each support a priori hypotheses based on theory and prior research, then conclusions should be based on the juxtaposition of different results rather than selecting a single “best” model based on goodness-of-fit. Indeed, our approach is consistent with Muthén and Asparouhov’s recommendation to juxtapose the results of the different models.
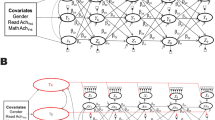
Alternative approaches to controlling for covariate effects in reciprocal effect models (REMs) positing relations between math self-concept (the X factor) and math achievement (the Y factor) over five annual waves of data. Note. See Fig. 2 for an explanation of the variables. Alternative 5 is a traditional random intercept approach, including paths leading from covariates to the global trait factor (Tx and Ty) and paths from the global trait factors to the measurement factors (Xs and Ys). In Alternatives 3 and 4, paths from the covariates lead directly to the measurement factors (i.e., their effects are not mediated by the T factors). For this alternative, it is possible to test the invariance of the covariate effects over time by fixing the effects to be invariant or not. Although we have shown this alternative in combination with random intercepts, testing this approach can be applied to models without random intercepts
In Fig. 1, we also introduce a “hypothetical” model with additional hypothetical waves falling somewhere between the actual data waves (i.e., wave 1 + t, falling between waves 1 and 2; wave 2 + t, falling between waves 2 and 3). This model cannot be tested because the additional waves are hypothetical and do not exist. Nevertheless, the model suggests that what would be interpreted as contemporaneous effects might actually represent the proximal effects of one or the other variables that have occurred between the data waves included in the design. Thus, contemporaneous effects might not reflect truly “instantaneous” effects, but merely the proximal effects of the variables occurring between the data waves. Responding to a similar concern, Muthén & Asparouhov (2023, p. 42) note that “There may truly be a distinct time lag but one that is much shorter than that of the interval between measurements so that the contemporaneous model is an approximation to a model with lag somewhat greater than zero.” This could possibly be tested with new data collections using alternative designs, including increasingly shorter time waves, but this may not be feasible.
However, even if contemporaneous effects are not genuinely instantaneous, the results provide important information about whether the design is based on the most appropriate time intervals or even whether one specific time interval is appropriate for both variables being considered. Thus, for example, are the effects of achievement on ASC more fast-acting than the effects of ASC on achievement? This is a critical consideration, as the length of the time interval between waves constitutes an essential consideration that has been given insufficient attention in CLPM studies. From this perspective, tests of contemporaneous (lag0) effect in CLPMs are heuristic and offer a practical sensitivity analysis of whether the research design is based on appropriate time intervals. Significant lag0 effects might not represent true instantaneous effects, but they might suggest considering the appropriateness of the time interval used.
The Present Investigation
Our study is a substantive-methodological synergy, extending the application of new and evolving statistical methodology in a way that has substantively important implications for theory, policy, and practice (Marsh & Hau, 2007). Substantively, our focus is on the REM predictions relating to math self-concept (MSC) and math achievement (MACH) across the five compulsory school years (Years 5–9) in the German secondary school system. Methodologically, we integrate and extend methodological advances introduced by Marsh et al. (2022; Pekrun et al., 2023) with newly proposed contemporaneous effects models proposed by Muthén & Asparouhov (2022; also see Muthén & Asparouhov, 2023).
In pursuit of these issues, we chose what we judged to be the strongest database relating MSC and MACH across secondary school years to juxtapose traditional REMs with lag1 effects, evolving models with lag2 and random intercepts (RIs), and new models with contemporaneous (lag0) effects. The Project for the Analysis of Learning and Achievement in Mathematics (PALMA; Bardach et al., 2023; Marsh et al., 2016a, 2016b, 2016c; Marsh et al., 2017; Marsh et al., 2018a; 2018b; Pekrun, 2006; Pekrun et al., 2007, 2017, 2019; Pekrun et al., 2023) is a longitudinal, large-scale study probing the development of math achievement and its basis across secondary school years. Although the directional ordering of MACH and MSC has been a component of earlier PALMA research, previous studies have not applied contemporaneous effects models. Thus, PALMA is well-suited for contrasting CLPMs, RI-CLPMs, and their extensions with newly proposed REMs of contemporaneous effects.
Cross-Lagged Panel Models: Lagged (Lag1 and Lag2) and Contemporaneous (Lag0) Effects
Here, we extend the contemporaneous effects models proposed by Muthén & Asparouhov (2022; also see Muthén & Asparouhov, 2023). We integrate these with extensions to CLPMs and RI-CLPMs proposed by Marsh et al. (2022) to test REMs of the reciprocal ordering of MSC and MACH over multiple school years. In these extended models, we posit latent rather than manifest measurement models, lag2 paths between non-adjacent school years, random intercept (global) trait factors, measurement factors, lagged and contemporaneous effects, and improved strategies to control covariates (gender; primary school math and reading achievement).
Because terminology concerning these models is inconsistent, we begin with defining terms for SEM diagrams in Figs. 2 and 3. We refer to all these models as reciprocal effect models (REMs) designed to test the reciprocal (bidirectional) effects of MSC and MACH. The models are latent in that there are multiple indicators of MSC (the five boxes for each data wave). We refer to these latent factors (X and Y factors in Fig. 2) as “measurement factors” that provide tests of the measurement model that are separate from the structural model (also see Marsh et al., 2022). Thus, the multiple MSC indicators define measurement X factors, and the X factors define the substantive MSC autoregressive factors over the five data waves (Ax1–Ax5 in Fig. 2). Although there is only one indicator of MACH, we still represent it as a single-item latent measurement and autoregressive factors. For the random intercept (RI) models, we posit global trait (RI) factors (Tx and Ty in Fig. 2) representing the grand mean over all waves of MSC (Tx) and MACH (Ty).
Relations between MSC and MACH are represented as covariances (curved, double-headed arrows) or single-headed straight lines (lag2, lag1, or lag0) paths. Lag1 paths are the effects of latent variables in adjacent waves; stability (test–retest) paths between matching variables (MSC→MSC, MACH→MACH) and reciprocal paths between non-matching variables (MSC→MACH and MACH→MSC). Similarly, lag2 paths relate variables in non-adjacent waves (e.g., from first to third, second to fourth, etc.). Lag0 paths are the pair of reciprocal paths (MSC→MACH and MACH→MSC) within each wave. Of particular relevance are the reciprocal paths (MSC→MACH and MACH→MSC) used to test REM predictions. We use the term “reciprocal effects” generically, referring to reciprocal effects based on any combination of lag1 or lag0 paths. Thus, support for REM predictions requires that at least one MSC→MACH path (lag1 or lag0) and at least one MACH→MSC (lag1 or lag0) is significant.
We focus on four basic models (Fig. 2): CLPMs (lag1 effects; no RI; no lag0 effects), RI-CLPMs (with lag1 and RI effects, but no lag0 effects), pure contemporaneous panel models with only contemporaneous effects (PCPM; RI and lag0 effects, but no lag1 cross-paths), and reciprocal models (RI-CCLPM; RI, lag0 and lag1 effects). We also posit alternatives with lag2 effects highlighted by Marsh et al. (2022; also see Lüdtke & Robitzsch, 2021, 2022). Of course, there are many possible variations of each of these models, some of which we explore. For example, the models can have lag2 effects, global trait factors representing random intercepts, or both. Most of our models assume invariance over time (metric invariance of factor loadings and invariance of cross-paths), but we relaxed these assumptions in some supplemental models. Of particular relevance, following recommendations by Muthén & Asparouhov (2022, 2023), we also test more parsimonious models in which some of the paths are constrained to zero to test a priori hypotheses or to achieve better-behaved models that circumvent convergence issues.
To avoid clutter, the correlated residuals relating responses to the same item in different waves (the boxes in Fig. 2) are not presented (see subsequent discussion), but we include them in all models. Lag2 autoregressive cross-paths are not shown in Fig. 2 because they are typically non-significant (Marsh et al., 2022), but we included them in some of our models (Table 3). For the fully reciprocal path models with lag1 and lag0 paths (CCLPMs in Fig. 2), we did not include residual covariances (RCOVs, covariances between residual variances within each wave. This follows recommendations by Muthén & Asparouhov (2022; also see Muthén & Asparouhov, 2023), indicating that these models typically do not converge. However, we included RCOVs in supplemental models, testing the robustness of interpretations (Table 3) and discussing their implications.
As shown in Fig. 3, we further extend REMs to incorporate multiple covariates. Covariate effects are modeled either by paths leading to the global trait (RI) factors (Tx and Ty in Fig. 3) or the measurement factors (X and Y factors in Fig. 3). [HM2] We juxtapose these approaches to controlling covariates, noting that their relative merits have been discussed but not assessed empirically (Mulder & Hamaker, 2021; but also see Marsh et al., 2022). The first approach requires RI models with global trait factors, but the second approach can also be applied to models without global trait factors. We illustrate these two approaches with the fully reciprocal model (lag1 and lag2 reciprocal effects in Fig. 3) but note that they can also be applied to other models.
We view these hypothesized reciprocal lag1 and lag2 effects as “causal” in the traditional Granger-causality where a cause is equated with a variable’s prospective/longitudinal effect, net of confounding factors of change (Granger, 1969). This Granger causality framework underpins all REMs of longitudinal correlational data and follows from previous research on reciprocal effects relating to academic achievement and self-concept. However, we use the more descriptive term “directional ordering” to avoid misunderstanding the terms causality and causal ordering concerning frameworks of causality presented by Pearl (2009, Causality), Rubin (Imbens & Rubin, 2015, Causal Inference), and VanderWeele (2015, Explanation in Causal Inference).
Lag0 effects that are truly instantaneous might not fit into the Granger framework of causality in the sense of being prospective effects but still qualify as predictive effects. However, to the extent that lag0 paths reflect the effects of variables occurring in the interval between data collections rather than being truly instantaneous, they are heuristic for the design of studies with more appropriate time intervals that would fit into the Granger framework of causality.
Research Hypotheses
The key issues here involve juxtaposing critical features in each model to establish the directional ordering of MSC and MACH. We offer the following research hypotheses based on our review of the substantive literature on MSC and achievement. Here, we use the term reciprocal effects generically, referring to reciprocal effects based on any combination of lagged (lag1) or contemporaneous (lag0) effects. Moreover, for increased generality, we also estimate total reciprocal effects (i.e., the sum of direct and mediated effects over multiple time lags).
Research Hypothesis 1: Lagged Effects
For alternative REMs without contemporaneous effects (i.e., REMs with lag1 effects, with some of them including lag2 effects or RIs but not lag0 effects), we hypothesize a priori that students’ MSC and math achievement (school grades from school records) will be reciprocally related. The paths from MSC in one wave to math achievement in the next wave will be significantly positive. Likewise, the paths from math achievement in one wave to MSC in the subsequent wave will be significantly positive (see Fig. 2). We hypothesize that this support will generalize over models, including random intercepts and lag2 effects. Our hypotheses are consistent with REM predictions and extensive research based on cross-lagged-panel models showing that MSC and math achievement are reciprocally related (e.g., Huang, 2011; Marsh & Craven, 2006; Marsh & Martin, 2011; also see Marsh et al., 2022).
Research Hypothesis 2: Contemporaneous Effects
Similarly, based on ASC theory and REM meta-analyses, for pure contemporaneous panel models with no lag1 reciprocal effects (RI-PCPMs), we hypothesize support for REMs. Contemporaneous paths from MSC to achievement and from achievement to MSC will be significant. However, we note that apparent lag0 effects might merely reflect lag1 effects not included in this model.
Research Hypothesis 3: Juxtaposing Cross-Lagged and Contemporaneous Reciprocal Effects
Self-concept theory (Marsh, 2006) posits that lagged effects of self-concept on achievement are mediated by processes (e.g., increased engagement, academic choice behaviors) that occur over time rather than instantaneously. Although typically not tested in REMs, this theoretical description is consistent with lagged (lag1) effects rather than contemporaneous (lag0) effects. Hence, we predict that MSC→MACH lag1 paths will be significant but leave the possibility of lag0 paths open. However, it is reasonable for MACH→MSC effects to be contemporaneous as well as lagged. In our data, MACH and MSC are collected near the end of each school year, so the effect of Lag1 achievement refers to achievement in the subsequent school year, whereas Lag0 refers to achievement in the current school year. Given the relatively long (one year) time interval between waves in the present dataset, we posit that there will be lag0 MACH→MSC effects reflecting events in the current school year after the final school grade in the previous school year has been received (see earlier discussion of the hypothetical model in Fig. 1). These lag0 effects might reflect events that have taken place following the last round of data collection (e.g., feedback on academic performance in the current school year; Marsh, 2006). However, we emphasize that these a priori hypotheses based on self-concept theory are reasonable, as are the proposed tests of these hypotheses. However, as is typically the case, the interpretation of empirical findings concerning a priori hypotheses is based on many explicit or implicit assumptions that might qualify support. This is particularly true for tests of lag0 paths that have not previously been considered in applied REM studies (see Muthén & Asparouhov, 2023). In this sense, we see tests of hypothesized lag0 paths as heuristic and providing a sensitivity test for critical assumptions that are usually ignored in panel model studies.
Furthermore, we leave open the question of whether there are also lag1 MACH→MSC effects from one school year to the next. Hence, we test whether there will be contemporaneous (lag0) paths, lagged (lag1) reciprocal paths, both (lag0 and lag1 reciprocal effects), or neither (i.e., MSC and MACH are not causally related). Significant contemporaneous (lag0) or lagged (lag1) reciprocal paths support REM predictions as long as significant paths represent both ASC→ACH and ACH→ASC paths. Also, following Muthén & Asparouhov’s (2022, 2023), we note that models with both lag0 and lag1 effects might have convergence issues. Hence, exploring alternative and more parsimonious models of these effects is important.
Research Hypothesis 4: Extended Models Including Covariates and Temporal Invariance of Their Effects
A critical issue for REMs is how best to control for covariates that may or may not be fixed and may have more or less stable effects over time. The RI models can potentially control fixed unmeasured covariates whose effects are stable over time. However, the RI model is based on strong modeling assumptions (e.g., no nonlinear effects) to identify these unmeasured covariates’ effects. Importantly, these assumptions are not easily tested and might overcorrect the effects of interest (i.e., the cross-lagged effect) if the model is misspecified (e.g., Lüdtke & Robitzsch, 2021, 2022). Furthermore, REMs with lag2 effects may be stronger for controlling for time-varying covariates (or fixed covariates whose effects vary over time), as compared with REMs only including lag1 effects. The lag2 effects help adjust for the effects of unmeasured confounders but do not rely on the RI models’ strong assumptions, some of which are not easily testable (see VanderWeele et al., 2020). Thus, RI and lag2 models are based on different assumptions, address different questions, and offer alternative perspectives on the control of covariates. From this perspective, Marsh, Pekrun, et al. (2022, 2023) argue that juxtaposing these competing models and the generalizability of conclusions based on them is valuable. Here, we explore alternative approaches for controlling fixed covariates and assessing whether their effects vary over time. Nevertheless, based on REM meta-analyses, we predict a priori that the pattern of results will support the robustness of REM predictions (and Research Hypotheses 1–3) over alternative approaches to handling covariates. Here, we focus on testing the effects’ robustness when controlling covariates.
Method
Sample
In our study, we used data from PALMA (Project for the Analysis of Learning and Achievement in Mathematics; see Frenzel et al., 2009; Marsh et al., 2018a, 2018b, 2022; Murayama et al., 2016; Pekrun et al., 2007, 2017, 2019, 2023), a comprehensive longitudinal investigation focusing on the development of math achievement throughout secondary school in Germany. The Data Processing and Research Center of the International Association for the Evaluation of Educational Achievement (IEA) conducted the sampling and assessments. Sampling was carried out in secondary schools in Bavaria, ensuring representativeness in terms of student demographics such as gender, urban or rural location, and socioeconomic status (SES), as detailed by Pekrun et al. (2007).
The dataset comprises five measurement waves covering Years 5 to 9, including school grades from the final year of primary school (Year 4). Questionnaires were administered to students during the first two weeks of July, near the conclusion of each academic year. Based on their performance in primary school, students (N = 3370; 50% girls; mean age = 11.7 at Year 5, SD = 0.7) were allocated to one of three school tracks: Gymnasium (high-achievement: 37%), Realschule (middle-achievement: 30%), or Hauptschule (low-achievement: 33%). Trained external test administrators conducted all assessments in the students’ classrooms. Participation in the study was voluntary, with parental consent secured for all students. Agreement to participate rates were remarkably good: 100% agreement among schools and over 90% among students at each data wave. Consequently, the final sample closely mirrored the intended sample and represented the broader population accurately (Pekrun et al., 2007). We anonymized responses, ensuring participants’ confidentiality.
Measures
We measured MSC in five secondary school Years (5–9) using the same six items and a 5-point Likert scale: “not true,” “hardly true,” “somewhat true,” “largely true,” or “absolutely true.” Coefficient alpha estimates of reliability were all substantial in each year (Year 5 α = 0.88; Year 6 α = 0.89; Year 7 α = 0.89; Year 8 α = 0.91; Year 9 α = 0.92). We measured MSC with the following items: “In math, I am a talented student;” “It is easy for me to understand things in math;” “I can solve math problems well;” “It is easy for me to write tests/exams in math;” “It is easy for me to learn something in math;” “If the math teacher asks a question, I usually know the right answer.” Students’ achievement was based on school grades (math in Years 4–9; German in Year 4). We obtained end-of-the-year final grades from school records. For present purposes, we treated gender and primary school grades (from Year 4) as covariates.
Statistical Analyses
We performed analyses with Mplus (Muthén & Muthén, 1998-2017, 8th edition) using the robust maximum likelihood estimator (MLR) that is robust against many violations of normality assumptions. Like most REM studies, our focus is on direct effects. However, we also computed indirect and total effects based on Mplus’s indirect model option.
In evaluating models, we relied substantially on traditional fit indices and accepted guidelines of fit (Hu & Bentler, 1999; Marsh et al., 2005a, 2005b), the comparative fit index (CFI; 0.95 is good, 0.90 is acceptable), the Tucker–Lewis index (TLI; 0.95 is good, 0.90 is acceptable), and the root-mean-square error of approximation (RMSEA;0.06 is good, 0.08 is acceptable). We supplemented these traditional fit measures with the Akaike information criterion (AIC), which is more closely related to the chi-square statistic (Muthén & Muthén, also see Marsh et al., 2005a). However, following Marsh et al. (2004) and others, we emphasize that the interpretation of the appropriateness of a model should not be based solely on goodness-of-fit.
Missing Data
Many students had missing data for at least one data-collection wave, due largely to students being absent or changing schools, as is typical in large longitudinal field studies. Across the five waves, 38% participated in all five waves (i.e., Years 5–9). However, 9%, 19%, 15%, and 19% participated in four, three, two, or one of the assessments, respectively.
We included all students with at least one data wave and employed full information maximum likelihood (FIML) estimation. FIML yields reliable and unbiased estimates for missing values, even in the presence of a substantial number of missing values, particularly in extensive longitudinal studies (Jelicić et al., 2009). Specifically, as highlighted in seminal discussions of missing data (e.g., Newman, 2014), FIML operates under the assumption of missing-at-random (MAR). This assumption allows for missingness to be conditional on all variables included in the analyses but independent of the values of variables that are missing. Consequently, missing values can be related to the values of the same variable collected in different waves in a longitudinal panel design. This data characteristic diminishes the likelihood of serious violations of the MAR assumption, as the primary instance of not-MAR occurs when missingness is linked to the variable itself. Therefore, the presence of multiple waves of parallel data serves as robust protection against such violations. Moreover, the suitability of FIML is reinforced by evidence supporting the invariance of parameter estimates over time, as discussed subsequently in the context of invariance constraints.
Transparency and Openness
The sample included all students responding to our survey, and there were no exclusions (see discussion in the “Missing Data” section). We analyzed the data using the Mplus statistical package (Muthén & Muthén, 1998-2017, 8th edition), and the Mplus code is presented as part of supplemental materials. Data are available by emailing the first author. This study’s design and its analysis were not pre-registered.
Preliminary Analyses: Measurement Model, Longitudinal Invariance, and Covariates
We began with a series of measurement models testing invariance over time (Marsh et al., 2014; Marsh et al., 2016b; Meredith, 1993; Millsap, 2012): configural (no invariance constraints), metric (factor loading invariance), and scalar (intercept invariance). We based these models on responses to 35 indicators—6 MSC items and one math school grade in each of five waves (i.e., 7 indicators × 5 waves). We standardized (Mn = 0, SD = 1) all MSC items to a common metric based on Year-5 responses (wave 1, the first year of secondary school). Following Marsh et al. (2013), we included in our a priori model correlated uniquenesses relating residual variances for the same item measured at different waves (for further discussion, see Marsh & Hau, 1996; Joreskog, 1979). As expected, the measurement model not including correlated uniquenesses provided an acceptable fit (RMSEA = 0.031, CFI = 0.965, TLI = 0.960; see MM0 in Table 1), but one that was poorer than other measurement models. The configural invariance model (MM1) with invariance constraints but correlated uniquenesses provided an excellent fit to the data (RMSEA = 0.020, CFI = 0.988, TLI = 0.984). The metric invariance model (MM2) with factor loading invariance also resulted in an excellent fit (RMSEA = 0.020, CFI = 0.986, TLI = 0.983). In the scalar invariance model (MM3), the intercept invariance constraint resulted in a slightly poorer fit (RMSEA = 0.023, CFI = 0.982, TLI = 0.979) but one that was still excellent in relation to traditional guidelines. The measurement models show that the factor structure is well-defined and generalizes over the five data waves—the first five years of secondary school.
Table 2 is a latent correlation matrix; correlations among the 15 factors (MSC and MACH in each of the five waves) and the three covariates. MSC and MACH demonstrate high stability in test–retest correlations over the five waves. For example, the average lag1 correlations (i.e., test–retest correlations in adjacent waves separated by one year) for matching traits is r = 0.71 (0.68–0.78) for MSC and 0.64 (0.59–0.69) for math achievement. Indeed, Year 5 factors are significantly correlated even with Year 9 factors for MSC (r = 0.50) and school grades (r = 0.45).
Our primary interest in covariates (gender and school grades from the end of primary school) is incorporating them into our various REMs. Boys have consistently higher MSCs, but there is little gender difference in math achievement. However, at the end of primary school, girls have higher verbal achievement, and boys have higher math achievement. In subsequent years, primary school math grades consistently correlated highly with math achievement and MSC. Compared to primary school math grades, primary school reading grades were less positively correlated with math achievement and were almost uncorrelated with MSC. These results demonstrate that primary school grades provide particularly strong covariates to control achievement levels during the subsequent five secondary school years.
Results
In Tables 3, 4, and 5 we present a wide variety of models incorporating various combinations of features illustrated in Figs. 2 and 3 (also see earlier discussion but also preliminary analyses of the measurement model). For present purposes, our focus is the effects of these different features on goodness-of-fit and how they influence particularly the lag1 reciprocal paths and lag0 contemporaneous paths. For simplicity of presentation, we impose invariance constraints over waves (also see earlier discussion of invariance of the measurement model in the “Preliminary Analyses: Measurement Model, Longitudinal Invariance, and Covariates” section). Thus, for example, the four paths representing lag1 MSC→MACH over the five waves are constrained to be equal so that a single estimate can represent them. However, we subsequently relax this invariance constraint to evaluate its impact on our results.
Traditional CLPMs (Research Hypothesis 1)
CLPMs Without Random Intercepts
As expected, the CLPM (CLPM-M1 in Table 3 with no lag2 effects or RI factors) provides the worst fit, but it is still excellent using traditional guidelines (RMSEA = 0.024; CFI = 0.975; TLI = 0.972). In support of the hypothesized REM (Research Hypothesis 1), both lag1 reciprocal paths are positive and highly significant: MSC→MACH = 0.128 (SE = 0.011) and MACH→MSC = 0.102 (SE = 0.011). Following Orth et al. (2022), we interpret these effects as medium (greater than 0.07) or large (greater than 0.12). However, the critical question is how the inclusion of additional features improves model fit, and changes support REM predictions.
CLPMs with Random Intercepts
The inclusion of lag2 paths (CLPM-M2 and M3), global trait (RI) factors (RI-CLPM-M1), or both lag2 paths and RI factors (RI-CLPM-M2 and M3) led to marginal improvements in fit. Critically, however, each model supported REM predictions more strongly than the traditional CLPM-M1. For example, the critical MSC→MACH was 0.128 in CLPM-M1 but higher in the subsequent models (0.129–0.145). Similarly, MACH→MSC was 0.102 in CLPM-M1 but higher in the subsequent models (0.109–0.125). Thus, stronger statistical models, including lag2 paths, random intercepts, or both, all resulted in stronger support for REM predictions. Consistent with previous research, eliminating lag2 reciprocal paths (but retaining lag2 stability paths; CLPM-M3 and RI-CLPM-M3) did not affect fit but resulted in marginally weaker lag1 reciprocal effects. In summary, all the traditional CLPMs and RI-CLPMs provided an excellent fit to the data and good support for CLPMs. In alternative models, most reciprocal lag1 effects were large (or at least medium) in size.
Contemporaneous Effects: Alone or in Combination with Lagged Effects
Contemporaneous Panel Models
We begin with the two basic contemporaneous effects models proposed by Muthén & Asparouhov (2022; also see Muthén & Asparouhov, 2023). The first (RI-PCPM in Table 3 and Fig. 2) is a pure contemporaneous panel model with lag0 contemporaneous effects but no lag1 reciprocal paths and no lag2 paths. RI-PCPM-M1’s fit was similar to traditional CLPMs, but the lag0 paths in support of REM predictions were much stronger than the associated lag1 effects in previous models: MSC→MACH = 0.324 (SE = 0.053) and MACH→MSC = 0.426 (SE = 0.070). The inclusion of lag2 stability paths (RI-PCPM-M2) improved the fit marginally but reduced the sizes of lag0 paths: MSC→MACH = 0.254 (SE = 0.045) and MACH→MSC = 0.381 (SE = 0.061).
CLPMs with Contemporaneous and Lagged Effects (RI-CCLPMs)
The second contemporaneous model (RI-CCLPM in Table 3 and Fig. 2) is a fully reciprocal effects model with lag0 contemporaneous paths and lag1 reciprocal paths. RI-CCLPM-M1’s fit was similar to the traditional REMs and RI-PCPMs. RI-CCLPM-M1 resulted in one significant lag1 reciprocal path (MSC→MACH) and one significant lag0 reciprocal path (MACH→MSC). These results support REM predictions and are consistent with self-concept theory but present a more complicated picture than the CLPM and PCPM models. Nevertheless, although the RI-CCLPM-M1 terminated normally (i.e., did not result in nonpositive definite matrices or out-of-range values) and had good fit indices, the multiple R squared values were undefined (see related discussion by Muthén & Asparouhov, 2022, 2023). Also, the substantially larger SEs dictate caution in the interpretation of results. Muthén & Asparouhov (2022, 2023) suggested constraints to resolve this issue that we implemented (i.e., non-duality constraints). Still, this RI-CCLPM-M1x in Table 3 resulted in a “boundary condition” in which an offending parameter (the lag0 MSC→MACH path) was estimated to be zero, and the fit was marginally poorer (technically, this was an improper solution, suggesting caution in interpretation).
Interestingly, when we added lag2 effects, the model (RI-CCLPM-M2) was well-defined. Like the first model (RI-CCLPM-M1) and consistent with Research Hypothesis 3, RI-CCLPM-M2 resulted in one significant lag1 reciprocal path (MSC→MACH) and one significant lag0 reciprocal path (MACH→MSC). However, even the RI-CCLPM-M2 solution was not ideal in that some SEs were large, again suggesting that the results should be interpreted cautiously. Thus, following Muthén & Asparouhov’s (2022, 2023) recommendations, we pursued alternative models to evaluate the robustness of the parameter estimates.
In additional models (RI-CCLPM-M3 to M5), we tested more parsimonious variations of the pure contemporaneous model, constraining various parameters to be zero (e.g., non-significant paths in RI-CCLPM-M1 and M2). All these models resulted in proper solutions and fit the data well. We chose RI-CCLPM-M5 as the “best” model based on parsimony, fit, and theory. Like all these models, RI-CCLPM-M5 resulted in one significant lag1 reciprocal path (MSC→MACH = 0.167, SE = 0.021) and one significant lag0 reciprocal path (MACH→MSC = 0.473, SE = 0.014). Indeed, there was relatively little difference in the fit of these models, and the pattern of lag0 and lag1 reciprocal effects was consistent over all reciprocal models.
Supplemental Models
Next, we evaluated support for the assumption made in models considered thus far, evaluating the robustness of parameter estimates of RI-CCLPM-M5 (our “best” model). In the first of these supplemental models, we eliminated the constraint that reciprocal paths are invariant over time. Eliminating this invariance constraint (RI-CCLPM-M6) led to a minimal improvement in fit (ΔCFI = 0.002, ΔTLI = 0.001, ΔRMSEA = 0.000; Table 3). In addition, the means of paths averaged over waves continued to support REM predictions (MSC→MACH = 0.152, SE = 0.021; MACH→MSC = 0.465, SE = 0.016), consistent with the other contemporaneous and cross-lagged models (e.g., RI-CCLPM-M5; also see the table note in Table 3 where we report effects for each wave separately).
Next, we evaluated the effects of adding to RI-CCLPM-M5 the covariances between the residual variance components (RCOVs) within each wave (RI-CCLPM-M7 in Table 3). Their addition did not affect goodness-of-fit. However, both the lag1 effect (MSC→MACH = 0.142, SE = 0.023) and the lag0 effect (MACH→MSC = 0.351, SE = 0.059) became marginally smaller, and their standard errors became marginally larger. Based on goodness-of-fit, we would typically reject RI-CCLPM-M8 (with RCOVs), retaining the more parsimonious RI-CCLPM-M5 (without RCOVs). However, we return to this issue in subsequent discussions of the ambiguous role of RCOVs in contemporaneous effects models.
Finally, we tested CCLPM-M5, the RI-CCLPM-M5 without random intercepts (but retaining all other parameters, including lag2 stability effects emphasized by Marsh et al., 2022; also see Lüdtke & Robitzsch, 2021, 2022). There was a noticeable decline in fit and weaker support for REM predictions. Thus, compared to RI-CCLPM-M5, reciprocal effect paths were smaller in CCLPM-M5 (0.332 vs. 0.473 for MACH → MSC; 0.117 vs. 0.167 for MSC→MACH). Hence, as observed with CLPMs and RI-REMs, adding controls for unobserved covariates in the RI-CCLPM-M5 compared to CCLPM-M5 resulted in a better fit to the data and stronger support for the generalizability of REM predictions. Nevertheless, we again emphasize that this control of unobserved covariates in RI models is based on strong (in part untestable) assumptions and that a better fit does not necessarily mean that the model successfully controlled the effects of unmeasured (time-invariant) confounders.
In summary, all the contemporaneous effects models support REM predictions of reciprocal effects of MSC and MACH—lag1 effects from MSC to MACH and contemporaneous lag0 effects from MACH to MSC.
Total (Direct and Indirect) Effects
Implicit in reporting CLPMs is a focus on direct (lag1) effects between adjacent waves. For contemporaneous effect models, we extend this to include direct (lag0) effects between variables in the same wave. However, particularly for longitudinal data, it is also important to consider total and indirect effects. For CLPM designs and all the models considered here, indirect effects have the same “causal” status as direct effects. For selected models, we evaluated the indirect and total effects (Table 4).
CLPM-M1’s total indirect effects (Table 4) between non-adjacent waves are substantial and marginally higher than the direct (lag1) effects between adjacent waves. For example, the direct (lag1) effect MSC1→MACH2 = 0.128 was marginally smaller than the corresponding total (lag2, lag3, and lag4) indirect effects from MSC1 (MACH3, 0.166; MACH4, 0.163; MACH5, 0.144). In contrast, RI-CLPM-M1’s direct (lag1) effects are marginally larger than those for the CLPM-M1, but the indirect effects are smaller than for the CLPM-M1.
RI-PCPM is a pure contemporaneous panel model with no lag1 reciprocal paths. The contemporaneous (lag0) effects are substantial and much larger than the corresponding lag1 effects in any CLPMs or RI-CLPMs. RI-PCPM is interesting because it has no direct lagged effects (i.e., no lag1 paths).For the fully reciprocal model (RI-CCLPM-M5 in Table 2), the interpretation is more complicated in that there are direct lag1 reciprocal paths (MSC→MACH = 0.167) and direct contemporaneous lag0 paths (MACH→MSC = 0.473). Total indirect MSC→MACH effects for lag2, lag3, and lag4 effects are all substantial. All of the lagged effects of MACH on MSC are indirect because there are no direct MACH→MSC lag1 effects. Nevertheless, these indirect effects are substantial as well. Indeed, these indirect MACH→MSC effects are larger than the total lagged effects (direct and indirect) of MACH on MSC for any other models, particularly for T > 1, as there are no contemporaneous effects at T1.
Control for Covariates
As in all non-experimental (but also experimental) designs, controlling covariates that might otherwise bias the results is a critical issue in REM studies. Although we treat the introduction of covariates as potentially reducing bias, we note that the addition of covariates can possibly introduce bias (e.g., Rohrer, 2018; also see Lüdtke & Robitzsch, 2022), particularly when covariates are collected at the same time as the central variables (i.e., self-concept and achievement in this study). Hence, interpreting models that include covariates should be based on appropriate theoretical models (see Li, 2021).
For present purposes, we classify covariates as time-varying and time-fixed. Nevertheless, even time-fixed covariates can have time-varying effects (e.g., gender differences might change over school years). The best way to control covariates is to include them in the model, but we did this in different ways that have important implications. However, more worrisome are the effects of unmeasured covariates (time-varying, fixed with time-invariant effects, and fixed with time-varying effects).
Here, we evaluated the effects of three fixed covariates (math and verbal achievement from primary school and gender) but left open the question of whether their effects are time-invariant. For selected models (Table 5), we evaluated alternative approaches to controlling the three covariates. Although the covariate effects are substantively interesting (see earlier discussion of Table 2), we focus on model fit and changes in lag1 reciprocal and lag0 contemporaneous effects. We did this for selected models including CLPM-M1, CLPM-M2, CLPM-M3, RI-CLPM-M1, and RI-CCLPM-M5 (our “best” model; see Table 5).
-
Alternative 1 (no covariates) excludes the covariates, treating them as unmeasured covariates (these are the models discussed so far and reported in Table 3, providing a baseline comparison for changes associated with covariates).
-
Alternative 2 (null effects) includes the covariates but constrains all relations (paths from covariates to MSC and MACH) to be zero. Reciprocal paths are the same for Alt1 and Alt2. However, the fit indexes differ between Alternatives 1 and 2 due to the inclusion of covariates. Alternative 2 provides a basis for comparison with models where the effects of covariates are not constrained to be zero.
-
Alternative 3 (invariant effects) estimates paths from each covariate to the measurement factors (Xs and Ys in Fig. 3) but constrains them to be invariant over time. This treats covariates as fixed and having time-invariant effects.
-
Alternative 4 (covariate effects freely estimated) estimates paths from each covariate to the measurement factors but does not impose invariance of effects over time. Comparison of Alternatives 4 and 2 indexes the size of covariates effects explained by the model, whereas comparison of Alternatives 4 and 3 tests whether the effects of covariates are time-varying.
-
Alternative 5 (effects of covariates on RIs) estimates paths from each covariate to the RI (global) trait factors for models with RIs (Tx and Ty in Fig. 3). Alternative 5 is equivalent to Alternative 3 (same df, fit, and estimates). However, Alternative 5 does not test the implicit assumption that covariate effects are invariant over time (i.e., it does not allow the comparison of Alternatives 3 and 4), and it cannot be used with models not incorporating RIs.
Regarding goodness of fit, all four models that included covariates showed clear evidence that the covariates are related to MSC and MACH (i.e., comparison of Alternative 2 with Alternatives 1 and 4; see Table 5). Alternative 4’s fit was best. However, in support of the invariance over time, the more parsimonious Alternative 3 models fit almost as well (e.g., all ΔCFI and ΔTLI < 0.005). Hence, there is reasonable support for the assumption in the present RI models that the effects of covariates are time-invariant.
Importantly, including covariate effects (Alternatives 3 and 4 models in Table 5) had relatively little impact on the lag1 and lag0 reciprocal paths. This suggests that our interpretations of models without covariates were relatively unbiased and that introducing covariates did not create any new biases. In most cases, the paths were relatively unchanged or marginally higher (e.g., RI-CLPM-M1); controlling covariates never led to substantial reductions in the sizes of lag1 and lag0 reciprocal paths. In summary, support for the REM predictions (and Research Hypothesis 4) is robust relative to the inclusion of these covariates.
Discussion
Our study is a substantive-methodological synergy (Marsh & Hau, 2007), applying evolving statistical practice to substantially important issues with critical implications for theory, policy, and practice. In pursuit of this overarching aim, we offer the following discussion, summarizing the results, substantive and methodological implications, and directions for further research.
Substantive Implications
Summary of Main Findings
All our models support REM predictions. Self-concept theory and much research show that MSC is partly formed based on MACH (MACH→MSC). Hence, the MSC→MACH path is critical for testing REMs. The lag1 reciprocal and lag0 contemporaneous paths for all the models provide good support for REM predictions. For all CLPM models, one and only one MSC→MACH path (i.e., a lag1 cross-path or a contemporaneous path) and one and only one MACH→MSC path are significant and meaningfully large. Nevertheless, the models differ substantially in the sizes of reciprocal paths.
CLPM-M1 (with RI and no lag2 or contemporaneous effects) provides the weakest support for REM predictions. However, even in this model, both reciprocal paths are in the expected direction and medium or large relative to Orth et al.’s (2023) criteria. RI-REM-M1’s fit was similar to REM-M2, but both lag1 reciprocal paths were stronger. For all CLPMs and RI-CLPMs (with no contemporaneous effects), all reciprocal paths are significant and greater than 0.10. Although MSC→MACH effects (0.104 to 0.145) tend to be larger than MACH→MSC effects ( 0.102 to 0.125), the differences are not substantial. These results support a priori REM predictions.
The fit of pure contemporaneous panel models (with lag0 but no lag1 effects) was comparable to the other models. However, the lag0 reciprocal paths are much higher (all greater than 0.25) than the corresponding lag1 estimates in CLPMs and RI-CLPMs. There were some problems in estimating the fully reciprocal (RI-CCLPM) models with both lag1 and lag0 effects. Interestingly, adding lag2 effects resolved this issue and resulted in better-behaved models. We then explored more parsimonious versions in which we constrained some of the non-significant paths to be zero. These versions fit the data as well as the RI-CCLPM-M1 and behaved better (e.g., in terms of the size of standard errors). Indeed, our final model (RI-CCLPM-M5 in Table 3) provides the strongest support for REM predictions of any of the models—particularly if indirect effects (Table 4) are also considered. Consistent with self-concept theory (Marsh, 2006) and Research Hypothesis 3, all the fully reciprocal models resulted in significant MSC→MACH paths (for lag1 but not lag0) and significant MACH→MSC paths (for lag0 but not lag1).
Substantive and Theoretical Implications
For present purposes, we discuss implications concerning academic self-concept theory but note that the issues generalize to all other CLPM studies of reciprocal ordering used in many disciplines. Theoretically, it is reasonable that MACH→MSC effects evolve over a shorter time span than MSC→MACH effects. Positive and negative MACH results are likely to impact MSC immediately. Thus, it is also reasonable that lag0 contemporaneous reciprocal paths are larger than lag1 reciprocal paths. However, this leaves open the question of whether there are also lag1 MACH→MSC effects from previous MACH. Our results suggest this is not the case, as lag1 MACH→MSC effects are consistently non-significant in all the fully reciprocal contemporaneous models.
Relatedly, it is theoretically reasonable that MSC→MACH effects evolve over a longer time span. Thus, changes in MSC are unlikely to have immediate effects on MACH. Instead, intervening processes must mediate MSC effects (e.g., academic choice, emotions, engagement, repeated effort, and time investment; Marsh, 2006; Pekrun, 2006). From this perspective, it is reasonable that there are lag1 effects but not lag0 effects. However, we note that lag2 MSC→MACH effects are non-significant. Hence, the MSC→MACH effects are primarily based on achievement in the previous school year—not instantaneous, but also not based on achievement from 2 years ago.
MACH→MSC effects are contemporaneous. However, whether sufficiently short intervals would result in significant lag1 reciprocal effects instead of (or in addition to) these lag0 effects remains an open question. Furthermore, it leaves the philosophical question of whether contemporaneous MACH→MSC effects are instantaneous. However, students must first perceive MACH and then translate this into an MSC self-perception; this might include various cognitive processes such as social comparison and causal attributions (e.g., attributions of MACH to ability). Hence, truly instantaneous effects seem unlikely.
For MSC→MACH, the effect clearly is not instantaneous. The 1-year interval might be appropriate because the lag0 effect was non-significant in the RI-CCLPM. Nevertheless, we leave open the question of whether lag1 effects would be smaller or larger with a shorter interval. However, it is not likely that shorter time intervals would increase the size of lag0 effects. Indeed, we argue that contemporaneous lag0 MSC (MACH effects that were truly instantaneous) would be inconsistent with the self-concept theory.
Appropriate Time-Lag Intervals in Cross-Lagged Panel Designs
The appropriate length of the time-lag interval in cross-lagged panel studies is a serious, largely unresolved problem (Dorman & Griffin, 2015; Gollob & Reichardt, 1987; Kuiper & Ryan, 2018). In particular, the failure to find reciprocal lagged effects for a given interval provides no basis for concluding that lagged effects would not be evident for other intervals. Common sense and real-world examples (e.g., the appropriate time interval for testing the effects of taking aspirin and reducing headache pain) make it clear that lagged effects might exist for appropriate intervals but not for intervals that are either too long or too short. We address these issues with contemporaneous effect models.
It is also important to re-emphasize that the contemporaneous models do not require that effects are truly instantaneous but only that the contemporaneous paths reflect proximal effects of occurrences subsequent to the previous wave of data. Particularly for annual data collections in educational settings, as in the present investigation, this merely means that the contemporaneous effects reflect occurrences in the current school year beyond those from the previous school year. In this sense, it might be more appropriate to think of the contemporaneous effects to reflect “proximal” effects and the lagged effects to reflect “distal” effects (e.g., Singh et al., 2023). Indeed, if a sufficiently large number of data waves with short intervals are analyzed with intensive longitudinal modeling, contemporaneous effects might disappear altogether. Nevertheless, testing lag0 effects in CLPMs has potentially important implications for the largely unresolved problem of the “ideal” time interval between data waves (Boele et al., 2023; Pekrun, 2023).
The contemporaneous and cross-lagged effects model (CCLPMs in Fig. 2) has both lagged and contemporaneous effects. The traditional lagged effects reflect the distal reciprocal effects that are likely idiosyncratic to a particular time interval. However, the contemporaneous effects provide estimates of reciprocal effects within each wave that might not depend on temporal ordering. These proximal reciprocal effects reflect processes occurring within the same time interval. In the present investigation based on annual waves at the end of each academic year, we interpret the contemporaneous MACH→MSC effect to reflect processes unfolding within the academic year (subsequent to data collection from the previous year) not captured by the distal effects. Thus, depending on the interval length and its appropriateness for the variables under consideration, evidence supporting reciprocal effects might be evident in either lagged or contemporaneous effects (see related discussion by Singh et al., 2023). For example, if the time interval is so long that lagged reciprocal effects are so attenuated as to become undetectable, the contemporaneous reciprocal effects might remain detectable. Thus, the interpretation of reciprocal effects should be based on the juxtaposition of different models positing lagged and contemporaneous reciprocal effects and the length of the time interval. Hence, the application of contemporaneous effects models provides an important tool to address the problem of the appropriate time interval.
Furthermore, there is sometimes an implicit assumption that some ideal interval is appropriate for all lagged effects in any particular cross-lagged-panel study (e.g., MSC→MACH and MACH→MSC in our study). However, as we showed, the new framework integrating multiple reciprocal effects (lagged and contemporaneous) enables testing which time interval matters most for each construct. In the present context, our results suggest that the 1-year interval is too long for MACH→MSC effects but might be more appropriate for the MSC→MACH effects. Thus, not only do we question the suggestion that there is a single ideal interval in a particular study, but we further suggest that the most appropriate interval might differ for MSC→MACH and MACH→MSC effects. This finding is essential to ASC studies but also has general implications for CLPM studies.
Methodological Implications
Goodness-of-Fit
Evaluating the measurement models’ goodness-of-fit and invariance over time is essential. Unless there is good support for at least configural invariance, applying any of the REMs considered here is dubious. Furthermore, unless there is reasonable support for metric invariance of the factor structure over time, then constraining critical autoregressive parameters to be invariant over time may be problematic (but see Robitzsch & Lüdtke, 2023). Metric invariance is particularly relevant for models positing RIs (RI-CLPMs, RI-PCPMs, and RI-CCLPMs) but also complicates the interpretation of CLPMs without random intercepts. Hence, REM studies should always begin by testing measurement models for ASC (and achievement when multiple indicators are available) and the invariance of the factor structure over multiple time waves. This presupposes that studies collect multiple indicators of each construct and incorporate them into their REMs. Establishing a good measurement model with at least configural invariance over time should be a starting point for all REMs.
Because the basic REM (CLPM-M1 in Table 3) is nested under the corresponding RI model (RI-REM-M1), the RI-REM-M1 will routinely fit better (except in unlikely situations when all global trait factors in the RI models have zero variance; Hamaker et al., 2015; 2023). However, model selection should also be based on theory, the purposes of the study, and the interpretation of the results (Marsh et al., 2022, 2023; also see Asendorpf, 2021; Orth et al., 2021). Furthermore, the improved fit of RI models due to the addition of RI global trait factors is similar to that of the REM with lag2 paths (CLPM-M2 in Table 3; see Marsh et al., 2022, 2023; also see Lüdtke & Robitzsch, 2021, 2022).
There are predictable differences in goodness-of-fit in the different models, but the differences are small (except for REM-M1, and even this model had an excellent fit: RMSEA = 0.024, CFI = 0.975, TLI = 0.972). For all the other models, differences in fit are tiny—particularly for indices that control for parsimony (e.g., RMSEA, 0.018 to 0.020; TLI = 0.980 to 0.984). Indeed, for the extended set of REMs considered here, there was almost no difference in the ability of different models (other than the REMs with no lag2 paths or RIs) to fit the data.
In summary, goodness-of-fit indices did not distinguish very well between alternative models positing lag1 and lag0 effects and were not very useful in selecting the “best” model. Muthén & Asparouhov (2022; also see Muthén & Asparouhov, 2023) consider goodness-of-fit as an essential starting point but similarly note that alternative models positing lag1 or lag0 effects could not be distinguished based on fit. However, evaluating the pattern of parameter estimates across different models provided a clear interpretation of the results of our study. Across all the models we considered, there was highly consistent support for REMs. For every model, one MSC→MACH path (lag1 or lag0) and one MACH→MSC (lag1 or lag0) path were significant. Furthermore, across all the fully reciprocal effects models (RI-CCLPM-M1 to M8), only the lag1 MSC→MACH path and only the lag0 MACH→MSC path were statistically significant. Particularly, as this pattern of results was consistent with a priori predictions based on ASC theory, we interpret the results as strong support for our REM predictions. However, it also represents a significant new contribution, showing that the two reciprocal effects unfold over different time intervals.
Juxtaposing Control for Covariates via Lag2 Paths and Random Intercepts
The primary structural difference between the CLPMs and RI-CLPMs is that RI-CLPMs include a stable trait factor (Tx and Ty in Fig. 2) whereas CLPMs do not. CLPMs evaluate an undecomposed between-person perspective; individual differences at each wave are related to those in subsequent waves. RI-CLPMs evaluate a decomposed between-person difference, how within-person deviations at each wave differ from a student’s stable trait, and how these within-person differences from one wave are related to those in the next wave (a within-person perspective). Thus, in CLPMs, the between-person terms reflect undecomposed between-person differences, whereas, in the RI-CLPMs, they reflect decomposed between-person differences. Neither of these models (or any others considered here) are truly within-person (idiographic) models configured separately for each person (see Marsh et al., 2022; Niepel et al., 2022; Pekrun et al., 2023; but also see Núñez-Regueiro et al., 2022).
Following Hamaker et al. (2015), many recent psychological studies argue that RI models provide more robust controls for unmeasured covariates that are fixed and have time-invariant effects. However, Marsh, Pekrun et al. (2022, 2023; also see Lüdtke & Robitzsch, 2022; Orth et al., 2021; Pekrun et al., 2023) argued that RI-CLPMs and CLPMs with lag2 paths are complementary rather than antagonistic models. Each has contrasting strengths and weaknesses concerning the control for unmeasured covariates (i.e., strong ignorability/no unobserved confounding assumptions underpinning both CLPMs and RI-CLPMs). RI models potentially control effects of unmeasured fixed covariates with time-invariant effects but are based on strong assumptions that are not easily tested (e.g., Lüdtke & Robitzsch, 2022). In particular, RI models might lead to over-correction (i.e., residualizing for the stable parts of all variables—also time-varying variables—that should not be controlled) when the assumptions are not met. However, including lag2 effects in CLPMs is a viable alternative that might be particularly useful in controlling for unmeasured time-varying covariates (VanderWeele et al., 2020). Importantly, because lag2 CLPMs and RI-CLPMS can be complementary rather than antagonistic, they can be combined in a way that is potentially stronger than using either in isolation. Here, we extended this previous research by including both lag2 stability effects and random intercepts as well as contemporaneous (lag0) effects.
Control of Covariates and Biases Associated with Omitted Covariates
We used gender and primary school achievement as covariates. These are substantively interesting (Table 2). However, we focused on controlling their effects and the consequences of not controlling them. We found that the critical reciprocal paths used to determine directional ordering in all our models were nearly unaffected by the inclusion or exclusion of these covariates. However, there is always the possibility of additional, unmeasured covariates. Thus, Hübner et al. (2023) suggested using a propensity score weighting approach based on a potentially large number of covariates. This presupposes that the appropriate covariates were measured and that covariates provide appropriate control for confounding, but the strategy warrants further investigation into a potentially serious ignorability problem in current approaches to CLPM studies.
Unmeasured covariates may manifest as fixed covariates with genuinely time-invariant effects, fixed covariates with varying effects across different waves (potentially reflecting additional, unmeasured process variables that fluctuate with time and interact with the time-invariant covariates), time-varying covariates specific to particular waves, or even auto-regressive covariates undergoing gradual or systematic changes over time. However, REM studies have given little attention to understanding the characteristics of these different covariate effects biases and their likelihood of occurrence (see Asendorpf, 2021; Lüdtke & Robitzsch, 2021; Schuurman & Hamaker, 2019 for further discussion on this matter).
In CLPMs without random intercepts, truly time-invariant covariates typically exert their strongest direct effects on the initial data wave (with potential exceptions such as gender effects that may change over time). However, compared to CLPMs and RI-CLPMs, models incorporating lag2 effects offer better control over unmeasured covariates.
For RI-CLPMs, the global trait factors largely absorb time-invariant effects of fixed covariates under appropriate assumptions. In our study, consistent with this rationale, stability and reciprocal paths in RI-CLPMs were largely unaffected by excluding covariates. However, unmeasured time-varying covariates are potentially worrisome confounders for all CLPMs (Marsh, Pekrun, et al., 2018a, 2018b, 2022; also see Lüdtke & Robitzsch, 2021, 2022; VanderWeele et al., 2020). Both lag2 and random-intercept approaches have complementary strengths and weaknesses and can be used in combination. Thus, we argue that this should not be seen as an either-or issue and recommend that researchers routinely juxtapose interpretations of models that include RIs, lag2 effects, or both.
Separating the measurement factors (the X and Y factors in Fig. 3) and the structural factors (the Axs and Ays in Fig. 3) is crucial. In particular, this allows random intercepts (the global trait factors labeled Tx and Ty in Fig. 3) to be incorporated into the measurement model rather than the structural model relating to MSC and MACH. These measurement factors are particularly relevant when covariates are included in the REMs. As shown in Fig. 3, we model covariates effects by paths either leading to the global trait (RI) factors (Tx and Ty; alternative 3 in Fig. 3) or the measurement factors (X and Y factors, Alternatives 3 and 4 in Fig. 3). Thus, the measurement factors also provide a valuable approach to incorporating covariates into REMs with no RI factors.
Furthermore, although not previously articulated (but see Marsh et al., 2022; Mulder & Hamaker, 2021), we explore the juxtaposition of these two approaches to controlling covariates in latent REMs. In particular, for RI models, the two models are equivalent (i.e., same df, goodness-of-fit, and parameter estimates) when paths from covariates to the measurement factors are constrained to be invariant (Alternative 3 in Fig. 3 and Table 5). The implicit assumption in the RI model that the effects of covariates are time-invariant is not easily tested in the first approach (Alternative 5 in Fig. 3); the critical paths can be invariant (Alternative 3) or free (Alternative 4) in the second approach. This provides a substantively important test of whether a covariate’s effects are stable over time, one easily incorporated into CLPMs, RI-CLPMs, and contemporaneous effects models.
Although it is appropriate to hypothesize the reciprocal directional ordering of self-concept and achievement are “causal” (i.e., the REM hypothesis), there typically are alternative interpretations of the results that might qualify this support. Thus, interpretations based on support for the REM hypothesis based on cross-lagged panel data rely on robust assumptions inherent in various statistical models used to test the assumptions. Here, we outline new and evolving statistical models to address this issue, particularly those related to fixed and time-varying covariates that are unmeasured and have different measurement lags. Nevertheless, the validity of causal interpretations remains susceptible to threats and might never be fully resolved with statistical models of longitudinal correlational data. However, an alternative avenue for future REM research lies in devising randomized control trials (RCTs) to rigorously test implications posited by non-experimental REM studies (e.g., Bailey et al., 2018). Thus, in a systematic review and meta-analysis, Wu et al. (2021) proposed that “Future investigation could use experimental design, quasi-experimental design, and invention strategies to directly test the causal ordering between achievement and ASC” (p. 1771).
Of particular relevance, Haney & Durlak’s (1998) meta-analysis of self-concept interventions, aligned with REM inferences, concluded that interventions specifically targeting self-concept not only significantly enhanced self-concept but also yielded positive effects on academic achievement. This experimental evidence supports the core REM hypothesis that improving academic self-concept leads to subsequent academic performance enhancement. REM research advocates for simultaneously enhancing both academic self-concept (ASC) and achievement, positing greater benefits than an exclusive focus on one construct. Expanding upon Haney & Durlak’s (1998) meta-analysis and REM research, Marsh et al. (2022) suggested that this implication could empirically test this implication through a 2 (ASC intervention or not) × 2 (achievement intervention or not) RCT design. The REM predicts that the group receiving both ASC and achievement interventions would exhibit significant advantages over groups receiving only one of the interventions. The efficacy of each intervention in isolation could be assessed in comparison to a no-treatment control group that received neither intervention. However, implementing this design is likely to encounter various complexities that may complicate the interpretation of results.
Contemporaneous (lag0) Reciprocal Paths and Covariances of Residual Variances
It is important to emphasize that CLPMs (CLPMs and RI-CLPMs) routinely posit contemporaneous relations between variables. However, they treat these as noncausal covariances between MSC and MACH residuals (RCOVs) rather than reciprocal causal effects. Because CLPMs and RI-CLPMs incorporate contemporaneous relations among factors, it is not surprising that the goodness-of-fit for these traditional models does not differ substantially from the fit of contemporaneous models. Hence, particularly as alternative models fit the data well, the critical issue is the appropriate interpretation of the results rather than goodness-of-fit. Here, we explore implications for interpreting results.
Residual variances (RVARs) have different interpretations for manifest factors and latent factors based on multiple indicators (e.g., MSC in Fig. 2). Latent factors control measurement error so that RVARs represent a state-specific shock (i.e., effects external to the system or transient processes) for a particular wave. Because these shocks might affect both MSC and MACH, CLPMs posit RCOVs. However, the RVARs confound the effects of measurement error and wave-specific shocks for manifest models. In this sense, the latent approach is stronger because it controls for measurement error and distinguishes between measurement error and shocks. However, if there are RCOVs due to wave-specific shocks to the system, these should be captured by manifest as well as latent models. Because these shocks are posited to be specific to each wave, RCOVs are freely estimated and not constrained to be invariant over time.
Contemporaneous reciprocal (lag0) models reflect the effects of MSC and MACH on each other within the same time wave. Contemporaneous models are consistent with a simultaneous model of causality in that they assume bidirectionality of effects within a given wave. However, consistent with a sequential model of causality, the contemporaneous effects can also reflect the prior effects of the variables on each other that occurred between waves, that is, short-term cross-lagged effects. The longer the time interval between waves, the more likely the reciprocal effects reflect events occurring between the waves that would be interpreted as contemporaneous effects. For purely contemporaneous panel models (i.e., PCPMs with no lag1 reciprocal effects), there is an implicit assumption that the lag0 effects capture all the meaningful bidirectional effects between these variables. For the fully reciprocal models, contemporaneous effects capture reciprocal effects occurring subsequent to the immediately previous wave of data. Including RCOVs assumes additional effects due to shocks to the system that potentially bias estimates of contemporaneous effects. However, the nature of these biases makes it challenging to predict a priori without positing specific processes and including appropriate variables representing these processes. To the extent that these shocks are really wave-specific, they are unlikely to be controlled by random intercepts.
Understandably, RCOVs are routinely included in CLPMs and RI-CLPMs. However, their interpretation in contemporaneous effect models is more challenging and depends on their putative status. If RCOVs reflect effects external to the system, their exclusion might positively bias lag0 estimates. If, on the contrary, RCOVs are conceived as reflecting contemporaneous effects of MSC and MACH, their inclusion is likely to isolate variance that should be attributed to reciprocal effects erroneously. Nevertheless, the basis of RCOVs, their interpretation, and how they influence other parameter estimates are almost always based on post hoc speculation about unmeasured variables. Furthermore, Muthén & Asparouhov (2022; also see Muthén & Asparouhov, 2023) found that fully reciprocal contemporaneous models with both RCOVs and lag0 effects typically fail to converge. This led them to recommend that they should not be routinely included. In our study, we proposed a comprise. Like Muthén & Asparouhov (2022; also see Muthén & Asparouhov, 2023), supplemental analyses of contemporaneous and cross-lagged models with RCOVs in our study did not converge. However, our best model was more parsimonious, with only two reciprocal paths—one lag1 and one lag0 (RI-CCLPM-M5 in Table 3). For this model, we were able to evaluate RCOVs in terms of goodness-of-fit and the influence of their inclusion on reciprocal paths (RI-CCLPM-M7).
Interestingly, adding RCOVs did not affect goodness-of-fit compared to the less parsimonious RI-CCLPM-M5 (with no RCOVs). Parsimony is closely related to goodness-of-fit. Traditional practice is to reject a less parsimonious model if it does make a meaningful contribution to goodness of fit—based on either formal tests of significance or subjective comparisons of indices of fit relative to a priori benchmarks (i.e., rules of thumb rather than “golden rules;” Marsh et al., 2004). Based on goodness-of-fit, the inclusion of RCOVs should be rejected. However, Marsh & Hau (1996, 1998) argued that although this practice is usually good advice, there are applications when additional parameters should be included that might bias interpretations of results if left out. They illustrated this for the inclusion of correlated uniquenesses relating to the same indicators administered on different occasions that typically lead to positively biased estimates of test–retest stability if excluded (see earlier discussion of this issue with our data). They cited Bollen and Long’s (1993, p.8) conclusion that “test statistics and fit indices are very beneficial, but they are no replacement for sound judgment and substantive expertise.”
Exemplifying this issue in our study, including four RCOVs in RI-CCLPM-M7, did not improve goodness-of-fit compared to RI-CCLPM-M5. However, their inclusion did meaningfully change the sizes of the reciprocal paths (but not their direction or pattern of significance). We argue that RCOV inclusion is important and offer the following interpretation supporting this contention. To the extent that RVARs represent shocks to the system that similarly influence both MSC and MACH, the RCOVs reflect a potential bias in interpreting reciprocal effects. Consistent with this supposition, corresponding reciprocal effects in RI-CCLPM-M7 (with RCOVs) are smaller than those in RI-CCLPM-M5 (without RCOVs). The differences appear to be meaningfully large, particularly for the lag0 MACH→MSC path: 0.473 (SE = 0.014) vs. 0.354 (SE = 0.059). Including RCOVs in RI-CCLPM-M7 did not explain any additional covariation among variables not already explained by the more parsimonious RI-CCLPM-M5. However, their inclusion allowed us to disentangle the confounded effects associated with external shocks to the system and reciprocal effects relating to MSC and MACH. Critically, the results did not change the pattern of significant reciprocal effects. Nevertheless, we recommend that RCOVs should be routinely included in REMs or at least in supplemental analyses. Even when their inclusion compromises model convergence, it might be possible to include them in more parsimonious models, as in the present investigation.
Appropriate Time-Lag Intervals in Cross-Lagged-Panel Designs—A Supplemental Sensitivity Analysis
As described earlier, the appropriate length of the time-lag interval is a critical, unresolved problem in CLPM studies and in longitudinal research, with serious substantive and methodological implications. Our study’s essential contribution is providing a new approach to address this issue. The juxtaposition of cross-lagged (lag1) and contemporaneous (lag0) effects is particularly relevant in the present investigation, where there is an a priori, theoretical basis for predicting that MACH→MSC effects are faster acting than MSC→MACH effects (see earlier discussion). More broadly, the conceptualization is relevant if the reciprocal effects are posited to unfold in time intervals that might be shorter than the interval between waves in the available data. Our new statistical models and findings provide an important new understanding of this issue. The juxtaposition of models with and without contemporaneous and cross-lagged reciprocal effects is clearly justified when there is such a strong theoretical basis concerning the relative timing of the effects, as will often be the case. However, a more general methodological question is whether researchers should routinely consider contemporary (lag0) effects even without an a priori theoretical basis.
Our response is a qualified yes—as a supplemental sensitivity analysis. On the one hand, we worry that naïve researchers will mindlessly free up contemporaneous (lag0) paths because it is easily done. Interpreting lag0 paths as causal effects in isolation is not appropriate—particularly in the absence of theoretical justifications and for the purely contemporaneous panel model (PCPM). Especially if lag1 effects are not significant in either CLPMs or CCLPMs, then the existence of significant lag0 effects provides a weak basis for claiming support for REM predictions. In particular, we do not recommend using a pure contemporaneous model (lag0 paths with no lag1, lag2, or random intercepts) in isolation. Although lag0 effects may reflect proximal reciprocal effects not identified with lag1 reciprocal effects with shorter time intervals, more work is needed on the assumptions and empirical evidence necessary to justify this conclusion.
However, the juxtaposition of results from different models considered here can provide insight into interpreting the results. Furthermore, adding lag0 paths can provide a supplemental sensitivity analysis concerning the appropriate time interval issues. For example, non-significant lag1 cross-paths would suggest no support for REM predictions. However, an alternative explanation might be that the time interval was too long, so a shorter time interval might support REM predictions. The lag0 paths provide a test for this alternative explanation. For example, if both the corresponding lag1 and lag0 paths are non-significant, then this alternative explanation is not supported. However, if lag0 paths are significant, then further research with shorter time intervals is warranted. Alternatively, suppose lag1 paths are consistently significant in CLPMs (with lag1 paths) and CCLPMs (with lag1 and lag2), but lag0 paths are non-significant. In that case, there is evidence that the interval length might be appropriate. If the pattern of lag1 and lag0 paths differ for the different variables—as in the present investigation—then the most suitable interval might not be consistent across the different variables.
In summary, without a clear theoretical justification for interpreting contemporaneous effects (like the rationale in the present investigation), we recommend the continued reliance on the juxtaposition of results for lag1 reciprocal paths based on alternative CLPMs. However, even in this case, tests of lag0 effects can be heuristic and provide a sensitivity analysis concerning the appropriate time interval. Thus, we also encourage researchers to explore further insights provided by contemporaneous reciprocal-effect models like those described here, as well as alternative approaches to evaluating the effects of different time intervals.
Muthén and and Asparouhov’s (2022) Caution: Goodness-of-Fit and Substantive Interpretation
Muthén & Asparouhov (2022; also see Muthén & Asparouhov, 2023) express caution about adequately selecting a “best” model and differentiating between CLPMs based on goodness-of-fit. Their concern was based primarily on goodness-of-fit. Because the fit of the different models was so similar, they could not differentiate between models based on fit. Nevertheless, as emphasized by many researchers, Marsh et al. (2004) underlined the importance of considering substantive and theoretical aspects in model evaluation. They argued that researchers should rely on the substantive and theoretical implications of their findings as well as goodness-of-fit; goodness-of-fit is not a magic bullet, and that fit indices should be considered rough rules of thumb rather than golden rules. Marsh & Hau (1996) said that model evaluation is as much art as it is science.
In the context of evaluating CLPMs, Orth et al. (2021) noted that the choice of models should also be based on theoretical grounds and appropriate interpretations of the results rather than only goodness-of-fit. Hence, goodness-of-fit should be only one of the considerations in the choice of models and their interpretation. Hayduk (1996) goes even further to argue that “goodness-of-fit indices provide a convenient and readily understandable summary of how well the implied model fits the observed data, but this summary is essentially irrelevant to the central scientific problem—testing a specific hypothesis about the way the data were generated,” whereas Humphreys (1978) claims that goodness-of-fit tests are simply not relevant to the goals and assumptions of a theory. In contrast to Muthén & Asparouhov’s (2022) pessimism, our optimistic perspective is that a cautious juxtaposition of goodness-of-fit, parameter estimates, underlying assumptions, and theoretical perspectives for alternative CLPMs such as those presented here offers valuable insight into interpreting the empirical results. Whereas the fit for many of our models was similar, the substantive interpretations of all the models were consistent with our a priori hypothesis that math achievement and self-concept are reciprocally related. In this sense, juxtaposing the different models is more important than choosing a single best model. This juxtaposition between goodness-of-fit and substantive interpretation is at the heart of our approach to substantive-methodological synergy.
Continuous Time Models (CTM)
The continuous time model (CTM) is an evolving statistical model. Although CTMs have only been applied to evaluate how cross-lagged panel effects vary over time (e.g., Hecht & Zitzmann, 2021a, 2021b; Kuiper et al., 2018; Lohmann et al., 2022; Voelkle et al., 2018), treating time as a continuous variable has theoretically important implications potentially relevant to our research. In order to juxtapose our extension to traditional approaches to CLPMs with CTMs, we reanalyzed our data with CTMs, explicitly modelled time as a continuous rather than a discrete variable (see supplemental materials).
However, there is a critical limitation to this CTM approach for our study. In particular, the CTM automatically fixes the Lag0 cross-paths to zero so that there is necessarily a steep decline in the extrapolated size of cross-lagged effects from Lag1 to Lag0 (see Supplemental Materials). Thus, within the CTM model, it is impossible for the cross-lagged effects to peak at some point between Lag0 and Lag1. However, from the perspective of our study, this limitation in the CTM is problematic as this is precisely what we want to test—that the peak of the ACH→ASC falls somewhere between Lag0 and Lag1 and may even be very close to Lag0. Hence, the CTM is unable to test our study’s central prediction.
The limitation of the CTM is that there is no data in our study with a time interval of less than one year that the CTM can use to extrapolate what would happen if the intervals were even shorter. Indeed, Voelkle et al. (2018) warn that CTM researchers should be cautious in extrapolating to unobserved intervals. This is particularly true for extrapolating results to the Lag0 to Lag1 interval where there is no data, and the Lag0 effect is automatically fixed at 0. Thus, the CTM model can never result in a peak effect within the Lag0 and Lag1 interval (i.e., less than one year) for our data. However, with sufficiently fine-grained data (with very short intervals of weeks or even days), the CTM model (as well as the various CLPMs) could test whether the optimal time interval is less than one year. Indeed, it is well-recognized that the CTM and CLPMs provide similar information for fixed time intervals (e.g., Voelkle et al., 2018), as was the case in our CTM analysis. Hence, the main advantage of the CTM is when the time intervals vary and may not be the same for all participants, a design not easily handled with traditional CLPMs but well-suited to CTMs (e.g., Voelkle et al., 2018; see Supplemental Materials for further discussion). We also note that Niepel et al. (2022) found support for the REM based on experience-sampling data using a dynamic structural equation modelling to analyze their intensive longitudinal data. Although beyond the scope of the present investigation, exploration of alternative data collection designs, continuous-time models, and dynamic structural equation models warrant further consideration in relation to limitations in CLPMs more generally and more specifically to our evaluation of lag0 models.
Strengths, Limitations, and Directions for Further Research
Our strongest substantive contribution is showing that support for the REM generalizes over different modelled approaches. These substantive results are important, demonstrating that support for REM hypotheses generalizes over the complementary interpretations based on CLPM, PCPMs, and CCLPMs with and without random intercepts, lag2 effects, and control for covariates. Although there are likely to be studies in which there is no such clear convergence over different statistical models, it is useful to apply the approach used here to evaluate why there are potential inconsistencies and how these might compromise support for REM hypotheses.
Our study is strong regarding the size and representativeness of the sample of German secondary students, the study design including annual waves over all five years of compulsory secondary schooling, and the statistical models we used. However, the generalizability of our results needs to be tested with other age groups, countries, and school settings. Thus, for example, Wu et al.’s (2021) important meta-analysis of REM studies of self-concept and achievement found that support for the REM hypothesis of reciprocal effects was stronger for students in secondary school (as in our study) than in primary school. Because this conclusion differs from Valentine et al.’s classic 2004 meta-analysis (but also see Guay et al., 2003 and related discussion by Marsh et al., 2022), considering younger age groups is an important direction for further research using strong methodological approaches like those used here.
More broadly, there is a need to test the relevance of our substantive and methodological contributions to the evaluation of CLPMs to other constructs in educational psychology (e.g., academic emotions and academic achievement: Pekrun et al., 2017; Pekrun et al., 2023; school-belonging and resilience: Bostwick et al., 2022; self-efficacy and academic achievement, Bandura, 1986; parental involvement and student outcomes, Epstein, 2001; Hill & Tyson, 2009; school bullying and depression; Kochel et al., 2012; Marsh et al., 2016a, b, c; Olwelus, 1993; use of technology and learning outcomes: Hattie, 2012; Hwang & Wu, 2012; motivation and learning goals: Coventry et al., 2023; Pintrich & Schunk, 2002; time investment and achievement: Liu et al., 2023; peer relationships and achievement: Miles & Stipek, 2006; Stenseng et al., 2022; Wentzel & Caldwell, 1997; Li & Wang, 2022; parental involvement and school engagement: Hoover-Dempsey & Sandler, 1995; Fan & Chen, 2001; parental aspirations and academic outcomes: Buchmann et al., 2022; Marsh et al., 2023; teacher self-efficacy and student outcomes: Hettinger et al., 2023; teacher support and academic engagement: Roorda et al. (2011); De Laet et al., 2015; Wu & Zhang, 2022). The same holds true for other disciplines that routinely use CLPMs. Indeed, as emphasized, for example, by Valentine et al. (2004) and Núñez-Regueiro et al. (2022), the reciprocal effects model approach unites most school motivation theories.
Methodologically, we introduce a more robust methodological framework for evaluating directional ordering, extending current research in education and psychology. Although there has been recent debate on the usefulness of CLPMs and RI-CLPMs (Hamaker et al., 2015; Marsh et al., 2022, 2023; Murayama et al., 2017; Niepel et al., 2022; Núñez-Regueiro et al., 2022; Orth et al., 2021, 2022), we extend that previous research to include contemporaneous effect models of directional ordering. The juxtaposition of lag0 and lag1 effects provides new insights into the largely neglected problem of interval length. In addition, we present alternative approaches to controlling covariates and how to test the implicit assumption that the effects of fixed covariates are stable over time. Finally, we offer a viable compromise on including residual covariances in contemporaneous and cross-lagged models containing both lag1 and lag0 effects.
Our study is a substantive-methodological synergy. Based on academic self-concept theory, we offered predictions about the nature of contemporaneous and lagged reciprocal effects relating MSC and MACH. We tested these predictions by applying and extending evolving statistical models of contemporaneous effects. The rationale for our tests is that MSC→MACH links must take place over time, mediated by intervening processes. In contrast, MACH→MSC links are more direct and can occur more quickly. Consistent with predictions, we found that the reciprocal effects were contemporaneous for MACH→MSC but lagged for MSC→MACH. Although these predictions are idiosyncratic to academic self-concept theory, we suspect that the rationale also applies to other studies. Thus, for example, in one of the few studies to have considered contemporaneous reciprocal effects, Ormel et al. (2002; also see Muthén & Asparouhov, 2022, 2023) found contemporaneous (lag0) effects from disability to depression but lagged (lag1) effects from depression to disability. Applying our logic, we suggest that intervening processes mediate the effects of depression on disability, whereas the effects of disability on depression are likely to be more immediate.
Our discussion of contemporaneous and lagged reciprocal effects also highlights the neglected issue of the time interval between waves in REM studies (but also see Hamaker, 2023). Contemporaneous effects reflect occurrences taking place within a given time interval. Support for contemporaneous effects suggests that the time interval might be too long. Shorter time intervals might demonstrate lagged reciprocal effects rather than contemporaneous effects. However, our results also indicate that even within a single study, the most appropriate time interval might vary for different variables (see also Pekrun, 2023). Thus, our results suggest that the time interval might have been too short to test the MACH→MSC contemporaneous effect because there were only contemporaneous effects in the CCLPMs. However, the time interval might have been appropriate for MSC→MACH relations because there were only lag1 reciprocal effects. From this perspective, we recommend that traditional tests of REM should routinely be extended to consider contemporaneous effects to evaluate the appropriateness of the time interval—a sensitivity analysis.
In our study, we assessed MSC with self-report measures. Self-report is criticized because its subjectivity might introduce method effects that bias parameter estimates. However, by its nature, self-concept is a self-perception, and students are the most appropriate source to evaluate their own MSCs. For RI models, method effects that are stable over time will probably be absorbed into the global (decomposed between-person) trait effects and have little influence on decomposed reciprocal paths (but also see discussion of measurement error). These method effects in CLPMs are likely to inflate MSC stability paths. Nevertheless, we considered the relations between MSC and objective achievement measures. Hence, self-report method effects are less concerning than in studies where self-reports are the basis of all the constructs (or even non-self-report measures that might be contaminated by shared method effects).
CLPM studies give insufficient attention to the underlying measurement model, especially studies that use manifest variables. The application of SEMs is questionable if the measurement model is not well-defined. The measurement model provides an essential basis for comparison for subsequent models and preliminary insights into the nature of the relations among the variables (see Table 1). For our longitudinal measurement models, we tested traditional factorial-invariance constraints (configural, metric, and scalar invariance over time). Support for at least configural invariance underpins the rationale for all CLPMs, and many implicitly assume that the factor loadings are invariant over time (metric invariance). We included multiple indicators MSC, allowing us to control for method effects idiosyncratic to specific items (using correlated uniqueness) that cannot readily be controlled with manifest-variable models. Although tangential to the issue of reciprocal effects, all CLPM studies should begin by evaluating the measurement model and its invariance over time, particularly for subjective outcomes like MSC that are based on self-report.
Random intercept models are claimed to reflect a within-person perspective. However, this should not be confused with a fully idiographic approach that models the effects separately for each individual (e.g., Beltz et al., 2016; Molenaar, 2004). Indeed, for all the random intercept models considered here, the relations between within-person deviations are modelled as typical between-person regressions (i.e., effects are constant across individuals). The critical difference is that all models considered here, including random-intercept models, start with one model for all individuals and not separate (potentially very different) models for each individual. In particular, none of the models addresses the idiographic question of what proportion of the students conform to REM hypotheses. Hence, none of the models considered enunciates within-person processes underpinning dynamic relations between ASC and achievement; these remain a black box (Niepel et al., 2022; also see Murayama et al., 2017; Núñez-Regueiro et al., 2022). A direction for further research is to evaluate REM predictions from a more idiographic approach, such as group iterative multiple model estimation (Beltz et al., 2016) or dynamic SEMs that integrate nomothetic and idiographic strategies (Niepel et al., 2022; Pekrun et al., 2023). Furthermore, idiographic research might better inform practice and policy designed to accommodate the distinct needs of specific individuals.
Here, we focus on tests of temporal ordering that provide information relevant to causal ordering. However, as Wunsch et al. (2021) emphasized, temporal ordering does not necessarily provide the correct causal ordering because individuals make decisions based on past experiences, present circumstances, and future expectations. Thus, it is important to distinguish between the operational and statistical models based on available data and the conceptual-theoretical models and the characteristics underlying the data-generating process. Temporal ordering is neither a necessary nor a sufficient basis for attributing causal ordering. Indeed, the typical randomized controlled trial approach to causality based on experimental control can be considered time-independent (i.e., not dependent on assumptions of temporal ordering). Furthermore, interpretations of temporal ordering are complicated because the critical events are not measured at the moment of occurrence and may evolve over time, whereas underlying processes and mechanisms (e.g., Machamer et al., 2000) are not instantaneous and may also change over time. Longitudinal data with many waves address these issues in part but need to be interpreted in relation to underlying theory, conceptual models, and knowledge of the variables under consideration.
Conclusions and Practical Implications
Our substantive-methodological synergy delves into the symbiotic relation between academic self-concept (ASC) and achievement, which holds implications across substantive, theoretical, policy, practice, and methodological domains. Substantively, our findings support the reciprocal relations between ASC and achievement, transcending potential conflicts among various statistical models built on divergent underlying assumptions. Unlike unidirectional models that solely emphasize either skill development or self-enhancement, our research provides robust backing for the REM predictions over an extensive temporal span.
The policy and practical implications of our research underscore the substantial and expanding body of REM studies. The directional relationship between ASC and achievement is pivotal in informing interventions. If the direction solely flowed from achievement to ASC, endeavors to enhance ASC would have minimal impact on achievement. Conversely, if ASC solely influenced achievement, efforts aimed at enhancing achievement would not necessarily improve ASC. In contrast to these unidirectional paradigms, REM research suggests that interventions targeting both achievement and ASC yield greater efficacy compared to interventions focusing solely on one of these constructs. Marsh & Craven (2006), in their narrative review of REM research, aptly articulated this point, stating: “If practitioners enhance self-concepts without improving performance, then the gains in self-concept are likely to be short-lived …. If practitioners improve performance without also fostering participants’ self-beliefs in their capabilities, then the performance gains are also unlikely to be long-lasting” (p. 159).
Here, we show that this support for REM predictions generalizes over newly evolving reciprocal contemporaneous and lagged effects models. Although we extended REM research in important ways and raised various issues that require further investigation, support for REMs was consistent with all the models we considered. On this basis, we recommend the interventions aimed at one of these constructs should also incorporate the other, as the enhancement of ASC and achievement are complementary and mutually reinforcing. Short-term gains in either construct are unlikely to be long-lasting unless there are changes in both (Marsh, 2006).
Theoretically, we focused on ASC theory and empirical research based on this framework. However, it would be useful to expand this theoretical approach and statistical framework to include other theoretical frameworks such as broaden-and-build theory (Fredrickson, 2001), social cognitive theory (Bandura, 1986), REMs of appraisals, emotions, and achievement (Pekrun, 1992, 2006; Pekrun et al., 2017, 2023), job-demand resources model (Bakker & Demerouti, 2014, 2017), and the conservation-of-resources model (Hobfoll & Shirom, 2001). Each of these theoretical models posits reciprocal effects from somewhat different theoretical bases.
Methodologically, the study outlines the importance of longitudinal design issues and the use of different statistical models to test directional ordering. Our most important methodological contribution is the extension of statistical models proposed by Muthén & Asparouhov (2022; also see Muthén & Asparouhov, 2023) and by Marsh, Pekrun et al. (2022, 2023), and our substantive interpretation of the results based on well-established theory—a substantive methodological synergy.
Researchers have tended to treat CLPMs and RI-CLPMs as antagonistic. However, following Marsh and colleagues (e.g., Marsh et al., 2022; 2023; also see Lüdtke & Robitzsch, 2021, 2022; Pekrun et al., 2023), we argue that they are complementary approaches with contrasting strengths and weaknesses. Likewise, Muthén & Asparouhov (2022; also see Muthén & Asparouhov, 2023) found that goodness-of-fit did not differentiate their models and that it was sometimes unclear whether reciprocal effects should be best represented as lag1 or lag0 effects. However, this conclusion relies mainly on goodness-of-fit rather than understanding the underlying causal mechanisms. For us, the critical value of these models is to juxtapose the interpretations of the models concerning substantive theory about the nature of the effects. Like Muthén & Asparouhov (2022; also see Muthén & Asparouhov, 2023), we recommend that applied researchers test alternative models and juxtapose their interpretations. CLPMs, RI-CLPMs, and contemporaneous models—and their variations—each have counter-balancing strengths and weaknesses, making their juxtaposition informative from substantive, theoretical, and methodological perspectives. These methodological insights are broadly generalizable to other disciplines and applied research. This conclusion might seem disappointing to researchers seeking a single best model that provides the one “true” result. However, it fits well with our approach to substantive-methodological synergy.
The critical, unresolved issue of the appropriate time interval length in cross-lagged panel studies is widely acknowledged. However, except for being mentioned as a limitation and a direction for further research, the issue is largely ignored in the design and analysis of cross-lagged panel studies. Concerning this issue, a major contribution of our study is a new approach to evaluating the appropriateness of the time interval, addressing this much-neglected topic in cross-panel designs. The support for our theoretical prediction upon which we base the lag0 predictions and the statistical methodology used to test it provides essential new contributions to this substantive area of research that will likely generalize to other research areas.
Ultimately, there is a need for substantive-methodological synergy (Marsh & Hau, 2007) that combines theory, measurement, and statistical analysis in a helpful way for research, intervention, policy, and practice. In their manifesto on substantive-methodological synergy, Marsh & Hau (2007) argued that applied researchers applying new and evolving methodologies should adopt the role of data detective. Using a construct validity approach, they should thoroughly evaluate the appropriateness of new methodological approaches and interpretations. Our study demonstrates this approach in extending REM research to include contemporaneous reciprocal effects relating MSC and MACH within the same wave. Substantively, our research focuses on ASC in an educational setting. However, we hope that our substantive-methodological approach and the issues raised will serve as an exemplar with broad applicability across psychology and other disciplines.
References
Asendorpf, J. B. (2021). Modeling developmental processes. In J. R. Rauthmann (Ed.), Handbook of Personality Dynamics and Processes, 815–835. London, UK. https://doi.org/10.1016/B978-0-12-813995-0.00031-5
Asparouhov, T., & Muthén, B. (2022). Residual structural equation models. Structural Equation Modeling: A Multidisciplinary Journal. https://doi.org/10.1080/10705511.2022.2074422
Bailey, D. H., Duncan, G. J., Watts, T., Clements, D. H., & Sarama, J. (2018). Risky business: Correlation and causation in longitudinal studies of skill development. American Psychologist, 73(1), 81–94. https://doi.org/10.1037/amp0000146
Bailey, D. H., Oh, Y., Farkas, G., Morgan, P., & Hillemeier, M. (2020). Reciprocal effects of reading and mathematics? Beyond the cross-lagged panel model. Developmental Psychology, 56, 912–921. https://doi.org/10.1037/dev0000902
Bakker, A. B., & Demerouti, E. (2014). Job demands-resources theory. In C. L. Cooper (ed.), Wellbeing: A Complete Reference Guide , 1–28. John Wiley & Sons, Ltd. https://doi.org/10.1002/9781118539415.wbwell019
Bakker, A. B., & Demerouti, E. (2017). Job demands-resources theory: Taking stock and looking for- ward. Journal of Occupational Health Psychology, 22(3), 273–285. https://doi.org/10.1037/ocp0000056
Bandura, A. (1986). Social foundations of thought and action: A social cognitive theory. Prentice-Hall.
Bardach, L., Yanagida, T., Goetz, T., Jach, H., & Pekrun, R. (2023). Self-regulated and externally regulated learning in adolescence: Developmental trajectories and relations with teacher behavior, parent behavior, and academic achievement. Developmental Psychology, 59(7), 1327–1345. https://doi.org/10.1037/dev0001537
Basarkod, G., Marsh, H., Guo, J., Dicke, T., Xu, K. M., & Parker, P. (2020). The big-fish-little-pond effect for reading self-beliefs: A cross-national exploration with PISA 2018. https://doi.org/10.35542/osf.io/7wbxj
Beltz, A. M., Wright, A. G., Sprague, B. N., & Molenaar, P. C. (2016). Bridging the nomothetic and idiographic approaches to the analysis of clinical data. Assessment, 23(4), 447–458. https://doi.org/10.1177/1073191116648209
Boele, S., Nelemans, S. A., Denissen, J. J. A., Prinzie, P., Bülow, A., & Keijsers, L. (2023). Testing transactional processes between parental support and adolescent depressive symptoms: From a daily to a biennial timescale. Development and Psychopathology, 35(4), 1656–1670. https://doi.org/10.1017/S0954579422000360
Bollen, K. A., & Long, J. S. (Eds.). (1993). Testing structural equation models. Sage Publications, Inc.
Bostwick, K. C. P., Martin, A. J., Collie, R. J., Burns, E. C., Hare, N., Cox, S., Flesken, A., & McCarthy, I. (2022). Academic buoyancy in high school: A cross-lagged multilevel modeling approach exploring reciprocal effects with perceived school support, motivation, and engagement. Journal of Educational Psychology, 114(8), 1931–1949. https://doi.org/10.1037/edu0000753
Brand, M. (1984). Intending and acting: Toward a naturalized action theory. Bradford Books.
Buchmann, M., Grütter, J., & Zuffianò, A. (2022). Parental educational aspirations and children’s academic self-concept: Disentangling state and trait components on their dynamic interplay. Child Development, 93(1), 7–24. https://doi.org/10.1111/cdev.13645
Calsyn, R. J., & Kenny, D. A. (1977). Self-concept of ability and perceived evaluation of others: Cause or effect of academic achievement? Journal of Educational Psychology, 69(2), 136–145. https://doi.org/10.1037/0022-0663.69.2.136
Campbell, D. T., & Stanley, J. C. (1963). Experimental and quasi-experimental designs for research. Chicago: Rand MçNally & Company.
Cartwright, N. (2004). Causation: One word, many things. Philosophy of Science, 71(5), 805–819. https://doi.org/10.1086/426771. Proceedings of the 2002 Biennial Meeting of The Philosophy of Science AssociationPart II: Symposia PapersEdited by Sandra D. Mitchell (December 2004).
Cook, T. D., & Campbell, D. T. (1979). Quasi-experimentation: Design and analysis issues for fields settings. Houghton Mifflin Company.
Coventry, W. L., Farraway, S., Larsen, S. A., Enis, T. P., Forbes, A. Q., & Brown, S. L. (2023). Do student differences in reading enjoyment relate to achievement when using the random-intercept cross-lagged panel model across primary and secondary school? PLoS ONE, 18(6), e0285739. https://doi.org/10.1371/journal.pone.0285739
Cramer, J. G. (1986). The transactional interpretation of quantum mechanics. Reviews of Modern Physics, 58(3), 647–688. https://doi.org/10.1103/RevModPhys.58.647
De Laet, S., Colpin, H., Vervoort, E., Doumen, S., Van Leeuwen, K., Goossens, L., & Verschueren, K. (2015). Developmental trajectories of children’s behavioral engagement in late elementary school: Both teachers and peers matter. Developmental Psychology, 51(9), 1292–1306. https://doi.org/10.1037/a0039478
Diener, E., Northcott, R., Zyphur, M. J., & West, S. G. (2022). Beyond experiments. Perspectives onPsychological. Science, 17(4), 1101–1119.
Dorman, C., & Griffin, M. A. (2015). Optimal time lags in panel studies. Psychological Methods, 20(4), 489–505. https://doi.org/10.1037/met0000041
Enders, C. K. (2010). Applied missing data analysis. books.google.com.
Epstein, J. L. (2001). School, family, and community partnerships: Preparingeducators and improving schools. Westview: Boulder CO.
Fan, X., & Chen, M. (2001). Parental involvement and students’ academic achievement: A meta-analysis. Educational Psychology Review, 13, 1–22. https://doi.org/10.1023/A:1009048817385
Fredrickson, B. L. (2001). The role of positive emotions in positive psychology. The broaden-and-build theory of positive emotions. The American Psychologist, 56(3), 218–226. https://doi.org/10.1037/0003-066X.56.3.218
Frenzel, A. C., Goetz, T., Lüdtke, O., Pekrun, R., & Sutton, R. (2009). Emotional transmission in the classroom: Exploring the relationship between teacher and student enjoyment. Journal of Educational Psychology, 101(3), 705–716. https://doi.org/10.1037/a0014695
Garfield, J. L. (1995). Fundamental wisdom of the middle way: Nagarjuna’s Mulamadhyamakakarika. Oxford University Press.
Giddens, A. (1984). The constitution of society: Outline of the theory of structuration. University of California Press.
Gollob, H. F., & Reichardt, C. S. (1987). Taking account of time lags in causal models. Child Development, 58(1), 80–92. https://doi.org/10.2307/1130293
Granger, C. W. J. (1969). Investigating causal relations by econometric models and cross-spectral methods. Econometrica, 37(3), 424–438. https://doi.org/10.2307/1912791
Greenberg, D. F., & Kessler, R. C. (1982). Equilibrium and identification in linear panel models. Sociological Methods & Research, 10, 435–451.
Guay, F., Marsh, H. W., & Boivin, M. (2003). Academic self-concept and academic achievement: Developmental perspectives on their causal ordering. Journal of Educational Psychology, 95(1), 124–136. https://doi.org/10.1037/0022-0663.95.1.124
Guo, J., Marsh, H. W., Morin, A. J. S., Parker, P. D., & Kaur, G. (2015a). Directionality of the associations of high school expectancy-value, aspirations, and attainment: A longitudinal study. American Educational Research Journal, 52(2), 371–402. https://doi.org/10.3102/0002831214565786
Guo, J., Parker, P. D., Marsh, H. W., & Morin, A. J. S. (2015b). Achievement, motivation, and educational choices: A longitudinal study of expectancy and value using a multiplicative perspective. Developmental Psychology, 51(8), 1163–1176. https://doi.org/10.1037/a0039440
Hamaker, E. L. (2023). The within-between dispute in cross-lagged panel research and how to move forward. Psychological Methods. https://doi.org/10.1037/met0000600
Hamaker, E. L., Kuiper, R. M., & Grasman, R. P. P. P. (2015). A critique of the cross-lagged panel model. Psychological Methods, 20(1), 102–116. https://doi.org/10.1037/a0038889
Haney, P., & Durlak, J. A. (1998). Changing self-esteem in children and adolescents: A meta-analytic review. Journal of Clinical Child Psychology, 27, 423–433.
Hansford, B. C., & Hattie, J. A. (1982). The relationship between self and achievement/performance measures. Review of Educational Research. https://doi.org/10.3102/00346543052001123
Hattie, J. (2012). Visible learning for teachers: Maximizing impact on learning. Routledge.
Hayduk, L. A. (1996). LISREL issues, debates and strategies. JHU Press.
Hecht, M., & Zitzmann, S. (2021a). Exploring the unfolding of dynamic effects with continuous-time models: Recommendations concerning statistical power to detect peak cross-lagged effects. Structural Equation Modeling, 28, 894–902. https://doi.org/10.1080/10705511.2021.1914627
Hecht, M., & Zitzmann, S. (2021b). Sample size recommendations for continuous time models: Compensating shorter time-series with higher numbers of persons and vice versa. Structural Equation Modeling, 28, 229–236. https://doi.org/10.1080/10705511.2020.1779069
Heine, S. (1994). Dogen and the Koan tradition: A tale of two Shobogenzo texts. State University of New York Press.
Heise, D. R. (1975). Causal analysis. John Wiley & Sons.
Hettinger, K., Lazarides, R., & Schiefele, U. (2023). Longitudinal relations between teacher self-efficacy and student motivation through matching characteristics of perceived teaching practice. European Journal of Psychology of Education. https://doi.org/10.1007/s10212-023-00744-y
Hill, N. E., & Tyson, D. F. (2009). Parental involvement in middle school: A meta-analytic assessment of the strategies that promote achievement. Developmental Psychology, 45(3), 740–763. https://doi.org/10.1037/a0015362
Hobfoll, S., & Shirom, A. (2001). Conservation of resources theory: Applications to stress and manage- ment in the workplace. In R. T. Golembiewski (Ed.), Handbook of organizational behavior (pp. 57–80). Marcel Dekker.
Hoover-Dempsey, K. V., & Sandler, H. M. (1995). Parental involvement in children’s education: Why does it make adifference? Teachers College Record, 97(2), 310–331. https://doi.org/10.1177/016146819509700202
Hu, L. T., & Bentler, P. M. (1999). Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Structural Equation Modeling, 6, 1–55. https://doi.org/10.1080/10705519909540118
Huang, C. (2011). Self-concept and academic achievement: A meta-analysis of longitudinal relations. Journal of School Psychology, 49(5), 505–528. https://doi.org/10.1016/j.jsp.2011.07.001
Hübner, N., Wagner, W., Zitzmann, S., et al. (2023). How strong is the evidence for a causal reciprocal effect? Contrasting traditional and new methods to investigate the reciprocal effects model of self-concept and achievement. Educational Psychology Review, 35, 6. https://doi.org/10.1007/s10648-023-09724-6
Huemer, M., & Kovitz, B. (2003). Causation as simultaneous and continuous. The Philosophical Quarterly, 53(213), 556–565. https://doi.org/10.1111/1467-9213.00331
Humphreys, L. G. (1978). Relevance of genotype and its environmental counterpart to the theory, interpretation, and nomenclature of ability measures. Intelligence, 2(2), 181–193. https://doi.org/10.1016/0160-2896(78)90008-9
Hwang, G. J., & Wu, P. H. (2012). Advancements and trends in digital game-based learning research: A review of publications in selected journals from 2001 to2010. British Journal of Educational Technology, 43(1), 19–23.
James, L. R., Mulaik, S. A., & Brett, J. M. (1983). Causal analysis: Assumptions, models, and data. Beverly Hills. CA. Sage Publications.
Jelicić, H., Phelps, E., & Lerner, R. M. (2009). Use of missing data methods in longitudinal studies: The persistence of bad practices in developmental psychology. Developmental Psychology, 45(4), 1195–1199. https://doi.org/10.1037/a0015665
Joreskog, K. G., & Sorbom, D. (1984). LISREL VI: Analysis $linear structural relationships by the method maximum likelihood, instrumental variables, and least squares methods. User’s Guide. Mooresville, Ind.: Scientific Software.
Joreskog, K. G. (1979). Statistical estimation of structural models in longitudinal investigations. (J. R. Nesselroade & B. Baltes, Eds.). Academic Press.
Kessler, R. C., & Greenberg, D. F. (1981). Linear panel analysis: Models of quantitative change. Academic Press.
Klein, L. R., & Goldberger, A. S. (1955). An econometric model of the United States 1929–1952. North-Holland Publishing Company.
Kochel, K. P., Ladd, G. W., & Rudolph, K. D. (2012). Longitudinal associations among youth depressive symptoms, peer victimization, and low peer acceptance: An interpersonal process perspective. Child Development, 83, 637–650. https://doi.org/10.1111/j.1467-8624.2011.01722.x
Kuiper, R. M., & Ryan, O. (2018). Drawing conclusions from cross-lagged relationships: Re-considering the role of the time-interval. Structural Equation Modeling, 25(4), 809–823. https://doi.org/10.1080/10705511.2018.1431046
Laland, K. N., Odling-Smee, J., & Feldman, M. W. (1999). Evolutionary consequences of niche construction and their implications for ecology. Proceedings of the National Academy of Sciences, 96(18), 10242–10247. https://doi.org/10.1073/pnas.96.18.10242
Leuridan, B. & Lodewyckx, T. (2019). Causality and time: An introductory typology. (2019). In S. Kleinberg (Ed.), Time and Causality across the Sciences, 14–36. Cambridge: Cambridge University Press. https://doi.org/10.1017/9781108592703.002
Lewis, D. (1973). Causation. The Journal of Philosophy, 70(17), 556–567. https://doi.org/10.2307/2025310
Li, T., & Wang, Z. (2022). Disaggregating the between-person and within-person associations between peer acceptance and academic achievement in early elementary school. Journal of Applied Developmental Psychology, 78. https://doi.org/10.1016/j.appdev.2021.101357
Li, J., Zyphur, M. J., Sugihara, G., & Laub, P. J. (2021). Beyond linearity, stability, and equilibrium: The edmpackage for empirical dynamic modeling and convergent crossmapping in Stata. The Stata Journal, 21(1), 220–258. https://doi.org/10.1177/1536867X211000030
Little, T. D. (2013). Longitudinal structural equation modeling. Guilford Press.
Liu, M., Vu, T., Van Atteveldt, N., & Meeter, M. (2023). Testing the reciprocal effect between value of education, time investment, and academic achievement in a large non-western sample. Journal of Intelligence, 11(7), 133. https://doi.org/10.3390/jintelligence11070133
Lohmann, J., Zitzmann, S., Voelkle, M., & Hecht, M. (2022). A primer on continuous-time modeling in educational research: An exemplary application of a continuous-time latent curve model with structured residuals (CT-LCMSR) to PISA data. Large-Scale Assessments in Education, 10, 1–32. https://doi.org/10.1186/s40536-022-00126-8
Lüdtke, O., & Robitzsch, A. (2021). A critique of the random intercept cross-lagged panel model. PsyArXiv. https://doi.org/10.31234/osf.io/6f85c
Lüdtke, O., & Robitzsch, A. (2022). A comparison of different approaches for estimating cross-lagged effects from a causal inference perspective. Structural Equation Modeling, 29(6), 888–907. https://doi.org/10.1080/10705511.2022.2065278
Machamer, P., Darden, L., & Craver, C. F. (2000). Thinking about mechanisms. Philosophy of Science, 67(1), 1–25.
Marsh, H. W. (1990). Causal ordering of academic self-concept and academic achievement: A multiwave, longitudinal panel analysis. Journal of Educational Psychology, 82(4), 646.
Marsh, H. W. (2023). Extending the reciprocal effects model of math self-concept and achievement: Long-term implications for end-of-high-school, age-26 outcomes, and long-term expectations. Journal of Educational Psychology, 115(2), 193–211. https://doi.org/10.1037/edu0000750
Marsh, H. W., & Craven, R. G. (2006). Reciprocal effects of self-concept and performance from a multi- dimensional perspective: Beyond seductive pleasure and unidimensional perspectives. Perspectives on Psychological Science, 1(2), 133–163. https://doi.org/10.1111/j.1745-6916.2006.00010.x
Marsh, H. W., & Hau, K.-T. (1996). Assessing goodness of fit: Is parsimony always desirable? The Journal of Experimental Education, 64(4), 364–390. https://doi.org/10.1080/00220973.1996.10806604
Marsh, H. W., & Hau, K.-T. (1998). Is parsimony always desirable: Response to Sivo and Willson, Hoyle, Markus, Mulaik, Tweedledee, Tweedledum, the Cheshire Cat, and Others. The Journal of Experimental Education, 66(3), 274–285. https://doi.org/10.1080/00220979809604412
Marsh, H. W., & Hau, K.-T. (2003). Big-fish–little-pond effect on academic self-concept: A cross-cultural (26-country) test of the negative effects of academically selective schools. American Psychologist, 58(5), 364–376. https://doi.org/10.1037/0003-066X.58.5.364
Marsh, H. W., & Hau, K.-T. (2007). Applications of latent-variable models in educational psychology: The need for methodological-substantive synergies. Contemporary Educational Psychology, 32, 151–171. https://doi.org/10.1016/j.cedpsych.2006.10.008
Marsh, H. W., & Martin, A. J. (2011). Academic self-concept and academic achievement: Relations and causal ordering. The British Journal of Educational Psychology, 81(Pt 1), 59–77. https://doi.org/10.1348/000709910X503501
Marsh, H. W., & O’Mara, A. (2008). Reciprocal effects between academic self-concept, self-esteem, achievement, and attainment over seven adolescent years: Unidimensional and multidimensional perspectives of self-concept. Personality and Social Psychology Bulletin, 34(4), 542–552. https://doi.org/10.1177/0146167207312313
Marsh, H. W., Hau, K.-T., & Wen, Z. (2004). In search of golden rules: Comment on hypothesis-testing approaches to setting cutoff values for fit indexes and dangers in overgeneralizing Hu and Bentler’s (1999) findings. Structural Equation Modeling: A Multidisciplinary Journal, 11(3), 320–341. https://doi.org/10.1207/s15328007sem1103_2
Marsh, H. W., Trautwein, U., Lüdtke, O., Köller, O., & Baumert, J. (2005b). Academic self-concept, interest, grades, and standardized test scores: Reciprocal effects models of causal ordering. Child Development, 76(2), 397–416. https://doi.org/10.1111/j.1467-8624.2005.00853.x
Marsh, H. W., Lüdtke, O., Nagengast, B., Morin, A. J. S., & Von Davier, M. (2013). Why item parcels are (almost) never appropriate: Two wrongs do not make a right—camouflaging misspecification with item parcels in CFA models. Psychological Methods, 18, 257–284. https://doi.org/10.1037/a0032773
Marsh, H. W., Morin, A. J. S., Parker, P. D., & Kaur, G. (2014). Exploratory structural equation modeling: An integration of the best features of exploratory and confirmatory factor analysis. Annual Review of Clinical Psychology, 10, 85–110. https://doi.org/10.1146/annurev-clinpsy-032813-153700
Marsh, H., Craven, R., Parker, P., Parada, R., Guo, J., Dicke, T., & Abduljabbar, A. (2016a). Temporal ordering effects of adolescent depression, relational aggression, and victimization over six waves is fully latent reciprocal effects models. Developmental Psychology, 52(12), 1994–2009. https://doi.org/10.1037/dev0000241
Marsh, H. W., Pekrun, R., Lichtenfeld, S., Guo, J., Arens, A. K., & Murayama, K. (2016c). Breaking the double-edged sword of effort/trying hard: Developmental equilibrium and longitudinal relations among effort, achievement, and academic self-concept. Developmental Psychology, 52(8), 1273–1290. https://doi.org/10.1037/dev0000146
Marsh, H. W., Pekrun, R., Parker, P. D., Murayama, K., Guo, J., Dicke, T., & Lichtenfeld, S. (2017). Long-term positive effects of repeating a year in school: Six-year longitudinal study of self-beliefs, anxiety, social relations, school grades, and test scores. Journal of Educational Psychology, 109(3), 425–438. https://doi.org/10.1037/edu0000144
Marsh, H. W., Pekrun, R., Murayama, K., Arens, A. K., Parker, P. D., Guo, J., & Dicke, T. (2018a). An integrated model of academic self-concept development: Academic self-concept, grades, test scores, and tracking over 6 years. Developmental Psychology, 54(2), 263–280. https://doi.org/10.1037/dev0000393
Marsh, H. W., Pekrun, R., Parker, P. D., Murayama, K., Guo, J., Dicke, T., & Arens, A. K. (2018b). The murky distinction between self-concept and self-efficacy: Beware of lurking jingle-jangle fallacies. Journal of Educational Psychology, 111(2), 331–353. https://doi.org/10.1037/edu0000281
Marsh, H. W., Pekrun, R., & Lüdtke, O. (2022). Directional ordering of self-concept, school grades, and standardized tests over five years: New tripartite models juxtaposing within- and between-person perspectives. Educational Psychology Review, 34(4), 2697–2744. https://doi.org/10.1007/s10648-022-09662-9
Marsh, H. W., Lüdtke, O., Pekrun, R., Parker, P. D., Murayama, K., Guo, J., Basarkod, G., Dicke, T., Donald, J. N., & Morin, A. J. (2023). School leaders’ self-efficacy and job satisfaction over nine annual waves: A substantive-methodological synergy juxtaposing competing models of directional ordering. Contemporary Educational Psychology, 73, 102170. https://doi.org/10.1016/j.cedpsych.2023.102170
Marsh, H. W., Hau, K.-T., & Grayson, D. (2005a). Goodness of fit evaluation in structural equation modeling. In A. Maydeu-Olivares & J. McArdle (Eds.), Psychometrics: A festschrift to Roderick P. McDonald, 275–340. Hillsdale, NJ: Erlbaum.
Marsh, H. W., Parker, P. D., & Morin, A. J. S. (2016b). Invariance testing across samples and time: Cohort-sequence analysis of perceived body composition. In N. Ntoumanis & N. Myers (eds.), Introduction to Intermediate and Advanced Statistical Analyses for Sport and Exercise Scientists. Wiley-Blackwell Publishing, Inc.
Marsh, H. W. (2006). Self-concept theory, measurement, and research into practice: The role of self- concept in educational psychology... British Psychological Society Vernon-Wall Lecture.
Meredith, W. (1993). Measurement invariance, factor analysis and factorial invariance. Psychometrika, 58(4), 525–543. https://doi.org/10.1007/BF02294825
Miles, S. B., & Stipek, D. (2006). Contemporaneous and longitudinal associations between social behavior and literacy achievement in a sample of low-income elementary school children. Child Development, 77(1), 103–117. https://doi.org/10.1111/j.1467-8624.2006.00859.x
Millsap, R. E. (2012). Statistical approaches to measurement invariance. Routledge. https://doi.org/10.4324/9780203821961
Molenaar, P. C. M. (2004). A manifesto on psychology as idiographic science: Bringing the person back into scientific psychology, This Time Forever. Measurement: Interdisciplinary Research and Perspectives, 2(4), 201–218. https://doi.org/10.1207/s15366359mea0204_1
Mulder, J. D., & Hamaker, E. L. (2021). Three extensions of the random intercept cross-lagged panel model. Structural Equation Modeling: A Multidisciplinary Journal, 28, 638–648. https://doi.org/10.1080/10705511.2020.1784738
Murayama, K., Pekrun, R., Suzuki, M., Marsh, H. W., & Lichtenfeld, S. (2016). Don’t aim too high for your kids: Parental overaspiration undermines students’ learning in mathematics. Journal of Personality and Social Psychology, 111(5), 766-779. https://doi.org/10.1037/pspp0000079
Murayama, K., Goetz, T., Malmberg, L. E., Pekrun, R., Tanaka, A., & Martin, A. J. (2017). Within-person analysis in educational psychology: Importance and illustrations. In P. D. W. & S. K. (eds.), Psychological Aspects of Education – Current Trends: The Role of Competence Beliefs in Teaching and Learning, 71–87. Wiley.
Muthén, B., & Asparouhov, T. (2022) Can cross-lagged panel modeling be relied on to establish cross-lagged effects? The case of contemporaneous and reciprocal effects. Mplus Web Talks: No. 5. https://www.statmodel.com/recentpapers.shtml. Accessed 1 Feb 2024.
Muthén, B. & Asparouhov, T. (2023). Can cross-lagged panel modeling be relied on to establish cross-lagged effects? The case of contemporaneous and reciprocal effects. Submitted for publication. https://www.statmodel.com/recentpapers.shtml. Accessed 1 Feb 2024.
Muthén, L. K., & Muthén, B. O. (1998–2017). Mplus User’s Guide. Eighth edition. Accessed 1 Feb 2024.
Newman, D. A. (2014). Missing data. Organizational Research Methods, 17(4), 372–411. https://doi.org/10.1177/1094428114548590
Niepel, C., Marsh, H. W., Guo, J., Pekrun, R., & Möller, J. (2022). Revealing dynamic relations between mathematics self-concept and perceived achievement from lesson to lesson: An experience-sampling study. Journal of Educational Psychology, 114(6), 1380–1393. https://doi.org/10.1037/edu0000716
Núñez-Regueiro, F., Juhel, J., Bressoux, P., & Nurra, C. (2022). Identifying reciprocities in school motivation research: A review of issues and solutions associated with cross-lagged effects models. Journal of Educational Psychology, 114(5), 945–965. https://doi.org/10.1037/edu0000700
Olwelus, D. (1993). Bullying at school: What we know and what we can do. Blackwell Publishing.
Ormel, J., Rijsdijk, F. V., Sullivan, M., van Sonderen, E., & Kempen, G. I. J. M. (2002). Temporal and reciprocal relationships between IADL/ADL disability and depressive symptoms in late life. Journal of Gerontology, Psychological Sciences, 57B, 338–347.
Orth, U., Clark, D. A., Donnellan, M. B., & Robins, R. W. (2021). Testing prospective effects in longitudinal research: Comparing seven competing cross-lagged models. Journal of Personality and Social Psychology, 120(4), 1013–1034. https://doi.org/10.1037/pspp0000358
Orth, U., Meier, L. L., Bühler, J. L., Dapp, L. C., Krauss, S., Messerli, D., & Robins, R. W. (2022). Effect size guidelines for cross-lagged effects. Advance online publication. https://doi.org/10.1037/met0000499
Paxton, P. M., Hipp, J. R., & Marquart-Pyatt, S. (2011). Nonrecursive models: Endogeneity, reciprocal relationships, and feedback loops. Sage.
Pearl, J., Glymour, M., & Jewell, N. P. (2016). Causal inference in statistics: A primer. John Wiley & Sons.
Pekrun, R. (1990). Social support, achievement evaluations, and self-concepts in adolescence. In L. Oppenheimer (Ed.), The self-concept (pp. 107–119). Springer.
Pekrun, R. (1992). The impact of emotions on learning and achievement: Towards a theory of cognitive/ motivational mediators. Applied Psychology, 41(4), 359–376. https://doi.org/10.1111/j.1464-0597.1992.tb00712.x
Pekrun, R. (2006). The control-value theory of achievement emotions: Assumptions, corollaries, and implications for educational research and practice. Educational Psychology Review, 18(4), 315–341. https://doi.org/10.1007/s10648-006-9029-9
Pekrun, R. (2023). Mind and body in students’ and teachers’ engagement: New evidence, challenges, and guidelines for future research. British Journal of Educational Psychology, 93(Suppl 1), 227–238. https://doi.org/10.1111/bjep.12575
Pekrun, R., Lichtenfeld, S., Marsh, H. W., Murayama, K., & Goetz, T. (2017). Achievement emotions and academic performance: Longitudinal models of reciprocal effects. Child Development, 88(5), 1653–1670. https://doi.org/10.1111/cdev.12704
Pekrun, R., Murayama, K., Marsh, H. W., Goetz, T., & Frenzel, A. C. (2019). Happy fish in little ponds: Testing a reference group model of achievement and emotion. Journal of Personality and Social Psychology, 117(1), 166–185. https://doi.org/10.1037/pspp0000230
Pekrun, R., Marsh, H. W., Suessenbach, F., Frenzel, A. C., & Goetz, T. (2023). School grades and students’ emotions: Longitudinal models of within-person reciprocal effects. Learning and Instruction, 83, 101626. https://doi.org/10.1016/j.learninstruc.2022.101626
Pekrun, R., Marsh, H. W., Elliot, A. J., Stockinger, K., Perry, R. P., Vogl, E., Goetz, T., van Tilburg, W. A. P., Lüdtke, O., & Vispoel, W. P. (2023). A three-dimensional taxonomy of achievement emotions. Journal of Personality and Social Psychology, 124(1), 145–178. https://doi.org/10.1037/pspp0000448
Pekrun, R., Frenzel, A. C., Goetz, T., & Perry, R. P. (2007). The control-value theory of achievement emotions. In P. Schutz & R. Pekrun (Eds.), Emotion in Education, 13–36. Elsevier. https://doi.org/10.1016/B978-012372545-5/50003-4
Pintrich, P. R., & Schunk, D. H. (2002). Motivation in education: Theory, research, and applications. Pearson.
Robitzsch, A., & Lüdtke, O. (2023). Why full, partial, or approximate measurement invariance are not a prerequisite for meaningful and valid group comparisons. Structural Equation Modeling: A Multidisciplinary Journal. https://doi.org/10.1080/10705511.2023.2191292
Rohrer, J. M. (2018). Thinking clearly about correlations and causation: Graphical causal models for observational data. Advances in Methods and Practices in Psychological Science. https://doi.org/10.1177/2515245917745629
Roorda, D. L., et al. (2011). The influence of affective teacher–student relationships on students’ school engagement and achievement: A meta-analytic approach. Review of Educational Research, 81(4), 493–529. https://doi.org/10.3102/0034654311421793
Samuelson, P. A., & Nordhaus, W. D. (2010). Economics (19th ed.). McGraw-Hill/Irwin.
Schuurman, N. K., & Hamaker, E. L. (2019). Measurement error and person-specific reliability in multilevel autoregressive modeling. Psychological Methods, 24(1), 70–91. https://doi.org/10.1037/met0000188
Seaton, M., Marsh, H. W., & Craven, R. G. (2009). Earning its place as a pan-human theory: Universality of the big-fish-little-pond effect across 41 culturally and economically diverse countries. Journal of Educational Psychology, 101(2), 403–419. https://doi.org/10.1037/a0013838
Simon, H.A. (1977). Scientific discovery and the psychology of problem solving. In: Models of Discovery. Boston Studies in the Philosophy of Science, vol 54. Springer, Dordrecht. https://doi.org/10.1007/978-94-010-9521-1_16
Singh, M., Dolan, C. V., & Neale, M. C. (2023). Integrating cross-lagged panel models with instrumental variables to extend the temporal generalizability of causal inference. Multivariate Behavioral Research, 58(1), 148–149. https://doi.org/10.1080/00273171.2022.2160954
Stenseng, F., Tingstad, E. B., Wichstrøm, L., & Skalicka, V. (2022). Social withdrawal and academic achievement, intertwined over years? Bidirectional effects from primary to upper secondary school. British Journal of Educational Psychology, 92(4), 1354–1365. https://doi.org/10.1111/bjep.12504
Strotz, R. H., & Wold, H. O. A. (1960). Recursive versus nonrecursive systems: An attempt at synthesis. Econometrica, 28, 417–427.
Ulanowicz, R. E. (1997). Ecology, the ascendent perspective. Columbia University Press.
Valentine, J. C., DuBois, D. L., & Cooper, H. (2004). The relation between self-beliefs and academic achievement: A meta-analytic review. Educational Psychologist, 39(2), 111–133. https://doi.org/10.1207/s15326985ep3902_3
VanderWeele, T. J., Mathur, M. B., & Chen, Y. (2020). Outcome-wide longitudinal designs for causal inference: A new template for empirical studies. Statistical Science, 35(3), 437–466. https://doi.org/10.1214/19-STS728
Voelkle, M. C., Gische, C., Driver, C. C., & Lindenberger, U. (2018). The role of time in the quest for understanding psychological mechanisms. Multivariate Behavioral Research, 53(6), 782–805. https://doi.org/10.1080/00273171.2018.1496813
Watts, A. (1951). The wisdom of insecurity: A message for an age of anxiety. Pantheon Books.
Wentzel, K. R., & Caldwell, K. (1997). Friendships, peer acceptance, and group membership: Relations to academic achievement in middle school. Child Development, 68(6), 1198–1209. https://doi.org/10.2307/1132301
Wu, C. H., & Griffin, M. A. (2012). Longitudinal relationships betweencore self-evaluations and job satisfaction. Journal of Applied Psychology, 97(2), 331–342. https://doi.org/10.1037/a0025673
Wu, G., & Zhang, L. (2022). Longitudinal associations between teacher-student relationships and prosocial behavior in adolescence: The mediating role of basic need satisfaction. International Journal of Environmental Research and Public Health, 19(22). https://doi.org/10.3390/ijerph192214840
Wu, H., Guo, Y., Yang, Y., Zhao, L., & Guo, C. (2021). A meta-analysis of the longitudinal relationship between academic self-concept and academic achievement. Educational Psychology Review, 1–30.
Wunsch, G., Russo, F., Mouchart, M., & Orsi, R. (2021). Time and causality in the social sciences. Time & causality in the social sciences. Time and Society. https://doi.org/10.1177/0961463X211029488
Zyphur, M. J., Allison, P. D., Tay, L., Voelkle, M. C., Preacher, K. J., Zhang, Z., Hamaker, E. L., Shamsollahi, A., Pierides, D. C., Koval, P., & Diener, E. (2020). From data to causes I: Building a general cross-lagged panel model (GCLM). Organizational Research Methods, 23(4), 651–687. https://doi.org/10.1177/1094428119847278
Funding
Open Access funding enabled and organized by CAUL and its Member Institutions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Marsh, H.W., Guo, J., Pekrun, R. et al. Cracking Chicken-Egg Conundrums: Juxtaposing Contemporaneous and Lagged Reciprocal Effects Models of Academic Self-Concept and Achievement’s Directional Ordering. Educ Psychol Rev 36, 53 (2024). https://doi.org/10.1007/s10648-024-09887-w
Accepted:
Published:
DOI: https://doi.org/10.1007/s10648-024-09887-w