Introduction

Rubrics have become commonplace in educational settings across all instructional levels and throughout the world. Educators and policymakers put their trust in rubrics because rubrics are effective for judging the quality of student performance against pre-set criteria, increasing scoring reliability (Jonsson & Svingby, 2007). Additionally, the use of rubrics may also support students’ academic achievement (e.g., Dawson, 2017).

Although there are several research reviews presenting evidence of positive effects on students’ academic performance, self-regulated learning, and self-efficacy (e.g., Brookhart, 2018; Brookhart & Chen, 2015; Panadero & Jonsson, 2013; Reddy & Andrade, 2010), these reviews are all narrative, making it difficult to estimate the strength of this effect or the contribution from different moderating factors. Such estimations are especially important in a field where the findings are mixed, and the number of potential moderating factors is large, which is the case with research on the use of rubrics. Our aim is therefore to conduct a meta-analysis in order to estimate the strength of the effects on students’ academic performance, self-regulated learning, and self-efficacy through the use of rubrics, while investigating the influence of moderating factors.

Definition of Rubrics and Terminology

Since it is not unusual that rubrics get confused with other tools such as checklist, rating scales, or performance list (Arter & McTighe, 2001; Brookhart, 2013, 2018), it is important to define what a rubric is. The definition of rubrics used in this study is taken from Brookhart (2018), where a rubric is described as a tool that: “articulates expectations for student work by listing criteria for the work and performance level descriptions across a continuum of quality” (p. 1). Rubrics are sometimes also described as containing “three essential features: evaluative criteria, quality definitions, and a scoring strategy” (Popham, 1997 p. 72). However, a rubric designed for formative purposes might not include an explicit scoring strategy, only assessment criteria, the corresponding performance levels, and a description on the intersections of criteria and performance levels. In this study, we will therefore not use the term “scoring rubrics,” as this implies the existence of a scoring strategy.

The most commonly used representation of a rubric is a table or matrix. Usually, the first column to the left presents the assessment criteria. The rest of the columns contain the different performance levels, which can vary in their direction from high to low quality or, vice versa, low to high. The first row may contain labels for the performance levels (e.g., “outstanding,” “deficient”, etc.), and may also (in “scoring rubrics”) include the points to be awarded for each level. Other, less common, designs also exist, which include the same features, but use a different representation (e.g., concentric circles).

Rubrics for formative purposes are usually created by the teachers, though other options are also possible, such as co-creation of rubrics with the students (e.g., Fraile et al., 2017) or implementing already existing rubrics from databases, such as (for example) the Writing Rubrics for the English Language Proficiency Assessments for California.

The Origin and History of Rubrics

The term “rubric” has been found to be in use at least from the fifteenth century, referring to “headings of different sections of a book…Christian monks…initiating each major section of a copied book with a large red letter. Because the Latin word for red is ruber, rubric came to signify the headings for major divisions of a book.” (Popham, 1997 p. 72). During the twentieth century, rubrics and similar tools were created to produce more reliable and valid inter-rater and intra-rater scores for qualitative judgments of student performance (i.e., a summative purpose). Turley and Gallagher (2008) refer to “A Scale for the Measurement of Quality in English Composition by Young People” by Hillegas (1912) as one of the first documented attempts to create a tool for increasing the objectivity in teachers’ scoring. Another publication that has been pointed out as a key contribution for rubric development, is a study by Diederich and colleagues (1961), in which they summarized nearly a decade of research and conclude with five factors on judgments of writing ability: ideas, form, flavour, mechanics, and wording. According to Broad (2003), this was the inception of “standard, traditional, five-point rubric, by some version of which nearly every large-scale assessment of writing since 1961 has been strictly guided” (p. 6).

Prior to 1970, the term “rubric” only appeared in a few studies per year, but from thereon the term appears more and more frequently. From somewhere around the early years in the twenty-first century, the growth appears almost exponential and Dawson (2017) suggests that a seminal publication on rubrics by Popham (1997) may have sparked the rapid evolution of rubrics and the associated research during this time.

In his review, Dawson (2017) presented a figure on the cumulative frequency of articles and books including the term rubric. That figure contained information for articles until 2014 and for books until 2008. As a way to test whether the interest on rubrics is still increasing, we performed a similar search. The search method is explained in Appendix 1. As can be seen in Fig. 1, the use of the term “rubrics” in abstracts and as a topic, has been steadily growing over the years. Whether the decline after 2019 depends on the Covid pandemic, an actual decline in interest, or that the databases need some time to fully represent what has been published in the last couple years, or a combination of the previous, is not known.

Fig. 1
figure 1

Publications per year

Full size image

In parallel to the increased interest in rubrics as a research topic, there has been an expansion of the use of rubrics across educational settings, from primary to higher education. As seen in the first research review on the use of rubrics (Jonsson & Svingby, 2007), this initial interest in rubrics was almost entirely for summative purposes. However, this was about to change, not least by the influential work by Grant Wiggins (1993, 1998), who on moral grounds argued against secrecy in assessment of student performance and advocated the use of rubrics to increase transparency in assessments, as well as to support formative feedback practices and student self-regulation. This growing interest in the formative use of rubrics can be seen in the review mentioned above, where Jonsson and Svingby (2007) found merely 15 studies with this focus, while a decade later Brookhart (2018) found 46, even though she searched for studies in a higher education context only.

The increased use of rubrics for formative purposes has also sparked a heated debate regarding the merits of transparency and use of rubrics to support student performance, where some authors claim, for instance, that sharing criteria with students is not beneficial and almost inevitably leads to instrumental learning and “criteria compliance” among students (e.g., Sadler, 2014; Torrance, 2007). However, by reviewing the arguments against the use of rubrics, Panadero and Jonsson (2020) show that the empirical evidence behind this critique is currently weak, and mainly based on anecdotal evidence and/or personal experiences. This debate is therefore likely to intensify, especially if the use of rubrics for formative purposes continues to grow.

Effects of Rubrics on Student Performance

In general, it has been argued that the bigger effects of rubrics on students’ learning occur when they are implemented for self-assessment or peer assessment purposes. In their review of research on the formative use of rubrics, Panadero and Jonsson (2013) suggest—in line with the arguments made by Wiggins (1998)—that rubrics provide a measure of transparency to the assessment situation. By making criteria, performance levels, and (when relevant) scoring strategies explicit, these may become objects of action and reflection themselves (i.e., students can use them to regulate their learning) helping students to improve their learning via self and peer assessment (Nicol, 2021; Panadero et al., 2019). This interpretation is supported by students, who are generally positive about being provided with rubrics and claim to use the rubrics to better understand (and meet) expectations (e.g., Andrade & Du, 2005; Jonsson, 2014; Reynolds-Keefer, 2010). Consequently, there is a number of studies where rubrics have been used to promote different aspects of self-regulated learning, such as establishing more accurate goals, monitoring progress, and increasing self-regulation and metacognition (Brookhart & Chen, 2015; Panadero & Jonsson, 2013), while reducing cognitive load (Krebs et al., 2022), and increasing self-efficacy (Reddy & Andrade, 2010). All of these aspects are likely to contribute to improved performance among students (Panadero & Jonsson, 2013).

Several rubric studies have found a positive impact on student performance, where the students using a rubric showed a greater improvement compared to a control group (e.g., Brookhart & Chen, 2015). However, the findings from other studies are not necessarily as straight forward, for instance by only reporting statistically significant effects for some criteria or some groups of students (e.g., Becker, 2016; Montanero et al., 2014; Sáiz-Manzanares et al., 2015). Furthermore, longer and larger interventions might be needed in order to produce positive results for younger students (Panadero & Jonsson, 2013).

In addition to encompassing many different educational levels, topics, research designs, etc., most studies combine the use of rubrics with other pedagogical tools, such as “model assignments” (Andrade et al., 2008), feedback (Panadero et al., 2012), or “Jonassen’s (1999) constructivist, reflective, purposeful, interactive cooperative learning environment model” (Bay & Kotaman, 2011 p. 286). This diversity makes it difficult to get an overview of the effects on student performance by the use of rubrics from the narrative reviews currently available, or the influence from different moderating factors.

In addition, since the transparency provided by rubrics is thought to support students’ self-regulation of learning (SRL) and self-efficacy (Panadero & Jonsson, 2013), thereby indirectly affecting students’ academic performance, both variables are of particular importance in this context. As mentioned, rubrics have been used to promote self- and peer assessment, as rubrics may help students to establish more accurate goals, monitor their progress, increase self-regulation and metacognition (Brookhart & Chen, 2015; Panadero & Jonsson, 2013). This points to the importance of considering self-, and peer assessment as moderators, as well as SRL-variables and self-efficacy as important outcomes of using rubrics, along with student performance.

Potential Moderator Variables

Given the extensive use of rubrics, a great variation in design and implementation is to be expected, including different moderating factors that may have an impact on the effects of using rubrics. For this reason, we explore eleven variables as possible moderators on the effect of using rubrics on academic performance. First, the year of publication could influence the effect found in rubric research. As shown by Dawson (2017), rubric research has become more and more widespread, which means that, by “standing on the shoulders of previous research”, the quality of interventions may have improved over time. Therefore, we will explore whether interventions are getting more precise and stronger over time by exploring the year of publication as a moderator.

Second, some studies have found different effects for boys and girls, where girls benefit more from the intervention (e.g., Andrade et al., 2009). A similar effect is reported in a meta-analysis on the effects of self-assessment interventions (Panadero et al., 2017). Some peer assessment studies have also found gender differences (Bloom & Hautaluoma, 1987; Wen & Tsai, 2006). As rubrics are often implemented in combination with self and peer assessment activities, we included gender as a moderating factor.

Third, mean age needs to be considered, as research seems to suggest that students in more advanced educational levels may benefit more from self- and peer assessment interventions (Yan et al., 2022). As the use of rubrics facilitates different aspects of self-regulation, it is of interest to explore if a similar pattern can be identified in relation to the use of rubrics. Fourth, educational level, obviously in close relationship with mean age, will also be explored as a potential moderator. Fifth, an additional aspect related to age, but also to educational level, is whether the rubric intervention takes place in compulsory education (e.g., primary, secondary) or higher education. To our knowledge, there are no studies on rubrics that empirically compare these levels, but using a meta-analytical approach, we can explore such relationships.

Sixth, the number of sessions in which the students use the rubric is another moderating factor that could influence the effect. Just handing out rubrics does not guarantee educational gains (Brookhart, 2018). Therefore, it could be expected that students need to work with the rubrics for a number of sessions before an effect can be documented.

Seventh and eighth, rubrics can vary in relation to the number of assessment criteria and performance levels (Brookhart, 2013). There are only general indications on what could be the adequate number, and this could be greatly influenced by the context and students’ knowledge. Therefore, we investigate if the number of criteria or performance levels make a difference in the effect of using rubrics.

Ninth, when implemented with the intention of improving students’ learning, rubrics are supposed to generate positive effects in combination with students’ self and peer assessment (Brookhart, 2018). As these two are different in nature and may affect the outcome, we will explore them as potential moderators.

Tenth, we also explore research design as a potential moderator. Stronger research designs (i.e., randomized controlled trials) have more control over potential cofounding variables and may therefore lead to more accurate results. Thus, we explore if there are differences based on research design.

Finally, eleventh, the empirical quality of the study can influence the effects of an intervention (Valentine, 2020). More robust research designs with a larger sample, more acute operationalizations of the variables, more precise measurements, etc., might be more capable of identifying educational effects with greater precision. The instrument designed and used to measure empirical quality can be found in Appendix 2.

Another moderator that we considered was the timing of the rubric. Studies can be divided into two broad categories: (1) studies where the students are provided with rubrics before task performance, and therefore can use the rubric to plan and monitor their performance; and (2) studies where the students use rubrics to revise (and hopefully improve) previous task performance (Jonsson, 2020). Unfortunately, when we coded this moderator, we found that in the vast majority of studies the rubric was provided before, making it statistically unfeasible to run the analysis.

Aim and Research Questions

Our aim is to investigate the effects of using rubrics on students’ academic performance, self-regulated learning, and self-efficacy through three meta-analyses. We formulated three research questions (RQ):

  • RQ1. What is the effect of using rubrics and its potential moderators on academic performance?

  • RQ2. What is the effect of using rubrics and its potential moderators on self-regulated learning?

  • RQ3. What is the effect of using rubrics on self-efficacy?

Method

Selection of Studies

The search was conducted in February 2022 in PsycINFO, ERIC, SCOPUS, Web of Science, and ProQuest databases. Authors used the following combinations of keywords for the fields of title and abstract: rubric* OR (assessment AND matrix) OR (scoring AND guide*) OR (scoring AND grid) OR (grading AND list). Additionally, since 2022 the first and second authors have been particularly attentive to any new publication on rubrics via journal and citation alerts.

The inclusion criteria were: (a) the study included empirical results on the use of rubrics in relation to cognitive and non-cognitive skills, (b) analyzed the individual use of rubrics (not group work), (c) had a control group, (d) had quasi- or experimental designs, (e) had been peer-reviewed, and (f) was published in English.

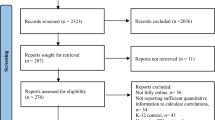
Figure 2 is a flowchart of the search and inclusion process. In total, 3,848 records were identified from the search. After removing duplicates, the first two authors independently screened the abstract of 200 out of 2,564 papers to assess the eligibility of the selected papers until a 100 percent agreement was reached. The remaining papers were divided among the first two authors to select the relevant empirical studies. The full texts of 97 selected studies were read and assessed. Reference lists of empirical articles and quotes from the included articles were also examined, resulting in 12 publications of interest. Based on the inclusion criteria, 24 studies were included in the data set. However, only 23 studies were included in the meta-analyses as there was only one study (Hongxia et al., 2020) exploring “engagement” as a variable, so it was not feasible to explore this variable due to the low number of studies. Of these 23 studies, 21 provided effect sizes for academic performance (54 effect sizes), 5 reported results on self-regulated learning (17 effect sizes), and 4 studies (with one effect size per study) reported results on self-efficacy.

Fig. 2
figure 2

Flowchart of search process and inclusion of articles

Full size image

If the studies did not include enough information to calculate an effect size, we contacted the authors and asked for the information. A total of thirteen authors were contacted, eight for statistical information, and five for information about the empirical procedure. Eleven authors replied, but only six provided the necessary information.

Coding the Articles

The first and second authors independently assessed the eligibility of 200 papers in two rounds, reaching a 98.5% inter-rater agreement. The screening of the remaining records was equally distributed between the first and second authors who also coded all the selected articles using a database containing the following categories: (a) aim; (b) research questions; (c) hypothesis; (d) characteristics of the sample (country of origin, percentage of women in the sample, mean age, grade, educational level); (e) self-assessment and peer assessment terminology, use of peer-assessment and whether they included grades; (f) use of other aids (exemplars, innovative computer scaffold, etc.); (g) length of intervention/training measured in number of sessions; (h) task and subject; (i) independent and dependent variables; (j) type and time of measurement, and type of data collection; (k) research design (type, use of pre-test and post-test and longitudinal data); (l) whether gender differences were found; (m) observations on the procedure; (o) results; (p) rubric characteristics (time when it was handed out, number of assessment criteria and levels); (q) conclusions; (r) direction of effect (whether dependent variables were inversed), (s) quality of the studies according to an “empirical quality” rubric (Panadero et al., 2023) and slightly modified for this study; and (t) statistical data (type, mean score, standard deviation, sample size, and Pearson correlation). A series of meetings among all the authors were held to discuss relevant aspects of the coding to maintain rigor throughout the process.

From the aforementioned variables, the following characteristics of the studies were further operationalized to be used as potential moderator variables: percentage of females in the sample, mean age of the sample, mean age imputed (i.e., when age was not reported, it was inferred from the specific educational gradeFootnote 1), educational level with the following categories: primary (from grade 1 to 6), middle (from grade 7 to 8), secondary (from grade 9 to 12), or higher education,Footnote 2 type of educational level (compulsory vs. higher education), length of the intervention (measured in number of sessions, and when it was not reported it was inferred from the intervention durationFootnote 3), performance levels of the rubric (the levels of executions usually presented as the number of columns), number of assessment criteria in the rubric (the areas to be evaluated usually presented in the first column), research design (quasi-experimental or experimental), and an empirical quality score obtained from an instrument designed for this study (Appendix 2).

This “empirical quality” instrument consists of a rubric with the following categories: research design, quality of the measurement tools, quality of the intervention (three subcategories: training, practice, length of the intervention), quality of dependent variables, and quality of the sample. Each study was evaluated according to all of these categories to calculate a summary score for quality.

The data and coding of all studies, including the measures of quality, can be found in the following link: https://osf.io/d6mry/?view_only=0db0f9c5617a492c84500c0a83a185b9.

Statistical analyses

We calculated and synthesized the standardized mean difference (Cohen’s d) as the main effect size, which indicates the magnitude of the difference in the dependent variable between the control group and the intervention group at a specific point in time. We applied Hedges’ correction to avoid overestimated standardized mean differences (Hedges, 1981), and the effect sizes are therefore referred to as Hedges’ g. A positive Hedges’ g indicates that the performance (or other outcome) of the intervention group was higher as compared to the control group. In addition, we calculated the standardized mean change (Becker, 1988)Footnote 4 for studies reporting pre-post measures for both the control and the intervention group. A standardized mean change indicates how much the outcome variable of the intervention group improved with respect to the improvement observed in the control group. A positive standardized mean change indicates that the outcome of the intervention group has improved to a greater extent (from the pre- to the post-test) as compared to the control group. To calculate the sampling variance of the standardized mean change, information on the correlation between pre-post measures in each group is needed. Since this correlation was not reported in the primary studies, we imputed a correlation of 0.4, which represents a moderate-to-high correlation according to Cohen’s cutoffs (Cohen, 1988). To interpret the overall effect size, we used the empirical cutoffs proposed by Hattie (2012). Specifically, Cohen’s d values from 0 to 0.2 were considered low, from 0.2 to 0.4 medium, and above 0.4 high (or “desired”) overall effect. We report overall effects together with their 95% confidence intervals and 95% prediction intervals. Prediction intervals indicate the range in which the effect size of a future study would be expected to fall within, if this study was chosen from the same population of studies included in one of these meta-analyses.

In some studies, several effect sizes could be calculated, either because the dependent variable was measured using different indicators, or because different types of rubrics were used (leading to multiple comparisons within that study). To model the dependency among effect sizes that were extracted from the same study, we applied a meta-analytic three-level model to synthesize effect sizes (Cheung, 2014; Van den Noortgate et al., 2013, 2015). This model takes into account the variability between effect sizes within studies (Level 2), and the variability among study effects across studies (Level 3). To test whether the variance within and between studies were significantly different from zero, we applied likelihood ratio tests, comparing the fit of a model that considers both sources of variance with the fit of a model that ignores one of these variances. If substantial variability among effect sizes was detected, we entered the moderator variables one by one in the three-level model. Continuous variables were previously centered. To avoid type I error rates above the nominal level (\(\alpha\) = 0.05), we applied the robust variance correction a posteriori to all these analyses (Fernández-Castilla et al., 2021a, 2021b; Tipton et al., 2019). Therefore, all the standard errors and confidence intervals reported in the result section are those obtained after applying the robust variance correction. At least ten effect sizes had to be available for each meta-regression to ensure minimal statistical power to detect an effect.

An analysis of outliers was carried out to detect extreme effect sizes. Specifically, we calculated the studentized deleted residuals for each effect size (Viechtbauer & Cheung, 2010), and we searched for effect sizes with studentized deleted residuals beyond ± 1.96. If potential outliers were detected, we removed them, and repeated all analyses without them.

Finally, we implemented several procedures to check for the presence of publication bias. First, we visually evaluated a figure known as the funnel plot, where effect sizes are plotted against their corresponding standard errors. In cases without publication bias, the distribution of effect sizes should exhibit symmetry within the funnel plot. When the distribution of effect sizes is asymmetrical—indicating a higher number of small studies contributing significant positive effects compared to small studies with considerable negative effects—it raises the possibility of the presence of publication bias. Second, we calculated the \({L}_{0}^{+}\) statistic of the Trim and Fill method (Duval & Tweedie, 2000), as according to Fernández-Castilla et al. (2021a, 2021b) this is currently the method with the highest power to detect the presence of publication bias (once controlled for the Type I error) given the characteristics of our dataset. If the value of \({L}_{0}^{+}\) was 3 or larger, we concluded that publication bias could exist. If publication bias was detected, we calculated a corrected overall effect size using the selection method of Vevea and Woods (2005). More information about how these methods can be used to detect and correct for publication bias can be found in the Supplementary material (Appendix 3).

All the analyses were carried out in R studio, using the following packages: metafor (Viechtbauer, 2010), clubSandwich (Pustejovsky, 2021), and weightr (Corbun & Vevea, 2019).

Results

RQ1. What Is the Effect of Using Rubrics and Its Potential Moderators on Academic Performance?

Meta-analysis on Standardized Mean Differences

A total of 54 standardized mean differences (Hedges’ g) were synthesized from 21 studies. The study-effects are depicted in Fig. 3. The black confidence interval around each study-effect represents the global study precision, whereas the gray confidence interval represents the precision provided only by the sample size of each study (Fernández-Castilla et al., 2020).

Fig. 3
figure 3

Forest plot of studies reporting effects on academic performance (standardized mean differences). Note: Black confidence intervals represent the global study-precision, whereas gray confidence intervals have been calculated using only sample size information. Therefore, the width of the gray confidence intervals is a direct function of the sample size, whereas the width of the black confidence intervals is a direct function of the global precision of the study, which depends on the sample size, the within study variability in that study, and the number of effect sizes reported. The dimensions of the squares correspond to the weights assigned to each study when computing the pooled effect size (larger squares indicate higher assigned weight). The J index denotes the count of effect sizes reported within the studies

Full size image

The overall Hedges’ g was 0.57 (SE = 0.125, t = 4.59, p-value < 0.001, 95% CI [0.312, 0.831], 95% PI [-0.558, 1.701]), which is a large overall effect. The variability between study-effects was statistically different from zero (\({\widehat{\sigma }}_{between }^{2}=\) 0.289, LRT = 4.22, p-value < 0.05) and the within-study variability as well (\({\widehat{\sigma }}_{within }^{2}=\) 0.028, LRT = 29.15, p-value < 0.001). No outliers were detected, and none of the potential moderator variables were significantly related to the observed effect sizes (see Table 1).

Table 1 Results from the moderator analyses for academic performance
Full size table

A slight asymmetry was detected in the visual inspection of the funnel plot (see Fig. 4): smaller studies tend to have larger effect sizes. However, the \({L}_{0}^{+}\) statistic was 0, meaning that the Trim and Fill test did not detect the presence of publication bias. Given the mixed evidence on the potential presence of publication bias, we decided to apply Vevea and Woods (2005) selection model to obtain a corrected, overall effect size. The corrected overall effect was 0.45 for moderate bias, and 0.33 for severe bias.

Fig. 4
figure 4

Funnel plot of standardized mean differences (Hedges’ g) for academic performance

Full size image

Meta-analysis on Standardized Mean Changes

A second meta-analysis was calculated with the twelve studies including 30 effect sizes that reported pre- and post-measures from both the intervention and control group, as in these studies standardized mean changes could be obtained. Figure 5 illustrates the study-effects of this subset of studies.

Fig. 5
figure 5

Forest plot of studies reporting effects on academic performance for which standardized mean changes could be calculated. Note. Black confidence intervals represent the global study-precision, whereas gray confidence intervals have been calculated using only sample size information. Therefore, the width of the gray confidence intervals is a direct function of the sample size, whereas the width of the black confidence intervals is a direct function of the global precision of the study, which depends on the sample size, the within study variability in that study, and the number of effect sizes reported. The dimensions of the squares correspond to the weights assigned to each study when computing the pooled effect size (larger squares indicate higher assigned weight). The J index denotes the count of effect sizes reported within the studies

Full size image

The overall standardized mean change was 0.38 (SE = 0.16, t = 2.34, p-value = 0.042, 95% CI [0.02, 0.75], 95% PI [-0.75, 1.51]), which is a medium overall effect. The variability between study-effects was statistically different from zero (\({\widehat{\sigma }}_{between }^{2}=\) 0.207, LRT = 6.01, p-value = 0.014), as well as the within-study variability (\({\widehat{\sigma }}_{within }^{2}=\) 0.098, LRT = 9.06, p-value = 0.003). Once again, no outliers were detected.

The mean age of the participants significantly predicted the variability of the standardized mean changes: for a one unit increase in the average age, there was a 0.062 unit decrease in the standardized mean changes, which suggests that the effect of the use of rubrics on academic performance decreases as the mean age of the sample increases (SE = 0.001, t = -243, p = 0.001). However, these results must be interpreted with caution, since they are based on only 14 effect sizes from two studies, and there were only two different values for the mean age. The overall standardized mean change also differed across educational levels: the overall effect for studies from secondary education was higher (g = 0.99, number of effects = 10) than the overall effect of studies from primary education (g = 0.03, number of effects = 10, difference = 0.96, p = 0.004) and middle school (g = 0.14, number of effects = 4, difference = 0.85, p < 0.001). No other effects were observed for the rest of the study variables (the results are provided in the supplementary material Appendix 3).

The funnel plot (Fig. 6) seems symmetric, meaning that publication bias might not be present. Furthermore, the Trim and Fill — \({L}_{0}^{+}\) statistic is equal to 0, which is another indicator suggesting that there is no publication bias.

Fig. 6
figure 6

Funnel plot of standardized mean changes for academic performance

Full size image

RQ2. What Is the Effect of Using Rubrics and Its Potential Moderators on Self-Regulated Learning?

A total of 17 effect sizes from five studies were synthesized. The study-effects are depicted in Fig. 7. The overall standardized mean difference was 0.23 (SE = 0.123, t = 1.82, p-value = 0.156, 95% CI [-0.15, 0.60], 95% PI [-0.65, 1.10]), which is small in magnitude. The variability between study-effects was not significantly different from zero (\({\widehat{\sigma }}_{between }^{2}=\) 0.017, LRT = 6.01, p = 0.014), but the within-study variability was (\({\widehat{\sigma }}_{within }^{2}=\) 0.168, LRT = 73.25, p < 0.001). No outliers were detected.

Fig. 7
figure 7

Forest plot of studies reporting effects on self-regulated learning (standardized mean differences). Note. Black confidence intervals represent the global study-precision, whereas gray confidence intervals have been calculated using only sample size information. Therefore, the width of the gray confidence intervals is a direct function of the sample size, whereas the width of the black confidence intervals is a direct function of the global precision of the study, which depends on the sample size, the within study variability in that study, and the number of effect sizes reported. The dimensions of the squares correspond to the weights assigned to each study when computing the pooled effect size (larger squares indicate higher assigned weight). The J index denotes the count of effect sizes reported within the studies

Full size image

Only one moderator variable explained part of the observed variability: when self-assessment and peer-assessment were used, the overall effect was significantly larger than when only self-assessment was used (see Table 2). However, since there are only five effect sizes available for the category “self-assessment and peer-assessment used”, these results should be interpreted with caution. The effect sizes seem to symmetrically distributed across the funnel plot (Fig. 8), meaning that publication bias is not likely not be present. This result is further supported by the Trim and Fill — \({L}_{0}^{+}\) statistic which is equal to 0.

Table 2 Results from the moderator analyses for self-regulated learning
Full size table
Fig. 8
figure 8

Funnel plot of standardized mean differences (Hedges g) for self-regulated learning

Full size image

Meta-analysis on Standardized Mean Changes

Only three studies provided enough information to calculate a standardized mean change (including five effect sizes). These five effect sizes were pooled using a standard random effects model. The pooled effect was 0.05 (SE = 0.189, Z = 0.263, p = 0.792, 95% CI [-0.32, 0.42], 95% PI [-0.81, 0.91], \({\widehat{\sigma }}_{between }^{2}\) = 0.156), which is a small (almost null) effect. Since the number of effect sizes available was very small, meta-regressions and publication bias analyses were not carried out.

RQ3. What Is the Effect of Using Rubrics on Self-Efficacy?

Only four effect sizes (coming from four different studies) summarized the effect of using rubrics on self-efficacy (see Fig. 9). Therefore, a standard random-effects model was applied. The overall effect was 0.18 (SE = 0.05, Z = 3.31, p < 0.001, 95% CI [0.07, 0.29], 95% PI [0.07, 0.29], \({\widehat{\sigma }}_{between }^{2}\)= 0.000), which is small in magnitude. No other analyses were performed due to the small number of effect sizes.

Fig. 9
figure 9

Forest plot of studies reporting effects on self-esteem (standardized mean differences). Note. Black confidence intervals represent the global study-precision, whereas gray confidence intervals have been calculated using only sample size information. Therefore, the width of the gray confidence intervals is a direct function of the sample size, whereas the width of the black confidence intervals is a direct function of the global precision of the study, which depends on the sample size, the within study variability in that study, and the number of effect sizes reported. The dimensions of the squares correspond to the weights assigned to each study when computing the pooled effect size (larger squares indicate higher assigned weight). The J index denotes the count of effect sizes reported within the studies

Full size image

Secondary Results from a Posteriori Hypothesis

Moderator analyses in relation to standardized mean changes of academic performance suggested that the effect of using rubrics decreases as the mean age of the sample increases. However, the overall effect for studies from secondary education was also higher than those from primary education, making the results contradictory. As it has been suggested in previous research (Panadero & Jonsson, 2013) that there is an interaction between age/educational level and the “time devoted to work with the rubric” (p. 140), secondary analyses were carried out, using the standardized mean differences (Hedges’ g) for academic performance, to explore this interaction.

The number of sessions (centered), mean age (centered), and the interaction were therefore entered in the meta-regression, producing a statistically significant and negative interaction effect (B = -0.041, SE = 0.001, t = -62.1, p < 0.001, 95% CI [-0.05, -0.03]), which means that the relationship between the number of sessions and the standardized mean differences decreases as the mean age increases (see Fig. 10). That is, the length of the intervention has less effect on the observed effect in samples with a larger mean age. Interpreting it in another way, this negative interaction effect indicates that the effect of the mean age on the observed effect sizes increases as the length of the intervention diminishes. When mean age imputed was entered instead of mean age, the interaction term was still negative, but not statistically significant (p = 0.677).

Fig. 10
figure 10

Effect of the interaction between mean age and number of sessions (both variables centered)

Full size image

Discussion

This meta-analysis has explored the effects of the use of rubrics on students’ academic performance, self-regulation, and self-efficacy, along with moderating variables assumed to have an impact on these effects. The use of rubrics was shown to have a positive and moderate effect on students’ academic performance, and a positive but smaller effect on students’ self-regulation and self-efficacy. In most analyses, the potential moderator variables were not significantly related to the observed effect sizes.

The Effect of Rubrics and Moderators on Students’ Academic Performance

In their review on the use of rubrics, Jonsson and Svingby (2007) claimed that it was not possible to draw any conclusions about student improvement related to the use of rubrics, as the findings were mixed. Similarly, Brookhart and Chen (2015) concluded that the “body of evidence that is accumulating is promising but not sufficient for establishing that using rubrics cause increased performance” (p. 363). The results from our meta-analyses, however, clearly lend support to the conclusion that the use of rubrics aid students during task performance, so that they may perform at a higher standard as compared to control groups and/or on assignments performed before they were provided with rubrics.

The strength of the effect of using rubrics on students’ academic performance was estimated by calculating Hedges’ g using 54 standardized mean differences from 21 studies, which showed an overall effect of 0.57. However, as a slight asymmetry was detected in the funnel plot, a selection model was used to obtain a corrected overall effect size, providing different effect sizes for moderate and severe bias respectively. Since the Trim and Fill test did not detect the presence of publication bias, a small to moderate bias is more likely, suggesting an effect size of 0.45. Furthermore, according to calculations made from 30 standardized mean changes in 12 studies reporting on pre- and post-measures from both the intervention and control group, the effect was 0.38. The effect of using rubrics can therefore be assumed to be positive and moderate.

As suggested by previous research (Jonsson & Svingby, 2007; Panadero & Jonsson, 2013), our results show that we can keep the hypothesis that by making criteria and performance levels explicit, students can use them to regulate their learning and improve their performance.

Recent studies have looked at how different rubric designs might influence student performance. However, these studies, including our own, found that the specifics of rubric design do not significantly affect the outcomes (Jonsson & Panadero, 2017; Brookhart, 2018). This finding is somewhat surprising because previous researchers, like Jonsson and Panadero (2017), believed that carefully designing rubrics could enhance student learning. They suggested using multiple quality levels and a detailed scoring method, rather than just a total score. Rubrics, by definition, include criteria and descriptions of performance levels (Brookhart, 2018). Most research on rubrics, therefore, already considers these elements in their design. The main differences in these studies are in the number of criteria and performance levels used, but these differences do not seem to have a major impact on how students perform. Brookhart (2018) also found no link between the type or quality of a rubric and student performance.

From the analyses of potential moderating variables, only mean age and educational level were found to have a statistically significant relationship to the observed effect sizes. Furthermore, this relationship was only seen when effect sizes were calculated from standardized mean changes (i.e., not standardized mean differences). Here, the effect of using rubrics was seen to decrease as the mean age of the sample increased (i.e., younger students benefited more from using rubrics). On the other hand, the effect for studies from secondary education was higher than the overall effect of studies from primary education and middle school, suggesting a reversed direction of effects as compared to students’ age. Results from analyses of these moderating variables are therefore inconclusive, although the results from studies reporting on educational level may be more reliable, as the analyses on mean age were based on fewer effect sizes reported in two studies only, which make this conclusion very tentative. This would suggest that secondary students might benefit more from using rubrics as compared to younger students. However, there are no similar findings from earlier reviews for comparison. Previous reviews either concentrated on studies in higher education (Brookhart, 2018; Reddy & Andrade, 2010) or indicated a link between a student's age/educational level and the effectiveness of comprehensive interventions. It has been suggested that younger students might need longer and more extensive interventions for positive outcomes (Panadero & Jonsson, 2013). This theory aligns with our study's results, which demonstrate that intervention length has a lesser effect on older students. In contrast, studies in higher education frequently report positive outcomes from using rubrics, irrespective of intervention length (Brookhart, 2018; Panadero & Jonsson, 2013).

Student gender is a potential moderating variable that has been discussed in previous reviews, where the use of rubrics has been shown to have different effects on boys and girls in some studies, but not significant in others (Panadero & Jonsson, 2013). Brookhart and Chen (2015) suggest that there may be a gender effect in relation to writing, where girls seem to have an advantage, but whether there is a more general effect is unknown. The results from the current study suggest that there is no such general effect of gender on student performance from using rubrics in the studies included here.

Other potential moderating variables are self- and peer assessment. Jonsson and Svingby (2007) wrote that, although they found only few studies on this topic, these studies indicated that “rubrics might be valuable in supporting student self- and peer assessment” (p. 139). If rubrics facilitate self- and peer assessment, this may in turn support student performance (cf. Andrade, 2019; Yan et al., 2022). Panadero and Jonsson (2013) also suggest that there is evidence supporting the claim that rubrics may aid in improving student performance if combined with “self-assessment or other meta-cognitive activities” (p. 140). Our results show that the use of rubrics produced similar effect sizes if combined with either self or peer assessment. As self and peer assessment usually involve the use of metacognitive and regulatory strategies, both seem to be equally effective when combined with rubrics. It was not possible to empirically compare the effects of using self- and peer assessment against a control, however, as all studies included one or both strategies in combination with the use of rubrics.

Taken together, no claims can be made from this study beyond the conclusion that the use of rubrics have a positive and moderate effect on students’ academic performance. It is important to note, however, that the exploration of some of the moderators is based on a narrow selection of studies, which might affect the stability of the results.

The Effect of Rubrics and Moderators on Students’ Self-Regulated Learning

To investigate the effect of the use of rubrics on students’ self-regulated learning, 17 effect sizes from five studies were synthesized. The overall effect was 0.23, which is considered a small effect. None of the moderator variables significantly explained the observed variability. Nevertheless, our study contributes by showing that there is indeed a positive effect of using rubrics on students’ self-regulated learning, suggesting that rubrics can be used as a facilitator for students’ self-regulation.

As noted by Panadero and Jonsson (2013), rubrics have been shown to facilitate several aspects of self-regulated learning. Improved self-regulation may therefore be a potential outcome of using rubrics. However, self-regulated learning is also a potential moderator, as students may use self-regulation strategies together with rubrics to improve their performance (see e.g., Jonsson, 2020). Complicating the matter further, self-regulation models comprise a wide range of cognitive, motivational, behavioral, and contextual variables, making Brookhart and Chen (2015) suggest that research on the relationships among these variables and rubrics still have a long way to go before we fully understand them. Unfortunately, the number of included studies did not allow for conducting specific analyses to contrast different self-regulatory strategies (e.g., motivation, emotions), thus one meta-analysis was performed for all effect sizes. Therefore, it can be recommended as a future direction of research to study more closely which parts of the self-regulation process rubrics can facilitate.

The Effect of the Use of Rubrics on Students’ Self-Efficacy

Panadero and Jonsson (2013) discuss the influence of using rubrics on students’ self-efficacy with reference to a study by Andrade et al. (2009), where the self-efficacy ratings of boys and girls are affected differently by long-term rubric use. Brookhart and Chen (2015) include a couple more studies in their discussion on rubrics and self-regulation of learning, but note that the evidence is mixed, where some studies reported increased student self-efficacy from the use of rubrics, while others reported non-significant effects.

In our study, the overall effect of the use of rubrics on students’ self-efficacy was small (0.18). However, this estimate is based on only four effect sizes from four different studies, which means that the result should be interpreted with caution. Still, it is interesting to note that this set of studies is particularly strong in terms of research design (i.e., either RCTs or well-planned quasi-experiments), they have substantial sample sizes (up to 762 participants in one of the studies), and some of the studies have control variables (e.g., self-regulated learning, different types of feedback as independent variables). Nevertheless, we still need to be careful with the interpretation of these results.

By providing transparency to the assessment situation, through criteria and performance levels, students could be expected to be in a better position to decide whether they are able to handle the assignment or not. If they think that they can, self-efficacy should increase, as should the use of productive self-regulation strategies. This is also the picture that emerges from studies investigating students’ perceptions of using rubrics, such as the studies by Andrade and Du (2005), Jonsson (2014), and Reynolds-Keefer (2010) mentioned above.

However, it is also possible that the rubric could make the assignment appear more complex or difficult to complete (in particular with high standards), which would lower students’ self-efficacy and potentially increasing the use of more negative self-regulation strategies, such as avoidance goals. This aspect is not well researched, although Panadero et al. (2013) report that the use of rubrics in fact decreased such negative self-regulation strategies. Similar to what was suggested in relation to self-regulation strategies above, the relationship between the use of rubrics and self-efficacy can be recommended as a future direction of research.

The Influence of Other Moderating Variables

In addition to the moderating variables discussed above, factors relating to the quality of research and publication were also explored, namely: (1) year of publication, (2) research design, and (3) the quality of the study. However, none of these were significantly related to the observed effect sizes. Since the range of research designs is very limited, encompassing only experimental and quasi-experimental studies, the lack of influence of this factor could perhaps be expected. Still, although the estimated quality among the studies provided greater variability (observed range was 5–13 points on a scale from 0–14), this factor did not seem to influence the outcomes either. Finally, it was assumed that later studies could have learnt from previous ones, resulting in larger effect sizes, but this assumption could not be confirmed.

Future Lines of Research

First, while the results from this meta-analysis are important for estimating the effects of the use of rubrics on students’ academic performance, self-regulation, and self-efficacy, the selected studies do not clarify the mechanisms for how rubrics influence students’ academic performance, self-regulation, and self-efficacy. Consequently, research is needed that investigates more closely how students use rubrics by using external data sources (e.g., eye-tracking, direct observation), along with stronger measures of students’ own perceptions and statements, such as thinking aloud protocols or validated self-report tools.

Secondly, more research is needed to understand the relationship between the use of rubrics and students’ self-regulated learning. This relationship is complex, not least since self-regulated learning is multifaceted, encompassing cognitive, motivational, behavioral, and contextual aspects, which can all interact with the use of rubrics. As already noted by Brookhart and Chen (2015), research in this area has only just begun to explore these intricacies and still has a long way to go.

Thirdly, for future research to have a bigger impact in what we know about rubrics, the quality of the reports needs to improve dramatically. It is almost a constant in assessment research that the quality of reports is low, as mentioned in other reviews (e.g., Panadero et al., 2023). In the context of rubrics, there is often limited information available regarding two crucial aspects: rubric design and implementation. Access to details about rubric design reflects the quality of the instrument, while additional information on implementation sheds light on how teachers and students actually used the rubric. This information is essential for enhancing our understanding of the effects of rubrics. With the purpose of improving the quality of rubric studies reports we have created an instrument (see Appendix 4) following the original idea from Panadero and colleagues (2023). Our intention is that researchers could include this instrument as supplementary material to their articles. By having that information, future readers and colleagues conducting reviews or replications will be able to better understand the research design and the intervention. The instrument is freely available online via: https://osf.io/3hgcv/?view_only=31b7b778c81a40a5a7a00b55e416ad94.

Fourth, it will be important to conduct studies that investigate the long-term effects of rubric interventions. Such research could offer insights about, for instance, the sustainability of rubrics interventions, or whether there is transfer of students’ knowledge about how to use rubrics from one subject to other subjects with different teachers.

Educational Implications

The major educational implication from this meta-analysis is that the use of rubrics has a positive influence on students’ academic performance, and to a lesser extent on students’ self-regulation strategies and self-efficacy. According to the analyses of potential moderating variables, it does not seem to matter how many criteria or quality levels the rubrics have, as long as they meet the basic definition of rubrics, and there are no clear indications of rubrics being more or less effective for younger or older students, or for students of different genders.

Conclusion

The use of rubrics has shown a positive and moderate effect on students’ academic performance, and a positive but smaller effect on self-regulation strategies and self-efficacy. These findings might not appear as particularly striking, as there are already a number of systematic reviews drawing similar conclusions. However, the meta-analytical approach has the additional benefit of quantifying such effects. The observed effects make sense, since well-designed rubrics draw students’ attention to the core aspects of how to execute the task with perfection. Furthermore, rubrics are used to evaluate whether students have indeed improved their performance, possibly reenforcing the effect even further. The finding that rubrics sometimes do not contribute to positive gains might therefore be seen as more startling.

To further our understanding of the processes underlying the effects, we explored the role of potential moderators. In most analyses, none of these potential moderator variables were significantly related to the observed effect sizes. An exception is that the length of the intervention was shown to have less impact on the observed effect in samples with older students, which means that older students, primarily in a higher education context, need less support to reap the benefits of using rubrics for formative purposes. It should be noted, however, that the lack of statistical significance in this analysis do not rule out a possible relationship between moderators and effects. In particular, there are two aspects of rubric research that limit the analysis of potential moderators. First, the number of studies exploring different moderators is relatively small, limiting the analysis. Second, there is quite some room for improvement when it comes to reporting important aspects of rubric design and implementation. To amend this situation, we are providing an instrument to support the report on rubric characteristics in future studies Appendix 4.

In conclusion, we assert that a key question to be answered by upcoming research is not whether rubrics work or not, but under what circumstances. In order to answer this question, future primary research need to clearly report on the specifics of the interventions, while future research reviews need to explore the characteristics of high-quality studies reporting on the successful implementation of rubrics, such as those identified in this meta-analysis.