How Strong Is the Evidence for a Causal Reciprocal Effect? Contrasting Traditional and New Methods to Investigate the Reciprocal Effects Model of Self-Concept and Achievement

Abstract

The relationship between students’ subject-specific academic self-concept and their academic achievement is one of the most widely researched topics in educational psychology. A large proportion of this research has considered cross-lagged panel models (CLPMs), oftentimes synonymously referred to as reciprocal effects models (REMs), as the gold standard for investigating the causal relationships between the two variables and has reported evidence of a reciprocal relationship between self-concept and achievement. However, more recent methodological research has questioned the plausibility of assumptions that need to be satisfied in order to interpret results from traditional CLPMs causally. In this substantive-methodological synergy, we aimed to contrast traditional and more recently developed methods to investigate reciprocal effects of students’ academic self-concept and achievement. Specifically, we compared results from CLPMs, full-forward CLPMs (FF-CLPMs), and random intercept CLPMs (RI-CLPMs) with two weighting approaches developed to study causal effects of continuous treatment variables. To estimate these different models, we used rich longitudinal data of N = 3757 students from lower secondary schools in Germany. Results from CLPMs, FF-CLPMs, and weighting methods supported the reciprocal effects model, particularly when math self-concept and grades were considered. Results from the RI-CLPMs were less consistent. Implications from our study for the interpretation of effects from the different models and methods as well as for school motivation theory are discussed.

Researchers in educational psychology have put considerable effort into investigating reciprocal relationships between self-concept and student achievement (e.g., Huang, 2011; Marsh & Craven, 2006; Valentine et al., 2004; Wu et al., 2021). Academic self-concept reflects a person’s perceptions about their abilities formed through self-experiences with performance and the environment (Marsh, 1990b; Marsh et al., 2016; Shavelson et al., 1976). Positive self-concepts are believed to have many desirable effects, particularly those related to academic outcomes (Brunner et al., 2010; Huang, 2011) but also regarding psychological and physical health and child development (Marsh & Martin, 2011; Möller et al., 2009).

Since the 1970s, three concurring models have been formulated (e.g., Arens et al., 2017): the skill development model, which assumes that achievement influences self-concept; the self-enhancement model (Calsyn & Kenny, 1977; Valentine et al., 2004), which assumes the opposite pattern; and the reciprocal effects model (REM; Marsh, 1990a), which assumes that the two constructs are reciprocally related. These three models have typically been investigated using statistical models from the family of cross-lagged panel models (CLPMs; e.g., Marsh & Craven, 2006; Usami, Murayama, & Hamaker, 2019a) claiming to investigate “causal relations between academic achievement and academic self-concept” (Marsh & Craven, 2006, p. 151). Thus, specific patterns of results in the cross-lagged parameters have often been interpreted causally and as evidence in favor of one of the three models outlined above (e.g., Helmke & van Aken, 1995; Marsh et al., 2005; Marsh & Martin, 2011; Pinxten et al., 2010; Sewasew et al., 2018).

However, the assumptions under which statistical relationships in different types of CLPMs can be interpreted causally have seldom been made explicit, thus leaving us with uncertainty about the strength of evidence for a causal reciprocal effect of self-concept on achievement using different models/methods. Methodological research has suggested that neither longitudinal data nor the specification of a CLPM per se is sufficient for estimating causal effects (e.g., Hamaker et al., 2015; Rogosa, 1980). More specifically, Usami et al. (2019a) argued that the assumptions required for CLPMs to allow for a causal interpretation might be rather unrealistic in practice. They argued that other models, such as the RI-CLPM or weighting methods, might provide promising alternatives to satisfy these assumptions and more safely estimate causal effects. On the basis of our review of the respective literature, these issues leave applied self-concept researchers with two sets of challenging questions: First, what are the assumptions for causal inference made by weighting methods, and how likely are they to be satisfied when reciprocal effects between self-concept and achievement are investigated? Second, is there evidence of reciprocal effects of academic self-concept and achievement when these methods are used for causal inference, and how do results from traditional and new methods compare with one another? In addressing these questions, we will investigate reciprocal relationships between student self-concept and achievement using (a) traditional CLPMs, (b) FF-CLPMs (e.g., Lüdtke & Robitzsch, 2022), (c) RI-CLPMs (Hamaker et al., 2015), and (d) two weighting approaches (covariate balanced generalized propensity score weighting [CBGPS-weighting] and entropy balancing [EB]). The two weighting approaches were explicitly developed to study causal effects of continuous treatment variables in observational studies (Fong et al., 2018; Hainmueller, 2012; Tübbicke, 2021). The results of this substantive-methodological synergy (Marsh & Hau, 2007) will shed new light on one of the core topics of prior educational psychological research, the reciprocal relations between student self-concept and achievement, and the robustness of these relations under different assumptions for causal inference. Beyond providing these new insights, the discussed methods are of general importance for the broader audience of educational psychologists interested in cross-lagged effects.

The Interplay Between Student Motivation and Achievement

In recent decades, many studies have investigated the association between students’ self-concept and their achievement (e.g., Arens et al., 2017; Huang, 2011; Wu et al., 2021). Academic self-concept reflects a person’s perceptions of their abilities, formed through self-experiences with performance and the environment (Marsh, 1990b; Marsh et al., 2016; Shavelson et al., 1976). Positive self-concept has been discussed as a potential gateway to enhance student learning via specific targeted interventions and educational reforms (Uchida et al., 2018; Valentine et al., 2004) and as a mediator of a host of further desirable social-emotional and behavioral outcomes (O'Mara et al., 2006). The statistical models from this research have consistently shown reciprocal relationships between academic self-concept and achievement, that is, positive partial regression coefficients. However, our review of the respective literature also showed that whether and under which assumptions these relationships can be interpreted as representing causal effects is an open question that has seldom been addressed by substantive researchers.

In a meta-analysis, Huang (2011) investigated longitudinal relationships between prior self-concept and achievement (i.e., grades or test scores) with subsequent achievement and self-concept using data from 39 independent samples. The study reported average correlations ranging from r = .20 to .27 between prior self-concept and later achievement and correlations ranging from r = .19 to .25 between prior achievement and subsequent self-concept, all of which were interpreted as evidence of reciprocal relationships. Wu et al. (2021) conducted another more recent meta-analysis in which they considered results from 68 longitudinal studies and found that prior achievement significantly predicted subsequent self-concept (β = .16, p < .01) after accounting for prior self-concept scores. In addition, prior self-concept predicted subsequent achievement (β = .08, p < .01) after accounting for prior achievement scores. Notably, this study also suggested that self-concept might be more strongly related to grades than to achievement on standardized tests. The authors argued that grades are often based on high-stakes assessments, which have strong implications for students and are therefore strongly influenced by motivational student characteristics, whereas achievement assessed by standardized achievement tests in educational studies is typically more low-stakes and might therefore be less strongly influenced by students’ self-concept (e.g., Arens et al., 2017; Hübner et al., 2022; Marsh et al., 2005; Wylie, 1979). Further studies have extended these findings by focusing on dimensional comparisons (e.g., internal and external frames of reference). A meta-analysis by Möller et al. (2020) found substantial positive path coefficients between achievement and self-concept in similar subjects but substantial negative path coefficients in dissimilar subjects. Taken together, these studies provide important evidence in favor of reciprocal relationships between self-concept and student achievement. But the questions of whether and under which assumptions these partial regression coefficients can be interpreted as causal have received little attention in substantive research on this topic.

Challenges and Assumptions Involved in Interpreting Cross-Lagged Coefficients as Causal: a Potential Outcome Perspective

Usami et al. (2019a) provided a comprehensive overview of requirements for causal inference in cross-lagged panel models that were based on the Rubin causal model (Rubin, 1974). The Rubin causal model defines causal effects in terms of potential outcomes. Potential outcomes are hypothetical values: For instance, Y(1) would be a person’s potential outcome that would have been observed if this person was assigned to the treatment condition (T = 1), and Y(0) would be the person’s potential outcome that would have been observed if that very same person had been assigned to the control condition (T = 0). These values are referred to as “potential outcomes” because the two different values can never be observed for one person at the same time under similar conditions. This is oftentimes conceptualized as the fundamental problem of causal inference (Shadish, 2010; West & Thoemmes, 2010). Note that in order to investigate a causal effect, it is also possible to define the treatment variable as continuous (e.g., Fong et al., 2018; Hirano & Imbens, 2004; Lüdtke & Robitzsch, 2022; Tübbicke, 2021; Voelkle et al., 2018). In such cases, a potential outcome of individual i (e.g., Y_i) takes a value, given a specific intensity of the continuous treatment/exposure variable (e.g., Y_i(e)). On the basis of this, one can define the causal cross-lagged effect in REM with panel data. In our case, this means that we can define achievement and self-concept as continuous treatment variables. Lüdtke and Robitzsch (2021) applied this framework to define the cross-lagged causal effect. Translated to the REM, one would define the causal cross-lagged effect of self-concept on grades as the following linear model:

$$\text{E}\left(G_{i3}\left({sc}_2\right)\right)={\mathrm\beta}_0+{\mathrm\beta}_1{sc}_2$$

where the outcome—the grades received by individual i (G_i3) given a specific value of self-concept (SC₂ = sc₂)—is predicted by an intercept β₀ and the causal effect β_1. Here, β₁ constitutes the causal effect of increasing self-concept at the second measurement occasion by 1 unit on grades at the third measurement occasion. Linearity suggests that this model is a linear combination of variables or functions thereof and does not exclude nonlinear terms (Hernán & Robins, 2020). Specifically, the linear model above displays a marginal structural mean model, and the outcome of this model is counterfactual and therefore never observed. The treatment parameters in such a structural mean model represent the average causal effect (Hernán & Robins, 2020). This suggests that if we are interested in causal cross-lagged effects, we will have to assume that parameters revealed from specified statistical models (e.g., CLPMs or weighting methods) have the same causal interpretation as β₁ in the model outlined above. Usami et al. (2019a) outlined three assumptions that need to be satisfied in order for CLPMs to identify causal effects: (a) consistency, (b) strong ignorability/no unobserved confounding, and (c) positivity (also see Lüdtke & Robitzsch, 2022). In reference to Rubin’s potential outcome framework (e.g., Holland, 1986; Rubin, 1974, 2004), consistency implies that the observed outcome of a person is identical to the potential outcome of this person, given their observed exposure history (Rehkopf et al., 2016). It requires that the treatment must be carefully and precisely defined so that variation in the exposure does not lead to different outcomes and thus ties the observed outcomes to the potential outcomes. Note that whereas Usami et al. (2019a) named consistency as one of three assumptions, other authors have considered it an integral part of the stable unit treatment value assumption (STUVA; Rubin, 1974; Vanderweele & Hernán, 2013). Again, other authors have not conceptualized consistency as an assumption but as a theorem (Pearl, 2010). A violation of this assumption in an experimental setting would occur, for instance, if multiple versions of a treatment exist (see Rehkopf et al., 2016). Related to this, Vanderweele and Hernán (2013) referred to literature that discusses how to handle settings with multiple versions of a treatment. The strong ignorability/no unobserved confounding assumption requires that all potential confounding variables are measured and adequately considered in the respective model (Rosenbaum & Rubin, 1983). Finally, the positivity assumption requires that all treatment × covariate combinations exist in the population. Practically, this suggests that the covariate distribution must show sufficient overlap across the different values of a treatment variable (Kang et al., 2016). This assumption could be explored by distributional balance checks (e.g., plots that display the overlap of covariate values between treatment and control units/different levels of the treatment variable) or cross-tables. As outlined by Thoemmes and Ong (2016) for continuous treatment variables and in settings with many covariates, however, such checks become increasingly difficult to implement, and some authors have argued that this assumption might be very strong in practice (e.g., Tübbicke, 2021).

Challenges and Assumptions Involved in Interpreting CLPM Results as Causal: a Structural Causal Model Perspective

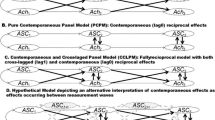
A conceptual look at the REM seems helpful for deriving potentially reasonable structural causal models on the relationship between self-concept and achievement from the literature. Structural causal models are models of reality that present considerations and assumptions about causal relationships between variables (Cunningham, 2021; Lüdtke & Robitzsch, 2022; Pearl et al., 2016). They consist of exogenous and endogenous variables, operators (arrows) that indicate the direction of the respective causal effects (see Fig. 1), and any functional form to link the two types of variables (not displayed). Researchers can easily apply these models to a scenario in which they would like to know the causal effect of self-concept (SC) on grades (G). Importantly, as outlined in more detail by Voelkle et al. (2018), in order to define and identify the causal effect, it is not necessary to be able to physically manipulate a variable in the real world (e.g., by setting SC to a specific value). Based on this, structural causal models are assumed to display causal relationships (Pearl, 2009).

Fig. 1

Potential structural causal models for the reciprocal relationships between self-concept, grades, and test achievement. Note. SC, self-concept; G, grades; T, test achievement. C denotes a vector of potential confounders. Indices indicate measurement occasions

By contrast, statistical models such as structural equation models (e.g., CLPMs), which are typically used in educational psychological literature on reciprocal relationships between self-concept and achievement (e.g., Arens et al., 2017; Ehm et al., 2019), are based on linear regressions and are related to specific data. Such statistical models have a specific causal interpretation only if they are linked to a causal framework via specific identification rules. There are different frameworks that can be used in this regard, for instance, Rubin’s potential outcome framework (Rubin, 1974; see above), sometimes synonymously referred to as a counterfactual framework (Shadish, 2010), or other frameworks, such as structural causal models (Pearl, 2009; Pearl et al., 2016; see above).

On the basis of prior research on reciprocal relationships between self-concept and achievement, we derived three types of structural models (e.g., Huang, 2011; Marsh et al., 2005; Marsh & Craven, 2006; Preckel et al., 2017; Seaton et al., 2015; Sewasew et al., 2018; Wu et al., 2021) that are depicted in Fig. 1: (a) a model with prior scores predicting post scores; (b) a model with additional lag-2 effects (e.g., with additional paths from the first to the third measurement occasion), also referred to as a full-forward model; and (c) a model with lag-2 effects and additional confounders.

In the simplest structural model (a) derived from the respective REM literature (e.g., Arens et al., 2017; Preckel et al., 2017), self-concept, grades, and test achievement (SC, G, and T in Fig. 1) are assumed to be reciprocally related. This means that the structural causal model assumes paths from all preceding variables to all variables at the next assessment timepoint. This model is indeed very (and probably overly) restrictive: It is based on the assumption that there are no other time-constant and time-varying variables that simultaneously influence academic self-concept and achievement (e.g., no hidden confounders, backdoor paths) and that there are no additional lagged effects (e.g., carry-over effects). In practice, this model seems unrealistic: It is well-known that achievement and self-concept are typically related to many variables beyond self-concept and achievement, such as socioeconomic status, gender, or school type (Chmielewski et al., 2013; Hübner et al., 2017; Sirin, 2005; Voyer & Voyer, 2014), and prior studies have found evidence of carry-over effects, particularly on autoregressive but also on cross-lagged coefficients (e.g., Arens et al., 2017; Ehm et al., 2019; Preckel et al., 2017).

Structural model (b) is similar to model (a) but additionally includes lag-2 effects (e.g., T1 to T3). Specifically, this model would imply that all preceding variables have effects on subsequent variables, but that self-concept, grades, and test achievement at the very first occasion also have long-term effects (e.g., carry-over effects) on all variables at the third measurement occasion. This model is more plausible as empirical results show that full-forward autoregressive and cross-lagged coefficients are quite commonly predictive in REMs (e.g., Arens et al., 2017). However, it still leaves out other confounding variables that are time-invariant properties of the students and time-varying states at the different measurement occasions. In the context of the REM of self-concept and achievement, time-invariant confounders could be trait-like differences, for example, in students’ achievement, school track, or gender. Time-variant, state-like confounding could result, for instance, from specific events that occur between measurement occasions and that have rather immediate effects on students’ self-concept and somewhat delayed effects on their achievement. As one example, students who recently received some praise from their teachers for their creativity in solving mathematical problems may immediately show higher self-concept in mathematics, but they will likely show higher achievement only after a while (e.g., due to increased effort in mathematics lessons, homework).

Finally, structural model (c) is similar to model (b) but also includes a vector of confounding variables that might be time-invariant or time-varying. For instance, as prior empirical research suggests, girls and boys differ in their math self-concept, and prior studies have also reported gender differences in math achievement to some extent, and these should be controlled for (e.g., Hübner et al., 2017; Watt et al., 2012; Watt et al., 2017). Furthermore, if confounders change over time, and/or change their association with grades, achievement tests, and self-concept over time (time-varying confounders), these would need to be controlled for in the model. Considering prior research on self-concept and achievement, this structural causal model seems to be most realistic compared with (a) and (b), as it explicitly considers confounders that influence the different variables in the REM.

Recent Methodological Advancements for Investigating Reciprocal Relationships

In recent years, several statistical models were discussed to overcome the shortcomings of the traditional CLPM with regard to confounders: the RI-CLPM, the FF-CLPM, and weighting methods. All of these models come with specific assumptions and requirements for revealing cross-lagged causal effects (see Table 1).

Table 1 Comparison of central assumptions between different methodological approaches to estimate reciprocal effects of self-concept and achievement

RI-CLPM

In 2015, Hamaker et al. introduced the RI-CLPM, a model that adds random intercepts to the CLPM. The conceptual idea for this model resulted from a multilevel perspective on longitudinal data, whereby repeated observations are nested within individuals. Technically, the CLPM is nested within the RI-CLPM, and the two models are identical if the variances and covariances of the random intercept factors are set to zero (Hamaker et al., 2015). The specific advantage of the RI-CLPM over the CLPM, particularly with regard to causal inference, was argued to result from the fact that it separates processes that take place within individuals from time-stable observed and unobserved differences between individuals. The idea of eliminating this time-stable between-person variation is less prominent in educational psychology but more common in econometric panel analysis, for instance, when using unit-centering or adding unit-dummy variables to regression models (Hamaker & Muthén, 2020). Related to this, Usami et al. (2019a) outlined that the RI-CLPM relaxes some of the strong assumptions inherent in CLPMs: It requires strong ignorability and positivity assumptions to hold only after controlling for time-invariant differences between individuals.

FF-CLPM

Recently, Lüdtke and Robitzsch (2022) raised concerns about the superiority of the RI-CLPM over the CLPM for investigating causal effects. Using simulated data, they showed that RI-CLPMs are not necessarily able to control for unobserved confounding (as suggested by Hamaker et al., 2015). Most interestingly, in their simulation study, they generated data for two variables X and Y based on a CLPM with three measurement occasions and showed that the RI-CLPM leads to biased estimates if the true model is a CLPM with lag-2 effects (i.e., FF-CLPM; and vice versa) and that model fit statistics do not seem suitable for deciding whether to use a RI-CLPM or a CLPM with lag-2 effects. Based on these findings, Lüdtke and Robitzsch highlight the value of considering FF-CLPM when cross-lagged effects are of interest.

Weighting Methods

Different ways of adjusting for confounders exist in nonexperimental studies, and one of the most prominent ways is regression adjustment (e.g., Shadish et al., 2008). However, regression adjustment (i.e., modeling the relationship between outcome, covariate, and exposure) may come with some challenges (e.g., regarding threats of extrapolation and cherry picking of covariates) that may lead to specific patterns of results (Thoemmes & Ong, 2016). Furthermore, not many studies have investigated sensible approaches for including (very many, potentially time-varying) covariates in prominent longitudinal models (e.g., FF-CLPMs or RI-CLPMs) with few exceptions (e.g., Marsh et al., 2022; Mulder & Hamaker, 2021). In addition, whether including many covariates might increase issues of previously reported nonconvergence in these models has not been investigated thoroughly (Orth et al., 2021; Usami, Todo, & Murayama, 2019b).

In contrast to traditional multiple regression approaches, weighting methods seem promising for addressing some of the challenges outlined above. Weighting methods are designed to model the relationships between observed covariates and exposure in a first step before estimating the treatment effect on the outcome variable. Thus, these approaches allow researchers to analytically disentangle these two steps, which is impossible in outcome modeling. Furthermore, weighting approaches can easily take large sets of observed (potentially time-stable and time-varying) covariates into account and combine this information in a weighting variable. In addition, they place a specific focus on the adequate balancing of covariates by modeling the exposure using the observed covariates before they estimate the treatment effect of interest. Thus, weighting approaches try to achieve covariate balance using observational data, similarly to what should be achieved by randomization in experimental designs (Thoemmes & Kim, 2011).

When introducing weighting methods on a conceptual level, it is helpful to start by considering the example of inverse probability weighting, which typically follows a four-step procedure as outlined by Thoemmes and Ong (2016) or Pishgar et al. (2021). First, researchers (a) identify potential confounders (e.g., Vanderweele, 2019; Vanderweele et al., 2020), and (b) then they specify a selection model and predict a treatment variable of interest from the set of confounders assessed prior to the treatment. On the basis of this selection model, weights are estimated by using information about the individual’s probability of having a specific value on the treatment variable. In the case of inverse probability weighting, these weights are the inverse of the estimated probability of having received the treatment given the different covariates. Thus, as more comprehensively outlined by Thoemmes and Ong (2016), in the case of a binary exposure variable, treated individuals would receive a weight of 1/P(Treatment = 1|Covariates), and untreated individuals would receive a weight of 1/(1 − P(Treatment = 1|Covariates)). In the case of inverse probability weighting, this formula can be extended to nonbinary treatments using conditional densities. However, the implementation is rather technical and goes beyond a conceptual presentation of the idea of weighting here. We therefore refer the reader to Fong et al. (2018) and Tübbicke (2021) for more information. (c) Next, researchers inspect and optimize the covariate balance if needed. As outlined by Thoemmes and Kim (2011), “Balance on covariates is desirable because a balanced covariate (which is by definition uncorrelated with treatment assignment) cannot bias the estimate of a treatment effect, even if the covariate itself is related to an outcome variable” (p. 92). Thus, very low standardized mean differences (binary treatments) or correlations (continuous treatments) are desirable and indicate a good covariate balance. (d) Finally, researchers use the weighted (i.e., covariate balanced) data to estimate the treatment effects (see also Fig. 2) for the (weighted) pseudo-population (Hernán & Robins, 2020), typically using outcome models with the treatment variable as the independent variable and the variable of interest as the outcome. Some researchers have argued that covariates should also be considered in this final estimation step again to adjust for remaining imbalances (Schafer & Kang, 2008), which is referred to as “doubly robust” estimation. Doubly robust estimation can be considered a combination of treatment/exposure modeling (i.e., weighing) and outcome modeling (i.e., regression adjustment). As more formally outlined by Hernán and Robins (2020), the particular benefit of doubly robust estimators is a correction of the regression for the outcome model by a function of the treatment model. Further, it has been mathematically shown that the bias is asymptotically zero if one of the two models is correct. Notably, this advantage of doubly robust estimators depends on the correct specification of the respective models (i.e., the inclusion of all relevant confounders).

Fig. 2

Example of the different steps when applying CBGPS weighting to estimate the effect of self-concept (T2) on grades (T3). Note. T1, first measurement occasion; T2, second measurement occasion; T3, third measurement occasion; D1, first data set; Dn, last data set; Test ACH, test achievement; Self-concept_w ➔ Grades, weighted regression of self-concept (T2) on grades (T3). Doubly robust estimation (e.g., Schafer & Kang, 2008)

In sum, several advantages of weighting methods have been outlined in the literature, for instance, related to addressing threats of cherry picking and extrapolation (Thoemmes & Ong, 2016), rigorous checks of covariate balance, applying doubly robust estimators (Hernán & Robins, 2020), or related to features of specific weighting algorithms (e.g., desirable properties of EB to achieve covariate balance; Hainmueller, 2012).

When comparing the assumptions of the different statistical models with the structural causal models (see Fig. 1), it becomes evident that if the structural causal model is similar to (a) or (b), the CLPM and the FF-CLPM (without covariates) are adequate choices for causal inference: More practically speaking, if associations between self-concept and achievement are similar to (a), where there are no 2-lag paths or confounder, or (b), where there is no confounder, statistical models such as the CLPMs/FF-CLPMs will reveal adequate causal effects. As outlined above, this seems unrealistic in the context of the REM. Regarding (c), different suggestions have been outlined in the literature. Whereas some studies have argued that RI-CLPMs constitute a reasonable improvement for testing this model, particularly regarding time-invariant confounders (e.g., Hamaker et al., 2015), others have challenged this proposition (Lüdtke & Robitzsch, 2021, 2022), and yet other studies have suggested that different methods might be even more promising in such contexts (e.g., weighting techniques; Usami et al., 2019a). Most importantly, if model (c) is the structural causal model with time-invariant and time-varying confounders, then most common specifications of the CLPM and the FF-CLPM (i.e., without covariates) will not reveal the desired causal effects of self-concept on achievement and vice versa because then the estimated coefficients would be biased due to unconsidered confounders.

The Present Study

The present study constitutes a substantive-methodological synergy (Marsh & Hau, 2007) to investigate relationships between self-concept and achievement using different traditional and more recently developed methods. Specifically, we went beyond prior research and applied new weighting methods to estimate reciprocal effects of self-concept on achievement and vice versa. These methods were developed to identify causal effects of continuous treatment variables and have many desirable features regarding causal inference (see Table 1).

Our study should therefore produce new insights into the existence and directions of reciprocal effects of self-concept and achievement. We investigated reciprocal relationships between student motivation and achievement using (a) traditional CLPMs; (b) suggested extensions of these models, namely, FF-CLPMs (Lüdtke & Robitzsch, 2022); and (c) RI-CLPMs (Hamaker et al., 2015). In addition to these three types of longitudinal structural equation models, we applied two weighting approaches, that is, entropy balancing (EB) and covariate balanced generalized propensity score (CBGPS) weighting to study the causal effects of the two variables on one another. Note that according to our review of the literature, most studies on the REM either did not control for any confounders when investigating reciprocal effects between self-concept and achievement or controlled for only a very small set of confounders at one measurement occasion (e.g., Arens et al., 2017; Ehm et al., 2019; Preckel et al., 2017; Seaton et al., 2015). This oversight may have resulted from the fact that, at the moment, there is a lack of research that researchers can consult to figure out which potentially time-varying and time-stable confounders should or should not be considered when investigating the reciprocal effects between self-concept and achievement and how such potential confounders should technically be considered (see Marsh et al., 2022, and Mulder & Hamaker, 2021, for initial suggestions and a more comprehensive discussion of specific challenges). To be able to estimate the degree to which differences between the different models/methods result from different sets of covariates, we also considered CLPMs, FF-CLPMs, and RI-CLPMs with and without a similar set of covariates as used in the weighting methods.

On the basis of prior research, we expected that traditional models, such as the CLPM and the FF-CLPM without covariates (Huang, 2011; Wu et al., 2021), would yield reciprocal effects of academic self-concept and achievement, particularly when high-stakes grades were considered rather than low-stakes standardized achievement tests when no feedback was given to students about their test results. In addition, on the basis of prior findings, we expected that cross-lagged coefficients in the RI-CLPM would be smaller and the respective standard errors would be larger than in the CLPM and the FF-CLPM (e.g., Bailey et al., 2020; Burns et al., 2020; Ehm et al., 2019; Lüdtke & Robitzsch, 2021, 2022; Mulder & Hamaker, 2021). Finally, we were not aware of any studies that have used the new weighting approaches to investigate the effect of self-concept on achievement or vice versa. However, as outlined above, we expected that these methods would show favorable characteristics with regard to the assumptions required to identify causal effects, particular the strong ignorability assumption. Theoretically, it seems reasonable to believe that CLPMs might overestimate cross-lagged coefficients to some degree if relevant confounding variables that actually explain variation in the dependent variable (e.g., general cognitive ability, personality, achievement in other subjects, effort) are ignored. However, not controlling for these confounders might also lead to a suppression of the true associations between the REM variables. Therefore, we had no expectations about whether or not evidence would be found in favor of the REM when using these new methods.

Method

Data

To investigate differences between the results from the different methods, we used secondary data from the Transition and Innovation (TRAIN) study hosted by the Hector Research Institute of Education Sciences and Psychology at the University of Tübingen in Germany (Jonkmann et al., 2013). Beginning in 2008, this study repeatedly assessed students once a year during lower secondary school (from grade 5 to grade 8). Specifically, in TRAIN, researchers applied a stratified sampling procedure where schools were first randomly drawn (separately in each state) from a list of all respective intermediate and lower track schools in each state, and then classes were randomly selected from these schools. All students in each class were asked to participate in the study. Notably, there were some peculiarities in the sampling design; for instance, at-risk lower track schools were oversampled, and in order to amass large enough sample sizes, the entire school cohorts (e.g., all grade 5 students) were considered in Saxony (see Rose et al., 2013). Overall, N = 3880 students participated in the TRAIN study. Here, we considered only the subset of students who participated in the mathematics assessment test, resulting in a sample of n = 3,757 students (45.3% female) from 136 classes in 105 schools. We considered data from all individuals who participated at least once in the 4 years, resulting in a sample of n = 2,869 students in grade 5 (44% female), n = 2925 students in grade 6 (45% female), n = 2969 students in grade 7 (46% female), and n = 2985 students in grade 8 (46% female). The majority of students participated in all four waves (n = 2206). The sample consisted of students from lower secondary schools in two German states (Baden-Württemberg [65.9%] and Saxony). The smaller proportion of female students in our sample adequately reflected the generally smaller proportion of female students in the population of lower and intermediate track schools in Germany at the time of assessment (Statistisches Bundesamt, 2010). Notably, the sample used in our secondary data analysis was not representative of the student population in the two German states due to its multistage sampling design with missing data (see Supplemental Material S4 for additional sample information). At the first measurement occasion, students were on average 11.2 years old. Access to the data and study material can be requested from the host of the study (see above). The main analysis code can be found in Supplemental Material S2-S3. We did not preregister this study. The TRAIN study was approved by the Ministries of Education in the respective states.

Instruments

As further outlined below, we considered students’ math self-concept, standardized test achievement, grades, and an additional rich set of covariates that were assessed at all four measurement occasions.

Subject-Specific Self-Concept in Mathematics

Students’ self-concept in mathematics was assessed with a German version of the Self-Description Questionnaire (SDQ) III (Marsh, 1992; Schwanzer et al., 2005). The instrument consisted of four items (e.g., “I am good in mathematics”), and students were required to rate their agreement from 1 (does not apply at all) to 4 (completely applies). Items with negative wording were reverse-coded. The reliability of the scale as indicated by Cronbach’s alpha was high (ranging from α = .78 to .86 across waves).

Achievement in Mathematics

Students’ achievement in mathematics was assessed with a standardized mathematics test oriented at the national standards for lower secondary school. Overall, 40 min were allocated for the math test. The test consisted of 74 to 87 items per measurement occasion, which were administered in a multimatrix design so that students had to work on 41 to 45 items per assessment. The majority of items were taken from prior large-scale studies, such as ELEMENT (Lehmann & Lenkeit, 2008) or BIJU (Baumert et al., 1996), and assessed primarily math literacy using exercises from five different guiding areas: numbers, measuring, shapes and space, functions, and data and chance. We used 20 plausible values, which were generated using a 2PL item response theory (IRT) model (Rose et al., 2013). The background model used to generate these PVs considered a rich set of variables, such as gender, age, different indicators of students’ socioeconomic background (e.g., immigration background, socioeconomic status, books at home, cultural practices, and goods at home), school grades, standardized achievement, reading speed, and a broad set of variables related to student motivation (e.g., self-concepts) and psychological well-being (see Supplemental Material S1 for additional information on these variables). The average weighted likelihood estimator (WLE) reliability of the test was .74, ranging from .71 to .77. In addition, grades were assessed on the basis of teachers’ reports at each measurement occasion, ranging from 1 (very good) to 6 (worst possible grade). We reverse-coded the grades so that higher values reflected better achievement.

Covariates

We also considered a broad set of covariates, which were used when we applied the weighting approaches and estimated the CLPMs, FF-CLPMs, and RI-CLPMs with covariates. When deciding which variables to consider, we followed recommendations from prior studies, specifically from Vanderweele (2019), who suggested a modified disjunctive cause criterion approach. This approach suggests that researchers (a) include all variables that might cause self-concept, achievement, or both, (b) exclude variables that could be instruments of self-concept or achievement, and (c) include proxy variables for potential confounders that might commonly cause self-concept and achievement. Notably, we followed his recommendations to (d) control for covariates that were measured prior to the treatment variable (i.e., the treatment variables at t-1 were conditioned on the covariates assessed at t-2). As suggested, this strategy can help satisfy the strong ignorability assumption by considering a large set of potential confounders while also mitigating challenges resulting from potential mediator variables or collider bias. However, it is important to note that even though the modified disjunctive cause criterion is very helpful to address the challenge of confounder selection, collider bias cannot ultimately be ruled out. On the basis of this strategy and theoretical considerations, we included five sets of variables: (1) demographic variables (e.g., school type, gender, and age), (2) variables related to the socioeconomic background of the student (e.g., migration background, socioeconomic background, and books at home), and (3) variables related to student achievement (e.g., standardized achievement in English) and general cognitive abilities. In addition, we considered (4) motivational variables, such as self-concepts in German and English and students’ subject-specific interests and effort in mathematics, German, and English. Finally, we also considered (5) variables related to students’ well-being as well as the Big Five personality traits. The variables included in (3), (4), and (5) were considered time-varying variables in the analysis of data from grades 6 to 8 (see the “Statistical Analysis” section). A comprehensive list of all the variables we considered can be found in Supplemental Material S1.

Statistical Analysis

The main statistical analysis followed three steps: First, we inspected and multiply imputed missing data. Next, we specified the respective longitudinal structural equation models. Finally, we applied the EB and CBGPS weighting approaches.

Inspection and Multiple Imputation

In the first step, we identified the relevant variables and compiled the data from the TRAIN study in R 4.1.1 (R Development Core Team, 2021). Next, we specified a multilevel imputation model in Mplus 8.6 (Muthén & Muthén, 1998-2017) with the school ID as a cluster variable, resulting in 20 complete data sets. Before multiple imputation, the missing data on the outcome variables ranged from 1 (grade 8) to 9% (grade 5) on math grades and from 17 (grade 8) to 28% (grade 5) on math self-concept. For standardized math achievement, missing values ranged from 3 (grade 5) to 8% (grade 6). Here, we used the plausible values provided by the data set (e.g., Rose et al., 2013). Data were transferred to Mplus using the MplusAutomation package (Hallquist & Wiley, 2018).

Specification of Longitudinal Structural Equation Models

Next, we specified (a) the CLPM, (b) the FF-CLPM, and (c) the RI-CLPM in Mplus. An annotated example of the Mplus code for the RI-CLPM can be found in Supplemental Material S2. In line with Lüdtke and Robitzsch (2022), we focused on cross-lagged coefficients between variables assessed at the second (T2) and third (T3) measurement occasions and, in separate models, the third (T3) and fourth (T4) measurement occasions (see Table 2) in our comparison because these are the coefficients provided by the weighting approaches, which require the user to distinguish between (a) pretreatment variables (T1/T2), (b) treatment variables (T2/T3), and (c) posttreatment outcomes (T3/T4). This means that in order to estimate causal effects, weighting approaches require variables that are assessed prior to the treatment variable and that cannot be influenced by the respective treatment variable itself (e.g., Hübner et al., 2021; Thoemmes & Kim, 2011; Thoemmes & Ong, 2016). Therefore, we ran two sets of models, each considering three measurement timepoints (i.e., grades 5–7 and grades 6–8). When estimating models using data from grades 5 to 7, we were interested in coefficients for the grades 6–7 time-lag, and when estimating models using data from grades 6 to 8, we were interested in the respective grades 7–8 coefficients. On the basis of prior recommendations (Orth et al., 2021), we provide results from models with and without equality constraints on the lag-1 paths. These models assume that cross-lagged and lag-1 autoregressive coefficients are similar across time and are most prominently used in the current REM literature (Usami et al., 2019a).

Table 2 Interpretations of the respective cross-lagged coefficients from the CLPM, the FF-CLPM, the RI-CLPM, and entropy balancing

The specification of the respective models closely followed recent recommendations (e.g., Mulder & Hamaker, 2021). As outlined in prior research (Hamaker et al., 2015), the CLPM is nested in the RI-CLPM. Therefore, in the CLPM and the FF-CLPM, the variances and covariances of the random intercepts were fixed to zero. The FF-CLPM also included additional lag-2 coefficients to predict variables assessed at measurement occasion t from variables assessed at measurement occasions t-1 and t-2. Note that when specifying CLPMs, FF-CLPMs, and RI-CLPMs to investigate the association between student achievement and self-concept, specifying residual covariances across the different constructs is a common practice, as can be seen in a range of different studies (e.g., Ehm et al., 2019; Marsh et al., 2022; Preckel et al., 2017). Thus, to be in line with this rich set of prior studies on the REM, we also decided to consider residual covariances (see Supplemental Material S2). Occasion-specific associations between residual variables suggest that there are additional common causes of students’ achievement and their self-concept that cannot be explained by cross-lagged or autoregressive variables. A common cause could be situation-specific influences that might affect both constructs, for instance, students’ mood or recent events that are not considered in the model but negatively or positively affect their situation-specific achievement and self-concept.

Finally, we also estimated CLPMs and FF-CLPMs, and for the grades 6–8 data, we estimated RI-CLPMs with an identical set of covariates as used in the weighting approaches. It was important to be able to better disentangle potential differences between models that resulted from the different methods from those that resulted from different choices of covariates. Note that according to Mulder and Hamaker (2021), the RI-CLPM requires the covariates to be assessed prior to the repeated measures. Therefore, we were able to specify RI-CLPMs with covariates only for the grades 6–8 data, and we used variables from grade 5 as covariates.

Specification of Weighting Approaches

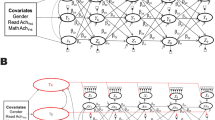
Following the specification of the longitudinal structural equation models, we specified the weighting approaches in R (R Development Core Team, 2021). Specifically, we made use of the MatchThem package (Pishgar et al., 2020), which extends functionalities of the WeightIt package (Greifer, 2021b) in such a way that models can be run with multiply imputed data sets. Figure 2 illustrates the general procedure and steps of the applied weighting approach for estimating the causal effect of self-concept on grades. Supplemental Material S3 presents example R code.

In our study, in the first step (selection step), three different selection models were specified in which either test achievement, self-concept, or grades in mathematics assessed at T2 was predicted by achievement, self-concept, and grades in mathematics plus a large set of covariates assessed prior to T2 (i.e., T1; see the “Instruments” section). These three selection models revealed three sets of weights. Before running these models, all continuous variables were standardized (M = 0 and SD = 1) across all imputed data sets using the miceadds package (Robitzsch et al., 2021) so that the results could be interpreted in terms of standard deviation units. We estimated the weights separately for each imputed data set (i.e., the within approach; Leyrat et al., 2019) using (a) the EB method (Tübbicke, 2021) and (b) the CBGPS weighting method (Fong et al., 2021). EB for continuous variables relies on a reweighting scheme that minimizes the loss function and imposes normalization constraints (i.e., weights have to be positive and sum to one). Practically speaking, EB reweights all participants to achieve a correlation of zero between covariates and the treatment variable (Tübbicke, 2021). Note that we did not consider higher order moments in the balancing condition and therefore assumed an underlying linear model between the covariates and exposure. Prior studies have found some evidence that EB can handle missing nonlinear terms quite well in the binary case (Hainmueller, 2012). However, this evidence needs to be more thoroughly investigated for the continuous extension of the EB algorithm. We considered only linear terms in our study in order to mimic the current standard when considering covariates in CLPMs, FF-CLPMs, and RI-CLPMs. In the case of nonlinearities, our results can be understood in terms of the best linear approximation of the true function between covariate and exposure (Angrist & Pischke, 2009). The reweighting scheme therefore ensures double robustness (Zhao & Percival, 2017). The CBGPS approach constitutes a parametric extension of Imai and Ratkovic’s (2014) CBPS approach for binary treatment variables to continuous variables. CBGPS applies a homoscedastic linear model to estimate the generalized propensity score and to minimize the covariate treatment correlation (Fong et al., 2018).

In the next step (inspection step), we inspected the weights and the correlation between covariates and the respective treatment variables (covariate balance) before and after weighting, using different functions from the cobalt package (Greifer, 2021a; see Fig. 3), and we also screened the quadratic and interaction terms. A common challenge when applying weighting approaches is that sometimes unrealistically large weights are estimated (Thoemmes & Ong, 2016). Ignoring large weights can yield unbiased but imprecise estimates (Cole & Hernán, 2008). In our study, large weights resulted when we applied CBGPS weighting. On the basis of the literature cited above, we decided to estimate 1% trimmed weights to assess the robustness of our findings (see Thoemmes & Ong, 2016).

Fig. 3

Covariate balance before and after weighting at T2 using EB and CBGPS weighting summarized across imputations. Note. A, standardized test achievement + EB; B, self-concept + EB; C, grades + EB; D, standardized test achievement + CBGPS; E, self-concept + CBGPS; F, Grades + CBGPS. The x-axis displays the size of the treatment-covariate correlation, and the y-axis displays all considered covariates. A detailed list of all covariates can be found in Supplemental Material S1. For the sake of clarity, dashed lines were plotted at r = .1/−.1. Lines within dots display variation in estimated correlations across imputations (ranging from the lowest to the highest estimated correlation per imputation)

In the next step (analytic step), we used the survey package (Lumley, 2018) to specify multiple regression models in which we predicted the T3 outcome variables (i.e., achievement and self-concept) using the T2 treatment variables (i.e., self-concept, achievement), the pretreatment covariates (Schafer & Kang, 2008), the respective sets of balancing weights from the first steps (see above), and the cluster-robust standard errors (based on information about students nested in schools). Thus, the causal effects resulted from the effect of the respective T2 variable (e.g., self-concept) on the respective T3 variable (e.g., achievement), using the weighted (multiply imputed) data sets and the respective covariates and considering nesting. In the final step (pooling step), we pooled the results from these 20 regression models using Rubin’s rules (Rubin, 1987). A similar procedure was applied when investigating effects of the T3 variables on the T4 variables (see Supplemental Material S3 for example code).

Interpretation of Effect Sizes

There are different approaches that can be applied to better understand and interpret the effect sizes presented in this article. First, one could identify the sizes of the effects typically found in CLPMs or RI-CLPMs as benchmarks. In this regard, Orth et al. (2022) recently published guidelines that were based on a sample of 1028 effect sizes. Using these guidelines, the authors estimated effect sizes for the 25th, 50th, and 75th percentiles of the distribution of cross-lagged effects and proposed .03, .07, and .12 as small, medium, and large effects in CLPMs and RI-CLPMs, respectively. From this perspective, the majority of our findings ranged from medium to large effects, with a slight tendency toward larger effect sizes when the weighting approaches were used. Notably, beyond these benchmarks, judging effect sizes could also be based on prior REM research. For instance, Wu et al. (2021) found that reciprocal effects for the REM of self-concept and achievement ranged from β = .08 to β = .16, values that were similar to our results. In addition, it is also important to account for the lengths of the time intervals when interpreting the effect sizes of cross-lagged effects (e.g., Hecht & Zitzmann, 2021).

Results

Preliminary Results

First, we inspected correlations between the different variables that are presented in Table 3. As can be seen, correlations between matching constructs ranged from r = .73 to .83 for math test achievement, from r = .37 to .60 for math self-concept, and from r = .41 to .65 for grades (all ps < .001). Correlations between subsequent measurement occasions (lag-1; e.g., G5 and G6 or G6 and G7) were stronger than the lag-2 correlations (e.g., G5 and G7), a finding that is in line with prior REM research (e.g., Ehm et al., 2019). Taken together, these results suggest that the different constructs seem to be relatively stable over time.

Table 3 Pooled correlations, means, and standard deviations across 20 imputed data sets for math self-concept, test scores, and grades from grades 5 (G5) to 8 (G8)

Next, we took a closer look at the correlations between nonmatching constructs. Although, as outlined above, these were also statistically significantly related (all ps < .001), they were smaller. For instance, the correlations between standardized test achievement and self-concept in mathematics ranged from r = .23 to .31, and the correlations between grades and self-concept ranged from r = .20 to .41. Grades and self-concept were slightly more strongly correlated than standardized test achievement and self-concept (on average Δr = .04), a finding that prior studies argued resulted from the fact that grades provide a stronger reflection of the motivational aspects of student behavior (Wu et al., 2021; Wylie, 1979). Similar to our findings for matching constructs, the correlations between the lag-1 paths tended to be larger than between the lag-2 paths.

Results from CLPMs, FF-CLPMs, and RI-CLPMs

Model Fit

In the next step, we inspected the model fit statistics of the specified CLPMs (see Table 4). For each of the three types of longitudinal structural equation models, we specified two types of models, one without and one with equality constraints over time (see the “Statistical Analysis” section). Table 4 presents the model fit statistics for CLPMs without equality constraints, χ²(9) = 359.27, p < .001, RMSEA = .10, CFI = .97, TLI = .89, SRMR = .03, and for CLPMs with equality constraints, χ²(18) = 485.80, p < .001, RMSEA = .08, CFI = .96, TLI = .93, SRMR = .05. These results were similar for CLPMs from grade 5 to grade 7 and for CLPMs from grade 6 to grade 8.

Table 4 Model fit statistics for the respective longitudinal structural equation models

Regarding the FF-CLPM, we found a slightly different picture. Here, the model with the respective lag-1 equality constraints had the following model fit when the grades 5–7 students were considered, χ²(18) = 260.11, p < .001, RMSEA = .09, CFI = .98, TLI = .92, SRMR = .05. When data from the grades 6 to 8 students were considered, the FF-CLPM fit the data well, χ²(9) = 137.16, p < .001, RMSEA = .06, CFI = .99, TLI = .97, SRMR = .04. Importantly, unconstrained FF-CLPMs with three measurement timepoints are saturated models (df = 0) and thus fit perfectly, which is why no model fit statistics were computed for these models.

Finally, we inspected the model fit statistics for the RI-CLPMs. As presented in Table 4, these models showed good fit to the data when the grades 5–7 data were considered; RI-CLPM _G56/G67: χ²(3) = 11.63, p < .01, RMSEA = .03, CFI = .99, TLI = .99, SRMR = .01, as well as when the grades 6–8 data were considered, RI-CLPM _G67/G78: χ²(3) = 13.77, p < .01, RMSEA = .03, CFI = .99, TLI = .99, SRMR = .01. Similarly, as can be seen in Table 4, RI-CLPMs with equality constraints also showed good fit to the data.

Model fit statistics for CLPMs, FF-CLPMs, and RI-CLPMs with covariates were very similar to those of the respective models without covariates. Notably, the TLI sometimes took on very small values in the models with covariates. We explored this result pattern, and it seems that, in our case, the fit of the baseline model could not be substantially improved because many of the covariates explained only a small amount of variance in the outcome variable. This finding means that, as assumed in the baseline model, these covariates are (in many cases) essentially uncorrelated with the outcome. For a more formal explanation, see Supplemental Material S5.

Autoregressive and Cross-Lagged Coefficients

In the next step, we inspected the different autoregressive and cross-lagged coefficients for the models. We first considered the grades 5–7 data. As shown in Table 5 and Fig. 4, we found substantial autoregressive coefficients in the CLPMs without model constraints for standardized test achievement (β = .75, p < .001), for self-concept (β = .55, p < .001), and for grades (β = .50, p < .001). These findings therefore mimic the correlational findings, as outlined above. Regarding opposing constructs, we found statistically significant associations between all the constructs (all ps < .05) except one: The association between prior self-concept in mathematics in grade 6 and standardized test achievement in grade 7 did not reach statistical significance (β = .02, p = .226). Results for CLPMs with time constraints were similar to these prior results except that the relationship between prior self-concept and subsequent standardized test achievement was also statistically significant (β = .04, p = .004). These findings from CLPMs are in line with the large number of prior studies that have found evidence in favor of the reciprocal effects model in which prior self-concept is a predictor of subsequent achievement (grades in particular), and prior achievement is positively associated with subsequent self-concept in mathematics (e.g., Ehm et al., 2019; Marsh & Craven, 2006).

Table 5 Autoregressive and cross-lagged coefficients (grades 6–7) for the different models

Fig. 4

Cross-lagged coefficients from different modeling strategies. Note. Model index A relates to Model 56/67 (grades 5–7) or 67/89 (grades 6–8), and model index B relates to Model 567 (grades 5–7) or Model 678 (grades 6–8) from Tables 5 and 6. The figure shows cross-lagged coefficients from Tables 5 and 6 and 95% confidence intervals. DV dependent variable, IV independent variable, ASC academic self-concept, CLPM cross-lagged panel model, FF-CLPM full-forward (lag-2) cross-lagged panel model, RI-CLPM random intercept cross-lagged panel model, EB entropy balancing, CBGPS covariate balanced generalized propensity score weighting, n.a. not available. Cov. including covariates. As suggested by Mulder and Hamaker (2021) who stated that covariates need to be assessed prior to the repeated measures in RI-CLPMs. These were only available for the grades 6–8 data. Trimmed = Trimmed at 1%

Results for the FF-CLPMs were quite comparable to the results of the CLPMs with two exceptions: The association between grades in grade 6 and test scores in grade 7 (see Fig. 4) was not statistically significant (β = .03, p = .319), similar to the relationship between grades in grade 6 and self-concept in grade 7 (β = .04, p = .096). In contrast to these findings, the constrained FF-CLPM results were largely comparable to those found in the constrained CLPM.

Next, we inspected results for the RI-CLPMs. Prior studies found differences between results from traditional CLPMs and RI-CLPMs (Bailey et al., 2020; Burns et al., 2020; Ehm et al., 2019) in terms of attenuating, direction-changing, or even vanishing associations. Our findings are in line with these prior findings and suggest that, of the six different cross-lagged coefficients, only the association between prior self-concept and subsequent grades remained statistically significant (β = .23, p < .001) in the unconstrained model, whereas in the respective FF-CLPM, this number came to three, and in the respective CLPM to five. However, when considering results of the constrained RI-CLPM, our findings were much more in line with results from the CLPM and the FF-CLPM in that both (a) prior grades were found to predict subsequent self-concept (β = .14, p < .001) and (b) prior self-concept was found to predict subsequent grades (β = .24, p < .001; see Table 5).

Comparisons of Estimates Across Grades

When comparing our findings for the grades 5–7 models with the results for the grades 6–8 models (see Table 6), we found large similarities, with few exceptions. Most important for the focus of this study, the association between grades and self-concept was not statistically significant for the RI-CLPM_G678 model, whereas this association was found when considering the grades 5–7 data (i.e., in the RI-CLPM_G567 model).

To sum up, the results from the three different models were largely in line with findings from prior studies on this topic (Burns et al., 2020; Ehm et al., 2019). They showed that whereas the CLPM and the FF-CLPM tend to produce evidence in favor of a reciprocal effects model between grades and self-concept and, depending on the model, also for standardized test achievement and self-concept, this finding is less consistent when using RI-CLPMs. Regarding cross-lagged coefficients, with the exception of the RI-CLPM_G567, only the association between prior self-concept and subsequent grades consistently reached statistical significance, thus offering evidence in favor of a self-enhancement model. However, it is important to keep in mind the interpretational differences when comparing the results for these models (see Table 2; e.g., Lüdtke & Robitzsch, 2021, 2022; Orth et al., 2021; Usami et al., 2019a).

Results from CLPMs, FF-CLPMs, and RI-CLPMs with Covariates

Finally, we inspected results from the longitudinal structural equation models with covariates. Overall, this model revealed a fairly similar picture compared with the models without covariates for CLPMs, FF-CLPMs, and RI-CLPMs. The most prominent changes were observed for the stability coefficients, which became smaller when the covariates were considered. This tendency was more visible for CLPMs than for FF-CLPMs. Considering cross-lagged coefficients between self-concept and achievement (and vice versa), the largest change in coefficients was found when predicting self-concept from test achievement in the CLPM for the grades 6–8 data, which came to β = .10 without the covariates and β = .19 when the covariates were included (both ps < .001). The second largest change was observed when predicting self-concept from test achievement in the FF-CLPM for the grades 6–8 data, which came to a nonsignificant β = .09 without the covariates and β = .14 (p = .004) with the covariates. However, the majority of differences for cross-lagged coefficients were small and came to |.01|.

Robustness Checks

Note that we also specified CLPMs, FF-CLPMs, and RI-CLPMs and applied the single indicator approach for self-concept to evaluate the impact of measurement error on our results. To do this, we specified latent variables for the self-concept scores and fixed the residual variance of the indicators to (1 − reliability) × sample variance, respectively. Overall, the average absolute differences between the beta coefficients were small for both the grades 5–7 models (M_|Δ| = 0.023) and the grades 6–8 models (M_|Δ| = 0.022). For the specified models, statistical significance changed in only three cases (CLPM _G56/67, ASC on grade = .787; FF-CLPM _G56/67, ASC on test = .084; FF-CLPM _G67/78, ASC on grade = .108). On the basis of these results, it seems unlikely that correcting for measurement error in self-concept would have led to substantially different results in our study.

Results of EB and CBGPS Weighting

Balance Before and After Weighting

Finally, we closely inspected the results from the two weighting methods for continuous treatment variables, namely, EB and CBGPS. To this end, we first checked the covariate balance for the different treatment conditions. Figure 3 shows the treatment-covariate correlation in the adjusted and unadjusted samples for all the covariates that were considered, separately for EB (A–C) and CBGPS weighting (D–F) and for the three different weighting variables. The x-axis displays the size of the treatment-covariate correlation (for the sake of clarity, dashed lines are plotted at r = .1/−.1), and the y-axis displays the different covariates (see Supplement S1 for a detailed list of all covariates). Lines within dots represent variation in the estimated treatment-covariate correlation across the imputed data sets. As can be seen, the correlations were substantial before weighting, particularly for matching constructs (e.g., self-concept at the first and second measurement occasions), but also for other variables, such as cognitive abilities. For instance, for standardized test achievement before weighting, the treatment-covariate correlations ranged from r = −.44 to .83 across the covariates. After weighting, these correlations were reduced to zero for all covariates when using EB (see Fig. 3 panel A). This finding suggests that the weights were estimated in such a way that the covariates were perfectly balanced across the different levels of the treatment variable and constituted a specific feature of EB (e.g., Zhao & Percival, 2017). Similar results were found for the other weighting variables (panels B and C) when EB was applied. With regard to CBGPS weighting, the covariate balance improved substantially and came to r < .1 for the large majority of variables. However, the balance was not as good as for EB, as can be seen in panels D–F in Fig. 3. For instance, for standardized test achievement, the balance after weighting improved with an average absolute correlation of M = .18 before and M = .05 after adjusting for CBGPS. The highest correlations after weighting were found for matching constructs (e.g., for achievement), whereas the correlations for all other constructs were substantially smaller, and in the large majority of cases, they were below |r| = .1. The screening of quadratic and interaction terms revealed a similar picture with better balance statistics for EB. On average, the correlations between the exposure variables and the higher order terms for EB ranged from M = −.002 (grades) to M = .002 (self-concept). For CBGPS, the average correlations ranged from M = .001 (self-concept) to M = .009 (test achievement). In line with suggestions from the respective literature (Hernán & Robins, 2020; Schafer & Kang, 2008), we added covariates from the conditioning step again in the estimation step. Note that in our study, this did not create any problems, but it might lead to challenges in scenarios with smaller samples and many covariates. As outlined above, one way out of these challenges might be to use EB, which typically leads to a much better balance than CBGPS as early as in the first step.

Effects of Self-Concept on Grades and Vice Versa

The results for EB presented in Table 5 (see also Fig. 4) suggest that prior grades had a positive effect on subsequent self-concept (all βs = 0.11, all ps ≤ .001), and self-concept had a positive effect on grades (β = .22/0.23, all ps < .001; results without trimming before the slash and trimmed results after the slash). When applying CBGPS weighting and using the resulting trimmed weights, we were able to replicate this finding for the effect of prior grades on self-concept (β = .12, p = .002) and prior self-concept on grades (β = .21/.22, all ps ≤ .001). It is important to note that in very few cases, very large weights were estimated when using CBGPS. This makes the solution with 1% trimmed weights more reliable to use in the case of CBGPS weighting (Thoemmes & Ong, 2016). For EB, no such extreme weights were computed.

Effects of Self-Concept on Standardized Test Achievement and Vice Versa

Next, we more closely examined results for the estimates of the effects of standardized test achievement on self-concept and vice versa. Here, we found statistically significant coefficients for the effect of math self-concept on subsequent standardized test achievement, ranging from β = .06 to .07 (all ps ≤ .01). However, the opposite effect of test achievement on math self-concept did not reach statistical significance (all ps > .05).

Comparison of Effect Estimates

When comparing estimates of the effects for the respective grade 6 variables on the grade 7 variables with those resulting from estimating effects of the grade 7 variables on the grade 8 variables (see the EB and CBGPS results in Tables 5 and 6), the results were fairly similar. When estimating the grade 7 on grade 8 effect, self-concept had a statistically significant effect on grades, ranging from β = .14 to .17 (all ps < .001), and grades had a statistically significant effect on self-concept, ranging from β = .15 to .17 (all ps < .001). In addition, the effect of test achievement on self-concept was statistically significant for all weighting methods (all βs = .17, all ps < .05); however, the reverse effect did not reach statistical significance in any of the models (all ps > .05).

Table 6 Autoregressive and cross-lagged coefficients (grades 7–8) for the different models

In sum, the results from the weighting methods produced evidence in favor of the REM because we consistently found positive effects of math self-concept on grades and vice versa with the exception of one of eight models, namely, the CBGPS_G67, in which we found only a one-sided statistically significant effect of grades on self-concept. Effects of standardized test achievement on self-concept and vice versa were consistent within but less consistent across the two grade groups G5–G7 and G6–G8 (see Tables 5 and 6). Depending on the grade group, we found evidence in favor of either the self-enhancement model or the skill-enhancement model.

Discussion

In this substantive-methodological synergy, we investigated the REM using different approaches: the CLPM, the FF-CLPM, and the RI-CLPM, all with and without covariates, as well as EB and CBGPS weighting. Prior research has suggested that the RI-CLPM might be superior to traditional CLPMs in identifying causal effects because it relaxes some of the strong assumptions of CLPMs by controlling for time-stable differences between individuals (e.g., Hamaker et al., 2015; Usami, 2021). By contrast, other studies have questioned the validity of this argument by underscoring interpretational differences and suggesting that the CLPM and particularly the FF-CLPM are more useful for addressing causal questions with rather large measurement timepoint intervals, as in our study with 1-year lags (Lüdtke & Robitzsch, 2022; Orth et al., 2021). In addition, researchers have also proposed making use of more recently developed weighting methods to investigate reciprocal causal effects through unidirectional causal effect estimates (Usami et al., 2019a), and we highlighted that these methods might be promising in terms of satisfying the assumptions required for causal interpretations, particularly when longitudinal models do not consider covariates (see Table 1). However, a large number of validly measured potential confounders can be included in the analyses as in the present study. We aimed to compare results of the different proposed models/methods in this study.

At the beginning of this manuscript, we proposed two sets of overarching questions: First, what are the assumptions for causal inference made by weighting methods, and how likely are they to be satisfied when reciprocal effects between self-concept and achievement are investigated? Second, is there evidence of reciprocal effects of academic self-concept and achievement when these methods are used for causal inference, and how do results from traditional and new methods compare with one another?

Regarding the first question, we provided insights into one of several options, that is, continuous treatment variable weighting, which comes with the advantage of making assumptions related to causality more plausible. This is particularly evident for the strong ignorability assumption, which is unlikely to hold in scenarios in which only two or three variables are considered over time when estimating CLPMs without covariates (e.g., Usami et al., 2019a). As outlined, we showed that weighting approaches easily allow for the inclusion of a broad set of potential time-stable and time-varying confounders and allow researchers to assess and potentially optimize the covariate balance before estimating the actual treatment effects. Therefore, the application of these methods for investigating reciprocal associations via unidirectional causal effect estimates might indeed provide a promising extension to prior strategies utilized in the field of educational psychology. Notably, the RI-CLPM was argued to control for all observed and unobserved time-stable differences between individuals, which relaxes the strong ignorability assumption to some degree (Usami et al., 2019a) when the assumption of stable traits across the time span under investigation seems plausible. This aspect certainly provides a benefit of this model, particularly when only a few potentially relevant confounders are assessed.

Regarding the second question, the CLPMs, FF-CLPMs (with and without covariates), and weighting methods all painted a fairly similar overarching picture and provided evidence of a REM for self-concept and grades, which is largely in line with prior studies (e.g., Arens et al., 2017; Ehm et al., 2019; Marsh & Craven, 2006). Overall, from an applied perspective and considering the year-to-year changes/stability of the respective constructs (see Table 3), these findings can be considered relevant in the majority of cases. Interestingly, the results were less consistent when standardized test achievement was considered, a tendency that has been noted in previous studies (Marsh et al., 2005; Wu et al., 2021) and may have resulted from differences in the stakes of the test versus grades (i.e., grades are high stakes, whereas tests are low stakes) or from the fact that the students were not aware of their test results because no feedback was provided at the individual student level in the TRAIN study. Support for this assumption can be found in Table 3. As can be seen, grades and self-concept were more strongly associated compared with achievement tests and self-concept. In addition, the TRAIN study focused on students in the low and intermediate tracks, which might have further contributed to these findings: That is, prior research has found the association between self-concept and test achievement to be considerably lower in the low tracks compared with the academic tracks (e.g., Penk et al., 2014).

When comparing results from the RI-CLPMs (with and without covariates) with those from the other models/methods, the similarities in the findings were slightly reduced: We found a statistically significant association only between prior self-concept and subsequent grades, whereas the reverse association was statistically significant in only one model (RI-CLPM_G567). In the remaining models, the standard errors of the cross-lagged coefficients were larger, whereas the standardized beta coefficients remained relatively comparable to the other cross-lagged models or the weighting approaches when considering the grades 5–7 data. This finding reflects results from prior studies that also reported differences between coefficients from CLPMs, FF-CLPMs, and RI-CLPMs to some extent (e.g., Bailey et al., 2020; Ehm et al., 2019) and found larger standard errors for cross-lagged and autoregressive parameters of RI-CLPMs compared with the traditional CLPM (Mulder & Hamaker, 2021; e.g., Usami, Todo, & Murayama, 2019b).

As outlined in Table 2 and mentioned in prior studies (Lüdtke & Robitzsch, 2021, 2022; Orth et al., 2021), it is important to recall that coefficients from RI-CLPMs have a different interpretation than those from the other models/methods and that they redefine the causal cross-lagged effect. The RI-CLPM’s autoregressive and cross-lagged coefficients represent within-person associations between temporal deviations from individuals’ average scores (typically referred to as within-person associations/associations between states), whereas CLPMs, FF-CLPMs, and weighting approaches all follow a selection-on-observable strategy and share a similar interpretation with average increases or decreases based on individuals’ prior scores relative to others’ (between-person associations). This difference is important to keep in mind when comparing the different coefficients. If the cross-lagged coefficients from RI-CLPMs and CLPMs were comparable, this would suggest that states (i.e., temporal deviations from the trait level) are associated with one another in a manner that is similar to coefficients between mixtures of states and traits. This could occur if, for instance, the random intercepts in the RI-CLPM have zero variance because no stable trait factor exists. Yet, it is unclear whether and when this constitutes a reasonable assumption. Although both approaches might be able to identify causal effects in theory under specific assumptions (i.e., within-person and between-person causal effects; e.g., Gische et al., 2021; Usami et al., 2019a; Voelkle et al., 2018), suggestions about when to choose a specific model over another one have just emerged in the respective literature (e.g., Lüdtke & Robitzsch, 2022; Orth et al., 2021). This shows that the way in which a causal cross-lagged effect is defined and interpreted clearly depends on the alignment of the structural causal model and the chosen statistical model.

Limitations

There are several limitations that should be mentioned when interpreting the results of our study. First, in this article, we showed that investigating reciprocal relationships between variables using weighting methods might constitute a promising alternative approach, which, compared with how longitudinal structural equation models are most commonly applied, more likely satisfies the strong ignorability assumption and is able to estimate autoregressive and cross-lagged effects that are the focus of many studies in educational psychology. However, we also identified some challenges for the application of these methods. For instance, the covariate balance of different weighting methods (i.e., EB and CBGPS weighting) differed to some extent. In line with prior research, we found that EB led to a perfect treatment-covariate balance of the covariates we considered (Zhao & Percival, 2017). By contrast, CBGPS weighting substantially improved the balance but was still not perfect, making the strong ignorability assumption less plausible compared with EB. In order to render the results comparable across the two methods, when we applied EB and CBGPS, we decided to use an identical set of covariates that we derived on the basis of prior theoretical considerations and prior suggestions (Thoemmes & Kim, 2011; Vanderweele, 2019). However, when following such recommendations, researchers should be warned because they might fall into a “propensity score tautology” (Imai et al., 2008) when weighting approaches other than EB are applied. Researchers are thus advised to repeatedly respecify the selection model by adding and dropping covariates to obtain an adequate balance, a process that can get tedious and can lead to even less balance (e.g., Hainmueller, 2012).

Second, as can be seen from Usami et al. (2019a), a broad variety of different models exist, all of which could be reasonably used to investigate reciprocal relationships between self-concept and achievement. In this study, we focused on three types of longitudinal models from recent research—the CLPM, the FF-CLPM, and the RI-CLPM (with and without covariates)—and ignored other models that have gained attention in more recent research (e.g., Núñez-Regueiro et al., 2021). Two arguments guided our decision to do so: The first is that the models that we compared in this study are most prominently used when investigating questions related to reciprocal associations between achievement and self-concept (though typically without covariates). This can be seen in a broad set of prior studies and meta-analyses (e.g., Arens et al., 2017; Burns et al., 2020; Ehm et al., 2019; Hamaker et al., 2015; Huang, 2011; Marsh et al., 2022; Marsh & Craven, 2006; Mulder & Hamaker, 2021; Preckel et al., 2017; Sewasew et al., 2018). The second point that guided our decision is that the interpretation of autoregressive and cross-lagged coefficients differed across different models. This difference was already noted when we compared the RI-CLPM results with results from the other models/methods in this study, but differences between models became even more visible when some of the other models were compared, for instance, the LCM-SR (also referred to as the RC-CLPM; Núñez-Regueiro et al., 2021) with the FF-CLPM (e.g., Orth et al., 2021). In addition, in this paper, we were particularly interested in estimating the causal effects of self-concept on achievement and vice versa, but not in modeling developmental processes, as prior work suggested that these two should be distinguished from one another (Lüdtke & Robitzsch, 2022). Therefore, aspects related to trends and the stationarity assumptions were not our key focus, and we did not consider models that have been suggested to control for trends. Such models were more comprehensively presented by Usami et al. (2019a) and might go along with different additional challenges. As suggested, if dynamics reflect relationships after controlling for developmental changes, such “new” models might throw “the baby out with the bathwater” (p. 649) because, if relationships between developmental processes are of interest, these processes move into the slope factor of such models. This has also led to discussions in the methodological literature on whether random slopes should generally be included in CLPMs or not (e.g., Berry & Willoughby, 2017; Curran et al., 2014; Núñez-Regueiro et al., 2021; Zyphur et al., 2020). Therefore, before applying these models to the debate about reciprocal causal effects, we feel that more research is required to thoroughly outline the respective assumptions and underlying developmental theories.

Furthermore, beyond all the potential advantages of weighting methods, there is one specific disadvantage that has not been given a lot of attention in previous research. In structural equation modeling frameworks, unreliability can easily be accounted for by using the single indicator approach (e.g., Ehm et al., 2019; Hoyle, 2012; Hübner et al., 2022) or a fully latent variable model. By contrast, for weighting approaches with continuous treatment variables, up to this point, it has been necessary to generate plausible values. Although there are statistical software packages that ease the application of weighting methods with multiple imputed data (e.g., Pishgar et al., 2021), generating PVs with a huge background model can be considered a cumbersome task (e.g., Khorramdel et al., 2020), and it is important to consider that the model for generating the PVs needs to be correct in order to avoid leading to biased results (Enders, 2010; Lechner et al., 2021). To hold the measurement model between the different models/methods constant, and on the basis of the good reliability of self-concept scales (see the Instruments section) and some checks using single indicator approaches, we decided not to model self-concept as a latent variable in our study. However, there is a need for future research to refine existing approaches and develop new approaches for dealing with measurement error more flexibly in weighting approaches.

Another important challenge that becomes especially visible when weighting approaches are applied is related to the selection of observed covariates. Although some suggestions in the literature have provided helpful guidance on covariate selection (e.g., Vanderweele, 2019; Vanderweele et al., 2020), recent recommendations still rely on specific assumptions about the underlying data-generating model that cannot be tested formally (e.g., to exclude variables known to be instruments or to add variables that function as proxies for other variables that were not assessed). However, this limitation does not apply only to weighting approaches, although it becomes especially visible in this situation. It applies to all other models/methods that rely on observed covariate adjustment strategies and require the strong ignorability assumption to be fulfilled. Obviously, such challenges are tackled when modeling strategies do somewhat “automatically” control for all (e.g., observed and unobserved) (time-stable) confounders, and this clearly points to benefits that have been discussed to be related to the RI-CLPM (Usami et al., 2019a).

Finally, it is important to note that generalizability constitutes an important research question on its own but was not the main focus of the current manuscript (Bryan et al., 2021; Tipton & Olsen, 2018). The existence and generalizability of the REM of self-concept and achievement has already been demonstrated and systematically investigated in different meta-analyses on this topic (Huang, 2011; Wu et al., 2021), whereas we were mainly interested in investigating differences between different approaches. It is possible that, because of this, many central studies on the REM have not considered representative data (e.g., Ehm et al., 2019; Marsh et al., 2022; Orth et al., 2021; Preckel et al., 2017; Sewasew et al., 2018). In Table S4 in the Supplemental Material, we included information about central demographic variables that might be useful for judging the generalizability of our findings.

Implications and Future Prospects

The results of our substantive-methodological synergy have important implications. First, from a theoretical perspective, when inspecting and comparing the assumptions behind the different structural causal models (see Fig. 1), it seems unlikely that true causal cross-lagged effects are being recovered in many application contexts in educational psychology using CLPMs, FF-CLPMs, or RI-CLPMs. This point was highlighted in prior research (e.g., Usami et al., 2015, 2019a) and results primarily from how these models are currently applied. Typically, only two or three endogenous variables are considered repeatedly over time (without covariates), and therefore, the strong ignorability assumption seems particularly implausible to satisfy. As this is not an inherent limitation of the statistical models, it seems important to invest time in reconsidering current standards when using these models. As one example, it seems relatively easy to extend traditional CLPMs, FF-CLPMs, and RI-CLPMs by including additional covariates (e.g., Usami et al., 2019a) in order to increase the likelihood that the strong ignorability assumption will hold, as we showed in this paper. Even though the differences between longitudinal models with and without covariates were small in our study, such comparisons should be conducted on a more regular basis in applied research. Our review of the literature suggested that controlling for large sets of covariates has seldom been done in practice until now. It is important to note that even though adding covariates to CLPMs, FF-CLPMs, and RI-CLPMs worked without any issues in our study, these models might quickly become overly complex and struggle to converge in other settings. Related to this issue, we also found that TLI values might decrease a lot when many of the predictors that are included are not strongly related to the outcome of interest. Thus, the value of such fit statistics might need to be reconsidered in situations in which many covariates need to be considered in CLPMs, FF-CLPMs, and RI-CLPMs. By contrast, weighting approaches can be used with large sets of observed covariates, and they require researchers to more thoroughly investigate and potentially optimize the covariate balance.

From a more substantial perspective related to the REM, although coefficients vary across the different models/methods, all models (besides the RI-CLPM) produced evidence in favor of the REM with regard to statistical significance. When considering standardized regression coefficients, results from the RI-CLPM were more comparable to the findings from the other models, but the standard errors were typically larger, which has also been noted in prior studies on this topic (e.g., Mulder & Hamaker, 2021; Usami, Todo, & Murayama, 2019b). This finding might suggest that the CLPMs and FF-CLPMs (at least in our data set) might actually not have performed as poorly as suggested by prior methodological studies as well as by the violation of the strong ignorability assumption outlined above. This tentative conclusion was also supported by the fact that the models with and without covariates produced comparable results. However, future studies and simulation studies are needed to determine whether this trend will emerge as a general pattern or whether it was specific to our study.

Another important aspect to consider for future research is related to the FF-CLPM. For these models, there are typically three types of arguments outlined in the literature about the benefits of including additional lags (Lüdtke & Robitzsch, 2022; Marsh et al., 2022). Such arguments consist of (a) statistical arguments regarding the fit of the model or threats of misspecifications when lag-2 effects are not included (Arens et al., 2017; Ehm et al., 2019; Marsh et al., 1999; Marsh et al., 2018); (b) arguments related to benefits in terms of causal inference (Vanderweele et al., 2020); and (c) content-related explanations, for instance, from a perspective of “accumulating self-concepts” (Ehm et al., 2019) or regarding curricular content that is relevant in specific grades (Marsh et al., 2018). Regarding (a), Marsh et al. (1999) argued that when investigating the REM, the FF-CLPM can be seen as the most general structural equation model, and the authors therefore suggested that researchers should start with this model before testing it against others. Related to this, as can be seen in a variety of different papers (e.g., Arens et al., 2017; Ehm et al., 2019; Marsh et al., 2022), the FF-CLPM often leads to better model fit statistics than the traditional lag-1 CLPM. Regarding (b), Vanderweele et al. (2020) suggested that controlling for lagged effects can help mitigate the problem of reverse causality and unmeasured confounding. Reverse causality in this case would suggest that a positive effect of X_t-1 on Y_t results primarily from the fact that, for instance, Y_t-2 (or lags further beyond) has a positive effect on X_t-1. Including confounder (e.g., self-concept and achievement measures) from prior lags (e.g., at t-2 or beyond) would be beneficial from a causal inference perspective because it would require a potential confounder C to be associated with achievement/self-concept at timepoint t, independent of the self-concept and achievement measures at t-1/t-2 (or beyond), but such an association seems less plausible in many applied cases. Finally, regarding (c), Ehm et al. (2019) suggested that considering self-concept as an “accumulation of all previous self-evaluations and achievements” (p. 2339) might help justify the theoretical inclusion of several lagged effects. From this perspective, it might be possible to understand the current outcome of self-concept only when information about multiple previous self-evaluations is included. In addition to this, Marsh et al. (2018) provided some additional explanations for including lagged effects in the context of the REM, namely, curricular content: Lag-2 effects might be reasonable and important to include if study-specific curricular content/study material (e.g., from grade 5) is of special importance in specific subsequent grades but not in others (e.g., in grade 7 but less so in grade 6). Such a pattern seems very likely in mathematics because, here, curricular content from earlier grades is often required in order to understand the material presented in later grades. Prior studies have articulated challenges in investigating the psychological mechanisms that can provide content-related explanations for lag-2 effects (Lüdtke & Robitzsch, 2022), and we can emphasize these challenges by putting out a call for future research that is needed to provide a better understanding of the ongoing processes and mechanisms. This might be possible, for instance, by more closely investigating instructional materials and identifying the sequences that are commonly used in teaching curricular content. On a related note, in such cases and depending on the implemented curriculum, it might also be particularly important to consider higher order lags beyond lag-2, for instance, if curricular content is relevant in grade 5/6 and grade 8/9. In such cases, longitudinal data with more than three measurement occasions is required. Empirical support for this assumption was provided by Arens et al. (2017), who found meaningful lag-4 stability coefficients for math test scores and meaningful lag-3 stability coefficients for math self-concept, test achievement, and grades.

In addition, there have recently been developments in dynamic structural equation models (DSEM; e.g., McNeish & Wolf, 2021) that offer valuable alternatives for providing insights into the reciprocal effects of self-concept and achievement. For instance, Niepel et al. (2021) recently considered longitudinal data collected on students across a 3-week period and applied DSEMs to investigate reciprocal relationships between state self-concepts and lesson-specific perceived achievement. By doing this, they found evidence in favor of the REM. These models (i.e., DSEMs) provide alternatives to more prominently discussed within-person discrete time models (e.g., the RI-CLPM), which seem very promising for better understanding within-person associations of the REM and related developmental processes.

Finally, this study shows that more studies are needed to clarify which causal effects different theoretical models discuss/define and which of these effects different statistical models actually estimate. This might include simulation studies but also theoretical work that helps applied researchers make better decisions regarding assumptions about the underlying structural causal model, which can then be transferred to adequate statistical models. In addition, a very lively discussion is currently taking place about whether within- or between-person coefficients are the “holy grail of longitudinal SEM” (i.e., within or between effects or mixtures of both of these effects), how they should be estimated (Voelkle et al., 2018), how they are defined from a causal perspective, and what they actually mean for theory and practice. At the moment, it seems that the methodological debate about the “right model” (either the RI-CLPM or the CLPM/FF-CLPM) has left applied researchers and even methodologists with bemusement about what model to choose for what kind of research question and data situation. Addressing this gap in the literature will be an important task for future research.

In sum, we have outlined many useful features of weighting approaches related to mitigating threats of extrapolation and the cherry picking of variables but also related to benefits of doubly robust estimation strategies and useful features of specific weighting methods, such as EB (e.g., great balance statistics, potentially even when higher order terms are missing; see Hainmueller, 2012). These methods seem to be particular useful for investigating reciprocal effects of self-concept and achievement when relevant confounders are available and the assumption of strong ignorability is plausible. Notably, as outlined by others, weighting methods also come with specific challenges that are related to, for example, how to handle measurement error or use latent variables. In addition, although there might be specific advantages of weighting methods in some situations (see the Theory section), regression methods could also be understood as a special form of weighting (Angrist & Pischke, 2009), and results by Shadish et al. (2008) suggest that, given a similar set of covariates, approaches such as propensity score weighting and regression adjustment typically lead to very comparable amounts of bias reduction. Related to this, as suggested by Schafer and Kang (2008), potential differences might especially occur when common support (i.e., the region of overlap on the covariate distribution) is low because, then, independence of the treatment effect and the covariates is less plausible. Although similar result patterns seem reasonable when considering multiwave longitudinal data and models, we are not aware of any studies that have investigated the amount of bias reduction in such settings more formally. Therefore, there is a need for future studies that can either simulate the required longitudinal data or use within-study comparison designs to be able to quantify the amount of bias reduction using different models/methods (e.g., Cook et al., 2008; Cook et al., 2009).

Our results from CLPMs and FF-CLPMs with covariates also tend to point in this direction when comparing them to the results from using weighting methods. However, before we will be able to provide researchers with definitive guidance on modeling choices, we see a need for further studies, including simulation studies, to investigate potential differences between the different methods when the true causal effect is known. Future research will also be important for determining whether prior evaluations of the comparability of outcomes and treatment modeling methods hold true for recently developed, new algorithms for weighting data with continuous treatment variables.

Summary

With this substantive-methodological synergy, we investigated the REM and aimed to contrast traditional and more recently developed methods in order to investigate reciprocal effects of students’ academic self-concept and achievement, one of the most prominent models in educational psychology (Wu et al., 2021). In this study, we investigated how different models/methods satisfy the requirements for estimating causal cross-lagged parameters: the CLPM, the FF-CLPM, the RI-CLPM, and weighting techniques to estimate causal effects of continuous treatment variables (Fong et al., 2018; Hainmueller, 2012; Tübbicke, 2021). CLPMs, FF-CLPMs, and results from weighting methods produced evidence in favor of the REM, whereas, in line with findings from prior studies (e.g., Bailey et al., 2020; Burns et al., 2020; Ehm et al., 2019), the results for the RI-CLPM were mixed.