Introduction

Populations of birds of prey have been affected by bioaccumulation of organochlorines like DDT and PCBs during the twentieth century (Grier 1982; Henny et al. 2009; Nygård and Gjershaug 2001; Helander et al. 2002). The relationships between DDT and PCBs exposure and reduced reproduction in sea eagles, i.e. white-tailed eagles (Haliaeetus albicilla) and bald eagles (Haliaeetus leucocephalus), have extensively been documented (Wiemeyer et al. 1993; Bowerman et al. 1995; Donaldson et al. 1999; Helander et al. 2008). Due to the ban on PCBs and DDT and due to conservation measures, most sea eagle populations are currently recovering (Hailer et al. 2006; Scharenberg and Struwe-Juhl 2006; Krüger et al. 2010). In some countries, however, reproduction rates of sea eagles are still low (Helander et al. 2002; Gill and Elliott 2003). In addition to toxic stress, non-toxic stress factors have been linked to low breeding success (Gende et al. 1997; Dykstra et al. 1998). Sea eagles are known to be sensitive to, for example, limited resource availability, climate change and poor habitat configuration, but also to frequent human disturbance, which can cause breeding failures (Buehler et al. 1991a; McGarigal et al. 1991; Grubb et al. 1992; Grim and Kallemeyn 1995; Steidl and Anthony 2000; Bowerman et al. 2005; Watts et al. 2008). To facilitate the return of sea eagles as an indigenous species in The Netherlands, impacts of toxic and non-toxic stress have to be integrated, quantified and assessed at population level endpoints (Sibly et al. 2005; Marris 2009). So far, most quantitative studies focussed on the impacts of single stressors. Besides, investigations of birds of prey, including sea eagle studies, usually assess impacts on reproduction, such as the number of young per pair, nestling brood size and fledging success, rather than population level endpoints.

The aims of the present study were to (1) develop a tool to quantify the impact of multiple stressors on the population development of white-tailed eagles; (2) determine if PCB and DDT were potentially limiting the establishment of white-tailed eagles in The Netherlands in the past; (3) assess the development potential of a white-tailed eagle population in The Netherlands. To that end, we extended an existing analytical single-species modelling framework to include the impacts of organochlorine contaminants as well as disturbance stress on white-tailed eagle populations. The model was parameterized using values collected from literature and validated on an independent field data set.

Model development and application

General approach

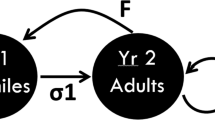
The toxic stress module of the model was based on a framework for assessing the impact of PCB contamination on reproduction, survival and population parameters of cormorants (Phalacrocorax carbo). The basic equations are briefly summarised, as details can be found elsewhere (Hendriks and Enserink 1996; Hendriks et al. 2005). The number of breeding individuals in a given year N(t) is calculated from the population in the preceding year N(t−Δt) by

$$ N\left( t \right) = N\left( {t - \Updelta t} \right) + \frac{{r\left( {C,t} \right)}}{{r\left( {0,t} \right)}} \cdot r\left( {0,t} \right) \cdot N\left( {t - \Updelta t} \right) \cdot \Updelta t \cdot \left( {1 - \frac{{N\left( {t - \Updelta t} \right)}}{N(\infty )}} \right) $$
(1)

where r(C,t) and r(0,t) represent the rates of increase at time t under contaminated conditions and under reference conditions respectively, N(∞) represents the carrying capacity, and the time step Δt was set at 1 year. The rate of increase under reference conditions r(0) was calculated by

$$ \sum\limits_{0}^{{a_{\max } }} {l\left( a \right)} \cdot m\left( a \right) \cdot e^{ - r\left( 0 \right) \cdot a} \cdot da = 1 $$
(2)

with l(a) as the fraction surviving until at least age a and a max as the maximum age. The age-specific fecundity or reproduction rate m(a) represents the number of juveniles fledged per individual during interval da (Birch 1948; Hendriks and Enserink 1996). The rate of increase under contaminated conditions r(C) can be related to the exposure concentration C according to (Hendriks and Enserink 1996)

$$ e^{r\left( C \right) \cdot t} = \sum\limits_{0}^{{a_{\max } }} {\frac{l\left( a \right)}{{1 + \left( {\tfrac{C}{LC50}} \right)^{1/\beta } }} \cdot \frac{m\left( a \right)}{{1 + \left( {\tfrac{C}{EC50}} \right)^{1/\beta } }}} \cdot da $$
(3)

where the median lethal concentration (LC50) and median effect concentration (EC50) represent 50% reductions of l(a) and m(a), respectively. Parameter ß characterises the slope of the concentration–response curve; the terms 1/(1+(C/LC50)1/ß) and 1/(1+(C/EC50)1/ß) represent the fractions of the population which are unaffected by toxic stress through survival and reproduction, respectively. The ratio between the rate of increase r(C) at concentration C and the rate of increase under reference conditions r(0) is calculated according to (Hendriks and Enserink 1996; Hendriks et al. 2005)

$$ {\frac{r\left( C \right)}{r\left( 0 \right)} = \frac{{ - \ln \left( {1 + \left( {\tfrac{C}{LC50}} \right)^{1/\beta } } \right) - \ln \left( {1 + \left( {\tfrac{C}{EC50}} \right)^{1/\beta } } \right)}}{R\left( 0 \right)} + 1} $$
(4)

with R(0) as the lifetime fecundity, i.e. the average number of offspring per individual per generation time, calculated as (Birch 1948; Hendriks and Enserink 1996)

$$ {R\left( 0 \right)} = \sum\limits_{0}^{{a_{\max } }} {l\left( a \right)} \cdot m\left( a \right) \cdot da $$
(5)

Non-toxic environmental stressors, like disturbance, may affect the population size N(t) by further reducing the rate of increase r(C) (Hendriks et al. 2005). Under the assumption that effects of toxic stress and disturbance are purely additive, the population fractions unaffected by either stressor can be multiplied to determine the population fraction unaffected by both stressors combined (Traas et al. 2002). Disturbance stress can then be implemented in Eq. 4 to arrive at

$$ {\frac{{r\left( {C,D} \right)}}{r\left( 0 \right)} = \frac{{ - \ln \left( {\left( {1 + \left( {\tfrac{C}{LC50}} \right)^{1/\beta } } \right) \cdot \left( {\frac{1}{{\left( {f_{L} } \right)}}} \right)} \right) - \ln \left( {\left( {1 + \left( {\tfrac{C}{EC50}} \right)^{1/\beta } } \right) \cdot \left( {\frac{1}{{f_{E} }}} \right)} \right)}}{R\left( 0 \right)} + 1} $$
(6)

where r(C,D)/r(0) represent the ratio of the rate of increase as a function of a chemical concentration C and disturbance D and the rate of increase in reference conditions r(0). The factors f L and f E represent the age independent population fractions which are unaffected by disturbance stress through survival and reproduction, respectively.

Ecological and toxicological parameters

The toxic stress module of the model was parameterised for the organic contaminants ∑PCB and DDE, which have been frequently linked to reduced reproduction in sea eagles (Wiemeyer et al. 1993; Bowerman et al. 1995; Donaldson et al. 1999; Helander et al. 2008). Where possible, white-tailed eagle data were used for model parameterization. If species-specific values were not available, values for the closely related bald eagle (Haliaeetus leucocephalus) were used instead. Assuming that bald eagle data can be applied instead of white-tailed eagle data seems reasonable because the life history patterns are sufficiently comparable. Besides, hazard values estimated for bald eagles have been used in previously published white-tailed eagle studies (Koistinen et al. 1997; Van Wezel et al. 1999). To cover variation and uncertainties in ecological data, the model was parameterised for both favourable and unfavourable conditions.

The rate of increase under reference conditions r(0) was obtained from age-specific reproduction rates of a bald eagle population living in uncontaminated areas and survival rates of white-tailed eagles (Table 1). Measured survival rates for juvenile white-tailed eagles of 0.86–0.95 were reported by Saurola et al. (2003). According to Nygård et al. (2000), survival rates for young birds in the first two years ranged from 0.90 to 0.95. Green et al. (1996) measured survival rates in a reintroduced population of 0.73 for young birds prior to settlement and 0.94 for established birds. In other studies, survival rates reported for white-tailed eagles range from 0.72 to 0.95 for juveniles and from 0.85 to 0.97 for adults (Evans et al. 2009; Krüger et al. 2010; Radovic and Mikuska 2009). Exceptionally low and high values could be attributed to location circumstances (e.g., Green et al. 1996) or were based on a small sample size (e.g. Krüger et al. 2010). Survival rates of 0.75–0.85 for juveniles and 0.90–0.95 for adults were found to be more common and were used for calculating the rate of increase under favourable and unfavourable conditions, respectively. For reproduction, we used data of a bald eagle population in Florida and Chesapeake Bay before widespread use of PCB and DDT (Broley 1947). The mean reproduction of 1.7 fledging juveniles per nest reported for 1936–1946 is among the highest published for sea eagles (Colborn 1991). Reproduction rates of 2 juveniles per nest over multiple years were common and some nests occasionally produced 3 fledging juveniles per year (Broley 1947). It was assumed that the somewhat lower average reproduction of 1.7 juveniles per nest included random nest failures due to inter-specific competition and bad weather (Broley 1947). Fledging success values of 1.7 (average) and 2 (maximum) juveniles per nest were converted following Bortolotti (1986) and Grim and Kallemeyn (1995) and used for parameterisation of the rate of increase under unfavourable and favourable reference conditions, respectively (Table 1). Following Watts et al. (2008) we assumed that the Chesapeake Bay bald eagle population had not reached its carrying capacity yet, implying that reproduction was not affected by intraspecific competition. The lifetime fecundity was based on the life history data given in Table 1.

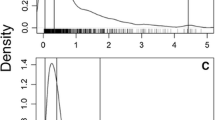
Table 1 Ecological parameters for unfavourable and favourable conditions
Full size table

Lethal concentrations LC50 for ∑PCB and DDE were estimated by calculating the geometric mean of the highest concentration reported in bald eagles with a non-toxic cause of death and the lowest concentration found in sea eagles known to have died from ∑PCB and DDE (Table 2; Fig. 1). The median effect concentration EC50 and the slope constant ß (Table 2; Fig. 1) were derived by fitting a sigmoid dose–response curve on reproduction data from a field study of white-tailed eagle populations in Sweden (Helander et al. 2002). Reproduction rates apply to three different sub-populations, monitored in 1965–1997 (Fig. 1). During this period, 249 dead eggs from 205 clutches were analysed for ∑PCB and DDE residues. Measured lipid weight concentrations were converted to wet weight concentrations using the average lipid fraction of 0.05 noted for eggs of white-tailed eagles (Helander et al. 2002; 2008). Data from Lapland were not used because this subpopulation suffered from food shortages, human disturbance and bad weather (Helander et al. 2002).

Table 2 Toxicological parameters used for simulation of white-tailed eagle population size as a function of ΣPCB and DDE
Full size table
Fig. 1
figure 1

The ratio r(C)/r(0) as a function of a ∑PCB and b DDE concentrations in white-tailed eagles for favourable and unfavourable conditions (Table 1) calculated according to Eq. 4. Concentration–response curves for average reproduction and survival were based on reproduction (dots) and survival (squares) data collected from literature

Full size image

Model testing and data acquisition for validation

The equations and the parameter settings used in the toxic module of the model were tested by comparing exposure concentrations C(t) and population size N(t) with field data collected from the literature. Exposure concentrations C(t) were quantified by estimating residues in eggs from sediment concentrations, according to a method described by Hendriks and Enserink (1996). Sediment levels comprised PCB118 and DDE concentrations measured in Lake Erie’s western basin in 1971 and 1996 (Frank et al. 1977; Painter et al. 2001; Marvin et al. 2004). To obtain a continuous data set, linear interpolation was applied. Interpolated PCB118 concentrations in sediment organic matter were converted to concentrations of the standard congener PCB153 by multiplying them by 1.8 (Hendriks 1993). The PCB153 concentrations were used to derive levels in fish using a biota lipid-organic sediment accumulation factor of 1.8 and a lipid fraction of 0.05 for vertebrates (Hendriks 1995; Hendriks and Enserink 1996). Concentrations in fish, in turn, were used to determine concentrations in eagle eggs using a biomagnification factor from fish to egg of 28 as previously reported for bald eagles (Bowerman et al. 1995). The ∑PCB residue in eggs was calculated by multiplying the estimated PCB153 concentration by a factor of 5 (Helander et al. 2002). For DDE, we used a biota lipid-organic sediment accumulation factor of 11.6 reported for fish, a lipid fraction of 0.05 for vertebrates (Hendriks and Enserink 1996; Hendriks et al. 1998) and a biomagnification factor from fish to egg of 22, as reported for bald eagles (Bowerman et al. 1995).

Next, the chemical residues of ∑PCB and DDE predicted in eagle eggs from sediment concentrations were compared with ∑PCB and DDE residues measured in bald eagle eggs obtained from the Lake Erie area (Donaldson et al. 1999). The predicted egg residues were also used for estimating the population size N(t). Predicted population sizes were compared with observed population data of bald eagles from Lake Erie from 1977 to 1993 reported by Bowerman (1993), which were converted to breeding individuals according to Bortolotti (1986) and Grim and Kallemeyn (1995).

Population development for The Netherlands

The model was applied to estimate the past and future population developments of white-tailed eagles in The Netherlands. For the period up to 1988, environmental concentrations of PCB118 were derived from measurements in sediment core samples obtained from Lake Ketelmeer (Beurskens et al. 1993). PCB118 sediment concentrations were used to derive ∑PCB concentrations in white-tailed eagle eggs as described above. For 1989–2050, emissions as well as degradation of ∑PCB were assumed to be negligible. For DDE, no sediment core data were available for The Netherlands. Instead, we used concentration trends of ∑DDT in European eels (Anguilla anguilla) caught in Lobith from 1978 till 1997 (Hendriks and Pieters 1993). The ∑DDT concentrations were converted to DDE, assuming that DDD and DDT had been transformed to DDE. As the DDE peak is expected to have occurred before 1978, for which no measurements were available in The Netherlands, the DDE trends observed in Sweden (Helander et al. 2002) and Germany (Scharenberg and Struwe-Juhl 2006) were extrapolated to our study area. For 1998–2050, emissions as well as degradation of DDE were assumed to be negligible.

So far, mortality rates of sea eagles due to disturbance stress have not been quantified, although several authors have reported anthropogenic causes of white-tailed eagle and bald eagle mortality (Reichel et al. 1984; Elliott et al. 1996; Krone et al. 2006; Müller et al. 2007). We calculated a disturbance-induced mortality fraction of 0.016 based on the casualties and population size reported for white-tailed eagles in Germany, yielding a surviving fraction F L of 0.984 (Kollman et al. 2002; Krone et al. 2003). The non-toxic and unnatural causes of mortality underlying this fraction were collision with trains, tissue or bone destruction with unknown origin (trauma), electrocution and collision with wires (wind turbines and deliberate poisoning were not included). Unfortunately, no quantitative data could be found regarding the effects of disturbance stress on white tailed eagles’ reproduction success in The Netherlands. In addition, the degree of disturbance stress likely varies as it depends highly on variables such as distance, degree, frequency and type of disturbance (e.g. McGarigal et al. 1991; Grubb et al. 1992; Steidl and Anthony 2000). To cover some of the uncertainty and variability in the effects of disturbance stress, we used reductions in reproduction of 10 and 50% in the simulations, corresponding with unaffected fractions f E of 0.9 and 0.5, respectively.

As the white-tailed eagle has only recently begun to breed in The Netherlands, we did not simulate the population size N(t) from 1950 till 2005 starting from an arbitrary number. Instead, the ratio of r(C)/r(0) was used to assess the potential impacts of ∑PCB and DDE on white-tailed eagles. The model simulations for the period 2006–2050 start from one breeding pair in 2006 (Van Rijn et al. 2010). Within The Netherlands, the majority of wintering white-tailed eagles were recorded at large open wetlands, i.e. Oostervaardersplassen, Lauwersmeer and enclosed estuaries such as Biesbosch, Hollandsch Diep, Haringvliet, Grevelingen and Krammer-Volkerak (Van Rijn et al. 2010). These areas provide a total of 56300 ha of riverine forest, macrophyte marshland and shallow open water (Ministry of Agriculture, Nature and Food Quality 2005), which constitute suitable habitat for the species (Reijnen et al. 1995). Based on an average density of one white-tailed eagle breeding pair per 3750 ha of suitable habitat (Reijnen et al. 1995), following Bortolotti (1986) and Grim and Kallemeyn (1995), we calculated a minimum carrying capacity of N(∞) of 30 breeding individuals for The Netherlands.

Results

Model testing and validation

The difference between the estimated and measured ∑PCB concentration in eagle eggs was less than a factor of 2.5 (Fig. 2a). The measured population size followed the scenario with a favourable parameter setting based on ∑PCB concentrations in eggs (Fig. 2b). For DDE, the maximum difference between estimated and measured concentrations was a factor of 10.7 (Fig. 2c) and the measured population densities followed the scenario with an unfavourable parameter setting based on sediment concentrations (Fig. 2d).

Fig. 2
figure 2

Comparison of measured and simulated a ∑PCB and c DDE residues in eggs (Donaldson et al. 1999; Frank et al. 1977; Painter et al. 2001; Marvin et al. 2004) and observed population size N(t) (Bowerman 1993) compared with N(t) as a function of the simulated b ∑PCB and d DDE concentration trend for both favourable and unfavourable conditions (Table 1). Note that no carrying capacity N(∞) was applied in the model validation

Full size image

Population development for The Netherlands

From 1950 till 1987, the simulated ∑PCB residues in white-tailed eagles exceeded the value of 6.45 × 104 μg·kg−1 wet weight, resulting in a negative ratio r(C)/r(0), corresponding to a population reduction (Fig. 3a). For DDE, ratios were close to 1, suggesting that the impact has been small even in unfavourable conditions (Fig. 3b). Therefore the impact of DDE was not assessed for the period 2006–2050.

Fig. 3
figure 3

The ratio of increase rates r(C)/r(0) for favourable (solid line) and unfavourable (dotted line) parameter setting as a function of a ∑PCB and b DDE concentrations in time. The grey area represents the concentrations simulated for white-tailed eagle eggs. Note that the impact of disturbance stress is not included

Full size image

The white-tailed eagle population projected for 2006–2050 increased and levelled off to the carrying capacity for favourable reference conditions and showed a steady increase for unfavourable reference conditions (Fig. 4). Model simulations including ∑PCB exposure showed a reduced population growth, but eventually resulted in population sizes comparable to those in reference conditions (Fig. 4a). Population sizes predicted for ∑PCB exposure were in between the values predicted for 10 and 50% reductions in reproduction, respectively (Fig. 4b). Under the assumption of additive effects, the combination of toxic and disturbance stress resulted mostly in a reduced population growth. However, under unfavourable conditions, a 50% reduction in reproduction combined with toxic stress resulted in a negative rate of increase and extinction of the population (Fig. 4c).

Fig. 4
figure 4

Trends in white-tailed eagle population size N(t) projected for 2006–2050 as a function of a ∑PCB exposure, b 10 or 50% reduction in annual reproduction and 1.6% reduction in annual survival due to disturbance stress and c both stressors combined, for both favourable and unfavourable parameter setting (Table 1)

Full size image

Discussion

Validation and assumptions

The model developed provides a tool to quantify the impact of toxic and other stressors, due to for example disturbance, on white-tailed eagle populations. For the prediction and evaluation of population trends related to toxic stress, most data were available in literature. Unfortunately, quantitative data that relate reproduction parameters to disturbance stress were not available for sea eagles. Hence, disturbance stress could not be included in the validation of the model. According to the validation of the toxic stress module of the model, the measured DDE concentrations were consistently higher than the simulated concentrations (Fig. 2c), but close to those estimated by Weseloh et al. (2002). Yet, the variability and uncertainty in ecological data (Table 1) have a larger effect on population development than uncertainty in the simulated egg concentrations (Fig. 2d).

Fixed fledging success values were used for calculating the reference rate of increase, which is a simplification. In reality, the fledging success often increases after first breeding and declines at the end of life (Best et al. 2010). Large variations were found in survival and reproduction rates. However, the survival and reproduction rates that were used resulted in reference rates of increase for favourable and unfavourable conditions (Table 1) that are close to the minimum and maximum rates of increase (0.07–0.19) reported for an exponentially growing bald eagle population (Buehler et al. 1991b).

The estimated EC50s and LC50s for ∑PCB and DDE are considered to be indicative because the values are based on reproduction data from field studies and they were not derived by standardised methods. The values may be overestimated due to cumulative effects of ∑PCB, DDE other chemicals, and other stressors. However, the threshold values for ∑PCB and DDE were close to those estimated for bald eagles (Wiemeyer et al. 1993; Elliott and Harris 2001; Best et al. 2010). In addition, the first signs of a reduction in reproduction were revealed at a ∑PCB concentration of 1 × 104 μg·kg−1 wet weight in eggs (Fig. 1a). This corresponds with ∑PCB concentrations in eggs of herring gull (Larus argentatus) and Caspian tern (Sterna caspia) that showed substantial PHA skin responses (Grasman 2002). An immuno-toxicological approach to threshold values is desirable, because immunologic and other sub-individual responses have been related with the establishment success and population development of birds (Grasman 2002; Møller and Cassey 2004).

Despite the assumptions and simplifications that were made in the validation simulation, like the exclusion of potential cumulative effects, a carrying capacity and possible density-dependence in survival and reproduction parameters, the predicted population densities showed no major deviations from field data.

Simulation of impact of ∑PCB, DDE and disturbance stress

In retrospection, the simulated ∑PCB and DDE concentrations in Dutch white-tailed eagle eggs (Fig. 3) are similar to levels previously reported for white-tailed eagle eggs from Sweden and Germany (Helander et al. 2002; Scharenberg and Struwe-Juhl 2006). From 2005 and further, the growing white-tailed eagle population is in line with the population dynamics of white-tailed eagles in Sweden (Helander et al. 2008), Germany (Scharenberg and Struwe-Juhl 2006; Krüger et al. 2010) and bald eagles in Canada and United States (Grier 1982; Bowerman et al. 1995; Donaldson et al. 1999; Buck et al. 2005).

For the simulation of the impact of disturbance stress, a mortality fraction of 0.016 per year was estimated based on mortality rates related to several anthropogenic, non-toxic causes reported for the German white-tailed eagle population (Kollman et al. 2002; Krone et al. 2003). A slightly lower mortality fraction of 0.01 was calculated for a white-tailed eagle population in Sweden, where electrocution and toxic stress were the major causes of death (Kollman et al. 2002; Krone et al. 2006). Yet, the mortality fraction of the German population was considered more representative, because of the resemblance of the infrastructure between Germany and The Netherlands. The calculated impact of a mortality fraction of 0.016 per year on the ratio of increase rates and on the population size N(t) was negligible. One may suggest that not all dead eagles were found the study of Krone et al. (2003) and that the mortality rate therefore is underestimated. However, tentative sensitivity analyses revealed that mortality fractions of 0.01, 0.04 and 0.08 yielded similar model outcomes N(2050) of 23, 23 and 24 in unfavourable reference conditions, respectively, indicating that the model is relatively insensitive to adult mortality.

Unfortunately, quantitative dose–response relationships relating reproduction parameters to human activities were not available for sea eagles, as such relationships are difficult to obtain for birds of prey (Steidl and Anthony 2000; McGarigal et al. 1991). To cover some of the uncertainty and variability in the effects of disturbance stress, we simulated reductions in reproduction of both 10 and 50%. This range is in line with reproduction reductions of 11% and 50–56% due to visitor and investigator disturbance previously reported for common eider (Somateria mollissima) and Leach’s storm-petrel (Oceanodroma leucorhoa), respectively (Bolduc and Guillemette 2003; Blackmer et al. 2004). Other reported values include 20% for black-legged kittiwake (Rissa tridactyla), 22% for golden plover (Pluvialis apricaria) and 44% for Egyptian vultures (Neophron percnopterus) (Beale and Monaghan 2005; Finney et al. 2005; Zuberogoitia et al. 2008). Relatively large impacts of disturbance stress were found for the 50% reduction in reproduction. Moreover, the model is sensitive to changes in the reproduction parameters (Hendriks and Enserink 1996), which further emphasises the need for quantitative dose–response relations between disturbing stress and reproduction parameters.

Conclusions

In the present study, we simulated the impacts of ∑PCB, DDE and disturbance stress on white-tailed eagle populations. The ∑PCB contamination from 1950 till 1987 was found to be too high to allow return of white-tailed eagle as a breeding species in The Netherlands. The impact of DDE concentrations was limited. Simulations of ∑PCB exposure for 2006–2050 indicated that the future population development is still hampered. Simulation of the impact of disturbance stress resulted in a reduced population development. The combination of both toxic and disturbance stress varied from a slower population development to a catastrophical reduction in population size, where the main cause was attributed to the reduction in reproduction of 50%. Despite the limited availability of dose–response relationships and the uncertainties in parameter setting and validation data, the model provides a first step in integrating and quantifying the impacts of multiple stressors on white-tailed eagle populations.