Some Unconventional Properties of New Keynesian DSGE Models

Abstract

We examine the theoretical and numerical properties of a prototypical New Keynesian DSGE model featuring endogenous capital accumulation and labour supply. We find that this completely conventional model yields implausible impact results following unanticipated and temporary shocks when the monetary closure rule is changed from a policy rule setting nominal interest rates (a Taylor Rule) to a fixed money supply rule. We compare and contrast a variety of New Keynesian models, featuring aggregate price stickiness, with their New Classical counterparts featuring perfectly flexible prices. In line with the literature we find that under a Taylor Rule the impulse-response functions following a technology shock are very similar. In contrast, with a fixed money supply the impact effects for the New Keynesian model are implausible. We demonstrate the robustness of this Implausible Result to alternative parameter values and show that it is ultimately caused by the inflexibility of the capital stock relative to that of the real money supply. We suggest several model extensions which will eliminate the Implausible Result from New Keynesian sticky-price models.

1 Introduction

Over the last two decades or so the once dominant IS-LM-AS framework of macroeconomic theory and policy has been largely superseded by a multitude of dynamic stochastic general equilibrium (DSGE hereafter) models with Keynesian features. Founded as it is on earlier DSGE models of the Real Business Cycle (RBC) variety, the New Keynesian approach has the following key features: (a) behavioural relations have microeconomic foundations, and (b) agents form rational expectations. In contrast, while RBC models invariably assume that (c) prices and wages are perfectly flexible, New Keynesian economists typically assume that price- and/or wage stickiness is a fact of life which must be included in a micro-based model of the monetary macroeconomy. Throughout this paper we consider New Keynesian DSGE models in which wages are perfectly flexible but (c) the aggregate price level is sticky.

The main purpose of our paper is to examine the theoretical properties of a prototypical New Keynesian DSGE model. The compelling reason for doing so lies in the fact that this completely conventional model yields implausible impact results following unanticipated and temporary shocks when the monetary closure rule is changed. In particular, such implausible results are obtained if the assumption of nominal interest rate targeting via a Taylor Rule¹ is replaced by the more traditional assumption that the nominal money supply is the instrument of monetary policy, a feature that is well known from the IS-LM-AS framework.

An additional purpose of our paper is to present a careful derivation and discussion of all the salient features of the New Keynesian DSGE model. Whilst these features are generally well-known by practitioners in the field and are taken for granted, our paper may be of use to new entrants in the field presenting and providing a more extensive discussion of the model. In a sense our paper can be seen as a “How To” manual for future builders of New Keynesian DSGE models.

The structure of the paper is as follows. In Sect. 2, we formulate the basic New Keynesian DSGE model, versions of which are used throughout the paper. The model is loosely based on Yun (1996) and (a simplified version) has been documented more extensively in Heijdra (2017, ch. 19). Firms in the intermediate good sector have some market power and engage in Chamberlinian monopolistic competition. Following much of the New Keynesian literature we capture imperfect aggregate price flexibility by adopting the Calvo (1977, 1983) pricing mechanism. The main features of the pricing approach are as follows. In each period a fraction, $1-\zeta$, of firms receive a “green light” from nature and get to charge a new price. They do so making use of all the information that is available to them and recognizing that it may be impossible to adjust prices in the near future (since we assume that $0<\zeta <1$). The remaining fraction, $\zeta$, of firms receive a “red light” and must charge their old price (that was set in the past). The advantage of the Calvo process is that the magnitude of $\zeta$ parameterizes the degree of aggregate price stickiness in the economy (with $\zeta =0$ representing perfect price flexibility). Individuals derive felicity from the consumption of final goods and real money balances and disutility from working. Since they are ultimately the owners of all financial assets (including the shares of intermediate goods producers), their optimal portfolio investment behaviour ensures that firms in the intermediate goods sector discount future profits using the nominal stochastic discount factor for discounting purposes. To complete the model description we must select the type of monetary closure that is assumed.

In Sect. 3 we start with our investigation of the New Keynesian DSGE model. We consider two types of monetary closure, namely a rule setting the nominal interest (Tayor Rule, or TR hereafter) under which the money supply is endogenous, and a fixed money supply rule (FMS hereafter) and an endogenous nominal interest rate (cf. Woodford, 2003; Gali, 2015). We commence the section by presenting the effects of a temporary productivity shock in the benchmark model commonly used in the New Keynesian model, namely the one featuring a TR. We label this model NK-TR and compare its properties to the New Classical model featuring perfectly flexible prices ($\zeta =0$) and a TR (we label this model NC-TR). Interestingly, we find that the impulse-response functions for the NK-TR and NC-TR models are very similar. The fact that prices in the former model are sticky does not essentially alter the dynamic pattern of adjustment following a real shock in the economy.

Next, in Sect. 3, we study the same technology shock in the New Keynesian and New Classical models featuring a constant nominal money supply, i.e. we compare and contrast NK-FMS and NC-FMS. Our main findings are twofold. First, apart from the impact effects, the impulse-response functions for the two models continue to be very similar. Second, and more importantly, the impact effects on output, investment, employment, factor prices, and real marginal cost are implausible in the NK variant of the model. Indeed, we show that a one percent increase in the productivity indicator causes output to decline by 0.18 percent whilst causing declines in investment and employment of, respectively, of 2.83 and 1.10 percent. So even though households get a little wealthier as a result of the shock, they respond at impact by consuming more (which is plausible) and by saving-investing less (which is implausible in view of the intertemporal smoothing motive of individuals). The remainder of the section is dedicated to a discussion of the robustness and intuitive reason behind what we label the Implausible Result of the NK-FMS model (a conjecture).

In Sect. 4, we construct and discuss a number of alternative models in the New Keynesian tradition and investigate for each specification whether it features the Implausible Result in the presence of a money demand function and a (passive or active) money supply rule. The main findings of this section are the following. First, the Implausible Result does not arise in versions of the New Keynesian model with (a) a fixed or absent capital stock, (b) an inflation-fighting money supply rule, (c) capital adjustment costs, and (d) a mix of sticky-price and flexible-price firms in the intermediate goods sector. Second, the Implausible Result persists (or even gets worse) in New Keynesian models with (e) quadratic price adjustment costs, (f) a predetermined price level, (g) a money supply rule that is countercyclical in output, (h) variable capital utilization, and (i) non-separable preferences. The evidence provides support for the conjecture (stated above) that the presence or absence of the Implausible Result hinges on the flexibility of the real money supply relative to the flexibility of the capital stock.

Finally, in Sect. 5 we provide some conclusions. Technical derivations and further material has been gathered in an extensive mathematical appendix labeled Supplementary Material (SM hereafter). This material will be made available to the interested reader.

2 Model

In this section we formulate the basic New Keynesian Dynamic Stochastic General Equilibrium (DSGE) model to be used throughout the remainder of this paper. The model is loosely based on Yun (1996) and (a simplified version) has been documented more extensively in Heijdra (2017, ch. 19).² We consider a closed economy inhabited by identical (representative) agents and normalize the population size to unity. For expositional reasons we first describe the production sector (in Subsect. 2.1). Next we turn to household behaviour (in Subsect. 2.2) after which we characterize the macroeconomic equilibrium (in Subsect. 2.3).

2.1 Firms

There are two production sectors in the economy. The final goods sector is perfectly competitive and it uses inputs produced by monopolistically competitive producers in the intermediate goods sector. The output of the final goods sector is consumed by households or the government and is used to augment the physical capital stock.

2.1.1 Production in the Final Goods Sector

The representative firm in the final goods sector produces a homogeneous good using varieties of a differentiated intermediate good as productive inputs. Production is subject to constant returns to scale (in these inputs) and perfect competition prevails. The number of inputs is constant and we write the aggregate production function as:

$$\begin{aligned} Y_{t}=\left[ \int _{0}^{1}Y_{t}\left( i\right) ^{1-1/\theta }di\right] ^{1/\left( 1-1/\theta \right) },\qquad 1<\theta \ll \infty , \end{aligned}$$

(1)

where $Y_{t}$ is homogeneous output, $Y_{t}\left( i\right)$ is the quantity of input i used in production, and $\theta$ is the substitution elasticity between any two inputs $Y_{t}\left( i\right)$ and $Y_{t}\left( j\right)$ (for $i\ne j$). Since $\theta$ is close to but strictly greater than unity the inputs are close but imperfect substitutes for each other. Denoting the price of input i by $P_{t}\left( i\right)$ we find that the unit-cost function is:

$$\begin{aligned} UC _{t}\equiv \left[ \int _{0}^{1}P_{t}\left( i\right) ^{1-\theta }di \right] ^{1/\left( 1-\theta \right) }. \end{aligned}$$

(2)

In the absence of fixed costs, unit cost equals marginal cost. Perfect competition in the final goods sector thus results in:

$$\begin{aligned} P_{t}= UC _{t}. \end{aligned}$$

(3)

For future reference we note that the derived demand function for input variety i can be written as:

$$\begin{aligned} Y_{t}\left( i\right) =Y_{t}\,\left( \frac{P_{t}\left( i\right) }{P_{t}} \right) ^{-\theta }. \end{aligned}$$

(4)

2.1.2 Production in the Intermediate Goods Sector

The intermediate goods sector is populated by a large number of small firms, each producing a single variety of the differentiated input. Firms engage in Chamberlinian monopolistic competition and, since all firms in the sector are assumed to be identical, we focus on the decisions made by firm i.

Firm i believes that it is too small to affect the overall market outcome, i.e. in setting its price $P_{t}(i)$ it takes the prices charged by other firms (as well as aggregate demand) as given. In formal terms it assumes that $\partial P_{t}(j)/\partial P_{t}(i)=0$ for $j\ne i$ and that $\partial Y_{t}/\partial P_{t}(i)=0$. The firm rents capital and labour from the household and faces a fixed cost in the form of “overhead labour.” The production function is given by:

$$\begin{aligned} Y_{t}(i)=F(K_{t}(i),Z_{t}\,(L_{t}(i)-{\bar{L}}))\equiv K_{t}(i)^{\alpha }\left[ Z_{t}\,(L_{t}(i)-{\bar{L}})\right] ^{1-\alpha }, \end{aligned}$$

(5)

where $K_{t}(i)$ and $L_{t}(i)$ denote the amounts of capital and labour, respectively, ${\bar{L}}$ is overhead labour (so that $L_{t}(i)-{\bar{L}}$ is the number of production workers), and $Z_{t}$ is a labour-augmenting technological term (which is stochastic and common to all firms in the sector).³ The second expression in (5) shows that the technology is of the Cobb-Douglas type with the capital coefficient such that $0<\alpha <1$.

Table 1 New Keynesian DSGE models

Firm i faces perfectly competitive input markets because capital and labour are assumed to be perfectly mobile across firms. This ensures that at any time t there exist common nominal rental rates, which we denote by $R_{t}^{K}$ for capital and $W_{t}$ for labour. At each moment in time the firm chooses its input mix in order to minimize total factor cost, $R_{t}^{K}K_{t}(i)+W_{t}L_{t}(i)$, subject to the production function (5). This results in:

$$\begin{aligned} TC _{t}(i)&= MC _{t}\,Y_{t}(i)+W_{t}{\bar{L}}, \end{aligned}$$

(6)

$$\begin{aligned} MC _{t}&\equiv \left( \frac{R_{t}^{K}}{\alpha }\right) ^{\alpha }\left( \frac{W_{t}}{(1-\alpha )Z_{t}}\right) ^{1-\alpha }, \end{aligned}$$

(7)

where $TC _{t}(i)$ is total cost, $MC _{t}$ is marginal cost, and $W_{t}{\bar{L}}$ is fixed cost. To produce anything at all the firm must hire ${\bar{L}}$ overhead workers. Variable cost is given by $MC _{t}\,Y_{t}(i)$ and depends on the firm’s output. Note that both marginal and fixed cost are the same for all firms in the intermediate goods sector. The derived demands for the two production factors are obtained by employing Shephard’s Lemma:

$$\begin{aligned} K_{t}(i)&=\frac{\partial TC _{t}(i)}{\partial R_{t}^{K}}=\frac{ \alpha }{R_{t}^{K}}\, MC _{t}\,Y_{t}(i), \end{aligned}$$

(8)

$$\begin{aligned} L_{t}(i)&=\frac{\partial TC _{t}(i)}{\partial W_{t}}={\bar{L}}+\frac{ 1-\alpha }{W_{t}}\, MC _{t}\,Y_{t}(i). \end{aligned}$$

(9)

In the absence of price adjustment costs firm i faces a static profit maximization problem which results in the (flex-price) optimal price, $P_{t}^{f}(i)$, which satisfies the usual markup formula:

$$\begin{aligned} P_{t}^{f}(i)=\frac{\theta }{\theta -1}\, MC _{t}. \end{aligned}$$

(10)

At that price the firm’s flex-price output level is $Y_{t}^{f}(i)=Y_{t} \,(P_{t}^{f}\left( i\right) /P_{t})^{-\theta }$ whilst its flex-price profit level is:

$$\begin{aligned} NP _{t}^{f}(i)=\frac{1}{\theta -1}\, MC _{t} \,Y_{t}^{f}(i)-W_{t}{\bar{L}}. \end{aligned}$$

(11)

Several things are worth noting. First, every firm chooses the same price and output level and attains the same profit. Second, since $\theta$ is greater than unity it follows from (10) that the gross markup is greater than one so that the firm more than covers its variable production cost. This explains why nominal profit is increasing in the firm’s output level in (11).

In the presence of price adjustment costs the choice facing the firm is a dynamic one. Following much of the New Keynesian literature Calvo pricing is used. The main features of the pricing approach are as follows. In each period a fraction $1-\zeta$ of firms receive a green light from nature and get to charge a new price, $P_{t}\left( i\right) =P_{t}^{n}\left( i\right)$ . The remaining fraction $\zeta$ of firms receive a red light and must charge their old price.

To derive the firm’s pricing decision when it receives a green light we first write nominal profit at some future time $t+\tau$ from the perspective of time t as follows:

$$\begin{aligned} NP _{t+\tau }(i)&=\left[ P_{t}(i)- MC _{t+\tau }\right] \,Y_{t+\tau }\,\left( \frac{P_{t}\left( i\right) }{P_{t+\tau }}\right) ^{-\theta }-W_{t+\tau }{\bar{L}} \nonumber \\&\equiv \Phi \left( P_{t}(i),X_{t+\tau }\right) , \end{aligned}$$

(12)

where $X_{t+\tau }$ is the vector of macroeconomic variables (expressed in nominal terms) that are taken as given by the firm, $X_{t+\tau }\equiv (P_{t+\tau },Y_{t+\tau },W_{t+\tau }, MC _{t+\tau })$. The objective function of a firm that has just received a green light and decides on $P_{t}\left( i\right)$ is given by:

$$\begin{aligned} V_{t}^{0}\left( i\right) =\Phi \left( P_{t}(i),X_{t}\right) +{\mathbb {E}}_{t} \left[ \sum _{\tau =1}^{\infty }\zeta ^{\tau }{\mathcal {N}}_{t,t+\tau }\Phi \left( P_{t}(i),X_{t+\tau }\right) \right] , \end{aligned}$$

(13)

where ${\mathcal {N}}_{t,s}$ is the nominal stochastic discount factor used for discounting nominal profits:

$$\begin{aligned} {\mathcal {N}}_{t,s}\equiv \left( \frac{1}{1+\rho }\right) ^{s-t}\frac{U_{C}(C_{s},L_{s},M_{s+1}/P_{s})}{U_{C} (C_{t},L_{t},M_{t+1}/P_{t})}\frac{ P_{t}}{P_{s}},\qquad s\ge t, \end{aligned}$$

(14)

and $U_{C}(\cdot )$ is the marginal felicity of consumption. Note that ${\mathcal {N}}_{t,s}$ appears in the firm’s objective function as a result of the portfolio investment decisions of the representative household (see Subsect. 2.2).

The firms sets $P_{t}^{n}\left( i\right)$ in order to maximize $V_{t}^{0}\left( i\right)$. The solution for this problem is (see Supplementary Material [SM], Sect. A.1.1):

$$\begin{aligned} P_{t}^{n}(i)=P_{t}^{n}=\frac{\theta }{\theta -1}\,\frac{P_{t}^{\theta }Y_{t} MC _{t}+{\mathbb {E}}_{t}\left[ \sum _{\tau =1}^{\infty }\zeta ^{\tau } {\mathcal {N}}_{t,t+\tau }P_{t+\tau }^{\theta }Y_{t+\tau } MC _{t+\tau } \right] }{P_{t}^{\theta }Y_{t}+{\mathbb {E}}_{t}\left[ \sum _{\tau =1}^{\infty }\zeta ^{\tau }{\mathcal {N}}_{t,t+\tau }P_{t+\tau }^{\theta }Y_{t+\tau }\right] }. \end{aligned}$$

(15)

Several things are worth noting in this expression. First, since firms face the same macroeconomic environment every green-light firm sets the same price! This symmetry property is convenient because it facilitates the computation of aggregates later on. Second, if firms would get a green light in every period for sure (so that $\zeta =0$) then equation (15) would reduce to $P_{t}^{n}(i)=P_{t}^{n}=\frac{\theta }{\theta -1} MC _{t}$ which is – of course – the flex-price solution stated in (10). Third, in the general case (with $0<\zeta <1$) the new price $P_{t}^{n}(i)$ depends in a complicated way on the current and expected future macroeconomic environment. The new price is explicitly forward looking.

The symmetry of pricing by green-light firms results in a very simple expression for the aggregate price level $P_{t}$ (see SM, Sect. A.1.1):

$$\begin{aligned} P_{t}=\left[ \left( 1-\zeta \right) \left( P_{t}^{n}\right) ^{1-\theta }+\zeta P_{t-1}^{1-\theta }\right] ^{1/(1-\theta )}. \end{aligned}$$

(16)

The current price level is a CES aggregate of the price set by current green-light firms and the lagged aggregate price level. The current price level thus contains both a backward-looking term ($P_{t-1}$) and a forward-looking term ($P_{t}^{n}$).

2.2 Households

There is a large number of identical households. Each individual household is infinitely small and is a price taker on all markets in which it operates. By normalizing the population size to unity we can develop the argument on the basis of a single representative agent. The representative household is infinitely lived and has an objective function based on expected lifetime utility. Denoting the planning period by t, expected lifetime utility, ${\mathbb {E}}_{t}\Lambda _{t}$, is given by:

$$\begin{aligned} {\mathbb {E}}_{t}\Lambda _{t}\equiv {\mathbb {E}}_{t}\sum _{\tau =t}^{\infty }U(C_{\tau },L_{\tau },M_{\tau +1}/P_{\tau })\left( \frac{1}{1+\rho }\right) ^{\tau -t}, \end{aligned}$$

(17)

where $U(C_{\tau },L_{\tau },M_{\tau +1}/P_{\tau })$ is the felicity function, $C_{\tau }$ is consumption, $L_{\tau }$ is labour supply, and $1/(1+\rho )$ is the discounting factor due to time preference (with $\rho >0$ ).We assume that real money balances provide instantaneous utility to the household. As far as timing is concerned, $M_{\tau }$ denotes nominal money balances held at the start of period $\tau$ so we assume that end-of-period real balances enter the felicity function. Following convention in the New Keynesian DSGE literature we assume that the felicity function takes the following form:

$$\begin{aligned} U(C_{\tau },L_{\tau },M_{\tau +1}/P_{\tau })\equiv \frac{C_{\tau }^{1-1/\sigma }-1}{1-1/\sigma }-\varepsilon _{l}\frac{L_{\tau }^{1+\kappa }}{ 1+\kappa }+\varepsilon _{m}\frac{\left( M_{\tau +1}/P_{\tau }\right) ^{1-1/\eta }-1}{1-1/\eta }, \end{aligned}$$

(18)

with $\varepsilon _{l}>0$, $\varepsilon _{m}>0$, $\sigma >0$, $\kappa >0$, and $\eta >0$. The felicity function is weakly separable in consumption, labour supply, and real money balances implying that money is superneutral in a model with perfectly flexible prices and nominal wages.

In order to simplify the exposition somewhat we assume that households are the direct owners of the capital stock and thus make the capital accumulation decision and derive income from renting out their capital stock to firms in the intermediate goods sector (described in Subsect. 2.1.2 above). The household also engages in portfolio investments by purchasing risk-free government bonds, by holding money balances, and by buying equity shares in firms in the intermediate goods sector.

The household’s periodic budget identity (in nominal terms) is given by:

$$\begin{aligned} P_{\tau }\left[ C_{\tau }+I_{\tau }\right] +M_{\tau +1}+B_{\tau +1}+\sum _{s=0}^{\infty }Q_{\tau }^{s}S_{\tau +1}^{s}&=W_{\tau }L_{\tau }+R_{\tau }^{K}K_{\tau }+\left( 1+R_{\tau -1}\right) B_{\tau } \nonumber \\&\quad +\sum _{s=0}^{\infty }X_{\tau }^{s}S_{\tau }^{s}+M_{\tau }-P_{\tau }T_{\tau }, \end{aligned}$$

(19)

where $P_{\tau }$ is the price level, $I_{\tau }$ is gross investment, $M_{\tau }$ is cash balances at the start of period $\tau$, $B_{\tau }$ is the nominal value of the stock of single-period bonds available at the start of period $\tau$, $R_{\tau -1}$ is the (risk-free) nominal interest rate received on such bonds, $Q_{\tau }^{i}$ is the nominal price of share type i in period $\tau$, $S_{\tau }^{s}$ is the number of shares of type s held at the start of period $\tau$, $X_{\tau }^{s}$ is the payoff from such shares (see below), $W_{\tau }$ is the nominal wage rate, $R_{\tau }^{K}$ is the nominal rental rate on capital, $K_{\tau }$ is the stock of capital available at the start of period $\tau$, and $P_{\tau }T_{\tau }$ is the nominal lump-sum tax. Note that – in principle – there are infinitely many firm types, i.e. $s=0,1,\ldots$where firm type $s=0$ is a green-light firm in period t, $s=1$ is a firm which had a green light in period $t-1$ (but a red light in period t), etcetera. The law of motion for the capital stock is given by:

$$\begin{aligned} K_{\tau +1}=I_{\tau }+\left( 1-\delta \right) K_{\tau }, \end{aligned}$$

(20)

where $\delta$ is the depreciation rate of capital ($0<\delta <1$).

The household chooses sequences for consumption, labour supply, investment, single-period bonds, share purchases, money balances, and the capital stock $\{C_{\tau },L_{\tau },I_{\tau },B_{\tau +1},S_{\tau +1}^{s},$ $M_{\tau +1},$ $K_{\tau +1}\}_{\tau =t}^{\infty }$ in order to maximize expected utility (17) subject to (19)–(20) and taking its initial stocks, $B_{t}$, $S_{t}^{s}$, $M_{t}$, and $K_{t}$ as given. In addition, the household treats as given the paths of prices and rental rates ($P_{\tau }$, $Q_{\tau }^{s}$, $W_{\tau }$ and $R_{\tau }^{K}$), the bond rate ($R_{\tau }$), payoffs ($X_{\tau }^{s}$), and taxes ($T_{\tau }$).

For the planning period t the key first-order conditions for this optimization problem are as follows (see SM, Sect. A.1.4). The optimal static choice regarding consumption and leisure is such that the marginal rate of substitution between labour supply and consumption is equated to the real wage rate:

$$\begin{aligned} \frac{-U_{L}(C_{t},L_{t},M_{t+1}/P_{t})}{U_{C}(C_{t},L_{t},M_{t+1}/P_{t})}= \frac{W_{t}}{P_{t}}. \end{aligned}$$

(21)

Furthermore, the first-order condition for optimal investment gives the consumption Euler equation for the representative household:

$$\begin{aligned} 1={\mathbb {E}}_{t}\left[ \frac{r_{t+1}^{K}+1-\delta }{1+\rho }\frac{ U_{C}(C_{t+1},L_{t+1},M_{t+2}/P_{t+1})}{U_{C}(C_{t},L_{t},M_{t+1}/P_{t})} \right] , \end{aligned}$$

(22)

where $r_{t+1}^{K}\equiv R_{t+1}^{K}/P_{t+1}$ is the next period’s real rental rate on capital. Optimal purchases of the risk-free nominal bond results in:

$$\begin{aligned} 1={\mathbb {E}}_{t}\left[ (1+R_{t}){\mathcal {N}}_{t,t+1}\right] , \end{aligned}$$

(23)

where ${\mathcal {N}}_{t,t+1}$ is the nominal stochastic discount factor defined in (14) above. Note that the interest factor $1+R_{t}$ can be taken out of the expectations operator because its value is known to the investor at time t. We thus have the usual result that the risk-free gross interest rate satisfies $1+R_{t}=1/E_{t}\left[ {\mathcal {N}}_{t,t+1}\right]$ (Cochrane, 2005, p. 11).

The first-order condition for nominal money balances is given by:

$$\begin{aligned} 1=\frac{U_{M/P}(C_{t},L_{t},M_{t+1}/P_{t})}{U_{C}(C_{t},L_{t},M_{t+1}/P_{t})} +{\mathbb {E}}_{t}\left[ {\mathcal {N}}_{t,t+1}\right] . \end{aligned}$$

(24)

Money provides not only direct felicity (captured by the first term on the right-hand side) but also acts as a store of value (second term). By using the expression for the risk-free interest rate from (23) we can rewrite (24) in a more intuitive form as:

$$\begin{aligned} \frac{U_{M/P}(C_{t},L_{t},M_{t+1}/P_{t})}{U_{C}(C_{t},L_{t},M_{t+1}/P_{t})}= \frac{R_{t}}{1+R_{t}}. \end{aligned}$$

(25)

Optimal demand for real money balances is such that the marginal rate of substitution between such balances and consumption is equated to the nominal interest factor on the right-hand side of (25).

The final (and most complicated) first-order condition is the one for optimal share purchases:

$$\begin{aligned} Q_{t}^{s}={\mathbb {E}}_{t}\left[ {\mathcal {N}}_{t,t+1}X_{t+1}^{s}\right] , \end{aligned}$$

(26)

where $X_{t+1}^{s}$ is the one-period payoff to purchasing a share in firm type s in period t. What is this payoff and why is it uncertain at time t? Assume that the investor purchases a share in a period-t green-light firm, i.e. $Q_{t}^{0}={\mathbb {E}}_{t}\left[ {\mathcal {N}}_{t,t+1}X_{t+1}^{0} \right]$. Whilst the firm has a green light in period t there are two possible outcome for the next period. With probability $1-\zeta$ it will have a green light again in period $t+1$ so that the payoff to the investor will be $Q_{t+1}^{0}+ NP _{t+1}^{0}$, where $Q_{t+1}^{0}$ is the share price for green-light firms and $NP _{t+1}^{0}$ is nominal profit of such a firm (both in period $t+1$). With probability $\zeta$, however, the firm gets a red light in period $t+1$ so that the payoff to the investor will be $Q_{t+1}^{1}+ NP _{t+1}^{1}$, where $Q_{t+1}^{1}$ and $NP _{t+1}^{1}$ denote the share price and nominal profit level of type $s=1$ firms in period $t+1$. Since the household is ultimately interested in what he or she can consume as a result of the payoff, the nominal stochastic discount factor is applied in the expression in (26). To answer the question at the start of this paragraph, the payoff is stochastic both because there are technology shocks affecting all firms and because the firm may change type between periods t and $t+1$. To summarize we note that for a firm of type s in period t the share price satisfies:

$$\begin{aligned} Q_{t}^{s}={\mathbb {E}}_{t}\left[ {\mathcal {N}}_{t,t+1}\left[ (1-\zeta )(Q_{t+1}^{0}+ NP _{t+1}^{0})+\zeta (Q_{t+1}^{s+1}+ NP _{t+1}^{s+1})\right] \right] . \end{aligned}$$

(27)

No matter how long a red-light firm has been in this sorry state there is always hope in the form of a non-zero probability of switching to the green-light status in the next period.

2.3 Macroeconomic Equilibrium

In this section we tie up some loose ends and define the macroeconomic equilibrium model using the functional forms for household preferences and the technology in the intermediate goods sector (as stated in, respectively, (18) and (5)). For convenience the equations defining the macroeconomic equilibrium have been gathered in Table 1.

Equation (T1.1) restates (20) and (T1.2) is the final goods market clearing condition for a closed economy. Equations (T1.3)–(T1.6) are obtained from, respectively, (23), (22), (25) and (21) by using the felicity function (18) and noting (14). Equations (T1.7)–(T1.8) are obtained by aggregating (8)–(9) over all firms in the intermediate sector (using the definition of $Y_{t}^{a}$) and by expressing the result in real terms. Equation (T1.9) is obtained from (15) by using the definition of the nominal stochastic discount factor from (14). Finally, equation (T1.12) just restates (16).

The remaining equations in Table 1 deal with the loose ends mentioned above. Since primary factors are used in the intermediate goods sector only, the equilibrium conditions in the rental markets for labour are given by:

$$\begin{aligned} L_{t}&=\int _{0}^{1}L_{t}(i)di, \end{aligned}$$

(28)

$$\begin{aligned} K_{t}&=\int _{0}^{1}K_{t}(i)di, \end{aligned}$$

(29)

where $L_{t}$ is total employment and $K_{t}$ is the capital stock. It turns out to be convenient to define an alternative output measure which can be tied directly to the aggregate factor supplies. The alternative output index is defined as:

$$\begin{aligned} Y_{t}^{a}\equiv \int _{0}^{1}Y_{t}(i)di=K_{t}^{\alpha }\left[ Z_{t}\,(L_{t}- {\bar{L}})\right] ^{1-\alpha }. \end{aligned}$$

(30)

Note that the expression in (30) differs from the true aggregate production function (1) in that it treats any two inputs $Y_{t}(i)$ and $Y_{t}(j)$ as if they are perfect substitutes whereas (1) says that they are not. But by defining the alternative price index:

$$\begin{aligned} P_{t}^{a}\equiv \left[ \int _{0}^{1}P_{t}\left( i\right) ^{-\theta }di\right] ^{-1/\theta }, \end{aligned}$$

(31)

we nevertheless find that $Y_{t}$ and $Y_{t}^{a}$ are related to each other according to the following expression:

$$\begin{aligned} Y_{t}=\left( \frac{P_{t}^{a}}{P_{t}}\right) ^{\theta }Y_{t}^{a}. \end{aligned}$$

(32)

Note that (30) and (32) have been restated in (T1.13) and (T1.15) respectively. The recursive relationship for $P_{t}^{a}$ in (T1.14) is obtained by repeating the steps leading to (16) above.

The nominal government budget identity is given by:

$$\begin{aligned} B_{t+1}+M_{t+1}=\left( 1+R_{t-1}\right) B_{t}+M_{t}+P_{t}(G_{t}-T_{t}). \end{aligned}$$

(33)

Together with an assumption regarding the money supply and a government solvency condition the macroeconomic equilibrium is determined. We implicitly assume that the lump-sum tax ensures government solvency. Since the model features Ricardian equivalence the timing of taxation does not matter.

3 Investigating the New Keynesian Model

The New Keynesian DSGE model developed in the previous section is seen by many as the natural successor to the IS-LM-AS model that was used widely in the postwar period. In the wake of the rational expectations revolution that started in the nineteen-seventies the latter model was severely criticized for its lack of consistent microeconomic foundations. Even though the IS-LM-AS model is still widely used in undergraduate textbooks on macroeconomics, its use in research applications has come to a virtual standstill.

Economists working in the New Keynesian tradition have presumably been willing to jettison their once most-preferred workhorse model because they take the New Keynesian DSGE model to be an eminently suitable replacement. On the one hand the model has strong and consistent microeconomic foundations, and on the other hand it seems quite robust and flexible in its usage. But does the New Keynesian model always deliver sensible and empirically plausible predictions? The standard New Keynesian DSGE model has been demonstrated to do so for productivity shocks, monetary shocks, and taste shocks when monetary policy is implemented via an interest rate rule (the so-called Taylor rule). See, for example, the exposition in Gali (2015, ch. 3). In this section, we deviate from such interest rate rules, and close our New Keynesian model with endogenous capital accumulation via a monetary policy that features a constant nominal money supply.

In order to investigate the (im)plausibility of the New Keynesian approach we focus on the impulse-response functions associated with temporary productivity shocks.⁴ Such shocks have been studied extensively in the early literature on Real Business Cycles (RBC). Since the New Keynesian model shares a lot of features with standard RBC models a comparison between the two is our point of departure. In the remainder of this section we proceed as follows. In Subsect. 3.1 we investigate the effects of a productivity shock in the benchmark New Keynesian DSGE model featuring a Taylor Rule (NK-TR hereafter). Next, in Subsect. 3.2 we discuss the standard New Classical model featuring perfectly flexible prices and a Taylor Rule (NC-TR). Finally, in Subsect. 3.3 we study the effects of the technology shock in the alternative New Keynesian DSGE featuring a fixed nominal money supply (NK-FMS hereafter) and an endogenous nominal interest rate and compare it with its New Classical counterpart (NC-FMS). In doing so we discover some highly implausible features of the sticky-price model.

3.1 The Benchmark Sticky-Price Model: NK-TR

In terms of the model listing stated in Table 1, the benchmark sticky-price model consists of equations (T1.1)–(T1.16) plus a countercyclical and inflation fighting policy rule for the nominal interest rate. In the absence of real economic growth and with zero steady-state inflation, such a Taylor Rule takes the form as given in equation (T1.17a), where $Y^{*}$ is the deterministic steady-state output level, $\pi _{t}\equiv (P_{t}-P_{t-1})/P_{t-1}$ is the inflation rate, and $\phi _{\pi }$ and $\phi _{y}$ are positive parameters. Of course, with the rule for the nominal interest rate as given in equation (T1.17a) in operation, the end-of-period nominal money supply, $M_{t+1}$ , becomes an endogenous variable.

The benchmark sticky-price model (labeled NK-TR) constitutes a high-dimensional and nonlinear system of expectational difference equations and contains a number of predetermined (‘non-jumping’) variables and some non-predetermined (‘jumping’) variables.⁵ We analyze the numerical effects of a productivity shock by focusing on the impulse-response functions for the different variables. In particular, we assume that at shock-time $t=0$ the system is in the deterministic steady state and we compute the effects at impact and over time of a single positive innovation term in the technology process, i.e. we set $\eta _{0}^{z}>0$ and $\eta _{t}^{z}=0$ for $t=1,2,\ldots$. The implied perturbation in the technology index is thus given by ${\tilde{Z}}_{t}=\xi _{z}^{t}\eta _{0}^{z}$ for $t=1,2,\ldots$

The perfect foresight solution of the technology shock is computed with the aid of Dynare using the parameter values reported in Table 3.⁶ Details of the parameterization approach are found in SM (Sect A.2). In essence we assume that government consumption is constant ($G_{t}={\bar{G}}$) and parameterize the benchmark model in such a way that the following targets are met for the deterministic steady state:

$$\begin{aligned} Y^{*}=1,\quad L^{*}=\frac{1}{3},\quad \frac{{\bar{G}}}{Y^{*}}= \frac{2}{10},\quad \frac{M^{*}}{P^{*}Y^{*}}=\frac{2}{10},\quad P^{*}=1,\quad \epsilon _{M\!R}\equiv -\frac{d\ln \left( M_{t+1}/P_{t}\right) }{dR_{t}}=0.08. \end{aligned}$$

Output and the equilibrium price level are both normalized to unity, employment is one-third of the available time endowment, and the government spending share of output is twenty percent. Finally we set the ratio of the money supply to nominal quarterly GDP equal to twenty percent. For the Netherlands in the Fall of 2020 we find that M^* ≈ 74 € 10⁹ and P^*Y^* ≈ 238 € 10⁹ yielding a slightly higher fraction of 0.31. Finally, we target the (local) interest semi-elasticity of the demand for real money balances to equal 0.08 in absolute value. This value is in the range of estimates reported by Ball (2012). The calibration parameters are $\Omega _{0},\eta$, $\varepsilon _{l}$, and $\varepsilon _{m}$. The resulting deterministic steady-state equilibrium is reported in Table 4.

Fig. 1

Transitory productivity shock under a Taylor Rule: sticky ($\bullet$) versus flexible ($\circ$) prices

The impulse-response function associated with the temporary technology shock are depicted with solid dots ($\bullet$) in Fig. 1, whilst the impact effects (for period $t=0$) on all variables are reported in column (a) of Table 5. We use the following notational conventions. For all variables except the nominal interest rate $R_{t}$ and inflation $\pi _{t}$ we use proportional rates of change, i.e. ${\tilde{x}} _{t}\equiv (x_{t}-x^{*})/x^{*}$, where $x^{*}$ is the deterministic steady-state value of $x_{t}$. For the remaining variables we define ${\tilde{R}}_{t}\equiv (R_{t}-\rho )/(1+\rho )$, ${\tilde{r}}_{t}\equiv (r_{t}-\rho )/(1+\rho )$, and $\pi _{t}\equiv {\tilde{P}}_{t}-{\tilde{P}}_{t-1}$.

As can be observed in Table 5, a one percent increase in the technology indicator (${\tilde{Z}}_{0}=1$) results in immediate upward jumps in output and investment equaling, respectively, ${\tilde{Y}}_{0}=0.65$ and ${\tilde{I}}_{0}=2.57$ percent. Intuitively, households react to the temporary increase in wages by consuming more (${\tilde{C}}_{0}=0.41$) and by saving-investing more. There is a slight decline in employment of ${\tilde{L}} _{0}=0.07$ percent at impact because the income effect dominates the substitution effect in labour supply. In Fig. 1 the impulse-response functions for the benchmark sticky-price model are depicted with solid dots. Panel (a) depicts the time path of the technology indicator following the shock (the “impulse”) whilst panels (b)–(l) illustrate the resulting time paths for the endogenous variables in the model (the “responses”). Output is boosted at impact and subsequently converges back to its original level (panel (b)). Both the capital stock and consumption display hump-shaped responses (see panels (d)–(e)). Several other things are worth noting. First, since the benchmark model features a Taylor rule, there is a huge decrease at impact in the nominal interest rate (panel (k)) which prompts a substantial increase in the real money supply (panel (l)). Second, the temporary technology shock induces a process of price deflation leading to a large long-run drop in the price level, i.e. the model with a Taylor rule features hysteresis in the price level (panel (i)).

3.2 The Flexible-Price Model: NC-TR

Before turning to our alternative sticky-price model we first compare and contrast the benchmark New Keynesian model of Subsect. 3.1 with a purely New Classical one featuring perfectly flexible prices and a Taylor Rule. Details of the latter model are reported in SM (Sect. A.3.4). All intermediate firms practice “static” marginal cost pricing at all times, i.e. $P_{t}=[\theta /\left( \theta -1\right) ] MC _{t}$, so that real marginal cost is constant in the flexible-price model:

$$\begin{aligned} mc _{t}=\frac{\theta -1}{\theta }. \end{aligned}$$

(34)

The New Classical model (labeled NC-TR) is listed in Table 2 and in this subsection equation (T2.11a) is used and (T2.11b) is ignored. As the comparison between Tables 1 and 2 reveals, the flexible-price model is structurally much simpler than the sticky-price model.

Table 2 New classical DSGE models

Table 3 Structural parameters

Table 4 Deterministic steady-state equilibrium in the benchmark model

Table 5 Impact effects of a persistent productivity shock: standard cases

Table 5(e) reports the impact effects of the technology shock for the NC-TR model. A one percent increase in the technology indicator results in increases in output, employment, and investment equaling, respectively, 0.93, 0.22, and 4.16 percent. In Fig. 1 the impulse-response functions for the New Keynesian and New Classical models are depicted using, respectively, solid dots ($\bullet$) and open dots ($\circ$). Interestingly, the impulse-response functions for output, the capital stock, consumption, and investment are very similar for the two models (see panels (b) and (d)–(f)). With perfect price flexibility there is a higher rate of price deflation during transition resulting in a larger long-run effect on the price level (panel (i)). Furthermore, during transition there is a lower nominal interest rate (panel (k)), and a higher real money stock (panel (l)) than in the sticky-price model.

3.3 The Alternative Sticky-Price Model: NK-FMS

With a Taylor Rule for nominal interest rates in place, the impulse-response functions for a temporary technology shock are qualitatively very similar for the New Keynesian and New Classical models. In this subsection we investigate whether this similarity result also holds for an alternative monetary policy rule, namely when the central bank maintains a constant nominal money supply instead of using the nominal interest rate as an instrument.

As we document in the remainder of this subsection, it turns out that the New Keynesian sticky-price model gives rise to implausible impact effects for a number of variables when the Taylor Rule is replaced by a passive money supply rule, i.e. if equation (T1.17a) in Table 1 is replaced by equation (T1.17b). As is evident Table 5(b), the alternative model (which we label NK-FMS from here on) yields implausible impact results for output, investment, employment, factor prices, and real marginal cost. Indeed, a one percent increase in ${\tilde{Z}}_{0}$ causes output to decline by 0.18 percent whilst causing declines in investment and employment of, respectively, of 2.83 and 1.10 percent. So households get wealthier and respond at impact by consuming more (which is plausible) and by saving-investing less (which is highly implausible in view of the intertemporal smoothing motive of individuals).

Fig. 2

Transitory productivity shock under a fixed money supply: sticky ($\bullet$) versus flexible ($\circ$) prices

That these results are highly implausible is further exemplified by the impulse-response functions in Fig. 2. In that figure the impulse-response functions for NK-FMS and the flexible-price model with a fixed money supply (labeled NC-FMS) are depicted using, respectively, solid dots ($\bullet$) and open dots ($\circ$). Indeed, from period $t=1$ onward, output, employment, investment, factor prices and real marginal cost respond to the technology shock in a very similar fashion in the NK-FMS and NC-FMS models (Table 6).

Fig. 3

Factor markets after a productivity shock

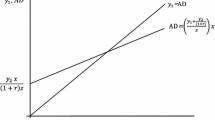
The effects occurring in periods $t=0$ and $t=1$ in the NK-FMS model can be further explained intuitively with the aid of Fig. 3(a)–(b).⁷ These figures make use of the linearized demand and supply of labour and the demand for capital units (see Table 7):

$$\begin{aligned} {\tilde{L}}_{t}&=\frac{1}{\kappa }\left[ {\tilde{w}}-\frac{1}{\sigma }{\tilde{C}} _{t}\right] ,\end{aligned}$$

(35)

$$\begin{aligned} {\tilde{L}}_{t}&=(1-\xi )\left[ \widetilde{ mc }_{t}+{\tilde{Y}}_{t}- {\tilde{w}}_{t}\right] , \end{aligned}$$

(36)

$$\begin{aligned} {\tilde{r}}_{t}&=\frac{\delta +\rho }{1+\rho }\left[ \widetilde{ mc }_{t}+{\tilde{Y}}_{t}-{\tilde{K}}_{t-1}\right] . \end{aligned}$$

(37)

In panel (a) the spot market for labour is illustrated. The solid lines depict the steady-state demand (D) and supply (S) curves. At impact, in period $t=0$, the labour supply shifts to the left, to $\hbox {S}_{{0}}$, as a result of the increase in consumption (${\tilde{C}}_{0}>0$). At the same time, the labour demand curve also shifts to the left to $\hbox {D}_{{0}}$ because $\widetilde{ mc }_{0}+{\tilde{Y}}_{0}<0$. It follows that the equilibrium shifts from point e to point $\hbox {e}_{{0}}$ and the wage rate and employment both fall. In panel (b) the rental market for units of existing capital is drawn. In this market $r^{K}=r+\delta$ is determined and we plot the real interest rate perturbation on the vertical axis. Again the solid lines depict the steady-state demand (D) and supply (S) curves. At time $t=0$, the capital stock is predetermined so that the supply curve at that time, $\hbox {S}_{{0}}$, coincides with the initial supply curve. The demand for capital units falls, again because $\widetilde{ mc }_{0}+{\tilde{Y}}_{0}<0$, and the demand curve shifts to $\hbox {D}_{{0}}$. The equilibrium shifts from point e to point $\hbox {e}_{{0}}$ directly below it. The rental rate on capital and thus the real interest rate falls.

The simultaneous drop in both factor prices in period $t=0$ explains why there is such a huge decrease in real marginal cost at that time, i.e. $\widetilde{ mc }_{0}=-1.7753$. Indeed, by linearizing equation (7) around the deterministic steady state we find the following expression for the perturbation in real marginal cost:

$$\begin{aligned} \widetilde{ mc }_{t}=\frac{\alpha (1+\rho )}{\rho +\delta }{\tilde{r}} _{t}+(1-\alpha )\left[ {\tilde{w}}_{t}-{\tilde{Z}}_{t}\right] , \end{aligned}$$

(38)

where we have used the fact that ${\tilde{r}}_{t}^{K}\equiv (r_{t}^{K}-(\rho +\delta ))/(\rho +\delta )=[(1+\rho )/(\rho +\delta )]{\tilde{r}}_{t}$. At impact we find that all variables on the right-hand side of (38) cause real marginal cost to fall, i.e. ${\tilde{r}}_{0}<0$, ${\tilde{w}}_{0}<0$, and $-{\tilde{Z}}_{0}<0$.

Next we consider what happens in period $t=1$. In panel (a) of Fig. 3 the supply curve shift further to the left, say to S$_{1}$, because consumption increases further (${\tilde{C}}_{1}>{\tilde{C}}_{0}$ ). At the same time the demand for labour experiences a ‘miraculous’ recovery, and the demand curve shifts to the right to $\hbox {D}_{{1}}$ (because $\widetilde{ mc }_{1}+{\tilde{Y}}_{1}>0$). It follows that in period $t=1$, the spot market equilibrium shifts from point $\hbox {e}_{{0}}$ to $\hbox {e}_{{1}}$. Both employment and the wage rate are higher than their steady-state values, i.e. ${\tilde{w}}_{1}>0$ and ${\tilde{L}}_{1}>0$. In panel (b) the effects in period $t=1$ consist of a rightward shift in demand, from $\hbox {D}_{{0}}$ to $\hbox {D}_{{1}}$ (because $\widetilde{ mc }_{1}+{\tilde{Y}}_{1}>0$), and a leftward shift in supply, from $\hbox {S}_{{0}}$ to $\hbox {S}_{{1}}$ (because investment in the impact period was negative, ${\tilde{I}}_{0}<0$). The equilibrium shifts from point e$_{0}$ to point $\hbox {e}_{{1}}$. The capital stock in period $t=1$ is less than its steady-state value but the real interest rate exceeds its steady-state value, i.e. ${\tilde{r}}_{1}>0$. Together with the increase in the wage rate this helps explain why the drop in real marginal cost is almost entirely eliminated in period $t=1$, i.e. $\widetilde{ mc }_{1}=-0.0541.$

What would happen in a flexible-price model? The answer is furnished by the New Classical model with a fixed money supply (NC-FMS) as listed in Table 2. To compare it to the NK-FMS model, the Taylor Rule, given in equation (T2.11a), is replaced by the fixed money supply assumption stated in (T2.11b). As is confirmed in column (f) of Table 5, the NC-FMS model does not feature the implausible impact results. Indeed, a one percent increase in the technology indicator results in immediate increases in output, investment, and employment equalling, respectively, 0.93, 4.16, and 0.22 percent.⁸

The effects occurring in periods $t=0$ and $t=1$ on factor markets can be further explained with the aid of Fig. 3(e)–(f). Since real marginal cost is constant under flexible prices (see (34) above), the expressions stated in (36)–(37) can be simplified by imposing $\widetilde{ mc }_{t}=0$ to obtain:

$$\begin{aligned} {\tilde{L}}_{t}&=(1-\xi )\left[ {\tilde{Y}}_{t}-{\tilde{w}}_{t}\right] , \end{aligned}$$

(39)

$$\begin{aligned} {\tilde{r}}_{t}&=\frac{\delta +\rho }{1+\rho }\left[ {\tilde{Y}}_{t}-{\tilde{K}} _{t-1}\right] . \end{aligned}$$

(40)

In panel (e) the situation on the spot market for labour is illustrated. In period $t=0$, the supply curve (35) shifts to the left to $\hbox {S}_{{0}}$ because consumption increases (${\tilde{C}}_{0}>0$), whilst the demand curve (39) shifts to the right, to $\hbox {D}_{{0}}$, because output has increased ( ${\tilde{Y}}_{0}>0$) and the capital stock is predetermined (${\tilde{K}} _{t-1}=0$). It follows that the equilibrium in the labour market shifts from point e to point $\hbox {e}_{{0}}$, i.e. the wage rate and employment both rise. In panel (f) the rental market for units of existing capital is drawn. At time $t=0$, the capital stock is predetermined so that $\hbox {S}_{{0}}$ coincides with the initial supply curve S. The demand for capital units increases (because ${\tilde{Y}}_{0}>0$) and the demand curve shifts to $\hbox {D}_{{0}}$. The equilibrium shifts from point e to point $\hbox {e}_{{0}}$ directly above it. The rental rate on capital and thus the real interest rate increases. In the flexible-price model real marginal cost is constant and the increase in productivity, ${\tilde{Z}}_{0}>0$, is accompanied by a rise in both factor prices, i.e. ${\tilde{w}}_{0}>0$ and ${\tilde{r}}_{0}>0$.

In period $t=1$ the supply of labour shifts to the left, to $\hbox {S}_{{1}}$, because ${\tilde{C}}_{1}>{\tilde{C}}_{0}$, and the demand for labour shifts to the left, to $\hbox {D}_{{1}}$, because ${\tilde{Y}}_{1}<{\tilde{Y}}_{0}$. The equilibrium shifts from point $\hbox {e}_{{0}}$ to $\hbox {e}_{{1}}$ in Fig. 3(e). Employment and the wage rate both fall. In Fig. 3(f) the supply curve of units of capital shifts to the right, to $\hbox {S}_{{1}}$, because ${\tilde{I}}_{0}>0$. The demand curve shifts to the left, to $\hbox {D}_{{1}}$, because $0<{\tilde{Y}}_{1}<{\tilde{Y}}_{0}$. The equilibrium shifts from $\hbox {e}_{{0}}$ to $\hbox {e}_{{1}}$ and the real interest rate falls somewhat ($0<{\tilde{r}}_{1}< {\tilde{r}}_{0}$).

3.4 The Implausible Result

3.4.1 Statement of the Problem

In the previous subsection we have identified and intuitively explained an implausible implication of the New Keynesian sticky-price model with a fixed nominal money supply. In order to streamline the discussion we define the implausible result as follows.

Definition 1

(Implausible Result) In the New Keynesian DSGE model with a constant nominal money supply and endogenous capital accumulation (NK-FMS), a temporary technology shock results in implausible effects in that: (i) output, employment, and investment fall at impact, (ii) the wage rate and the rental rate on units of capital both drop at impact, (iii) there is a large reduction in real marginal cost at impact,(iv) output, employment, investment, the wage rate, and the rental rate all increase whilst the drop in real marginal cost is virtually eliminated one period after the shock, (v) the capital stock declines one period after the shock but more than recovers immediately thereafter.

In the remainder of this subsection we investigate the parametric and theoretical robustness of the Implausible Result.

3.4.2 Parametric Robustness

It might be argued that the Implausible Result is merely an artifact of the particular set of structural parameters that was chosen in the parameterization. As it turns out, however, the result is quite robust. In Table 6 we present a number of pairwise comparisons featuring different combinations of structural parameters. In panel (A) we report the impact effects on output, investment, and real marginal cost for different $(\zeta ,\sigma )$ combinations. The benchmark NK-FMS model features $(\zeta ,\sigma )=(0.75,1)$, along the row different values of $\sigma$ are considered, and along the column the $\zeta$ parameter is varied. For a given value of $\sigma$, the Implausible Result disappears for output and investment and becomes less extreme for marginal cost provided prices are sufficiently flexible, i.e. the lower is the probability of a red light, $\zeta$. Similarly, holding constant $\zeta$, the Implausible Result becomes less pronounced provided the intertemporal substitution mechanism in consumption is sufficiently strong, i.e. the higher is $\sigma$.

Table 6 Impact effects on output, investment, and marginal cost under alternative parameter settings

In Table 6(B) we report the impact effects for different $(\zeta ,\kappa )$ combinations. Recall that the benchmark NK-FMS model features $(\zeta ,\kappa )=(0.75,1)$. Just as in panel (A), within any column the Implausible Result disappears for output and investment and becomes less extreme for marginal cost for sufficiently flexible prices. Similarly, holding constant $\zeta$, the Implausible Result disappears for output and invstment but becomes more pronounced for marginal cost provided the Frisch elasticity of labour supply is sufficiently low, i.e. the higher is $\kappa$.

In Table 6(C) we report the impact effects for different $(\zeta ,\theta /(\theta -1))$ combinations, where we recall that $\theta /(\theta -1)$ represents the gross monopoly markup. The benchmark NK-FMS model features $(\zeta ,\theta /(\theta -1))=(0.75,9/8)$. With regard to price flexibility a similar pattern is obtained as in panels (A)–(B). Interestingly, holding constant $\zeta$, the Implausible Result is not essentially affected by the size of the monopoly markup.

Finally, in Table 6(D) we report the impact effects for different $(\zeta ,\epsilon _{ M\!R })$ combinations, where $\epsilon _{ M\!R }$ represents the (absolute value of) the interest semi-elasticity of money demand. The benchmark NK-FMS model features $(\zeta ,\epsilon _{ M\!R })=(0.75,0.08)$. For the parameter of price flexibility we fid the same pattern as in panels (A)–(C). Furthermore, holding constant $\zeta$, the Implausible Result disappears for output and investment and becomes less extreme for marginal cost the less elastic is money demand, i.e. the smaller is $\epsilon _{ M\!R }$.

3.4.3 Theoretical Robustness

Loosely put the New Keynesian model presented here has two ‘parents.’ On the one hand it contains the Old Keynesian idea of price stickiness which is captured with the Calvo friction, and on the other hand it embraces the New Classical notion of clearing markets, perfect wage flexibility, endogenous labour supply and capital accumulation and rational expectations. So the question arises whether the Implausible Result arises because of one of the model’s parents. Indeed, is it the Keynesian or the Classical component that is causing the Implausible Result? Of all the models considered up to this point, NK-TR, NC-TR, NC-FMS do not feature the Implausible Result whilst NK-FMS does. So there is a strong suspicion that the Keynesian component is ‘somehow’ causing the problems.

The capital accumulation mechanism As a first case we compare the NK-FMS model with a special case of this model in which there is a fixed stock of a non-depreciating production input (say capital or land). We refer to the latter model as NK-$\hbox {FMS}_{{ff}}$ and provide details on it in SM (Sect. A.3.1). The representative agent can buy or sell units of land. The household’s periodic budget identity (19) is changed to:

$$\begin{aligned}&P_{\tau }C_{\tau }+P_{\tau }^{K}(K_{\tau +1}-K_{\tau })+M_{\tau +1}+B_{\tau +1}+\sum _{s=0}^{\infty }Q_{\tau }^{s}S_{\tau +1}^{s}\nonumber \\&\quad =W_{\tau }L_{\tau }+R_{\tau }^{K}K_{\tau } +\left( 1+R_{\tau -1}\right) B_{\tau }+\sum _{s=0}^{\infty }X_{\tau }^{s}S_{\tau }^{s}+M_{\tau }-P_{\tau }T_{\tau }, \end{aligned}$$

(41)

where $P_{\tau }^{K}$ is the price of land at time $\tau$. Equation (22) is changed to:

$$\begin{aligned} 1={\mathbb {E}}_{t}\left[ \frac{r_{t+1}^{K}+p_{t+1}^{K}}{p_{t}^{K}}\frac{1}{ 1+\rho }\left( \frac{C_{t}}{C_{t+1}}\right) ^{1/\sigma }\right] , \end{aligned}$$

(42)

where $p_{t}^{K}\equiv P_{t}^{K}/P_{t}$ is the real price of land. Furthermore, investment is zero, $I_{t}=0$, and the total stock of land is constant, $K_{t}=K$.

Fig. 4

The sticky-price model: with ($\bullet$) and without ($\circ$) variable capital

In Fig. 4 the impulse-response function for the two models are depicted, with solid dots for the NK-FMS model and open dots for the NK-$\hbox {FMS}_{{ff}}$ model (featuring a fixed factor). As is confirmed in column (c) of Table 5, the NK-$\hbox {FMS}_{{ff}}$ model does not feature the Implausible Result. Indeed, a one percent increase in the technology indicator results in an increase in output of 0.30 percent and a decrease in employment of 0.53 percent.

The effects occurring in periods $t=0$ and $t=1$ are visualized in Fig. 3(c)–(d). Consider panel (c) first. In period $t=0$ , labour supply shifts to the left, from S to $\hbox {S}_{{0}}$, because consumption increases (${\tilde{C}}_{0}>0$). Labour demand shifts to the left, from D to D$_{0}$, because $\widetilde{ mc }_{0}+{\tilde{Y}}_{0}<0$ (just as in the NK-FMS model). It follows that the equilibrium shifts from point e to point e $_{0}$ so the wage rate and employment both fall at impact. In panel (d) the rental market for units of existing land is drawn. The stock of land is fixed and supplied inelastically on the rental market–see the supply curve S. The demand for land units falls (because $\widetilde{ mc }_{0}+ {\tilde{Y}}_{0}<0$) and the demand curve shifts to $\hbox {D}_{{0}}$. The equilibrium shifts from point e to point $\hbox {e}_{{0}}$ directly below it. The rental rate on land decreases. In view of the fact that ${\tilde{w}}_{0}<0$, ${\tilde{r}}_{0}<0$ , and $-{\tilde{Z}}_{0}<0$ we find that real marginal cost falls substantially, i.e. $\widetilde{ mc }_{0}=-1.0430$ in Table 5(c).

In period $t=1$ the supply of labour shifts further to the left, to $\hbox {S}_{{1}}$, because ${\tilde{C}}_{1}>{\tilde{C}}_{0}$, but the demand for labour shifts to the right, to $\hbox {D}_{{1}}$, because $\widetilde{ mc }_{0}+{\tilde{Y}}_{0}< \widetilde{ mc }_{1}+{\tilde{Y}}_{1}<0$. The equilibrium shifts from point $\hbox {e}_{{0}}$ to $\hbox {e}_{{1}}$ in Fig. 3(c). Both employment and the wage rate increase. In Fig. 3(d) the demand curve for units of land shifts to the right, say from $\hbox {D}_{{0}}$ to $\hbox {D}_{{1}}$, again because $\widetilde{ mc }_{0}+{\tilde{Y}}_{0}< \widetilde{ mc }_{1}+{\tilde{Y}}_{1}<0$. The equilibrium shifts from e$_{0}$ to $\hbox {e}_{{1}}$ and the land rental rate increases (${\tilde{r}}_{0}<{\tilde{r}} _{1}<0$).

Glancing at the impulse response function for the NK-$\hbox {FMS}_{{ff}}$ model in Fig. 4 we note that the highly implausible response functions for output and employment of the NK-FMS model are replaced by much more plausible counterparts, i.e. there is a hump-shaped response in output and a monotonic recovery of employment following the technology shock in the NK-$\hbox {FMS}_{{ff}}$ model.

The verdict: Too much rigidity in the NK-FMS model The upshot of the discussion thus far is that the Implausible Result cannot be contributed solely to one of the three major mechanisms at work in New Keynesian models, namely (a) nominal price stickiness, (b) the form of monetary closure that is adopted, and (c) endogenous capital accumulation. But this means that the only remaining potential ‘culprit’ causing the Implausible Result in the NK-FMS model is the combination of sticky prices, endogenous capital accumulation, and a constant money supply (or inactive money supply rule). Monetary non-neutrality is the key feature distinguishing the New Keynesian model from its Classical flexible-price counterpart. And this implies that the monetary model closure affects the real equilibrium attained in the economy. Intuitively, with a sufficiently high degree of price stickiness and a constant nominal money supply, the real money supply is more of less fixed at impact and it is this real rigidity which, in combination with a predetermined capital stock, causes the Implausible Impact effects of technology shocks. We summarize these insights in the following conjecture.

Conjecture 1

(Excessive Real Monetary Rigidity) The New Keynesian sticky-price model with a constant nominal money supply and endogenous capital accumulation (NK-FMS) features the Implausible Result provided nominal prices are sufficiently sticky. This is caused by the resulting stickiness of the real money supply in combination with an endogenous capital stock which is predetermined at impact.

The conjecture can be motivated more extensively by revisiting the impulse-response functions for the different models. First, we consider the New Keynesian and New Classical models under a Taylor rule for which the Implausible Result does not occur–see Fig. 1. In panel (l) of that figure we illustrate the impulse response functions for the real money supply in the two models. Note that in both TR models there are huge swings in the real money supply. Price stickiness does not matter here because the policy maker controls the nominal interest rate and real money demand is determined residually.

Second, we consider the New Keynesian and New Classical models under a fixed money supply for which the Implausible Result does occur with sticky prices–see Fig. 2. Panel (l) in that figure shows that in both FMS models there are rather small fluctuations in the real money supply. For the New Classical model the ‘straightjacket’ of a fixed nominal money supply has no effect on the real macroeconomic variables. In contrast, for the New Keynesian model the ‘near rigidity’ of the real money supply does spill over into the real economy at impact. In particular, agents wish to engineer a sharp reduction in the capital stock one period after the shock and do so by reducing saving-investment dramatically (see, respectively, panels (d) and (f)).

Third, we consider the New Keynesian model with an endogenous or constant capital stock in Fig. 4.⁹ In the latter case the Implausible Result does not occur because the perverse pattern for the capital stock and investment is excluded a priori. Instead, the near fixity of the real money supply now shows up in the form of a substantial fall in labour supply and employment at impact and during transition (see panel (c)).

4 Possible Remedies and Blind Alleys

In this section we discuss a number of alternative models in the New Keynesian tradition and investigate for each specification whether it features the Implausible Result in the presence of a money demand function and a (passive or active) money supply rule. For each alternative model we recalibrate the model in such a way that it yields the same deterministic steady state as the NK-FMS model. Details of this procedure are found in SM. For the sake of convenience the quantitative results for the impact period have been collected in Table 8. For ease of comparison column (a) in that table restates the results for the NK-FMS model.

Table 7 The linearized New Keynesian DSGE models

Table 8 Alternative model specifications

4.1 Quadratic Price Adjustment Costs

As a first alternative model specification we consider the case for which the Calvo (1977, 1983) pricing friction is replaced by the Rotemberg (1982) assumption featuring symmetric firms facing quadratic price adjustment costs. We first sketch the main theoretical changes implied by this alternative modeling assumption. Details can be found in SM (Sect. A.3.3). See also Ascari and Rossi (2012) for a model without capital.

In the absence of a Calvo friction each firm is free to re-optimize its current and planned future prices. Indeed, at time t firm i in the intermediate goods sector chooses its price path $P_{t+\tau }(i)$ in order to maximize the present value of its nominal profits:

$$\begin{aligned} V_{t}(i)&\equiv {\mathbb {E}}_{t}\sum _{\tau =0}^{\infty }{\mathcal {N}}_{t,t+\tau }\Bigg [\left( P_{t+\tau }(i)- MC _{t+\tau }\right) Y_{t+\tau }(i)-W_{t+\tau }{\bar{L}} \nonumber \\&\quad -\frac{\chi }{2}\left( \frac{P_{t+\tau }(i)}{P_{t+\tau -1}(i)} -1\right) ^{2}P_{t+\tau }Y_{t+\tau }\Bigg ], \end{aligned}$$

(43)

where $\chi$ is the price-adjustment cost parameter (such that $\chi >0$) and ${\mathcal {N}}_{t,t+\tau }$ is the nominal stochastic discount factor defined in (14) above. After some manipulation we find that the first-order condition for the optimal price at time t can be written as:

$$\begin{aligned} \theta \left[ 1- mc _{t}\right]&=1-\chi \left( \frac{P_{t}}{P_{t-1}}-1\right) \frac{P_{t}}{P_{t-1}} \nonumber \\&\quad +\frac{\chi }{1+\rho }{\mathbb {E}}_{t}\left[ \left( \frac{C_{t}}{ C_{t+1}}\right) ^{1/\sigma }\left( \frac{P_{t+1}}{P_{t}}-1\right) \frac{ Y_{t+1}}{Y_{t}}\frac{P_{t+1}}{P_{t}}\right] . \end{aligned}$$

(44)

The national income identity in the presence of price-adjustment cost is changed from (T1.2) to:

$$\begin{aligned} Y_{t}=C_{t}+I_{t}+{\bar{G}}+\frac{\chi }{2}\left( \frac{P_{t}}{P_{t-1}} -1\right) ^{2}Y_{t}. \end{aligned}$$

(45)

Since firms are symmetric they all choose the same price and set the same quantity so there is no price- and quantity dispersion, i.e. $P_{t+\tau }(i)=P_{t+\tau }$, $Y_{t+\tau }(i)=Y_{t+\tau }$, and $Y_{t+\tau }^{a}=Y_{t+\tau }$.

The augmented model consists of equations (T1.1), (45), (T1.3)–(T1.5), (44), (T1.6)–(T1.8), (T1.13), and (T1.16). The endogenous variables are $Y_{t}$, $L_{t}$, $K_{t}$, $C_{t}$, $I_{t}$, $Y_{t}$, $w_{t}$, $r_{t}^{K}$, $P_{t}$, $mc _{t}$, and $Z_{t}$. The exogenous variables are $\eta _{t}^{z}$, ${\bar{G}}$, and $M_{t+1}$. The model features the same deterministic steady state as the NK-FMS model. In order to make the dynamics of the linearized model observationally equivalent (to a first order) with the dynamics of the linearized NK-FMS model we set the adjustment cost parameter as follows (Ascari and Rossi, 2012, p. 1122):

$$\begin{aligned} \chi =\frac{\zeta (\theta -1)\left( 1+\rho \right) }{\left( 1-\zeta \right) \left( 1+\rho -\zeta \right) }. \end{aligned}$$

(46)

The simulation results for the Rotemberg-pricing model are reported in Table 8(b). The quantitative results are rather similar to those of the NK-FMS model. Output, investment, and employment fall at impact only to more than recover from the next period onward. The huge impact drop in marginal cost is also virtually eliminated immediately after the impact period. Replacing Calvo pricing by Rotemberg pricing does not eliminate the Implausible Result from the new Keynesian model with a constant money supply. This conclusion is in accordance with the conjecture stated above.

4.2 Predetermined Price Level

As a second alternative model specification we consider the case featuring a predetermined price level. Indeed, in this subsection we assume that a firm which gets a green light in period t sets its price to be charged from the next period onward. There is thus an implementation lag of one period. We first briefly comment on the model changes that occur as a result of this assumption.

Instead of (13), the objective of the green-light firm at time t is now given by:

$$\begin{aligned} V_{t}^{0}\left( i\right)&\equiv \left[ P_{t-1}(i)- MC _{t}\right] \,Y_{t}\,\left( \frac{P_{t-1}\left( i\right) }{P_{t}}\right) ^{-\theta }-W_{t}{\bar{L}} \nonumber \\&\quad + {\mathbb {E}}_{t} \left[ \left[ P_{t}(i)- MC _{t+1}\right] \,Y_{t+1}\,\left( \frac{P_{t}\left( i\right) }{P_{t+1}}\right) ^{-\theta }-W_{t+1}{\bar{L}} \right] {\mathcal {N}}_{t,t+1} \nonumber \\&\quad + {\mathbb {E}}_{t}\left[ \left[ P_{t}(i)- MC _{t+2}\right] \,Y_{t+2}\,\left( \frac{P_{t}\left( i\right) }{P_{t+2}}\right) ^{-\theta }-W_{t+2}{\bar{L}}\right] \zeta {\mathcal {N}}_{t,t+2} \nonumber \\&\quad + {\mathbb {E}}_{t}\left[ \left[ P_{t}(i)- MC _{t+3}\right] \,Y_{t+3}\,\left( \frac{P_{t}\left( i\right) }{P_{t+3}}\right) ^{-\theta }-W_{t+3}{\bar{L}} \right] \zeta ^{2}{\mathcal {N}}_{t,t+3} \nonumber \\&\quad +\ldots \end{aligned}$$

(47)

Redoing the derivations (see SM, Sect. A.3.5) we find that (T1.10)–(T1.11) in Table 1 in the paper are replaced by:

$$\begin{aligned} \Xi _{t}^{N}&=\frac{\zeta }{1+\rho }{\mathbb {E}}_{t}C_{t+1}^{-1/\sigma }P_{t+1}^{\theta }Y_{t+1} mc _{t+1}+\frac{\zeta }{1+\rho }{\mathbb {E}} _{t}\Xi _{t+1}^{N}, \end{aligned}$$

(48)

$$\begin{aligned} \Xi _{t}^{D}&=\frac{\zeta }{1+\rho }{\mathbb {E}}_{t}C_{t+1}^{-1/\sigma }P_{t+1}^{\theta -1}Y_{t+1}+\frac{\zeta }{1+\rho }{\mathbb {E}}_{t}\Xi _{t+1}^{D}. \end{aligned}$$

(49)

Similarly, (T1.12) and (T1.14) in Table 1 are replaced by:

$$\begin{aligned} P_{t}&=\left[ \left( 1-\zeta \right) \left( P_{t-1}^{n}\right) ^{1-\theta }+\zeta P_{t-1}^{1-\theta }\right] ^{1/(1-\theta )}, \end{aligned}$$

(50)

$$\begin{aligned} P_{t}^{a}&=\left[ \left( 1-\zeta \right) \left( P_{t-1}^{n}\right) ^{-\theta }+\zeta P_{t-1}^{-\theta }\right] ^{-1/\theta }. \end{aligned}$$

(51)

Since both $P_{t-1}^{n}$ and $P_{t-1}$ are predetermined at time t, both $P_{t}$ and $P_{t}^{a}$ are also predetermined at that time. The rest of the model is unchanged.

The simulation results for the New Keynesian model with a predetermined price level are reported in Table 8(c). The quantitative results are in the same direction but are even more implausible than those of the NK-FMS model. Output, investment, and employment fall dramatically at impact only to more than recover from the next period onward (see the impulse-response functions in SM, Sect. A.3.5). The huge impact drop in marginal cost is also virtually eliminated immediately after the impact period. Making the price level more inflexible than in the NK-FMS model exacerbates the Implausible Result yielded by the new Keynesian model with a constant money supply from Sect. 3. Again this conclusion is in accordance with the conjecture stated above.

4.3 Money Supply Rule

As a third alternative model specification we consider the case featuring a money supply rule. Indeed, in this subsection we assume that the monetary authority does not maintain a constant nominal money supply but instead allows it to react to macroeconomic circumstances. In its most general form we postulate:

$$\begin{aligned} \frac{M_{t}-{\bar{M}}}{{\bar{M}}}=-\mu _{y}\frac{Y_{t}-Y^{*}}{Y^{*}}-\mu _{\pi }\pi _{t}, \end{aligned}$$

(52)

where $\pi _{t}\equiv (P_{t}-P_{t-1})/P_{t-1}$ is the current inflation rate, ${\bar{M}}$ is a constant, and $\mu _{y}$ and $\mu _{\pi }$ are non-negative parameters. Equation (52) is added to the NK-FMS model and the money supply becomes an endogenous variable. We consider two prototypical subcases.

The first subcase assumes a countercyclical money supply rule (in the vein of Tobin), i.e. we set $\mu _{y}>0$ and $\mu _{\pi }=0$. If output falls short of (exceeds) its full-employment level then the monetary authority attempts to boost (slow down) economic activity by increasing (decreasing) the nominal money supply. The simulation results for the New Keynesian model with a countercyclical money supply rule are reported in Table 8(d). As in the case with a predetermined price level, the quantitative results are in the same direction but are even more implausible than those of the NK-FMS model. Output, investment, and employment fall dramatically at impact only to more than recover from the next period onward (see the impulse-response functions in SM, Sect. A.3.6). The huge impact drop in marginal cost is also virtually eliminated immediately after the impact period. Although rather Keynesian in spirit, a countercyclical money supply rule does not remove the Implausible Result from the new Keynesian model.

Matters are quite different for the second subcase in which the monetary authority adopts an inflation fighting stance. We model such an inflation-fighting money supply rule by setting $\mu _{y}=0$ and $\mu _{\pi }>100$.¹⁰ If inflation is negative (positive) then the monetary authority attempts to boost (slow down) economic activity by increasing (decreasing) the nominal money supply. The simulation results for the New Keynesian model with an inflation-fighting money supply rule are reported in Table 8(e). Interestingly, despite the fact that prices are sticky the Implausible Result does not appear under the inflation-fighting rule. Indeed, the impulse-response functions for this model variant are quite similar to those for the Classical model with perfectly flexible prices (see Tables 5(f) and 8(e) and SM, Sects. A.3.4 and A.3.6). The inflation-fighting money supply rule thus largely removes the stickiness in the real money supply.

4.4 Capital Adjustment Costs

As a fourth alternative model specification we consider the case in which large changes (in either direction) in the capital stock are costly. We capture this feature by postulating adjustment costs in the form suggested by Uzawa (1969) and Hayashi (1982). We postulate the existence of a representative investment firm which constructs the macroeconomic capital stock and rents out units of capital to firms in the intermediate goods sector. The investment firm’s objective function is given by:

$$\begin{aligned} V_{t}\equiv {\mathbb {E}}_{t}\sum _{\tau =t}^{\infty }\left[ R_{\tau }^{K}K_{\tau -1}-P_{\tau }I_{\tau }\right] {\mathcal {N}}_{t,\tau }, \end{aligned}$$

(53)

where ${\mathcal {N}}_{t,\tau }$ is the nominal stochastic discount factor defined in (14) above. The net capital accumulation function is given by:

$$\begin{aligned} \frac{K_{\tau }-K_{\tau -1}}{K_{\tau -1}}=\Phi \left( \frac{I_{\tau }}{ K_{\tau -1}}\right) , \end{aligned}$$

(54)

where $\Phi \left( x\right)$ is an installation function satisfying $\Phi (\delta )=0$, $\Phi ^{\prime }(\delta )=1$ (where $\delta >0$ is the constant rate of capital depreciation), and $\Phi ^{\prime \prime }(\cdot )<0$. In period t the first-order conditions are given by (54) and:

$$\begin{aligned} 1&=q_{t}\Phi ^{\prime }\left( \frac{I_{t}}{K_{t-1}}\right) , \end{aligned}$$

(55)

$$\begin{aligned} q_{t}&=\frac{1}{1+\rho }\frac{C_{\tau }^{1/\sigma }}{C_{\tau +1}^{1/\sigma } }\left( r_{\tau +1}^{K}+q_{\tau +1}\left( 1+\Phi \left( \frac{I_{\tau +1}}{ K_{\tau }}\right) \right) -\frac{I_{\tau +1}}{K_{\tau }}\right) , \end{aligned}$$

(56)

where $q_{t}$ is Tobin’s (marginal) q measuring the shadow price of installed capital and thus the profitability of investment.

To implement the adjustment cost model we assume that the installation function takes the following form:

$$\begin{aligned} \Phi \left( x\right) \equiv \frac{{\bar{z}}}{1-\sigma _{x}}\left[ \left[ \frac{ {\bar{z}}+x-\delta }{{\bar{z}}}\right] ^{1-\sigma _{x}}-1\right] , \end{aligned}$$

(57)

with $\sigma _{x}>1$ and ${\bar{z}}>0$. By using (57) we find that (54)–(56) are given by:

$$\begin{aligned} K_{t}&=\left[ 1+\frac{{\bar{z}}}{1-\sigma _{x}}\left[ q_{t}^{(1-\sigma _{x})/\sigma _{x}}-1\right] \right] K_{t-1}, \end{aligned}$$

(58)

$$\begin{aligned} I_{t}&=\left[ \delta +{\bar{z}}\left( q_{t}^{1/\sigma _{x}}-1\right) \right] K_{t-1}, \end{aligned}$$

(59)

$$\begin{aligned} q_{t}&=\frac{1}{1+\rho }\left( \frac{C_{t}}{C_{t+1}}\right) ^{1/\sigma } \left[ r_{t+1}^{K}+q_{t+1}\left( 1+\frac{{\bar{z}}}{1-\sigma _{x}}\left[ q_{t+1}^{(1-\sigma _{x})/\sigma _{x}}-1\right] \right) -\frac{I_{t+1}}{K_{t}} \right] . \end{aligned}$$

(60)

Equation (59) is added to the NK-FMS model and $q_{t}$ becomes an additional non-predetermined state variable. Equations (58) and (60) replace, respectively, equations (T1.1) and (T1.4).

The simulation results for the New Keynesian model with capital adjustment costs are reported in Table 8(f). The Implausible Result does not appear. At impact output and investment increase. Employment and factor prices fall but by much less than in the NK-FMS model. As a result the drop in real marginal cost is much smaller also. In the presence of capital adjustment costs the temporary productivity increase is fully incorporated in Tobin’s q which increases at impact. This explains why investment is boosted at impact. The impulse-response functions for output, employment, consumption, factor and goods prices, and real marginal cost implied by this model variant are quite similar to those for the New Keynesian model with a fixed nondepreciating capital stock (see Tables 5(d) and 8(f) and SM, Sects. A.3.1 and A.3.7).

4.5 Endogenous Capital Utilization Rate

As a fifth alternative model specification we consider the case in which the utilization rate of capital is flexible. In particular we assume that the household determines the utilization rate of capital, $u_{t}$ , and that firms rent capital services, which we define as $K_{t-1}^{s}(i)\equiv u_{t}K_{t-1}(i)$, in order to produce output. The physical depreciation rate of the capital stock is assumed to be increasing in its rate of utilization, i.e. heavy usage brings about more severe wear and tear. The household’s periodic budget identity in real terms is now given by:

$$\begin{aligned} P_{\tau }\left[ C_{\tau }+I_{\tau }\right] +M_{\tau +1}+B_{\tau +1}+\sum _{s=0}^{\infty }Q_{\tau }^{s}S_{\tau +1}^{s}&=W_{\tau }L_{\tau }+R_{\tau }^{K}u_{\tau }K_{\tau -1}+\left( 1+R_{\tau -1}\right) B_{\tau }\nonumber \\&\quad +\sum _{s=0}^{\infty }X_{\tau }^{s}S_{\tau }^{s}+M_{\tau }-P_{\tau }T_{\tau }, \end{aligned}$$

(61)

whilst the capital accumulation identity is changed to:

$$\begin{aligned} K_{\tau }=I_{\tau }+\left( 1-\delta \left( u_{\tau }\right) \right) K_{\tau -1}. \end{aligned}$$

(62)

To implement this model we assume that the depreciation function takes the form suggested by Baxter and Farr (2005, p. 338):

$$\begin{aligned} \delta (u_{t})\equiv \delta _{0}+\frac{a_{0}}{1+a_{1}}u_{t}^{1+a_{1}}, \end{aligned}$$

(63)

with $\delta _{0}>0$, $a_{0}>0$, and $a_{1}>0$. In period t the first-order necessary conditions are given by (63) and:

$$\begin{aligned} r_{t}^{K}&=\delta ^{\prime }\left( u_{t}\right) , \end{aligned}$$

(64)

$$\begin{aligned} 1&={\mathbb {E}}_{t}\left[ \frac{r_{t+1}^{K}u_{t+1}+1-\delta \left( u_{t+1}\right) }{1+\rho }\left( \frac{C_{t}}{C_{t+1}}\right) ^{1/\sigma } \right] . \end{aligned}$$

(65)

Equation (64) is added to the NK-FMS model and $u_{t}$ is endogenous. Equation (62) replaces (T1.1) whilst (65) replaces (T1.4). Finally, in (T1.8) and (T1.13) $K_{t-1}$ is replaced by $u_{t}K_{t-1}$.

The simulation results for the New Keynesian model with an endogenous capital utilization rate are reported in Table 8(g). The quantitative results are in the same direction but are even more implausible than those of the NK-FMS model. Output, investment, and employment fall dramatically at impact only to more than recover from the next period onward (see the impulse-response functions in SM, Sect. A.3.9). The huge impact drop in marginal cost is also virtually eliminated immediately after the impact period. The introduction of an endogenous capital utilization rate does not remove the Implausible Result from the NK-FMS model.

4.6 Hybrid Synthesis Model

As a sixth alternative model specification we consider the hybrid case in which there are two types of firm operating in the intermediate goods sector, namely sticky-price and flexible-price firms. In particular, we assume that a constant fraction $\psi$ of firms in the intermediate sector face the Calvo friction whilst the remaining fraction $1-\psi$ of firms can freely adjust their prices at all times. Flexible-price firms set their price according to the usual markup formula:

$$\begin{aligned} P_{t}^{f}=\frac{\theta }{\theta -1}P_{t} mc _{t}, \end{aligned}$$

(66)

and sticky-price firms (which get a green light in period t) set the new price according to the usual rule:

$$\begin{aligned} P_{t}^{ns}=\frac{\theta }{\theta -1}\frac{\Xi _{t}^{N}}{\Xi _{t}^{D}}, \end{aligned}$$

(67)

where $\Xi _{t}^{N}$ and $\Xi _{t}^{D}$ evolve according (T1.10) and (T1.11). The regular and alternative price indices for all sticky-price firms together are given by:

$$\begin{aligned} P_{t}^{s}&=\left[ \left( 1-\zeta \right) \left( P_{t}^{ns}\right) ^{1-\theta }+\zeta \left( P_{t-1}^{s}\right) ^{1-\theta }\right] ^{1/(1-\theta )}, \end{aligned}$$

(68)

$$\begin{aligned} P_{t}^{as}&=\left[ \left( 1-\zeta \right) \left( P_{t}^{ns}\right) ^{-\theta }+\zeta \left( P_{t-1}^{as}\right) ^{-\theta }\right] ^{-1/\theta }. \end{aligned}$$

(69)

Finally, the regular and alternative aggregate price levels are:

$$\begin{aligned} P_{t}&=\left[ \left( 1-\psi \right) (P_{t}^{f})^{1-\theta }+\psi \left( P_{t}^{s}\right) ^{1-\theta }\right] ^{1/(1-\theta )}, \end{aligned}$$

(70)

$$\begin{aligned} P_{t}^{a}&=\left[ \left( 1-\psi \right) (P_{t}^{f})^{-\theta }+\psi \left( P_{t}^{as}\right) ^{-\theta }\right] ^{-1/\theta }. \end{aligned}$$

(71)

In summary, the changes to the NK-FMS model are as follows: equation (66) is added to the model, equation (67) replaces (T1.9) (and $P_{t}^{n}$ is dropped from the model), and (68)–(71) replace (T1.12) and (T1.14). The additional endogenous variables are $P_{t}^{f}$, $P_{t}^{ns}$, $P_{t}^{s}$, $P_{t}^{as}$, and $P_{t}^{a}$.

The simulation results for the hybrid model are reported in Table 8(h). These results are based on the assumption that eighty percent of firms face the Calvo friction ($\psi =0.8$). Interestingly, despite the fact that flex-price firms constitute a relatively small fraction of the intermediate goods sector, the Implausible Result is no longer observed at the macroeconomic level. Indeed, the impulse-response functions for ${\tilde{Y}}_{t}$, ${\tilde{C}}_{t}$, ${\tilde{I}}_{t}$, ${\tilde{K}} _{t}$, ${\tilde{w}}_{t}$, ${\tilde{r}}_{t}^{K}$, and $\widetilde{ mc } _{t}$ implied by this model variant are quite similar in shape to those for the New Keynesian FMS model with capital adjustment costs (see Table 8(f) and (h) and SM, Sects. A.3.7 and A.3.10).

4.7 Non-Separable Preferences

As a seventh and final alternative model specification we consider the case in which the household’s felicity function is non-separable. In particular we change the felicity function in equation (17) to:

$$\begin{aligned} U\left( C_{\tau },L_{\tau },M_{\tau +1}/P_{\tau }\right) \equiv \frac{\left[ C_{\tau }^{\gamma }(M_{\tau +1}/P_{\tau })^{1-\gamma }\right] ^{1-1/\sigma }-1}{1-1/\sigma }-\varepsilon _{l}\frac{L_{\tau }^{1+\kappa }}{1+\kappa }, \end{aligned}$$

(72)

with $\sigma >0$ and $0<\gamma <1$. Note that for $\sigma \rightarrow 1$ the expression used for the NK-FMS model is obtained. With this specification of preferences, equations (T1.3)–(T1.6) and (T1.10)–(T1.11) are replaced by:

$$\begin{aligned} 1&={\mathbb {E}}_{t}\left[ \frac{1+R_{t}}{1+\rho }\left( \frac{C_{t}}{C_{t+1}} \right) ^{1+\gamma (1/\sigma -1)}\left( \frac{P_{t}}{P_{t+1}}\right) \left( \frac{M_{t+1}/P_{t}}{M_{t+2}/P_{t+1}}\right) ^{(1-\gamma )(1/\sigma -1)}\right] , \end{aligned}$$

(73)

$$\begin{aligned} 1&={\mathbb {E}}_{t}\left[ \frac{1+r_{t+1}^{K}-\delta }{1+\rho }\,\left( \frac{ C_{t}}{C_{t+1}}\right) ^{1+\gamma (1/\sigma -1)}\left( \frac{M_{t+1}/P_{t}}{ M_{t+2}/P_{t+1}}\right) ^{(1-\gamma )(1/\sigma -1)}\right] , \end{aligned}$$

(74)

$$\begin{aligned} \frac{M_{t+1}}{P_{t}}&=\frac{1-\gamma }{\gamma }C_{t}\frac{1+R_{t}}{R_{t}}, \end{aligned}$$

(75)

$$\begin{aligned} \varepsilon _{l}L_{t}^{\kappa }&=\gamma w_{t}C_{t}^{-[1+\gamma (1/\sigma -1)]}\left( \frac{M_{t+1}}{P_{t}}\right) ^{-(1-\gamma )(1/\sigma -1)} \end{aligned}$$

(76)

$$\begin{aligned} \Xi _{t}^{N}&=\gamma C_{t}^{-(1+\gamma (1/\sigma -1))}\left( \frac{M_{t+1}}{ P_{t}}\right) ^{-(1-\gamma )(1/\sigma -1)}P_{t}^{\theta }Y_{t} mc _{t}+\frac{\zeta }{1+\rho }{\mathbb {E}}_{t}\left[ \Xi _{t+1}^{N}\right] , \end{aligned}$$

(77)

$$\begin{aligned} \Xi _{t}^{D}&=\gamma C_{t}^{-(1+\gamma (1/\sigma -1))}\left( \frac{M_{t+1}}{ P_{t}}\right) ^{-(1-\gamma )(1/\sigma -1)}P_{t}^{\theta -1}Y_{t}+\frac{\zeta }{1+\rho }{\mathbb {E}}_{t}\left[ \Xi _{t+1}^{D}\right] . \end{aligned}$$

(78)

Compared to the NK-FMS model, the evolution of the real money supply plays a much more prominent role in the non-separable model.

The simulation results for the New Keynesian model with non-separable preferences are reported in Table 8(i). These results are based on a parameter setting featuring $\sigma =0.7$ and $\gamma =0.8$. The quantitative results are in the same direction but are even more implausible than those of the NK-FMS model. Output, investment, and employment fall dramatically at impact only to more than recover from the next period onward (see the impulse-response functions in SM, Sect. A.3.11). The huge impact drop in marginal cost is also virtually eliminated immediately after the impact period. The introduction of non-separable preferences does not remove the Implausible Result from the NK-FMS model.

4.8 Discussion

The main findings of this section are the following. First, the Implausible Result does not arise in versions of the New Keynesian model with (a) a fixed or absent capital stock, (b) an inflation-fighting money supply rule, (c) capital adjustment costs, and (d) a mix of sticky-price and flexible-price firms. Second, the Implausible Result persists (or even gets worse) in New Keynesian models with (e) Rotemberg quadratic price adjustment costs, (f) a predetermined price level, (g) a countercyclical money supply rule, (h) variable capital utilization, and (i) non-separable preferences.

The evidence suggests that the presence or absence of the Implausible Result hinges on the flexibility of the real money supply relative to the flexibility of the capital stock. In models with sufficiently perfectly flexible prices and in the NK-TR model both the real money stock and the capital stock are flexible. With a fixed money supply (as in the NK-FMS model) the real money supply is virtually fixed at impact, whereas the capital stock is perfectly flexible. Following a temporary shock, all adjustment occurs at impact via gross investment and the capital stock thus leading to the Implausible Result. An endogenous utilization rate for capital makes the use of capital services even more flexible and reinforces the Implausible Result. Similarly, pre-determined prices eliminates all variability in the real money supply at impact which also worsens the Implausible Result. The introduction of capital adjustment reduces the flexibility of the capital stock so that the relative flexibility with respect to the real money supply is also reduced and the Implausible Result does not arise.

5 Conclusions

In this paper we show that a standard New Keynesian model with endogenous capital accumulation that is closed with a constant nominal money supply (and an endogenous interest rate) delivers an implausible result in response to a positive productivity shock. Specifically, we find that output and investment decrease on impact in response to the positive productivity shock, which contrasts with the model where monetary policy is implemented via a standard Taylor rule where output and investment increase in response to a positive productivity shock. The implications of the latter model are, of course, both economically and empirically much more plausible. After the impact period, the model with a constant nominal money supply delivers impulse-response functions that are qualitatively very similar to those of the model with a standard Taylor rule.

The intuition behind what we refer to as the “Implausible Result” is that the real money supply becomes more or less fixed when the nominal money supply is fixed and prices are sticky dus to price staggering. When the capital stock can freely adjust, all the adjustment from the productivity shock falls on the capital stock, which causes investment and output to decrease on impact. This Implausible Result is removed when variations in the capital stock are subject to adjustment costs or impossible altogether (for example when a fixed supply of land is an input in the production function). In that case, the adjustment falls on the (replacement) price of capital (or land), which increases in response to the productivity shock. Furthermore, the Implausible Result also disappears when prices become more flexible. However, we also show that the Implausible Result becomes quantitatively stronger when prices become more sticky or even pre-determined, or when capital essentially becomes more flexible by introducing an endogenous utilization rate of capital. Therefore, the Implausible Result is driven by the relative flexibilities of the real money supply on the one hand and the capital stock on the other.

Modern central banks implement their monetary policy via an endogenous interest rate policy rule, for which the Implausible Result does not arise. In addition, graduate students are typically exposed to the New Keynesian model version without endogenous capital accumulation for which the Implausible Result also does not arise when the nominal money supply is constant (Gali, 2015). This might explain why the Implausible Result has not been picked up by the literature thus far. However, further research is necessary to identify the exact factors that drive our results.