1 Introduction

In June 2020, after more than a decade of negotiations, social partners concluded a political agreement on a reform of the second pillar pension system in the Netherlands.Footnote 1 A four-year transition period towards this new pension system is planned to start in 2023. As of 2027, all pension funds should have finalized this transition.Footnote 2, Footnote 3 A key element of the pension reform is a refined allocation rule to share collective risks. This allocation rule replaces the one-size-fits-all approach in the current Dutch pension system.

The purpose of this paper is to show that, under stylized assumptions, the new allocation rule leads to a Pareto optimal allocation of risks among current participants. First, we consider a simple Black-Scholes financial market setting with a single risk factor. We derive Pareto optimal allocations to collectively share financial market risk among individual participants. In this analysis, we consider the aggregate investment exposure of collective pension fund wealth as exogenously given. Obviously, when we would allow for optimization of this aggregate exposure, we simply obtain well-known optimal (individual) life-cycle investment strategies.

Second, we show how the presence of a (traded or non-traded) annuity risk factor affects Pareto optimal risk allocations. Annuity risk is a crucial ingredient, since the retirement income is the number of annuities that a retiree can obtain with his/her financial wealth. We do not specify the exact source of the annuity risk. It can be thought of as any risk that affects the price of an annuity, such as interest rate risk, longevity risk, or inflation risk.

We find that the new Dutch pension contract can incorporate Pareto optimal sharing of risks between current participants. In other words, the outcome of one participant can only be improved at the expense of another participant. In addition, we show how the optimal risk sharing rule depends on the weights attached to different participants.

The new Dutch pension contract contains an additional instrument, the so-called solidarity reserve, that enables risk sharing with future (‘unborn’) participants. We ignore this type of intergenerational risk sharing in the present paper and refer to Van Bilsen et al. (2022) for an analysis.

The ideas in this paper are strongly based on optimal risk sharing rules as originally studied in Borch (1962). Bao et al. (2017) and Pazdera et al. (Pazdera et al., 2017) use Borch’s general risk sharing rules in more specific settings than in Borch (1962), in particular risk sharing within a pension fund. An even more specific analysis for the Dutch pension system can be found in Muns and Werker (2019). The analysis in the present paper, jointly taking into account life-cycle investment risk and annuity risk, is new. Since the retirement income is the number of annuities that a retiree can buy with his/her financial wealth, we consider for the retirement income both the nominator risk (investment risk) and the denominator risk (annuity risk).

Our paper is also connected to the strand of literature that optimizes investments over the life cycle of an individual participant; see Gomes (2020) for a recent overview. In this literature, however, the risk allocation is not restricted to a certain collective risk exposure as we consider. More specifically, the new Dutch pension contract prescribes an allocation principle, and not an investment policy. To illustrate the difference between the two concepts in the new pension system, pension funds agree with stakeholders upon (i) a certain collective investment policy to invest total fund wealth and (ii) allocation rules to allocate fund returns, i.e., ex-ante risk, among participants (including the solidarity reserve).

Subsequently, pension funds stick to this agreement for a longer period of time. During this period, multiple fund returns are allocated to participants, each period according to the same investment policy and agreed allocation rule. Clearly, from a mathematical point of view, optimizing a collective fund investment strategy given optimal risk-sharing rules is equivalent to deriving individually optimized life-cycle investment strategies. However, the first approach is more in the spirit of the new Dutch pension contract.

The rest of this paper is organized as follows. The institutional setting is discussed in more detail in Sect. 2. Section 3 introduces notation and assumptions. In Sect. 4 we analyze our baseline model with a single investment risk factor and no annuity risk. In Sect. 5 we extend our analysis to a setting, which is more relevant in a pension fund context, with a (traded or non-traded) annuity risk factor. Section 6 contains a numerical illustration and Sect. 7 concludes.

2 Institutional Framework

In this section, we outline the most important characteristics of the current and new pension system in the Netherlands. A detailed description on the transition towards the new pension system is given in Metselaar et al. (2022).

2.1 Current Pension System

Most Dutch pension schemes are formally called defined benefit (DB) schemes.Footnote 4 Collective risks are shared based on the DB notion of a uniform adjustment of accruals. The funding ratioFootnote 5 determines this uniform adjustment. At first sight, this may seem a simple approach, but risk sharing through a single measure (funding ratio) is suboptimal by (i) the heterogeneity in risk exposures among different participants and (ii) the presence of multiple risk factors.Footnote 6 As such, it will generally not lead to an ex-ante optimal sharing of collective risks among participants. In addition, the denominator of the funding ratio—the marked to market accounting value of funds’ liabilities – has turned out to be much more sensitive to the discount rate than the numerator of the funding ratio, i.e., the value of funds’ assets.Footnote 7 This has substantially affected pension outcomes.

Up to the financial crisis of 2007–2008, inflation-based indexation of pension benefits was nevertheless deemed almost certain by participants in DB schemes. This perception was based on (i) past experiencesFootnote 8, (ii) a favorable financial position of pension fundsFootnote 9, (iii) the possibility to impose (accrual-free) recovery contributions on employees in case of distress, and (iv) an employer commitment to deposit (accrual-free) additional funds in case of financial distress.Footnote 10

Nowadays, many participants have missed inflation-linked indexation up to a cumulative total of 20% from 2009 until 2021Footnote 11, with the current Dutch inflation rate showing a sharp increase to above 5% at the end of 2021.Footnote 12 In some periods, they even faced a threat of cutting pensions, thereby conflicting a perceived certain (nominal or real) retirement income in DB schemes. As a result, all participants increasingly faced uncertainty in their pension benefits, because of the low interest rate environment and an ageing population. First, lower interest rates have led to low funding ratios. In the first half of 2020, funding ratios below 90% were no exception, including some larger pension funds.Footnote 13 Second, from an actuarial point of view even contribution rates at historically high levels are too low to attain a replacement rate of typically 75 percent.Footnote 14 In response to the lower interest rates, some pension funds lowered accrual rates substantially as further increases in the contribution rate were deemed impossible. In the long run, low accrual rates can lead to low replacement rates. Third, pension funds with an ageing population have more difficulties to impose a recovery contribution. In fact, a smaller share of working participants should pay a higher recovery rate to compensate the same loss. A recovery contribution is even more difficult to impose in case contribution rates are already high. Fourth, globalization and liberalization have forced firms into a more competitive economic environment. This has reduced the willingness of employers to commit to deposit additional funds if their pension fund is in financial distress.

All this triggered a vigorous political debate among many stakeholders on the “appropriate” way to calculate the discounted value of accruals. Particularly, the legal discount rate—based on the default-free term structureFootnote 15—was subject of this heated debate. Obviously, different generations had different interests in this debate. In the end, social partners agreed that it is preferable if the discount rate plays no longer any (crucial) role in the pension system.

2.2 New Dutch Pension SystemFootnote 16

The new Dutch pension contract is best characterized as a CDC system. While pension risks are still shared collectively, a key element of the pension reform is the new mechanism to share collective risks. Foremost, risk sharing is no longer based on a funding ratio; this concept is no longer used. Instead, each pension scheme should specify a predefined allocation mechanism that prescribes how returns are allocated to the participants. This allocation mechanism consists of two components:Footnote 17

  1. (1)

    a hedge return (‘beschermingsrendement’) to compensate participants for the realization of annuity risks such as interest rate risk. The realization as well as the corresponding compensation will differ by participant. For instance, the price of a pension annuity of young participants varies with long-term interest rates. If annuity risk (in nominal terms) for outcomes in the far future is considered to be less relevant, the hedge return may only partly compensate young participants for their exposure to (long-term) nominal interest rate risk, i.e., price changes in deferred annuities that match their pension payout scheme. In a similar vein, the hedge return can compensate participants for macro longevity risk.

  2. (2)

    a mechanism to allocate the (positive or negative) excess return (‘overrendement’). The excess return is the collective fund return that remains after allocating the hedge returns to all participants in Step (1). Dutch pension funds will generally adopt life-cycle principles for this allocation to take into account the human capital of (non-retired) participants.Footnote 18

Both components of the allocation mechanism will generally differ by individual participant. Ideally, the allocation mechanism is fine-tuned to the individual preferences of each participant. We show how this heterogeneity depends on individual characteristics such as risk appetite, financial wealth, and total wealth.

3 Assumptions and Notation

Consider a pension fund with a finite number of participants indexed by \(i=1,\ldots ,n\). Participants are, at time t, equipped with financial wealth \(F_{it}\) and human capital \(H_{it}\).

3.1 Financial Wealth

Financial wealth \(F_{it}>0\) represents retirement savings to finance a retirement income after the pension date of participant i. For simplicity, our analysis does not consider other possible sources to finance a retirement income, such as a state pension, partner income, and housing. The pension fund invests collective financial wealth

$$\begin{aligned} F_t = \sum _{i=1}^n F_{it}. \end{aligned}$$

The (continuously compounded) instantaneous risk-free interest rate r describes the evolution of the risk-free rate. Uncertainty is generated in a Black-Scholes financial market by a standard Brownian motion Z. The time t stock price \(S_t\) satisfies \(S_0=1\) and follows a geometric Brownian motion (GBM), i.e.,

$$\begin{aligned} \mathrm{d}S_t=(r+\lambda \sigma ) S_t \mathrm{d}t+\sigma S_t \mathrm{d}Z_t, \end{aligned}$$

where the price of risk, or Sharpe ratio, \(\lambda \) of the Brownian motion Z and the volatility of the stock \(\sigma >0\) are given constants.

Through the pension fund, financial wealth \(F_{it}\) of participant i at time t has an effective exposure \(w_{it}\) to the excess return of the stock price S.Footnote 19 As such, the return allocated to financial wealth \(F_{it}\) can be seen as the sum of (in this case risk-free) hedge return \(r \mathrm{d}t\) and excess return \(w_{it}\sigma (\lambda \mathrm{d}t + \mathrm{d}Z_t )\). In addition, financial wealth increases with the pension contribution \(h_{it} \mathrm{d}t\):

$$\begin{aligned} \mathrm{d}F_{it} = [(r+w_{it} \lambda \sigma ) F_{it}+h_{it} ]\, \mathrm{d}t+w_{it} \sigma F_{it} \, \mathrm{d}Z_t \end{aligned}$$
(1)

3.2 Human Capital

Human capital \(H_{it}\) is the present value of future pension contributions \(h_{it}\). In our model, pension contributions are deterministic and known with perfect foresight.Footnote 20 Starting the retirement date \(T_i\) no labor income is earned, i.e., \(H_{it}=h_{it}=0\) if \(t\ge T_i\). In other words, human capital \(H_{it}\) can be interpreted as a riskless bond with coupon \(h_{is}\) at time \(s\in [t,T_i ]\):

$$\begin{aligned} H_{it} = \int _{s=t}^{T_i} {\exp } (-r (s-t) ) h_{is} \, \mathrm{d}s \end{aligned}$$

This gives time dynamics

$$\begin{aligned} \mathrm{d} H_{it} = (r H_{it} - h_{it} ) \, \mathrm{d}t. \end{aligned}$$
(2)

In this formalization human capital is considered a nominal riskless bond. We do so to keep the analysis simple. In Sect. 5, we extend our analysis to a setting where human capital can be considered as a risky real bond.

Note that in practice it is difficult to assess the level of human capital of individual participants accurately. The same holds for their risk aversion (to be discussed below). The contract we specify will lead to suboptimal exposures when either of these is incorrectly assessed. In relation to a standard individual life-cycle DC contract this is paramount to specifying a suboptimal glide path. In that case investment exposures are suboptimal, though no wealth transfers take place between participants.

3.3 Total Wealth

The allocation rules derived below depend on the ratio of financial capital \(F_{it}\) to total wealth \(F_{it}+H_{it}\) available to finance the private pension of participant i. Adding (1) and (2), total wealth randomly evolves over time according to the GBM,

$$\begin{aligned} \frac{\mathrm{d}(F_{it}+H_{it}) }{ F_{it}+H_{it} }&= \left( r+w_{it} \lambda \sigma \frac{F_{it}}{F_{it}+H_{it} } \right) \mathrm{d}t+w_{it} \sigma \frac{F_{it}}{F_{it}+H_{it} } \, \mathrm{d}Z_t. \end{aligned}$$
(3)

Note that the pension contribution rate \(h_{it}\) is not included in (3), because the pension contribution is transferred from \(H_{it}\) to \(F_{it}\). Under the assumption that labor income is a nominal riskless bond, the present value \(H_{it}\) is the characteristic of the pension contribution scheme \(h_{it}\) that affects the optimal allocation. Also (3) takes the standard form for the value of a self-financing portfolio where the expected excess returns equals the risk exposure \(w_{it} \sigma \frac{F_{it}}{F_{it}+H_{it} }\) multiplied by the price of risk \(\lambda \).

3.4 Annuity

At participant i’s retirement date \(T_i\ge t\), total wealth \(F_{iT_i}+H_{iT_i}=F_{iT_i}\) is converted into a pension annuity. Let \(A_{it}\) denote the annuity price (sometimes called annuity factor) to convert total wealth into a pension income. We simply start without annuity risk:

$$\begin{aligned} \frac{ \mathrm{d}A_{it}}{A_{it}} = r \, \mathrm{d}t \end{aligned}$$
(4)

In Sect. 5, we include annuity risk in this expression.

Since our focus is on risk sharing among working generations, we will not model the payout scheme of the annuity explicitly. For instance, the payout scheme may include an optional 10% lumpsum around pension date, which is planned to be introduced as of 2023 in the Netherlands.Footnote 21

3.5 Utility

Using his total wealth \(F_{it}+H_{it}\), a participant i can buy at time t the annuitized pension incomeFootnote 22

$$\begin{aligned} Y_{it}&= \frac{F_{it}+H_{it}}{A_{it}}. \end{aligned}$$
(5)

Both components \(F_{it}+H_{it}\) and \(A_{it}\) in (5) follow a geometric Brownian motion. By It’s quotient rule, annuitized pension income \(Y_{it}\) evolves as a geometric Brownian motion as well:

$$\begin{aligned} \frac{\mathrm{d}Y_{it}}{Y_{it}}&= \mu _{Y_{it}} \, \mathrm{d}t + \sigma _{Y_{it}} \, \mathrm{d}Z_t \end{aligned}$$
(6)

The parameters \(\mu _{Y_{it}}\) and \(\sigma _{Y_{it}}\) change when we allow for annuity risk in Sect. 5.

As we will assume \(\mathrm{CRRA}\) preferences, the optimal consumption path and the optimal risk allocation path follow from independent decisions (Samuelson 1969). As a consequence, we can assume that utility is generated by annuitized pension income, and consider the impact of the risk allocation on annuitized pension income. This approach is standard in the literature on optimal risk allocations.

Let \(R_{it}\) denote the continuously compounded growth rate in annuitized pension income \(Y_{it}\). The pension fund assumes for participant i \(\mathrm{CRRA}(\gamma _i)\) preferences on the growth rate \(\exp \left( R_{it} \right) \):Footnote 23

$$\begin{aligned} U\!\left( R_{it} \right) = {\left\{ \begin{array}{ll} \frac{1}{1-\gamma _i} E\!\left[ \exp \left( \left( {1-\gamma _i} \right) R_{it} \right) -1 \right] &{} \gamma _i\ne 1\\ E\!\left[ {R_{it}}\right] &{} \gamma _i=1 \end{array}\right. } \end{aligned}$$
(7)

Note that, as \(R_{it}\) denotes a continuously compounded return, a risk-neutral agent is represented by \(\gamma _i=0\) for which utility \(U_{it}\!\left( R_{it} \right) = E[\exp (R_{it})]\) is proportional to the discretely compounded return \(\exp (R_{it})\). We exclude risk-neutral participants from our analysis by assuming \(\{ \gamma _i \ne 0 \}\) for each participant i. Risk-neutral participants (\(\gamma _i = 0\)) simply maximize their expected end-of-period wealth. They prefer an infinite exposure \(w_{it}\) to benefit from the risk premium \(\lambda \).Footnote 24

3.6 Certainty Equivalent

Proposition 1 gives us a well-known simple expression for the certainty equivalent \(\mathrm{CEQ}_{it}\) of \(R_{it}\). The reader is referred to Appendix A for the proofs.

Proposition 1

The certainty equivalent of the continuously compounded growth rate \(R_{it}\) in (7) is

$$\begin{aligned} \mathrm{CEQ}_{it}&= \mu _{Y_{it}} - \frac{\gamma _{i}}{2} \sigma _{Y_{it}}^2. \end{aligned}$$
(8)

Intuitively, utility increases with the mean \(\mu _{Y_{it}}\) of the return \(\mathrm{d}Y_{it}/Y_{it}\), while it decreases with the volatility \(\sigma _{Y_{it}}^2\) particularly if the risk aversion \(\gamma _i\) is high.

Social welfare \(\mathrm{CEQ}_t\) is the weighted average of individual certainty equivalents \(\mathrm{CEQ}_{it}\) with weights \(\left\{ \alpha _i> 0\right\} _{i=1}^n\)Footnote 25:

$$\begin{aligned} \mathrm{CEQ}_{t}&= \sum _{i=1}^n \alpha _i \mathrm{CEQ}_{it} \end{aligned}$$
(9)

A higher weight \(\alpha _i\) indicates that the social planner attaches more weight to the outcome of participant i. Without loss of generality, we assume \(\sum _{i=1}^n \alpha _i=1\) such that (9) is a weighted average. The functional form (9) will enable a quadratic optimization that provides us with closed-form solutions.

Note that social welfare \(\mathrm{CEQ}_t\) in (9) can also be obtained from a linearization of (7) around \(\mathrm{CEQ}_{it}=0\) (see also (A5)):

$$\begin{aligned} \mathrm{CEQ}_t=\sum _i U_{it}\!\left( \alpha _i \mathrm{CEQ}_{it} \right) = \sum _i \alpha _i \mathrm{CEQ}_{it} + O\!\left( \mathrm{CEQ}_{it}^2\right) . \end{aligned}$$

The second-order term \(O\!\left( \mathrm{CEQ}_{it}^2\right) \) is negligible in continuous time since \(\mathrm{CEQ}\) is small.

4 Collective Risk Sharing in a Pension Fund: No Annuity Risk

In this section, we assume that the dynamics of annuity risk are represented by (4).

4.1 Certainty Equivalent

Applying Its quotient rule on (6) and substituting (3) and (4),

$$\begin{aligned} \frac{\mathrm{d}Y_{it}}{Y_{it}}&= \frac{A_{it}}{F_{it}+H_{it}} \, \mathrm{d} \frac{F_{it}+H_{it}}{A_{it}}\nonumber \\&= \frac{ \mathrm{d}(F_{it}+H_{it}) }{ F_{it}+H_{it} }-\frac{\mathrm{d} A_{it}}{A_{it}} + \left( \frac{\mathrm{d}A_{it}}{A_{it}} \right) ^2- \frac{\mathrm{d}(F_{it}+H_{it}) }{F_{it}+H_{it}} \frac{\mathrm{d}A_{it}}{A_{it}}\nonumber \\&= \mu _{Y_{it}} \, \mathrm{d}t + \sigma _{Y_{it}} \, \mathrm{d}Z_t, \end{aligned}$$
(10)

where

$$\begin{aligned} \mu _{Y_{it}}&=w_{it}\lambda \sigma \frac{F_{it}}{ F_{it}+H_{it} }&\sigma _{Y_{it}}&= w_{it}\sigma \frac{F_{it}}{F_{it}+H_{it}}. \end{aligned}$$
(11)

Substituting (11) into Proposition 1,

$$\begin{aligned} \mathrm{CEQ}_{it}&= w_{it}\lambda \sigma \frac{F_{it}}{ F_{it}+H_{it} } - \frac{\gamma _{i}}{2} \left( w_{it}\sigma \frac{F_{it}}{F_{it}+H_{it}} \right) ^2. \end{aligned}$$
(12)

The certainty equivalent (12) increases with the risk premium \(\lambda \). This is intuitive, because a higher risk premium increases the reward for risk. The pattern for \(\sigma \) is mixed. The certainty equivalent increases in \(\sigma \) if and only if the reward for taking risk is sufficiently high, i.e., \(\lambda >\sigma \).

4.2 First-Best Optimal Exposure

We first define the well-known first-best solutions that maximize the corresponding certainty equivalents.

Proposition 2

(i):

When \(w_{it}\) can be chosen freely for participant \(i\), the first-best investment weight equals

$$\begin{aligned} w_{it}^{\text {FB}}&= \frac{F_{it} + H_{it}}{F_{it}}\frac{\lambda }{\gamma _{i}\sigma }. \end{aligned}$$
(13)
(ii):

The first-best investment of the fund is

$$\begin{aligned} w^{\text {FB}}_t&= \frac{F_t + H_t}{F_t}\frac{\lambda }{{\tilde{\gamma }}\sigma }, \end{aligned}$$
(14)

where \(F_t = \sum _{i = 1}^{n}F_{it}\), \(H_t = \sum _{j = 1}^{n}H_{jt}\), and \({\tilde{\gamma }}\) is the (harmonic) total wealth weighted risk-aversion:

$$\begin{aligned} \frac{F_t + H_t}{{\tilde{\gamma }}}&= \sum _{j = 1}^{n}\frac{F_{jt} + H_{jt}}{\gamma _{j}} \end{aligned}$$
(15)
(iii):

The first-best certainty equivalent of participant i is

$$\begin{aligned} \mathrm{CEQ}_{it}^{\mathrm{FB}}&= \frac{\lambda ^{2}}{2\gamma _{i}}. \end{aligned}$$
(16)

Proposition 2 is a well-known adaption of the Merton-Samuelson solution of the CRRA consumption problem in a Black-Scholes financial market (Samuelson (1969) and Merton (1969)). Our solution is adapted for the presence of riskless human capital \(H_{it}\). Intuitively, the first-best exposure \(w_{it}^{\mathrm{FB}}\) in (13) decreases with \(\gamma _i\) and \(\sigma \).

When \(H_{it} \equiv 0\), the standard mean-variance optimal investment weight \(\frac{\lambda }{\gamma _{i}\sigma }\) is obtained. When \(H_{it} > 0\) the first-best solution (13) states that stock exposures for financial capital \(F_{it}\) have to be leveraged up. This is done in such a way that the effective stock exposure for total wealth \(F_{it} + H_{it}\) equals the standard Merton-Samuelson solution

$$\begin{aligned} w_{it}^{\text {FB}}\frac{F_{it}}{F_{it} + H_{it}}&= \frac{\lambda }{\gamma _{i}\sigma }. \end{aligned}$$
(17)

Therefore, total wealth, and thus also annuitized retirement income \(Y_{it} = \left( F_{it} + H_{it} \right) /A_{it}\), have a constant stock exposure \(\lambda /(\gamma _i \sigma )\) over time \(t\) and across states \(Z_{t}\).Footnote 26

These results are well known and can be related to the Rao-Blackwell-Kolmogorov theorem in statistical inference; see Nikulin (2001). The optimal exposure implies that the i.i.d. shocks \(\mathrm{d}Z_{t}\), for all \(t\), have an identical effect on the retirement income. More precisely, retirement income \(Y_t\) (and total wealth) is invariant with respect to a reordering of increments of the Brownian motion \(Z\). Indeed, the Rao-Blackwell-Kolmogorov theorem states that, for a given expectation, a statistic becomes more stable, in the sense of a smaller variance, when it is measurable with respect to a sufficient statistic. In the present setting, the sufficient statistics are the order statistics of the increments of the Brownian motion (as these are i.i.d.). Alternatively, observe that an equal exposure of a participant’s retirement income to previous shocks implies that collective fund returns should be allocated in such a way that they affect each participant’s annuitized retirement income equally. This is precisely what we will find below.

4.3 Second-Best Optimal Exposure

Besides the first-best exposure \(w_{it}^{\text {FB}}\) above, we are also interested in the collective fund problem. Suppose a funds’ investment policy has pinned down the collective exposure to financial market risk at a certain level \(w\). This setting is common in Dutch pension funds where the (collective) fund’s investment policy is often decided separately from the allocation rules. One possible explanation may be the difficulty of assessing participants’ risk aversions.

Given the—possibly suboptimal—collective exposure \(w\), financial market risk is optimally allocated to the individual participants. This constrained optimum is referred to as the second-best optimal allocation.

To formalize this, by (9) and (12),

$$\begin{aligned} \mathrm{CEQ}_t&= \sum _{i=1}^{n}{\alpha _{i} \text {CEQ}_{it}}\nonumber \\&= \sum _{i=1}^{n} {\alpha _{i}\left( w_{it}{\sigma \lambda } \frac{F_{it}}{F_{it} + H_{it}} - \frac{\gamma _{i}}{2}\left( w_{it}\sigma \frac{F_{it}}{F_{it} + H_{it}} \right) ^{2} \right) }, \end{aligned}$$
(18)

where, as before, we assume that the social planner adopts weights \(\left\{ \alpha _i> 0\right\} _{i=1}^n\) with \(\sum _i \alpha _i = 1\). The social planner solves

$$\begin{aligned} \max _{ \left\{ w_{it} \right\} _{i = 1}^{n} } \mathrm{CEQ}_t, \end{aligned}$$
(19)

subject to an exogenously given collective exposure \(w\) of fund wealth \(F_t = \sum _{i = 1}^{n}F_{it}\) to the stock \(S_{t}\). Thus, the social planner faces the constraint

$$\begin{aligned} \sum _{i=1}^{n}{w_{it}F_{it}}&= w_t F_t. \end{aligned}$$
(20)

Proposition 3

For given w the optimal risk allocation of the social planner is

$$\begin{aligned} w_{it}^{\mathrm{SB}} = w_{it}^{\mathrm{FB}} + \frac{v_{it}}{\sum _{j}^{}v_{jt}}\frac{1}{F_{it}}\left[w_t F_t - \sum _{j = 1}^{n}{w_{jt}^{\mathrm{FB}}F_{jt}} \right]&v_{jt} = \frac{\left( F_{jt} + H_{jt} \right) ^{2}}{\alpha _{j}\gamma _{j}}. \end{aligned}$$
(21)

Proposition 3 characterizes, indexed by all possible sets of weights \(\left( \alpha _{i} > 0 \right) _{i = 1}^{n}\), the Pareto optimal allocations \(\left\{ w_{it}^{\mathrm{SB}} \right\} _{i = 1}^{n}\) of the collective pension exposure to individual pension savings accounts. For each Pareto risk allocation \( w_{it}^{\mathrm{SB}} \), the utility of one participant cannot be increased without reducing the utility of another participant.

The optimal exposure \(\left\{ w_{it}^{\mathrm{SB}} \right\} _{i = 1}^{n}\) is invariant under a scaling of the weights \(\left( \alpha _{i} > 0 \right) _{i = 1}^{n}\) by a positive scalar. For instance, doubling all weights does not change the optimal exposure.

If the collective exposure \(w_t\) equals the first-best collective optimum \(w^{\text {FB}}_t\), we find again \(w_{it}^{\mathrm{SB}} = w_{it}^{\text {FB}}\) in Proposition 3. More formally, including \(w_t\) as an additional free parameter would give the first-order condition \(\eta ^{\mathrm{SB}} = 0\), and, indeed, \(w^{\text {FB}}_t F_t = \sum _{j = 1}^{n}{w_{jt}^{\text {FB}}F_{jt}}\), which gives the first-best result in Proposition 2. For this special case where \(w_t = w^{\text {FB}}_t\), total welfare U is maximized, and the optimal allocation \(\left\{ w_{it}^{\mathrm{SB}} \right\} _{i = 1}^{n} = \left\{ w_{it}^{\text {FB}} \right\} _{i = 1}^{n}\) is independent of the weights \(\alpha _{i}\).

If the collective investment \(w_t F_t\) is above (below) the first-best collective investment \(w^{\text {FB}}_t F_t\), the difference \(w_t F_t - \sum _{i = 1}^{n}{w_{it}F_{it}}\) is allocated to the participants according to the weights \(\left\{ {v_{it}}/{\sum _{j}v_{jt}} \right\} _{i=1}^n\) and added to each individual’s first-best exposure \(w_i^{\mathrm{FB}}\). Provided \(\left\{ \gamma _i>0\right\} _{i=1^n}\), all weights \(v_i\) are also positive and the exposure of each participant i is above (below) the first-best exposure \(w_{it}^{\text {FB}}\).

Note that the stock characteristics \(\lambda \) and \(\sigma \) affect the first-best allocation (see Proposition 2), but have no effect on the distribution \(v_{it}\) in Proposition 3 of an excess fund exposure.Footnote 27 Vice versa, the weights \(\alpha _{i}\) only determine the distribution of an excess fund exposure, but not the first-best allocation.

The allocation in Proposition 3 specifies the second-best optimal exposure of the financial wealth \(F_{it}\) of each individual participant. The induced second-best optimal exposure of total wealth \(F_{it} + H_{it}\) is

$$\begin{aligned} w_{it}^{\mathrm{SB}}\frac{F_{it}}{F_{it} + H_{it}}&= \frac{\lambda }{\gamma _{i}\sigma } + \frac{v_{it}}{\sum _{j}^{}v_{jt}}\frac{1}{F_{it} + H_{it}}\left[w_t F_t - \sum _{j = 1}^{n}{w_{jt}^{\text {FB}}F_{jt}} \right],\\ v_{it}&= \frac{\left( F_{it} + H_{it} \right) ^{2}}{\alpha _{i}\gamma _{i}}. \end{aligned}$$

Again, we are back at the standard Merton-Samuelson optimum \(\lambda /(\gamma _i\sigma )\) if \(H_{it}=0\) and \(w_t=w_t^{\mathrm{FB}}\).

The following proposition characterizes the set of Pareto optimal allocations.

Proposition 4

(i):

For given \(w_t\), the set of Pareto efficient allocations \(\left\{ w_{it}^{\mathrm{SB}} \right\} _{i = 1}^{n}\) can be characterized by the convex hull

$$\begin{aligned} w_{it}^{\mathrm{SB}}\left( \left\{ \xi _{j} \right\} _{j = 1}^{n} \right)&= w_{it}^{\text {FB}} + b_{i}\xi _{i},&i = 1,\ldots ,n, \end{aligned}$$
(22)

with \(\left\{ \xi _{i} \in \left[0,1 \right]\right\} _{i=1}^n\) normalized to \(\sum _{j}^{}\xi _{j} = 1\), and

$$\begin{aligned} b_{i} = \frac{1}{F_{it}}\left( w_t F_t - \sum _{j = 1}^{n}{w_{jt}^{\text {FB}}F_{j}} \right) . \end{aligned}$$
(ii):

Suppose \(w_t \ne w_t^{\text {FB}}\). Each \(\left\{ w_{it}^{\mathrm{SB}} \right\} _{i = 1}^{n}\) in (i) corresponds to a unique \(\left\{ \alpha _{i} > 0 \right\} _{i = 1}^{n}\) with \(\sum _i \alpha _i = 1\).

(iii):

For \(\alpha _{i} \downarrow 0\),

$$\begin{aligned} w_{it}^{\mathrm{SB}} \rightarrow w_{it}^{\text {FB}} + b_{i},&w_{j}^{\mathrm{SB}} \rightarrow w_{j}^{\text {FB}} \quad (j\ne i). \end{aligned}$$
(iv):

For \(\alpha _{i} \uparrow 1\),

$$\begin{aligned} w_{it}^{\mathrm{SB}} \rightarrow w_{it}^{\text {FB}}. \end{aligned}$$

Given a certain fund exposure w, Proposition 4(i) indicates that the exposures \(\left\{ w_{it}^{\mathrm{SB}} \right\} _{i = 1}^{n}\) that are optimal for some weights \(\left\{ \alpha _{i} > 0 \right\} _{i = 1}^{n}\) can be characterized by a convex hull. In other words, a convex combination of Pareto optimal allocations is again Pareto optimal. For the special case \(w_t = w^{\text {FB}}_t\), the convex hull consists of exactly one point with the individual first-best exposures \(\left\{ w_{it}^{\text {FB}}\right\} _{i=1}^n\).

Proposition 4(ii) states that if \(w_t \ne w^{\text {FB}}_t\), each optimal allocation \(w_{it}^{\mathrm{SB}}\) is associated with a unique set of weights \(\left\{ \alpha _{i} > 0 \right\} _{i = 1}^{n}\) (up to a normalization factor).

Proposition 4(iii) characterizes the n extremal points of the convex hull. All other Pareto optimal allocations are a convex combinations of the n extremal points.

Proposition 4(iv) indicates that for \(w_t \ne w^{\text {FB}}_t\), \(w_{it}^{\mathrm{SB}} \rightarrow w_{it}^{\text {FB}}\) can only be attained if \(\alpha _{i} \! \uparrow \! 1\). By \(\sum _j \alpha _j = 1\), the social planner must then attach an infinitely larger weight to participant i than all other participants.

We now consider allocations that are obtained under particular choices for the social planner’s weights \(\alpha _{i}\) and risk aversions \(\gamma _{i}\).

Proposition 5

Suppose that the social planner weighs individual participants proportional to their total wealth, i.e., \(\alpha _i \propto F_{i} + H_{i}\). At the second-best optimum,

(i):
$$\begin{aligned} w_{it}^{\mathrm{SB}}&= \frac{F_{it} + H_{it}}{F_t + H_t}\frac{F_t}{F_{it}}\frac{{\tilde{\gamma }}}{\gamma _{i}}w_t, \end{aligned}$$
(23)
$$\begin{aligned} w_{it}^{\mathrm{SB}}&= \frac{w_t}{w_t^{\mathrm{FB}}}w_{it}^{\mathrm{FB}}&\mathrm{if~} \lambda \ne 0, \end{aligned}$$
(24)
$$\begin{aligned} \mathrm{CEQ}_{it}^{\mathrm{SB}}&= \frac{1}{\gamma _i} \left[ \lambda \sigma \frac{F_{t}}{ F_{t}+H_{t} }{{\tilde{\gamma }}} w_{t} - \frac{1}{2} \left( \sigma \frac{F_{t}}{ F_{t}+H_{t} }{{\tilde{\gamma }}} w_{t} \right) ^2 \right] . \end{aligned}$$
(25)
(ii):

If in addition \(\gamma _i \equiv {{\tilde{\gamma }}}\), then (23) and (25) simplify further to

$$\begin{aligned} w_{it}^{\mathrm{SB}}&= \frac{F_{it} + H_{it}}{F_t + H_t}\frac{F_t}{F_{it}}w_t, \end{aligned}$$
(26)
$$\begin{aligned} \mathrm{CEQ}_{it}^{\mathrm{SB}}&= \lambda \sigma \frac{F_{t}}{ F_{t}+H_{t} } w_{t} - \frac{{{\tilde{\gamma }}}}{2} \left( \sigma \frac{F_{t}}{ F_{t}+H_{t} } w_{t} \right) ^2. \end{aligned}$$
(27)

We have the following results from Proposition 5 where each participant is weighted by his/her total wealth. By (24), the second-best optimal exposure \(w_{it}^{\mathrm{SB}}\) of each participant i is a constant \((w_t/w_t^{\mathrm{FB}})\) times the first-best individual exposure \(w_{it}^{\text {FB}}\). This result holds even if the risk aversion differs among participants. Further, the individual second-best exposures \(w_{it}^{\text {SB}}\) are proportional to the fund exposure \(w_t\). Of course, at the first-best fund exposure, where \(w_t=w^{\mathrm{FB}}_t=\frac{F_t + H_t}{F_t}\frac{\lambda }{{\tilde{\gamma }}\sigma }\) (see (14)), the second-best certainty equivalent \(\mathrm{CEQ}_{it}^{\mathrm{SB}}\) in (25) equals the first-best \(\mathrm{CEQ}_{it}^{\mathrm{FB}}\) in (16).

Under the assumptions of (26), the second-best exposure of total retirement wealth is

$$\begin{aligned} w_{it}^{\mathrm{SB}}\frac{F_{it}}{F_{it} + H_{it}}&= \frac{w_t F_t}{F_t + H_t}. \end{aligned}$$
(28)

Note that the exposure in the right-hand side of (28) is the same for each participant i, i.e., collective financial returns are allocated in such a way that the effect of total retirement wealth for each participant is, in relative terms, the same. This life-cycle idea is precisely the underlying idea of the new Dutch pension contract.

At the first-best (14), we find of course in (27) again the first-best certainty equivalent (16).

5 Collective Risk Sharing in a Pension Fund: With Annuity Risk

The previous section characterized Pareto optimal risk-sharing rules within a stylized pension fund. In particular we derived an allocation of risk such that the effect on total retirement wealth for each participant is the same. However, the setting did not allow for interest rate, longevity, or inflation risk. These annuity risks are potentially important (Koijen et al. 2011). In this section, we do take annuity risk, in an abstract setting, into account. With annuity risk we mean that the utility of participants takes into account that pension wealth \(F_{iT_{i}}\) at the retirement date \(T_{i}\) has to be converted into an income stream, e.g., a lifelong annuity. The conversion rate is exposed to some risk factor. We model a single underlying risk factor to account for this annuity risk. The model can be extended to multiple (traded and non-traded), possibly, correlated factors, but this is not needed to describe the core ideas.

To allow for interest rate risk, we generalize the constant interest rate \(r\) to the time-varying instantaneous interest rate \(r_{t}\). Since this rate is a risk-free rate, exposure to this random rate is not rewarded with a risk premium.Footnote 28 The evolution of \(r_{t}\) will not be specified further.

Each participant \(i\) can face a different annuity price at time t to convert total wealth into a pension annuity. We denote this annuity conversion factor by the annuity price \(A_{it}\). The annuitized pension income at retirement date \(T_{i}\) is equal to \(\frac{F_{iT_{i}}}{A_{iT_{i}}}\) as we imposed \(H_{iT_{i}} = 0\). We extend (4) by assuming that the annuity price \(A_{it}\) follows a GBM that depends on the instantaneous interest rate and the exposure to a risk factor \(Z_{A}\):

$$\begin{aligned} \frac{ \mathrm{d}A_{it} }{ A_{it} }&= \left( r_{t} + \lambda _{A}\sigma _{A_{it}} \right) \mathrm{d}t + \sigma _{A_{it}} \, \mathrm{d}Z_{At}, \end{aligned}$$
(29)

with \(A_{i0} = 1\), \(\sigma _{A_{it}} > 0\), and \(\lambda _{A}\) the price of risk for the Brownian motion \(Z_{A}\). We assume, for notational simplicity, that \(Z\) and \(Z_{A}\) are independent.Footnote 29

It is not necessary that \(\lambda _{A}\) represents a market price of risk. It may also reflect a price that has been agreed upon within the pension fund. In principle, both the risks \(Z\) and \(Z_{A}\) can represent a traded or a non-traded risk. For a traded risk such as interest rate risk and stock market risk, the collective fund exposure can be chosen by the pension fund (unless a particular restriction applies). The corresponding price-of-risk is observable from market prices. In contrast, for non-traded risk the fund exposure is exogenously given. Nonetheless, we can still allow for sharing of nontraded risks within the fund at some internal price-of-risk \(\lambda _{A}\).

Like the annuity price, human capital may also have an exposure to the risk factor \(Z_{A}\). For instance, interest rates are a discount rate to determine annuity prices as well as human capital. Therefore, we allow for the possibility that human capital \(H_{it}\) has an exogenously given exposure \(D_{it} \ge 0\) to \(Z_{A}\). Since the exposure to this risk factor is rewarded with a risk premium \(\lambda _{A}\), we extend (2) to:

$$\begin{aligned} \mathrm{d}H_{it} = \left[\left( r_{t} + \lambda _{A}D_{it} \right) H_{it} - h_{it} \right]\mathrm{d}t + D_{it}H_{it}\,\mathrm{d}Z_{At}. \end{aligned}$$
(30)

The special case \(D_{it} = 0\), represents a risk in \(A_{it}\) unrelated to \(H_{it}\), such as longevity risk at ages after the retirement date. Then, equation (30) is the same as (2).

We allow the pension fund to share the risk associated with \(Z_{A}\) between the participants. If we denote the (chosen by the fund) exposure of participant \(i\)’s financial wealth \(F_{it}\) to \(Z_{At}\) by \(a_{it}\) we can extend (1) to

$$\begin{aligned} \mathrm{d}F_{it}&= \left[\left( r_{t} + w_{it}\lambda \sigma + \lambda _{A}a_{it} \right) F_{it} + h_{it} \right]\mathrm{d}t + w_{it}\sigma F_{it}\mathrm{d}Z_{t} + a_{it}F_{it}\mathrm{d}Z_{At}. \end{aligned}$$
(31)

For a non-traded risk \(Z_A\), the collective exposure \(\sum _i a_i F_i\) of the funds financial wealth is exogenously given.

Next, we generalize the evolution of pension income (10) to this setting.

Proposition 6

Consider the dynamics (29)-(31). The evolution of annuitized pension income \(Y_t = (F_t+H_t)/A_t\) is

$$\begin{aligned} \frac{\mathrm{d}Y_{it}}{Y_{it}}&= \mu _{Y_{it}} \, \mathrm{d}t + \sigma _{Y_{it}} \, \mathrm{d}Z_t, \end{aligned}$$

where

$$\begin{aligned} \mu _{Y_{it}}&= \frac{F_{it}}{F_{it} + H_{it}} \left( w_{it}\lambda \sigma + a_{it}^{\mathrm{net}}\lambda _{A} + \sigma _{A_{it}}^{2}\frac{F_{it} + H_{it}}{F_{it}} - a_{it}\sigma _{A_{it}}\right) , \end{aligned}$$
(32)
$$\begin{aligned} \sigma _{Y_{it}}^2&= \left( w_{it}^{2}\sigma ^{2} + \left( a_{it}^{\mathrm{net}} \right) ^{2} \right) \left( \frac{F_{it}}{F_{it} + H_{it}} \right) ^{2}, \end{aligned}$$
(33)
$$\begin{aligned} a_{it}^{\mathrm{net}}&= a_{it} + D_{it}\frac{H_{it}}{F_{it}} - \frac{F_{it} + H_{it}}{F_{it}}\sigma _{A_{it}}. \end{aligned}$$
(34)

The exposure \(a_{it}^{\mathrm{net}}\) refers to the exposure of financial wealth to \(Z_A\) as if human capital \(H_{it}\) has no exposure to \(Z_A\). In contrast, the exposure \(a_{it}\) includes a hedge for the exposure of \(H_{it}\) to \(Z_A\).

We can now extend the analysis above to obtain the optimal social planner’s allocation in the presence of annuity risk.

Proposition 7

  1. (i)

    The first-best exposures to financial market risk and annuity risk are for participant i

    $$\begin{aligned} w_{it}^{\text {FB}}&= \frac{F_{it} + H_{it}}{F_{it}}\frac{\lambda }{\gamma _{i}\sigma }, \end{aligned}$$
    (35)
    $$\begin{aligned} a_{it}^{\text {FB}}&= a_{it}^{\mathrm{net,FB}} - D_{it}\frac{H_{it}}{F_{it}} + \frac{F_{it} + H_{it}}{F_{it}}\sigma _{A_{it}}, \end{aligned}$$
    (36)

    where

    $$\begin{aligned} a_{it}^{\mathrm{net,FB}}&= \frac{F_{it} + H_{it}}{F_{it}}\frac{\lambda _{A} - \sigma _{A_{it}}}{\gamma _{i}}. \end{aligned}$$
    (37)
  2. (ii)

    The following three statements are equivalent:

    1. (1)
      $$\begin{aligned} \frac{\lambda _{A} - \sigma _{A_{it}}}{\gamma _{i}} > D_{it} - \sigma _{A_{it}}. \end{aligned}$$
    2. (2)

      A new entrant (who has \(H_{it}/F_{it} \rightarrow \infty \)) has a positive first-best exposure \(a_{it}^{\mathrm{FB}}\).

    3. (3)

      The first-best exposure \(a_{it}^{\mathrm{FB}}\) increases with \(H_{it}/F_{it}\) (and thus decreases with age).

  3. (iii)

    The first-best fund exposures to financial market risk and annuity risk are

    $$\begin{aligned} w_{t}^{\text {FB}}&= \frac{F_{t} + H_{t}}{F_{t}}\frac{\lambda }{\gamma _{i}\sigma }, \end{aligned}$$
    (38)
    $$\begin{aligned} a_{t}^{\text {FB}}&= a_{t}^{\mathrm{net,FB}} + \frac{1}{F_{t}}\left( \sum _{j=1}^n \left( F_{jt} + H_{jt}\right) \sigma _{A_{jt}} - D_{jt} H_{jt} \right) , \end{aligned}$$
    (39)

    where

    $$\begin{aligned} a_{t}^{\mathrm{net,FB}}&= \frac{1}{F_{t}} \sum _j \left( F_{jt} + H_{jt}\right) \frac{\lambda _{A} - \sigma _{A_{jt}}}{\gamma _{j}}. \end{aligned}$$
    (40)
  4. (iv)

    The first-best certainty equivalent of the return \(R_i\) of participant i is

    $$\begin{aligned} \mathrm{CEQ}_{it}^{\mathrm{FB}}&= \frac{\lambda ^2 + \left( \lambda _A-\sigma _{A_{it}} \right) ^2}{2\gamma _i} + D_{it} \frac{H_{it}}{F_{it}+H_{it}}\sigma _{A_{it}}. \end{aligned}$$
    (41)

Let us discuss the statements in Proposition 7 in more detail. The result in (35) is actually the same as in (13). In other words, the first-best optimal exposure \(w_{i}^{\mathrm{FB}}\) is not affected by the exposure to \(Z_{A}\). That makes sense, given the assumed independence of \(Z\) and \(Z_{A}\). Thus, also the results in Sect. 4 for different choices of \(\alpha _{i}\) and \(\gamma _{i}\) still hold for \(w_{i}^{\mathrm{FB}}\).

In contrast to (16), the first-best exposure \(a_{it}^{\text {FB}}\) in (36) and the first-best certainty equivalent in (41) vary by individual even if \(\gamma _i \equiv \gamma \). The reason is that the return on the hedge for human capital risk differs by individual.Footnote 30

The intuition behind (ii1) and (ii2) is that the first-best exposure \(a_{it}^{\mathrm{net,FB}}\) exceeds the exposure \(D_{it}-\sigma _{A_{it}}\) to \(Z_A\), which is inherited from the exposure of human capital \(H_{it}\) and annuity risk \(A_{it}\). Hence, the first-best exposure \(\left( \lambda _{A} - \sigma _{A_{it}}\right) /\gamma _{i}\) of initial financial wealth compensates for the shortfall in exposure to \(Z_A\). For the equivalence of (ii1) and (ii3), the first-best exposure \(a_{it}^{\mathrm{FB}}\) is linear in \(H_{it}/F_{it}\) with slope \(\left( \lambda _{A} - \sigma _{A_{it}}\right) /\gamma _{i} - D_{it} + \sigma _{A_{it}}\).

Suppose now that the fund exposures to financial market risk (\(w_t\)) and annuity risk (\(a_t\)) are both exogenously determined. For instance, the investment strategy can be fixed for a longer period of time and annuity risk can be non-traded. The exposure \(a_t\) of financial wealth to the risk factor \(Z_A\) can be zero, but this is necessary. For instance, long-term bond prices are exposed to changes in the annuity price by the common exposure to long-term interest rates. As a result, financial wealth is sensitive to annuity risk, i.e., \(a_t > 0\). In contrast, longevity risk may not affect the fund’s financial wealth \(F_{t}\), such that \(a_t = 0\) for this type of annuity risk.

Proposition 8

Given fund exposures \(w_t\) and \(a_t\), the second-best exposures of participant i are

$$\begin{aligned} w_{it}^{\mathrm{SB}}&= w_{it}^{\text {FB}} + \frac{v_{it}}{\sum _{j}^{}v_{jt}}\frac{1}{F_{it}}\left[w_t F_t - \sum _{j = 1}^{n}{w_{jt}^{\text {FB}}F_{jt}} \right], \end{aligned}$$
(42)
$$\begin{aligned} a_{it}^{\mathrm{SB}}&= a_{it}^{\text {FB}} + \frac{v_{it}}{\sum _{j}^{}v_{jt}}\frac{1}{F_{it}}\left[a_t F_t - \sum _{j = 1}^{n}{a_{jt}^{\text {FB}}F_{jt}} \right], \end{aligned}$$
(43)

where \(w_{it}^{\mathrm{SB}}\) and \(a_{it}^{\mathrm{SB}}\) are given in Proposition 7, and \(v_{it} = \frac{\left( F_{it} + H_{it} \right) ^{2}}{\alpha _{i}\gamma _{i}}\).

Let us study in more detail the allocation of financial market risk \(Z\) and annuity risk \(Z_{A}\) to the financial wealth of individual participants. Similar to the first-best, the result in (42) is actually the same as Proposition 3. In other words, the second-best optimal exposure \(w_{i}^{\mathrm{SB}}\) is not affected by the exposure to \(Z_{A}\). That makes sense, given the assumed independence of \(Z\) and \(Z_{A}\). Thus, also the results in Sect. 4 for different choices of \(\alpha _{i}\) and \(\gamma _{i}\) still hold.

Of course, the structure in (43) is very similar to (42). The optimal exposure is, again, the individual first-best exposure and a share in the excess fund exposure. This share is the same for \(w_{i}^{\mathrm{SB}}\) and \(a_{i}^{\mathrm{SB}}\), because of the similar structure of the restrictions in (A19) that determine this share. For the exposure to \(Z_A\) of total wealth,

$$\begin{aligned} \frac{F_{it}}{F_{it} + H_{it}}a_{it}^{\mathrm{SB}}&= \frac{\lambda _{A}}{\gamma _{it}} - D_{it}\frac{H_{it}}{F_{it} + H_{it}} + \frac{1}{F_{it} + H_{it}}\frac{v_{it}}{\sum _{j}^{}v_{jt}}\left[aF - \sum _{j = 1}^{n}{a_{j}^{\text {FB}}F_{jt}} \right]. \end{aligned}$$

Indeed, total wealth of new hires (\(F_{it} \downarrow 0\)) has a nonzero exposure, because of the future pension contributions \(H_{it}\) that already finance a nonzero pension annuity.

Next, we consider the similarities between the optimal allocation in Proposition 8 and the new Dutch pension system. The optimal exposures in Proposition 8 can be decomposed as

$$\begin{aligned} w_{it}^{\mathrm{SB}}&= \overset{\text {FB\ speculative}}{\overbrace{\frac{F_{it} + H_{it}}{F_{it}}\frac{\lambda }{\gamma _{i}\sigma }}} + \overset{\text {suboptimal\ speculative}}{\overbrace{\frac{v_{it}}{\sum _{j}^{}v_{jt}}\frac{1}{F_{it}}\left[wF - \sum _{j = 1}^{n}{w_{jt}^{\text {FB}}F_{jt}} \right]}} \end{aligned}$$
(44)
$$\begin{aligned} a_{it}^{\mathrm{SB}}&= \underset{\text {FB\ hedge}}{\underbrace{\frac{F_{it}+H_{it}}{F_{it}}\left( 1-\frac{1}{\gamma _i}\right) \sigma _{A_{it}}-\frac{H_{it}}{F_{it}}D_{it}}} + \underset{\text {FB speculative}}{\underbrace{\frac{F_{it}+H_{it}}{F_{it}}\frac{\lambda _A}{\gamma _i}}} \nonumber \\&\quad+ \underset{\text {suboptimal\ speculative}}{\underbrace{\frac{v_{it}}{\sum _{j}^{}v_{jt}}\frac{1}{F_{it}}\left[aF - \sum _{j = 1}^{n}{a_{jt}^{\text {FB}}F_{jt}} \right]}}, \end{aligned}$$
(45)

where \(v_{it} = \frac{\left( F_{it} + H_{it} \right) ^{2}}{\alpha _{i}\gamma _{i}}\).

These terms have a clear interpretation. We discuss the terms in (45):

(i):

\(\frac{F_{it} + H_{it}}{F_{it}}\left( 1 - \frac{1}{\gamma _{i}} \right) \sigma _{A_{it}}\): this is the ‘leveraged up’ hedge of risk in the annuity factor \(A_{it}\). The term with \(\frac{1}{\gamma _{i}}\) is only included if \(\mathrm{d}\!\left( F_{it} + H_{it} \right) \) and \(\mathrm{d}A_{it}\) both depend on \(Z_{A}\).

(ii):

\(- \frac{H_{it}}{F_{it}}D_{it}\): ‘natural’ hedge to neutralize effects from human capital (30). This term is particularly important for participants with a large exposure \(\mathrm{D}_{it}\) to \(A_{it}\).

(iii):

\(\frac{F_{it} + H_{it}}{F_{it}}\frac{\lambda _{A}}{\gamma _{i}}\): This term is the first-best net exposure to \(Z_{A}\). It is the speculative demand for \(Z_{A}\) linearly depending on \(\lambda _{A}\).

(iv):

\(\frac{v_{it}}{\sum _{j}^{}v_{jt}}\frac{1}{F_{it}}\left[aF_{t} - \sum _{j = 1}^{n}{a_{j}^{\text {FB}}F_{jt}} \right]\): this is the ‘leveraged up’ hedge of (29) due to the fact that annuity risk may not be traded or that the aggregate fund exposure \(a\) is exogenously given. This exposes the fund to the risk factor \(Z_{A}\) sub-optimally. This term is absent in case \(a\) is chosen optimally, i.e., \(a = a_{t}^{\text {FB}}\). The weights \(v_{it} > 0\) determine how the collective risk from the mismatch in period t is shared among the participants. Total wealth determines these weights. More specifically, the weights \(v_{it} = \frac{\left( F_{it} + H_{it} \right) ^{2}}{\alpha _{i}\gamma _{i}}\) are proportional to the ratio of \(\eta F_{it}\) (marginal benefit in satisfying the constraint on \(a_{it}\) in (A19)) to \( \frac{\alpha _{i}\gamma _{i}F_{it}}{\left( F_{it} + H_{it}\right) ^{2}} \) (additional marginal cost for each \(a_{it}\) in excess of \(a_{it}^{\text {FB}}\)). At the optimum, this marginal cost equals the marginal benefit.

The optimal allocation \(a_{it}^{\mathrm{SB}}\) is strongly related to the new Dutch pension contract. To see this, notice first that each first-best component in (44)-(45) depends on the ratio \(H_{it}/F_{it}\). This individual-specific ratio may be approximated by an age-specific exposure in the new pension contract, since it may be difficult to obtain a reliable estimate of \(H_{it}\) for each individual participant.

Now, consider the case where \(Z_{A}\) represents interest rate risk:

  1. (1)

    In the new Dutch pension contract, the hedge return (the so-called ‘beschermingsrendement’) to hedge the exposure of the annuity to interest rate risk is represented by the first component in \(a_{it}^{\mathrm{SB}}\).

  2. (2)

    The second component in \(a_{it}^{\mathrm{SB}}\) corrects for interest rate risk due to human capital (28). For working generations, this mitigates the optimal exposure of financial capital to interest rate risk. In the new pension contract, a pragmatic response to this exposure is to scale the exposures in the hedge return by an age-specific factor below 100% for working generations.

  3. (3)

    The third and the fourth component in \(a_{it}^{\mathrm{SB}}\) are jointly included in the excess fund return that remains after allocating the hedge returns in the new pension contract (the so-called ‘overrendement’). For \(\alpha _{i} \propto F_{it} + H_{it}\), the optimal allocation of this excess return is proportional to \(\frac{1}{\gamma _{i}}\frac{F_{it} + H_{it}}{F_{it}}\). Then, the optimal exposure of total wealth to this excess return is simply proportional to \(\frac{1}{\gamma _{i}}\). This holds for the speculative return in both (44) and (45).

6 Numerical Example

We illustrate some of our results for a fund with \(N=40\) participants facing a flat (in monetary terms) annual contribution rate, normalized to one: \(h_i\equiv 1\). Participant i has contributed for i years of a total of N contribution years. Let \(\rho \) denote the expected return on financial assets, and let r denote the the discount rate to value human capital. Suppressing time subscripts for convenience gives (\(i=1,\ldots ,N\))

$$\begin{aligned} \text {Financial wealth:}&F_i&=\sum _{j=0}^{i-1} (1+\rho )^j = \frac{1}{\rho }\left[ (1+\rho )^{i}-1 \right] \end{aligned}$$
(46)
$$\begin{aligned} \text {Human capital:}&H_i&=\sum _{j=1}^{N-i}(1+r)^{-j} = \frac{1}{r}\left[ 1 - (1+r)^{i-N} \right] , \end{aligned}$$
(47)

and for the pension funds’ wealth

$$\begin{aligned} F&= \sum _{i=1}^{N} F_i = \frac{1}{\rho }\left( \frac{1}{\rho }\left[ (1+\rho )^{N+1}-1 \right] -(N+1) \right) \\ H&= \sum _{i=1}^{N} H_i = \frac{1}{r}\left( (N - 1) - \frac{1}{r}\left[ 1 - (1+r)^{1-N} \right] \right) . \end{aligned}$$

Suppose the discount rate r and expected return \(\rho \) are both \(1\%\), and assume a risk premium of \(\lambda = 20\%\) and stock volatility of \(\sigma = 20\%\). The top plot in Fig. 1 shows that \(F_i\) and \(H_i\) are almost linear with age. This is due to the interest rate r and discount rate \(\rho \) being close to zero. For young participants the ratio \(H_i/F_i\) is high, which implies a high leverage in the first-best allocations.

6.1 No Annuity Risk

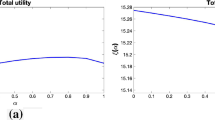
The first-best exposure \(w_i^{\mathrm{FB}}\) of financial wealth from (13) is much higher at young ages, because then financial wealth is only a small proportion of total wealth. Since \(F=H\) and \(\lambda =\sigma \), it follows from (14) that \(w^{\mathrm{FB}}=2/{{\tilde{\gamma }}}\). The top plot in Fig. 2 shows the first-best fund exposure \(w^{\mathrm{FB}}\) for different risk perceptions \({{\tilde{\gamma }}}\). Intuitively, a higher risk aversion (higher \({{\tilde{\gamma }}}\)) means a lower first-best fund exposure \(w^{\mathrm{FB}}\). Note that \(w_i^{\mathrm{FB}}\) in (13) differs across individual participants.

Next, consider the second-best where \(w=w^{FB}\) does not necessarily hold. Suppose \(\alpha _i \propto F_i + H_i\) and \(\gamma _i\equiv {{\tilde{\gamma }}}\). Recall from (27) that each participant has then the same second-best optimal certainty equivalent, regardless whether \(w=w^{\mathrm{FB}}\) holds. The bottom plot in Fig. 2 shows how this second-best certainty equivalent \(\mathrm{CEQ}_i^{\mathrm{SB}}\) of \(R_t\) changes with the fund exposure w. Naturally, the fund exposure \(w=0\) is equivalent to a certain payoff of zero. At \(w=1\), we find from (27) that participants prefer a certain payoff of zero over the uncertain payoff of a full stock exposure of financial wealth if their risk aversion satisfies

$$\begin{aligned} {{\tilde{\gamma }}} > \frac{2\lambda }{\sigma }\frac{ F+H }{F} \approx 3.36. \end{aligned}$$

At higher levels of the fund exposure w, the certainty equivalent becomes more sensitive to the risk aversion \(\gamma \). Likewise, the certainty equivalent of risk averse participants is more sensitive to the fund exposure w, which makes sense.

Fig. 1
figure 1

Top: Financial wealth \(F_i\) (46) and human capital \(H_i\) (47), by age. Bottom: First-best stock exposure \(w^{\mathrm{FB}}_i\) (13), by age

Full size image
Fig. 2
figure 2

Top: First-best fund exposure \(w^{\mathrm{FB}}\) in (14), by risk perceptions \({{\tilde{\gamma }}}\). Bottom: Second-best optimal certainty equivalent from (9) and (27), by fund exposure w for different risk perceptions \({{\tilde{\gamma }}}\)

Full size image

6.2 Annuity Risk

We add annuity risk to the setting in the previous section. Each participant i has the first-best stock exposure \(w_i^{\mathrm{FB}}\). We set the risk premium at \(\lambda _A = 10\%\) for each unit of exposure on \(Z_A\), the exposure of \(A_i\) to \(Z_A\) is \(\sigma _{A_{it}} = 0.006 (N + 21 - i)/2\), and the exposure of human capital to \(Z_A\) is \(D_i = 0.006 (N + 1 - i)/2\). The linearity of \(\sigma _{A_{it}}\) and \(D_i\) in i reflects the linearity of the duration by maturity (see top plot in Fig. 3). The slope coefficient of 0.006 is based on the annualized standard deviation of historical monthly returns on zero coupon bonds.Footnote 31

In contrast to \(w_i^{\mathrm{FB}}\), the first-best optimal \(a_i^{\mathrm{FB}}\) to the annuity risk factor \(Z_A\) depends on the age of participant i, even if \(\gamma _i\equiv {{\tilde{\gamma }}}\) (see (36)). The bottom plot in Fig. 3 shows the first-best exposure \(a^{\mathrm{FB}}_i\) by age for different values of the risk perception \(\gamma _i\). The first-best allocation \(a_{it}^{\mathrm{FB}}\) in Proposition 7 is no longer proportional to \(1/\gamma _i\), as was the case with \(w_{i}^{\mathrm{FB}}\) in Fig. 1. In our example, Proposition 7(ii1) and (ii2) imply that \(\gamma _{i} > \frac{0.1 - 0.18}{0.12-0.18} = \frac{4}{3}\) suffices for a positive first-best exposure \(a_i^{\mathrm{FB}}\) for new entrants. Proposition 7(ii1) and (ii3) imply that the first-best positive exposure \(a_i^{\mathrm{FB}}\) is independent of \(\gamma _i\) at \(i = 27\frac{2}{3}\) (and \(N-i=12\frac{1}{3}\)) where \(\lambda = \sigma _{A_{it}}\).

The risk aversion \(\gamma _i\) has a large impact on \(a_i^{\mathrm{FB}}\) for young participants with \(\gamma _i\) not to close to 4/3. The intuition is that young participants with \(\gamma _i>\!\!> 4/3\)) have a strong appetite to hedge annuity risk, while less risk-averse participants (\(\gamma _i<\!\!< 4/3\)) may not be willing to do this if the risk premium is considered too low \(\lambda _A < \sigma _{A_{it}}\). Relatedly, the individual first-best fund allocations are particularly sensitive to \(\gamma _i\) at low levels of \(\gamma \), also at the fund level (Fig. 4). The sensitivity is much lower at a higher level of risk aversion \(\gamma \). However, at such \({{\tilde{\gamma }}}\) the fund exposure a has a pronounced impact on the second-best certainty equivalent return (left panel in Fig. 5). This reflects that the duration effect through \(A_t\) on to the annuity risk factor \(Z_A\) can be large, particularly for young participants. For instance, a social planner with \(\gamma =8\) is willing to pay a nine percentage point certain annual return to substitute the exposure \(a=0.4\) for the first-best exposure \(a=a^{\mathrm{FB}}\).

A similar exercise is in the right panel in Fig. 5, where \(a_i=a_i^{SB}\) varies with w for some different levels of risk aversion \(\gamma _i\). The certainty equivalent \(\mathrm{CEQ}^{\mathrm{SB}}\) is higher in the right panel in Fig. 5 than in the bottom panel in Fig. 2. The reason is that \(a_i^{\mathrm{FB}}\) captures a risk premium, which increases the certainty equivalent. Nonetheless, the sensitivity of \(\mathrm{CEQ}^{\mathrm{SB}}\) is comparable in both figures. In sum, welfare effects are more sensitive to the fund exposure a to annuity risk than to the exposure w to financial market risk, in particular for risk averse participants.

Fig. 3
figure 3

Top: Exposure to \(Z_A\) of \(A_i\) (in (29)) and of \(H_i\) (in (30)), by age i. Bottom: First-best annuity risk exposure \(a^{\mathrm{FB}}_i\) in (36) by age i

Full size image
Fig. 4
figure 4

First-best fund exposure \(a_i^{\mathrm{FB}}\) from (36) and \(a^{\mathrm{FB}}\) from (39) by risk perception \(\gamma \)

Full size image
Fig. 5
figure 5

Second-best certainty equivalent fund return \(\mathrm{CEQ}^{SB}\). Left: \(\mathrm{CEQ}^{SB}\) by fund exposure a to the annuity risk factor \(Z_A\). Each participant i has the first-best exposure \(w_i^{\mathrm{FB}}\) from (35) and the second-best optimal risk exposure \(a_i^{\mathrm{SB}}\) from (43). Right: \(\mathrm{CEQ}^{SB}\) by fund exposures w to the financial market risk factor Z. Each participant i has the first-best exposure \(a_i^{\mathrm{FB}}\) from (36) and the second-best optimal risk exposure \(w_i^{\mathrm{SB}}\) from (42)

Full size image

7 Conclusion

We have shown that an allocation where the relative effect on total retirement wealth (the sum of financial wealth and human capital) is the same for each participant is Pareto optimal. This stylized lifecycle fact inspired the new Dutch retirement system. Under stylized assumptions, we characterized the Pareto optimal risk allocations. Subsequently, we extended the optimal allocation rule to a setting with annuity risk. This optimal allocation rule consists of one part that hedges annuity risk and human capital risk, and another part to benefit from a risk premium on risky assets. The latter part is also present in the case with only financial market risk.

Our optimal allocation rule is very similar to the allocation rule in the proposed new Dutch pension system. One potential difference between these two allocation rules is that the individual-specific ratio of human capital to financial wealth plays a key role in our optimal allocation role, while in the proposed new Dutch pension system this ratio is allowed to be approximated by an age-dependent life-cycle. In future research, one can estimate the welfare loss due to this approximation.

A numerical example indicates that the fund risk allocation has substantial welfare effects. With our settings, an appropriate hedge of annuity risk is particularly important for risk averse participants. For them, the exposure to long-duration annuity risk is most important to hedge sufficiently.

Our model is a basic model with some limitations, which opens up some opportunities for future research. We mention a few without intending to be exhaustive. First, the model can be calibrated to empirical data. Then, one can identify the impact of different risk factors such as interest rate risk, stock market risk, inflation risk, real wage risk, and mortality risk. Second, household characteristics (partner income, number of children and housing assets) can enrich our concepts of financial wealth and human capital. Particularly, the interrelation of different sources of wealth can affect the optimal allocation. Third, a policy relevant question is to optimize the welfare gains when adding the so-called solidarity reserve to our model or, relatedly, when anticipating the entry of future generations to the pension fund. A fourth avenue for further research is to include more advanced time-series properties, e.g., non-normality, by extending our simple geometric Brownian motion framework. Finally, risk preferences other than CRRA preferences are another interesting topic for future research.