Abstract
The diffusion of a novel taxing scheme (among Dutch municipalities over the period 1998–2005) is studied in which the waste disposal tax is increasing in the amount of waste a household produces. Inspection of the rise and spread of this tax shows that it is contagious: the probability of introduction is increasing in the number of neighboring municipalities that have already introduced this taxing scheme. A possible rationale is that the tax encourages the dumping of waste in neighboring municipalities. These municipalities may then introduce a similar tax to prevent dumping (spillover effect). Using panel data and a recently developed spatial probit approach (Elhorst et al. in J Appl Econom 32:422–439, 2017), it is possible to distinguish this spillover effect from time-specific effects. The results indicate the presence of strong spillovers.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Policy decisions of governments often have effects beyond its own borders. This is especially true for local governments, where borders are nothing more than a dotted line on a map. For example, cities that offer amenities, like (subsidized) theatres, often attract visitors from surrounding areas, and decreasing tax rates on business activities may cause the relocation of firms. In turn this affects the policy decisions of neighboring jurisdictions (not sustaining a theatre when a nearby city already has one, also decreasing tax rates on business activities). However, often it is difficult to disentangle these spillover effects from other factors.
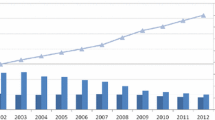
In this paper, we investigate the diffusion of differentiated waste disposal taxes across municipalities in the Netherlands, where the waste disposal tax is increasing in the amount of waste a household produces. At the start of our observation period in 1998 this kind of taxation barely existed. Figure 1 shows that since then its diffusion rapidly increased, as well as that this process is highly clustered. In total 110 of the 467 municipalities employed some form of DIFferentiated TARiffs (DIFTAR hereafter) in 2005.Footnote 1 The purpose of this paper is to examine the causes and strength of this process and the corresponding spillover effects.
Spillover effects may occur for two reasons. First, (illegal) dumping of waste will become more prevalent, which may not be confined to the municipality that introduces DIFTAR. A study cited by Linderhof et al. (2001) confirms this: in the Dutch municipality of Oostzaan 4–5% of total waste reduction resulted from dumping in neighboring municipalities out of a total of 30% waste reduction. A second spillover is an informational one. If a particular municipality introduces DIFTAR, the policymakers and citizens of neighboring municipalities obtain valuable information about the impact of this taxing scheme, which may help them to decide whether it is also suitable for them. We will show how these kinds of externalities determine the introduction of DIFTAR.
The data that we use to identify the presence of spillovers, consists of a panel with yearly observations for all Dutch municipalities over the period 1998–2005. For each municipality it is known in which year it introduced DIFTAR and what its bordering municipalities are. The results of local elections are also known, as well as a number of time-independent characteristics of the municipality. With cross-section data, it might be problematic to identify the existence of spillovers since the introduction of DIFTAR could equally well be attributed to an unobserved trend. Therefore, in this paper, we use a spatial panel data model to separate potential spillover effects from time-specific effects. The results indicate the existence of significant spillover effects.
The paper is organized as follows. An overview of the literature is given in Sect. 2. Section 3 presents a theoretical model. The institutional details and an overview of the data are given in Sect. 4. In Sect. 5, we present the econometric model and in Sect. 6 we discuss the estimation results. Section 7 summarizes the main results and discusses the welfare implications of the contagious nature of introducing DIFTAR.
2 Overview of the Literature
Most research on DIFTAR focuses on the question whether and to what extent it reduces the amount of waste produced by a household. Notable studies are Linderhof et al. (2001) and Fullerton and Kinnaman (1996). The former study uses data for each household in the Dutch municipality of Oostzaan before and after the introduction of a DIFTAR-regime that taxes households for each kilogram of waste produced. This allows estimation of short- and long-run price effects, which they find to be strong and negative. Fullerton and Kinnaman (1996) use similar data for the city of Charlotteville, Virginia. The main difference is that the households are taxed per bag produced. In order to estimate weight reduction, the bags were weighed for a selection of households. The effect of the tax caused a significant reduction in the amount of waste. Besides the aforementioned studies, there are dozens of studies that use aggregated data. Dijkgraaf (2004) is the most interesting of these studies from our perspective since it uses Dutch data. In the Netherlands, municipalities use a variety of DIFTAR-regimes: pricing per kilogram, pricing per bag, etc. Dijkgraaf finds that each of the regimes lowers the total amount of waste collected but the scheme with the most direct incentives (i.e. pricing per kilogram) reduces it by the largest amount.
The aim of this study is not to present further evidence that DIFTAR reduces the amount of waste collected, but to show that the introduction of DIFTAR imposes externalities on neighboring municipalities. Consequently, introducing DIFTAR raises strategic coordination issues. The externality can be a physical one (in the form of waste dumping), but this is not necessarily the case.
Before continuing our discussion, it is to be noted that waste dumping refers to two activities. The first is illegal dumping of waste on publicly owned land, such as parks or forests. The second activity is either carrying waste to family or friends in neighboring municipalities that do not charge households per kilogram of waste produced or dumping the waste at work. The latter activity is usually referred to as waste tourism. Although legal, it is a form tax evasion.Footnote 2
Both Fullerton and Kinnaman (1996) and Linderhof et al. (2001) provide evidence that DIFTAR increases the incidence of waste dumping. Fullerton and Kinnaman (1996) refer to the first activity and claim that it may account for 43% of waste reduction. Linderhof et al. refer to the second activity and suggest that 4–5% of waste is dumped in neighboring municipalities. Moreover, Linderhof et al. explicitly mention that illegal dumping of waste on publicly owned land is a minor problem in the Netherlands. If DIFTAR implies the second kind of activity, then a municipality without DIFTAR can diminish the effect of waste tourism by introducing DIFTAR itself. This is an additional reason for a municipality to introduce DIFTAR: by doing so, it will avoid the cost of waste tourism. This argument is elaborated on in the theoretical model presented in Sect. 3.
There is a large literature, both theoretical and empirical, on policy diffusion. The two largest strands in the theoretical literature are on the Tiebout-hypothesis and yardstick competition. As a short remark on terminology, we use both diffusion and spillovers to denote any kind of diffusion whereas the Tiebout-hypothesis and yardstick competition denote two particular forms of diffusion which we will define shortly.
Tiebout (1956) argues that citizens vote with their feet and move toward municipalities that offer the best combination of provision of local public goods and taxation. If local public goods are indeed local then the outcome is efficient, which is usually referred to as the Tiebout-hypothesis. This conclusion does not hold if local public goods have an effect on neighboring municipalities (and the government cannot internalize all externalities): then the outcome can be far from efficient.
Yardstick competition takes a different approach (Salmon 1987). In this approach citizens are unable to directly evaluate the performance of local politicians. Citizens can observe policy outcomes, but they are unaware if a better outcome was available but not implemented. Assuming that politicians in neighboring municipalities face the same trade-offs, comparing outcomes with neighboring municipalities might provide an opportunity to indirectly evaluate the performances of these local politicians. This leads politicians in neighboring municipalities to make the same choices. This theory does not predict that the outcome will be efficient or in which direction policy will move. In general, yardstick competition differs from the Tiebout-hypothesis and the theory presented in this paper, because the externality is not physical. Other non-physical externalities include learning models. The cost and benefits of introducing a new policy are uncertain. Consequently, the introduction of DIFTAR in a neighboring municipality might be a useful experiment to examine the associated cost and benefits. If it is successful, then DIFTAR may spur the introduction in surrounding municipalities.
A plethora of studies finds empirical evidence of both the Tiebout-hypothesis and yardstick competition. To name a few: Brown and Rork (2005) study lottery taxes among American states and find evidence supporting the Tiebout-hypothesis. It appears that American states lower their lottery tax in order to generate more revenue from state lotteries by attracting out-of-state buyers. Case et al. (1993) observe strong correlation between the size of expenditures of American states and present this as evidence of fiscal interdependence. In a related study, Besley and Case (1995) study the effect of income taxation on outcomes in gubernatorial elections: lower taxes in neighboring states lead to a higher probability that the incumbent loses the election. This is in line with the yardstick competition theory. Allers and Elhorst (2005) study property taxes among Dutch municipalities and also find evidence in support of yardstick competition.
The above studies focus on tax rates and not on a tax innovation like DIFTAR. Following Walker (1969), political scientists and economists alike have also devoted many studies to the diffusion of innovative tax instruments, see Ashworth et al. (2006) and the references therein. The latter find that the rapid diffusion of a novel environmental tax among Flemish municipalities during the 1990s could be partly determined by the implementation of such a tax among neighboring municipalities. However, they do not explain why the probability of implementation is increasing in the number of neighboring municipalities that have implemented the tax. Since the environmental tax amounts to reserving part of the budgets for environmental purposes, this tax is a purely symbolic act. Hence, there seems to be no reason for any spillover effect beyond imitation. In the case of DIFTAR studied in this paper, there is an externality present, which could explain spillover effects.
3 A Theoretical Model
In the model presented in this section, the diffusion of DIFTAR is explained solely by dumping in neighboring municipalities. In a guide for introducing DIFTAR (AOO 2004), aimed at municipalities, waste tourism is explicitly mentioned as an effect of introducing DIFTAR. As discussed in Sect. 2, this is by no means the only possible rationale for its diffusion. However, by focusing entirely on the waste-tourism motive, we want to give some insight in the incentives of a municipality to introduce DIFTAR and how it depends on the decisions of neighboring municipalities.
Suppose there are two, neighboring municipalities: \(i=1,2\). Consumers in municipality i have the following utility function:
where D is a (dirty) good that produces waste and C is a (clean) good that does not produce waste. It is assumed that if a household consumes one unit of D, it also produces one unit of waste. A fraction \(\rho _i\) of waste remains in the municipality of origin. The remaining fraction \((1-\rho _i)\) is dumped in the neighboring municipality. A municipality can only tax the waste that is not dumped.
Assume that, for \(i,j=1,2\) with \(i\ne j\) and \(0<\rho <1\), we have:
where \(t_i\) is the tax rate per unit of waste in municipality i. Waste of municipality i is dumped in municipality j if and only if municipality i has introduced DIFTAR and municipality j has not. This is in line with the waste tourism explanation: consumers will only dump their household waste at friends in neighboring municipalities if these friends can dump extra waste without additional cost. For the sake of simplicity, we do not explicitly model the decision to dump waste; it is assumed to occur at a rate independent of the cost of waste disposal.
If municipality 1 introduces a value tax per unit of waste and municipality 2 does not, then consumers in municipality 1 will try to avoid taxation by dumping waste in municipality 2. Since consumers in municipality 2 have no incentive to dump waste, the tax in municipality 1 will lead to an increase in waste for municipality 2. The cost of waste disposal in municipality 2 increases. In municipality 1 the cost goes down for two reasons. First, the price per unit of the dirty good increases (since consumers also pay for the disposal of the good) and thus less waste is produced. Second, part of this waste is dumped in the neighboring municipality 2, causing a further decrease in waste.
The (indirect) price of consuming one unit of D (assuming, to avoid cumbersome notation, that all prices are normalized to one) is \(1+t_i\rho _i\). The budget equation is:
where m is income and \(\beta _i\) is a lump-sum tax to cover the cost of waste disposal. If \(t_i=0\), then the municipality will raise revenue through the lump-sum tax \(\beta _i\) per household. Otherwise the municipality will raise revenue solely through the value tax \(t_i>0\) and \(\beta _i\) will be zero. Observe that \(\beta _i\) also depends on \(t_j\), since in case \(t_j>0\) and \(t_i=0\), waste from municipality j is dumped in municipality i, which increases the lump-sum tax compared to the case in which \(t_i=t_j=0\). Since utility is quasi-linear, consumption of D does not depend on m or \(\beta _i\) as long as the cost of the optimal consumption of D does not exceed \(m-\beta _i\). It is assumed that every household can afford this.Footnote 3
Solving the consumer’s maximization problem, we see that household waste production by a consumer in municipality i is:
Total waste production in municipality i is:
where \(S_i\) is the total number of inhabitants in this municipality. Utility of the consumer in the optimum is:
The government takes into account the welfare of the consumers (i.e. consumers’ surplus \(CS_i\)) when deciding to introduce DIFTAR. Suppose a single consumer can only buy the non-waste producing good C and receives a compensation \(CS_i/S_i\) in terms of good C such that his utility is the same as in the optimum of (6). We compare the situation with a tax \(t_i\) and \(\beta _i\) with a situation in which all consumption is clean and there is no tax. Then \(CS_i/S_i\) is such that:
It follows that:
Since Dijkgraaf and Gradus (2003) present evidence that the cost of waste disposal has constant returns to scale, we assume that the cost function is linear in the amount of waste: \(c\Omega _i\), where \(c>0\) is given, and that there are no additional costs if a municipality decides to change from \(t_i=0\) to \(t_i>0\) (i.e. implement DIFTAR).
Suppose the local government tries to maximize consumers’ surplus and to minimize the amount of waste subject to a financing constraint. This reflects two considerations the local government might take into account. It wants to be reelected and hence it must try to please the electorate. At the same time, the local government and the citizens might, out of environmental concerns, want to minimize waste collected in their municipality. Since the cost of waste collection also needs to be covered, the government in municipality i faces the following maximization problem:
where \(\delta _i>0\) is a parameter that signifies the strength of the environmental concerns. Since \(t_i>0\) implies \(\rho _j=1\), the first constraint simplifies to marginal cost pricing: \(t_i=c\). Alternatively, \(t_i=0\), pointing to the option to raise money by taxing each household with a lump-sum tax \(\beta _i=c(\Omega _i + (1-\rho _j)\Omega _j)/S_i\).
The following game is played: the municipalities simultaneously and independently decide to implement DIFTAR (i.e. set \(t_i=c\)) or not. It can be shown that all four pure strategy Nash equilibria are possible (for varying parameter values). Subsequently, we will characterize the best-response for municipality \(i=1,2\) for varying parameter values in an attempt to provide insight when certain equilibria occur.
Suppose municipality \(j\ne i\) has chosen \(t_j=0\). Then municipality i will introduce DIFTAR if:
where \(CS_i(\cdot )\) and \(\Omega _i(\cdot )\) are respectively consumers’ surplus and total waste production as a function of \(t_i\). After rearranging (11) the following expression is obtained
Inspecting (12), and using \(\frac{\rho }{(1+c\rho )^2}<1\), we see that if \(\delta _i\) is large enough, municipality i’s best response is to introduce DIFTAR. One would expect green parties to have a high aversion of waste, implying a high \(\delta _i\) and therefore be more likely to introduce DIFTAR even if the neighboring municipality has not. If \(\rho \) equals zero, then (12) reduces to \(1\ge 1 - c -\delta _i\). Consequently, if \(\rho \) is low, it is also beneficial to introduce DIFTAR since both the cost of waste disposal and total waste production are reduced severely when DIFTAR is implemented. A Nash equilibrium in which no municipality introduces DIFTAR will not occur in the situation when \(\rho \) is low. Moreover, if c is high enough, then DIFTAR will also be implemented since a reduction in waste production becomes more attractive.
Suppose municipality j has chosen \(t_j=c\). Then municipality i will introduce DIFTAR if:
which after some manipulations yields:
Note that all terms in brackets represent non-negative quantities. Hence, a municipality i that either has a large enough \(\delta _i\) or a neighbor that is large enough relative to its own number of inhabitants (i.e. \(S_j/S_i\) large) introduces DIFTAR. So, having a large neighbor that chooses to introduce DIFTAR can be the reason to introduce DIFTAR.
Now suppose that a social planner, e.g. a central government, determines the tax rates. The social planner maximizes \(CS_1 + CS_2 - \delta _s (\Omega _1 + \Omega _2)\) subject to a financing constraint. The weight attached by the social planner to the amount of waste produced is \(\delta _s>0\) and is not necessarily equal to \(\delta _1\) and/or \(\delta _2\). Observe that the only reason for the social planner to introduce DIFTAR is a strong enough dislike of the amount of waste produced, i.e. a high \(\delta _s\), while the dumping of waste is irrelevant to this decision.
The theoretical analysis set out above results in three major findings:
-
1.
The model can explain the existence of an isolated DIFTAR-municipality. An isolated DIFTAR-municipalities probably has a high \(\delta _i\) and will introduce DIFTAR regardless of whether neighboring municipalities have introduced DIFTAR. These neighboring municipalities on the other hand have a low \(\delta _i\) and not enough neighboring municipalities that have introduced DIFTAR.
-
2.
The model can explain how DIFTAR spreads. A domino effect can occur: if a municipality introduces DIFTAR, the best response of a neighboring municipality could be to also introduce DIFTAR.
-
3.
The Nash equilibrium is not necessarily socially optimal. As the previous point shows, a municipality might be coerced to introduce DIFTAR through waste dumping. The social planner internalizes these externalities and could choose to not introduce DIFTAR in the neighboring municipality.
From an empirical viewpoint, the essence of this model can be captured by a panel data model controlling for time-period specific effects (indicating the tendency to introduce DIFTAR over time) and variables that represent the proportion of neighboring municipalities that have introduced or that did not yet introduce DIFTAR (representing the threshold of \(S_i/S_j\) in (14)). Using these proportions as explanatory variables yields a model that has recently been considered in the spatial econometrics literature (Elhorst et al. 2017).
4 Description of Institutional Details and the Data
4.1 Institutional Details
The Netherlands is, as of January 1, 2005, divided in 467 municipalities.Footnote 4 The average municipality has an area of slightly less than 90 square kilometer, or less than \(10\times 10\) kilometer. The number of inhabitants ranges from one thousand to 750 thousand. A municipality usually consists of one larger city or a collection of villages. Despite these large differences, they have broadly the same obligations and means of taxation. They are required to execute several tasks, but have considerable autonomy regarding the details.
Local politics decides on these details. The political system in municipalities is based on proportional representation. Apart from a handful of municipalities, no single party has a majority. As in national politics, it is common to form a coalition with a majority backing. The coalition parties provide aldermen. We will use the political alignment of the aldermen to construct two political indicators: the percentage of aldermen aligned with a certain political view and a measure of concentration of the coalition with respect to the political alignment. It is posited that heavily fragmented coalitions are less effective in causing major changes.
One of the public services a municipality is required to offer is the collection and disposal of household waste. It raises revenues by taxing households to pay for the associated cost. The municipality is free to hire a company to take care of the collection and disposal of waste, but it can also choose to organize the collection of waste itself. In practice, small municipalities outsource completely and larger municipalities usually outsource only the disposal of waste.
No matter how waste is collected, it is the municipality that determines the tax system and the height of the tax rates. Until the mid 1990s, practically all municipalities taxed consumers according to a flat fee (although possibly dependent on the size of the household). Since then many municipalities have made the tax dependent on the amount of waste a household produces. The main types of DIFTAR-schemes are:
-
Weight-based: Collected waste is weighed and households are charged per kilogram.
-
Volume-based: Households are equipped with a container of a certain size and they have to pay each time the container is presented at the curbside and emptied.
-
Expensive bag: Waste is only collected if it is presented in a particular bag. A household buys these bags in advance in a nearby shop. The main advantage of this scheme are the low cost of implementation and the small administrative cost.
All these schemes lower the amount of waste (in kilograms), but the effect is most pronounced for the weight-based scheme (Dijkgraaf 2004; Fullerton and Kinnaman 1996).
We end this section with one final remark on the politics of DIFTAR and one on the problem of dumping. Empirical evidence suggests that at the individual level the relation between income and waste production, if anything, is decreasing (Fullerton and Kinnaman 1996). Then the introduction of DIFTAR is actually the introduction of a regressive tax where the poor may end up paying more than the rich. Of course, this effect is weakened by the incentive to produce less waste, but this could well explain why left-wing parties with a strong voter base among the lower classes (in the Netherlands, this applies to the Socialist Party) are vehemently against the introduction of DIFTAR schemes.
Both Linderhof et al. (2001) and Fullerton and Kinnaman (1996) find evidence that a substantial part of the reduction in waste is due to dumping. Fullerton and Kinnaman (1996) even hypothesize that in a large, anonymous city like New York, a DIFTAR scheme would lead to near-100% dumping of waste. It is clear that the introduction of a DIFTAR scheme can only be successful if laws against waste dumping are enforced. This may well be the reason that larger cities are reluctant to introduce DIFTAR. Even in cities like Groningen (in the northern part of the Netherlands) where the necessary infrastructure is present (i.e. underground collection bins that record how much each household dumps) DIFTAR has not been introduced.Footnote 5
4.2 The Data
We use yearly data over the period 1998–2005 for all Dutch municipalities. A slightly complicating factor is the merging of municipalities.Footnote 6 In 1998 there were 553 municipalities of which 467 are left at the end of the sample period and 462 are used.Footnote 7 All data is for municipalities that existed in 2005.Footnote 8
We introduce the following variables:
- \(Y_{it}\)::
-
Value 1 if municipality i or a part of municipality i has DIFTAR in year t, and zero otherwise. A municipality that has already adopted DIFTAR in year t will also be denoted below by \(Y_{it}^1\), and a municipality that has not by \(Y_{it}^0\).
- \(W_{ij}\)::
-
Value \(1/\text {(total number of neighbors of municipality} \)i) if municipality i and municipality j share a border, and zero otherwise.Footnote 9 Fig. 2 provides a simple illustration of the construction of the border matrix W. The matrix \(W^{00}_{t}\) denotes a submatrix extracted from the full border matrix expressing the spatial relations between municipalities that have not adopted DIFTAR yet in year t, and \(W^{01}_t\) between municipalities that have not adopted DIFTAR yet and those that already did in year t.
- \(RURAL_{i}\)::
-
The rurality of the municipality (None \(=1\), ...,Very \(=5\)).
- \(LEFT_{it}\)::
-
The percentage of aldermen representing a left-wing party (i.e. PvdA, GroenLinks, SP and local left-wing parties).Footnote 10
- \(LOCAL_{it}\)::
-
The percentage of aldermen representing a local party (as opposed to a party that operates nationally) including local left-wing and local christian parties. Local parties do not participate in national elections.
- \(CONFES_{it}\)::
-
The percentage of aldermen representing a christian party (i.e. CDA, SGP, ChristenUnie and local christian parties).Footnote 11
- \(HI_{it}\)::
-
The Herfindahl-index of the coalition, i.e. the sum over the parties of the squared percentage of aldermen representing a party.
In addition, it is to be noted that only the last four variables, just as the DIFTAR-variable, vary over time.
4.3 Descriptive Statistics
Table 1 shows the number of DIFTAR-municipalities for the different categories of \(RURAL_i\). Almost all DIFTAR-municipalities are rural (\(RURAL_i=\) 4 or 5) and most of them are located in North-Brabant or Limburg (see Fig. 1). Presence is notably increasing in Gelderland and Overijssel, as well as in smaller cities (i.e. \(RURAL_i=\) 2 or 3). In line with this, Tables 2 and 3 show that the typical DIFTAR-municipality tends to have few inhabitants, to be (relatively) sparsely populated, and to have relatively high incomes and large households. Politically, the local and christian parties are overrepresented.Footnote 12
Table 4 shows the average number of neighboring DIFTAR-municipalities for both DIFTAR- and non-DIFTAR-municipalities. On average, DIFTAR-municipalities have more neighboring DIFTAR-municipalities than non-DIFTAR-municipalities. Naturally, since many municipalities have introduced DIFTAR during the sample period, the figure is rising for both types, but it has risen faster for DIFTAR-municipalities: the average for DIFTAR-municipalities has increased by 1.04, whereas this number has only increased by 0.34 for non-DIFTAR-municipalities.
5 Econometric Model
The basic idea behind the econometric model is the following. The probability that municipality i that has not adopted DIFTAR yet but will do so in year t is explained by the proportion of neighboring municipalities that also have not introduced DIFTAR yet, \(\sum _{j=1}^{N} W^{00}_{ij} Y_{jt}^0\), by the proportion of neighboring municipalities that have already done so, \(\sum _{j=1}^{N} W^{01}_{ij} Y_{jt}^1\), a set of explanatory variables (a row vector \(X^0_{it}\)), which consist of the political variables \(LEFT_{it}\), \(LOCAL_{it}\), \(CONFES_{it}\) and \(HI_{it}\), as well as their spatial counterparts observed in neighboring municipalities, \(\sum _{j=1}^{N} W^{00}_{ij}X^0_{jt}\), and a time fixed effect \(\xi _t\). This is broadly in line with the theory presented in Sect. 3. The model reads as:
where \(\epsilon _{it}\) are i.d.d. normally distributed error terms, and F represents the corresponding cumulative multivariate normal distribution function. The dependent variable and the independent variables only cover the behavior of municipalities without having DIFTAR at the start of each time period (denoted by the superscript 0). If \(N_t^0\) denotes the corresponding number of observations, the total number of observations to estimate the parameters of this model amounts to \(\sum ^{T}_{t=1} N_t^0\), which is 3078. Municipalities that did not yet introduce DIFTAR may be affected by neighboring municipalities that also did not introduce this system yet, and vice versa, and by neighboring municipalities that already did so. The first variable on the right-hand side, \(\sum _{j=1}^{N} W^{00}_{ij}Y_{jt}^0\), denotes the spillover effect caused by first set of municipalities. Since they are also in state 0, this variable needs to be treated as an endogenous explanatory variable. The second variable on the right-hand side, \(\sum _{j=1}^{N} W^{01}_{ij}Y_{jt}^1\), denotes the spillover effect caused by the second set of municipalities. This variable may be treated as an exogenous explanatory since observations on municipalities after they adopted DIFTAR are removed from the sample, in line what is common in the duration literature and the fact that the decision to adopt DIFTAR represents an absorbing state,Footnote 13 as a result of which they cannot be affected by municipalities that are still in state 0. Furthermore, since it is reasonable to assume that neighboring municipalities without DIFTAR may have a different impact than those that already introduced it, we allow these two variables to have different coefficients \(\lambda \) and \(\gamma \). Hence, the parameters in (15) can be estimated similarly to those of a standard spatial probit model. Nevertheless, their estimation remains a computational challenge since the corresponding likelihood function cannot be written as the product of \(N_t^0\) one-dimensional normal distributions in each time period, as is the case with a standard (non-spatial) probit model. This is because the individual error terms \(\epsilon _{it}\) (\(i=1,\ldots ,N_t^0\)) are not independent of each other due to the endogenous explanatory variable \(\sum _{j=1}^{N} W^{00}_{ij}Y_{jt}^0\).
A recent and extensive overview of spatial econometric models for limited dependent variables dealing with these kind of issues is provided by Baltagi et al. (2017), while the ins and outs of the model used here are set out in Elhorst et al. (2017). The software to run this model is also taken from that study (see http://qed.econ.queensu.ca/jae/datasets/elhorst001/), while the estimation technique, Efficient Importance Sampling Simulated Maximum Likelihood (EIS-SML), is taken from Liesenfeld et al. (2017). Time-period fixed effects are added to control for potential non-stationarity issues related to diffusion processes and to avoid that the spillover effects are overestimated (Ciccarelli and Elhorst 2017).
Direct interpretation of the the parameters in (15) is difficult, because they do not represent true partial derivatives LeSage and Pace (2009). Elhorst et al. (2017) show that the matrix of (true) partial derivatives of the expected value of the dependent variable with respect to the \(k^{th}\) independent variable for \(i=1,\ldots ,N\) in year t is given by the N by N matrix (note N is used here rather than \(N_t^0\) to simplify notation)
where \(\tau =(I_N - \lambda W^{00}_t)^{-1} (\gamma W^{01}_t Y^1_t + X^0_t \theta + WX^0_t \eta )\) denotes the predicted values of \(Y_t^0\), and \(Y^1_t\), \(Y^0_t\), and \(X^0_t\) are denoted in vector or matrix form. The average diagonal element of this matrix can be used as a summary indicator for the direct effect, and the average row sum of off-diagonal elements as a summary indicator of the indirect effect. These summary indicators reflect the impact on the dependent variable that result from a change in the \(k^{th}\) independent variable respectively in the own municipality and in other municipalities. Note that these indirect effects on other municipalities are a main interest in and beyond regional science. In linear spatial econometric models with continuous variables, the outcomes are generally independent from the time index (LeSage and Pace 2009), but in this case they are not since the spatial weight matrix changes over time. To obtain one summary indicator for the direct effect and one for the indirect effect of every explanatory variable in the model, we therefore also average the outcomes over time. To achieve that the the ratio between the indirect effect and direct effect may be different from one explanatory variable to another, we also take up spatial lags of the explanatory variables in the model, i.e., \(\sum _{j=1}^{N} W^{00}_{ij}X^0_{jt}\), known as spatial Durbin terms (Elhorst 2014, p.9). Without these variables these ratios would be the same for every explanatory variable, which is unlikely from an empirical point of view.
6 Estimation Results
Table 5 reports the coefficient estimates and their t-statistics, as well as the direct and indirect effects of changes in the explanatory variables on \(Y^*\) and Y, respectively denoting the unobserved willingness of a municipality to adopt DIFTAR and the binary value (0/1) of the actual decision. The parameter estimates and corresponding variance-covariance matrix to determine their t-values are obtained by estimating (15). The effects estimates are determined using (16) and their significance levels by the standard deviation obtained by recalculating these direct and indirect effects based on 1000 draws of the relevant parameters from the estimated variance-covariance matrix.
We find that the coefficient estimates \(\lambda \) and \(\gamma \) of the two spillover effects are both positive and significant, respectively 0.637 (t-value 15.32) and 0.505 (t-value 2.55). The findings imply that both the fear for waste tourism and the information that can be obtained from municipalities that already adopted DIFTAR are important drivers for municipalities to adopt or not to adopt DIFTAR. The fact that many municipalities still did not adopt DIFTAR yet is because the strength of environmental concerns of the local population (the parameter \(\delta \) in the theoretical model) in these municipalities is apparently still not high enough.
In contrast to the descriptive statistics, not many variables appear to produce significant parameter estimates. One exception is the percentage of aldermen representing a left-wing party. The probability that municipalities adopt DIFTAR is negatively affected by this percentage. The explanation is twofold. First, one potential disadvantage of DIFTAR is that the poor may end up paying more than the rich. Second, left-wing parties have a stronger voter base in bigger cities where the introduction of DIFTAR is more difficult to organize and therefore more expensive.
It is to be noted that the parameter estimates reported in Table 5 are different from the direct effects. This is due to the feedback effects that arise as a result of impacts passing through neighboring municipalities back to the municipality that instigated a change in one of the explanatory variables. Suppose that the percentage of aldermen representing a left-wing party increases after an election. The parameter estimate of this variable is \(-\,0.731\), while the direct effect on the unobserved willingness to adopt DIFTAR \((Y^*)\) amounts to \(-\,0.788\). This implies that the feedback effect equals \(-\,0.788-(-\,0.731)=-\,0.057\), which corresponds to 7.3% of the direct effect. The magnitude of this feedback effect is in line with previous results commonly found \((<\,10\%)\) in the spatial econometric models literature (Elhorst 2014, Sections 2.9, 3.6 and 4.7). Larger percentages are found for some of the other variables, but since the parameter and direct effects estimates of these variables are not significant, we should not attach too much value to this.
The direct effects further change when considering the actual value of Y; Equation (16) shows that the previous results then also need to be multiplied with the probability to adopt DIFTAR, \(\text {diag}(\phi (\tau ))\). Since 110 of the 462 municipalities adopted DIFTAR, the probability is \(23.8\%\) over the whole sample period, and approximately \(3.0 \%\) in a particular year. Due to this probability, the direct effect of the percentage of aldermen representing a left-wing party drops to − 0.275. It indicates that the probability to adopt DIFTAR has a greater impact on the direct effect of this explanatory variable than the corresponding feedback effect. Despite this fall the significance level of the direct effect nonetheless remains almost the same.
A rather different story occurs for the indirect effects. Four variables appear to produce significant (5%-level) or weakly significant (10%-level) indirect effects. The share of municipalities that already adopted DIFTAR has a positive effect on neighboring municipalities that did not adopt DIFTAR yet, in line with the theoretical finding that they may be coerced through waste dumping. Municipalities surrounded by municipalities that are not typically urban or typically rural but in between (rurality = 2 or 3) or by municipalities that are politically fragmented negatively affects the probability to adopt DIFTAR, often because these surrounding municipalities behave the same. In line with this, many indirect effects exceed their direct counterparts. The ratio between the indirect effect and the direct effect of the share of municipalities that already adopted DIFTAR on the actual decision Y appears to be \(0.229/0.158=1.45\), while even larger ratios are obtained for the other explanatory variables producing weakly significant indirect effects. In other words, not only the two spillover effects are significant, but also the indirect effects of four of the nine explanatory variables considered in this paper. This result justifies the inclusion of the spatial Durbin terms (spatial lags of the explanatory variables). The log-likelihood function value of the model amounts to 405.08. Without the spatial Durbin terms it drops to 394.83. This implies that the likelihood ratio test whether these spatial Durbin terms (8 in total) are jointly significant amounts to 20.50, while the 5% critical value of the corresponding chi-squared distribution is 15.51. Despite the fact that none of the individual spatial Durbin terms is statistically significant, they are therefore better not removed from the model.
Generally, it is harder to find empirical evidence in favor of significant indirect effects than in favor of significant spillover effects. This is because the former are composed of three parameters \(\lambda , \theta _k,\eta _k\), as well as the probability to adopt DIFTAR, which depends on all parameters in the model. If already one of the first three parameters happens to be insignificant, often the indirect effect also becomes insignificant, as a result of which only a fraction of the explanatory variables eventually produces significant indirect effects. The fact that we find result opposite to this trend is therefore all the more remarkable. It explains why the rise and spread shown in Fig. 1 is so clustered.
7 Concluding Remarks
In this paper, a theoretical model is developed to explain the diffusion of a local differentiated waste disposal tax on the amount of waste a household produces across municipalities in the Netherlands. Next, an advanced spatial probit model allowing for transitions of municipalities at different moments in time is used to test this theoretical setting. The two diffusion parameters considered in this model, \(\lambda \) and \(\gamma \), appear to be positive and significant, and so are the parameter estimate and direct effect of the percentage of aldermen representing a left-wing party, and the indirect effects estimates of the share of municipalities that already adopted DIFTAR, municipalities of rural type 2 and 3, and political fragmentation. These results provide solid evidence that a taxation scheme which imposes externalities on neighboring communities might be the cause of its rise and spread in the Netherlands over the period 1998–2005. This empirical evidence corroborates the theory set out in Sect. 3.
The theory is also supported by the accuracy of the prediction that the adoption of DIFTAR represents an absorption state: there are no instances of municipalities abandoning DIFTAR in the data. Our final prediction—municipalities that introduce DIFTAR first are likely to have a high aversion of waste production—cannot be tested by the methods used in this paper, although anecdotal evidence suggests that pioneering municipalities do have a unique legislative composition. For instance, in the municipality of Oostzaan, GroenLinks was the largest party when DIFTAR was introduced, but nationally GroenLinks is one of the smaller parties.
From a supramunicipal viewpoint, the diffusion process may or may not be beneficial. This depends on whether the central government would choose to implement DIFTAR for all municipalities. If the central government is in favor of DIFTAR, then the contagious nature of DIFTAR helps to enforce this process, while at the same time municipalities do not lose their autonomy. By contrast, if the central government opposes DIFTAR, the conclusion reverses. In that case the central government should restrict the freedom of municipalities especially in areas where non-local externalities are important or facilitate coordination.
Notes
After 2005, municipalities have continued to introduce DIFTAR, but at a diminishing rate. Our observation period corresponds to the period when DIFTAR was a relatively new innovation and most municipalities switched to DIFTAR.
There are other ways to reduce the output of waste. In Ireland, the introduction of DIFTAR has led people to burn waste in their backyard. Unfortunately this seems to have caused an increase in the number of burn victims (Murphy et al. 2007).
While it may seem strange that the amount of waste produced does not depend on income, first of all note that Fullerton and Kinnaman (1996) in their empirical analysis find a negative relation between waste and income instead of the expected positive relation. This is difficult to reconcile with a theoretical framework of waste producing goods and non-waste producing goods. The theoretical model employed in Fullerton and Kinnaman (1993), which explicitly considers the option to recycle, predicts that low-income households with their low opportunity cost recycle more. This would lead to a positive relation between waste and income. Our results only require that DIFTAR is more effective in reducing waste than a lump-sum tax, which is always true when both forms of taxation yield the same revenue.
Due to an ongoing process of municipal reorganization, as of January 1, 2019, only 354 municipalities will remain. Nonetheless, we opt to refer to institutional details in the present tense.
Dumping in some areas already occurs even though there are no monetary cost of throwing a bag in the bin.
There used to be more than 1000 municipalities in the Netherlands, some having less than 500 inhabitants. In recent decades the Dutch government has striven to increase the size of municipalities.
The Wadden-islands off the northern coast (Texel, Vlieland, Terschelling, Ameland and Schiermonnikoog, each of which is a separate municipality) do not share a land border with any other municipality and therefore have been left aside in this study.
There is a great deal of policy synchronizing in the years leading up to a merger. Therefore treating municipalities, that are to merge, as if they have already merged seems to be the natural choice.
Note that \(W_{ii}=0\) and that \(\sum _{j}W_{ij}=1\) for all municipalities. The \((462\times 462)\) matrix \(W\equiv \{W_{ij}\}_{i,j=1}^{462}\) is symmetric in the sense that \(W_{ij}>0 \iff W_{ji}>0\), but not in the sense that \(W=W^\top \).
The PvdA is a social democratic party comparable to the British Labour Party, GroenLinks (literally GreenLeft) is a left-wing environmental party, SP is a socialist party.
CDA is the mainstream christian-democratic party, both SGP and ChristenUnie represent orthodox protestants.
In North-Brabant and especially Limburg, the two provinces where most DIFTAR municipalities are situated, in local elections mainly local parties participate.
See Cameron and Trivedi (2005, Ch. 17) for an excellent overview. Up to now municipalities that adopted DIFTAR did not abandon it later.
References
Allers, M., & Elhorst, P. (2005). Tax mimicking and yardstick competition among local governments in the Netherlands. International Tax and Public Finance, 12, 493–513.
AOO (2004). Eerste hulp bij discussie over DIFTAR.
Ashworth, J., Geys, B., & Heyndels, B. (2006). Determinants of tax innovation: The case of environmental taxes in Flemish municipalities. European Journal of Political Economy, 22, 223–247.
Baltagi, B. H., LeSage, J. P., & Pace, R. K. (2017). Spatial Econometrics: Qualitative and limited dependent variables (advances in econometrics) (Vol. 37). Bingley: Emerald Group Publishing Limited.
Besley, T., & Case, A. (1995). Incumbent behavior: Vote-seeking, tax-setting, and yardstick competition. American Economic Review, 85, 25–45.
Brown, R., & Rork, J. (2005). Copycat gaming: A spatial analysis of state lottery structure. Regional Science and Urban Economics, 35, 795–807.
Cameron, C. A., & Trivedi, P. K. (2005). Microeconometrics. U.S.:Methods and applications. Cambridge: Cambridge University Press.
Case, A., Rosen, H., & Hines, J. (1993). Budget spillovers and fiscal policy interdependence. Journal of Public Economics, 52, 285–307.
Ciccarelli, C., & Elhorst, J. P. (2017). A dynamic spatial econometric diffusion model with common factors: The rise and spread of cigarette consumption in Italy. Regional Science and Urban Economics,. https://doi.org/10.1016/j.regsciurbeco.2017.07.003.
Dijkgraaf, E. (2004). Regulating the Dutch waste market. Ph.D. thesis, Erasmus University Rotterdam.
Dijkgraaf, E., & Gradus, R. (2003). Cost savings of contracting out refuse collection. Empirica, 30, 149–161.
Elhorst, J. P. (2014). Spatial econometrics: From cross-sectional data to spatial panels. Heidelberg: Springer.
Elhorst, J. P., Heijnen, P., Samarina, H., & Jacobs, J. P. A. M. (2017). State transfers at different moments in time: A spatial probit approach. Journal of Applied Econometrics, 32, 422–439.
Fullerton, D. & Kinnaman, T. (1993). Garbage, recycling and illicit burning and dumping. NBER Working Paper No. 4374.
Fullerton, D., & Kinnaman, T. (1996). Household responses to pricing garbage by the bag. American Economic Review, 86, 971–984.
LeSage, J. P., & Pace, R. K. (2009). Introduction to spatial econometrics. Boca Raton: Chapman&Hall/CRC.
Liesenfeld, R., Richard, J.-F., & Vogler, J. (2017). Likelihood evaluation of high-dimensional spatial latent gaussian models with non-gaussian response variables. In B. H. Baltagi, J. P. LeSage, & R. K. Pace (Eds.), Spatial Econometrics: Qualitative and limited dependent variables (advances in econometrics) (Vol. 37, pp. 35–77). Bingley: Emerald Group Publishing Limited.
Linderhof, V., Kooreman, P., Allers, M., & Wiersma, D. (2001). Weight-based pricing in the collection of household waste: The Oostzaan case. Resource and Energy Economics, 23, 359–371.
Murphy, S., Davidson, C., Kennedy, A., Eadie, P., & Lawlor, C. (2007). Backyard burning. Journal of Plastic and Reconstructive Surgery,. https://doi.org/10.1016/j.bjps.2006.11.033.
Salmon, P. (1987). Decentralisation as an incentive scheme. Oxford Review of Economic Policy, 3, 24–43.
Tiebout, C. (1956). A pure theory of local expenditures. Journal of Political Economy, 64, 416–424.
Walker, J. (1969). The diffusion of innovations among the American states. American Political Science Review, 63, 880–899.
Author information
Authors and Affiliations
Corresponding author
Additional information
Maarten Allers and Eduard Gerritsen are much obliged for providing the data and background knowledge of municipal politics and organization. The authors would also like to thank Peter Kooreman, Bert Schoonbeek, and participants of several conferences for helpful comments. Financial support by the Netherlands Organization for Scientific Research (NWO) is gratefully acknowledged.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Heijnen, P., Elhorst, J.P. The Diffusion of Local Differentiated Waste Disposal Taxes in the Netherlands. De Economist 166, 239–258 (2018). https://doi.org/10.1007/s10645-018-9321-3
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10645-018-9321-3