Teacher Literacy and Numeracy Skills: International Evidence from PIAAC and ALL

Abstract

Using the OECD-studies PIAAC and ALL, this paper shows that teachers on average have better literacy and numeracy skills than other respondents in almost all of the 15 countries in the samples. In most countries, teachers outperform others in the bottom percentiles, while in some countries they perform better than others throughout the skill distribution. These results imply that the scope to improve teachers’ skills varies between countries and that policy makers should take the shape of the skills distribution into account when designing interventions in order to most efficiently raise teachers’ skills.

1 Introduction

Teachers are essential for the development of human capital in society. Their skills are formed in teacher training programs, but are also highly influenced by the type and overall quality of the students who enter these programs and become teachers. Understanding which segment of the population is part of the teacher corps is important in order to determine the focus of interventions which can improve the quality of teachers.

This paper compares the dispersions of literacy and numeracy skills of primary and secondary school teachers relative to those of other respondents. We use international data of 15 different countries from the Programme for the International Assessment of Adult Competencies (PIAAC) and the Adult Literacy and Lifeskills Survey (ALL), both conducted by the OECD. These data sets are representative samples of the adult population in various countries. They include reading and math test scores, and contain detailed information about occupations. For each country, we compare average math and literacy skills between teachers and other respondents, and we investigate differences at the $10{\mathrm{th}}$ and $90{\mathrm{th}}$ percentiles of the distributions.

In virtually all countries, both primary and secondary school teachers score on average higher on literacy and numeracy tests than the country average. Secondary school teachers score higher than primary school teachers on both skill measures. Our analyses of the differences in skill distributions between teachers and others show that the lowest scoring teachers significantly outperform the lowest scoring other respondents both on literacy and numeracy tests. At the top of the distributions, we find that the best secondary school teachers are not strongly outperformed by the best other respondents, and that the best primary school teachers score only slightly lower than the best other respondents.

The extent to which low scoring teachers outperform other low scoring respondents differs substantially across countries. For instance, in the Netherlands, primary school teachers at the $10{\mathrm{th}}$ percentile perform much better than other respondents at the $10{\mathrm{th}}$ percentile, while in Denmark, primary school teachers at the $10{\mathrm{th}}$ percentile do not outperform other respondents at the $10{\mathrm{th}}$ percentile that strongly. In Denmark, it might therefore be an effective policy to focus on the bottom of the distribution (e.g., by raising barriers to enter into teaching, or focusing training on the worst teachers), while in the Netherlands little can be gained in becoming more restrictive at the lower end.

The main message of the paper is that it is important to investigate the shape of the relative skill distributions in addition to the differences in average skills when designing policy to improve the teacher corps. Our results persist when restricting the comparison to the tertiary educated subsample. The results are not driven by age or gender, and are not sensitive to the inclusion of measures for the frequency of skill use.

This paper contributes to the literature on teacher characteristics and teacher quality. Teacher quality has been recognized as one of the most important determinants of educational productivity (Hanushek 2011; Barber and Mourshed 2007). Hanushek (1992) finds that being taught by a high quality teacher results on average in 1.5 years’ worth of progress in one academic year, while being taught by a low quality teacher results on average in 0.5 years’ worth of progress. Although the exact characteristics of teacher quality are not well-defined (Hanushek and Rivkin 2006), teachers’ skills as measured by scores on achievement tests have been found to be associated with educational productivity (Metzler and Woessmann 2012; Eide et al. 2004). Hanushek et al. (2014) furthermore show that teachers’ cognitive skills are an important factor in explaining international differences in student performance.

While such studies explore how the relative differences between individuals within the teaching population relate to educational outcomes (e.g., Hanushek 2003; Rivkin et al. 2005) and long-term economic outcomes (e.g., Chetty et al. 2014; Hanushek 2011), our study addresses international differences in the dispersion of math and language skills of teachers relative to others. Investigating the differences in the distribution rather than the average skill level allows us to pinpoint the focus of potential policy interventions that aim to improve the quality of teachers. Our analysis reveals that the focus of interventions should lie on different parts of the distribution of skills in different countries.

The remainder of this paper is organized as follows. Section 2 explains the relationship between skill dispersions and policy interventions. Section 3 describes the data. In Sect. 4, the research strategy is discussed. Section 5 gives the results. Section  6 shows several robustness checks and Sect. 7 concludes.

2 Skill Dispersions and Policy Interventions

In the analysis, we investigate math and language skill dispersions of teachers relative to the dispersions of the skills of others in society. These relative dispersions give an indication at which part of the distribution teachers perform relatively well, and where they perform worse than others. Potential policy interventions which aim to increase teacher skills can take different forms, e.g. increasing wages, installing entry barriers, training the current teacher force, or improving the training of new teachers in teacher colleges. A key aspect in each of these examples is that there is an implicit or explicit choice to improve teachers’skills in some part of the distribution.

The costs of these policy measures vary highly. Increasing the wage for all teachers for instance is very costly, especially if the aim is to raise the level of low skilled teachers only. A cheaper and probably more effective solution for countries with a large percentage of low skilled teachers might be to install entry barriers or intensify elementary training programs. In a situation where the lowest skilled teachers already perform relatively well on basic skills, it may make more sense to provide training that adds value to highly skilled teachers. To conclude, getting insight into the dispersion of skills in a country helps to form a decision about which part of the distribution should be targeted and about which tools can be most effective and efficient to reach the target.

In order to show the relative skill dispersions, we compute the score on a measure of a skill (numeracy, literacy) for each percentile of (1) the distribution of the skills for teachers only and (2) the distribution of skills of other respondents, and then subtract these two distributions. The results can be plotted in a figure, such as Fig. 1A. The horizontal axis displays the percentile of the distribution and the vertical axis displays the difference in the score on the measure of the skill between teachers and others. A positive difference at the first percentile implies that teachers in the first percentile of the teacher distribution score higher than other respondents in the first percentile of their distribution.

Fig. 1

A Hypothetical relative skill distributions: differences at all percentiles. B Hypothetical relative skill distributions: differences at the $10{\mathrm{th}}$ percentile

Figure 1A illustrates four hypothetical relative skill distributions.¹ In the first scenario, represented by the horizontal line at zero, teachers and non-teachers are equally skilled across the entire distribution. The lowest scoring teachers are as skilled as the lowest scoring non-teachers, and the highest scoring teachers are as skilled as the highest scoring non-teachers. In this scenario, a possible policy suggestion to increase the average quality of teachers may be to implement entry barriers to avoid low-skilled teachers from entering. Another policy suggestion is to give teachers better training, either in school or in the labor market.

Increasing barriers to entry might result in a situation such as scenario 2, represented by the uninterrupted convex line. In this situation, teachers outperform the rest of the population mainly in the lower parts of the distribution. Policies aimed at increasing the quality of the lowest skilled teacher by becoming even more selective might result in teacher shortage, and in this case, policies aimed at increasing the attractiveness of the teaching profession for highly skilled individuals might be more effective to increase the quality of the teacher corps.

In scenario 3, represented by the dashed line at one, teachers outperform non-teachers consistently across the entire distribution. Here, teaching appears to be an attractive alternative for people across the full skill distribution. Highly skilled people are sorting into the profession, preferring teaching jobs over non-teaching jobs. An effective policy option may be to install entry barriers for lower skilled people, allowing more highly skilled people to enter the profession and increasing overall quality. In this scenario, however, the teachers are already skilled above average across the board, which raises the question whether the costs associated with intervening would be worth the benefits.

Scenario 4 is the opposite of scenario 3 in the sense that represented teachers are consistently outperformed by non-teachers across the entire distribution. This would imply that at any given level of skills, people choose a different occupation rather than the teaching profession. In this case, making the profession more attractive for people across the distribution (e.g., by raising wages) may be most effective.

These examples show the importance of investigating skill distributions above and beyond analyzing differences in means only: if we would only investigate average teacher quality, scenario 2 and scenario 3 would lead to similar conclusions. Looking at the distributions is more informative because it allows policy makers to design interventions aimed at a specific part of the distribution, which will be more effective and efficient than untargeted interventions. The differences in relative skill distributions across countries also give an indication of the result of different standing policies regarding teacher recruitment and teacher training and serve to illustrate why policies to attract better teachers need to differ between countries.

Figure 1A shows the differences in scores between teachers and others at all percentiles. In order to reduce complexity, we report the differences in scores in the analyses only at the mean, $10{\mathrm{th}}$ percentile, and $90{\mathrm{th}}$ percentile. This is shown in Fig. 1B, which displays the difference between teachers and non-teachers at the $10{\mathrm{th}}$ percentile only.

3 Data

We combine data from the Programme for the International Assessment of Adult Competencies (PIAAC) and the Adult Literacy and Lifeskills Survey (ALL), both conducted by the OECD. These surveys were designed to measure adult skills and competencies across different countries. In this section, we describe the ALL and PIAAC dataset, and provide descriptive statistics.

3.1 The ALL Data

The ALL measured literacy and numeracy skills of nationally representative samples of 16–65 year olds in participating countries in two rounds. The first round was conducted in 2003 and the second round was conducted between 2006 and 2008. The six countries that took part in the first round were Canada, Italy, Norway, Switzerland, the United States, and Bermuda. In the second round, Australia, Hungary, the Netherlands, and New Zealand participated. The ALL study is the successor of the International Adult Literacy Survey (IALS), which was the first international comparative survey of adult skills undertaken between 1994 and 1998.² Measured skills in the ALL survey include prose literacy, document literacy, numeracy, and problem solving. Literacy was defined as “the knowledge and skills needed to understand and use information from texts and other written formats.” Numeracy was defined as “the knowledge and skills required to manage mathematical demands of diverse situations.”

3.2 The PIAAC Data

PIAAC measures skills in three domains: literacy, numeracy and problem solving in technology-rich environments. PIAAC has two cycles of assessment: the first cycle is conducted in two rounds, while the second cycle is expected to take place from 2018 to 2023. The first round of the first cycle took place from January 2008 to October 2013. We use data from the first round of the first cycle. The countries that took part in the first round of the first cycle were Australia, Austria, Belgium, Canada, Cyprus, Czech Republic, Denmark, Estonia, Finland, France, Germany, Ireland, Italy, Japan, Korea, the Netherlands, Norway, Poland, Russia, the Slovak Republic, Spain, Sweden, the United Kingdom and the United States.

3.3 Merging the Datasets and Descriptive Statistics

We identify teachers based on their 4 digit ISCO-88 occupation code.³ The occupation codes allow us to distinguish between primary and secondary school teachers. For some countries, no teachers are present in the dataset or the occupation code is not detailed enough to correctly identify them. We exclude these countries from our analyses. The countries that are dropped are Australia, Austria, Canada, Cyprus, Estonia, Finland, Germany, Ireland, Sweden, and the United States.

Table 1 shows the summary statistics by country. Italy, Norway and the Netherlands have most respondents; these are also the countries which were sampled in both PIAAC and ALL. In most countries there is approximately an equal amount of men and women in the samples. The Russian data are not representative for the entire population as inhabitants of the Moscow municipal area were not included in the PIAAC survey. For this reason, we exclude Russia from our analyses.

The number of tertiary educated people differs substantially across countries. This implies that in our analyses, it is better to relate the skills of teachers to all other respondents in a country than to the tertiary educated sub-sample only. In a robustness check, we nonetheless make the latter comparison.

Table 1 Sample characteristics per country

Table 2 shows the number of teachers and the number of primary and secondary school teachers per country sample. The Netherlands, Denmark, Norway, New Zealand, and the United Kingdom have relatively many teachers in their sample, while in other countries like Bermuda, Switzerland and Japan few teachers were sampled. For these latter countries our results are less generalizable to the entire teacher population. In our analyses, we will therefore restrict our sample to those countries for which more than 50 primary or secondary school teachers can be identified.⁴ Practically, this means that when analyzing primary school teachers Japan, Korea, Bermuda and Switzerland will be excluded. When analyzing secondary school teachers we exclude Japan, Korea, Bermuda, Denmark, Slovakia and the Czech Republic.

Tables 1 and 2 reveal that the average teacher is somewhat older than the average respondent. They are also more highly educated on average and the proportion of women is higher for teachers. In robustness analyses, we control for these differences.

Both the ALL and PIAAC surveys measure the skill domains on a 0–500-point scale. While ALL and PIAAC both aim to measure the same skills and use the same measurement scale, they do not employ the same tests. In order to be able to pool the two datasets, we standardize the test results based on the full sample, so that they have a mean of 0 and a standard deviation of 1.⁵

Table 2 Number of teachers in the sample by country and teacher demographics

Table 3 shows the mean and standard deviation for the skills in all countries that have teachers in the sample. The results are depicted separately for all respondents and for teachers only. For each country, the mean test score of teachers is higher than the average score of all respondents.

This table reveals the differences in the absolute skill level for teachers between countries. In this article, we study the relative differences of skill levels between teachers and others within countries in order to indicate which segment of the population has become a teacher. We choose to focus on relative differences within a country because we are interested in studying the scope for improvement of the skill level of the teacher population. I.e., if the teacher population is relatively low skilled, then it will be more feasible to improve its skill level because there is a large pool of other people in society which may be induced to become a teacher. If this pool is smaller, improving the teachers’ skill level is less feasible.

However, the absolute differences of skill levels for teachers between countries also provide an important source of information. Policy to improve teacher skills will partly depend on a minimal required skills level. Hence, the interplay between absolute and relative skill levels is policy relevant. Using the table, we can see that literacy and numeracy levels of teachers are lowest in Italy, while Japanese teachers score highest. Teachers in the Netherlands score very highly both on the literacy and numeracy tests relative to teachers in other countries.

Table 3 Mean and standard deviation of test scores by country

4 Methodology

To compare the average skills of teachers to those of the other respondents, we respectively regress literacy and numeracy scores on a dummy for being a primary school teacher. We do these analyses for each country separately. We perform a similar set of regressions on a dummy for being a secondary school teacher. This yields the difference in test scores between teachers and other respondents, expressed in standard deviations. We use full sample weights present in the datasets to account for sampling bias and to ensure our results are representative for the population. We generate bar charts to graphically represent teacher skill levels compared to the country average levels. In the baseline analyses, we do not control for other variables. In robustness analyses, we do control for potential confounders.

Next, we investigate the shape of the distributions. We show this by plotting differences in scores at the $10{\mathrm{th}}$ percentile and the $90{\mathrm{th}}$ percentile on the measure of a skill (numeracy, literacy) between non-teachers and primary and secondary school teachers, respectively.

We perform several robustness checks. Because most countries require their teachers to be relatively highly educated, we compare teachers with the college educated part of the population for each country. These results should be interpreted with caution since the percentage of individuals with a tertiary education differs substantially between countries (see also Table 1). Still, it is instructive to see whether our results could be explained purely by differences in educational attainment.

Another interesting question is whether differences in skills are driven by selection or whether these are due to the nature of the profession. Teachers are likely to use their literacy and numeracy skills more than others. Therefore, our results could reflect frequency of use rather than innate ability. To address this possible alternative explanation, we present regression adjusted graphs where we control for skill use at the workplace.

In each graph, we highlight the Netherlands because we use this country as an example to describe the results.

5 Results

5.1 Differences in the Averages of Skills

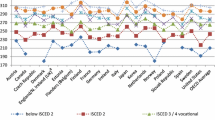
Figure 2 shows how primary and secondary school teachers perform on literacy and numeracy skills compared to the rest of the population per country. In virtually all countries, teachers significantly outperform the average other respondent on both skill measures. The difference is slightly larger for secondary school teachers.⁶

Fig. 2

Mean skill difference: teachers vs. other respondents Note: Bars indicate the mean test score difference in standard deviations between teachers and non-teachers for each country on the horizontal axis. The error bars indicate the 95 % confidence interval. Differences were calculated using full sample weights

The graphs in Fig. 2 suggest that the scores for numeracy and literacy are highly related. To test the relationship, we calculate the correlation between literacy and numeracy skills for non-teachers, primary school teachers and secondary school teachers separately. These results can be found in Table 4. As expected, literacy and numeracy skills are highly correlated within individuals.

Table 4 Correlation between Literacy and Numeracy scores for non-teachers, primary school teachers and secondary school teachers

5.2 Differences in the Distribution of Skills

As argued in Sect. 2, the shape of the skill distribution can be more informative for policy makers than the average skill level, as different distributions might warrant different interventions. For each available country, we depict the test scores at the $10{\mathrm{th}}$ and $90{\mathrm{th}}$ percentiles for teachers and non-teachers.

Fig. 3

Differences in literacy and numeracy scores at the $10{\mathrm{th}}$ and $90{\mathrm{th}}$ percentile for primary school teachers

Note: Bars indicate the test score difference at the $10{\mathrm{th}}$ and $90{\mathrm{th}}$ percentile in standard deviations between primary school teachers and non-teachers for each country on the horizontal axis. Differences were calculated using full sample weights

Figure 3 shows the difference between primary school teachers and others in society at the $10{\mathrm{th}}$ and $90{\mathrm{th}}$ percentiles for literacy and numeracy skills. For both skills, primary school teachers at the $10{\mathrm{th}}$ percentile strongly outperform the other respondents at the $10{\mathrm{th}}$ percentile in most countries. Interestingly, primary school teachers at the $90{\mathrm{th}}$ percentile are not outperformed by the non-teachers at the $90{\mathrm{th}}$ percentile, suggesting that there are some very highly skilled teachers. Given that wages for teachers are substantially lower than potential private sector wages at the high end of the skills distribution (Chevalier et al. 2007; Stinebrickner 2001), these results suggest that non-pecuniary factors (e.g. job security, secondary benefits, intrinsic motivation) may play an important role in the decision to become a teacher for highly skilled people. In Fig. 4, we show the results focusing on secondary school teachers. The results are similar to those found for primary school teachers.

Fig. 4

Differences in literacy and numeracy scores at the $10{\mathrm{th}}$ and $90{\mathrm{th}}$ percentile for secondary school teachers

Note: Bars indicate the test score difference at the $10{\mathrm{th}}$ and $90{\mathrm{th}}$ percentile in standard deviations between secondary school teachers and non-teachers for each country on the horizontal axis. Differences were calculated using full sample weights

These findings provide a guideline for policy makers who design interventions aimed at increasing the average skill level of teachers. For example, if we compare the results from Denmark and the Netherlands in Fig. 2, we see that the average primary school teacher outperforms the average respondent in both countries (this difference is smaller in Denmark than in the Netherlands). Comparing the average difference across countries is informative for descriptive purposes, but for policy makers it is much more relevant to know at which part of the skill distribution the differences are most apparent. As argued in Sect. 2, different shapes of the distribution warrant different kinds of interventions. When looking at the differences at the $10{\mathrm{th}}$ and $90{\mathrm{th}}$ percentile in Fig. 3, we see that in the Netherlands the primary school teachers at the $10{\mathrm{th}}$ percentile perform very well compared to the $10{\mathrm{th}}$ percentile of other respondents, while in Denmark primary school teachers at the $10{\mathrm{th}}$ percentile are not that much better than the $10{\mathrm{th}}$ percentile of other respondents. At the $90{\mathrm{th}}$ percentile the relative performance of primary school teachers in the two countries is much more similar. By looking at the skills dispersions, we may conclude that in Denmark an effective policy appears to be to focus on the bottom of the distribution (e.g., by raising barriers to entry into teaching), while in the Netherlands there is little to be gained in becoming more restrictive at the lower end. This example clearly shows the benefit of analyzing differences in distributions relative to differences in means as the conclusions could not have been drawn if only country means were compared.

It is interesting to investigate whether the order of the countries in the graphs above is similar for numeracy and literacy scores. The order of the scores may be different, for instance, because some countries prioritize numeracy skills over literacy skills in their education system. This preference could be reflected in the relative skills of their teachers. It is important to take into account different orderings of the countries, as policy recommendations become less clear-cut when relative literacy and numeracy scores differ strongly. For example if low literacy scores are accompanied by high numeracy scores it is unclear whether interventions aimed at the bottom of the distribution would be effective in raising teaching quality as much as when low literacy is accompanied by low numeracy. Furthermore, if countries prioritize numeracy, low scores on literacy may not warrant any corrective intervention. In Table 5, we investigate the correlations of the differences at the $10{\mathrm{th}}$ or $90{\mathrm{th}}$ percentile for numeracy and literacy skills. It appears that the differences at the $10{\mathrm{th}}$ percentile of literacy scores are highly correlated with the $10{\mathrm{th}}$ percentile differences in numeracy scores, both for primary and secondary school teachers. This implies that at the $10{\mathrm{th}}$ percentile, the order of the countries is similar for the numeracy and literacy scores. At the $90{\mathrm{th}}$ percentile, the results for literacy and numeracy skills correlate substantially for primary school teachers but less so for secondary school teachers. This suggests that within countries the relative literacy and numeracy skills of teachers are quite strongly related.

Table 5 Correlations of the differences in skills between teachers and non-teachers at the $10{\mathrm{th}}$ and $90{\mathrm{th}}$ percentiles

Fig. 5

Mean skill difference of teachers vs. tertiary educated subsample per country, controlling for age and gender

Note: Bars indicate the mean test score difference in standard deviations between teachers and non-teachers for each country on the horizontal axis. The error bars indicate the 95 % confidence interval. Differences were calculated using full sample weights using only the tertiary educated subsample and controlling for age and gender

Fig. 6

Differences in literacy and numeracy scores at the $10{\mathrm{th}}$ and $90{\mathrm{th}}$ percentile: primary school teachers vs. highly educated

Note: Bars indicate the test score difference at the $10{\mathrm{th}}$ and $90{\mathrm{th}}$ percentile in standard deviations between primary school teachers and tertiary educated non-teachers for each country on the horizontal axis. Differences were calculated using full sample weights and controlling for age and gender

Fig. 7

Differences in literacy and numeracy scores at the $10{\mathrm{th}}$ and $90{\mathrm{th}}$ percentile: secondary school teachers vs. highly educated

Note: Bars indicate the test score difference at the $10{\mathrm{th}}$ and $90{\mathrm{th}}$ percentile in standard deviations between secondary school teachers and tertiary educated non-teachers for each country on the horizontal axis. Differences were calculated using full sample weights and controlling for age and gender

6 Robustness

6.1 Comparison with the Tertiary Educated

In order to become a teacher, one must have a certain level of education. In most countries, only people with a tertiary degree are eligible for teaching jobs (OECD 2014). One may therefore argue that it could be meaningful to restrict our analyses to that part of the sample which has a tertiary degree. Notice, however, that the percentage of people with a tertiary education differs dramatically between countries. Therefore, in our baseline analyses, we compare teachers’ skills to those of all other respondents instead of only tertiary educated respondents. In this robustness check, we restrict the sample to the tertiary educated. Additionally, we add controls for gender and age.

Figure 5 compares the average scores between teachers and tertiary educated other respondents. We find mixed results. Primary school teachers in Japan, South Korea and the UK significantly outperform the average tertiary educated respondent on both skill measures. Interestingly, in almost none of the countries primary school teachers score significantly below average. This suggests that in the countries we observe, teachers are not recruited from the lower part of the college graduate skill distribution. Our findings contrast with earlier results from studies in the United States that showed that the average teacher is less skilled than the average college graduate (e.g., Hanushek and Pace 1995; Bacolod 2007). For secondary school teachers, the results are even more pronounced. In New Zealand, the UK, Norway and Spain, secondary school teachers outperform the average tertiary educated respondent on both skill measures and secondary school teachers do not score significantly lower than others on either skill measure in any country.

It is also instructive to look at the difference in the distribution of skills between teachers and non-teachers who have finished tertiary education. The graphs depicting these analyses can be found in Figs. 6 and 7. The combined findings in Figs. 5, 6 and 7 suggest that the average teacher is approximately as skilled as the average college graduate. The differences in average test scores we observe in some countries are mainly due to teachers outperforming other graduates in the bottom of the distribution, while in the top of the distribution, (especially secondary school) teachers keep up with the best scoring other graduates.

6.2 Controlling for Differences in Skill Use

One potential concern with our results is that literacy and numeracy might be skills that sustain or improve because they are used at work. The nature of their profession may make it more likely that teachers use these skills more often than others. This could mean that their higher performance relative to the rest of the population is driven by experience rather than innate ability. PIAAC and ALL allow us to check for this alternative explanation. Both surveys ask respondents a variety of questions regarding the frequency of their literacy and numeracy skill use in the workplace. Table 6 shows the correlations of the differences at the $10{\mathrm{th}}$ and $90{\mathrm{th}}$ percentile for numeracy and literacy between the original results and the results when controlling for frequency of skill use, age and gender. This allows us to see whether the results are stable across the different specifications.

Table 6 Correlations of the differences in skills between teachers and non-teachers at the $10{\mathrm{th}}$ and $90{\mathrm{th}}$ percentiles between the original results and the results when controlling for skill use, age and gender

The table shows that the differences are highly correlated across both specifications. For primary school teachers, the order of the countries is very similar for the $10{\mathrm{th}}$ percentile of both skill measures and the $90{\mathrm{th}}$ percentile of literacy. The $90{\mathrm{th}}$ percentile for numeracy differs slightly between the two specifications. For secondary school teachers, the order of the countries is very similar for all of our outcomes of interest. In absolute terms, controlling for skill use, age and gender decreases the difference between teachers and the rest of the population mainly in the lower part of the distribution. Teachers still outperform the other respondents across the main part of the distribution. These results can be seen in Figs. 9, 10 and 11 of the appendix.

Note that skill use and raw ability are most likely not independent. Skilled people probably sort into jobs in which they can utilize their talents. Also, highly educated people tend to sort into professions where literacy and numeracy skills are more likely to be needed. To show that skill use is not merely a proxy for educational attainment, we also created correlation tables comparing teachers to the tertiary educated subset of the population controlling for frequency of skill use. These results can be found in Table 7. The results are qualitatively similar as the baseline results: the differences between teachers and other college graduates do not appear to be driven by differences in use of literacy and numeracy skills in the workplace. The absolute differences between teachers and other tertiary educated respondents when controlling for skill use can be seen in Figs. 12, 13 and 14 of the appendix. Controlling for skill use increases the performance of both primary and secondary school teachers relative to others in numeracy but decreases it in literacy across the distribution. This could be an indication that teachers use their literacy skills relatively more than their numeracy skills compared to the rest of the working age population.

Table 7 Correlations of the differences in skills between teachers and tertiary educated non-teachers at the $10{\mathrm{th}}$ and $90{\mathrm{th}}$ percentiles between the original results and the results when controlling for skill use, age and gender

7 Conclusions and Policy Implications

We investigated teachers’ relative literacy and numeracy skills in 15 countries, using the OECD’s PIAAC and ALL datasets. We not only analyzed differences in average skills, but also focused on differences in the distribution of skills. Our main conclusions are that the skill distributions differ between countries and that these differences are more informative for policy makers than average teacher skills.

We find that in virtually all countries, teachers are more highly skilled than the average respondent. Looking at the differences in the skills distributions, we find that in most countries teachers outperform the average respondent mainly in the lower percentiles of the distribution. The lowest scoring teachers perform better than the lowest scoring other respondents. These findings hold when restricting the analyses to the tertiary educated subsample and controlling for skill use, age and gender. The results are robust across the ALL and PIAAC data sets.

The extent to which teachers outperform other respondents in the lower parts of the distribution varies between countries. This variation is informative for policy makers aiming to increase teacher quality. Interventions focusing on the bottom part of the distribution will, for instance, be less effective in countries in which the difference in the lower parts of the distribution between teachers and others is already large. Such interventions can be more effective in countries where these differences are close to zero or negative.

Considering that earnings for teachers compared to potential earnings in the private sector are relatively low (Stinebrickner 2001), the finding that the best teachers are not outperformed by the best non-teachers is a result which suggests that non-pecuniary factors may motivate these highly skilled people to enter the teaching profession. For policy makers, it is relevant to investigate what drives these highly skilled individuals to become a teacher. If some of these factors can be identified, attempting to select on these factors may prove a cost-effective way to attract more highly skilled individuals into the teaching corps. This could potentially allow policy makers to increase average teacher quality without having to resort to costly salary increases.

While our policy recommendations are based on teachers’ relative skills, there are other facets that need to be taken into account when deciding on a specific intervention. For example costs and feasibility may differ vastly between interventions. A policy intervention that may be optimal from a skills distribution perspective may not be optimal in terms of other factors. Increasing barriers to entry may for example lead to teacher shortages, while increasing pay for high skilled teachers may create inequality between teachers and decrease overall teacher job satisfaction. Nevertheless, the shape of the current teachers’ skills distribution is important information to consider in order to accurately predict the costs and benefits of any policy intervention.

The substantial variation in the skill dispersion across the different countries leads to the conclusion that different interventions are likely to be optimal in different countries. In countries where the teachers with the lowest skills do not outperform the low skilled other college graduates (e.g., Denmark), interventions like increased barriers to entry might be more cost-effective than trying to aim at the top of the distribution. However, in countries where the lowest skilled teachers are already performing relatively well there is less scope for improvement at the bottom and shifting focus to the top end of the distribution might be more efficient. All in all, we conclude that it is important to take the shape of the skills distribution into account when designing policies aimed at improving teacher skills.

Fig. 8

Comparing the difference in distributions for PIAAC and ALL for the Netherlands

Note: Percentile graphs depicting the difference in the distribution of skills of teachers and all non-teachers for the Netherlands (the graphs for Italy and Norway are available upon request). The uninterrupted (interrupted) line depicts the scores in PIAAC (ALL). All differences are in standard deviations from the full sample standardized test scores. Results were calculated using full sample weights

Fig. 9

Regression adjusted mean skill difference of teachers vs. other respondents

Note: Bars indicate the mean test score difference in standard deviations between teachers and non-teachers for each country on the horizontal axis adjusted for frequency of skill use. The error bars indicate the 95 % confidence interval. Differences were calculated using full sample weights

Fig. 10

Regression adjusted differences at the $10{\mathrm{th}}$ and $90{\mathrm{th}}$ percentile of primary school teachers vs. non-teachers

Note: Bars indicate the test score difference at the $10{\mathrm{th}}$ and $90{\mathrm{th}}$ percentile in standard deviations between primary school teachers and non-teachers for each country on the horizontal axis adjusted for frequency of skill use in the workplace. Differences were calculated using full sample weights

Fig. 11

Regression adjusted differences at the $10{\mathrm{th}}$ and $90{\mathrm{th}}$ percentile of secondary school teachers vs. non-teachers

Note: Bars indicate the test score difference at the $10{\mathrm{th}}$ and $90{\mathrm{th}}$ percentile in standard deviations between secondary school teachers and non-teachers for each country on the horizontal axis adjusted for frequency of skill use in the workplace. Differences were calculated using full sample weights

Fig. 12

Regression adjusted mean skill difference teachers vs. tertiary educated other respondents

Note: Bars indicate the mean test score difference in standard deviations between teachers and tertiary educated non-teachers for each country on the horizontal axis adjusted for frequency of skill use and controlling for age and gender. The error bars indicate the 95 % confidence interval. Differences were calculated using full sample weights

Fig. 13

Regression adjusted differences at the $10{\mathrm{th}}$ and $90{\mathrm{th}}$ percentile of primary school teachers vs. tertiary educated non-teachers

Note: Bars indicate the test score difference at the $10{\mathrm{th}}$ and $90{\mathrm{th}}$ percentile in standard deviations between primary school teachers and tertiary educated non-teachers for each country on the horizontal axis adjusted for frequency of skill use in the workplace. Differences were calculated using full sample weights and controlling for age and gender

Appendix: Additional Results

See Figs. 8, 9, 10, 11, 12, 13 and 14.

Fig. 14

Regression adjusted differences at the $10{\mathrm{th}}$ and $90{\mathrm{th}}$ percentile of secondary school teachers vs. tertiary educated non-teachers

Note: Bars indicate the test score difference at the $10{\mathrm{th}}$ and $90{\mathrm{th}}$ percentile in standard deviations between secondary school teachers and tertiary educated non-teachers for each country on the horizontal axis adjusted for frequency of skill use in the workplace. Differences were calculated using full sample weights and controlling for age and gender