Low-Carbon Investment and Credit Rationing

Abstract

This paper develops a principal-agent model with adverse selection to analyse firms’ decisions between an existing carbon-intensive technology and a new low-carbon technology requiring an externally funded initial investment. We find that a Pigouvian emission tax alone may result in credit rationing and under-investment in low-carbon technologies. Combining the Pigouvian tax with interest subsidies or loan guarantees resolves credit rationing and yields a first-best outcome. An emission tax set above the Pigouvian level can also resolve credit rationing and, in some cases, yields a first-best outcome. If a carbon price is (politically) not feasible, intervention on the credit market alone can promote low-carbon development. However, such a policy yields a second-best outcome. The issue of credit rationing is temporary if the risks of low-carbon technologies decline. However, there are social costs of delay if credit rationing is not addressed.

1 Introduction

Climate change has been recognised as one of the greatest challenges in the 21st century. Limiting global warming to well below $2^{\circ }$C, as agreed under the Paris Agreement (UN 2015), will only be possible with a climate policy that is substantially more ambitious than current policies (Nordhaus 2018; Stern 2018). Without ambitious policies, the private sector lacks sufficient incentives for required investments to achieve the transition to a low-carbon economy. Emission externalities and spillovers from low-carbon innovation are the frequently discussed market failures impeding low-carbon development (Bennear and Stavins 2007; Jaffe et al. 2005; Jaffe and Stavins 1995). More recently, scholars have stressed the role of functioning financial markets for enabling low-carbon investments (Ghisetti et al. 2017; Kempa and Moslener 2017; Pahle and Schweizerhof 2016; Polzin 2017; Steckel and Jakob 2018). Financial market failures are largely caused by information asymmetries between the borrower (agent) and the lender (principal), which may result in unfavourable loan conditions or completely deter socially desirable transactions (Jaffee and Stiglitz 1993). This leads to non-optimal allocation of capital in the economy (Akerlof 1970; Stiglitz and Weiss 1981; Stiglitz 1993).

Despite the increasing evidence for deterring effects of financing constraints on low-carbon investments (see Sect. 2), theoretical analyses of this issue are lacking. However, to reach the ambitious climate targets, it is essential to understand how low-carbon investments are affected by financial markets. Can frictions on credit markets, such as information asymmetries, deter firms’ investment in low-carbon innovation and thus favour existing carbon-intensive technologies? What are the options for policymakers to address this issue? We offer a novel theoretical framework that addresses these questions.

This paper is not the first theoretical analysis considering the role of financial markets within an environmental context. Several studies focus on the effect of external financing on environmental performance of firms. Andersen (2017) analyses firms’ investments in different assets that require external borrowing. The findings indicate that credit constraints affect the asset composition of polluting firms and ultimately result in higher emission intensities. Andersen (2016, 2020) use general equilibrium frameworks to analyse the effect of credit constraints and default risks. The effect on emissions, however, is not clear from a theoretical perspective due to several confounding effects.¹ Other studies analyse the effectiveness of taxes on externalities in the presence of financial frictions (Hoffmann et al. 2017; Heider and Inderst 2022; Döttling and Rola-Janicka 2023). They show that the government can improve efficiency by combining a Pigouvian tax with a grant scheme or by setting a tax rate that differs from the Pigouvian level. A different methodological approach is chosen by D’Orazio and Valente (2019). Using a computational agent-based model, the authors find that government intervention through a public bank can reduce financing constraints and lead to more environmental innovation.

This paper contributes to the literature by proposing a novel theoretical approach that explicitly models firms’ choice between a clean and a dirty production technology with external borrowing. Rather than adding lending to an environmental model framework, we build on credit market models from the finance literature (Arping et al. 2010; Besanko and Thakor 1987; Gale 1990; Philippon and Skreta 2012). Based on Janda (2011), we develop a principal-agent model, where firms can choose between two technologies: a carbon-intensive (dirty) technology and a low-carbon (clean) technology, which requires external funding for an initial risky investment.² Due to asymmetric information, the lender (bank) cannot distinguish between different firm types, which might induce credit rationing, i.e., some firm types do not receive financing for the socially desirable investment in low-carbon technology. Another major contribution is our comparative analysis of different individual policy instruments and policy mixes. We analyse environmental policy (Pigouvian emission tax) and its combination with an intervention on the credit market through interest rate subsidies and loan guarantees. We then investigate whether either an emission tax or credit market interventions alone can effectively address both the environmental externality and credit rationing.

Our main findings are as follows. A Pigouvian emission tax incentivises high emission firms to switch to the clean technology. However, a Pigouvian tax might not be sufficient, as credit rationing may occur, which leads to a socially undesirably low level of low-carbon investment. Introducing an interest rate subsidy or a loan guarantee can successfully eliminate credit rationing, which resembles the findings of the theoretical finance literature (Arping et al. 2010; Gale 1990; Janda 2011; Minelli and Modica 2009; Philippon and Skreta 2012). Combining the Pigouvian tax with an intervention on the credit market can always yield the first-best outcome. The policymaker further has some flexibility: the tax rate can be lowered if expenditures for credit market interventions are increased and vice versa. Using only the emission tax can resolve credit rationing if the tax rate is set above the Pigouvian level and, in some cases, yields a first-best outcome. For the situation without emission tax, we show that an interest rate subsidy can promote low-carbon investment but cannot yield a first-best outcome.

The paper is structured as follows. Section 2 reviews the empirical literature on low-carbon investments and external financing (constraints). Section 3 presents the model setup and the laissez-faire and full information outcomes. Section 4 introduces information asymmetry, analyses different policy interventions, and compares their welfare impacts. Section 5 discusses the findings and derives policy recommendations before Sect. 6 concludes.

2 Financing Low-Carbon Investment

Empirical evidence suggests that access to external financing and the development of the finance sector are core drivers of low-carbon investments such as renewable energy (Ang et al. 2017; Best 2017; Brunnschweiler 2010; Haščič et al. 2015; Kim and Park 2016) or energy efficiency (Apeaning and Thollander 2013; Fleiter et al. 2012; Kostka et al. 2013). Furthermore, innovative high-tech firms face financing constraints (Carpenter and Petersen 2002), in particular clean technology firms (Howell 2017; Kempa et al. 2021; Nanda et al. 2015; Noailly and Smeets 2021; Olmos et al. 2012).

Due to their capital intensity, renewable energy investments highly rely on financial markets, in particular debt provision (Evans et al. 2009; Painuly 2001; Wiser et al. 1997).³ Non-recourse project finance structures, where debt typically covers 65–80% of the investment expenditure (McCrone et al. 2017; Pollio 1998), are frequently used to finance renewable energy investments (Steffen 2018).⁴ Long amortisation periods of 15 years or more (Couture and Gagnon 2010) foster the susceptibility to financing constraints that increases with the time horizon of the lending contract (Stiglitz 1993).

Similar to renewable energy, energy efficiency investments have high up-front costs and long amortisation periods (Gillingham et al. 2009). Information asymmetries can prevent the lender from distinguishing investments with high from those with low potential energy savings (Gillingham and Palmer 2014). Thus, credit constraints might contribute to the energy efficiency gap (Golove and Eto 1996). Access to external financing for energy efficiency investments seems less problematic in developed countries (Fleiter et al. 2012; Trianni et al. 2016), while credit rationing can be an issue in developing and emerging economies with typically less developed financial sectors (Apeaning and Thollander 2013; Kostka et al. 2013).

Clean technology firms require access to external funds to finance the initial technology investment, e.g., R&D or initial production capacities. Empirical evidence suggests that young firms using new technologies face difficulties to source debt financing (Carpenter and Petersen 2002; Guiso 1998; Revest and Sapio 2012). This is mainly driven by lenders’ information asymmetries concerning the new technologies, who may find it too costly or even impossible to assess the firms through screening. In the absence of a carbon price, new clean technologies have a double disadvantage compared to incumbent dirty technologies. In addition to information asymmetries, clean technologies’ positive externalities for the climate are often not priced appropriately (Howell 2017). Moreover, the lender is likely to be hesitant to finance innovation involving assets that are firm-specific and intangible and thus difficult to collateralise (Berger and Udell 2002; De Haas and Popov 2019). These issues are particularly pronounced in the case of clean technology firms (Erzurumlu et al. 2010; Nanda et al. 2015). Noailly and Smeets (2021) show that innovative firms specialising in clean technology are substantially more vulnerable to financing constraints than fossil fuel firms.

Transactions between lender and borrower reduce the information asymmetry. Thus, credit constraints are more likely if the borrowing firm does not have a lending relationship with a bank (Bharath et al. 2011; Jiménez and Saurina 2004; Petersen and Rajan 1995). Innovative clean energy firms tend to be rather small (Noailly and Smeets 2015) and do not have such a relationship with a lender, which renders securing debt financing more difficult.⁵ A closely related issue is the banks’ technological conservatism. If the information gathered by banks is technology specific, technological progress will erode their knowledge on mature (carbon-intensive) technologies (Minetti 2010). Hence, the lender may have an incentive not to finance new (low-carbon) technologies.

3 The Model

For our analysis, we use a principal-agent model with adverse selection. The idea of the model in a nutshell is as follows. The economy consists of three types of actors: firms, the lender (bank) providing loans for firms, and the government. The firms can choose between either an immature low-carbon (clean) or a mature carbon-intensive (dirty) technology for production. Their choice depends on the expected returns from producing with the respective technology. The immature clean technology requires an initial risky investment, which can be thought of as R&D expenditures or other costs of introducing it. This investment is financed through a loan from a bank, which has all the bargaining power in the model.⁶ The dirty technology is mature and does not require such an initial investment.⁷

Agents in the economy make the following decisions. Firms decide which technology to choose based on expected profits. Firms that chose the clean technology apply for a bank loan to finance their initial expenditure. However, firms are heterogeneous with respect to their risk, i.e., their probability of successfully introducing the clean technology, which the lender does not observe. By designing loan contracts, the bank then selects which firms to lend to. Firms that do not receive a bank loan use the dirty technology for production. In the model, all these decisions are made simultaneously.

3.1 Model Setup

In the model, the lender faces a perfectly elastic supply of funds at unit cost $\rho$. Each firm has both a dirty and a clean production technology. There are two types of clean technologies, indexed as type $c \in \left\{ s, u\right\}$, with identical output $y_{c}$. Skilled firms with s-type technologies have a higher probability of successfully investing into the clean technology compared to unskilled firms with u-type technologies: $0<\delta _{ u}<\delta _{ s}\equiv 1$.⁸ The required loan for investing is normalised to 1. $\theta _u \in (0,1)$ is the proportion of firms with u-type technologies and $1-\theta _u$ is the proportion of firms with s-type technologies in the economy. Similarly, there are two types of dirty technologies, indexed as type $d \in \left\{ l, h\right\}$. Outputs of both types are identical, $y_{d}$, but lead to different carbon emission levels. Firms with l-type technologies have lower emission levels compared to firms with h-type technologies, $e_{l}<e_{h}$. Emissions are associated with social per unit costs of $\kappa$, which we normalise to one, $\kappa \equiv 1$. $\theta _h \in (0,1)$ is the proportion of firms with h-type technologies and $1-\theta _h$ is the proportion of firms with l-type technologies. Table 1 depicts the overall four types of firms differing in their clean and dirty technologies, i.e., uh-, ul-, sh-, and sl-firms.

Table 1 Contingency table of firm types in the economy

We assume that the private net present value of using the clean technology is below the returns to using the dirty technology. From social planer’s perspective, i.e., also considering emission externalities associated with dirty production, high-emission firms (H-firms) should rather choose the clean technology, while low-emission firms (L-firms) should use the dirty technology. This setup is captured by the following assumption:

Assumption 1

      $y_{d}>y_{d}-e_{ l}>\delta _c y_{c}-\rho>y_{d}-e_{ h}> 0$.

Figure 1 illustrates this setup. Panel (a) depicts the private perspective: expected private returns from using the dirty technology ($y_{d}$) exceed those from the clean technology for all firm types, which corresponds to the left inequality in Assumption 1. The difference in expected returns from using the clean technology is due to the difference in success probabilities. Panel (b) in Fig. 1 depicts the societal perspective: here, the social costs of emissions ($e_d$) lead to lower returns from using the dirty technology. This results in higher relative returns to clean investments for H-firms, while returns from using the dirty technology are still higher for L-firms, which corresponds to the inner inequalities in Assumption 1.

Firms (borrowers) are risk neutral and have full information. The lender and the government do not observe firms’ clean and dirty technologies, and thus cannot distinguish between the types of borrowers. This information asymmetry can lead to adverse selection. Other than that, all parameters are known to all actors in the economy.

Fig. 1

Illustration of expected a private and b social returns of all four firm types

A contract between a borrowing firm and a lender comprises two parts, $\pi _k$ and $R_k$, with $k \ \in \lbrace uh, u l, s h, sl\rbrace$, where $\pi _k\in [0,1]$ is the probability of receiving the loan and $R_k>0$ denotes the loan repayment (1+interest rate).⁹ Like Besanko and Thakor (1987), we assume that both technology alternatives (clean or dirty) are mutually exclusive, such that the returns from dirty production represent the opportunity costs of choosing the clean technology. The expected profit of a borrower of type cd who applies for a contract designed for a borrower k is the difference between the expected profit from using the clean technology and the opportunity cost of not using the dirty technology:

$$\begin{aligned} P_{cd,k}=\pi _k\left[ \delta _c\left( y_{c}-R_k\right) -y_{d}\right] . \end{aligned}$$

(1)

The lender’s expected profit of a loan to a borrower of type k is the difference between the loan repayment, given that the borrower is successful and hence able to repay the loan, and the bank’s marginal cost to obtain funds:

$$\begin{aligned} B_k=\pi _k\left[ \delta _cR_k-\rho \right] . \end{aligned}$$

(2)

Following Janda (2011), we assume that, in the case of indifference between providing and not providing the loan, the bank chooses to provide the loan. When the borrower is indifferent between accepting the loan contract to finance the clean technology investment and choosing the dirty technology, they will decide in favour of the loan contract. The lender can observe the technology choice such that the firm cannot take a loan and then use the dirty technology to repay it. In order to conduct welfare analyses, expected social welfare is defined as the sum of firms’ profits, bank profits, and government budget, less social costs of emissions.

3.2 Laissez–Faire and Full Information Outcome

We first characterise the equilibrium under laissez-faire, i.e., an economy without government intervention, and then the socially optimal equilibrium under full information. The latter serves as a baseline comparison for the subsequent main analyses of different policy interventions under asymmetric information.

The bank maximises its benefits from lending to the respective borrower of type k. The lender is subject to the borrowers’ participation constraints, i.e. their expected profits using the clean technology after repaying the loan are at least as high as their returns from dirty production ($P_{cd,k}\ge 0$). All potential borrowers know the bank’s per unit cost to obtain funds for lending, $\rho$ and hence the minimum interest $R_k$ the bank has to set in order to break even. In laissez-faire, the firms’ returns from dirty production are very high compared to using the clean technology, as firms do not internalise the social costs ($e_d$). All firms know that the lender cannot offer interest rates that are low enough to raise the profits from clean over those of dirty production without the lender incurring losses. Thus, all firms favour the dirty technology. This outcome is not socially optimal, as H-firms use their emission-intensive dirty technology instead of the clean technology. Lemma 1 summarises the laissez-faire equilibrium.

Lemma 1

Without government intervention, all firms use the dirty technology.

Proof

See Appendix 7.1. $\square$

We now turn to the socially optimal equilibrium under full information. The government introduces policy addressing the externalities of carbon emissions, namely a Pigouvian tax $\tau$ on emissions that equals their per unit social costs $\kappa \equiv 1$, such that firms internalise the true social costs of their decisions (Knittel and Sandler 2018). Following from this and Assumption 1, L-firms will not apply for a loan. Those firms know that the bank cannot offer them a loan contract that makes the clean investment more attractive and, at the same time, allows the bank to break even. This is due to these firms’ ability to produce the dirty output at a low emission level $e_{l}$: despite the emission tax, using the dirty technology is still more profitable than investing in the clean technology, independent of the success probability $\delta _c$. Hence, only H-firms have an incentive to invest in the clean technology.

The group of H-firms applying for a loan to fund the initial investment for the clean technology contains both firms with a low and firms with a high success probability. The bank maximises its benefits from lending subject to the participation constraint (PC) of the respective type of borrower. The lender’s maximisation problem can be written as:

$$\begin{aligned} \max _{\pi _{ch},R_{ch}}\ B=&\,\pi _{ch}\left( \delta _cR_{ch}-\rho \right) \\ \text {subject to} \quad (PC_{ch}) \quad&\pi _{ch}\left[ \delta _c\left( y_{c}-R_{ch}\right) -\left( y_{D}-\tau e_{ h}\right) \right] \ge 0,\\&0\le \pi _{ch} \le 1. \end{aligned}$$

With full information, the solution to this problem is given by:

$$\begin{aligned} R^*_{ch}=y_{c}-\frac{y_{d}-\tau e_{ h}}{\delta _c} \quad \quad \quad \pi ^*_{ch}=1. \end{aligned}$$

The bank can identify each type and offers them different contracts. Lemma 2 sums up the results of the baseline case.

Lemma 2

With Pigouvian emission tax and perfect information, H-firms use the clean technology and L-firms use the dirty technology.

Proof

See Appendix 7.2. $\square$

4 Policy Interventions Under Information Asymmetry

We now introduce information asymmetry between lender (principal) and borrower (agent): the lender cannot distinguish between borrower types. We show that, in contrast to the full information outcome, a Pigouvian tax may not be sufficient to achieve a first-best allocation, as credit rationing might occur. We then investigate how interest subsidies or loan guarantees can resolve this issue. Subsequently, we analyse whether one instrument can effectively address both market failures. We consider alternative tax rates (higher than the Pigouvian tax) and the case where an emission tax is (politically) not feasible and only credit market interventions are available. Finally, we compare welfare levels of all policy mixes.

4.1 Pigouvian Emission Tax and Credit Market Instruments

In an economy with a Pigouvian tax, the bank maximises its expected benefit from lending subject to the participation constraints (PCs) and incentive compatibility constraints (ICs) of both borrower types:

$$\begin{aligned} \max _{\pi _{ uh}, R_{ uh},\pi _{ s h},R_{ s h}} \ B=&\,\theta _h\left[ \theta _u B_{ uh}+\left( 1-\theta _u\right) B_{ s h}\right] = \theta _h\left[ \theta _u \pi _{ uh}\left( \delta _{ u}R_{ uh}-\rho \right) +\left( 1-\theta _u\right) \pi _{ s h}\left( R_{ s h}-\rho \right) \right] \\ \text {subject to}\quad (PC_{ch}) \quad&\pi _{ch}\left[ \delta _c\left( y_{c}-R_{ch}\right) -\left( y_{d}-\tau e_{ h}\right) \right] \ge 0\\ (IC_{sh,uh}) \quad&\pi _{ s h}\left[ \left( y_{c}-R_{ s h}\right) -\left( y_{d}-\tau e_{ h}\right) \right] \ge \pi _{ uh}\left[ \left( y_{c}-R_{ uh}\right) -\left( y_{d}-\tau e_{ h}\right) \right] \\ (IC_{uh,sh}) \quad&\pi _{ uh}\left[ \delta _{ u}\left( y_{c}-R_{ uh}\right) -\left( y_{d}-\tau e_{ h}\right) \right] \ge \pi _{ s h}\left[ \delta _{ u}\left( y_{c}-R_{ s h}\right) -\left( y_{d}-\tau e_{ h}\right) \right] \\&0\le \pi _{ch} \le 1. \end{aligned}$$

The solution to this problem is given by:

$$\begin{aligned} \begin{aligned} R^*_{ s h}&= {\left\{ \begin{array}{ll} y_{c}-\left( y_{d}-\tau e_{ h}\right) \quad if \quad \pi ^*_{ u h}=0\\ y_{c}-\frac{y_{d}-\tau e_{ h}}{\delta _{ u}} \quad otherwise \end{array}\right. } \end{aligned}&\begin{aligned} \pi ^*_{ s h}&=1 \end{aligned}\\ \quad \quad \quad \begin{aligned} R^*_{ uh}&= {\left\{ \begin{array}{ll} any \ value \quad if \quad \pi ^*_{ u h}=0\\ y_{c}-\frac{y_{d}-\tau e_{ h}}{\delta _{ u}} \quad otherwise \end{array}\right. } \end{aligned}&\begin{aligned} \pi ^*_{ uh}&= {\left\{ \begin{array}{ll} 0 &{}if \quad \frac{\left( \delta _{ u}y_{c}-\rho \right) -\left( y_{d}-\tau e_{ h}\right) }{\left( y_{d}-\tau e_{ h}\right) }<\frac{1-\theta _u}{\theta _u}\frac{1-\delta _{ u}}{\delta _{ u}}\\ 1 &{}otherwise. \end{array}\right. } \end{aligned} \end{aligned}$$

Like in the case with full information, H-firms prefer the clean technology and hence apply for a loan. There are two possible equilibrium outcomes: in the first equilibrium, both the skilled and the unskilled firms receive the same loan contract for their low-carbon investments and get served by the lender. In the second equilibrium, only the skilled firms receive a loan, as the lender offers a contract that only skilled firms are willing to accept, whereas unskilled firms with a low success probability $\delta _{ u}$ do not receive a loan. The latter outcome is referred to as credit rationing and occurs if the condition for $\pi ^*_{ uh}=0$ holds.

This credit rationing condition holds if the difference between the success probabilities of both borrowers, $1-\delta _{ u}$, is large enough. This means that credit rationing is more likely for immature and risky clean technologies. When the credit rationing condition holds, it is more profitable for the lender to only serve the sh-firms by setting a high interest rate $R^*_{ s h}= y_{c}- \left( y_{d}-\tau e_{ h}\right)$, which the uh-firms cannot afford, than setting a low the interest rate and offering loans to both firm types. Figure 2 panel (a) depicts the resulting technology choices of firms. Proposition 1 sums up the results.

Proposition 1

With Pigouvian tax and if the credit rationing condition holds, L-firms use the dirty production technology. H-firms prefer the clean technology, but only sh-firms use the clean technology, as uh-firms do not receive a loan and hence use the dirty technology.

Proof

See Appendix 7.3. $\square$

Fig. 2

Technology choices and resulting returns with a Pigouvian tax and b Pigouvian tax and interest subsidy or loan guarantee. Panel a depicts the case with credit rationing of uh-firms

The outcome with credit rationing is socially inferior to the full information baseline. In the next step, we consider two alternative instruments the government can use to address the friction on the financial market resulting in credit rationing: interest rate subsidies or credit guarantees. These policy instruments are typically suggested in the theoretical literature on financial market failures (Arping et al. 2010; Gale 1990; Janda 2011; Minelli and Modica 2009; Philippon and Skreta 2012) and frequently used to support low-carbon investment (Buchner et al. 2019; Kempa and Moslener 2017). In order to enable socially optimal clean technology investments of H-firms, the government defines an overall budget for its intervention on credit markets based on the optimal level of the interest subsidy or the loan guarantee. The key difference between both instruments is the event triggering the associated payment. The interest rate subsidy lowers the repayment of the borrower by driving a wedge between the market interest rate and the interest rate the borrower must pay. Thus, we model it as a payment to the borrower. As the interest repayment only occurs in the case of a successful investment, the interest rate subsidy is only paid in this case. With an interest subsidy $\sigma >0$, the expected profit of a borrower, Eq. (1), changes to:

$$\begin{aligned} P_{cd,k}=\pi _k\left[ \delta _c\left( y_{c}-\left( R_k-\sigma \right) \right) -\left( y_{d}-\tau e_{d}\right) \right] . \end{aligned}$$

(3)

In contrast, a loan guarantee $\gamma \in (0,\rho /(1-\delta _u))$ is only paid if an investment is unsuccessful and the borrower cannot repay the loan.¹⁰ As the loan guarantee is the share of the loan that is recovered in the case of clean investment failure, the lender’s expected profit changes to:

$$\begin{aligned} B_k=\pi _k\left[ \delta _cR_k+\left( 1-\delta _c\right) \gamma -\rho \right] . \end{aligned}$$

(4)

With a given interest rate subsidy $\sigma$ or a loan guarantee $\gamma$, the bank maximises its expected benefit subject to the participation and incentive compatibility constraints of both borrowers¹¹:

$$\begin{aligned} \max _{\pi _{ uh}, R_{ uh},\pi _{ s h},R_{ s h}} \ B&= \ \theta _h\left[ \theta _u B_{ uh}+\left( 1-\theta _u\right) B_{ s h}\right] \\&=\ \theta _{d}\left[ \theta _u \pi _{ uh}\left[ \delta _{ u}\left( R_{ uh}\right) -\rho +\left( 1-\delta _{ u}\right) \gamma \right] +\left( 1-\theta _u\right) \pi _{ s h}\left( R_{ s h}-\rho \right) \right] \\ \text {subject to} \quad&PC_{ch},\ IC_{sh,uh},\ IC_{uh,sh},\ \le \pi _{ uh} \le 1. \end{aligned}$$

The solution to this problem is given by:

$$\begin{aligned} \begin{aligned} R^*_{ s h}&= {\left\{ \begin{array}{ll} y_{c}+\sigma -\left( y_{d}-\tau e_{ h}\right) \quad if \quad \pi ^*_{ u h}=0\\ y_{c}+\sigma -\frac{y_{d}-\tau e_{ h}}{\delta _{ u}} \quad otherwise \end{array}\right. } \end{aligned}&\begin{aligned} \pi ^*_{ s h}&=1 \end{aligned}\\ \begin{aligned} R^*_{ uh}&= {\left\{ \begin{array}{ll} any \ value \quad if \quad \pi ^*_{ u h}=0\\ y_{c}+\sigma -\frac{y_{d}-\tau e_{ h}}{\delta _{ u}} \quad otherwise \end{array}\right. } \end{aligned}&\begin{aligned} \pi ^*_{ uh}&= {\left\{ \begin{array}{ll} 0 &{}if \quad \frac{\left( \delta _{ u}\left( y_{c}+\sigma \right) -\rho \right) -\left( y_{d}-\tau e_{ h}\right) +\left( 1-\delta _{ u}\right) \gamma }{\left( y_{d}-\tau e_{ h}\right) }<\frac{1-\theta _u}{\theta _u}\frac{1-\delta _{ u}}{\delta _{ u}}\\ 1 &{}otherwise. \end{array}\right. } \end{aligned} \end{aligned}$$

Figure 2 panel (b) illustrates the results. As in Fig.  2 panel (a), the low-risk borrowers (sh-firms) always receive a loan. For the borrowers with a lower success probability, we can derive conditions for $\gamma$ and $\sigma$, under which this borrower receives a loan as well. Solving the credit rationing condition, i.e. the condition for $\pi ^*_{ uh}=0$, for $\sigma$ yields the minimum interest rate subsidy assuring that also uh-firms receive a loan and hence no credit rationing occurs. Similarly, there is a minimum share of the loan that has to be covered by the guarantee, $\gamma$, such that all H-firms receive a loan. The following proposition sums up the results for both cases.

Proposition 2

With Pigouvian tax combined with either an interest rate subsidy of $\sigma \ge \sigma ^*= \frac{\rho +\left( y_{d}-\tau e_{ h}\right) \left[ 1+\frac{1-\theta _u}{\theta _u}\frac{1-\delta _{ u}}{\delta _{ u}}\right] }{\delta _{ u}}-y_{c}$ or a loan guarantee of $\gamma \ge \gamma ^*=\frac{\rho +\left( y_{d}-\tau e_{ h}\right) \left[ 1+\frac{1-\theta _u}{\theta _u}\frac{1-\delta _{ u}}{\delta _{ u}}\right] }{1-\delta _{ u}}$, there is no credit rationing of uh-firms. H-firms use the clean technology, L-firms use the dirty technology. The government expenditures for $\sigma ^*$ are higher than for $\gamma ^*$.

Proof

See Appendix 7.3. $\square$

One difference between both instruments is that the applicability of the loan guarantee is limited, i.e. it cannot be used if the required guarantee is above its upper limit of $\rho /(1-\delta _u)$. The interest rate subsidy can always achieve the first-best outcome. However, the government budget required to fund the guarantee programme is smaller than for interest rate subsidies. Hence, the combination of the Pigouvian tax with the loan guarantee is the preferable option for the government in most cases. Only if the guarantee cannot yield a first-best outcome, the government should use the interest rate subsidy.

The policymaker further has some flexibility when combining an emission tax with a credit market instrument. In equilibrium, the tax and loan guarantee or interest subsidy have an inverse relationship. The government can yield a first-best outcome by reducing the tax below the Pigouvian level if it increases the guarantee or the subsidy, and vice versa.

Lemma 3

The two combined policy instruments required for the outcome characterised in Proposition 2have an inverse relationship, $d\sigma ^*/d\tau <0$ and $d\gamma ^*/d\tau <0$.

Proof

See Appendix 7.3. $\square$

4.2 Non-Pigouvian Emission Taxes

We now turn to the cases, where not all first-best policy instruments are available. First, we consider the case of an emission tax and build on the literature on optimal environmental taxes with more than one externality. Previous studies found that a tax rate equal to the social costs of the emission may not be optimal in the presence of different other market failures, such as consumption externalities (Diamond 1973), knowledge externalities (Acemoglu et al. 2012; Fischer et al. 2021), imperfect competition (Baumol and Oates 1988), or constraints and frictions on financial markets (Hoffmann et al. 2017; Heider and Inderst 2022; Döttling and Rola-Janicka 2023). If the government can substitute an emission tax for other taxes, tax rates above or below the Pigouvian level can be optimal (Lee and Misiolek 1986).

Based on these findings, we explore whether tax rates above the Pigouvian level can effectively address the emission externality and the issue of credit rationing. Increasing the tax reduces the profits of dirty production, which is the outside option of a firm applying for a loan for the clean technology investment. Hence, it increases the incentives of firms to choose the clean technology. At the same time, it becomes more attractive for the lender to offer loans. Due to the reduced value of firms’ outside options, the lender has, ceteris paribus, higher profits from lending, as the borrowers’ opportunity costs, which the lender has to compensate, are lower (recall Eq. 1). We distinguish two relevant cases: first, a tax rate above the Pigouvian tax can resolve credit rationing and the first-best outcome is achieved. Second, in addition to the H-firms, some of the L-firms, in particular those with a higher success probability (sl-firms), successfully apply for loans and produce with the clean instead of their low-emission dirty technology, which is social undesirable. To analyse these cases, we assume that $[y_{d}-(\delta _u y_{c}-\rho )]/e_l>y_{d}/e_h$. If this assumption holds, ul-firms cannot successfully apply for a loan and hence always use the low-emission dirty technology. This assumption does not affect our analysis of the two relevant cases, while it reduces the complexity of the maximisation problem.¹²

With $\tau >1$, the bank maximises its expected benefit from lending subject to the participation and incentive compatibility constraints of three borrowers¹³:

$$\begin{aligned} \max _{\pi _{uh}, R_{uh},\pi _{sh},R_{sh},\pi _{sl},R_{sl}} \ {}&B= \ \theta _h\left[ \theta _u B_{uh}+\left( 1-\theta _u\right) B_{sh}\right] +(1-\theta _u)(1-\theta _h)B_{sl}\\&=\ \theta _{h}\left[ \theta _u \pi _{ uh}\left( \delta _{ u}R_{ uh}-\rho \right) +\left( 1-\theta _u\right) \pi _{ s h}\left( R_{ s h}-\rho \right) \right] +(1-\theta _u)(1-\theta _h)\pi _{sl}\left( R_{sl}-\rho \right) \\ \text {subject to} \quad&PC_{ch},\ PC_{sl},\ IC_{sh,uh},\ IC_{sh,sl},\ IC_{uh,sl},\ 0\le \pi _{sh} \le 1,\ 0\le \pi _{uh} \le 1,\ 0\le \pi _{sl} \le 1. \end{aligned}$$

The solution to this problem is given by:

$$\begin{aligned} \begin{aligned} R^*_{sh}&= {\left\{ \begin{array}{ll} y_{c}-\left( y_{d}-\tau e_{h}\right) \quad if \quad \pi ^*_{uh}=\pi ^*_{sl}=0\\ y_{c}-\frac{y_{d}-\tau e_{h}}{\delta _{u}}\quad if \quad \pi ^*_{uh}>0, \pi ^*_{sl}=0\\ y_{c}-\left( y_{d}-\tau e_{l}\right) \quad if \quad \pi ^*_{uh}>0, \pi ^*_{sl}>0 \end{array}\right. } \end{aligned}&\begin{aligned} \pi ^*_{ s h}&=1 \end{aligned}\\ \begin{aligned} R^*_{ uh}&= {\left\{ \begin{array}{ll} any \ value \quad if \quad \pi ^*_{uh}=0\\ y_{c}-\frac{y_{d}-\tau e_{ h}}{\delta _{u}}\quad if \quad \pi ^*_{uh}>0, \pi ^*_{sl}=0\\ y_{c}-\left( y_{d}-\tau e_{l}\right) \quad if \quad \pi ^*_{uh}>0, \pi ^*_{sl}>0 \end{array}\right. } \end{aligned}&\begin{aligned} \pi ^*_{ uh}&= {\left\{ \begin{array}{ll} 0 &{}if \quad \tau< \min \left\{ \tau _{uh};\tau _{sl}\right\} \\ 1 &{}otherwise; \end{array}\right. } \end{aligned}\\ \begin{aligned} R^*_{ uh}&= {\left\{ \begin{array}{ll} any \ value \quad if \quad \pi ^*_{uh}=0\\ y_{c}-\left( y_{d}-\tau e_{l}\right) \quad if \quad \pi ^*_{uh}>0, \pi ^*_{sl}>0 \end{array}\right. } \end{aligned}&\begin{aligned} \pi ^*_{sl}&= {\left\{ \begin{array}{ll} 0 &{}if \quad \tau <\tau _{sl}\\ 1 &{}otherwise; \end{array}\right. } \end{aligned} \end{aligned}$$

with $\tau _{uh} \equiv \frac{y_{d}-A\left( \delta _uy_{c}-\rho \right) }{e_h}$, $A\equiv \frac{\theta _h\theta _u\delta _u}{\theta _h\theta _u\delta _u+\theta _h(1-\theta _u)\left( 1-\delta _u\right) }$, $\tau _{sl} \equiv \frac{\left[ 1-B\left( (1-\delta _u)/\delta _u\right) \right] y_{d}-\left( y_{c}-\rho \right) }{\left[ 1-B\left( (e_h-e_l\delta _u)/(e_l\delta _u)\right) \right] e_l}$, $B\equiv \frac{\theta _h(1-\theta _u)+\theta _h\theta _u\delta _u}{(1-\theta _h)(1-\theta _u)}$.

Like in the case of the Pigouvian tax, H-firms always have an incentive to use the clean technology and the firms with the high success probability (sh-firms) always receive a loan. For uh- and sl-firms, we obtain two credit rationing conditions. Solving those conditions for $\tau$ yields the tax rates to resolve credit rationing of the respective firm type.

Whether a first- or a second-best outcome can be achieved depends on the ratio of both tax rates. If $\tau _{uh}<\tau _{sl}$, the government can set the tax equal to $\tau _{uh}$ resolve socially undesirable credit rationing of uh-firms and all high-emission firms use the clean technology, whereas the low-emission firms use the dirty technology. If $\tau _{uh}\ge \tau _{sl}$, also sl-firms successfully apply for a loan and use the clean technology. This yields a second-best outcome, as it would be optimal if those firms used their low-emission dirty technology instead.

The likelihood of the latter, second-best outcome depends on the uncertainty related to clean technologies and the emission levels of the two dirty technologies. If $1-\delta _{u}$ is large, credit rationing of uh-firms is very strong, i.e. the lender has low incentives to offer a loan to this firm type. Hence, the policymaker needs to set a rather high tax $\tau _{uh}$ to resolve credit rationing. If the emission level of sl-firms $e_l$ is rather high, then the tax required to induce a successful switch from the dirty towards the clean technology $\tau _{sl}$ is rather small. Hence, the larger $1-\delta _{u}$ and the smaller $e_h-e_l$, the higher is the likelihood that resolving credit rationing of uh-firms also induces a welfare-reducing switch towards clean technologies by sl-firms. The following proposition sums up the results.

Proposition 3

With $\tau \ge \min \left\{ \tau _{uh};\tau _{sl}\right\}$, there is no credit rationing of uh-firms. If $\tau _{uh}<\tau _{sl}$, H-firms use the clean technology, L-firms use the dirty technology. However, if $\tau _{uh}\ge \tau _{sl}$, sl-firms also successfully apply for a loan and use the clean instead of the low-emission technology.

Proof

See Appendix 7.4. $\square$

4.3 Credit Market Instruments

We now analyse an economy without (a sufficiently high) emission tax. In practice, emission taxes often cannot be imposed. If policymakers rely on votes, it is more attractive to support clean technologies rather than impose additional costs for the dirty technologies (Bowen 2011; Green and Yatchew 2012; Ito 2015). Lobbying can also deter taxation (Fredriksson 1997).

As shown in Sect. 3.2, there is no incentive for firms to use the clean technology without an appropriate price on carbon emissions. Here, we show that the government can alternatively use the interest rate subsidy, which is paid to the borrower, to incentivise firms to switch to low-carbon technologies. As argued in Sect. 4.1, the bank cannot offer an interest rate that is low enough to render the low-carbon investment more attractive for firms without incurring losses. The government can use the interest rate subsidy to fill this gap, such that (at least some) firms choose the clean technology, while the lender is able to break even.

There are two relevant levels of the interest rate subsidy $\sigma$. Figure 3 illustrates both cases. If the interest rate subsidy reaches the first threshold $\sigma _{S}$, it becomes profitable for all skilled firms (S-firms) to switch from the dirty to the clean technology, while unskilled firms (U-firms) still prefer the dirty technology (see Fig. 3 panel (a)). Hence, only S-firms apply for loans. As S-firms are identical in the absence of an emission tax, there are no information asymmetries and credit rationing cannot occur. However, new inefficiencies are introduced. Recall that the emission tax incentivises high-emission firms (H-firms) to switch to the clean technology, while low-emission firms (L-firms) keep using the dirty technology. Without tax, there is no self-selection of H-firms into choosing the clean technology. Instead, a fraction $\theta _h\theta _u$ of H-firms, the uh-firms, uses the dirty technology, resulting in overall higher emissions compared to the economy with emission tax. At the same time, the subsidy incentivises a fraction $\left( 1-\theta _h\right) \left( 1-\theta _u\right)$ of L-firms, the sl-firms, to choose the low-carbon technology, whereas it would be preferable if those firms chose their low-emission dirty technology. Proposition 4 summarises the results.

Fig. 3

Technology choices and resulting returns without emission tax and with a low interest rate subsidy $\sigma _{S}$ and b high interest rate subsidy $\sigma _{SU}$ combined with a loan guarantee $\gamma ^*$

Proposition 4

Without emission tax and with an interest subsidy $\sigma =\sigma _{S}= y_{d}-y_{c}+\rho$, S-firms use the clean technology and U-firms use the dirty technology.

Proof

See Appendix 7.5. $\square$

At the second, relevant and higher threshold of the interest subsidy, denoted as $\sigma _{SU}$, all firms choose the clean technology (see Fig. 3 panel (b)). An advantage of $\sigma _{SU}$ is the abatement of emissions produced by emission-intensive uh-firms, which use the dirty technology at lower subsidies levels. At the same time, however, $\sigma _{SU}$ also incentivises all L-firms to use the clean technology, although it would have been socially desirable if ul-firms used the dirty technology. As all firms choose the clean technology for $\sigma _{SU}$, firms with both low and high success probabilities now apply for a loan. Hence, with $\sigma _{SU}$ credit rationing is a potential issue that does not exist for $\sigma _{S}$. Credit rationing can be resolved by either increasing $\sigma$ above $\sigma _{SU}$ or combining it with a loan guarantee, where the latter is the preferable option (see Proposition 2). Proposition 5 sums up the results.

Proposition 5

Without emission tax and with an interest subsidy $\sigma =\sigma _{SU}= \frac{y_{d}}{\delta _{ u}}-\left( y_{c}-\rho \right)$ and a loan guarantee $\gamma _{n\tau }^*=\frac{1-\theta _u}{\theta _u}\frac{1}{\delta _{ u}}\left( \delta _{ u}y_{c}-\rho \right)$, all firms use the clean technology.

Proof

See Appendix 7.5. $\square$

4.4 Comparative Welfare Analysis

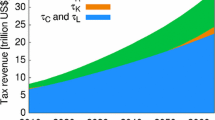
The welfare levels under laissez-faire and under full information with Pigouvian tax represent the lower and the upper bound of total welfare, respectively. If an emission tax is introduced, firms internalise the social costs of emissions, which increases welfare. With information asymmetries, credit rationing may occur, and some firms are deterred from using low-carbon technologies and thus use carbon-intensive technologies, which results in a welfare below the welfare-maximum. Credit rationing can be effectively addressed by a loan guarantee or an interest rate subsidy. This combination of Pigouvian tax and intervention on the credit market resembles the first-best outcome under full information and thus yields the welfare maximum.

An emission tax level above the Pigouvian tax can also resolve socially undesirable credit rationing. If clean technology risks and emission levels of low-emission firms are low, a tax alone can yield the welfare optimum. Alternatively, the tax can induce a reallocation of some low-emission firms towards the clean technology.

If an emission tax is (politically) not feasible, emission externalities are not internalised, but can be indirectly addressed by financial instruments. There are two relevant subsidy levels, as outlined in Propositions 4 and 5. Their ordering with respect to welfare depends on two factors. Firstly, the order is driven by the share of the H-firms in the economy and their actual emission levels $e_{h}$: the larger the share of H-firms and the higher $e_{h}$, the higher are the social costs of emissions if those firms use the dirty technology. The higher these social costs of emissions, the higher is the welfare resulting from the high subsidy $\sigma _{SU}$ that incentivises all firms to use the clean technology. Secondly, relative welfare is affected by the success probability of U-firms, $\delta _{ u}$, that are incentivised to use the clean technology by $\sigma _{SU}$. The higher their success probability, the higher is the resulting welfare compared to $\sigma _{S}$, where those firms use the dirty technology. However, if emission levels of dirty technologies and thus their social costs are relatively low, while low-carbon alternatives are relatively risky, it is socially optimal if the government does not intervene at all.¹⁴

The following corollary sums up the core results of the comparative welfare analysis:

Corollary 1

The reference scenario with Pigouvian tax and full information yields the welfare optimum (upper bound) $\tilde{W}_{P}$. Laissez-faire yields the lower bound, $W_L$. With Pigouvian tax, welfare is higher than in laissez-faire and can resemble the welfare optimum if no credit rationing occurs, $W_L<W_{P}\le \tilde{W}_{P}$. The combined use of Pigouvian tax and a credit market instrument, $\sigma ^*$ or $\gamma ^*$, can resemble the welfare optimum, $W_{P \gamma }=W_{P \sigma }=\tilde{W}_{P}$. Without credit market intervention and with an emission tax above the Pigouvian level, welfare can be lower or equal to the welfare optimum, $W_{\tau _{sl}}<W_{\tau _{uh}}=\tilde{W}_{P}$. Without emission tax, either low interest rate subsidy $\sigma _{S}$ or the combination of high interest rate subsidy $\sigma _{SU}$ and $\gamma _{n\tau }^*$ cannot resemble the first-best outcome, $W_{\sigma _{S}},W_{\sigma _{SU}}<\tilde{W}_{\tau }$, with $W_{\sigma _{S}}\gtreqqless W_{\sigma _{SU}}\Leftrightarrow y_{d}-\left[ \left( 1-\theta _h\right) e_{ l}+\theta _h e_{ h}\right] \gtreqqless \delta _{ u}y_{c}-\rho$.

Proof

See Appendix 7.6.$\square$

5 Discussion and Policy Recommendations

In this section, we elaborate when credit rationing is likely to occur, discuss how risk aversion would affect our results, and derive policy recommendations. Our results show that the likelihood of credit rationing increases with the level of low-carbon technology risk, i.e., the difference between investment success probabilities. Empirical evidence supports this prediction. Firms face issues to source debt for their renewable energy investments when using new technologies, as banks are largely unfamiliar with their risks (Geddes et al. 2018). However, when clean technologies mature and are perceived as less risky, firms have less or no issues to access debt for their investments (Egli et al. 2018; Geddes et al. 2018; Mazzucato and Semieniuk 2018). This process is further enhanced by learnings in the financial sector (Egli et al. 2019). As outlined in Sect. 2, the development of the financial sector is of key importance. The more developed a country’s financial sector, the better is the ability of lenders to initially screen firms and assess risks of low-carbon investments. This reduces information asymmetries and thus the likelihood of credit rationing. Consequently, the more mature a low-carbon technology and the more developed an economy’s financial sector, the lower is the likelihood of credit rationing impeding low-carbon investments.

In the model, we assume risk neutral actors. One might argue that firms or, in particular, banks might be risk averse, which would affect our results as follows. Risk aversion of banks would lead to higher interest rates and hence loan repayments, as banks would request a higher compensation for a specific risk than in the case of risk neutrality. Risk averse firms would be less likely to decide in favour of the risky low-carbon technology vis-à-vis the risk-free dirty one. As a consequence, risk aversion could increase the likelihood of socially undesirable credit rationing.¹⁵ In general, all the policy mixes analysed above would still be suitable to resolve the issue of credit rationing. Interventions on credit markets, however, would be more costly for the government, as higher interest rate subsidies or loan guarantees would be required to incentivise the risk-averse bank to offer a loan to high-risk firms. Furthermore, the applicability of an emission tax as the sole instrument would be limited. Due to the penalisation of high risks by a risk-averse bank, the required tax rate to prevent socially undesirable credit rationing of high-emission firms, $\tau _{uh}$, is higher to make sure that also high-risk firms receive loans. Consequently, it is less likely that the condition $\tau _{uh}<\tau _{sl}$ holds, which guarantees that none of the L-firms receive loans, but rather use their low-emission dirty technology. Overall, the issue of credit rationing would be more severe in case of risk aversion and resolving it would be more difficult and costly for the policymaker.

We now turn to the key insights for policymakers. Our analysis shows that combining environmental policy with an intervention on credit markets can resolve credit rationing and thus induce higher low-carbon investments. This finding is in line with empirical evidence. Access to public funding is an important driver for low-carbon innovations, in particular for SMEs (Cecere et al. 2020), and renewable energy investments (Haščič et al. 2015). Public guarantees and interest subsidies reduce credit rationing and have de-risking effect on low-carbon investments (Cowling et al. 2018; Geddes et al. 2018). Hence, combining an environmental policy that internalises the externality with an interest rate subsidy or a loan guarantee is the preferred option for the policymaker. An additional advantage of this policy mix is that policymakers have some flexibility in combining an emission tax with credit market interventions and still reach a first-best outcome. If setting a tax at the Pigouvian level is, e.g., politically difficult, the government can lower the emission tax and instead increase its financial support through subsidies or loan guarantees. Alternatively, the government can lower the latter as long as this goes along with an emission tax above the Pigouvian level. The second option might be relevant if the government wants to reduce the burden for its budget.

We further find that only using an emission tax can also result in a first-best outcome if it is set above the Pigouvian level. From a political economy perspective, however, it might be difficult to introduce such a policy if the emission tax rate required to resolve credit rationing is high. It may also introduce an additional distortion if clean technology risk and the emission intensity of low-emission firms are rather high. In the case of the former, the required tax rate to resolve socially undesirable credit rationing is rather high. If the emission intensity of low-emission firms is too high, some of these firms might choose to also invest in the low-carbon technology, although it would be socially desirable if they used their efficient dirty technology. This means that an emission tax above the Pigouvian level bears the risk of welfare-reducing over-investment in low-carbon technologies. Hence, using an emission tax alone seems to be a good option for the policymaker if clean technologies are rather mature and not too risky and if emission-levels of low-emission dirty technologies are rather low. Otherwise, the government should rather combine a Pigouvian tax with a loan guarantee or an interest rate subsidy.

Given that technological progress reduces the risk of low-carbon technologies, our findings indicate that credit rationing is only a temporary issue.¹⁶ In our setup, this would mean that the difference between the success probabilities of low-carbon innovations of skilled and unskilled firms diminishes. As long as there is an emission tax that incentivises high-emission firms to choose the clean technology, socially undesirable credit rationing ultimately disappears if this difference gets sufficiently small. Until that point, however, there are welfare losses if credit rationing is not addressed by interventions on the credit market or an emission tax above the Pigouvian tax level. The main reason is that some high-emission firms, i.e., those that do not receive a loan for their clean technology investment, use their dirty technology. Hence, not addressing credit rationing results in social costs of delay.

In addition, it is worth noting that our results are not specific to an emission tax. Consider, e.g., an emission standard: the government sets a firm-level emission standard somewhere between the emission levels of high- and low-emission firms. In this case, high-emission firms would incur some costs to reduce their emissions to comply with the standard.¹⁷ If these costs reach a threshold, then, like in the case of the Pigouvian tax, high-emission firms would choose to apply for a loan to invest in a low-carbon technology and credit rationing could occur. Alternatively, these firms would have to reduce their dirty output if they do not have any abatement options, which would also make the clean investment more attractive. Overall, other environmental policy instruments should lead to results similar to an emission tax, as long as they increase high-emission firms’ incentives to switch to clean technologies.

Finally, our results offer insights for policymakers if an emission tax is (politically) not available. Although the coverage of carbon prices has been increasing over time, they only cover around 23% of global emissions (World Bank 2022). At the same time, an increasing public involvement in financing for low-carbon investment can be observed. Currently, there are 160 loan/debt financing or guarantee programmes mainly for renewable energy and energy efficiency in force worldwide.¹⁸ According to Buchner et al. (2021), annual average public climate finance flows increased from USD 300 billion in 2017 and 2018 to USD 321 billion in 2019 and 2020. For this current scenario with a limited global price coverage of carbon emissions, our model offers valuable guidelines on the choice of finance instruments to incentivise low-carbon investments. The socially optimal choice of financial market interventions largely depends on the risk profiles of low-carbon technologies and the emission intensities of dirty technologies. High subsidies are the preferable option if clean technology risks are rather low and dirty technologies are very emission intensive. However, if clean technologies are still immature, whereas dirty alternatives are not too emission-intensive, the government should refrain from using too high subsidies as inducing too high levels of clean technology investments can actually be welfare reducing.

6 Conclusion

This paper offers a novel theoretical framework to analyse firms’ decisions between low-carbon (clean) and carbon-intensive (dirty) technologies that explicitly models external financing. We show how information asymmetries between lender and firms might induce credit rationing and thus a socially undesirably low level of investments and analyse how different policy interventions might resolve this issue. We find that a Pigouvian emission tax alone may not be sufficient to achieve a first-best outcome, as credit rationing occurs if the low-carbon technology is immature and risky. Introducing interest rate subsidies or loan guarantees can solve the issue of credit rationing and achieve a first-best outcome, which is consistent with the Tinbergen rule (Tinbergen 1956). Credit market instruments have an inverse relationship with the emission tax in equilibrium and allow some flexibility. The government can reduce the emission tax below the Pigouvian level if it increases the interest rate subsidy or loan guarantee and vice versa.

We further analyse the effectiveness of using only one instrument, i.e., either an emission tax or an intervention on credit markets. We find that setting an emission tax above the Pigouvian tax level can resolve the issue of credit rationing. A tax alone might even yield a first-best outcome, if the risks of clean technologies are rather low and hence the issue of credit rationing is not too severe. Alternatively, a second-best outcome is achieved. Given the low coverage of carbon pricing worldwide, we also consider the relevant case, where an emission tax is (politically) not feasible. In this scenario, an interest rate subsidy can be used as an alternative to the emission tax to induce a switch to low-carbon technologies. We find that, independent of the size of the interest subsidy or its combination with a loan guarantee, credit market interventions alone cannot resemble the fist-best outcome. This finding stresses the importance of a price on emissions. Using only finance instruments bears the risk of substantially increasing the social costs of the transition to a low-carbon economy and should be only considered if an emission price is (politically) not feasible.

Finally, we discuss some dynamic aspects of credit rationing. As ongoing technological progress results in decreasing risks of low-carbon technologies over time, e.g., due to innovation spillovers, the issue of credit rationing eventually vanishes. While this happens even without policy intervention on the credit market, there are, however, costs of delay if the government does not intervene if credit rationing occurs.

There are relevant aspects that are not covered in this paper and might be valuable directions of future research. A promising approach would be a dynamic analysis considering learning effects on the part of the firms or learning effects for the lender that could reduce information asymmetries. In the model, we consider risks to be exogenous. Realistically, the level of risk is at least partly endogenous to firm’s choice, e.g., if projects with high risks also have higher returns. Alternatively, firm outcomes might depend on effort. This could be analysed in an alternative principal-agent setup with moral hazard, as opposed to our model with adverse selection. Finally, a general equilibrium approach modelling consumers and a budget constraint for the government may provide additional insights.

7. Appendix

1.1 7.1. Laissez-Faire

Profit maximisation of firms requires the expected profit from investing in the clean technology to be non-negative, i.e. (1) $\ge 0$. Furthermore, profit maximisation of the bank requires the expected profit from lending to a firm to be non-negative. Solving (2) $\ge 0$ for $R_k$ yields the minimum loan repayment for loans that are provided with positive probability: $R_k\ge \rho /\delta _c \in (\rho ,\infty )$. We use the lower limit and define $R^{min}_k\equiv \rho$. Substituting $R^{min}_k$ into (2) reveals that under Assumption 1 expected profit from the clean investment of a firm can only be positive if expected profit of the bank is negative and vice versa. Therefore, without an emission tax and without credit market instruments, profit maximising behaviour of the bank and the firms is only compatible with the bank providing no loans and all firms choosing the dirty technology.

1.2 7.2. Full Information Outcome

With a Pigouvian tax $\tau =1$ (and $\sigma =\gamma =0$), there exists no contract with a positive probability that fulfils the PCs of L-firms, i.e. (1) $\ge 0$. This can be shown by substituting the minimum loan repayment (solving (2) $=0$ for $R_k$) into the expected profit of L-firms, (1). Hence, the reduced¹⁹ Lagrangian to the profit maximisation problem of the bank is:

$$\begin{aligned}&L(\pi _{ch},R_{ch},\lambda _1,\lambda _2,\lambda _3)=\pi _{ch}\left( \delta _c R_{ch}-\rho \right) +\lambda _1\pi _{ch}\left[ \delta _c\left( y_{c}-R_{ch}\right) -\left( y_{D}-\tau e_{ h}\right) \right] +\lambda _2\left( \pi _{ch}\right) +\lambda _3\left( 1-\pi _{ch}\right) . \end{aligned}$$

The (first-order) Kuhn–Tucker conditions for this problem are:

$$\begin{aligned}&\frac{\partial L(\cdot )}{\partial R_{ch}}=\pi _{ch}\delta _c-\lambda _1\pi _{ch}\delta _c\le 0, \quad R_{ch} \ge 0, \\&\frac{\partial L(\cdot )}{\partial \pi _{ch}}=\delta _cR_{ch}-\rho +\lambda _1\left[ \delta _c\left( y_{c}-R_{ch}\right) -\left( y_{d}-\tau e_{ h}\right) \right] +\lambda _2-\lambda _3\le 0, \quad \pi _{ch}\ge 0, \\&\frac{\partial L(\cdot )}{\partial \lambda _1}= \pi _{ch}\left[ \delta _c\left( y_{c}-R_{ch}\right) -\left( y_{d}-\tau e_{ h}\right) \right] \ge 0, \quad \lambda _1\ge 0,\\ &\frac{\partial L(\cdot )}{\partial \lambda _2}=\pi _{ch}\ge 0 , \quad \lambda _2\ge 0,\\&\frac{\partial L(\cdot )}{\partial \lambda _3}=1-\pi _{ch}\ge 0 , \quad \lambda _3\ge 0. \end{aligned}$$

With $R_{ch}>0$ it follows that $\partial L(\cdot )/\partial R_{ch}=0$ (follows from complementary slackness) and hence $\lambda _1=0$; with $\pi _{ch}>0$ it follows that $\partial L(\cdot ) / \partial \pi _{ch}=0$ (follows with complementary slackness) and hence $\lambda _3>0$ (see Assumption 1). From this it follows that $\pi _{ch}=1$ and with this and $\partial L(\cdot )/\partial \lambda _1$ it follows (for a global maximum) that $R_{ch}=y_{c}-\frac{y_{d}-\tau e_{ h}}{\delta _c}$.

1.3 7.3. Imperfect Information with Pigouvian Tax and Credit Market Instruments

In this subsection, we derive equilibrium contracts and the associated allocation of firms in a scenario with the combined use of a Pigouvian tax ($\tau =1$) and a credit market instrument and under the assumption of information asymmetries between borrowers, the lender, and the government. Given the four types of firms, we distinguish between 16 technical (groups of) regimes based on their respective allocation of the firm types. We restrict the presentation of the analysis to a set of regimes that are economically interesting, describe the local maxima in these regimes and under what conditions they apply, and show that they are global maxima.

The relevant (group of) regimes are characterised by:

Regime 1

(under-investment): $\pi _{sh}>0$, $\pi _{uh}=0$, $\pi _{sl}=0$, $\pi _{ul}=0$,

Regime 2

(optimal investment): $\pi _{sh}>0$, $\pi _{uh}>0$, $\pi _{sl}=0$, $\pi _{ul}=0$.

1.3.1 7.3.1. Maximisation Problem

The bank maximises its expected benefit from lending subject to the participation (PCs) and incentive compatibility constraints (ICs) of two types of borrowers. The reduced maximisation problem is²⁰:

$$\begin{aligned} \max _{\pi _{sh},R_{sh},\pi _{uh}, R_{uh}} \ B= & {} \, \ \theta _h\left[ \theta _u B_{ uh}+\left( 1-\theta _u\right) B_{ s h}\right] \nonumber \\= & {} \,\ \theta _{h}\left[ \theta _u \pi _{ uh}\left[ \delta _{ u}\left( R_{ uh}\right) -\rho +\left( 1-\delta _{ u}\right) \gamma \right] +\left( 1-\theta _u\right) \pi _{ s h}\left( R_{ s h}-\rho \right) \right] ,\nonumber \\ \text {subject to} \quad (PC_{ch})\ {} & {} \pi _{ch}\left[ \delta _c\left( y_{c}+\sigma -R_{ch}\right) -\left( y_{d}-\tau e_{ h}\right) \right] \ge 0,\nonumber \\ (IC_{sh,uh})\ {} & {} \pi _{ s h}\left[ \left( y_{c}+\sigma -R_{s h}\right) -\left( y_{d}-\tau e_{ h}\right) \right] \ge \pi _{ uh}\left[ \left( y_{c}+\sigma -R_{uh}\right) -\left( y_{d}-\tau e_{ h}\right) \right] ,\nonumber \\ 0\le & {} \pi _{sh} \le 1, 0\le \pi _{uh} \le 1. \end{aligned}$$

(5)

1.3.2 7.3.2. Kuhn–Tucker Approach

The Lagrangian to the maximisation problem (5) is given by:

$$\begin{aligned}&L(\pi _{ s h},R_{ s h},\pi _{ uh},R_{ uh},\lambda _1,\lambda _2,\lambda _3,\lambda _4,\lambda _5,\lambda _6)=\\&\quad \left( 1-\theta _u\right) \pi _{ s h}\left[ R_{ s h}-\rho \right] +\theta _u \pi _{ uh}\left[ \delta _{ u}R_{ uh}+\left( 1-\delta _{ u}\right) \gamma -\rho \right] \\&\quad +\lambda _1\pi _{ uh}\left[ \delta _{ u}\left( y_{c}+\sigma -R_{ uh}\right) -\left( y_{d}-\tau e_{ h}\right) \right] \\&+\lambda _2\left[ \pi _{ s h}\left[ \left( y_{c}+\sigma -R_{ s h}\right) -\left( y_{d}-\tau e_{ h}\right) \right] - \pi _{ uh}\left[ \left( y_{c}+\sigma -R_{ uh}\right) -\left( y_{d}-\tau e_{ h}\right) \right] \right] \\&\quad +\lambda _3\pi _{ uh}+\lambda _4\left( 1-\pi _{ uh}\right) +\lambda _5\pi _{ s h}+\lambda _6\left( 1-\pi _{ s h}\right) . \end{aligned}$$

The (first-order) Kuhn–Tucker conditions for this problem are given by:

$$\begin{aligned}&\frac{\partial L(\cdot )}{\partial R_{ uh}}=\theta _u\pi _{ uh}\delta _{ u}-\lambda _1\pi _{ uh}\delta _{ u}+\lambda _2\pi _{ uh}\le 0, \quad R_{ uh} \ge 0;\\&\quad \frac{\partial L(\cdot )}{\partial R_{ s h}}=\left( 1-\theta _u\right) \pi _{ s h}-\lambda _2\pi _{ s h}\le 0, \quad R_{ s h} \ge 0;\\&\quad \frac{\partial L(\cdot )}{\partial \pi _{ uh}}=\theta _u\left( \delta _{ u}R_{ uh}+\left( 1-\delta _{ u}\right) \gamma -\rho \right) +\lambda _1\left[ \delta _{ u}\left( y_{c}+\sigma -R_{ uh}\right) -\left( y_{d}-\tau e_{ h}\right) \right] ,\\&\quad \quad \ -\lambda _2\left[ \left( y_{c}+\sigma -R_{ uh}\right) -\left( y_{d}-\tau e_{ h}\right) \right] +\lambda _3-\lambda _4\le 0, \quad \pi _{ uh}\ge 0;\\&\quad \frac{\partial L(\cdot )}{\partial \pi _{ s h}}=\left( 1-\theta _u\right) \left( R_{ s h}+\left( 1-\theta _{ s}\right) \gamma -\rho \right) +\lambda _2\left[ \left( y_{c}+\sigma -R_{ s h}\right) -\left( y_{d}-\tau e_{ h}\right) \right] +\lambda _5-\lambda _6\le 0,\\&\quad \quad \quad \pi _{ s h}\ge 0;\\&\quad \frac{\partial L(\cdot )}{\partial \lambda _1}= \pi _{ uh}\left[ \delta _{ u}\left( y_{c}+\sigma -R_{ uh}\right) -\left( y_{d}-\tau e_{ h}\right) \right] \ge 0, \quad \lambda _1\ge 0; \\&\quad \frac{\partial L(\cdot )}{\partial \lambda _2}= \pi _{ s h}\left[ \left( y_{c}+\sigma -R_{ s h}\right) -\left( y_{d}-\tau e_{ h}\right) \right] -\pi _{ uh}\left[ \left( y_{c}+\sigma -R_{ uh}\right) -\left( y_{d}-\tau e_{ h}\right) \right] \ge 0, \quad \lambda _2\ge 0;\\&\quad \frac{\partial L(\cdot )}{\partial \lambda _3}=\pi _{ uh}\ge 0 , \quad \lambda _3\ge 0;\\&\quad \frac{\partial L(\cdot )}{\partial \lambda _4}=1-\pi _{ uh}\ge 0 , \quad \lambda _4\ge 0;\\&\quad \frac{\partial L(\cdot )}{\partial \lambda _5}=\pi _{ s h}\ge 0 , \quad \lambda _5\ge 0;\\&\quad \frac{\partial L(\cdot )}{\partial \lambda _6}=1-\pi _{ s h}\ge 0 , \quad \lambda _6\ge 0. \end{aligned}$$

1.3.3 7.3.3. Analysis of Regimes

Regime 1: $\pi _{sh}>0,\ \pi _{uh}=0,\ \pi _{sl}=0,\ \pi _{ul}=0$.

$R_{ch}>0$ if $\pi _{ch}>0$. With $\pi _{ s h}>0 \ \Rightarrow \ \lambda _5=0$ and $\partial L(\cdot )/\partial \pi _{ s h}=0$ (both follow from complementary slackness) and with $R_{ s h}>0\ \Rightarrow \ \partial L(\cdot )/\partial R_{ uh}=0$ (follows from complementary slackness). From that $\lambda _2=\left( 1-\theta _u\right)$. With $\lambda _2>0 \ \Rightarrow \ \partial L(\cdot ) / \partial \lambda _2=0$. Together with $\pi _{ uh}=0$ and $\pi _{ s h}>0$ it follows that $R_{ s h}=y_{c}+\sigma -y_{d}+\tau e_{ h}$. Furthermore, with $\lambda _2>0, \ \lambda _5=0, \ \pi _{ s h}>0, \ \partial L(\cdot )/\partial \pi _{ s h}=0 \ \Rightarrow \lambda _6>0$ and hence $\partial L(\cdot ) / \partial \lambda _6=0 \ \Rightarrow \ \pi _{ s h}=1$ (follows from complementary slackness). Regime 2: $\pi _{sh}>0,\ \pi _{uh}>0,\ \pi _{sl}=0,\ \pi _{ul}=0$.

With $\pi _{ uh}>0 \ \Rightarrow \ \lambda _3=0$ and $\pi _{ s h}>0 \ \Rightarrow \ \lambda _5=0$ (both follow from complementary slackness). With $R_{uh}>0 \ \Rightarrow \ \partial L(\cdot ) / \partial R_{ uh}=0$ and $R_{ s h}>0 \ \Rightarrow \ \partial L(\cdot ) / \partial R_{ s h}=0$ (both follow from complementary slackness). With $\partial L(\cdot ) / \partial R_{ s h}=0, \ \pi _{ s h}>0 \ \Rightarrow \lambda _2=\left( 1-\theta _u\right) >0$ and together with $\lambda _5=0, \ \partial L(\cdot ) / \partial \pi _{ s h}=0 \Rightarrow \ \lambda _6>0 \ \Rightarrow \ \ \pi _{ s h}=1$ (follows from complementary slackness). With $\partial L(\cdot ) / \partial R_{ uh}=0, \ \lambda _2=\left( 1-\theta _u\right) \ \Rightarrow \ \lambda _1=\theta _u+\left( 1-\theta _u\right) /\delta _{ u}$. Together with $\partial L(\cdot ) / \partial \pi _{ uh}=0$ it follows that:

$$\begin{aligned} \lambda _4\gtreqqless 0 \Leftrightarrow \delta _{ u}\left( y_{c}+\sigma \right) -y_{d}+\tau e_{ h}-\rho \gtreqqless \frac{1-\theta _u}{\theta _u}\left( y_{d}-\tau e_{ h}\right) \left( \frac{1}{\delta _{ u}}-1\right) -\left( 1-\delta _{ u}\right) \gamma . \end{aligned}$$

(6)

Note that (in)equality of the RHS of (6) determines the sign of $\lambda _4$. It follows that if $\delta _{ u}\left( y_{c}+\sigma \right) -y_{d}+\tau e_{ h}-\rho> \frac{1-\theta _u}{\theta _u}\left( y_{d}-\tau e_{ h}\right) \left( \frac{1}{\delta _{ u}}-1\right) -\left( 1-\delta _{ u}\right) \gamma \ \Rightarrow \lambda _{4}>0$ and hence $\pi _{ uh}= 1$ (follows from complementary slackness). If $\delta _{ u}\left( y_{c}+\sigma \right) -y_{d}+\tau e_{ h}-\rho = \frac{1-\theta _u}{\theta _u}\left( y_{d}-\tau e_{ h}\right) \left( \frac{1}{\delta _{ u}}-1\right) -\left( 1-\delta _{ u}\right) \gamma \ \Rightarrow \lambda _{4}=0$ and hence $\pi _{ uh}\in [0,1]$ is compatible with complementary slackness. If $\delta _{ u}\left( y_{c}+\sigma \right) -y_{d}+\tau e_{ h}-\rho< \frac{1-\theta _u}{\theta _u}\left( y_{d}-\tau e_{ h}\right) \left( \frac{1}{\delta _{ u}}-1\right) -\left( 1-\delta _{ u}\right) \gamma \ \Rightarrow \lambda _{4}<0$ and hence does not fulfil the first order conditions. That is, (6) yields the credit rationing condition for type uh:

$$\begin{aligned} \frac{\delta _{ u}\left( y_{c}+\sigma \right) -\rho +\left( 1-\delta _{ u}\right) \gamma -\left( y_{d}-\tau e_{ h}\right) }{\left( y_{d}-\tau e_{ h}\right) }< \frac{1-\theta _u}{\theta _u}\frac{1-\delta _u}{\delta _{ u}}. \end{aligned}$$

(7)

If (7) holds, uh-firms will not receive a loan and Regime 1 applies. If (7) does not hold, it follows: With $\partial L(\cdot ) \partial \lambda _2=0, \ \pi _{ s h}=1, \ R_{ uh}=y_{c}+\sigma -\frac{y_{d}-\tau e_{ h}}{\delta _{ u}}\ \Rightarrow \ R_{ s h}=y_{c}+\sigma -\left( \pi _{ uh}\left( (1-\delta _{ u})/\delta _{ u}\right) +1\right) \left( y_{d}-\tau e_{ h}\right)$. For $\pi _{ uh}=1\ \Rightarrow R_{ s h}=y_{c}+\sigma -\frac{y_{d}+-\tau e_{ h}}{\delta _{ u}}$.

Summary: For the case of a Pigouvian tax $\tau =1$ and given Assumption 1: Regime 2 is profit maximising if the credit rationing condition (7) does not hold. H-firms receive a loan and produce using the clean technology. L-firms do not apply for a loan and produce using the dirty technology.

Regime 1 is profit maximising if the credit rationing condition (7) holds. Only sh-firms receive a loan and produce with the clean technology. uh-firms would be able to pay the social cost of a clean investment ($\rho /(1-\delta _u)$) but do not receive a loan (credit rationing). L-firms do not apply for a loan and produce using the dirty technology.

It follows from Regimes 1 and 2 that $\pi ^*_{ s h}=1$, $R^*_{ s h}=y_{c}+\sigma -\frac{\left( \pi _{ uh}\left( 1-\delta _{ u}\right) +\delta _{ u}\right) \left( y_{d}-\tau e_{ h}\right) }{\delta _{ u}}$, and:

$$\begin{aligned} \pi ^*_{ uh}&= {\left\{ \begin{array}{ll} 1 \quad \text {if} \ \quad \delta _{ u}\left( y_{c}+\sigma \right) -y_{d}+\tau e_{ h}-\rho \ge \frac{1-\theta _u}{\theta _u}\left( y_{d}-\tau e_{ h}\right) \left( \frac{1}{\delta _{ u}}-1\right) -\left( 1-\delta _{ u}\right) \gamma \\ 0 \quad \text {if} \ \quad \delta _{ u}\left( y_{c}+\sigma \right) -y_{d}+\tau e_{ h}-\rho< \frac{1-\theta _u}{\theta _u}\left( y_{d}-\tau e_{ h}\right) \left( \frac{1}{\delta _{ u}}-1\right) -\left( 1-\delta _{ u}\right) \gamma \end{array}\right. }\\ R^*_{ uh}&= {\left\{ \begin{array}{ll} y_{c}+\sigma -\frac{y_{d}-\tau e_{ h}}{\delta _{ u}} \quad \text {if} \ \quad \delta _{ u}\left( y_{c}+\sigma \right) -y_{d}+\tau e_{ h}-\rho \ge \frac{1-\theta _u}{\theta _u}\left( y_{d}-\tau e_{ h}\right) \left( \frac{1}{\delta _{ u}}-1\right) -\left( 1-\delta _{ u}\right) \gamma \\ any \ value \quad \text {if} \ \quad \delta _{ u}\left( y_{c}+\sigma \right) -y_{d}+\tau e_{ h}-\rho < \frac{1-\theta _u}{\theta _u}\left( y_{d}-\tau e_{ h}\right) \left( \frac{1}{\delta _{ u}}-1\right) -\left( 1-\delta _{ u}\right) \gamma \end{array}\right. } \end{aligned}$$

1.3.4 7.3.4. Policy Instruments

With (7), we define:

$$\begin{aligned}&\Lambda \equiv \delta _{ u}\left( y_{c}+\sigma \right) -\rho -\left( y_{d}-\tau e_{ h}\right) \left[ 1+\frac{1-\theta _u}{\theta _u}\frac{1-\delta _{ u}}{\delta _{ u}}\right] +\left( 1-\delta _{ u}\right) \gamma , \end{aligned}$$

such that with $\Lambda <0$ there is credit rationing (and with $\Lambda \ge 0$ there is no credit rationing). Solving $\Lambda =0$ for $\sigma$ yields the minimum interest subsidy that resolves credit rationing:

$$\begin{aligned} \sigma ^*\equiv \frac{\rho +\left( y_{d}-\tau e_{ h}\right) \left[ 1+\frac{1-\theta _u}{\theta _u}\frac{1-\delta _{ u}}{\delta _{ u}}\right] -\left( 1-\delta _{ u}\right) \gamma }{\delta _{ u}}-y_{c}. \end{aligned}$$

(8)

Solving $\Lambda =0$ for $\gamma$ yields the minimum loan guarantee that resolves credit rationing:

$$\begin{aligned} \gamma ^*=\frac{\rho +\left( y_{d}-\tau e_{ h}\right) \left[ 1+\frac{1-\theta _u}{\theta _u}\frac{1-\delta _{ u}}{\delta _{ u}}\right] -\delta _{ u}\left( y_{c}+\sigma \right) }{1-\delta _{ u}}. \end{aligned}$$

(9)

Differentiation of (8) with $d\gamma =0$ yields the following relation between $\sigma ^*$ and $\tau$:

$$\begin{aligned} \frac{d\sigma *}{d\tau }=-\frac{e_h}{\delta _u}\left[ 1+\frac{1-\theta _u}{\theta _u}\frac{1-\delta _u}{\delta _u}\right] <0. \end{aligned}$$

(10)

Differentiation of (9) with $d\sigma =0$ yields the following relation between $\gamma ^*$ and $\tau$:

$$\begin{aligned} \frac{d\gamma *}{d\tau }=-\frac{e_h}{1-\delta _u}\left[ 1+\frac{1-\theta _u}{\theta _u}\frac{1-\delta _u}{\delta _u}\right] <0. \end{aligned}$$

(11)

1.3.5 7.3.5. Analysis of Profit Maximum

We show that the derived allocation in Regime 2 maximises the profit of the bank (global maximum). For brevity, we only consider Regime 2 which applies if the government chooses the social optimal combination of policy instruments. We define the aggregate expected profit from lending to the four types of firms as:

$$\begin{aligned}&B\equiv \Theta _{sh}\left( R_{sh}-\rho \right) +\Theta _{uh}\left[ \delta _u R_{uh}+\left( 1-\delta _u\right) \gamma -\rho \right] \\&+\Theta _{sl}\left( R_{sl}-\rho \right) +\Theta _{ul}\left[ \delta _u R_{ul}+\left( 1-\delta _u\right) \gamma -\rho \right] , \end{aligned}$$

(12)

where $\Theta _{cd}$ is the mass of loans provided to type cd. The maximum loan repayment of each type is given by solving the respective (binding) participation constraint (expected profit=0) for $R_k$. We use these upper limits of $R_{sl}$ and $R_{ul}$ to show that even if the bank could provide loans to sl- and ul-firms at the maximum level of the loan repayment and if this would not affect levels of $R^*_{sh}$ and $R^*_{uh}$ except for the potential reallocation of interest subsidies, providing loans to sl- and ul-firms decreases aggregate expected profit (B). To show this, we substitute $R^*_{sh}$, $R^*_{uh}$, and the maximum loan repayments for sl- and ul-firms into the aggregate expected profit and further split the profits from lending to each firm type into three main components, i.e. the profits of the borrowing firm, denoted with pr, the interest rate subsidy, denoted with $\sigma$, and the loan guarantee, denoted with $\gamma$:

$$\begin{aligned} B'&\equiv \Theta ^{pr}_{sh}\left[ \delta _u\left( y_c-\frac{y_d-\tau e_h}{\delta _u}\right) -\rho \right] +\Theta ^{\sigma }_{sh}\sigma \\&+ \Theta ^{pr}_{uh}\left[ \delta _u\left( y_c-\frac{y_d-\tau e_h}{\delta _u}\right) -\rho \right] +\Theta ^{\sigma }_{uh}\delta _u\sigma +\Theta ^{\gamma }_{uh}\left( 1-\delta _u\right) \gamma \\&+\Theta ^{pr}_{sl}\left( y_c-y_d+\tau e_l-\rho \right) +\Theta ^{\sigma }_{sl}\sigma \\&+ \Theta ^{pr}_{ul}\left[ \delta _u\left( y_c-\frac{y_d-\tau e_l}{\delta _u}\right) -\rho \right] +\Theta ^{\sigma }_{ul}\delta _u\sigma +\Theta ^{\gamma }_{ul}\left( 1-\delta _u\right) \gamma . \end{aligned}$$

(13)

Total differentiation, assuming $d\sigma =d\gamma =0$, yields:

$$\begin{aligned} dB'&\equiv d\Theta ^{pr}_{sh}\left[ \delta _u\left( y_c-\frac{y_d-\tau e_h}{\delta _u}\right) -\rho \right] +d\Theta ^{\sigma }_{sh}\sigma ,\\&\quad + d\Theta ^{pr}_{uh}\left[ \delta _u\left( y_c-\frac{y_d-\tau e_h}{\delta _u}\right) -\rho \right] +d\Theta ^{\sigma }_{uh}\delta _u\sigma +d\Theta ^{\gamma }_{uh}\left( 1-\delta _u\right) \gamma ,\\&\quad +d\Theta ^{pr}_{sl}\left( y_c-y_d+\tau e_l-\rho \right) +d\Theta ^{\sigma }_{sl}\sigma , \\&\quad + d\Theta ^{pr}_{ul}\left[ \delta _u\left( y_c-\frac{y_d-\tau e_l}{\delta _u}\right) -\rho \right] +d\Theta ^{\sigma }_{ul}\delta _u\sigma +d\Theta ^{\gamma }_{ul}\left( 1-\delta _u\right) \gamma . \end{aligned}$$

(14)

With a fixed budget chosen according to the funding requirements of credit market instruments in Regime 2, the following relations can be derived:

$$\begin{aligned} \text {Interest rate subsidy:} \quad&\left( \Theta ^{\sigma }_{sh}+\Theta ^{\sigma }_{uh}\delta _u+\Theta ^{\sigma }_{sl}+\Theta ^{\sigma }_{ul}\delta _u\right) \sigma =\left[ \theta _h(1-\theta _u)+\theta _h\theta _u\delta _u\right] \sigma ,\\ \end{aligned}$$

(15)

$$\begin{aligned} \text {Loan guarantee:} \quad&\left[ \Theta ^{\gamma }_{uh}(1-\delta _u)+\Theta ^{\gamma }_{ul}(1-\delta _u)\right] \gamma =(1-\delta _u)\theta _h\theta _u\gamma . \end{aligned}$$

(16)

Total differentiation, assuming $d\sigma =d\gamma =0$, yields:

$$\begin{aligned} \text {Interest rate subsidy:} \quad&\left( d\Theta ^{\sigma }_{sh}+d\Theta ^{\sigma }_{uh}\delta _u+d\Theta ^{\sigma }_{sl}+d\Theta ^{\sigma }_{ul}\delta _u\right) \sigma =0\\ \end{aligned}$$

(17)

$$\begin{aligned} \text {Loan guarantee:} \quad&\left[ ]d\Theta ^{\gamma }_{uh}(1-\delta _u)+d\Theta ^{\gamma }_{ul}(1-\delta _u)\right] \gamma =0. \end{aligned}$$

(18)

Now, consider $\sigma =\gamma =0$. Using (14) and setting $d\Theta ^{i}_{sh}=d\Theta ^{i}_{uh}=d\Theta ^{i}_{ul}=0$ with $i\in \lbrace pr, \sigma , \gamma \rbrace$, expanding lending to sl-firms, i.e. $d\Theta ^{i}_{sh}>0$, yields:

$$\begin{aligned} dB'=d\Theta ^{pr}_{sl}\left[ \left( y_c-\left( y_d-\tau e_l\right) \right) -\rho \right] <0. \end{aligned}$$

(19)

Setting $d\Theta ^{i}_{sh}=d\Theta ^{i}_{uh}=d\Theta ^{i}_{sl}=0$ with $i\in \lbrace pr, \sigma , \gamma \rbrace$, expanding lending to ul-firms, i.e. $d\Theta ^{i}_{ul}>0$, yields:

$$\begin{aligned} dB'=d\Theta ^{pr}_{ul}\left[ \delta _u\left( y_c-\frac{y_d-\tau e_l}{\delta _u}\right) -\rho \right] <0. \end{aligned}$$

(20)

Both inequalities follow immediately with (1).

Now, consider the case with $\sigma =\sigma ^*,\gamma =\gamma ^*$ and $\Theta ^{i}_{sh}=\theta _h(1-\theta _u), \Theta ^{i}_{uh}=\theta _h\theta _u$, with $i\in \lbrace pr,\sigma ,\gamma \rbrace$, and expanding lending to sl-firms, i.e. $d\Theta ^{i}_{sl}>0$. By assumption, there is no effect on $\Theta ^{pr}_{sh}$, $\Theta ^{pr}_{uh}$, $\Theta ^{pr}_{ul}$, i.e. $d\Theta ^{pr}_{sh}=d\Theta ^{pr}_{uh}=\Theta ^{pr}_{ul}=0$. However, due to the fixed budget for the credit market instruments, the reallocation of capital market instruments has to be taken into account. Using (17) and (18) in (14) yields:

$$\begin{aligned} dB'=&\, d\Theta ^{\sigma }_{sh}\sigma +d\Theta ^{\sigma }_{uh}\delta _u\sigma +d\Theta ^{\gamma }_{uh}\left( 1-\delta _u\right) \gamma +d\Theta ^{pr}_{sl}\left( y_c-y_d+\tau e_l-\rho \right] \\&\quad -\left( d\Theta ^{\sigma }_{sh}+d\Theta ^{\sigma }_{uh}\delta _u+d\Theta ^{\sigma }_{ul}\delta _u\right) \sigma -\left[ d\Theta ^{\gamma }_{uh}(1-\delta _u)+d\Theta ^{\gamma }_{ul}(1-\delta _u)\right] \gamma \\&\quad + d\Theta ^{\sigma }_{ul}\delta _u\sigma +d\Theta ^{\gamma }_{ul}\left( 1-\delta _u\right) \gamma =d\Theta ^{pr}_{sl}\left( y_c-y_d+\tau e_l-\rho \right) <0, \end{aligned}$$

(21)

where the inequality follows immediately with (1). Analogously, it can be derived that expanding lending to ul-firms decreases aggregate profit. Hence, any deviation from the allocation derived in Regime 2 decreases profit of the bank and therefore the allocation in Regime 2 is a global maximum.

1.3.6 7.3.6. Government Budgets

To determine the cheaper option from the government’s perspective, we compare the costs of both instruments. The government budgets for the interest rate subsidy, $G_{\sigma }$, and the loan guarantee, $G_{\gamma }$, are:

$$\begin{aligned} G_{\sigma }&=\theta _h\left[ \theta _u \delta _u \sigma ^*+ \left( 1-\theta _u\right) \sigma ^*\right] ,\\ \end{aligned}$$

(22)

$$\begin{aligned} G_{\gamma }&=\theta _h\left[ \theta _u\left( 1-\delta _u\right) \gamma ^*\right] . \end{aligned}$$

(23)

We can use Eqs. (8) and (9) to determine the relation of $\sigma ^*$ and $\gamma ^*$ (if both instruments are used isolated):

$$\begin{aligned} \sigma ^*=\frac{1-\delta _u}{\delta _u}\gamma ^*. \end{aligned}$$

(24)

Combining (24) with Eqs. (22) and (23) yields:

$$\begin{aligned} G_{\sigma }-G_{\gamma }=\theta _h\left( 1-\theta _u\right) \gamma ^*\frac{1-\delta _u}{\delta _u}>0 \quad if \quad \delta _u<1. \end{aligned}$$

1.4 7.4. Imperfect Information with Non-Pigouvian Emission Taxes

In this subsection, we derive equilibrium contracts and the associated allocation of firms in a scenario with the use of an emission tax only and under the assumption of information asymmetries between borrowers, the bank, and the government. As above, we restrict the presentation of the analysis to the economically interesting (group of) regimes:

Regime 1

(under-investment): $\pi _{sh}>0$, $\pi _{uh}=0$, $\pi _{sl}=0$, $\pi _{ul}=0$;

Regime 2

(optimal investment): $\pi _{sh}>0$, $\pi _{uh}>0$, $\pi _{sl}=0$, $\pi _{ul}=0$;

Regime 3

(over-investment): $\pi _{sh}>0$, $\pi _{uh}>0$, $\pi _{sl}>0$, $\pi _{ul}\ge 0$.

1.4.1 7.4.1. Maximisation Problem

The bank maximises its expected benefit from lending subject to the PCs and ICs of three borrowers:

$$\begin{aligned} \max _{\pi _{uh}, R_{uh},\pi _{sh},R_{sh},\pi _{sl},R_{sl}} \ B=&\, \ \theta _h\left[ \theta _u B_{uh}+\left( 1-\theta _u\right) B_{sh}\right] +(1-\theta _u)(1-\theta _h)B_{sl}\\ =&\,\ \theta _{h}\left[ \theta _u \pi _{ uh}\left( \delta _{ u}R_{ uh}-\rho \right) +\left( 1-\theta _u\right) \pi _{ s h}\left( R_{ s h}-\rho \right) \right] +(1-\theta _u)(1-\theta _h)\pi _{sl}\left( R_{sl}-\rho \right) \\ \text {subject to} \quad (PC_{ch}) \quad&\pi _{ch}\left[ \delta _u\left( y_{c}-R_{ch}\right) -\left( y_{d}-\tau e_{ h}\right) \right] \ge 0\\ \quad (PC_{sl}) \quad&\pi _{sl}\left[ \left( y_{c}-R_{sl}\right) -\left( y_{d}-\tau e_{ l}\right) \right] \ge 0\\ (IC_{sh,uh}) \quad&\pi _{sh}\left[ \left( y_{c}-R_{sh}\right) -\left( y_{d}-\tau e_{h}\right) \right] \ge \pi _{uh}\left[ \left( y_{c}-R_{uh}\right) -\left( y_{d}-\tau e_{ h}\right) \right] \\ (IC_{sh,sl}) \quad&\pi _{sh}\left[ \left( y_{c}-R_{sh}\right) -\left( y_{d}-\tau e_{h}\right) \right] \ge \pi _{sl}\left[ \left( y_{c}-R_{sl}\right) -\left( y_{d}-\tau e_{ h}\right) \right] \\ (IC_{uh,sl}) \quad&\pi _{uh}\left[ \delta _u\left( y_{c}-R_{uh}\right) -\left( y_{d}-\tau e_{h}\right) \right] \ge \pi _{sl}\left[ \delta _u\left( y_{c}-R_{sl}\right) -\left( y_{d}-\tau e_{ h}\right) \right] \\&0\le \pi _{sh} \le 1, \quad 0\le \pi _{uh} \le 1, \quad 0\le \pi _{sl} \le 1. \end{aligned}$$

(25)

1.4.2 7.4.2. Kuhn–Tucker Approach

The Lagrangian to the profit maximisation problem of the bank is:

$$\begin{aligned}&L\left( \pi _{sh},R_{sh},\pi _{uh},R_{uh},\pi _{sl},R_{sl},\lambda _0,\lambda _1,\lambda _2, \lambda _3,\lambda _4,\lambda _5,\lambda _6,\lambda _7,\lambda _8,\lambda _9,\lambda _{10},\lambda _{11}\right) =\\&\quad \theta _h(1-\theta _u)\pi _{sh}\left( R_{sh}-\rho \right) +\theta _h\theta _u\pi _{uh}\left( \delta _{u}R_{uh}-\rho \right) +(1-\theta _h)(1-\theta _u)\pi _{sl}\left( R_{sl}-\rho \right) \\&\quad +\lambda _{0}\pi _{sh}\left[ \left( y_{c}-R_{sh}\right) -\left( y_{d}-\tau e_h\right) \right] \\&\quad +\lambda _{1}\pi _{uh}\left[ \delta _{u}\left( y_{c}-R_{uh}\right) -\left( y_{d}-\tau e_h\right) \right] +\lambda _{2}\pi _{sl}\left[ \left( y_{c}-R_{sl}\right) -\left( y_{d}-\tau e_l\right) \right] \\&\quad +\lambda _{3}\left[ \pi _{sh}\left[ \left( y_{c}-R_{sh}\right) -\left( y_{d}-\tau e_h\right) \right] -\pi _{uh}\left[ \left( y_{c}-R_{uh}\right) -\left( y_{d}-\tau e_h\right) \right] \right] \\&\quad +\lambda _{4}\left[ \pi _{sh}\left[ \left( y_{c}-R_{sh}\right) -\left( y_{d}-\tau e_h\right) \right] -\pi _{sl}\left[ \left( y_{c}-R_{sl}\right) -\left( y_{d}-\tau e_h\right) \right] \right] \\&\quad +\lambda _{5}\left[ \pi _{uh}\left[ \delta _u\left( y_{c}-R_{uh}\right) -\left( y_{d}-\tau e_h\right) \right] -\pi _{sl}\left[ \delta _u\left( y_{c}-R_{sl}\right) -\left( y_{d}-\tau e_h\right) \right] \right] \\&\quad +\lambda _{6}\pi _{sh}+\lambda _{7}\left( 1-\pi _{sh}\right) +\lambda _{8}\pi _{uh}+\lambda _{9}\left( 1-\pi _{uh}\right) +\lambda _{10}\pi _{sl}+\lambda _{11}\left( 1-\pi _{sl}\right) \end{aligned}$$

The (first-order) Kuhn–Tucker conditions are given by:

$$\begin{aligned} \frac{\partial L(\cdot )}{\partial \pi _{sh}}=&\, \theta _h(1-\theta _u)\left( R_{sh}-\rho \right) +\left( \lambda _0+\lambda _3+\lambda _4\right) \left[ \left( y_{c}-R_{sh}\right) -\left( y_{d}-\tau e_h\right) \right] +\lambda _6-\lambda _7 \le 0, \quad \pi _{sh}\ge 0;\\ \frac{\partial L(\cdot )}{\partial R_{sh}}=&\, \pi _{sh}\left[ \theta _h(1-\theta _u)-\lambda _0-\lambda _3-\lambda _4\right] \le 0, \quad R_{sh}\ge 0;\\ \frac{\partial L(\cdot )}{\partial \pi _{uh}}=&\, \theta _h\theta _u\left( \delta _u R_{uh}-\rho \right) +\left( \lambda _1+\lambda _5\right) \left[ \delta _u\left( y_{c}-R_{uh}\right) -\left( y_{d}-\tau e_h\right) \right] \\&\quad -\lambda _3\left[ \left( y_{c}-R_{uh}\right) -\left( y_{d}-\tau e_h\right) \right] +\lambda _8-\lambda _9 \le 0, \quad \pi _{uh}\ge 0;\\ \frac{\partial L(\cdot )}{\partial R_{uh}}=&\,\pi _{uh}\left[ \delta _u\left( \theta _h\theta _u-\lambda _1-\lambda _5\right) +\lambda _3\right] \le 0, \quad R_{uh}\ge 0;\\ \frac{\partial L(\cdot )}{\partial \pi _{sl}}=&\, (1-\theta _h)(1-\theta _u)\left( R_{sl}-\rho \right) +\lambda _2\left[ \left( y_{c}-R_{sl}\right) -\left( y_{d}-\tau e_l\right) \right] -\lambda _4\left[ \left( y_{c}-R_{sl}\right) -\left( y_{d}-\tau e_h\right) \right] \\&\quad -\lambda _5\left[ \delta _u\left( y_{c}-R_{sl}\right) -\left( y_{d}-\tau e_h\right) \right] +\lambda _{10}-\lambda _{11}\le 0, \quad \pi _{sl}\ge 0;\\ \frac{\partial L(\cdot )}{\partial R_{sl}}=&\,(1-\theta _h)(1-\theta _u)\pi _{sl}+\left( \lambda _4-\lambda _2\right) \pi _{sl}+\lambda _5\pi _{sl}\delta _u \le 0, \quad R_{sl}\ge 0;\\ \frac{\partial L(\cdot )}{\partial \lambda _{0}}=&\, \pi _{sh}\left[ \left( y_{c}-R_{sl}\right) -\left( y_{d}-\tau e_h\right) \right] \ge 0, \quad \lambda _0 \ge 0;\\ \frac{\partial L(\cdot )}{\partial \lambda _{1}}=&\, \pi _{uh}\left[ \delta _u\left( y_{c}-R_{uh}\right) -\left( y_{d}-\tau e_h\right) \right] \ge 0, \quad \lambda _1 \ge 0;\\ \frac{\partial L(\cdot )}{\partial \lambda _{2}}=&\, \pi _{sl}\left[ \left( y_{c}-R_{sl}\right) -\left( y_{d}-\tau e_l\right) \right] \ge 0, \quad \lambda _2 \ge 0;\\ \frac{\partial L(\cdot )}{\partial \lambda _{3}}=&\, \pi _{sh}\left[ \left( y_{c}-R_{sh}\right) -\left( y_{d}-\tau e_l\right) \right] - \pi _{uh}\left[ \left( y_{c}-R_{uh}\right) -\left( y_{d}-\tau e_h\right) \right] \ge 0, \quad \lambda _3 \ge 0;\\ \frac{\partial L(\cdot )}{\partial \lambda _{4}}=&\, \pi _{sh}\left[ \left( y_{c}-R_{sh}\right) -\left( y_{d}-\tau e_h\right) \right] - \pi _{sl}\left[ \left( y_{c}-R_{sl}\right) -\left( y_{d}-\tau e_h\right) \right] \ge 0, \quad \lambda _4 \ge 0;\\ \frac{\partial L(\cdot )}{\partial \lambda _{5}}=&\, \pi _{uh}\left[ \delta _u\left( y_{c}-R_{uh}\right) -\left( y_{d}-\tau e_h\right) \right] - \pi _{sl}\left[ \delta _u\left( y_{c}-R_{sl}\right) -\left( y_{d}-\tau e_h\right) \right] \ge 0, \quad \lambda _5 \ge 0;\\ \frac{\partial L(\cdot )}{\partial \lambda _{6}}=&\,\pi _{sh}\ge 0, \quad \lambda _6\ge 0; \quad \frac{\partial L(\cdot )}{\partial \lambda _{7}}=\left( 1-\pi _{sh}\right) \ge 0, \quad \lambda _7\ge 0; \quad \frac{\partial L(\cdot )}{\partial \lambda _{8}}=\pi _{uh}\ge 0, \quad \lambda _8\ge 0;\\ \quad \frac{\partial L(\cdot )}{\partial \lambda _{9}}=&\,\left( 1-\pi _{uh}\right) \ge 0, \quad \lambda _9\ge 0; \quad \frac{\partial L(\cdot )}{\partial \lambda _{10}}=\pi _{sl}\ge 0, \quad \lambda _{10}\ge 0; \quad \frac{\partial L(\cdot )}{\partial \lambda _{11}}=\left( 1-\pi _{sl}\right) \ge 0, \quad \lambda _{11}\ge 0. \end{aligned}$$

1.4.3 7.4.3. Analysis of Regimes

We analyse the different regimes in two steps. First, we use the characteristics of Regime 3 to show under what conditions the bank will prefer (i) Regime 2 over Regime 1 (credit rationing condition of uh-firms) and (ii) Regime 3 over Regime 2 (credit rationing condition of sl-firms). Second, we complement the analyses of the regime boundaries (equilibrium allocation of funds) and derive equilibrium values of the loan repayment for the different regimes.

For Regime 3, with $\pi _{sh}>0$, $\pi _{uh}>0$, $\pi _{sl}>0$, it follows: With $\pi _{sh}>0 \Rightarrow \lambda _6=0$; with $\pi _{uh}>0 \Rightarrow \lambda _8=0$; and with $\pi _{sl}>0 \Rightarrow \lambda _{10}=0$ (all follow from complementary slackness). With $R_{sh}>0 \Rightarrow \partial L(\cdot )/\partial R_{sh}=0$; with $R_{uh}>0 \Rightarrow \partial L(\cdot )/\partial R_{uh}=0$; and with $R_{sl}>0 \Rightarrow \partial L(\cdot )/\partial R_{sl}=0$ (all follow from complementary slackness).

Solving $\partial L(\cdot )/ \partial R_{sh}=0$ for $\lambda _3+\lambda _4$, substituting into $\partial L(\cdot )/ \partial \pi _{sh}\le 0$ and solving for $\lambda _7$ yields: $\lambda _7\ge \theta _h(1-\theta _u)\left[ \left( y_{c}-\rho \right) -\left( y_{d}-\tau e_h\right) \right]$, where the RHS is greater than 0, which follows with Assumption 1 and $\tau \ge 1$. With $\lambda _7>0 \Rightarrow \partial L(\cdot )/\partial \lambda _7 =0$ and hence $\pi _{sh}=1$ (follows from complementary slackness).

Profit maximisation requires $R_{sl}=y_{c}-\left( y_{d}-\tau e_l\right)$, i.e. the participation constraint of sl-firms holds with equality (if $\pi _{sl}>0$). From this it follows that $\partial L(\cdot )/\partial \lambda _2=0$. With $\partial L(\cdot )/\partial \lambda _2=0$ it follows that $\pi _{sl}\left[ \delta _u\left( y_{c}-R_{sl}\right) -\left( y_{d}-\tau e_h\right) \right] >0$, and with $\partial L(\cdot )/\partial \lambda _{5}\ge 0$ it follows that $\pi _{uh}\left[ \delta _u\left( y_{c}-R_{uh}\right) -\left( y_{d}-\tau e_h\right) \right] >0$ and hence $\partial L(\cdot )/\partial \lambda _{1}>0$. From this it follows that $\lambda _1=0$ (follows from complementary slackness).

Now, we show that for the relevant parameter space $\lambda _4=0$. Note that profit maximisation requires choosing $R_{uh}\ge R_{sl}$ and $\pi _{uh}\ge \pi _{sl}$. We consider two cases, (i) $\pi _{uh}>\pi _{sl}$ and (ii) $\pi _{uh}=\pi _{sl}$. For (i) $\pi _{uh}>\pi _{sl}$: Combining $\partial L(\cdot )/\partial \lambda _3>0$ and $\partial L(\cdot )/\partial \lambda _4>0$ yields the condition for which $\partial L(\cdot )/\partial \lambda _3>\partial L(\cdot )/\partial \lambda _4$:

$$\begin{aligned} y_{c}-\left( y_{d}-\tau e_h\right) \ge \frac{\pi _{uh}R_{uh}-\pi _{sl}R_{sl}}{\pi _{uh}-\pi _{sl}}. \end{aligned}$$

(26)

Rearranging $\partial L(\cdot )/\partial \lambda _5>0$ yields:

$$\begin{aligned} \delta _uy_{c}-\left( y_{d}-\tau e_h\right) \ge \frac{\pi _{uh}R_{uh}-\pi _{sl}R_{sl}}{\pi _{uh}-\pi _{sl}}. \end{aligned}$$

(27)

Note that if weak inequality (27) holds, weak inequality (26) holds with strict inequality (follows immediately with $1>\delta _u$). Hence, for (i) $\pi _{uh}>\pi _{sl}$: If $\partial L(\cdot )/\partial \lambda _5\ge 0$ and $\partial L(\cdot )/\partial \lambda _3\ge 0$, the shadow price of relaxing the incentive compatibility constraint that sh-firms do not choose a contract designed for sl-firms is zero, i.e. $\lambda _4=0$. For (ii) $\pi _{uh}=\pi _{sl}$: If $\pi _{uh}=\pi _{sl} \Rightarrow R_{uh}=R_{sl}$, which follows from $\partial L(\cdot )/\partial \lambda _5\ge 0$ and Assumption 1. In this case, $\partial L(\cdot )/\partial \lambda _3\ge 0$, $\partial L(\cdot )/\partial \lambda _5\ge 0$ hold with strict equality, $\partial L(\cdot )/\partial \lambda _4\ge 0$ just holds with strict equality and hence $\lambda _4=0$.

Solving $\partial L(\cdot )/ \partial R_{uh}=0$ for $\lambda _1+\lambda _5$, substituting into $\partial L(\cdot )/ \partial \pi _{uh}\le 0$, using $\lambda _1=0$, $\lambda _4=0$, and $\lambda _3=\theta _h(1-\theta _u)$ (follows with $\lambda _4=0$ and $\partial L(\cdot )/ \partial R_{uh}=0$), and solving for $\lambda _9$ yields: $\lambda _9= \theta _h\theta _u\left[ \left( \delta _u y_{c}-\rho \right) -\left( y_{d}-\tau e_h\right) \right] -\theta _h(1-\theta _u)\left( y_{d}-\tau e_h\right) (1-\delta _u)/\delta _u$. It follows that if $\theta _h\theta _u\left[ \left( \delta _u y_{c}-\rho \right) \right.$ $\left. - \left( y_{d}-\tau e_h\right) \right] \ge \theta _h(1-\theta _u)\left( y_{d}-\tau e_h\right) \left( (1-\delta _u)/\delta _u\right)$ $\Rightarrow$ $\lambda _9\ge 0$ and hence $\pi _{uh}=1$ (follows from complementary slackness).

Substituting $\lambda _3=\theta _h(1-\theta _u)$ (follows with $\lambda _4=0$ and $\partial L(\cdot )/ \partial R_{uh}=0$), $\lambda _5=\lambda _3(\delta _ds/\delta _u)+\theta _h\theta _u$ (follows with $\lambda _1=0$), and $\lambda _{10}$ into $\partial L(\cdot )/ \partial \pi _{sl}=0$ yields: $\lambda _{11}=(1-\theta _h)(1-\theta _u)\left[ \left( y_{c}-\rho \right) -\left( y_{d}-\tau e_l\right) \right] +\theta _h(1-\theta _u)\left[ \frac{1}{\delta _u}\left( y_{d}-\tau e_h\right) -\left( y_{d}-\tau e_l\right) \right] +\theta _h\theta _u\left[ \left( y_{d}-\tau e_h\right) -\delta _u\left( y_{d}-\tau e_l\right) \right]$.

It follows that if $(1-\theta _h)(1-\theta _u)\left[ \left( y_{d}-\tau e_l\right) -\left( y_{c}-\rho \right) \right] \le \theta _h(1-\theta _u)\left[ \frac{1}{\delta _u}\left( y_{d}-\tau e_h\right) -\left( y_{d}-\tau e_l\right) \right] +\theta _h\theta _u\left[ \left( y_{d}-\tau e_h\right) -\delta _u\left( y_{d}-\tau e_l\right) \right]$ $\Rightarrow$ $\lambda _{11}\ge 0$ and hence $\pi _{sl}=1$ (follows from complementary slackness).

Summing up: There are two credit rationing conditions:

$$\begin{aligned} \theta _h\theta _u\left[ \left( \delta _u y_{c}-\rho \right) - \left( y_{d}-\tau e_h\right) \right]&\le \theta _h(1-\theta _u)\left( y_{d}-\tau e_h\right) \left( (1-\delta _u)/\delta _u\right) ; \end{aligned}$$

(28)

$$\begin{aligned}&(1-\theta _h)(1-\theta _u)\left[ \left( y_{d}-\tau e_l\right) -\left( y_{c}-\rho \right) \right] \\ \ge \theta _h(1-\theta _u)\left[ \frac{1}{\delta _u}\left( y_{d}-\tau e_h\right) -\left( y_{d}-\tau e_l\right) \right]&+\theta _h\theta _u\left[ \left( y_{d}-\tau e_h\right) -\delta _u\left( y_{d}-\tau e_l\right) \right] . \end{aligned}$$

(29)

Solving (28) and (29), respectively, for $\tau$ yields:

$$\begin{aligned} \tau&=\frac{y_{d}-A\left( \delta _uy_{c}-\rho \right) }{e_h}\equiv \tau _{uh}, \quad with \quad A\equiv \frac{\theta _h\theta _u\delta _u}{\theta _h\theta _u\delta _u+\theta _h(1-\theta _u)\left( 1-\delta _u\right) },\\ \tau&=\frac{\left[ 1-B\left( \frac{1-\delta _u}{\delta _u}\right) \right] y_{d}-\left( y_{c}-\rho \right) }{\left[ 1-B\left( \frac{e_h-e_l\delta _u}{e_l\delta _u}\right) \right] e_l}\equiv \tau _{sl}, \quad with \quad B\equiv \left[ \frac{\theta _h(1-\theta _u)+\theta _h\theta _u\delta _u}{(1-\theta _h)(1-\theta _u)}\right] . \end{aligned}$$

In the next step, we distinguish two cases. First, the tax that resolves credit rationing of uh-firms will result in credit rationing of sl-firms. Second, the tax that resolves credit rationing of uh-firms will also resolve credit rationing of sl-firms.

Note that any contract that is accepted by sl-firms fulfils the participation constraint of uh-type firms. Profit maximising behaviour of the bank then ensures that if sl-firms receive a loan, there is no credit rationing of uh-firms. Hence, $\tau =\min \left\{ \tau _{uh},\tau _{sl}\right\}$ resolves credit rationing of uh-type.

For the first case, it is sufficient to show that there exists a (non-empty parameter space with) $\tau _{uh}\le \tau <\tau _{sl}$, in particular $\tau _{uh}<\tau _{sl}$ for some parameter values. With $\theta _h(1-\theta _u)\rightarrow 0$, $(1-\theta _h)(1-\theta _u)\rightarrow 0$ it follows:

$$\begin{aligned} \left. \tau _{uh}\right| _{\theta _h(1-\theta _u)\rightarrow 0,(1-\theta _h)(1-\theta _u)\rightarrow 0}<\left. \tau _{sl}\right| _{\theta _h(1-\theta _u)\rightarrow 0,(1-\theta _h)(1-\theta _u)\rightarrow 0} \Leftrightarrow \frac{y_d-\left( \delta _u y_c-\rho \right) }{y_d}< \frac{e_h}{e_l}, \end{aligned}$$

which is true (see Assumption 1).

For the second case, it is sufficient to show that there exists a (non-empty parameter space with) $\tau _{sl}\le \tau =\tau _{uh}$: With $\theta _h\theta _u\rightarrow 0$ it follows:

$$\begin{aligned}&\left. \tau _{sl}\right| _{\theta _h\theta _u\rightarrow 0}<\left. \tau _{uh}\right| _{\theta _h\theta _u\rightarrow 0} \Leftrightarrow \frac{\left[ 1-\frac{\theta _h(1-\theta _u)}{(1-\theta _h)(1-\theta _u)}\left( \frac{1-\delta _u}{\delta _u}\right) \right] y_{d}-\left( y_{c}-\rho \right) }{\left[ 1-\frac{\theta _h(1-\theta _u)}{(1-\theta _h)(1-\theta _u)}\left( \frac{e_h-e_l\delta _u}{e_l\delta _u}\right) \right] e_l}<\frac{y_d}{e_h}\\&\Leftrightarrow \left[ \left[ 1-\frac{\theta _h(1-\theta _u)}{(1-\theta _h)(1-\theta _u)}\left( \frac{1-\delta _u}{\delta _u}\right) \right] -\left[ 1-\frac{\theta _h(1-\theta _u)}{(1-\theta _h)(1-\theta _u)}\left( \frac{e_h-e_l\delta _u}{e_l\delta _u}\right) \right] \frac{e_l}{e_h}\right] y_{d}\\&\quad = \left( 1+\frac{\theta _h(1-\theta _u)}{(1-\theta _h)(1-\theta _u)}(1-\frac{e_l}{e_h})-\frac{e_l}{e_h}\right) y_{d}<\left( y_{c}-\rho \right) . \end{aligned}$$

The above inequality holds for sufficiently large $(1-\theta _h)(1-\theta _u)$ and $e_h/e_l$ (in line with Assumption 1). Note that multiplication by the term $\left[ 1-\frac{\theta _h(1-\theta _u)}{(1-\theta _h)(1-\theta _u)}\left( \frac{e_h-e_l\delta _u}{e_l\delta _u}\right) \right] e_l$ (line 2 in the inequality above) does not change the inequality as resolving credit rationing of sl-firms requires inequality of the credit rationing condition (29) to decrease (weaken) in $\tau$, which is the case only if: $\delta _u\left( 1+\frac{\theta _{s_l}}{\theta _h(1-\theta _u)+\delta _u\theta _h\theta _u}\right) >\frac{e_h}{e_l}$ (follows from differentiation of (29)) and hence $\left[ 1-\frac{\theta _h(1-\theta _u)}{(1-\theta _h)(1-\theta _u)}\left( \frac{e_h-e_l\delta _u}{e_l\delta _u}\right) \right] e_l>0$. Therefore, potential credit rationing of uh-firms can be addressed by choosing a sufficiently large emission tax. However, this might result in misallocation of sl-firms (choosing clean investment).

Equilibrium conditions for the loan repayment are derived using binding participation constraints of sh-, uh-, and sl-firms, i.e. $\partial L(\cdot )/\partial \lambda _0=0$, $\partial L(\cdot )/\partial \lambda _1=0$, $\partial L(\cdot )/\partial \lambda _2=0$, respectively: If (28) and (29) hold, $\pi _{sh}=1$, $\pi _{uh}=0$, $\pi _{sl}=0$. Hence, $\lambda _3=\lambda _5=0$, with $\partial L(\cdot ) / \partial R_{sh}\ge 0$ it follows that $\lambda _0>0$ and hence $\partial L(\cdot )/\partial \lambda _0=0$ (follows from complementary slackness). Therefore, $R^*_{sh}=y_c-(y_d-\tau e_h)$.

If (29) holds and (28) does not hold, $\pi _{sh}=1$, $\pi _{uh}=1$, $\pi _{sl}=0$. As derived above, $\lambda _1>0$ and hence $\partial L(\cdot )/\partial \lambda _1=0$ (follows with complementary slackness). Therefore, $R^*_{uh}=y_c-(y_d-\tau e_h)/\delta _u$. With $\pi _{sh}=\pi _{uh}=1$, $\lambda _3>0$, $\partial L(\cdot )/\partial \lambda 3=0$ (follows from complementary slackness) and hence $R^*_{sh}= y_c-(y_d-\tau e_h)/\delta _u$.

If (28) and (29) do not hold, $\pi _{sh}=1$, $\pi _{uh}=1$, $\pi _{sl}=1$. As derived above, $\lambda _2>0$ and hence $\partial L(\cdot )/\partial \lambda _2=0$ (follows with complementary slackness). Therefore, $R^*_{sl}=y_c-(y_d-\tau e_l)$. With $\pi _{uh}=\pi _{sl}=1$, $\lambda _5>0$ it follows that $\partial L(\cdot )/\partial \lambda 5=0$ (follows from complementary slackness) and hence $R^*_{uh}= y_c-(y_d-\tau e_l)$. With $\pi _{sh}=\pi _{uh}=1$, $\lambda _3>0$ it follows that $\partial L(\cdot )/\partial \lambda 3=0$ (follows from complementary slackness) and hence $R^*_{sh}= y_c-(y_d-\tau e_l)$.

1.5 7.5. Imperfect Information with Credit Market Instruments

In this subsection, we derive equilibrium contracts and the associated allocation of firms in a scenario with the use of an interest rate subsidy (potentially combined with a loan guarantee) and under the assumption of information asymmetries between borrowers, the bank, and the government. Without an emission tax, the private returns from using the dirty technology are identical for all firms. Therefore, the relevant (group of) regimes are:

Regime 1

(under-investment): $\pi _{sd}=0$, $\pi _{ud}=0$    ($\Leftrightarrow$ $\pi _{sh}=0$, $\pi _{uh}=0$, $\pi _{sl}=0$, $\pi _{ul}=0$),

Regime 2

(misallocation): $\pi _{sd}>0$, $\pi _{ud}=0$    ($\Leftrightarrow$ $\pi _{sh}>0$, $\pi _{sl}>0$, $\pi _{uh}=0$, $\pi _{ul}=0$),

Regime 3

(over-investment): $\pi _{sd}>0$, $\pi _{ud}>0$    ($\Leftrightarrow$ $\pi _{sh}>0$, $\pi _{sl}>0$, $\pi _{uh}>0$, $\pi _{ul}>0$).

Note that a necessary condition for Regime 2 is that the participation constraint ((3) $\ge 0$) of S-firms is fulfilled. Solving (3) $\ge 0$ for $\sigma$ yields: $\sigma \ge y_d/\delta _c-y_c+R_{k}$. Furthermore, profit maximisation of the bank requires the expected profit from lending to a firm to be non-negative. Solving (2) $\ge 0$ for $R_k$ yields the minimum loan repayment for loans that are provided with positive probability: $R_k\ge (\rho -(1-\delta _c)\gamma )/\delta _c$. Combining minimum $R_k$ with minimum $\sigma$ yields the threshold level for the interest rate subsidy for which the participation constraint of S-firms is compatible with profit maximisation of the bank:

$$\begin{aligned} \sigma =y_d+\rho -y_c\equiv \sigma _{S}. \end{aligned}$$

(30)

Analogously, a necessary condition for Regime 3 is that the participation constraints ((3) $\ge 0$) of S- and U-firms are fulfilled. As above, combining the minimum $R_k$ with the minimum $\sigma$ yields the threshold level for the interest rate subsidy for which the participation constraint of U-firms is compatible with profit maximisation of the bank:

$$\begin{aligned} \sigma =\frac{y_d+\rho -(1-\delta _u)\gamma }{\delta _u}-y_c\equiv \sigma _{SU}. \end{aligned}$$

(31)

As $\sigma _{SU}>\sigma _{S}$ (follows immediately from $1>\delta _u$), the participation constraint of S- and U-firms can be fulfilled if $\sigma \ge \sigma _{SU}$.

1.5.1 7.5.1. Maximisation Problem

The bank maximises its expected benefit from lending subject to the participation and incentive compatibility constraints of two types of borrowers:

$$\begin{aligned} \max _{\pi _{sd},R_{sd},\pi _{ud}, R_{ud}} \ B=&\, \ \left( 1-\theta _u\right) B_{sd}+\theta _u B_{ ud}\\ =&\,\ \left( 1-\theta _u\right) \pi _{sd}\left( R_{sd}-\rho \right) +\theta _u \pi _{ud}\left[ \delta _{ u}\left( R_{ud}\right) -\rho +\left( 1-\delta _{ u}\right) \gamma \right] \\ \text {subject to} \quad (PC_{cd}) \quad&\pi _{cd}\left[ \delta _c\left( y_{c}+\sigma -R_{cd}\right) -y_{d}\right] \ge 0\\ (IC_{sd,ud}) \quad&\pi _{sd}\left[ \left( y_{c}+\sigma -R_{sd}\right) -y_{d}\right] \ge \pi _{ud}\left[ \left( y_{c}+\sigma -R_{ud}\right) -y_{d}\right] \\&0\le \pi _{sd} \le 1, 0\le \pi _{ud} \le 1. \end{aligned}$$

(32)

1.5.2 7.5.2. Kuhn–Tucker Approach

The Lagrangian to the maximisation problem is:

$$\begin{aligned}&L(\pi _{ sd},R_{ sd},\pi _{ ud},R_{ ud},\lambda _0,\lambda _1,\lambda _2,\lambda _3,\lambda _4,\lambda _5,\lambda _6)=\\&\quad \left( 1-\theta _u\right) \pi _{ sd}\left[ R_{ sd}-\rho \right] +\theta _u \pi _{ ud}\left[ \delta _{ u}R_{ ud}+\left( 1-\delta _{ u}\right) \gamma -\rho \right] \\&\quad +\lambda _0\pi _{sd}\left[ \left( y_{c}+\sigma -R_{ sd}\right) -y_{d}\right] \\&\quad +\lambda _1\pi _{ ud}\left[ \delta _{ u}\left( y_{c}+\sigma -R_{ ud}\right) -y_{d}\right] \\&\quad +\lambda _2\left[ \pi _{ sd}\left[ \left( y_{c}+\sigma -R_{ sd}\right) -y_{d}\right] - \pi _{ ud}\left[ \left( y_{c}+\sigma -R_{ ud}\right) -y_{d}\right] \right] \\&\quad +\lambda _3\pi _{ ud}+\lambda _4\left( 1-\pi _{ ud}\right) +\lambda _5\pi _{ sd}+\lambda _6\left( 1-\pi _{ sd}\right) . \end{aligned}$$

The (first-order) Kuhn–Tucker conditions are given by:

$$\begin{aligned}&\frac{\partial L(\cdot )}{\partial R_{ sd}}=\left( 1-\theta _u\right) \pi _{ sd}-\lambda _2\pi _{ sd}\le 0, \quad R_{ sd} \ge 0;\\&\quad \frac{\partial L(\cdot )}{\partial \pi _{ sd}}=\left( 1-\theta _u\right) \left( R_{ sd}+\left( 1-\theta _{ s}\right) \gamma -\rho \right) +\lambda _2\left[ \left( y_{c}+\sigma -R_{ sd}\right) -y_{d}\right] +\lambda _5-\lambda _6\le 0 \quad \pi _{ sd}\ge 0;\\&\quad \frac{\partial L(\cdot )}{\partial R_{ ud}}=\theta _u\pi _{ ud}\delta _{ u}-\lambda _1\pi _{ ud}\delta _{ u}+\lambda _2\pi _{ ud}\le 0, \quad R_{ ud} \ge 0;\\&\quad \frac{\partial L(\cdot )}{\partial \pi _{ ud}}=\theta _u\left( \delta _{ u}R_{ ud}+\left( 1-\delta _{ u}\right) \gamma -\rho \right) +\lambda _1\left[ \delta _{ u}\left( y_{c}+\sigma -R_{ ud}\right) -y_{d}\right] \\&\quad \quad \ -\lambda _2\left[ \left( y_{c}+\sigma -R_{ ud}\right) -y_{d}\right] +\lambda _3-\lambda _4\le 0, \quad \pi _{ ud}\ge 0;\\&\quad \frac{\partial L(\cdot )}{\partial \lambda _1}= \pi _{ ud}\left[ \delta _{ u}\left( y_{c}+\sigma -R_{ ud}\right) -y_{d}\right] \ge 0, \quad \lambda _1\ge 0;\\&\quad \frac{\partial L(\cdot )}{\partial \lambda _2}= \pi _{ sd}\left[ \left( y_{c}+\sigma -R_{ sd}\right) -y_{d}\right] -\pi _{ ud}\left[ \left( y_{c}+\sigma -R_{ ud}\right) -y_{d}\right] \ge 0, \quad \lambda _2\ge 0;\\&\quad \frac{\partial L(\cdot )}{\partial \lambda _3}=\pi _{ ud}\ge 0 , \quad \lambda _3\ge 0;\\&\quad \frac{\partial L(\cdot )}{\partial \lambda _4}=1-\pi _{ ud}\ge 0 , \quad \lambda _4\ge 0;\\&\quad \frac{\partial L(\cdot )}{\partial \lambda _5}=\pi _{ sd}\ge 0 , \quad \lambda _5\ge 0;\\&\quad \frac{\partial L(\cdot )}{\partial \lambda _6}=1-\pi _{ sd}\ge 0 , \quad \lambda _6\ge 0. \end{aligned}$$

1.5.3 7.5.3. Analysis of Regimes

Regime 1: $\pi _{sd}=0,\ \pi _{ud}=0$.

No firm type receives funding for the clean investment.

Regime 2: $\pi _{sd}>0,\ \pi _{ud}=0$.

With $\sigma \ge \sigma _{S}$ it follows: With $\pi _{ sd}>0 \ \Rightarrow \ \lambda _5=0$ and $\partial L(\cdot )/\partial \pi _{ sd}=0$ (both follow from complementary slackness) and $R_{ sd}>0\ \Rightarrow \ \partial L(\cdot )/\partial R_{ ud}=0$ (follows from complementary slackness). From that $\lambda _2=\left( 1-\theta _u\right)$. With $\lambda _2>0 \ \Rightarrow \ \partial L(\cdot ) / \partial \lambda _2=0$. Together with $\pi _{ ud}=0$ and $\pi _{ sd}>0$ it follows that $R_{ sd}=y_{c}+\sigma -y_{d}$. Furthermore, with $\lambda _2>0, \ \lambda _5=0, \ \pi _{ sd}>0, \ \partial L(\cdot )/\partial \pi _{ sd}=0 \ \Rightarrow \lambda _6>0$ and hence $\partial L(\cdot ) / \partial \lambda _6=0 \ \Rightarrow \ \pi _{ sd}=1$ (follows from complementary slackness).

Regime 3: $\pi _{sd}>0,\ \pi _{ud}>0,\ \pi _{sl}=0,\ \pi _{ul}=0$.

For $\sigma \ge \sigma _{SU}$ it follows: With $\pi _{ ud}>0 \ \Rightarrow \ \lambda _3=0$ and $\pi _{ sd}>0 \ \Rightarrow \ \lambda _5=0$ (both follow from complementary slackness). With $R_{ud}>0 \ \Rightarrow \ \partial L(\cdot ) / \partial R_{ ud}=0$ and $R_{ sd}>0 \ \Rightarrow \ \partial L(\cdot ) / \partial R_{ sd}=0$ (both follow from complementary slackness). With $\partial L(\cdot ) / \partial R_{ sd}=0, \ \pi _{ sd}>0 \ \Rightarrow \lambda _2=\left( 1-\theta _u\right) >0$ and together with $\lambda _5=0, \ \partial L(\cdot ) / \partial \pi _{ sd}=0 \Rightarrow \ \lambda _6>0 \ \Rightarrow \ \ \pi _{ sd}=1$ (follows from complementary slackness). With $\partial L(\cdot ) / \partial R_{ ud}=0, \ \lambda _2=\left( 1-\theta _u\right) \ \Rightarrow \ \lambda _1=\theta _u+\left( 1-\theta _u\right) /\delta _{ u}$. Together with $\partial L(\cdot ) / \partial \pi _{ ud}=0$ it follows that

$$\begin{aligned} \lambda _4\gtreqqless 0 \Leftrightarrow \delta _{ u}\left( y_{c}+\sigma \right) -y_{d}-\rho \gtreqqless \frac{1-\theta _u}{\theta _u}\left( y_{d}\right) \left( \frac{1}{\delta _{ u}}-1\right) -\left( 1-\delta _{ u}\right) \gamma . \end{aligned}$$

(33)

Note that (in)equality of the RHS of (33) determines the sign of $\lambda _4$. With this it follows that if $\delta _{ u}\left( y_{c}+\sigma \right) -y_{d}-\rho> \frac{1-\theta _u}{\theta _u}y_{d}\left( \frac{1}{\delta _{ u}}-1\right) -\left( 1-\delta _{ u}\right) \gamma \ \Rightarrow \lambda _{4}>0$ and hence $\pi _{ ud}= 1$ (follows with complementary slackness). If $\delta _{ u}\left( y_{c}+\sigma \right) -y_{d}-\rho = \frac{1-\theta _u}{\theta _u}\left( \frac{1}{\delta _{ u}}-1\right) y_{d}-\left( 1-\delta _{ u}\right) \gamma \ \Rightarrow \lambda _{4}=0$ and hence $\pi _{ ud}\in [0,1]$ is compatible with complementary slackness. If $\delta _{ u}\left( y_{c}+\sigma \right) -y_{d}-\rho< \frac{1-\theta _u}{\theta _u}\left( \frac{1}{\delta _{ u}}-1\right) y_d-\left( 1-\delta _{ u}\right) \gamma \ \Rightarrow \lambda _{4}<0$ and hence does not fulfil the first order conditions. That is, (33) yields the credit rationing condition for ud-firms:

$$\begin{aligned} \frac{\delta _{ u}\left( y_{c}+\sigma \right) -\rho +\left( 1-\delta _{ u}\right) \gamma -y_{d}}{y_{d}}< \frac{1-\theta _u}{\theta _u}\frac{1-\delta _u}{\delta _{ u}}. \end{aligned}$$

(34)

If (34) holds, ud-firms will not receive a loan and Regime 1 applies. If (34) does not hold, it follows: With $\partial L(\cdot ) \partial \lambda _2=0, \ \pi _{ sd}=1, \ R_{ ud}=y_{c}+\sigma -\frac{y_{d}}{\delta _{ u}}\ \Rightarrow \ R_{ sd}=y_{c}+\sigma -\left( \pi _{ ud}\left( (1-\delta _{ u})/\delta _{ u}\right) +1\right) y_{d}$. For $\pi _{ ud}=1\ \Rightarrow R_{ sd}=y_{c}+\sigma -\frac{y_{d}}{\delta _{ u}}$.

Summary:

Without emission tax and with $\sigma <\sigma _{S}$: PCs of all firms are incompatible with profit maximising behaviour of the bank. Hence, Regime 1 is profit maximising. All firms produce using the dirty technology.

Without emission tax and with $\sigma _{S}\le \sigma <\sigma _{SU}$: PC of S-firms is compatible, PC of U-firms is incompatible with profit maximising behaviour of the bank. S-firms receive a loan and produce using the clean technology, U-firms do not apply for a loan and produce using the dirty technology.

Without emission tax and with $\sigma _{S}<\sigma _{SU}\le \sigma$: PCs of all types are compatible with profit maximising behaviour of the bank. If the credit rationing condition for U-firms, (34), holds, only S-firms receive a loan. If (34) does not hold, U- and S-firms receive a loan.

It follows from Regimes 2 and 3 that $\pi ^*_{ sd}=1$, $R^*_{ sd}=y_{c}+\sigma -\frac{\left( \pi _{ ud}\left( 1-\delta _{ u}\right) +\delta _{ u}\right) y_{d}}{\delta _{ u}}$, and:

$$\begin{aligned} \pi ^*_{ ud}&= {\left\{ \begin{array}{ll} 1 \quad \text {if} \ \quad \delta _{ u}\left( y_{c}+\sigma \right) -y_{d}+\tau e_{ h}-\rho \ge \frac{1-\theta _u}{\theta _u}\left( y_{d}-\tau e_{ h}\right) \left( \frac{1}{\delta _{ u}}-1\right) -\left( 1-\delta _{ u}\right) \gamma \\ 0 \quad \text {if} \ \quad \delta _{ u}\left( y_{c}+\sigma \right) -y_{d}+\tau e_{ h}-\rho< \frac{1-\theta _u}{\theta _u}\left( y_{d}-\tau e_{ h}\right) \left( \frac{1}{\delta _{ u}}-1\right) -\left( 1-\delta _{ u}\right) \gamma \end{array}\right. }\\ R^*_{ ud}&= {\left\{ \begin{array}{ll} y_{c}+\sigma -\frac{y_{d}-\tau e_{ h}}{\delta _{ u}} \quad \text {if} \ \quad \delta _{ u}\left( y_{c}+\sigma \right) -y_{d}+\tau e_{ h}-\rho \ge \frac{1-\theta _u}{\theta _u}\left( y_{d}-\tau e_{ h}\right) \left( \frac{1}{\delta _{ u}}-1\right) -\left( 1-\delta _{ u}\right) \gamma \\ any \ value \quad \text {if} \ \quad \delta _{ u}\left( y_{c}+\sigma \right) -y_{d}+\tau e_{ h}-\rho < \frac{1-\theta _u}{\theta _u}\left( y_{d}-\tau e_{ h}\right) \left( \frac{1}{\delta _{ u}}-1\right) -\left( 1-\delta _{ u}\right) \gamma \end{array}\right. } \end{aligned}$$

1.6 7.6. Welfare analysis

Expected social welfare is defined as the sum of firms’ profits, bank profits, and government budget, less social costs of emissions. Using Lemma 1, total welfare in laissez-faire is:

$$\begin{aligned} W_L=y_{d}-\left( 1-\theta _{d}\right) e_{ l}-\theta _h e_{ h}. \end{aligned}$$

(35)

Using Lemma 2, total welfare in the reference scenario with full information and Pigouvian tax is:

$$\begin{aligned} \tilde{W}_{P}=\theta _hy_{c}\left[ \left( 1-\theta _u\right) +\theta _u\delta _{ u}-\rho \right] +\left( 1-\theta _h\right) \left( y_{d}- e_{ l}\right) . \end{aligned}$$

(36)

Using Proposition 1, total welfare with Pigouvian tax if no credit rationing occurs is:

$$\begin{aligned} W_{P}= \left( 1-\theta _h\right) \left( y_{d}- e_{ l}\right) +\theta _h\theta _u\left( y_{d}- e_{ h}\right) +\theta _h\left( 1-\theta _u\right) \left( y_{c}-\rho \right) . \end{aligned}$$

(37)

Using Proposition 2, total welfare with Pigouvian tax and credit market intervention is:

$$\begin{aligned} W_{P \sigma }=W_{P \gamma }=\theta _hy_{c}\left[ \left( 1-\theta _u\right) +\theta _u\delta _{ u}-\rho \right] +\left( 1-\theta _h\right) \left( y_{d}- e_{ l}\right) . \end{aligned}$$

(38)

Using Proposition 3, there are two possible total welfare levels with emission tax above the Pigouvian level. If $\tau _{uh}\ge \tau _{sl}$, total welfare is:

$$\begin{aligned} W_{\tau _{sl}}=\theta _hy_{c}\left[ \left( 1-\theta _u\right) +\theta _u\delta _{ u}-\rho \right] +\left( 1-\theta _h\right) \left( 1-\theta _u\right) \left( y_{c}-\rho \right) + \left( 1-\theta _h\right) \theta _u\left( y_{d}- e_{ l}\right) \end{aligned}$$

(39)

If $\tau _{uh}<\tau _{sl}$, total welfare is:

$$\begin{aligned} W_{\tau _{uh}}=\theta _hy_{c}\left[ \left( 1-\theta _u\right) +\theta _u\delta _{ u}-\rho \right] +\left( 1-\theta _h\right) \left( y_{d}- e_{ l}\right) . \end{aligned}$$

(40)

Using Proposition 4, total welfare with interest subsidy $\sigma _{S}$ is:

$$\begin{aligned} W_{\sigma _{S}}=\left( 1-\theta _u\right) \left[ y_{c}-\rho \right] +\theta _u\left[ y_{d}-\theta _h e_{ h}-\left( 1-\theta _h\right) e_{ l}\right] . \end{aligned}$$

(41)

Using Proposition 5, total welfare with interest subsidy $\sigma _{SU}$ and loan guarantee $\gamma _{n\tau }^*$ is:

$$\begin{aligned} W_{\sigma _{SU}}=\left( 1-\theta _u\right) y_{c}+\theta _u\delta _{ u}y_{c}-\rho . \end{aligned}$$

(42)

Corollary 1 follows immediately from combining respective Eqs. (35)–(42).