A Novel HydroEconomic - Econometric Approach for Integrated Transboundary Water Management Under Uncertainty

Abstract

The optimal management of scarce transboundary water resources among competitive users is expected to be challenged by the effects of climate change on water availability. The multiple economic and social implications, including conflicts between neighbouring countries, as well as competitive sectors within each country are difficult to estimate and predict, to inform policy-making. In this paper, this problem is approached as a stochastic multistage dynamic game: we develop and apply a novel framework for assessing and evaluating different international strategies regarding transboundary water resources use, under conditions of hydrological uncertainty. The Omo-Turkana transboundary basin in Africa is used as a case study application, since it increasingly faces the above challenges, including the international tension between Kenya and Ethiopia and each individual country’s multi-sectoral competition for water use. The mathematical framework combines a hydro-economic model (water balance, water costs and benefits), and an econometric model (production functions and water demand curves) which are tested under cooperative and non-cooperative conditions (Stackelberg “leader–follower” game). The results show the cross-country and cross-sectoral water use—economic trade-offs, the future water availability for every game case, the sector-specific production function estimations (including residential, agriculture, energy, mining, tourism sectors), with nonparametric treatment, allowing for technical inefficiency in production and autocorrelated Total Factor Productivity, providing thus a more realistic simulation. Cooperation between the two countries is the most beneficial case for future water availability and economic growth. The study presents a replicable, sophisticated modelling framework, for holistic transboundary water management.

1 Introduction

Transboundary river basins should be treated as single units, and be modelled accordingly to maintain the physical integrity of the hydro-economic system and consider overall optimum solutions. Water Resources Management and Economics have gone beyond the traditional approach of monitoring and measuring the spatiotemporal allocation of resources, costs, and benefits, and seek the optimal way to control and manage systems in a way that maximizes the users’ welfare under environmental constraints (Gupta et al. 2016). The problem of covering competitive and increasing needs with limited (and often deteriorating) resources becomes more complicated when considering the broad impacts of transboundary water decisions on the context of multiple competitive economic sectors. Additionally, in the coming years, it is expected that the impacts of the changing climate will stress water balances by reduced water availability and increased demand, sharpening thus the competition among different water uses and deteriorating the ecological status of water bodies (Alamanos et al. 2018; Pastor et al. 2022). The negative impacts of scarcer water resources on the economic, production, energy sectors, social stability, and environmental sustainability (Khan et al. 2022a, b; Tang et al. 2022) are calling for multi-disciplinary solutions. Subsequently, integrated and detailed modelling is increasingly used in the decision-making process, to provide science-supported policies, especially in cases where holistic approaches and cooperative management can be hardly found (Uitto and Duda, 2003).

Game theory has been used to describe the actions of the countries-players (Frisvold and Caswell 2000; Dinar and Hogarth 2015). Kucukmehmetoglu (2012) analysed the problem of scarce water resources allocation combining game theory and Pareto frontier, using also linear programming to maximize net economic benefits. Zeng et al. (2019) proposed a hybrid game theory and mathematical programming model for solving transboundary water conflicts, by the optimal water allocation, considering water quality and quantity and the associated benefits and costs. Menga (2016) highlights the interplay between domestic and foreign policy for transboundary waters through the example of the two-level game theory of Putnam (1988). Hu et al. (2017) used the case of hydropower and water supplies within the water-energy nexus using stochastic competitive and cooperative (Nash–Cournot model) analysis. However, there are fewer contributions assessing cross-country together with cross-sectoral water and economic parameters. The aforementioned papers suggest that future studies need to also include uncertainty in hydrological processes. Indeed, the consideration of uncertainty for long-term planning is increasingly used in recent applications (Wine 2019; Kryston et al. 2022), combined with game theory (Bhaduri et al. 2011). Some examples follow: Degefu et al. (2017) analysed the uncertain characteristics of water flow in transboundary waters through a stochastic game. A similar analysis was performed by Janjua and Hassan (2020), who introduced the ‘weighted bankruptcy’ approach which favors agents with ‘high agricultural productivity’. Jiang et al. (2019) used a stochastic differential game to analyze transboundary pollution control options, comparing the non-cooperative and Stackelberg cooperative game pollution results. However, these applications refer to allocation (resource or pollution) and include only economic extensions, as add-ons to the main model, while they focus on the one or two main sectors (water users). In order to better combine hydrological and economic parameters, and increase the number of different sectors considered, integrated hydro-economic models have been highlighted as promising tools for science-supported policies (Booker et al. 2012; Alamanos 2021; Wang et al. 2020). However, the use of hydro-economic models in uncertain transboundary management problems (e.g. Jeuland 2010) has been very limited (Tayia 2019), mainly because of their complexity and data requirements (Alamanos et al. 2020).

This study attempts to build on all these gaps of the literature mentioned, by proposing an integrated approach that considers hydrological and economic aspects (based on a hydro-economic model), where the economic aspects are emphasized through econometric modelling, in the context of game theory investigation of transboundary water management strategies, under conditions of hydrological uncertainty. The integrated character of the proposed approach is an added value, which is highly desirable for cross-sectoral transboundary resources management (Bernauer and Böhmelt 2020). We demonstrate how the potential of hydro-economic modelling to simulate in an integrated and expandable way multistage stochastic and dynamic processes under uncertainty can fits into the concept of a transboundary water management-game. The proposed framework combines hydrological (precipitation, runoff, outflows from the upstream country, and water stock, stochastically) and economic components (social benefits, marginal and total costs), considering the five sectors-drivers of water demand and economy (mining, energy, tourism, residential, and agriculture), as well as their water demand curves through production functions and productivity. This study provides also specific modelling advances, as the estimation of the latter relations has been one of the most challenging econometric processes: Biases, inconsistencies, and correlation among the regressors (explanatory variables, e.g. capital or labor, with the error term) often cause endogeneity problems. Traditional approaches (Olley and Pakes 1996; Levinsohn and Petrin 2003) lack of instruments to control for the endogenous inputs and suffer from collinearity problems (Ackerberg et al. 2015; Gandhi et al. 2017). Endogeneity problems are still a challenge for stochastic frontier models in efficiency analysis, too (Shee and Stefanou 2014). It usually biases the commonly used tools (e.g. DEA), and Monte Carlo techniques are recently suggested to control the effects of endogeneity in efficiency analysis and estimates (von Cramon-Taubadel and Saldias 2014; Santín and Sicilia 2017). We present a new estimation method of sector-level productivity as an extension of the model proposed by Gandhi et al. (2017), to tackle the existing limitations, introducing technical inefficiency in production, and allowing for autocorrelation of Total Factor Productivity (TFP).

The whole framework is tested under a non-cooperative and a cooperative (Stackelberg leader–follower) game, considering the agreements (e.g. food or energy trade-offs) between the upstream and downstream countries, providing thus a direct link to Water-Food-Energy (WEF) nexus. The transboundary Omo-Turkana River Basin in Africa is used as an example to showcase the framework, while highlighting the significance and impacts of proper management of scarce resources to the economic and WEF issues of the area under baseline and future scenarios. The specific case study results demonstrate the benefits of the cooperation between the two countries towards maximizing the efficiency of all economy sectors, and prolonging the water resources availability, under varying hydrological conditions.

With respect to the novelties of the study, its integrated character and the coupled modelling approach (to our knowledge, no study has combined all the above components in a single framework), are significant. Also, there are specific modelling advances such as: the proposed way for the stochastic description of the hydrological components; the connection of the follower’s reaction to the leader’s strategy, together with the (quantitatively tractable) optimization of their objective functions over all possible strategies of the stochastic game; the realistic production functions estimations, controlling-allowing for endogeneity, technical inefficiency and autocorrelated TFP. Finally, this study significantly contributes to the transboundary water management in the African context, where there are limited applications (Basheer et al. 2019; Hughes 2019; Mumbi et al. 2021). To our knowledge, this is also the first study of its kind for the Omo-Turkana basin, with the exception of Giuliani et al. (2022), which was more focused on the hydrology of the area though.

2 Study Area

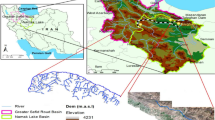
The Omo-Turkana (Omo River and Lake Turkana) basin in Eastern Africa is an area of 130,860 km² across Ethiopia and Kenya, and small encroachments into Uganda and South Sudan (95% of the basin is in Ethiopian and Kenya) (Fig. 1). The water-land uses of the broader area are agriculture (main use, including livestock), energy production, mining, residential, and touristic. Lake Turkana receives its inflows from Omo River, which defines its levels and water quality. Turkana concentrates over 70% of Kenya’s population, relying on food aid, flood retreat farming along Omo River, cattle-grazing, and fishing (Kaijage and Nyagah 2010; Reta 2016; Oakland Institute 2014; Anaya 2010). A five-plant hydroelectric dam cascade is being constructed in Ethiopia (three of them- GIBE I, GIBE II, GIBE III, are already operating in Omo River) to fulfill energy demand and electricity export ambitions (Regi 2011; Ficquet 2015).

The case is controversial as there are studies highlighting the engineering achievement of the dams’ construction, or criticising it from the ecological point of view (Ambelu et al. 2013). Hydrological studies argue that the impact on the water level of Lake Turkana is negligible (Yesuf, 2012), or dependent on the rainfall and the lake’s initial level (Velpuri and Senay 2012), while there are reported phenomena of extreme hunger in the Omo Valley, attributing it to the GIBE III reservoir which holds back the Omo River’s annual floods, preventing retreat agriculture for local pastoralists, (Avery 2013) and around Lake Turkana where people (and ethnic groups) are already fighting over dwindling resources (Avery 2013; Carr 2012, 2017). In any case, there are transboundary tensions and territorial conflicts/border disputes around the Lake Turkana border, in contrast with the Ethiopian agricultural and rural-factories development (Kamski 2016; Sugar Corporation 2019). Kenya sees the dam construction as growing poverty because of increased water scarcity; Ethiopia is concerned by land erosion, water access increased poverty, change in livelihood, while points out the positive impact of regulating floods to provide a more constant water availability throughout the downstream (DAFNE 2019). The broader area was in the spotlight last year because of the food crisis caused from a historic locust swarm invasion.¹

Fig. 1

The study area, with the constructed works in Kenya (Gebresenbet 2015

The dams’ construction allows Ethiopia to export electricity to Kenya, Sudan, and Djibouti. This agreement exists only in a form of Memorandum of Understanding (MoU), that only Kenya’s Electricity Company has signed in 2006 (Eastern Electricity Highway Project—construction of a 1000 km power line from Ethiopia to Kenya), while other trade-offs refer to food production (irrigation and fishing) and tourism (DAFNE 2019). In particular, the downstream country offers a discounted price for food exports to the upstream country, in exchange for greater transboundary water flow (and hydropower) that results in a higher water reserve accumulation and sequentially in a higher production of food (Fig. 2). The environmental and social impact assessment report was approved in 2012, although it has been criticised as it was conducted after any objection could be made (Abbink 2012). Following a World Bank loan of US$684 million (World Bank 2012), construction began in June 2016.² While the 2016 agreement is not yet publicly available, it is reported that the agreement will allow Ethiopia to supply Kenya with 400 megawatts of hydropower at less than 1 US cent/kwh.³ However, the hydropower source (or sources) that will supply this transmission line is not officially stated, although the World Bank modified an official project report specifying that power would be sourced “from Ethiopia’s GIBE hydropower scheme”, changing the reference to the dam in its next report instead to “Ethiopia’s power grid” (AthiWater 2018).

Fig. 2

Conceptual flowchart with the factors considered and their brief description

3 Conceptual Framework: Hydro-Economic Model

The situation described is a typical example of transboundary water management problem, where the links to the WEF nexus are expressed as agreements and social welfare for both the Upstream (h = U) and Downstream (h = D) countries. Hydrological, economic, WEF, uncertainty factors and leader–follower games can describe the general form of the problem (Fig. 2).

The proposed framework enables the quantitative estimation of the influence of stochastic water resources on transboundary water allocation over multiple (all the five) sectors of the economy, following a multistage dynamic cooperative game (Stackelberg “leader–follower”) framework.

Deconstructing the flowchart, the proposed approach is based on the following pillars:

3.1 Water Resources

Hydrological cycle’s components such as water availability, losses, and runoff, that are necessary for integrated modelling often face many data limitations and their accurate simulation is accompanied with many uncertainties. Hydrological modelling itself is not always enough for their complete and integrated simulation (Van Emmerik et al. 2014). Thus, in this framework these components are expressed stochastically, by geometric Brownian motion functions, which have been proved to simulate flows better than other deterministic models (Lefebvre 2002), and its proportional changes describe the most natural continuous random movements. Given the different hydrological-social-future regional climate conditions that may affect the flows in the upstream and downstream countries, we provide the option (and develop the framework accordingly) to use Brownian motions with different characteristics in terms of variance between the upstream and the downstream country. Additionally, this allows to determine how the water abstraction of the riparian countries will change in the long run, considering the greater variability of water availability caused by climate change or other uncertainties. Another benefit of this approach is the ability to model the water allocation between the upstream and the downstream country, with and without any cooperation in water sharing, taking into account how uncertainty in water supply affects the water abstraction rates of the countries, and explore the underlying conditions that may influence allocation decisions. The upstream country has the upper riparian right to unilaterally divert water while the freshwater availability of the downstream one partially depends on the water usage in the upstream country.

Following Bhaduri et al. (2011), we consider at first a complete filtered probability space (Ω, J, J_t, P) for the stochastic water flow. Then the annual renewable water resource (mainly precipitation) due to the river basin, W_t, evolves through time according to the Geometric Brownian motion:

$$dW_{t} = \sigma^{W} W_{t} dz_{t}^{W} ,\;\;t \ge 0$$

(1)

where ${\sigma }^{W}$ is the volatility of water flow in the upstream country,${z}_{t}^{W}$ is a standard Wiener process—standard Brownian Motion, (see also next paragraph).

In Fig. 2, the term losses refer to the natural outflows and evaporation/ evapotransiration (ET), here denoted by O_t which can be formulated by another Geometric Brownian motion:

$$dO_{t} = \sigma^{O} O_{t} dz_{t}^{O} ,\;\;t \ge 0$$

(2)

where ${\sigma }^{O}$ is the volatility of the losses and ${z}_{t}^{O}$ a standard Wiener process.

The water availability in D depends on the total water consumption in U and runoff (to the Lake), denoted by R, which is expressed by a third Geometric Brownian motion as:

$$dR_{t} = \sigma^{R} R_{t} dz_{t}^{R} ,\;\;t \ge 0$$

(3)

where ${\sigma }^{R}$ is the runoff volatility and ${z}_{t}^{R}$ the standard Wiener process (${z}_{t}^{W}, {z}_{t}^{O}, {z}_{t}^{R}$ are independent Wiener processes).

3.2 Water Demand

As mentioned above, the framework provides the option to use all the involved sectors-water consumers i (here i = 5), and their water use in a way that highlights the scarce character of the input resource, unlike with previous studies (as in Eq. 4, for the upstream country h = U):

$${dW}_{jt}^{U}=\left[{W}_{t}-{\sum }_{i=j}^{5}{w}_{it}^{U}\right] dt\text{, }{T}_{j-1}^{U}\le t< {T}_{j}^{U}, \quad j=1,2,\ldots,5$$

(4)

where ${W}_{i}^{h}$ is the total freshwater utilization (see Eq. 1) by country U,${w}_{it}^{U}$ is the water utilization per sector i in U, for a specific time: ${T}_{i}^{h}$ is the end of use (exit) time⁴ of the i-th sector of U (T₀ = 0 and T₅ = ∞). So, Eq. (4) expresses the water stock (available resources) change in the upstream country, ${W}_{jt}^{U}$, for the j-th exit stage.

The stock of water (water storage D = water balance, as in Fig. 2) in country D (i.e. in the lake), where agricultural products and fisheries are produced, is denoted by S and is actually based on the general water balance equation: ΔS = Available–Use + Runoff–Losses. Thus, Eq. (5) is a function of the stochastic water resources and the control (water use) variables = ${w}_{i}^{h}$(${w}_{1}^{h}$, ${w}_{2}^{h}$,…, ${w}_{5}^{h}$) per country h = U, D. For the (j,k)-th exit stage of U and D, respectively, it follows the dynamics:

$$d{S}_{jkt}=\left\{{W}_{t}-{\sum }_{i=j}^{5}{w}_{it}^{U}-{\sum }_{l=k}^{5}{w}_{lt}^{D}+{R}_{t}-{O}_{t}\right\}dt, \quad {T}_{j-1}^{U}\le t< {T}_{j}^{U}$$

(5)

with ${T}_{k-1}^{D}\le t< {T}_{k}^{D}\text{, }j,k=1,2,...,5$ and S(0) = S₀ (initial condition).

So, the inverse demand function takes into account the water utilization ${w}_{i}^{h}$ of the j-th exit stage, and the price of water ${p}_{jt}^{h}$ which is the same for the different sectors i:

$${p}_{jt}^{h}=\frac{{a}_{i}^{h}}{{b}_{i}^{h}}-\frac{1}{{b}_{i}^{h}}\cdot {w}_{it}^{h}, \, {T}_{j-1}^{h}\le t< {T}_{j}^{h}, \quad i=j,...,5, \, j=1,2,...,5$$

(6)

where ${a}_{i}^{h}\in {\mathbb{R}}\text{, }{b}_{i}^{h}>0$ are constant sector-specific parameters that define their water demand.

The sector-specific inverse demand curves are ordered so that ${a}_{1}^{h}/{b}_{1}^{h}<{a}_{2}^{h}/{b}_{2}^{h}<\cdots <{a}_{5}^{h}/{b}_{5}^{h}$, which implies that water demand for each of the five sectors reaches zero sequentially over time as the price of water increases over time, leading to the endogenously defined exit times ${T}_{j}^{h}$, giving thus piecewise linear demand functions.

3.3 Costs

Water abstraction from rivers may be taken directly from the flowing waters in the channel (surface water abstraction) or can be achieved through inter-basin flow transfer schemes. Thus, we may assume that the marginal extraction cost (MC) for the j-th exit stage of the upstream country is a decreasing function of the available water W^U of the form:

$${MC}^{U}\left({W}_{j}^{U}\right)={k}_{2}^{U}-{k}_{1}^{U}{W}_{j}^{U}, \quad j=1,2,...,5$$

(7)

where ${k}_{1}^{U}, {k}_{2}^{U}>0$ given constants which define the cost magnitudes.

As water becomes increasingly scarce in the economy, the government will exploit water through appropriating and purchasing a greater share of aggregate economic output, in terms of dams, pumping stations, supply infrastructure, etc. (Barbier 2004). Given the high cost of building infrastructure and expanding supplies, this will lead to a higher marginal cost of water. Then the Total Cost (TC) function of water withdrawing ${w}_{i}^{U}$ from the river per sector i = j, …,5, for the j-th exit stage of the upstream country is given by an increasing function of the water extraction variable:

$${TC}^{U}\left({W}_{j}^{U},{w}_{i}^{U}\right)=({k}_{2}^{U}-{k}_{1}^{U}{W}_{j}^{U}){w}_{i}^{U}, \quad i=j,...,5, \, j=1,2,...,5$$

(8)

On the other hand, D country extracts water from its available stock, thus for the (j,k)-th exit stage the MC of the downstream country is a decreasing function of the available water stock ${S}_{jk}$ (Eq. 9). Similarly, the TC function of water withdrawing ${w}_{l}^{D}$ from the water stock per sector l = k, …, 5 for the (j,k)-th exit stage is given by Eq. (10).

$${MC}^{D}\left({S}_{jk}\right)={k}_{2}^{D}-{k}_{1}^{D}{S}_{jk}, \quad j,k=1,2,...,5$$

(9)

$${TC}^{D}\left({S}_{jk},{w}_{l}^{D}\right)=({k}_{2}^{D}-{k}_{1}^{D}{S}_{jk}){w}_{l}^{D}, \quad l=k,...,5, \ k=1,2,...,5$$

(10)

where ${k}_{1}^{D}, {k}_{2}^{D}>0$ given constants.

3.4 Social Benefits

The last component of Figure’s 2 flowchart refers to the Benefits. Since consumers are deriving benefits from water, the inverse demand curve (Eq. 6) is the marginal social benefit curve. Hence, consider further the benefit of water consumption ${w}_{i}^{h}$ per sector i of country h, namely social benefit (SB), as:

$$S{{B}_{i}}^{h}\left({w}_{i}^{h}\right)={\int }_{0}^{{w}_{i}^{h}}\left(\frac{{a}_{i}^{h}}{{b}_{i}^{h}}-\frac{1}{{b}_{i}^{h}}\cdot {w}_{i}^{h}\right)d{w}_{i}^{h}=\frac{{a}_{i}^{h}}{{b}_{i}^{h}}{w}_{i}^{h}-\frac{1}{2{b}_{i}^{h}}\cdot ({w}_{i}^{h}{)}^{2}$$

(11)

It is obvious that the benefit function is strictly concave for all possible values of ${w}_{i}^{h}$.

As mentioned, D country’s benefits occurring from storing water, while U country receives an additional benefit in the cooperation case, from their agreement, as the net consumer surplus or economic benefit from food (agricultural product and fisheries) production. This can be described by a linear function of water stock S_jk per (j,k)-th exit stage:

$$F \left( {S_{jk} } \right) = \eta_{1} S_{jk} + \eta_{2} , \, j,k = 1,2,\ldots ,5{ , }\;\; \eta_{1} > 0,\;\; \eta_{2 } \in R\;\;\left( {{\text{constants}}} \right)$$

(12)

This relation’s form describes these benefits, and allow us to use the coefficient η₁ to represent the intensity of the contribution that the water storage of the lake has to the corresponding food benefits enjoyed by the upstream country.

3.5 Game

Figure 2 also shows the two game-cases we define, using an inter-sectoral Stackelberg leader (U)-follower (D) game. Bhaduri et al. (2011) used a stochastic differential Stackelberg game to produce qualitative results on the optimal transboundary water allocation between an upstream and a downstream area. The leader (U) applies its strategy first, a priori knowing that the follower (D) observes its actions and posteriori moves accordingly. In contrast to Bhaduri et al. (2011), who had to restrict the U’s strategy space to quadratic functions of the state variable in order to obtain a sub-optimal qualitative solution of the problem, we maximize the leader’s objective function, using the D’s reaction strategy, over all possible strategies to provide an optimal solution of our stochastic game problem that is also quantitatively tractable. Assuming that both countries use Markovian perfect strategies, since all model coefficients are deterministic functions of time, a subgame perfect equilibrium and an equilibrium set of decisions dependent on previous actions are defined. These strategies are decision rules that dictate the optimal action, conditional on the current values of the state variables (e.g. water resources of U, water stock of D), that summarize the latest available information of the dynamic system. The following sections analyse the two cases of the game.

4 Non-Cooperative Case

In the case of a non-cooperative framework, where there is no agreement between the two countries regarding either water or food sharing, the benefit maximization and the impact on water balance is presented for each country (hydro-economic model).

4.1 Upstream

The upstream country chooses the economically potential rate of water utilization that maximizes its own net benefit (NB) per j-th exit stage:

$$N{{B}_{j}}^{U}={\sum }_{i=j}^{5}S{{B}_{i}}^{U}({{w}_{i}}^{U})-{\sum }_{i=j}^{5}{TC}^{U}\left({W}_{j}^{U},{w}_{i}^{U}\right), \quad j=1,2,...,5$$

(13)

Thus, U country’s maximization problem is based on its net social benefit (${J}_{j}^{U}$) of the j-th exit stage (j = 1,2,…,5), and is formulated as follows:

$$\begin{aligned} J^{U} & = \mathop {\max }\limits_{{w^{U} }} \mathop \sum \limits_{j = 1}^{5} J_{j}^{U} = \mathop {\max }\limits_{{w^{U} }} \mathop \sum \limits_{j = 1}^{5} E\left\{ {\mathop \smallint \limits_{{T_{j - 1}^{U} }}^{{T_{j}^{U} }} e^{ - rt} NB_{j}^{U} dt} \right\} \\ & = \mathop {\max }\limits_{{w^{U} }} \mathop \sum \limits_{j = 1}^{5} E\left\{ {\mathop \smallint \limits_{{T_{j - 1}^{U} }}^{{T_{j}^{U} }} e^{ - rt} \mathop \sum \limits_{i = j}^{5} \left[ {SB_{i}^{U} \left( {w_{it}^{U} } \right) - TC^{U} \left( {W_{jt}^{U} ,w_{it}^{U} } \right)} \right]dt} \right\} \\ & = \mathop {\max }\limits_{{w^{U} }} \mathop \sum \limits_{j = 1}^{5} E\left\{ {\mathop \smallint \limits_{{T_{j - 1}^{U} }}^{{T_{j}^{U} }} e^{ - rt} \mathop \sum \limits_{i = j}^{5} \left[ {\frac{{a_{i}^{U} }}{{b_{i}^{U} }}w_{it}^{U} - \frac{1}{{2b_{i}^{U} }} \cdot (w_{it}^{U} )^{2} + c_{i}^{U} - \left( {k_{2}^{U} - k_{1}^{U} W_{jt}^{U} } \right)w_{it}^{U} } \right]dt} \right\} \\ \end{aligned}$$

(14)

Which subjects to the renewable water (precipitation) in U (Eq. 1), and the water stock change in U (Eq. 4). An explicit solution of this stochastic control problem via a decoupling method for forward–backward stochastic differential equations (FBSDEs) is analytically derived in Appendix A.

4.2 Downstream

On the other hand, the water consumption/production of D depends on the inflow from U, and the runoff generated within the country’s share of the water stock in D (Fig. 2). Based on the given water availability, D maximizes its NB per exit stage (j,k) as:

$${\mathrm{NB}}_{\mathrm{jk}}^{\mathrm{D}}={\sum }_{\mathrm{l}=\mathrm{k}}^{5}\mathrm{S}{{\mathrm{B}}_{\mathrm{l}}}^{\mathrm{D}}\left({\mathrm{w}}_{\mathrm{jl}}^{\mathrm{D}}\right)-{\sum }_{\mathrm{l}=\mathrm{k}}^{5}{\mathrm{TC}}^{\mathrm{D}}\left({\mathrm{S}}_{\mathrm{jk}},{\mathrm{w}}_{\mathrm{jl}}^{\mathrm{D}}\right) ,\quad k=1, 2,\ldots ,5$$

(15)

Thus, putting together Eqs. (11), and (10) in the above relation, the maximization problem of the net social benefit (${J}_{j}^{D}$) of the j-th exit stage (j = 1,2,…,5), is:

$${\mathrm{J}}^{\mathrm{D}}=\underset{{\mathrm{w}}^{\mathrm{D}}}{\mathrm{max}}{\sum }_{\mathrm{k}=1}^{5} {\sum }_{\mathrm{j}=1}^{5}{\mathrm{J}}_{\mathrm{jk}}^{\mathrm{D}}=\underset{{\mathrm{w}}^{\mathrm{D}}}{\mathrm{max}}{\sum }_{\mathrm{k}=1}^{5} {\sum }_{\mathrm{j}=1}^{5}\mathrm{E}\left\{{\int }_{\left\{{\mathrm{T}}_{\mathrm{j}-1}^{\mathrm{U}}\le \mathrm{t}< {\mathrm{T}}_{\mathrm{j}}^{\mathrm{U}}\right\} \cap \left\{{\mathrm{T}}_{\mathrm{k}-1}^{\mathrm{D}}\le \mathrm{t}< {\mathrm{T}}_{\mathrm{k}}^{\mathrm{D}}\right\}}{\mathrm{e}}^{-\mathrm{rt}}{\mathrm{NB}}_{\mathrm{jk}}^{\mathrm{D}}\mathrm{dt}\right\}$$

$$=\underset{{\mathrm{w}} ^{\mathrm{D}}}{\mathrm{max}}{\sum }_{\mathrm{k}=1}^{5} {\sum }_{\mathrm{j}=1}^{5}\mathrm{E}\left\{{\int }_{\left\{{\mathrm{T}}_{\mathrm{j}-1}^{\mathrm{U}}\le \mathrm{t}< {\mathrm{T}}_{\mathrm{j}}^{\mathrm{U}}\right\} \cap \left\{{\mathrm{T}}_{\mathrm{k}-1}^{\mathrm{D}}\le \mathrm{t}< {\mathrm{T}}_{\mathrm{k}}^{\mathrm{D}}\right\}}{\mathrm{e}}^{-\mathrm{rt}}\left[\begin{array}{c}{\sum }_{\mathrm{l}=\mathrm{k}}^{5}\mathrm{S}{{\mathrm{B}}_{\mathrm{l}}}^{\mathrm{D}}\left({\mathrm{w}}_{\mathrm{lt}}^{\mathrm{D}}\right)\\ -{\sum }_{\mathrm{l}=\mathrm{k}}^{5}{TC}^{\mathrm{D}}\left({\mathrm{S}}_{\mathrm{jkt}},{\mathrm{w}}_{\mathrm{lt}}^{\mathrm{D}}\right)\end{array}\right]\mathrm{dt}\right\}$$

$$\underset{{\mathrm{w}}^{\mathrm{D}}}{\mathrm{max}}{\sum }_{\mathrm{k}=1}^{5} {\sum }_{\mathrm{j}=1}^{5}\mathrm{E}\left\{{\int }_{\left\{{\mathrm{T}}_{\mathrm{j}-1}^{\mathrm{U}}\le \mathrm{t}< {\mathrm{T}}_{\mathrm{j}}^{\mathrm{U}}\right\} \cap \left\{{\mathrm{T}}_{\mathrm{k}-1}^{\mathrm{D}}\le \mathrm{t}< {\mathrm{T}}_{\mathrm{k}}^{\mathrm{D}}\right\}}{\mathrm{e}}^{-\mathrm{rt}}\left[\begin{array}{c}{\sum }_{\mathrm{l}=\mathrm{k}}^{5}\left(\frac{{\mathrm{a}}_{\mathrm{l}}^{\mathrm{D}}}{{\mathrm{b}}_{\mathrm{l}}^{\mathrm{D}}}{\mathrm{w}}_{\mathrm{jlt}}^{\mathrm{D}}-\frac{1}{2{\mathrm{b}}_{\mathrm{l}}^{\mathrm{D}}}\cdot ({\mathrm{w}}_{\mathrm{jlt}}^{\mathrm{D}}{)}^{2}\right)\\ -({\mathrm{k}}_{2}^{\mathrm{D}}-{\mathrm{k}}_{1}^{\mathrm{D}}{\mathrm{S}}_{\mathrm{jkt}}){\sum }_{\mathrm{l}=\mathrm{k}}^{5}{\mathrm{w}}_{\mathrm{jlt}}^{\mathrm{D}}\end{array}\right]\mathrm{dt}\right\}$$

(16)

where ${J}_{jk}^{D}$ represents the downstream country’s net social benefit of the (j,k)-th exit stage, j, k = 1,2,…,5, and ${w}_{jlt}^{D}$=(${w}_{1lt}^{D}$, ${w}_{2lt}^{D}$,…, ${w}_{5lt}^{D}$) is the sectorial water extraction vector for D. This relation subjects to the river basin annual renewable water resource Eq. (1), outflow Eq. (2), runoff Eq. (3), the upstream area water resources Eq. (4), and the stock of water (state variable) in the downstream area Eq. (5). The analytical solution of this stochastic optimization problem can be found in Appendix A.

5 Cooperative Case

In this case the agreements described earlier apply, so the formed Stackelberg game determines the inter-sector optimal water allocation between U and D countries. First, we find the solution to the follower’s (D) problem of maximizing a payoff function, and then, using D’s reaction strategy, we maximize the U’s objective function.

5.1 Downstream

Receiving now hydropower benefits, denoted by a variable hydro, from U at a discount rate and given its announced intersectoral water abstraction policy ${w}_{jkt}^{U}$=(${w}_{1kt}^{U}$, ${w}_{2kt}^{U}$,…, ${w}_{5kt}^{U}$) per (j,k)-th exit stage, the follower D is faced with an optimal water management problem as in the non-cooperative case, i.e., maximise Eq. (16) augmented by hydro subject to the state Eqs. (2)–(6). For every j, k = 1, 2, …, 5, the (j,k)-th exit stage Hamiltonian of the system is also given by Eq. (A.14), whose necessary optimality conditions Eqs. (A15) and (A16) result in the optimal water allocation path of Eq. (A17) and in the same FBSDEs system which will constitute a state system for the upstream country, too.

5.2 Upstream

U receives now food benefits from D as in Eq. (12), and its NB function (Fig. 2) is given by:

$${\mathrm{NB}}_{\mathrm{jk}}^{\mathrm{U}}={\sum }_{\mathrm{i}=\mathrm{j}}^{5}\mathrm{S}{{\mathrm{B}}_{\mathrm{i}}}^{\mathrm{U}}({{\mathrm{w}}_{\mathrm{it}}}^{\mathrm{U}})+{\mathrm{F}}\left({\mathrm{S}}_{\mathrm{jk}}\right)-{\sum }_{\mathrm{i}=\mathrm{j}}^{5}\mathrm{T}{{\mathrm{C}}}^{\mathrm{U}}\left({\mathrm{W}}_{\mathrm{j}}^{\mathrm{U}},{\mathrm{w}}_{\mathrm{i}}^{\mathrm{U}}\right)\text{, }\mathrm{j},\mathrm{k}=1,2,...,5$$

(17)

Therefore, U, anticipating the D’s optimal response as analysed in the previous case, chooses the optimal water abstraction vector process ${w}^{U}=({w}_{1}^{U}, {w}_{2}^{U}, ..., {w}_{5}^{U})$ under cooperation by solving the maximization problem:

$$\begin{aligned}{J}^{U}&=\underset{{w}^{U}}{max}{\sum }_{j=1}^{5} {\sum }_{k=1}^{5}{J}_{jk}^{U}=\underset{{w}^{U}}{max}{\sum }_{j=1}^{5} {\sum }_{k=1}^{5}E\left\{{\int }_{\left\{{T}_{j-1}^{U}\le t\le {T}_{j}^{U}\right\} \cap \left\{{T}_{k-1}^{D}\le t\le {T}_{k}^{D}\right\}}{e}^{-rt}N{B}_{jk}^{U}dt\right\}\\&= \underset{{w} ^{U}}{max}{\sum }_{j=1}^{5} {\sum }_{k=1}^{5}E\left\{{\int }_{\left\{{T}_{j-1}^{U}\le t\le {T}_{j}^{U}\right\} \cap \left\{{T}_{k-1}^{D}\le t\le {T}_{k}^{D}\right\}}{e}^{-rt}\left[\begin{array}{c}{\sum }_{i=j}^{5}S{{B}_{i}}^{U}\left({{w}_{ikt}}^{U}\right)+{F}_{jk}\left({S}_{jkt}\right)\\ -{\sum }_{i=j}^{5}T{{C} }^{U}\left({W}_{jt}^{U},{w}_{ikt}^{U}\right)\end{array}\right]dt\right\} \\&=\underset{{w} ^{U}}{max}{\sum }_{j=1}^{5} {\sum }_{k=1}^{5}E\left\{{\int }_{\left\{{T}_{j-1}^{U}\le t\le {T}_{j}^{U}\right\} \cap \left\{{T}_{k-1}^{D}\le t\le {T}_{k}^{D}\right\}}{e}^{-rt}\left[\begin{array}{c}{\sum }_{i=j}^{5}\left(\frac{{a}_{i}^{U}}{{b}_{i}^{U}}{w}_{it}^{U}-\frac{1}{2{b}_{i}^{U}}\cdot ({w}_{it}^{U}{)}^{2}\right)\\ +{\eta }_{1}{S}_{jkt} ,+{\eta }_{2}-({k}_{2}^{U}-{k}_{1}^{U}{W}_{jt}^{U}){\sum }_{i=j}^{5}{w}_{it}^{U}\end{array}\right]dt\right\}\end{aligned}$$

(18)

subject to the state equation subject to the river basin annual renewable water resource Eq. (1), the upstream country water demand Eq. (4), the runoff Eq. (2), the outflow Eq. (3), and the Hamiltonian FBSDEs state system of the downstream country, Eq. (A18). In Appendix B one can find an explicit solution of this stochastic maximization problem.

6 Econometric Model: Production Functions Through Stochastic Frontier Estimation and Water Demand Curves

The hydro-economic model shows how all parts of the economy—in our case the sectors (agriculture, residential, mining industry, energy production, tourism) are based on water use directly or indirectly, so are the benefits of U and D. Water is an input (as well as labour, capital, natural capital, etc.) for the production process, hence the inverse demand curves we imposed in Sect. 3, as a way to express the input price-quantity relation. The marginal contribution of water in consumption and production of each sector, can be obtained if in Eq. (6), we collapse all variables, except of ${w}_{i}$, to their means (ceteris paribus). Then we will have a relation of the form ${p}_{i}={\widehat{f}}_{i}^{^{\prime}} ({w}_{i})$, where ${\widehat{f}}_{i}$ expresses the maximum Willingness-To-Pay (WTP) by sector i for each unit of water, in a price ${p}_{i}$. The integration of this curve will result the SB of each sector.⁵

We propose a stochastic frontier model and a typical quadratic production function, the form of which remains unknown (Brems 1968). Copulas are used to estimate non-parametrically the dependence between the endogenous regressors and the composed error terms directly, and thus the marginal product function of our hydro-economic model without biases. Bayesian analysis is performed using a Sequential Monte Carlo/Particle-Filtering approach for the computations (Tsionas 2017; Tsionas and Mamatzakis 2019; Tsionas and Mallick 2019, see Appendix B).

Consider the following stochastic frontier model for the production function(s):

$${y}_{it}=\varphi ({x}_{it},{z}_{it};\beta )+{v}_{it}-{u}_{it},\quad i=1,\ldots ,n,t=1,...,T$$

(19)

where ${y}_{it}$ is the output of sector $i$ in time $t$, $\varphi ()$ is an unknown functional form, ${z}_{it}$ is a $p\times 1$ vector of exogenous inputs, ${x}_{it}$ is a $p\times 1$ vector of endogenous inputs, $\beta$ is a $d\times 1$ vectors of unknown parameters, ${v}_{it}$ is a symmetric random error, ${u}_{it}$ is the one-sided random disturbance representing technical inefficiency.⁶ We assume that ${z}_{it}$ is uncorrelated with ${v}_{it}$ and ${u}_{it}$ but ${x}_{it}$ is allowed to be correlated with ${v}_{it}$ and possibly with ${u}_{it}$. This, of course, generates an endogeneity problem. We also assume that ${u}_{it}$ and ${v}_{it}$ are independent and leave the form of ${u}_{it}$ unrestricted. The model can be easily extended to the case of exogenous (environmental) variables are included in the distribution of technical inefficiency (e.g. Battese and Coelli 1995; Caudill et al. 1993). To address the endogeneity problem, we propose a copula function approach to determine the joint distribution of the endogenous regressors and the composed errors that effectively capture the dependency among them.⁷

We first assume that ${v}_{it}{\sim}i i.i.d.N(0,{\sigma }_{v}^{2})$ and ${u}_{it}{\sim}i i.i.d.\left|N(0,{\sigma }_{u}^{2})\right|$. Then the density of ${\varepsilon }_{it}={v}_{it}-{u}_{it}={y}_{it}-\varphi ({x}_{it},{z}_{it};\beta )$ is given by:

$$g({\varepsilon }_{it})={\int }_{0}^{\infty }{f}_{v}({\varepsilon }_{it}+{u}_{it}){f}_{u}({u}_{it})d{u}_{it}=\frac{2}{\sigma }\varphi \left(\frac{{\varepsilon }_{it}}{\sigma }\right)\Phi \left(-\frac{\lambda {\varepsilon }_{it}}{\sigma }\right)$$

(20)

where ${\sigma }^{2}={\sigma }_{v}^{2}+{\sigma }_{u}^{2}$, $\lambda ={\sigma }_{u}/{\sigma }_{v}$, $\varphi (\cdot )$ and $\Phi (\cdot )$ are the Probability Density Function (PDF) and cumulative distribution function of a standard normal random variable, respectively. To avoid the non-negativity restrictions, we make use of the following transformation: $\bar{\lambda }=\mathit{log}(\lambda )$ and${\bar{\sigma }}^{2}=\mathit{log}({\sigma }^{2})$. Let $\theta =({\beta }^{^{\prime}},\bar{\lambda },{\bar{\sigma }}^{2}{)}^{^{\prime}}$ then the conditional PDF of $y$ given $x$ and $z$ is:

$$f({y}_{it}|{x}_{it},{z}_{it})=\frac{2}{\bar{\sigma }}\varphi \left(\frac{{y}_{it}-\varphi ({x}_{it},{z}_{it};\beta )}{\bar{\sigma }}\right)\Phi \left(-\frac{\bar{\lambda }}{{\bar{\sigma }}_{v}}(y-\varphi ({x}_{it},{z}_{it};\beta ))\right)$$

(21)

and conditional log-likelihood is then given by:

$$\mathit{log}L(\theta )={\sum }_{i=1}^{n}{\sum }_{t=0}^{T}\mathit{log}f({y}_{it};\theta |x,z)$$

(22)

From the estimated production function for each of the two countries (considering regional differences in productivity) we can easily obtain their corresponding marginal product function, which is connected with the water use (${w}_{i}^{h}$) input variable via Eq. (23) (see first paragraph of this section). Consequently, the derived demand curve for water of the producer is represented at Eq. (24):

$$Marginal~product=\alpha +\beta \cdot {w}_{i}^{h}$$

(23)

$${w}_{i}^{h}=a+b\cdot price$$

(24)

where α,β are water demand parameters (coefficients) of each sector and b water demand price elasticity, estimated as:

$$price~ elasticity=\frac{d({w}_{it}^{h})}{d(price)}\cdot \frac{price}{{w}_{it}^{h}}$$

(25)

As mentioned, copulas will determine the joint distribution of the endogenous regressors and the composed errors that capture their dependencies (Nelsen 2006). In Appendix B we scrutinise this concept, taking the function $\varphi ()$ as given, and we elaborate on the dynamic latent productivity.

Overall, the proposed methodological framework allows to assess multiple economic and social parameters, for all different economic sectors, with their dependance on variable water resources. The knowledge of the trade-offs among these factors is crucial for identifying the best management strategies. The societal implications are expected to be significant, as conflicts between neighbouring countries can be avoided by following more reasonable practices. Moreover, the ability of the adaptation of the best practices according to the strategy followed by the neighbouring country is expected to be particularly useful for the economic stability, for any region, but especially for the study area: The Omo-Turkana river basin is historically facing transboundary management problems and cross-sectoral conflicts, and is to our opinion an overlooked case in terms of scientific-supported policy-making. In the near future such problems are expected to get worse due to more challenging climatic conditions that affect the hydrologic variability (Sidibe et al. 2020). Thus, it would be highly valuable to consider tools able to estimate and predict with detail hydrologic, economic, and policy parameters, under such uncertain conditions.

7 Results and Discussion

7.1 Production Functions and Water Demand Functions

In this section we present a simple nonparametric estimation of the production function per sector in Ethiopia and Kenya. Human input (labour, machinery), land, and ecosystem-based inputs need to be accounted in production function estimations, which lead to the integrated hydro-economic modelling (the existence of natural capital⁸ is necessary to characterise water resources in each country). For each sector involved data on Natural Capital were collected using Environmental Indices (EI) as approximations of both quality and quantity, indicatively shown in Table 1, in detail described in Appendix D. The Eora global supply chain database consists of a Multi-Region Input–Output table (MRIO) model that provides time series of high-resolution Input–Output (IO) tables with matching environmental and social satellite accounts for 190 countries (35 types of EI air pollution, energy use, greenhouse gas emissions, water use, land occupation, N and P emissions, etc.). 16 IO tables, each for the period 2000–2017 for Ethiopia and Kenya were used.

Table 1 Factors (data) used per sector

The results of the nonparametric estimation are presented below (Table 2), following the Copula function approach and production frontier analysis, described in the previous section. From the estimated production functions we can easily obtain their corresponding marginal product function, which is connected with the water use input variable, according to Eq. (23) (see also Fig. 5). The estimated α, β parameters have the expected signs, which define the form of the demand curves.

Table 2 Parameters α, β and price elasticities per sector

Regarding the price elasticity, which is also presented in Table 2, based on Eqs. (24)–(25), as expected, all sectors are exceptionally inelastic to a price change for water use (price cannot affect water use). Agriculture seems to be perfectly inelastic to any price change, which means that in both countries the demand will remain stable for any price change. This implies an extremely strong relationship between the input (w_i) and the corresponding crop output, since the producer lacks alternatives, actually depends on the scarce water resources, which is highly valued. These well-known findings that are confirmed by our results, strengthen the validity of the proposed framework.

The respective demand curves (Eq. (24)), provide an ordering of these sectors via their demand function intercepts (Fig. 3). Sequential “exits from the market” are defined by the relative importance of sector-specific demand parameter ratio a, with a = α/β. As w_i reaches zero sequentially, its price increases revealing producers’ preferences for water use. At these prices, in Ethiopia, Tourism sector should exit the market first followed by Residential and Energy sectors, while in Kenya, Mining would exit the market first trailed by the Tourism sector. Moreover, mining producers in Kenya value higher the water than in Ethiopia, and that happens because Kenya relies strongly on groundwater for mining production. In both cases, in case of river/lake depletion, agriculture sector should be the last one to exit the market, since it is valuing water use more than any other sector.

Fig. 3

Water demand curves per sector for each country

The water price elasticity (Eq. 25, b) sampling distributions tend not to vary significantly between the two countries (Fig. 4). Except of the Ethiopian residential sector’s distribution which seems like a normal distribution, the others slightly diverge from the normal distribution at their tails, showing disorders during extreme cases. None of these means is the mode of the distribution as well, although the chasm between those values is not notable. In economic terms, the elasticities for water demand in each sector do not deviate remarkably, letting so similar behavioural patterns to be observed in each sector across the two countries.

Fig. 4

Sampling distributions of water price elasticities by sector for both countries

The second parameter of the inverse demand curve is the constant term (α), which is responsible for the starting point of the demand curve, revealing the stakeholders’ WTP per sector. Figure 5 shows the distributions of constant terms of the inverse demand functions and interestingly we can see that in most cases the WTP for water use in energy sector is greater than the corresponding one in agriculture and tourism, which implies greater profitability in energy sector. Additionally, in terms of WTP, mining sector in Ethiopia, which follows a leptokurtic distribution seems to be the most stable one. The technical inefficiency parameter ${u}_{it}$ (Eqs. (19) and (33)) shows how (in)efficiently the water-input is transformed into production output (Fig. 5). Mining and Residential sectors in Ethiopia follow exactly the same distribution with a positive skew to the right. Energy and Tourism in both countries, ${u}_{it}$ has two district peaks (bimodal distribution), which indicates that in these sectors there are two groups of producers: some of them achieve to maximize their outputs given their inputs, while some others do not with technical inefficiency taking greater values than the former group. However, it is noteworthy that Energy sector is more technically efficient compared with Tourism, since the lowest peak of Tourism is as great at the biggest one of Energy sector.

Fig. 5

Sampling distributions of constant terms (up) and technical inefficiency (down) by sector for each country

All the above ‘clues’ derived from the two graphs, justify the proposed framework in terms of selecting a multi-sectorial approach, and introducing the term of technical inefficiency. Those novel elements give a significantly added value compared with the more ‘narrowed’ approaches so far.

7.2 Games Under Uncertainty

Historical hydrological data of the basin (e.g. precipitation, runoff of the Omo River to Lake Turkana, and evaporation/ ET), can be used to estimate their corresponding historical volatilities, σ, as in Eqs. (1)–(3), and storage of the lake, as in Eq. (5), while pumping costs per country can be used to represent water tariffs (detailed data and parameters of the solved models can be found in Appendix D, Table D.2). Subsequently, the stochastic optimization hydro-economic model, for both game cases can be solved with the described decoupling method for linear FBSDEs (Sect. 3). For the sake of scale consistency, the optimal water abstraction and the resulting NB are presented via the percentage of the water availability inside the river basin over the total water availability of each of the two countries.

Regarding the game, both players have two available strategies:

• myopic (the country follows short-term water exploitation, without considering the benefits coming from the natural resource sustainable use, i.e. from the river for U and from the lake for D): A myopic strategy amounts to the depletion of the resource that is owned as a common property. In the myopic equilibrium, the marginal benefit of the water use equals current marginal extraction cost, ignoring the water scarcity rents (conventional user costs) that represent instantaneous benefit of foregoing water extraction currently as a means of reducing future extraction costs. Analytically, the NB function is maximized without taking into account the constraint imposed by the resource (state) equation.

• non-myopic (consider natural resource and long-term plan–preservation benefits). In a non-myopic strategy, the marginal benefit of the water use equals current marginal extraction cost plus marginal user cost (as defined above). Analytically, the NB function is maximized subject to the constraint imposed by the resource (state) equation.

7.2.1 Non-Cooperative Case

The optimal scenario would be a Non-myopic–Non-myopic combination, where the lake runs out of water after 33 years, while the worst-case scenario in environmental terms is realised when both countries follow a myopic strategy, where the Lake Depletion Time (LDT) is 15 years, accompanied by lack of trust, institutions bridging the limited disposable information, or a limited technical support (Table 3).

Table 3 Non-cooperative case for myopic and non-myopic combinations

Although Kenya on average seems to gain more at the myopic case, the total losses of that strategy surpass the gains, as for fifteen more years it could have an average net benefit equal to $2.2543･10⁷, while from the myopic perspective it is zero. So, if Kenya (D) controls its water use over time (non-myopic), it can increase its total benefits from $743,919,000 to $1,321,810,000 no matter what Ethiopia decides, while in the myopic equilibrium it gains only $342,435,000. At the same time, Ethiopia (U) has every time higher NBs in the non-myopic strategy. However, Ethiopia’s negative externalities to Kenya in the event of both following the myopic strategy can be seen at the LDT (in half of the time compared to the non-myopic strategies).

NB values represent the average value of the economy as long as there is water. Ethiopia’s benefit curves are the average of a 200-year period, where there is no sector exit, while Kenya’s benefit curves are the average of 15- to 33-year period, until the point, where first all sectors leave, and the lake depletes. Hence, in myopic-myopic combination, the 16^th year in Kenya is characterized by zero SB and costs, while all the demand for goods and services is met by imports.

The water use of all sectors in both countries (Fig. 6) is characterised by increased rates and faster depletion in the myopic-myopic case, compared to the non-myopic–non-myopic one. Kenya’s water use becomes zero at the LDT (15.5 years for the myopic-myopic and 33.4 years for the non-myopic–non-myopic case). Ethiopia’s time horizon is 200 years, to indicate the lack of limitations on water reserves of Omo River.

Fig. 6

Total water use for the two extreme strategy-combinations

7.2.2 Cooperative Case

In this case that the players benefit from their goods’ exchange, NBs are higher for both.⁹ So, the most crucial concept is relative efficiency. After a three-case numerical exploration of η₁ coefficient of Eq. (12), for a number of periods, it seems that the lake does not deplete under the cooperative case. This very promising outcome is important for both countries, because since they trade, there is interest in the sustainable development of the neighbours. Table 4 presents the indicative results of the solutions in terms of maximized NBs and lake depletion times.

Table 4 Cooperative case: a numerical simulation of different n values to optimize NB

Apparently, for all possible outcomes given the preferences of Ethiopia, NB are outstandingly greater than the non-cooperative case (Fig. 7—indicatively for the least possible rate of η₁), not to mention the sustainability of the lake (LDT = never). Thus, indisputably the cooperative is the best strategy, and the more beneficial for both players as η₁ increases.

Fig. 7

Total water use in for the best non-cooperative case versus the cooperative case (for the lower η₁)

In this graph, Ethiopia realises the upcoming benefits coming from giving up a considerable amount of water in exchange of food supply produced by the downstream country. In response (reaction), Kenya significantly increases its water use over the years, to increase production. Moreover, the total water use of both countries in the cooperative case is less compared to the non-cooperative (Kenya’s peak in the 20^th year is seven times less than Ethiopia’s maximum use).

7.3 Uncertainty Effects

As analysed, the impact of altering the volatility of the hydrological variables, will affect both water stocks and NBs. The comparative results for the non-cooperative and cooperative cases, are presented in Table 5, for the maximum observed historical changes.

Table 5 Hydrological variability impacts on NBs and LDT

In the non-cooperative case (Fig. 8a, b), Kenya tries to adjust its water consumption due to the increased outflow volatility (so to save water). In the cooperative case, no country changes its behaviour, as there is no risk of drought due to mutual assistance. Ethiopia’s water consumption (Fig. 8c, d) tends to zero, indicating the short-term planning. In cooperation, the behaviour is almost the same, allowing the trades, and NBs are also higher compared to the non-cooperative case. That difference would be enough to motivate both countries to keep on trading even under extremes. Although runoff decreased (Fig. 8e,f), NBs and water consumption do not change significantly. Under cooperation, even with uncertain runoff, Ethiopia and Kenya can continue to use almost the same water quantity, unlike to the non-cooperative case, where Kenya slightly reduces its water use, to gain $2,002,000 more, but the lake depletes earlier than the BAU scenario.

Fig. 8

σ_Ο variability’s effects on Kenya’s water use (first row), σ_W variability’s effects on Ethiopia’s water use (second row), σ_R variability’s effects on Kenya’s water use (third row): Comparison of non-cooperative non-myopic–non-myopic (left column), and cooperative case (right column)

In the studied basin, the life-dependance between water resources and survival (not just economy) is well described in the demand curves. This mandates a rational and sustainable water resources management that will lead to overall optimum results. Having scientific support from integrated and sophisticated tools that will provide detailed estimations of water availability, demand per sector, production, costs and economic benefits, as well as the interactions and responses of the “game players”, is crucial (Loucks 2021). The results also indicated the most vulnerable sectors for each country, and this can be generalised easily, having thus significant policy implications: It can assist decisions on what sector will be prioritized or not (exiting the market, as shown), and how the others will respond in order to maximize their benefits. In this particular case, we see that under any conditions, cooperation seems to be a win–win sustainable strategy, for both countries, environment, and economy. Furthermore, in case of river/lake depletion, agriculture sector that values water more compared to the other sectors would be the last one to exit the market. The technically efficient and inefficient sectors are also an important output that should be considered in policy-making, as it directly indicates the ‘stability’ of each sector, their ability to transform the water inputs into production outputs, and how uniform this is among the different producers per sector (Song et al. 2018; Lombardi et al. 2019; Tsionas and Mallick 2019). While there is no one-size-fits-all approach for how to exploit these findings for maximizing the overall benefits, cooperation seems to be a necessary initial condition to build on it and achieve sustainable growth. The results are in agreement with previous studies, showing the importance of cooperation, mutual investments and shared economic benefits, especially important for downstream countries (Vinca et al. 2021). Dinar (2009) argues that under increased water supply variability, cooperation should be preferred to address the risks, and this is now proved. An international agreement would strengthen this strategy, because at the time any trade-offs depend on governmental decisions. Hydrological uncertainties put into risk most cooperative decisions: Dinar et al. (2010) found a bell-shaped relationship between water supply variations and cooperation agreements; Ansink and Ruijs (2008) also demonstrate that a decrease in average river flows reduces the stability of an agreement, while an increase in variance may have both positive and negative effects.

8 Conclusions

In this work, a framework for scarce transboundary water resources management was presented. Game theory, hydro-economics, and econometrics were combined to explore the optimal strategies in environmental and economic terms, while the whole system was tested under hydrological uncertainty.

The conceptual framework is quite simple, while the analytical solution is provided, to make possible its replication. It is based on the principles of water balance, marginal and total costs, net and social benefits, while a novel element was the stochastic consideration of its hydrological components. The stochastic Stackelberg differential game approach was successfully applied and enabled the evaluation of numerous potential strategies. The econometric model’s contribution is also deemed essential for planning, as it provided production functions for all sectors for both countries, which was expressed as their social benefits, and the derived water demand curves. A novel mathematical approach was demonstrated to address the endogeneity issues of the production functions’ inputs, combining different tools, in order to provide a realistic representation of the problem. As said in the previous section, the findings that can be derived from the results of the technical inefficiency in water use, and the participation of all the five sectors of the economy, could not be obtained with any previous approach. The management insights that a policymaker can consider from the results are very important both in the short- and long-term planning. The conceptual hydro-economic model, with the game cases under uncertainty that we presented, completes the integrated character of the proposed framework. The present paper provides a case-study specific application of the developed framework, which however, can be easily modified (e.g. assuming more water sources, more or different sectors, decentralized water management decision allowing more interactions, etc.). The novel character of this contribution is based on its detailed hydro-economic/ econometric and sophisticated mathematical modelling, which identifies easily the most solid and “win–win” management strategies, supporting thus sustainable decision-making and planning. In the future, we aim to further test the developed methodology in other contexts and case studies, compare and potentially generalize the findings.

A limitation of this study is that we were not able to present in detail all models used, given the length of the paper. However, the mathematical expressions presented in the main text and the Appendices allow the replication of the modelling framework. Another limitation is that we analysed the five economic sectors—same for both Kenya and Ethiopia. In our case, this was not a big assumption, because the two countries have similar characteristics in terms of their economic development. If the framework is applied in other contexts, then the sectors considered can be easily modified. Integrated modelling needs integrated data—a challenge for any integrated assessment. The data used are presented in detail in Appendix D. While the aim of this work was to demonstrate the proposed framework, rather than a case-study application, it is worthy to mention some specific conclusions: The analysis proved the vital role of water resources to any continuation and development of the economic activities. It is well known that as the price of a good rises, buyers will choose to buy less of it, and as its price falls, they buy more: as water price increases over time due to water scarcity, the demand for all economic sectors reaches zero sequentially. The way this finding was proved (showing also the ordering of the sectors who will reach zero) is a novel element, and combined with the examined game strategies, it is proved that under any circumstances, cooperation is the overall optimal strategy. Under cooperation scenario, the upstream country realises the upcoming benefits coming from giving up a considerable amount of water to the downstream country, in exchange of their produced food supply, over time. The reaction of the downstream country is the increment of its water use to increase production. So over time, it turns out to be more profitable for both countries the case where the downstream one uses more water than the upstream, which currently seems utopic. A swift in selfish and opportunistic mindsets is required, so both countries can secure a future water availability, sustainable access to the input resource-driver of their economic growth, and exploit the mutual benefits of cooperation and collaboration.

Appendices

Appendix A

Non-Cooperative Case

2.1 Upstream

The Hamiltonian for the j-exit stage is:

$$\begin{aligned} H_{j}^{U} \left( {W_{jt}^{U} ,\, w_{jt}^{U} ,\, \ldots ,\, w_{5t}^{U} ,\lambda_{jt}^{U} } \right) & = \mathop \sum \limits_{i = j}^{5} \left[ {\frac{{a_{i}^{U} }}{{b_{i}^{U} }}w_{it}^{U} - \frac{1}{{2b_{i}^{U} }} \cdot (w_{it}^{U} )^{2} - \left( {k_{2}^{U} - k_{1}^{U} W_{jt}^{U} } \right)w_{it}^{U} } \right] \\ & + \, \lambda_{jt}^{U} \left[ {W_{jt}^{U} - \mathop \sum \limits_{i = j}^{5} w_{it}^{U} } \right],\;\;j = 1,2,...,5 \\ \end{aligned}$$

(A1)

where ${\lambda }_{jt}^{U}$ is the j-exit stage adjoint variable that represents water scarcity rents for U country. The necessary conditions for the optimality are given as follows:

$$\frac{{\partial H_{j}^{U} }}{{\partial w_{it}^{U} }} = \frac{{a_{i}^{U} }}{{b_{i}^{U} }} - \frac{1}{{b_{i}^{U} }}w_{it}^{U} - \left( {k_{2}^{U} - k_{1}^{U} W_{jt}^{U} } \right) - \lambda_{jt}^{U} \;\;\;i = j,...,5,\;\;j\, = \,1,2, \ldots ,5$$

(A2)

$${d\lambda }_{jt}^{U}= \left[-\frac{\partial {H}_{j}^{U}}{\partial {W}_{it}^{U}}+r{\lambda }_{jt}^{U} \right]dt= \left[-{k}_{1}^{U}{\sum }_{i=j}^{5}{w}_{it}^{U}+r{\lambda }_{jt}^{U} \right]dt$$

(A3)

The first optimality condition gives:

$$w_{it}^{U} = a_{i}^{U} - b_{i}^{U} \left( {k_{2}^{U} - k_{1}^{U} W_{jt}^{U} } \right) - b_{i}^{U} \lambda_{jt}^{U} ,\;\;\;i = j,...,5$$

(A4)

Then substituting to the state equation (Eq. 4), we have:

$${dW}_{jt}^{U}=\left[-{\text{k}}_{1}^{\text{U}}({\sum }_{\text{i=j}}^{5}{b}_{\text{i}}^{\text{U}}\text{)}{W}_{jt}^{U}+({\sum }_{\text{i=j}}^{5}{b}_{\text{i}}^{\text{U}}\text{)}{\lambda }_{jt}^{U}+{W}_{t}-{\sum }_{\text{i=j}}^{5}{a}_{\text{i}}^{\text{U}}+{k}_{2}^{U}{\sum }_{\text{i=j}}^{5}{b}_{\text{i}}^{\text{U}}\right]{\text{dt}}$$

(A5)

while substituting to the adjoint Eq. (A3) we have

$$d{\lambda }_{jt}^{U}=\left\{-{\left({k}_{1}^{U}\right)}^{2}\left({\sum }_{i=j}^{5}{b}_{i}^{U}\right){W}_{jt}^{U}+\left[{k}_{1}^{U}\left({\sum }_{i=j}^{5}{b}_{i}^{U}\right)+r\right]{\lambda }_{jt}^{U}-{k}_{1}^{U}{\sum }_{i=j}^{5}{a}_{i}^{U}+{k}_{1}^{U}{k}_{2}^{U}{\sum }_{i=j}^{5}{b}_{i}^{U}\right\}dt$$

(A6)

Setting ${A}_{j}^{U}\triangleq {\sum }_{i=j}^{5}{a}_{i}^{U}$ and ${B}_{j}^{U}\triangleq {\sum }_{i=j}^{5}{b}_{i}^{U}$ we obtain the forward–backward stochastic differential equations system (FBSDEs):

$$\begin{aligned}&d{W}_{jt}^{U}=\left[-{k}_{1}^{U}{B}_{j}^{U}{W}_{jt}^{U}+{B}_{j}^{U}{\lambda }_{jt}^{U}+{W}_{t}-{A}_{j}^{U}+{k}_{2}^{U}{B}_{j}^{U}\right]dt,\\&d{\lambda }_{jt}^{U}=\left[-{\left({k}_{1}^{U}\right)}^{2}{B}_{j}^{U}{W}_{jt}^{U}+\left({k}_{1}^{U}{B}_{j}^{U}+r\right){\lambda }_{jt}^{U}-{k}_{1}^{U}{A}_{j}^{U}+{k}_{1}^{U}{k}_{2}^{U}{B}_{j}^{U}\right]dt,\\&{W}_{00}^{U}={w}_{0}, \, \underset{t\to \infty }{lim}{\lambda }_{jt}^{U}=0, \, j=1,2,...,5\end{aligned}$$

(A7)

To solve the above system of FBSDEs we impose a solution of the form:

$${\lambda }_{jt}^{U}={N}_{jt}^{U}{W}_{jt}^{U}+{M}_{jt}^{U}, \, i=j,...,5$$

(A8)

where $N_{jt}^{U}$ and $M_{jt}^{U}$ are stochastic processes to be determined. Taking differentials, we have:

$$d{\lambda }_{jt}^{U}={W}_{jt}^{U}d{N}_{jt}^{U}+{N}_{jt}^{U}d{W}_{jt}^{U}+d{M}_{jt}^{U}={W}_{jt}^{U}d{N}_{jt}^{U}+d{M}_{jt}^{U}+\left\{[{B}_{j}^{U}{\left({N}_{jt}^{U}\right)}^{2}- {k}_{1}^{U}{B}_{j}^{U}{N}_{jt}^{U}]{W}_{jt}^{U}+{{B}_{j}^{U}{N}_{jt}^{U}{M}_{jt}^{U}}+\left[{W}_{t}{-A}_{j}^{U}+{k}_{2}^{U}{B}_{j}^{U}\right]{N}_{jt}^{U}\right\}dt$$

(A9)

while from the backward equation of the system (Eq. A7) we have:

$$d{\lambda }_{jt}^{U}=\{[\left({k}_{1}^{U}{B}_{j}^{U}+r\right){N}_{jt}^{U}-{\left({k}_{1}^{U}\right)}^{2}{B}_{j}^{U}]{W}_{jt}^{U}+\left({k}_{1}^{U}{B}_{j}^{U}+r\right){M}_{jt}^{U}-{k}_{1}^{U}{A}_{j}^{U}+{k}_{1}^{U}{k}_{2}^{U}{B}_{j}^{U}\}dt$$

(A10)

Sufficient conditions for the last two relationships to be equivalent are:

$$\begin{aligned}&d{N}_{jt}^{U}=\left[-{B}_{j}^{U}{\left({N}_{j}^{U}\right)}^{2}+\left(2{k}_{1}^{U}{B}_{j}^{U}+r\right){N}_{jt}^{U}-{\left({k}_{1}^{U}\right)}^{2}{B}_{j}^{U}\right]dt,\\&\quad\underset{t\to \infty }{lim}{N}_{jt}^{U}=0\end{aligned}$$

(A11)

which is a Backward Riccatti Equation (BRE) that can be solved numerically for ${N}_{jt}^{U}$x

And.

$$\begin{aligned}&d{M}_{jt}^{U}=\left[\left(-{B}_{j}^{U}{N}_{j}^{U}+{k}_{1}^{U}{B}_{j}^{U}+r\right){M}_{jt}^{U}-\left({W}_{t}-{A}_{j}^{U}+{k}_{2}^{U}{B}_{j}^{U}\right){N}_{j}^{U}-{k}_{1}^{U}{A}_{j}^{U}+{k}_{1}^{U}{k}_{2}^{U}{B}_{j}^{U}\right]dt\\&\\quad \mathop {\lim }\limits_{t \to \infty } M_{jt}^{U} = 0,\;j\, = \,1,2, \ldots ,5 \end{aligned}$$

(A12)

Substituting the linear solution form of Eq. (A8) to the forward equation of the FBSDEs system:

$$\begin{aligned}&{\mathrm{dW}}_{\mathrm{jt}}^{\mathrm{U}}=\left[\left(-{\mathrm{k}}_{1}^{\mathrm{U}}+{\mathrm{N}}_{\mathrm{jt}}^{\mathrm{U}}\right){\mathrm{B}}_{\mathrm{jt}}^{\mathrm{U}}{\mathrm{W}}_{\mathrm{jt}}^{\mathrm{U}}+{\mathrm{B}}_{\mathrm{j}}^{\mathrm{U}}{\mathrm{M}}_{\mathrm{j}}^{\mathrm{U}}+{\mathrm{W}}_{\mathrm{t}}-{\mathrm{A}}_{\mathrm{j}}^{\mathrm{U}}+{\mathrm{k}}_{2}^{\mathrm{U}}{\mathrm{B}}_{\mathrm{j}}^{\mathrm{U}}\right]\mathrm{dt},\\&\quad {\mathrm{W}}_{00}^{\mathrm{U}}={\mathrm{w}}_{0}\end{aligned}$$

(A13)

Which is a forward linear SDE that can be solved for ${\mathrm{W}}_{\mathrm{jt}}^{\mathrm{U}}.$ Then the backward adjoint variable ${\lambda }_{\mathrm{jt}}^{\mathrm{U}}$ follows from Eq. (A8) and the optimal water use ${\mathrm{w}}_{\mathrm{jt}}^{\mathrm{U}}$ follows from the optimality condition (Eq. A4).

2.2 Downstream

The maximization function, as described in the main text (water balance concept) and also shown in Fig. 2, it subjects to water balance of U, the runoff in D, water stock of D (state equation), and the water use of D. For the (j,k)-th exit-stage, we have the Hamiltonian:

$${H}_{jk}^{D}\left({S}_{jk},{w}_{jkt}^{D},...,{w}_{j5t}^{D},{\lambda }_{jkt}^{D}\right)\triangleq {\sum }_{l=k}^{5}\left[\frac{{a}_{l}^{D}}{{b}_{l}^{D}}{w}_{jlt}^{D}-\frac{1}{2{b}_{l}^{D}}\cdot ({w}_{jlt}^{D}{)}^{2}\right]-({k}_{2}^{D}-{k}_{1}^{D}{S}_{jkt}){\sum }_{l=k}^{5}{w}_{jlt}^{D}\text{+}{\uplambda }_{jkt}^{D}\left[{W}_{t}-{\sum }_{i=j}^{5}{w}_{it}^{U}-{\sum }_{l=k}^{5}{w}_{jlt}^{D}+{R}_{t}-{O}_{t}\right], \, j,k=1,2,...,5$$

(A14)

where ${\lambda }_{jkt}^{D}$ is the (j,k)-th exit stage adjoint variable that represents water scarcity rents for D. The necessary conditions for optimality are given as follows:

$$\frac{\partial {\mathrm{H}}_{\mathrm{jk}}^{\mathrm{D}}}{\partial {\mathrm{w}}_{\mathrm{jlt}}^{\mathrm{D}}}=\frac{{\mathrm{a}}_{\mathrm{l}}^{\mathrm{D}}}{{\mathrm{b}}_{\mathrm{l}}^{\mathrm{D}}}-\frac{1}{{\mathrm{b}}_{\mathrm{l}}^{\mathrm{D}}}\cdot {\mathrm{w}}_{\mathrm{jlt}}^{\mathrm{D}}-\left({\mathrm{k}}_{2}^{\mathrm{D}}-{\mathrm{k}}_{1}^{\mathrm{D}}{\mathrm{S}}_{\mathrm{jkt}}\right)-{\uplambda }_{\mathrm{jkt}}^{\mathrm{D}}=0, \, \mathrm{l}=\mathrm{k},...,5, j,k=1,2,..,5$$

(A15)

$$\mathrm{d}{\uplambda }_{\mathrm{jkt}}^{\mathrm{D}}=\left[-\frac{\partial {\mathrm{H}}_{\mathrm{jk}}^{\mathrm{D}}}{\partial {\mathrm{S}}_{\mathrm{jkt}}}+\mathrm{r}{\uplambda }_{\mathrm{jkt}}^{\mathrm{D}}\right]\mathrm{dt} \, \iff \, \mathrm{d}{\lambda }_{\mathrm{jkt}}^{\mathrm{D}}=\left[-{\mathrm{k}}_{1}^{\mathrm{D}}{\sum }_{\mathrm{l}=\mathrm{k}}^{5}{\mathrm{w}}_{\mathrm{jlt}}^{\mathrm{D}}+\mathrm{r}{\uplambda }_{\mathrm{jkt}}^{\mathrm{D}}\right]\mathrm{dt}$$

(A16)

From the first condition we have that:

$${w}_{jkt}^{D}={a}_{l}^{D}-{b}_{l}^{D}\left({k}_{2}^{D}-{k}_{1}^{D}{S}_{jkt}\right)-{b}_{l}^{D}{\lambda }_{jkt}^{D}, \quad l=k,...,5,\mathrm{ and j},\mathrm{k}=1,2,\ldots 5$$

(A17)

Setting again ${A}_{j}^{U}\triangleq {\sum }_{i=j}^{5}{a}_{i}^{U}$ and ${B}_{j}^{U}\triangleq {\sum }_{i=j}^{5}{b}_{i}^{U}$, the water storage state Eq. (5), and the adjoint equation Eq(A16) are reformulated as:

$$\begin{aligned}&d{S}_{jkt}=\left[-{k}_{1}^{D}{B}_{k}^{D}{S}_{jkt}+{B}_{k}^{D}{\lambda }_{jkt}^{D}+{W}_{t}-{\sum }_{i=j}^{5}{w}_{it}^{U}+{R}_{t}-{O}_{t}-{A}_{k}^{D}+{k}_{2}^{D}{B}_{k}^{D}\right]dt\\& d{\lambda }_{jkt}^{D}=\left\{{-\left({k}_{1}^{D}\right)}^{2}{B}_{k}^{D}{S}_{jkt}+{(k}_{1}^{D}{B}_{k}^{D}+r){\lambda }_{jkt}^{D}-{k}_{1}^{D}{A}_{k}^{D}+{k}_{1}^{D}{k}_{2}^{D}{B}_{k}^{D}\right\}dt\\&{S}_{000}={s}_{0}, \, \underset{t\to \infty }{lim}{\lambda }_{jkt}^{D}=0, \, j,k=1,2,...,5\end{aligned}$$

(A18)

To solve the above system of FBDEs we impose a solution of the form:

$${\lambda }_{jkt}^{D}={N}_{jkt}^{D}{S}_{jkt}+{M}_{jkt}^{D}$$

(A19)

where ${N}_{jkt}^{D}$ and ${M}_{jkt}^{D}$ are stochastic processes to be determined. Taking differentials in Eq. (A19), we have:

$$\begin{aligned}d{\lambda }_{jkt}^{D}&={S}_{jkt}d{N}_{jkt}^{D}+{N}_{jkt}^{D}d{S}_{jkt}+d{M}_{jkt}^{D}\\&={S}_{jkt}d{N}_{jkt}^{D}+d{M}_{jkt}^{D}+\left\{[{B}_{k}^{D}{\left({N}_{jkt}^{D}\right)}^{2}-{k}_{1}^{D}{B}_{k}^{D}{N}_{jkt}^{D}]{S}_{jkt}+{B}_{k}^{D}{N}_{jkt}^{D}{M}_{jkt}^{D}+\left[{W}_{t}-{\sum }_{i=j}^{5}{w}_{it}^{U}+{R}_{t}-{O}_{t}-{A}_{k}^{D}+{k}_{2}^{D}{B}_{k}^{D}\right]{N}_{jkt}^{D}\right\}dt\end{aligned}$$

(A20)

while from the backward equation of the system (Eq. A18) we have:

$$d{\lambda }_{jkt}^{D}=\left\{\left[{(k}_{1}^{D}{B}_{k}^{D}+r){N}_{jkt}^{D}-{\left({k}_{1}^{D}\right)}^{2}{B}_{k}^{D}\right]{S}_{jkt}+\left[{k}_{1}^{D}{B}_{k}^{D}+r\right]{M}_{jkt}^{D}-{k}_{1}^{D}{A}_{k}^{D}+{k}_{1}^{D}{k}_{2}^{D}{B}_{k}^{D}\right\}dt$$

(A21)

A sufficient condition for the latter to be equal is given by

$$d{N}_{jkt}^{D}=\left[-{B}_{k}^{D}{\left({N}_{jkt}^{D}\right)}^{2}+\left(2{k}_{1}^{D}{B}_{k}^{D}+r\right){N}_{jkt}^{D}-{\left({k}_{1}^{D}\right)}^{2}{B}_{k}^{D}\right]dt, \underset{t\to \infty }{lim}{N}_{jkt}^{D}=0$$

(A22)

which is a BRE that can be solved numerically for ${N}_{jkt}^{D}$. Also:

$$\begin{aligned}&d{M}_{jkt}^{D}=\left[\begin{array}{c}\left(-{B}_{k}^{D}{N}_{jkt}^{D}+{k}_{1}^{D}{B}_{k}^{D}+r\right){M}_{jkt}^{D}-\left({W}_{t}-{\sum }_{i=j}^{5}{w}_{it}^{U}+{R}_{t}-{O}_{t}-{A}_{k}^{D}+{k}_{2}^{D}{B}_{k}^{D}\right){N}_{jkt}^{D}\\ \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, -{k}_{1}^{D}{A}_{k}^{D}+{k}_{1}^{D}{k}_{2}^{D}{B}_{k}^{D}\end{array}\right]dt\\&\underset{t\to \infty }{lim}{M}_{jkt}^{D}=0\end{aligned}$$

(A23)

which given the above solution is a backward linear first-order SDE that can be solved for ${M}_{jkt}^{D}$. Substituting the linear solution form of Eq. (A19) to the forward equation of the FBSDEs system (Eq. A18), we get:

$$\begin{aligned}{\mathrm{dS}}_{\mathrm{jkt}}=\left[\left(-{\mathrm{k}}_{1}^{\mathrm{D}}+{\mathrm{N}}_{\mathrm{jkt}}^{\mathrm{D}}\right){\mathrm{S}}_{\mathrm{jkt}}+{\mathrm{B}}_{\mathrm{k}}^{\mathrm{D}}{\mathrm{M}}_{\mathrm{jkt}}^{\mathrm{D}}+{\mathrm{W}}_{\mathrm{t}}-{\sum }_{\mathrm{i}=\mathrm{j}}^{5}{\mathrm{w}}_{\mathrm{it}}^{\mathrm{U}}+{\mathrm{R}}_{\mathrm{t}}-{\mathrm{O}}_{\mathrm{t}}-{\mathrm{A}}_{\mathrm{k}}^{\mathrm{D}}+{\mathrm{k}}_{2}^{\mathrm{D}}{\mathrm{B}}_{\mathrm{k}}^{\mathrm{D}}\right]\mathrm{dt}\\& {\text{S}}_{000} = {\text{s}}_{0} ,\quad j,k\, = \,1,2, \ldots ,5 \end{aligned}$$

(A24)

which is a forward linear SDE that can be solved numerically for ${\mathrm{S}}_{\mathrm{jkt}}$. Thus, the backward adjoint variable ${\lambda }_{jkt}^{D}$ follows from the linear transformation of Eq. (A19) and the optimal water use ${w}_{jlt}^{D}$ follows from the optimality condition Eq. (A17).

Cooperative Case

3.1 Upstream

For the (j,k)-th exit stage we have the augmented Hamiltonian:

$${H}_{jk}^{U}\left({W}_{jt}^{U},{S}_{jkt},{\lambda }_{jkt}^{D},{w}_{jkt}^{U},...,{w}_{5kt}^{U},{\mu }_{j\kappa t},{\nu }_{j\kappa t},{\xi }_{j\kappa t}\right)\triangleq {\sum }_{i=j}^{5}\left[\frac{{a}_{i}^{U}}{{b}_{i}^{U}}{w}_{it}^{U}-\frac{1}{2{b}_{i}^{U}}\cdot ({w}_{it}^{U}{)}^{2}-({k}_{2}^{U}-{k}_{1}^{U}{W}_{jt}^{U}){w}_{it}^{U}\right]+{\upeta }_{1}{S}_{jkt}+{\eta }_{2}+{\mu }_{jkt}\left[{W}_{t}-{\sum }_{i=j}^{5}{w}_{it}^{U}\right]+{\upnu }_{jkt}\left[{W}_{t}-{\sum }_{i=j}^{5}{w}_{ikt}^{U}+{R}_{t}-{O}_{t}-{A}_{k}^{D}+{B}_{k}^{D}({k}_{2}^{D}-{k}_{1}^{D}{S}_{jkt})+{B}_{k}^{D}{\lambda }_{jkt}^{D}\right] {+}{\upxi }_{jkt}\left\{-{k}_{1}^{D}\left[{A}_{k}^{D}-{B}_{k}^{D}({k}_{2}^{D}-{k}_{1}^{D}{S}_{jkt})\right]+\left(r+{k}_{1}^{D}{B}_{k}^{D}\right){\lambda }_{jkt}^{D}\right\}$$

(A25)

where $\left({\mu }_{j\kappa },{\nu }_{j\kappa },{\xi }_{j\kappa }\right)$ is the vector of the associated adjoint variables.

The necessary conditions for optimality for the maximization problem of U are given below:

$$\frac{\partial {H}_{jk}^{U}}{\partial {w}_{ikt}^{U}}=\frac{{a}_{i}^{U}}{{b}_{i}^{U}}-\frac{1}{{b}_{i}^{U}}\cdot {w}_{ikt}^{U}-\left({k}_{2}^{U}-{k}_{1}^{U}{W}_{jt}^{U}\right)-{\mu }_{jkt}-{\nu }_{jkt}=0, \, i=j,...,5,\mathrm{ j},\mathrm{k}=1,2,\ldots 5$$

(A26)

$$d{\mu }_{jkt}=\left[-\frac{\partial {H}_{j\kappa }^{U}}{\partial {W}_{jt}^{U}}+r{\mu }_{jkt}\right]dt \, \iff \, d{\upmu }_{jkt}=\left[-{k}_{1}^{U}{\sum }_{i=j}^{5}{w}_{it}^{U}+r{\mu }_{jkt}\right]dt$$

(A27)

$$d{\nu }_{jkt}=\left[-\frac{\partial {H}_{j\kappa }^{U}}{\partial {S}_{jkt}}+r{\nu }_{jkt}\right]dt \, \iff$$

$$\mathrm{d}{\upnu }_{\mathrm{jkt}}=\left\{-{\upeta }_{1} +{\mathrm{k}}_{1}^{\mathrm{D}}{{\mathrm{B}}_{\mathrm{k}}^{\mathrm{D}}\upnu }_{\mathrm{jkt}}+{\left({\mathrm{k}}_{1}^{\mathrm{D}}\right)}^{2}{\mathrm{B}}_{\mathrm{k}}^{\mathrm{D}}{\upxi }_{\mathrm{jkt}}+\mathrm{r}{\upnu }_{\mathrm{jkt}}\right\}\mathrm{dt}$$

(A28)

$$d{\xi }_{jkt}=\left[-\frac{\partial {H}_{j\kappa }^{U}}{\partial {\lambda }_{jt}^{D}}+r{\xi }_{jkt}\right]dt \, \iff d{\upxi }_{jkt}=\left[-{B}_{k}^{D}{\nu }_{jkt}-{k}_{1}^{D}{B}_{k}^{D}{\xi }_{jkt}\right]dt,$$

$${\xi }_{000}=0$$

(A29)

From the first optimality condition (Eq. A26) we have:

$${w}_{ikt}^{U}={a}_{i}^{U}-{b}_{i}^{U}\left({k}_{2}^{U}-{k}_{1}^{U}{W}_{jt}^{U}\right)-{b}_{i}^{U}{\mu }_{jkt}-{b}_{i}^{U}{\nu }_{jkt}, \, i=j,...,5,\mathrm{ j},\mathrm{k}=1,2,\ldots ,5$$

(A30)

It can be easily seen that the adjoint variables of both Eqs. (A28) and (A29) satisfy the system of FBSDEs:

$$d{\xi }_{jkt}=-\left[{k}_{1}^{D}{B}_{k}^{D}{\xi }_{jkt}+{B}_{k}^{D}{v}_{jkt}\right]dt,$$

$${\mathrm{d\nu }}_{\mathrm{jkt}}=\left\{{\left({\mathrm{k}}_{1}^{\mathrm{D}}\right)}^{2}{B}_{k}^{D}{\upxi }_{\mathrm{jkt}}+(\mathrm{r}+{\mathrm{k}}_{1}^{\mathrm{D}}{{B}_{k}^{D})\upnu }_{\mathrm{jkt}}-{\upeta }_{1}\right\}dt$$

$$\xi_{000} = 0,\;\mathop {\lim }\limits_{t \to \infty } v_{jkt} = 0,\quad j,k\, = \,1,2, \ldots .,5$$

(A31)

In order to solve this FBSDEs system we are looking for solutions (${\xi }_{jkt},{\upnu }_{jkt})$ that satisfy the linear transformation:

$${v}_{ikt}={N}_{jkt}{\xi }_{jkt}+{M}_{jkt}, \quad \mathrm{ j},\mathrm{k}=1,2,\ldots ,5$$

(A32)

where ${N}_{jkt}$ and ${M}_{jkt}$ are stochastic processes to be determined. Taking differentials in Eq. (A32) we get:

$${dv}_{ikt}={N}_{jkt}{\xi }_{jkt}+{\xi }_{jkt}d{N}_{jkt}+{dM}_{jkt}={\xi }_{jkt}d{N}_{jkt}+{dM}_{jkt}-[\left({B}_{k}^{D}{{N}_{jkt}^{2}{+{k}_{1}^{D}B}_{k}^{D}{N}_{jkt})\xi }_{jkt}{+B}_{k}^{D}{N}_{jkt}{M}_{jkt}\right]dt$$

(A33)

While the backward equation of Eq. (A31) may be written as

$${dv}_{ikt}=\{[\left(\mathrm{r}+{\mathrm{k}}_{1}^{\mathrm{D}}{{B}_{k}^{D})\mathrm{N}}_{\mathrm{jkt}}+{\left({k}_{1}^{D}\right)}^{2}{B}_{k}^{D}\right]{\xi }_{jkt}+(\mathrm{r}+{\mathrm{k}}_{1}^{\mathrm{D}}{{B}_{k}^{D})\mathrm{M}}_{\mathrm{jkt}}-{\upeta }_{1}\}dt$$

(A34)

Sufficient conditions for the latter to be equivalent are provided by

$$\begin{aligned} & dN_{jkt} = [B_{k}^{D} \cdot N_{jk}^{2} + \left( {2k_{1}^{D} B_{k}^{D} + r)N_{jkt} + \left( {k_{1}^{D} } \right) ^{2} B_{k}^{D} } \right]dt, \\ & \mathop {\lim }\limits_{t \to \infty } N_{jkt} = 0,\;\;\;j,k\, = \,1,2, \ldots .,5 \\ \end{aligned}$$

(A35)

which is a BRE that can be solved numerically for ${N}_{jkt}^{D}$ and by

$$d{M}_{jkt}=\left[\left({B}_{k}^{D}{N}_{jt}^{U}+r+{k}_{1}^{D}{B}_{k}^{D}\right){M}_{jkt}-{\eta }_{1}\right]dt,$$

$$\mathop {\lim }\limits_{t \to \infty } M_{jkt} = 0,\;\;j,k\, = \,1,2, \ldots .,5$$

(A36)

which given the above solution is a backward linear first-order SDE that can be easily solved for ${M}_{jkt}$.

Substituting the linear solution form of Eq. (A32) to the forward equation of the FBSDEs system Eq. (A31), we obtain:

$$d{\xi }_{jkt}=\left[-{B}_{k}^{D}\left({N}_{jkt}+{k}_{1}^{D}\right){\xi }_{jkt}-{B}_{k}^{D}{M}_{jkt}\right]dt,$$

$${\xi }_{000}=0, \quad j,k=1,2,...,5$$

(A37)

which is a forward linear SDE that can be solved for ${\xi }_{jkt}$. Then the backward adjoint variable ${v}_{jkt}$ follows from the linear transformation of Eq. (A32).

Given the obtained solution $\left({\xi }_{jk},{\nu }_{jk}\right), \, j,k=1,2,...,5,$ of the FBSDEs system, as described above, we may put in use Eq. (A30) to derive that U’s water resources state Eq. (4) and adjoint variable of Eq. (A27) form the subsequent system of FBSDEs:

$$\begin{aligned}&d{W}_{jt}^{U}=\left[-{k}_{1}^{U}{B}_{j}^{U}{W}_{jt}^{U}+{B}_{j}^{U}{\mu }_{jkt}+{B}_{j}^{U}{\nu }_{jkt}+{W}_{t}-{A}_{j}^{U}+{k}_{2}^{U}{B}_{j}^{U}\right]dt,\\&d{\mu }_{jkt}=\left[-{\left({k}_{1}^{U}\right)}^{2}{B}_{j}^{U}{W}_{jt}^{U}+\left({k}_{1}^{U}{B}_{j}^{U}+r\right){\mu }_{jkt}+{k}_{1}^{U}{B}_{j}^{U}{\nu }_{jkt}-{k}_{1}^{U}{A}_{j}^{U}+{k}_{1}^{U}{k}_{2}^{U}{B}_{j}^{U}\right]dt,\\&{W}_{00}^{U}=w{r}_{0}, \, \underset{t\to \infty }{lim}{\mu }_{jkt}=0, \, j,k=1,2,...,5\end{aligned}$$

(A38)

To find a solution process pair $\left({W}_{jt}^{U},{\mu }_{jk}\right){, }j,k=1,2,...,5,$ for this system of FBSDEs, we impose the linear transformation:

$${\mu }_{jkt}={\Lambda }_{jkt}{W}_{jt}^{U}+{\Xi }_{jkt}, \quad j,k=1,2,...,5$$

(A39)

where ${\Lambda }_{jk}$ and ${\Xi }_{jkt}$ are stochastic processes to be determined. Taking differentials in Eq. (A39) we have that:

$$d{\mu }_{jkt}={\Lambda }_{jkt}d{W}_{jt}^{U}+{W}_{jt}^{U}d{\Lambda }_{jkt}+d{\Xi }_{jkt}={W}_{jt}^{U}d{\Lambda }_{jkt}+d{\Xi }_{jkt} \, +\left\{\left[{B}_{j}^{U}{\Lambda }_{jkt}^{2}-{k}_{1}^{U}{B}_{j}^{U}{\Lambda }_{jkt}\right]{W}_{jt}^{U}+{B}_{j}^{U}{\Lambda }_{jkt}{\Xi }_{jkt}+{B}_{j}^{U}{\nu }_{jkt}{\Lambda }_{jkt}+\left[{W}_{t}-{A}_{j}^{U}+{k}_{2}^{U}{B}_{j}^{U}\right]{\Lambda }_{jkt}\right\}dt$$

(A40)

while the backward Eq. (A38) may be reformulated as:

$$d{\mu }_{jkt}=\left\{\left[-{\left({k}_{1}^{U}\right)}^{2}{B}_{j}^{U}+\left({k}_{1}^{U}{B}_{j}^{U}+r\right){\Lambda }_{jkt}\right]{W}_{jt}^{U}+\left({k}_{1}^{U}{B}_{j}^{U}+r\right){\Xi }_{jkt}+{k}_{1}^{U}{B}_{j}^{U}{\nu }_{jkt}-{k}_{1}^{U}{A}_{j}^{U}+{k}_{1}^{U}{k}_{2}^{U}{B}_{j}^{U}\right\}dt$$

(A41)

Sufficient conditions for the latter to be equivalent are given as follows:

$$\begin{aligned}&d{\Lambda }_{jkt}=\left[-{B}_{j}^{U}{\Lambda }_{jkt}^{2}+\left(2{k}_{1}^{U}{B}_{j}^{U}+r\right){\Lambda }_{jkt}-{\left({k}_{1}^{U}\right)}^{2}{B}_{j}^{U}\right]dt,\\&\quad \underset{t\to \infty }{lim}{\Lambda }_{jkt}=0, \quad j,k=1,2,...,5\end{aligned}$$

(A42)

which is a BRE that can be solved numerically for ${\Lambda }_{jkt}{, }j,\; k=1,2,...,5,$ and

$$\begin{aligned}&d{\Xi }_{jkt}=\left\{\begin{array}{c}\left[-{B}_{j}^{U}{\Lambda }_{jkt}+\left({k}_{1}^{U}{B}_{j}^{U}+r\right)\right]{\Xi }_{jkt}-{B}_{j}^{U}{\nu }_{jkt}{\Lambda }_{jkt}-\left[{W}_{t}-{A}_{j}^{U}+{k}_{2}^{U}{B}_{j}^{U}\right]{\Lambda }_{jkt}\\ +{k}_{1}^{U}{B}_{j}^{U}{\nu }_{jkt}-{k}_{1}^{U}{A}_{j}^{U}+{k}_{1}^{U}{k}_{2}^{U}{B}_{j}^{U}\end{array}\right\}dt,\\&\quad \underset{t\to \infty }{lim}{\Xi }_{jkt}=0, \quad j,k=1,2,...,5\end{aligned}$$

(A43)

which given the above solution is a backward linear first-order SDE that can be easily solved for ${\Xi }_{jkt}{, }\; j,k=1,2,...,5.$

Substituting the linear transformation of Eq. (A39) to the forward equation of the FBSDEs system Eq. (A38) we deduce that:

$$\begin{aligned}&d{W}_{jt}^{U}=\left\{\left[-{k}_{1}^{U}{B}_{j}^{U}+{B}_{j}^{U}{\Lambda }_{jkt}\right]{W}_{jt}^{U}+{B}_{j}^{U}{\Xi }_{jkt}+{B}_{j}^{U}{\nu }_{jkt}+{W}_{t}-{A}_{j}^{U}+{k}_{2}^{U}{B}_{j}^{U}\right\}dt,\\&{W}_{00}^{U}={w}_{0}^{U}, \quad j,k=1,2,...,5\end{aligned}$$

(A44)

which is a forward linear SDE that can be solved for ${W}_{jt}^{U}{, }\; j=1,2,...,5.$ Then the backward adjoint variable ${\mu }_{jkt}{, }\; j,k=1,2,...,5$ follows readily from the linear transformation of Eq. (A39).

Given now the solutions $\left({\xi }_{jk},{\nu }_{jk}\right), \left({W}_{jt}^{U},{\mu }_{jkt}\right), \, j,k=1,2,...,5,$ of the FBSDEs systems Eq. (A31) and Eq. (A38), respectively, together with Eq. (A30) to write equivalently the Hamiltonian FBSDEs state system of the downstream country as:

$$\begin{aligned}&d{S}_{jkt}=\left[\begin{array}{c}-{k}_{1}^{U}{B}_{j}^{U}{W}_{jt}^{U}-{k}_{1}^{D}{B}_{k}^{D}{S}_{jkt}+{B}_{k}^{D}{\lambda }_{jkt}^{D}+{B}_{j}^{U}{\mu }_{jkt}+{B}_{j}^{U}{\nu }_{jkt}+{W}_{t}-{A}_{j}^{U}+{k}_{2}^{U}{B}_{j}^{U}\\ +{R}_{t}-{O}_{t}-{A}_{k}^{D}+{k}_{2}^{D}{B}_{k}^{D}\end{array}\right]dt,\\&d{\lambda }_{jkt}^{D}=\left[-{\left({k}_{1}^{D}\right)}^{2}{B}_{k}^{D}{S}_{jkt}+\left(r+{k}_{1}^{D}{B}_{k}^{D}\right){\lambda }_{jkt}^{D}-{k}_{1}^{D}{A}_{k}^{D}+{k}_{1}^{D}{k}_{2}^{D}{B}_{k}^{D}-{\eta }_{1}\right]dt,\\&{S}_{000}={s}_{0}, \, \underset{t\to \infty }{lim}{\lambda }_{jkt}^{D}=0, \quad j,k=1,2,...,5\end{aligned}$$

(A45)

Imposing once again a solution $\left({S}_{jkt},{\lambda }_{jkt}^{D}\right), \, j,k=1,2,...,5,$ that satisfies the linear transformation:

$${\lambda }_{jkt}^{D}={\Pi }_{jkt}{S}_{jkt}+{\Sigma }_{jkt}, \, j,k=1,2,...,5$$

(A46)

To determine the stochastic processes ${\Pi }_{jkt}$ and ${\Sigma }_{jkt}$, we take differentials in Eq. (A46) we have that:

$$d{\lambda }_{jkt}^{D}={\Pi }_{jkt}d{S}_{jkt}+{S}_{jkt}d{\Pi }_{jkt}+d{\Sigma }_{jkt}={S}_{jkt}d{\Pi }_{jkt}+d{\Sigma }_{jkt}+\left\{\begin{array}{c}\left[{B}_{k}^{D}{\Pi }_{jkt}^{2}-{k}_{1}^{D}{B}_{k}^{D}{\Pi }_{jkt}\right]{S}_{jkt}+{B}_{k}^{D}{\Pi }_{jkt}{\Sigma }_{jkt}-{k}_{1}^{U}{B}_{j}^{U}{W}_{j}^{U}{\Pi }_{jkt}\\ +\left[{B}_{j}^{U}{\mu }_{jkt}+{B}_{j}^{U}{\nu }_{jkt}+{W}_{t}-{A}_{j}^{U}+{k}_{2}^{U}{B}_{j}^{U}+{R}_{t}-{O}_{t}-{A}_{k}^{D}+{k}_{2}^{D}{B}_{k}^{D}\right]{\Pi }_{jkt}\end{array}\right\}dt,$$

(A47)

while the backward Eq. (A45) may be written equivalently as:

$$d{\lambda }_{jkt}^{D}=\left\{\left[-{\left({k}_{1}^{D}\right)}^{2}{B}_{k}^{D}+\left(r+{k}_{1}^{D}{B}_{k}^{D}\right){\Pi }_{jkt}\right]{S}_{jkt}+\left(r+{k}_{1}^{D}{B}_{k}^{D}\right){\Sigma }_{jkt}-{k}_{1}^{D}{A}_{k}^{D}+{k}_{1}^{D}{k}_{2}^{D}{B}_{k}^{D}\right\}dt$$

(A48)

Sufficient conditions for the latter to be equivalent are provided by:

$$\begin{aligned}&d{\Pi }_{jkt}=\left[-{B}_{k}^{D}{\left({\Pi }_{jk}^{U}\right)}^{2}+\left(2{k}_{1}^{D}{B}_{k}^{D}+r\right){\Pi }_{jkt}^{U}-{\left({k}_{1}^{D}\right)}^{2}{B}_{k}^{D}\right]dt,\\&\quad \underset{t\to \infty }{lim}{\Pi }_{jkt}=0, \quad j,k=1,2,...,5\end{aligned}$$

(A49)

which is a BRE that can be solved numerically for ${\Pi }_{jkt}, j,k=1,2,...,5,$ and by:

$$d{\Sigma }_{jkt}=\left\{\begin{array}{c}\left[-{B}_{k}^{D}{\Pi }_{jkt}+\left({k}_{1}^{D}{B}_{k}^{D}+r\right)\right]{\Sigma }_{jkt}\\ -\left[-{k}_{1}^{U}{B}_{j}^{U}{W}_{j}^{U}+{B}_{j}^{U}{\mu }_{jkt}+{B}_{j}^{U}{\nu }_{jkt}+{W}_{t}-{A}_{j}^{U}+{k}_{2}^{U}{B}_{j}^{U}+{R}_{t}-{O}_{t}-{A}_{k}^{D}+{k}_{2}^{D}{B}_{k}^{D}\right]{\Pi }_{jkt}\\ -{k}_{1}^{D}{A}_{k}^{D}+{k}_{1}^{D}{k}_{2}^{D}{B}_{k}^{D}\end{array}\right\}dt,\quad \underset{t\to \infty }{lim}{\Sigma }_{jkt}=0, \, j,k=1,2,...,5$$

(A50)

which given the above solution is a backward linear first-order SDE that can be easily solved for ${\Sigma }_{jkt}, j,k=1,2,...,5.$

Substituting the linear transformation Eq. (A46) to the forward equation of the FBSDEs system Eq. (A45), we obtain:

$$\begin{aligned}&d{S}_{jkt}=\left\{\begin{array}{c}{B}_{k}^{D}\left[{\Pi }_{jkt}-{k}_{1}^{D}\right]{S}_{jkt}+{B}_{k}^{D}{\Sigma }_{jkt}-{k}_{1}^{U}{B}_{j}^{U}{W}_{jt}^{U}+{B}_{j}^{U}{\mu }_{jkt}+{B}_{j}^{U}{\nu }_{jkt}\\ +{W}_{t}-{A}_{j}^{U}+{k}_{2}^{U}{B}_{j}^{U}+{R}_{t}-{O}_{t}-{A}_{k}^{D}+{k}_{2}^{D}{B}_{k}^{D}\end{array}\right\}dt,\\&\quad S_{000} = s_{0} ,\quad j,k = 1,2,...,5 \end{aligned}$$

(A51)

which is a forward linear SDE that can be solved for $S_{jkt} {, }j,k = 1,2,...,5.$ Then the backward adjoint variable $\lambda_{jkt}^{D} {, }j,k = 1,2,...,5,$ follows immediately from the linear transformation of Eq. (A46). Clearly, the optimal water abstraction policies $w_{jkt}^{U} {, }w_{jkt}^{D} {, }j,k = 1,2,...,5,$ of U and D follow from Eqs. (A30) and (A17), respectively.

Appendix B

Econometric Modeling

5.1 Copula Approach

As mentioned, copulas will determine the joint distribution of the endogenous regressors and the composed errors that capture their dependencies (Nelsen, 2006). In this sub-section we scrutinise this concept, taking the function $\varphi ()$ as given, while in Sect. 6.2 we elaborate on the dynamic latent productivity.

To this end, let $F({x}_{1},\ldots ,{x}_{p},\varepsilon )$ be the joint distribution of $({x}_{1},\ldots ,{x}_{p})$ and ${\varepsilon }_{i}$. Since the information contained in the correlation between $({x}_{1},\ldots ,{x}_{p})$ and ${\varepsilon }_{i}$ is also contained in its joint distribution, and if this is known to belong to a class of parametric density, then consistent estimates of the model parameters can be obtained by simply maximizing the log-likelihood function derived from $F({x}_{1},\ldots ,{x}_{p},\varepsilon )$. Thus, there is no need for resorting to instruments nor to consistently estimate the parameters of the model. However, in practice $F({x}_{1},\ldots ,{x}_{p},\varepsilon )$ is typically unknown. Following Park and Gupta (2012) and suggesting a copula to determine this joint density, we can capture the dependence in the joint distribution of the endogenous regressors and the composed errors. More precisely, suppose the joint distribution of $({x}_{1},\ldots ,{x}_{p},\varepsilon )$ with joint density $f({x}_{1},\ldots ,{x}_{p},\varepsilon )$, and let ${f}_{j}({x}_{j})$, ${F}_{j}({x}_{j})$, for $j=1,\ldots ,p$, $g(\varepsilon )$ and $G(\varepsilon )$ denote the marginal density and Cumulative Distribution Function (CDF) of ${x}_{j}$ and $\varepsilon$, respectively. Also, $C$ denotes the “copula function” defined for $({\xi }_{1},\ldots ,{\xi }_{p+1})\in [\mathrm{0,1}{]}^{p+1}$ by:

$$C({\xi }_{1},\ldots ,{\xi }_{p+1})=P({F}_{1}({x}_{1})\le {\xi }_{1},\ldots ,{F}_{p}({x}_{p})\le {\xi }_{p},G(\varepsilon )\le {\xi }_{p+1})$$

(B1)

so that the copula function is itself a CDF.

Moreover, since ${F}_{j}({x}_{j})$ and $G(\cdot )$ are marginal distribution functions, each component ${U}_{j}={F}_{j}({x}_{j})$ and ${U}_{\varepsilon }=G(\varepsilon )$ has a uniform marginal distribution (Li and Racine 2007).¹⁰ Let $c({\xi }_{1},\ldots ,{\xi }_{p})$ denote the PDF associated with $C({\xi }_{1},\ldots ,{\xi }_{p})$, then by Sklar’s theorem (Sklar 1959), we have:

$$f({x}_{1},\ldots ,{x}_{p},\varepsilon )=c\left({F}_{1}({x}_{1}),\ldots ,{F}_{p}({x}_{p}),G(\varepsilon )\right)g(\varepsilon ){\prod }_{j=1}^{p}{f}_{j}({x}_{j})$$

(B2)

Thus, Eq. (B1) shows that the copula function completely characterizes the dependence structure of $({x}_{1},\ldots ,{x}_{p},\varepsilon )$, and $c({\xi }_{1},\ldots ,{\xi }_{p})=1$ if and only if $({x}_{1},\ldots ,{x}_{p},\varepsilon )$ are independent of each other. To obtain the joint density, we need to specify the copula function; here the Gaussian copula is used¹¹:

Let ${\Phi }_{\Sigma ,p+1}$ denote a $(p+1)$-dimensional CDF with zero mean and correlation matrix $\Sigma$. Then the $(p+1)$ -dimensional CDF with correlation matrix $\Sigma$ is given by:

$$C\left( {w;\Sigma } \right) = \Phi_{\Sigma ,p + 1} \left( {\Phi^{ - 1} \left( {U_{1} } \right), \ldots ,\Phi^{ - 1} \left( {U_{p} } \right),\Phi^{ - 1} \left( {U_{\varepsilon } } \right)} \right),$$

where

$$w = \left( {U_{1} , \ldots ,U_{p} ,U_{\varepsilon } } \right) = \left( {F_{1} \left( {x_{1} } \right), \ldots ,F_{p} \left( {x_{p} } \right),G\left( \varepsilon \right)} \right)$$

(B3)

The copula density is:

$$c(w;\Sigma )={\left(\mathit{det}(\Sigma )\right)}^{-1/2}\times \mathit{exp}\left\{-\frac{1}{2}{\left({\Phi }^{-1}({U}_{1}),\ldots ,{\Phi }^{-1}({U}_{p}),{\Phi }^{-1}({U}_{\varepsilon })\right)}^{^{\prime}}\left({\Sigma }^{-1}-{I}_{p+1}\right)\left({\Phi }^{-1}({U}_{1}),\ldots ,{\Phi }^{-1}({U}_{p}),{\Phi }^{-1}({U}_{\varepsilon })\right)\right\}$$

(B4)

And the log-likelihood function is:

$$\mathit{log}L(\theta ,\Sigma )={\sum }_{i=1}^{n}{\sum }_{t=1}^{T}\left\{\mathit{ln}c({F}_{1}({x}_{1,it}),\ldots ,{F}_{p}({x}_{p,it}),G({\varepsilon }_{it};\theta );\Sigma )+{\sum }_{j=1}^{p}\mathit{ln}{f}_{j}({x}_{j,it})+\mathit{ln}g({\varepsilon }_{it};\theta )\right\}$$

(B5)

where $\theta =({\beta }^{^{\prime}},\bar{\lambda },{\bar{\sigma }}^{2}{)}^{^{\prime}}$ and the form of $c(.)$ is given in Eq. (22). Notice that the first term in the summation of Eq. (B5) is derived from the copula density and reflects the dependence between endogenous variables and composed errors. In addition, since the marginal density ${f}_{j}({x}_{j})$ does not contain any parameters of interest, the second term in the summation of Eq. (B5) can be dropped from the log-likelihood function. Finally, it is clear that if there is no endogeneity problem, Eq. (B5) collapses to the log-likelihood function of the standard stochastic frontier models.

By maximizing the log-likelihood function, consistent estimates of $(\theta ,\Sigma )$ can be obtained, and this can be done as we described by the algorithm below:

5.2 Estimation of${F}_{j}\left({x}_{j}\right),j=1,\ldots ,p$; and $G(\varepsilon ;\theta )$

Since ${F}_{j}({x}_{ji})$ are unknown and we have an observed sample of ${x}_{ji},j=1,\ldots ,p;i=1,\ldots ,n$; in the first step, we can estimate ${F}_{j}({x}_{ji})$ by

$${\widetilde{F}}_{nj}=\frac{1}{nT+1}{\sum }_{i=1}^{n}1\left({x}_{j,it}\le {x}_{0j}\right), j=1,\ldots ,p$$

(B6)

where $1(.)$ is an indicator function. Note that we used the rescaling factor $1/(nT+1)$ rather than $1/nT$ to avoid difficulties arising from the potential unboundedness of the $\mathit{ln}c\left({F}_{1}({x}_{1,it}),\ldots ,{F}_{p}({x}_{p,it}),G({\varepsilon }_{it};\theta );\Sigma \right)$ as some of the ${F}_{j}({x}_{j})$ tend to one. To estimate$G({\varepsilon }_{it};\theta )$, note that its density $g({\varepsilon }_{it} ;\theta )$ is given in Eq. (20) and by definition,$G({\varepsilon }_{it};\theta )={\int }_{-\infty }^{{\varepsilon }_{it}}g(s;\theta )ds$, thus $G(\varepsilon ;\theta )$ can be estimated using numerical integration, and let denotes the estimator of$G(\varepsilon ;\theta )$.

5.2.1 Maximization of the Log-Likelihood Function

Maximization of the log-likelihood function of Eq. (B5) where ${F}_{j}({x}_{j})$ and $G({\varepsilon }_{it} ;\theta )$ are replaced by their estimates ${\widetilde{F}}_{j}({x}_{j})$ and${\widetilde{G}}({\varepsilon }_{j};\theta )$, respectively:

$$(\widehat{\theta },\widehat{\Sigma })=\underset{\theta \in \Theta ,\Sigma }{argmax}{\sum }_{i=1}^{n}\left\{\mathit{ln}c({\widetilde{F}}_{1}({x}_{1i}),\ldots ,{\widetilde{F}}_{p}({x}_{pi}),\widetilde{G}({\varepsilon }_{i};\theta );\Sigma )+\mathit{ln}g({\varepsilon }_{i};\theta )\right\}$$

(B7)

5.3 Estimating Technical Inefficiency

Once the parameters have been estimated, the ultimate goal is to predict the technical inefficiency values (term ${u}_{i}$). This can be calculated based on Jondrow et al. (1982):

$${\widehat{u}}_{it}=\widehat{E}\left({u}_{it}|{\varepsilon }_{it}\right)=\frac{\widehat{\sigma }\widehat{\lambda }}{1+{\widehat{\lambda }}^{2}}\left[\frac{\varphi \left(\frac{\widehat{\lambda }{\widehat{\varepsilon }}_{it}}{\widehat{\sigma }}\right)}{1-\Phi \left(\frac{\widehat{\lambda }{\widehat{\varepsilon }}_{it}}{\widehat{\sigma }}\right)}-\frac{\widehat{\lambda }{\widehat{\varepsilon }}_{it}}{\widehat{\sigma }}\right]$$

(B8)

where ${\widehat{\varepsilon }}_{it}={y}_{it}-\varphi ({x}_{it},{z}_{it};\widehat{\beta })$ and $\widehat{\beta },\widehat{\lambda }$ and ${\widehat{\sigma }}^{2}$ are the parameter estimates obtained from the approach discussed above.

5.4 Local Likelihood Estimation

The functional form $\varphi ({x}_{it},{z}_{it};\beta )$ was left unspecified so far. By all means, any parametric form can be used, but here we focus on non-parametric estimation by the local likelihood method. We use the simpler notation $\varphi ({x}_{it};\beta )$ as the extension to the case of exogenous covariates is straightforward. Since we have a multivariate covariate, we use the method of local linear estimation. This means that all parameters of the model become functions of $x$, and they are denoted by $\theta (x)$. We denote the conditional density of $y$ given $x$ by $p(y|x)=g(y;\theta (x)),$ where $\theta \left(x\right)\in {\mathbb{R}}^{k}$ is unknown and we define $q(y;\theta (x))=\mathit{log}g(y;\theta (x))$. For example, a standard frontier would take the form:

$${y}_{it}=m\left({x}_{it}\right)+{v}_{it}-{u}_{it},$$

where

$$v_{it} \left| {x_{it} {\sim}iN\left( {0,\sigma_{v}^{2} \left( {x_{it} } \right)} \right), u_{it} } \right|x_{it} {\sim}iN\left( {0,\sigma_{u}^{2} \left( {x_{it} } \right)} \right).$$

(B9)

Then:

$$\uptheta (\mathrm{x})={\left[\mathrm{m}(\mathrm{x}),{\upsigma }_{\mathrm{v}}^{2}(\mathrm{x}),{\upsigma }_{\mathrm{u}}^{2}(\mathrm{x})\right]}^{\mathrm{^{\prime}}}$$

(B10)

Our fundamental departure from the standard model is the introduction of productive performance or technical efficiency:

$${y}_{it}=m({x}_{it},{z}_{it})+{v}_{it}+{\omega }_{it}-{u}_{it}$$

(B11)

where the productivity process is:

$${\omega }_{it}|{x}_{it},{\omega }_{i,t-1}{\sim}i N\left(r\left({\omega }_{i,t-1},{x}_{it},{z}_{it}\right),{\sigma }_{\omega }^{2}\left({\omega }_{i,t-1},{x}_{it},{z}_{it}\right)\right)$$

(B12)

In this specification, $r({\omega }_{i,t-1},{x}_{it},{z}_{it})$ is a non-parametric productivity mean process, and ${\sigma }_{\omega }^{2}({\omega }_{i,t-1},{x}_{it},{z}_{it})$ is the variance. For ease in notation, we omit explicit dependence on z and we continue to denote $\theta \left(x\right)\in {\mathbb{R}}^{k}$ with

$$\theta (x)={\left[m(x),r({\omega }_{-1},x),{\sigma }_{v}^{2}(x),{\sigma }_{u}^{2}(x),{\sigma }_{\omega }^{2}({\omega }_{-1},x)\right]}^{^{\prime}}$$

(B13)

where ${\omega }_{-1}$ denotes the lagged value of productivity. As productivity is latent special problems are introduced into the analysis.

There is a multivariate kernel which satisfies:

$$\int K\left(u\right)du=1, \int u{u}^{^{\prime}}K\left(u\right)du={\mu }_{2}{\rm I}_{d}$$

(B14)

To fix notation, we start with the analysis of the simpler model in Eq. (B11). The conditional local linear log-likelihood is given by¹²:

$$\mathit{log}L\left({\theta }_{o},{\Theta }_{1}\right)={\sum }_{i=1}^{n}{\sum }_{t=1}^{T}q({y}_{it},{\theta }_{o}+{\Theta }_{1}({x}_{it}-x)){K}_{H}({x}_{it}-x)$$

(B15)

where ${\theta }_{o},{\Theta }_{1}$ is a vector ($k\times 1$) and matrix ($k\times d$) respectively, $H$ is a bandwidth matrix which is symmetric, positive definite and ${K}_{H}\left(u\right)={\left|H\right|}^{-1}K\left({H}^{-1}u\right)$. We choose a multivariate product kernel so that $K(u)={\prod }_{j=1}^{d}{K}_{j}({u}_{j})$ in which case $\int u{u}^{^{\prime}}K(u)du=\left(\int {u}_{1}^{2}{K}_{1}({u}_{1})d{u}_{1}\right){I}_{d}.$

The local linear estimator is $\widehat{\theta }(x)={\widehat{\theta }}_{o}(x)$ where ${\widehat{\theta }}_{o}(x)$ and ${\widehat{\Theta }}_{1}\left(x\right)$ maximize the log-likelihood $L({\theta }_{o},{\Theta }_{1})$ with respect to ${\theta }_{o},{\Theta }_{1}$.

For the model with latent productivity ${\omega }_{it}$ as in Eq. (B12) the likelihood function is

$$\mathrm{L}({\uptheta }_{\mathrm{o}},{\Theta }_{1})={\int }_{{\mathbb{R}}^{\mathrm{nT}}}\left\{{\prod }_{\mathrm{i}=1}^{\mathrm{n}}{\prod }_{\mathrm{t}=1}^{\mathrm{T}}\mathrm{g}({\mathrm{y}}_{\mathrm{it}},{\upomega }_{\mathrm{it}},{\uptheta }_{\mathrm{o}}+{\Theta }_{1}\left({\Lambda }_{\mathrm{it}}-\Lambda \right))\cdot {\mathrm{K}}_{\mathrm{H}}\left({\Lambda }_{\mathrm{it}}-\Lambda \right)\right\}\mathrm{d\omega }$$

(B16)

where ${\Lambda }_{it}={\left[{x}_{it}^{^{\prime}},{\omega }_{i,t-1}\right]}^{^{\prime}}$,$\Lambda ={\left[{x}^{^{\prime}},{\omega }_{-1}\right]}^{^{\prime}}$, and

$$\mathrm{g}\left(\mathrm{y},\upomega ;\uptheta (\Lambda )\right)=\frac{2}{\upsigma (\mathrm{x})}\mathrm{\varphi }\left(\frac{{\mathrm{y}}_{\mathrm{it}}-\mathrm{\varphi }({\mathrm{x}}_{\mathrm{it}};\upbeta (\mathrm{x}))-{\upomega }_{\mathrm{it}}}{\upsigma (\mathrm{x})}\right)\Phi \left(-\frac{\uplambda (\mathrm{x})}{{\upsigma }_{\mathrm{v}}(\mathrm{x})}(\mathrm{y}-\mathrm{\varphi }({\mathrm{x}}_{\mathrm{it}};\upbeta (\mathrm{x})))-{\upomega }_{\mathrm{it}}\right)\cdot \frac{1}{{\upsigma }_{\upomega }(\mathrm{x},{\upomega }_{-1})}\mathrm{\varphi }\left(\frac{{\upomega }_{\mathrm{it}}-\mathrm{r}({\mathrm{x}}_{\mathrm{it}},{\upomega }_{\mathrm{i},\mathrm{t}-1};\upgamma (\mathrm{x},{\upomega }_{-1}))}{{\upsigma }_{\upomega }(\mathrm{x},{\upomega }_{-1})}\right)$$

(B17)

Moreover, $\gamma \left(x,{\omega }_{-1}\right)$ denotes the localized parameters in the r() function of Eq. (37). For ease in notation, we define $\theta \left(x,{\omega }_{-1}\right)={\left[\beta {\left(x\right)}^{^{\prime}},\gamma {\left(x,{\omega }_{-1}\right)}^{^{\prime}}\right]}^{^{\prime}}\in {\mathbb{R}}^{k}$. In Eq. (B16) there is an $nT$-dimensional integral which cannot be evaluated analytically, which is obvious from the definition of Eq. (42). The computation relies in two steps:

Step 1: Integrate out $\left\{{\omega }_{it}\right\}$ from Eq. (B16) using a Sequential Monte Carlo (SMC) algorithm (Pitt and Shephard 1999).

Step 2: Maximize the resulting expression using numerical optimization techniques.

For reasons of computational convenience and without sacrificing generality we assume:

$$\omega_{it} = \rho \omega_{i,t - 1} + \xi_{it} , \left\{ {\xi_{it} } \right\}{\sim}ii.i.d. N\left( {0,\sigma_{\xi }^{2} } \right)$$

(B18)

We will still need the SMC algorithm in step 1 (Appendix B), for which we used 10⁶ particles per likelihood evaluation, and a standard conjugate gradients algorithm for maximization. Our results were insensitive to using ${10}^{5}$ or ${10}^{7}$ particles per likelihood evaluation.

Appendix C

Sequential Monte Carlo

The particle filter methodology can be applied to state space models of the general form:

$${y}_{T}{\sim}i p({y}_{t}|{x}_{t}),\hspace{0.33em}{s}_{t}{\sim}i p({s}_{t}|{s}_{t-1})$$

(C1)

where ${s}_{t}$ is a state variable. For general introductions see Gordon (1997), Gordon et al. (1993), Doucet et al. (2001) and Ristic et al. (2004). Given the data ${Y}_{t}$ the posterior distribution $p({s}_{t}|{Y}_{t})$ can be approximated by a set of (auxiliary) particles $\left\{{s}_{t}^{(i)},i=1,...,.N\right\}$ with probability weights $\left\{{w}_{t}^{(i)},i=1,...,N\right\}$ where ${\sum }_{i=1}^{N} {w}_{t}^{(i)}=1$. The predictive density can be approximated by:

$$p({s}_{t+1}|{Y}_{t})=\int p({s}_{t+1}|{s}_{t})p({s}_{t}|{Y}_{t})d{s}_{t}{\sim}ieq {\sum }_{i=1}^{N} p({s}_{t+1}|{s}_{t}^{(i)}){w}_{t}^{(i)}$$

(C2)

and the final approximation for the filtering density is:

$$p\left({s}_{t+1}|{Y}_{t}\right)\propto p({y}_{t+1}|{s}_{t+1})p({s}_{t+1}|{Y}_{t}){\sim}ieq p({y}_{t+1}|{s}_{t+1}){\sum }_{i=1}^{N} p({s}_{t+1}|{s}_{t}^{(i)}){w}_{t}^{(i)}$$

(C3)

The basic mechanism of particle filtering rests on propagating $\left\{{s}_{t}^{(i)},{w}_{t}^{(i)},i=1,\ldots ,N\right\}$ to the next step, viz. $\left\{{s}_{t+1}^{(i)},{w}_{t+1}^{(i)},i=1,\ldots ,N\right\}$ but this often suffers from the weight degeneracy problem. If parameters $\theta \in \Theta \in {\mathfrak{R}}^{k}$ are available, as is often the case, we follow Liu and West (2001) parameter learning takes place via a mixture of multivariate normals:

$$p\left(\theta |{Y}_{t}\right)={\sum }_{i=1}^{N}{w}_{t}^{\left(i\right)} {\rm N}(\theta |\alpha {\theta }_{t}^{\left(i\right)}+\left(1-a\right)\overline{{\theta }_{t}},{b}^{2}{V}_{t})$$

(C4)

where $\mathop {\overline{\theta }}\nolimits_{t} = \sum\nolimits_{i = 1}^{N} \,w_{t}^{(i)} \theta_{t}^{(i)}$, and $V_{t} = \sum\nolimits_{i = 1}^{N} \,w_{t}^{(i)} (\theta_{t}^{(i)} - \mathop {\overline{\theta }}\nolimits_{t} )(\theta_{t}^{(i)} - \mathop {\overline{\theta }}\nolimits_{t} )^{\prime}$. The constants $a$ and $b$ are related to shrinkage and are determined via a discount factor $\delta \in (\mathrm{0,1})$ as $a=(1-{b}^{2}{)}^{1/2}$ and ${b}^{2}=1-[(3\delta -1)/2\delta {]}^{2}$(see also Casarin and Marin 2007). Andrieu and Roberts (2009), Flury and Shephard (2011) and Pitt et al. (2012) provide the Particle Metropolis-Hastimgs (PMCMC) technique which uses an unbiased estimator of the likelihood function $\mathop {\hat{p}}\nolimits_{N} (Y|\theta )$ as $p(Y|\theta )$ is often not available in closed form.

Given the current state of the parameter ${\theta }^{(j)}$ and the current estimate of the likelihood, say $L^{j} = \mathop {\hat{p}}\nolimits_{N} (Y|\theta^{(j)} )$, a candidate ${\theta }^{c}$ is drawn from $q({\theta }^{c}|{\theta }^{(j)})$ yielding $L^{c} = \mathop {\hat{p}}\nolimits_{N} (Y|\theta^{c} )$. Then, we set ${\theta }^{(j+1)}={\theta }^{c}$ with the Metropolis—Hastings probability:

$$A={\text{min}}\left\{1,\hspace{0.33em}\frac{p({\theta }^{c}){L}^{c}}{p({\theta }^{(j)}{L}^{j}}\frac{q({\theta }^{(j)}|{\theta }^{c}}{q({\theta }^{c}|{\theta }^{(j)})}\right\}$$

(C5)

otherwise we repeat the current draws: $\left\{{\theta }^{(j+1)},{L}^{j+1}\right\}=\left\{{\theta }^{(j)},{L}^{j}\right\}$.

Hall et al. (2014) propose an auxiliary particle filter which rests upon the idea that adaptive particle filtering (Pitt et al. 2012) used within PMCMC requires far fewer particles that the standard particle filtering algorithm to approximate $p(Y|\theta )$. From Pitt and Shephard (1999) we know that auxiliary particle filtering can be implemented easily once we can evaluate the state transition density $p({s}_{t}|{s}_{t-1})$. When this is not possible, Hall et al. (2014) present a new approach when, for instance, ${s}_{t}=g({s}_{t-1},{u}_{t})$ for a certain disturbance. In this case we have:

$$p({y}_{t}|{s}_{t-1})=\int p({y}_{t}|{s}_{t})p({s}_{t}|{s}_{t-1})d{s}_{t}$$

(C6)

$$p({u}_{t}|{s}_{t-1};{y}_{t})=p({y}_{t}|{s}_{t-1},{u}_{t})p({u}_{t}|{s}_{t-1})/p\left({y}_{t}|{s}_{t-1}\right)$$

(C7)

If one can evaluate $p({y}_{t}|{s}_{t-1})$ and simulate from $p({u}_{t}|{s}_{t-1};{y}_{t})$ the filter would be fully adaptable (Pitt and Shephard 1999). One can use a Gaussian approximation for the first-stage proposal $g({y}_{t}|{s}_{t-1})$ by matching the first two moments of$p({y}_{t}|{s}_{t-1})$. So in some way we find that the approximating density$p({y}_{t}|{s}_{t-1})=N\left(E({y}_{t}|{s}_{t-1}),V({y}_{t}|{s}_{t-1})\right)$. In the second stage, we know that $p({u}_{t}|{y}_{t},{s}_{t-1})\propto p({y}_{t}|{s}_{t-1},{u}_{t})p({u}_{t})$. For $p({u}_{t}|{y}_{t},{s}_{t-1})$ we know it is multimodal so suppose it has $M$ modes are $\mathop {\hat{u}}\nolimits_{t}^{m}$, for$m=1,\ldots ,M$. For each mode we can use a Laplace approximation.

Let $l({u}_{t})=log\left[p({y}_{t}|{s}_{t-1},{u}_{t})p({u}_{t})\right]$. From the Laplace approximation we obtain:

$$l\left({u}_{t}\right)=l\left(\widehat{{u}_{t}^{m}}\right)+\frac{1}{2}{\left({u}_{t}-\widehat{{u}_{t}^{m}}\right)}^{^{\prime}}\nabla \, ^{2}l\left(\widehat{{u}_{t}^{m}}\right)\left({u}_{t}-\widehat{{u}_{t}^{m}}\right)$$

(C8)

Then we can construct a mixture approximation:

$$g(u_{t} |x_{t} ,s_{t - 1} ) = \sum\limits_{m = 1}^{M} \,\lambda_{m} (2\pi )^{ - d/2} |\Sigma_{m} |^{ - 1/2} exp\left\{ {\tfrac{1}{2}(u_{t} - \mathop {\hat{u}}\nolimits_{t}^{m} )^{\prime}\Sigma_{m}^{ - 1} (u_{t} - \mathop {\hat{u}}\nolimits_{t}^{m} } \right\},$$

(C9)

where ${\Sigma }_{m}=-$$\mathop {\left[ {\nabla^{2} l(\mathop {\hat{u}}\nolimits_{t}^{m} )} \right]}\nolimits^{ - 1}$ and ${\lambda }_{m}\propto \mathit{exp}\left\{l({u}_{t}^{m})\right\}$ with${\sum }_{m=1}^{M} =1$. This is done for each particle ${s}_{t}^{i}.$ This is known as the Auxiliary Disturbance Particle Filter (ADPF). An alternative is the independent particle filter (IPF) of Lin et al. (2010). The IPF forms a proposal for ${s}_{t}$ directly from the measurement density $p({y}_{t}|{s}_{t})$ although Hall et al. (2014) are quite right in pointing out that the state equation can be very informative. In the standard particle filter of Gordon et al. (1993) particles are simulated through the state density $p({s}_{t}^{i}|{s}_{t-1}^{i})$ and they are re-sampled with weights determined by the measurement density evaluated at the resulting particle, viz.$p({y}_{t}|{s}_{t}^{i})$. The ADPF is simple to construct and rests upon the following steps, for $t=0,\ldots ,T-1$ given samples ${s}_{t}^{k}{\sim}i p({s}_{t}|{Y}_{1:t})$ with mass ${\pi }_{t}^{k}$ for$k=1,\ldots ,N$:

• 1. For $k=1,\ldots ,N$ compute ${\omega }_{t|t+1}^{k}=g({y}_{t+1}|{s}_{t}^{k}){\pi }_{t}^{k},$ ${\pi }_{t|t+1}^{k}={\omega }_{t|t+1}^{k}/{\sum }_{i=1}^{N} {\omega }_{t|t+1}^{i}$ .

• 2. For $k=1,\ldots ,N$ draw $\widetilde{{s}_{t}^{k}}={\sum }_{i=1}^{N} {\pi }_{t|t+1}^{k}{\delta }_{St}^{i}(d{s}_{t})$

• 3. For $k=1,\ldots ,N$ draw ${\delta }_{St}^{i}$= g(${u}_{t+1}|\widetilde{{ s}_{t}^{k}}, {y}_{t+1}$ and set ${s}_{t+1}^{k}=h({s}_{t}^{k};{u}_{t+1}^{k})$

• 4. For $k=1,\ldots ,N$ compute

  $$\upomega _{t + 1}^{k} = \frac{{p(y_{t + 1} |s_{t + 1}^{k} )p(u_{t + 1}^{k} )}}{{g(y_{t + 1} |s_{t}^{k} )g(u_{t + 1}^{k} |\mathop {\tilde{s}}\nolimits_{t}^{k} ,y_{t + 1} )}}, \,\uppi _{t + 1}^{k} = \frac{{\upomega _{t + 1}^{k} }}{{\sum\nolimits_{i = 1}^{N} \,\upomega _{t + 1}^{i} }}.$$

  (C10)

It should be mentioned that the estimate of likelihood from ADPF is:

$$p({Y}_{1:T})={\prod }_{t=1}^{T} \left({\sum }_{i=1}^{N} {\omega }_{t-1|t}^{i}\right)\left({N}^{-1}{\sum }_{i=1}^{N} {\omega }_{t}^{i}\right)$$

(C11)

Particle Metropolis Adjusted Langevin Filters

Nemeth et al. (2014) provide a particle version of a Metropolis Adjusted Langevin algorithm (MALA). In Sequential Monte Carlo we are interested in approximating $p\left({s}_{t}|{Y}_{1:t},\theta \right)$. Given that:

$$p({s}_{t}|{Y}_{1:t},\theta )\propto g({y}_{t}|{x}_{t},\theta )\int f({s}_{t}|{s}_{t-1},\theta )p({s}_{t-1}|{y}_{1:t-1},\theta )d{s}_{t-1}$$

(C12)

where $p({s}_{t-1}|{y}_{1:t-1},\theta )$ is the posterior as of time $t-1$. If at time $t-1$ we have a set of particles $\left\{{s}_{t-1}^{i},i=1,\ldots ,N\right\}$ and weights $\left\{{w}_{t-1}^{i},i=1,\ldots .N\right\}$ which form a discrete approximation for $p({s}_{t-1}|{y}_{1:t-1},\theta )$ then we have the approximation:

$$\widehat{p}({s}_{t-1}|{y}_{1:t-1},\theta )\propto {\sum }_{i=1}^{N} {w}_{t-1}^{i}f({s}_{t}|{s}_{t-1}^{i},\theta )$$

(C13)

See Cappé et al. (2005) and Andrieu et al. (2010) for reviews. From (B13) Fearnhead (2007) makes the important observation that the joint probability of sampling particle ${s}_{t-1}^{i}$ and state ${s}_{t}$ is:

$${\omega }_{t}=\frac{{w}_{t-1}^{i}g({y}_{t}|{s}_{t},\theta )f(s|{s}_{t-1}^{i},\theta )}{{\xi }_{t}^{i}q({s}_{t}|{s}_{t-1}^{i},{y}_{t},\theta )}$$

(C14)

where $q({s}_{t}|{s}_{t-1}^{i},{y}_{t},\theta )$ is a density function amenable to simulation and:

$${\xi }_{t}^{i}q({s}_{t}|{s}_{t-1}^{i},{y}_{t},\theta ){\sim}ieq cg\left({y}_{t}|{s}_{t},\theta \right)f\left({s}_{t}|{s}_{t-1}^{i},\theta \right)$$

(C15)

and $c$ is the normalizing constant in (B12).

In the MALA algorithm of Roberts and Rosenthal (1998)¹³ we form a proposal:

$${\theta }^{c}={\theta }^{(s)}+\lambda z+\frac{{\lambda }^{2}}{2}\nabla {\text{log}}p({\theta }^{(s)}|{Y}_{1:T})$$

(C16)

where $z{\sim}i N(0,I)$ which should result in larger jumps and better mixing properties, plus lower autocorrelations for a certain scale parameter $\lambda$. Acceptance probabilities are:$a({\theta }^{c}|{\theta }^{(s)})=\mathit{min}\left\{1,\frac{p({Y}_{1:T}|{\theta }^{c})q({\theta }^{(s)}|{\theta }^{c})}{p({Y}_{1:T}|{\theta }^{(s)})q({\theta }^{c}|{\theta }^{(s)})}\right\}$

Using particle filtering it is possible to create an approximation of the score vector using Fisher’s identity:

$$\nabla \mathit{log}p({Y}_{1:T}|\theta )=E\left[\nabla \mathit{log}p({s}_{1:T},{Y}_{1:T}|\theta )|{Y}_{1:T},\theta \right]$$

(C17)

which corresponds to the expectation of:

$$\nabla \mathit{log}p({s}_{1:T},{Y}_{1:T}|\theta )=\nabla \mathit{log}p(|{s}_{1:T-1},{Y}_{1:T-1}|\theta )+\nabla \mathit{log}g({y}_{T}|{s}_{T},\theta )+\nabla \mathit{log}f({s}_{T}|s{|}_{T-1},\theta )$$

over the path ${s}_{1:T}$. The particle approximation to the score vector results from replacing $p({s}_{1:T}|{Y}_{1:T},\theta )$ with a particle approximation $\widehat{p}({s}_{1:T}|{Y}_{1:T},\theta )$.

With particle i-th at time t-1, we can associate a value ${\alpha }_{t-1}^{i}=\nabla \mathit{log}p({s}_{1:t-1}^{i},{Y}_{1:t-1}|\theta )$ which can be updated recursively. As we sample ${\kappa }_{i}$ in the APF (the index of particle at time $t-1$ that is propagated to produce the $i$ th particle at time t) we have the update:

$${\alpha }_{t}^{i}={a}_{t-1}^{{\kappa }_{i}}+\nabla \mathit{log}g({y}_{t}|{s}_{t}^{i},\theta )+\nabla \mathit{log}f({s}_{t}^{i}|{s}_{t-1}^{i},\theta )$$

(C18)

To avoid problems with increasing variance of the score estimate $\nabla \mathit{log}p({Y}_{1:t}|\theta )$ we can use the approximation:

$${\alpha }_{t-1}^{i}{\sim}i N({m}_{t-1}^{i},{V}_{t-1})$$

(C19)

The mean is obtained by shrinking ${\alpha }_{t-1}^{i}$ towards the mean of ${\alpha }_{t-1}$ as follows:

$${m}_{t-1}^{i}=\delta {\alpha }_{t-1}^{i}+(1-\delta ){\sum }_{i=1}^{N} {w}_{t-1}^{i}{\alpha }_{t-1}^{i}$$

(C20)

where $\delta \in (\mathrm{0,1})$ is a shrinkage parameter. Using Rao-Blackwellization one can avoid sampling ${\alpha }_{t}^{i}$ and instead use the following recursion for the means:

$${m}_{t}^{i}=\delta {m}_{t-1}^{{\kappa }_{i}}+(1-\delta ){\sum }_{i=1}^{N} {w}_{t-1}^{i}{m}_{t-1}^{i}+\nabla \mathit{log}g({y}_{t}|{s}_{t}^{i},\theta )+\nabla \mathit{log}f\left({s}_{t}^{i}|{s}_{t-1}^{{\kappa }_{i}},\theta \right)$$

(C21)

which yields the final score estimate:

$$\nabla \widehat{\mathit{log}p}({Y}_{1:t}|\theta )={\sum }_{i=1}^{N} {w}_{t}^{i}{m}_{t}^{i}$$

(C22)

As a rule of thumb Nemeth et al. (2014) suggest taking $\delta =0.95$. Furthermore, they show the important result that the algorithm should be tuned to the asymptotically optimal acceptance rate of 15.47% and the number of particles must be selected so that the variance of the estimated log-posterior is about 3. Additionally, if measures are not taken to control the error in the variance of the score vector, there is no gain over a simple random walk proposal.

Of course, the marginal likelihood is:

$$p({Y}_{1:T}|\theta )=p({y}_{1}|\theta ){\prod }_{t=2}^{T} p({y}_{t}|{Y}_{1:t-1},\theta )$$

(C23)

where

$$p({y}_{t}|{Y}_{1:t-1},\theta )=\int g({y}_{t}|{s}_{t})\int f({s}_{t}|{s}_{t-1},\theta )p({s}_{t-1}|{Y}_{1:T-1},\theta )d{s}_{t-1}d{s}_{t}$$

(C24)

provides, in explicit form, the predictive likelihood.

Appendix D

Data Mentioned in Results Section

The Environmental Indices derived from the factors presented in Sect. 7, as well as the parameters of the hydro-economic model (same section) were obtained from official databases.

The Eora global supply chain database consists of a Multi-Region Input–Output table (MRIO) model that provides a time series of high-resolution Input–Output (IO) tables with matching environmental and social satellite accounts for 190 countries (35 types of EI air pollution, energy use, greenhouse gas emissions, water use, land occupation, N and P emissions, etc.). 16 IO tables, each for the period 2000–2017 for Ethiopia and Kenya were used. Additional data, as well as pumping costs and hydrological timeseries were collected from scientific journals, official reports, governmental websites, and other forms of grey literature databases, including: African development bank, including African development bank, ILO (International Labor Organization) and the World Bank Group: Climate Change Knowledge Portal For Development Practitioners and Policy Makers, the United Nations Statistics Division, Food and Agriculture Organization of United Nations (FAOSTAT, AQUASTAT), Unesco World Heritage list, OpenDataSoft, Environment and Climate Change Data Portal, and offices of national statistics.

See Tables 6 and 7.

Table 6 Description of Indices of Ecosystem Services

Table 7 Parameters of the hydro-economic model