On the Interpretation and Measurement of Technology-Adjusted Emissions Embodied in Trade

Abstract

We propose a new method for standardizing the production technology at the world average level and derive interpretations for the resulting carbon emission concepts. The technology-adjusted emission balance measures net weak carbon leakage defined as the difference between the foreign emissions avoided by exports and the foreign emissions generated by imports. We use global multi-regional input–output tables to document the variable’s spatio-temporal variation for 49 economies between 1995 and 2015. There is a positive cross-country correlation between net leakage and per-capita income. Changes in net leakage are generally small and do not account for country-specific emission trends, that is, domestic emission decreases were not offset by foreign emission increases.

1 Introduction

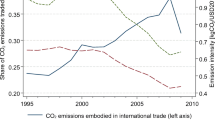
International emission transfers are measured by the balance of emissions embodied in trade (BEET), meaning the difference between the emissions embodied in exports (EEX) and the emissions embodied in imports (EEM), which equals the difference between production-based emissions (PBE) and consumption-based emissions (CBE). The analysis of global multi-regional input–output tables has revealed how international emission transfers vary over time, across countries, and by income level (e.g. Peters and Hertwich 2008; Hertwich and Peters 2009; Davis and Caldeira 2010). Between 1990 and 2011, the Kyoto-relevant territorial emissions decreased in the developed (Annex-B) countries while the CBE increased (Kanemoto et al. 2014). In 2008, the Annex-B countries transferred 1.6 GtCO2 to non-Annex-B countries; this amount exceeds the reductions achieved in the Kyoto protocol period until then (Peters et al. 2011). In general, the developed countries are “net importing” emissions (PBE < CBE) while the developing countries are “net exporting” emissions (PBE > CBE).

How to interpret these facts? Economic activity and the associated emissions may simply have migrated from the developed to the developing world. Trade liberalization might have encouraged the developing countries to specialize in the production and export of emission-intensive products. “Emission outsourcing” might explain the advanced-economy decoupling success. National emission decreases apparently did not translate into corresponding global emission decreases. Jakob and Marschinski (2013) caution against premature conclusions and emphasize that the interpretation of international emission transfer patterns, and the derivation of climate policy implications, requires better understanding of the underlying driving forces. The size and direction of international emission transfers are determined to a large extent by international technology differences, that is, cross-country differences in the carbon intensity of energy and the energy intensity of production. In the presence of technology differences, exchanging identical products at equal prices would imply emission transfers (Jakob and Marschinski 2013; Jakob et al. 2014). Kander et al. (2015) propose a new scheme to account for the emissions embodied in trade – technology-adjusted accounting – which standardizes the emission intensity at the world average level. Jiborn et al. (2018), Baumert et al. (2019), and Jiborn et al. (2020) implement the technology adjustment in order to appraise competing narratives about the advanced-economy decoupling. These studies seek to evaluate the claim that the developed countries are “systematically outsourcing emissions” to the developing countries, and to assess the extent to which developed-country PBE trends are driven by international trade. The scale of emission outsourcing, it turns out, is much smaller than previously suggested, and the clear divide between the developed world and the developing world disappears. Many developed countries, especially in Europe, are “insourcing” emissions and not “outsourcing” them (Baumert et al. 2019).

How to interpret the new facts revealed by technology-adjusted accounting? We propose a new method for technology-adjusted accounting and develop interpretations for the resulting emission concepts. We interpret the technology-adjusted emission balance as a measure of net weak carbon leakage, document how the variable varies across space and over time, analyze its cross-country relationship with per-capita income, and discuss what technology-adjusted accounting implies with respect to the decoupling of emissions and economic growth.

The “technology adjustment” implemented thus far really is an emission intensity adjustment: the direct emission intensities (the ratios of emissions to gross outputs) are standardized but not the input intensities (the ratios of intermediate inputs to gross outputs). In input–output analysis (Leontief 1986), the ratios of inputs to outputs are said to represent the production technology (the “production recipes”). This point is not merely a semantic quibble but matters in practice. The observed cross-country differences in the input intensity are non-negligible, e.g. China’s cement, lime, and plaster production requires 0.82 euros worth of inputs per unit worth of output while the same sector in Germany requires just 0.64 euros. On average, Chinese producers require 0.61 euros worth of inputs per euro worth of gross output while German producers require only 0.48 euros.¹ The same demand will generate greater environmental impacts, ceteris paribus, if more inputs are required per unit of output. A comparative standard intended to represent the world average production technology should also eliminate international differences in the input intensity. In this article we build on the decomposition proposed by Xu and Dietzenbacher (2014) in order to standardize the input intensities across countries. We implement the technology adjustment using EXIOBASE3 (Stadler et al. 2018), which offers finer sector detail than the MRIO tables used by our antecedents.

The emission intensity adjustment has a curious feature: it tends to be inconsequential when the analysis draws on highly dis-aggregated data, i.e. input–output tables with fine sector detail. The intensity adjustment is inconsequential, in particular, when the electricity sector is broken down by green and brown energy sources. The energy mix of the domestic electricity sector is a key driver of embodied emissions. As a rough approximation, the emission intensity of Sweden’s aggregate electricity sector is low because Sweden uses hydro power rather than coal, and not because Sweden’s hydro electricity production is exceptionally clean. In general, the emission intensity of the aggregate electricity sector varies a lot more across countries than the emission intensities of electricity sub-sectors vary across countries. Therefore, with fine sector detail, standardizing only the emission intensity – substituting a sector’s world average value for the sector’s country-specific emission intensity – will be relatively inconsequential. Our proposed technology adjustment behaves differently, because the technology adjustment standardizes the direct emission intensities and the intermediate input requirements. Standardizing the input requirements implies, for example, that the aluminum sectors of Sweden and China require the same amount of hydro electricity input per unit of output. As a result, the technology adjustment is consequential even when based on highly dis-aggregated data (EXIOBASE3 provides global MRIO tables with 163 sectors per country).

Section 2 discusses related literature and introduces the key concepts used in this study. We explain why we apply the technology-adjustment only to the export side, and why interpret the technology-adjusted emission balance as a measure of net weak carbon leakage. Section 3 introduces the notation for the environmentally-extended MRIO model, describes how the model is used to calculate emissions embodied in trade, and explains the modifications needed for standardizing the production technology. Section 5 discusses the results. The patterns of net weak carbon leakage are quantitatively and qualitatively different from international emission transfers. Emissions in most countries follow country-specific trends, regardless of the emission concept. Weak carbon leakage cannot be considered an important driver of national emission trends.

2 Related Literature and Key Concepts

Kander et al. (2015) first proposed the emission intensity adjustment to address concerns over the incentives implicit in PB and CB accounting. PB accounting does not hold countries responsible for the emissions associated with the production of imported products, while CB accounting does not hold countries responsible for the emissions associated with the production of exported products. In either case, there are no incentives for taking mitigation action with respect to certain emissions attributed to trading partners. The emission-intensity adjustment was designed to serve the principle that national “actions that contribute to reduced global emissions should be credited, and actions that increase them should be penalized” (Kander et al. 2015, p. 431). Kander et al. (2015) propose to hold countries responsible for the emission intensity-adjusted consumption-based emissions (EICBE), calculated as EICBE $=$ PBE − EIEEX $+$ EEM, where EIEEX are the emission intensity-adjusted emissions embodied in exports. Compared to regular CB accounting, this scheme introduces a new mitigation incentive by rewarding countries for cleaning up their export production. As such it contributes to the normative debate about the merit of alternative carbon accounting schemes, which discusses how emission responsibility should be attributed in order to support mitigation incentives, equity and fairness, and other principles (Rodrigues et al. 2010; Afionis et al. 2017; Zhang 2018; Dietzenbacher et al. 2020; Jakob et al. 2021).

The existing empirical implementations of the emission intensity adjustment do not discuss implicit incentive structures and normative principles, but interpret the results of positive ex-post empirical analyses of trade and emission flows. Jiborn et al. (2018) use data for Sweden and the UK to investigate if the decoupling of national emissions and production is a delusion. The decoupling would be a delusion if the emission decreases observed in Sweden and the UK were in fact offset by emission increases in the ROW. The underlying issue, at a general level, is how and to what extent “trade-driven” emission changes in individual countries are related to emission changes in the ROW. Baumert et al. (2019) extend the analysis to the global economy and implement the emission intensity adjustment for 40 countries and 35 sectors between 1995 and 2009, drawing on data from the World Input–Output Database, 2013 Release (Timmer et al. 2015). Jiborn et al. (2020) implement the emission intensity adjustment for 43 countries and 56 sectors between 2000 and 2014, drawing on the World Input–Output Database, 2016 Release. These studies ask if the emission trends in the developed countries are in fact driven by trade, and they seek to evaluate the claim that the developed countries are “systematically outsourcing” emissions to the developing countries.

It is important to be clear about the meaning of “emission outsourcing”, and about what is being measured for which region when embodied emission flows are adjusted for intensity differences. “Emission displacement means that a country’s foreign trade contributes to (i) reduced domestic emissions and (ii) increased emissions abroad compared to a no-trade scenario with the same domestic and foreign consumption” (Jiborn et al. 2018, p. 27). Note that the authors use the terms displacement, outsourcing, and weak leakage interchangeably. As explained below, the intensity-adjusted emission balance does not actually say something about the contribution of trade to domestic emissions—it represents the contribution of trade to foreign emissions—and therefore we settle on the term (net weak) leakage. Strong carbon leakage refers to policy-driven emission increases in the ROW, the idea being that e.g. more ambitious European climate policy will lead to increased production and emissions in China.² Weak carbon leakage refers to “demand-driven” emission increases in the ROW, the idea being that e.g. higher European import demand will lead to increased production and emissions in China (Peters 2008, 2010). The original definitions refer to the relation between Kyoto-constrained Annex-B countries and unconstrained non-Annex B countries, but many later studies simply analyze the relation between a focus country and the ROW. In either case, leakage refers to emission changes outside a focus country. The accounting for emissions embodied in trade was developed largely in response to concerns over weak leakage. Peters (2008) proposed to measure weak leakage by the emissions embodied in imports.

Jakob and Marschinski (2013) suggest that assessing a net impact of trade on emissions requires answering a but-for question: what would emissions be without trade? In this spirit Kander et al. (2015) imagine a counterfactual no-trade scenario that considers “what would be the case if a certain commodity were not to be exported from the country in question” (Kander et al. 2015, p. 432). The counterfactual scenario takes domestic and foreign demand as given, meaning a foreign producer using foreign technology will have to produce the focus country’s exports instead. Without further knowledge about the counterfactual producer, “the most plausible, and least demanding, assumption is that a similar good would have been produced at the average emissions intensity on the world market for the relevant sector” (Kander et al. 2015, p. 432). Thus, when the emission intensity adjustment is applied to the emissions embodied in exports, the resulting variable (EIEEX) has to be interpreted as a measure of the foreign emissions avoided by exports (i.e. the PBE avoided in the ROW by the focus country’s exports).

Kander et al. (2015) and Jiborn et al. (2020) define the intensity-adjusted emission balance as EIBEET $=$ EIEEX − EEM. If applied only to the export side, the intensity adjustment violates scale invariance (Domingos et al. 2016). Scale invariance is a desirable property of carbon accounting schemes (the emission responsibility attributed to an aggregate region must equal the sum of the emission responsibility attributed to its sub-regions). To preserve it, Jiborn et al. (2018) and Baumert et al. (2019) also adjust the emissions embodied in imports. But what the resulting variable measures is not so clear. The emission-intensity adjusted emissions embodied in imports (EIEEM) has no obvious interpretation. There is a conflict between methodological choices that serve the attribution of emission responsibility and methodological choices that serve the ex-post analysis of trade and emission flows. We are performing the latter, we like to preserve clean interpretations of the technology-adjusted emission concepts, and therefore we adjust only the export side.

The intensity-adjusted emission balance (EIBEET $=$ EIEEX − EEM) compares the foreign emissions avoided by exports to the foreign emissions generated by imports; with reversed sign, it can be interpreted as a measure of net weak carbon leakage. A positive EIBEET indicates that a country’s trade is net avoiding emissions in the ROW, or net avoiding foreign emissions for short. The contribution of trade to domestic emissions would be given by the difference between the observed emissions embodied in exports and the counterfactual emissions avoided by imports, and is typically measured by the balance of avoided emissions.³

3 Methods

3.1 Emissions Embodied in Trade and the Emission Intensity Adjustment

We use the environmentally-extended MRIO model to calculate carbon dioxide emissions embodied in trade (Leontief 1970; Miller and Blair 2009). For ease of exposition we simplify to the two-country setting and follow the notation of Jiborn et al. (2020) to write the MRIO model in compact form:

$$\begin{aligned} \begin{bmatrix} e^{11} &{} e^{12}\\ e^{21} &{} e^{22}\\ \end{bmatrix} = \begin{bmatrix} \hat{q}^{1} &{} 0\\ 0 &{} \hat{q}^{2}\\ \end{bmatrix} \begin{bmatrix} L^{11} &{} L^{12}\\ L^{21} &{} L^{22}\\ \end{bmatrix} \begin{bmatrix} y^{11} &{} y^{12}\\ y^{21} &{} y^{22}\\ \end{bmatrix} \end{aligned}$$

(1)

Here the global emission matrix E, the global direct emissions intensity vector q (the hat denotes a diagonal matrix formed by the vector), the global Leontief inverse L, and the global final demand matrix Y are partitioned into sub-matrices and sub-vectors for countries 1 and 2. Country 1 can be considered as the focus country and country 2 as the ROW. $e^{11}$ and $e^{22}$ each represent the “domestic-domestic” emissions ($DDE ^1$ and $DDE ^2$), meaning domestic emissions embodied in domestic final demand. From the perspective of country 1, $e^{12} = \hat{q}^{1}L^{11}y^{12} + \hat{q}^{1}L^{12}y^{22}$ represents the emissions embodied in exports ($EEX ^1$), meaning the domestic emissions embodied in foreign final demand. $e^{21} = \hat{q}^{2}L^{21}y^{11} + \hat{q}^{2}L^{22}y^{21}$ represents the emissions embodied in imports ($EEM ^1$), meaning the foreign emissions embodied in domestic final demand. Country 1’s production-based emissions ($PBE ^1$) are the sum of $DDE ^1$ and $EEX ^1$. Its consumption-based emissions ($CBE ^1$) are the sum of $DDE ^1$ and $EEM ^1$. Country 1’s balance of emissions embodied in trade ($BEET ^1$), the net emissions transfer, is given by $BEET ^1 = EEX ^1 - EEM ^1 = PBE ^1 - CBE ^1$. A positive BEET ($EEX ^1 > EEM ^1$) indicates that country 1 is net transferring, or net exporting, emissions to the ROW.⁴

The emission intensity adjustment replaces country-specific values of the each sector’s emission intensity by the respective sector’s world average value. We use a gross output-weighted average:⁵

$$\begin{aligned} \dot{q}_{i} = \sum _s \frac{x_{i}^{s}}{x_{i}} \cdot q_i^s \end{aligned}$$

(2)

$\dot{q}_{i}$ denotes sector i’s standardized emission intensity, $q_i^s$ the direct emission intensity of sector i in country s, $x_i^s$ the gross output of sector i in country s, $x_i = \sum _s x_i^s$ sector i’s global gross output, and i and s sector and country indices.

The calculation would more accurately capture the target concept (the emissions avoided in the ROW by the focus country’s export production) if the world average intensity was calculated excluding the focus country. This calculation would yield country-specific ROW emission intensities, rather than a single global average for each sector. For most countries it will not matter much, but even China and the USA make up only 15% of global GDP each (a rough indication of the average industry weight for these countries). In our view, this is acceptable, especially because there are also benefits to using a single global average: (i) the results are comparable to previous studies and (ii) the comparison of each country to the same global comparative standard has intuitive appeal.

Using the standardized emission intensities, the MRIO system is:

$$\begin{aligned} \begin{bmatrix} \dot{e}^{11} &{} \dot{e}^{12}\\ \dot{e}^{21} &{} \dot{e}^{22}\\ \end{bmatrix} = \begin{bmatrix} \hat{\dot{q}}^{1} &{} 0\\ 0 &{} \hat{\dot{q}}^{2}\\ \end{bmatrix} \begin{bmatrix} L^{11} &{} L^{12}\\ L^{21} &{} L^{22}\\ \end{bmatrix} \begin{bmatrix} y^{11} &{} y^{12}\\ y^{21} &{} y^{22}\\ \end{bmatrix} \end{aligned}$$

(3)

The domestic-domestic emissions should be ignored, only the emissions embodied in trade are relevant in what follows. From the perspective of country 1, $\dot{e}^{12} = \hat{\dot{q}}^{1}L^{11}y^{12} + \hat{\dot{q}}^{1}L^{12}y^{22}$ represents the emission intensity-adjusted emissions embodied in exports ($EIEEX ^1$), and $\dot{e}^{21} = \hat{\dot{q}}^{2}L^{21}y^{11} + \hat{\dot{q}}^{2}L^{22}y^{21}$ the emission intensity-adjusted emissions embodied in imports ($EIEEM ^1$). The no-trade scenario assumes foreign sectors produce country 1’s exports using the world average emission intensity, so the EIEEX measure the foreign emissions avoided by country 1’s exports. We follow Kander et al. (2015) and Jiborn et al. (2020) and define country 1’s emission intensity-adjusted balance of emissions embodied in trade as $EIBEET ^1 = EIEEX ^1 - EEM ^1$. Only the exports are adjusted. The EIBEET therefore compares the hypothetical foreign emissions avoided by exports to the observed foreign emissions generated by imports. A positive EIBEET implies a net decrease in foreign emissions.

3.2 The Technology Adjustment

We propose to adjust not only the direct emission intensity but also the intermediate input intensity, the quantity of inputs per unit of output. The technology-adjusted MRIO system is:

$$\begin{aligned} \begin{bmatrix} \ddot{e}^{11} &{} \ddot{e}^{12}\\ \ddot{e}^{21} &{} \ddot{e}^{22}\\ \end{bmatrix} = \begin{bmatrix} \hat{\dot{q}}^{1} &{} 0\\ 0 &{} \hat{\dot{q}}^{2}\\ \end{bmatrix} \begin{bmatrix} \dot{L}^{11} &{} \dot{L}^{12}\\ \dot{L}^{21} &{} \dot{L}^{22}\\ \end{bmatrix} \begin{bmatrix} y^{11} &{} y^{12}\\ y^{21} &{} y^{22}\\ \end{bmatrix} \end{aligned}$$

(4)

The equations for embodied emissions are the same as before: from the perspective of country 1, $\ddot{e}^{12} = \hat{\dot{q}}^{1}\dot{L}^{11}y^{12} + \hat{\dot{q}}^{1}\dot{L}^{12}y^{22}$ represents the technology-adjusted emissions embodied in exports ($TEEX ^1$), and $\ddot{e}^{21} = \hat{\dot{q}}^{2}\dot{L}^{21}y^{11} + \hat{\dot{q}}^{2}\dot{L}^{22}y^{21}$ represents the technology-adjusted emissions embodied in imports ($TEEM ^1$). The only difference to system (3) is the appearance of the technology-adjusted Leontief inverse $\dot{L}$, which is derived from adjusted technical coefficients. The adjustment is inspired by Xu and Dietzenbacher (2014) and explained in the remainder of this section.

Consider the aluminum sector in Sweden and its intermediate input purchases of nuclear electricity. We so adjust the technical coefficients that Sweden’s aluminum sector directly requires as much nuclear electricity per unit of output as the world average aluminum sector. To this end we calculate the technological coefficients, which represent direct sector-by-sector intermediate input requirements regardless which country supplies the inputs. Let $a_{ij}^{sr}$ be an element of the global technical coefficient matrix A representing country-sector pair rj’s intermediate input purchases from the country-sector pair si. Summing over all supplying countries s gives the technological coefficient:⁶

$$\begin{aligned} h_{ij}^{r} = {\sum _{s=1}^{m} a_{ij}^{sr}} \end{aligned}$$

(5)

Country r’s technological coefficient matrix $H^{r}$ (size $n \times n$) collects these coefficients:

$$\begin{aligned} H^{r} = {\sum _{s=1}^{m} A^{sr}} \end{aligned}$$

(6)

where $A^{sr}$ is a $n \times n$ sub-matrix of the global technical coefficient matrix A.

The trade structure matrix T reflects the origin (geographical composition) of the intermediate inputs:

$$\begin{aligned} T = \begin{bmatrix} T^{11} &{} \cdots &{} T^{1m}\\ \vdots &{} \ddots &{} \vdots \\ T^{m1} &{} \cdots &{} T^{mm} \end{bmatrix} \end{aligned}$$

(7)

Its elements represent the share of all inputs i (required per unit of output by sector j in country r) that originates in country s, calculated as:

$$\begin{aligned} t_{ij}^{sr} = a_{ij}^{sr} / h_{ij}^{r} \end{aligned}$$

(8)

The sum over all countries s necessarily adds up to one: ${\sum _{s=1}^{m} t_{ij}^{sr}} = 1$.

We have introduced all the objects needed to decompose the global technical coefficients matrix:

$$\begin{aligned} A = \begin{bmatrix} T^{11}\otimes H^{1} &{} \cdots &{} T^{1m}\otimes H^{m}\\ \vdots &{} \ddots &{} \vdots \\ T^{m1}\otimes H^{1} &{} \cdots &{} T^{mm}\otimes H^{m} \end{bmatrix} \end{aligned}$$

(9)

where $\otimes$ represents the Hadamard product (element-wise multiplication). The technology adjustment replaces country-specific values of the technological coefficients by world average values. The standardized coefficients are calculated as gross output-weighted averages:

$$\begin{aligned} \dot{h}_{ij} = \sum _s \frac{x_{i}^{s}}{x_{i}} \cdot h_{ij}^s \end{aligned}$$

(10)

where $x_i = \sum _s x_i^s$ is sector i’s global gross output. Using the same technological coefficients for all countries, $\dot{H} = H^{1} = H^{2} = \ldots$, the new technical coefficients matrix is:

$$\begin{aligned} \dot{A} = \begin{bmatrix} T^{11}\otimes \dot{H} &{} \cdots &{} T^{1m}\otimes \dot{H}\\ \vdots &{} \ddots &{} \vdots \\ T^{m1}\otimes \dot{H} &{} \cdots &{} T^{mm}\otimes \dot{H} \end{bmatrix} \end{aligned}$$

(11)

$\dot{A}$ defines the technology-adjusted Leontief inverse, $\dot{L} = (I - \dot{A})^{-1}$, which is used to calculate the technology-adjusted emissions embodied in trade per system (4).

The regular emission balance is defined as BEET $=$ EEX − EEM and the technology-adjusted balance as TBEET $=$ TEEX − EEM. The BEET compares domestic emissions generated by foreign demand and foreign emissions generated by domestic demand. The BEET measures international emission transfers; when it is positive, we say the country is net exporting emissions or net transferring emissions to the ROW. The TBEET focuses on foreign emissions only, comparing hypothetical foreign emissions avoided by exports and observed foreign emissions generated by imports. The TBEET measures net weak carbon leakage; when it is positive, we say the country is net avoiding emissions in the ROW or simply net avoiding foreign emissions. When the TBEET is negative, we say the country is net generating foreign emissions or net leaking emissions.

4 Data

Our source for the annual MRIO tables are the monetary industry-by-industry tables from EXIOBASE3 (Stadler et al. 2018). The main inputs to EXIOBASE3 are macroeconomic data from the UN National Accounts Main Aggregates Database, goods trade data from BACI (Gaulier and Zignago 2010), services trade data from the UN Service Trade Database, product and industry output data from the Detailed Tables of the UN National Accounts Statistics and national statistical offices, as well as supply- and use tables from national statistical offices. Stadler et al. (2018) describe the principles guiding the relations between different classification systems, the filling of gaps, and the reconciliation and balancing needed for the MRIO table construction. The resulting MRIO tables, covering 44 countries and five ROW aggregate regions between 1995 and 2015, stand out for their detailed sector classification dividing economic activity into 163 sectors per country. Notably, electricity production is not merely part of some larger utilities sector but is dis-aggregated by energy source (in total there are 12 different electricity sectors: coal, nuclear, hydro, etc.).

EXIOBASE3 includes environmental satellite accounts matching the sector classification of the MRIO tables. We select total CO2 emissions (kg) as the environmental stressor variable. Only up to 2015 does EXIOBASE3 use detailed emissions data as input to the values of the environmental stressor; we prioritize data quality and restrict our analysis to the period 1995–2015.

EXIOBASE3 covers mostly developed countries with the exceptions of Brazil, China, Indonesia, India, Mexico, and South Africa. The five ROW aggregates are largely composed of developing countries, though the average per-capita income of the Middle East ROW aggregate is at the same level as Greece and Hungary. EXIOBASE3 fills input data gaps for single countries and the ROW regions, so that the final database is exhaustive in that it covers the global economy. Values in the economic transactions tables are estimated in a way that global totals from the UN National Accounts Main Aggregates Database are preserved. The construction of exhaustive environmental satellite accounts involves the estimation of emission factors for the ROW regions (using weighted averages of all available countries) (Stadler et al. 2018, Supporting Information S3). The appendix gives the complete list of countries and country codes (Table 1).

We supplement the environmentally-extended IO tables with country-level population and national accounts data from the Penn World Table Version 10 (PWT10, Feenstra et al. 2015). As an indicator of income per capita, we use output-side real GDP at chained PPPs in 2017US$ divided by population.

5 Results and Discussion

5.1 The Technology-Adjusted Balance of Emissions in Trade

We plot the technology-adjusted balance of emissions embodied in trade (TBEET) for two big developed countries with trade deficits and relatively large service sectors (the USA and the UK), two big developed countries with export orientation and relatively large manufacturing sectors (Germany and Japan), and the two biggest developing countries (China and India, Fig. 1). For comparison and contrast we also plot the regular emission balance (BEET) and the emission intensity-adjusted emission balance (EIBEET). The USA records a negative TBEET, meaning the USA avoids less emissions in the ROW than it generates in the ROW, in other words, the USA net generates foreign emissions (or is net leaking emissions). No region in the whole sample net generates more foreign emissions than the USA (0.5 GtCO2 in 2015).⁷ China net avoids foreign emissions, that is, China’s participation in global value chains helps countries in the ROW to reach their climate targets—the “Factory of the World” provides a mitigation service to its trading partners. The amount of foreign emissions net avoided is modest and smaller, by a factor of four, than the amount of emissions transferred (China’s TBEET in 2015 is 0.3 GtCO2 and its BEET is 1.2 GtCO2). For the USA, the difference between the TBEET and the BEET is less pronounced (the TBEET is $-0.5$ GtCO2 and the BEET is $-0.8$ GtCO2).

Fig. 1

Balance of Emissions Embodied in Trade, GtCO2

For India, Japan, and the UK, the size of the TBEET is relatively modest. These countries do not contribute very much to emissions in the ROW, neither in absolute terms nor relative to national PBE. No single country in the whole sample net avoids more foreign emissions than Germany (0.5 GtCO2 in 2015). Germany, China and other trade-surplus countries are producing more than they are consuming, which helps the ROW to avoid emissions.

There is a well-known negative cross-country relationship between the regular BEET and per-capita income. There is no analogous relationship between the TBEET and per-capita income—in fact there is a positive correlation between the two variables (Fig. 3). Germany, the Netherlands, and many other developed countries are net avoiding foreign emissions while India and Indonesia are net generating foreign emissions. But the strength of the TBEET-income relationship should not be overestimated (see the regression analysis in “Appendix”). The rich USA is net generating foreign emissions while China and South Africa are net avoiding foreign emissions.

The negative cross-country BEET-income relationship is driven to a large extent by international technology differences, as producers tend to generate less emissions per unit of output in developed countries than in developing countries (Jakob and Marschinski 2013; Baumert et al. 2019). The EEX depend on the focus country’s production technology, but the technology adjustment replaces the country-specific technology by a common global standard, eliminating a key source of variation in EEX. The EEM calculation is based on a mix of production technologies. The more geographically diversified are the import partners, the more will the average import partner technology resemble the world average technology. The role of international technology differences thus dampened, the TBEET will significantly depend on the trade balance, i.e. the scale of exports and imports, and the composition of exports and imports.

Structural decomposition methods could shed light on the TBEET’s proximate drivers, and quantify how much certain drivers contribute to the differences between the TBEET and the BEET. That type of analysis is beyond the scope of this study, but some patterns can be inferred from the reported results. First, the monetary trade balance is an important driver of the TBEET. This is evident from the TBEET’s variation over time and across countries. For China, Germany, and the USA, the TBEET roughly tracks the trade balance. Prominent surplus countries (China, Germany, and the Netherlands) record positive TBEETs, while the most prominent deficit country (USA) records negative TBEETs (Appendix, Table 3). Second, the trade composition might explain why resource-abundant countries exporting mined raw materials tend to record positive TBEETs. Examples are Canada, Norway, Russia, and the Middle East ROW aggregate (Appendix, Table 3). Trade surpluses may partly explain the pattern, but the trade composition probably plays a role as well, as the cleaning and processing of resources can be quite emission intensive. Composition effects should be most visible in commodity-exporting countries, due to the export concentration. The exports of China, Germany, and the USA are more diversified, thus the trade composition plays a smaller role and trade balance effects are brought to light. Third, the regular BEET depends heavily on international differences in the input intensity. This can be inferred from the difference between the TEEX and the EEX: for most countries this difference is large and larger than the difference between the EIEEX and the EEX (Appendix, Table 7). Standardizing technology is more consequential than standardizing only the direct emission intensity.⁸

The Chinese production technology is browner than the world average, and the technology adjustment roughly halves China’s EEX. The American production technology is greener than the world average, and the technology adjustment roughly doubles the USA’s EEX (Appendix, Table 7). The technology adjustment triples Germany’s EEX, and it is even more consequential for small countries like Austria, Croatia, Finland, Hungary, Slovenia, Sweden, and Switzerland, where the ratios of TEEX to EEX exceed four (Appendix, Table 6). Austria, Germany, and Hungary do not house exceptionally clean electricity sectors, so the energy mix is only part of the story, and the adjustment to the intermediate input intensities of the producing sectors matters as well.

5.2 Technology-Adjusted Consumption-Based Emissions

This section evaluates the national emission trends in the six focus countries. Our main interest rests with the PBE and the TCBE, but we also plot the CBE and EICBE for comparison and contrast (Fig. 2). The TCBE represent the production-based emissions plus the emissions net generated in the ROW. Assuming the economy is growing, decreasing PBE indicates successful decoupling. The decoupling would be a delusion, following Jiborn et al. (2018), if the TCBE increased over the same period, for then the increase in the net generation of foreign emissions was larger than the PBE decrease.

Fig. 2

Consumption-based Emissions, GtCO2

Fig. 3

TBEET vs. Income per Capita, 2015 Snapshot. Notes Own calculations based on EXIOBASE3 and PWT10 using data from 2015. The TBEET is measured in % of PBE, income per capita in thousand PPP-adjusted US$. The right panel excludes economies whose 2015 population is lower than 10 million. The lines represent the best linear fit from simple OLS cross-country regressions (see “Appendix”)

The overall picture is that emissions are increasing in the two big developing countries, are decreasing in Germany, show ups and downs while remaining overall roughly constant in Japan, and are increasing first and then decreasing in the UK and the USA. This picture emerges regardless of which emission concept is being considered. For each country, there are level differences between the PBE and TCBE, but the two variables tend to change in the same direction, following country-specific trends. Changes in the net generation of foreign emissions, as a rule, are too small to cause qualitative divergence between the existing emission concepts.

In much of the developed world, economic growth has decoupled from any of the existing emission concepts. Europe’s CBE peaked in 2006 (Karstensen et al. 2018; Wood et al. 2019). Both PBE and CBE decreased in 18 developed countries between 2005 and 2015 (Quéré et al. 2019). Jiborn et al. (2020) analyze the period 2000–2014 and report that 21 countries record decreases in PBE, CBE, and the emission intensity-adjusted CBE. Our sample covers the period 1995–2015 and shows that PBE are decreasing in 24 countries (out of 44), the technology-adjusted CBE are decreasing in 29 countries, and both variables are decreasing in 19 countries (Appendix, Tables 4 and 8). That said, the absolute decoupling of emissions and economic growth in the developed countries is insufficient—reaching climate targets requires far greater mitigation rates (e.g. Quéré et al. 2019).

While most developed countries record decreasing emissions, all the developing countries in our sample record increasing emissions. The proximate drivers are relatively clear. Production-side decompositions based on the Kaya identity show that energy intensity improvements (more than decarbonization) account for the bulk of the emission decreases in the developed countries. Meanwhile in the developing world, income and population growth are pushing emissions up more than decarbonization efforts and energy intensity improvements are pulling them down (Quéré et al. 2019; Xia et al. 2020). The importance of changes in the scale of economic activity is also visible from demand-side decompositions based on the input–output model. Rising domestic demand—more than the increased participation in global supply chains—has driven the emission increases in the developing countries (de Vries and Ferrarini 2017). Alone the increased domestic production serving domestic final demand in China accounts for nearly 50% of the increase in global emissions between 2000 and 2014 (Jiborn et al. 2020).

Net weak carbon leakage as measured by the technology-adjusted emission balance cannot be regarded as an important driver of national emission trends. To avoid misunderstanding, this does not mean that international trade hardly influences national or global emissions. It may be true that the key proximate determinants of China’s rapid emission growth are the (coal-fueled) buildup of the domestic capital stock and the rising consumption demand from the growing middle class, rather than observed trade flows. But this economic development is hard to imagine without the export-oriented growth strategy China was able to pursue in the increasingly integrated world economy. Without technology diffusion and learning spurred by foreign investment, without the foreign demand for manufactured products, China’s domestic demand would never have increased as much. The input–output model rules out mechanisms through which trade influences technology and demand.⁹ Net weak carbon leakage represents the contribution of a country’s trade to foreign emissions, where this contribution is calculated for given technologies and demands. The interpretation is analogous to the balance of avoided emissions, also an input–output based concept that takes technology and demand as given, which represents the contribution of a country’s trade to domestic emissions (e.g. Dietzenbacher and Mukhopadhyay 2007; Zhang et al. 2017).

6 Summary and Concluding Remarks

We proposed and implemented a new method for the technology-adjusted accounting for emissions embodied in trade. Following the logic of emission intensity-adjusted accounting (Kander et al. 2015), the standardization should be extended to the production recipes.

Technology-adjusted accounting can be viewed as a contribution to the normative debate about the attribution of emission responsibility, which considers the design of incentive-compatible accounting schemes that would credit countries only for those national mitigation actions that lead to global emission reductions (Kander et al. 2015; Dietzenbacher et al. 2020; Jakob et al. 2021). Such schemes should not ignore international differences in the input intensity. Exploring the merits of alternative accounting schemes, irrespective of political and practical constraints, is a worthwhile enterprise. At the same time, there is little political momentum for adopting an alternative to territorial or PB accounting, and any scheme that depends on accurate input–output tables for all countries faces severe practical challenges (e.g. Liu 2015; Afionis et al. 2017).

The technology adjustment can also be viewed as a tool for the positive analysis of emissions embodied in trade. After examining what the resulting emission concepts measure, we interpreted the technology-adjusted emission balance (with reversed sign) as a measure of net weak carbon leakage. A country’s imports generate emissions in the ROW, while its exports avoid emissions in the ROW. The technology-adjusted EEX represent a measure of the foreign emissions avoided by exports, and the technology-adjusted BEET represents a measure of the foreign emissions net avoided by trade. The technology-adjusted CBE represent production-based emissions plus emissions net avoided in the ROW.

International emission transfers and net weak carbon leakage show different patterns. In contrast to the regular BEET, the TBEET exhibits a positive cross-country correlation with per-capita income. Most developed economies are net avoiding foreign emissions. China helps its trading partners to avoid emissions, though the amounts are modest and much smaller than China’s net emission exports. Emissions are decreasing in many developed countries while they are increasing in the developing countries, regardless of the emission concept. The modest decoupling success in the developed countries would be tainted if the PBE decreases had been accompanied by trade-driven emission increases in the ROW. This is not the case, changes in net weak leakage do not account for the decreases.

Appendix: Cross-Country Regressions

To assess the strength of the positive cross-country correlation between the TBEET and per-capita income, we regress the TBEET in % of PBE on per-capita GDP in thousand PPP-adjusted US$ (Table 9). The columns 1 and 2 report simple OLS regressions with heteroskedasticity-consistent standard errors based on the 2015 cross section (Fig. 3 shows the regression lines). The columns 3 and 4 report pooled OLS regressions with country-cluster-robust standard errors based on panel data from 1995–2015. The pooled OLS estimator is consistent for the parameters $\varvec{\beta }$ of the model:

$$\begin{aligned} y_{it} = \varvec{x}_{it} \varvec{\beta } + v_{it} \end{aligned}$$

(12)

where the regressor vector $\varvec{x}_{it}$, which includes per-capita income and year dummies, does not correlate with the composite error (the unobserved country effect plus the idiosyncratic error $v_{it} = c_i + u_{it}$), i.e. $E(\varvec{x}_{it} v_{it}) = \varvec{0}$. The regressions yield coefficients that measure statistical association and should be viewed as a tool of descriptive analysis. A causal analysis would at the very least address the potential correlation between per-capita income and the unobserved effects (i.e. use the fixed effects estimator), and possibly deal with reverse causality as well. Our goal is merely to show how net weak carbon leakage and per-capita income are related in the cross-section.

Fig. 4

Balance of emissions embodied in trade 1995–2015, line plots by country

Fig. 5

Consumption-based and production-based emissions 1995–2015, line plots by country

Fig. 6

Emissions embodied in exports 1995–2015, line plots by country

The slope coefficient, statistically significant (5%) in one regression (Column 3), is always greater than zero and varies between 0.44 and 0.95. A coefficient of one would indicate that one thousand dollar higher income is associated with one percentage point higher TBEET. The R squares are low, the variation around the best linear fit is large, many factors other than income explain the TBEET.

Table 1 Countries in EXIOBASE3

Table 2 Balance of emissions embodied in trade, GtCO2

Table 3 Balance of emissions embodied in trade, % of PBE

Table 4 Consumption-based emissions, GtCO2

Table 5 Consumption-based emissions, % of PBE

Table 6 Emissions embodied in exports, GtCO2

Table 7 Emissions embodied in exports, % of PBE

Table 8 Production-based emissions, GtCO2

Table 9 TBEET vs. income per capita: cross-country regressions