Welfare Effects of Changing Technological Efficency in Regulated Open-Access Fisheries

Abstract

Small-scale fisheries often operate under conditions of regulated open access; that is, the fishery is subject to natural or regulatory constraints on fishing technology, including regulations of fishing gear and fishing practices, but typically there is no direct regulation of catches. We study how an increase in harvesting efficiency changes the different components of welfare—consumer surplus and producer surplus—in such a regulated open-access fishery, taking t the feedback of harvesting on stock dynamics, i.e. the dynamic common-pool resource externality into account. We find that both components of welfare change in the same direction. If, and only if, initial efficiency is low enough so that there is no maximum sustainable yield (MSY) overfishing, an improvement of harvesting efficiency increases welfare.

Introduction

About 90% of the world’s fishers and over half of the fish consumed each year are captured by small scale, often inshore fisheries, under conditions of open access, regulated open access, or local common pool resources (Ostrom 1990, p. 27; Homans and Wilen 1997; FAO 2007; World Bank 2012). This means, catch quantities are not directly regulated. Harvesting efficiency in those fisheries is limited, however, by the current state of technology, and often by regulations that further constrain the efficieny of harvesting technologies, e.g. by restricting fishing gear and practices, or limiting the length of fishing seasons (Homans and Wilen 1997). Whereas improving technical efficiency would unambiguously enhance welfare in a first-best setting (see, e.g., Clark 1990, Ch. 2), this is far from obvious in the actual second-best world of most fisheries, with the imperfect regulation and enforcement of resource use and thus common-pool externalities in place. The reason is that improving technical efficiency tends to increase harvesting and reduce the stock, which may undermine long-run productivity of the resource and thus ultimately reduce welfare.

This paper aims to characterize conditions under which a costless improvement of technical harvesting efficiency will increase or decrease welfare in an imperfectly regulated fishery. To this end, we formulate a bioeconomic model of a regulated open-access fishery. In this setting, individual fishermen ignore the effect of their harvest on the dynamics of the fish population; that is, exploitation takes place in a myopic manner. The supply of fish is thus determined by current marginal fishing costs, ignoring the dynamic stock externality of the resource use, and dissipating resource rent, similar as in Reimer and Wilen (2013). Welfare includes producer surplus and consumer surplus (Copes 1972; Quaas et al. 2018; Jensen et al. 2019), which is certainly relevant for small-scale fisheries in developing countries that serve as an important local source of livelihoods and food supply.

We find that in biological equilibrium where the harvest equalizes natural growth of the fish stock, the components of welfare—consumer and producer surplus—in the regulated open access fishery, change with technical efficiency in a non-monotonic fashion. This shows how more efficient fishing methods, or more lenient gear regulations, may be a mixed blessing not only for the catch and fish abundance, but also for the profitability and the welfare of the local fishing community. Importantly, we characterize under which conditions technical efficiency will improve, or reduce welfare. We find that if technical efficiency increases from a low level, this will improve both consumer and producer surplus, while beyond some point a further increase in technical efficiency will reduce both components of welfare. We further find that the turning point is the same for both welfare components. It is the level of efficiency for which the fish population size would give rise to the maximum sustainable yield (MSY) harvesting. MSY as welfare-maximizing harvesting is indeed a surprising result, given that the model includes the feature that fishing costs decrease wth fish abundance. This result holds for a large range of specifications for benefits and costs derived from harvesting, allowing for stock-dependency of both benefits and costs. It is demonstrated that the result stems from the stock-agumenting property of harvesting efficiency, i.e. that a change in harvesting efficiency is equivalent to a change in resource stock size. We show that under this condition, welfare in biological and market equilibrium can be expressed as an increasing function of harvest alone and thus long run welfare effects of harvesting efficiency depend on the steady-state harvest level only.

The main contribution of this paper is to show how an improvement of technical efficiency in a common-pool resource affects the different components of welfare. That a more efficient fishing technology can be a mixed blessing has been discovered before (Whitmarsh 1990; Murray 2007). In particular, Squires and Vestergaard (2013a, b) show that the rapid technological progress in the past contributed to the decline of most, if not all, global fisheries. Gordon and Hannesson (2015) gives an in depth analysis of technological progress and the stock collapse in the Norwegian winter herring fishery, and provide evidence that the introduction of the power block technology was the principal factor in the demise of the stock. Hannesson et al. (2010) and Eide et al. (2003) find similar results for other fisheries. Here, we show that this mixed blessing of improving fishing technology is a systematic property of fisheries operating under regulated open access, and that in the long-term welfare effects are negative if the stock is below the one that generates the maximum sustainable yield, i.e. if the stock is overfished according to the definition of the FAO (2020). The result that improving technical efficiency can reduce harvest—and hence welfare—in the long run can be interpreted as a form of bio-economic rebound effect, in a sense related to the rebound effect known in energy economics (Gillingham et al. 2016). This bio-economic rebound effect works over two links: In the short run, increased technical efficiency increases harvest in market equilibrium. In the long run, increased technical efficiency thus reduces the (steady state) resource stock, which feeds back on the biological resource productivity.

The next section presents our bioeconomic model and Sect. 3 presents the main results. In Sect. 4 the results are illustrated for a case study; the Sengalese small scale fishery on Sardinella Aurita. The final Sect. 5 discusses our findings and concludes. The appendix considers extensions of the model to show that our main results generalize to a wider class of fishing technologies and utility functions, and how results are qualified if dynamics and discounting are considered.

Model of a Small-Scale Fishery Under Regulated Open Access

We consider a single fish stock exploited in a myopic manner in a local fishing community. The population dynamics in continuous time is described by:

$$\frac{{dX_{t} }}{dt} = F(X_{t} ) - H_{t} ,$$

(1)

where $X_{t}$ is the stock size (measured in biomass) at time $t$, $H_{t} \ge 0$ is the aggregate harvest by the entire fishing community, and $F(X_{t} )$ is the natural growth function. We adopt the standard assumptions $F(0) = F(K) = 0$, where $K > 0$ is the carrying capacity of the fish stock, and where growth is positive for biomass positive and below carrying capacity, $F(X_{t} ) > 0$ for $X_{t} \in (0,K),$$F^{\prime\prime}(X_{t} ) < 0$. Additionally, $F(X_{t} )$ is single-peaked, i.e. there is a unique stock size $X^{msy}$ that maximizes $F(X_{t} )$, i.e. where $F^{\prime}(X^{msy} ) = 0$.

Harvest from the small-scale fishery is sold on a local market, where the fish price depends on the amount of fish available. This is modelled by the inverse demand function $p_{t} = P(H_{t} )$, with $P^{\prime}(H_{t} ) < 0.$ Fishermen have no market power and hence take the price $p_{t}$ as given.

We analyze a search fishery where the harvest depends on the current stock size, and the harvesting technology is assumed to follow the generalised Gordon (1954) and Schaefer (1957) model. The harvest function is thus given as $H_{t} = q{\kern 1pt} E_{t}^{\xi } {\kern 1pt} X_{t}^{\chi }$ with $0 < \chi \le 1$ and $0 < \xi \le 1$, such that the harvest is increasing in fishing effort $E_{t}$ and stock size $X_{t}$. The technical efficiency parameter q, commonly also referred to as ‘catchability coefficient’, is assumed to be exogenous, with a higher value indicating a more efficient fishing technology. We can think of an increase in $q$ as the result of technical progress (Squires and Vestergaard 2013a, b), or as a result of a more lenient regulation of fishing gear, equipment or methods. In other words, a value of q below the current state of technology reflects the effects of regulation on the fishery that otherwise is operating under open access, i.e. without direct restrictions on total harvest (Homans and Wilen 1997). While the focus of our analysis is on changes in $q$, changes in demand and fishing cost parameters can be studied in a similar way. We sketch this in the subsequent analysis. All the time, changing the value of $q$ is assumed to be costless.

On the other hand, fishing effort $E_{t}$ is costly, and $\hat{C}(E_{t} )$ yields the effort cost function. Marginal effort costs are positive, $\hat{C^{\prime}}(E_{t} ) > 0$, and non-decreasing $\hat{C}^{\prime\prime}(E_{t} ) \ge 0$.We think of this cost function as describing the (opportunity) costs of fishing for the whole fishing community, reflecting different productivity (fishing skill) among the various fishermen (Péreau et al. 2012; Grainger and Costello 2016) and different productivities of outside options (Baland and Francois 2005; Okonkwo and Quaas 2019). In Appendix 1 we show how the reduced-form model we present here can be derived from a model that explicitly considers a large number of heterogeneous fishers. The cost function $\hat{C}(E_{t} )$ therefore represents a smoothing of the costs of the various fishermen in this fishing community and where the fishermen with high fishing skill, or low opportunity costs of fishing, earn high intramarginal rent, and vice versa. Based on the Gordon-Schaefer harvest function, effort can be written as $E_{t} = (H_{t}^{{}} /(q{\kern 1pt} {\kern 1pt} X_{t}^{\chi } ))_{{}}^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \xi }}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$\xi $}}}}$. Using this in the effort cost function $\hat{C}(E_{t} )$, we can formulate the harvesting cost function for our search fishery as a function of harvest H_t, stock size X_t and catchability q:

$$C_{t} = C\left( {H_{t} ,X_{t} ,q} \right) \equiv \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{C} \left( {\left( {\frac{{H_{t} }}{{qX_{t}^{\chi } }}} \right)^{{1/\xi }} } \right).$$

(2)

From the above assumptions, it follows that fishing cost are increasing and (weakly) convex in total catch, $C_{{H_{t} }}^{{}} > 0$, $C_{{H_{t} H_{t} }}^{{}} \ge 0$, decreasing and convex in stock size and catchability coefficient, $C_{{X_{t} }}^{{}} < 0$, $C_{{X_{t} X_{t} }}^{{}} \ge 0$, $C_{q}^{{}} < 0$, $C_{qq}^{{}} \ge 0$. Furthermore, the cross derivatives with respect to $H_{t}$ and both stock size and catchability are negative, $C_{{H_{t} X_{t} }}^{{}} < 0$, $C_{{H_{t} q}}^{{}} < 0$, i.e. marginal fishing cost decrease both with stock size and technical efficiency. The current profit, or producer surplus, reads then:

$$\pi_{t}^{{}} = p_{t} {\kern 1pt} H_{t} - C^{{}} (H_{t} ,X_{t} ,q).$$

(3)

In general, current welfare derived from the fishery is the sum of consumer surplus, producer surplus, and resource rent (Copes 1972; Quaas et al. 2018; Jensen et al. 2019). As formally shown below, resource rent is dissipated in the fishery unter regulated open access, such that the remaining welfare components are consumer and producer surplus. Given the inverse demand function $p_{t} = P(H_{t} )$ welfare is expressed as:

$$U_{t}^{{}} = \int_{0}^{{H_{t} }} P(h){\kern 1pt} dh - p_{t} {\kern 1pt} H_{t} + p_{t} {\kern 1pt} H_{t} - C\left( {H_{t} ,X_{t} ,q} \right) = \int_{0}^{{H_{t} }} P(h){\kern 1pt} dh - C(H_{t} ,X_{t} ,q).$$

(4)

Analysis and Results for the Small-Scale Fishery Under Regulated Open Access

Short-Run Analysis: Market Equilibrium at a Given Fish Stock Size

Myopic profit maximization for the given stock $X_{t} > 0$, and where hence the fishing impact on the stock is neglected, yields $\frac{{\partial \pi_{t} }}{{\partial H_{t} }} = p_{t} - C_{{H_{t} }} \le 0.$ This condition defines the (inverse) supply function of fish to the local market, for a given size of the fish stock. If marginal harvesting costs are increasing, inverse supply is a smoothly increasing function of catch $H_{t}$. If marginal harvesting costs are constant, inverse supply is a ‘bang-bang’ curve, i.e. zero whenever marginal costs are above $p_{t}$ and maximum possible if they are below $p_{t}$ (Pindyck 1984). In market equilibrium (denoted by a ^* superscript to the variables), it must hold that the supply equals demand, and for $H_{t}^{*} > 0$ thus:

$$P(H_{t}^{*} ) = C_{{H_{t}^{{}} }}^{{}} \left( {H_{t}^{*} ,X_{t} ,q} \right).$$

(5)

Note that the downward-sloping inverse demand function $P^{\prime}(H_{t} ) < 0$ guarantees a unique market equilibrium even for constant marginal harvesting costs.

It follows that harvest in the above myopic exploited fishery market equilibrium condition (5) is positive or zero according to:

$$H_{t}^{*} = \left\{ {\begin{array}{*{20}l} {H(X_{t} ,q) = 0} \hfill & {{\text{if}}\,P(0) - C_{{H_{t} }}^{{}} (0,X_{t} ,q) \le 0} \hfill \\ {H(X_{t} ,q) > 0,} \hfill & {{\text{else}}.} \hfill \\ \end{array} } \right.$$

(6)

Therefore, $H_{t}^{*}$ is an increasing function of fish abundance $X_{t}$, whenever harvest is positive. Differentiating Eq. (5), using the implicit function theorem, yields:

$$\frac{{dH_{t}^{*} }}{{dX_{t} }} = \frac{{C_{{H_{t} X_{t} }}^{{}} }}{{P^{\prime}(H_{t} ) - C_{{H_{t} H_{t} }}^{{}} (H_{t} ,X_{t} ,q)}} > 0\,\,,\,\,\,{\text{for}}\,\,\,H_{t}^{*} > 0.$$

(7)

The harvest locus may be concave or convex, depending on third order derivatives of inverse demand and cost functions.

Furthermore, technically more efficient fishing through a higher value of $q$ shifts down both the cost function and the marginal cost function, and hence increases total harvest for a given size of the fish stock. This follows from differentiating condition (5) with respect to $q$, which yields, using the implicit function theorem:

$$\frac{{dH_{t}^{*} }}{dq} = \frac{{C_{{H_{t} q}}^{{}} }}{{P^{\prime}(H_{t} ) - C_{{H_{t} H_{t} }}^{{}} (H_{t} ,X_{t} ,q)}} > 0\,\,,\,\,\,\,{\text{for}}\,\,\,H_{t}^{*} > 0.$$

(8)

Multiplying both sides of the market equilibrium condition (5) with total harvest H^*, we obtain the condition that total revenues, harvest quantity times marginal harvesting costs, equal consumer expenditures—there is no resource rent. Using (2), total revenues can also be written as a function of effort, $R\left( {E_{t}^{*} } \right)$, and thus the condition that total revenues equal consumer expenditures can be formulated as:

$$R\left( {E_{t}^{*} } \right) \equiv \frac{1}{\xi }{E_{t}^{*}} {\hat{C}^{\prime}}\left( {E_{t}^{*} } \right) = {H_{t}^{*}} C_{{H_{t} }} \left( {{H_{t}^{*}} ,\,X_{t} ,\,q} \right) = P\left( {H_{t}^{*} } \right){H_{t}^{*}} .$$

(9)

As marginal effort costs are positive and non-decreasing, total revenues are monotonically increasing in effort from zero for $E_{t}^{*} = 0$ to infinity for $E_{t}^{*} \to \infty .$ Thus, the inverse function $R_{{}}^{ - 1} \left( . \right)$ exists. Using this in the condition that expenditures equal total revenues, we find that effort in market equilibrium can be expressed as an increasing function of total harvest:

$$E_{t}^{*} = R_{{}}^{ - 1} \left( {H_{t}^{*} P\left( {H_{{}}^{*} } \right)} \right).$$

(10)

Current producer surplus, or profit, and consumer surplus in market equilibrium are now:

$$\pi_{t}^{*} = C_{{H_{t} }}^{{}} (H_{t}^{*} ,X_{t} ,q){\kern 1pt} H_{t}^{*} - C^{{}} (H_{t}^{*} ,X_{t} ,q)$$

(11)

and

$${\text{C}}S_{t}^{*} = \int_{0}^{{H_{t}^{*} }} P(h)dh - P(H_{t}^{*} )H_{t}^{*} ,$$

(12)

respectively. We have the following result.

Result 1

In the short-term market equilibrium, i.e. for given fish abundance $X_{t}$, more efficient fishing technology.

• 1. Increases producer surplus if the elasticity of the inverse demand is smaller than unity, $- H{\kern 1pt} P^{\prime}(H)/P(H) < 1$,

• 2. Increases consumer surplus.

Proof

See Appendix

Therefore, as expected, we find that in the short run and for a given fish abundance $X_{t}$, a more efficient harvesting technology unambigously improves consumer surplus through the reduced market price effect. For producer surplus, more efficient fishing equipment through reduced costs $C_{q}^{{}} < 0$ works in the direction of higher profit and this effect dominates the negative price effect due to a higher harvest and reduced price if the inverse demand elasticity is small enough. Under this condition, more efficient technology is therefore not only beneficially for the local fishermen in the short-term, as also shown in a somewhat different setting by Anderson (1986), but it also improves the consumer surplus and welfare of the local community.

Long-Run Analysis: Market Equilibrium and Biological Equilibrium Combined

The more interesting question is, however, the welfare effect of increased harvesting efficiency in the long run; that is, when the feedback effect of a higher valued $q$, and thus higher short-run harvest level, on the stock dynamics is taken into account as well. With the myopic optimized harvest function $H_{t}^{*} = H(X_{t} ,q) \ge 0$ from Eq. (6) inserted into the stock growth Eq. (1), the dynamics of the harvested fish population is described by:

$$\frac{{dX_{t} }}{dt} = F(X_{t} ) - H(X_{t} ,q).$$

(13)

The biological equilibrium is defined by the condition that the stock is at long-term steady state, $dX_{t} /dt = 0$.With total harvest equals natural growth, the steady-state stock size $X^{*}$ is determined by:

$$F(X^{*} ) = H(X^{*} ,q).$$

(14)

A long-run equilibrium of the regulated open-access fishery is thus defined by both the market equilibrium condition (demand = supply; Eq. 5) and the biological equilibrium conditoin (harvest = natural growth; Eq. 14).

Moreover, the biological equilibrium described by Eq. (14) is locally stable if:

$$F^{\prime}(X^{*} ) - H_{X} (X^{*} ,q) < 0.$$

(15)

Therefore, under condition (15), a small deviation from the steady-state stock size generates a dynamic that drives the stock back to the biological equilibrium. That is, if the stock is slightly smaller (larger) than the steady-state size, biological growth exceeds (falls short of) harvest. The stock accordingly increases (decreases) again up (down) to the biological equilibrium level.

The given assumptions on the natural growth function, and the result that the harvest locus is strictly increasing in fish biomass, as described by Eq. (7), are not sufficient to characterize the number of steady states, i.e., the number of solutions to the biological equilibrium condition (14). If the inverse demand function is bounded from above, $P(0) < \infty$, there will always be an interval of sufficiently small stock sizes where marginal harvesting costs exceed the price of fish (see also Nævdal and Skonhoft 2018). Combined with the result that harvest is (weakly) increasing with stock size, Eq. (7), this implies that $P(0) < \infty$ is a sufficient condition for the existence of at least one steady state.

We now turn to the main question studied in this paper; how does increased technical efficiency affect consumer surplus and producer surplus in the long run? To this end, differentiate Eq. (14) that describes the biological equilibrium with respect to $q$ and apply the implicit function theorem. This leads to:

$$\left( {F^{\prime}(X^{*} ) - H_{X}^{{}} (X^{*} ,q)} \right){\kern 1pt} \frac{{dX^{*} }}{dq} = H_{q}^{{}} (X^{*} ,q).$$

(16)

Through Eq. (8), a higher $q$ increases total harvest, i.e. the right-hand-side of Eq. (16) is positive. As we are considering a locally stable biological equilibrium, the factor in brackets on the left-hand side of Eq. (16) is negative. Hence, a small increase in technical efficiency will consistently lower the steady-state stock, $dX^{*} /dq < 0$. On the other hand, more efficient technology may either reduce or increase biological growth $F(X^{*} )$, and hence through Eq. (14) also either reduce or increase harvest in biological equilibrium. The critical stock size is here $X^{{{\text{m}}sy}}$, and where harvest in biological equilibrium increases with technical efficiency if $X_{{}}^{*} > X_{{}}^{msy}$. As consumer surplus unambiguously increases with harvest, we have:

$${\text{sign}}\left( {X^{*} - X^{{{\text{msy}}}} } \right) = {\text{sign}}\left( {\frac{{d{\text{CS}}^{*} }}{dq}} \right).$$

(17)

Thus, if the initial technical efficiency is low enough such that the stock is not MSY-overfished, improved fishing efficiency—be it due to technical progress or changes in fishing gear regulations—will increase the long run consumer surplus.

However, the long-run effect of an increase in $q$ on producer surplus, or profit, is not quite as straightforward, as producer surplus is also directly affected by the recuced stock size triggered by an increase in $q$. To study the effect of a small change on $q$ on the producer surplus defined through Eq. (11) at market equilibrium, we differentiate this expression with respect to q, while taking the effect of $q$ on $X^{*}$ and on $H^{*} = F(X^{*} )$ into account. Using Eq. (5) for $H^{*} > 0$, this yields (omitting arguments of functions):

$$\frac{{d\pi^{*} }}{dq} = C_{HH}^{{}} {\kern 1pt} H^{*} {\kern 1pt} H_{q}^{*} + C_{Hq}^{{}} {\kern 1pt} H^{*} - C_{q}^{{}} + \left( {C_{HX}^{{}} {\kern 1pt} H^{*} + C_{HH}^{{}} {\kern 1pt} H^{*} {\kern 1pt} H_{X}^{*} - C_{X}^{{}} } \right){\kern 1pt} X_{q}^{*} .$$

(18)

This expression contains positive and negative terms. Therefore, while Result 1 indicates that the short-run effect of more efficient fishing increases producer surplus (provided that the elasticity of the inverse demand function is less than one), the long-term effect, when also biological equilibrium is taken into account, is generally ambiguous. The reason is that the long-run effect comprises two opposite forces, and where the direct positive effect of a higher $q$ working through the cost function (the first three terms on the right-hand side of Eq. 18) is counterbalanced by a negative indirect effect also working through the cost function by a reduction in the fish abundance (the last term on the right-hand side of Eq. 18).

Under the given assumptions, we can characterize the sign of the net effect of technical efficiency on welfare where harvest is determined by market equilibrium (demand = supply; Eq. 5), and the feedback of harvesting on fish stock in biological equilibrium (natural growth = harvest; Eq. 14) is taken into account. To this end, we use the total revenue function (9) to write producer surplus in market equilibrium as $\pi_{t}^{*} = P\left( {H_{t}^{*} } \right)H_{t}^{*} - \hat{C}\left( {R_{{}}^{ - 1} \left( {H_{t}^{*} P\left( {H_{t}^{*} } \right)} \right)} \right).$ This indicates that producer surplus can be expressed as an (increasing) function of harvest alone. Thus, the long-run effect of technical efficiency on producer surplus and on harvest will go in the same direction—just as it is the case for consumer surplus and havest. In sum, we have the following result:

Result 2

• 1. Consumer surplus increases with technical efficiency if and only if the steady state stock size is above the stock that generates the maximum sustainable yield.

• 2. Producer surplus increases with technical efficiency if and only if the steady state stock size is above the stock that generates the maximum sustainable yield.

Formally,

$${\text{sign}}\left( {X^{*} - X^{{{\text{msy}}}} } \right) = {\text{sign}}\left( {\frac{{d{\text{CS}}^{*} }}{dq}} \right) = {\text{sign}}\left( {\frac{{d\pi^{*} }}{dq}} \right).$$

(19)

Proof

See Appendix.

Result 2 shows that in a situation with a high exploitation pressure, channeled through a high harvesting efficiency and $X^{*} < X^{msy}$, more efficient technology will reduce steady-state producer surplus while the opposite happens when initially $X^{*} > X^{msy}$. Result 2 contrasts the outcome of the standard sole owner, or social planner, biomass model where improved harvesting technology, and hence lower catch costs, unambiguously increases the equilibrium rent (again, see Clark 1990, Ch. 2).

In the long run, both consumer surplus and producer surplus will therefore be at its maximum when the steady stock size is equal to the stock size that generates the maximum sustainable yield, $X^{*} = X^{{{\text{m}}sy}}$. As consumer surplus increases unambiguously with harvest, the maximum of consumer surplus will be higher the larger the MSY is. Therefore, the maximum consumer surplus will be higher for larger biological productivity. Maximum producer surplus in our search fishery can be written as $\pi^{\max } = P(H^{{{\text{m}}sy}} ){\kern 1pt} H^{{{\text{m}}sy}} - C\left( {H^{{{\text{m}}sy}} ,X^{{{\text{m}}sy}} ,q} \right)$. For a cost function with a constant elasticity of cost with respect to harvest, i.e. where $C = \beta {\kern 1pt} H_{t} {\kern 1pt} C_{{H_{t} }}^{{}}$ with some constant $\beta \ge 1$, we have, using Eq. (5), $\pi^{\max } = P(H^{{{\text{m}}sy}} ){\kern 1pt} H^{{{\text{m}}sy}} - C\left( {H^{{{\text{m}}sy}} ,X^{{{\text{m}}sy}} ,q} \right) = (1 - \beta ){\kern 1pt} P(H^{{{\text{m}}sy}} ){\kern 1pt} H^{{{\text{m}}sy}}$, which does not depend on harvesting efficiency $q$. We thus have the following result.

Result 3

For an iso-elastic harvesting cost function, and in particular for constant marginal harvesting cost, the maximum steady state welfare is unrelated to fishing efficiency.

However, while the maximum rent in our model is not contingent upon the technology level, it is also clear that there will be a certain value of $q$ that yields the highest rent. This technical efficiency level $q = q^{\max }$ solves the stock equilibrium equation $F(X^{msy} ) = H^{*} (X^{msy} ,q^{\max } )$ and is hence contingent upon all the parameters of the model.

Case study: Senegalese Small Scale Fishery on Sardinella Aurita

To illustrate our results, we consider a quantitative case study on the Senegalese small scale fishery on Sardinella Aurita, which is operating under conditions of open access and myopic exploitation. Sardinella Aurita are the main target of the Senegalese artisanal fishery. The catch of this small pelagic fish is consumed mostly locally in Senegal, and the artisanal purse seine fishery contributes substantially to local food security and livelihoods. Harvesting efficiency is changing due to technical progress (e.g., improved motorization of fishing vessels) and climate change, which changes the spatial distribution and accessibility of the resource (Lancker et al. 2019a, b).

We base the specification of our case study on the estimates from Lancker et al. (2019b). Functional forms and parameter values are given in Tabe 1. Lancker et al. (2019b) estimate economic parameters for four regions along the Senegalese coastline, here we consider the estimates for Thiès Sud, and we also scale down the natural growth function by the catches in Thiès Sud relative to total catches by the Senegalese purse seine fleet to focus on this region. The cost function is based on the generalized Gordon-Schaefer harvesting function (Sect. 2) with $\xi = 1$, $\chi = 0.22$, and effort cost function $C(E_{t} ) = \tfrac{1}{2}cE_{t}^{2} .$ We set $c = 160$ (Central African Francs/unit of effort) by choice of measurement units for the catchability coefficient $q$, which we vary in the analysis. Market equilibrium catch is thus $H_{t}^{*} = \left( {\frac{160}{c}{\kern 1pt} \left( {q{\kern 1pt} X_{t}^{0.22} } \right)^{2} } \right)^{{\frac{1}{1 + 0.3}}} = \left( {q{\kern 1pt} X_{t}^{0.22} } \right)^{1.54}$.¹ In the baseline calculation we use $q = 4.65$(1/unit of effort) to obtain the observed annual harvest $H_{t} = 64$ (thousand tons) at the observed biomass $X_{t} = 200$ (thousand tons) (Lancker et al. 2019b, Tables 1 and A5).

Table 1 Specification of empirical model for Senegalese small scale fishery on Sardinella Aurita

Figure 1 shows the resulting consumer and producer surplus for this Senegalese Sardinella fishery for these parameter values.

Fig. 1

Consumer surplus and producer surplus for the Senegalese Sardinella Aurita small-scale fishery, measured in Central African Francs (CFA)

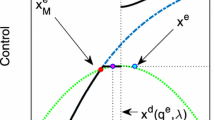
Welfare is the sum of consumer and producer surplus in this fishery, and depends on both harvest and stock size in this search fishery. Welfare can thus be considered through indifference curves in the stock-harvest space. Varying the welfare level, we then obtain an entire set of indifference curves of instantaneous welfare as illustrated in Fig. 2. Note that according to (5), the market (short-run) equilibrium catch is determined by the condition that instantaneous welfare is maximized with respect to $H_{t}$. For any given $X_{t}$, the market equilibrium harvest thus corresponds to the vertical point of a welfare indifference curve. Therefore, the curve showing market equilibrium harvest as a function of fish population size connects the vertical points of the set of welfare indifference curves. Long-run equilibria of the regulated open-access fishery are obtained as the points of intersection between the market equilibrium harvest curve and the natural growth curve.

Fig. 2

Harvest and natural growth for the case of the Senegalese Sardinella Aurita small-scale fishery. The green line shows fish population biomass growth function, the violet line the (current) market equilibrium harvest schedule, the blue and red lines show a set of indifference curves of instantaneous welfare, and the purple line, connecting the vertical points of welfare indifference curves, indicates market equilibrium harvest. The filled circle marks a stable (market and biological) equilibrium, the empty circle an unstable one, and the dashed circle the biological equilibrium that would maximize welfare (zero discount rate, but which is not a market equilibrium in regulated open-access)

Under the given assumptions and the given value of technical efficiency $q$, there are three points of intersection between the curve showing the natural growth function and the harvest locus and hence three long-run equilibria. The biological equilibrium is stable if the slope of the market equilibrium harvest function exceeds the biomass growth function (Eq. 15), and unstable otherwise. Figure 2 shows a stable equilibrium at a high biomass with a filled circle and an unstable one at a low biomass with an empty circle.

The figure also shows the harvest and stock combination that maximizes welfare in biological steady-state equilibrium, determined by the stock size and harvest where a welfare indifference curve and the biomass growth function are tangents to each other. Therefore, this point coincides with the equilibrium stock and harvest that solves the present-value welfare maximization problem with zero discounting. As this allocation is not a myopic exploited fishery market equilibrium, it does not lie on the purple line, but rather below. This shows the well-known issue of resource overuse in open-access.

Discussion and Concluding Remarks

Our key finding is that the effect of more efficient harvesting goes in the same direction for the different components of welfare, and that increased harvesting efficiency has an ambiguous long-term effect on consumer as well as producer surplus, or more generally, on the welfare in the considered fishing community. Both components of welfare increase with harvesting efficiency in the long run equilibrium (where both demand is equal to supply and harvest is equal to natural growth) if the fish stock exceeds the size that would generate the maximum sustainable yield (MSY). In contrast, if the equilibrium fish population is smaller than the MSY stock size, i.e., if there is MSY overfishing, increasing harvesting efficiency reduces welfare. As the equilibrium stock size decreases with harvesting efficiency in regulated open access, it depends on the initial harvesting efficiency whether an increase is welfare-enhancing or detrimental. It is shown that the critical level of harvesting efficiency depends on demand conditions and the market price of harvest, and on the biological productivity of the considered fish stock. MSY as welfare maximizing harvesting is a surprising result as the model includes fishing costs.

The central property of the harvesting technology that leads to this result is the stock-augmenting harvesting efficiency, as formally shown in Appendix 4. This property means that for any increase in harvesting efficiency there is an equivalent increase in the resource stock size that would lead to the same productivity effect, an assumption that is ubiquitous in resource economics. We have focused on biological equilibrium, or steady-state analysis. We show in Appendix 5 how our analysis generalizes to a dynamic setting with discounting. As to be expected, the critical stock size below which an increase in harvesting efficiency reduces welfare is determined by the condition that marginal stock growth equals the discount rate.

Our results have clear policy relevance, especially in situations where fish stocks and resource use are subject to regulations that affect harvesting efficiency, but where no direct individual, or total, catch regulations are in place (e.g. due to prohibitively high transaction costs), and thus the first-best optimal regulation is out of reach. In addition to gear regulations, regulations of harvesting efficiency may include restrictions on harvesting locations, season length, and so forth. Our results imply that whenever the stock is MSY-overfished, a regulation that reduces harvesting efficiency increases welfare. On the other hand, if the current stock size exceeds the one that would produce the MSY, a marginal increase in harvesting efficiency improves welfare. Therefore, any gear regulations that increase harvesting efficiency needs to be considered with caution. Our analysis also has shown that there may be situations in which critical bifurcations exist such that an equilibrium becomes unstable with increasing harvesting efficiency, and the resource stock eventually collapses to a lower and less productive size.

It has also been shown that these main results are very general. Although we have basically considered small-scale fishery, the results hold equally for recreational fisheries and other resources that are exploited under regulated open access conditions. This may include many cases of wildlife hunting, timber and non-timber use forests, or rangelands. In all these cases, a stock-augmenting increase in harvesting efficiency has the described ambiguous welfare effect.

Appendices

Appendix

Model of Regulated Open Access with Many Heterogeneous Fishers

Here we derive the aggregate cost function for the whole fishing community from individual fishers entry-exit decisions in response to profitability of fishing relative to outside opportunities. The model follows Quaas and Requate (2013), allowing for heterogeneous fishing skills and opportunity costs of effort.

Consider a continuum of fishers $i$, where fisher $i$ has fishing skill (idiosyncratic productivity parameter) $\varphi \left( i \right)$. Assume that each fisher is endowed with one unit of effort. If the fisher uses $e_{i} \in [0,1]$ units of effort in fishing, the catch $h_{i}$ of that fisher is $h_{i} = q{\kern 1pt} \varphi \left( i \right)e_{i} {\kern 1pt} X_{t}^{\chi } .$ As in Baland and Francois (2005), each fisher $i$ has the choice between using effort in fishing or in a private project outside the fishery, which would yield a return $\omega \left( i \right)(1 - e_{i} )$. Given these opportunity costs, and a fish price $p$, fisher $i$’s net gain of fishing is:

$$\pi_{i} = p{\kern 1pt} q{\kern 1pt} \varphi \left( i \right){\kern 1pt} e_{i} {\kern 1pt} X_{t}^{\chi } - \omega \left( i \right){\kern 1pt} e_{i} = \left( {p{\kern 1pt} q{\kern 1pt} \varphi \left( i \right){\kern 1pt} X_{t}^{\chi } - \omega \left( i \right)} \right){\kern 1pt} e_{i} .$$

(20)

All individuals with positive net gain will spend the entire effort fishing, all others don’t fish at all. The marginal fisher i.^* is the one where

$$p{\kern 1pt} q{\kern 1pt} \varphi \left( {i_{{}}^{*} } \right){\kern 1pt} X_{t}^{\chi } = \omega \left( {i_{{}}^{*} } \right).$$

(21)

Thus, all fishers with fishing skill higher than $\varphi \left( {i_{{}}^{*} } \right) = \omega \left( {i_{{}}^{*} } \right)/\left( {p{\kern 1pt} q{\kern 1pt} X_{t}^{\chi } } \right)$, and all fishers with opportunity costs of fishing effort lower than $\omega \left( {i_{{}}^{*} } \right) = p{\kern 1pt} q\varphi \left( {i_{{}}^{*} } \right){\kern 1pt} X_{t}^{\chi }$, will go fishing. We use $E_{t}$ to denote the number of active fishers. As they are endowed with one unit of effort each, this is also aggregate effort.

We specifically assume a Pareto distribution of fishing skills, $\phi (i) = \xi {\kern 1pt} i^{\xi - 1}$, as common also in other fields of economics where heterogeneous productivity is considered, such as international trade (Arkolakis et al. 2008, 2012). Thus, aggregate harvest by all active fishers is given by:

$$H_{t} = q{\kern 1pt} \left( {\int_{0}^{{E_{t} }} \varphi \left( i \right){\kern 1pt} {\kern 1pt} di} \right){\kern 1pt} X_{t}^{\chi } = q{\kern 1pt} E_{t}^{\xi } {\kern 1pt} X_{t}^{\chi } ,$$

(22)

which is the generalized Gordon-Schaefer harvest function specified in the main text.

Total harvesting costs are $C_{t} = \int_{0}^{{E_{t} }} \omega (i){\kern 1pt} di.$ Relative to the marginal fisher with skill $\omega \left( {i_{{}}^{*} } \right)$, individuals with lower opportunity costs are fishing and individuals with higher opportunity costs are using their effort outside the fishery. Thus, $\omega^{\prime}\left( {E_{t}^{{}} } \right) > 0$, and we obtain that marginal costs of effort are positive and increasing. Finally, it follows that the zero-profit condition for the marginal fisher, equation (21), is equivalent to condition (5), as:

$$\frac{{dC_{t} }}{{dH_{t} }} = \omega (E_{t} ){\kern 1pt} \frac{{dE_{t} }}{{dH_{t} }} = \frac{{\omega (E_{t} )}}{{\frac{{dH_{t} }}{{dE_{t} }}}} = \frac{{\varpi (E_{t} )}}{{q{\kern 1pt} \xi {\kern 1pt} E_{t}^{\xi - 1} {\kern 1pt} X_{t}^{\chi } }} = \frac{1}{{q{\kern 1pt} X_{t}^{\chi } }}{\kern 1pt} \frac{{\omega (E_{t} )}}{{\varphi (E_{t} )}} = p,$$

(23)

as we have $E_{t} = i_{{}}^{*}$.

Proof of Result 1

We first state some properties of the cost function (2). We get the following derivatives of the cost function (2)

$$C_{q} = - \frac{1}{{\xi {\kern 1pt} q}}{\kern 1pt} \left( {\frac{{H_{t}^{*} }}{{q{\kern 1pt} X_{t}^{\chi } }}} \right)^{{\frac{1}{\xi }}} {\kern 1pt} \hat{C}^{\prime}\left( {\left( {\frac{{H_{t}^{*} }}{{q{\kern 1pt} X_{t}^{\chi } }}} \right)^{{\frac{1}{\xi }}} } \right),$$

(24)

$$C_{{X_{t} }} = - \frac{\chi }{{\xi {\kern 1pt} X_{t} }}{\kern 1pt} \left( {\frac{{H_{t}^{*} }}{{q{\kern 1pt} X_{t}^{\chi } }}} \right)^{{\frac{1}{\xi }}} {\kern 1pt} \hat{C}^{\prime}\left( {\left( {\frac{{H_{t}^{*} }}{{q{\kern 1pt} X_{t}^{\chi } }}} \right)^{{\frac{1}{\xi }}} } \right),$$

(25)

and

$$C_{{H_{t} }} = \frac{1}{{\xi {\kern 1pt} H_{t}^{*} }}{\kern 1pt} \left( {\frac{{H_{t}^{*} }}{{q{\kern 1pt} X_{t}^{\chi } }}} \right)^{{\frac{1}{\xi }}} {\kern 1pt} \hat{C}^{\prime}\left( {\left( {\frac{{H_{t}^{*} }}{{q{\kern 1pt} X_{t}^{\chi } }}} \right)^{{\frac{1}{\xi }}} } \right).$$

(26)

Thus, we can also write $H_{t}^{*} {\kern 1pt} C_{{H_{t} }} = - q{\kern 1pt} C_{q}$, and $\chi {\kern 1pt} H_{t}^{*} {\kern 1pt} C_{{H_{t} }} = - X_{t} {\kern 1pt} C_{{X_{t} }}$. Differentiating the former equation with respect to $H_{t}^{*}$ we get:

$$C_{{H_{t} H_{t} }} = - \frac{q}{{H_{t}^{*} }}{\kern 1pt} C_{{qH_{t} }} + \frac{q}{{\left( {H_{t}^{*} } \right)_{{}}^{2} }}{\kern 1pt} C_{q} \Leftrightarrow H_{t}^{*} {\kern 1pt} C_{{qH_{t} }} - C_{q} = - \frac{{\left( {H_{t}^{*} } \right)_{{}}^{2} }}{q}{\kern 1pt} C_{{H_{t} H_{t} }} .$$

(27)

Moreover, multiplying $H_{t}^{*} {\kern 1pt} C_{{H_{t} }} = - q{\kern 1pt} C_{q}$ with $C_{{H_{t} H_{t} }}$ and rearranging a bit, we get

$$C_{{H_{t} H_{t} }} {\kern 1pt} C_{q} = - C_{{H_{t} H_{t} }} {\kern 1pt} \frac{{H_{t}^{*} }}{q}{\kern 1pt} C_{{H_{t} }} .$$

(28)

Differentiating Eq. (11) in the main text with respect to $q$, using the envelope theorem and doing small rearrangements, we find (omitting arguments):

$$\frac{{d\pi_{t}^{*} }}{dq} = C_{{H_{t} H_{t} }}^{{}} {\kern 1pt} H_{t}^{*} {\kern 1pt} \frac{{dH_{t}^{*} }}{dq} + C_{{H_{t} {\kern 1pt} q}}^{{}} {\kern 1pt} H_{t}^{*} - C_{q}^{{}}$$

(29)

$$\mathop = \limits^{{(8)}} \frac{{C_{{H_{t} H_{t} }}^{{}} {\kern 1pt} H_{t}^{*} {\kern 1pt} C_{{H_{t} {\kern 1pt} q}}^{{}} }}{{P^{\prime}(H_{t}^{*} ) - C_{{H_{t} H_{t} }}^{{}} }} + C_{{H_{t} {\kern 1pt} q}}^{{}} {\kern 1pt} H_{t}^{*} - C_{q}^{{}} = \frac{{P^{\prime}(H_{t}^{*} ){\kern 1pt} \left( {H_{t}^{*} {\kern 1pt} C_{{H_{t} {\kern 1pt} q}}^{{}} - C_{q}^{{}} } \right) + C_{{H_{t} H_{t} }}^{{}} C_{q}^{{}} }}{{P^{\prime}(H_{t}^{*} ) - C_{{H_{t} H_{t} }}^{{}} }}$$

(30)

$$\mathop = \limits^{(27)} \frac{{P^{\prime}(H_{t}^{*} ){\kern 1pt} \frac{{\left( {H_{t}^{*} } \right)_{{}}^{2} }}{q}{\kern 1pt} C_{{H_{t} H_{t} }} - C_{{H_{t} H_{t} }} {\kern 1pt} \frac{{H_{t}^{*} }}{q}{\kern 1pt} C_{{H_{t} }} }}{{P^{\prime}(H_{t}^{*} ) - C_{{H_{t} H_{t} }} }}$$

(31)

$$\mathop = \limits^{(28)} \frac{{C_{{H_{t} H_{t} }} {\kern 1pt} C_{q} }}{{P^{\prime}(H_{t}^{*} ) - C_{{H_{t} H_{t} }} }}\left( {1 - \left( { - \frac{{H_{t}^{*} {\kern 1pt} P^{\prime}(H_{t}^{*} )}}{{P(H_{t}^{*} )}}} \right)} \right){\kern 1pt} .$$

(32)

The result that consumer surplus increases with $q$ directly follows from the assumption of a downward sloping inverse demand function according to which consumer surplus increases with and the result that catch increases with $q$ as stated in Eq. (8).

Proof of Result 2

We have already proven the result for consumer surplus. Here we show that we obtain the same for producer surplus. Using Eqs. (16) in (18) from the mai text, we find:

$$\frac{{d\pi^{*} }}{dq} = \frac{1}{{(F^{\prime}(X^{*} ) - H_{X}^{*} )}}{\kern 1pt} \left( {\left( {C_{HX}^{{}} {\kern 1pt} H^{*} + C_{HH}^{{}} {\kern 1pt} H^{*} {\kern 1pt} H_{X}^{*} - C_{X}^{{}} } \right){\kern 1pt} H_{q}^{*} + \left( {C_{HH}^{{}} {\kern 1pt} H^{*} {\kern 1pt} H_{q}^{*} + C_{Hq}^{{}} {\kern 1pt} H^{*} - C_{q}^{{}} } \right){\kern 1pt} \left( {F^{\prime}(X^{*} ) - H_{X}^{*} } \right)} \right)$$

(33)

Differentiating condition (5), which determines the market equilibrium harvest, with respect to $X$ and $q$, we obtain:

$$\left( {P^{\prime}(H^{*} ) - C_{HH}^{{}} } \right){\kern 1pt} H_{X}^{*} = C_{HX}^{{}}$$

and

$$\left( {P^{\prime}(H^{*} ) - C_{HH}^{{}} } \right){\kern 1pt} H_{q}^{*} = C_{Hq}^{{}} .$$

Combining these two conditions, we have $C_{HX}^{{}} {\kern 1pt} H_{q}^{*} = C_{Hq}^{{}} {\kern 1pt} H_{X}^{*}$. Note that the cost function (2) implies $X{\kern 1pt} C_{X}^{{}} = \chi q{\kern 1pt} C_{q}^{{}}$ and $X{\kern 1pt} C_{HX}^{{}} = \chi q{\kern 1pt} C_{Hq}^{{}}$ (see Appendix 2). We thus also have $C_{X}^{{}} {\kern 1pt} H_{q}^{*} = C_{q}^{{}} {\kern 1pt} H_{X}^{*}$. Using these results, Eq. (C.1) simplifies to:

$$\frac{{d\pi^{*} }}{dq} = \frac{{F^{\prime}(X^{*} )}}{{F^{\prime}(X^{*} ) - H_{X}^{*} }}{\kern 1pt} \left( {C_{HH}^{{}} {\kern 1pt} H^{*} {\kern 1pt} H_{q}^{*} + C_{Hq}^{{}} {\kern 1pt} H^{*} - C_{q}^{{}} } \right).$$

(34)

The term in brackets is the short-term effect of more efficient fishing technology on profit, as given in Eq. (20). Under the assumptions stated in Result 1, this term is positive. Thus, the sign of $d\pi^{*} /dq$ depends on the sign of the first factor. For a stable steady state, the denominator is negative. Thus, $d\pi^{*} /dq > 0$ if and only if $F^{\prime}(X^{*} ) < 0$, which is the case if and only if $X^{*} > X^{{{\text{m}}sy}}$.

Generalized Model of Welfare from Myopic Explotation and Regulated Open-Access Fishery

To obtain some indications of how robust the above results are, we will look at a very general model of harvesting and welfare derived from the fishery. In general, aggregate instantaneous welfare derived from the fishery is described by a utility function:

$$U_{t} = U(H_{t} ,X_{t} ,q),$$

(35)

which is increasing in harvest, $U_{{H_{t} }} > 0$, nondecreasing in stock size, $U_{{X_{t} }} \ge 0$, and increasing in efficiency, $U_{q} > 0$. We further assume that marginal utility of catch weakly increases with stock size, $U_{{H_{t} X_{t} }} \ge 0$, and increases with efficiency, $U_{{H_{t} q}} > 0$. As above, the assumption $U_{q} > 0$ implies that the short-run effect of increasing efficiency—while keeping stock size constant—is positive. The instantaneous welfare function (35) can capture net economic surplus—the sum of consumer and producer surplus. The general formulation (35), applied to a commercial fishery, also allows to take into account that consumers’ willingness to pay for fish may include concerns for sustainability, for example in a way that the demand for fish positively depends on stock size.²

The condition determining market equilibrium harvest in myopic exploitation is then simply:

$$U_{H} (H_{t}^{*} ,X_{t} ,q) = 0.$$

(36)

We assume that the net utility is separable as follows:

$$U(H_{t}^{{}} ,X_{t}^{{}} ,q) = \hat{U}(H_{t}^{{}} ,y(X_{t}^{{}} ,q))$$

(Assumption 1)

Harvesting profit with a Gordon-Schaefer harvest function is a special case, where $y\left( {X_{t}^{{}} ,q} \right)$ can be interpreted as the catch per unit of effort. Formally, given the separability of utility, the condition (36) for harvest under restricted open access fixes the relationship between harvest and $y(X,q).$ Thus, utility can be expressed as a function of harvest only.

More intuitively, Assumption 1 imposes a condition how harvesting efficiency affects instantaneous welfare; namely in a way such that an equivalent effect on welfare could be obtained by keeping harvesting efficiency constant, but changing the resource stock size in a specific way. This shows that Assumption 1 is related to the idea of labor-augmenting technical change in growth theory (Robinson 1938) where improving technology has the same effect on output as an expansion of labor force. Thus, we can interpret Assumption 1 as the property of ‘stock-augmenting’ harvesting efficiency.

Differentiating (36) with respect to $X$ and $q$ gives, adopting the assumption of stock-augmenting harvesting efficiency:

$$U_{HH} {\kern 1pt} H_{X}^{*} = - U_{HX} = - \hat{U}_{Hy} {\kern 1pt} y_{X}$$

(37)

and

$$U_{HH} {\kern 1pt} H_{q}^{*} = - U_{Hq} = - \hat{U}_{Hy} {\kern 1pt} y_{q} ,$$

(38)

respectively. Under Assumption 1, it follows that $U_{X} {\kern 1pt} H_{q}^{*} = U_{q} {\kern 1pt} H_{X}^{*}$, where $U_{x} = \hat{U}_{y} {\kern 1pt} y_{X}$ and $U_{q} = \hat{U}_{y} {\kern 1pt} y_{q}$. From the assumptions on $U$ it also follows that $H_{q}^{*} > 0$.

Differentiating the biological equilibrium condition $F(X^{*} ) = H^{*}$ with respect to q gives:

$$\left( {F^{\prime} - H_{X}^{*} } \right){\kern 1pt} X_{q}^{*} = H_{q}^{*} .$$

(39)

As stability requires $F^{\prime} - H_{X}^{*} < 0$ (Eq. 15 main text), this equation implies, $X_{q}^{*} < 0$. Now consider a steady state in which changes in $q$ lead to changes in $H^{*}$ giving repercussions on the steady state stock size $X^{*}$. Taking these feedbacks into account, we obtain the following long-term relationship between $U$ and q:

$$\frac{{dU^{*} }}{dq} = U_{q} + U_{X} {\kern 1pt} X_{q}^{*} = U_{q} + U_{X} {\kern 1pt} H_{q}^{*} {\kern 1pt} \frac{1}{{F^{\prime} - H_{X}^{*} }} = U_{q} {\kern 1pt} \frac{{F^{\prime}}}{{F^{\prime} - H_{X}^{*} }}.$$

(40)

The first equality holds by virtue of the envelope theorem while the second equality uses Eq. (39) that states how steady state stock size reacts to changes in $q$ via changes in $H$. In the last step we have used the Assumption 1 of stock-augmenting harvesting efficiency, which implies $U_{X} {\kern 1pt} H_{q}^{*} = U_{q} {\kern 1pt} H_{X}^{*}$, as shown above. Thus, we can conclude that our main results hold for this generalized model of welfare as well. This is summarized as follows.

Theorem 1

The long-run equilibrium stock size is above the stock that generates the maximum sustainable yield if and only if the long-run equilibrium welfare increases with harvesting efficiency. Formally,

$${\text{sign}}\left( {X^{*} - X^{{{\text{msy}}}} } \right) = {\text{sign}}\left( {\frac{{dU^{*} }}{dq}} \right).$$

(41)

To illustrate this result a bit further, consider the Sengalesian case study again, but for the sake of the argument we assume a stock elasticity $\chi = 0.65$(Sect. 4), such that the market equilibrium harvest is a linear function of stock size.

Fig. 3

Effects of increasing harvesting efficiency (from the left to the right), $q_{0} < q_{1} < q_{2}$. Stock-augmenting increase in harvesting efficiency compresses the welfare indifference curves to the left. The three blue indifference curves correspond to the same welfare level in all three graphs. The red indifference curve corresponds to different welfare levels, as the maximum attainable (long-run) equilibrium welfare level is increasing in harvesting efficiency

Figure 3 illustrates the effect of increasing harvesting efficiency, $q_{0} < q_{1} < q_{2}$. Stock-augmenting increase in harvesting efficiency compresses the welfare indifference curves to the left, i.e. at a given level of harvest welfare is the same, no matter what the level of harvesting efficiency is. Thus only the resulting harvest level affects the equilibrium level of welfare. For the increase in harvesting efficiency from $q_{0}$ to $q_{1}$, equilibrium harvest increases and thus the new equilibrium is reached at a higher welfare level. With the further increase from $q_{1}$ to $q_{2}$ the new equilibrium attains a lower welfare level.

Extension to Dynamic Setting

Here we extend the analysis to a dynamic setting by considering the problem to determine the time path of $q$ that maximizes the present value of welfare, at a discount rate $\rho$, subject to the biological dynamics and the condition for restricted open-access market equilibrium. Formally, the problem reads:

$$\mathop {\max }\limits_{{q_{t} }} \int_{0}^{\infty } e^{{ - \rho {\kern 1pt} t}} {\kern 1pt} U(H^{*} (X_{t} ,q_{t} ),X_{t} ,q_{t} ){\kern 1pt} dt$$

(42)

subject to Eq. (13) (main text) with $X_{0}$ given and where $H^{*} (X_{t} ,q_{t} )$ is implictly defined by the restricted open-access condition $U_{{H_{t} }} (H^{*} (X_{t} ,q_{t} ),X_{t} ,q_{t} ) = 0$.

The current-value Hamiltonian for this problem is

$${\mathbb{H}} = U(H^{*} (X_{t} ,q_{t} ),X_{t} ,q_{t} ) + \mu_{t} {\kern 1pt} \left( {F(X_{t} ) - H^{*} (X_{t} ,q_{t} )} \right)$$

(43)

The first-order conditions for the optimal time path of $q_{t}$ are, using $U_{{H_{t} }} = 0$,

$$\frac{{\partial {\mathbb{H}}}}{{\partial q_{t} }} = U_{{q_{t} }} (H^{*} (X_{t} ,q_{t} ),X_{t} ,q_{t} ) - \mu_{t} {\kern 1pt} H_{{q_{t} }}^{*} (X_{t} ,q_{t} ) = 0$$

(44)

and

$$\frac{{\partial {\mathbb{H}}}}{{\partial X_{t} }} = U_{{X_{t} }} (H^{*} (X_{t} ,q_{t} ),X_{t} ,q_{t} ) + \mu_{t} {\kern 1pt} \left( {F^{\prime}(X_{t} ) - H_{{X_{t} }}^{*} (X_{t} ,q_{t} )} \right) = \rho {\kern 1pt} \mu_{t} - \dot{\mu }_{t}$$

(45)

Equation (44) states that the immediate marginal benefit of improved harvesting efficiency should equal the marginal opportunity costs in terms of reducing the stock. Condition (45) is closely related to the fundamental equation of resource economics (Clark 1990), but here it includes the effect of the stock size on the harvest quantity in regulated open access.

Given Assumption 1, it follows from Eq. (44) that $U_{{X_{t} }} (H^{*} (X_{t} ,q_{t} ),X_{t} ,q_{t} ) - \mu_{t} {\kern 1pt} H_{{X_{t} }}^{*} (X_{t} ,q_{t} ) = 0$. Thus, the optimality conditions simplify to:

$$U_{{q_{t} }} (H^{*} (X_{t} ,q_{t}^{*} ),X_{t} ,q_{t}^{*} ) = \mu_{t} {\kern 1pt} H_{{q_{t} }}^{*} (X_{t} ,q_{t}^{*} )$$

(46)

and

$$F^{\prime}(X_{t} ) - \rho = - \frac{{\dot{\mu }_{t} }}{{\mu_{t} }}.$$

(47)

These equations define, for any given stock size $X_{t}^{{}}$, a level $q_{t}^{*} = q^{*} (X_{t} )$ of harvesting efficiency that maximizes the present value of welfare. Figure 4 shows the numerical result for the case of the Senegalese small-scale fishery on Sarinella Aurita detailed in Sect. 4, for a zero discount rate $\rho = 0$. We use AMPL with Knitro to numerically solve the dynamic optimization problem; the code is available from the authors on request. In line with intuition, the figure shows that larger the current stock size, the larger is the current harvesting efficiency that maximizes the present value of welfare. The steady state equilibrium stock size and harvesting efficiency that optimize welfare is indicated by the intersection of the black vertical and horizontal lines.

The result corresponding to Theorem 1 is the following: Whenever the actual harvesting efficiency is above (below) $q^{*} (X_{t} )$, an instantaneous increase of harvesting efficiency decreases (increases) the present value of welfare.

Fig. 4

The level of harvesting efficiency that maximizes the present value of welfare as a function of the current stock size for the Senegalese Sardinella Aurita small-scale fishery