Stranded Assets: How Policy Uncertainty affects Capital, Growth, and the Environment

Abstract

The paper considers stochastic environmental policy and its effects on the environment, portfolio composition, and economic growth. Capital accumulation causes pollution which is reduced by private green services and public abatement. The government subsidizes green services and taxes dirty capital albeit at a rate which may become random, causing unexpected capital write-offs. Tax jumps depend on natural degradation and environmental activism. We derive how uncertainty and political activism affect the risk premia for investors. We analyze the incentives for firms to increase the greenness of production in order to reduce political uncertainty. Stochastic taxation is shown to act as a substitute for green subsidies when uncertainty decreases in the ratio of green services to capital and agents use their green activities strategically. Tax uncertainty may trigger precautionary savings, causing additional growth and enhanced environmental deterioration.

1 Introduction

1.1 Environmental Policy Uncertainty

It is common practice in environmental economics to derive optimal policies from a theoretical framework and to advise an implementation by the government without a delay. However, it is evident that in reality environmental policy works significantly different. Governments depend on the voters and are subject to political lobbying; as a consequence, they are often reluctant to implement new policy measures. This especially applies when a structural change of the economy is required as in the case of climate policy, which involves adjustments in consumption and production patterns affecting central activities such as transportation, heating, and manufacturing. Nevertheless, recent experience clearly shows that policies may alter unexpectedly when natural catastrophes, scientific reports, or legal decisions affect public opinion or pave the ground for political action. Prominent examples are the decisions on a nuclear phaseout in Germany and Switzerland after the nuclear accident in Fukushima or the partial ban of diesel vehicles in European cities like Copenhagen, Berlin, and Paris to combat local air pollution which in the German case was the result of an unexpected court decision.¹ To mitigate climate change it is uncertain yet very likely that many countries will implement more policies or make the existing ones more stringent in the future. Reasons for this are the country commitments under the Paris Climate Agreement but also the expected intensification of climate shocks and a public process of further evolving social norms and of possible stigmatization of fossil fuels. Summarizing current development in environmental policy, two characteristics of political uncertainty stand out. First, it is the implementation date of policies which is often impossible to predict for market participants. Second, the intensity of the policies appears to follow specific patterns. But these are not necessarily based on general welfare considerations but rather on the imperative of political economy. According to recent investigations, all major German car manufacturers colluded to prevent effective exhaust gas cleaning technology in petrol cars. Instead, they agreed on a political lobbying strategy to weaken and delay stronger limits for the emission of particles in gasoline engines as long as possible.² Norway is heavily supporting electric mobility and taxing traditional cars which is politically well accepted as the share of green technology in the economy is already large. These two elements of uncertainty will be used to determine the intensity of environmental policy we will introduce in this paper.

Uncertain policies pose a special challenge for decisions on long-run investments, the basic driver of economic growth. If asset conversion is constrained by irreversibilities or high adjustment costs, assets may lose part of their market value or become completely worthless after policy implementation (McKibben 2011), which affects household wealth as well as the economic growth rate. It is said that assets become ”stranded” when suffering from unanticipated or premature write-offs, downward revaluations, or conversions to liabilities, see International Energy Agency (IEA 2013, p.134) and Generation Foundation (2013, p.26).³ Policy risks are often not fully accounted for in asset allocation which has resulted in a high exposure of portfolios to carbon-intensive activities. From the perspective of production, capital which is used jointly with fossil fuels as an input to production is potentially affected by environmental policy. Hence, in the non-oil countries, most of the stranded assets belong to companies that use ”dirty” machines, i.e. machinery running with fossils fuels. Environmental policy usually does not involve a complete capital loss but rather a lower capital return for capital investments. This is what we will incorporate in our model prominently featuring a dirty capital input and its impact on economic growth. That capital may become stranded in a market economy may also be related to the effect of ‘creative destruction’ (Schumpeter 1942). However, the Schumpeterian creation and destruction of values is caused by innovations and technical breakthroughs which are, by their nature, not fully predictable yet crucial for development. Conversely, environmental policy is uncertain due to the complex conditions of the political process framed by political majorities and lobbying.⁴

As a novel contribution to the literature, the present paper develops a basic endogenous growth model with clean and dirty inputs and pollution abatement in which policy formation departs radically from existing literature. Policy is not optimal according to standard welfare criteria but occurs in shocks which are random. The size of the shocks is affected by the state of the natural environment, because we posit that with larger environmental damages voters are willing to accept higher stringency of environmental policy. As motivated by the recent examples of Germany and Norway, shock size will also depend on the shares of dirty and clean activities, reflecting the distribution of political power; this may become effective through coalition building and lobbyism of firms and consumers. As the focus of the paper is on the important effects of random and suboptimal policies we do not assume a rationally optimizing government but rather rely on a core tax equation reflecting policy uncertainty. With this approach we derive the different effects of policy uncertainty on environmental quality and economic growth; we show that the impact depends crucially on risk aversion and may give rise to strategic behavior.

To underline the core contribution of the present paper and to distinguish it from existing environmental economics literature, we highlight some empirical observations supporting our main policy mechanism. We argue that an environmental tax which is implemented once and forever and whose value is close or equal to the optimal level is basically nowhere observed in the world. What is a normal case and highly relevant in our view is that private investors are confronted with a randomness in terms of time of policy implementation and a policy stringency that depends on political conditions rather than on welfare economics. It has been found that in general tax policy provides a ”key source of uncertainty” about the costs of capital for firms in the US and the UK (Hassett and Metcalf 1999, p. 372). In the few countries that have actually implemented carbon taxes this has exactly been the experience: in Sweden carbon tax rates have increased several times in the past and in Switzerland the jumps have frequently occurred for taxation of heating oil. Randomness and jump patterns are also documented by other examples addressing externality problems such as the tobacco tax (NCI and WHO 2016). Smoking is an especially illuminating case because we have a much larger country sample and longer time series than for carbon taxes. In all major countries, cigarette tax rates have in no way been on an optimal level from the beginning but have rather jumped upward many times in the past; tax rates have increased at irregular dates and the size of the tax jumps has varied widely. Tax jumps can be attributed to a variety of reasons, such as increasing government budget needs or public awareness of the health problems caused by smoking. However, from our perspective, it is important to note that the largest tax jumps were made after smokers became a minority, while nonsmoking became a widely accepted social norm; smokers and nonsmokers are also voters at the same time. In the same way, we believe it is not accidental that the two countries with the highest market shares of electric cars, Norway and the Netherlands, were the first to seriously consider a ban of internal combustion engine cars. More generally, when production technology has become sufficiently environmentally friendly, households rely less on dirty capital, and thus can be expected to be more favorably disposed to environmental policies. Moreover, emission levels, catastrophic environmental events, and the awareness of pollution problems are important promoters of (sudden) environmental policy reforms; the decision on a nuclear phaseout in Germany and Switzerland followed right after the Fukushima accident. One can foresee that stringency of future climate policy will be affected by the severity of climate events which are contingent on the degradation of the atmosphere.

1.2 Contribution to the Literature

The paper topic relates to different strands of literature dealing with environment, uncertainty, finance, and endogenous growth. The effects of environmental shocks on the economy and on optimal policy were first studied formally by Tsur and Zemel (1996, 1998, 2008) with a special focus on endogenous hazard rates. Deriving optimal carbon policies, de Zeeuw and Zemel (2012) apply different hazard functions to various types of environmental risks. Featuring endogenous growth like in the present paper and including different capital stocks, Ikefuji and Horii (2012) assume that climate shocks are idiosyncratic which allows agents to diversify their risk.⁵ We will refer to this literature in terms of the methodology but will apply the techniques dealing with uncertainty not to the state of the environment but to policy, which opens up a completely new perspective on uncertain decisions in a market economy. To study tax rate changes, the Poisson rather than the Wiener process is the appropriate mechanism to represent uncertain shocks.⁶

Political uncertainty has been largely neglected in general and environmental economics literature so far. An early exception is the contribution of Xepapadeas (2001) who studies the effects of uncertainty in environmental policy in combination with uncertainty in prices and technology.⁷ More recently, referring to rare macroeconomic disasters, Barro (2015) has shown that optimal environmental investments decrease with uncertainty about policy effectiveness, pointing at the importance of risks stemming not only from the environment but also from environmental policy. Pommeret and Schubert (2017) introduce policy uncertainty in an emission permit system; their result that abatement and clean technology activities can grow with uncertainty appears in our stochastic endogenous growth approach only under certain parameter conditions. With the analysis of stranded assets in a growth context the paper is related to Rozenberg et al. (2014) who introduce two types of capital to analyze the transition to clean capital when polluting investment is irreversible, which imposes a transition cost to the economy. Their paper shows that avoiding stranded assets by appropriate policy comes at the cost of lower efficiency in emission reduction and higher transition cost. We differ from their approach by using a model of endogenous growth and by introducing a random process generating policy shocks. Kalkuhl et al. (2018) study how irreversible investments and imperfect commitment by regulators affect climate policy outcomes. Stranded assets result from the government strategically deviating from the previously announced policy. Their paper uses a partial equilibrium approach and assumes that the government maximizes its objective function.⁸ We take a different route by analyzing a general equilibrium framework and introducing a government that is driven by pollution and greenness of the economy but not fully predictable for the investors. We add to the literature by studying stranded assets which are associated with capital investments under the conditions of a policy that deviates from first best.⁹ Our extension of traditional economic tax analysis also relates to different strands of recent tax literature. It has been shown how the assumption of behavioral agents with biases such as misperceptions and internalities leads to modifications of optimal tax formulas, see Farhi and Gabaix (2020). Fleurbaey and Maniquet (2018) provide a survey on optimal taxation when traditional welfare functions are supplemented by fairness principles such as desert or responsibility. In the present paper, taxes deviate from the social optimum because they are subject to shocks which are driven by the state of the environment and the state of production inducing strategic political action.

Building on the insights of the cited literature we develop a model with endogenous economic growth, environmental pollution, and stochastic tax policies. In our setup, environmental policy is neither optimal nor predictable but comes with significant shocks. The government is not an autonomous institution acting like a benevolent dictator but rather a decision unit reacting to specific developments yet in a not fully-predictable manner. Unexpected policy changes need not be inconsistent with optimal government decisions when new information arrives that suggests a sudden change in policy;¹⁰ this case is included in the analysis below. We are well aware that compared to the standard procedures this is a novel and very different approach. We highlight that nothing has to change in our fundamental economic position that appropriately designed policies are suitable to restore the social optimum with environmental externalities. But as governments are often not willing and/or not able to directly implement such policies, we posit that political reality is probably better characterized by a process in which pending issues like climate change are debated for a period of time while the implementation of concrete policy measures happens suddenly and unexpectedly. Given the evidence and the importance of the topic it is quite surprising that the literature has not covered the issue of uncertain environmental policy so far. The present paper aims to fill this gap.

In our model, random tax policy is supplemented by subsidies to green activities and by public and private abatement activities. We study how uncertain environmental policy interacts with optimal subsidies and private green services. We believe that private activities may play an important part in mitigation but that, under realistic conditions, agents have suboptimally low incentives to undertake these efforts. We also derive the optimal portfolio choices in the presence of policy uncertainty and the effects of the tax jumps on economic growth. After a tax jump, the capital return is reduced which devaluates the capital stock. For the agents, the shocks to capital return come unexpectedly which entails the form of stranded assets we consider in our model.

Referring to the visible public campaigns and the big impact of lobbies in environmental policy, we explicitly consider the possibility of coordinated action with the aim to affect the policy measures. Accordingly, we analyze an equilibrium in which producer or consumer lobbies are able to implement common action and compare it to the case with purely atomistic agents. As a first major result, we characterise the portfolio of investors in the two types of equilibria and show how the investments in polluting capital may be used strategically as an insurance against major tax increases. Our main results with respect to environmental policy reveal that, in the absence of optimal subsidies and taxes, a social optimum can also be achieved with stochastic taxation, provided that actors use their efforts in green activities in a strategic manner. Moreover, we show under which conditions firms will increase the greenness of production strategically in order to reduce policy uncertainty. Specifically, we derive that stochastic taxation serves as a substitute for deterministic green services subsidies, if uncertainty decreases in the ratio of green services to capital. Finally, we derive that tax uncertainty triggers precautionary savings, causing additional growth and enhanced environmental deterioration, if relative risk aversion is sufficiently large. We believe that our results are useful for a positive analysis. Normative conclusions on how to exploit the derived outcome in terms of actual policy or policy design are more difficult. One of the results is that raising policy uncertainty can push the economy into a greener state or onto a higher growth trajectory, which may be evaluated positively under some conditions. However, creating unnecessary risks is not a good proposal. We think a fair normative conclusion is that the existence of policy uncertainty, which is inevitable to a certain degree, does not prevent us from achieving our enviromental targets in an efficient manner. The paper explains the mechanics of the argument and provides more detailed results in the different sections.

The remainder of the paper is organized as follows. Section 2 develops the model. Section 3 develops the dynamic growth path with stochastic capital taxation. In Sects. 4 and 5 we analyze short and long-run effects of uncertain taxation. Section 6 concludes.

2 Modelling Framework

Our analytical approach encompasses several building blocks. We start from including capital and endogenous capital investments into the production process of the economy. Physical capital investments are crucial for the portfolio composition and for determining economic growth but are, at the same time, harming the environment by raising emissions. We posit that environmental externalities are taxed by the government albeit at a non-deterministic rate. As a consequence, investors aim to anticipate the shocks by a change in investment behavior; however, they may also be subject to unexpected capital losses. Policy does not solely rely on taxes but is broader, including public abatement activities and subsidies to private abatement efforts. In our model, the private sector devotes resources to build a productive input reducing emissions which we label ”green services.” We consider household-producers which have access to the production technology and decide on consumption and investment as well as on green services expenditures. Given our assumption of non-altruistic behavior, private efforts are strictly positive when they are associated with a private return. We ensure private clean activity by assuming that green services are an input to final goods production which substitutes for dirty capital.

Capital taxation has a deterministic and a stochastic component. Tax policy is complemented by public abatement and subsidies to green services. Finally, public emission mitigation is supplemented by spillovers from private provision of green services. Equipped with this framework we analyze portfolio decisions, policy design, and economic growth in the following.

2.1 Production and Pollution

Output Y is produced by dirty capital stock K and green services G according to

$$\begin{aligned} Y_{t}=F(K_{t},G_{t})\equiv AK_{t}^{\alpha }G_{t}^{1-\alpha } \end{aligned}$$

(1)

where t is the time index; $A>0$ and $0<\alpha <1.$ The use of capital causes environmental degradation, i.e. emissions E grow proportional to K with a pollution intensity factor $\phi$. The second input labeled G is green i.e it does not pollute the natural environment. For simplicity, it is produced from output at constant marginal costs which we normalize to unity.¹¹ Like capital, services G are provided by the private sector consisting of an infinite number of household-producers who earn income by renting capital and selling services to the output goods market. The public sector reduces emissions by spending on abatement, H, i.e. it does not harm but improve the natural environment. To highlight the parallel role of the private sector for environmental quality and to show the interactions with public activities we explore the case of green services reducing emissions via positive spillovers.¹²

The level of emissions, E, is then increased by physical capital and reduced by public abatement expenditures and green services, each term multiplied by the associated intensity, so that¹³

$$\begin{aligned} E_{t}=\phi {K_{t}}-\theta {H_{t}}-\psi {G_{t}}\qquad \text {with }\phi ,\theta ,\psi>0,\quad \theta >\phi ,\psi . \end{aligned}$$

(2)

$\phi$ denotes the pollution intensity of physical capital, $\theta$ describes the efficacy of abatement activity, and $\psi$ the efficacy of green services, respectively. In order to analyse ongoing growth, we consider a production technology with constant returns to the accumulable factor, physical capital. Consequently on the steady state growth path physical capital is proportional to output and consumption. Hence the outcomes are invariant to the assumed source generating pollution. On the whole the results would remain unchanged with pollution caused by consumption or production.

2.2 Households

Instantaneous utility depends on consumption and emissions as given by

$$\begin{aligned} U(C_t,E_t) = \frac{(C_t E_t^{-\beta })^{1-\sigma }}{1-\sigma } \end{aligned}$$

(3)

where $0<\beta <1$ determines disutility out of pollution, $1/\sigma >0$ denotes the intertemporal elasticity of substitution. We assume intertemporal utility to be additively separable in time, with $\rho >0$ denoting the constant rate of time preference. In the presence of uncertainty, we consider expected utility maximization according to

$$\begin{aligned} E_{0}\int _{0}^{\infty }\frac{(CE^{-\beta })^{1-\sigma }}{1-\sigma }e^{-\rho t}dt \end{aligned}$$

(4)

where $\sigma > 0$ can be interpreted as the constant degree of relative risk aversion.

Recall that emissions are determined by the aggregate levels of physical capital stock, abatement and green services. With a continuum of households, the impact of individual decisions on these aggregate variables vanishes, hence individuals consider emissions to be exogenous to their decisions.

2.3 Government

Due to the negative environmental externalities of physical capital accumulation the government imposes a tax on capital. Similar to the existing literature we use a deterministic tax with rate $\tau$ but, in addition, thoroughly study the case when the government changes the tax rate in a stochastic manner.¹⁴ Notably, the tax levied on capital follows a Poisson process according to

$$\begin{aligned} dT_{t}=K_{t}(\tau dt+\gamma _{t}dq). \end{aligned}$$

(5)

The Poisson process is denoted by $\gamma _{t}$ indicating the change in the tax rate at time t driven by the stochastic process q with an increment dq and the arrival rate $\lambda$. It reflects the unanticipated changes in taxation due to environmental and/or political reasons.¹⁵ The size of the tax jumps is influenced by the greenness of the economy and the state of environmental degradation, both explained in detail in the following subsection. Note that, although the production technology is riskless as given in (1), net return from production becomes uncertain as soon as taxation follows a stochastic process, so that

$$\begin{aligned} Y_{t}dt-dT_{t}=(Y_{t}-\tau K_{t})dt-\gamma _{t}K_{t}dq. \end{aligned}$$

(6)

To internalize the positive environmental benefits of green private services the government may apply a deterministic subsidy rate s for service expenditures. Subsidies, sG, as well as public abatement spendings, H, are financed by the revenues from deterministic capital taxation so that deterministic and stochastic policy effects can clearly be distinguished.

Given our stochastic policy framework, we do not explicitly require the government’s budget to be balanced at every time increment. We highlight the non-optimal aspects of policy making and this includes a suboptimal budgeting in our view. Formally, we could ensure a balanced budget by assuming lump-sum transfers between households and governments, which would not affect any of the results. Moreover, below we will introduce a safe asset to fully exploit the effects of stranded assets; then, the government can issue bonds at the riskless rate at any time, which again would not change our analysis. For the sake of brevity, we do not specify the public budget further in our model.

2.4 Stochastic Capital Taxation

Random tax shocks can be a major cause of asset stranding. In our model, we add the stochastic tax rate $\gamma$ to deterministic capital taxation at rate $\tau$. We assume that the time of arrival of tax shocks is random, so that investors are indeed caught by surprise by policy changes. To specify the size of the jump, we distinguish between a constant term $\bar{\gamma },$ which reflects general uncertainty about regulation, and two structural terms. In fact, as extensively discussed and motivated by empirical observations in Sect. 1, the size of the tax jumps, $\gamma _{t},$ depends on specific conditions. First, we assume that it depends positively on the green service ratio, G/K, which reflects the relative importance and associated political power of green and dirty technology in the economy. Second, we posit that it is affected by the state of environmental degradation that causes policy urgency, which we capture by the ratio of emissions E to green services G,  E/G . Hence, the change in taxation is given by

$$\begin{aligned} \gamma _{t}=\bar{\gamma }+\eta \left( \frac{G_{t}}{K_{t}}\right) ^{\chi }+\varepsilon \left( \frac{E_{t}}{G_{t}}\right) ^{\xi } \end{aligned}$$

(7)

where $0<\chi ,\xi <1$ and $\eta ,\varepsilon >0$.¹⁶

With respect to the individual impact on stochastic taxation, we consider two alternative model variants for the green service ratio. In a first variant, we assume that agents act in isolation i.e. they consider aggregate green services and aggregate capital stock as exogenous that is independent of their individual decisions. Then, the tax shocks depend purely on aggregate macroeconomic conditions, which cannot be influenced by individual action. We label this case the ”fragmented equilibrium” (short: FE). The assumption of atomistic agents without individual impact is widely used in economics. However, the broad waves of recent protests for environmental policy, the evidence of political lobbying against policies, and the documented collusion of car and other manufacturers suggest that cooperation needs to be considered in the model as well. Hence, as a second variant, we study the case where agents have the power and willingness to cooperate. Specifically, we assume they use the green service ratio as a strategic device to frame the political process, which we will label the ”activist equilibrium” (AE). The scenario reflects producer or consumer lobbies encouraging and implementing common action. Keeping more dirty capital may be effective to moderate environmental policy, while public campaigns pushing for more green services would raise political support for higher pollution taxes, see Eq. (7). Conversely, a movement aiming at a reduced public support of green tax policies may push for a lower green service ratio, i.e. a higher capital share because this raises households’ exposure to unexpected capital write-offs. We can conveniently include the case of common action in the logic of our model by adding the green service ratio to the variables which are subject to optimization in the case of the AE. Further strategic decisions like the private coordination of individual emissions are not included because they lack empirical motivation and we do not want to add unnecessary complexity to the framework.

3 Dynamic Equilibrium

In each point of time, the levels of consumption, investment, and green services are decided by individual decisions. Environmental policy affects these decisions; it consists of subsidies for green services at a rate s, the stochastic capital tax, $\gamma$, and public abatement as given by $H=\delta K$ where ${\delta }$ is a (possibly non-optimal) expenditure rate e.g. resulting from the political process.

3.1 Wealth Development

As we focus on investment decisions in the presence of uncertain environmental policy, we follow the finance literature and additionally include a safe asset with riskless interest rate r. This asset has no interrelation with the production sector of the economy and thus offers the possibility to avoid or reduce uncertain investments revealing important insights in the effects of environmental policy on portfolio composition.¹⁷ Individual wealth W is composed of physical capital, K, and the safe asset, B, where n denotes the portfolio share of physical capital. So physical capital is given by nW, the value of the safe asset is $(1-n)W$ and wealth accumulation results in

$$\begin{aligned} dW & = \;Y(K,G)dt - \tau Kdt - \gamma Kdq + rBdt - Cdt - (1 - s)Gdt \\ &= \;[Y(nW,G) - \tau nW + r(1 - n)W - C - (1 - s)G]dt - nW\gamma dq \end{aligned}$$

(8)

Since the household-producers are faced with uncertain future income, they maximize expected lifetime utility subject to the (stochastic) evolution of wealth

$$\begin{aligned} \max _{C,n,W}\quad&E_{0}\int _{0}^{\infty }\frac{(CE^{-\beta })^{1-\sigma }}{ 1-\sigma }e^{-\rho t}dt \end{aligned}$$

(9)

$$\begin{aligned} \text {s.t.}\quad&dW=[Y(nW,G)-\tau nW+r(1-n)W-C-(1-s)G]dt-nW\gamma dq \end{aligned}$$

(10)

and in addition to the optimal consumption path they choose the optimal portfolio composition, n.

Due to uncertainty, the Hamilton-Jacobi-Bellman equation is used to solve the intertemporal maximization problem. The value function is denoted by V(W) and $\tilde{W}=(1-\gamma n)W$ gives the level of wealth after the tax increase occurred. The Hamilton-Jacobi-Bellman equation for the underlying situation is given by

$$\begin{aligned} \rho V(W)=\max _{C,n}\Bigg \{\frac{(CE^{-\beta })^{1-\sigma }}{1-\sigma }&+V_{W}[A(nW)^{\alpha }G^{1-\alpha }-\tau nW+r(1-n)W-C-(1-s)G] \nonumber \\&+\lambda (V(\tilde{W})-V(W))\frac{{}}{{}}\Bigg \} \end{aligned}$$

(11)

The first-order condition with respect to consumption

$$\begin{aligned} C^{-\sigma }E^{-\beta (1-\sigma )}-V_{W}=0 \end{aligned}$$

(12)

allows for the conjecture that consumption and physical capital will grow at the same rate in dynamic equilibrium and that portfolio composition will also remain constant. We define the consumption-capital-ratio $\mu =C/K$. Together with the portfolio share n consumption reads $C=\mu nW$ and using $\tilde{\sigma }=\sigma +\beta (1-\sigma )$ results directly in

$$\begin{aligned} V_{W}&=(\mu nW)^{-\sigma }E^{-\beta (1-\sigma )} \nonumber \\&=\mu ^{-\sigma }\left( \phi -\theta \delta -\psi \frac{G}{K}\right) ^{-\beta (1-\sigma )}(nW)^{-\tilde{\sigma }} \end{aligned}$$

(13)

The effective intertemporal elasticity of substitution, $1/\tilde{\sigma }$ is modified by environmental preferences. For empirically relevant parameter values, $\sigma >1$, environmental preferences increase the effective intertemporal elasticity of substitution, which is a familiar result in environmental economics.

3.2 Portfolio

Individuals optimally adjust their portfolios to policy risks. Again, we distinguish between the fragmented equilibrium (FE) and the activist equilibrium (AE). In the FE, individuals neglect their impact on macroeconomic variables, hence they perceive the tax jumps as purely exogenous. Contrarily, the AE describes the case where agents strategically cooperate in order to influence environmental policy. Therefore they are informed that all household-producers will display the same behavior. As a consequence, (coordinated) individual decisions have an impact on the aggregate green service ratio in the AE.

We obtain the portfolio composition directly by the derivative of the Hamilton-Jacobi-Bellman equation¹⁸ with respect to n; in the fragmented equilibrium agents do not optimize $\gamma$ over the portfolio share of capital, n, irrespective of the impact of capital accumulation on stochastic taxation because without coordination their individual action has no impact.

Optimal portfolio composition for the two equilibria is expressed in Proposition 1.

Proposition 1

Given uncertain environmental taxation, the portfolio of investors in the fragmented equilibrium (FE) and the activist equilibrium (AE) is characterized by the two arbitrage conditions:

$$\begin{aligned}&A\alpha \left( \frac{G}{K}\right) ^{1-\alpha } - \tau = r + \underbrace{\lambda (1-\gamma {\bar{n}})^{-{\tilde{\sigma }}}\gamma }_{\text {risk premium FE}} \end{aligned}$$

(14)

$$\begin{aligned}&A\alpha \left( \frac{G}{K}\right) ^{1-\alpha } - \tau = r + \underbrace{\lambda (1-\gamma {\check{n}})^{-{\tilde{\sigma }}} \left( \gamma - \eta \chi \left( \frac{G}{ K} \right) ^\chi \right) .}_{\text {risk premium AE}} \end{aligned}$$

(15)

The proposition shows that the deterministic part of capital return must equal the riskless interest rate plus a risk premium.¹⁹ With an increase in risk (rising probability $\lambda$ or rising loss $\gamma$) or in risk aversion $\sigma$, the risk premium becomes larger. It can be increased (or reduced, respectively) by an increase (or reduction) of the portfolio share of physical capital, the risky asset in the portfolio.

The interest rate of the safe asset, r, is given exogenously, and households compose their portfolio such that the necessary condition (14) or (15) is met. Rearranging terms gives the respective equilibrium portfolio composition ${\bar{n}}$ for the fragmented equilibrium and ${\check{n}}$ for the activist equilibrium

$$\begin{aligned} {\bar{n}} = \frac{1}{\gamma }\left( 1-\left( \frac{\lambda \gamma }{A\alpha \left( \frac{G}{K}\right) ^{1-\alpha } - \tau - r}\right) ^{\frac{1}{{\tilde{\sigma }}}} \right) , \qquad \qquad {\check{n}} = \frac{1}{\gamma }\left( 1-\left( \frac{ \lambda \left( \gamma - \eta \chi \left( \frac{G}{K} \right) ^\chi \right) }{ A\alpha \left( \frac{G}{K}\right) ^{1-\alpha } - \tau - r}\right) ^{\frac{1}{ {\tilde{\sigma }}}} \right) . \end{aligned}$$

(16)

The individuals unambiguously choose a higher portfolio share n of risky physical capital when the safe interest rate, r, becomes lower or when uncertainty decreases (decreasing $\lambda$). The derivations are given in the appendix and the relation is illustrated in Fig. 1 which displays²⁰ Eq. (16). The implications of the equilibrium type (FE or AE) and of the specific design of stochastic environmental taxation can be seen in the numerators in Eq. (16). Since in the FE the size of the tax shock, $\gamma$, is perceived to be exogenous to the portfolio decision, only $\gamma$ itself is relevant for the portfolio composition and appears in the numerator.

Fig. 1

Portfolio share of capital (16); dotted lines: FE, solid lines: AE

Contrarily, in the AE, the risk-increasing impact of the greenness of production (due to $\eta ,\chi >0$) increases the portfolio share of capital, n. The reason is that, with increasing physical capital, the green service ratio decreases and a sudden depreciation of physical capital due to taxation gets less probable. Put differently, investors know that the increase of tax rate in case of a tax shock grows with the green service ratio which raises the revaluation of capital i.e. intensifies the stranded capital-effect. As a consequence, investments in polluting capital act as a political ”insurance” against major tax increases; capital portfolio shares rise compared to the FE, as illustrated in Fig. 1. This increase in physical capital investment is strategic behavior in the AE: it is due to the investors’ knowledge that tax increases get less politically feasible with larger capital accumulation. And concerning the environment, a larger portfolio share of capital is attended by faster capital accumulation and hence more pollution.

It is worth noting that the impact of pollution level E on tax shocks does not influence the portfolio decision in either equilibrium setting, at least not directly. Recall that the last term in (7) to determine $\gamma$ reflects increasing tax jump as a consequence of environmental degradation. However, aggregate emissions cannot be changed by individual decisions. Accordingly, individuals do not consider the impact of individual capital accumulation on pollution when deciding on their portfolio. Nevertheless, the fact that tax jumps are larger in a society with higher pollution is included in our analysis: $\gamma$ is an argument in the determination of optimal portfolio shares. Put differently, this aspect of uncertain taxation only affects portfolio composition indirectly through the resulting size of the tax jump $\gamma$, like the exogenous part of the jump, $\bar{\gamma }$.

3.3 Green Services

In our setup, household-producers decide on the level of green service provision. Green services are productive and — in the stochastic context — affect the size of the tax jumps. Again, we distinguish between the fragmented equilibrium (FE) and the activist equilibrium (AE).

In both types of equilibria individuals are fully informed about productivity as well as costs of green services. But only in the AE they (jointly) can affect the change in the size of the tax jump $\gamma$ by an increase in green services. In the FE, however, the stochastic tax rate is perceived to be independent of the individual choice of green services; consequently, individuals will not optimize their tax burden over the green service ratio. Moreover, in both settings (FE and AE), households have free-rider behavior with respect to the aggregate emission level that is relevant for intertemporal utility. Hence, we will show that individually optimal and socially optimal emissions diverge.

In the FE setting, maximization of the Hamilton-Jacobi-Bellman Eq. (11) with respect to G results in

$$\begin{aligned} V_{W}\left( A(1-\alpha )\left( \frac{G}{K}\right) ^{-\alpha }-(1-s)\right) =0. \end{aligned}$$

(17)

Here, household-producers have no influence on aggregate environmental quality, the aggregate green service ratio, and thus the uncertainty in taxation. Consequently, all variables related to uncertainty are absent.

In the AE case, maximization of the Hamilton-Jacobi-Bellman equation with respect to G includes the change in uncertainty via the stochastic tax rate

$$\begin{aligned} V_{W}\left( A(1-\alpha )\left( \frac{G}{K}\right) ^{-\alpha }-(1-s)\right) -\lambda V_{W}(\tilde{W})\left( \eta \chi \left( \frac{G}{K}\right) ^{\chi }-\varepsilon \xi \left( \frac{E}{G}\right) ^{\xi }\right) \left( \frac{G}{K} \right) ^{-1}=0. \end{aligned}$$

(18)

It is straightforward to see that in both settings (FE and AE), green services and physical capital grow at the same rate in steady state, hence we can write $G=\omega K$, where we will use the variable label $\bar{\omega }$ for the fragmented equilibrium and ${\check{\omega }}$ for the activist equilibrium. This determines the conditions for the individually optimal green service ratios $\bar{\omega }$ and ${\check{\omega }}$ in the FE and the AE setting according to

$$\begin{aligned} \text {FE: } \quad&A(1-\alpha )\left( \bar{\omega }\right) ^{-\alpha }-(1-s)=0 \end{aligned}$$

(19)

$$\begin{aligned} \text {AE: } \quad&A(1-\alpha )\check{\omega }^{-\alpha }-(1-s)-\lambda (1-\gamma n)^{-\tilde{\sigma }}(\eta \chi \check{\omega }^{\chi -1}-\varepsilon \xi (\phi -\theta \delta -\psi \check{\omega })^{\xi }\check{ \omega }^{-\xi -1})=0 \end{aligned}$$

(20)

which will be analyzed further in the following section.

4 Environmental Policy

In our model, agents do not consider the impact of their investments on aggregate emissions. Therefore, in a market equilibrium green services tend to be suboptimally low and emissions become suboptimally high. A general formulation for the emissions to capital ratio is given by

$$\begin{aligned} \frac{E}{K}=(\phi -\theta \delta -\psi \omega )\gtrless \left( \frac{E}{K} \right) ^{*}\quad \Longleftrightarrow \quad \omega \lessgtr \omega ^{*}. \end{aligned}$$

(21)

where $\omega ^{*}$ is the green service ratio in social optimum.

The socially optimal growth path can be derived from maximization of intertemporal utility (3) subject to goods market clearing $\dot{ K}=Y-C-G-H$. The optimal ratio $\omega ^{*}$ results from maximization of the corresponding Hamiltonian²¹ with respect to G

$$\frac{\uppsi}{\uptheta} + A(1-\upalpha){(\frac{G}{K})^{-\upalpha}}-1=0 \to \frac{G}{K} = \left(\frac{A(1-\upalpha)}{1-\frac{\uppsi}{\uptheta}}\right)^\frac{1}{\upalpha} \equiv \upomega^*$$

(22)

Note that, if green services had no impact on emissions (i.e. $\psi =0$), the optimal ratio of capital to green services would be identical to the Barro (1990) model. With positive $\psi$, there is an additional positive effect of green services, hence the optimal greenness of production increases.

It is well known that environmental externalities can be internalized by appropriate policies to achieve the social optimum, where the green service ratio, $\omega$, is at the optimal level. When we introduce random tax jumps like in our approach, tax and subsidy policies could, in principle, be adjusted to accommodate the underlying risks for the private agents. However, first-best characteristics of planner solutions are only a benchmark in our setup. In fact, we continue to argue that the government is not an autonomous rational decision unit but rather a body that depends on political support inducing uncertain policy implementation. Hence, our next task is to analyze the effects of uncertain policies on the green service ratio in decentralized equilibrium.

In the fragmented equilibrium (FE), agents do not adjust the green service ratio in the presence of stochastic taxation. According to (19), the green service ratio is given by

$$\begin{aligned} \bar{\omega }=\left( \frac{A(1-\alpha )}{1-s}\right) ^{\frac{1}{\alpha }} \end{aligned}$$

(23)

In the absence of any environmental policy ($\tau =s=0$), individuals choose the green service ratio according to $\omega =(A(1-\alpha ))^{\frac{1}{ \alpha }}$, as can be seen from equation (23). Due to the environmental externality, green services remain to be suboptimally low, like in the deterministic setting.²² A political process generating unanticipated environmental capital tax jumps will affect capital accumulation, and thereby lead to stranded assets (as will be shown in the next section). However, it does not have any impact on the greenness of production when individuals act in isolation and are not actively shaping the political process via common action.

Random taxation of dirty capital will only lead to an increase in green services if individuals perceive the possibility to affect taxation by means of greener production. In fact, in the activist equilibrium (AE) the green service ratio is used by agents to have an impact on tax development. This effect on the stochastic tax is included in the optimization of the green service ratio as shown in Eq. (20). With the deterministic subsidy and — additionally — the stochastic tax rate, the optimal green service ratio, $\omega ^{*},$ can be realized by any combination fulfilling $A(1-\alpha )(\omega ^{*})^{-\alpha }=1-\frac{\psi }{\theta }$ from (22) and $\check{\omega }=\omega ^{*}$ such that

$$\begin{aligned} s-\frac{\psi }{\theta }=\lambda (1-\gamma \check{n})^{-\tilde{\sigma }}(\eta \chi \check{\omega }^{\chi -1}-\varepsilon \xi (\phi -\theta \delta -\psi \check{\omega })^{\xi }\check{\omega }^{-\xi -1}) \end{aligned}$$

(24)

and hence

$$\begin{aligned} s^{*}\gtrless \frac{\psi }{\theta }\quad \Longleftrightarrow \quad \eta \chi \check{\omega }^{\chi -1}-\varepsilon \xi (\phi -\theta \delta -\psi \check{\omega })^{\xi }\check{\omega }^{-\xi -1}\gtrless 0. \end{aligned}$$

(25)

Note that under certainty ($\lambda =0$), the optimal subsidy rate is simply given by $s^{*}=\frac{\psi }{\theta }$. It is determined by the efficiency $\psi$ of green services in the reduction of pollution relative to the efficiency $\theta$ of the alternative, which is public abatement activity.

Condition (24) can easily be interpreted: If uncertainty in taxation can be reduced by green services (that is, if $\varepsilon \xi$ is high) there is an additional incentive to engage in green services and therefore less need for the deterministic subsidy. If instead uncertainty in taxation rises in the greenness of production (that is, if $\eta \chi$ is high), green services are discouraged and the subsidy rate has to be increased to reach the optimal green service ratio. With the same argument, the adoption of cleaner technologies may be discouraged if firms have to fear environmental tax increases as soon as they are able to use less polluting technologies. This distinction of cases will also be crucial in our further argumentation below although socially optimal environmental taxation only serves as a reference point in our analysis.

Rearranging terms from equation (20)

$$\begin{aligned} A (1-\alpha ) {\check{\omega }}^{-\alpha } - (1-s) = \lambda (1-\gamma \check{n})^{-{\tilde{\sigma }}}( \eta \chi {\check{\omega }}^{\chi -1} - \varepsilon \xi (\phi - \theta \delta - \psi {\check{\omega }})^\xi {\check{\omega }}^{-\xi -1}) \end{aligned}$$

(26)

shows the impact of tax uncertainty on green service provision when looking at the right hand side of (26). Its direction depends on whether the risk increasing impact ($\eta \chi$) of green services or the risk reducing impact ($\varepsilon \xi$) dominates. In both settings, the safe asset lowers the impact of tax uncertainty on the individually optimal green service ratio (since $(1-\gamma {\check{n}})^{-{\tilde{\sigma }}}<(1-\gamma )^{-{\tilde{\sigma }}}$). As individuals have access to safe return, only part of individual wealth is exposed to taxation uncertainty. Hence the effect of taxation uncertainty on individual decisions is smaller.

Implicit differentiation of Eq. (20) demonstrates the influence of uncertainty in taxation on the individual choice of the green service ratio

$$\begin{aligned} \frac{d{\check{\omega }}}{d\lambda } = - \frac{-(1-\gamma \check{n})^{-{\tilde{\sigma }}}( \eta \chi {\check{\omega }}^{\chi -1} - \varepsilon \xi (\phi - \theta \delta - \psi {\check{\omega }})^\xi {\check{\omega }}^{-\xi -1})}{\mathcal {N}}&\gtrless 0 \\ \Longleftrightarrow (\eta \chi {\check{\omega }}^{\chi -1} - \varepsilon \xi (\phi - \theta \delta - \psi {\check{\omega }})^\xi {\check{\omega }}^{-\xi -1})&\lessgtr 0 \quad \text {with } \mathcal {N} <0 \nonumber \end{aligned}$$

(27)

Increasing the arrival frequency of the tax shock, $\lambda$, implies rising uncertainty. The sign of Eq. (27) depends on the sign of the term in parenthesis in the numerator,²³$(\eta \chi {\check{\omega }}^{\chi -1} - \varepsilon \xi (\phi - \theta \delta - \psi {\check{\omega }})^\xi {\check{\omega }}^{-\xi -1})$. We find that rising uncertainty has two opposing effects on the green service ratio.

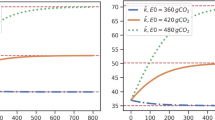
First, if the importance of $\varepsilon \xi$ — representing the impact of emissions in the determination of tax changes — dominates, risk will be reduced in a greener economy as illustrated²⁴ in Fig. 2a. An economy with a higher ratio of green services, $\omega$, will experience a reduction in environmental emissions, e.g. through effective climate mitigation or reduction of environmentally harmful technologies, which curbs the size of environmentally motivated tax increases. The reduction of political risk is an additional benefit of green service provision which raises the green service ratio. In this respect the stochastic tax has the same effect as the subsidy to green services. If the government is constrained to pay substantial subsidies it can obtain the same effect by simply ”threatening” the private economy by a highly stochastic tax setting. This effect is even present when no deterministic tax is implemented as it is effective through the individual aversion against (tax) shocks.

Fig. 2

Structure of the stochastic tax

Second, if the importance of $\eta \chi$ — representing the impact of greenness in the determination of tax changes — dominates, larger tax increases get more likely in a greener economy as illustrated in Fig. 2b. The increase in green services induces an additional effect on policy uncertainty due to stronger political support. At the same time, it induces more stringent environmental policy in the end. Current examples are countries with high market shares of green technologies and renewable energies considering even stricter emission abatement policies, e.g. in traffic and for heating. A government which values environmental policy highly can increase its subsidies to green services in order to obtain more political support in tax policy. In this sense, the time sequence first subsidies and then taxes becomes a very rational strategy for public policy.

In an activist equilibrium and if $\eta \chi$ dominates, firms anticipate the increasing stochastic taxation and know that this is an additional cost of green services. Hence, they use the amount of green services as strategic variable and agree upon reducing the green service ratio in order to decline the size of tax shocks and thereby diminish uncertainty. Firms in this case decide to reduce the greenness of production to prevent more severe environmental policy measures. Put differently, firms present themselves less green in order to reduce the political feasibility of large tax cuts.

Hence, whether the green service ratio will decrease or increase as a response to tax risks depends on two well defined effects which have an opposite impact. The impact of uncertainty on the optimal green services subsidy, $s^*$, depends on whether green services increase or decrease uncertainty in the economy. If tax risks become lower in a green economy (if $\varepsilon \xi$ dominates), this additional incentive to use green service reduces the need for internalization through the subsidy rate. This kind of stochastic taxation is a substitute for the deterministic subsidy rate. The individually optimal green service ratio increases due to tax uncertainty and the optimal level of the subsidy rate decreases. If the tax risk becomes higher in a greener economy (if $\eta \chi$ dominates), the stochastic taxation reduces the incentive to use green services. This kind of stochastic taxation restrains the internalization through the subsidy rate. Increasing uncertainty in this case results in an additional cost of green services which discourages environmentally friendly behavior. Hence, individually optimal green services expenditures decrease due to this stochastic taxation and the subsidy rate would have to be increased in order to ensure the optimal green service ratio.

The following proposition summarizes our findings in three parts a) - c).

Proposition 2

With uncertain taxation, environmental policy is characterized as follows:

• (a) There exists an optimal policy design with subsidies and purely deterministic taxes; if political restrictions prevent adopting such a design, the optimum can also be achieved in an activist equilibrium through the use of stochastic tax policies.

• (b) With lower (higher) tax risks in a green economy, firms will increase (decrease) the greenness of production strategically in order to reduce uncertainty.

• (c) Stochastic taxation serves as a substitute (complement) to deterministic green services subsidy, if uncertainty decreases (increases) in the green service ratio.

With an increase in the constant term ${\bar{\gamma }}$, the size of the tax jumps increases and the green service ratio is adjusted accordingly. Implicit differentiation of (20) results in

$$\begin{aligned} \frac{d{\check{\omega }}}{d{\bar{\gamma }}} = - \frac{-\lambda \sigma {\check{n}}(1-\gamma {\check{n}})^{-{\tilde{\sigma }}-1}( \eta \chi {\check{\omega }}^{\chi -1} - \varepsilon \xi (\phi - \theta \delta - \psi {\check{\omega }}) {\check{\omega }}^{\xi -1})}{\mathcal { N}}&\gtrless 0 \\ \Longleftrightarrow (\eta \chi {\check{\omega }}^{\chi -1} - \varepsilon \xi (\phi - \theta \delta - \psi {\check{\omega }}) {\check{\omega }}^{\xi -1})&\lessgtr 0. \nonumber \end{aligned}$$

(28)

In an activist equilibrium, an increased level of tax jumps ${\bar{\gamma }}$ has opposing effects which depend on the specific structure of the stochastic tax system. An increase in ${\bar{\gamma }}$ causes a positive level effect of tax jumps, immediately increasing uncertainty. Hence there is an incentive to change the green service ratio in order to reduce uncertainty. The remaining argument is the same as given above. Individuals will increase the green service ratio as response to increasing general uncertainty of stochastic taxation, if $\varepsilon \xi$ are high and stochastic taxation will be less uncertain in a greener economy. On the contrary, they will decrease the green service ratio, if $\eta \chi$ are high and stochastic taxation involves higher risks in a greener economy.

5 Growth Effects of Stochastic Taxation

In any dynamic equilibrium, environmental policy uncertainty will also affect the accumulation decision and thereby economic growth. First, savings are increased or decreased depending on the degree of risk aversion due to the precautionary motive. Additionally, investment in the safe asset reduces capital accumulation. And in the activist equilibrium, savings are adjusted in order to shape the political process via common action.

The growth rate of wealth between the tax shocks (for $dq=0$), which we label the ”trend growth rate”, is characterized by the following proposition.²⁵

Proposition 3

The trend growth rate of the economy is given by

$$\begin{aligned} g_W =&A \omega ^{1-\alpha } n - \tau n + r (1-n) -\mu n - (1-s)\omega n\end {aligned}$$

$$\begin{aligned} \text {FE:}\quad {\bar{g}}_W=&\frac{1}{{\tilde{\sigma }}}\left( A \alpha {\bar{\omega }}^{1-\alpha } - \tau - \rho \right) + \frac{\lambda }{ {\tilde{\sigma }}} \Big ((\underbrace{(1-\gamma {\bar{n}})^{1-{\tilde{\sigma }}} - 1} _{(ps)} \; \underbrace{- (1-\gamma {\bar{n}})^{-{\tilde{\sigma }}} \gamma (1-{\bar{n}})} _{(sa)}\Big ) \end{aligned}$$

(29)

$$\begin{aligned} \text {AE:}\quad {\check{g}}_W=&\frac{1}{{\tilde{\sigma }}}\left( A \alpha {\check{\omega }}^{1-\alpha } - \tau - \rho \right) + \frac{\lambda }{ {\tilde{\sigma }}} \Big ((\underbrace{(1-\gamma {\check{n}})^{1-{\tilde{\sigma }}} - 1} _{(ps)} \underbrace{- (1-\gamma {\check{n}})^{-{\tilde{\sigma }}} \gamma (1-{\check{n}}) }_{(sa)} \, \nonumber \\&\quad + \underbrace{(1-\gamma {\check{n}})^{-{\tilde{\sigma }}}\eta \chi {\check{\omega }}^\chi }_{(unc)} \Big ) \; \end{aligned}$$

(30)

Stochastic environmental taxation affects capital accumulation differently, depending on whether individuals jointly can an affect the change in the size of the tax jump. In the activist equilibrium, they have an additional incentive to invest in physical capital, since in an economy with a lower green service ratio tax jumps are smaller. The resulting decrease in uncertainty is an extra benefit of the investment in physical capital. Equations (29) and (30) show that growth is unequivocally higher in the activist equilibrium (AE) than in the fragmented equilibrium (FE). This effect can also be observed in Fig. 3: The trend growth rate is higher in AE (solid lines) than in FE (dotted lines) for all degrees of risk aversion and for all levels of exogenous tax uncertainty, ${\bar{\gamma }}$.

Fig. 3

Impact of exogenous uncertainty ${\bar{\gamma }}$ on trend growth (29), (30); dotted lines: FE, solid lines: AE

Direct tax uncertainty, given by the exogenous tax jump, ${\bar{\gamma }}$, is equivalent to an unforeseeable and exogenous depreciation of physical capital. The impact on the resulting trend growth rate is ambiguous due to the precautionary savings motive and displayed²⁶ in Fig. 3. If relative risk aversion, $\sigma$, is sufficiently low, the growth decreasing impact of uncertainty dominates, see Fig. 3a. Tax uncertainty decreases the incentive to accumulate capital and thereby supports environmental policy. However, if relative risk aversion, $\sigma$, is sufficiently large, the growth increasing impact of uncertainty dominates and tax uncertainty ends up in even larger physical capital taxation and environmental deterioration, see Fig. 3c.

The entire impact of stochastic taxation on the trend growth rate is more complex and displayed in the second parenthesis in equations (29) and (30) respectively; the three impact channels can be discussed by inspection of the terms (ps), (sa) and (unc). The precautionary savings motive is captured with term (ps), the reduction in capital accumulation due to the existence of a safe asset is given in term (sa) and term (unc) describes the additional capital accumulation in order to reduce tax uncertainty. Figure 4 displays the three effects.

Fig. 4

Impact of uncertainty on trend growth, terms, (ps), (sa) and (unc)

First, as can be seen in term (ps) and Fig. 4a, policy uncertainty causes a precautionary savings motive; the agents adjust capital accumulation with the aim to decrease uncertainty. In this respect, the model outcome is in full accordance with the results of stochastic growth theory. If relative risk aversion is sufficiently high such that ${\tilde{\sigma }} > 1$, term (ps) is positive. As a response to uncertainty, savings are increased in order to increase future consumption possibilities and compensate for the utility loss induced by uncertainty (see the black line in Fig. 4a). If instead relative risk aversion is low (${\tilde{\sigma }}<1$), term (ps) is negative and individuals decrease savings in order to substitute away from uncertainty (see the gray line). Precautionary behavior is a specific aspect of the stranded assets problem: Given the probability of a future capital devaluation or even capital loss, investors deviate from their optimal plans to accommodate uncertainty in an optimal way. Put differently, investors try to alleviate the consequences of sudden capital depreciation and react correspondingly.

In term (sa) and Fig. 4b we see that individuals will adjust portfolio composition in order to evade tax uncertainty. This is a key feature of the stranded assets problem, harming the growth rate of the economy, whenever $n<1$ i.e. not all wealth is invested in physical capital. In our model, the availability of a safe asset allows the agents to reduce the tax risk by investing part of the wealth in a way to have a safe return. Individuals substitute away from uncertain capital accumulation and shift wealth into the safe asset which is not subject to stochastic environmental taxes.

Term (unc), displayed in Fig. 4c, shows the effect that capital accumulation alters the green service ratio G/K and with it policy uncertainty. If more capital is accumulated the risk of a sizeable tax increase is reduced, because there is less political support. Capital accumulation reacts positively on the decrease in uncertainty which fosters the growth process. Both effects work in the same direction, i.e. this effect is unambiguously growth enhancing. We interpret this as a further stranded assets effect: capital investments reduce the threat of large tax jumps via the political support channel which in turn incentivizes capital accumulation. Of course, this effect only applies in the activist equilibrium. In the fragmented equilibrium setting, individuals perceive stochastic taxation as purely exogenous to their decisions, hence there is no attempt to reduce the risk of taxation by means of individual capital accumulation.

The following proposition summarizes our findings in three parts.

Proposition 3

Increasing uncertainty in environmental taxation affects the trend growth rate as follows:

• (a) Growth increases due to precautionary savings if the degree of relative risk aversion is sufficiently high (ps).

• (b) Growth decreases due to portfolio adjustment because the portfolio share of the safe asset is increased (sa).

• (c) Growth increases in the AE since capital accumulation serves as strategic variable to decrease political uncertainty (unc).

Fig. 5

Trend growth rate (29),(30) and relative risk aversion; dotted lines: FE, solid lines: AE

Figures 5 and 6 show that the overall impact of uncertainty in taxation on the trend growth rate is ambiguous. The stranded assets which arise from unforeseeable capital taxation may lead to a growth decreasing impact of uncertainty. But depending on the specific structure of stochastic environmental taxation, the accumulation increasing incentives may dominate. For sufficiently high relative risk aversion, the precautionary savings argument dominates and the trend growth rate increases with rising uncertainty, see Fig. 5a. Stochastic environmental taxation leads to decreasing growth, if relative risk aversion is small enough, see Fig. 5b. The growth decreasing impact of stochastic taxation may dominate even for relative risk aversions above unity despite of the precautionary savings motive. Individuals then increase the share of the safe asset in their portfolio and substitute away from risky capital. Figure 5b displays this case.

Additionally, Figs. 5 and 6 again reveal that growth rates in the fragmented equilibrium are always lower than in the activist equilibrium. The reason is that firms in the activist equilibrium have an additional incentive to accumulate capital: Capital accumulation can be used as a strategic variable to reduce the greenness of the economy and to undermine political support for sudden environmental tax increases.

Fig. 6

Trend growth rate (29), (30) and importance of political support; dotted lines: FE, solid lines: AE

The impact of the specific structure of the stochastic tax system is illustrated in Fig. 6. $\eta$ represents the degree to which environmental policy is dependent from political support. For low values of $\eta$ and in the fragmented equilibria increasing uncertainty in environmental taxation leads to decreasing growth. But if $\eta$ is large (Fig. 6a) and if we consider an activist equilibrium, the incentive to increase capital accumulation is sufficiently large to reverse the result. Increasing uncertainty in taxation then even has a growth accelerating impact which is due to the strategic reduction of political support for tightening environmental taxation.

6 Conclusions

The paper has analyzed investment decisions and their macroeconomic consequences when environmental policy is not deterministic but uncertain, following the Poisson process. This is a different perspective compared to standard environmental economics models where proposed policies are welfare-maximizing and implemented immediately. As a consequence, we have not derived an optimal policy design when assets tend to become stranded but have rather focused on the impacts of uncertain environmental policies on asset values and the adjustments of individual investment behavior.

We have shown how policy shocks affect capital accumulation, composition of the capital stock, green services, and economic growth and have obtained some major results. First, we have derived the formal relationship between random taxation and environmental subsidies. In an activist equilibrium, stochastic taxation serves as a substitute for a green service subsidy if uncertainty decreases in the green service ratio; in the opposite case it is a complement. Second, we have found that capital accumulation alters the level of green service provision and with it policy uncertainty. When agents cooperate strategically, capital investments may act as a political ”insurance” against future tax increases. Third, policy uncertainty causes precautionary savings. Given the probability of stranded assets i.e. of a future capital devaluation or capital loss, investors deviate from their optimal plans to accommodate the uncertainty in an optimal way. If relative risk aversion is sufficiently high, savings are increased in order to compensate for the utility loss induced by uncertainty. Fourth, individuals adjust portfolio composition in order to reduce tax uncertainty; with increasing policy risk they invest more in the safe assets which harms the growth rate of the economy.

Our analysis highlights that most effects of uncertain policies decrease the welfare in the economy as would be expected. Agents have to adjust their optimal savings and portfolio plans or to cooperate strategically in order to optimally cope with uncertain policy conditions and to reduce the risk of stranded assets. These induced adjustments of individual behavior have adverse effects on income level and income growth. One aspect of policy uncertainty turned out to be less negative, however: the use of unpredictable emission tax policies to discourage polluting investments. We have shown that — under certain conditions — this may restore the optimal green service ratio and thus act like a deterministic environmental policy. To threaten the markets with possible taxes is indeed efficient and may even be seen as relatively ”cheap,” because agents change their plans ”voluntarily.” However, if the threat principle in policy is transferred to a general context the conclusion loses much of its attractiveness. In a holistic policy framework, unpredictable behavior of the government is not generally desirable because it not only discourages polluting investments but all kind of investments in the economy. Moreover, the threat principle may also be used for a less favorable purpose than environmental protection, which is likely to harm overall welfare.

The present framework can be extended in several ways. While we have already introduced green services in our model as an alternative input to polluting capital we have sidestepped the option of green capital stock as an investment alternative. We expect that such an extension of the model would strengthen our results on green services. In the same way, the introduction of different production sectors with different degrees of green service or green capital ratios would be a rewarding object to study. Environmental policy uncertainty in this case could harm the adoption of less polluting technologies. This is left for future research.

Appendix

1.1 Portfolio Composition in Fragmented and Activist Equilibrium

Maximization of the Hamilton-Jacobi-Bellman Eq. (11) with respect to the portfolio share of capital, n, differs with respect to the equilibrium setting

$${\text{FE:}}\quad 0 = \;V_{W} (A\alpha (nW)^{{\alpha - 1}} WG^{{1 - \alpha }} - rW - \tau W) - \lambda V_{W} (\tilde{W})W\left( {\gamma - \eta \chi \left( {\frac{G}{K}} \right)^{\chi } } \right)$$

(31)

$${\text{AE:}}\quad 0 = \;V_{W} (A\alpha (nW)^{{\alpha - 1}} WG^{{1 - \alpha }} - rW - \tau W) - \lambda V_{W} (\tilde{W})W\gamma$$

(32)

Inserting (13) for $V_W$ and replacing $nW=K$ directly leads to Proposition 1.

Portfolio composition for both types of equilibrium are given in Eq. (16). In the following, it will be shown that the portfolio share of capital decreases unambiguously in $\lambda$ and r:

$$\begin{aligned}&\frac{\partial {\bar{n}}}{\partial \lambda } = - \frac{1}{\gamma \lambda \tilde{\sigma }} \left( \frac{\lambda \gamma }{A\alpha \left( \frac{G}{K} \right) ^{1-\alpha }-\tau -r} \right) ^\frac{1}{{\tilde{\sigma }}} < 0 \end{aligned}$$

(33)

$$\begin{aligned}&\frac{\partial {\bar{n}}}{\partial r} = - \frac{1}{\gamma ^2\lambda {\tilde{\sigma }}} \left( \frac{\lambda \gamma }{A\alpha \left( \frac{G}{K}\right) ^{1-\alpha }- \tau -r} \right) ^{\frac{1}{{\tilde{\sigma }}}+1} < 0 \end{aligned}$$

(34)

$$\begin{aligned}&\frac{\partial {\check{n}}}{\partial \lambda } = - \frac{1}{\gamma \lambda \tilde{\sigma }} \left( \frac{\lambda (\gamma -\eta \chi \left( \frac{G}{K}\right) ^\chi )}{ A\alpha \left( \frac{G}{K}\right) ^{1-\alpha }-\tau -r} \right) ^\frac{1}{ {\tilde{\sigma }}} < 0 \end{aligned}$$

(35)

$$\begin{aligned}&\frac{\partial {\check{n}}}{\partial r} = - \frac{1}{\gamma ^2\lambda \tilde{\sigma }} \left( \frac{\lambda (\gamma -\eta \chi \left( \frac{G}{K}\right) ^\chi )}{ A\alpha \left( \frac{G}{K}\right) ^{1-\alpha }-\tau -r} \right) ^{\frac{1}{ {\tilde{\sigma }}}+1} < 0 \end{aligned}$$

(36)

Solely the signs of the second derivatives are ambiguous and depend on the specific parameter setting, predominantly on ${\tilde{\sigma }}$. Figure 1 is done for the empirically relevant case of an effective intertemporal elasticity of substitution below unity $1/{\tilde{\sigma }}<1$ which results in positive second derivatives $\partial ^2 {\bar{n}} /\partial \lambda ^2>0$ and $\partial ^2 {\check{n}} /\partial \lambda ^2>0$. The signs of the second derivatives $\partial ^2 {\bar{n}} /\partial r^2$ and $\partial ^2 {\check{n}} /\partial r^2>0$ are smaller than those with respect to $\lambda$ and may well be negative as displayed in Fig. 1. However, the signs of the second derivatives are not crucial for the results.

Moreover, the portfolio share of capital is unambiguously larger in the activist equilibrium:

$$\begin{aligned} {\bar{n}}< {\check{n}}&\quad \Longleftrightarrow \quad \frac{1}{\gamma } \left( 1 - \left( \frac{\lambda \gamma }{A\alpha \left( \frac{G}{K}\right) ^{1-\alpha }- \tau -r}\right) ^\frac{1}{{\tilde{\sigma }}} \right) < \frac{1}{\gamma } \left( 1 - \left( \frac{\lambda (\gamma -\eta \chi \left( \frac{G}{K}\right) ^\chi )}{ A\alpha \left( \frac{G}{K}\right) ^{1-\alpha }-\tau -r}\right) ^\frac{1}{ {\tilde{\sigma }}} \right) \nonumber \\&\quad \Longleftrightarrow \quad \left( \frac{\lambda \gamma }{A\alpha \left( \frac{G}{K}\right) ^{1-\alpha }-\tau -r}\right) ^\frac{1}{{\tilde{\sigma }}}> \left( \frac{\lambda (\gamma -\eta \chi \left( \frac{G}{K}\right) ^\chi )}{A\alpha \left( \frac{G}{K}\right) ^{1-\alpha }-\tau -r}\right) ^\frac{1}{{\tilde{\sigma }}} \nonumber \\&\quad \Longleftrightarrow \quad \frac{\lambda \gamma }{A\alpha \left( \frac{G}{ K}\right) ^{1-\alpha }-\tau -r}> \frac{\lambda (\gamma -\eta \chi \left( \frac{G}{K }\right) ^\chi )}{A\alpha \left( \frac{G}{K}\right) ^{1-\alpha }-\tau -r} \nonumber \\&\quad \Longleftrightarrow \quad \gamma > \gamma -\eta \chi \left( \frac{G}{K} \right) ^\chi \end{aligned}$$

(37)

These results are illustrated in Fig. 1.

1.2 The Social Optimum

The social planner maximizes intertemporal utility of the households (3) with respect to the budget constraint $\dot{K} = Y - G - H - C$. Without stochastic taxation, the setting is merely deterministic. As a consequence, any riskless return must equal marginal capital productivity, the safe asset becomes irrelevant.

The program of the social planner is given by the Hamiltonian

$$\begin{aligned} \mathcal {H} = e^{-\rho t} \frac{(CE^{-\beta })^{1-\sigma }}{1-\sigma } + \nu (AK^{\alpha }G^{1-\alpha } - G - H - C) \end{aligned}$$

(38)

Maximisation with respect to consumption, C, and abatement expenditures, H, shows that emissions are proportional to consumption and hence grow with the same rate as consumption on the social optimal time path

$$\begin{aligned} E = \beta \theta C \end{aligned}$$

(39)

Maximization of the Hamiltonian with respect to capital, K, allows deriving the growth rate of consumption

$$\begin{aligned} g_C = \frac{1}{\tilde{\sigma }} \left( A \alpha \left( \frac{G}{K} \right) ^{1-\alpha } - \frac{\phi }{\theta } - \rho \right) \qquad \text {with } \tilde{\sigma } = \sigma + \beta (1-\sigma ) . \end{aligned}$$

(40)

The direct marginal return of physical capital in production is reduced by $\frac{\phi }{\theta }$ due to the need of abatement activity. The pollution intensity $\phi$ indicates the environmental damage caused by physical capital and $\theta$ is the efficiency of abatement expenditures.

Maximisation with respect to green services, G, determine the optimal green service ratio

$$\begin{aligned} \psi + \theta \left( A (1-\alpha ) \left( \frac{G}{K}\right) ^{-\alpha } - 1 \right) =0 \end{aligned}$$

(41)

1.3 Environmental Policy and Structure of the Stochastic Tax

The denominator $\mathcal {N}$ in Eq. (27) results from the derivation of (20) with respect to ${\check{\omega }}$ as given by

$$\begin{aligned} \mathcal {N} =&-\alpha (1-\alpha )A{\check{\omega }}^{-\alpha -1} \nonumber \\&- \lambda {\tilde{\sigma }} n (1-\gamma n)^{-{\tilde{\sigma }}-1}(\eta \chi {\check{\omega }}^{\chi -1} - \varepsilon \xi (\phi - \theta \delta - \psi {\check{\omega }})^{\xi -1} {\check{\omega }}^{-\xi -1} (\phi - \theta \delta ))\cdot \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \cdot (\eta \chi {\check{\omega }}^{\chi -1} - \varepsilon \xi (\phi - \theta \delta - \psi {\check{\omega }})^\xi {\check{\omega }}^{-\xi -1}) \\&- \lambda (1-\gamma n)^{-{\tilde{\sigma }}}(\eta \chi (\chi -1){\check{\omega }}^{\chi -2} + \varepsilon \xi (\phi - \theta \delta -\psi {\check{\omega }})^{\xi -1} {\check{\omega }}^{-\xi -2}((\phi - \theta \delta )(\xi +1)-\psi {\check{\omega }}) ) < 0. \end{aligned}$$

The critical term in Eq. (27) can be understood using the differentiation of the tax jump $\gamma$ with respect to $\omega$. Equation (7) defines the assumptions on political determinants of tax jumps. In the steady state, the green service ratio, $\omega = G/K$, is shown to be constant. Together with Eq. (2), the tax jump $\gamma$ results in

$$\begin{aligned} \gamma =\bar{\gamma }+\eta \omega ^{\chi }+\varepsilon ( \underbrace{\phi -\theta \delta -\psi \omega }_{>0} )^{\xi } \omega ^{-\xi } \end{aligned}$$

(42)

The green service ratio, $\omega$, has a positive impact on the tax jump through the second term and a negative impact through the third term. The positive impact dominates if $\eta$ and $\chi$ are sufficiently large and the negative impact dominates if $\varepsilon$ and $\xi$ are sufficiently large. This argument can be derived mathematically with

$$\begin{aligned} \frac{\partial \gamma }{\partial \omega } = \eta \chi \omega ^{\chi -1} - \varepsilon \xi ( \phi -\theta \delta -\psi \omega )^{\xi -1} \omega ^{-\xi -1} ( \underbrace{\phi - \theta \delta }_{>0}) \end{aligned}$$

(43)

It is straightforward that the sign of the derivative is positive for $\varepsilon ,\xi \rightarrow 0$ and negative for $\eta ,\chi \rightarrow 0$. Summing up, the slope of $\gamma$ with respect to $\omega$ is positive if $\eta$ and $\chi$ are sufficiently large compared with $\varepsilon$ and $\xi$ , and negative if $\eta$ and $\chi$ are sufficiently small compared with $\varepsilon$ and $\xi$. Both cases are illustrated in Fig. 2.

1.4 Capital Accumulation and Growth Effects of Stochastic Taxation

Individually optimal wealth accumulation is given by the derivative of the Hamilton-Jacobi-Bellman Eq. (11) with respect to wealth. Again this differs with respect to the equilibrium setting

$$\begin{aligned} \text {FE:}\quad \rho V_W =&V_{WW} \left( A\omega ^{1-\alpha } nW - \tau n W + r(1-n)W -C- (1-s)\omega nW\right) \nonumber \\&+ V_W \left( A\alpha \omega ^{1-\alpha }n - \tau n + r (1-n)\right) + \lambda \left( V_{{\tilde{W}}}(\tilde{W}) (1 - \gamma n) - V_W \right) \end{aligned}$$

(44)

$$\begin{aligned} \text {AE:}\quad \rho V_W =&V_{WW} \left( A\omega ^{1-\alpha } nW - \tau n W + r(1-n)W -C- (1-s)\omega nW\right) \nonumber \\&+ V_W \left( A\alpha \omega ^{1-\alpha }n - \tau n + r (1-n)\right) + \lambda \left( V_{{\tilde{W}}}(\tilde{W}) (1 - \gamma n + n \eta \chi \omega ^\chi ) - V_W \right) \end{aligned}$$

(45)

Together with the conjecture of the value function (13) this first-order condition allows for the derivation of the consumption ratio in the respective equilibrium setting

$$\begin{aligned} \text {FE:}\quad {\tilde{\sigma }} {\bar{\mu }} {\bar{n}} =&\rho + ({\tilde{\sigma }} - 1) (A\alpha {\bar{\omega }}^{1-\alpha } - \tau )+ {\tilde{\sigma }} A{\bar{\omega }}^{1-\alpha } {\bar{n}} (1-\alpha ) - {\tilde{\sigma }} (1-s){\bar{\omega }} {\bar{n}} \nonumber \\&- \lambda \left( (1-\gamma {\bar{n}})^{1-{\tilde{\sigma }}} - 1 - (1-\gamma \bar{n})^{-{\tilde{\sigma }}} (1-{\tilde{\sigma }}) (1-{\bar{n}}) (\gamma - \eta \chi {\bar{\omega }}^\chi ) \right) \end{aligned}$$

(46)

$$\begin{aligned} \text {AE:}\quad {\tilde{\sigma }} {\check{\mu }} {\check{n}} =&\rho + ({\tilde{\sigma }} - 1) (A\alpha {\check{\omega }}^{1-\alpha } - \tau )+ {\tilde{\sigma }} A{\check{\omega }}^{1-\alpha } {\check{n}} (1-\alpha ) - {\tilde{\sigma }} (1-s){\check{\omega }} {\check{n}} \nonumber \\&- \lambda \left( (1-\gamma {\check{n}})^{1-{\tilde{\sigma }}} - 1 + (1-\gamma {\check{n}})^{-{\tilde{\sigma }}} {\check{n}} \eta \chi {\check{\omega }}^\chi \right. \nonumber \\&\quad \left. - (1-\gamma {\check{n}})^{-{\tilde{\sigma }}} (1-{\tilde{\sigma }}) (1-{\check{n}}) (\gamma - \eta \chi {\check{\omega }}^\chi ) \right) \end{aligned}$$

(47)

which verifies that consumption and wealth grow at a common rate and therefore confirms the existence of the steady state growth path. The impact of stochastic environmental taxation on capital growth is discussed in Sect. 5.

The trend growth rate of wealth is directly derived from the equation of motion of capital (8), the portfolio decision (14) and the consumption ratio (46) for FE, and (15) with (46) for AE respectively, and taking into account that $dq=0$.