Implications of Entry Restrictions to Address Externalities in Aquaculture: The Case of Salmon Aquaculture

Abstract

This paper investigates production license management when regulation constrains the number of production licenses to address production externalities. This is increasingly relevant for aquaculture production where disease issues threaten future seafood supply. The regulatory problem is analyzed in the context of Norwegian salmon aquaculture where a stop in issuance of new production licenses has been implemented to address social costs of parasitic sea lice. Our theoretical model shows that restricting number of licenses raises prices and shifts production efforts excessively towards greater stocking of fish per license. Hence, the policy cannot achieve a first-best welfare-maximizing allocation. Furthermore, restricting entry by limiting number of licenses can create regulatory rents, which effectively subsides rather than tax the source of the externality.

1 Introduction

This paper investigates the difficulty of efficiently limiting production growth by restricting number of licenses without also addressing other available production margins. This relates our paper to other work in regulation theory showing the problem and complexity of regulating single decision variables when multiple margins are available (Smith 2012; Squires 2016). Good resource regulations can improve markets by recovering dissipated rents (Gordon 1954; Smith 1969), or by reducing incentives for socially wasteful investments (Homans and Wilen 1997). With decentralized production decisions, getting specific regulations right is difficult, getting them wrong is easy.

Aquaculture has been one of the fastest growing food production sectors, but disease issues threaten future seafood supply growth (Stentiford et al. 2012). In Norwegian salmon aquaculture, the major current issue is the prevalence and spread of parasitic sea lice associated with salmon production (Smith et al. 2010; Asche et al. 2009; Abolofia et al. 2017). This has led to a stop in the issuance of new production licenses. Little research exists on aquaculture farmers responses to such a regulation, which is worrying as it is well known that private adaptations to regulations can lead to unintended consequences not consistent with the policy objective. It is the purpose of this paper is to investigate how farmers manage production licenses when regulators limit the number of licenses to address an environmental externality. The regulatory problem will be analyzed in the context of Norwegian salmon farming.

We develop a simple economic model of salmon farming with externalities in production. Regulators set the number of production licenses, while private farmers decide on the use of their licenses, which for the salmon farming involves decisions on stocking of fish per license and harvest timing. We use a calibrated version of the model to show how restricting the number of available licenses raises the market price and shifts production efforts excessively towards higher stocking density. This will reduce the effectiveness of policy in addressing the externality. Specifically, the first-best welfare-maximizing allocation cannot be achieved by a regulation that only limits the number of licenses. Furthermore, limiting the number of licenses imposes a barrier to entry that can generate regulatory rents. This will further strengthen incentives to grow production along unregulated margins. The policy will privilege incumbent license owners and subsidize rather than tax the source of the externality.

While specifying the exact social costs of the sea lice externality in Norwegian salmon farming is beyond the scope of this paper, we argue that the policy response of excessive stocking density is unlikely to be compatible with the objective of the policy. While a policy that reduces number of licenses will ultimately reduce the social cost of the externality through reducing aggregate production, the resulting more intensive use of the licenses makes it an inefficient means to reduce the social cost of the externality. The lesson from the first-best solution is that reducing number of licenses should be accompanied by regulations that addresses the incentives for excessive stocking, such as a per fish production fee. The results in this paper is applicable to licensed production where producers are free to decide the use of their licenses. This includes most of aquaculture production.

In Norway, the major environmental concern is the growth and spread of sea lice parasites (Abolofia et al. 2017). Sea lice has a direct private cost for farmers (such as increased mortality and regulatory imposed treatment costs), but also a social cost by adversely affecting the health of wild fish stocks, as well as cross farm location contagion (Krkošek et al. 2005, 2007; Torrissen et al. 2013). Number of fish at farm locations raises the abundance of sea lice and the rate of spread of lice between farms (Kragesteen et al. 2019; Jansen et al. 2012). As such, private stocking decisions are related to both private and social costs of sea lice abundance. We provide empirical evidence that stopping the issuance of new licenses did not stop salmon production growth. Rather, production growth continued, although at a lower rate, through higher stocking of fish per license. Furthermore, because of the maximum standing biomass restriction on each license, the higher stocking induced by the policy has led to a shortening of the grow-out period and smaller harvested fish.

Restrictive licensing that limits entry can create regulatory rents that will reward the incumbent license owners, risking potentially subsidizing negative externalities. This is consistent with what has been the development in the Norwegian salmon aquaculture industry since around 2011. Strong demand for salmon with limited opportunities to grow production has supported high profitability in the industry. Norway currently has a resource tax on petroleum income and has been evaluating the basis for such a tax in salmon farming. Our findings suggest that the rent in salmon farming is not a resource rent, but a regulatory rent. The tax should be justified based on efficiently regulating negative externalities, not as a transfer of resource rent to the public as for the petroleum tax. For the sea lice issue, the proper Pigouvian tax requires an assessment of the social cost of any negative effects of production on the health of wild fish stocks, as well as any excess costs due to cross farm location contagion.

Our main findings highlight the difficulty of efficiently limiting production growth by restricting number of licenses without also addressing other available production margins. This relates our paper to other work in regulation theory showing the problem and complexity of regulating single decision variables when multiple margins are available (Smith 2012; Squires 2016). Good resource regulations can improve markets by recovering dissipated rents (Gordon 1954; Smith 1969), or by reducing incentives for socially wasteful investments (Homans and Wilen 1997). With decentralized production decisions, getting specific regulations right is difficult, getting them wrong is easy.

Previous research on environmental issues in aquaculture has focused on the sustainability of aquaculture growth and its wider environmental impact (Naylor et al. 2000; Ashley 2007; Naylor et al. 2009; Meijboom and Bovenkerk 2013; Olesen et al. 2011). Comparatively little research exists on the problem of regulating aquaculture production to deal with externalities. Some insights can be found in the literature on regulations in fisheries. For instance, research here has shown that restricting fishing vessel inputs leads vessels to substitute unregulated for regulated inputs to maintain catches (Squires 1987, 1994; Dupont 1991). Research suggests that regulating a single fishery can generate spillovers from regulated to unregulated sectors (Squires and Kirkley 1991; Asche et al. 2007; Chan and Pan 2016). Similarly, Cunningham et al. (2016) show that restrictions on efforts in one region can free up capital that is reallocated spatially to another region. Deacon et al. (2010) investigate substitution towards an unrestricted input when the fishery is subject to restricted entry and season length. Amongst other findings, they show that a higher price can reduce rents by raising efforts along the unregulated margin leading to a necessary shortening of the season length and a raise in total cost due to lower capacity utilization. We investigate the intensive use of aquaculture licenses when number of production license is regulated, allowing for explicit private cost as well as social cost escalations due to private responses. Policy spillover effects can occur when regulations are compartmentalized while private decisions are multifaceted. With stronger property rights, more complete regulations are possible, however when specific controls rather than objectives are targeted, unintended effects are likely to manifest.

2 Background

Norway is the largest producer of Atlantic Salmon, accounting for around 60% of global production (Asche and Bjorndal 2011). The major environmental issue facing Norwegian salmon farming is sea lice (Lepeophtheirus salmonis), a parasite that attaches to the skin of the salmon, affecting appetite and growth (Johnson et al. 2004). Prevalence of sea lice causes higher private costs of production (Liu and van Bjelland 2014; Abolofia et al. 2017; Dresdner et al. 2019). In addition, treatment of sea lice leads to increased stress and adult mortality.¹

Sea lice can transmit to wild salmon and trout populations, with negative effects on the health of wild fish stocks (Krkošek et al. 2005, 2007; Torrissen et al. 2013). Sea lice can also spread between farm locations. Aldrin et al. (2013) document that 66% of the expected salmon lice abundance at a location was attributed to infections within farms, 28% was attributed to infection from neighboring farms, and 6% to non-specified sources of infection. In addition, the number of fish at a farm location raises abundance of sea lice and the rate of spread between farms (Kragesteen et al. 2019; Jansen et al. 2012). As such, private stocking decisions are related to social costs of sea lice. Kragesteen et al. (2019) argue that the spread of lice between farms leads to a tragedy of the common operational environment, with well-known coordination issues. Furthermore, chemical treatments for sea lice can interact negatively with the environment. Contagion in open water sea pens means the sea lice becomes a negative externality in salmon farming.

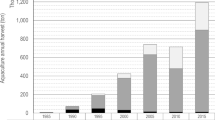
The sea lice problem has led to a stop in issuance of new grow-out production licenses. Grow-out licenses are licenses to grow fish in seawater pens for commercial harvest and sales. Licenses are issued by the Norwegian Ministry of Trade, Industry and Fisheries, and are administered by the Directorate of Fisheries.² Licenses are awarded in perpetuity but may be withdrawn under breaches of legal conditions. Each license has an associated maximum allowable biomass (MAB) of 780 tons. This means that the standing biomass of fish associated with a license cannot at any time during the year exceed 780 tons. In 2016, there were 990 grow-out production licenses in Norway, and almost all were in commecrial use (around 97% according to the Directorate of Fisheries license utilization data).

Figure 1 shows number of grow-out production licenses in Norway, along with global salmon production. From 2000 to 2010, global production of Atlantic salmon grew by 5% p.a. on average, and Norway accounted for 92% of this growth. From 2011 to 2016, world production grew by 7.5% p.a., with Norway accounting for only 32% of the growth. For Norway, 2009 was the last year of a major issuance of new production licenses.

Fig. 1

Global Atlantic Salmon production and production licenses for Norway

Production of salmon, $Y_{t}$, is the product of the number of licences $L_{t}$ (the extensive margin) and average production per licence $S_{t} = Y_{t} /L_{t}$ (the intensive margin). Growth is the sum of growth in these margins, $\Delta y_{t} \equiv \Delta l_{t} + \Delta s_{t}$, where lower case letters refer to natural logs. When the extensive margin is restricted, any further growth must occur along the intensive margin.

This is demonstrated for Norwegian salmon farming in Fig. 2. The left panel shows total production and production per license,$S_{t}$, normalized to unity in year 2000. Production tripled over the 17-year period, and almost all growth can be accounted for by growth along the intensive margin. From 2010, all growth is due to the growth along the intensive margin.

Fig. 2

Normalized production and production per license (left panel) and internal margin growth and lagged one-year growth in smolt purchases (right panel)

We measure stocking density as the number of smolt purchased per license. The right panel in Fig. 2 shows the one-year lagged growth rate in stocking density and the growth rate in production per license. The one-year lag is necessary to account for the production lag from smolt to harvest ready fish; it takes around 18 months to produce harvest ready salmon from smolt. The correlation between the two is 0.57. A linear regression shows a significant positive elasticity of 0.83 (t-value of 2.6 using HACSE robust standard error estimator). That data suggests that increased stocking per license has been the major driver of production growth in the industry.

On the market side, high demand for salmon has resulted in record high salmon prices (Brækkan and Thyholdt 2014; Asche and Oglend 2016; Brækkan et al. 2018). Norway is the world’s largest producer of farmed salmon (around 60% production share), and production trends in Norway will have price effects. It is also the case that salmon production growth has also been limited in other main production countries (Asche and Bjorndal 2011).

Figure 3 plots annual average salmon sales prices and private unit production costs (left panel), as well as long-run and short-run average accounting profits (defined as price less total unit cost for the long run margin, and price less feed cost for the short run margin). Both the price of salmon and private profit margins has grown over the sample period. The high profitability in salmon farming is discussed in Asche and Sikveland (2015), Asche et al. (2018) and Misund and Nygård (2018). Margins have grown at a lower rate than price because of escalating unit costs. Increasing cost is consistent with diminishing returns from the substantial growth along the intensive margin.

Fig. 3

Price and profit developments in Norwegian salmon production

3 License Utilization Under Restricted Entry

Fish farmers have two major controls when determining the production per license: stocking density and harvest timing.³ For Norwegian salmon aquaculture, stocking of salmon per license more than doubled from 2005 to 2016. In Fig. 4 we show the harvest time and harvest weight of salmon.⁴ Over the sample period the average grow-out period and harvest weight of has been declined. There is a trend break in 2011 associated with the end of major issuance of new production licenses. This break is informative as it is consistent with a binding maximum biomass restriction. This will be revisited later in the model results section.

Fig. 4

Average fish lifespan (left panel) and harvest weight (right panel). Weight developments have been adjusted for an increasing linear trend over the period due to improvements in technology and larger smolt and so reflects somewhat lower weight levels than normal harvest weight

We now present the economic model used to investigate how farmers utilize their private production licenses when regulators determine the number of available production licenses. We postulate theoretical social cost of externality functions and investigate first-best and second-best policy outcomes. This will allow us to compare equilibrium private outcomes to the optimal policy outcomes. In the first-best outcome, the regulator chooses number of licenses, stocking per license and harvest time to maximize social welfare. In the second-best outcome the regulator can choose only number of licenses, while private farmers decide stocking density and harvest time. This latter case reflects the recent Norwegian regulatory regime. The maximum allowed biomass (MAB) per license is assumed fixed, but we show some comparative static effects of altering this constraint.

The management of a production license, once acquired, requires the management of successive cohorts, or age-classes, of salmon - like other animal production or forestry. In salmon farming the start of the production cycle, the initial stocking period, coincides with specific times during the year when conditions are especially favorable for stocking (primarily spring and fall). Since the stocking time is seasonally determined, the optimal harvest problem is equivalent to a single-rotation Faustman forestry problem. This way of modelling farm production is consistent with earlier literature on optimal harvest timing in aquaculture. This literature highlights that fish in pens are productive capital, equivalent to a standing forest (Bjørndal 1988; Cacho 1997; Guttormsen 2009; Karp et al. 1986). Grow-out production from juvenile to harvest ready fish occurs in ocean pens and takes on average 18 months. As such, salmon production takes longer than one year, and any single producer will at any time have multiple cohorts of fish in the ocean (i.e. juvenile released this year, last year, and the year before that) to allow harvesting fish every year. The main decision variables for any cohort, which determines production for that cohort, are how many juvenile fish to stock for the cohort and at which age to harvest the fish. We introduce a growth function that models the weight of the fish as a function of time since stocking, which together with the other parameters of the decision problem discussed below allow us to determine cohort production. Each cohort decision problem is identical, we are considering a stationary setting with fixed parameters such that farm production can be modelled by choosing stocking density and harvest time for a single cohort.

The total supply in the market is farm production times number of farms. Each farm is identical and manages one production license. Our model extends the previous literature by introducing the joint stocking density decision to the license management problem. In addition, as in Asche et al. (2017) we solve for equilibrium market outcome rather than just the single farm outcome.

3.1 The Model

There are $m$ production licenses (farmers). The farmer chooses initial stocking level $n_{0}$ (number of fish) and harvest time $t$. Harvest time is continuous. Each fish grows at a rate $g_{t}$. There is a constant mortality rate of $\delta$. To make the solution well-defined, we that $\mathop {\lim }\limits_{t \to \infty } g_{t} < \delta$, i.e. at some point fish growth decreases below the mortality rate and stays below that level.

An important part of the model is the Maximum Allowed Biomass (MAB) constraint. The MAB constraint is such that the standing biomass of fish associated with a license cannot exceed MAB limit (currently 780 tons). Denote the total biomass per license at time $t$ by $q_{t}$. Then the regulation imposes the constraint $q_{t} \le MAB$ for all $t$. This regulation differs from individual fishing quotas in fisheries as it does not directly regulate production, but rather the stock size of private fish.

Figure 5 displays model-generated equilibrium growth paths of fish biomass for a given license both with a high (top panel) and low (bottom panel) $MAB$. When the $MAB$ is high enough, as in the top panel, the farmer harvests everything at the optimal harvest time, which we denote by $t^{*}$. If the $MAB$ constraint binds along the growth path we denote the first point in time when it binds by $t_{MAB}$. The get as close as possible to the unconstrained optimum, farmer uses early harvesting to keep the biomass exactly on the level of the constraint (horizontal line). The rest of the harvest is done at the optimal harvest time $t^{*}$ (marked by the vertical lines). The marginal revenue product of stocking one more smolt will be a key variable throughout the analysis. If the MAB constraint does not bind during the optimal growth-path, the marginal product of a fish is computed at the optimal harvest time $t^{*} .$ With a binding $MAB$ constraint, harvest will have to occur at sub-optimal times which reduces the marginal product of fish relative to the unconstrained harvest time.

Fig. 5

Model-generated growth-paths of biomass when the MAB constraint does not bind (top panel) and when it binds (bottom panel). The horizontal dashed line is the MAB limit determined by the regulator. The vertical dashed line is the optimal harvest time determined by Eq. (1). The point in time which corresponds to the left end of the flat part in the bottom panel is the earliest harvest time which we denote by ${\text{t}}_{\text{MAB}}$ in “Appendix 1”. Note that an increase in initial stocking density effectively shifts the growth-paths upwards. Harvest time starts at zero at the beginning of the first year after fish was stocked, fish is never harvested the year that it is stocked, this makes the harvest time in the above figure lower than the actual harvest time counting from the month it was stocked

If $w_{0}$ is the initial weight of stocked fish, the weight of a fish at time $t$ is $w_{t} = e^{{\mathop \int \limits_{0}^{t} g_{v} dv}} w_{0}$. Denote a farmer’s total biomass of fish at time $t$ by $q_{t}$. Total biomass per license is given by:

$$q_{t} = { \hbox{min} }\left( {e^{ - \delta t} n_{0} w_{t} ,MAB} \right)$$

The biomass expression accounts for mortality, stocking density and growth of fish. Note that for high enough levels of MAB or low levels of $n_{0}$, the MAB constraint will never bind. If the MAB constraint binds, early harvest in necessary and the farmer will harvest fish such that $q_{t} = MAB$ holds exactly. “Appendix 1” derives a closed-form solution for the total amount of early harvest and other relevant measures when the MAB constraint binds. As our data allows estimation of fish growth rate, the estimation procedure can account for the presence of the MAB constraint in a computationally efficient manner.

A farm’s private cost of production over the production cycle is the sum of initial stocking cost $C\left( {n_{0} } \right)$, accumulated feed cost $c_{t}$, and a fixed cost $f$. We assume increasing costs of stocking $C'\left( {n_{0} } \right) > 0$. The accumulated feed cost is,

$$c_{t} = \mathop \int \limits_{0}^{t} c q_{v} dv$$

i.e., feed cost is proportional to the total biomass of fish at that time. Here $c > 0$ is feed cost per kilogram fish. Feed is supplied at a constant price by independent fish feed producers.

We assume all costs and revenues are in present value terms relative to the production cycle. The farmer’s decision problem is,

$$\mathop {\hbox{max} }\limits_{{t,n_{0} > 0}} p\left( Q \right)h_{t} - c_{t} - C\left( {n_{0} } \right) - f,$$

where $h_{t}$ is total harvest per license and $c_{t}$ is defined above, $p$ is the aggregate inverse demand function, and $Q = mh_{t}$ is total quantity produced by all farmers. We assume a competitive market such that an individual producer cannot affect the market price. Coordinated effects of regulations can affect the price through aggregate production.

The first-order condition with respect to harvest time $t$ is

$$p\left( Q \right)\left( {g_{{t^{*} }} - \delta } \right) = c .$$

(1)

Optimal harvest time is characterized by the growth rate of revenues being equal to the cost required to obtain that marginal revenue. Interest costs if modelled would enter the decision problem directly as an augmentation to right-hand side the feed cost rate $c$, i.e. a higher economic cost of delaying harvest.

The first-order condition with respect to stocking density $n_{0}$ is,

$$p\left( Q \right)MP = \frac{{c_{t} }}{{n_{0} }} + C'\left( {n_{0} } \right) ,$$

(2)

where $MP = e^{ - \delta t} w_{t}$ is the marginal product of an additional fish, where $t$ is either the optimal harvest time $t^{*}$ if the MAB constraint does not bind, or $t_{MAB}$ if the MAB constraint binds. Optimal stocking of fish requires the marginal revenue product from stocking one more fish (left hand side) to equal its marginal cost (comprising average feed cost and marginal stocking cost).

Equations (1) and (2) characterizes optimal private license management. If number of licenses $m$ is decreased, total production $Q = mh_{t}$ decreases, and the market price $p\left( Q \right)$ in (2) increases. Hence optimal stocking $n_{0}$ increases. From (1), the optimal unconstrained grow-out time will increase, given growth is subject do diminishing returns. Whether observed harvest time increases or not will depend on the MAB constraint. If it does not bind, harvest time and fish weight will increase. If it binds, harvest will occur between $t_{MAB}$ and $t^{*}$, and the average harvest time and fish weight will decline relative to the non-binding MAB outcome.

Finally, with a fixed number of production licenses in the market, there is limited entry, and farmers can earn positive economic profits. However, given the stocking decision (2), which does not enter private fisheries decisions, there is no rent on the margin. This is necessarily so because the aquaculture farmer can adjust the number of fish, and so there are no stock externalities. Regulators can extract any profits by auctioning licenses, or tax, but we do not consider such transfer effects.

3.1.1 First-Best Solution

We proceed to welfare considerations. Fish production imposes a social cost of $f\left( {m,n_{0} } \right)$, where the social cost is increasing in both arguments. The externality is measured in monetary terms.

The first-best outcome maximizes total private profits minus social cost. The optimal allocation is the solution to,

$$\mathop {\hbox{max} }\limits_{{m,t,n_{0} > 0}} p\left( Q \right)Q - f\left( {m,n_{0} } \right) - m\left( {c_{t} + C\left( {n_{0} } \right) + f} \right)$$

The first-order conditions with respect to $m$,$t$ and $n_{0}$ are

$$p\left( Q \right)h_{t} - f_{1} \left( {m,n_{0} } \right) - \left( {c_{t} + C\left( {n_{0} } \right) + f} \right) = 0,$$

(3)

$$p\left( Q \right)\left( {g_{{t^{*} }} - \delta } \right) = c,$$

(4)

$$p\left( Q \right) MP - \frac{1}{m}f_{2} \left( {m,n_{0} } \right) - \left( {\frac{{c_{t} }}{{n_{0} }} + C^{\prime}\left( {n_{0} } \right)} \right) = 0,$$

(5)

where subscripts to the externality function indicate partial derivatives with respect to that argument. We assume the $MAB$ constraint applies to the first-best case as well. These three equations characterize the first-best solution.

3.1.2 Second-Best Solution

We consider a second-best solution where the social planner can choose only the number of licenses $m$, while farmers choose stocking $n_{0}$ and harvest time $t$ given $m$ and the $MAB$ constraint. This approximates the policy regime in Norwegian salmon farming. We maximize welfare using the first-order conditions (1) and (2) as constraints. Formally:

$$\begin{array}{*{20}c} {\mathop {\hbox{max} }\limits_{{m,t,n_{0} > 0}} \begin{array}{*{20}c} {p\left( Q \right)Q - f\left( {m,n_{0} } \right) - m\left( {c_{t} + C\left( {n_{0} } \right) + f} \right)} \\ {s.t.} \\ \end{array} } \\ {p\left( Q \right)\left( {g_{{t^{*} }} - \delta } \right) = c} \\ {p\left( Q \right)MP = \frac{{c_{t} }}{{n_{0} }} + C'\left( {n_{0} } \right)} \\ \end{array}$$

Once again, if the $MAB$ constraint binds there will be early harvest, which is kept as small as possible.

3.1.3 Externality Function Specifications and Numerical Calibration

The exact outcome of regulations will necessarily depend on how the extensive and intensive production margins map to the social cost of the externality. To move forward, we assume margins map into social costs in a linear quadratic way, $f\left( {m,n_{0} } \right) = \alpha \frac{1}{2}m^{2} + \left( {1 - \alpha } \right)\frac{1}{2}n_{0}^{2}$ for some $\alpha \in \left( {0,1} \right)$. Increasing either $m$ or $n_{0}$ will lead to social costs that are initially small but grows increasingly larger as the margins grow. Based on this functional form, we expect a planner to impose a “balanced mix” of $m$ and $n_{0}$. The weight $\alpha$ measures the relative impacts of the two margins, $m$ and $n_{0}$, on social costs. As $\alpha$ decreases (higher relative social costs of stocking density), the first-best solution will choose lower $n_{0}$ than the equilibrium outcome with the same number of licenses.

In Sect. 4, we also present results for the case where the environmental externality is on total industry production, i.e. it takes the functional form $f\left( Q \right) = \frac{1}{2}Q^{2}$.

We assume quadratic stocking costs, $C\left( {n_{0} } \right) = \frac{1}{2}bn_{0}^{2}$, where $b > 0$ defines the marginal cost slope. Furthermore, we demand is iso-elastic with inverse demand function, $p\left( Q \right) = \gamma Q^{ - \mu }$ where $\mu$ is the price flexibility parameter, and $\gamma$ is a parameter that will be calibrated to make model predictions match price data.

We rely on numerical analysis to investigate model outputs. To do so, we calibrate the model to match the average price and production quantity of the Norwegian industry from 2005 to 2016. The parameters to specify are $\alpha$ in the externality function, $\mu$ and $\gamma$ in the inverse market demand function, the mortality rate $\delta$, and cost parameters $b$, $c$ and $f$. The following parameter values are chosen:

• We set $\mu = 0.3$ and $\delta = 1\%$, and choose the scaling of the inverse demand function $\gamma$ so that the model replicates the average price during the sample period.

• We set $\alpha = 0.5$ such that externality cost is weighed equally towards stocking density and number of licenses. We do not have enough information to tune this parameter and so chooses an uninformed prior where both margins are given equal weight.

• Based on the data described earlier in the paper, we know the average production by a Norwegian farmer. Furthermore, we have data on the average weight of a fish by month of the production cycle, which allows us to construct a measure of the period growth rate $g_{t}$ in (1). Hence it is possible to choose $c$ in (1) such that model production is equal to actual production.⁵

• We also know $n_{0}$ from the data. Hence, we can choose $b$, the marginal cost slope, such that Eq. (2) binds exactly.

The fixed cost of production is not identified by the data and is set to zero for the numerical analysis. With the parametrization we compute equilibrium allocations for various levels of $m$ along with the first-best and second-best allocations. The parametrization is deemed realistic of qualitative aspects of salmon farming, but as with any such exercises, exact numeric outcomes will depend on chosen functional forms and parameter values. This will necessarily differ across industries and externalities.

4 Results

Figure 6 shows the relationship between the number of licenses $m$ and the optimal stocking density $n_{0}$, farm revenue, private cost and private cost per kg salmon produced. The solid blue equilibrium curves display equilibria of the model for various number of licenses, $m$. The red dot shows the first-best regulatory outcome, the blue dots the second-best outcome.

Fig. 6

Initial stocking level, firm revenue, firm private cost and private cost per kg as a function of number of licenses

We note that for the range of licenses (x-axis) in the figures, the MAB constraint is always binding. Our calibrated model hence predicts that farmers fully utilize their licenses. The appendix replicates the figures for a wider range of number of licenses, showing that for sufficiently high number of available licenses the MAB will not bind.

Equilibrium stocking density is decreasing in $m$ (top left panel). When number of licenses declines, the optimal response is to intensify the use of existing licenses by increasing stocking density. The first-best allocation lies below the equilibrium curve, meaning the first-best allocation will choose a lower stocking density $n_{0}$. For the second-best allocation, blue dot, the planner is not able to restrict producers from increasing stocking density, $n_{0}$. In this case, the regulator will choose a lower number of licenses $m$ in order to reduce the externality cost.

Firm revenue and cost are declining in number of licenses. Revenues decline because more licenses lead to higher aggregate production and lower price. Furthermore, the lower stocking density resulting from more licenses reduces costs. The first-best allocation will lead to reduced farm revenue. While the allocation raises price due to constraining aggregate production, it reduces farm level production due to lower stocking such that in total farm revenue declines. However, the first-best allocation as also reduces private costs as the competitive push along the stocking margin is cut off by the regulation.

Figures 7 displays equivalent plots for private profits, social costs and price. The combined private revenue and cost effects are such that license profits decrease in number of licenses. In other words, restricting the number of licenses can put existing license owners in a privileged position, raising profits. The second-best solution that regulates only number of licenses has a higher private profit than the first-best solution. This highlights the private economic cost of fully internalizing the externality.

Fig. 7

Private profits, social cost 1 (separate quadratic externality costs for stocking density than number of licenses), social cost 2 (quadratic externality cost on aggregate industry production), and the equilibrium price as a function of number of licenses. Note that the above price is considerably lower than historically average prices due to not accounting for variable costs unrelated to the decision margins investigated in this paper (i.e. labor costs, harvest costs, logistic costs)

Social cost 1 uses the baseline specification of the externality function, whereas Social cost 2 puts the externality on aggregate production volume. Both cases show increasing social cost with increasing number of licenses. The figures also show that the first-best allocations are not supported by the private equilibrium. Interestingly, when the social cost is on the individual farm margins, the second-best allocation will have lower total social cost. This is because the second-best allocation will have to choose lower number of licenses to compensate for the private response of increasing the stocking density. In total this reduces the social cost when the externality loads on the stocking density margin. This changes somewhat when the externality is quadratic in total industry production. Because the first-best allocation will choose a lower aggregate production, this will reduce the social cost when it is a function of aggregate production. These outcomes highlight that the outcome of the first- and second-best allocations on social cost will depend on exactly how production maps to the social cost. Given the behavioral responses of farmers to the regulation controls, this information is important for successful policy design.

As suggested by the revenue plot above, the equilibrium price of salmon will be decreasing in number of licenses, and the first-best price is above the equilibrium curve due to the lower enforced total production.

Figures 8 displays production outcomes showing equilibrium harvest weight, earliest harvest time, production per license and total industry production. The average harvest weight is computed by computing the percentage of biomass harvested in each period. As the number of licenses increases, equilibrium harvest weight and time increase. This is due to the binding maximum biomass restriction, as can be seen in the appendix Fig. 13 which includes the production regime when the MAB is not binding. When the MAB is binding, more licenses lead to lower stocking density and to the MAB binding later in the production cycle, raising harvest weight and time. Because of the lower stocking density in the first-best allocation, the production cycle and fish weight will be larger than the equilibrium outcome. Even though fish weight increases in number of licenses, the reduction in stocking leads to lower production per license. However, an additional license adds more to total industry production than the decline in incumbent licenses production removes from production such that total production in the industry will increase in number of licenses.

Fig. 8

Harvest weight, average harvest time, harvested quantity per license and total harvest as a function of number of licenses. The above harvest time is lower than the actual harvest time reported in Fig. 4 as it starts at zero at the beginning of the first year after fish is stocked, while Fig. 4 counts from the month it was stocked

To summarize, a stricter licensing regime reduces supply such that the market price increases. The reduced production will also reduce the social cost of the externality. However, if the regulation only consists of reducing the reduction number of licenses, private farmers will respond to the regulation by raising stocking density. This will moderate the decline in social costs induced by the regulation. The degree to which this happens will depend on how the stocking margin maps into the social cost. Because of this private response the restricted entry regulation alone is sub-optimal. The first-best allocation will moderate the increased stocking density, but this allocation is not supported by the private equilibrium.

Until now we have assumed the $MAB$ level is fixed. Figure 9 shows optimal stocking, harvested biomass, harvest weight and harvest time as a function of the MAB when the number of licenses is fixed at the industry average over the sample period from 2005 to 2016. We see that for lower MAB levels, the constraint binds and any further increases in the $MAB$ raises optimal stocking, harvested biomass, harvest weight and harvest time. At some level the MAB no longer binds, and further increases has no effect on the optimal level of the endogenous variables.

Fig. 9

Initial stocking level, harvest per license, harvest weight and average harvest time as a function of MAB

In Fig. 10 we explore impacts of changes in the demand parameter γ, where higher γ corresponds to an upward shift in the demand curve. The kinks in the plots is due to the MAB constraint. At higher demands, the MAB tends to bind, and so further increases in demand raises stocking and production at a lower rate. We observe how harvest weight and harvest time increases in demand until the MAB binds, after which it decreases due to forced early harvest to comply with the restriction. This contributes to limiting production growth in response to higher demand and explains the lower rate of growth in stocking and production at demand growth above the kink point. These results are consistent with Fig. 2 showing a slow-down in Norwegian production from around 2011, and the trend breaks in Fig. 5 showing actual average harvest time and harvest weight developments. It clearly suggests that the observed behavior of production, harvest time and harvest weight can be explained by stronger demand for salmon in a regime restricted entry.

Fig. 10

Initial stocking level, harvest per license, harvest weight and average harvest time as a function of demand parameter γ. An increase in γ corresponds to an upward movement of the demand curve

Our findings support a holistic approach to regulations aimed at addressing externalities in aquaculture. Private incentives across all available production margins need to be consistent with the policy objective; a view of regulation promoted by amongst others Smith (2012) and Squires (2016). A textbook Pigouvian tax equal to the social cost of the externality can achieve the first-best outcome. For instance, the first-best optimality conditions (Eqs. 3–5) suggest that the first-best outcome can be supported by the private equilibrium if regulators choose the first-best number of licenses together with a tax equal to the average intensive margin marginal social cost, $\frac{{f_{2} \left( {m,n_{0} } \right)}}{m}$, per fish stocked. However, the correct numeric value of this tax is not clear. In addition, any tax imposes administrative costs, but given the second-best regulation also has associated administrative costs this is a lesser concern than the correct tax. Norway already has a resource rent tax on petroleum incomes and has been evaluating the basis for such a tax for salmon farming. However, it should be noted that the rent in salmon farming is not a resource rent. It is a rent supported by the restrictive licensing regulation in a regime of demand growth. Such a tax should be justified based on efficiently regulating negative externalities, not as a transfer of resource rent to the public. For the sea lice issue, the proper Pigouvian tax requires an assessment of the social cost of any negative effects of production on the health of wild fish stocks, as well as any excess costs due to cross farm location contagion.

5 Concluding Remarks

Addressing a negative externality by limiting the number of production licenses is a potentially attractive policy measure and is commonly used in food production and natural resource industries. This paper has highlighted some possible consequences of such a policy in the context of aquaculture production.

We investigate the policy as a measure to limit social costs of externalities related to sea lice in Norwegian salmon farming. Sea lice can spread to wild salmon and trout stocks, as well as between farm locations, generating negative externalities. Although the case is specific, the results in this paper apply to any production where access is licensed, and producers face private decisions on the intensive utilization of their licenses.

We have shown how limiting number of licenses reduces aggregate production and raises price. This shifts private production efforts towards more intensive utilization of existing licenses. The model of salmon farming shows that the licensing policy is unable to support the first-best policy that maximizes social welfare. This is because the policy is unable to constrain competitive efforts to increase stocking density to raise production in response to the higher price. Depending on how stocking density maps into social costs, this will moderate the reduction in the externality cost from limiting number of production licenses. Restrictive licensing that limits entry can create regulatory rents that will reward the incumbent license owners, risking potentially subsidizing negative externalities. Furthermore, when each production license is subject to a maximum standing biomass constraint, the regulation will reduce harvest time and harvested fish weight as farmers that raise stocking density will be forced to harvest earlier to avoid violating the maximum biomass restriction. This is consistent with what has been the development in the Norwegian aquaculture industry since around 2011. Strong demand for salmon with restricted entry has reduced the growth rate in production as it can only grow through higher stocking density. This has led to binding a binding maximum biomass with smaller harvested fish.

The higher stocking density arising from the regulation has likely not contributed to improving sea lice issues. While our stocking density measure is an industry aggregate, it likely translates to higher in situ densities given the incentive of greater stocking per production license. Excessive in situ stocking density has been shown to increase contagion to wild fish, impair fish growth, health and general fish welfare (Ellis et al. 2002; Ashley 2007; Baldwin 2011; Turnbull et al. 2005; Sveen et al. 2016).

Appendices

Appendix 1: Derivation of Harvested Quantities in the Presence of a Binding MAB Constraint

This Appendix derives expressions for the harvested quantities in the presence of a binding MAB constraint. Let us assume that $n_{0}$ is large enough so that the MAB constraint binds before the optimal harvest time given by Eq. (1). We denote the first point in time when the MAB binds by $t_{MAB}$. This can be solved for by using $n_{0} \exp \left( { - \delta t_{MAB} } \right)w_{{t_{MAB} }} = MAB$ along the unconstrained growth path.

We will proceed to derive an expression for the total amount of early harvest between $t_{MAB}$ and $t^{*}$, where the latter refers to the optimal harvest time given by (1). Since the effective fish growth rate $g_{t} - \delta$ is positive in this time interval, the farmer will have to harvest some of the fish by gradually decreasing $n_{0}$ over time. In this Appendix we use notation $n = n\left( t \right)$ to account for the number of fish in the pen as a function of time. In the beginning, $n = n_{0}$ but after $t_{MAB}$ the farmer will have to decrease $n$ in order to satisfy the constraint. More specifically, in the interval where MAB binds we have $n\exp \left( { - \delta t} \right)w_{t} = MAB$ at all times. Taking logs and time-differentiating gives

$$\frac{{\dot{n}}}{n} - \delta + \frac{{\dot{w}}}{w} = 0$$

where $\dot{n} = \frac{{\mathop {dn}\limits^{.} }}{dt}$ and $\dot{w} = \frac{{\mathop {dw}\limits^{.} }}{dt}$. The instantaneous harvest weight in a point in time is given by $- \dot{n} \exp \left( { - \delta t} \right)w_{t}$ and therefore the total early harvest is given by

$$- \mathop \int \limits_{{t_{MAB} }}^{{t^{*} }} \dot{n} \exp \left( { - \delta t} \right)w_{t} dt = - \mathop \int \limits_{{t_{MAB} }}^{{t^{*} }} {\text{n }}\left( {\delta - \frac{{\dot{w}}}{w}} \right)\exp \left( { - \delta t} \right)w_{t} dt$$

where the equality follows from the earlier expression for $\dot{n}$. By construction, $\dot{n}$ is such that $n\exp \left( { - \delta t} \right)w_{t} = MAB$always holds. The integral above simplifies to

$$- MAB\mathop \int \limits_{{t_{MAB} }}^{{t^{*} }} \left( {\delta - \frac{{\dot{w}}}{w}} \right)dt = - MAB\mathop \int \limits_{{t_{MAB} }}^{{t^{*} }} \left( {\delta - \frac{dlog \left( w \right)}{dt}} \right)dt$$

Evaluating this integral gives an expression for the total early harvest:

$$h_{early} = - MAB\left( {\delta \left( {t^{*} - t_{MAB} } \right) - \log \left( {{\text{w}}_{{t^{*} }} } \right) + {\text{log}}\left( {{\text{w}}_{{t_{MAB} }} } \right)} \right)$$

In addition to the total early harvest, the farmer will harvest $MAB$, the remainder of the fish, at $t^{*}$. The need for fish feed is computed based on the total biomass summed up over time. This biomass is given by $n_{0} \exp \left( { - \delta t} \right)w_{t}$ between time 0 and $t_{MAB}$, and by $MAB$ between time $t_{MAB}$ and $t^{*}$.

Finally, the harvest time is computed as a weighted average of harvest times where the weight is the quantity of harvested fish at that point in time. If $h_{early}$ denotes the total early harvest and $h_{{t^{*} }} = MAB$ denotes the harvest at the optimal harvest time, the harvest time is given by

$$t_{harvest} = \frac{{h_{early} }}{{h_{early} + h_{{t^{*} }} }}t_{early} + \frac{{h_{{t^{*} }} }}{{h_{early} + h_{{t^{*} }} }}t^{*}$$

where the weighted average time for early harvest is given by

$$t_{early} = \frac{{ - \mathop \int \nolimits_{{t_{MAB} }}^{{t^{*} }} t \dot{n} \exp \left( { - \delta t} \right)w_{t} dt}}{{h_{early} }}$$

In the last expression, $\frac{{ - \dot{n} \exp \left( { - \delta t} \right)w_{t} }}{{h_{early} }}$ is the weight, i.e. the ratio of early harvest at a given point in time to the total early harvest. Multiplying this by $t$ and integrating over the relevant interval gives the average time for early harvest. As before, the expression for $t_{early}$ can be simplified further along the same lines as before. However, in practice this term is computed by numerical integration.

Appendix 2: Model Outputs for Extended Range of Licenses

The below figures reproduce Figs. 6,7 and 8 in the main document but extends the range of number of licenses (x-axis). Licenses greater than the kink-point thresholds reflect outcomes with a non-binding MAB constraint.

See Figs. 11, 12, 13.

Fig. 11

Initial stocking level, firm revenue, firm private cost and private cost per kg as a function of number of licenses. At a sufficiently high number of licenses, the MAB constraint no longer binds, and results reflect unconstrained license production

Fig. 12

Private profits, social cost 1 (externality cost on aggregate industry production), social cost (externality cost on farm stocking density and number of licenses), and equilibrium price as a function of number of licenses

Fig. 13

Harvest weight, average harvest time, harvested quantity per license and total harvest as a function of number of licenses