Optimal Siting, Sizing, and Enforcement of Marine Protected Areas

Abstract

The design of protected areas, whether marine or terrestrial, rarely considers how people respond to the imposition of no-take sites with complete or incomplete enforcement. Consequently, these protected areas may fail to achieve their intended goal. We present and solve a spatial bio-economic model in which a manager chooses the optimal location, size, and enforcement level of a marine protected area (MPA). This manager acts as a Stackelberg leader, and her choices consider villagers’ best response to the MPA in a spatial Nash equilibrium of fishing site and effort decisions. Relevant to lower income country settings but general to other settings, we incorporate limited enforcement budgets, distance costs of traveling to fishing sites, and labor allocation to onshore wage opportunities. The optimal MPA varies markedly across alternative manager goals and budget sizes, but always induce changes in villagers’ decisions as a function of distance, dispersal, and wage. We consider MPA managers with ecological conservation goals and with economic goals, and identify the shortcomings of several common manager decision rules, including those focused on: (1) fishery outcomes rather than broader economic goals, (2) fish stocks at MPA sites rather than across the full marinescape, (3) absolute levels rather than additional values, and (4) costless enforcement. Our results demonstrate that such naïve or overly narrow decision rules can lead to inefficient MPA designs that miss economic and conservation opportunities.

1 Introduction

Many countries are expanding their protected area (PA) networks, terrestrial and marine, to achieve both ecological goals, which often align with international conservation agreements (Pereira et al. 2013), and economic goals (Gaines et al. 2010; Jentoft et al. 2011), which often prioritize sustainable resource management for the benefit of nearby resource-dependent communities (Cabral et al. 2019; Carr et al. 2019). However, for any of these goals, economic efficiency requires that PA siting and management decisions anticipate and consider the response of potential resource extractors, especially in settings of limited enforcement budgets (Cabral et al. 2017). Empirical economic analyses of terrestrial park effectiveness often rely on von Thunen-inspired models to predict the level of deforestation that would occur if a location was not in a PA, and then calculate the level of “avoided deforestation” created by the PA as a measure of its effectiveness (e.g. Pfaff et al. 2014). Working from the opposite starting point, we use a model of villagers’ fishing site and labor decisions to predict how villagers react to a marine protected area (MPA), and incorporate these villager best responses into optimal MPA design to determine the optimal size, location, and enforcement of an MPA intended to maximize either ecological or economic objectives.

To predict how villagers react to an MPA, we develop a game-theoretic model in which villagers make individual fishing site and labor effort decisions that aggregate through a Nash equilibrium with spatially explicit micro-foundations. To be general to lower-income country settings, we explicitly model labor allocation decisions across fishing and non-fishing income-generating activities and a fishing site choice, rather than allocating fishing effort until achieving rent dissipation in each fishing site (Sanchirico and Wilen 2001).¹ By modeling fixed distance costs of traveling to each potential fishing site, we incorporate the spatial interactions between fishers’ site choice and managers’ MPA size, sites, and enforcement decisions (Robinson et al. 2014; Madrigal-Ballestero et al. 2017). Specifically, we model biologically homogeneous fishing sites with density dispersal across sites, but heterogeneous distance costs induce heterogeneous returns to fishing across sites. Finally, acting as a Stackelberg leader and to maximize a specific goal, our manager chooses the optimal size, sites, and enforcement level considering villagers’ spatial equilibrium best responses to the MPA.

MPAs are often used for fisheries management and ecological conservation goals, including ecological objectives around fish populations or marine biodiversity and economic goals around livelihood objectives and fish yields (Batista et al. 2011; Pajaro et al. 2010; Pomeroy et al. 2005). To reflect the varied objectives for MPAs worldwide, we consider two central goals: maximize income as an economic goal and maximize the avoided fish stock losses in the marinescape as an ecological goal. Our economic goal emphasizes a broad objective similar to maximizing welfare, rather than following the fishery economics literature’s emphasis on aggregate yield and fishery profits, because aggregate income is inclusive of fishery profits and onshore wage earnings.² Our ecological goal of maximizing avoided stock losses in the marinescape corresponds with the systematic conservation planning literature’s emphasis on evaluating conservation policy at the landscape level and on the additional conservation created.³

Regardless of the manager’s goal, we consider the optimal MPA design both when a manager is constrained by an enforcement budget and when this constraint does not bind. By considering the budget-constrained managers, we can address a central issue for PAs in lower-income countries: PAs without sufficient enforcement become “paper parks” that provide few additional PA benefits because people continue to extract resources (e.g. Adams et al. 2019; Brown et al. 2018; Bonham et al. 2008). In our model, villagers’ respond to the “carrot” of MPA configuration’s impact on dispersal (i.e. increased fish stocks in a particular site) and to the “stick” of the MPA’s potentially incomplete enforcement (i.e. increased probability of being caught and losing their harvest), in addition to other characteristics of the setting. We find that the optimal MPA differs markedly across management goals and non-monotonically across budgets in ways that reflect the villagers’ spatially explicit response, in the form of a spatial Nash equilibrium, to the MPA at the long run steady state fish stock. Previous studies that consider enforcement costs and the response to incomplete enforcement in making MPA siting decisions either conduct that analysis with assumptions about constant fishing effort (Byers and Noonburg 2007) or in an implicitly spatial setting without modeling distance as a component of the fishers’ site choice (Yamazaki et al. 2014).

Furthermore, we show the potential shortcomings of establishing an MPA based on often-used goals that do not consider either the full livelihood of the villagers (i.e. fishing income and non-fishing income) or the full marinescape (i.e. stock inside and outside the MPA). First, while the economics literature on marine protection typically considers only economic outcomes within fisheries (e.g. Smith and Wilen 2003), MPAs may shift labor out of fishing and into other sectors of the economy. By introducing onshore wage labor as an outside option, we can compare the standard goal of yield-maximization with a more holistic goal of maximizing income for the villagers (i.e. a better measure of welfare). By allowing for onshore wage labor and constraining the manager’s enforcement capacity, our model highlights the distinction between yield- and income-maximization that is particularly salient in low- and middle-income countries where artisanal fishers frequently work multiple jobs and limited enforcement capacity cannot completely deter illegal harvest. Second, while ecological conservation goals typically focus on outcomes within the geographic footprint of the PA itself, incomplete enforcement can cause economic activity to spillover to nearby areas just outside the enforced zone (Robalino et al. 2017) and fish dispersal from sites of high relative fish density influence fishing site decisions such as “fishing the line” (Kellner et al. 2007). If a naïve manager designs an MPA to maximize avoided stock loss only within the MPA itself, spillovers to adjacent fishing sites are likely to undermine its ecological impact across the full marinescape. By explicitly modeling how both fish and people move across space, including across MPA borders, we compare standard ecological MPA-focused goals with a broader objective to maximize avoided stock loss across the full marinescape.

Our results reveal qualitative and quantitative differences in optimal MPAs established to achieve different goals; show changes in MPA design across budget levels; elucidate relationships between enforcement levels and MPA outcomes; and inform a policy discussion. Specifically, we make three main contributions. First, we extend the economic analysis of MPAs by including multiple sites and spatially explicit modeling of villager labor and site decisions with heterogeneous distance costs and incomplete enforcement. Second, we extend the systematic conservation planning and reserve site selection literatures by including a model of fishers’ MPA response directly in the decision framework for selecting MPA sites. Third, by incorporating constrained enforcement budgets, our results speak to real-world challenges faced by PA managers. This article continues with the development of a model that considers several manager goals. Section III presents the open access decisions of villagers in IIIA, the optimal MPAs from a manager who maximizes income and one who maximizes avoided stock loss across the marinescape in IIIB, and interprets those results in IIIC. Section IV reports and interprets the MPA results of 3 “naïve” managers. Section V discusses the policy implications of the results and section VI concludes.

2 Model

2.1 Overview

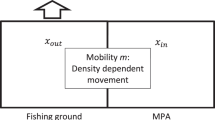
We develop a spatial bio-economic model to study the MPA manager’s siting, sizing, and enforcement level decisions, given the presence of villagers who either fish or work onshore. First, we define our stylized marinescape spatial setting as an $R \times C$ matrix with a village located next to the first site (Fig. 1). The biological part of the model is a fish metapopulation structure with density dispersal. The economic part of the model includes two types of participants: $N$ identical villagers and one manager. As the Stackelberg leader, the manager defines the MPA, comprised of no-take sites within the marinescape and the level of enforcement that maximizes the manager’s goal, considering both fish dynamics and the villagers’ equilibrium response. Each individual villager allocates labor across onshore wage labor and fishing labor to maximize their individual income. Each villager considers the other villagers’ choices, the location and level of enforcement within the MPA, distance costs, and fish stocks per site, which results in a spatial Nash equilibrium that constitutes the villagers’ best response to the Stackelberg leader’s MPA.

Fig. 1

Spatial setting. The dashed lines represent the distance from the village to each fishing site and the wide arrows show the dispersal of the fish within the marinescape. The vector below the marinescape figure corresponds to the vectorization of the marinescape matrix

2.2 Fish Dynamics

In common with much of the marine economics literature, we define the biological and spatial setting as a fish metapopulation structure with adult fish density dispersal across the $R \times C$ marinescape. A fishing site, $i$, is one cell in that matrix, indexed from $1$ to $(R \cdot C)$. Cells—or fishing sites—in the first row, $i \in \left\{ {1, \ldots , C} \right\}$, are closest to the shore (see Fig. 1). Fish net growth, harvest, and dispersal over time change the fish stock in each site:

$$\begin{array}{*{20}c} {\varvec{X}_{{\varvec{t} + {\mathbf{1}}}} = \varvec{X}_{\varvec{t}} + G\left( {\varvec{X}_{\varvec{t}} ,\varvec{K}} \right) + \varvec{DX}_{\varvec{t}} - \varvec{H}_{\varvec{t}} ,} \\ \end{array}$$

(1)

where $\varvec{X}_{\varvec{t}}$ is a $\left( {R \cdot C} \right) \times 1$ vector of fish stocks over fishing sites $x_{i}$ at time $t$, $\varvec{K}$ is a $\left( {R \cdot C} \right) \times 1$ vector of site carrying capacities, $\varvec{D}$ is a $\left( {R \cdot C} \right) \times \left( {R \cdot C} \right)$ dispersal matrix, and $\varvec{H}_{\varvec{t}}$ is a $\left( {R \cdot C} \right) \times 1$ vector of the sum of all individual fishers’ harvests from each site $i$ at time $t$. The logistic function $G(\varvec{X}_{\varvec{t}} ,\varvec{K}) = g\varvec{X}_{\varvec{t}} \left( {1 - \frac{{\varvec{X}_{\varvec{t}} }}{\varvec{K}}} \right)$ depicts natural population net growth at each specific site, with $g$ indicating the intrinsic net growth rate. The dispersal matrix $\varvec{D}$ operationalizes the density dependent dispersal process as a linear function of fish stocks of all sites with net dispersal to lower density neighbors that share a boundary through rook contiguity (Sanchirico and Wilen 2001; Albers et al. 2015; see Appendix 1). Our results hold in the steady state stock of fish, $\varvec{X}_{{\varvec{SS}}}$, which occurs when $\varvec{X}_{\varvec{t}} = \varvec{X}_{{\varvec{t} + {\mathbf{1}}}}$.

2.3 Manager Decisions

Each manager selects sites to define an MPA that maximizes either an economic or an ecological goal. First, for the economic goal, we posit a manager who maximizes total income from fishing and non-fishing activities. This goal aligns with the objective function of a benevolent social planner and many lower income country managers (Carr et al. 2019; Madrigal-Ballestero et al. 2017). Consistent with the optimal enforcement literature, the income-maximizing manager accounts for both legal and illegal harvest (Stigler 1970; Milliman 1986).⁴ Second, for the ecological goal, we posit a manager who maximizes avoided aggregate fish stock losses (ASL) across the marinescape, recognizing the fundamental role that fish dispersal plays across the marinescape (Jentoft et al. 2011; Pressey and Bottrill 2009). This ASL-marinescape manager considers both the spatial leakage of fishing effort that generates stock losses in non-MPA sites and fish dispersal across MPA borders. In addition, this manager’s goal considers the additional benefits created by the MPA through the focus on “avoided stock loss” (Andam et al. 2008; Pfaff et al. 2014). The managers choose the size of the MPA (i.e. number of sites in the MPA) and the specific location of the MPA sites, creating an $\left( {R \cdot C} \right) \times 1$ element vector, S, where each element of the vector depicts whether that site is within the MPA:

$$s_{i} = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\text{if site}}\; i\; {\text{is in the MPA}}} \hfill \\ 0 \hfill & {\text{otherwise}} \hfill \\ \end{array} .} \right.$$

The manager chooses one level of enforcement that is constant throughout the MPA at level $\phi \in \left[ {0,1} \right]$, where $\phi = 1$ denotes complete enforcement and implies a probability of being caught and punished of 1.⁵ Following the optimal enforcement literature, managers incur enforcement costs, $\beta$, which here follow a linear and additive form with marginal cost $c$ per unit $\phi$ per unit (Nostbakken 2008; Milliman 1986; Sutinen and Andersen 1985):

$$\beta = \mathop \sum \limits_{i} s_{i} [c\phi ]$$

Each manager accounts for the villagers’ optimal responses to the MPA; thus, the manager optimizes over the outcome of villagers’ Nash equilibrium location and labor choices in response to the MPA at the steady state for fish stocks.

The income-maximizing manager’s decision is:

$$\mathop {\hbox{max} }\limits_{{\varvec{S},\phi }} \mathop \sum \limits_{i} pH_{i} (1 - \phi_{i} ) + \mathop \sum \limits_{n} w\left( {l_{w,n} } \right)^{\gamma } ,$$

The ASL-marinescape maximizing manager’s decision is:

$$\mathop {\hbox{max} }\limits_{{\varvec{S},\phi }} \mathop \sum \limits_{i} [x_{i} - x_{i,OA} ],$$

where $x_{i,OA}$ depicts the open access equilibrium and steady state stock value in site $i$, $p$ is the exogenous price of fish per unit harvest, $l_{w,n}$ is the villager $n$’s allocation of onshore wage labor, $w$ is the exogenous onshore wage, and $\gamma \in \left( {0,1} \right)$ creates diminishing returns to onshore labor (reflecting imperfect labor markets). Both managers make these maximization decisions subject to fish dispersal (Eq. 1) and the best response of the villagers’ optimization and Nash equilibrium, which determine $\varvec{H}$ and $\varvec{X}$. To consider a lower income country setting, we evaluate the managers’ decisions subject to an enforcement budget constraint: $B \ge \beta .$

To reflect common goals of the fishery economics literature, systematic conservation literature, conservation economics literature, and lower income country regional development and conservation managers, we also consider several “naïve” managers who do not consider the entire setting in their decisions. First, a naïve manager with an economic goal maximizes the yield or the fishery profits from the marinescape but disregards the MPA’s impact on total income. Second, two other naïve managers with ecological goals consider only the stock inside the MPA: An ASL-MPA manager considers only the avoided stock loss within the MPA rather than considering the marinescape, and an MPA-stock manager maximizes the fish stock within the MPA rather than considering the additional benefits created by the MPA.

The yield-maximizing manager’s decision is:

$$\mathop {\hbox{max} }\limits_{{\varvec{S},\phi }} \mathop \sum \limits_{i} H_{i} (1 - \phi_{i} )$$

The ASL-MPA maximizing manager’s decision is:

$$\mathop {\hbox{max} }\limits_{{\varvec{S},\phi }} \mathop \sum \limits_{i} s_{i} [x_{i} - x_{i,OA} ]$$

The MPA-stock maximizing manager’s decision is:

$$\mathop {\hbox{max} }\limits_{{\varvec{S},\phi }} \mathop \sum \limits_{i} s_{i} [x_{i} ]$$

We also consider two naïve managers—one based on the ASL-marinescape maximizer and one based on the income-maximizer—who make MPA decisions assuming either that their budget is large enough to induce complete deterrence or that their MPA automatically produces complete deterrence.

2.4 Villagers

We include one village with $N$ identical villagers who have full information about the MPA and the resource setting. Each villager, $n$, seeks to maximize income by allocating labor across two activities: fishing and onshore wage labor. This labor allocation framework reflects the reality that many villagers allocate time across several activities, including between fishing and tourism-related activities (Muthiga 2009; Madrigal-Ballestero et al. 2017) and between fishing and subsistence agriculture (Rahman et al. 2012; Robinson et al. 2014).⁶ To achieve his goal, each villager chooses either to not fish at all, or to fish in one site; and if the latter, how much time to fish, how much time to work onshore, and the fishing site. Each villager recognizes that he has a fixed amount of labor time ($L_{n}$) to allocate to working onshore ($l_{w}$), fishing in a given site ($l_{f,i}$), and traveling in his boat from the village to the fishing site ($l_{d\left( i \right)}$):

$$\begin{array}{*{20}c} {L_{n} \ge l_{w,n} + l_{f,i,n} + l_{d\left( i \right),n} .} \\ \end{array}$$

(2)

Labor time in fishing represents the marginal cost of fishing and labor time for travel to a fishing site captures the fixed distance costs of fishing, both valued at the opportunity cost of time (i.e. the onshore wage). Fishing sites in our model differ due to two types of spatial heterogeneity, in contrast with the standard spatially homogeneous frameworks (e.g. Sanchirico and Wilen 2001). First, each fishing site is located at a different distance from the village, inducing heterogeneous travel costs $l_{d(i)}$. Second, fish dispersal patterns are spatially explicit, inducing heterogeneous returns to fishing across sites.

We assume a standard harvest function:

$$\begin{array}{*{20}c} {h_{i,n} = l_{f,i,n} x_{i} q,} \\ \end{array}$$

(3)

where an individual villager’s harvest in a given site i, $h_{i,n} ,$ depends on the amount of labor time that villager allocates to fishing in the site ($l_{f,i,n} )$ as the marginal cost of fishing, the stock of fish in the site, ($x_{i}$), and the catchability coefficient ($q$). The individual villager’s harvest does not directly depend on the number of other villagers in the site (i.e. no congestion costs), but it indirectly depends on the other villagers’ harvest in the site through the steady state equilibrium stock effect, as in Eq. 1. The total harvest in a given site is the sum of all villagers’ harvests in the site i:

$$H_{i} = \mathop \sum \limits_{n} h_{i,n}$$

(4)

Dynamic stock effects occur through the impact of the total harvest on the state variable $x_{i}$ (an element of $\varvec{X}$ in the equation of fish dynamics) in the steady state. Given this interaction of villagers’ decisions in determining the steady state, a steady state spatial Nash equilibrium defines the fishing locations and fishing labor for each villager, in which each villager has no incentive to move to another site nor to alter their optimally chosen labor allocation. In addition, to simplify the problem, we constrain each villager to fish in at most one site and assume that villagers know the resource stock sizes and distance costs in choosing that site.⁷

Finally, all $n$ villagers share the same goal of maximizing their individual income:

$$\begin{array}{*{20}c} {\mathop {\hbox{max} }\limits_{{i,l_{f,i} ,l_{w} }} \left[ {ph_{i} \left( {1 - \phi_{i} } \right) + w(l_{w} )^{\gamma } } \right],} \\ \end{array}$$

(5)

with $p$, $w$, and $\gamma$ as previously defined. Unlike other models with a fixed entry cost, by explicitly incorporating the onshore wage option in decisions, this model permits exploration of villagers’ responses to MPAs including both changes at the intensive margin of fishing effort and the extensive margin (i.e. exit from fishing). The enforcement parameter $\phi_{i}$ enters each villager’s objective function to reflect the probability that the manager detects and punishes illegal harvesting, which reduces a villager’s expected income from that location and labor choice. In keeping with the lower income country setting, the model posits that villagers lose their illegal harvest if caught, and incur time costs, but not an additional fine. The parameter $\phi_{i}$ is equal to 0 if the site $i$ is not a protected area and equal to $\phi \in [0,1]$ otherwise. $\phi = 1$ implies that no illegal harvesting goes undetected; no-enforcement, $\phi = 0$, implies that no illegal harvesting is detected; and intermediate levels of enforcement, $0 < \phi < 1$, can deter some or all illegal harvesting depending on the fishers’ alternatives.

2.5 Solution Method and Parameters

The model is not analytically tractable, and we solve it using numerical methods in MATLAB for the specific spatial setting in Fig. 1 (see "Appendix 2" for details). We use a $2 \times 3$ grid (i.e. 6 fishing sites) with one fish subpopulation located at the centroid of each cell of the grid.⁸ Sites in column 2 disperse with 3 neighbors through rook dispersal, while sites in columns 1 and 3 disperse with only 2 neighbors, creating heterogeneity in dispersal. A single village comprised of 12 villagers located at the top of the leftmost column, nearest to the first site, provides an asymmetric benchmark marinescape with six biologically identical fish sites (i.e. each site’s carrying capacity and intrinsic growth are identical) that differ only in their distance from the village.⁹ The villagers’ travel time is simply the Cartesian distance from the village to the centroid of the fishing site (parameters in Table 1). The solution is the spatial Nash equilibrium of the $N$ identical villagers’ best response to the MPA setting, including each villagers’ fishing site choice and optimal labor allocation decisions at the long-run biological (i.e. fish stock) steady-state. We parameterize the model to achieve an open access baseline setting with rents dissipated in each fishing site to reflect an overfished pre-policy setting. In our parameterization, adding a marginal unit of labor per villager or adding more villagers leads to no change in fishing labor or location decisions because rents are dissipated above covering fixed distance costs to each site. Additional labor, or villagers, is optimally allocated to onshore wage work because no fishing rents exist in the marinescape that cover distance costs.¹⁰

Table 1 Parameter values

3 Results and Interpretation

Section A presents the open-access results of fisher decisions that generate the baseline, no-MPA setting. Section B presents the optimal MPAs of the income-maximizing and ASL-maximizing managers across budgets. Section C discusses each of the manager control variables for their impact on villager decisions and develops intuition and general statements about optimal MPA design.

3.1 Open-Access (Baseline)

To determine the impact of an MPA policy, we use the model of open access equilibrium to define a baseline, working from the opposite starting point of, but in similar fashion to, the empirical park effectiveness analyses’ use of a von Thunen model to predict patterns of resource extraction without a PA. Villagers’ equilibrium labor allocation and fishing site decisions depend directly on the onshore wage, distance costs (opportunity cost of time), time spent fishing, and the fishing site choice.¹¹ Returns from fishing reflect total fishing effort at a site and net fish stock following dispersal. In the open-access equilibrium, for our specific calibration, all villagers choose to fish, and fishing occurs in 5 of the 6 sites. Villagers’ labor allocations differ (Fig. 2a); more villagers fish in sites close to the village than far from the village due to distance costs (Fig. 2b). Site 1, closest to the village, hosts the highest number of villagers and total fishing labor (Fig. 2b), which drives down fish stock there (Fig. 2c). The stock levels in each site are the elements of the vector of open access baseline stocks, $\varvec{X}_{{\varvec{OA}}}$.

Fig. 2

Open access. a Depicts the labor allocation per villager in each site. For example, each villager who fishes in site 1 spends about 11 h fishing (white), about 1 h traveling to the fishing site (light gray), and the remaining 12 h working onshore (black). This graph does not fully reflect the spatial configuration of the setting demonstrated in Fig. 1 because it uses the vectorized matrix of sites travel time increases the farther from the village to the fishing site, and it increases monotonically in the first row of the matrix (sites 1, 2, and 3). However, site 4 (row 2, column 1) is closer to the village than site 3 (row 1, column 3), and has a shorter travel time. In sites with no bar indicated in the figure, such as site 6, no one fishes. b Total fishing labor across all villagers per site and the number of villagers in each site (numbers over bars). Panel C shows the fish stock in each site

The open access baseline reflects both distance costs and dispersal. Distance costs alone keep villagers from the most distant site (site 6) despite high equilibrium fish stocks there (Fig. 2c), just as distance protects the interior of forests surrounded by encroaching or extracting villagers (Albers 2010; Robinson et al. 2011). Distance acts as a fixed cost to entry in a particular site, implicitly valued at the wage rate, and reduce the labor time available for wage work and fishing. Therefore, in a labor-constrained setting, sites with high marginal fishing values can remain unfished. The many villagers who fish in site 1 each face low travel costs but also low steady state stocks, and allocate the least time to fishing of all villagers (Fig. 2a). Heterogeneity in dispersal results in sites in column two (sites 2 and 5) supporting more fishing than sites in column three (sites 3 and 6), and only slightly less than sites in column one (sites 1 and 4).¹² The baseline parameterization and pattern of fishing effort reflects observations in Costa Rica, where villagers who fish agglomerate near shore and fish less per person than the smaller number of villagers located at more distant sites (Madrigal-Ballestero et al. 2017).

3.2 Optimal MPA Location, Size, and Enforcement Level

The optimal MPAs—set of sites and enforcement level—of the income-maximizing manager and the ASL-marinescape manager differ from each other, and across budgets, in size (number of MPA sites), configuration (specific set of sites), and enforcement levels ($\phi$) (Fig. 3).¹³ With no budget constraint, the ASL-maximizing manager includes the entire marinescape in the MPA, deterring all fishing. Avoided stock losses in the marinescape rise monotonically as the enforcement budget is parametrically increased from zero until complete deterrence occurs at $\phi = 0.584$ (Fig. 3, last column), at which point all villagers have exited fishing. In contrast, the unconstrained income-maximizing manager places the MPA in the 2 most fished pre-MPA sites and includes a third MPA site (site 5), but chooses not to fully enforce the MPA. For our specific calibration, 2 villagers are induced to exit fishing, which reduces the over-extraction pressure in non-MPA and MPA sites and improves aggregate income (first and last column, Fig. 4b), yet does not completely deter extraction in the MPA (Fig. 3). The income-maximizing MPA creates avoided stock loss within the MPA that is partially offset by increased stock loss in two non-MPA sites, including the most distant site (6), in which no fishing occurs without the MPA (Fig. 4c).

Fig. 3

Optimal MPA for each goal. The first column depicts the open access distribution of villagers. The number of villagers in each site is identified in the marinescape figure, and the number of villagers who choose not to fish is indicated by that number in the village location on the marinescape. The highlighted sites are the optimal MPA sites for each row’s manager. This figure’s last column contains the unconstrained budget scenarios discussed in Sect. 3.1

Fig. 4

Optimal MPA to maximize income. Each column represents a different budget level from 0 (i.e. open access) to unlimited. a Labor allocation per villager; the white bars represent time spent fishing, the gray bars represent time traveling, and the black bars represent time spent working on shore. b Total fishing labor per site and the number of villagers in each site. c The fish stock. In b, c, black bars represent sites within the MPA

In many settings, particularly in lower-income countries, budget constraints limit the level of enforcement that a manager can exert within an MPA. For both manager types, as we parametrically increase the enforcement budget from zero, the budget-constrained-optimal MPA changes until the budget permits the optimal amount of enforcement for the optimal MPA size and siting (Figs. 3, 5 and 6). The ASL-maximizing manager typically selects larger MPAs and enforces at higher levels than income-maximizing managers (Fig. 3, 5 and 6). At most budget levels, villagers respond to the ASL-maximizer’s MPAs by exiting fishing, concentrating fishing effort in some sites that receive dispersal, and avoiding fishing in some MPA sites (Fig. 7). In contrast, the income-maximizing manager typically locates their MPAs close to the village where the MPA restrictions solve some of the open-access over-extraction problem that arises from low distance costs in near-village sites. Villagers respond to the MPA by exiting fishing and distributing remaining fishing across the marinescape.

Fig. 5

Changes in size and configuration when maximizing ASL Marinescape with different budgets. The gray sites are the optimal MPA sites for each budget level and the MPA size is the number of sites included in the MPA. Although the optimal enforcement level increases between budget levels reported here, this figure contains every MPA size and configuration, which vary discretely as budget increases

Fig. 6

Changes in size and configuration when maximizing income with different budgets. The gray sites are the optimal MPA sites for each budget level and the MPA size is the number of sites included in the MPA. Although the optimal enforcement level increases between budget levels reported here, this figure contains every MPA size and configuration, which vary discretely as budget increases

Fig. 7

Optimal MPA to maximize avoided fish stock in the marinescape. Each column represents a different budget level from 0 (i.e. open access) to unlimited. a Labor allocation per villager; the white bars represent time spent fishing, the gray bars represent time traveling, and the black bars represent time spent working on shore. b Total fishing labor per site and the number of villagers in each site. c The fish stock. In b, c, black bars represent sites within the MPA

3.3 MPA Instruments to Determine Villager Responses

The specific choices of location/configuration, size, and enforcement of an MPA—the MPA manager’s control variables in the model and policy instruments in practice—determine the reaction of villagers to the MPA, which determines the MPA’s ecological and economic outcomes. Considering how each instrument influences villager responses, and how the instruments interact in that influence, informs general rules for MPA design across settings.

3.3.1 Configuration of the MPA

The configuration of MPA sites enters villagers’ decisions through the impact of distance costs on fishing site choice and through how dispersal affects returns to fishing in non-MPA sites. With low enforcement budgets, an income maximizing manager relies on MPA configuration to create dispersal patterns that provide incentives—a carrot—for villagers to choose particular sites for fishing. For example, for our specific calibration, at a low budget, the income-maximizer includes site 5 in the MPA, which creates enough dispersal to sites 2, 4, and 6 to encourage villagers to spread out across sites 1 and 2 near the village and sites 4 and 6 (Figs. 3 and 4). The ASL-marinescape manager’s particular configuration of MPA sites varies considerably as budget increases (Fig. 5). At high budgets, for our specific calibration, this manager’s configuration creates deterrence in sites that increase dispersal to the near-village site (site 1), which results in both high levels of fishing and negative avoided stock loss in that site (Figs. 3, 5 and 7).

3.3.2 Enforcement Level

Enforcement reduces expected fishing returns in a protected site, which enters villagers’ decisions as a disincentive—a stick—to fishing and fishing effort in particular sites and to fishing effort. For our specific calibration, the ASL-maximizing manager is able to deter all fishing in the marinescape with $\phi \le 0.6$ (Fig. 3); perfect detection, $\phi = 1$, is not necessary to deter all fishing. However, the minimum level of enforcement that produces complete deterrence does require relatively large budgets (Fig. 3). In contrast, the income-maximizing manager achieves their optimal MPA management at relatively low enforcement and budget levels because this manager does not deter all fishing and instead deters enough fishing effort to reduce over-extraction from open access by inducing exit and limiting extraction in near-village sites (Fig. 3). While the income-maximizing manager finds an internal optimum enforcement level that does not deter all fishing in their MPAs, the ASL-maximizing manager spends their entire enforcement budget until achieving complete deterrence.

3.3.3 MPA Size

With enforcement budgets spread across the MPA, decisions reflect trade-offs between size and enforcement levels when budget constraints bind. For the income maximizing manager, in general, MPA size increases with the budget until the budget-unconstrained optimal size is reached (Fig. 3). For the ASL-marinescape maximizing manager, however, increases in the budget lead unambiguously to increases in avoided stock loss, but the optimal size of the MPA varies non-monotonically with budget because of tradeoffs between the size of the MPA and the level of enforcement possible across the MPA (Figs. 3, 5 and 7). A budget increase can decrease the optimal MPA size when the extra budget permits increased enforcement across a smaller MPA, resulting in increased ASL.

3.3.4 Combining Control Variable Choices

Budget-constrained managers face interactions and trade-offs among their choice variables. The choice of enforcement level interacts with the choice of MPA size and location because the enforcement budget is spread evenly across the whole MPA; because more distant sites require lower levels of enforcement to deter fishing (Albers 2010; Robinson et al. 2010; Albers et al. 2015); and because can enforcement result in “policy-induced” fish sources for dispersal to other sites that villagers have a positive incentive to choose.

3.3.5 General Rules for MPA Siting

Although the details of our optimal MPA results are specific to one calibration, examining the open access villager response to other settings of distance costs and wages, in combination with how MPAs alter villagers’ decisions, reveals general rules for MPA siting in other settings.¹⁴ The central idea of this paper is that managers make effective policy when they incorporate the expected response of resource users—site, effort, and exit decisions—in the MPA policy design, which implies that managers can design and enforce MPAs to induce changes in villager decisions. First, if distance costs are either small or homogeneous, managers cannot take advantage of distance-enforcement trade-offs. Instead, the optimal MPA configuration alters villagers’ site decisions only through the impact of MPAs on dispersal (Appendix 3). Second, settings with a high onshore wage induce villagers to allocate relatively less labor to fishing due to marginal returns tradeoffs and to choose low-distance cost fishing sites due to the high opportunity cost of time (Albers et al. 2015). Similarly, settings with high distance costs also induce low fishing labor allocations and near-village fishing site choices (Albers et al. 2015).

Based on these observations, a general rule for real world managers with an income-maximization goal is to locate moderate-sized MPAs in sites where enforcement leads to enough exit and reduction in fishing effort to solve the open access over-extraction problem—using some “stick” of enforcement and some “carrot” of directing dispersal. In contrast, a general rule for real world managers with an ASL-maximizing goal is to use their limited budgets to locate and size MPAs that create effective no-take sites that direct fish dispersal to sites close to the village where fishing effort is higher. ASL-managers with higher budgets can induce exit from fishing—primarily relying on the “stick” of enforcement to deter fishing and using the “carrot” of directing dispersal to sites of high fishing. In high wage or high distance cost settings, optimal MPA locations move closer to the village and require lower levels of enforcement due to the lower level of over-extraction generated by either the high wage or the high distance costs pulling villagers out of fishing overall and discouraging distant site fishing (Albers et al. 2015).

4 Results and Analysis of Naïve Manager Decisions

In our model, managers’ constrained-optimal MPA choices are made considering the impact on villagers’ livelihood or the full marinescape; and fully accounting for the response of all villagers to an MPA and its enforcement level. For livelihood considerations, our managers focus on total labor income rather than only that generated by fishing. Villagers, in turn, respond to the actual enforcement level in MPAs when making fishing effort and site decisions. However, many MPA economic models and practical siting decisions ignore one or more these aspects. This section explores how such “naïve” assumptions impact MPA design and outcomes.

4.1 Yield-Maximizing and Fishery Profit-Maximizing MPA Decisions

Much of the fishery policy and fishery economics literature focuses on how policies such as MPAs improve yield (harvest) and fishery profits.¹⁵ We posit a “naïve” yield-maximizing manager and compare their optimal MPA choice with a manager who optimizes over the MPA’s full impact on economic development, as measured by total income rather than fishing income alone. First, in the absence of an onshore wage option, income is isomorphic with yield, and the two manager types choose identical MPAs. Second, across a range of enforcement budgets and on-shore wage options, the income-maximizing manager’s optimal choice of MPA differs from the yield-maximizing manager’s in size, configuration/location, and enforcement level. For our specific calibration, the income-maximizer’s MPA contains 3 sites, whereas the budget-unconstrained optimal MPA for the yield maximizer contains two near-village sites and uses a lower level of enforcement (Figs. 3 and 14 in the Appendix). The income-maximizers’ strategy induces exit, whereas the yield-maximizing manager’s MPA induces villagers to choose fishing sites that reduce the stock effect of over-extraction in particular sites and creates patterns of effort that generate, or take advantage of, dispersal. These differences in MPA strategies imply that analysts who focus only on fishery yield and profits miss opportunities to use MPAs to improve regional incomes. In addition, yield analyses cannot address policies that pair MPAs with income-generating projects that can reduce pressure on fishery resources by inducing villagers to replace fishing effort with new on-shore income-generating activities.

4.2 MPA-Focused Decisions

Many conservation goals rely on metrics such as the size of the PA rather than metrics that convey the additional conservation benefits created by PA. For example, the Convention on Biodiversity identifies percentages of land and marinescapes to be in PAs. Similarly, PA managers’ face mandates to focus on the management and conservation of their particular PA rather than considering the PA’s contribution to conservation at the system or landscape level. Here, we explore how the choices of two MPA-focused naïve managers differ from a marinescape perspective.

4.2.1 Maximizing Avoided Stock Loss in MPAs

Although policy and economics literatures describe the leakage of extraction activities, and spatial spillovers of ecosystem services, from protected areas into other areas, many PA siting decisions and park effectiveness evaluations do not consider these landscape effects (Delacote and Angelsen 2015; Robinson et al. 2013). Here, a manager who focuses only on the avoided stock loss in the MPA and is “naïve to the marinescape”, the ASL-MPA manager, places the entire marinescape within the MPA at an unconstrained budget level (Figs. 3 and 16 in the Appendix), exactly as does the ASL-marinescape manager. At lower budgets that reflect low and middle income settings, managers face a tradeoff between the MPA size and the level of enforcement achievable at each budget and consequently choose smaller MPAs to ensure that the probability of being caught is sufficient to reduce extraction within the MPA. The “naïve” ASL-MPA manager typically chooses an MPA that is larger, where the probability of a fisher being caught is smaller, and with a different configuration, than the ASL-marinescape choice of MPA (Figs. 5 and 17 in the Appendix). The ASL-MPA manager’s MPAs include sites with complete deterrence, often including the most village-distant sites (3 and 6) that are easiest to protect due to distance; but also include near-village site 1 when the probability of being caught encourages villagers to exit. In settings where sites both in and outside of the MPA contribute ecological benefits, these differences imply inefficiencies associated with designing MPAs without considering marinescape-wide impact.

4.2.2 Maximizing MPA Stock

Some frameworks for selecting MPA sites focus on conserving the highest possible stocks within the MPA rather than using MPAs to produce the highest avoided stock losses within the MPA or across the marinescape; the emphasis is on stock levels rather than on the additionality of the policy.¹⁶ We define the MPA-stock maximizing manager’s optimal MPA across budgets (Appendix 4 and Appendix Figs. 18 and 19). The MPA-stock maximizing manager’s MPA creates 18, 34, 57, and 78 percent of the avoided stock loss generated by the ASL-MPA maximizing manager at budgets 5, 15, 25, and 35, respectively. These results demonstrate that ecological triage methods of establishing MPAs, such as basing MPA locations on the level of a metric as opposed to basing MPA decisions on the additional conservation created by the MPA, lead to less conservation than can be achieved at each budget.

4.3 Assuming Full Enforcement

MPA managers in lower-income countries must often choose the location and size of an MPA while considering limited enforcement budgets that are insufficient to prevent all fishing within the MPA. Yet economic models, implementation software, and managers often tacitly assume that enforcement is costless or leads to perfect compliance (Albers et al. 2016; Watts et al. 2009). We define a naïve ASL-marinescape and a naïve income-maximizing manager who assume that any MPA completely deters harvest or that their budget is large enough to generate the desired level of deterrence. For each of their optimal MPAs, we calculate the level of enforcement possible for that MPA per budget and determine the villager response to the MPA at that level of enforcement rather than at the assumed complete deterrence. We compare these budget constrained outcomes from the complete-deterrence MPA to the outcomes from the optimal MPAs across budgets.

The enforcement-naïve ASL-maximizing manager chooses an MPA covering the entire marinescape, and assumes all villagers will become wage-specializers (Appendix 7). Yet with low enforcement budgets spread over the large MPA, the MPA creates little actual deterrence, and this strategy has minimal impact on villager’s decisions with only marginal decreases in fishing effort (Appendix 7). As compared to the ASL-maximizing manager who concentrates the limited budget for enforcement in a smaller number of sites, the enforcement-naïve ASL-maximizing manager’s MPA with budget-constrained enforcement generates 30 percent of the avoided stock losses at a budget of 5, and 83 percent at a budget of 25 (Appendix Figs. 20 and 21).

The enforcement-naïve income-maximizer does not aim to deter all fishing, yet, at low budgets, they incorrectly assume their budget is large enough to create their desired level of deterrence. In this case, their “naïve” choice of MPA is larger and has less enforcement at low budgets than the income-maximizer MPA (Appendix 7). In contrast, if the enforcement-naïve income-maximizer assumes that any MPA generates complete deterrence, our baseline income-maximizing manager remains in open-access rather than use MPAs that over-deter villagers from fishing, which reduces income. This type of naivete loses the gains possible from using incompletely enforced MPAs, as in the optimal income-maximizing MPAs.

5 Discussion and Policy Implications

5.1 Management Goals

MPAs are recognized as an important tool for fishery management by both resource economists and fishery practitioners (Carr et al. 2019; Rassweiler et al. 2012; Castilla 2010). Other conservation and regional development organizations view MPAs as tools for broader development or conservation goals (Jentoft et al. 2011; Geange et al. 2017). More generally, MPAs are viewed as mechanisms to provide both marine conservation values and fishery incomes (Jentoft et al. 2011; Smith and Wilen 2003; Gaylord et al. 2005; Gaines et al. 2010). Here, we find considerable differences across all budget levels in the optimal MPAs designed for economic goals and for ecological goals. Economic goals that appear similar—maximizing yield and maximizing income—lead to different optimal MPA sites and enforcement levels across many budget levels, which serves as a caution to economists and managers about inappropriate interpretations of MPA frameworks based on yield profits alone. Because many villagers’ income derives from labor allocation decisions between fishing and onshore wage activities, and because reaching more distant fishing sites requires labor that could otherwise be spent on income-generating activities, a focus on yield in MPA siting and analysis fails to fully characterize the impact of MPAs on villagers’ total income. Similarly, two ecological goals—avoided stock loss at the marinescape level and at the MPA level—are achieved with different MPA sites and enforcement levels until the budget is sufficient for the entire marinescape to be fully protected from fishing. Because ecological benefits derive from the whole marinescape, including leakage of fishing and spillovers of fish across MPA borders, a focus on in-MPA metrics fails to capture benefits both lost and created outside of the MPA. The differences in constrained and unconstrained MPAs across budgets and managers demonstrate that efficient MPA site selection and management requires careful consideration of the appropriate goal of creating MPAs and of the relevant budget level.

5.1.1 Policy Effectiveness

Economists may evaluate policy based on its effectiveness at creating positive net change or preventing negative outcomes. Conservation policy may follow a triage approach, such as focusing limited budgets on conserving high-stock areas. Although the bulk of our analysis considers avoided fish stock losses, we also show that managers who seek to maximize the stock within the MPA—rather than the avoided stock loss—employ marinescape-wide MPAs that, with low budgets, produce limited additional benefits because they fail to change villager behavior. These results demonstrate the missed conservation opportunities that derive from decisions based on total stock size within MPAs rather than on the conservation additionality created by the MPA.

5.2 Incomplete Enforcement

In the systematic conservation planning and PA economics literatures, protected area siting decisions rarely consider the impact of incomplete enforcement on extractor decisions and instead assume costless and complete enforcement (Ando et al. 1998; Sanchirico and Wilen 2001). In practice, no protected area siting software, such as Marxan, contains enforcement costs with a reaction of villagers (fishers or terrestrial extractors) to that enforcement within the site or sizing decision (Watts et al. 2009; Arafeh-Dalmau et al. 2017). Although the practical implementation of MPAs addresses villagers’ needs, including the use of benefits-sharing or community management and sometimes re-design of MPAs based on villagers’ concerns, such programs typically occur after the selection of the MPA sites. Similarly, the economic literature on terrestrial park effectiveness largely ignores the impact of enforcement spending on that effectiveness. Although transponder signals present a low-cost enforcement mechanism, incomplete enforcement occurs in both low- and high-income country MPAs. Given the “paper park” phenomenon and suggestions from MPA managers that enforcement budgets are lower than needed to induce full compliance, our results demonstrate that ignoring enforcement costs and villager reactions to incomplete enforcement limits the conservation gains possible from MPAs. Economic efficiency requires decisions based on the reality of costly and incomplete enforcement—whether due to budget constraints or optimal marginal tradeoffs.

5.3 Broader Policy Implications

The results here inform discussion about the implementation of MPAs that are not no-take reserves; marinescape versus MPA perspectives; and other settings.

5.3.1 Beyond No-Take Zones: IUCN Classifications

Limited enforcement budgets in lower-income country no-take PAs lead to illegal harvest, or poaching, within PAs. Our analysis identifies situations in which the yield or income maximizing manager chooses not to use the full enforcement budget but rather chooses to allow some illegal harvest. This situation arises when a no-take mandate contradicts a manager’s preference to maximize yields or income across a marine or landscape. To avoid costly conflict between PA guards and villagers, but still achieve their objectives, managers in lower-income country settings might choose less restrictive IUCN classifications of their MPA rather than implementing incompletely enforced no-take reserves (Robinson et al. 2010, 2013; Ferraro and Hanauer 2011). For example, some of Tanzania’s MPAs permit villagers to harvest within MPAs, with managers enforcing gear restrictions or community access restrictions instead of a complete ban on fishing. Similarly, in one of Tanzania’s IUCN category II PAs, the management committee permitted limited harvesting inside the perimeter of the reserve to reduce overall ecological damage and conflict resulting from imperfect efforts to fully enforce the no-take mandate (Robinson et al. 2011). In addition, some empirical terrestrial research suggests that extraction-permitting PAs can avoid more deforestation than more restrictive PAs (Pfaff et al. 2014; Ferraro et al. 2013). Some PAs have managed to stop land-use change and degradation in cases where PAs use co-management and allow multiple uses (Nelson and Chomitz 2011; Herrera et al. 2019; UNEP-WCMC 2016; Robinson et al. 2008). Our framework of PA choices as a function of villagers’ responses could be the basis for future research of access restrictions or IUCN classification—beyond no-take reserves—as a choice variable to achieve both ecological and economic goals and for analyzing co-managed MPAs instead of enforced MPAs (Robinson et al. 2008).

5.3.2 MPA- Versus Marinescape-Focused Resource Conservation

Our analysis demonstrates clear inefficiencies at the level of the marinescape when the MPA manager does not account for the impact of leakage of fishing effort, or the impact of dispersal of fish, to non-MPA sites. Although inefficient, many organizations and managers base their assessment of success on in-MPA status and economists evaluating park effectiveness often consider the avoided losses within the park rather than across a landscape. In contrast, in other settings, such as establishing REDD forests, landscape perspectives and the role of leakage are central to the discussion, albeit often without a model of how resource extractors respond to a policy to create leakage. In our open access with distance costs setting, fishers’ effort can only “leak” to sites to which the MPA generates enough dispersal to support additional effort above the starting point equilibrium effort levels (as in Sanchirico and Wilen 2001). Organizations seeking efficient production of avoided stock losses across the marinescape must charge the MPA implementation team with that marinescape goal rather than assume that a high in-MPA effectiveness at avoiding stock losses correlates well with avoided stock losses at the marinescape level. To make such marinescape decisions, however, managers must predict the pattern of extraction that results from villagers’ response to the MPA in their MPA design decisions, as is done here.

5.3.3 Across Settings

This research focuses on settings in which resource extractors make labor allocation decisions across income-generating activities facing time constraints and distance costs; and on costly enforcement settings. To apply this model and results to other settings, parameters can be changed and budget constraints removed. For example, settings in which fishers only fish can be considered by setting wage to zero (as in Albers et al. 2015, 2020). Similarly, settings in which distance costs do not dominate fisher site choices can be considered by setting distance costs to zero (as in Albers et al. 2015, 2020). Although enforcement budget constraints appear particularly binding in many lower income settings, the sheer size of PAs and diversity of illegal activities in high-income country settings pose challenges to enforcement of MPA restrictions. For example, illegal fishing in MPAs can be difficult and costly to identify if fishers employ avoidance activities such as turning off transponders. Our framework focuses on using MPAs to alter fishing activities, which can generalize to considering MPAs as part of conservation policies to achieve ecological goals beyond the fish stocks considered here, such as removing long-line fishing from turtle or whale migration paths (Capitán et al. 2020; Hayes et al. 2018). Given the emphasis on fisher decisions, however, this framework does not generalize well to settings in which non-fishing activities generate threats to MPA goals, such as tourists harassing protected marine animals (NOAA 2020).

5.4 Relationship to Research and Policy Literatures

5.4.1 Ongoing and Future Research

This framework forms a foundation to explore other aspects of MPA siting and management. In addition to detailed case study analysis, ongoing research explores socioeconomic aspects of these settings such as making on-shore wages endogenous to the labor supply and to MPA quality, incomplete labor and resource markets, and the role of alternative income-generating projects or conditional and non-conditional payments in inducing conservation. Similarly, analyses of different ecological settings in terms of dispersal patterns, of heterogeneity across marine sites including hotspots, and of ecological goals other than resource stocks will provide information for managers of these complex systems (Capitán et al. 2020; Albers et al. 2015, 2020). Further work on heterogeneous enforcement patterns and contrasting enforcement through “caught in the act” versus “caught with contraband” will also improve the efficiency of MPA management. In addition, analysis of the optimal MPA decisions during a dynamic transition from degraded resources to a steady state resource will prove particularly important for the lower income country context in which complete moratoria on fishing presents a problematic policy tool in the presence of subsistence fishers, slack labor markets, and limited regulatory capacity.

5.4.2 Contributions to Research and Planning Literatures

This research contributes directly to the fishery economics literature in several ways. First, the open access baseline and all MPA policy analyses here employ a novel spatially-explicit model of individual fisher behavior that contains the micro-foundations of fishing site choice and fishing effort decisions in settings with distance costs and labor tradeoffs, and aggregates individual fishing decisions across all fishers in a spatial Nash equilibrium. While many models assume away heterogenous distance costs, enforcement costs, and labor allocation decisions, the modeling framework here is inclusive of artisanal fishing settings with such characteristics while being general to many other settings by varying parameters—such as setting wage, enforcement costs, or distance costs to zero. Second, the analysis of multi-site MPAs informs the fishery economics literature on MPAs as a fishery management tool in which enforcement operates as a deterrent to fishing while the size and configuration of the MPA influences dispersal to encourage fishing in particular sites. Third, considering income instead of the more common fishery profits (here equivalent to yield) broadens the impact of fishery economics because income is a useful metric in many settings; fishery profits does not generate the same MPA policy as income; and evaluating broader policies, such as those that link income-generating projects to MPA designation, requires addressing income and labor allocation decisions. This research also informs the systematic conservation planning literature by using economic analysis of the response to MPAs in defining optimal MPAs rather than addressing people’s needs separately, as is common in practice. Integrating people’s response into the MPA site selection increases economic efficiency, as does the emphasis here on the additional benefits created by the MPA rather than levels of benefits. In addition, this analysis identifies the importance of MPA design that reflects the reality of limited enforcement budgets and incomplete enforcement in many settings.

6 Conclusion

The model results here inform MPA design decisions—including size, location, and enforcement—over a for a range of goals in settings where villagers face labor allocation decisions and distance costs and where managers face limited enforcement budgets. We demonstrate explicitly how the response of villagers to an MPA policy influences the optimal choice of the MPA. Yet few models—and few practical MPA siting and implementation procedures—consider those reactions at the point of selecting MPA sites. Overall, MPA siting and management decisions that do not reflect the equilibrium villager response to the MPA overestimate conservation benefits and establish inefficient MPAs, due to the misrepresentation of the villagers’ reaction to the MPA and its enforcement in terms of illegal fishing, fishing site choices, and fishery exit.

Appendices

Appendix 1: Dispersal Matrix

In common with much of the marine economics literature, a fish metapopulation structure on a grid with density dispersal defines the biological and spatial setting. Here, we follow Sanchirico and Wilen (2001), Smith and Wilen (2003), and Albers et al. (2015) in characterizing the fish dispersal in a patchy setting. Fish stock changes in each site occur through growth over time, harvest, and dispersal:

$$X_{t + 1} = X_{t} + G\left( {X_{t} ,K} \right) + DX_{t} - H_{t}$$

(6)

where $X_{t}$ is a vector of fish stocks in each location in time $t$, $K$ is a vector of carrying capacities, $G(X_{t} ,K)$ is the net growth function, $D$ is the dispersal matrix, and $H_{t}$ is a vector of the sum of all fishers’ harvest in a location at time $t$. All vectors are $1 \times IJ$ (i.e. the dimensions of the closed system are $I \times J$), and each element of $X_{t} , K, H_{t}$ refers to a specific $i \times j$ site. The logistic growth function $G\left( {X_{t} ,K} \right) = gX_{t} \left( {1 - \frac{{X_{t} }}{K}} \right)$ depicts the specific per-site growth with $g$ indicating the intrinsic net growth rate.

The $IJ \times IJ$ dispersal matrix $D$ operationalizes the dispersal process as a linear function of fish stocks and densities of all sites (Sanchirico and Wilen 2001). For example, in a three-site system with patches indexed $\left\{ {1,2,3} \right\}$, the following dispersal matrix contains the information about dispersal across all possible combinations of the three patches:

$$DX_{t} = \left[ {\begin{array}{*{20}c} {d_{11} } & {d_{12} } & {d_{13} } \\ {d_{21} } & {d_{22} } & {d_{23} } \\ {d_{31} } & {d_{32} } & {d_{33} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {X_{t1} } \\ {X_{t2} } \\ {X_{t3} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {a_{1} \left( {\frac{{X_{t2} }}{{K_{2} }} - \frac{{X_{t1} }}{{K_{1} }} } \right) + a_{2} \left( {\frac{{X_{t3} }}{{K_{3} }} - \frac{{X_{t1} }}{{K_{1} }} } \right)} \\ {a_{1} \left( {\frac{{X_{t1} }}{{K_{1} }} - \frac{{X_{t2} }}{{K_{2} }} } \right) + a_{3} \left( {\frac{{X_{t3} }}{{K_{3} }} - \frac{{X_{t2} }}{{K_{2} }} } \right)} \\ {a_{2} \left( {\frac{{X_{t1} }}{{K_{1} }} - \frac{{X_{t3} }}{{K_{3} }} } \right) + a_{3} \left( {\frac{{X_{t2} }}{{K_{2} }} - \frac{{X_{t3} }}{{K_{3} }} } \right)} \\ \end{array} } \right]$$

(7)

This matrix implies that

$$D = \left[ {\begin{array}{*{20}c} {d_{11} } & {d_{12} } & {d_{13} } \\ {d_{21} } & {d_{22} } & {d_{23} } \\ {d_{31} } & {d_{32} } & {d_{33} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\frac{{ - (a_{1} + a_{2} )}}{{K_{1} }}} & {\frac{{a_{1} }}{{K_{2} }}} & {\frac{{a_{2} }}{{K_{3} }}} \\ {\frac{{a_{1} }}{{K_{1} }}} & {\frac{{ - (a_{1} + a_{3} )}}{{K_{2} }}} & {\frac{{a_{3} }}{{K_{3} }}} \\ {\frac{{a_{2} }}{{K_{1} }}} & {\frac{{a_{3} }}{{K_{2} }}} & {\frac{{ - (a_{2} + a_{3} )}}{{K_{3} }}} \\ \end{array} } \right]$$

(8)

Here, $\left\{ {a_{1} ,a_{2} ,a_{3} } \right\}$ represent pairwise dispersal coefficients for each pair of sites. For example, $a_{1}$ affects dispersal between sites 1 and 2. Each column of $D$ sums to zero, which guarantees (mechanically) zero net dispersal.

For an $I \times J$ grid, we generalize an $IJ \times IJ$ dispersal matrix, where each element is $d_{kl} = \frac{{b_{kl} }}{{K_{l} }}$.¹⁷ In this paper, dispersal occurs between neighbors that share a boundary through rook contiguity and not across site corners as in queen-contiguity. Numerators $b_{kl}$ derive from a system-wide dispersal coefficient $m \in [0,1]$, where

$$\begin{aligned} & b_{kl} = 0,\quad {\text{if}}\;k \ne l\,{\text{and patches}}\;k\;{\text{and}}\;l\; {\text{are not neighbors}} \\ & b_{kl} = \frac{m}{{\nu_{l} }},\quad {\text{if}}\;k \ne l\; {\text{and patches}}\;k\;{\text{and}}\;l\; {\text{are neighbors,where}}\;\nu_{l} \; {\text{is patch}}\;l'{\text{s total number of neighbors (i}} . {\text{e}} . ,\;\nu_{l} = 2 \;{\text{for a corner patch}}) \\ & b_{ll} = - \mathop \sum \limits_{k \ne l} b_{kl} ,\quad {\text{ constraining each column of}}\;D\; {\text{to sum to zero}}. \\ \end{aligned}$$

(9)

These conditions ensure, respectively, that direct dispersal only occurs between contiguous sites, that the same fish cannot disperse to multiple neighboring sites, and that the dispersal matrix maintains a constant aggregate fish stock.

Appendix 2: Description of Numerical Methods

We solve the villagers’ problem (i.e. optimize income) for each unique MPA policy defined by the combination of three policy parameters (i.e. size of the MPA, sites protected, and enforcement level). For a given set of policy parameters, this solution is characterized by three conditions: (1) stock in steady-state, (2) labor is optimally allocated, and (3) fishers are in a spatial Nash equilibrium. Finally, the output is villagers’ best response to each unique MPA.¹⁸

Figure 8 outlines the solution method; each box represents a Matlab script. The script managerProblem.m controls the execution of the code. First, we set all parameters (setParameters.m) and create the spatial setting (defineNeighbors.m, defineDispersal.m, and distanceFromVillage.m). Second, we define all possible MPA configurations that can be set given the parameters (in our case, with 2 rows and 3 columns, there are 64 different MPA configurations. See Fig. 9).

Fig. 8

Solution method

Fig. 9

All possible MPA configurations

Third, we iterate over all 64 possible MPA configurations and 500 possible enforcement levels (from 0 to 1 with a step size of 0.002). Inside this nested loop (32,000 iterations) we call the script to solve the villager’s problem (fishersProblem.m).¹⁹ For a given set of policy parameters (i.e. iteration in the nested loop), we start by creating a vector with all possible spatial distributions of fishers (in our case, with 12 fishers, there are 18,564 distributions. See Fig. 10).

Fig. 10

All possible fishers’ distributions

In the next step, we iterate over all the 18,564 spatial distributions of fishers and solve for the steady state and their optimal allocation of labor (getSteadyStateOptima.m, nlsSolver3.m, and steadyStateFunction.m).²⁰ In the last step of the solution of the villagers’ problem (given a set of policy parameters), we identify which of the solutions previously identified are a spatial Nash equilibrium (findNashEquilibrium.m). To do so, we discard all solutions in which any fisher has an incentive to move (getStartDeviations.m, getMoveDeviations.m, and getIndices.m). The resulting solutions (i.e. non-discarded solutions) are then saved and used for the output of villagers’ best responses.

Appendix 3: No-Dispersal and Equidistance Cases

The spatial setting of density-dispersal between sites and heterogeneous distance to fishing sites forms a foundation for exploring optimal MPA decisions but examining settings without these spatial components further elucidates the interactions occurring within the spatial setting.

3.1 Dispersal

A model experiment with zero dispersal mimics a sedentary species case and demonstrates the impact of dispersal in determining fishing patterns and the optimal MPAs. The fishers and MPA managers make their decisions according to the model described above but the dispersal matrix, D, is set to zero, converting Eq. 6 to:

$$\varvec{X}_{{\varvec{t} + 1}} = \varvec{X}_{\varvec{t}} + G\left( {\varvec{X}_{\varvec{t}} ,\varvec{K}} \right) - \varvec{H}_{\varvec{t}}$$

The stock dynamics of each fishing site now depend only on the growth and harvest in that particular site.

With zero dispersal and no MPA, two villagers choose to become wage specializers and the remaining 10 fishers spread out across space more than for the baseline (Fig. 11). Without dispersal, villagers must incur distance costs to access fish stocks directly because the fish do not disperse to nearer village sites. The resulting equilibrium maintains the agglomeration of fishers near the village due to the distance cost but the most distant site contains one fisher. In this context, the yield-maximizing manager optimally locates an MPA near the village with enough enforcement to deter some fishing labor to reduce open access over-extraction yield losses, at all budgets. The income-maximizing manager always includes site 4 in MPAs, which induces one additional villager to exit fishing, and also selects the near village location at higher budgets to reduce over-extraction there. Both the ASL-marinescape and the ASL-MPA manager aim to induce exit from fishing and complete deterrence of fishing where possible (Fig. 11). Across budgets and manager types, the no-dispersal case’s optimal MPAs contain fewer column two sites than the dispersal case because those locations cannot contribute to other sites through dispersal, which allows the enforcement-distance relationship to dominate the MPA location decisions. As in the baseline above, yield and income maximizing managers reach their optimal configuration and enforcement level at moderately low budgets, with illegal fishing optimal in the MPAs.

Fig. 11

Optimal MPAs for no-dispersal case. The number in each of the six fishing sites in this figure depicts the number of villagers who fish in that site in equilibrium, while the number below the first column is the number of villagers who undertake no fishing and work for wage full-time

3.2 Homogenous Distance Costs

Despite fishers’ statements about the role of distance in choosing fishing sites, most of the MPA economics literature assumes either zero or homogenous distance costs. Here, setting all distance costs to the distance to the nearest site to the village in the baseline (1.75) as a new baseline elucidates the impact of the heterogeneity of distance costs (Fig. 12). The fishers’ income maximization problem remains the same, but the fishing site choice does not rely on differences in the labor time allocated to traveling to different sites but instead relies on the homogeneous distance cost, l_d, and the labor constraint becomes:

$$\begin{array}{*{20}c} {L_{n} \ge l_{w,n} + l_{f,i,n} + l_{d,n} .} \\ \end{array}$$

Fig. 12

Optimal MPAs for equidistance case. The number in each of the six fishing sites in this figure depicts the number of villagers who fish in that site in equilibrium, while the number below the first column is the number of villagers who undertake no fishing and work for wage full-time

That homogeneity often produces multiple equilibria in the spatial distributions of fishers, especially mirror image equilibria, which we identify but do not explore further here.

With homogeneous distance costs at the baseline level and no MPA, no villager becomes a wage specializer (results vary with higher distance costs). Instead, villagers spread out evenly across sites because they face no trade-off between distance and stock effects. As in the heterogeneous distance baseline, in the no-MPA case here, the center column can support more fishing than the edge columns due to dispersal benefits from 3 rather than 2 neighboring sites, which also permits more fishers. The income maximizing manager focuses MPAs on the center column to facilitate fishing near in the remaining columns. For the ASL marinescape maximizing manager there are multiple equilibria masked in non-integers fishers and we do not attempt to explore it further. Eventually, both ASL-maximizer managers protect the complete marinescape when the budget is high enough. In general, fishers’ decisions reflect the lack of heterogeneous distance costs by spreading out across the marinescape while MPA managers’ choices focus on taking advantage of the center column’s dispersal role. Again, income and yield maximizing managers achieve their objective at moderate budgets, with the yield maximizing MPA containing optimal illegal fishing.

3.3 Overall

Removing either dispersal or heterogeneous distance costs from the marinescape setting leads to different optimal MPAs than the baseline and isolates the individual contribution of each aspect to the choice of MPA. Most economic MPA analyses consider only dispersal, which leads to MPA locations that focus on protecting sites that can contribute beyond the MPA through dispersal and to fishers spread evenly across the marinescape. Employing such an MPA in a setting of artisanal fishers that consider distance costs as part of labor allocation decisions may not achieve the desired outcomes as fishers tend to choose sites closer to the village rather than spreading out (Figs. 11 and 12).

Appendix 4: Distance-Dependent Enforcement Costs

In the baseline, we implicitly assume a site-specific distance cost of $1$ for all sites and calculate the enforcement cost as²¹:

$$cost = enf \times wage \times L \times \left( {\mathop \sum \limits_{i = 1}^{6} mpa_{i} \times 1} \right) = enf \times wage \times L \times size_{MPA} ,$$

where $mpa_{i}$ is 1 if site $i$ is protected and 0 otherwise. Here we relax the assumption and find the optimal MPA when enforcement costs are higher farther away from the village. To make it comparable to the budgets explored in the baseline, we choose the enforcement costs to (1) be proportional to the distance from the site to the village and (2) have the same average cost of enforcement (across sites) as in the baseline (i.e. 1). We present the relationship between distance cost and distance from the village in Table 2.

Table 2 Site-specific distance costs

Therefore, with “Distance cost” or “$cost_{i}$” as the site-specific distance cost (last column in Table 2), the enforcement costs are calculated as²²:

$$cost = enf \times wage \times L \times \left( {\mathop \sum \limits_{i = 1}^{6} mpa_{i} \times cost_{i} } \right)$$

Finally, Fig. 13 shows the results. Comparing the ecological goals with the baseline confirms that the effect of having distance-dependent enforcement costs is to make enforcement easier close to the village. Because it is now easier to enforce near the village, the optimal MPAs, in general, shift towards the first site and, consequently, fishing there decreases.

Fig. 13

Optimal MPA with distance-dependent enforcement costs

Appendix 5: Optimal MPAs to Maximize Yield and ASL-MPA

See Figs. 14, 15, 16 and 17.

Fig. 14

Optimal MPA to maximize yield. Each column represents a different budget level from 0 (i.e. open access) to unlimited. a Labor allocation per villager; the white bars represent time spent fishing, the gray bars represent time traveling, and the black bars represent time spent working on shore. b Total fishing labor per site and the number of villagers in each site. c The fish stock. In b, c, black bars represent sites within the MPA

Fig. 15

Changes in size and configuration when maximizing yield with different budgets

Fig. 16

Optimal MPA to maximize avoided fish stock in the MPA. Each column represents a different budget level from 0 (i.e. open access) to unlimited. a Labor allocation per villager; the white bars represent time spent fishing, the gray bars represent time traveling, and the black bars represent time spent working on shore. b Total fishing labor per site and the number of villagers in each site. c The fish stock. In b, c, black bars represent sites within the MPA

Fig. 17

Changes in size and configuration when maximizing ASL-MPA with different budgets. The gray sites are the optimal MPA sites for each budget level and the MPA size is the number of sites included in the MPA. Although the optimal enforcement level increases between budget levels reported here, this figure contains every MPA size and configuration, which vary discretely as budget increases

Appendix 6: Maximizing MPA Stock

The park effectiveness literature argues that the impact of policy—in this case a park—derive not from the ecological benefits generated by the park but instead by the additional ecological benefits generated that would not have been generated without the establishment of the park. In contrast, some managers seek to maximize the ecological benefits rather than the additional ecological benefits. In the case here, a “MPA stock-maximizing manager”²³ seeks to maximize the stock in the MPA:

$$\mathop {\hbox{max} }\limits_{{\varvec{S},\phi }} \mathop \sum \limits_{i} s_{i} [X_{i} ]$$

Such managers create different MPA networks than ASL-MPA managers (Fig. 18). At high enough budgets, both the MPA stock maximizing manager and the ASL-MPA manager put the entire marinescape into the MPA system. At lower budgets, however, the MPA stock maximizing manager includes the whole marinescape in the MPA to “get credit” for all site’s stocks. In contrast, at those lower budgets, the ASL-MPA manager uses smaller MPA systems that permit higher levels of enforcement and more effectiveness at generating conservation; and typically emphasizes either MPA units with zero fishing or MPA configurations that encourage fishers to exit fishing. The MPA stock maximizing manager generates a fraction of the avoided stock loss benefits created by the ASL-MPA manager’s MPAs, with that fraction becoming large at high budgets (Figs. 18 and 19). In particular, this manager’s MPA creates 18.3, 33.9, 57.3, and 77.7 percent of the ASL-MPA’s optimal MPA at budgets 5, 15, 25, and 35, respectively. The focus on within-MPA stock also generates lower marinescape avoided stock loss than created by the ASL-marinescape’s MPAs, until large budgets (Fig. 19). These results demonstrate the missed conservation opportunities that derive from decisions based on total stock size rather than on the conservation additionality created by the MPA.

Fig. 18

Optimal MPAs for stock and ASL maximizers

Fig. 19

ASL marinescape outcome for different goals

Appendix 7: Assuming Perfect Enforcement

See Figs. 20 and 21.

Fig. 20

Naïve ASL marinescape manager

Fig. 21

Naïve income manager

Note the distinction between (1) assuming perfect enforcement, and (2) assuming unlimited budget. In the case of the ASL-marinescape manager, the difference is not consequential. However, with the income goal, if the manager is naïve assuming (2), the MPAs chosen lead to the outcomes in Fig. 21. In contrast, if the manager is naïve assuming (1), then the naïve optimal is open access (i.e. the manager does not protect anything because she thinks the protection would lead to complete deterrence. In that case, the right side of Fig. 20 would be replaced by Open access at all budget levels).