Buy Coal or Kick-Start Green Innovation? Energy Policies in an Open Economy

Abstract

This paper analyses two unilateral policies available to countries that want to rapidly curb carbon emissions in the global economy, but do not own any fossil fuel resources. If fossil fuel owners do not cooperate in $\hbox {CO}_2$ emission reduction efforts, the only strategy to reduce their fossil fuels’ use is to exploit the interconnectedness of production given by international trade. We compare a Pigouvian approach, namely a subsidy for renewable energy prices, and a Coasian supply-side strategy, buying extractive rights over fossil fuel deposits abroad. Using a dynamic North–South trade model with endogenous innovation, we show how these policies, designed to prevent an environmental disaster, have different cost and welfare profiles. If fossil fuel deposits can be purchased at their market price, the supply-side policy achieves the highest welfare. If instead the fossil fuel owners require a full compensation for their income loss, subsidies for renewable energy inputs can result in higher welfare, but only if the resource-rich region has less advanced technologies for green energy production than the countries implementing the policy.

1 Introduction

Sustainable development is one of the key challenges for the future of the world economy. Currently, most productive activities rely upon energy from fossil fuels, with unsustainable damage to the global environment. Climate scientists estimate that a large fraction of fossil fuel reserves—as much as 80% of coal deposits—should remain unexploited if we want to meet a $2\hbox {C}^{\circ }$ climate target (McGlade and Ekins 2015). However, some of the largest coal and oil producers in the world are developing countries with prominent greenhouse gas emission profiles, as in the case of China and India for absolute emissions, or Qatar, Kuwait, and Saudi Arabia in per capita terms (European Commission 2019; British Petroleum 2019). Naturally, the governments of these countries are not inclined to restrict fossil fuel extraction (Friedrichs and Inderwildi 2013; Tvinnereim and Ivarsflaten 2016). What policies could induce them to forego their resource wealth? In particular, can countries that do not own carbon deposits induce their resource-rich trade partners to shift to other energy sources to avoid a climate disaster?

Unilateral climate policies have been topical since the 2015 Paris Agreement, which required voluntary pledges from individual governments in the form of ‘Intended Nationally Determined Contributions’, instead of coordinated global actions such as carbon pricing. Following the negotiations, countries focused on several possible unilateral measures, including R&D in clean energy technology and financing climate actions in developing countries, for instance through the Green Climate Fund (Dagnet et al. 2016). However, these unilateral policies can be successful only if they address the substantial productivity advantage that fossil fuels still have in the energy sector, either by adjusting energy prices, or directly tackling the abundance of cheap carbon deposits.

In this article, we compare two unilateral policies that can promptly address fossil fuels’ use in an open economy. These policies consist of a “pigouvian” solution, acting on the world price of renewable energy, and a “Coasian” supply-side solution, creating a market for fossil fuel deposits to prevent their exploitation. Both policies rely on the interconnectedness of the global economy to redirect the path of production and innovation: since energy inputs are traded, the North can foster its competitiveness in renewables with a price subsidy, or stop the leading source of comparative advantage in the production of fossil fuels by purchasing extractive rights over carbon deposits in the South. Both interventions immediately reverse the process of environmental degradation, but the costs of the two policies can vary substantially depending on the characteristics of the countries involved. To compare these two strategies, we develop a dynamic trade model with endogenous innovation and asymmetric fossil fuel endowments, which allows us to examine the monetary costs and welfare implications of the policies.

The design of our theoretical framework is close to the directed technical change models of Acemoglu et al. (2012) and Hémous (2016). Similar to Hémous, we model two regions connected by international trade, North and South, and assume that the South does not cooperate in the fight against climate change, so that a global carbon tax is not feasible. In this context, we argue that a key difficulty for tackling climate change with unilateral policies arises if the non-cooperative region controls most of the global reserves of fossil fuels. We model this issue by introducing a large asymmetric endowment of fossil fuel deposits, which are present only in the South. This region can extract fossil fuels, use them to satisfy domestic energy demand if no cheaper alternative is available, and export them to the North. Thus, the South might emit greenhouse gases for its own local economic activities, even if the North completely stops importing and consuming carbon-intensive goods. The connection between the two regions through international trade is then the only instrument¹ available to the North to shift Southern production away from burning fossil fuels.

We model two unilateral interventions that immediately shut down fossil fuel production: a price subsidy for energy-intensive inputs made with renewable energy (the Pigouvian policy), and the purchase of extractive rights over fossil fuel deposits in the South (the Coasian policy). This latter option is directly related to the work of Harstad (2012) and the long-standing literature on supply-side interventions (Bohm 1993). These models, however, do not consider the effect that carbon deposits have on the export profile of a country through sectoral innovation, which over time can amplify trade specialization.² Hence, unlike Harstad (2012), we evaluate this policy in a general equilibrium model with trade and directed technical change. Even if our model is related to the one of Hémous (2016), we depart from his policy analysis because of some key differences in initial assumptions. Hémous (2016) studies a combination of R&D subsidies for green innovation and trade taxes to achieve sustainability. However, the effectiveness of his policy package rests on three conditions: (1) the policies are not enacted too late, when environmental degradation is too advanced; (2) the South does not consume polluting goods domestically;³ and (3) fossil fuels, if present, are exhaustible resources with rapidly rising prices as they become more scarce (similar to Acemoglu et al. 2012). In our model, instead, we consider policies that could work at any degree of environmental degradation, even if the South has home-consumption of polluting goods, and even in the presence of large endowments of fossil fuels that will not become scarce any time in the near future. This last point is based on current research on stranded carbon assets, which argues that fossil fuel resources are too abundant to rely on their exhaustibility to prevent a climate disaster under business as usual (Jakob and Hilaire 2015; van der Ploeg and Rezai 2017). Therefore, in our model we assume that scarcity does not limit the availability of fossil fuel deposits within the time horizon under consideration.

With a simple calibration of the model, we find that the choice between the Pigouvian and the Coasian approach depends primarily on the cost of purchasing fossil fuel deposits in the South, and secondly on the relative technological development of renewable energy in the two regions. If the North can purchase deposits at their market price, the Coasian policy yields the highest welfare. Buying deposits at market prices is in fact substantially cheaper than paying them at full-income compensation and, unlike the price subsidy, does not distort the international production of energy, thus it is the least disruptive intervention in terms of welfare. However, if the South requires a full compensation for abandoning fossil fuel deposits, the policy choice depends on which region has the best technology for clean energy production. Whenever the North has a large advantage in green technologies over the resource-rich South, a price subsidy yields a higher welfare for the North than paying full income compensation for the deposits. Conversely, if the North does not have a substantial technological advantage, buying fossil fuel deposits is always preferable for Northern welfare. This result arises because, in the subsidy scenario, unsubsidized Southern energy firms cannot compete with Northern ones, which produce all energy inputs worldwide. Thus, if the North starts with relatively backward green technologies, it will take a long time before its firms catch up with fossil fuels’ productivity, and thus more substantial welfare costs. We also discuss the direct costs of the policies, which might be a more tangible measure for politicians of the feasibility of each intervention, even if they do not capture their general equilibrium welfare effects. We find that monetary costs can be substantial, in the range of 20–60% of Northern income in the baseline parametrization. Both policies can be removed once the market price of energy inputs from renewables falls below the one of fossil fuels, as countries change their specialization patterns and innovation fosters alternative energy production.

Our results bridge different strands of the literature on international environmental policies. Previous studies propose a variety of instruments to tackle global environmental externalities, from trade, to innovation, to supply-side policies.⁴ The trade literature was the first to highlight that environmental policies cannot ignore the role of competitiveness effects and the international reallocation of production (Barrett 1994; Copeland and Taylor 2004). These international effects may dampen the optimism of the directed technical change literature, which argues that temporary innovation policies can redirect countries permanently to green growth paths (Newell et al. 1999; Acemoglu et al. 2012; Gans 2012; Acemoglu et al. 2014; Aghion et al. 2014; Gupta 2015).⁵ In an open economy context, a combination of innovation and trade policies can effectively shift economies to clean energy production (Di Maria and Smulders 2005; Di Maria and Werf 2008; Hémous 2016; van den Bijgaart 2017). These models of trade and directed technical change provide important insights concerning the dynamic problem of pollution havens and the location of dirty production. However, they leave a marginal role for large asymmetries in polluting endowments, such as fossil fuel ownership. Instead, we want to highlight how the abundance of fossil fuel reserves in non-participating countries creates path dependence and specialization that are hard to contrast, but that can still be reversed in an interconnected world economy.

As noted by van den Bijgaart (2017), the size of the coalition implementing unilateral policies relative to the non-complying nations is a crucial determinant of the ability of few countries to redirect dirty production.⁶ We focus on a situation in which the South is ‘large’, not only because its mass of scientists is as large as the Northern one, but also because it owns abundant fossil fuel deposits, giving the region a significant comparative advantage in dirty energy production. Moreover, the South has its own domestic consumption of energy inputs that is unaffected by Northern restrictions. This setting reflects the characteristics of many large resource-rich developing countries like China, India, Indonesia, or South Africa (OECD 2012; World Energy Council 2013). Therefore, in our framework, the trade and innovation policies examined by models with a ‘smaller’ South, like Hémous (2016) and van den Bijgaart (2017), are not sufficient to address environmental degradation.

Lastly, our approach is related to Müller-Fürstenberger and Schumacher (2017) , who consider two regions producing a global externality, but with only one of them suffering the external damages. In our model, the non-cooperative South is indifferent to the pollution externality, but also the sole owner of fossil fuel deposits for the production of polluting energy. In their non-cooperative framework, they find that the region affected by the externality has to spend a large share of its income to offset it, even to the point of an environmental poverty trap. Our paper arrives at a similar conclusion: we find that implementing those policies that can always stop a climate disaster requires substantial income transfers from North to South.

The paper proceeds as follows. In Sect. 2 we develop the theoretical model. Section 3 characterizes the laissez-faire equilibrium. In Sects. 4 and 5 we define and compare the two policy instruments with a simple calibration of the model. Section 6 discusses some modelling assumptions and concludes.

2 Model

We consider a dynamic trade model characterized by two asymmetric regions of the world, North N, and South S, linked by international trade and transboundary pollution. The North comprises those countries that, for geological reasons, do not possess any deposits of oil, coal, or gas within their boundaries. This definition can be extended to countries that own some fossil fuel deposits, but have agreed on strict regulations of $\hbox {CO}_{{2}}$ emissions and thus are legally bound to leave the deposits untouched.⁷ The South, instead, is a region that owns cheap and abundant fossil fuel reserves and is not willing to restrict their exploitation. Each region $k\in \{N, S\}$ produces two types of intermediate inputs necessary for the production of final consumption goods: non-energy inputs n, such as raw materials, manufacturing or service inputs, and energy inputs e, like fossil fuel products, electricity or solar panels. Countries trade intermediate inputs internationally and assemble them in final goods Y. The local factors of production (labour, scientists, capital, carbon deposits) cannot be traded. Each economy specializes and trades according to relative factor abundance (à la Heckscher–Ohlin) and its relative technological productivity (with a Ricardian mechanism).

2.1 Welfare

In each region, we consider an economy with one representative agent who lives for one period. The utility of time t agent living in region k is given by $U^k_t \left( C^k_{t} \;, \mu ^k \;, G_{t} \right)$ and depends on the consumption of final goods $C^k$ and on the quality of the global environment G. The country’s social planner considers aggregate welfare over multiple generations as the discounted sum of utility over time. Welfare is given by

$$\begin{aligned} W^k_{\tau }= \;\; \overset{\infty }{\underset{t=\tau }{\sum }} \,\frac{1}{\left( 1+ \rho \right) ^{t-\tau }} \; \; U^k_t \left( C^k_{t} \;, \mu ^k \;, G_{t} \right) \end{aligned}$$

(1)

where $0<\rho <1$ is the social discount factor, $\mu ^k$ is the weight that determines the relative amenity value of the global environment (or sensitivity to climate change), and $U^k$ is a region-specific function. If a region assigns a positive value to the environment in its utility function, whenever environmental quality G reaches the lower bound of 0, the utility value goes to $-\infty$. This case of infinitely negative utility is defined as an environmental disaster and is irreversible.

Definition D.1

An environmental disaster is an irreversible event that occurs when global environmental quality reaches or falls below a critical threshold, $G_{\nu }=0$, at some finite time $\nu <\infty$.

The disaster captures the problem of tipping points identified by the climate change literature, thresholds beyond which ecosystems abruptly switch to a critical state and cannot recover (Lenton et al. 2008). The instantaneous utility in the North takes the following functional form

$$\begin{aligned} U^N_t\left( C^N_{t}, \mu ^N, G_{t} \right)&=\left\{ \begin{array}{cc} \frac{1}{1-\eta }\left( \mu ^N G_{t} + (1-\mu ^N) \; C^N_{t} \; \right) ^{1-\eta } &{} \quad \text{ if } \; G_t>0 \;\; \text{ with } \;\; t < \nu \\ -\infty &{} \quad \text{ if } \; G_t\le 0 \;\; \text{ with } \;\; t \ge \nu \end{array}\right. \end{aligned}$$

(2)

where $1/\eta$ represents the elasticity of inter-temporal substitution, with $\eta \le 1$, and $0<\mu ^N<1$. The difference between the two regions is that the South derives no utility from the state of the global environment: it is indifferent to improvements in environmental quality and to its degradation. Thus, utility in the South is

$$\begin{aligned} U^S_t\left( C^S_{t} \right) =\frac{1}{1-\eta }\left( C^S_{t} \; \right) ^{1-\eta } \end{aligned}$$

(3)

This indifference to environmental damage could be the result of a socio-political regime that is not concerned with global climate degradation, or that denies the possibility of climate change and its consequences, or that believes that the country will not be affected by climate shocks. We do not model explicitly Southern socio-political processes, but take the pessimistic stance that this region will not spontaneously restrict fossil fuel use. It might be an extreme characterization, but in reality some fossil fuel owners are climate change deniers or authoritarian regimes unconcerned with the country’s environment or natural disasters. We can then abstract from any strategic interactions between the North and the South on pollution abatement and consider the Southern region as fully non-cooperative in the prevention of climate catastrophes.

2.2 Production

The production of final consumption goods Y requires two intermediate inputs: energy and non-energy components, assembled in a Cobb–Douglas aggregate by perfectly competitive firms around the world⁸$^,$⁹

$$\begin{aligned} Y= (Q_{n} )^{\upsilon } \;\; (Q_{e} )^{1-\upsilon } \;\;\;\;\;\;\;\;\text {with} \;\; \;\; \;\;\;\; Q_{e}=Q_{eC}+Q_{eF} \end{aligned}$$

(4)

where $Q_z$ refers to the use of an intermediate input $z\in \{n, eC, eF \}$. Non-energy inputs n represent parts, components, raw materials and services (such as design), while e refers to energy inputs that rely on either fossil fuels (eF) or on renewable energy sources (eC). We assume that, from the point of view of final goods producers, the two energy forms are perfect substitutes (second part of Eq. 4), and it does not matter whether the source is fossil fuels or renewable energy. Firms always choose the cheapest option.¹⁰ For example, to make clothes, final goods’ producers can process cotton with electricity-powered weaving machines, but do not care if the energy is produced using coal or hydroelectric power. We assume that if the prices of the two energy inputs are exactly equal, final goods’ producers choose clean energy inputs, to avoid multiple equilibria in which any combination of $Q_{eF}$ and $Q_{eC}$ is acceptable. Because of free trade, intermediate inputs do not need to be produced in the country that assembles them into final goods. The global demand for intermediate energy and non-energy inputs is met by production in the two regions under perfect competition

$$\begin{aligned} Q_{n} = \sum _k Y^k_n \;\;\;\;\;\;\;\;Q_{e} = \sum _k Y^k_{eC}+Y^S_{eF} \end{aligned}$$

(5)

The production of tradable intermediate inputs $Y_z$ works as follows.

Non-energy Intermediates ($Y_{n}$) The production function for these inputs requires three factors of production: labour, machines, and (indirectly) scientists, through sector-specific technologies, combined as

$$\begin{aligned} Y^k_{n}=\left( L^k_{n}\right) ^{1-\gamma }\int _{0}^{1} A^k_{ni} (x^k_{ni})^{\gamma }di \end{aligned}$$

(6)

where $L_{n}$ is the labour employed in this sector n, $x_{ni}$ are the machines used and $A_{ni}$ is the technological productivity associated with machine i. The technologies A depend on the sectoral allocation of scientists, as discussed in Sect. 2.3. The parameter $0<\gamma <1$ is the share of machines in the production function.

Energy Intermediates ($Y_{e}$) The production of these inputs requires the same factors of production as non-energy goods, but in addition it uses nature more intensively. Energy products requires water, air and soil, regardless of whether the energy comes from renewable resources or fossil fuels—consider how solar panels occupy land, hydroelectric dams flood valleys, fracking requires large amounts of water, and so on. We define this required natural capital as K, present in both regions. Moreover, the production of fossil fuel energy inputs $Y_{eF}$ requires a specific type of natural capital, namely the geological deposits of carbons that formed in sedimentary rocks over the past millennia, R (only present in the South). The two intermediate inputs made in the energy sector are

$$\begin{aligned} Y^{k}_{eC}= & {} \left( (L^{k}_{eC})^{\psi }(K^{k}_{eC})^{1-\psi }\right) ^{1-\gamma }\int _{0} ^{1}A^{k}_{eCi}(x^{k}_{eCi})^{\gamma }di \end{aligned}$$

(7)

$$\begin{aligned} Y^S_{eF}= & {} \left( (L^S_{eF})^{\beta }(K^S_{eF})^{1-\alpha -\beta }(R^S)^{\alpha }\right) ^{1-\gamma }\int _{0}^{1}A^S_{eFi}(x^S_{eFi})^{\gamma }di \end{aligned}$$

(8)

where $0<\psi , \alpha , \beta <1$ are fixed parameters capturing factors’ shares. Fossil fuels products $Y_{eF}$ capture energy inputs like coal, crude oil and natural gas, but also processed fuels like refined oil or coke that are not consumed directly, but are needed to generate energy for final goods’ production. Renewable energy inputs $Y_{eC}$ represent electricity (only tradable within integrated grid systems) and other products that ‘embed’ renewable energy, such as solar panels or biofuels. Since deposits R are only present in the South, the North cannot produce fossil fuel products $Y_{eF}$. Like all other factors of production, natural capital K and deposits R are non-tradable, since countries cannot ship away pieces of their land and environment.

In our model, deposits R are non-exhaustible within the time scale of critical climate degradation, capturing the problem of excess availability of fossil fuels.¹¹ Our approach differs from other models of green directed technical change, which treat them as classic exhaustible resources. In our framework, the flow of fossil fuel products $Y_{eF}$—for instance the coal extracted from a mine—does not deplete the stock of deposits R—the mine itself—and hence scarcity does not encourage R&D in clean technologies (differently from Acemoglu et al. 2012). In practice, inflows like new discoveries and outflows from extraction are likely to cancel out. For both oil and natural gas, in the past 3 decades the discovery of new reserves roughly equalled consumption in that year, maintaining a stable reserves-to-consumption ratio, independently of the large variation in prices. Coal’s reserves-to-production ratio instead has decreased historically, but since the early 2000s it stabilized and more recently even increased slightly. A stable reserve-to-consumption ratio indicates that the supply of fossil fuels is unlikely to ‘run out’ in the medium term (Covert et al. 2016, pp. 119). On the contrary, in our model the productivity of the South in fossil fuels $Y_{eF}$ can increase over time if extractive technologies $A_{eF}$ improve, so that for a given amount of reserves more fossil fuels can be produced.

Machines Each region produces a unit mass of varieties i of machines $x_{zi}$, with $i\in \left[ 0,1\right]$, made under monopolistic competition, so that their owners can charge a mark-up above marginal costs and make a profit.¹² Following Acemoglu et al. (2012), producing a machine has a fixed cost of $\varsigma \equiv \gamma ^{2}$ units of final output. Machines are not traded. The quantity of machines $x_{zi}$ in each sector is determined every period by the market equilibrium at price $p_{xzi}$.

Endowments and Market Clearing Condition Each country has fixed endowments of production factors available in each period. Labour L, natural capital K, and fossil fuel deposits R can be purchased by intermediates producers at their respective prices: wages w, price of natural capital r, and price for fossil fuel deposits q. Market clearing implies that $L^k_n+L^k_{eC}+L^k_{eF} = {\overline{L}}^k$ and $K^k_{eC}+K^k_{eF} \le {\overline{K}}^k$ and $R^S\le {\overline{R}}^S$, with ${\overline{L}}^k$, ${\overline{K}}^k$ and ${\overline{R}}^S$ being the total exogenous endowment of each factor available every period in a country. The last factor of production used in these economies is scientists m, described in the next Sect. 2.3. Countries cannot run surpluses or deficits, and use all their output for consumption and machine production, so that

$$\begin{aligned} Y^k = C^k + \gamma ^{2} \int _{i} x^k_{i} \, di \end{aligned}$$

(9)

where the amount of final consumption goods that accrues to each country $Y^k$ depends on how valuable is their production of intermediate goods. National income I is the total monetary value of intermediates produced nationally $I^k=\sum _z p_z Y_{z}^k$ and hence the share of final output is just $Y^k = Y \, [I^k / (I^N + I^S)]$.

2.3 Innovation

Innovation occurs in each intermediate sector $z\in \{n,eC, eF\}$ in a cumulative process, with technological productivity A growing in the manufacturing and energy sectors independently. We assume no technology spillovers across countries or sectors. The growth of sectoral technologies within each country is determined by the allocation of a fixed mass of scientists $m^k$, equal to one in both countries: $m^{k} \equiv m_{n}^{k}+m_{eC}^{k}+m^k_{eF}=1$. The crucial choice for scientists is in which sector to work: they cannot choose a specific machine, but each of them is randomly allocated to a machine i within their sector of choice. Each machine is paired at most with one scientist to avoid congestion. If innovation is successful, the productivity of that machine is augmented by a factor $\varphi \in \left( 0,1\right)$, so that the associated technology becomes $A_{zi, t}=(1+\varphi )A_{zi, t-1}$ and the scientist has a one-period patent to make monopoly profits. If innovation is not successful, the machine operates with its old technology $A_{zi, t-1}$ and, since no patent is deposited, the monopoly rights to use the old machine is allocated randomly to the pool of potential entrepreneurs in that sector. This short-term patent system creates an intertemporal knowledge externality. Innovators do not internalize the long-term effects of their innovative activities on the future productivity of the different sectors: innovation permanently raises the stock of knowledge in that sector and all future generations benefit from it (Aghion and Howitt , 1992, pp. 330). We define $A^k_{z}$ as the country-specific average productivity in sector z, such that

$$\begin{aligned} A^k_{z} \equiv \int _{0}^{1}(A^k_{zi})\; di \end{aligned}$$

(10)

Scientists consider the aggregate productivity of each sector to decide where to work, on the basis of the expected profitability of each sector. “Appendix B”. illustrates the allocation mechanism for scientists. Average sectoral productivity then evolves according to the following law of motion

$$\begin{aligned} A^k_{z,t}=\left[ 1+\varphi \left( \, m^k_{z,t}\right) \right] A^k_{z,t-1} \end{aligned}$$

(11)

which “builds on the shoulders of giants”, improving upon existing technologies in each period.

2.4 Environment

Beyond the intertemporal knowledge externality, the second significant market failure in this economy is due to environmental externalities from the energy sector. If the South extracts and sells fossil fuel products, the emissions from their use accumulate in the atmosphere, causing damage to the global environment. However, since the South is unconcerned with environmental destruction, only the North suffers the environmental externality. Instead, energy from renewable resources causes no global damage (we discuss possible local damages from renewable energy production in Sect. 6). In each period, environmental quality falls within the interval $G_{t}\in [0,{\overline{G}}]$, where ${\overline{G}}$ denotes the initial, pristine level of the global atmosphere before industrialization, and $G_t=0$ is the environmental disaster of Definition D.1. Environmental quality evolves between these two thresholds according to the following law of motion

$$\begin{aligned} G_{t}\;&=\left\{ \begin{array}{ll} 0 &{} \quad \text{ if } \;\; G_{t-1} \le \varepsilon \\ \left( 1+\Delta \right) G_{t-1}-\xi \; Y^S_{eF, t-1}&{}\quad \text{ if } \;\; \varepsilon< G_{t-1} < {\overline{G}}/(1+\Delta )+\varepsilon \\ {\overline{G}} &{}\quad \text{ if } \;\; G_{t-1} \ge {\overline{G}}/(1+\Delta )+\varepsilon \end{array}\right. \end{aligned}$$

(12)

where $\varepsilon \equiv \xi (Y^S_{eF, t-1})/(1+\Delta )$. Environmental quality depends on the previous state of the environment $G_{t-1}$, given a fixed regeneration capacity $\Delta \ge 0$ and on the production of fossil fuels $Y_{eF}$ in the South. The damage from fossil fuels is captured by the parameter $\xi >0$. Note that deposits R of fossil fuels do not produce pollution per se, but only once the resources are extracted and burnt in the form of intermediate fossil fuel products $Y_{eF}$. This stylized formulation of global environmental dynamics captures two key problems in international environmental negotiations: the transnational spillovers from global pollution, which affects not only the jurisdictions in which the fossil fuels are burnt but also their neighbours (the global environment G is not region-specific); and the intertemporal externalities from fossil fuels, which impacts future generations in the following time periods. International negotiations over carbon controls are thus challenging because countries do not fully internalized the global environmental damage of their economic activity and because future generations are less represented in current political debates.

3 Laissez Faire

The model presented above captures some key features of the global fossil fuel challenge. It considers two types of energy inputs, with the globally polluting one—fossil fuels—controlled by one region, endogenous sectoral innovation, and asymmetric concerns for the environment (non-cooperative South). The core market failures are the transboundary environmental externality caused by fossil fuels and the knowledge externality caused by a short-term patent system that does not internalize future evolutions of technology in the returns to current innovation. We now present the solution of the model to show that, under laissez-faire, this setting leads to unsustainable outcomes. The laissez-faire equilibrium is defined as follows.

Definition D.2

An equilibrium is defined as a sequence of demands for factors of production ($L^{k}_{z},K^{k}_{e},R^S_{eF}$) and factor prices (wages $w^{k}$, price of natural capital $r^{k}$ and price for fossil fuel deposits $q^S$), demand and price for machines ($x^{k}_{zi}$ and $p^k_{xzi}$), scientists’ allocations ($m^{k}_{z}$), and quality of the environment (G) such that, for every period t: (1) the price and quantity of machines $p^k_{xzi}$ and $x^{k}_{zi}$ maximize profits for machine owners; (2) $L^{k}_{z}, K^{k}_{e}$ and $R^S_{eF}$ maximize profits of producers of energy and non-energy intermediates; (3) Y and $Q_{z}$ maximizes the profits of final goods producers; (4) consumers of the final good Y maximize their utility; (5) the allocation of scientists $m_z^k$ maximizes the expected profits of researchers; (6) factor prices clear the factor markets, and intermediates and final goods prices clear the market for Y, $Y^k_{n}$ and $Y^k_{e}$; and (7) the evolution of the environment G is given by the law of motion in Eq. (12).

The Online Appendix provides a full derivation of this equilibrium. In the North, given the absence of fossil fuel deposits, scientists can only work in sectors n or eC. Ex ante, they face an expected ratio of profits of

$$\begin{aligned} \frac{E(\pi _{n, t}^{N})}{E(\pi _{eC, t}^{N})}=\frac{L_{n, t}^{N}}{\left( L_{eC, t}^{N}\right) ^{\psi }}\frac{1}{\left( K_{eC, t}^{N}\right) ^{1-\psi }}\left( \frac{p_{n, t}}{p_{eC, t}}\right) ^{\frac{1}{1-\gamma }}\left( \frac{A_{n, t-1}^{N} }{A_{eC, t-1}^{N}}\right) ^{\frac{1}{1-\gamma }} \end{aligned}$$

(13)

where E is the expectation operator. This ratio is derived from the machine producers’ optimization (“Appendix B”.). It features the three driving forces found in Acemoglu et al. (2012): size, price and technology effects. Everything else equal, more scientists are present in (1) the largest sector, as captured by the ratio of labour and natural capital, (2) the most valuable sector, where the price ratio is higher, and (3) the most advanced sector, where productivity levels are higher, from the ratio of $A_{z}$. In the South, depending on which energy sector is active, scientists face a ratio of expected profits that is either identical to the Northern one, when renewable energy inputs are produced, or that takes the following form, when fossil fuels are produced

$$\begin{aligned} \frac{E\left( \pi _{n, t}^{S}\right) }{E\left( \pi ^S_{eF, t}\right) }=\frac{L_{n, t}^{S}}{\left( L^{S}_{eF, t}\right) ^{\beta }} \frac{1}{\left( K^{S}_{eF, t}\right) ^{1-\alpha -\beta }\left( {R^S_t}\right) ^{\alpha }}\left( \frac{p_{n, t}}{p_{eF, t}}\right) ^{\frac{1}{1-\gamma }}\left( \frac{A_{n, t-1}^{S}}{A^S_{eF, t-1}}\right) ^{\frac{1}{1-\gamma }} \end{aligned}$$

(14)

This condition captures again size, price and technology effects, plus a carbon-abundance effect, which pushes scientists towards the fossil fuel sector due to the endowment of deposits R. We impose the following assumption, so that initially fossil fuels are preferred to renewable energy.

Assumption 1

We assume that, in the initial period $\hbox {t}=1$, fossil fuels are always strictly cheaper than renewable energy, namely $p^*_{eC,t=1}> p^*_{eF,t=1} \; \forall m_{z, t=1}^k$.

This assumption implies that the relationship between technologies $A_{eF, t=0}^S$, $A^k_{eC, t=0}$ and $A^k_{n,t=0}$, given the countries’ endowments of labour ${\overline{L}}^k$, capital ${\overline{K}}^k$ and fossil fuel deposits ${\overline{R}}^S$, is such that, independently of the allocation of scientists, fossil fuels are preferred at first. “Appendix C” shows the necessary and sufficient condition to ensure that this assumption holds. If instead fossil fuels were not cheaper ($p_{eF,t=1} \ge p_{eC,t=1}$), they would be irrelevant because they would be too expensive to use. In that case, models without any R would be better suited to analyse unilateral policies. Since the industrial revolution, however, renewable energy sources have not been significantly cheaper than coal, oil or gas, so we find Assumption 1 reasonably justified in the real world. Whenever fossil fuels are cheaper, there is no demand for renewable energy products eC, since energy inputs are prefect substitutes. Hence, the sector is inactive and does not employ workers, capital, or scientist because its expected profits are non-existent. In the North, given that no fossil fuel sector is present, only manufacturing will innovate. For the South, we add the following initial assumption.

Assumption 2

We assume that, in the initial period $t=1$, innovation in the South occurs only in the fossil fuel sector, such that $E(\pi ^S_n(m_{n, t=1}=0))< E(\pi ^S_{eF}(m_{n, t=1}=0))$ and $m_{n, t=1}^*=0$. This situation arises if

$$\begin{aligned} \left[ \frac{A_{n,t=0}^S}{(1+\varphi ) A^N_{n, t=0}}\right] ^{\frac{1}{1-\gamma }}\frac{{\bar{L}}^S}{{\bar{L}}^N} < \frac{1+\beta (1+\varphi )^{\frac{1}{1-\gamma }}}{\frac{\upsilon }{1-\upsilon }(1-\varphi )^{\frac{1}{1-\gamma }-1}} \end{aligned}$$

(15)

Lemma 1 in “Appendix B” derives this condition. After the first period, scientists can operate in any sector they expect to be the most profitable. Combining Assumptions 1 and 2 we derive the following Proposition.

Proposition 1

Under laissez-faire, given Assumptions 1and  2, the price of renewable energy inputs never falls below that of fossil fuel inputs and the production of dirty intermediates $Y_{eF}$strictly increases over time.

Proof

A full derivation is presented in “Appendix D”. $\square$

Proposition 1 shows that, since the energy inputs of the South are valuable in international markets, there is no incentive to reduce their production, and instead the region invests in innovation to make them increasingly competitive and hard to replace. Since fossil fuels are cheaper and initially attract all scientists in the South, it is easy to see that renewable energy sources cannot compete without an intervention external to the markets. After one period, since fossil fuel technologies $A_{eF}^S$ have grown by a factor $(1+\varphi )$, while Southern manufacturing technologies $A_{n}^S$ have not changed, it is still an equilibrium for the South to allocate all scientists to the fossil fuel sector, considering Eq. (15) iterated one period. In the North, without an active energy sector, all scientists do R&D in manufacturing. As a consequence, the condition $p_{eF}< p_{eC}$ holds also in the following period. This is shown formally in “Appendix D”. In this context, $Y_{eF}$ is strictly increasing every period because fossil fuel energy production is a function of the ever-growing Southern technologies, that cannot decrease or stay constant. Again, “Appendix D” shows formally that this is the case with the equilibrium production of $Y_{eF}$, for any allocation of scientists. This production path under laissez-faire leads inexorably to an environmental disaster, as stated in the following Proposition.

Proposition 2

Under laissez-faire, over time the world reaches an environmental disaster.

Proof

For a formal proof, see “Appendix E”. Intuitively, since the environment cannot regenerate above its pristine level ${\overline{G}}$, even if the growth in fossil fuels is slow, there exists a point in time when the extraction and burning of fossil fuel energy will start overwhelming the regeneration rate of the global environment $\Delta$ and bring it to a decline. Environmental disaster then follows from the dynamics of Eq. (12). $\square$

Proposition 2 abstracts from free movements of capital, since factors of production are not traded in our model. Capital movements might actually reduce the chances of an environmental disaster as countries become bound by a common interest rate (Müller-Fürstenberger and Schumacher 2017). There is substantial evidence, however, that innovation in fossil fuel technologies is indeed expanding in the problematic direction identified in this setting (Covert et al. 2016) and drastic climate change is predicted to occur over the next century if major policies are not adopted (Nordhaus 2018). Next, we analyse two policies available to the North to unilaterally prevent this disaster in the global economy.

4 Policy Instruments

In our model, as in current international politics, there is no world social planner that implements policies at a global level. Taxes and regulations are chosen separately by each region. Hence, shifting an uncooperative South away from global emissions requires a significant intervention from the North in global energy markets to remove the competitive edge of fossil fuel energy $Y_{eF}$. The North can alter the price of energy or the availability of the key factor of production for ‘dirty’ energy products, namely carbon deposits R. Other policies, such as re-directing technical change with green innovation subsidies, or reducing the consumption of fossil fuels with taxes or trade barriers, slows down environmental degradation but cannot ensure that a global disaster will be avoided at any point in time, since they do not necessarily shut down the fossil fuel sector. We consider instead two policies that would work even under the most unfavourable conditions, regardless of the degree of environmental degradation.

4.1 Price Subsidy for Renewable Energy

Under laissez-faire, renewable energy inputs are not competitive at market prices with cheap fossil fuel products. To remedy this lack of competitiveness, the North can offer a price subsidy to its producers of clean energy intermediates to level the difference between the two energy inputs. To stop fossil fuel use worldwide, the price subsidy should make renewables as cheap as fossil fuels both for domestic energy users and for importers from the South. The value of the subsidy (s) equals the gap between the price of fossil fuels in laissez-faire and that of renewable energy.¹³ Producers of green energy inputs $Y^N_{eC}$ in the North receive the subsidy from their government and serve total world energy demand $Q_e$, selling their output to final goods’ producers for ${\tilde{p}}_{eC}\equiv p_{eC}^*-s = p^*_{eF}$, where $^{\sim }$ denotes equilibrium variables during the policy implementation, while $^*$ refers to laissez-faire equilibrium values. The total cost P of the subsidy is

$$\begin{aligned} P\equiv s \times Y_{eC}^N \end{aligned}$$

(16)

Proposition 3

A unilateral price subsidy ‘s’ for green energy inputs produced in the North ensures that the price of renewables is competitive with that of fossil fuels, namely ${\tilde{p}}_{eC} \equiv p^*_{eC}-s = p^*_{eF}$. The subsidy leads to (1) an immediate halt to the use of fossil fuels worldwide, and (2) specialization of the South in non-energy production for the whole duration of the policy.

Proof

The first part (1) follows straightforwardly from the perfect substitutability of energy intermediates stated in Eq. (4). Since the subsidy is defined precisely to equalize the prices of energy inputs under laissez-faire, and since we assumed that when those prices are exactly equal green energy inputs are used, it follows that ${\tilde{Q}}_{eF}=0$ and ${\tilde{Q}}_{eC}>0$. Point (2) is due to the target of the unilateral price subsidy: only Northern energy producers receive it, so if Southern firms were to produce clean energy inputs, they would sell them at the uncompetitive free market price $p^{*}_{eC}$. For this price, they have no demand, since the laissez-faire $p^{*}_{eC}$ is higher than the subsidized one ${\tilde{p}}_{eC}$—otherwise, firms should have been selling green energy inputs in laissez-faire instead of $Y_{eF}$, contradicting Proposition 1. Hence ${\tilde{Y}}^S_{eC}=0$ as long as the subsidy is in place. $\square$

The goal of a subsidy for clean energy generation is to support the price received by renewables’ producers, while putting downward pressure on the price at which the clean energy is sold, making it competitive against fossil fuels (Fischer and Newell 2008; Andor and Voss 2016). The effectiveness of the price subsidy in our model rests on the assumption that fossil fuel and renewable energy are perfect substitutes from the point of view of final goods’ producers. If instead the technologies’ characteristics (for instance the intermittent nature of some renewable energy sources) made the two energy inputs weak complements, the subsidy would not bring a full switch away from fossil fuels, but could even increase fossil fuels’ use. The literature on subsidies for clean backstop technologies has evidenced that innovation subsidies or capacity expansion for renewable energy technologies might lead to a short term rise in emissions—the so-called Green Paradox (Gronwald et al. 2017). However, recent evidence shows that, contrary to the older literature on interfuel substitution, the elasticity of substitution between clean and dirty energy inputs in most countries is greater than one, indicating that complementarity is becoming less common (Papageorgiou et al. 2017).

4.2 Purchase of Fossil Fuel Deposits: ‘Buy Coal’

Alternatively, the North can stop the supply of energy from fossil fuels by purchasing or leasing Southern carbon deposits. This way, the North acquires extractive rights over oil and gas fields and coal mines to leave them idle. For brevity, we borrow Harstad (2012)’s article title and call this policy ‘buy coal’ - even though we refer to multiple fossil fuels and to their deposits, rather than the coal itself. Depending on the bargaining power of the two regions, the annual cost of purchasing deposits can vary between two extremes: the market price of deposits R, equivalent to their rental rate, and a full compensation for the foregone income from fossil fuel exploitation in the South.¹⁴ In the first case, the cost M of buying deposits is

$$\begin{aligned} M \equiv q^* \times R_{min} \end{aligned}$$

(17)

where $q^*$ is the reward for R as a factor of production in the laissez-faire equilibrium (see the Online Appendix)¹⁵ and $R_{min}$ is the minimum stock of deposits that the North must buy to ensure the shut-down of the fossil fuel industry, derived in “Appendix F”. Instead, buying deposits compensating the income loss L costs

$$\begin{aligned} L \equiv { \sum _z p^*_z Y_z^{*S} - \sum _z {\tilde{p}}_z {\tilde{Y}}_z^S } \end{aligned}$$

(18)

where $\sum _z p^*_z Y_z^{*S}$ is the income that the South would have earned under laissez-faire and $\sum _z {\tilde{p}}_z {\tilde{Y}}_z^S$ is the income it earns under the ‘buy coal’ policy. Prior to the policy, the income of the South comes from $Y_n^S$ ($p_n$ normalized to one) and $p_{eF} Y_{eF}^S$, while after the policy from ${\tilde{Y}}_n^S$ and ${\tilde{p}}_{eC} {\tilde{Y}}_{eC}^S$. L is the Southern opportunity cost for abandoning fossil fuels. Independently of the price paid for the carbon deposits, once the ‘buy coal’ policy is implemented, both regions compete in the production of energy inputs from renewable energy sources.

Proposition 4

A sufficiently large purchase of the extractive rights over fossil fuel deposits by the North induces (1) an immediate halt to the extraction of fossil fuels and their global use (2) competition between the two regions in renewable energy inputs’ production.

Proof

$R_{min}$ is calculated so that $p_{eF}\ge {\tilde{p}}_{eC}$. From the perfect substitutability of energy source (Eq. 4), it follows that fossil fuel intermediates ${\tilde{Y}}_{eF}^S=0$. Since energy inputs are necessary for final goods’ production, renewable energy production $\sum _k {\tilde{Y}}_{eC}^k>0$ develops in the two regions depending on their competitiveness. $\square$

4.3 Policy Comparison

The key difference between the two policies is with respect to the production of energy products. The price subsidy for renewable energy inputs made in the North automatically removes energy production from the South, while the supply-side policy of buying fossil fuel deposits leaves a levelled playing field for competition between Northern and Southern renewable energy firms. Both policies can be removed when renewable energy inputs become sufficiently competitive, namely when the equilibrium price $p_{eC}^*$ (without any intervention) gets as cheap as the laissez-faire one $p_{eF}^*$.

We resort to a simple calibration to illustrate the effects of the two policies. We use calibration parameters as close as possible to Hémous (2016), with the South endowed with more labour and natural capital than the North, but technologically less advanced in every sector of production, especially in renewable technologies (see “Appendix G”). For the implementation of the two policies, we take the analytic results from the laissez-faire equilibrium (summarized in “Appendix A”) and after five periods modify them with each policy. Policy costs are subtracted as lump-sum taxes from the income of the North, reducing local consumption and welfare, as discussed in Sect. 5.1. Figure 1 summarize the production paths after each policy.

Fig. 1

Production of non-energy inputs (top panels) and energy inputs (bottom panels) under the two policies. Vertical bars represent the start of the policy (year 5) and its end (year 174)

In our baseline parametrization, since Southern green energy technologies lag substantially behind those of the North, both policies redirect Southern production towards manufacturing intermediates, while the North reduces its production of them (top panels). The response of the $Y_n^k$ sector in the two countries is the same under the two policy regimes. In the energy sector instead, even if both policies immediately shut down the fossil fuel sector (not shown in Fig. 1), the production paths of green energy intermediates is different (bottom panels). In both cases, the North starts producing a large amount of renewable energy inputs. In the price subsidy scenario, while the policy is in place, the South cannot compete with the subsidized Northern firms, so its green energy production is zero. When the price subsidy is discontinued, however, Southern firm can freely compete in the clean energy market and start producing some energy inputs, with a small spike in the bottom-left panel.¹⁶ With a deposit purchase, instead, both regions can produce renewable energy. The South initially ramps-up green energy production as soon as the policy is implemented, then reduces it as its manufacturing sector grows, and lastly experiences a slow but steady increase when manufacturing stabilizes (bottom-right panel, right scale). When manufacturing in the North plateaus, the expected profits for scientists in the South in the manufacturing sector are no longer as attractive as in the previous periods, when Northern production was declining and the Southern one could raise in its place. Thus, for scientists the energy sector returns more profitable (in expectations) than being in manufacturing (with an increasing profit ratio, this corresponds to condition 1.b in “Appendix B”), and all innovation moves into the energy sector also in the South. In the next section, we show how the North chooses between these policies, comparing other parametrizations of the model for the two regions.

5 Policy Choice

A core property of our framework is that whenever the environment reaches disaster ($G=0$), this causes an irreversible drop in utility for the North. To avoid this perpetual catastrophe, Northern policymakers must encourage a global substitution away from emission intensive energy inputs $Y_{eF}$ and into renewable energy inputs $Y_{eC}$. Both strategies described in the previous paragraphs achieve this goal, independently of their starting time, the degree of relative specialization reached by the two countries, and the environmental degradation reached by the world. From an environmental perspective, the policies are identical (Fig. 2).

Fig. 2

Environmental trajectories under business as usual (BaU) and the two policies

As soon as a policy is implemented, the disaster is averted and the global environment returns to its pristine state. However, in terms of monetary costs and welfare, the two policies can differ substantially.

5.1 Policy Costs

First, we examine the direct monetary costs of each policy. From the point of view of Northern politicians, monetary costs can be a key concern for the feasibility of these environmental actions, since both policies entail a transfer to the South, either in the form of a subsidy for Southern consumers of energy inputs, or through a payment for the fossil fuel deposits. Figure 3 shows the yearly monetary costs of each policy (as a share of Northern income) over time.¹⁷

Fig. 3

Monetary costs as a percentage of Northern income over time. Baseline parametrization

We present four different cost paths. ‘Buying coal’ at income loss compensation (solid line) costs more than double than paying deposits at their market price (dashed line).¹⁸ The cost of a green price subsidy is somewhere in between.¹⁹ All policies end at the same time, since they induce the same innovation patters, which in turn implies an equal fall in the price of green energy inputs under both policies. If we consider total costs summed over the whole policy horizon, discounted with the same factor as for welfare in Eq. (1), the price subsidy costs around 35% of total income,²⁰ while buying coal at market prices costs around 23%, and at income compensation more than 60% of Northern income.²¹

These costs depend on the parametrization of the model: in particular, one of the strongest assumptions that we make is that the South has substantially backward green energy technology relative to the North, more than ten times smaller, making it uncompetitive in renewable energy inputs production. Figure 4 illustrates the sensitivity of total discounted costs to these initial green technology values.

Fig. 4

Total costs (% of Northern income, discounted) and initial levels of renewable energy technology

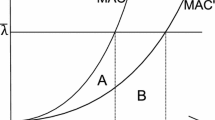
On the horizontal axis, each panel shows different levels of green technology at time zero in the North (top panels) and South (bottom panels). The vertical red line indicates the level of initial green technology in the other country. In Panel A, Southern green technology is not developed, as in our baseline parametrization, and, if initial Northern green tech surpasses it just by a little, a price subsidy is the most affordable policy option. However, if the North has substantially better renewable technology, ‘buying coal’ at market prices is the cheapest policy (but not at income-compensating values). Conversely, in Panel B Southern technology $A_{eC, t=0}^S$ is very high—we set is as high as the North in the baseline parametrization—and the subsidy is always the cheapest option; however, even if subsidy costs are nearly zero, almost no green energy inputs $Y_{eC}$ are produced worldwide in that setting. The same happens when the North has low $A_{eC, t=0}^N$ and the South has higher $A_{eC, t=0}^S$ (Panel C): again, the subsidy seems virtually free, but the general equilibrium effects of the policy are not so favourable for the North, as we show in the next section. Lastly, if the North has advanced green technologies (Panel D), as in our baseline model, ‘buying coal’ at market prices is the cheapest option when the South has underdeveloped green technologies, but if the South has more advanced technologies, closer to the ones of the North, the subsidy is cheaper.²²

Overall, these graphs show that our baseline result that ‘buying coal’ at market prices is the cheapest option hinges on the fact that the North starts with an advanced level of green technology, while the South is substantially less advanced. However, even if monetary costs are a tangible criterion for choosing among policies, they do not capture how much production is depressed by a policy, which is why we need a welfare analysis that includes general equilibrium effects. The next section discusses this issue.

5.2 Welfare of the North

The welfare of the North after implementing these policies is a function of the global environment and consumption. Under both policy scenarios, the environment recovers at the same rate (Fig. 2). What differs is the consumption available after paying the costs of a policy. Consumption depends on how much is produced by the North and hence on its income. Since the two policies have different production profiles, welfare outcomes do not necessarily correspond to monetary costs. We subtract the cost of a policy from income, calculate consumption from Eq. (9) and compute welfare from Eq. (1). In our baseline calibration, ‘buying coal’ at market prices is again the preferred option, resulting in the highest total discounted welfare. The second best choice is the price subsidy, followed by the purchase of deposits at income-compensating values, while the subsidy with the full dead-weight loss is the policy that yields the lowest total welfare. This policy ranking is again driven by the initial technology values. Figure 5 illustrates the sensitivity of total welfare to the initial levels of green technology in the two regions.

Fig. 5

Total Northern welfare and initial level of renewable energy technology

Welfare under all policy scenarios is very similar, with a variation of less than 1.5% between the maximum and minimum attainable welfare under all sensitivity scenarios, unlike the large differences in costs found before. Again, the vertical red line indicates the level of initial green technology in the other country. Comparing monetary costs from Fig. 4 and welfare in Fig. 5, we see that even if subsidies are often the cheapest policy, they never grant the highest welfare. In fact, subsidies depress global production and income because the South cannot make any green energy inputs. Instead, if fossil fuel deposits can be bought at market prices, this policy always provides the highest welfare. The second best option depends on the relative technological development of the two regions. In Fig. 5, when the North has worse green technologies than the South, the ‘buy coal’ policy is always preferable (Panel B on the left of the vertical line indicating green tech in the South, panel C, panel D on the right of the vertical line indicating green tech in the North). If instead the South has significantly less advanced green technologies, the second best can be the price subsidy (Panel A, panel B towards the right side, panel D on the left side).

In sum, if fossil fuel deposits can be purchased at market prices, for a wide range of different initial technologies this is the best option from the point of view of total welfare. If this option is not available (for instance because the South does not accept this lower-bound payment), the choice depends on technological advantage in green energy technologies. If the North is largely superior, it can afford to shut down all energy production in the South with the price subsidy; but if instead the South has very similar or even better green technologies, then buying the deposits and letting the South compete in the market for energy inputs is preferable. These sensitivity graphs in Figs. 4 and 5 also illustrate what would happen with a technology transfer from the North to the South: if green patents were transferred to the fossil fuel region, improving $A_{eC, t=0}^S$, they would make the subsidy policy cheaper (Panel D of Fig. 4), but also they would make it more appropriate for welfare maximization to adopt the ‘buy coal’ policy, and let the South use the imported technologies to produce some energy inputs (as per Fig. 5).

6 Conclusion

Countries endowed with abundant carbon resources are unlikely to give them up gratuitously. Fossil fuels provide a cheap source of competitiveness for the production of energy. This “dirty” comparative advantage builds up over time, reinforced by endogenous innovation. Countries that care the most about global environmental outcomes might therefore be the only ones taking the initiative to reduce carbon emissions, dealing with the costs of restructuring the global energy mix. Our model provides a simple policy comparison to analyse two options that can rapidly halt an environmental collapse, even when the non-cooperating region has a large comparative advantage from fossil fuels. In this framework, both Pigouvian and Coasian policies require an income transfer to fossil fuel owners abroad, either in the form of subsidized renewable energy or with a purchase of resource deposits. Depending on the relative technological development of the two regions, these policies entail different monetary costs and different welfare outcomes.

We find that the first best option in terms of Northern welfare is to buy fossil fuel deposits in the South at their market price. However, if this option was not available and the South required a full compensation for the foregone income from its fossil fuel deposits, the choice between ‘buying coal’ and a price subsidy for green energy inputs depends on the relative development of green technologies in the North and the South. The subsidy is preferable only if the North has a much higher initial level of renewable technology, as it would become the sole producer of energy worldwide for the duration of the policy. If that was not the case, a Northern region with relatively underdeveloped green energy technologies should always prefer the ‘buy coal’ policy, even with full income compensation. Therefore, if the Southern region comprises large fossil fuel owners like China, India, South Africa, Indonesia, Russia, with technologies and a capacity to produce solar panels, wind turbines or hydroelectric energy almost equivalent to the richest nations, the best solution would be to purchase their fossil fuel deposits and preserve them, while letting these countries compete in the production of (clean) energy inputs. Much of the current climate challenge indeed derives from these large developing nations, which perceive a significant opportunity cost in abandoning fossil fuels, so this might be the most realistic scenario.

Our model relies on a number of simplifications to make it tractable. First, the model focuses on the damage from fossil fuels only, but in reality generating and processing energy is an environmentally intensive activity, even when done with renewable energy sources. No current energy source is free from some environmental externalities. Nuclear energy production imposes rare but sizeable risks on the countries producing it, in addition to the cost of managing radioactive waste. Hydroelectric energy requires the flooding of valleys to build dams. Biomass and wood burning releases local air pollutants like $\hbox {SO}_{{X}}$ and $\hbox {NO}_{{X}}$. Wind turbines produce noise and landscape impacts. Even if these energy sources do not have significant global spillovers, their local impacts are far from neutral (Markandya 2012). Introducing local externalities in the model would make the North less keen to produce energy, and thus favour the Coasian policy of buying deposits abroad, letting the South produce some amount of renewable energy inputs.

Second, in our model fossil fuel and renewable energy inputs are perfect substitutes. In reality, the two forms of energy often coexist, especially because renewable energy poses significant challenges in terms of intermittent availability and storage. Practically, many plants that rely on solar energy also use fossil fuels to compensate volatility in supply (Sinn 2016). Moreover, technical limitations reduce the substitutability between fossil fuel inputs and renewables’ ones. For example, the production of steel requires extremely high temperatures and coking coal remains a vital input with no easy substitutes (World Coal Associaltion 2014). We leave the analysis of these technical hindrances to substitution for future research.

Third, in our model the use of fossil fuels automatically results in environmental degradation and, without any policies, the South continues using these polluting resources until a disaster is reached. However, in reality there could be a number of counterbalancing effects. For example, the South could at some point become active and tax or ban fossil fuels. Another option is that the scarcity of fossil fuel resources could make them more expensive to extract (although, as we discussed in the introduction, at least coal is unlikely to become significantly more expensive in the coming century). Moreover, carbon capture and storage technologies could appear, so that part of existing fossil fuel reserves could still be burnt, with limited damages from their emissions. In our model we consider a worse-case scenario, whereby none of these factors exists and the North needs to halt the use of fossil fuels abroad alone. An interesting extension could be to model the Southern decision-making process: this would also allow an examination of the monitoring costs for the deposits purchased, showing in what circumstances the South might still have an incentive to illegally use some fossil fuels.

Overall, our model provides a benchmark for a pessimistic scenario in which no cooperation is reached and unilateral policies are required to hastily remove fossil fuels from a non-cooperating region. As shown in the literature, with sufficient time available, innovation policies combined with other instruments such as trade restrictions can be enough to redirect the world towards cleaner energy production. But this is not guaranteed to work under all circumstances. ‘Scale and speed matter’, observed Nicholas Stern at the 25th Annual meeting of the European Bank for Reconstruction and Development, following the Paris COP21 agreements. In this spirit, our model highlights that the scale of major fossil-fuel owners plays against unilateral interventions and calls for expensive policy actions to reshape global energy production rapidly. Such costly interventions might become the only option available as countries postpone a multilateral solution, imposing a continuous degradation of the global climate.

Appendices

Appendices

A: Laissez-Faire Equilibrium

A complete derivation of the laissez-faire equilibrium is provided in the Online Appendix. In this section, we summarize the main equilibrium results. To solve the model, first we use the profit maximization of final goods producers Y to get the demand for intermediates $Q_z$. Second, the profit maximization of intermediate goods producers generates a demand for machines, which leads to the price for machines, their optimal quantity and the profits that can be realized if a scientist successfully patents an innovation on a given machine. Third, we obtain factor demands for L, K and R and express intermediate products’ prices $p_z$ as functions of factors’ prices. Lastly, combining all results from the three levels of optimization above, we obtain the equilibrium conditions as functions of innovative technologies A, as follows

$$\begin{aligned} (p_{eC}^*)^{\phi }= & {} \left( \frac{1}{\psi }\right) ^{\frac{\psi }{1-\psi }}(X_\psi ) \frac{\left[ \left( A_{n}^k\right) ^\psi \left( A_{n}^{(k-1)}\right) ^\psi \right] ^{\phi }}{\left[ A_{eC}^k\left( A_{n}^{(k-1)}\right) ^\psi \right] ^{\phi }\overset{\_}{K}^k + \left[ A_{eC}^{(k-1)}\left( A_{n}^k\right) ^\psi \right] ^{\phi }\overset{\_}{K}^{(k-1)}} \end{aligned}$$

(19)

$$\begin{aligned} (p_{eF}^*)^{\frac{1}{1-\gamma }}= & {} \left( \frac{1}{\beta }\right) ^{\beta } (X_\beta )^{1-\beta } \left( \frac{(A_n^S)^\beta }{A_{eF}^S}\right) ^{\frac{1}{1-\gamma }} \left( \frac{1}{\overset{\_}{R}^{S}}\right) ^{\alpha } \left( \frac{1}{\overset{\_}{K}^S}\right) ^{1-\alpha -\beta } \end{aligned}$$

(20)

where $\phi \equiv \frac{1}{(1-\psi )(1-\gamma )}$, $X_\psi \equiv \frac{1-\upsilon }{\upsilon + \psi (1-\upsilon )} \left( (A_n^N)^{\frac{1}{1-\gamma }}\overset{\_}{L}^{N} + (A_n^S)^{\frac{1}{1-\gamma }} \overset{\_}{L}^{S}\right)$ and $X_\beta \equiv \frac{(1-\upsilon )}{\upsilon +\beta (1-\upsilon )} \left( (A_n^N)^{\frac{1}{1-\gamma }}\overset{\_}{L}^{N} + (A_n^S)^{\frac{1}{1-\gamma }} \overset{\_}{L}^{S}\right)$, and the price of non-energy goods is set as the numeraire, $p_n\equiv 1$. If fossil fuels are being produced, the equilibrium factor demands are

$$\begin{aligned} L_{eC}^{S*}= & {} L_{eC}^{N*}=0 \;\;\;\;\;\;\;\; L_{n}^{N*}=\overset{\_}{L}^{N} \;\;\;\;\;\;\;\;L_{n}^{S*}= \overset{\_}{L}^{S} - L_{eF}^{S*} \end{aligned}$$

(21)

$$\begin{aligned} L_{eF}^{S*}= & {} min \;\; \left\{ \overset{\_}{L}^{S}\;\; ; \;\; \frac{\beta (1-\upsilon )}{\upsilon + \beta (1-\upsilon )} \frac{(A_n^N)^{\frac{1}{1-\gamma }}\overset{\_}{L}^{N} + (A_n^S)^{\frac{1}{1-\gamma }} \overset{\_}{L}^{S}}{{A_{n}^S}^\frac{1}{1-\gamma }} \right\} \end{aligned}$$

(22)

$$\begin{aligned} K_{eF}^{S*}= & {} \overset{\_}{K}^{S} \;\;\;\;\;\;\;\; K_{eC}^{S*}=K_{eC}^{N*}=0 \;\;\;\;\;\;\;\; R_{eF}^{S*}=\overset{\_}{R}^S \end{aligned}$$

(23)

and the optimal amount of fossil fuel intermediates produced is

$$\begin{aligned} Y^{*S}_{eF}=\frac{A_{eF}}{\left( A_n^{S}\right) ^\beta }\;\;\left( X_{\beta }\right) ^{\beta +\gamma (1-\beta )}\;\;\; \left[ \beta ^{\beta } \left( \overset{\_}{K}^{S}\right) ^{(1-\alpha -\beta )} \left( \overset{\_}{R}^S\right) ^{\alpha }\right] ^{1-\gamma } \end{aligned}$$

(24)

If instead fossil fuels are not being produced, the equilibrium values are

$$\begin{aligned} L_{eF}^{S*}= & {} 0 \;\;\;\;\;\;\;\; L_{n}^{k*}=\overset{\_}{L}^k-L_{eC}^{k *} \end{aligned}$$

(25)

$$\begin{aligned} L_{eC}^{k*}= & {} min \left\{ \overset{\_}{L}^k ; \frac{\psi (1-\upsilon )}{\upsilon + \psi (1-\upsilon )} \frac{\left( (A_n^k)^{\frac{1}{1-\gamma }}\overset{\_}{L}^{k} + (A_n^{k-1})^{\frac{1}{1-\gamma }} \overset{\_}{L}^{k-1}\right) \left( A_{eC}^k \left( A_n^{(k-1)}\right) ^\psi \right) ^{\phi } \overset{\_}{K}^k}{\left( A_n^k\right) ^{\frac{1}{1-\gamma }} \left( \left[ A_{eC}^k\left( A_{n}^{(k-1)}\right) ^\psi \right] ^{\phi }\overset{\_}{K}^k + \left[ A_{eC}^{(k-1)}\left( A_{n}^k\right) ^\psi \right] ^{\phi } \overset{\_}{K}^{(k-1)}\right) } \right\} \end{aligned}$$

(26)

$$\begin{aligned} K_{eF}^{S*}= & {} 0 \;\;\;\;\;\;\;\;K_{eC}^{k*}=\overset{\_}{K}_{eC}^{k} \;\;\;\;\;\;\;\; R_{eF}^{S*}= 0 \end{aligned}$$

(27)

B: Innovation Dynamics

The allocation of scientists in equilibrium depends on the expected profitability of working in a sector. Profits are zero if innovation is not successful. From the profit maximization of machine producers, we get

$$\begin{aligned} E(\pi ^k_{n, t})= & {} \gamma \left( 1-\gamma \right) L^k_{n, t}\left( p_{n, t}(1+\varphi ) A^k_{n,t-1}\right) ^\frac{1}{1-\gamma } + 0 \end{aligned}$$

(28)

$$\begin{aligned} E(\pi ^k_{eC, t})= & {} \gamma \left( 1-\gamma \right) (L^k_{eC, t})^{\psi }(K^k_{eC, t})^{1-\psi }\left( p_{eC, t}(1+\varphi ) A^k_{eC,t-1}\right) ^\frac{1}{1-\gamma } + 0 \end{aligned}$$

(29)

$$\begin{aligned} E(\pi ^S_{eF, t})= & {} \gamma \left( 1-\gamma \right) (L^S_{eF, t})^{\beta }(K^S_{eF, t})^{1-\alpha -\beta } (R^S_{t})^{\alpha } \left( p_{eF, t}(1+\varphi ) A^S_{eF,t-1}\right) ^\frac{1}{1-\gamma } + 0 \end{aligned}$$

(30)

Only Southern scientists can work in the fossil fuel sector. The ratio of expected profits in Eqs. (28) and (29) or (30) yields the ratios of Eqs. (13) and (14) in the main text. In equilibrium, they become

$$\begin{aligned} \frac{E(\pi _{n,t}^{k})}{E(\pi _{eC,t}^{k})}= & {} \frac{\left( \frac{\upsilon }{1-\upsilon }\right) f(k)_t-\psi f(k-1)_t +\left( \frac{\upsilon }{1-\upsilon }+\psi \right) \frac{g(k-1)_t}{g(k)_t}}{f(k-1)_t +f(k)_t}\left( \frac{1+\varphi (1-m_{n,t}^k)}{1+\varphi m_{n,t}^k}\right) ^{\frac{1}{1-\gamma }} \end{aligned}$$

(31)

$$\begin{aligned} \frac{E(\pi _{n,t}^{S})}{E(\pi ^S_{eF,t})}= & {} \frac{\left( \frac{\upsilon }{1-\upsilon }\right) f(S)_t-\beta f(N)_t}{f(N)_t +f(S)_t}\left( \frac{1+\varphi (1-m_{n,t}^S)}{1+\varphi m_{n,t}^S}\right) ^{\frac{1}{1-\gamma }} \end{aligned}$$

(32)

where $f(k)_t\equiv [(1+\varphi m_{n,t}^k) A_{n,t-1}^k]^{\frac{1}{1-\gamma }} \overset{\_}{L}^{k}$ and $g(k)_t\equiv \left[ (1+\varphi (1-m_{n,t}^k))A_{eC, t-1}^k\left( (1+\varphi m_{n,t}^{k-1})A_{n, t-1}^{k-1}\right) ^\psi \right] ^{\phi }\overset{\_}{K}^{k}$.

We then have three possible cases, depending on the effect of scientists on the ratio of profits.²³

• 1. Profit ratio increasing in scientists—$\partial \frac{E(\pi _n)}{E(\pi _e)}/ \partial m_n>0$. In this case, when the number of scientists in n rises, the profits of the manufacturing sector also rise relative to the energy sector. Thus, it must hold that

  $$\begin{aligned} \frac{E(\pi _{n} (m_n=1))}{E(\pi _{e} ((m_n=1))}> \frac{E(\pi _{n} (m_n=0))}{E(\pi _{e} ((m_n=0))} \end{aligned}$$

  (33)

  The equilibrium allocations of scientists (such that none would want to move to a more profitable sector) are

  • (a) If $\frac{E(\pi _{n} (m_n=1))}{E(\pi _{e} ((m_n=1))}> \frac{E(\pi _{n} (m_n=0))}{E(\pi _{e} ((m_n=0))} > 1$—the only equilibrium is $m^*_n=1$, as manufacturing is always more profitable than energy.

  • (b) If $1> \frac{E(\pi _{n} (m_n=1))}{E(\pi _{e} ((m_n=1))} > \frac{E(\pi _{n} (m_n=0))}{ E(\pi _{e} ((m_n=0))}$—the only equilibrium is $m^*_n=0$, viceversa.

  • (c) If $\frac{E(\pi _{n} (m_n=1))}{E(\pi _{e} ((m_n=1))}> 1 > \frac{E(\pi _{n} (m_n=0))}{ E(\pi _{e} ((m_n=0))}$—the equilibrium is either $m^*_n=1$, $m^*_n=0$, or an interior solution $m^*_n \in (0,1)$ such that $[E(\pi _{n} (m_n=m_n^*))]/[E(\pi _{e} ((m_n=m_n^*))]=1$.

• 2. Profit ratio decreasing in scientists—$\partial \frac{E(\pi _n)}{E(\pi _e)}/ \partial m_n<0$. Now, the opposite of (33) must hold, so the options for equilibrium allocations are

  • (a) If $\frac{E(\pi _{n} (m_{n}=0))}{E(\pi _{e} ((m_{n}=0))} < 1$—the only equilibrium is $m_{n}^*=0$. It would not be profitable for scientist to move to manufacturing, because that would only lower the profit ratio.

  • (b) If $\frac{E(\pi _{n} (m_{n}=1))}{E(\pi _{e} ((m_{n}=1))} > 1$—the only equilibrium is $m_{n}^*=1$, opposite to the above case.

  • (c) If neither of the two corner solutions apply, we have an interior solution such that $\frac{E(\pi _{n} (m_n=m_n^*))}{E(\pi _{e} ((m_n=m_n^*))}=1$.

• 3. Profit ratio independent of scientists—$\partial \frac{E(\pi _n)}{E(\pi _e)}/ \partial m_n = 0$. If the ratio is independent of scientists, then

  • (a) If $E(\pi _n)< E(\pi _e)$, the only equilibrium is $m_n^*=0$

  • (b) If $E(\pi _n)> E(\pi _e)$, the only equilibrium is $m_n^*=1$

Applying the conditions above, we can find the equilibrium allocation of scientists, either with a corner solution if the conditions of point (1) or (2) are fulfilled, or finding an interior solution $m^*$ if case (3) applies.²⁴ Rearranging the profit ratios in Eq. (32) with laissez-faire equilibrium values and the respective equilibrium scientists’ allocation, we develop the following Lemma.

Lemma 1

Under laissez-faire, it is an equilibrium for innovation in the South at time t to occur:

(1) only in the fossil fuel sector when $E(\pi ^S_n(m_n=0))< E(\pi ^S_{eF}(m_n=0))$ , so that $m_n^*=0$, if

$$\begin{aligned} \left[ \frac{A_{n,t-1}^S}{(1+\varphi m_{n,t}^N)A^N_{n,t-1}} \right] ^{\frac{1}{1-\gamma }}\frac{{\bar{L}}^S}{{\bar{L}}^N} < \frac{1+\beta (1+\varphi )^{\frac{1}{1-\gamma }}}{\frac{\upsilon }{1-\upsilon }(1-\varphi )^{\frac{1}{1-\gamma }-1}} \end{aligned}$$

(34)

(2) only in the manufacturing sector when $E(\pi ^S_n(m_n=1))> E(\pi ^S_{eF}(m_n=1))$, so that $m_n^*=1$, if

$$\begin{aligned} \left[ \frac{A_{n,t-1}^S}{(1+\varphi m_{n,t}^N) A^N_{n,t-1}}\right] ^{\frac{1}{1-\gamma }}\frac{{\bar{L}}^S}{{\bar{L}}^N} > \frac{1+\beta (1+\varphi )^{\frac{1}{\gamma -1}}}{\frac{\upsilon }{1-\upsilon }(1-\varphi )^{\frac{1}{\gamma -1}}-1} \end{aligned}$$

(35)

(3) in both sectors when $E(\pi ^S_n({\tilde{m}}))=E(\pi ^S_{eF}({\tilde{m}}))$(so when Eq. (32equals to 1), such that $m_n^*={\tilde{m}}$.

Thus the following condition ensures that all Southern scientists work in the fossil fuel industry

$$\begin{aligned} \left[ \frac{A_{n,t-1}^S}{(1+\varphi )A^N_{n,t-1}} \right] ^{\frac{1}{1-\gamma }}\frac{{\bar{L}}^S}{{\bar{L}}^N} < \frac{1+\beta (1+\varphi )^{\frac{1}{1-\gamma }}}{\frac{\upsilon }{1-\upsilon }(1-\varphi )^{\frac{1}{1-\gamma }-1}} \end{aligned}$$

(36)

which corresponds to the initial condition at time zero imposed in Assumption 2.

If the fossil fuel sector is the most profitable innovation activity in the first period, as imposed in Assumption 2, then it necessarily remains the most profitable also in the next period if fossil fuels are still produced, because with this scientists’ allocation $A_{n, t}^S=A_{n, t-1}^S$ and $A_{n, t}^N\ge A_{n, t-1}^S$, and thus Eq. (36) keeps being valid.

C: Regularity Condition: Initial Prices

According to Assumption 1, in the first period under fossil fuels are cheaper than renewable resources, so $\frac{p_{eF, t=1}^*}{p_{eC, t=1}^*}<1$. This requires that fossil fuel technologies have an initial advantage such that, rearranging the equilibrium prices (19) and (20), the following condition holds

$$\begin{aligned} \dfrac{(A_{eF, t=1}^{S}) ^\phi }{\Omega } > \dfrac{ \left( \dfrac{\left( A_{n,t=1}^S\right) ^{\beta }}{(A_{n,t=1}^N)^\psi } \; A_{eC,t=1}^N\right) ^\phi \overset{\_}{K}^N + \left( \dfrac{\left( A_{n,t=1}^S\right) ^{\beta }}{(A_{n,t=1}^S)^\psi }\; A_{eC,t=1}^S\right) ^\phi \overset{\_}{K}^S}{\left[ (A_{n,t=1}^N)^{\frac{1}{1-\gamma }}\overset{\_}{L}^{N} + (A_{n,t=1}^S)^{\frac{1}{1-\gamma }} \overset{\_}{L}^{S}\right] ^{\frac{\beta - \psi }{1-\psi }} } \;\; \forall m^k_1\in [0,1] \end{aligned}$$

(37)

where for brevity we write the A technologies at time $t=1$, but each of them contains the initial technology $A_{t=0}$ and the contemporaneous allocation of scientists, namely $A_{z, t=1}^k= (1+\varphi m_{z,t=1}^k) A_{z, t=0}^k$. Omega is a time-invariant component such that $\Omega ^{1-\psi } \; \equiv \frac{\left[ \psi (1-\upsilon )\right] ^\psi }{\left[ \beta (1-\upsilon )\right] ^\beta } \; \frac{\left[ \upsilon +\psi (1-\upsilon )\right] ^{1-\psi }}{\left[ \upsilon +\beta (1-\upsilon )\right] ^{1-\beta }} \frac{1}{{\left( \overset{\_}{K}^S\right) ^{1-\alpha -\beta } \left( \overset{\_}{R}^S\right) ^\alpha }}$. A sufficiently large endowment of fossil fuel deposits in the South, R, or a sufficiently advanced fossil fuel technology $A_{eF, t=0}$ can by themselves ensure that this condition holds.

D: Proof of Proposition 1

Proof

For $Y_{eF}$ to be strictly increasing in time, we must show that $p_{eC, t} >p_{eF, t} \;\; \forall t$, so that fossil fuels are always preferred to renewable energy intermediates, and that $Y_{eF, t+1} > Y_{eF,t} \; \forall t$, so that fossil fuels increase every period. For the prices, we know from Assumption 1 that in the first period $p_{eC, t=1}/p_{eF, t=1}>1$. From Assumption 2, we also know that, if fossil fuels are the cheapest input, the equilibrium allocation of scientists is $m_n^S=0$ and $m_{eF}^S=1$. Hence, only fossil fuel technology $A_{eF}^S$ grows in the South. In the North, since there is no active energy sector, all scientists are in manufacturing ($m_n^N=1$) and only the $A_n^N$ technology grows over time. Then, the regularity condition in Eq. (37) must hold in the subsequent period: its left-hand side grows by $(1+\varphi )^\phi$—the increase in $A_{eF}^S$ with all scientists in that sector, while the right-hand side falls since $A_n^N$ increases the denominator. All other factors are constant, so the inequality holds in the following period. Iterating this process over time, fossil fuels are always cheaper than renewable energy inputs.

For the second point, using the equilibrium for fossil fuel intermediates $Y_{eF}^*$ from Eq. (24) we show that

$$\begin{aligned} Y_{eF, t+1}= & {} \frac{(1+\varphi m_{eF, t+1}^S)A_{eF, t}}{\left[ \left( 1+\varphi m_{n, t+1}^S\right) A_{n,t}^{S} \right] ^\beta }\;\left[ \left( \left( 1+\varphi \right) A_{n, t}^N\right) ^{\frac{1}{1-\gamma }}\overset{\_}{L}^{N} + \left( \left( 1+\varphi m_{n, t+1}^S\right) A_{n, t}^S\right) ^{\frac{1}{1-\gamma }} \overset{\_}{L}^{S}\right] ^{\beta +\gamma (1-\beta )} \nonumber \\&> Y_{eF, t}= \;\;\frac{A_{eF, t}}{\left( A_{n, t}^{S}\right) ^\beta }\;\;\left[ \left( (A_{n, t}^N)^{\frac{1}{1-\gamma }}\overset{\_}{L}^{N} + (A_{n, t}^S)^{\frac{1}{1-\gamma }} \overset{\_}{L}^{S}\right) \right] ^{\beta +\gamma (1-\beta )}\;\;\; \end{aligned}$$

(38)

All scientists in the North are in manufacturing, since the energy sector is non-existent. Simplifying

$$\begin{aligned} \begin{aligned}&\left( A_{n, t}^N\right) ^{\frac{1}{1-\gamma }}\overset{\_}{L}^{N}\left[ \left( \frac{1+\varphi m_{eF, t+1}^S}{\left( 1+\varphi m_{n, t+1}^S\right) ^\beta }\right) ^{\frac{1}{{\beta +\gamma (1-\beta )}}}\left( 1+\varphi \right) ^{\frac{1}{1-\gamma }} -1\right] +\\&\left( A_{n, t}^S\right) ^{\frac{1}{1-\gamma }} \overset{\_}{L}^{S} \left[ (1+\varphi m_{eF, t+1}^S)^{\frac{1}{{\beta +\gamma (1-\beta )}}} \left( 1+\varphi m_{n, t+1}^S\right) ^{\frac{1}{1-\gamma } - \frac{\beta }{\beta +\gamma (1-\beta )}} -1 \right] > 0 \end{aligned} \end{aligned}$$

(39)

We can show that both square brackets are greater than zero, so that the following conditions hold

$$\begin{aligned} \left( \frac{(1+\varphi m_{eF, t+1}^S)}{\left[ 1+\varphi m_{n, t+1}^S\right] ^\beta }\right) ^{\frac{1}{{\beta +\gamma (1-\beta )}}}\left( 1+\varphi \right) ^{\frac{1}{1-\gamma }} > 1 \end{aligned}$$

(40)

and

$$\begin{aligned} \left( 1+\varphi m_{eF, t+1}^S\right) ^{\frac{1}{{\beta +\gamma (1-\beta )}}} \left( 1+\varphi m_{n, t+1}^S\right) ^{\frac{\gamma }{(1-\gamma )(\beta +\gamma (1-\beta ))}} > 1 \end{aligned}$$

(41)

Since $\varphi >0$ and $1 \ge m_{eF}, m_n \ge 0$, the terms $(1+\varphi m_{eF}^S)\ge 1$ and $(1+\varphi m_{n}^S)\ge 1$. It is not possible for both terms to be equal to one at the same time, because $m_{eF}^S+m_n^S=1$. Moreover, since $1>\beta , \gamma >0$, then $\beta +\gamma (1-\beta )>0$ and all exponents are positive. The first condition (D.22) is least likely to hold when the denominator has its largest value with $m_{n}=1$

$$\begin{aligned} \left( \frac{1}{1+\varphi }\right) ^{\frac{\beta }{\beta +\gamma (1-\beta )}}\left( 1+\varphi \right) ^{\frac{1}{1-\gamma }} > 1 \end{aligned}$$

(42)

which holds if $\frac{1}{1-\gamma } > \frac{\beta }{\beta +\gamma (1-\beta )}$, which is indeed the case, since their difference is $\frac{\gamma }{(1-\gamma )(\beta +\gamma (1-\beta ))} > 0$. For any lower value of $m_{n}^S$ the denominator is smaller, so the above condition necessarily holds. Also the second condition 41 holds, since the two terms are both positive and cannot be simultaneously equal to one, as stated before. Thus, $Y_{eF}^S$ always strictly increases in time. $\square$

E: Proof of Proposition 2

Proof

To prove Proposition 2 we must show that the global use of fossil fuels under laissez-faire inevitably causes an environmental catastrophe. From Proposition 1, we know that the production of fossil fuel inputs $Y^S_{eF, t}$ is strictly increasing over time. The environment is a decreasing function of fossil fuel production, according to Eq. (12). Since the other parameters determining the quality of the global environment $\Delta$, $\xi$ and ${\overline{G}}$ are fixed and of finite magnitude, while $Y^S_{eF}$ keeps growing boundlessly, even if we start with a small amount of fossil fuels’ use, necessarily there will be a time d when the production of fossil fuels surpasses the regenerative capacity of the environment to return to its initial pristine state

$$\begin{aligned} G_{d}=\left( 1+\Delta \right) {\overline{G}} -\xi Y^S_{eF,d-1} < {\overline{G}} \end{aligned}$$

(43)

After this point, the environment starts declining more and more every year. Iteratively substituting the values of the environment over time in the above equation, with ever growing values of fossil fuels, we would get to a generic time T when $Y_{eF}$ makes $G_T\le 0$, namely when

$$\begin{aligned} \left( 1+\Delta \right) ^{T-d+1} {\overline{G}} \le \xi \sum _{a=d-1}^{T-1} \left( 1+\Delta \right) ^{T-a-1} Y^S_{eF,a} \end{aligned}$$

(44)

At which point the economy will be in a disaster, as per Definition D.1. $\square$

F: Minimum Purchase of Deposits R

The North only needs to buy the extractive rights for the minimum amount of deposits R that forces a switch away from fossil fuel production, by making renewable energy inputs less costly than fossil fuels, $p_{eF}> {\tilde{p}}_{eC}$. Rearranging the equilibrium prices from Eqs. (20) and (19) we get that, at a given point in time, the maximum amount of R that can be left to the South is

$$\begin{aligned} \left( {\tilde{R}}^S\right) ^{\alpha } \le \dfrac{\psi ^\psi \left( X_\beta \right) ^{1-\beta }}{\beta ^\beta \left( X_\psi \right) ^{1-\psi }} \left( \dfrac{(A_{n_{(eF)}}^S)^{\beta }}{\left( A_{n_{(eC)}}^N\right) ^\psi \left( A_{n_{ (eC)}}^{S}\right) ^\psi }\right) ^{\frac{1}{1-\gamma }} \dfrac{\left( \left[ A_{eC}^N\left( A_{n_{ (eC)}}^{S}\right) ^\psi \right] ^{\phi }\overset{\_}{K}^N + \left[ A_{eC}^{S}\left( A_{n_{ (eC)}}^N\right) ^\psi \right] ^{\phi } \overset{\_}{K}^{S}\right) ^{1-\psi }}{(A_{eF}^{S})^{\frac{1}{1-\gamma }}\left( \overset{\_}{K}^S\right) ^{1-\alpha -\beta }} \end{aligned}$$

(45)

In the notation, we distinguish among the $A_{n_{(e)}}$ technologies arising in the equilibrium with fossil fuel energy $A_{n_{(eF)}}$ from those in the renewable energy equilibrium $A_{n_{(eC)}}$, since they need not be equal. Again, as in Sect. C, all the A technologies are at time t (time subscript omitted for brevity), but contain the contemporaneous allocation of scientists and past technologies, namely $A_{z, t}^k= (1+\varphi m_{z,t}^k)A_{z,t-1}$, so this condition must apply in the context of the final scientists’ equilibrium. The deposits available for production in the South must be less than ${\tilde{R}}^S$ to ensure no production of fossil fuel energy occurs. Therefore, $R_{min}={\overline{R}}^S-{\tilde{R}}^S$.

G: Calibration

For the calibration exercise we select values as close as possible to Hémous (2016). Initial values for our simulations are based on the 2003–2007 world economy (from the UNIDO database). A standard approach is to identify Annex I countries with the North²⁵ and non-Annex I countries with the South²⁶. The energy intensive sector is identified with chemical, petrochemical, non-ferrous metals, non-metallic minerals, and iron and steel, while the manufacturing sector is identified with all other sectors. For fossil fuel resources, we use the Statistical Review of World Energy 2013, taking coal production for non-Annex I countries (million tonnes of oil equivalent) across all years under consideration. The discount rate is, as in Nordhaus (2008), 0.0015. We rely on Hémous’ calibration for the initial values of environment and productivity. The polluting factor associated with the use of fossil fuel is equalized to the polluting factor of the South in Hémous, the most polluting country in his model. Table 1 presents the full list of parameters.

Table 1 Calibration parameters