Do Benefits from Dynamic Tariffing Rise? Welfare Effects of Real-Time Retail Pricing Under Carbon Taxation and Variable Renewable Electricity Supply

Abstract

We analyze the gross welfare gains from real-time retail pricing in electricity markets where carbon taxation induces investment in variable renewable technologies. Applying a stylized numerical electricity market model, we find a U-shaped association between carbon taxation and gross welfare gains. The benefits of introducing real-time pricing can accordingly be relatively low at relatively high carbon taxes and vice versa. The non-monotonous change in welfare gains can be explained by corresponding changes in the inefficiency arising from “under-consumption” during low-price periods rather than by changes in wholesale price volatility. Our results may cast doubt on the efficiency of ongoing roll-outs of advanced meters in many electricity markets, since net benefits might only materialize at relatively high carbon tax levels and renewable supply shares.

Introduction

Facing the challenge to accommodate increasing shares of variable renewable electricity supply, regulators, academia and practitioners consider price-responsive demand as an integral part of low-carbon power markets (Joskow 2012; Kopsakangas et al. 2012; Mills and Wiser 2014; ACER 2014; CEER 2014; IEA 2016; BMWi 2016; The White House 2016; CAISO 2017). Several jurisdictions in the U.S. and Europe with different renewable supply shares have started to roll out advanced metering infrastructure at large scale, or are planning to do so. While this would technically allow consumers to receive and respond to price signals in real time, it is unclear at what stage of renewable market penetration the resulting benefits would outweigh the related costs. This paper analyzes how and why the gross welfare gains from implementing real-time pricing could change under carbon emissions taxation and growing variable renewable supply shares.

While the majority of electricity consumers usually faces time-invariant retail prices, introducing real-time retail pricing that reflects the temporal variation in the marginal costs of electricity supply is often found to result in significant allocative efficiency gains (Borenstein and Holland 2005; Borenstein 2005; Holland and Mansur 2006; Joskow and Tirole 2007; Allcott 2011, 2012). It seems likely, however, that these gross welfare gains would be outweighed in many markets by the relatively high upfront costs of advanced metering infrastructure as well as by the related transaction costs, deeming the large-scale roll-out of real-time retail pricing inefficient (Leautier 2014). The market penetration of variable renewable energy technologies (VRE) such as wind or solar is widely assumed to change this in part because of the projected increase of wholesale price volatility, which is seen to drive the welfare loss from consuming either “too little” or “too much” under common flat retail rate schemes (Allcott 2011; Borenstein 2012; Leautier 2014; Mills and Wiser 2014; ACER 2014; IEA 2016).

We quantify the change in the potential gross welfare gains from introducing real-time retail pricing (RTP) for different carbon taxes and variable renewable market penetration rates. We investigate the economic mechanisms underlying these changes and whether they are associated with wholesale price volatility as common intuition would suggest. To do so, we simulate long-run market equilibria, applying a deterministic electricity market model following Borenstein and Holland (2005), which mimics a competitive wholesale and retail market with exogenous shares of real-time and flat-priced consumers. Our model adaptation includes endogenous investment in variable renewable generation technologies, which is induced through taxing carbon dioxide emissions from fossil-fuel technologies. We calibrate the model to German market data using long-run projections about technology-specific cost parameters. We conduct a comparative static welfare analysis of varying RTP consumer shares, carbon taxes and renewable supply shares in total annual electricity supply. Our research complements related studies which ignore the welfare effects of RTP between zero and very high renewable supply shares and thus do not account for different stages of renewable market penetration (Chao 2011; Kopsakangas et al. 2012; Fell and Linn 2013; Brouwer et al. 2016).

Our main finding suggests that the welfare gains from real-time pricing change in a U-shaped fashion with the carbon tax. Contrary to common intuition, this means that high shares of variable renewable electricity supply do not necessarily imply high welfare gains from introducing RTP (cf. Mills and Wiser 2014). For a wide range of carbon tax scenarios, we find that these welfare gains can actually be higher in cases where carbon taxation does not induce renewable supply compared to cases where carbon taxes and renewable supply shares are relatively high. Hence, given that introducing real-time pricing in conventional electricity markets may result in net losses when accounting for related infrastructure costs, as found by Leautier (2014), for instance, current roll-out plans for smart meters in U.S. and EU markets might be too optimistic about the renewable supply share at which real-time pricing is becoming net beneficial.

Moreover, while wholesale price volatility is an important driver of the potential welfare gains from real-time pricing, our results suggest that it does not fully explain the observed changes of welfare gains across different carbon tax scenarios. Specifically, welfare gains can be comparatively low even if wholesale price volatility is comparatively high and vice versa. Hence, to the extent that smart meter roll-out policies are based on the expectation that price volatility has sufficiently increased and that it is the sole driver of efficiency gains from time-based pricing schemes, these policies might be misguided (cf. Allcott 2011; Borenstein 2012; Leautier 2014; ACER 2014; IEA 2016).

We instead illustrate that the U-shaped change in the welfare gains from real-time pricing closely follows the changing inefficiency arising from “under-consumption”. That is, the extent to which flat-priced consumers consume “too little” during low-price periods changes with the carbon tax and renewable supply share. Specifically, we can show that the average level of under-consumption initially decreases with the carbon tax and increases again as soon as it induces market entry of wind and solar capacity. Changes in the levels of under-consumption result from a shift in the wholesale price distribution towards a higher mean, combined with an increasing incidence of zero-prices as soon as renewable technologies enter the market. As a result, the inefficiency arising from under-consumption gradually increases, leading to gradually increasing welfare gains from RTP. Initially, however, carbon emission taxation leads to a more elastic aggregate supply curve, since the marginal costs of carbon-intensive and less carbon-intensive fossil-fuel technologies converge. This results in lower retail price spreads and thus also decreasing welfare gains from adopting real-time pricing.

The paper proceeds as follows. In Sect. 2 we present an adaptation of the partial equilibrium model of real-time retail pricing by Borenstein and Holland (2005) and Allcott (2012). Data, the model calibration, scenarios and central simulation results are described and discussed in Sects. 4 and 5, respectively. Section 6 concludes.

Model

We employ a two-stage wholesale and retail electricity market model largely building on Borenstein and Holland (2005) and Allcott (2012), but also incorporate carbon tax driven investments and a detailed representation of variable renewable generation technologies. The details of the model are described below. For the numerical application, we formulate it as a mixed complementarity problem in GAMS (Rutherford 1995). The code is available as open-source using the acronym LORETTA (“LOng-run Electricity market model with Time-varying retail TAriffing”).¹

Electricity Demand

Wholesale electricity supply has to match aggregate demand ${\overline{Q}}_{t}\left( p_{t}+pc_{t},{\bar{p}}+pc\right)$ in each hour t$\in$T, where $p_{t}+pc_{t}$ is the retail real-time price and ${\bar{p}}+pc$ is the flat retail rate. In line with previous work, we assume that consumers have the same underlying demand function $Q_{t}\left( p\right)$ and reduce demand if their respective retail rate p increases, so that $\frac{\partial Q_{t}}{\partial p}<0.$ An exogenously given share of consumers, $\alpha \in \left[ 0,1\right]$, consists of real-time priced customers facing an hourly varying retail electricity price $p_{t}$, while the remaining $\left( 1-\alpha \right)$ flat-rate consumers pay the time-invariant tariff ${\bar{p}}.$ Additionally, consumers pay separately for generation capacity and reserves. While flat-rate consumers pay a constant capacity price pc per unit of electricity, RTP consumers pay the time-varying capacity price²$pc_{t}$. That is, RTP consumers face scarcity prices, whereas flat-rate consumers do not. Hence, in each period t RTP consumers consume $\alpha Q_{t}\left( p_{t}+pc_{t}\right)$ units of electricity, while flat-rate consumers’ demand is equal to $\left( 1-\alpha \right) Q_{t}\left( {\bar{p}}+pc\right)$. Hourly aggregate electricity demand is then given by ${\overline{Q}}_{t}\left( p_{t}+pc_{t},{\bar{p}}+pc\right) =\alpha Q_{t}\left( p_{t}+pc_{t}\right) +\left( 1-\alpha \right) Q_{t}\left( {\bar{p}}+pc\right)$. Increasing the RTP share $\alpha$ makes aggregate demand more price elastic, which implies that it rotates around the point $\left( {\overline{Q}}_{t}\left( p_{t}+pc_{t},{\bar{p}}+pc\right) ,{\bar{p}}+pc\right)$.³ For the simulation, we assume an isoelastic demand function, $Q_{t}\left( p\right) =a_{t}p^{\epsilon }$, where $\epsilon <0$ is the constant own-price elasticity and $a_{t}$ a scaling parameter capturing structural demand variations over time. Hourly aggregate demand in the simulation is thus ${\overline{Q}}_{t}\left( p_{t}+pc_{t},{\bar{p}}+pc\right) =a_{t}\left[ \alpha \left( p_{t}+pc_{t}\right) ^{\epsilon }+\left( 1-\alpha \right) \left( {\bar{p}}+pc\right) ^{\epsilon }\right].$

Electricity Supply and Capacity Investment

There are I generation technologies available indexed by $i=\left\{ 1,\ldots ,I\right\}$ where $V\subset I$ and $NV\subset I$ is the subset of variable renewable energy technologies (VRE) and non-variable, carbon dioxide (${\text{CO}}_{2}$) emitting technologies,⁴ respectively. Denoting $av_{it}$ as the technology specific capacity factor in period t,  installed capacity of each non-variable technology i, $K_{i}^{NV},$ is always fully available, that is $av_{it}=1\,\forall i\in NV,\,t\in T$, whereas capacity of VRE technology i, $K_{i}^{V}$, is time-varyingly available due to varying wind speeds or solar radiation, that is $av_{it}\in [0,1]\,\forall i\in V,\,t\in T$. Up to available capacity $av_{it}K_{i},$ technology i produces each megawatt hour (MWh) of electricity at constant marginal costs $mc_{i}\left( \tau \right)$, where $\tau$ is the exogenous per unit carbon dioxide emissions tax which increases marginal production costs of non-variable technology i by $\frac{\partial mc_{i}^{NV}}{\partial \tau }>0.$ Annuitized fixed costs of capacity amount to $fc_{i}$ units per megawatt (MW) and year. If assuming that the carbon tax is zero, non-variable technologies can be ordered by increasing marginal production costs $mc_{i}^{NV}>mc_{j}^{NV}\,\forall i>j$ and decreasing annual fixed costs $fc_{i}^{NV}<fc_{j}^{NV}\,\forall i>j$, principally allowing for entry of each technology type in the long-run equilibrium (Crew et al. 1995).⁵ Since VRE technologies produce at negligible or zero marginal costs without emitting carbon dioxide (${\text{CO}}_{2}$), that is $mc_{i}^{V}=0$ and $\frac{\partial mc_{i}^{V}}{\partial \tau }=0\,\forall i\in V$, they become relatively cheaper than non-variable technologies as the carbon tax $\tau$ is raised from zero. Likewise, non-variable technology i becomes relatively cheaper than technology j given that $\frac{\partial mc_{i}}{\partial \tau }<\frac{\partial mc_{j}}{\partial \tau }\,\forall i>j.$ That is, we assume that higher marginal cost technologies such as natural gas plants emit less ${\text{CO}}_{2}$ per MWh than low marginal cost technologies such as hard coal fired plants. Therefore, the carbon tax increases the marginal generation costs of coal fired plants stronger than those of natural gas fired plants. The tax $\tau$ is thus also the main driver ofcapacity portfolio changes in the non-variable technology set.

By maximizing total annual profits $\pi _{i}\left( q_{it},K_{i}\mid w_{t},r\right)$ under perfect foresight and perfect competition and thus taking wholesale electricity price $w_{t}$ as given, generators decide upon investment in capacity $K_{i}$ of technology i and output $q_{it}.$ Output choice is always constrained by available installed capacity, such that $q_{it}\le av_{it}K_{i}\,\forall t,i.$ In addition to their short-run profits from energy sales $q_{it}\left( w_{t}-mc_{i}\right) ,$ non-variable technologies receive a separate, uniform capacity payment r, which is determined in the capacity market equilibrium discussed below. This gives their total annual profit as

$$\begin{aligned} \pi _{i}^{NV}\left( q_{it},K_{i}\mid w_{t},r\right)&= {} \sum _{t=1}^{T}\left[ w_{t}-mc_{i}^{NV}\right] q_{it}^{NV}+rK_{i}^{NV}-fc_{i}^{NV}K_{i}^{NV}. \end{aligned}$$

(1)

Each VRE technology $i\in V$ fully depends on remuneration from energy sales and thus makes annual profits equal to

$$\begin{aligned} \pi _{i}^{V}\left( q_{it},K_{i}\mid w_{t}\right)&= {} \sum _{t=1}^{T}\left[ w_{t}-mc_{i}^{V}\right] q_{it}^{V}-fc_{i}^{V}K_{i}^{V}. \end{aligned}$$

(2)

Each generator using technology i optimally produces at capacity and supplies $q_{it}=av_{it}K_{i}$ each time marginal revenue is larger than marginal costs, that is $w_{t}>mc_{i}$. If $w_{t}=mc_{i}$, a generator is indifferent between any output level, that is $q_{it}\ge 0$, but produces nothing if $w_{t}<mc_{i}.$⁶ Hence, each generating unit has an inverse L-shaped supply curve so that aggregate wholesale supply is a step function (merit order) where each plateau reflects the constant marginal costs of all technologies present in equilibrium (cf. Holland and Mansur 2006).

Under perfect competition, generators invest in capacity of non-variable technology i until (annualized) the fixed costs per unit of capacity $fc_{i}$ equal the accumulated short-run profits $\sum _{t=1}^{T}\left[ w_{t}-mc_{i}\right]$ plus the price of capacity and reserves r⁷

$$\begin{aligned} \sum _{t=1}^{T}\left[ w_{t}-mc_{i}^{NV}\right] +r&= {} fc_{i}^{NV},\forall i\in NV. \end{aligned}$$

(3)

Likewise, generators invest in VRE capacity of technology i until the fixed costs $fc_{i}$ equal the respective stream of short-run profits $\sum _{t=1}^{T}\left[ w_{t}-mc_{i}\right]$ weighted by the hourly varying capacity factor $av_{it}$

$$\begin{aligned} \sum _{t=1}^{T}\left[ w_{t}-mc_{i}^{V}\right] av_{it}&= {} fc_{i,}^{V}\forall i\in V. \end{aligned}$$

(4)

As indicated above, we assume that investment in VRE technologies only becomes profitable, if they become sufficiently cheap through increasing the carbon tax. Equation (4) implies that VRE profitability is strongly determined by the technology specific correlation of capacity availability $av_{it}$ with the wholesale price $w_{t}$ (Lamont 2008). If more capacity of the same VRE technology type enters the market, wholesale prices drop particularly when $av_{it}$ is relatively high, resulting in decreasing profitability. Hence, if a certain VRE share is supposed to materialize in the long-run equilibrium, wholesale prices have to rise disproportionately in periods, where $av_{it}$ is relatively low. As shown by Green and Léautier (2015), this also implies that supportive measures, such as the carbon tax in our case, likely require to rise disproportionately with the VRE market penetration, ceteris paribus. In combination with the typically low average availability of VRE sources, $av_{it}$, this decreasing profitability effect has the important implication that equilibrium wholesale prices settle at relatively high levels on average in presence of VRE market entry. This crucially drives the differences found in the benefits from real-time retail pricing in a market with and without VRE supply.

The Reserve Capacity Mechanism

Previous findings suggest that most of the efficiency gains from introducing RTP result from mitigating the inefficiency from “over-consumption” during high-price periods through savings in costly peak-generation capacity. These savings can be particularly large in the presence of planning reserve margins (PRM), which are implemented in many U.S. markets to induce a certain amount of excess generation capacity. To account for this excess-capacity effect in our numerical application, we impose a planning reserve margin constraint on hourly output by non-variable generation capacity, $q_{it}^{NV},$ similar to Allcott (2012) as follows

$$\begin{aligned} \sum _{i}^{NV}q_{it}^{NV}\le \frac{\sum _{i}^{NV}K_{i}^{NV}}{\left( 1+m\right) },\forall t, \end{aligned}$$

(5)

noting that in equilibrium $\sum _{i}^{NV}q_{it}^{NV}$ is equal to aggregate net demand, ${\overline{Q}}_{t}\left( p_{t}+pc_{t},{\bar{p}}+pc\right) -\sum _{i}^{V}q_{it}$, i.e. total demand less supply from VRE technologies. Constraint (5) effectively requires that non-variable capacity is installed in excess of net peak demand by m percent. Technically it implies that the hourly aggregate supply curve becomes inelastic each time aggregate net demand exceeds installed non-variable capacity less reserves, $\frac{\sum _{i}^{NV}K_{i}^{NV}}{\left( 1+m\right) }$.⁸ The associated Karush–Kuhn–Tucker multiplier, $\rho _{t}$, reflects the time-varying shadow value of non-variable generation capacity plus reserves, $\left( 1+m\right) K^{NV}$, and equals the scarcity price at the intersection of net demand and the inelastic part of the supply curve each time constraint (5) binds.⁹ RTP consumers face this scarcity price via the real-time capacity retail price, $pc_{t}$ (see Sect. 2.4), and correspondingly reduce their demand during peak-demand periods. Flat-rate consumers do not and instead face a constant capacity price component in their retail rate, pc.

This set up basically mimics a perfectly competitive market for installed capacity with perfect foresight regarding peak-demand.Since available capacity always exceeds demand, the wholesale price, $w_{t}$, never exceeds the marginal production costs of the most expensive technology deployed in equilibrium.¹⁰ Accordingly, generators do not face $\rho _{t}$ as it occurs, and therefore do not change their output decisions. Instead, they are assumed to receive a single forward payment per unit of installed capacity, r, which equals the stream of scarcity prices, $\sum _{t=1}^{T}\rho _{t}$, and thus influences only their investment decision regarding non-variable generation capacity, $K_{i}^{NV}$ [cf. expression (3)].¹¹ The capacity payment, r, can be interpreted as the uniform clearing price of a forward capacity market auction, which would provide a secure return on investments in non-variable generation capacity (cf. Cramton et al. 2013).

Retail Market Equilibrium

In the perfectly competitive retail market homogeneous retail firms buy electricity at wholesale prices $w_{t}$ and sell it on to the final consumers either at the real-time price $p_{t}$ or flat rate tariff ${\bar{p}}$. We abstract from transmission and distribution costs and corresponding charges. Additionally, retail firms have to procure non-variable generation capacity in proportion to net demand served plus reserves, the total costs of which amount to $\left( 1+m\right) \sum _{t=1}^{T}\rho _{t}\left( {\overline{Q}}_{t}\left( p_{t}+pc_{t},{\bar{p}}+pc\right) -\sum _{i}^{V}q_{it}\right) .$ Retailers refinance these costs through charging RTP consumers the time-varying capacity price $pc_{t}$ during hours of scarce capacity, and charging flat-rate consumers the time-invariant capacity price pc per unit of consumed electricity. Total annual retail profits, $\pi ^{rt}$, are hence given by

$$\begin{aligned} \pi ^{rt}&= {} \sum _{t=1}^{T}\left( p_{t}-w_{t}\right) \alpha Q_{t}\left( p_{t,}+pc_{t}\right) \nonumber \\&\quad+ \left( {\bar{p}}-w_{t}\right) \left( 1-\alpha \right) Q_{t}\left( {\bar{p}}+pc\right) \nonumber \\&\quad+ pc_{t}\alpha Q_{t}\left( p_{t}+pc_{t}\right) -\rho _{t}\left( 1+m\right) \alpha \left( Q_{t}\left( p_{t}+pc_{t}\right) -\sum _{i}^{V}q_{it}\right) \nonumber \\&\quad+ pc\left( 1-\alpha \right) Q_{t}\left( {\bar{p}}+pc\right) -\rho _{t}\left( 1+m\right) \left( 1-\alpha \right) \left( Q_{t}\left( {\bar{p}}+pc\right) -\sum _{i}^{V}q_{it}\right) . \end{aligned}$$

(6)

The first and second term in (6) represent retail profits from selling electricity to RTP and flat-rate consumers, while the subsequent terms comprise profits from capacity plus reserves sales. For given $w_{t}$ and $\rho _{t}$, each retailer determines the retail real-time price $p_{t}$, the flat tariff ${\bar{p}}$, the constant and time-varying retail capacity price pc and $pc_{t}$, respectively, by maximizing $\pi ^{rt}$. Free entry of retail firms and the absence of transaction costs of switching retailers, which we assume, imply that retailers earn zero-profits in equilibrium. Moreover, we exclude cross subsidization of costs in retail rates such that the following zero-profit conditions have to hold in equilibrium:

$$\begin{aligned} \sum _{t=1}^{T}\left( p_{t}-w_{t}\right) \alpha Q_{t}\left( p_{t}+pc_{t}\right)&=0, \end{aligned}$$

(7)

$$\begin{aligned} \sum _{t=1}^{T}\left( {\bar{p}}-w_{t}\right) \left( 1-\alpha \right) Q_{t}\left( {\bar{p}}+pc\right)&=0, \end{aligned}$$

(8)

$$\begin{aligned} \sum _{t=1}^{T}\alpha Q_{t}\left( p_{t}+pc_{t}\right) \left( pc_{t}-\rho _{t}\left( 1+m\right) \right)&+\rho _{t}\left( 1+m\right) \alpha \sum _{i}^{V}q_{it}=0, \end{aligned}$$

(9)

$$\begin{aligned} \sum _{t=1}^{T}\left( 1-\alpha \right) Q_{t}\left( {\bar{p}}+pc\right) \left( pc-\rho _{t}\left( 1+m\right) \right)&+\rho _{t}\left( 1+m\right) \left( 1-\alpha \right) \sum _{i}^{V}q_{it}=0. \end{aligned}$$

(10)

Equation (7) implies that the competitive real-time retail price $p_{t}$ equals the electricity wholesale price $w_{t}$ in each period, that is $p_{t}=w_{t}\,\forall t.$ The solution to (8) yields the competitive flat retail price ${\bar{p}}$ the demand weighted average of $w_{t}$:

$$\begin{aligned} {\bar{p}}&= {} \frac{\sum _{t=1}^{T}w_{t}Q_{t}\left( {\bar{p}}+pc\right) }{\sum _{t=1}^{T}Q_{t}\left( {\bar{p}}+pc\right) }. \end{aligned}$$

(11)

Furthermore, following (9) $pc_{t}$ has to equal the costs for capacity per unit of consumed electricity in each period of scarce capacity, i.e.

$$\begin{aligned} pc_{t}&=\frac{\left( 1+m\right) \rho _{t}\left( Q_{t}\left( p_{t}+pc_{t}\right) -\sum _{i}^{V}q_{it}\right) }{Q_{t}\left( p_{t}+pc_{t}\right) }. \end{aligned}$$

(12)

Equation (10) implies that the time-invariant capacity price pc is a weighted average of the hourly capacity price $\rho _{t}$, where the weights equal the ratio of hourly net demand plus reserves and total demand by flat-rate consumers

$$\begin{aligned} pc&=\frac{\sum _{t=1}^{T}\left( 1+m\right) \rho _{t}\left( Q_{t}\left( {\bar{p}}+pc\right) -\sum _{i}^{V}q_{it}\right) }{\sum _{t=1}^{T}Q_{t}\left( {\bar{p}}+pc\right) }. \end{aligned}$$

(13)

Consequently, RTP and flate rate consumers respectively pay $p_{t}+pc_{t}$ and ${\bar{p}}+pc$ in each period t.¹²

Wholesale Market Equilibrium

Borenstein (2005) as well as Allcott (2012) demonstrate that the above model yields a unique long-run equilibrium in the wholesale, retail and capacity market. It is defined by the vector of installed capacity ${\mathbf {K}}$, the uniform capacity price for generators r, the flat electricity and capacity retail price ${\bar{p}}$ and pc. Moreover, it is defined by the set of equilibrium wholesale prices $\left\{ w_{t}\right\}$ as well as retail prices $\left\{ p_{t}\right\}$ and $\left\{ pc_{t}\right\}$, which clear demand and supply in each hour t, that is ${\overline{Q}}_{t}\left( p_{t}+pc_{t},{\bar{p}}+pc\right) =S\left( p_{t}\right) \,\forall t$ , noting that the retail market equilibrium implies $w_{t}=p_{t}\,\forall t.$

The wholesale clearing prices and quantities can be described in more detail by first noting that hourly aggregate supply is an upward sloping step function of $p_{t}$ due to the the clearly ranked marginal production costs $mc_{i}\in \left[ 0,mc_{NV}\right]$, where we now use the index $i=0$ for denoting each technology from the variable technology subset V. For $0\le i\le I$, the set of equilibrium electricity prices can be defined by the vertical segment between each step, $v_{i}=\left\{ t:\,mc_{i}<p_{t}<mc_{i+1}\right\}$, and the horizontal segment representing the marginal costs of the marginal technology $h_{i}=\left\{ t:\,p_{t}=mc_{i}\right\}$ (cf. Green and Léautier 2015). Let $u_{it}\in \left[ 0,1\right]$ denote the hourly degree of capacity utilization, that is the dispatch rate of technology i. Then on $h_{0}$, VRE technology $v\in \left[ 1,V\right]$ produces at the margin so that demand and supply clear at ${\overline{Q}}_{t}\left( p_{t}+pc_{t},{\bar{p}}+pc\right) =\sum _{v=1}^{V}u_{v,t}av_{v,t}K_{v}$. On $h_{i}$ for $i\ge 2$, technology i produces at the margin and VRE technologies at available capacity, therefore ${\overline{Q}}_{t}\left( p_{t}+pc_{t},{\bar{p}}+pc\right) =u_{i,t}K_{i}+\sum _{j=1}^{i-1}K_{j}+\sum _{v=1}^{V}{av_{v,t}K_{v}}$. On $v_{i}$ demand intersects a vertical segment of the supply curve where technology $i\ge 1$ produces at capacity, while technology $i+1$ is not dispatched, which gives the equilibrium quantity as ${\overline{Q}}_{t}\left( p_{t}+pc_{t},{\bar{p}}+pc\right) =\sum _{j=1}^{i}K_{j}+\sum _{v}^{V}{av_{v,t}K_{v}}$. Market clearing on $v_{I}$ implies that demand is rationed by the scarcity price $pc_{t}>0$, such that ${\overline{Q}}_{t}\left( p_{t}+pc_{t},{\bar{p}}+pc\right) =\frac{\sum _{i=1}^{I}K_{i}}{\left( 1+m\right) }+\sum _{v}^{V}av_{v,t}K_{v}.$

Finally, recall that due to free entry each technology $i\in I$ of the long-run equilibrium capacity vector ${\mathbf {K}}$ earns zero-profits, that is $\pi _{i}=0\,\forall i.$

Welfare Changes from Real-Time Pricing Under Carbon Taxation and Variable Renewable Electricity Supply

In this section, we briefly delineate the mechanisms through which carbon taxation and induced variable renewable generation affect the welfare changes from RTP. In order to do so, we start by defining and decomposing the aggregate welfare change from introducing real-time pricing, which represents the main variable analyzed in Sect. 5.1.

Welfare Changes from Real-Time Pricing

Since retailers and generators make zero-profits in the long-run equilibrium, total welfare changes from changing the RTP share, $\Delta CS$, equal the sum of consumer surplus changes of consumers who switch from flat to real-time pricing, who remain on the flat rate and who are already real-time priced (Borenstein and Holland 2005).¹³ Increasing the share of RTP consumers from $\alpha ^{0}$ to $\alpha ^{1}$ entails corresponding changes in the equilibrium real-time retail price from $p_{t}^{0}+pc_{t}^{0}$ to $p_{t}^{1}+pc_{t}^{1}$ and in the flat rate from ${\bar{p}}^{0}+pc^{0}$ to ${\bar{p}}^{1}+pc^{1}.$ Total net consumer surplus changes of incumbent RTP consumers,$\Delta CS^{R}$, equal the sum of all hourly surplus changes $\sum _{t=1}^{T}\left[ \intop _{p_{t}^{1}+pc_{t}^{1}}^{p_{t}^{0}+pc_{t}^{0}}\alpha ^{0}a_{t}x^{\epsilon }dx\right]$, i.e.

$$\begin{aligned} \Delta CS^{R}&=\sum _{t=1}^{T}&\left[ \frac{\alpha ^{0}a_{t}}{\epsilon +1}\left( \left( p_{t}^{0}+pc_{t}^{0}\right) ^{\epsilon +1}-\left( p_{t}^{1}+pc_{t}^{1}\right) ^{\epsilon +1}\right) \right] . \end{aligned}$$

(14)

Consumers who switch to RTP are paying ${\bar{p}}^{0}+pc^{0}$ before and $p_{t}^{1}+pc_{t}^{1}$ after switching, yielding hourly net surplus changes as $\intop _{p_{t}^{1}+pc_{t}^{1}}^{{\bar{p}}^{0}+pc^{0}}\left( \alpha ^{1}-\alpha ^{0}\right) a_{t}x^{\epsilon }dx$ and thus total surplus changes from switching as

$$\begin{aligned} \Delta CS^{S}&= {} \sum _{t=1}^{T}\left[ \frac{\left( \alpha ^{1}-\alpha ^{0}\right) a_{t}}{\epsilon +1}\left( \left( {\bar{p}}^{0}+pc^{0}\right) ^{\epsilon +1}-\left( p_{t}^{1}+pc_{t}^{1}\right) ^{\epsilon +1}\right) \right] . \end{aligned}$$

(15)

Finally, hourly surplus changes for customers who remain on the flat retail rate equal $\intop _{{\bar{p}}^{1}+pc^{1}}^{{\bar{p}}^{0}+pc^{0}}\left( 1-\alpha ^{1}\right) a_{t}x^{\epsilon }dx$, giving their total consumer surplus gains as

$$\begin{aligned} \Delta CS^{F}&= {} \sum _{t=1}^{T}\left[ \frac{\left( 1-\alpha ^{1}\right) a_{t}}{\epsilon +1}\left( \left( {\bar{p}}^{0}+pc^{0}\right) ^{\epsilon +1}-\left( {\bar{p}}^{1}+pc^{1}\right) ^{\epsilon +1}\right) \right] . \end{aligned}$$

(16)

Borenstein and Holland (2005) demonstrate that under general assumptions, total welfare increases with the RTP share, i.e. $\Delta CS>0$, although incumbent RTP consumer lose, i.e. $\Delta CS^{R}<0$, while switching consumers benefit, i.e. $\Delta CS^{S}>0$, and also make consumers who remain flat-priced better off, i.e. $\Delta CS^{F}>0$, since their changed consumption behavior exerts a positive pecuniary externality, that is the equilibrium flat rate decreases. In the numerical applications of their models, both Borenstein (2005) and Allcott (2012) show that the tariff switching gains $\Delta CS^{S}$ make up for the largest part of total welfare changes $\Delta CS$. In the following we try to illustrate graphically how these switching gains are affected by carbon taxation and variable renewable energy supply.

Effects of Carbon Taxation and Variable Generation on the Retail Price Spreads and Tariff Switching Benefits

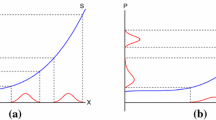
Hourly consumer surplus losses and gains from switching to RTP during peak and off-peak periods are depicted by the dark and gray areas in each panel of Fig. 1. Figure 1a–c respectively give a stylized representation of the peak and off-peak spot market equilibrium in the absence of carbon taxation as well as in the presence of carbon taxation without and with VRE technologies in the market.¹⁴ These three exemplary long-run equilibria roughly characterize the effect of zero, low and high carbon taxes on the long-run technology portfolio and aggregate supply curve S, which are relevant to explain the numerical welfare results presented in Sect. 5.

Each of the different carbon tax equilibria results in characteristic changes in both the wholesale price distribution and the consumer surplus gains from switching. That is, changes in the total consumer surplus gains $\Delta CS^{S}$ are driven by changes in the distribution of hourly flat-to-real-time price spreads, $\Delta p_{t}={\bar{p}}-p_{t}$, which in turn are determined by the corresponding wholesale price distribution. Intuitively, consumers switching to RTP gain whenever their real-time retail rate $p_{t}=w_{t}$ is below their previously paid flat rate ${\bar{p}}$, i.e. when ${\bar{p}}>p_{t}$¹⁵, and lose if otherwise. Positive and negative price spreads can be interpreted as an indicator for the level of “under-” and “over-consumption”, when consumers are on flat rates. Following equation (15), $\Delta CS^{S}$ increases if the sum of positive price spreads $\Delta p_{t}>0$ outweighs the sum of negative price spreads.

Fig. 1

Peak and off-peak wholesale spot market equilibrium with and without VRE supply

Moving from Fig. 1a and b shows that the aggregate supply curve becomes more elastic in the low carbon tax case without VRE entry. This is indicated by the upward shift and rotation of the black aggregate supply curve compared to the gray supply curve in Fig. 1b. The reason for this is that the carbon tax raises the marginal supply costs of relatively carbon-intensive fossil-fuel technologies such as coal stronger than those of less carbon-intensive technologies, noting that carbon-intensive technologies are originally at the low and less carbon-intensive ones at the high end of the aggregate supply curve. Importantly, Fig. 1b implies that this can reduce the level of under-consumption during low-price periods, i.e. $\Delta p_{t}>0$ becomes smaller on average, as the hourly spread between the flat rate ${\bar{p}}$ and the off-peak real-time price $p_{t}$ decreases. That is, off peak prices, which are set by the carbon-intensive technologies, increase faster than the (demand-weighted) mean price. This can in turn lead to lower switching gains during low-price periods, as is indicated by the gray area below the aggregate off-peak demand curve with RTP consumers, $D_{op}^{rtp}.$

Figure 1c shows the case where the carbon tax is high enough to induce VRE entry and where carbon-intensive generation technologies have been fully crowded-out of the market. The aggregate supply curve changes accordingly in two major ways. It becomes steeper or more inelastic at the right part, as the marginal generation costs of the remaining carbon emitting technologies increase with the carbon tax, and it is more or less flat where wind and solar power generate electricty at nearly zero marginal costs. In periods where VRE supply is high, the fossil fuel supply is driven out of the market such that the aggregate supply curve shifts to the right. Note that Fig. 1c depicts a special case, where VRE supply fully covers off-peak demand but carbon emitting technologies, e.g. natural gas fired plants, are needed to serve peak demand. Peak demand could, however, also be served at zero or very low marginal cost, if available VRE capacity is sufficiently high, i.e. peak prices drop to zero or are very low (supply curve shifts further to the right). In turn, off-peak demand may have to be served by high marginal cost technologies such that off-peak prices can now be relatively high (supply curve shifts to the far left). These latter two cases are not depicted in Fig. 1c but they hint to the importance of the covariance between demand and renewable generation profiles for determining the welfare gains of introducing RTP in markets with a high carbon tax and large VRE capacities.

The main effect on the wholesale price distribution in such markets is indicated by the higher flat rate ${\bar{p}}$ in Fig. 1c, implying that wholesale prices mostly settle at a higher levels and that demand D intersects supply at its steep part more frequently. The mean price inflation is a result of both the relatively low average availability of wind and solar power for generating electricity, particularly when wholesale prices are high, and the accordingly decreasing profitability per unit of VRE capacity (cf. Sect. 2.2). That is, as the carbon tax and VRE market penetration increases, higher average wholesale prices especially during periods of low VRE availability have to materialize in order to allow for making zero-profits with the installed VRE capacity.

These changes can have two major effects on the potential size and relative frequency of positive and negative price spreads, $\Delta p_{t}>0$ and $\Delta p_{t}<0$. On the one hand, positive retail price spreads, and thus the level of under-consumption can increase significantly, due to the flat rate inflation combined with the incidence of almost zero-wholesale prices in periods of relatively high VRE supply. This situation is indicated by the gray area under the off-peak demand curve in Fig. 1c. On the other hand, positive price spreads can occur less frequently than at low carbon taxes and VRE supply shares, since prices have to remain high most of the time, such that switchers to RTP mostly face retail price increases and flat-rate consumers mostly over-consume. The higher the carbon tax and the more VRE capacity is installed, the more often prices drop to nearly zero. Simultaneously, the flat rate paid before switching to RTP inflates further such that positive price spreads increase in size and relative frequency.

This implies that the overall effect of carbon taxation on the change in total consumer surplus gains from switching to RTP can be ambiguous. At low carbon taxes, the average level of positive price spreads and the inefficiency from under-consumption could decrease compared to a situation without carbon taxation and renewable supply. Additionally, there can be states in the transition towards high carbon taxes and VRE supply shares in which the welfare gains from RTP could be lower in the presence than in the absence of VRE deployment. As prices mostly settle above or close to the mean price, the average under-consumption and the corresponding switching gains could be relatively low at relatively high carbon tax levels and VRE supply shares. However, beyond a certain critical tax level and VRE supply share, the welfare gains from RTP might be strictly larger than at lower carbon taxes, since the level of average under-consumption increases with the growing incidence of zero-wholesale prices and the inflation of the mean price. At what carbon tax these different cases obtain greatly depends on the market specific covariation of aggregate demand and variable renewable output patterns, which primarily motivates the numerical analysis in the following.

Scenarios, Data and Calibration of the Simulation

The model described in Sect. 2 serves as the basis for the numerical model LORETTA, which is applied to simulate counterfactual carbon tax and RTP scenarios. In order to analyze how carbon taxation and VRE supply¹⁶ affect the welfare gains from implementing real-time pricing, we raise the carbon tax from zero up to EUR 450 per ton of ${\text{CO}}_{2}$ (${\text{tCO}}_{2}$) in discrete steps. These scenarios cover long-run projections based on German ${\text{CO}}_{2}$ emissions mitigation targets (cf. DLR et al. 2012; Bertsch et al. 2016).

Table 1 Technology cost assumptions

We simulate competitive long-run equilibrium prices and quantities for a representative year, that is for 8760 hours, using the PATH solver algorithm (Ferris and Munson 2000). We loosely calibrate the model to the German power system drawing on hourly price and load data of the German electricity spot market at the European Power Exchange (EPEX Spot SE) from 2013.¹⁷ The stylized set of supply technologies comprises onshore wind power and solar photovoltaic (solar PV) as VRE technologies, lignite and hard coal as non-variable base- and mid-load technologies as well as combined cycle and open cycle gas turbines (CCGT and OCGT) as peak and super-peak technologies. To compute technology specific marginal generation costs, $mc_{i}=\left( f_{i}+e_{i}\tau \right) \eta _{i}^{-1}+c_{i}^{om}$, we use long-run projections about average fuel prices $f_{i}$ and on operation and maintenance costs $c_{i}^{om}$, both taken from the IEA World Energy Outlook 2014 (IEA 2014), as well as prospective energy conversion (thermal) efficiency rates $\eta _{i}$, based on a meta-study by Schröder et al. (2013). Fuel specific ${\text{CO}}_{2}$-efficiency factors $e_{i}$ from Icha (2013) are used to determine marginal cost increases of carbon emitting technologies from corresponding increases in the carbon tax $\tau$, i.e. $\frac{\partial mc_{i}^{NV}}{\partial \tau }=e_{i}\eta _{i}^{-1}>0$. Each technology’s annualized fixed costs $fc_{i}$, also taken from Schröder et al. (2013), consist of overnight construction costs for the most part. Table 1 includes all relevant cost parameters of the stylized technology portfolio used for the simulation. Additionally, we apply publicly available data from 2013 provided by the German TSOs¹⁸, to compute capacity factors $av_{it}$ for all 8760 hours and each VRE technology. To do so, we divide hourly feed-in data from wind onshore and solar PV units by the respective installed capacity data.

Using the isoelastic demand function described in chapter 3.1, our numerical model results are largely driven by the parameter assumptions regarding own-price elasticity, $\epsilon$, and the distribution of the demand shifter, $a_{t}$. The demand shifter captures the characteristic seasonal and hourly aggregate consumption pattern and its distribution over 8760 hours is computed by using the mentioned price and load time series data. Since electricity demand in Germany is mostly non-responsive to price, we assume that $\alpha =0$ and solve for $a_{t}$, by first calculating the break-even retail flat rate from the real spot price time-series and inserting this flat-price and hourly load into the demand equation in 3.1 (cf. Borenstein 2005).¹⁹ Finally, in the base case we set own-price elasticity $\epsilon$ to -0.05 which is at the low end of empirical estimates (cf. Faruqui and Sergici 2010; Allcott 2011). Whether our qualitative findings hold for higher levels of price elasticity is checked in "Appendix 3". We also conduct sensitivity analyses regarding the impact of the PRM by running additional simulations assuming a PRM of zero and of 15% of net peak demand (see "Appendix 2"). In the base case the PRM is set to 5% of net peak demand.

Results

Welfare Effects of Introducing RTP Under Carbon Taxation

Panel 2a illustrates the main result that the welfare gains from introducing RTP change non-monotonously with the carbon tax $\tau$. Specifically, Panel 2a shows that the total annual consumer surplus gains (TCS) from raising the RTP share $\alpha$ from 1 to either 20% (blue curve) or 50% (red curve) follow a U-shaped curve across increasing carbon tax levels. As $\tau$ is raised in discrete steps starting from zero up to EUR 450 per ton of ${\text{CO}}_{2}$ emissions, the TCS gains initially drop and reach a minimum of about EUR 94 and 179 million/year, respectively, when the carbon tax equals approximately EUR 60/t${\text{CO}}_{2}$. At this tax level, VRE capacity starts to enter the market (see blue curve in Fig. 2b) and the TCS gains strictly rise with the carbon tax and corresponding VRE supply share as common intuition would suggest.²⁰

Fig. 2

Total annual consumer surplus gains from increasing the RTP share $\alpha$ from 1%, VRE supply shares in total electricity supply and standard deviation of the wholesale price $w_{t}$ for varying carbon taxes

Contrary to common intuition, however, there is a wide range of equilibria with relatively high carbon taxes and VRE supply shares, where RTP can be significantly less beneficial than at low carbon taxes, where no VRE entry occurs. This is the case between the kink at EUR 60/t${\text{CO}}_{2}$ and the dashed vertical line in Fig. 2a, where the TCS gains amount to about EUR 460 million/year, $\tau$ equals EUR 210/t${\text{CO}}_{2}$ and VRE supply reaches about 54% of total annual electricity (see blue curve in Fig. 2b). At this critical carbon tax increasing the RTP consumer share leads to approximately the same welfare gains as when the carbon tax and investment in VRE capacity is zero (compare rows 1 and 2 with 7 and 8 in Table 2). Beyond the vertical line, TCS gains are strictly larger than in all carbon tax scenarios where no VRE capacity entry occurs. At EUR 450/${\text{tCO}}_{2}$, where VRE supply about 67% of total annual electricity, the welfare gains are about twice as large as in the zero-tax-scenario.²¹

Table 2 Total and decomposed annual consumer surplus changes from increasing the RTP share from 1% for varying carbon tax levels and VRE supply shares

Hence, if implementing RTP is inefficient in conventional markets, where its gross benefits are often found to be outweighed by the costs of advanced metering infrastructure and other related costs, our results suggest that this could remain the case until carbon taxes and VRE supply shares reach critical levels, which may be higher than current roll-out plans in U.S. and EU markets assume.

The common reasoning for why welfare gains from RTP should increase with VRE supply shares is the increasing price volatility due to the variability in electricity generation. While wholesale price volatility is an important driver of the welfare gains from RTP, our results suggest that it is not the only driver. Specifically, we find that relatively low welfare gains can be associated with a relatively high wholesale price volatility and vice versa. This can be taken from the red curve in Fig. 2b, which gives the standard deviation of hourly wholesale price $\sigma \left( w_{t}\right)$ for different carbon taxes and $\alpha =1\%$.²² At EUR 210/t${\text{CO}}_{2}$, for instance, $\sigma \left( w_{t}\right)$ is about twice as large as in the zero-carbon tax scenario, where $\sigma \left( w_{t}\right)$ equals 30.8, while the TCS gains from RTP are about the same. From $\tau =$ EUR 90/t${\text{CO}}_{2}$ onwards, where the VRE share surges to slightly over 40%, we find several cases in which the corresponding TCS gains are lower than in the no-VRE scenarios, despite higher price volatility. Hence, while the price volatility follows a U-shaped pattern with increasing carbon tax levels and therefore seems to be perfectly associated with the corresponding change in the welfare gains, volatility does not clearly predict the potential welfare gains from RTP as common intuition would suggest.

The reason for this is that the volatility of prices does not indicate whether prices vary to high or low levels and, thus, whether and to what extent consumers “over-” or “under-consume”. The inefficiency from “under-consumption”, that is from consuming “too little” when wholesale prices are low or even zero, translates intuitively into gains from switching to RTP. We thus illustrate in the following section that the inefficiency caused by “under-consumption” is key to fully explain the observed changes in the welfare gains from RTP.

Wholesale and Retail Price Effects

This section demonstrates that changes in the welfare gains from RTP for increasing carbon taxes reflect the changing inefficiency arising from “under-consumption”. These changes result from both the shift of the long-run wholesale price distribution towards a higher mean price at high carbon tax levels and the incidence of zero-wholesale prices during periods of high supply from VRE technologies.

Table 3 Selected simulation results

In order to identify changes in the level of under-consumption and over-consumption, we examine the ranked distribution of hourly spreads between the flat and RTP rate in Fig. 3a, which shows $\Delta p_{t}=\left( {\bar{p}}+pc\right) -\left( p_{t}+pc_{t}\right)$ at $\tau$ equal to 0 and EUR 450/t${\text{CO}}_{2}$. A positive price spread $\Delta p_{t}>0$ implies that flat-rate consumers under-consume. The resulting inefficiency or, in turn, the potential efficiency gains from switching to RTP are proportional to the level and frequency of $\Delta p_{t}>0$, as follows from expression (15). Figure 3a illustrates that flat-rate consumers under-consume less frequently at high carbon tax levels. The duration of $\Delta p_{t}>0$ decreases from more than 80% of all hours in the zero-carbon-tax case (blue graph) to 34% at $\tau =$ EUR 450/t${\text{CO}}_{2}$ (red graph). While under-consumption hence occurs less often in the high carbon tax case, the hump of the red graph indicates that its level increases significantly. The price spread $\Delta p_{t}$ amounts to about EUR 153.2/MWh on average, which is about seven times larger than in the zero-tax case (EUR 22/MWh). Tariff switching consumers increase consumption during these periods accordingly by up to 18 GWh and by 11 GWh on average. This is indicated by the hump of the red graph in Fig. 3b, showing the ranked distribution of aggregate consumption changes $\Delta Q_{t}$, if the RTP share $\alpha$ increases from 1 to 20%. The average and maximum consumption increase in the zero-carbon tax case (blue graph) reach around 0.39 and 0.5 GWh, respectively. As our welfare results suggest, these consumption changes imply a significantly larger average level of under-consumption, which renders RTP at $\tau =$ EUR 450/t${\text{CO}}_{2}$ almost twice as beneficial than at $\tau =0$.

Fig. 3

Ranked hourly retail price spreads $\Delta p_{t}$ and aggregate consumption changes $\Delta Q_{t}$ from increasing the RTP share $\alpha$ from 1 to 20% in the zero-carbon-tax scenario and at $\tau = \hbox {EUR }450/\hbox {t}{\text{CO}}_{2}$ (VRE supply share = 67%)

The U-shaped change in the welfare gains thus results from an initial decrease in the average under-consumption until $\tau$ equals EUR 60/t${\text{CO}}_{2}$, and a gradual increase beyond that level. To measure the potential extent of average under-consumption for each carbon tax scenario, we define $\overline{\Delta p_{t}}$ as the mean of $\Delta p_{t}>0$ weighted by the relative frequency of positive price spreads. The resulting curve is given by the blue graph in Fig. 4 and basically matches the U-shaped change in the welfare gains found above. At EUR 60/t${\text{CO}}_{2}$, $\overline{\Delta p_{t}}$ decreases compared to the zero-tax-scenario by 27%, that is from about EUR 18.9 to 13.7 EUR per MWh. At EUR 210/t${\text{CO}}_{2}$, $\overline{\Delta p_{t}}$ reaches about the same value as in the zero-tax-case (EUR 22.1/MWh) and more than doubles to about EUR 52.4/MWh at $\tau =$ EUR 450/t${\text{CO}}_{2}$, which is also in line which the welfare results from the previous section. Since wholesale prices drop to nearly zero as soon as the VRE supply share is sufficiently high, maximum price spreads (black-dashed graph in Fig. 4) coincide with the respective flat rate (red graph) beyond EUR 60/t${\text{CO}}_{2}$. The maximum price spread or flat rate and the average under-consumption parameter $\overline{\Delta p_{t}}$ start to diverge at EUR 90/tCO2 due to the relatively low frequency of zero- and low-price periods.

Fig. 4

Average under-consumption $\overline{\Delta p_{t}}$, maximum retail price spread $\Delta p_{t}$ and flat retail rate across carbon tax scenarios

The change in $\overline{\Delta p_{t}}$ and thus the frequency and level of $\Delta p_{t}>0$ is a result of a shift in the wholesale price distribution towards a higher mean combined with an increasing incidence of zero-prices as soon as carbon taxation induces VRE entry. Both changes are depicted by the characteristic ranked distributions of hourly wholesale prices $w_{t}$ in Fig. 5, which materialize in the zero-tax-case and at $\tau =$ EUR 450/MWh. The blue curve shows the distribution of $w_{t}$ in the zero-tax case, where wholesale prices mostly settle at the marginal costs of lignite, that is at about EUR 18/MWh during roughly 83% of all hours. This value is below the demand-weighted average price, i.e. the flat rate ${\bar{p}}$, of about EUR 40.3/MWh (column 10 in Table 3), resulting in the equally frequent positive retail price spreads shown in Fig. 3a. The negative price spreads in Fig. 3a arise when peak technologies such as gas and oil fired OCGT units raise the wholesale price to about 96.8 and 173.9 EUR per MWh in the remaining periods. The demand-weighted average price increases by a factor of about four to EUR 153.8/MWh at $\tau =$ EUR 450/MWh (column 10 in Table 3), while $w_{t}$ settles at 212 EUR/MWh (CCGT) or higher in about 76% of the time, which is shown by the red graph in Fig. 5. Flat-rate consumers thus over-consume, i.e. $\Delta p_{t}<0$, during about the same amount of time. Wholesale prices drop to zero during 34% of all hours, resulting in the large positive price spreads indicated by the hump of the red graph in Fig. 3a.²³ The point where wholesale prices start to mostly settle above the demand weighted average price is at $\tau =$ EUR 150/MWh. Flat-rate consumers mostly over-consume from this point onwards and mostly under-consume at lower carbon taxes.

Fig. 5

Ranked distribution of hourly wholesale electricity prices $w_{t}$ for $\alpha =1\%$ in the zero-tax case and at $\tau = \hbox {EUR }450/\hbox {ton}$ of ${\text{CO}}_{2}$ (VRE supply share = 67%)

The change in the price distribution basically reflects how carbon taxation alters the long-run generation technology portfolio and thus the aggregate supply curve, as described in Sect. 3.2. The carbon tax causes a gradual switch from carbon- and capital-intensive base-load technologies to natural gas fired peak-load technologies, which are characterized by relatively low emission rates and low fixed investment costs but high marginal costs. Beyond a certain level it also induces entry of VRE technologies, characterized by relatively high fixed costs, zero-marginal-costs and relatively low capacity factors. Put differently, the aggregate supply curve becomes initially more elastic at relatively low and more inelastic at relatively high carbon tax levels. It becomes more elastic, since the marginal costs of supply from the lignite technology converge towards the marginal costs of natural gas based technologies (CCGT) due to the higher emission rate per MWh. As a result, the spread between off-peak prices and the mean price decreases, leading to the initial decline in average under-consumption and the welfare gains from RTP. The supply curve becomes more inelastic at about EUR 90/t${\text{CO}}_{2}$, where VRE entry is significant and the base-load technology is fully crowded out of the market (see column 1–6 in Table 3). The technology-switch leads to an increasing incidence of zero-prices, while the mean price increases further. The inflation of the mean price is largely required to allow for VRE capacity investments to break-even in equilibrium, as discussed in Sect. 3.2.²⁴ This inflation effect, in turn, increases the average under-consumption and positive retail price spreads during periods where only VRE technologies supply electricity at almost zero-marginal-costs. As the tax and VRE supply share increase, both the mean price as well as the incidence of zero-prices increase further, resulting in ever larger retail price spreads, which occur more frequently. As a result the average under-consumption gradually rises again.

Robustness and Limitations

The welfare changes from RTP found in our analysis could be underestimated for several reasons. First, we omit the cross-price elasticity of demand and, thus, the effect of substituting demand in high-price periods with demand in low-price periods (demand shifting). This also includes effects of utilizing “behind-the-meter” storage facilities (e.g. small batteries) or other technologies that facilitate demand shifting (e.g. Power-to-Heat or electric vehicles). Given the large price spreads between off-peak and peak demand periods found when VRE technologies enter the market, it seems plausible that welfare gains from RTP could actually grow faster with the VRE supply share than in our simulations, if the cross-price elasticity of demand would be accounted for. Thus, while the welfare gains from RTP may still change in a U-shaped fashion with the carbon tax, they may exceed those obtained in the absence of VRE supply and carbon taxation at an earlier stage of VRE market penetration.

Additionally, we may underestimate the growth in the benefits from RTP by ignoring the locational variation in electricity prices. We therefore do not account for potential cost savings in transmission capacity expansion and congestion management caused by deploying VRE technologies. If consumers would face real-time prices that also reflect the locational constraints in the grid, some costly transmission lines might not have to be built and less generation plants might have to be re-dispatched ahead and behind of a congested line. If the related costs would rise sufficiently strong due to the deployment of wind and solar power in the system, RTP could entail relatively large efficiency gains even at very low VRE penetration rates.

The effect of long-run changes in demand patterns or consumption behavior is more complex to assess and appears ambiguous. On the one hand, progress in information and communication technology could affect the benefits from RTP positively by reducing the private transaction costs related to optimally adjusting demand to time-varying prices. For instance, advanced meters combined with in-home displays providing high frequency information not only about prices but about consumption costs at the appliance level could significantly increase consumers’ elasticity to price, and thus the welfare gains from RTP (Jessoe and Rapson 2014). Home automation and the utilization of smart appliances able to communicate with advanced meters could amplify this positive effect (Bollinger and Hartmann 2015).²⁵ On the other hand, dynamics in consumer behavior may also reduce the potential benefits from introducing RTP. For instance, owners of rooftop solar PV capacity and small storage capacities could become more “attentive” to energy consumption related costs and adapt their behavior to the output profile of their PV unit (Sallee 2014). To some extent such behavioral adjustments could reduce the efficiency gains from implementing real-time pricing.

Apart from this, we omit other relevant factors which could also significantly reduce the potential welfare gains from RTP. First, our model does not account for cross-border-trade with adjacent electricity markets. Accordingly, hourly price spreads may actually be lower than in our simulations. Second, we ignore any kind of utility-scale storage technology, which could foster renewable capacity entry and have a dampening effect on hourly price spreads. Thus, we may in turn underestimate welfare gains, particularly in the scenarios with low carbon taxes, to the extent that trade with adjacent markets and the availability of storage affect renewable capacity entry positively.²⁶ Earlier market entry by renewables could also be driven by favourable fossil fuel price dynamics, from which we abstract. We think, however, that omitting these three factors has quantitative rather than qualitative implications for our results.

Finally, our welfare results crucially hinge on the electricity price effects of carbon taxation. Direct renewable support policies such as feed-in-tariffs for renewable energy or renewable portfolio standards would have different portfolio and price effects in the long-run equilibrium. In particular, renewable subsidy schemes can induce large-scale entry of VRE technologies, while allowing carbon intensive technologies with relatively low marginal generation costs like coal or lignite fired power plants to stay in the market at the same time.²⁷ Long-run wholesale prices could therefore reside at low levels most of the time and increasingly shift to zero as VRE supply shares rise. Compared to the carbon tax regime, this could render real-time pricing strictly more beneficial with than without supply from VRE. However, if renewable subsidies are refinanced via volumetric surcharges, consumption decisions by real-time-priced consumers are distorted. We analyze how these distortions affect the welfare gains from RTP by simulating equilibria in which VRE capacity is subsidized and subsidies are financed by surcharges included in the retail rates. We find that welfare gains from RTP now follow a U-shaped curve with renewable capacity subsidies and with the VRE supply share, as is shown by Fig. 6a–b in the Appendix 1. This outcome mainly results from the time-invariant surcharge. The surcharge increases with the VRE supply share and is added on top of both the retail real-time and flat rate, while wholesale prices settle at low levels or drop to zero with rising VRE supply. The underlying mechanism are explained in more detail in the "Appendix 1".²⁸

Conclusion

This paper analyzes the welfare effects of real-time retail pricing (RTP) in the presence of carbon taxation and variable electricity supply from renewable technologies such as wind and solar power. To do so, we simulate long-run electricity market equilibria by applying German market data and quantify the gross welfare gains from introducing RTP for different carbon tax scenarios.

We find a U-shaped relationship between the benefits of RTP and carbon emissions taxation. Contrasting common intuition, this can imply that introducing RTP can be significantly more beneficial at relatively low compared to relatively high carbon taxes, which also means that it can be more beneficial in the absence than in the presence of variable renewable electricity supply. This is the case until the carbon tax and corresponding renewable supply share reach relatively high levels. Our analysis illustrates that this result is majorly driven by the changing average “under-consumption” during low-price periods, which translates into the welfare gains from adopting real-time pricing. The change in average under-consumption results from a characteristic shift in the wholesale price distribution towards a higher mean price and a gradual increase in the incidence of zero-prices. This shift stems from the generation portfolio effects of carbon taxation as well as from the supply characteristics of variable renewable technologies.

These findings provide insights on the timing of rolling out costly advanced metering infrastructure. Given the relatively high costs for necessary infrastructure investments and the private transaction costs related to adopting real-time pricing, our results might question the efficiency of a large-scale roll-out at relatively low renewable market penetration rates. The ongoing roll-out of advanced metering infrastructure in many U.S. and European electricity markets may therefore not be well-timed.

Since the marginal costs of electricity supply usually vary between different locations in a power grid, further research should analyze the potential welfare gains from both temporally and locationally varying electricity retail prices. Doing so would capture the effects of geographically unevenly dispersed renewable generation capacity.

Moreover, realizing the potential efficiency gains from real-time pricing or other time-varying pricing schemes naturally requires consumers to adopt them. Our analysis abstracts from individual tariff choices and feasibility issues regarding time-varying pricing schemes in general. To tackle possible feasibility issues would, for instance, require to analyze the role of individual transaction costs in tariff choices or of psychological factors such as inattention to individual consumption costs and the misperception of individual benefits from retail pricing schemes. The determinants of retail tariff choice thus remains a promising future research topic.

Appendices

Appendix 1: Welfare Gains from RTP with VRE Capacity Subsidization

In this section we demonstrate that welfare gains from rising RTP shares also change non-monotonously with the VRE share if VRE capacity is subsidized.²⁹ Figure 6a, b show that up to a VRE share of 40%, TCS gains from raising the RTP share to 20% or 50% decrease compared to the levels obtained without VRE supply. From this point onward TCS gains rise again but remain below the level achieved without VRE supply when the RTP share is raised to 20%. When the RTP share is raised to 50%, corresponding TCS gains are lower than without VRE supply unless the VRE share amounts to 70% (Fig. 6b). Interestingly and in difference to the carbon tax scenarios, switching to RTP remains less beneficial than in the equilibrium without VRE supply (blue bars in Fig. 6). Flat-rate consumers, however, increasingly benefit from a switch to RTP by other consumers with rising VRE shares (red bars in Fig. 6). Hence, overall welfare gains from RTP at higher VRE shares are more and more determined by the TCS gains of flat-rate consumers and less by the benefits of consumers switching to RTP.

Fig. 6

Total annual consumer surplus gains from RTP share increases under VRE capacity subsidization

The above results now stem less from wholesale price changes but rather from the presence of a uniform per unit tax $\tau$ included in retail rates to finance the VRE subsidy. As each consumer pays $\tau$ per consumed unit of energy, this tax constitutes a time-invariant wedge between retail and wholesale electricity prices. Importantly, this wedge increases on average with VRE entry because of both VRE technologies set wholesale prices increasingly often to zero and the VRE subsidy as well as the corresponding tax rise simultaneously. The rise in subsidies follows from a decrease in short-run profits at the wholesale market by VRE technologies (cf. Lamont 2008). As VRE market profitability declines disproportionately with VRE capacity entry, subsidies to refinance VRE capacity costs have to rise disproportionately with the given VRE target (cf. Green and Léautier 2015). In the equilibria shown in Fig. 6, $\tau$ rises from EUR 3 to EUR 73 per MWh. Simultaneously, ${\bar{p}}$ drops from EUR 40 per MWh to around EUR 31 per MWh.

Fig. 7

Positive retail price spreads, i.e. ${\bar{p}}-p_{t}>0,$ at $\alpha =1\%$ faced by consumers switching to RTP at 0%, 30% and 70% VRE supply shares in total supply

These changes in retail price components entail several effects on switching and flat-rate consumers’ surplus gains. Flat retail rates ${\bar{p}}+\tau$ increase with the VRE share as $\tau$ rises faster than ${\bar{p}}$ declines. This would make switching to RTP in principle more beneficial, if hourly RTP rates could drop to the marginal costs of supply. However, this is not the case due to the tax mark up that RTP consumers pay per unit of consumption. Instead, the majority of positive price spreads if switching to RTP, $\triangle p_{t}>0$, declines at low VRE shares as shown by the solid red curve in Fig. 7. At relatively low VRE shares, VRE set prices relatively infrequently such that real-time retail prices mostly equal the marginal production costs of coal or lignite units plus the tax $\tau$. The corresponding positive price spread for switching consumers therefore equals ${\bar{p}}-mc_{i}^{NV}$ most of the time, which is lower than without VRE entry, since ${\bar{p}}$ decreases (slightly) with increasing VRE shares. Hence, comparing the large plateaus of the blue and red solid graphs in Fig. 7 gives that ${\bar{p}}-mc_{i}^{NV}$ amounts to EUR 22 per MWh without VRE entry (blue graph) and EUR 21 per MWh with a 30% VRE share during about 85% of the time. When the equilibrium VRE share equals 70%, these price spreads fall to EUR 15 per MWh in about 60% of all hours (dashed red line in Fig. 7). In most of the remaining hours of this scenario, price spreads rise to ${\bar{p}}=31\,\text {EUR/}MWh$, which is when VRE supply sets wholesale prices to zero. Thus, as price spreads increase comparatively, TCS gains from switching become larger again (blue bars in Fig. 6), at least if the RTP share is raised to 50%, yet not as large as without VRE supply.

Flat-rate consumers’ benefits from higher RTP shares rise with the VRE share, since their rate ${\bar{p}}+\tau$ declines more sharply when other consumer switch to RTP (not shown). As RTP consumers raise consumption when prices are low, wholesale prices rise during hours where a large part of VRE capacity supplies energy. VRE technologies thus become more profitable and less subsidies are needed to reach a given VRE share, so that$\tau$ decreases. This positive pecuniary externality increases with the VRE share and thus leads to the increasing benefits of flat consumers for given RTP share increases. Simultaneously, ${\bar{p}}$ decreases with the RTP share as explained above, but the decrease does not differ by much for different VRE shares.

In consequence, welfare gains from RTP change non-monotonously with VRE supply shares either if VRE entry is carbon tax or subsidy induced, however, the mechanisms responsible for this result differ.

Appendix 2: Impact of the Planning Reserve Margin on Welfare Gains from RTP

Table 4 illustrates that the PRM has a negligible quantitative, yet no qualitative impact on the welfare results found in the previous sections. In the absence of a PRM constraint, total annual consumer surplus gains from raising the RTP consumer share $\alpha$ to 50% change non-monotonously as follows from comparing columns 2 to 4. If the PRM equals 15%, annual consumer surplus gains are approximately 11% higher than without PRM constraint and about 4% higher than in the base case (cf. Table 2). This can be taken from comparing the values in the last column.

Table 4 Absolute and relative consumer surplus gains from RTP for a planning reserve margin (PRM) of zero and 15% (base case 5%) of net peak demand and for varying carbon taxes $\tau$ and VRE supply shares

Appendix 3: Impact of Own-Price Elasticity Assumptions

Total welfare gains from given increases in the RTP share rise proportional to own-price elasticity $\epsilon$. This follows directly from comparing the corresponding values given in Tables 2 and 5, which also shows that welfare gains nonetheless change non-monotonously with the carbon tax.

Table 5 Decomposed annual consumer surplus changes from increasing RTP with higher price elasticity (base case $\epsilon =-0.05$)