Abstract
This study analyzes socially optimal environmental policy for a mine with a model that takes into account waste or waste rock production and abatement possibilities of the mine. We develop a model, in which the mine produces an externality related to the waste rocks, such as acid mine drainage. We find that the extraction rate tends to be lower in a mine with higher waste rock production, and that the optimal tax on the waste rock production is strictly increasing in time. We extend the model to incorporate an additional externality in the form of a stock pollutant. We analyze the optimal taxes and show that the typical result that the time path of the tax on the stock pollutant is inverted U-shaped may be lost in a mine model with abatement possibility and fixed operation period.
Similar content being viewed by others
Notes
White et al. (2012) analyze the optimal mine rehabilitation and Pigovian taxation using a discrete-time model and apply it to Australian context.
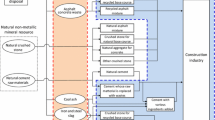
Lottermoser (2010) explains, that to reach the ore vein and to obtain eventually the valuable material, say metal, the topsoil and waste rocks must be first removed. Then the ore is mined and processed for example in a mill from which additional mine wastes called tailings are produced. Afterwards further processing is still needed. See Lottermoser (2010) for additional information.
More precisely, the mines in Finland produced 29,544,560 tons of ore (plus valuable stones) and 45,299,631 tons of waste rocks in 2014 (Tukes 2014).
In this paper disposing the waste rocks is always costly, although we acknowledge that some types of waste rocks can include valuable side products for the mine.
In underground mining the waste rocks are often used to fill old mining tunnels, but presumably not without cost.
An exception is carbon capture and storage, which is essentially abatement (Moreaux and Withagen 2015). Compared to our model, they have and infinite time horizon model. In addition to this, our model has two externalities and is related specifically to mining.
We often drop the time argument from the notation.
According to Dold (2014, p. 635) the AMD formation takes several years even after the mine shut-down.
If we would assume that acid mine drainage causes damages during the production stage, then many of the paper’s results would change. For example, the exponential development of the shadow value of the waste rock stock plays a crucial role in the Proof of Propositions 4, 5, 12, 13. If the waste rock stock causes damages during the production stage, the shadow value would not develop exponentially, which might imply that these propositions would not hold in this case. Similarly, if the waste rock production coefficient \(\alpha \) depends on the remaining stock and \(\alpha '(X)<0\) (exploitation implies higher amount of waste rocks per extracted unit), then the results would change since the shadow value of the resource stock would not develop exponentially.
Also Roan and Martin (1996) make this assumption although they are implicit about it.
Note that the fixed horizon does not exclude the physical or economical exhaustion of the mine. The choice of fixed horizon simplifies the analysis. If T is a choice variable, then the problem may not have a solution, since increasing T postpones the damages from AMD. This postponement is the benefit of waiting, and it may not have a corresponding cost unless there are fixed costs in production.
Theorem 5 in Chapter 3 of Seierstad and Sydsæter (1987).
By \(0 \le \lambda (T)=\lambda (0)e^{\rho T}\), \(\lambda (0)\ge 0\), so that \(\lambda (t)\ge 0\).
We also use superscript H for extraction rates and shadow values of the mine with a high coefficient value and superscript L in case of the mine with a low coefficient value.
It is a plausible possibility that both mines are exhausted. Tilton and Juan (2016) argue on page 142, that a mine often continues to operate until the ore body is exhausted due to high capital cost of mining. However, because these costs are not included in the model and because the terminal time is fixed, we study all the cases including ’both mines are exhausted’, ’only one of the mines is exhausted’ and ’neither of the mines are exhausted’.
This modeling choice is different than for example in Chakravorty and Krulce (1994), Farzin (1996) and Chakravorty et al. (2005), who use an inverse demand function. We are modeling the optimal policy of a single mine, which takes the price as given and therefore so does the regulator. This price can be interpreted as the world market price.
Also, whenever \({\dot{\gamma }}<0\), the induced decrease in the optimal value of the program from a unit increase in the pollution stock is increasing. Intuition suggests and Part (iv) of Proposition 7 confirms, that in this case it is optimal to increase abatement.
Note that the points, in which \({\dot{\gamma }}=0\), cannot be inflection points of \(\gamma \). If they were, we would obtain a contradiction as in the proof of Proposition 9, because \({\dot{\gamma }}<0\) between these two points.
See for example the proof of Proposition 4.
See their Section 3.2.
Our model has not analyzed the actual implementation of the two taxes, which is an important practical aspect.
Stollery (1985) studies this in a set-up with flow pollution.
Market structure and exhaustible resources have received much attention, see for example Benchekroun et al. (2009).
References
Ambec Stefan, Coria Jessica (2013) Prices vs Quantities with Multiple Pollutants. Journal of Environmental Economics and Management 66:123–140
Amigues Jean-Pierre, Moreaux Michael (2013) The Atmospheric Carbon Resilience Problem: A Theoretical Analysis. Resource and Energy Economics 35:618–636
Benchekroun Hassan, Halsema Alex, Withagen Cees (2009) On Nonrenewable Resource Oligopolies: The Asymmetric Case. Journal of Economic Dynamics & Control 33:1867–1879
Boukas E-K, Haurie A, Michel P (1990) An optimal control problem with a random stopping time. J Optim Theory Appl 64:471–480
Cairns RD (2001) Capacity choice and the theory of the mine. Environ Resour Econ 18:129–148
Cairns RD, Shinkuma T (2003) The choice of the cutoff grade in mining. Resour Policy 29:75–81
Campbell HF (1980) The effect of capital intensity on the optimal rate of extraction of a mineral deposit. Can J Econ 13:349–356
Caputo MR (1990) A qualitative characterization of the competitive nonrenewable resource extractive firm. J Environ Econ Manag 18:206–226
Caputo MR, Wilen JE (1995) Optimal cleanup of hazardous wastes. Int Econ Rev 36:217–243
Chakravorty U, Krulce DL (1994) Heterogenuous demand and order of resource extraction. Econometrica 62:1445–1452
Chakravorty U, Krulce DL, Roumasset J (2005) Specialization and non-renewable resources: Ricardo meets Ricardo. J Econ Dyn Control 29:1517–1545
Clarke HR, Reed WJ (1994) Consumption/pollution tradeoffs in an environment vulnerable to pollution-related catastrophic collapse. J Econ Dyn Control 18:991–1010
Dold B (2014) Evolution of acid mine drainage formation in sulphidic mine tailings. Minerals 4:621–641
Farzin YH (1992) The time path of scarcity rent in the theory of exhaustible resources. Econ J 102:813–830
Farzin YH (1996) Optimal pricing of environmental and natural resource use with stock externalities. J Public Econ 62:31–57
Farzin YH, Tahvonen OI (1996) Global carbon cycle and the optimal time path of a carbon tax. Oxf Econ Pap 48:515–536
Hoel M, Kverndokk S (1996) Depletion of fossil fuels and the impacts of global warming. Resour Energy Econ 18:115–136
Holland SP (2003) Extraction capacity and the optimal order of extraction. J Environ Econ Manag 45:569–588
Krautkraemer JA (1988) The cut-off grade and the theory of extraction. Can J Econ 21:146–160
Lèbre É, Corder GD, Golev A (2017) Sustainable practices in the management of mining waste: a focus on the mineral resource. Miner Eng 107:34–42
Lottermoser BG (2010) Mine wastes: characterization, treatment and environmental impacts, 3rd edn. Springer, Berlin
Lozada GA (1993) The conservationist’s dilemma. Int Econ Rev 34:647–662
Michielsen TO (2014) Brown backstops versus the green paradox. J Environ Econ Manag 68:87–110
Moreaux M, Withagen C (2015) Optimal abatement of carbon emission flows. J Environ Econ Manag 74:55–70
Moslener U, Requate T (2007) Optimal abatement in dynamic multi-pollutant problems when pollutants can be complements or substitutes. J Econ Dyn Control 31:2293–2316
Mudd GM (2010) The environmental sustainability of mining in australia: key mega-trends and looming constraints. Resour Policy 35:98–115
Nordstrom DK (2011) Mine waters: acidic to circumneutral. Elements 7:393–398
Roan PF, Martin WE (1996) Optimal production and reclamation at a mine site with an ecosystem constraint. J Environ Econ Manag 30:186–198
Schumacher I (2011) When should we stop extracting non-renewable resources? Macroecon Dyn 15:495–512
Seierstad A, Sydsæter K (1987) Optimal control theory with economic applications, 2nd edn. North-Holland, Amsterdam
Shinkuma T (2000) A generalization of the Cairns–Krautkraemer model and the optimality of the mining rule. Resour Energy Econ 22:147–160
Sinn H-W (2008) Public policies against global warming: a supply side approach. Int Tax Public Finance 15:360–394
Statistics Canada (2012) Human activity and the environment: waste management in Canada. http://www.statcan.gc.ca/pub/16-201-x/16-201-x2012000-eng.pdf
Stollery KR (1985) Environmental controls in extractive industries. Land Econ 61:136–144
Sullivan J, Amacher GS (2009) The social costs of mineland restoration. Land Econ 85:712–726
Tahvonen OI (1997) Fossil fuels, stock externalities, and backstop technology. Can J Econ 30:855–874
Tiess G (2010) Minerals policy in Europe: some recent developments. Resour Policy 35:190–198
Tilton JE, Juan IG (2016) Mineral economics and policy, 1st edn. RFF Press, Washington
Tsur Y, Zemel A (2003) Optimal transition to backstop substitutes for nonrenewable resources. J Econ Dyn Control 27:551–572
Tukes (2014) Tilastotietoja vuoriteollisuudesta 2014. http://www.tukes.fi/Tiedostot/kaivokset/tilastot/Tilastotiedot_vuoriteollisuus_2014.pdf
Ulph A, Ulph D (1994) The optimal time path of a carbon tax. Oxf Econ Pap 46:857–868
van der Meijden G, van der Ploeg F, Withagen C (2015) International capital markets, oil producers and the green paradox. Eur Econ Rev 76:275–297
van der Ploeg F, Withagen C (2012) Is There really a green paradox? J Environ Econ Manag 64:342–363
White B, Doole GJ, Pannell DJ, Florec V (2012) Optimal environmental policy design for mine rehabilitation and pollution with a risk of non-compliance owing to firm insolvency. Aust J Agric Resour Econ 56:280–301
Winter RA (2014) Innovation and the dynamics of global warming. J Environ Econ Manag 68:124–140
Author information
Authors and Affiliations
Corresponding author
Additional information
We would like to thank Olli Tahvonen and Anna-Kaisa Kosenius for useful discussions. We thank the referee, the editor, Karen Pittel and other EAERE2016 participants for helpful comments.
Appendix
Appendix
1.1 Proof of Proposition 1
(i) Since the control set \(U:=\{ (q,z) \in \mathbb {R}^2 \ | \ q\ge 0, z\ge 0\}\) is convex and H is strictly concave in (q, z), the control functions are continuous functions.
(ii) First we show that \(q(t)>0\) at some t. Assume not, that is \(q(t)\equiv 0\). Then \(X(T)=x_0>0\), and therefore by (16) \(\lambda (T)=0\). This implies \(\lambda (t)\equiv 0\). Equation (13) together with boundary condition \(S(T) \ge 0\), implies \(z(t)\equiv 0\). Then by assumption \({C^s}'(0)=0\) (recall Assumption 1) and by condition (11), \(\mu (t)\ge 0\) for every t. This yields a contradiction since (10), that is, condition
and assumption \(p-C'(0)>0\), imply \(\mu (t)< 0\). Therefore \(q(t)>0\) at some t. Since q(t) is continuous, it must be that \(q(t)>0\) at some interval \([t_0,t_1]\).
Now we show that the rate of extraction is strictly decreasing, when the rate of extraction is positive. We first show that \(\mu (0)<0\). Note that \(z>0\) somewhere: Suppose not, that is, suppose \(z\equiv 0\). Then \(S(T)>0\) and \(G'(S(T))>0\). By (11) and assumption \({C^s}'(0)=0\), \(\mu \ge 0\), which implies by (15) that \(\mu (0) \ge 0\). Hence \(\mu (T)\ge 0\). Because \(\mu (T)\ge 0\) and \(G'(S(T))>0\), also \(\mu (T)+G'(S(T))>0\), which implies by condition (17) that \(S(T)=0\). This contradicts \(S(T)>0\). Therefore \(z>0\) somewhere. Because \({C^s}'(z)=-\mu (0)e^{\rho t}\) for some t, \(\mu (0)<0\). To show that the rate of extraction is strictly decreasing let \(t_0^+, t_1^+ \in [t_0,t_1]\) with \(t_0^+< t_1^+\). We obtain, after using (10) twice and subtracting, that on the interval where \(q(t)>0\),
This implies \(q(t_1^+)<q(t_0^+)\) by assumption \(C''(q)>0\).
Continuity of q(t) implies that we can choose \(t_0=0\), because otherwise q(t) would be discontinuous or increasing somewhere.
(iii) Recall that \(z(t)>0\) at some interval \([t_2,t_3]\). At this interval, control z(t) is strictly increasing. This is true because on this interval, \({C^s}'(z)=-\mu (0)e^{\rho t}\), which clearly implies that z(t) must increase: Let \(t_2^+, t_3^+ \in [t_2,t_3]\) with \(t_2^+< t_3^+\). Using (11) twice and subtracting, we get
This implies \(z(t_3^+)>z(t_2^+)\) by assumption \({C^s}''(q)>0\). Note in addition that because \(\mu (0)<0\), \(\mu (t)<0\) for all t. Because z(t) is strictly increasing and continuous, there can be only one interval, where \(z(t)>0\). In addition, since \(\mu (0)<0\), \(z(0)>0\): Suppose not. By condition (11)
Then by assumption \({C^s}'(0)=0\), \(\mu (0)\ge 0\), which contradicts \(\mu (0)<0\).
(iv) When \(q(t)>0\),
Because \(\lambda (0)>0\) and \(\mu (0)<0\), the instantaneous marginal profit rises at the rate of interest.
1.2 Proof of Proposition 3
Note first that \(\mu (T)<0\) and (17) imply \(G'(S(T))>0\). This implies \(S(T)>0\). For the second part of the result, we show first that \(\alpha q(0)\le z(0)\) is generally impossible at optimum. Suppose that \(\alpha q(0)\le z(0)\) holds. Then \({\dot{S}}(0)\le 0\), and because \({\dot{q}}<0\) for every \(t\in [0,{\overline{t}})\) and \({\dot{z}}>0\) for every \(t\in [0,T]\), \({\dot{S}}(t)<0\) for all \(t\in (0,T]\). Then \(S(T) > 0\) cannot be satisfied. Therefore, inequality \(\beta q(0)>z(0)\) holds implying that \({\dot{S}}(0)>0\). Note that the time path of S cannot have a minimum: Suppose it has a minimum. At such a point extraction is positive and \({\ddot{S}}\ge 0\), which is equivalent with \(\alpha {\dot{q}} \ge {\dot{z}}\) by Eq. (13). But since \({\dot{z}}>0\), we obtain \({\dot{q}}>0\), which contradicts Part (ii) Proposition 1.
Hence the time path is either strictly increasing or has a maximum value on (0, T). If the path is strictly increasing, the maximum value is at \(t=T\). We show next, that if the path has a maximum value on (0, T), the maximum value is unique. To this end, suppose that the stock has a maximum value at \(t_0<T\), which is denoted by \(S(t_0)\). The stock cannot have another local maximum: Suppose it does. Two possibilities exists in this case: either there exists \(t_1\) with a local maximum satisfying \(S(t)<\max \{S(t_0),S(t_1) \}\) for all \(t \in (t_0,t_1)\), or there exists a local maximum \(t_2\) satisfying \(S(t)=S(t_0)\) for all \(t\in (t_0,t_2)\). The first case is ruled out, because it implies that S has a local minimum on \((t_0,t_1)\), which contradicts the above reasoning. To rule out the second possibility, we note that \({\dot{S}}(t_0)=0\) and \({\dot{S}}(t)>0\) for every \(t \in (0,t_0)\). Equation \({\dot{S}}(t_0)=0\) is equivalent to \(\beta q(t_0)=z(t_0)\). Since \({\dot{q}}\le 0\) and \({\dot{z}}>0\), it must hold that after \(t_0\) we have \({\dot{S}}(t)<0\). This contradicts \(S(t)=S(t_0)\) for all \(t\in (t_0,t_2)\).
1.3 Proof of Proposition 4
Let \(t^{L}\) be the time instant when the mine is exhausted with the waste rock production rate \(\alpha ^L\) and let \(t^{H}\) be the respective time instant with coefficient \(\alpha ^H\). We show first that \(t^{L}>t^{H}\) is impossible, so assume that \(t^{L}>t^{H}\) holds. In both cases \({\dot{q}}<0\) whenever \(q>0\). Because of this and because extraction is zero after exhaustion, \(q^{H}\) hits zero before \(t^{L}\). Since the mine is exhausted in both cases,
It follows from these, that there exists a time instant \({\hat{t}}<t^{H}\) for which
From this and from the necessary conditions of the models’ problems, we obtain the following equations
From (A.8)–(A.10) we obtain that
Furthermore, by the necessary conditions,
Define now function f with \(f(t):=\lambda ^{L}(t)-\alpha ^{L} \mu ^{L}(t)-\lambda ^{H}(t)+\alpha ^{H} \mu ^{H}(t)\), and note that \(f(t)=f(0)e^{\rho t}\) and \(f({\hat{t}})=f(0)e^{\rho {\hat{t}}}\). Since by (A.11) \(f({\hat{t}})=0\), we obtain that \(f(0)=0\). Hence \(f(t)\equiv 0\). Since (A.9) and (A.10) hold also for other time instants with positive extraction, we obtain equation
Hence \(q^{L}(t)=q^{H}(t)\) for all t with positive \(q^{L}\) and \(q^{H}\). But then
which contradicts (A.7).
By the same principles and after minor changes, \(t^{L}<t^{H}\) is also impossible. Hence \(t^{L}=t^{H}\). Similar arguments as used above show that the extraction rates are the same.
1.4 Proof of Proposition 5
(i) Since the mine with coefficient \(\alpha ^{H}\) is not exhausted, \(\lambda ^H(T)=0\), and therefore \(\lambda ^H(t)\equiv 0\). The rate of extraction with coefficient \(\alpha ^{H}\), \(q^H\), cannot be anywhere greater than the rate of extraction with coefficient \(\alpha ^{L}\), \(q^L\): Suppose otherwise, that is, suppose that \(q^{H}(t)>q^{L}(t)\) for some \(t \in [0,T]\). Then there exists a time instant \({\hat{t}}<T\) for which
and we obtain using similar arguments as in the proof of Proposition 4 that \(\lambda ^{L}(t)-\alpha ^{L} \mu ^{L}(t)=-\alpha ^{H} \mu ^{H}(t)\) for every t with positive extraction levels. This means that \(q^{H}(t)= q^{L}(t)\) (when extraction is positive), which yields a contradiction with \(q^{H}(t)>q^{L}(t)\).
Since the mine with \(\alpha ^{L}\) is exhausted and the mine with \(\alpha ^{H}\) is not, the extraction rates cannot be equal at any time instant, because similar arguments as above show that the extraction rates are equal for all time instants in such a case.
(ii) We will show that \(q^H<q^L\) for all \(t \in [0,T ]\) by contradiction. To this end, we assume \(q^H\ge q^L\) for some \(t \in [0,T ]\). Note then that \(q^H\ge q^L\) for all \(t \in [0,T ]\): Otherwise (that is, if \(q^H < q^L\) for some t) there would exist a time instant \({\hat{t}}\) such that \(q^H=q^L\), which implies using similar arguments as in the proof of Proposition 4 that \(q^H\equiv q^L\), which contradicts inequality \(q^H < q^L\) for some t.
Because neither of the mines are exhausted, \(\lambda ^H=\lambda ^L\equiv 0\). Since \(q^H\ge q^L\), \(p-C'(q^H)\le p-C'(q^L)\). Combining this with (10) gives us \(-\alpha ^H \mu ^H\le -\alpha ^L \mu ^L\) when extraction is positive. Then
since \(\alpha ^H>\alpha ^L\). This implies together with equation \({C^s}'(z)=-\mu \) from (11), that \(z^L>z^H\) for all \(t \in [0,T ]\). This and \(q^H\ge q^L\) for all \(t \in [0,T ]\) imply by (13) that \({\dot{S}}^H>{\dot{S}}^L\) for all \(t \in [0,T ]\). Combining this with \(S^H(0)=S^L(0)=0\) gives
Hence \(G'(S^H(T))> G'(S^L(T))\). We obtain using these and (17) that
but \(-\mu ^H(T)>-\mu ^L(T)\) contradicts (A.18). Hence \(q^H<q^L\) for all \(t \in [0,T ]\).
1.5 Proof of Proposition 6
Since the mine with a high waste rock production rate is exhausted and the one with a low rate is not, we have
This clearly implies that there exists a time instant at which \(q^H>q^L\). Then \(q^H>q^L\) for all \(t \in [0,T ]\) (otherwise we would again obtain a contradiction). Note that \(\lambda ^L\equiv 0\). When \(q^L>0\), condition (10) gives us after subtraction that
Since the left-side of this is strictly negative, we obtain
This implies
Because \(q^H>q^L\) for all \(t \in [0,T ]\) and \(-\mu ^H<-\,\mu ^L\) for all \(t \in [0,T ]\), we obtain a contradiction using similar lines of reasoning as in the proof of Part (ii) of Proposition 5. Hence it is impossible that a mine with a high waste rock production rate is exhausted, but the mine with a lower rate is not.
1.6 Proof of Proposition 7
(i) Similar to the proof of Part (i) of Proposition 1. (ii) Assume that q is always zero. With similar reasoning as in the proof of Part (ii) of Proposition 1, it follows from this that \(\mu (t)\ge 0\) for all t. (Note: Because of \(\gamma (t)\), we cannot argue directly for a contradiction using condition \(H_q\le 0\) in (27).) Since \(q(t)\equiv 0\), (32) becomes
whose solution using the given initial condition is
Then, because \(a(t)\ge 0\),
implying that \(a(t)\equiv 0\). Condition (29) and assumption \(A'(0)=0\), imply \(-\,\gamma \le 0\) or equivalently \(\gamma \ge 0\). Condition \(H_q\le 0\) becomes now
implying that \(\mu < 0\). This contradicts \(\mu \ge 0\). Therefore there exists a time instant where \(q(t)>0\). Again, by continuity of q, there is an interval, where \(q(t)>0\). (iii) Similar to the proof of Part (iii) of Proposition 1. (iv) Let \(t_1,t_2\in I \subset [0,T]\) with \(t_1<t_2\), where I is an interval with \(a(t)>0\). Using (29) twice, we obtain equation
The conclusion follows from this, since \(A''>0\).
1.7 Proof of Lemma 1
(i) Suppose on the contrary to the claim that \(N(t)=0\) on [0, T]. Recall that by Proposition 7 there exists an interval \(I \in [0,T]\), where \(q>0\). Then on that interval \(\beta q=a>0\) (by (32)) and \({\dot{\gamma }}=(\delta +\rho )\gamma \) (by (35) and by \(D'(0)=0\)). By (29), \(A'(a)=-\gamma >0\) on I, implying that \({\dot{\gamma }}<0\). Then a grows on I by Proposition 7. But by (27), \(p-C'(q)=\lambda -\mu \alpha -\gamma \beta \) on I, which implies that q is decreasing on I. This contradicts equation \(\beta q=a\) for all \(t\in I\). (ii) Suppose on the contrary to the claim that there exists an interval \(I \subset [0,T]\) such that \({\dot{\gamma }}=0\) and \(\gamma \ne 0\) for every \(t \in I\). Then it holds on the interval I that
Since \({\dot{\gamma }}=0\) and (A.30) holds, \({\dot{N}}=0\). This implies that \(\beta q-a=\delta N\) for every \(t \in I\). Differentiating this with respect to time yields \(\beta {\dot{q}}-{\dot{a}}=0\). This is equivalent with \(\beta {\dot{q}}=0\), since (A.31) holds. But this contradicts (A.32).
1.8 Proof of Lemma 2
(i) Suppose on the contrary to the claim that such a time instant does not exists, that is, suppose that \(a(t)=0\) for every \(t \in (t^0,{\hat{t}})\), where \(|{\hat{t}}-t^0| < \epsilon \) for any small \(\epsilon > 0\). By the definition of \({\hat{t}}\), \(N(t)>0\) on the interval \((t^0,{\hat{t}})\) for sufficiently small \(\epsilon \). Let \(t^1 \in (t^0,{\hat{t}})\). Then we obtain that
by the above assumption about abatement. Because \(q(t)\ge 0\), we obtain that \(N({\hat{t}})\ge N(t^1)\). However, the definition of \({\hat{t}}\) implies that \(N(t^1)>N({\hat{t}})\). These yield a contradiction \(N({\hat{t}})>N({\hat{t}})\). (ii) Since \(\gamma (t)<0\) for every \(t\in (t^+,{\hat{t}})\), \(\gamma ({\hat{t}})\le 0\) by the continuity of the costate. The solution to (35) is
This can be used to rewrite \(\gamma ({\hat{t}})\le 0\) as
Let \(t\ge {\hat{t}}\). Then
where the last equality follows from assumption \(D'(0)=0\), since after \({\hat{t}}\) we know that \(N(t)=0\) by definition, and the inequality follows from (A.37)–(A.38).
1.9 Proof of Lemma 3
(i) Since \(N(t) = 0\) for all \(t\in [{\hat{t}},T]\), it must be that \(\beta q(t)=a(t)\) there. Assume contrary to the claim that there exists \(I \subset [{\hat{t}}, T]\) such that \(a(t)>0\) on I. Then \(\gamma (t)<0\) on I and therefore \({\dot{a}}>0\) on I, because \({\dot{\gamma }}=(\delta +\rho )\gamma <0\) on I. But by \(p-C'(q)=\lambda -\mu \alpha -\gamma \beta \), \({\dot{q}}<0\) on I. This contradicts condition
(ii) Let \(t\ge {\hat{t}}\). Part (ii) of Lemma 2 says that \(\gamma (t) \le 0\). Part (i) of the current Lemma says that \(a(t)=0\). Condition (29) and assumption \(A'(0)=0\) give then that \(-\gamma (t) \le 0\). These imply \(\gamma (t)=0\) for all \(t \in [{\hat{t}},T]\).
1.10 Proof of Proposition 9
The proof has similarities with the proof of Proposition 1 in Tahvonen (1997).
Note first that \({\dot{\gamma }}(t) > 0\) for all \(t \in [0,{\hat{t}})\) is not true, since \({\dot{\gamma }}(0)=D'(N(0))+(\delta +\rho )\gamma (0)=(\delta +\rho )\gamma (0)<0\).
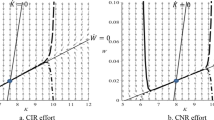
Recall that \(\gamma (T)=0\) and suppose that the time path has an inverted U-shape somewhere. There must exist a closed interval \(I=[t_1,t_2]\), where \({\dot{\gamma }}<0\) on the interior of I and \({\dot{\gamma }}(t_1)={\dot{\gamma }}(t_2)=0\). This implies that \({\dot{q}}<0\) and \({\dot{a}}\ge 0\) on I, so that
Note that \(\ddot{\gamma }(t_1)\le 0\) and \(\ddot{\gamma }(t_2)\ge 0\). By Eq. (35), \(\ddot{\gamma }(t)=D''(N(t)){\dot{N}}(t)\) at \(t=t_1\) and at \(t=t_2\), implying that
The derivative \(\ddot{\gamma }=D''(N(t)){\dot{N}}(t)+(\delta +\rho ){\dot{\gamma }}\) is positive somewhere on the interval \([t_1,t_2]\), implying that \({\dot{N}}(t)>0\) there, since \({\dot{\gamma }}<0\) on \((t_1,t_2)\). Then there exists \(t_3 \in [t_1,t_2)\) such that \({\dot{N}}(t_3)=0\). But then
which is a contradiction with (A.44). Hence the time path is U-shaped.
1.11 Proof of Proposition 10
We argue that \(a(T)=0\). Assume on the contrary that \(a(T)>0\). Then \(\gamma (T)<0\). However, condition (38) together with \(N(T)=0\) and \(R'(0)=0\) imply \(\gamma (T)\ge 0\), which contradicts \(\gamma (T)<0\). Hence \(a(T)=0\). Since \({\hat{t}}=T\), \(N(t)>0\) for all \(t \in (T-\epsilon ,T)\) for some (small) \(\epsilon >0\). Note that
which is non-positive at optimum. Since \(\beta q(T)\le a(T)=0\), we have that \(q(T)=0\). By Lemma 2, we have \(a(t)>0\) for all \(t \in (T-\epsilon ,T)\). For these instants of time, \(\gamma (t)<0\), implying that \(\gamma (T)\le 0\). This and \(\gamma (T)\ge 0\) obtained using condition (38) as above, imply that \(\gamma (T)=0\). Thus, when \({\hat{t}}=T\) and \(N(T)=0\), the shadow value of the pollution stock, \(\gamma \), has a U-shaped time path by the same principles as in the proof of Proposition 9.
1.12 Proof of Proposition 11
Note that in this case condition (38) implies \(-\,\gamma (T)=R'(N(T))\). Since the right-side is strictly positive, we obtain \(\gamma (T)<0\). This implies together with
that also \(\gamma (0)<0\). By (35) and assumption \(D'(0)=0\),
Note that \({\dot{\gamma }}(0)<0\) excludes the possibility that \({\dot{\gamma }}(t)>0\) for all \(t \in [0,T]\). This leaves four possibilities:
-
(1)
\({\dot{\gamma }}(t)<0\) for all \(t \in [0,T]\);
-
(2)
\({\dot{\gamma }}(t)<0\) for all \(t \in [0,T]\) except at an isolated time instant at which \({\dot{\gamma }}(t)=0\);
-
(3)
The time path is U-shaped;
-
(4)
The time path is first decreasing, then increasing and lastly decreasing again.
There are no other possibilities: Suppose on the contrary that the time path has three points with \({\dot{\gamma }}(t)=0\). Then the path has an inverted U-shape somewhere, and the same arguments as in the proof of Proposition 9 produce a contradiction.
1.13 Proof of Proposition 12
(i) Assume on the contrary to the claim that \(t^{L}\ge t^{H}\). Given the time invariant taxes and strictly positive extraction rates, the necessary conditions of the mining firms’ problems include the following conditions:
Since both mines are exhausted and \(t^{L}\ge t^{H}\), the time paths of the mines’ extraction rates must cross at least once.
Consider first the possibility that \(t^{L}>t^{H}\). Since there exists a smallest time instant \({\hat{t}}\) such that \(q^{H}({\hat{t}})=q^{L}({\hat{t}})\), Eqs. (51), (A.50) and (A.51) imply that
Note that the function \(t \mapsto \lambda ^{H}(t)-\lambda ^{L}(t)\) is then an exponentially decreasing function, obtains strictly negative values, and
This and Eqs. (A.50) and (A.51) imply
Hence
If \({\hat{t}}\) is unique, then \(q^{L}(t)>q^{H}(t)\) for all t except at \(t={\hat{t}}\). This clearly implies that the total extraction for mine L is strictly greater than \(x_0\), which is impossible. Suppose that \({\hat{t}}\) is not unique. Then Eq. (A.52) holds for at least two time instants, which contradicts the fact that the function \(\lambda ^{H}(t)-\lambda ^{L}(t)\) decreases exponentially.
Consider the possibility that \(t^{L}=t^{H}\). Note that continuity implies that Eqs. (A.50) and (A.51) hold also at \(t^{L}\). Because \(t^{L}=t^{H}\) and \(t^{H}<T\), there are two possibilities: either the extraction paths cross at some instant of time smaller than \(t^{L}\), or the paths don’t cross. If they cross, then Eq. (A.52) holds for two time instants, which again contradicts the fact that the function \(\lambda ^{H}(t)-\lambda ^{L}(t)\) decreases exponentially. If they don’t cross, then one of the mines is not exhausted, which is a contradiction.
(ii) Assume on the contrary to the claim that \(t^{L}>t^{H}\) or \(t^{L}<t^{H}\). First, let \(t^{L}>t^{H}\). Following the reasoning of Part (i), Eq. (A.52) implies that \(\lambda ^{H}({\hat{t}})=\lambda ^{L}({\hat{t}})\). Hence \(q^{L}(t)=q^{H}(t)\) for all t. But \(q^{L}(t)\) is strictly positive on \([t^{H},t^{L})\). These imply that the total extraction under profile \(q^{L}(t)\) is strictly greater than \(x_0\), which is a contradiction. The proof for the other case, \(t^{L}<t^{H}\), is similar.
1.14 Proof of Proposition 13
The proof is divided into two cases, one with \(t^H<T\) and the other with \(t^H=T\). Consider the first possibility. The proof of Proposition 12 shows that \(t^L<t^H\) and that there exists \({\hat{t}}\) such that \(q^{L}({\hat{t}})=q^{H}({\hat{t}})\). There is only one such time instant, since otherwise \(\lambda ^{H}(t)-\lambda ^{L}(t)\) would not decrease exponentially. Since \(t^{L}<t^{H}\), \(q^{L}(t)<q^{H}(t)\) for all \(t \in ({\hat{t}},t^H]\). This implies that \(q^{L}(t)>q^{H}(t)\) for all \(t \in [0,{\hat{t}})\).
Consider then the second possibility. If \(t^H=T\), then either \(t^L<T\) or \(t^L=T\). If \(t^L<T\), the extraction profiles of the mines must cross, since otherwise mine L is not exhausted. This can occur only once, since otherwise the function \(\lambda ^{H}(t)-\lambda ^{L}(t)\) does not evolve exponentially. Then it must be that the extraction path \(q^L\) crosses path \(q^H\) from the above. Next it is shown that if \(t^L=T\), then \(q^H(T)>q^L(T)\). To see this, suppose \(q^H(T)\le q^L(T)\), and note that \(q^H\) cannot always equal \(q^L\), since \(K>0\). Hence the paths are not the same, but they nevertheless must cross. As in the proof of Proposition 12, there exists \({\hat{t}}\) such that \(q^L(t)>q^H(t)\) for all \(t \in [0,{\hat{t}})\). But since \(q^H(T)\le q^L(T)\), the paths cross twice, which again means that the function \(\lambda ^{H}(t)-\lambda ^{L}(t)\) does not decrease exponentially. Hence \(q^H(T)>q^L(T)\), and the extraction path \(q^L\) crosses path \(q^H\) from the above.
Rights and permissions
About this article
Cite this article
Lappi, P., Ollikainen, M. Optimal Environmental Policy for a Mine Under Polluting Waste Rocks and Stock Pollution. Environ Resource Econ 73, 133–158 (2019). https://doi.org/10.1007/s10640-018-0253-9
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10640-018-0253-9