Abstract
The paper analyzes the effects of varying climate impacts on the social cost of carbon and economic growth. We use polynomial damage functions in a model of an endogenously growing two-sector economy. The framework includes nonrenewable natural resources which cause greenhouse gas emissions; pollution stock harms capital and reduces economic growth. We find a big effect of the selected damage function on the social cost of carbon and a significant impact on the growth rate. In our calibration a quartic damage function raises the social cost of carbon by more than a factor of ten compared to the linear function. In the social optimum the growth rate remains positive even when the damage function is highly convex. We test the robustness of the results by adding pollution decay, lowering the elasticity of intertemporal substitution, and addressing uncertainty, which does not alter our results. We find that high marginal climate damages require stringent climate policies but do not preclude positive economic growth despite convexity, provided that policies are designed in an efficient manner.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Climate Impacts
There is broad agreement that climate change has widespread effects on the economy and the natural environment. It causes economic damages which worsen with increasing temperatures.Footnote 1 For a thorough assessment of the consequences and the formulation of appropriate climate policies the determination and the use of an appropriate damage function is indispensable: it lies “at the heart” of the economic analysis of climate change (Farmer et al. 2015, p. 332). Such a function specifies how economic damages change as a function of greenhouse gas concentration in the atmosphere. The present paper thoroughly explores the impact of damage modeling in a theoretical setup of an economy with climate change and endogenous growth.
The economic impacts from climate change are difficult to be estimated on a global level (IPCC 2014b). So far, there is no agreement on the form and the parametrization of a general climate damage function. Nordhaus and Boyer (2000, p. 23) state that “estimating the damages from greenhouse warming has proven extremely elusive.” According to Weitzman the literature offers “little guidance on why one specification or another” of a damage function has been selected (Weitzman 2010a). It is thus admitted that a strong empirical basis for the damage functions used in the best-known models is lacking. What is more, climate damages have implausibly small effects on economic growth in most integrated assessment models even under extreme temperature scenarios (Stern 2013; Revesz et al. 2014).
The big challenge for formulating a comprehensive climate damage function is to properly aggregate various highly heterogeneous effects. Climate impacts on different regions and ecosystems are provided in IPCC (2014b) and Roson and Sartori (2016).Footnote 2 Yet, for a global analysis of climate damages, the available data are not sufficiently complete. Bottom-up studies may be used to inspire a general formula, but by their nature they are limited in scope. It thus remains unclear which functional form for the damage function is suitable (Moore and Diaz 2015) and where the limitations are to capture “everything by a simple function” (Farmer et al. 2015, p. 332). Damage functions are one of various elements of integrated assessment models which have recently been criticized. Farmer et al. (2015, p. 329) conclude that also the issues of risks, heterogeneity, and technical change are “inadequately addressed” by climate modelers. In all these areas, model specifications strongly affect the results and associated policy recommendations (Revesz et al. 2014). While recent contributions have addressed the additional issues under critique,Footnote 3 the functional form of the climate damage function has received little attention,Footnote 4 although its potential impact on optimal policies is substantial and the critique has been especially sharp.Footnote 5 The present paper shows how important the specifications of the damage functions are in climate economics. We use higher-order polynomial functions up to a cubic and quartic form to assess the impact of climate damages on welfare and growth. In our model, damages affect the capital stock, reducing both current income and economic growth; for a long-run ecological phenomenon economic dynamics become crucial.
The agreed temperature targets of international climate policy suggest that marginal climate damages become very large or even infinite once the temperature ceiling is reached. Conversely, most economic models use constant or quadratic functions for climate damages so that a specific threshold temperature does not emerge and optimum warming can exceed the ceiling, depending on the benefits of climate policy. We want to keep the assumption of a continuous damage function but aim at including high marginal damages by considering highly convex damage functions. This brings the economic view of optimal pollution closer to the view of climate physics and policymakers favoring temperature targets.Footnote 6
We find a big effect of the damage function on the social cost of carbon and a significant impact on the economic growth rate. Using a theoretical framework, this paper shows that the negative impact of climate damages on economic growth grows with the degree of convexity of the assumed damage function. Moreover, contrary to the prevalent opinion in public discourse, optimally designed climate policies do not prevent the world economy from experiencing positive growth rates despite the convexity of damage functions. However, if climate policies aiming to correct the pollution externality are sub-optimally chosen, damages to capital become higher and the economic growth rate may become negative in the long run.Footnote 7 Calibrating our model, we confirm that in the social optimum economic growth rates are still positive in the long run even for highly convex damage functions and assuming non logarithmic utility, i.e. for a quartic damage function and a low intertemporal elasticity of consumption substitution. Specifically, a quartic damage function raises the social cost of carbon by more than a factor of ten compared to the linear function, already after 14 years.Footnote 8
1.2 Contribution to the Literature
Modeling externalities in the form of greenhouse gas emissions includes two components: climate sensitivity, i.e. the increase in long-term temperature caused by growing concentration of carbon dioxide in the atmosphere, and climate damage functions, capturing the relationship between temperature rise and induced losses in the economy. Regarding the former, the broadly used RICE/DICE model (Nordhaus and Boyer 2000) uses a small structural model to describe the relationship between pollution stock, radiative forcing, and climate change, suggesting that temperature is a concave function of pollution stock. This crucial assumption is used in most of the climate economics literature, e.g. in Golosov et al. (2014) and van den Bijgaart et al. (2016, p. 78) where it is said that the relation “between atmospheric \(\mathrm{CO}_{2}\) concentrations and equilibrium temperatures can be described through a logarithmic curve..”. However, the IPCC has recently summarized all the relevant research and explains: “Multiple lines of evidence indicate a strong, consistent, almost linear relationship between cumulative \(\mathrm{CO}_{2}\) emissions and projected global temperature change to the year 2100 ..” IPCC (2014a, p. 9). This suggests the IAM tradition should be abandoned and climate sensitivity should be modelled using a linear rather than a concave function, as we will apply below.
With respect to the second component —climate damage functions—, RICE/DICE assumes that climate change affects current output negatively. Specifically, climate damages \(D(\cdot )\) are a quadratic function of temperature while a “damage coefficient” \(\Omega =\)\(1/\left[ 1+D(\cdot )\right] \) is used to multiply final output to reflect the impact of climate change (\(0<\Omega <1\)). The higher the damage, the lower the coefficient and thus output and income.Footnote 9 The functional form of the damage function and its parametrization has been inspired by numerical estimations of predicted climate damages. Nordhaus (2007) estimates that damages are 1.7 percent of output at 2.5 \({^\circ }\)C warming, which provides a parameter value for the quadratic term; Hanemann (2008) presents estimates for the same temperature which are 2.4 times as much, so a different value appears warranted.Footnote 10 To deal with higher temperatures one could use extrapolations of these models. However, Ackerman and Stanton (2012) find that this procedure lets damages grow very slowly with temperature. Only half of world output would be lost when temperatures increase by 19 \({^\circ }\)C in the Nordhaus case or 12 \({^\circ }\)C for the Hanemann specification neither of which is very plausible. Weitzman (2010b) argues that scientific evidence implies much greater losses, especially at higher temperatures. He modifies the RICE/DICE setup by adding a term to the damage function where temperature is raised to the power of 6.76. As a result, damages turn out to be 50 percent of output at 6 \({^\circ }\)C warming and 99 percent at 12 \({^\circ }\)C, which is closer to what natural science predicts. Evidently, adding a quadratic or a higher order term to a linear specification of the D-function increases output loss for any given temperature. But the use of the damage coefficient \(\Omega \) for multiplication with output implies that, with rising temperature, a total collapse of the economy is only reached asymptotically, i.e. only a temperature of infinity would entail a total income loss, which is an extreme assumption. Put differently, the relationship between temperature and damages (measured as a share of output \(1-\Omega )\) becomes concave for high temperatures (Ackerman and Stanton 2012, p. 11), which contradicts general expectations. We will use polynomial damage functions including terms of higher order to reach a significant degree of convexity but use the D-function for damages instead of coefficient \(\Omega \) so that damage concavity is removed. We will thoroughly analyze the impact of variations of the damage functions in a climate economy model with endogenous growth where emissions occur endogenously through exhaustible resource use.Footnote 11
While the DICE model considers damages of climate change on current productivity, Weitzman (2010a) analyzes climate effects on individual utility.Footnote 12 We highlight that damages affect not only the output level but also the growth rate of an economy, which is an important aspect of climate change (Moore and Diaz 2015; Bretschger and Vinogradova 2016; Bretschger and Karydas 2017). Moore and Diaz (2015) add induced capital depreciation to the DICE model and find that this entails more stringent climate policies in the optimum and slows down growth, especially in poor countries. We continue this line of research by including the dynamic effects of climate change in a full-fledged macroeconomic growth model with focus on highly convex climate damage functions. We close the gap between the moderately convex cost functions and the strict temperature targets of international climate policy implying that marginal damages become very high when the temperature target is exceeded. An alternative approach is to include a ceiling constraint for pollution stock as presented in Amigues and Moreaux (2013). In the optimum, carbon concentration increases up to the cap where the economy is constrained as long as natural resources are still abundant and natural decay too weak. Conversely, in our model, damages already occur at a level which is lower than the cap and increase in a continuous way so that discontinuities in consumption do not arise. Acemoglu et al. (2012) also assume that the deterioration of environmental quality may induce an environmental disaster in finite time. Such a state would cause infinite damage but in their model it is never formally reached because policy is able to avoid it.
The literature agrees that damages are a convex function of temperature but the degree of the convexity is an open issue, inevitably subject to uncertainty, see for instance Dietz and Stern (2015). The previous idea of IAMs (e.g. Golosov et al. 2014) that the mapping from the atmospheric carbon dioxide concentration to economic damages would amount to a composition of a convex and a concave function and could potentially become almost linear has to be discarded however; the concave relation between carbon emissions and global temperature is not existent. The economic impact of climate change crucially depends on the degree of the convexity of the damage function, which we explore in this contribution.
The structure of the paper is the following: In Sect. 2 the baseline model’s setup, assumptions, and solution are described. In Sect. 3, the long-run steady state of the economy is analysed. Section 4 describes the transition phase of the economy. Section 5 introduces the extensions to the baseline model, namely pollution decay, non-logarithmic utility and uncertainty. Section 6 concludes.
2 Baseline Model
2.1 The Setup
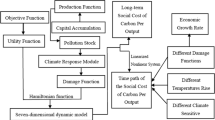
The model includes two sectors, one for final goods production and one for capital accumulation; it assumes that nonrenewable resource use causes emissions which accumulate aggregate pollution stock. Pollution negatively affects the existing capital stock; capital loss is a highly convex function of pollution stock. Emissions, the social cost of carbon and economic growth are endogenously determined from the model in closed-form solutions. To reduce emissions, the economy needs to decrease resource use and will use and accumulate more capital by reallocating inputs between the sectors.
Specifically, we assume that a fraction \(0<\epsilon _{t}<1\) of total capital \(K_{t}\) is used for the production of final goods \(Y_{t}\) where it is combined with nonrenewable natural resources \(R_{t}\), think of oil or gas, so that
where F denotes a function and t the time index. The remaining fraction \(1-\epsilon _{t}\) of capital \(K_{t}\) is used for the accumulation of new capital which is harmed by climate damages. Specifically, we denote by \(\dot{K_{t}}\) the time derivative of capital and by \(D(P_{t})\) a polynomial function expressing the damages of the pollution stock \(P_{t}\) on capital, with the depreciation rate \(\eta D(P_{t})\le 1\) for any \(P_{t}\), so that
where \(B>0\) is capital productivity in the investment sector.Footnote 13 That climate change enters the capital accumulation equation rather than the utility function follows a prominent request by Stern (2013). The stock of greenhouse gases in the atmosphere is accumulated with resource use according to
with \(\phi >0\). When pollution decay is neglected, \(\theta \) is set equal 0, whereas when pollution decay is present, \(\theta \) is positive. \(\bar{P}\) denotes the preindustrial level of pollution, which is assumed to be the lower bound of pollution. The stock of nonrenewable natural resource, is depleted according to
with \(S_0\) the initial stock of the resource being exogenously given. As we follow the IPCC (2014a) in assuming a linear relationship between pollution stock and temperature, we do not need to introduce temperature as a separate variable. The utility function of households \(U_{t}=U(C_{t})\) closes the model.
2.2 Assumptions
-
1.
Production
For the production of final goods of Eq. (1) we assume the Cobb–Douglas specification
$$\begin{aligned} Y_{t}=A(\epsilon _{t}K_{t})^{\alpha }R_{t}^{1-\alpha } \end{aligned}$$(5)with \(A>0.\) Both inputs are essential so that resources are always needed to obtain positive output.
-
2.
Utility
When \(\sigma \) denotes the coefficient of relative risk aversion, the utility function takes the form
$$\begin{aligned} U(C_{t})=\frac{C_{t}^{1-\sigma }-1}{1-\sigma } \end{aligned}$$(6)for \(\sigma \ne 1\) and
$$\begin{aligned} U(C_{t})=\ln C_{t} \end{aligned}$$(7)for \(\sigma =1\). For the sake of clarity we assume \(\sigma =1\) in the main part of the paper and provide a separate discussion for the case \(\sigma \ne 1\) in a separate section below.
-
3.
Pollution decay
It has been found that a small fraction of greenhouse gases in the atmosphere decays rapidly in the short run and a substantial fraction remains in the atmosphere for a very long time period (more than a thousand years). To highlight the second part of the process we abstract in the baseline model from pollution decay, i.e. set \(\theta =0\) but will extend the model in a separate section by adopting a positive decay rate (\(\theta >0\)).
2.3 Solving the Model
The social planner problem is characterized by the maximization of Eq. (7) under the restrictions Eqs. (2)–(5) and the fact that output is entirely consumed at each t, that is \(Y_t=C_t\). The associated Hamiltonian reads
The first-order and transversality conditions of this problem as well as the necessary proofs are given in the Appendix. In particular we show that the share of capital used in the final goods sector instantaneously jumps to its steady state value \(\epsilon =\rho /B.\) We next derive optimal resource extraction and pollution growth. The growth rates of output and capital are found by using the production function, \(Y_{t}=A(\epsilon _{t}K_{t})^{\alpha }R_{t}^{1-\alpha }\), the capital accumulation constraint, \(\dot{K_{t}}=B(1-\epsilon _{t})K_{t}-\eta D(P_{t})K_{t} \), and the steady state value of \(\epsilon \). Hence, we get \(\hat{Y}_{t}=\alpha \hat{K}_{t}+(1-\alpha )\hat{R}_{t}\) and \(\hat{K}_{t}=B-\rho -\eta D(P_{t})\).
Using (34), (39), and (31), from the appendix, yields the growth of the pollution costate variable as \(\hat{\mu }_{Pt}=\rho +\eta D^{\prime }(P_{t})\dfrac{\alpha }{\rho }\dfrac{1}{\mu _{Pt}}.\) Invoking (32) we write for resource growth \(-\hat{R} _{t}=\dfrac{\mu _{St}}{\mu _{St}-\phi \mu _{Pt}}\hat{\mu }_{St}-\dfrac{\phi \mu _{Pt}}{\mu _{St}-\phi \mu _{Pt}}\hat{\mu }_{Pt}\). By defining the relative shadow price of the resource stock according to \(\psi _{t}\equiv \dfrac{\mu _{St}}{\mu _{St}-\phi \mu _{Pt}}\) , where \(0<\psi _{t}<1\), using Eqs. (34) and (35) we have
as well as
Following Eq. (10) the growth rate of resource use \(\hat{R}_{t}\) is negative; it becomes more negative with an increasing discount rate and rising marginal damage of climate change \(D^{\prime }(P_{t})\). Higher convexity brings forward the resource use due to more severe consequences of pollution in the future.
The social cost of carbon (SCC) reflects total damages from releasing greenhouse gas emissions to the atmosphere at every point in time. This essential guideline for optimal climate policies has been the subject of many recent contributions (e.g. Van den Bijgaart et al. 2016; Ackerman and Stanton 2012). In our model we label SCC by \(\chi _{t}\), which is equal to the marginal damage due to pollution, that is \(\chi _{t}\equiv -\dfrac{\mu _{Pt}}{\mu _{Yt}}\), whereas the social cost of carbon per unit of output, which under general conditions equals the optimal carbon tax in decentralized equilibrium, is \(\tilde{\chi }_{t}\equiv \dfrac{\chi _{t}}{Y_{t}}=-\dfrac{\mu _{Pt}}{\mu _{Yt}Y_{t}}=-\mu _{Pt}\ \)so that \(\hat{\tilde{\chi }}_{t}=\hat{\mu }_{Pt}\).
By defining the resource depletion rate as \(u_{t}=\dfrac{R_{t}}{S_{t}}\), Eqs. (3) and (4) can be modified to \(\hat{P}_{t}=\phi u_{t}\dfrac{S_{t}}{P_{t}}\) and \(\hat{S}_{t}=-u_{t}\). We can then represent the model dynamics by a system of five variables according to
Using Eqs. (14) and (15) as well as the fact that pollution and resource stock at \(t=0\) are known, we can solve for pollution stock \(P_{t}\) following
To better understand the dynamic characteristics of the system and the long-run equilibrium it is useful to state that the growth rate of the resource depletion rate \(u_{t}=\dfrac{R_{t}}{S_{t}}\) is asymptotically constant and equal to zero; the formal proof is given in the Appendix. We next present the main model solutions for the long-run equilibrium before we will turn to the characteristics of the transition phase.
3 Long-run Steady State
We first analyse the long-run value of the social cost of carbon (SCC) and then turn to economic growth. Starting from Eq. (34) and denoting that \(\mu _{Kt}K_{t}=\dfrac{\alpha }{\rho }\), we find the value of \(\tilde{\chi }_{t}\) at any time t according to
For the long-run value of SCC per unit of output we then obtain
Equation (17) shows that in our model the social cost of carbon per unit of output is the discounted stream of all the future marginal damages due to pollution and depends on a few variables only. Importantly, steady-state SCC per unit of output grows with the marginal climate damage. We thus confirm that the algebraic form and the parametrization of the damage function directly affect a society’s valuation of the externality. Long run SCC per unit of output increases with the capital share \(\alpha \)—because climate change affects the capital input and therefore the cost climate change has on society—and with the damage impact parameter \(\eta \) measuring pollution intensity caused by resource use. SCC per unit of output is reduced by the discount rate which appears in the quadratic form in the denominator, representing both the impatience in capital buildup and resource depletion. In the next section we will use specific parameter values to directly determine SCC for different specifications of the damage function.
We also want to explore whether the economy is still growing in the optimum with climate change. Setting the system of Eqs. (11) to (15) equal to zero, we can obtain the asymptotic steady state values of the variables, namely
The dynamic system of (11) to (15) can be solved by using the linearization method.Footnote 14 The Jacobian matrix evaluated at the steady state gives us the eigenvalues, \(\{0,-\rho ,-\rho ,\rho ,\rho \}\), and the corresponding eigenvectors that specify the solution. At this point it is interesting to note that the linearized dynamic system is subject to a zero eigenvalue. This would mean that the dynamic system shows hysteresis. However in our case this does not happen because the corresponding coefficient of this eigenvector has to be set equal to zero, given our initial conditions. Moreover, in order to avoid solutions that result in diverging values of the variables in infinity, we set the coefficients that correspond to positive eigenvalues equal to zero and use appropriate initial values for \(u_{0}\) and \(\chi _{0}\), while taking as exogenous the initial values \(\psi _{0}\), \(P_{0}\) and \(S_{0}\).Footnote 15
Returning now to the initial variables, the growth rates of capital and output in infinite time are given by
According to Eq. (18) the long-run growth rate of output is positive provided that capital productivity B is high enough (\(B>\eta D(P_{\infty })\)) and the discount rate is sufficiently low \((\rho <\alpha (B-\eta D(P_{\infty })))\). The range of possible \(\rho \) that result in positive growth becomes wider with a higher capital share \(\alpha \).Footnote 16 Thus, in order to have \(\hat{Y}_{\infty }>0\Leftrightarrow \frac{B-\rho /\alpha }{\eta }>D(P_{\infty })\), there is an upper bound to damage size. For the choice of parameters and further conclusions we proceed to the analysis of transitional dynamics.
4 Transition Phase
We now determine how the form of the damage function has an impact not only on long-run equilibrium but also on the time paths of the variables. Specifically, the time path of the social cost of carbon (SCC) per output, given by \(\tilde{\chi }_{t}=\dfrac{\alpha \eta }{\rho }\int \limits _{t}^{\infty }D^{\prime }(P_{\nu })e^{-\rho (\nu -t)}d\nu \) and approximated by \(\tilde{\chi }_{t}=\dfrac{\alpha \eta D^{\prime }(P_{\infty })}{\rho ^{2}}-\dfrac{\alpha \eta \phi D^{\prime \prime }(P_{\infty })S_{0}e^{-\rho t}}{2\rho ^{2}}\) close to the steady state, is increasing and concave in time. Its concavity depends on the second derivative of the damage function evaluated at infinite time. Hence, the higher the degree of the polynomial damage function, the more concave the time path of \(\tilde{\chi }_{t}\). The connection between the convexity of the damage function and the concavity of the SCC per output can be better understood if we consider the fact that with higher convexity of \(D(P_t)\), marginal damages increase more steeply when pollution increases. In the social planner context, this leads to a higher value on every unit of pollution added to the stock, and a higher SCC per output at every level of pollution. Therefore, and given that pollution increases over time in the absence of decay, a more convex damage function results in a more concave time path for the SCC per output. At the special linear case, \(\tilde{\chi }_{t}\) is constant throughout time. Moreover, as can be seen from the expressions for \(\tilde{\chi }_{t}\) as well as in Fig. 1, the social cost of carbon per output converges asymptotically to a constant level given in Eq. (17), which was discussed in the previous section. For capital and output growth we get the two following equations for the transition phase
To further specify the transition paths we calibrate the model, using standard parameter values of literature. Specifically, we use for the discount rate \(\rho =0.015\), the output elasticity of capital \(\alpha =0.9\), and capital productivity \(B=0.04\) as well as the initial values \(P_{0}=830GtC\), \(S_{0}=6000GtC\), and \(Y_{0}=49.8\) trillion US$ which applies to the year 2010. The following figures show the SCC and economic growth as a function of time for different damage functions. In the graphs, the solid thin line corresponds to a linear damage function, i.e. \(D(P_{t})=\kappa _{1}P_{t}\), the largely dashed to a quadratic of the form \(D(P_{t})=\kappa _{1}P_{t}+\kappa _{2}P_{t}^{2}\), the solid thick to a cubic, i.e. \(D(P_{t})=\kappa _{1} P_{t}+\kappa _{2}P_{t}^{2}+\kappa _{3}P_{t}^{3}\), and finally the thinly dashed to a quartic one, \(D(P_{t})=\kappa _{1}P_{t}+\kappa _{2}P_{t}^{2}+\kappa _{3}P_{t}^{3}+\kappa _{4}P_{t}^{4}\).
Figure 1 depicts the social cost of carbon (SCC) per output corresponding to the different damage functions, when there is no decay in pollution and the utility is of logarithmic form. The calibration of the coefficients \(\kappa _{1}\), \(\kappa _{2}\), \(\kappa _{3}\) and \(\kappa _{4}\) is based on the literature where SCC in 2010 lies within the range of 20 US\(\$/tC\) to 120 US\(\$/tC\) (Van den Bijgaart et al. 2016) and global output is 49.8 trillion US$. To reflect that initial SCC depends positively on the convexity of the damage function we use as a first calibration the following assumptions for expositional convenience: With a linear damage function \(\chi _{0}\) is set to be 20 US\(\$/tC\), with a quadratic it is 50 US\(\$/tC\), with a cubic it is 80 US\(\$/tC\), and with a quartic it is 120 US\(\$/tC\); an alternative calibration approach is provided below.
It can be seen from the figures that a linear damage function results in a constant SCC per output, while higher degree polynomial damage functions cause a higher level of SCC per output that is reached in infinite time. While the increase is not very pronounced for the quadratic case it is highly visible for the cubic and quartic damage functions. It is striking that already after 14 years, the SCC per output differs by more than a factor of ten when the quartic instead of the linear damage function is used.
In Fig. 2 the growth rate of output can be seen. According to the figure, growth is decreased by climate damages and the growth rate becomes lower with higher convexity of the damage function. Put differently, for all the damage functions the optimal growth rate of output declines over the next centuries and more convex damage functions require lower growth rates of output, as a result of the negative impact of pollution on the accumulation of capital. The difference in the resulting growth rates of output between the various damages functions is significant albeit not of the same size as in the case of the SCC. Annual output growth \(\hat{Y_{t}}\) stays almost constant in the case of a linear damage function only moving from 2.1 to \(2.04\%\), while in the quadratic, cubic and quartic case it falls to 1.95, 1.70 and \(1.38\%\), respectively. Provided the economy is in the social optimum, the economy can still have positive growth with climate change. For the decentralized equilibrium it says positive growth is feasible provided that efficient climate policies replicating the social optimum are implemented.
The first calibration nicely exposes the analytical results using initial values of SCC per output which are based on the range given in the IAM literature. Let us now assume, as an alternative, that all the damage functions start from an equal SCC per output in the beginning of global climate policy, which we set at the year 2000. For the sake of clarity we restrict the analysis to the linear, quadratic, and quartic damage functions and present again the results for the SCC per output and the growth rate (Figs. 3,4).
With the new initial SCC per output we find a significant distinction between two different scenarios. The first is to assume a linear or a quadratic function, where it turns out that the time paths for \(\tilde{\chi }_{t}\) as well as \(\hat{Y}_{t}\) are almost identical. This result illustrates that a second-degree polynomial damage function, despite being convex, does not affect the variables as much as one would probably expect. Conversely, in the second scenario, when we use a quartic damage function we can show that this introduces high-enough convexity to have significant effects on both model variables; the same applies for the cubic function to a somewhat lower degree.Footnote 17
5 Model Extensions
5.1 Pollution Decay
In the following we modify the setup to allow for positive pollution decay. It is assumed that pollution cannot be lower than the preindustrial level, noted by \(\bar{P}\). Hence, the change in the stock of pollution needs an additional term and now reads
where \(0<\theta <1\) and \(P_{t}\ge \bar{P}\). With the new assumptions, the dynamic system is given by
Due to the pollution decay, the stock of pollution does not evolve monotonically but has a peak, which is seen in Fig. 5.
The four different damage functions are again calibrated so that the SCC in 2010 corresponds to values often reported in the literature, namely \(20\$/tC\), \(50\$/tC\), \(80\$/tC\), \(120\$/tC\), in the linear, quadratic, cubic and quartic case, respectively (Figs. 6, 7).
We derive the decay rate from the representation of the carbon cycle in Nordhaus and Boyer (2000) where the atmosphere, upper ocean layers and deep oceans are the three main carbon reservoirs. The calibrated transfer rates from the atmosphere to the upper ocean layer and from the upper oceans to the deep oceans imply an indirect transfer rate from the atmosphere to deep oceans of approximately 0.0038 per year, see Bretschger and Vinogradova (2016), which we use as the value of \(\theta \) in our model.
In this case, pollution stock does not reach the maximum, as in the previous case of \(\theta =0\), but eventually reaches the preindustrial level \(\bar{P}\). Since the social cost of carbon per output is directly affected by the time path of pollution stock, its time path for different damage functions now can be seen on Fig. 6.
From these graphs, it can be seen that the maximum level of pollution stock is reached after the maximum level of the SCC per output is attained. This is due to the fact that future damages are being discounted in the present.
Finally, the growth rate of output is declining to lower levels compared to the no decay case, before it starts increasing again and return almost to its initial level in the very long run. More precisely, the lowest growth rates of output for the four cases are \(2.05\%\) for the linear damage function, \(1.99\%\) for the quadratic, \(1.83\%\) for the cubic and \(0.94\%\) for the quartic. The reason for this behavior is that in addition perfect foresight, there is also pollution decay in this extension of the model. Hence, \(\hat{Y}_{t}\) first reacts sharply to the increasing pollution and eventually returns to a higher level, after pollution has been absorbed by the environment.
5.2 Non-logarithmic Utility
We now turn to the case where the intertemporal elasticity of consumption substitution is unequal unity by assuming that utility be given by Eq. (6) where \(\sigma \ne 1.\) Apart from that, the optimization problem is identical to Eq. (8); the first-order conditions of this problem are given in the Appendix. In the non-logarithmic case, the share of capital does not jump to its steady state value but asymptotically approaches a steady-state value. In order to prove that there is such a steady-state value of \(\epsilon _{t}\), we start from the transversality condition \(\lim _{t\rightarrow \infty }\mu _{Kt}K_{t}e^{-\rho t}=0\) and Eq. (41), from which we can see that \(\hat{\mu }_{Kt}+\hat{K}_{t}-\rho <0\Leftrightarrow \epsilon _{t}>0\). However, from the equation of capital accumulation and in order for the growth rate of capital to be constant in the long run, we need \(\lim _{t\rightarrow \infty }\hat{\epsilon }_{t}\le 0\). Hence, we can conclude that \(\lim _{t\rightarrow \infty }\hat{\epsilon }_{t}=0\).
Using the same auxiliary variables as in the logarithmic case, we can convert the system of equations into
The long-run steady state values of these variables are, respectively
The eigenvalues of the Jacobian matrix at the steady states are \(\{0\text {, }-\frac{\rho +\alpha (\sigma -1)(B-\eta D(P_{\infty }))}{\sigma }\text {, } -\frac{\rho +\alpha (\sigma -1)(B-\eta D(P_{\infty }))}{\sigma }\text {, }\frac{\rho +\alpha (\sigma -1)(B-\eta D(P_{\infty }))}{\sigma }\text {, }\frac{\rho +\alpha (\sigma -1)(B-\eta D(P_{\infty }))}{\sigma }\text {, }\frac{\rho +\alpha (\sigma -1)(B-\eta D(P_{\infty }))}{\sigma }\}\). For realistic values of the parameters, we have that \(\alpha (\sigma -1)(B-\eta D(P_{\infty }))>0\). Therefore, the last three eigenvalues are positive and the respective coefficients are set equal to zero in order to eliminate non-convergent solutions.
The long-run growth rate of output is given by
which is very similar to the previous result given in Eq. (18) but more general as now we do not impose \(\sigma =1.\) We now turn to the characterization of transitional dynamics with the help of calibrations and plotting of different time paths. As before, the solid thin line corresponds to a linear damage function, the largely dashed to a quadratic, the solid thick to a cubic, and finally the thinly dashed to a quartic one (Figs. 8, 9, 10).
For the characterization of the transition path we first look at sectoral capital allocation. In the previous case with \(\sigma =1,\) the share of capital in the final output sector immediately jumped to its steady state value (\(\epsilon =\rho /B)\). Now, with a lower intertemporal elasticity of substitution (\(\sigma >1)\), present consumption becomes more preferable compared to future consumption, which in turn results in lower savings. Consequently, a higher share of capital, \(\epsilon _{t}\), is used in the final output production in order to satisfy the higher current consumption.Footnote 18 The share converges to a steady state, which is higher than \(\rho /B\) for all damage functions, as can be seen from Fig. 8.
It is also worth noting that as convexity increases, \(\epsilon _{\infty }\) reaches a lower value. That is because in the long run capital has to be shifted towards the capital producing sector, as damages become more severe and a higher portion of the capital stock gets destroyed.
For non-logarithmic utility, the social cost of carbon per output for given parameters is presented in Fig. 9. By comparing it to Fig. 1 we can see that when \(\sigma >1\), \(\tilde{\chi }_{t}\) is reduced in terms of levels but grows more rapidly, approximating its long-run value sooner.
Regarding growth rates of output with non-logarithmic utility, they are lower compared to the baseline case at every point in time, which is due to the lower input allocation to the capital sector. Higher polynomial-degree damage functions result in an interesting time path for the growth rate \(\hat{Y}_{t}\), see Fig. 10.Footnote 19 We find a peak after several decades (at 35 and 40 years for cubic and quartic damage functions, respectively) before the growth rate starts decreasing again. This is because the initially increased use of the polluting resource causes the economy to grow in a first phase, without inducing sufficient capital accumulation as a compensation for pollution losses in the second phase. As expected from Eq. (29), the long-run growth rate of output for the calibarated value \(\sigma =2\) is half the respective value of the baseline case where \(\sigma =1\).
5.3 Uncertainty
In our framework, we can also assess the impact uncertainty has on the social cost of carbon per output and on the growth rate of output. Assuming that there is uncertainty as to whether the damage function is of linear or quartic form, let \(\pi \in [0,1]\) note the positive probability that the damage function is quartic. Therefore, \(\bar{D}_t\), which is the expected damage function, is given by \(\mathbb {E}[D_t]=\pi (\kappa _{1}P_t+\kappa _{2}P_t^2+\kappa _{3}P_t^3+\kappa _{4}P_t^4) + (1-\pi )\kappa _{1}P_t\). The time paths are of the usual form, as derived in section 4. However, now these time paths depend on the value of the probability \(\pi \) (Figs 11, 12).
The graphs above illustrate the implications of \(\pi \). More specifically, we can see that uncertainty on the form of the climate damage function may lead to miscalculating the SCC, which in turn results in a poorly designed climate policy. Additionally, uncertainty creates a range within which the growth rate of output lies. In other words, policy makers cannot correctly estimate the time path of a critical variable.
6 Conclusions
The paper shows that the choice of a specific climate damage function has a big impact on optimal climate policy and economic growth. We derive the effects of different damage functions on the social cost of carbon and the growth rate of the economy for various model specifications. In our baseline model, increasing convexity of the function raises the social cost of carbon sharply, suggesting more stringent climate policy is needed with growing pollution stock. The theory presented in this paper does not provide a criterion for the selection of the most realistic function but derives the economic consequences when high convexity of climate damage functions is significant. This is strongly suggested by empirical findings and implicitly assumed in the fixed temperature targets of international climate policy. In our calibrated model we find that the long-run growth rate is still positive for highly convex functions provided that we are in a social optimum which in reality is achievable by efficient climate policies.
Assuming a natural decay for pollution stock entails a peak in the social cost of carbon and a U-shaped pattern for optimal growth. Over time, the pollution stock grows less rapidly because of fading resource use as before but is now also reduced by natural forces. Note that the turning point of pollution stock is only reached after a very long time delay so that a long first phase of development is very similar to the baseline case without decay. When we posit that the intertemporal elasticity of consumption substitution is below unity we find that the growth rate of the economy becomes lower, resource use is brought forward, and the social cost of carbon grows less rapidly with damage convexity compared to the baseline case. Uncertainty, on the other hand, affects optimal policy, since the SCC per output and the growth rate of the economy now depend on the probability of a higher order damage function.
Our approach can be extended both in the direction of the assumed growth mechanics and the considered climate impact. It would also be rewarding to extend our analysis on risk and uncertainty. A broader use of the damage functions of this paper in integrated assessment models would potentially give rise to novel policy conclusions. This is left for future research.
Change history
20 February 2018
The original article displays figure errors caused by miscommunication during the proofing stage.
Notes
The effects range from sea level rise, drop in crop yields, and human health to energy demand; in 2017, strong hurricanes have caused immense damage: according to the Economist “Hurricane Harvey already set records as America’s most severe deluge.. The UN reckons that, in the 20 years to 2015, storms and floods caused $1.7trn of destruction; the World Health Organisation estimates that, in real terms, the global cost of hurricane damage is rising by 6% a year. Flood losses in Europe are predicted to increase fivefold by 2050.” Economist (2017, 2 Sept).
These authors present estimations of damage functions parameters for 140 countries and regions and for six climate impacts: sea level rise, variation in crop yields, heat effects on labor productivity, human health, tourism and household energy demand showing the heterogeneity of the different damages.
Technological change is addressed in Acemoglu et al. (2012), the impact of risk in Bretschger and Vinogradova (2016), the spatial distribution in Brock and Xepapadeas (2017), the time distrubution in Gerlagh and Liski (2017) and Bretschger and Karydas (2017) and the North–South aspects in Bretschger and Suphaphiphat (2014).
In a well-known contribution, Pindyck (2013, p. 860) writes: “the models’ descriptions of the impact of climate change are completely ad hoc, with no theoretical or empirical foundation.”
Temperature targets (2 \( {^\circ } \)C resp. 1.5 \( {^\circ } \)C warming) are an important part of the Paris Climate Agreement.
In this paper, we focus on analysing the social planner solution, so this result does not arise.
The quartic damage function has a parallel in physics, such as in the Stefan–Boltzmann law.
Golosov et al. (2014) adopt a slightly different functional form for D by assuming exponential damages but this approximates the other function well.
Even the higher estimate of Hanemann (2008) is not compatible with the 2 \( {^\circ }\)C target of international climate policy which implicitly assumes that damages of temperature rise exceeding 2 \( {^\circ }\)C are very high.
Optimal resource depletion is characterized in the seminal contributions of Dasgupta and Heal (1974) and Stiglitz (1974); endogenous growth with pollution builds on Bovenberg and Smulders (1995), Barbier (1999), Smulders (1999), and Xepapadeas (2005); optimal carbon taxes in a growing economy have been analyzed by Golosov et al. (2014) and Van der Ploeg and Withagen (2014). As a consequence of optimal resource extraction the use of resources decreases over time so that pollution stock accumulates as a concave function of time which affects the optimal solutions in our model.
An early contribution on the effects of stock pollution on utility in an endogenous growth model is Michel and Rotillon (1995).
By construction of the method the precision of the values is high when we are close to the steady state.
The linearized solution of the dynamic system can be found in the Appendix.
For a CIES function (with \(\sigma \) for the relative risk aversion) and damages given by \(D_{t} =\frac{\eta }{S_{0}-S_{t}}P_{t}\)\((P_{0}=0)\) Bretschger and Karydas (2017) calculates growth as \(\hat{Y}=\left[ \alpha (B-\eta \phi )-\rho \right] /\sigma \) which is very similar to the result here.
To complete the analysis, the time paths for the model variables \(u_{t}\) (depletion rate), \(\psi _{t}\) (ratio of shadow prices), as well as for pollution stock \(P_{t}\) and resource stock \(S_{t}\) are shown in figures that are available from the authors upon request.
Additionally, due to lower IES, the polluting resource extraction is shifted towards the present.
For ease of comparison, the same damage functions as in the initial baseline case are being used in this extension.
This result is modified below when we discuss the model extensions.
References
Acemoglu D, Aghion P, Bursztyn L, Hemous D (2012) The environment and directed technical change. Am Econ Rev 102(1):131–166
Ackerman F, Stanton EA (2012) Climate risks and carbon prices: revising the social cost of carbon. Econ E J 6(2012–10):1–25
Amigues, J.-P, Moreaux M (2013) Optimal growth under a climate constraint. LERNA Working Paper, Toulouse School of Economics
Barbier EB (1999) Endogenous growth and natural resources carcity. Environ Resour Econ 14(1):51–74
Bovenberg AL, Smulders S (1995) Environmental quality and pollution-augmenting technological change in a two-sector endogenous growth model. J Public Econ 57:369–391
Bretschger L, Suphaphiphat N (2014) Effective climate policies in a dynamic north–south model. Eur Econ Rev 69:59–77
Bretschger L, Vinogradova A (2016) Escaping Damocles’ Sword: endogenous climate shocks in a growing economy, Working Paper, ETH Zurich
Bretschger L, Karydas C (2017) Optimum growth and carbon policies with lags in the climate system. Environ Resour Econ. https://doi.org/10.1007/s10640-017-0153-4
Brock W, Xepapadeas A (2017) Climate change policy under polar amplification. Eur Econ Rev 94:263–282
Dasgupta PS, Heal GM (1974) The optimal depletion of exhaustible resources. Review of Economic Studies, Symposium, pp 3–28
Dietz S, Stern N (2015) Endogenous growth, convexity of damage and climate risk: how Nordhaus’ framework supports deep cuts in carbon emissions. Econ J 125(583):574–620
Economist (2017) How to cope with floods, Leaders section of the print edition, Sept 2nd
Farmer JD, Hepburn C, Mealy P, Teytelboym A (2015) A third wave in the economics of climate change. Environ Resour Econ 62:329–357
Gerlagh R, Liski M (2017) Carbon prices for the next hundred years. Econ J. https://doi.org/10.1111/ecoj.12436
Golosov M, Hassler J, Krusell P, Tsyvinski A (2014) Optimal taxes on fossil fuel in general equilibrium. Econometrica 82(1):41–88
Grimaud A, Rouge L (2003) Non-renewable resources and growth with vertical innovations: optimum, equilibrium and economic policies. J Environ Econ Manag 45(2):433–453
Hanemann WM (2008) What is the economic cost of climate change? eScholarship. UC Berkeley, Berkeley
IPCC (2014a) Climate change, synthesis report, summary for policymakers, www.ipcc.ch
IPCC (2014b) Summary for policymakers. In: Climate Change 2014: impacts, adaptation, and vulnerability. Contribution of working group II to the fifth assessment report, Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, pp 1–32
Michel P, Rotillon G (1995) Disutility of pollution and endogenous growth. Environ Resour Econ 6:279–300
Moore FC, Diaz DB (2015) Temperature impacts on economic growth warrant stringent mitigation policy. Nat Clim Change 5:127–131
Nordhaus WD (2007) Accompanying notes and documentation on development of DICE-2007 model: notes on DICE-2007.v8 of September 21, 2007 New Haven. Yale University, CT
Nordhaus WD, Boyer J (2000) Warming the world. MIT Press, Cambridge
Pindyck RS (2013) Climate change policy: What do the models tell us? J Econ Lit 51(3):860–872
Rebelo S (1991) Long-run policy analysis and long-run growth. J Polit Econ 99(3):500–521
Revesz RL et al (2014) Global warming: improve economic models of climate change. Nature 508:173–175
Roson R, Sartori M (2016) Estimation of climate change damage functions for 140 regions in the GTAP9 database, IEFE Working Paper Series Working Paper n. 86, Bocconi University
Smulders S (1999) Endogenous growth theory and the environment. In: van den Bergh JCJM (ed) Handbook of environmental and resource economics. Edward Elgar, Cheltenham
Smulders S, de Nooij M (2003) The impact of energy conservation on technology and economic growth. Resour Energy Econ 25(1):59–79
Stern N (2013) The structure of economic modeling of the potential impacts of climate change: grafting gross underestimation of risk onto already narrow science models. J Econ Lit 51:838–859
Stiglitz JE (1974) Growth with exhaustible natural resources: efficient and optimal growth paths. Rev Econ Stud 41:123–137
Van den Bijgaart I, Gerlagh R, Liski M (2016) A simple formula for the social cost of carbon. J Environ Econ Manag 77:75–94
Van der Ploeg F, Withagen C (2014) Growth, renewables and the optimal carbon tax. Int Econ Rev 55(1):283–311
Weitzman ML (2010a) What is the damages function for global warming and what difference might it make? Clim Change Econ 1(1):57–69
Weitzman ML (2010b) GHG targets as insurance against catastrophic climate damages. National Bureau of Economic Research, Cambridge
Xepapadeas A (2005) Economic growth and the environment. In: Mäler KG, Vincent JR (eds) Handbook of environmental economics, vol 3. Elsevier, Amsterdam, pp 1219–1271
Acknowledgements
We thank Christos Karydas, Andreas Schaefer and Aryestis Vlahakis, as well as an anonymous referee for valuable comments.
Author information
Authors and Affiliations
Corresponding author
Additional information
The original article displays figure errors caused by miscommunication during the proofing stage. The original article has been corrected.
Appendix
Appendix
1.1 Appendix 1: Baseline Model
The first-order conditions of the maximization problem given in Sect. 2.3 read
and the transversality conditions are
1.2 Appendix 2: Capital Share
To derive optimal capital allocation we use (33) and (31) to write \(-\,\hat{\epsilon }_{t}=\rho -B\epsilon _{t}\Leftrightarrow \dot{\epsilon } _{t}=B\epsilon _{t}^{2}-\rho \epsilon _{t}\). This differential equation is of the Riccati form, hence its solution is given by \(\epsilon _{t}=\dfrac{\rho C_{1}e^{-\rho t}}{BC_{1}e^{-\rho t}+B\rho C_{2}}\). Using the transversality condition (36) results in
and therefore
which says that the share of capital used in the final goods sector instantaneously jumps to its steady state value. Put differently, capital allocation to the two sectors is determined optimally in the beginning and does not change over time.Footnote 20 From (31) and (39) we also obtain \(\mu _{Kt}K_{t}=\dfrac{\alpha }{\rho }\equiv \mu _{K}K\) which says that capital stock multiplied with its shadow price is a constant.
1.3 Appendix 3: Depletion Rate
Starting from the transversality condition (38) and given that for product \(\mu _{St}S_{t}e^{-\rho t}\) is non-negative and declining over time, using (35) we have \(\hat{\mu }_{St}+\hat{S}_{t}-\rho<0\Rightarrow \hat{S}_{t}<0\Rightarrow -\,u_{t}<0\Rightarrow \lim _{t\rightarrow \infty }u_{t}>0\). Due to the Cobb–Douglas form of the production function and logarithmic utility resource extraction never ends, i.e. it only stops at infinite time, i.e. \(\lim _{t\rightarrow \infty }S_{t}=0\) where \(\hat{S}_{\infty }\) is a negative constant. In order for consumption to be asymptotically constant in infinite time, we need \(\lim _{t\rightarrow \infty }\hat{u}_{t}\le 0\) and since \(u_{t}\) cannot be negative, we conclude that \(\lim _{t\rightarrow \infty }\hat{u}_{t}=0\). As a consequence, the growth rate of resource use in infinite time, \(\hat{R}_{\infty }\), needs to be constant and non-positive.
1.4 Appendix 4: Solution of the Linearized System
Following the standard linearization procedure, the solution of the dynamic system of Eqs. (11)–(15) can be approximated close to the long-run steady state by
1.5 Appendix 5: Pollution Decay Model
The long-run values of the variables with \(\theta >0\) are
1.6 Appendix 6: Non-logarithmic Utility
The first order conditions of the maximization problem given in Sect. 5.2 read
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Bretschger, L., Pattakou, A. As Bad as it Gets: How Climate Damage Functions Affect Growth and the Social Cost of Carbon. Environ Resource Econ 72, 5–26 (2019). https://doi.org/10.1007/s10640-018-0219-y
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10640-018-0219-y