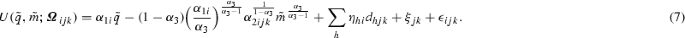Abstract
The reformed U.S. Corporate Average Fuel Economy (CAFE) standards have not only tightened the efficiency levels to be achieved by automakers, but also made substantial changes to the regulatory design and structure by introducing three new policy instruments (footprint-based targeting, intra-firm transferring of fuel economy credits across vehicle categories, and inter-firm trading of credits). While there are a number of economics studies on tightening CAFE standards, little attention has been paid to the design aspects. This paper uses policy simulation to evaluate the new policy instruments. First, I model and estimate vehicle purchase and utilization decisions by American households. Based on estimation results, I simulate the effects of four counterfactual CAFE policies with or without the three instruments. Simulation results suggest (1) footprint-based targeting has little impact at the aggregate market level, while at the individual automaker level it favors firms selling relatively large vehicles; (2) allowing intra-firm credit transferring (but not inter-firm credit trading) cuts aggregate gasoline consumption by 0.1–0.3%; and that (3) inter-firm credit trading significantly lowers the aggregate compliance costs (by $110–$140 million), and thus achieves the highest social welfare among the simulated policies.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Corporate Average Fuel Economy (CAFE) standards are a set of U.S. federal regulations that require each automaker to achieve a certain level of fleet average fuel economy. The standards have played a key role in curbing automotive fuel consumption. Recently, CAFE standards have been radically reformed in terms of stringency and structure. The standards for model years (MYs) 2012–2016 improved the combined fleet average fuel economy of new passenger cars (PCs) and new light-duty trucks (LDTs) to 32.5 miles per gallon (mpg) in MY 2016 (based on estimated sales data), compared to 29.3 mpg in MY 2010. The standards for MYs 2017–2021 are projected to achieve 40.3–41.0 mpg in MY 2021, and the provisional standards for MYs 2022–2025 aim at 48.7–49.7 mpg in MY 2025.Footnote 1
In addition to increased stringency, CAFE standards have also undergone significant structural and design changes. From the 1970s until recently, CAFE standards required an automaker’s average fuel economy in each vehicle category to meet a specified level, which is common to all automakers.Footnote 2 The new CAFE standards have completely reformed this structure. The three most important instruments introduced are footprint-based targeting, intra-firm credit transferring, and inter-firm credit trading.
Footprint-based targeting makes an automaker’s standards dependent on the size (footprint, i.e., the area enclosed by the points at which the tires touch the ground) of the vehicles it sells. Roughly speaking, the smaller the average footprint of a manufacturer’s fleet in a category, the better category-average fuel economy it is required to achieve. Relative to the conventional standards that are independent of vehicle size, footprint-based standards aim to discourage automakers from downsizing vehicles to meet CAFE standards: vehicle downsizing is the easiest way to improve fuel economy, but smaller vehicles are considered to involve higher fatality risks in case of traffic accidents. Footprint-based targets may favor automakers who tend to produce large vehicles and thus face less stringent standards under the new approach.
The other two instruments intend to provide flexibility in how to meet the standards, and thus reduce the overall compliance costs for automakers. Intra-firm credit transferring allows an automaker to over-comply in a category and earn credits, then use the credits to offset under-compliance in another category. With inter-firm credit trading, an automaker can sell extra credits from over-compliance to other automakers; conversely, one can buy credits from other automakers to offset under-compliance. The three new instruments have structurally changed CAFE standards, and can have various impacts on the vehicle market and gasoline consumption.
A number of previous studies use policy simulation to analyze how CAFE standards and other policies affect consumers, producers and gasoline consumption. For example, Goldberg (1998), Kleit (2004), Klier and Linn (2012), Jacobsen (2013) and Whitefoot et al. (2012) examine tightening of CAFE standards. Bento et al. (2009) look at an increase in gasoline taxes. Austin and Dinan (2005) compare the effects of tightening CAFE standards and increasing gasoline taxes.
This paper also simulates CAFE standards, but centers around a different aspect than most of the above-mentioned studies. Specifically, I focus on the design of CAFE standards, rather than their stringency, by simulating counterfactual policies that differ in structure, but not in stringency. These counterfactual policies are with or without the three instruments above.
Some of the previous studies include analysis on the design of CAFE standards in addition to tightening. Coleman and Harrington (2010) and Whitefoot et al. (2012) look into footprint-based targets and intra-firm credit transferring between categories, but not inter-firm credit trading. Austin and Dinan (2005) simulate inter-firm credit trading, but not footprint-based targets or intra-firm credit transferring.Footnote 3
This paper adds a few distinctive features to the previous studies on the design of CAFE standards. First, I consider all the three new instruments of the reformed CAFE standards, including the case in which they are in effect at once as in the actual reformed standards.
Second, I set parameters of counterfactual rules, which determine fuel economy standards for each automaker, in such a way that the market average fuel economy in simulated market equilibrium is essentially the same across all policies. This ensures that different policies are almost at the same level of stringency as measured by market average fuel economy. The difference between any counterfactual policies is less than 0.1% in this paper, while it is in some cases larger than 1% in Coleman and Harrington (2010), for example. As we want to evaluate the effectiveness of different policy instruments in terms of social welfare (automakers’ profits \(+\) consumer surplus − fuel use externalities), it is important that counterfactual policies featuring these instruments are at the same level of stringency. Otherwise, it is unclear whether differences in simulation outcomes are attributable to differences in design or stringency.
Third, I make use of a variant of the recent approach developed by Bento et al. (2009) that simultaneously estimates consumers’ vehicle purchase and utilization decisions. This approach can analyze the two connected decisions in a unified framework that is consistent with economic theory. Previous studies on the structure of CAFE standards model vehicle choice decisions only. Because the value of fuel economy to consumers depends on how much the vehicle is driven, incorporating a model of VMT (vehicle miles traveled) demand is important for evaluating policies relating to fuel economy and gasoline consumption.
The simulations carried out in the paper provide a number of interesting implications about the three instruments, as compared to the traditional structure that sets identical standards for all automakers, and does not allow intra-firm transferring across categories or inter-firm trading. First, introducing footprint-based targets has only a small impact on market-level outcomes such as consumer surplus and aggregate gasoline consumption. As for the profits of individual automakers, footprint-based targets relatively benefit those firms that tend to sell large vehicles and thus get their standards relaxed, compared to those selling small vehicles.
Second, allowing intra-firm credit transferring (but not inter-firm trading) is effective in reducing aggregate gasoline consumption, relative to the traditional structure. This policy induces automakers constrained by CAFE standards to make LDTs more fuel efficient but PCs less efficient, and then transfer credits across the two categories to comply. Because LDTs are typically driven for longer distances than PCs (National Highway Traffic Safety Administration, 2006), this leads to a reduction in aggregate gasoline use (by 0.1–0.3%).
Third, introducing inter-firm credit trading lowers the aggregate compliance costs to achieve a given level of market average fuel economy by $110–$140 million in comparison with the traditional structure. Inter-firm trading shifts the role of improving fuel economy at additional production costs to automakers that can do so relatively cheaply. With the compliance cost reduction, inter-firm credit trading increases social welfare: the policy with inter-firm trading gives the highest social welfare among the counterfactual policies considered.
The rest of the paper is organized as follows. Section 2 describes the data sets used in the study. Section 3 considers the demand side of the new vehicle market, and estimates a model of consumers’ vehicle and VMT choices. Based on the results of Sect. 3, Sect. 4 simulates four counterfactual CAFE policies to evaluate and compare the effects of footprint-based targeting, credit transferring, and credit trading. Section 5 concludes.
2 Data
This paper uses data from various sources. First, the 2001 National Household Travel Survey (NHTS), a national survey conducted by the Department of Transportation between mid-2001 and mid-2002, provides household-level data on the name and estimated annual VMT of each vehicle owned, as well as various household characteristics. To analyze the purchase and utilization of new vehicles (as opposed to used ones), I focus on households owning a model year 2001 vehicle, which is most likely purchased new. I construct gasoline prices (inclusive of federal and state fuel taxes) for each household with the State Energy Data System of the Energy Information Administration. Data on vehicle models (such as sales, price, fuel economy, horsepower, weight, and footprint) are obtained from several sources: Wards Automotive Yearbook, the Environmental Protection Agency’s “Fuel Economy Test Car List Data”, MSN Autos (http://www.msn.com/en-us/autos), and manufacturers’ automotive fuel economy reports submitted to the National Highway Traffic Safety Administration (available at https://www.regulations.gov).
A particular innovation of this paper is to use U.S. market sales data specific to vehicle models. Generally, U.S. market sales data is available at the nameplate level (e.g., Chevrolet Malibu, Ford Explorer, and Toyota Camry) at best, while each nameplate usually offers multiple vehicle models, which typically (and often significantly) differ in powertrain specifications (e.g., Toyota Camry CE and Toyota Camry LE). Manufacturers’ automotive fuel economy reports, which to my knowledge have not been used in the related literature, contain the U.S. market sales information at the more disaggregate, vehicle model level. With the detailed data, the following estimation and simulation can distinguish vehicle models under the same nameplate, and thus better approximate the choices made by actual consumers and producers. On the other hand, the NHTS identifies vehicles only at the nameplate level, so model-level data on household vehicle choice is unavailable. Despite this situation, an estimation procedure is contrived that makes analysis and simulation at the model level possible (see Online Appendix A for details).
Fuel economy values contained in the manufacturers’ reports are unadjusted values used by regulatory agencies. The U.S. Environmental Protection Agency downgrades fuel economy ratings seen by consumers (roughly by 15%) to account for actual driving conditions. Throughout the paper, I take account of this difference by using adjusted fuel economy in dealing with the consumer side (e.g., calculating gasoline spending), and unadjusted fuel economy in considering CAFE regulations.
Table 1 reports the descriptive statistics of the sample of vehicles and households used in the study: 457 MY 2001 vehicle models under 185 nameplates, and 5884 households with MY 2001 vehicles. Panel (a) shows that LDTs (i.e., vans, SUVs, and pickup trucks) are on average more expensive, less fuel efficient, larger, heavier, and more powerful than PCs. In Panel (b), LDTs are on average driven for longer distances than PCs. LDT buyers tend to be larger in household size, live in less populated areas, and own more vehicles than PC buyers. Additionally, van and SUV buyers on average earn more than PC and pickup truck buyers.
Relatively stable gasoline prices prior to 2001 make MY 2001 vehicles a suitable sample for our framework. Like several of the previous studies above, the paper is based on an equilibrium model in which manufacturers set fuel economy of vehicles in response to consumers’ demand (willingness to pay) for it. The price of gasoline is a crucial factor affecting such demand: the higher the price, the more consumers are willing to pay for better fuel economy. In practice, consumers’ demand for fuel economy can change quickly with gasoline prices, while it is hard for automakers to respond to such demand changes by frequently adjusting fuel economy of their models. Thus, gasoline price changes disturb the “market” for fuel economy in such a way that demand and supply do not balance as demand adjusts much more quickly than supply. Therefore, applying the equilibrium model to a situation where gasoline prices are changing significantly may lead to inaccurate results. Gasoline prices in the U.S. remained relatively stable since the 1990s until around 2002, and then started to increase sharply and became volatile, especially around 2008 (Fig. 1).Footnote 4 For this reason, I analyze vehicle sales and utilization in 2001, as the later NHTS from mid-2008 to mid-2009 is characterized by a period of extremely volatile gasoline prices.
Simulations based on the 2001 data can provide useful insights for understanding and predicting consumer and producer behavior under more recent market conditions as well. Table 2 lists selected firms’ regulatory standards, average fuel economy values, and total sales in the U.S. market in MYs 2001 and 2014. The firms in the table are the six largest automakers in the U.S. market in 2001, and continue to be in 2014. In both years, the U.S. Big Three are usually less fuel efficient and more constrained by CAFE standards than the Japanese automakers, a situation which is reproduced in my simulations.Footnote 5 Additionally, a robustness check suggests that the simulation model yields reasonable predictions even under much higher gasoline prices as we have currently. My simulations will thus offer helpful policy implications for analyzing the current market and CAFE standards.
3 Estimating the Demand for Vehicles and Driving
This section considers the demand side of the new vehicle market. I set up and estimate a model of household vehicle and VMT choices, and discuss the results. In essence, the following is a discrete-continuous model of consumer demand pioneered by Dubin and McFadden (1984). Mannering and Winston (1985) and West (2004) apply the Dubin–McFadden model to the vehicle market to analyze the discrete choice of vehicle purchase and the continuous choice of VMT. In place of the sequential estimation approach of Dubin and McFadden (1984), I employ a variant of the more recent approach developed by Bento et al. (2009) that simultaneously estimates the two choices in a full information maximum likelihood framework. Other papers with a similar approach include Gillingham (2011) and Spiller et al. (2016).
3.1 Econometric Model
Suppose that household i is choosing a new vehicle to purchase. Given a utility function and vehicles available in the market, the household predicts the utility level attained by owning each vehicle. Comparing all the options, it buys what is expected to give the highest utility. In calculating the utility from owning vehicle model jk (model k of nameplate j), household i considers the following utility maximization problem.
where \(\tilde{m}\) is vehicle miles traveled (VMT); \(\tilde{q}\) is the consumption of the numéraire good (the composite of all goods and services other than VMT); \(r_{ijk}\) is the price of household i driving model jk; \(y_i-p_{jk}\) is household i’s budget available after buying model jk (\(y_i\) is household i’s budget before vehicle purchase and \(p_{jk}\) is model jk’s price); and \(\varvec{\varOmega }_{ijk}\) is a vector of variables that are predetermined for this problem, but shift the utility function, such as household characteristics and vehicle attributes. \(V(r_{ijk},y_i-p_{jk};\varvec{\varOmega }_{ijk})\) is the indirect utility function resulting from the maximization problem, which is interpreted as the maximum achievable utility if household i buys model jk. For the sake of econometric tractability, this problem explicitly considers only one period, while vehicles are likely used over years. Section 3.2 below discusses how to incorporate the multi-period nature of vehicle ownership into this framework.
I parameterize the indirect utility function \(V(r_{ijk},y_i-p_{jk};\varvec{\varOmega }_{ijk})\) as follows.
where \(\epsilon _{ijk}\) is an i.i.d. error drawn from the standard type I extreme value distribution for each i-jk combination; \(d_{hjk}\) is a dummy variable that takes 1 if model jk is of vehicle type h, and 0 otherwise;Footnote 6\(\xi _{jk}\) is model jk’s fixed effect; \(\pmb {x}_{i}\) is a vector of household i’s (observed) characteristics; \(\pmb {z}_{jk}\) is a vector of model jk’s attributes (including dummy variables for vehicle types); \(\delta _{1i}\), \(\delta _{2i}\), and \(\eta _{hi}\)’s represent household i’s unobserved characteristics and preferences, which are randomly and independently drawn from respective normal distributions.Footnote 7 Under this framework, the probability that household i buys model jk is
where \(\tilde{V}_{ijk}\) is as defined in (3)–(6), and summation in the denominator is over all new vehicle models available in the market.Footnote 8
Applying Roy’s identity to the indirect utility function and taking the logarithm of both sides yields
where \(\tilde{m}_{ijk}\) is VMT planned by household i, conditional on the purchase of model jk. The logarithm of planned VMT is expressed as a linear function of household characteristics, vehicle attributes and (the logarithm of) the price of driving. Particularly, note that \(\alpha _{3}-1\) is interpreted as the elasticity of VMT with respect to the price of driving, conditional on vehicle choice.
In practice, the household’s planned VMT is unobservable to the econometrician, who observes only the household’s VMT reported in the NHTS. Therefore, in order to work with observed VMT, I add to (9) an (independently, identically, and normally distributed) error term \(\mu _{ijk}\):
where \(m_{ijk}\) is observed VMT for household i that has purchased model jk. The error \(\mu _{ijk}\) consists of unobserved (by the econometrician) factors that affect reported VMT, but not planned VMT or vehicle choice. For example, \(\mu _{ijk}\) may include unpredicted changes in the household’s driving demand that occur after vehicle purchase.
Parameters and variables that appear in both (2)–(6) and (10) affect both vehicle and VMT choices in a way that is consistent with Roy’s identity. In other words, they introduce correlation between the two choices, where, for example, a household with higher demand for driving is likely to buy a more fuel efficient vehicle, holding other vehicle attributes fixed. \(\pmb {x}_i\) and \(\pmb {z}_{jk}\) are, respectively, observed household characteristics and vehicle attributes that affect both choices. On the other hand, \(\delta _{1i}\) and \(\delta _{2i}\) are unobserved (by the econometrician) household characteristics affecting both choices. For example, \(\delta _{1i}\) and \(\delta _{2i}\) may include whether or not household i plans to use the vehicle for commuting.
The remaining terms \(\xi _{jk}\), \(\sum _h \eta _{hi} d_{hjk}\), and \(\epsilon _{ijk}\) all appear in (2)–(6), but not in the VMT equation (10). Thus, they affect the discrete vehicle choice, but not the continuous VMT choice. Model fixed effect \(\xi _{jk}\) represents the part of the utility from model jk that does not vary across households. Including model fixed effects is important because they allow us to equate a vehicle model’s econometrically predicted market share with its observed counterpart by applying the method of Berry et al. (1995), making estimation and simulation results more realistic. The random parameter \(\eta _{hi}\), which varies over i but not over jk, represents i’s unobserved preferences on vehicle type h that is common to all vehicles of type h. Thus, \(\sum _h \eta _{hi} d_{hjk}\) makes the household’s unobserved preferences correlated between two vehicles of the same type, but uncorrelated between two vehicles of distinct types. With these terms, the econometric model is analogous to a nested logit model (Train, 2009). Lastly, \(\epsilon _{ijk}\) is the unobserved portion of utility that varies over both i and jk.
Conditional on household i buying model jk and planning to drive it \(\tilde{m}_{ijk}\) miles, (10) implies that the probability that we observe household i drive the vehicle \(m_{ijk}\) miles is
where \(f\bigl [\cdot \bigr ]\) is the probability density function for the normally distributed error \(\mu _{ijk}\).
Then, the probability that household i buys model jk and we observe the vehicle driven for \(m_{ijk}\) miles is
where \(\text {Pr}_i(jk)\) and \(\text {Pr}_i(m_{ijk}|jk)\) are as defined in (8) and (11), respectively.
3.2 Automobiles as Durable Goods
In practice, automobiles are durable goods that consumers usually plan to use over several years. Because fuel efficiency reduces fuel costs over the years of vehicle ownership, its value at the time of vehicle purchase depends on the consumer’s expectation about, for example, the length of ownership, and the VMT schedule and gasoline prices during ownership. In the utility maximization problem (1) and the following argument so far, however, I have considered only one period to make the model simple.
The multi-period nature of vehicle ownership can be reflected into the above framework through the following interpretation. First, \(\tilde{q}\) in (1) is considered the present value of the sum of spending on the numéraire good (the composite of all goods and services other than VMT) over multiple years, and \(y_i-p_{jk}\) is interpreted similarly. As for fuel costs \(r_{ijk}\tilde{m}\) in (1), if we consider multiple periods, the present value of total fuel costs over the ownership of the vehicle is calculated as
where \(T(\ge 1)\) is the length (in years) of the household’s planning horizon, \(r_{ijkt}\) and \(\tilde{m}_t\) are, respectively, the anticipated price of driving and planned VMT in year t, and \(d_f\) is a discount factor for future fuel costs.
Assuming that the household expects the price of driving to change over years based on \(r_{ijkt}=d_r^{t-1} r_{ijk1}\) (due to fuel price changes or fuel efficiency deterioration over time), and also that VMT changes based on \(\tilde{m}_t=d_m^{t-1} \tilde{m}_1\), we can write the present value of total fuel costs anticipated at the time of vehicle purchase as
where \(K \equiv \frac{1-(d_f d_r d_m)^{T}}{1-d_f d_r d_m}\) if \(d_f d_r d_m \ne 1\), and \(K \equiv T\) if \(d_f d_r d_m = 1\). That is, the constant K is the ratio of the present value of anticipated total fuel costs over the ownership of the vehicle to anticipated fuel costs in the first year.Footnote 9 Note that K increases with T, \(\frac{\partial K}{\partial d_f} \ge 0\), \(\frac{\partial K}{\partial d_r} \ge 0\), and \(\frac{\partial K}{\partial d_m} \ge 0\).Footnote 10
Thus, we can take account of the durable good nature of automobiles through the following interpretation of \(r_{ijk}\) and \(\tilde{m}\) in (1):
Equation (14) means that the present value of anticipated fuel cost savings from a marginal improvement in fuel efficiency (gallons per 100 miles) is given by the product of K, first year VMT \(\tilde{m}_{1}\) (measured in 100 miles), and the price of gasoline. So the larger the multiplier K (i.e., the larger T, \(d_f\), \(d_r\), or \(d_m\)), the more valuable a fuel efficiency improvement, and thus the more consumers are willing to pay for such an improvement.Footnote 11 Through this mechanism, K is concerned with the elasticity of vehicle demand with respect to fuel economy.
In addition, responding to the larger (marginal) willingness to pay, in equilibrium manufactures will provide greater fuel efficiency improvements by using more advanced (thus expensive) technologies. That is, the larger the multiplier K, the higher the equilibrium marginal cost of further improving fuel economy. For this reason, K relates to the supply side of fuel economy as well.
The following estimation will use first year VMT and K as defined below. The 2001 NHTS includes (an estimate of) actual yearly VMT of each surveyed vehicle. For a model year 2001 vehicle, we interpret that the survey reports the first year’s observed VMT (\(m_{ijk1}\)). K is unobservable in the data, so I instead choose a few reasonable values of K and report results for each case.Footnote 12 More specifically, I set \(K=1, 4\), or 7, considering that the average length of new-vehicle ownership is about 4 years in 2001, and 6.5 years in 2015.Footnote 13
With the above argument, I replace \(m_{ijk}\) and \(r_{ijk}\) in (10) with \(Km_{ijk1}\) and \(r_{ijk1}\), respectively:
Therefore, (11) and (12) become
In (19), the discrete vehicle choice part \(\text {Pr}_i(jk)\) is defined by (8), and the continuous VMT choice part \(\text {Pr}_i(Km_{ijk1}|jk)\) is defined by (18).
A log-likelihood function is set up based on (19), and parameters are estimated with the maximum simulated likelihood (MSL) estimator, with vehicle model fixed effects estimated based on the contraction mapping of Berry et al. (1995) by equating the predicted and actual market shares of each vehicle model. The specific estimation procedure is discussed in Online Appendix A.
3.3 Estimation Results
Tables 3 and 4 summarize the results of the maximum simulated likelihood estimation. Each column corresponds to a specific value of K, the multiplier for annual VMT, as reported in the last row. Household characteristics included are the logarithm of the following variables: household size, population density, the number of vehicles owned, and household annual income. As for annual income, I fit a linear spline with two knots (\(\text {knot}_1=\log (46{,}715)\) and \(\text {knot}_2=\log (73{,}580)\)).Footnote 14 Vehicle attributes included are dummy variables for vans, SUVs, and pickup trucks (PCs as the base type), (the logarithm of) footprint, and (the logarithm of) horsepower per weight, which is a measure of acceleration capacity.Footnote 15
First, I discuss the implications of the estimates in terms of the discrete vehicle choice (Table 3). Note that with the utility function in consideration, \(\alpha _{1i}\) is the marginal utility of money, and each element of the vector \(\varvec{\beta }_{1}\) is the elasticity of \(\alpha _{1i}\) with respect to the corresponding household characteristic (household size, population density, number of vehicles owned, or household income). A negative element of \(\varvec{\beta }_{1}\) means that the marginal utility of money decreases with the corresponding characteristic. That is, the larger the value of the characteristic, the less sensitive the household is to vehicle prices and the more likely it purchases an expensive vehicle. A positive element of \(\varvec{\beta }_{1}\) indicates the opposite. Table 3 suggests that the marginal utility of money decreases with income, and does so faster (in terms of elasticity) for households with higher income.Footnote 16 Also, the marginal utility of money increases with population density. Other things equal, households with low income (or in densely populated areas) are more sensitive to vehicle prices and thus more likely to buy inexpensive vehicles than households with high income (or in sparsely populated areas, respectively).
A positive element of \(\varvec{\beta }_2\) means that the negative effect of the price of driving (\(r_{ijk}\)) on the utility from (and the probability of) choosing model jk gets stronger with the corresponding household characteristic. That is, a household with a larger value of the characteristic is more sensitive to \(r_{ijk}\) (and thus to fuel economy and the price of gasoline). A negative element indicates the opposite. The estimates suggest that, other things equal, households of larger size or in a more populated area are more sensitive to \(r_{ijk}\), and households owning more vehicles or earning higher income are less sensitive to it. In particular, the negative coefficient on log(# of vehicles owned) implies that as a household owns more vehicles, the possibility of substitution among them makes \(r_{ijk}\) a less important factor in its decision to purchase another vehicle.Footnote 17
Next, we turn to the VMT demand equation (17). The difference \(\varvec{\beta }_{2}-\varvec{\beta }_{1}\) constitutes the coefficients of household characteristics \(\pmb {x}_{i}\). Table 4 reports the point estimate and standard error of each element of \(\varvec{\beta }_{2}-\varvec{\beta }_{1}\). Other things equal, households of larger size, in a less populated area, with fewer vehicles owned, or with higher income plan to drive a newly-purchased vehicle for longer distance. All these would be reasonable relationships between the listed household characteristics and VMT demand.
In Table 4, estimates on \(\varvec{\gamma }_2\) suggest that, other things equal, consumers expect to drive SUVs and pickup trucks (in comparison to PCs), or larger vehicles (within each vehicle type) for longer distances.Footnote 18 In terms of Table 3 [that is, the indirect utility function (2)–(6)], this means that if model jk is an SUV or pickup truck, or it is relatively large within its type, then household i’s indirect utility conditional on buying model jk (\(V_{ijk}\)) is more sensitive to the price of driving (\(r_{ijk}\)), as it is expected to be used more intensively.
In Eq. (17), \(\alpha _3-1\) is the elasticity of VMT with respect to \(r_{ijk}\), conditional on vehicle choice.Footnote 19 In Table 4, the estimates of \(\alpha _3-1\) from the three different specifications range from − 0.17 to − 0.27.Footnote 20 This range is on the whole consistent with previous studies. Bento et al. (2009) find the long-run VMT elasticities for different classes of new vehicles to be around − 0.2 to − 0.3. Reviewing the literature, Small and Van Dender (2007) also regard the range of − 0.2 to − 0.3 as compatible with previous studies.Footnote 21
We now look at the overall performance of the econometric model. First, using parameter estimates of columns [1]–[3] of Table 3, Table 5 shows predicted choice probabilities of two selected vehicle models (the economical Toyota Corolla 1.8 L engine model and the luxurious Cadillac DeVille 4.6 L engine model) for three hypothetical households. Each household’s annual income is set at the 5th, 50th, or 95th percentile of the sample, and other household characteristics are set at the sample averages. Table 5 confirms a reasonable tendency that low income households prefer small, cheap vehicles, while wealthy households favor large, luxurious vehicles.
Based on Table 3, Table 6 reports the mean and standard deviation of the elasticity of a model’s sales with respect to its own price (\(p_{jk}\)) or fuel economy (mpg), which is obtained by aggregating (over households) the change in each household’s probability of choosing the model. The average elasticity with respect to the vehicle price \(p_{jk}\) is estimated at − 1.9 to − 2.3, which is similar in magnitude to the findings by other studies that use micro cross-sectional data (e.g., Berry et al. 2004; Bento et al. 2009; Train and Winston 2007). The average elasticity with respect to fuel economy (mpg) is estimated at 0.1 to 0.5. The larger K, the more valuable consumers consider fuel economy, hence the larger the impact of a fuel economy change on vehicle sales. We also notice that, for all of the three cases, the fuel economy elasticity is much smaller (in magnitude) than the vehicle price elasticity.
4 Simulating the Impacts of Counterfactual CAFE Standards
4.1 Actual CAFE Standards in Model Year 2001
First, I briefly discuss the CAFE standards for MY 2001, which serve as a baseline for the following counterfactual policies. Under MY 2001 CAFE standards, an automaker’s sales-weighted harmonic average mpg in each vehicle category (domestic PCs, import PCs, or LDTs) needs to be equal to or above the corresponding standard (27.5 mpg for domestic and import PCs, and 20.5 for LDTs). If a firm does not comply in a category, it must pay a fine (civil penalty) of $5 for each 0.1 mpg below the standard, for each vehicle sold in the category.
There are three types of responses from automakers to CAFE standards. First, the average mpg is consistently above the standard, and the firm is in compliance (e.g., Toyota in all categories). Second, the average mpg is consistently below the standard over years, as the firm chooses to pay the fines rather than meet the standard (e.g., BMW and Porsche for import PCs). In the third case, the average mpg is equal to or above the standard for some years and below for other years, and the firm uses intertemporal banking and borrowing to comply and avoid the fines (e.g., Ford’s LDTs).Footnote 22 Most of the automakers with non-trivial market shares comply with the standards (the first and third cases above). Some European automakers that concentrate on luxury, high performance vehicles, such as BMW and Porsche, consistently violate the standards and pay the fines (the second case above).Footnote 23
4.2 Overview of the Simulation
Based on the above analysis of the demand side, I explore the effectiveness of different features of CAFE standards by simulating a new-vehicle market under counterfactual regulations. Specifically, I evaluate the impacts of three policy instruments that were recently introduced to CAFE standards:
-
Instrument A: “footprint-based” functions that assign target values based on vehicle size;
-
Instrument B: intra-firm transferring of fuel efficiency credits across vehicle categories;
-
Instrument C: inter-firm trading of fuel efficiency credits.Footnote 24
Combining these instruments, I construct four counterfactual policies to be simulated. These policies are summarized as follows.
-
Policy 1 mirrors the actual CAFE standards for MY 2001.
-
Policy 2 replaces Policy 1’s “flat” functions with Instrument A.
-
Policy 3 adds Instrument B to Policy 2.
-
Policy 4 adds Instrument C to Policy 3, mirroring the actual CAFE standards for MYs 2012–2016.Footnote 25
I set parameter values of these counterfactual policies so that they will essentially be at the same level of stringency as measured by the market average fuel economy in equilibrium (approximately 24.39 mpg, which is about equal to the actual average in 2001). This allows us to compare the effects of the three instruments without being confounded by stringency differences as in previous studies.
The overall framework of the simulation is as follows. I find a Nash equilibrium in which each automaker sets the price and fuel economy of its models to maximize profits, given a counterfactual policy, the other attributes (e.g., size and power) of its models, and the price and all the attributes of other automakers’ models. The optimization problem represents the firm’s consideration as to how the sales and production cost of its models will change according to its price and fuel economy choices. Vehicle sales are determined by the demand side estimated above. The production cost changes with fuel economy: improving efficiency incurs additional production costs. As in previous studies (e.g., Bento et al. 2009; Coleman and Harrington 2010; Klier and Linn 2012), the incremental cost of improvement for each model is also calculated based on the demand side estimates.Footnote 26 I obtain various measures (such as fuel economy, profits, consumer surplus, fuel savings) in equilibrium, and then compare the four policies in terms of these measures to evaluate the impacts of the three policy instruments. The next subsection explains the four policies in detail.
4.3 Counterfactual CAFE Standards
The CAFE constraint for category g is expressed as
where summation is over all vehicle models in category g that are produced by automaker n (denoted by \(\mathcal {J}^g_{n}\)); \(\bar{e}_{jk}\) and \(e_{jk}\) are the target and actual fuel efficiency (in gallons per 100 miles, or gphm) of model jk, respectively; and \(s_{jk}\) is the U.S. market sales of jk. Note that in (20) and the following CAFE-constrained profit maximization problems, fuel efficiency is expressed in terms of gphm rather than mpg because this significantly simplifies a producer’s problem by making it linear in fuel efficiency, a choice variable. Dividing (20) by the producer’s total sales in the category (i.e., \(\sum _{{jk}\in \mathcal {J}^g_{n}} s_{jk}\)) and rearranging terms, we see that the constraint (20) is equivalent to the requirement that the sales-weighted arithmetic average of \(e_{jk}\)’s be less than or equal to the sales-weighted arithmetic average of \(\bar{e}_{jk}\)’s.Footnote 27 In other words, the latter average is the regulatory standard for automaker n in category g.
The constraint can be interpreted as follows. If model jk of category g is more fuel efficient than its target value (i.e., \(\bar{e}_{jk}>e_{jk}\)), then for each unit of model jk sold, automaker n earns a positive entry (“credit”) of \(\bar{e}_{jk}-e_{jk}\) in category g. On the other hand, if model jk is less fuel efficient than its target value (i.e., \(\bar{e}_{jk}<e_{jk}\)), then for each unit of model jk sold, it earns a negative entry (“debit”) of \(\bar{e}_{jk}-e_{jk}\) in category g. Automaker n meets the standard for category g if the total balance is non-negative after summing all entries in the category.
To focus on primary aspects of the regulations (namely, Instruments A–C above), counterfactual CAFE standards below ignore or simplify some features of actual CAFE standards. First, I do not distinguish between domestic and import PCs, so all PCs are grouped into a single category. I also do not consider banking and borrowing of credits over years, or bonus credits for selling flex-fuel vehicles.
4.3.1 Policy 1: Flat Targets/No Transferring/No Trading
Policy 1 mirrors the actual CAFE standards for MY 2001. Automakers face two CAFE constraints, one for PCs and the other for LDTs. The constraints are given by setting \(\bar{e}_{jk} = 100/27.5 \approx 3.64\) for all PCs, and \(\bar{e}_{jk} = 100/20.7 \approx 4.83\) for all LDTs. Notice that within each category, the target value is common to all vehicles, regardless of vehicle size (“flat standards”). As an illustration, Fig. 2 plots the target values and actual gphm of all new PC and LDT models in 2001. Credits earned in one category may not be used in the other category (“no transferring” of credits), and credits may not be sold to or bought from other producers (“no trading” of credits). If an automaker does not fulfill the requirement in a category, it must pay a fine as in the actual CAFE standards (see Sect. 4.1).
Under Policy 1, a complying automaker solves the following profit maximization problem:
where \(p_{jk}\) and \(c_{jk}\) are the price and unit production cost of model jk, respectively; \(\mathcal {J}_{n}^c\) denotes automaker n’s PC models, \(\mathcal {J}_{n}^t\) denotes n’s LDT models, and \(\mathcal {J}_{n} = \mathcal {J}_{n}^c \cup \mathcal {J}_{n}^t\).
4.3.2 Policy 2: Footprint-based Targets/No Transferring/No Trading
Policy 2 sets target values based on vehicle size (footprint, or the area enclosed by the points at which the tires touch the ground). Target value \(\bar{e}_{jk}\) in (20) varies across jk and is a function of jk’s footprint. Figure 3 plots footprint-based target functions used in the simulations. Comparing Policy 2 (Fig. 3) to Policy 1 (Fig. 2), we note that the target is tightened (relaxed) for PCs with footprint smaller (larger) than 44.70 \(\hbox {ft}^2\). For LDTs, the threshold is 51.73 \(\hbox {ft}^2\). This means that selling small (large) vehicles under Policy 2 does not generate as many positive (negative) credits as Policy 1. In other words, the required level of category average fuel efficiency (“standard”) depends on the footprint distribution of each firm’s fleet, and therefore varies across firms: compliance requires automakers that on average sell small PCs or LDTs to achieve better average efficiency than those selling large PCs or LDTs on average. In the footprint-based target functions in Fig. 3, slopes of the linearly increasing parts and footprint values at kink points (41, 56, and 66 \(\hbox {ft}^2\)) are the same as the actual footprint-based CAFE standards for 2012–2016. For each category, the vertical position of the function is determined so that the market average fuel economy will be effectively equal under Policies 1 and 2.Footnote 28 Like Policy 1, Policy 2 does not allow intra-firm transferring or inter-firm trading. The rule for the non-compliance penalty remains the same as Policy 1.
Under Policy 2, a complying automaker solves the following profit maximization problem:
where \(\bar{e}_{jk}\) is given in Fig. 3. This problem is identical to (21) except that target \(\bar{e}_{jk}\) varies over jk.
4.3.3 Policy 3: Footprint-based Targets/Transferring/No Trading
Policy 3 adds to Policy 2 intra-firm credit transferring between PCs and LDTs, so positive credits from a category may be used to offset negative credits in the other category.Footnote 29 Otherwise, Policies 2 and 3 are equivalent. Credit transferring offers flexibility in how to meet the standards.
Under Policy 3, a complying automaker solves the following profit maximization problem:
where \(\bar{e}_{jk}\) is given in Fig. 3. Credit transferring means that an automaker faces just one unified CAFE constraint that covers both PCs and LDTs.
4.3.4 Policy 4: Footprint-based Targets/Transferring/Trading
Policy 4 adds inter-firm credit trading to Policy 3. Credit trading between automakers is another flexibility that may reduce the social cost of achieving a given regulatory goal. This policy includes all the three new features of the actual reformed CAFE standards.
Under Policy 4, a complying automaker solves the following profit maximization problem:
where z is the price of a fuel efficiency credit (measured in gphm) and determined in the simulations to clear the credit trading market. If the automaker does not meet its standard alone, it is required to purchase credits from others and offset the shortage. There is no explicit CAFE constraint in (24) because it is replaced by trading of fuel efficiency credits. Under the actual CAFE regulations, a manufacturer can choose to pay a fine for the shortage, instead of buying credits. However, my simulations suggest that penalty payment for a given shortage is much greater than the cost of required credit purchase. Therefore, I assume that manufacturers choose to buy credits and solve the optimization problem defined in (24).
For Policy 4 to attain the same market average fuel economy as previous policies, I make target values (\(\bar{e}_{jk}\)’s) under Policy 4 more stringent than those under Policies 2 and 3 by vertically shifting down the functions in Fig. 3.Footnote 30
4.4 Simulation Results
Given one of the four counterfactual policies above, I follow the procedure detailed in Online Appendix C to simulate Nash equilibria in which manufacturers optimally set vehicle prices and fuel economy values by solving the corresponding profit maximization problem.Footnote 31 I first explain Tables 7, 8, 9, 10 and 11, then evaluate and compare the four counterfactual policies in terms of various market-level and automaker-level outcomes.
To show how footprint-based standards typically work, Table 7 reports seven largest automakers’ average footprint, standard, and average fuel economy under Policies 1 and 2.Footnote 32 The column “Bind” indicates whether a constraint is binding in an automaker’s optimization problem. Table 7 shows that introducing footprint-based targeting loosens the standards for General Motors (GM) and Ford, who tend to sell large cars and trucks, but tightens other automakers’ standards as they sell relatively small cars and trucks.
For selected automakers, Table 8 shows Lagrange multipliers (\(\lambda ^c\), \(\lambda ^t\), and \(\lambda \)) from profit maximization under Policies 1–3 [problems (21), (22), and (23)], along with the price of a fuel efficiency credit (z) and the net revenue from credit trading (\(\sum _{jk \in \mathcal {J}_n} z \bigl ( \bar{e}_{jk} - e_{jk} \bigr ) s_{jk}\)) under Policy 4 [problem (24)]. If there are two constraints (under Policies 1 and 2), \(\lambda ^c\) is for the PC constraint, and \(\lambda ^t\) is for the LDT constraint. Under Policy 3, \(\lambda \) is the Lagrange multiplier for the single constraint on the combined fleet of PCs and LDTs. A positive multiplier implies that the corresponding CAFE constraint is binding, and it is the shadow price of the constraint. We can interpret the Lagrange multipliers as follows: if every model’s target is increased (i.e., relaxed) by 0.1 gphm, and consequently the automaker’s standard, which is obtained as the sales-weighted arithmetic average of individual targets, is increased by the same amount, then the automaker’s profits per vehicle sold goes up by \({\$}\lambda /10\). The larger the Lagrange multiplier, the more costly the constraint is for the automaker. In relation to the fine (civil penalty) for violating the standards, if \(\lambda \) is less than the corresponding penalty rate (converted to the unit of gphm), it is less costly to comply than to violate the standards and pay the fine, so the manufacturer has an incentive to improve its average fuel economy and comply in the corresponding category.Footnote 33 Note that, if a constraint is relaxed by the introduction of footprint-based targets (GM and Ford), the corresponding Lagrange multiplier declines under Policy 2 relative to Policy 1. On the other hand, DaimlerChrysler’s standards are tightened by footprint-based targets, so its multipliers are greater under Policy 2.
Tables 9, 10 and 11 summarize various market-level, aggregate outcomes from the simulations. They first report the sales-weighted average mpg or footprint of different fleets (PCs, LDTs, or the entire fleet of PCs and LDTs), and the share of PCs in the entire fleet. Tables 9, 10 and 11 also show aggregate outcomes relating to the sales/purchase and use of the year 2001 fleet of new PCs and LDTs: automakers’ profits [1]; consumer surplus [2];Footnote 34 technology costs for fuel efficiency adjustment;Footnote 35 fuel used over the vehicles’ lives; external costs relating to the fuel use [3];Footnote 36 and social welfare (\(= [1] + [2] - [3]\)). Values per new vehicle sold are shown in the lower part of the tables. Values for Policies 2–4 are given as changes from Policy 1.
4.4.1 Effects of Footprint-based Targets
Comparing Policies 1 and 2 in Tables 9, 10 and 11, we find that footprint-based targets alone have little effect at the market level, as long as the two policies are set to achieve the same market average fuel efficiency. Vehicle size (footprint) and the share of PCs in the market change only slightly. Changes (relative to Policy 1) in profits, consumer surplus, technology costs, fuel use, and social welfare are relatively small in magnitude, and the same measure sometimes changes in opposite directions in different equilibria (even with the same K). Coleman and Harrington (2010) also obtain similar results that the impact of footprint-based targets is generally small. As this paper assumes vehicle attributes including footprint to be fixed, market average footprint changes only through adjustments in market shares of individual models. Further evaluating the effect of footprint-based targeting on vehicle size would require modeling the choice of vehicle size by manufacturers (Whitefoot and Skerlos, 2012).
At the individual automaker level, Table 12 presents how the Big Three’s profits change by switching from Policy 1 to Policy 2. The three firms are all constrained under both policies, but the difference in the footprint of their fleets makes Policy 2 standards relaxed for GM and Ford, and tightened for DaimlerChrysler, relative to Policy 1 (Table 7). Overall, Table 12 shows that GM and Ford are affected relatively favorably by Policy 2 as compared to DaimlerChrysler, implying that footprint-based targeting could work to the advantage of CAFE-constrained automakers that produce large vehicles.Footnote 37
4.4.2 Effects of Credit Transferring Within an Automaker
Tables 9, 10 and 11 show that, compared to Policies 1 and 2, Policy 3 on average makes PCs less efficient (about 2–5%), and LDTs more efficient (about 2–4%), although the efficiency of the entire fleet remains almost the same (as intended). Fuel efficiency improves in the LDT fleet and deteriorates in the PC fleet because automakers that are constrained in both categories under Policy 2 (GM, Ford, and DaimlerChrysler) now choose to earn positive credits in the LDT category, and use them to offset negative credits in the PC category.
In the paper’s framework in which vehicle prices and fuel economy ratings are endogenously determined given other vehicle attributes, the manufacturers’ choice as above is mainly explained by the estimated difference in the (average) elasticity of demand between PCs and LDTs when a vehicle model’s fuel economy is improved at additional production costs, with other attributes fixed. Improved fuel economy increases the demand for the model, while applying more/better technologies for the improvement pushes up its price and lowers the demand. The total effect on the model’s sales is given by the sum of the two terms: \(\frac{ds_{jk}}{de_{jk}}=\frac{\partial s_{jk}}{\partial e_{jk}} + \frac{\partial s_{jk}}{\partial p_{jk}} \times \frac{\partial p_{jk}}{\partial e_{jk}}\), where a decrease in \(e_{jk}\) is a fuel economy improvement. For the manufacturers constrained in both categories under Policy 2, the total derivative for a PC model is on average greater than that for an LDT model, so PC demand decreases more elastically than LDT demand when fuel efficiency is marginally improved at extra production costs.Footnote 38 Thus, these manufacturers can increase profits by making PCs less efficient but cheaper, and conversely LDTs more efficient but more expensive, and then transferring credits between the categories.
Among the four counterfactual policies, Policy 3 is most effective in reducing gasoline consumption. It lowers aggregate gasoline consumption (by 0.1–0.3% compared to Policies 1 and 2) because LDTs are on average driven for longer distances than PCs both annually and over their lives (as seen in National Highway Traffic Safety Administration, 2006, or Table 1 of this paper). That is, a fuel economy improvement in an LDT generally provides more fuel savings than the same improvement in a PC. Shrinking the fuel efficiency difference between PCs and LDTs is an effective way of cutting fuel consumption, and Policy 3 generates this substitution through producers’ and consumers’ choices in the market.
4.4.3 Effects of Credit Trading Across Automakers
Of the four counterfactual policies, Policy 4 attains the highest social welfare conditional on meeting the required level of market average fuel economy. Social welfare is increased primarily because Policy 4 significantly reduces the aggregate technology costs for fuel efficiency adjustment.Footnote 39 The technology costs are reduced by about $110–$140 million relative to Policy 1 because automakers with higher marginal costs of improving fuel efficiency (GM, Ford, and DaimlerChrysler) choose not to meet the standards independently, but to purchase credits from other automakers that can improve efficiency at lower costs. In one of their simulations, Austin and Dinan (2005) find a similar effect of inter-firm trading of fuel efficiency credits on the aggregate technology costs, although their counterfactual policies seem to differ in stringency, so their results likely show the combined effect of design (i.e., with or without credit trading) and stringency. My simulations suggest that the $110–$140 million cost reduction from inter-firm credit trading offsets the increase in the aggregate technology costs due to a 0.35–0.9% tightening of CAFE standards.Footnote 40
We next refer to Tables 8 and 13 to see the effect of credit trading on individual automakers. Table 8 shows the net revenue from credit sales (\(\sum _{jk \in \mathcal {J}_n} z \bigl ( \bar{e}_{jk} - e_{jk} \bigr ) s_{jk}\)). Table 13 lists each automaker’s standard and average fuel economy under Policies 3 and 4. Under Policy 4, the average efficiency (in mpg) of each of the Big Three is less than the corresponding standard (Table 13), meaning that they are purchasers of credits (Table 8).Footnote 41 On the contrary, the other manufactures in the tables set the average efficiency (in mpg) larger than the corresponding standard (Table 13), and thus are sellers of credits (Table 8).
Inter-firm credit trading is not as useful for reducing gasoline consumption as intra-firm credit transferring. Policy 3, which features intra-firm transferring without inter-firm trading, reduces aggregate fuel consumption mainly through efficiency improvement in the Big Three’s LDT fleet. Under Policy 4, buying credits from other firms is a better option for the Big Three, so their LDT fuel economy does not improve as much as under Policy 3. Thus, Policy 4 does not provide large fuel savings relative to Policy 1.
4.4.4 Robustness Against High Gasoline Prices
As a robustness check of the paper’s approach, I test how the simulation model will perform under increased gasoline prices, an important change in the vehicle market that took place after 2001. Specifically, in the simulation model (with \(K=4\)) I increase gasoline prices by $1.28 (86.5%) to match the average price in 2008 (prices are inflation-adjusted and in year 2001 U.S. dollars) as well as set (flat) CAFE standards to the actual levels in 2008 (8.7% more stringent for LDTs than in 2001, and no change for PCs). Table 14 reports the simulated market average fuel economy (mpg) under counterfactual Policy 1 with 2001 or 2008 gasoline prices and CAFE standards, along with the actual average fuel economy in both years. The table shows that the simulation model provides good estimates of fleet-wide fuel economy not only for 2001, but also for 2008, indicating the robustness of the simulation model against gasoline prices.Footnote 42
5 Conclusion
This paper has examined three major policy instruments recently introduced to the U.S. Corporate Average Fuel Economy (CAFE) standards: footprint-based targeting, intra-firm credit transferring, and inter-firm credit trading. The design and structure of CAFE standards has attracted relatively little attention in previous studies, compared to the stringency (i.e., the level of required fuel economy). This paper has particularly focused on the design aspects, and is the first study to compare all the three instruments simultaneously. I have modeled and estimated household vehicle purchase and utilization decisions in the U.S. new vehicle market regulated by CAFE standards. Based on estimation results, I have simulated market equilibria under various counterfactual CAFE policies, where manufacturers optimally pick the price and fuel economy of their vehicles. Importantly, these counterfactual policies are set at the same level of stringency, making it possible to identify the effects of the three instruments without being confounded by stringency differences as in previous studies.
Counterfactual simulations provide the following key policy implications. First, simply replacing flat targets with footprint-based targets (as in Policy 2) has little impact at the market level, while at the individual automaker level it relatively favors firms that tend to produce large vehicles. Second, allowing intra-firm transferring without inter-firm trading (as in Policy 3) is useful for cutting aggregate gasoline consumption by inducing constrained firms to improve LDTs’ fuel economy to offset PCs’ worsened fuel economy. Policy 3 sees a 0.1–0.3% reduction relative to Policy 1. Third, further introducing inter-firm trading (as in Policy 4) attains a given market average fuel economy at the lowest aggregate technology costs ($110–$140 million lower than Policy 1) because fuel economy is “produced” by automakers that can improve fuel economy at relatively low costs. This makes Policy 4 the most effective among the four simulated policies in terms of social welfare. As Policy 4 mirrors the actual reformed CAFE standards, simulation results are overall in favor of the reform.
This paper has several limitations and possible extensions. First, the household utility function as defined in (2)–(7) captures the interaction between household demand for VMT and that for fuel economy, where a household with higher demand for driving is likely to buy a more fuel efficient vehicle, conditional on other vehicle attributes. However, this functional specification does not allow us to capture a different, indirect channel that might exist between VMT and fuel economy, where VMT demand interacts with the demand for other vehicle attributes (e.g., size and power) which can in turn affect fuel economy. Addressing this point lies beyond the scope of this paper as it would add considerable complexity to the analysis, but reflecting it into the demand estimation framework is an interesting avenue for future research.
Second, I have not considered alternative fuel vehicles such as hybrid and electric vehicles because their market share was negligible in 2001. Their share has been steadily growing since then. Though expensive, these vehicles have substantially better fuel economy ratings than conventional fuel vehicles (even conditional on footprint). With the growing presence of these vehicles in the current market, manufacturers may be strategically utilizing them as a means to meet CAFE standards. Considering this aspect will be a useful extension of the paper.
Third, this paper has focused on the new vehicle market, so the possibility of substitution between new and used vehicles is ignored. In practice, used cars account for a large part of the vehicle market, and Bento et al. (2009) point out the importance of considering used cars in analyzing the vehicle market. Because the National Household Travel Survey has data on used car purchases, it will be possible in future work to include used cars in the demand estimation.
Lastly, in my framework automakers choose only the price and fuel economy of vehicles. Studies such as Klier and Linn (2012) and Whitefoot et al. (2012) additionally endogenize the choice of other vehicle attributes such as weight and horsepower, and consider the trade-offs between these attributes and fuel economy. Incorporating their approach into my framework will enrich the analysis of the paper.
Adding used cars and endogenizing other vehicle attributes would be especially important when we focus on significant stringency changes, which will substantially affect consumers’ and producers’ decisions, and thus market outcomes. Because I compare policies that are essentially at the same level of stringency, the effects of overlooking these features would be relatively small.
Notes
Large economic benefits are expected from the reformed fuel economy regulations: for example, the net benefits (in 2007 dollars) over the useful lives of MYs 2012–2016 vehicles are estimated at $130.7 billion (with a 3% discount rate) or $94.5 billion (with a 7% discount rate), where nearly 80% of gross benefits result from fuel savings (Environmental Protection Agency and Department of Transportation, 2010).
CAFE standards after 1996 use three vehicle categories: domestic PCs, import PCs, and LDTs.
Jacobsen (2013) also simulates a simplified version of footprint-based targets as an extension to his analysis.
In 2008, the highest price was over $4.10, and the lowest was around $1.60.
In the table, footprint-based targets make MY 2014 standards differ across automakers even within the same category. Intra-firm credit transferring and inter-firm credit trading are available in 2014, but not in 2001.
I consider four types: \(h=1\) for PCs, 2 for vans, 3 for SUVs, and 4 for pickup trucks. Vans, SUVs, and pickup trucks constitute LDTs.
This indirect utility function is associated with the following quasi-linear utility function:
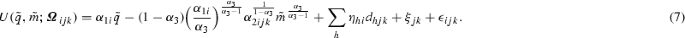
Note that if \(0<\alpha _{3}<1\), \(U(\tilde{q},\tilde{m};\varvec{\varOmega }_{ijk})\) is concave in \(\tilde{m}\).
In the maximum likelihood estimation of the econometric model, \(\alpha _{1i} y_i\) in (3) can be dropped because, constant over alternatives (jk), it does not affect the likelihood defined by (8). This is practically favorable because data on \(y_i\) (household i’s budget before vehicle purchase, which is generally different from its income) is unavailable.
K is assumed to be exogenous in this paper. The government may, however, be able to affect K, particularly T, through policies such as vehicle taxation.
The equality holds for the three derivatives only in the trivial case where \(T = 1\).
Conceptually, a vehicle’s fuel efficiency can be improved by 1) compromising other vehicle attributes such as weight and power, or 2) using more/better efficiency-improving technologies without affecting other attributes. (In reality, it is usually improved by a mixture of the two.) As will be discussed later, this paper focuses on improvement of the second form. Vehicle attributes are assumed to be fixed, and thus the first form is beyond its scope.
K may vary across households. In the econometric model, this possible heterogeneity is absorbed in household-specific random parameters, so we assume that K is common to all households.
As an illustration, if \((T, d_f, d_r, d_m)=(2,0.8,0.95,0.9)\), then \(K=1.68\). If \((T, d_f, d_r, d_m)=(4,0.9,1,0.95)\), then \(K=3.21\). If \((T, d_f, d_r, d_m)=(7,0.97,1.05,0.97)\), then \(K=6.75\).
Roughly, a third of the households in my data set have annual income less than $46,715, another third between $46,715 and $73,580, and the other third above $73,580.
I follow the vehicle classification used by the NHTS, where crossover utility vehicles (CUVs) are included in the SUV class except for one model in the PC class. As CUVs are relatively close substitutes for PCs, I have checked the robustness of the estimation results against this grouping by moving all CUVs to the PC class. The results remain almost the same after the re-grouping.
The elasticity of the marginal utility of money with respect to annual household income is estimated at − 0.31 to − 0.35 if annual household income is less than $46,715; − 0.66 to − 0.71 if it is between $46,715 and $73,580; − 2.05 to − 2.59 if it is greater than $73,580. The elasticity for households with income between $46,715 and $73,580 is given by summing the coefficients of log(hh income) and max[log(hh income/46,715), 0]. Similarly, the elasticity for households with income greater than $73,580 is given by summing the coefficients of log(hh income), max[log(hh income/46,715), 0], and max[log(hh income/73,580), 0].
As in most previous studies, for the sake of econometric tractability I do not control for the composition (\(\ne \) number) of vehicles owned by a household, and how it affects household vehicle and VMT choices. This could potentially cause bias. See Spiller et al. (2016) for an attempt to overcome the issue.
As in Bento et al. (2009), my estimation is based on cross-sectional data, so elasticity estimates should be interpreted as long-run elasticities.
With fuel efficiency (and driving patterns) held constant, VMT is proportional to gasoline consumption, and the price of driving is proportional to the price of gasoline. Therefore, under this assumption, \(\alpha _3-1\) can also be interpreted as the elasticity of gasoline consumption with respect to the price of driving, and the elasticity of VMT or gasoline consumption with respect to the price of gasoline, conditional on vehicle choice. A recent study (Gillingham, 2014) estimates the elasticity of VMT with respect to the price of gasoline at − 0.22.
A firm is allowed to bank and borrow credits over years within each category.
For MY 2001, fines were paid by BMW ($28 million for import PCs, and $1.5 million for LDTs), Porsche ($5 million for import PCs), Volkswagen ($0.2 million for LDTs), and two other European producers with very small sales volume (Fiat and Lotus). The data is available at the CAFE Public Information Center website (https://one.nhtsa.gov/CAFE_PIC).
Environmental Protection Agency and Department of Transportation (2010) gives a complete description of these instruments.
I add Instruments B and C in this order for two main reasons: first, intra-firm transferring is likely to be an easier option for both the government and automakers than inter-firm trading which by definition involves interactions with other automakers; second, simulating a policy with Instrument C but without Instrument B is computationally much more demanding as it needs to separately clear credit trading markets for different vehicle categories.
The methodology is detailed in Online Appendix B.
Equivalently, the sales-weighted harmonic average of actual fuel economy values in mpg needs to be greater than or equal to the sales-weighted harmonic average of target values in mpg.
In the actual CAFE standards for 2012–2016, slope parameters and footprint values at kink points remain constant over time, while vertical positions are lowered every year, leading to more stringent standards.
I have also considered a counterfactual policy that adds intra-firm credit transferring to Policy 1, that is, a policy with flat targets and credit transferring, but without credit trading. Simulation results under this policy are very similar to those under Policy 3.
Under Policies 2 and 3, CAFE constraints are not binding for a number of automakers, but their positive credits have no value because no inter-firm trading is allowed. If the same functions are used under Policy 4, these positive credits will be sold to the automakers constrained by or violating the standards under Policies 2 or 3, and lower their average efficiency (increase their average gphm). As a result, the market average efficiency will also deteriorate.
Manufacturers considered in the simulations are General Motors, Ford, DaimlerChrysler, Toyota, Honda, Nissan, Volkswagen, Hyundai, BMW, Kia, Subaru, Suzuki, and Porsche. As in actual CAFE standards, I consider ownership relations to group manufacturers, so General Motors includes Isuzu and Saab; Ford includes Jaguar, Mazda, and Volvo; and DaimlerChrysler includes Mitsubishi. In a robustness check, I treat Daimler and Chrysler as two distinct companies, and find that the following simulation results are robust to this change.
Table 7 is based on a Nash equilibrium with \(K=4\). I obtain almost the same values in other equilibria.
Consumer surplus is calculated with the method of Small and Rosen (1981).
Each model’s fuel efficiency is adjusted by changing the technology level applied. This adjustment leads to an increase or decrease in its production costs, which is defined as the technology costs for fuel efficiency adjustment. Tables 9, 10 and 11 report the sum of these technology costs over different vehicle models.
Fuel use external costs over the vehicles’ lives are calculated with an estimated lifetime VMT schedule and survival probability of the average car or truck (Tables 4–3 and 4–4 of Environmental Protection Agency and National Highway Traffic Safety Administration, 2010). A 5% discount rate is applied to future external costs. Fuel use externality is evaluated at $0.42 per gallon, based on an estimate by Parry et al. (2007). With these assumptions, I estimate fuel use external costs over a vehicle’s lifetime by multiplying first year’s fuel use external costs obtained from a simulation by 8.457 for PCs and by 8.389 for LDTs.
In Table 12, market interaction in equilibrium among all firms causes negative changes in profits even for GM and Ford in some cases.
With \(\frac{\partial c_{jk}}{\partial e_{jk}}\) replacing \(\frac{\partial p_{jk}}{\partial e_{jk}}\) as an approximation, the mean of \(\frac{ds_{jk}}{de_{jk}}\) is 0.098 for PCs, and 0.056 for LDTs (with \(K=4\)).
Refer to footnote 35 for an explanation on the technology costs for fuel efficiency adjustment.
Based on our simulated fuel economy values and VMT schedule data in National Highway Traffic Safety Administration (2006), this size of tightening would lower aggregate gasoline consumption over the lifetime of the year 2001 vehicles (PCs and LDTs) by about 0.2–0.65%, which is smaller than 0.35–0.9% because many automakers remain unconstrained and thus make almost no change in fuel economy after the 0.35–0.9% tightening.
With the Big Three’s standards and average fuel economy values in Table 13, along with the price of a credit (z) in Table 8 and the rate of the CAFE fine (in 2001, $5 per 0.1 mpg short of the corresponding standard), we can calculate whether credit purchase or fine payment is a better option for the Big Three. Back-of-the-envelope calculations suggest that fine payment is four to six times more costly than credit purchase for each of them, making credit purchase a rational choice given the level of the penalty. The current (year 2017) penalty rate of $5.5 per 0.1 mpg magnifies the gap.
The simulation model does not account for the extra credits that some manufacturers earned under the actual 2001 or 2008 CAFE standards by selling flex-fuel vehicles. This is the main reason that simulated PC fuel economy for 2001 (28.4) is less efficient than the actual value (28.8).
References
Austin D, Dinan T (2005) Clearing the air: the costs and consequences of higher CAFE standards and increased gasoline taxes. J Environ Econ Manag 50:562–582
Bento AM, Goulder LH, Jacobsen MR, von Haefen RH (2009) Distributional and efficiency impacts of increased U.S. gasoline taxes. Am Econ Rev 99:667–699
Berry S, Levinsohn J, Pakes A (1995) Automobile prices in market equilibrium. Econometrica 63:841–890
Berry S, Levinsohn J, Pakes A (2004) Differentiated products demand systems from a combination of micro and macro data: the new car market. J Polit Econ 112:68–105
Coleman C, Harrington W (2010) A simulation model of the new vehicle market. Mimeo, New York
Dubin JA, McFadden DL (1984) An econometric analysis of residential electric appliance holdings and consumption. Econometrica 52:345–362
Environmental Protection Agency, Department of Transportation (2010) Light-duty vehicle greenhouse gas emission standards and corporate average fuel economy standards; final rule. Federal Register 75(88):25324–25728
Environmental Protection Agency, National Highway Traffic Safety Administration (2010) Joint technical support document: rulemaking to establish light-duty vehicle greenhouse gas emission standards and corporate average fuel economy standards. http://www.nhtsa.gov/staticfiles/rulemaking/pdf/cafe/Final_Joint_TSD.pdf
Gillingham K (2011) The consumer response to gasoline price changes: empirical evidence and policy implications. Ph.D. thesis, Stanford University
Gillingham K (2014) Identifying the elasticity of driving: evidence from a gasoline price shock in California. Reg Sci Urban Econ 47:13–24
Goldberg PK (1998) The effects of the corporate average fuel efficiency standards in the U.S. J Ind Econ 46:1–33
Jacobsen MR (2013) Evaluating U.S. fuel economy standards in a model with producer and household heterogeneity. Am Econ J Econ Policy 5(2):148–187
Kleit AN (2004) Impacts of long-range increases in the fuel economy (cafe) standard. Econ Inq 42:279–294
Klier T, Linn J (2012) New vehicle characteristics and the cost of the corporate average fuel economy standards. RAND J Econ 43:186–213
Mannering F, Winston C (1985) A dynamic empirical analysis of household vehicle ownership and utilization. RAND J Econ 16:215–236
National Highway Traffic Safety Administration (2006) Vehicle survivability and travel mileage schedules. https://crashstats.nhtsa.dot.gov/Api/Public/ViewPublication/809952
Parry I, Walls M, Harrington W (2007) Automobile externalities and policies. J Econ Liter. 45:374–400
Small KA, Rosen HS (1981) Applied welfare economics with discrete choice models. Econometrica 49:105–130
Small KA, Van Dender K (2007) Fuel efficiency and motor vehicle travel: the declining rebound effect. Energy J 28:25–51
Spiller E, Stephens HM, Chen Y (2016) Understanding the heterogeneous effects of gasoline taxes across income and location. Working paper. http://dx.doi.org/10.2139/ssrn.2113594
Train K (2009) Discrete choice methods with simulation, 2nd edn. Cambridge University Press, Cambridge
Train KE, Winston C (2007) Vehicle choice behavior and the declining market share of U.S. automakers. Int Econ Rev 48:1469–1496
West SE (2004) Distributional effects of alternative vehicle pollution control policies. J Public Econ 88:735–757
Whitefoot K, Fowlie M, Skerlos S (2012) Product design response to industrial policy: evaluating fuel economy standards using an engineering model of endogenous product design. Energy Institute at Haas Working Paper
Whitefoot KS, Skerlos SJ (2012) Design incentives to increase vehicle size created from the U.S. footprint-based fuel economy standards. Energy Policy 41:402–411
Acknowledgements
I am very grateful to my thesis advisors Ted McConnell, Maureen Cropper, and Rob Williams for their guidance. I would also like to thank Euan Phimister, Catia Montagna, Keith Bender, and two anonymous referees for helpful comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kiso, T. Evaluating New Policy Instruments of the Corporate Average Fuel Economy Standards: Footprint, Credit Transferring, and Credit Trading. Environ Resource Econ 72, 445–476 (2019). https://doi.org/10.1007/s10640-017-0200-1
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10640-017-0200-1
Keywords
- Corporate Average Fuel Economy (CAFE) standards
- Footprint
- Credit transferring
- Credit trading
- Policy simulation