Abstract
Many real world fisheries have an individual vessel quota system with restrictions on transferability of quota or entrance of new vessels into the fishery. While the standard economic reasoning is that these institutional constraints lead to welfare losses, the size of those losses and optimal second-best policies are usually unknown. We develop a dynamic bioeconomic model, in which a scientific body provides an optimal TAC given restrictions on (i) transferability between vessel segments and (ii) entrance of new vessels. Further, we also quantify welfare losses arising from not maximizing economic welfare, but physical yield—which is actually the case in many fisheries. We apply the model to the Northeast Arctic cod fishery, and estimate not only the cost and harvesting functions of the various vessel types, but also the parameters of the biological model as well as those of the demand function. This allows us to determine optimal second-best policies and quantify corresponding welfare effects for our case study fishery.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Determining dynamically optimal harvests in a fishery is a canonical textbook example in resource economics, yet these insights are hardly applied in reality. One of the main reasons for this discrepancy lies in the political nature of fisheries management, where governance systems are typically highly convoluted (Wilen 2000; Mikalsen and Jentoft 2008; Aanesen and Armstrong 2016). In particular, it is common that science and policy are closely intertwined (Kvamsdal et al. 2016). Often, the size of the total allowable catch (TAC) is determined by a scientific body, usually striving for some biological criteria, such as the maximum sustainable yield (MSY) or some other target reference point. Policy makers, on their side, address distributional questions on how to divide a certain TAC, for example by issuing individual transferable quotas (ITQs). In reality, this setup rarely coincides with the social optimum for at least two reasons. First, a purely biological criterion ignores information on the costs and benefits of fishing which depend on the policy decisions, in particular the rules for buying or receiving vessel quotas. Second, while ITQs make sure that the TAC is distributed in the most efficient way (Wilen 2000), policy makers tend to impose restrictions on which vessels can participate in a fishery, and how quotas can be traded. These institutional constraints push a fishery further away from the socially optimal outcome.
The aim of this study is to provide a general model that captures the essential features of a fishery in which a TAC is set under institutional constraints with a specific application for the North East Arctic (NEA) cod (Gadus morhua) fishery. As Homans and Wilen (1997), we model fisheries regulation as a two stage process. First, the TAC is allocated to individual vessels through an ITQ mechanism, with and without restrictions on quota transferability and entrance of vessels imposed by policy makers. Second, the optimal TAC is determined by a scientific body taking into account the fleet structure, as vessels differ in terms of costs and benefits. Since there is a dependence between fleet structure and optimal TAC, we solve the model jointly. We then assess the associated welfare losses of (i) imposing restrictions on quota transfer between segments, (ii) imposing restrictions on entrance, and (iii) ignoring economic costs and benefits by setting a TAC that maximizes yield, rather than economic welfare.
We apply our theoretical model to NEA cod, which is distributed along the coast of Norway and in the Barents Sea. It is is one of the world’s most important fisheries consisting of a wide variety of boat types including trawlers, longliners, and coastal vessels with conventional gear (Sandberg 2006; Standal 2008). The Norwegian system is one of individual vessel quotas, where quotas are transferable between vessels of the same segment, and non-transferable between segments. The distribution of the quotas happens in two stages; see Hersoug (2005) and Guttormsen and Roll (2011). First, the annual TAC is implemented based on recommendations from the International Council for the Exploration of the Sea (ICES), the scientific body in this matter. Second, the quotas are distributed between fleet segments according to the so-called trawl-ladder, an allocation key that determines how the quota is divided between coastal and ocean-going vessels, which is a policy choice (Hersoug 2005).Footnote 1 We contribute to the existing literature in several ways. First, this paper adds to the literature of suboptimal controls in fisheries (Karpoff 1987). The focus does not lie on the political economy considerations that may explain why a fishery is managed suboptimally (Boyce 2004; Johnson and Libecap 1982), but rather on providing second-best management strategies given institutional constraints and corresponding welfare effects. This idea is related to Kroetz et al. (2015) who quantify the welfare effects of constraints on quota tradability from the Alaska halibut and sablefish fishery. Their paper empirically disentangles the welfare losses from restricting quota use on specific vessel classes, and having the quota in indivisable blocks, effectively posing a cap on the quota each vessel can hold.Footnote 2 Our paper is complementary, because we provide insights from a different fishery and develop a theoretical model for such a case, which is the second contribution to the literature. Our model adds to the tradition of fisheries models that considers the setting of a TAC and the distribution between vessels as separate processes (Homans and Wilen 1997).Footnote 3 We add to this branch of literature by assuming that there are different segments in the fishery, which differ in terms of cost structure, technology, and also the quality of the catch and hence the price that can be obtained (Asche et al. 2015). Furthermore, we assume that the fishery is not characterized by open access, but there is a quota system in place that allows participants to make profits in excess of any infra-marginal profits. While the distribution of quotas is a political decision, we assume that the TAC is endogenously set by a scientific body and optimal given the imposed institutional constraints. Third, this paper delivers important insights that are relevant for the Norwegian cod fishery. These are particularly useful to evaluate potential gains that could be made by either implementing a second-best solution or removing constraints in order to achieve a first-best outcome. This links to work by Asche et al. (2009) who look at rent, as well as capacity for the fleet of Norwegian trawlers. Using data from 1997 and 1998, they estimate optimal quota for each vessel and find substantial overcapacity in the fleet, which implies suboptimal rent generation. In general, it has been emphasized that substantial efficiency gains can be made by establishing an ITQ system (Hannesson 2004; Grafton et al. 2006). However, it is a priori unclear whether these efficiency gains come from an improvement in the quality of fish supplied with higher sales prices, or from lower costs of catching it, and usually very little is known about potential distributional aspects (Squires 2009).
The NEA cod fishery is remarkable to the extent in which it is perceived and managed as a single species fishery. This focus on cod has historical, cultural, and biological causes: Cod products, in particular dried cod (stockfish) are priced commodities at least since the Viking ages and they are inextricably linked to both the settlement patterns along the Northern Norwegian coast as well as to the rise of the hanseatic city of Bergen during the Middle Ages (Eide et al. 2012). Still today, the cod fishery is the most important fishery for many Norwegian fishing firms. Because it has such a well defined seasonal character (depending on the gear, the fish are only, or most easily, accessible during the cod’s spawning migration) fishing vessels participating in the cod fishery target little else during this period.Footnote 4
A main feature of this study is that we combine the empirically estimated functions into our analytical model to derive the most efficient allocation of individual vessel quotas for each vessel segment, and the optimal levels of biomass and the associated TAC with or without institutional constraints. More specifically, we estimate the cost and production functions of the various vessel types in the industry (coastal vessels, ocean-going longliners, and trawlers), the demand function for cod (to determine how its value changes with quantity supplied), as well as the parameters of the growth function of cod. Furthermore, we are the first to estimate the demand function for cod with instrumental variables using data on cod exports. In this respect we improve on the earlier work by Arnason et al (2004) and Kugarajh et al. (2006). We also explicitly acknowledge that there are not only variable costs associated with harvesting cod, but that there are fixed costs, too (Asche 2009).
This paper is organized as follows. Section 2 develops the theoretical model, while Sect. 3 gives an overview of the NEA cod fishery and presents the estimated production, cost, and demand functions as well as the biological model. Next, Sect. 4 combines the theoretical and empirical results and derives the optimal policy for NEA cod, while Sect. 5 concludes.
2 The Model
2.1 Allocation of Individual Vessel Quota
We model the vessels participating in the cod fishery and assume cod to be the only output variable, even though vessels may target other species during the rest of the year. Suppose the fishing fleet is divided in Z segments. Each segment \(z = 1,2,\dots ,Z\) consists of \(N_z\) individual vessels \(i = 1,2,\dots ,N_z\) that each have the following harvest function:
where \(X_t\) is the (common) stock of fish biomass at time t, \(q_z\) is a segment-specific catchability coefficient. Stock-output elasticity \(1>\alpha _z>0\) and effort-output elasticity \(1>\beta _z>0\) are also segment-specific, while effort \(e_{i,t}\) is chosen at the vessel level. Costs of effort are given by
where \(f_z\) are (quasi-)fixed costs and \(v_z\) are variable costs, which are assumed to be the same for all vessels in segment z. Fixed costs include adjustment costs, such as changing the vessel’s gear to make it suitable for catching the targeted fish species, while variable costs are proportional to effort.
The group quota for segment z is denoted by \(H_{z,t}\), and by definition, the aggregate amount of fish to be caught by all boats of segment z is equal to \(H_{z,t}\) (that is, \(N_{z,t} q_zX_t^{\alpha _z}e_{i,t}^{\beta _z}=H_{z,t}\).) Following Weninger and Just (1997) and Weninger (1998), we can determine the minimal cost of harvesting \(H_{z,t}\) with fleet segment z as
See “Appendix 1” for details. This implies that the cost per vessel are U-shaped with respect to effort. Consequently, there is an optimal effort level per vessel of each segment \(e^*_z\). This leads to an efficient scale of operation for each segment, as illustrated in panel a of Fig. 1. Therefore, there is an optimal number of vessels \(N^*_{z,t}\) in each segment harvesting \({H}_{z,t}\); see “Appendix 1”. Throughout the analysis we ignore the fact that individual vessels can typically enter only in full integers.
Illustration of the model with two segments that differ in efficiency. a Costs per vessel are U-shaped with respect to effort with the minimum cost at \(e^*_z\) for both segments. b All active vessels operate at \(e^*_z\) and therefore average fleet costs are constant. If two segments are used that differ in efficiency, the average costs must be higher than employing only segment 1, but lower than employing only the less efficient segment 2. c With entrance constraints, costs are constant, until all vessels of the most efficient segment \({\bar{N_1}}\) are active. Then, effort \(e_1\) is increased up to a point, where it would be as efficient to use the second segment operating at \(e^*_2\). After the first vessel of segment 2 enters, \(N_2\) is increased up to a point where all vessels \({\bar{N_2}}\) are active
2.2 Group Quotas and the Total Allowable Catch
The sum of the group quotas is equal to the total quota \(Q_t\) (the total allowable catch, TAC) as determined by the scientific body for that year (that is, \(Q_t= \sum _{z=1}^Z H_{z,t}\)). The output price \(p_{z,t}(Q_t)\) depends on the segment that has landed the catch because of differences in quality, but also on the total catch of all boats, due to an adverse effect of fleet landings on the sales price. Consequently, total fleet profits are given by \(\sum _{z=1}^Z (p_{z,t} (Q_t) H_{z,t} - C_{z} (X_t, H_{z,t}))\). To characterize the unconstrained first-best situation, we assume that the objective of the scientific body is to maximize long-term profits. The scientific body chooses the total quota that will then be allocated to a fleet as individual transferable quota, either via an auction or by grandfathering. As a result, the most efficient vessel group(s) will hold a certain share \(\theta _{z,t}\) of the total allowable catch. In practice, it is not necessary to know \(\theta _{z,t}\) for allocation purposes, since the market will automatically allocate the quotas to the most efficient vessels (since they are the ones with the highest willingness to pay), but \(\theta _{z,t}\) is needed to find the optimal TAC. Consequently, the long-term profit maximizing allocation of the total quota can be found by jointly determining \(Q{_t}\) and a share that is allocated to each vessel group \(\theta _{z,t}\). In practice, this implies that only the most efficient segment will be catching the whole TAC. Two segments z and \(z'\) will only be employed simultaneously if \(p_z(Q_t) = \frac{\Omega _{z}}{q_zX_t^{\alpha _z}}\) and \(p_{z'}(Q_t) = \frac{\Omega _{z'}}{q_{z'}X_t^{\alpha _{z'}}}\) hold at the same time;Footnote 5 see “Appendix 2”.
To characterize the second-best situation under institutional constraints, we will first consider restrictions on the tradability of quota. In particular, we assume that quotas can be traded within one segment but not between different segments. Each segment is allocated a specific share \(\theta _z\) of the total allowable catch \(Q_t\), which implies that \(H_{z,t}= \theta _z Q_t\). Unless the policy makers choose an allocation key \(\theta _z\) that coincides with the optimal allocation \(\theta ^*_z\), the net revenues are lower than without such constraint; see “Appendix 3”. In panel b of Fig. 1 the case is shown where two arbitrary segments are employed. The average costs are horizontal, since all active vessels operate at the efficient scale \(e^*_z\). If two segments are used that differ in efficiency, the average costs must be higher than just employing the most efficient fleet segment.
Now consider the case of entrance constraints. While there is no constraint on tradability of quota, new vessels cannot enter freely into a given segment, i.e. \(N_z \le {\bar{N}}_z\). This changes the segment-specific cost function \(C_z\) to (see “Appendix 4”):
Panel c in Fig. 1 illustrates how costs change as total effort increases. Consider the case where the most efficient segment \(z=1\) will be employed, before a less efficient segment \(z=2\) enters. There is no welfare loss due to the entrance constraint if \(Q_t \le {\bar{H}}_{1,t}\). Then there is an interval \(Q_t \in ({\bar{H}}_{1,t}, \bar{Q}_{2,t}]\) in which each vessel in the first segment increases effort, while \(N_{1,t}\) stays at \({\bar{N}}_z\). As can be seen from Eq. (4), marginal harvest cost are increasing in this interval. Then there is an interval in which segment \(z=2\) enters and a further increase in quota does not lead to an increase in marginal harvesting cost (at the fleet level) until \(Q_t > \bar{Q}_{2,t} + {\bar{H}}_{2,t}\). Then follows an interval \(Q_t \in (\bar{Q}_{2,t} + {\bar{H}}_{2,t}, \bar{Q}_{3,t}]\) in which marginal harvesting costs are increasing again. Both segment 1 and segment 2 increase effort beyond \(e^*_{z,t}\). For \(Q_t > \bar{Q}_{3,t}\) the third segment enters, etc.
To sum up, constraints in quota tradability introduce an inefficiency because quota cannot flow from less efficient segments to to the most efficient one. Entrance constraints introduce an inefficiency because the number of vessels in the most efficient segment cannot increase. As a result, (i) vessels from that segment may operate at a higher than optimal effort level, and (ii) vessels from a less efficient segment may be active.
3 An Empirical Application for the Northeast Arctic Cod Fishery
Today, Northeast Arctic (NEA) cod is the world’s largest stock of cod, and the history of this fishery since World War II is one of continued increase in harvesting pressure, giving way to a near collapse of the fishery in 1989. Since the 1930s (and especially after the second world war), technological developments facilitated the introduction of large ocean-going trawlers and increasing fishing pressure in the feeding grounds in the Barents Sea (Godø 2003). Until the early 1970 s the number of trawlers steadily increased and total landings for the whole fleet (comprising coastal vessels, longliners, and trawlers) have been as high as one million tonnes per annum for some years: this implies that the chances for an individual fish to end up in a fishing net instead of surviving a given year were as high as 70% (Eikeset 2010). In the late 1970 s it became clear that the NEA cod fishery was overexploited. In 1977 the Norwegian government responded by barring the entry of new trawlers (Hersoug 2005; Standal 2008). Also, a TAC was introduced on the total amount of cod caught per year. However, the TACs in the 1980 s were both too lenient and not enforced for the coastal vessels, so that the cod crisis that occurred in 1989 could not be prevented. As a consequence, the TAC in 1989 had to be reduced dramatically with severe consequences for the cod fishing industry (Hersoug et al. 2000). To deal with the crisis, a system was introduced that gave each vessel in the industry a quota to catch a certain amount of cod. These quotas were non-transferable at first, but later on the regulations were revised to allow some vessels to transfer harvesting rights within certain segments (Hersoug et al. 2000; Standal 2008; Armstrong et al. 2014).Footnote 6
In this section we estimate the production and cost function from individual vessel data from the Directorate of Fisheries (Bergen, Norway).Footnote 7 Since the NEA cod fishery is not a small scale fishery, its landings affect the export price, and hence also the ex-vessel prices. We empirically derive the percentage decrease in the landing price (or ex-vessel price) resulting from a 1% increase in the quantity of cod harvested i.e. the price flexibility. Finally, we estimate the biological model for the NEA cod stock. All data sources are described in “Appendix 5”.
3.1 Estimating the Production and the Cost Function
To estimate the cost and production functions of the various boat types, we use data from the profitability survey of the Norwegian Directorate of Fisheries. The Directorate sends an annual obligatory survey to a stratified sample of all active vessels. From this unbalanced panel with information on vessel characteristics, economic variables, the harvested amount and the harvest value, we use data from 1998 to 2010.Footnote 8 We match this with information on the stock biomass of NEA cod and remove all observations where the share of cod in total harvest is >5% to exclude those truly pelagic boats that catch cod only as undirected bycatch (removing 490 out of originally 3205 observations). The final selection contains 862 unique vessels over 13 years (in total, we have 2715 observations; on average ca. 200 observations per year). Of these 862 vessels, 80 are conventional ocean-going vessels (these are predominantly longliners, so that we denote this segment by \(z=L\)), 120 vessels are trawlers (we denote this segment by \(z=T\)), and 665 are coastal vessels (conventional vessels below 28 m length; \(z=C\)). Table 1 provides summary statistics of our economic data. This table also exemplifies the large diversity of the Norwegian NEA cod fishery.
Now we take our model to the dataFootnote 9 and estimate the production and cost functions, as specified in Eqs. (1) and (2). Given that we have a good proxy for effort, we can estimate those relationships directly, rather than imposing a cost function that assumes fishermen choices to be cost-minimizing (Felthoven and Morrison Paul 2004).Footnote 10 First, we estimate the production function for each fleet type z. We define effort as the number of days a boat is fishing cod north of 62\(^\circ \) latitude, multiplied by its size (gross tonnage; GT). Including the size of the boat takes differences in operational intensity into account (Asche 2009). We cannot rule out an omitted variable bias caused for example by differences in the skill of individual skippers (Squires and Kirkley 1999; Sandberg 2006), and therefore use the Hausman specification test to decide whether Fixed or Random effects should be chosen.Footnote 11 We estimate Eq. (1) for each segment separately, thus allowing all parameters to be segment specific:
where \(\epsilon _{i,z,t}\) is an error term, while \(\eta _{i,z}\) is the individual effect. The regression results are reported in the lower part of Table 2.
Next, we estimate the fixed and variable costs of harvesting cod as follows. The available cost data for each vessel covers expenses made for fuel, salt and packing, wages, payroll-related social expenses, vessel insurance, other insurance, vessel maintenance, gear and equipment maintenance, provisions, vessel depreciation, and a category “other costs”. In total, there are 11 cost components, which are indexed \(k= 1,\dots ,11\). Total costs incurred by vessel i from segment z in year t are given by the vector of nominal cost components, \(C_{i,z,k,t}\) which are subsequently corrected for inflation using the Producer Price Index \(\text {PPI}_t\). We calculate the part of the total costs incurred for catching cod by the share of days vessel i spends on catching cod in the total number of days vessel i is operating in a given year. Using index j to enumerate the different main target species (with cod being \(j=1\)) and using \(D_{i,z,j,t}\) to denote the number of days in year t that vessel i of type z catches species j, the costs attributed to catching cod by a vessel i of type z in year t are:
To estimate Eq. (2), we use the right-hand-side of Eq. (6) as the dependent variable and regress it on an intercept as well as on the number of tonnage-days vessel i spent harvesting cod in year t. We estimate
where \(f_{z}\) equals the fixed costs per boat operating in the cod fishery, while \(v_{z}\) reflect variable costs per tonnage-day spent fishing cod, and \(\eta _{z,i}\) is the individual effect. The regression results are presented in the upper part of Table 2.
The fixed costs per year are 0.96 million NOK per coastal vessel, 1.03 million NOK per longliner, and 3.67 million NOK per trawler.Footnote 12 The variable costs per tonnage-day are 117 NOK for coastal vessels, 192 NOK per longliner, and 185 NOK per trawler. Hence, the variable costs for one day of fishing cod are 9594 NOK per coastal vessel [of average size 82 Gross Tonnage (GT)], 55,488 NOK per longliner (of average size 289 GT), and 80,290 NOK per trawler (of average size 434 GT). Concerning the production function, the stock-output elasticity \(\alpha \) is estimated to be 0.21 for coastal vessels, 0.42 for longliners, and 0.60 for trawlers. The effort-output elasticity \(\beta \) is estimated to be 0.39 for coastal vessels, 0.97 for longliners, and 0.79 for trawlers. The coefficients for the fleet of trawler are similar to the ones found by Diekert (2013) for the same fishery and by Kronbak (2004) for the Baltic cod fishery.Footnote 13
3.2 Estimating the Demand Function
Estimating an inverse demand function for cod is complicated, because the price and quantity data are equilibrium outcomes of market interactions, and hence are the result of both demand and supply. In particular, there may be supply effects if (i) the TAC is set at a higher level when world prices are high, (ii) there is a tendency to harvest illegally when prices are high, or (iii) the quotas are not fully exercised when prices are really low. Because of these reasons we use Two Stage Least Squares (2SLS), instrumenting for landings in the first stage using biomass levels of the past two years as instruments. These are good instruments because supply is affected by past biomass levels, while demand is not. In the NEA cod fishery, ex-vessel prices and export prices are co-integrated (Asche et al. 2002) and therefore one can use the price flexibility to construct segment-specific linear demand functions. Hence, our regression model is
where \(P_t\) is the deflated export price of cod, \(Q_t\) are the total landings of the whole stock of NEA cod, \(I_t\) is our list of instruments, \(W_t\) is our list of control variables, and \(\epsilon _t\) is the error term. As control variable we include disposable income (given by real GDP in Europe), and the price of a substitute white fish product (Saithe, Pollachius virens). The time series for landings and biomass suffer from autocorrelation. We therefore estimate Eq. (8) as an ARMA(1,1) process. Following Fair (1984), the lagged values of \(P_t\) and \(Q_t\) will be added to the list of instruments; see also Pindyck and Rubinfeld (1991). We obtain the following estimates (with standard errors in parentheses):

and an adjusted R\(^2\) of 0.97 and a Durbin–Watson (DW) statistic of 1.27. We find that the price flexibility is 0.5 (implying that the export price of cod falls by 0.5% if the supply of cod increases by 1%). The DW statistic suggests that we may not have fully succeeded in solving the issue of autocorrelation, but several robustness tests corroborate these findings.Footnote 14
The price flexibility can be used to construct linear demand functions for all vessel segments by using landings and price data for the four vessel types for the year 2006. The average inflation-corrected ex-vessel price obtained for one kilogram of cod fish are 17.88 NOK for coastal vessels, 19.91 NOK for trawlers, and 22.43 NOK for large longliners. Together with the price flexibility, and the information that 537,642 tonnes of cod were landed in 2006, we can solve for the parameters in a linear demand function.Footnote 15 The price of a kilogram of cod is given in our model as:
3.3 Estimating the Biological Model
Net growth of a fish stock is typically dependent on total stock size and various environmental factors, which may increase or inhibit stock productivity. For NEA cod, the most important environmental factors are interactions with other species and climate, in particular temperature (Ottersen et al. 2006; Hjermann et al. 2007). There are several channels through which climate may affect cod recruitment (Kjesbu et al. 2014). First, temperature may have an effect on the intrinsic growth rate of cod (Brander 1995). However, for NEA cod temperature affects very young individuals differently than old ones, making the overall effect on the population somewhat ambiguous (Kjesbu et al. 2014). Second, warmer years may lead to enhanced recruitment independent of the size of stock biomass (Hjermann et al. 2007). Third, a warmer climate may increase the carrying capacity, which is effectively facilitated by a range expansion into Northern waters (Ottersen et al. 1998; Kjesbu et al. 2014). Concerning multi-species interactions, capelin (Marshall et al. 1999) and Norwegian Spring-Spawning (NSS) herring (Clupea harengus) are the two most important fish species that the cod interacts with (Hjermann et al. 2007). Herring feeds on capelin larvae (Gjøsæter and Bogstad 1998) and is therefore competing with cod for the prey species capelin.
Our starting point is the canonical model of renewable resources in discrete time (Conrad and Clark 1987), where the annual change of the resource stock is given by
where r is the intrinsic population growth rate, K is the carrying capacity, \(X_{t-1}\) is biomass and \(Q_{t-1}\) is the amount harvested. We augment the model by considering climatic forces that are transmitted through (i) the growth rate, (ii) the carrying capacity, (iii) random recruitment. As a climatic variable, we include the sea surface temperature that stretches from the Kola meridian transect (\(33^{\circ }50\)E, \(70^{\circ }50\)N to \(72^{\circ }50\)N) in the winter months prior to the spawning season (November–March), which has been shown to be a good indicator for NEA cod recruitment (Bochkov 1982; Tereshchenko 1996; Ottersen and Stenseth 2001). To facilitate comparability, we use deviations from the average temperature, which sum up to zero when aggregating over all years. In addition, we consider potential predator-prey interactions with herring and capelin. Following Hjermann et al. (2007), we include biomass data for capelin and juvenile herring. Again, we do not include absolute values, but deviations from the average biomass levels. We use ordinary least squares to estimate
where \(\epsilon _t\) are unobserved scalar errors, and Env\(_{t}\) is a vector of the various environmental interactions. Table 3 gives the regression results.
Model 1 gives the standard logistic growth model without any environmental covariates. Model 2 allows for random recruitment and shows that temperature has a positive and significant effect on net growth. Model 3 shows—in line with Kjesbu et al. (2014)—that temperature has no significant effect on the growth rate of cod. Model 4 indicates weak evidence for temperature having significant effect (at the 10% level) on carrying capacity. Concerning multi-species interactions, model 5 does not find any evidence for an interaction effect with herring, while model 6 finds a positive and significant relationship for capelin. When it comes to selecting the best model, the AIC suggests that model 6, which contains climatic and multi-species effects gives the best fit. The drawback of this model is that it uses only 40 years of data (compared to 63 years in all other specifications). For this reason, we selected model 4 as our baseline model, as it performs best of all models exploiting the full range of data. In general, we find that the estimates for the intrinsic growth rate and carrying capacity are very similar across all models, comforting us that the results are robust and the appropriate model can be selected based on the scientific question at hand.
In general, \(\beta _1\) gives the point estimate for the intrinsic population growth rate r, and \(-\beta _1/\beta _0\) is our point estimate for K. Using the estimates from model 4, the growth function (in tonnes) of cod reads as
The total biomass that supports a maximum sustainable yield (MSY) stock thus equals 816,000 tonnes of cod, and the associated MSY stock is equal to 2.85 million tonnes.
4 Results
We can now use the estimates obtained in Sect. 3 to derive the optimal quota size per vessel of each segment, the optimal amount of biomass, and the associated economic profits as indicated in Sect. 2. We start by calculating the optimal scale of operation \(e^*_{z}\) (measured in tonnage-days, td) for each of the three segments. We find that the optimal amount of effort is 5100 td for coastal vessels, 74,650 td for trawlers and 174,900 td for longliners. This large range partly reflects the fact that trawlers and longliners are much bigger than coastal vessels, but it mostly mirrors the differences in effort-output elasticity; see Table 2.
We proceed by analyzing how an optimal total allowable catch would look like for the different vessel segments. Formally, this is the solution to the dynamic optimization problem in “Appendix 3” assuming \(\theta _L=1\) and \(\theta _C=\theta _T=0\) for the case of longliners. \(\theta _T=1\) represents the case of trawlers, and \(\theta _C=1\) considers the case of having only coastal vessels. These stylized cases are useful to shed light on the question whether the different vessel segments require different TAC in optimum. The results are presented for discount rates (\(\delta \)) of 0, 3, and 10% in Table 4. First, and perhaps surprisingly, we find that discounting has a negligible impact on optimal management. The optimal biomass levels for a discount rate of 0% are >1% smaller than for a discount rate of 10%. The intuitive explanation is that it does not make economic sense to increase harvest beyond a certain point, because the drop in price (and to a lesser extent higher search cost) outweigh any gains accruing from higher yield irrespective of discounting; see Eq. (25). Indeed, independent of the fleet composition, we find that the optimal biomass is always larger than the MSY stock of 2.85 million tonnes of cod. Hence, search costs and the price effect outweigh the impact of discounting (even when using a discount rate of \(10\%\)). Further, we find that longliners are the most profitable segment, while trawlers are about \(7\%\) less profitable and coastal vessels are about half as profitable.Footnote 16 Finally, we find that trawlers and longliners would call for a very similar TAC in optimum (around 600,000 tonnes), while coastal vessels would require a little >500,000 tonnes in optimum.
We now turn towards analyzing the effects of the institutional constraints we have theoretically analyzed in Sect. 2. From now on we will proceed assuming a discount rate of \(3\%\). The first-best situation is the one where there are no constraints on quota trade and entry. In such a case, only the most profitable vessels—longliners—would participate in the fishery. The first-best situation can be derived from Table 4, where 125 longliners participate in the fishery harvesting 604,000 tonnes of fish. Annual profits are 8.42 billion NOK and the equilibrium biomass level is 4.28 million tonnes. In Fig. 2, we present efficiency losses as deviations from those optimal values. The first-best case is included for comparison. We find that under the presence of quota trade constraintsFootnote 17 (i.e. using also vessels from less efficient segments) it would be (second) best to reduce equilibrium harvests by about \(7\%\), which will then lead to an increase in biomass by \(3\%\).
The relative changes to profits (\(\pi \)), harvest (H) and stock biomass (X) under different scenarios. The different colors in the bars for profits and harvest represent the relative contribution of the different fleet segments. The different scenarios are: a first-best (no constraints), b Quota trade constraints, c entrance constraints, d MSY (maximize yield, no constraints), e status quo (maximize yield and quota trade constraints)
The loss in profits is 26%, reflecting the loss from employing less efficient vessels, both in terms of costs of operation, but also lower revenues. The entrance constraintsFootnote 18 on the other hand, lead only to a 1% loss for the fishing fleet. The reason is that the entire harvest can be caught by the most efficient segment—longliners. The constraint is however binding, since the vessels operate beyond \(e^*_L\)—see the first upward sloping line in Fig. 1c. If the policy objective is to maximize yield, rather than profits, we find that profits are \(21\%\) lower compared to the first-best. This loss in profits is primarily transmitted through the lower price, which is only partially offset by an increase in harvests by \(36\%\). Apart from having a too high TAC there are no further efficiency losses, since there are no further institutional constraints. Hence, the entire TAC is caught by longliners operating at the optimal scale \(e^*_L\). Finally, we proceed by analyzing the status quo: there are quota tradability constraints and in addition yield is maximized. We find that under the presence of those constraints, economic profits are half as large as under the first-best scenario. It is noteworthy that this loss is larger than the sum of just having quota trade constraints and pursuing MSY as a policy objective. Intuitively, a too high harvest aggravates the efficiency loss of the quota trade constraints.
We proceed by analyzing the sensitivity of our results with respect to some of the key parameters in Fig. 3. In particular, we analyze a change in two standard deviations (SD) of (i) variable costs, (ii) elasticity of demand, and (iii) carrying capacity.Footnote 19 The probability of a change by two sd is about 5% under the assumption that the data is normally distributed. The purpose of this analysis is to gauge how robust management is to external changes that may occur in the future.
Sensitivity of results with regard to key external factors that are often mentioned as drivers that may influence the fishery in the future. We consider a two standard deviation (SD) change in (i) variable costs, (ii) elasticity of demand, (iii) carrying capacity. The probability of a two SD change is about 5% if the data is normally distributed
First, we analyze how a change in variable costs alter optimal management. Such change may be brought about by technological innovations (a reduction in costs), but also a change in fuel costs, or alternative activities, such as oil exploitation, raising the cost to hire suitable crew members. Not surprisingly, a reduction in variable costs by two sd leads to a higher TAC (by \(6\%\)) and an increase in profits by \(11\%\). An increase in costs shows the opposite picture—-a decrease in TAC by \(5\%\) and a decrease in profits by \(10\%\). A change in elasticity of demand may be brought about by shifting consumer preferences, but also by market developments of substitute species, such as a large expansion of aquaculture in Asia. We find that a decrease in price elasticity increases the TAC by \(23\%\) and increases profits by \(9\%\). An increase in price elasticity calls for a reduction of the TAC by \(14\%\), but only to a \(1\%\) decrease in profits. Carrying capacity may be altered, for example, by range expansion brought about by climatic changes. A reduction of carrying capacity, leads to a \(6\%\) reduction in profits and TAC. An increase in the carrying capacity leads to an increase by \(6\%\) in profits and \(5\%\) in TAC, while biomass increases by \(30\%\).
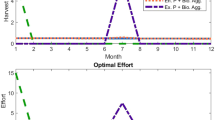
Optimal paths towards the steady states of a biomass, b harvests, and c the shadow value \(\phi _t\) for the first-best situation (dark line with circles), quota trade constraints (grey line with squares), and entrance constraints (light line with stars). Starting values are the observed biomass and harvest levels for 2013, the latter being so high that the shadow value is negative. From the second year on, optimal harvest levels are slightly lower than the steady state values, which are gradually approached. In c, an axis break has been inserted between \(-14\) and 0 to improve visualization (indicated by two small bars)
While the main analysis gives steady state values, we have also calculated optimal trajectories, using the observed values in 2013 as starting values; see Fig. 4.Footnote 20 Remarkably, the harvest level in 2013 is much higher than what we found to be optimal, and so high that marginal profits are negative, which is due to the demand effect. Additional revenues from an increase in landings are more than outweighed by the drop in price, which is reflected by the negative shadow value for 2013. From the second year on, optimal harvest levels are slightly lower than the steady state values, which are gradually approached as biomass levels increase. The optimal trajectories for catch shares and effort unfold as follows: for the first-best situation, only longliners are operating. While their number changes (following the harvest level), each longliner operates at the optimal effort scale. If quota trade constraints are imposed, the distribution of catch over the different segments is fixed (by definition). Again, the number of vessels change over time and follow the harvest, but effort is always at the (segment-specific) optimal scale for each vessel in operation. Finally, if entrance constraints are in place, all longliners in the fleet are operating and their number does not change. Effort levels are higher than optimal and follow harvest levels.
5 Conclusion and Discussion
In this paper we developed a model portraying a fishery in which the TAC is set by a scientific body for a set of institutional constraints that are imposed by policy makers. The model allows us to determine the optimal allocation of a TAC with and without restrictions of transferability of quotas between segments and entrance of vessels. Our application to the Northeast Arctic (NEA) cod fishery shows that tradability constraints lead to welfare losses of 26% in this case, which amounts to about 2.2 billion NOK. Entrance constraints lead to much smaller welfare losses (110 million NOK), as there are only welfare losses due to operating beyond the efficient scale, but not by using an inferior vessel type. The welfare losses of pursuing an MSY strategy are substantial as well, amounting to 1.75 billion NOK. Interestingly, the combination of quota trade constraints and pursuing an MSY strategy—a scenario that is somewhat close to the status quo—amounts to the largest losses (about 4.16 billion NOK) and to larger losses than the sum of both welfare losses in isolation. The key lesson here is that if the policy objective is not to maximize economic welfare, but something else, such as maximum yield, this could aggravate welfare losses from other restrictions in place. This finding is in line with literature on “immiserizing growth” (Bhagwati 1968; Brander and Taylor 1998) that shows that welfare losses from one distortion can be magnified by an increase in production.
Management of the NEA cod fishery is inherently complex, and any useful model—as the one developed here—has inevitably to sacrifice certain details. First of all, this study ignores important ecosystem effects. At the end of the year, the mature fish migrate out of the Barents Sea for about 3 months to spawn, returning to the feeding grounds in spring. The cod eggs drift up along the Norwegian coast and the immature fish stay in the feeding grounds until maturation when they start reproducing. Obviously, management could be substantially improved by acknowledging the age-structure and the productivity of the stock (Diekert et al. 2010). Second, and in a similar vein, the fact that older cod tend to cannibalize on younger cod may have management implications that are ignored here (Armstrong and Sumaila 2000). Third, if harvesting pressure is very high this may induce an evolutionary response that leads to economic repercussions (Eikeset et al. 2013a). Fourth, food-web dynamics and climate interactions may be more complex than sketched in our biological model. In particular, climate also plays an important role in ecosystem dynamics through fish physiology, competition and feeding relationships between the different species; especially as in our case, between cod, capelin and herring, and the lower trophic levels, zooplankton (Stige et al. 2010; Roderfeld et al. 2008). See Kjesbu et al. (2014) and Diekert and Schweder (2017) for studies that look at the interaction of climate and management. Finally, we focus our analysis on steady state harvest levels, while in reality the NEA cod fishery is managed via a harvest control rule. See Eikeset et al. (2013b) for a study that derives optimal harvest control rules for the NEA cod fishery.
Furthermore, while we include multi-species interactions below the sea-surface and on the marketplace in our analysis, we do not consider optimal management of a multi-species fishery (Kasperski 2015). This would be an interesting avenue for further research, though in reality the fishery is managed from a single-species perspective. Also, it is not feasible to have optimal multi-species management in a model that is analytically tractable and detailed at the fleet level like this one. Further, we assume that each segment can be represented by a typical boat, which is a common assumption (Salvanes and Squires 1995). Yet, in reality, a fleet comprises many boats that differ in age, size, productivity, and costs, which is not accounted for in our model. Finally, we restrict our analysis to the Norwegian fleet, while in practice, NEA cod is jointly managed and shared between Norway and Russia (Eide et al. 2012).
In our model, we kept it deliberately open how the policy makers decide, in particular whether policy preferences are stable (and random), the result of lobbyism, or reflecting the full array of preferences society holds concerning how natural resources should be optimally managed. This allowed us to take political preferences as constraints, while preserving the normative foundation on which the scientific body makes their decision. Obviously, it would be very interesting to endogenize the political preferences, ideally allowing for a strategy space that does not only include profit maximization. Environmental considerations, for example, are now higher on the political agenda than some years ago. The voices that suggest to rely more on small scale coastal vessels because they are less destructive for the habitat, use less fuel, and contribute more to quality of life in coastal villages are certainly getting louder. These institutional processes behind the scene of the fisheries management are not always visible, but they are certainly dynamic and part of the slowly evolving social-ecological system. Taking these institutional dynamics into account in combination with normative analysis as presented here seems like an exciting avenue for further research.
Notes
Our model is obviously an abstraction from reality, where science and policy are much more intervowen (Eide et al. 2012; Kvamsdal et al. 2016). The actual TAC is set by the joint Norwegian–Russian Commission that sometimes deviates from ICES recommendations. Also, policy makers, who decide on how to allocate the quota, are advised by a committee that comprises various stakeholders and also scientists.
In addition, there are also restrictions on who is entitled to enter the fishery, but these are outside the scope of Kroetz et al. (2015).
This framework has been extended by Anderson (2000) to account for disaggregated fleet behavior and considering several tactical tools, such as effort restrictions or trip limits, temporal closures, or an aggregate quota. Da Rocha and Gutiérrez (2012) have included uncertainty and stochasticity of the resource stock into a similar framework. An important addition has been made by Homans and Wilen (2005) by considering not only the cost side, but also the revenue side by distinguishing revenues that can be obtained for frozen and fresh fish. Finally, Valderrama and Anderson (2010) have addressed the case for a limited-entry fishery.
Nevertheless, there are three areas where multispecies aspects play an important role, which we take into account as follows: First, multispecies aspects are important on the demand side, where other whitefish species caught in the Barents Sea serve as (weak) substitutes in some markets. When estimating the demand schedule in Sect. 3.2, we therefore include the substitute species Saithe (Pollachius virens) as a control. Second, although the cod fishery is the most important fishery for most vessels, it is not the only fishery that the boats participate in over the year. When estimating the production function in Sect. 3.1, we carefully select those boats that target cod out of the sample of all Norwegian boats and scale their effort by the degree to which their landings come from this fishery. Third, multispecies aspects play a large biological role, of course. In Sect. 3.3, when we estimate the biological growth function, we go at length to include possible biotic and abiotic interactions.
Quota transfer within segments is typically approved by authorities, though the legal basis has yet to be clarified. However, there are some restrictions on transferability between regions and a deduction of the quota takes place upon transfer. Also, there are entrance constraints via vessel licenses and annual permits. In addition, there are typical technical regulations, such as a minimum mesh size, trawl closure areas and some subsidies when it comes to decommissioning vessels; see Armstrong et al. (2014) for a comprehensive overview of regulation.
Other studies have provided similar estimations for the Norwegian fleet of trawlers for different years. Salvanes and Squires (1995), Asche (2009), and Jensen (2007) have estimated a translog cost function, while Diekert (2013) and Guttormsen and Roll (2011) have estimated a Cobb-Douglas production function. Kumbhakar et al. (2013) have estimated return to the outlay, i.e. optimal quantities of inputs and outputs jointly chosen.
Importantly, we were able to pool the data from all Norwegian coastal vessels: The directorate usually publishes its data in two separate sections, classifying a boat as belonging to the “demersal fleet” when more than 50% of its harvest is from demersal species and as belonging to the “pelagic fleet” otherwise. However, as the harvest composition varies substantially from year to year, it is important to obtain data from all boats, regardless of classification. This allows us to study the fate of a boat even if, for example, 52% of its catch are demersal species in 2008 (and it is listed in the demersal dataset) and 48% of its catch are demersal species in 2009 (and it is listed in the pelagic dataset).
There are some caveats that are worth mentioning. First, we estimate our model for a given institutional context that was present at the time of the data. Therefore, we implicitly assume that our estimations carry over to alternative institutional settings. Second, when estimating the production function, we treat biomass as an exogenous variable. In reality, the fate of the stock depends on the decisions taken by the scientific body, as addressed in the theoretical model. Considerations such as profitability may play a role here, so there may be an endogeneity issue (although biomass will still be exogenous to the single vessel owner). Third, the biological data are the result of stock assessments which are obviously imperfect and essentially model outcomes. Therefore, any biases or errors from stock assessment will find its way into our model as well.
If the minimizing-cost assumption holds, it is actually preferred to estimate the cost function using a flexible form and infer the production function from the prices of the inputs and outputs. After all, one does not need to assume a certain technological structure a priori (as we did in Eq. 1) and it is statistically more efficient because the cost function and the first-order condition for cost minimization can be estimated jointly. However, there are a number of practical reasons that make this approach less appealing in fisheries (Felthoven and Morrison Paul 2004). First of all, the standard cost function approach cannot be applied because one of the inputs in the production process, biomass, cannot be chosen freely by individual fishermen, and introducing quasi-fixed factors in the cost function typically complicates the estimation procedure considerably (van Soest et al. 2006). Second, fishermen are unlikely to always operate at minimum costs at all times. Markets are usually incomplete, fishermen face informational constraints, and payments of all inputs are not always determined by market prices directly because crew members may receive shares of the harvesting revenues rather than a fixed wage (McConnell and Price 2006; Sandberg 2006). Finally, it is not necessarily the case that all fishermen always try to maximize profits because other considerations (including status seeking) may also play a role (Gezelius 2007; Holland 2008). Given that we have good data on input and output quantities, we estimate the cost and production functions directly.
This poses a particular problem if the skipper effect is positively correlated with the size of the boat, which may be the case if the best skippers run the largest boats. In that case, a model estimated with random effects would be inconsistent, and one would have to use vessel-specific fixed effects.
In 2010, one NOK was about 0.15 US dollars.
Eide et al. (2003), however, find an effort-output elasticity larger than one, which is unexpected for a demersal fishery. This result may be explained by the fact that they use daily data, where effort is given by hours of trawling—marginally decreasing returns do not necessarily materialize in the very short run.
Estimating the model as an ARIMA (0,1,0) process gives a price flexibility of 0.40, for a Durbin Watson of 1.92, but the model has in general less explanatory power (indicated by the AIC). Our results are also fairly robust towards adding or omitting instruments. Finally, using export quantity, rather than landing, gives a price flexibility of 0.61. These robustness checks support our finding of a price flexibility of 0.5.
For a linear demand function \(Q= a - bP\), the price elasticity \(\Delta Q/ \Delta P (P/Q)\) is equal to \(-b(P/Q)\). Knowing P, Q, and b, one can also calculate the choke price a.
Guttormsen and Roll (2011) (G&R) estimate technical efficiency for the same fishery and conclude that trawlers are the most efficient segment. Our results may be different for several reasons. First, the time period of the data used by G&R and our study is different. Second, while our study uses a Cobb Douglas function with effort and biomass as inputs, G&R estimate a Cobb Douglas function with labor, capital, and fuel. Third, while we estimate segment-specific coefficients, G&R assume coefficients to be the same for all segments. The fixed effects are then interpreted as a measure of efficiency. Fourth, we look at landings values, taking into account differences in prices between segments, while G&R only look at quantity of landings. Finally, G&R find a large diversity within groups (which we do not look at). Even though trawlers—as a group—are most efficient, the most efficient vessel is a longliner, which is also in line what we find.
In 2013, \(43\%\) of all harvests were caught by trawlers, \(46\%\) by coastal vessels, and \(11\%\) by longliners (Fiskeridirektoratet 2013). Therefore, we set \(\theta _T = 0.43\), \(\theta _C = 0.46\) and \(\theta _L = 0.11\).
In 2013, 24 longliners, 40 trawlers, and 993 coastal vessels were active in the Norwegian cod fishery (Fiskeridirektoratet 2013), which will be used as the maximum number of vessels from each segment that can be employed.
The following parameter values were used: (A) decrease in costs: \(v_L=0.15\), increase in costs: \(v_L=0.23\). (B) decrease in demand elasticity to 0.3: \(a_L=29.17, b_L= - 1.25 \times 10^{-8} Q_t\), increase in demand elasticity to 0.7: \(a_L=38.14, b_L=- 2.92 \times 10^{-8} Q_t\). (C) decrease in carrying capacity: \(K=4817544\), increase in carrying capacity: \(K=6970714\).
Optimal trajectories have been found by using the fmincon program of Matlab, which finds the minimum or maximum of the constrained nonlinear multivariable function.
Available at: http://www.ices.dk/community/groups/Pages/AFWG.aspx.
The OECD data has been accessed via www.SourceOECD.org/database/OECDStat.
References
Aanesen M, Armstrong CW (2016) The political game of European fisheries management. Environ Resour Econ 63(4):745–763
Anderson L (2000) Open access fisheries utilization with an endogenous regulatory structure: an expanded analysis. Ann Oper Res 94(1–4):231–257
Armstrong CW, Eide A, Flaaten O, Heen K, Kaspersen IW (2014) Rebuilding the Northeast Arctic cod fisheries–economic and social issues. Arct Rev 5(1):11–37
Armstrong CW, Sumaila UR (2000) Cannibalism and the optimal sharing of the North-East Atlantic cod stock: a bioeconomic model. J Bioecon 2:99–115
Arnason R, Sandal L, Steinshamn S, Vestergaard N (2004) Optimal feedback controls: comparative evaluation of the cod fisheries in Denmark, Iceland, and Norway. Am J Agric Econ 86(2):531–542
Asche F (2009) Adjustment cost and supply response in a fishery: a dynamic revenue function. Land Econ 85(1):201–215
Asche F, Bjørndal T, Gordon DV (2009) Resource rent in individual quota fisheries. Land Econ 85(2):279–291
Asche F, Chen Y, Smith MD (2015) Economic incentives to target species and fish size: prices and fine-scale product attributes in Norwegian fisheries. ICES J Mar Sci 72(3):733–740
Asche F, Flaaten O, Isaksen JR, Vassdal T (2002) Derived demand and relationships between prices at different levels in the value chain: a note. J Agric Econ 53(1):101–107
Bhagwati JN (1968) Distortions and immiserizing growth: a generalization. Rev Econ Stud 35(4):481–485
Bochkov Y (1982) Water temperature in the 0–200m layer in the Kola-Meridian in the Barents sea, 1900–1981. Sb Nauchn Trud PINRO 46:113–122
Boyce JR (2004) Instrument choice in a fishery. J Environ Econ Manag 47(1):183–206
Brander JA, Taylor SM (1998) Open access renewable resources: trade and trade policy in a two-country model. J Int Econ 44(2):181–209
Brander K (1995) The effect of temperature on growth of atlantic cod (Gadus morhua L.). ICES J Mar Sci 52(1):1–10
Conrad J, Clark C (1987) Natural resource economics. Cambridge University Press, Cambridge
Da Rocha JM, Gutiérrez MJ (2012) Endogenous fishery management in a stochastic model: why do fishery agencies use TACs along with fishing periods? Environ Resour Econ 53(1):25–59
Diekert FK, Hjermann DØ, Nævdal E, Stenseth NC (2010) Spare the young fish: optimal harvesting policies for North-East Arctic cod. Environ Resour Econ 47(4):455–475
Diekert FK (2013) The growing value of age: exploring economic gains from age-specific harvesting in the Northeast Arctic cod fishery. Can J Fish Aquat Sci 70(9):1346–1358
Diekert FK, Schweder T (2017) Disentangling effects of policy reform and environmental changes in the norwegian coastal fishery for cod. L Econ (forthcoming)
Eide A, Heen K, Armstrong CW, Flaaten O, Vasiliev A (2012) Challenges and successes in the management of a shared fish stock–the case of the Russian-Norwegian Barents sea cod fishery. Acta Boreal 30(1):1–20
Eide A, Skjold F, Olsen F, Flaaten O (2003) Harvest functions: the Norwegian bottom trawl cod fisheries. Mar Resour Econ 18(1):81–93
Eikeset AM (2010)The ecological and evolutionary effects of harvesting Northeast Arctic cod—insights from economics and implications for management. PhD thesis, University of Oslo
Eikeset AM, Richter A, Dunlop ES, Dieckmann U, Stenseth NC (2013a) Economic repercussions of fisheries-induced evolution. Proc Nat Acad Sci 110(30):12259–12264
Eikeset AM, Richter AP, Dankel DJ, Dunlop ES, Heino M, Dieckmann U, Stenseth NC (2013b) A bio-economic analysis of harvest control rules for the Northeast Arctic cod fishery. Mar Policy 39:172–181
Fair R (1984) Specification, estimation, and analysis of macroeconometric models. Harvard University Press, Cambridge
Felthoven RG, Morrison Paul CJ (2004) Multi-output, nonfrontier primal measures of capacity and capacity utilization. Am J Agric Econ 86(3):619–633
Fiskeridirektoratet (2013) Profitability survey on the Norwegian fishing fleet. Technical report, Fiskeridirektoratet
Gezelius S (2007) The social aspects of fishing effort. Hum Ecol 35(5):587–599. doi:10.1007/s10745-006-9096-z
Gjøsæter H, Bogstad B (1998) Effects of the presence of herring (Clupea harengus) on the stock–recruitment relationship of barents sea capelin (Mallotus villosus). Fish Res 38(1):57–71
Godø OR (2003) Fluctuation in stock properties of North-East Arctic cod related to long-term environmental changes. Fish Fish 4(2):121–137
Grafton R, Arnason R, Bjørndal T, Campbell D, Campbell H, Clark C, Connor R, Dupont D, Hannesson R, Hilborn R (2006) Incentive-based approaches to sustainable fisheries. Can J Fish Aquat Sci 63(3):699–710
Guttormsen AG, Roll KH (2011) Technical efficiency in a heterogeneous fishery: the case of Norwegian groundfish fisheries. Mar Resour Econ 26(4):293–307
Hannesson R (2004) The privatization of the oceans. MIT Press, Cambridge
Hersoug B (2005) Closing the commons: Norwegian fisheries from open access to private property. Eburon, Delft
Hersoug B, Holm P, Rånes SA (2000) The missing T. path dependency within an individual vessel quota system—the case of Norwegian cod fisheries. Mar. Policy 24(4):319–330
Hjermann DØ, Bogstad B, Eikeset AM, Ottersen G, Gjøsaeter H, Stenseth NC (2007) Food web dynamics affect Northeast Arctic cod recruitment. Proc R Soc B Biol Sci 274(1610):661–669
Holland D (2008) Are fishermen rational? A fishing expedition. Mar Resour Econ 23(3):325–344
Homans FR, Wilen JE (1997) A model of regulated open access resource use. J Environ Econ Manag 32(1):1–21
Homans FR, Wilen JE (2005) Markets and rent dissipation in regulated open access fisheries. J Environ Econ Manag 49(2):381–404
Huang L, Smith MD (2014) The dynamic efficiency costs of common-pool resource exploitation. Am Econ Rev 104(12):4071–4103
Jensen S (2007) Catching cod with a translog. Master’s thesis, Department of Economics, University of Oslo
Johnson RN, Libecap GD (1982) Contracting problems and regulation: the case of the fishery. Am Econ Rev 1005–1022
Karpoff JM (1987) Suboptimal controls in common resource management: the case of the fishery. J Polit Econ 95(1):179–194
Kasperski S (2015) Optimal multi-species harvesting in ecologically and economically interdependent fisheries. Environ Resour Econ 61(4):517–557
Kjesbu OS, Bogstad B, Devine JA, Gjøsæter H, Howell D, Ingvaldsen RB, Nash RD, Skjæraasen JE (2014) Synergies between climate and management for Atlantic cod fisheries at high latitudes. Proc Nat Acad Sci 111(9):3478–3483
Kroetz K, Sanchirico JN, Lew DK (2015) Efficiency costs of social objectives in tradable permit programs. J Assoc Environ Resour Econ 2(3):339–366
Kronbak L (2004) The dynamics of an open access fishery: Baltic sea cod. Mar Resour Econ 19(4):459–480
Kugarajh K, Sandal L, Berge G (2006) Implementing a stochastic bioeconomic model for the North-East Arctic cod fishery. J Bioecon 8(1):35–53
Kumbhakar SC, Asche F, Tveterås R (2013) Estimation and decomposition of inefficiency when producers maximize return to the outlay: an application to Norwegian fishing trawlers. J Prod Anal 40(3):307–321
Kvamsdal SF, Eide A, Ekerhovd N-A, Enberg K, Gudmundsdottir A, Hoel AH, Mills KE, Mueter FJ, Ravn-Jonsen L, Sandal LK (2016) Harvest control rules in modern fisheries management. Elem Sci Anthropocene 4(1):000114
Maddison A(2010) Historical Statistics of the World Economy. Groningen Growth and Development Center
Marshall CT, Yaragina NA, Lambert Y, Kjesbu OS (1999) Total lipid energy as a proxy for total egg production by fish stocks. Nature 402(6759):288–290
McConnell KE, Price M (2006) The lay system in commercial fisheries: origin and implications. J Environ Econ Manag 51(3):295–307
Mikalsen KH, Jentoft S (2008) Participatory practices in fisheries across Europe: making stakeholders more responsible. Mar Policy 32(2):169–177
Norwegian Directorate of Fisheries (annually). Lønnsomhetsundersøkelser for helårsdrivende fiskefartøy. Technical report, Fiskeridirektoratet, Bergen, Norway
Ottersen G, Hjermann D, Stenseth NC (2006) Changes in spawning stock structure strengthens the link between climate and recruitment in a heavily fished cod stock. Fish Oceanogr 15(3):230–243
Ottersen G, Michalsen K, Nakken O (1998) Ambient temperature and distribution of North-East Arctic cod. ICES J Mar Sci 55(1):67–85
Ottersen G, Stenseth NC (2001) Atlantic climate governs oceanographic and ecological variability in the barents sea. Limnol Oceanogr 46(7):1774–1780
Pindyck R, Rubinfeld D (1991) Econometric models and economic forecasts, 3rd edn. McGraw Hill, London
Roderfeld H, Blyth E, Dankers R, Huse G, Slagstad D, Ellingsen I, Wolf A, Lange MA (2008) Potential impact of climate change on ecosystems of the Barents sea region. Clim Change 87(1–2):283–303
Salvanes KG, Squires D (1995) Transferable quotas, enforcement costs and typical firms: an empirical application to the Norwegian trawler fleet. Environ Resour Econ 6(1):1–21
Sandberg P (2006) Variable unit costs in an output-regulated industry: the fishery. Appl Econ 38(9):1007–1018
Squires D (2009) Opportunities in social science research. In: Beamish RJ, Rothschild BJ (eds) The future of fisheries science in North America, vol 31., Fish & Fisheries seriesSpringer, Dordrecht, pp 637–696
Squires D, Kirkley J (1999) Skipper skill and panel data in fishing industries. Can J Fish Aquat Sci 56(11):2011–2018
Standal D (2008) The rise and fall of factory trawlers: an eclectic approach. Mar Policy 32(3):326–332
Stige LC, Ottersen G, Dalpadado P, Chan K-S, Hjermann DØ, Lajus DL, Yaragina NA, Stenseth NC (2010) Direct and indirect climate forcing in a multi-species marine system. Proc R Soc B Biol Sci 277(1699):3411–3420
Tereshchenko V (1996) Seasonal and year-to-year variations of temperature and salinity along the kola meridian transect. ICES C.M., p C:11
Timmer M, Richter A (2009) Estimating terms of trade levels. Groningen Growth and Development Centre Working Paper
Valderrama D, Anderson JL (2010) Market interactions between aquaculture and common-property fisheries: recent evidence from the Bristol Bay sockeye salmon fishery in Alaska. J Environ Econ Manag 59(2):115–128
van Soest DP, List JA, Jeppesen T (2006) Shadow prices, environmental stringency, and international competitiveness. Eur Econ Rev 50(5):1151–1167
Weninger Q (1998) Assessing efficiency gains from individual transferable quotas: an application to the mid-Atlantic surf clam and ocean quahog fishery. Am J Agric Econ 80(4):750–764
Weninger Q, Just R (1997) An analysis of transition from limited entry to transferable quota: non-Marshallian principles for fisheries management. Nat Resour Model 10(1):53–83
Wilen JE (2000) Renewable resource economists and policy: what differences have we made? J Environ Econ Manag 39(3):306–327
Acknowledgements
We are grateful to Linda Nøstbakken and Martin Quaas, as well as the editor and two anonymous reviewers for valuable comments on a previous version of this manuscript. We thank Per Sandberg from the Directorate of Fisheries (Bergen, Norway) for providing the data on individual vessels and very helpful advice and discussions concerning this data. We are also grateful to Bjarte Bogstad and Geir Ottersen from the Institute of Marine Research (Bergen, Norway) for providing some of the biological data and helpful advice. The authors gratefully acknowledge funding from the Norwegian Research Council (grant agreements 243892 & 215831). This paper is a deliverable of the project Green Growth Based on Marine Resources: Ecological and Socio-Economic Constraints (GreenMAR), which is funded by Nordforsk.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Minimal Cost of Catching Group Quota \({\bar{H}}_{z,t}\) for Fleet Segment z
We assume that each segment can be represented by a typical boat (Salvanes and Squires 1995) and find the efficient solution to harvest a given group quota \({\bar{H}}_{z,t}\) by choosing the optimal number of vessels \(N^*_{z,t}\) operating at scale \(e^*_{z,t}\) minimizing total cost. Formally, the problem is given as
The corresponding Lagrangian is \(\mathcal {L} = N_{z,t} (f_z + v_z e_{z,t}) - \lambda N_{z,t} (q_zX_t^{\alpha _z}e_{z,t}^{\beta _z})\) and the first order conditions are:
Re-writing (14) as \(\lambda = \frac{f_z + v_z e_{z,t} }{q_zX_t^{\alpha _z}e_{z,t}^{\beta _z}}\) and inserting this into (15) gives the efficient effort level per vessel
We can proceed by finding an optimal number of vessels \( N^*_{z,t}\) that harvest the group quota \({\bar{H}}_{z,t}\). Combining Eqs. (1) and (16) gives \( N^*_{z,t} = \frac{1}{ \left( \frac{\beta _z}{1-\beta _z}\frac{f_z}{v_z}\right) ^{\beta _z}} \frac{{\bar{H}}_{z,t}}{q_zX_t^{\alpha _z}}\). Thus, the total costs of catching \({\bar{H}}_{z,t}\), described in Eq. (3), is given as
Appendix 2: First-Best Allocation
The scientific body chooses the total quota \(Q_t\) for the whole fleet (i.e. \(Q_t = \sum _z H_{z,t}\)) that maximizes the net present value of the fishery. The quota allocation between different segments is determined by a market mechanism (e.g. an auction). As a result, each segment z holds a share of the total quota \(\theta _{z,t}\ge 0\), so that \(H_{z,t} = \theta _{z,t} Q_t\). While it is not important to know \(\theta _{z,t}\) to allocate \(Q_t\) most efficiently (the market takes care of that), this information is needed to set the total quota optimally. This happens because the optimal quota depends on costs and revenues—which both depend on \(\theta _z\). Formally, the problem is given as
Call the discrete time Hamiltonian corresponding to this problem \(\mathcal {H}^{fb}\), and let \(\phi _t\) be the adjoint multiplier at time t, which yields
Necessary conditions for an optimum are:
Equation (19) reveals that all fleet segments—when active—harvest an amount up to the point where their marginal profit equals the shadow value of the stock. However, Eqs. (20) and (21) show that two arbitrary segments z and \(z'\) can only be active at the same time when \(p_z(Q_t) = \frac{\Omega _{z}}{q_zX_t^{\alpha _z}}\) and \(p_{z'}(Q_t) = \frac{\Omega _{z'}}{q_{z'}X_t^{\alpha _{z'}}}\).
Appendix 3: Quota Trade Constraints
When the scientific body seeks to maximize profits, but is constrained to divide a total quota \({Q_t}\) according to some predetermined share \(\theta _z\) (with \(\sum _z \theta _z = 1\)), the maximization problem looks as follows:
Call the discrete time Hamiltonian corresponding to this problem \(\mathcal {H}^{tc}\) which is given as
Necessary conditions include:
We immediately see that there is no condition corresponding to (20) and (21) above, since the values of \(\theta _{z}\) are given. This implies that marginal cost will not equalize and the cost of harvesting a given quota will not be achieved at least cost (unless in the special case that \(\theta _z = \theta _z^*\) for all z).
Appendix 4: Entrance Constraints
We derive the entrance-constrained cost function \(C^{ec}_z\) by adding the condition \(N_z \le {\bar{N}}_z\) to the cost minimization problem (13). The corresponding Lagrangian is then \(\mathcal {L}^{ec} = N_{z,t} (f_z + v_z e_{z,t}) - \lambda N_{z,t} (q_zX_t^{\alpha _z}e_{z,t}^{\beta _z}) + \mu N_{z,t}\) and the first order conditions are:
Optimal effort is now given by: \(e^{ec}_{z,t} = \frac{\beta _z}{1-\beta _z}\frac{f_z + \mu }{v_z}\) and \(N^{ec}_{z,t} = \min \{\frac{{\bar{H}}_z}{h^*_{z,t}} ; {\bar{N}}_z \}\). This is intuitive: when the quota can be caught with all active vessels operating at the efficient scale harvesting \(h^*_{z,t}\), we have \(\mu = 0\). When the entrance constraint becomes binding (i.e. \(\mu > 0\)), each boat increases its effort beyond that scale. In such a case, effort is simply given by \(e^{ec}_{z,t} =\left( \frac{{\bar{H}}_{z,t}}{ {\bar{N}}_{z} q_z X_t^{\alpha _z}}\right) ^\frac{1}{\beta _z}\), while the shadow price of doing so is given by \(\mu =\frac{e^{ec}_{z,t} v_z (1-\beta _z)}{\beta _z} - f_z\). Effort is increased in the active segment until a switching point where it becomes more profitable to utilize vessels from the next segment. The above calculations allow us to write the cost of employing segment z by:
This gives the following dynamic optimization problem:
Necessary conditions for an optimum are:
Structurally, the first-order conditions (31)–(34) are parallel to (19)–(22). However, it is clear that (32) can hold for more than one fleet. This happens because marginal costs are no longer constant, but \(\frac{\partial ^2 C^{ec}_z(\theta _{z,t},Q_t,X_t)}{(\partial H_z)^2}>0\) for \({\bar{H}}_{z,t} > {\bar{N}}e^*_{z,t}\). So there must be a switching point where it is most efficient to change to a different segment rather than increasing \({\bar{H}}_z\).
Appendix 5: Data Sources
The biological data is obtained through International Council for the Exploration of the Sea (ICES) and Institute of Marine Research (IMR, Norway) and mostly runs from 1950 to 2013. The biomass data for cod is from Virtual Population Analysis (VPA), the cod landings are total caught NEA cod, both from 1950 to 2013. The capelin time-series starts in 1973. All these data is obtained from Arctic Fisheries Working Group (AFWG) annual reports.Footnote 21 The data on Herring is from 1950 to 2013 and is provided by IMR.
The annual sea surface temperature data were obtained by the Knipovich Polar Research Institute of Marine Fisheries and Oceanography (PINRO). We use vertical averages (0–200m) of mean temperature along the Kola meridian transect (\(33^{\circ }50\)E, \(70^{\circ }50\)N to \(72^{\circ }50\)N) which has been averaged between stations along the transect and interpolated to monthly values (Bochkov 1982; Tereshchenko 1996). Since the interannual variability in the (southern part of the) Barents Sea is dominated by the dynamics in winter time, we averaged monthly values over the winter months, i.e. from November in year \(t-1\) to March in year t. Data for all fleet segments and their harvests, costs and effort has been obtained by the Directories of Fisheries, Bergen. The cost data has been deflated with the Producer Price index for Norway taken from the OECD, using the year 2000 as a benchmark.Footnote 22 Export prices for cod and saithe (the substitute product) are inferred from export values and export quantities; see Timmer and Richter (2009) for more information on the method. For each export commodity (“Atlantic cod, fresh or chilled”, “Atlantic cod, frozen”, “Atlantic cod, salted, or in brine”, “Cod, dried, unsalted”, “Cod, salted, and dried” a price is calculated by dividing the total value in a given year by the total quantity: \(P_{i,t}=V_{i,t}/Q_{i,t}\). A weighted export price is obtained by multiplying each price by its value and dividing it by the value of all exports given by \(\sum _{i=1}^5 P_{i,t}V_{i,t}/\sum _{i=1}^5 V_{i,t}\). The data for saithe is given by “Saithe, dried, salted or in brine”. This data was accessed with Fish Stat Plus (FAO, data from “FAO Yearbook of Fishery Statistics—Commodities”; the data was collected originally by Statistics Norway). These are annual data for the period 1976–2006. European income is proxied by real European GDP (Maddison 2010). The data has been corrected for inflation, and has been converted from US Dollar into Norwegian Kroner using exchange rates from the OECD (2010). The price for cod is given by the off-boat sales prices (“Varepriser fra sluttseddel”), as given by the Norwegian Fishermen’s Sales Organization (“Norges Råfisklag”). For 2006, we use the average landings price that has been obtained by Norwegian vessels in the following categories: Coastal vessels: Fresh cod of the size 2.5+ KG, landed in Lofoten/Salten, caught with gill net (“Settegarn”), price: 21.04 NOK. Large longliners: Frozen cod of the size 1–2.5 KG, landed in Troms, caught with longliners (“autoline”), price: 26.41 NOK. Trawlers: Frozen cod of the size 1–2.5 KG, landed in Troms, caught with bottom trawlers (“bunntrål”), price 23.43 NOK. To make the price data comparable with the costs data we have used, again, the producer price index from the OECD. The baseline year was as before 2000.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Richter, A., Eikeset, A.M., van Soest, D. et al. Optimal Management Under Institutional Constraints: Determining a Total Allowable Catch for Different Fleet Segments in the Northeast Arctic Cod Fishery. Environ Resource Econ 69, 811–835 (2018). https://doi.org/10.1007/s10640-016-0106-3
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10640-016-0106-3